Buckling Characteristics of Bio-Inspired Helicoidal Laminated Composite Spherical Shells Under External Normal and Torsional Loads Subjected to Elastic Support
Abstract
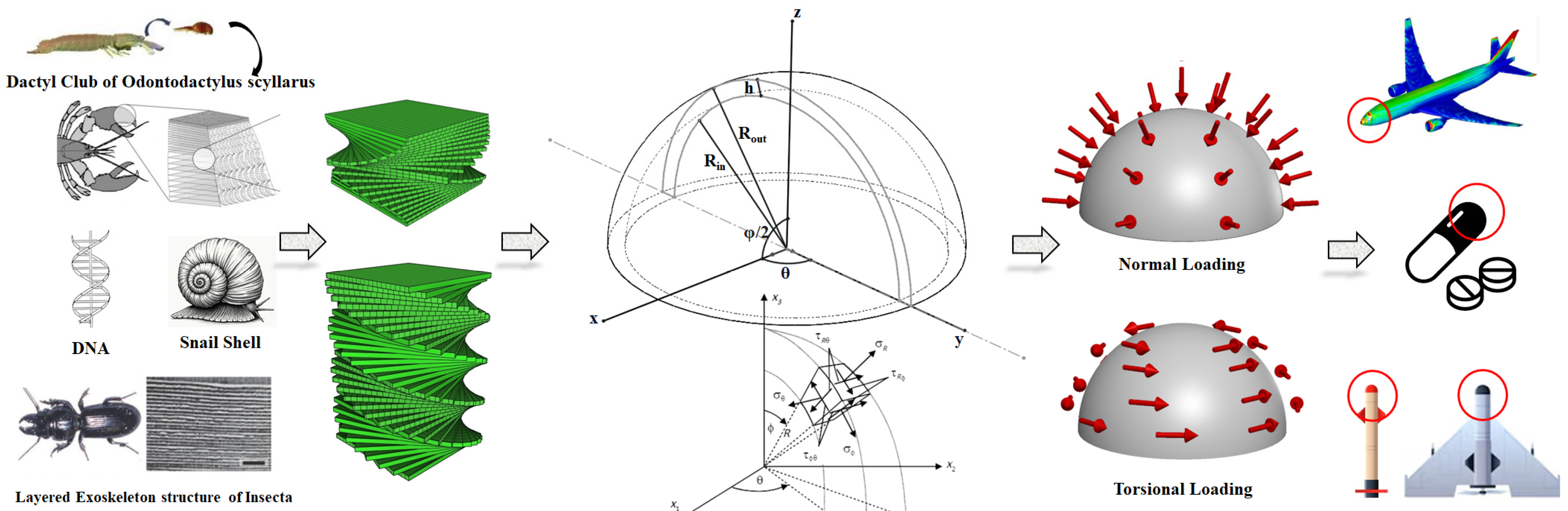
1. Introduction
2. Problem Definition
3. Governing Equations
3.1. Basic Formulations
3.2. Finite Element Modeling
4. Numerical Solution
4.1. Verification Studies
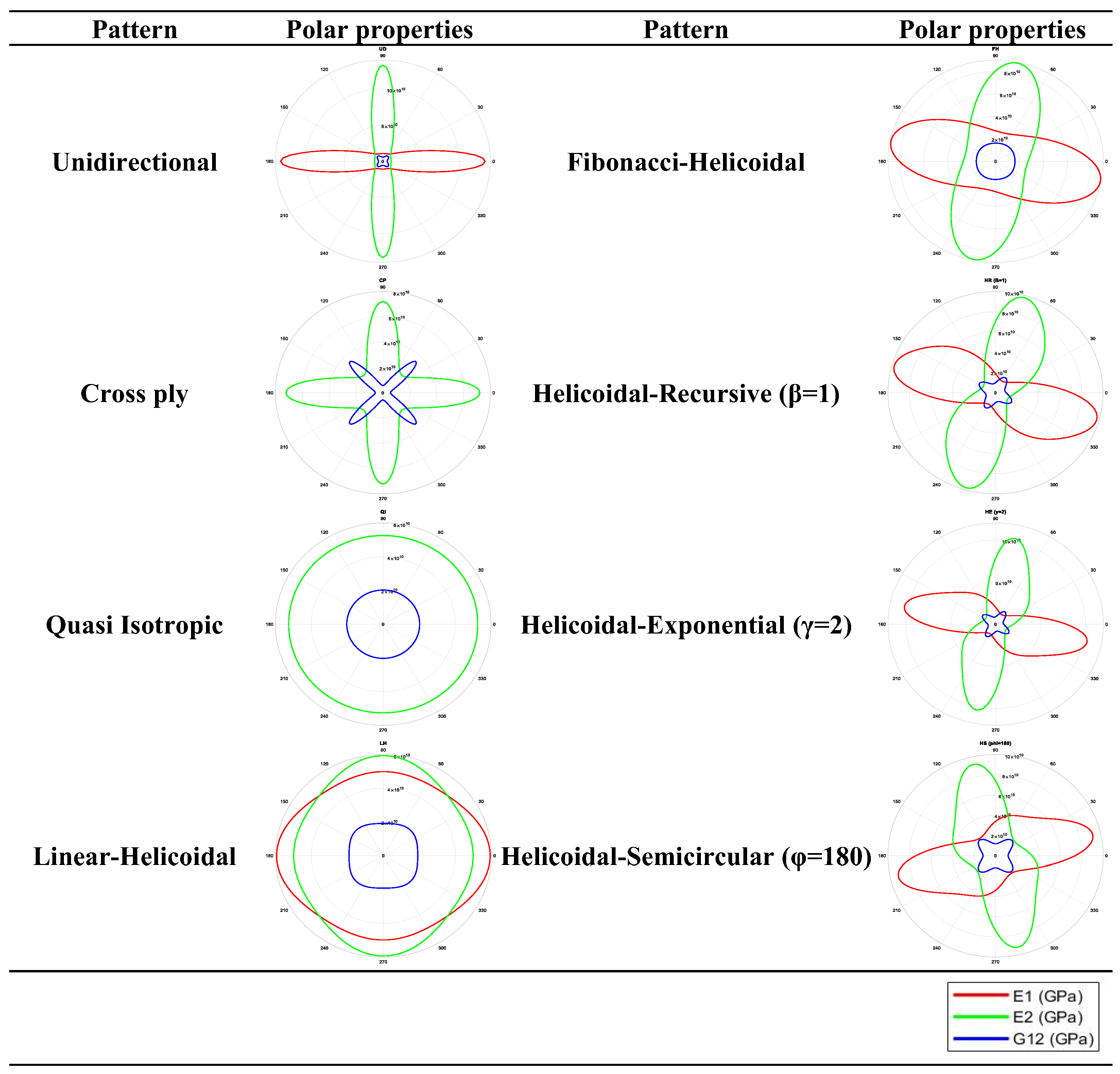
4.2. Results and Discussion
5. Conclusions
- -
- Quasi-isotropic (QI) lamination consistently delivered the highest buckling resistance under both normal and torsional loads, while unidirectional (UD) and cross-ply (CP) configurations exhibited the poorest performances in normal and torsional buckling, respectively.
- -
- For normal buckling, the performance rankings (from lowest to highest) are as follows: UD, HR (β = 1), HS (φ = 45°), HE (γ = 2), HE (γ = 3), HS (φ = 90°), CP, HE (γ = 2.5), HR (β = 2), HS (φ = 180°), FH, HR (β = 3), LH, and QI.
- -
- In terms of the torsional-buckling performance, the ranking order from lowest to highest is as follows: CP, UD, HR (β = 2), HR (β = 1), HE (γ = 3), HE (γ = 2), HS (φ = 45°), HR (β = 3), FH, HE (γ = 2.5), HS (φ = 90°), HS (φ = 180°), LH, and QI.
- -
- Increasing the number of layers generally enhanced the buckling resistance for QI and helicoidal (FH, HR, HE, HS) laminations, with HE configurations (γ = 2) exhibiting the most pronounced sensitivity. In contrast, UD, CP, and LH configurations showed negligible changes in the buckling load regardless of the layer count.
- -
- Increasing the thickness ratio (reducing the relative thickness) drastically reduced the buckling capacity, with normal buckling showing greater sensitivity than torsional buckling. CP laminations were most affected by thickness changes under normal loads, while UD configurations were the least sensitive. Conversely, under torsional loads, FH laminations exhibited the highest thickness dependency, whereas CP laminations proved the most resilient.
- -
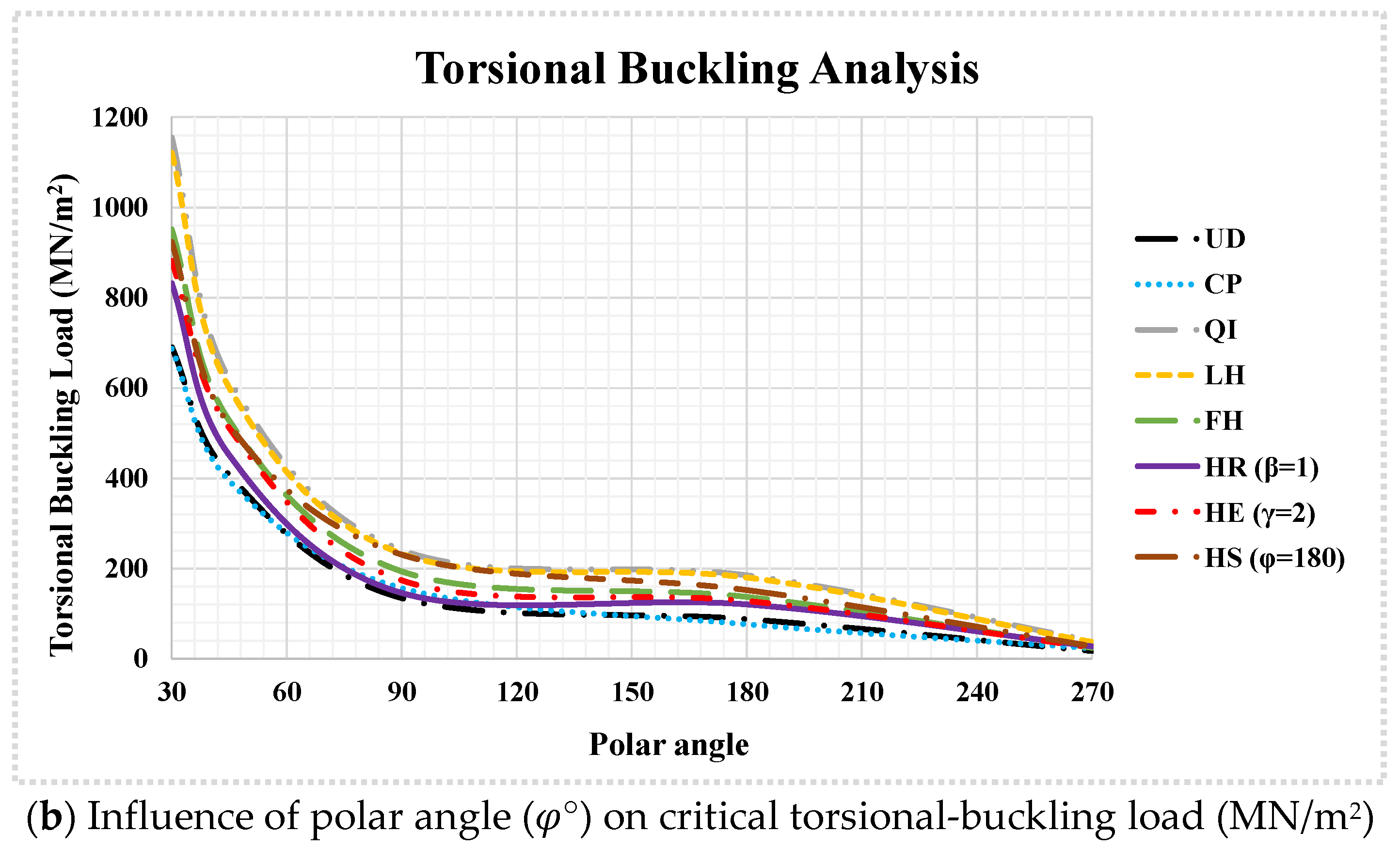
- Both reduced boundary constraints (clamped → simply supported) and an increased polar angle significantly diminished the buckling capacity, with smaller polar angles exhibiting greater sensitivity to boundary conditions. Additionally, clamped shells displayed stronger polar angle dependency under torsional loads compared to normal loads. In contrast, simply supported shells showed minimal load-type dependence, underscoring the critical interplay between the geometry, boundary conditions, and loading regime in spherical shells.
- -
- Increasing the polar angle reduced the buckling loads nonlinearly, with diminishing sensitivity at larger angles. Crucially, torsional buckling exhibited extreme polar angle dependence—expanding from 30° to 270°, causing a 32.51× reduction, far exceeding the 2.44× drop for normal loads.
- -
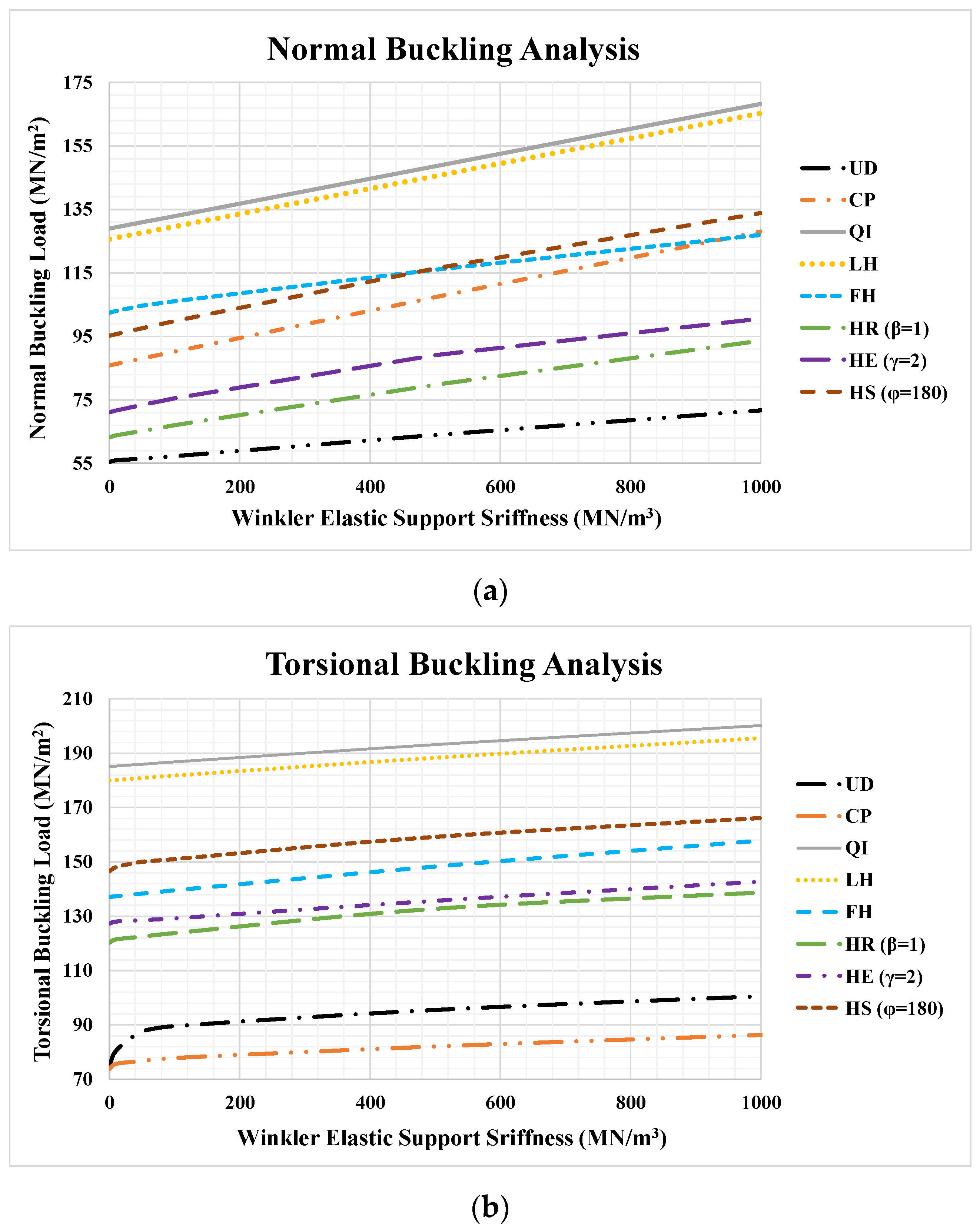
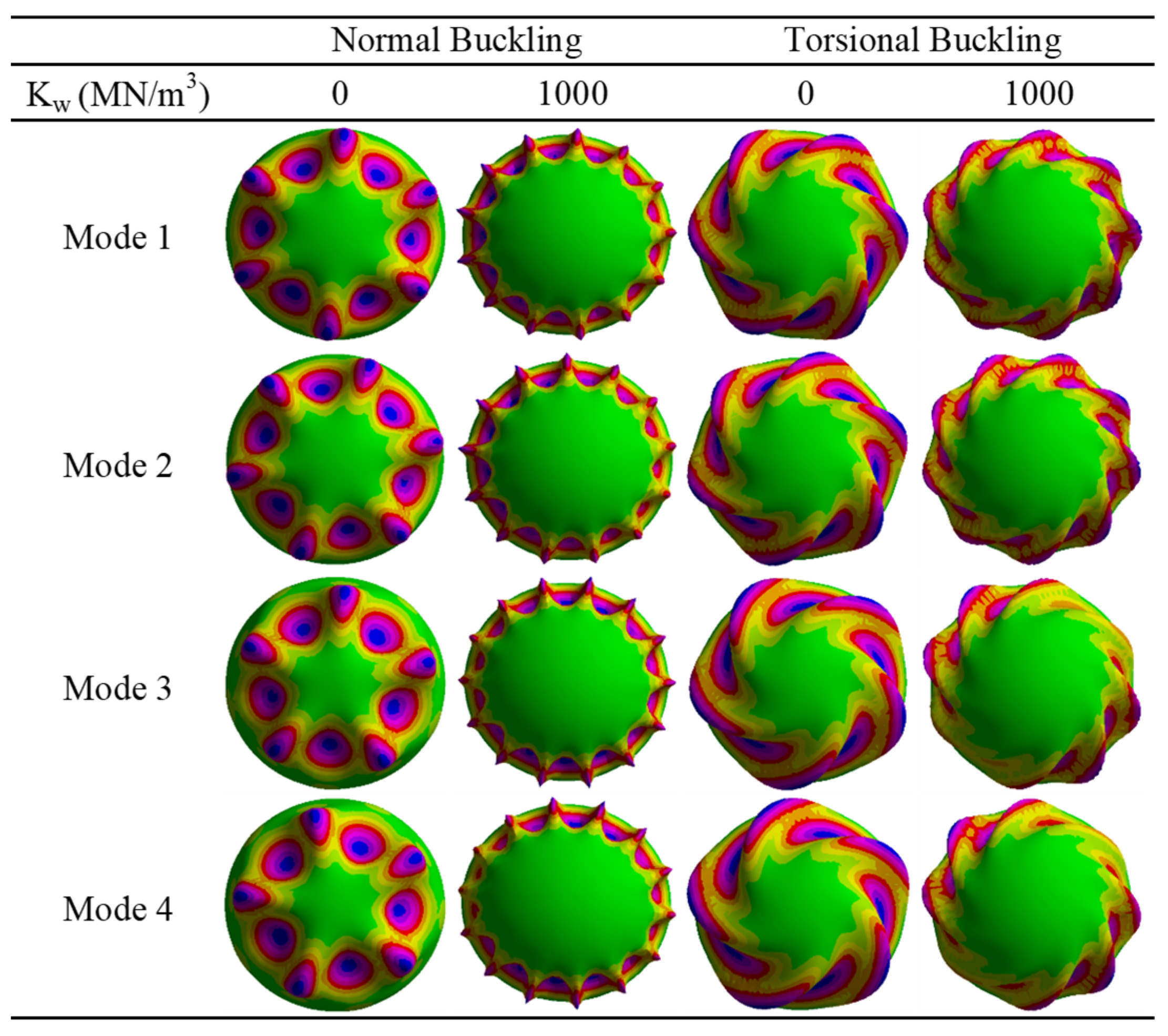
- Increasing the Winkler-type elastic foundation stiffness enhanced the buckling resistance, with normal buckling exhibiting a 1.36× improvement (from 0 to 1000 MN/m2) compared to only 1.14× for torsional buckling. This reveals that elastic support significantly improves the normal-load-bearing capacity while having relatively modest effects on the torsional stability. Similarly, mode shape analysis reveals that elastic foundations exert a more pronounced effect on normal-buckling-mode shapes than on torsional ones, inducing localized deformation patterns with elevated wave numbers and intensified modal humps.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, D.; Zaheri, A.; Russell, B.; Espinosa, H.; Zavattieri, P. Fiber reorientation in hybrid helicoidal composites. J. Mech. Behav. Biomed. Mater. 2020, 110, 103914. [Google Scholar] [CrossRef]
- Jiang, H.; Ren, Y.; Liu, Z.; Zhang, S.; Lin, Z. Low-velocity impact resistance behaviors of bio-inspired helicoidal composite laminates with non-linear rotation angle based layups. Compos. Struct. 2019, 214, 463–475. [Google Scholar] [CrossRef]
- Rawlinson, J.M.; Cox, H.J.; Hopkins, G.; Cahill, P.; Badyal, J.P.S. Nature-inspired trapped air cushion surfaces for environmentally sustainable antibiofouling. Colloids Surf. A Physicochem. Eng. Asp. 2023, 656, 130491. [Google Scholar] [CrossRef]
- Yang, T.; Wu, Z.; Chen, H.; Zhu, Y.; Li, L. Quantitative 3D structural analysis of the cellular microstructure of sea urchin spines (I): Methodology. Acta Biomater. 2020, 107, 204–217. [Google Scholar] [CrossRef]
- Naleway, S.E.; Porter, M.M.; McKittrick, J.; Meyers, M.A. Structural design elements in biological materials: Application to bioinspiration. Adv. Mater. 2015, 27, 5455–5476. [Google Scholar] [CrossRef]
- Chen, P.-Y.; McKittrick, J.; Meyers, M.A. Biological materials: Functional adaptations and bioinspired designs. Prog. Mater. Sci. 2012, 57, 1492–1704. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chen, P.-Y.; Lin, A.Y.-M.; Seki, Y. Biological materials: Structure and mechanical properties. Prog. Mater. Sci. 2008, 53, 1–206. [Google Scholar] [CrossRef]
- Weaver, J.C.; Milliron, G.W.; Miserez, A.; Evans-Lutterodt, K.; Herrera, S.; Gallana, I.; Mershon, W.J.; Swanson, B.; Zavattieri, P.; DiMasi, E. The stomatopod dactyl club: A formidable damage-tolerant biological hammer. Science 2012, 336, 1275–1280. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J. The hierarchical structure and mechanics of plant materials. J. R. Soc. Interface 2012, 9, 2749–2766. [Google Scholar] [CrossRef]
- Bouligand, Y. Sur une architecture torsadée repondue dans de nombreuses cuticules d’arthropodes. CR Acad. Sci. 1965, 261, 3665–3668. [Google Scholar]
- Bouligand, Y. Twisted fibrous arrangements in biological materials and cholesteric mesophases. Tissue Cell 1972, 4, 189–217. [Google Scholar] [CrossRef]
- Greco, F.; Leonetti, L.; Pranno, A.; Rudykh, S. Mechanical behavior of bio-inspired nacre-like composites: A hybrid multiscale modeling approach. Compos. Struct. 2020, 233, 111625. [Google Scholar] [CrossRef]
- Sharma, A.; Shukla, N.K.; Belarbi, M.-O.; Abbas, M.; Garg, A.; Li, L.; Bhutto, J.; Bhatia, A. Bio-inspired nacre and helicoidal composites: From structure to mechanical applications. Thin-Walled Struct. 2023, 192, 111146. [Google Scholar] [CrossRef]
- Ha, N.S.; Lee, T.-U.; Ma, J.; Li, J.; Xie, Y.M. Energy absorption of a bio-inspired cylindrical sandwich structure. Thin-Walled Struct. 2024, 195, 111378. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Shafighfard, T.; Jankowski, R.; Yoo, D.-Y. Machine-learning methods for estimating performance of structural concrete members reinforced with fiber-reinforced polymers. Arch. Comput. Methods Eng. 2025, 32, 571–603. [Google Scholar] [CrossRef]
- Bayat, M.-J.; Kalhori, A.; Asemi, K.; Babaei, M. Plates, Beams and Shells Reinforced by CNTs or GPLs: A Review on Their Structural Behavior and Computational Methods. Comput. Model. Eng. Sci. 2025, 142, 1351–1458. [Google Scholar] [CrossRef]
- Saurabh, S.; Kiran, R.; Singh, D.; Vaish, R.; Chauhan, V. A comprehensive investigation on nonlinear vibration and bending characteristics of bio-inspired helicoidal laminated composite structures. Appl. Math. Mech. 2025, 46, 81–100. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Mohamed, N.; Eltaher, M.A. Bending, buckling and linear vibration of bio-inspired composite plates. Ocean Eng. 2022, 259, 111851. [Google Scholar] [CrossRef]
- Do, N.-T.; Pham, Q.-H. Dynamic analysis of bio-inspired helicoid laminated composite plates resting on Pasternak foundation excited by explosive loading. Def. Technol. 2023, 30, 126–140. [Google Scholar] [CrossRef]
- Baakeel, F.K.; Eltaher, M.A.; Basha, M.A. Impact response of bio-inspired curved laminated composite plates: A numerical simulation. Adv. Aircr. Spacecr. Sci. 2025, 11, 331–361. [Google Scholar]
- Garg, A.; Shukla, N.K.; Belarbi, M.-O.; Mukherjee, D.; Pushpavalli, M.; Raman, R.; Avcar, M.; Narula, M.S.; Li, L. Bird strike-induced damage studies on bio-inspired laminated plates with holes. Aerosp. Sci. Technol. 2025, 162, 110200. [Google Scholar] [CrossRef]
- Melaibari, A.; Wagih, A.; Basha, M.; Kabeel, A.; Lubineau, G.; Eltaher, M. Bio-inspired composite laminate design with improved out-of-plane strength and ductility. Compos. Part A Appl. Sci. Manuf. 2021, 144, 106362. [Google Scholar] [CrossRef]
- Doan, T.S.; Tran, T.T.; Thao, P.H.; Luong, H.G.; Do, N.-T. Free vibration and buckling analysis of bio-inspired helicoid laminated composite plates resting on Pasternak foundation using the first-order meshfree. Lat. Am. J. Solids Struct. 2025, 22, e8346. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Hazell, P.J.; Wright, A.; Zhang, Z.; Lan, X.; Zhang, K.; Zhou, M. Insights into the high-velocity impact behaviour of bio-inspired composite laminates with helicoidal lay-ups. Polym. Test. 2021, 103, 107348. [Google Scholar] [CrossRef]
- Garg, A. Finite element-based buckling analysis of bio-inspired laminated composite plates. J. Ceram. Compos. 2025, 1, 1–5. [Google Scholar]
- Lu, T.; Shen, H.-S.; Wang, H.; Chen, X.; Feng, M. Optimization design and secondary buckling of bio-inspired helicoidal laminated plates under thermomechanical loads. Compos. Struct. 2023, 321, 117344. [Google Scholar] [CrossRef]
- Garg, A.; Shukla, N.K.; Avcar, M.; Belarbi, M.-O.; Zheng, W.; Raman, R.; Kiran, R.; Li, L. Free vibration analysis of annular and flat plates with sinusoidal corrugations using isogeometric analysis and machine learning-based stiffness modeling. Thin-Walled Struct. 2025, 215, 113492. [Google Scholar] [CrossRef]
- Bayat, M.J.; Kalhori, A.; Asemi, K.; Babaei, M. Static and vibrational characteristics of bio-inspired helicoid laminated composite annular sector plates embedded on Winkler elastic foundation. Eng. Struct. 2025, 334, 120194. [Google Scholar] [CrossRef]
- Garg, A.; Shukla, N.K.; Belarbi, M.-O.; Barnawi, A.B.; Raman, R.; Sharma, A.; Li, L. Free Vibration Analysis of Bio-Inspired Helicoidal Laminated Composite Square and Annular Plates Having Circular Openings Using Isogeometric Analysis, Structures; Elsevier: Amsterdam, The Netherlands, 2024; p. 107429. [Google Scholar]
- Almitani, K.H.; Mohamed, N.; Alazwari, M.A.; Mohamed, S.A.; Eltaher, M.A. Exact solution of nonlinear behaviors of imperfect bioinspired helicoidal composite beams resting on elastic foundations. Mathematics 2022, 10, 887. [Google Scholar] [CrossRef]
- Mohamed, N.; Mohamed, S.A.; Eltaher, M.A. Nonlinear static stability of imperfect bio-inspired helicoidal composite beams. Mathematics 2022, 10, 1084. [Google Scholar] [CrossRef]
- Karamanli, A.; Pham, S.D.; Lee, S.; Vo, T.P. A Comprehensive Bending Analysis of Laminated Composite, Sandwich and Bio-Inspired Helicoidal Composite Curved Beams. Sandw. Bio-Inspired Helicoidal Compos. Curved Beams 2024. [Google Scholar] [CrossRef]
- Amara, R.; Riadh, B.; Hassen, A.A.; Mokhtar, N.; Hadji, L. Hygrothermal effect of bio-inspired helicoid laminate plate for strengthening damaged RC beam. Mech. Adv. Mater. Struct. 2025, 32, 3319–3336. [Google Scholar] [CrossRef]
- Yang, F.; Xie, W.; Meng, S. Impact and blast performance enhancement in bio-inspired helicoidal structures: A numerical study. J. Mech. Phys. Solids 2020, 142, 104025. [Google Scholar] [CrossRef]
- Garg, A.; Zheng, W.; Avcar, M.; Belarbi, M.-O.; Kiran, R.; Li, L.; Raman, R. Free vibration behaviour of curved Miura-folded bio-inspired helicoidal laminated composite cylindrical shells using HSDT assisted by machine learning-based IGA. Compos. Struct. 2025, 357, 118933. [Google Scholar] [CrossRef]
- Khotjanta, P.; Aimmanee, S. Optimal interply angle of bio-inspired composite curved panels with helicoidal fiber architecture. Compos. Struct. 2024, 343, 118269. [Google Scholar] [CrossRef]
- Garg, A.; Shukla, N.K.; Li, L.; Birla, S.; Zheng, W. Machine learning assisted buckling analysis of cantilever bio-inspired helicoidal laminated composite cylindrical shells with cutouts. Mech. Based Des. Struct. Mach. 2024, 53, 3711–3735. [Google Scholar] [CrossRef]
- Kalhori, A.; Bayat, M.J.; Asemi, K. Torsional and axial buckling analysis of bio-inspired helicoidal laminated composite cylindrical shells. Results Eng. 2025, 26, 104808. [Google Scholar] [CrossRef]
- Garg, A.; Li, L.; Zheng, W.; Belarbi, M.-O.; Raman, R. Free vibration behaviour of bio-inspired helicoidal laminated composite panels of revolution under thermal conditions: Multi-output machine learning approach. Eng. Anal. Bound. Elem. 2024, 169, 106024. [Google Scholar] [CrossRef]
- Thu, T.T.T.; Anh, T.N.; Thi, H.N.; Thi, H.N. Transient response of doubly-curved bio-inspired composite shells resting on viscoelastic foundation subject to blast load using improved first-order shear theory and isogeometric approach. Def. Technol. 2024, 38, 171–193. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, Y.; Zhang, S.; Dimitri, R.; Tornabene, F.; Asemi, K. Numerical study on the buckling behavior of FG porous spherical caps reinforced by graphene platelets. Nanomaterials 2023, 13, 1205. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, Y.; Wang, F.; Tang, W. Buckling of stainless steel spherical caps subjected to uniform external pressure. Ships Offshore Struct. 2018, 13, 779–785. [Google Scholar] [CrossRef]
- Iarriccio, G.; Zippo, A.; Pellicano, F. Asymmetric vibrations and chaos in spherical caps under uniform time-varying pressure fields. Nonlinear Dyn. 2022, 107, 313–329. [Google Scholar] [CrossRef]
- Malek, S.; Wierzbicki, T.; Ochsendorf, J. Buckling of spherical cap gridshells: A numerical and analytical study revisiting the concept of the equivalent continuum. Eng. Struct. 2014, 75, 288–298. [Google Scholar] [CrossRef]
- Shen, X.; Li, T.; Xu, L.; Kiarasi, F.; Babaei, M.; Asemi, K. Free vibration analysis of FG porous spherical cap reinforced by graphene platelet resting on Winkler foundation. Adv. Nano Res. 2024, 16, 11–26. [Google Scholar]
- Minh, T.Q.; Dong, D.T.; Duc, V.M.; Van Tien, N.; Phuong, N.T.; Nam, V.H. Nonlinear axisymmetric vibration of sandwich FGM shallow spherical caps with lightweight porous core. In CIGOS 2021, Emerging Technologies and Applications for Green Infrastructure: Proceedings of the 6th International Conference on Geotechnics, Civil Engineering and Structures; Springer: Singapore, 2021; pp. 381–389. [Google Scholar]
- Yadav, R.K.; Gupta, S.S. Inextensional vibrations of thin spherical shells using strain gradient elasticity theory. Thin-Walled Struct. 2024, 202, 112061. [Google Scholar] [CrossRef]
- Kalleli, S.; Hajlaoui, A.; Dammak, F. Improved-FSDT-based solid-shell element for buckling analysis of plate, spherical cap, and cylindrical shell of FG porous materials. Comput. Math. Appl. 2024, 157, 1–14. [Google Scholar] [CrossRef]
- Ameri, E.; Aghdam, M.; Shakeri, M. Global optimization of laminated cylindrical panels based on fundamental natural frequency. Compos. Struct. 2012, 94, 2697–2705. [Google Scholar] [CrossRef]
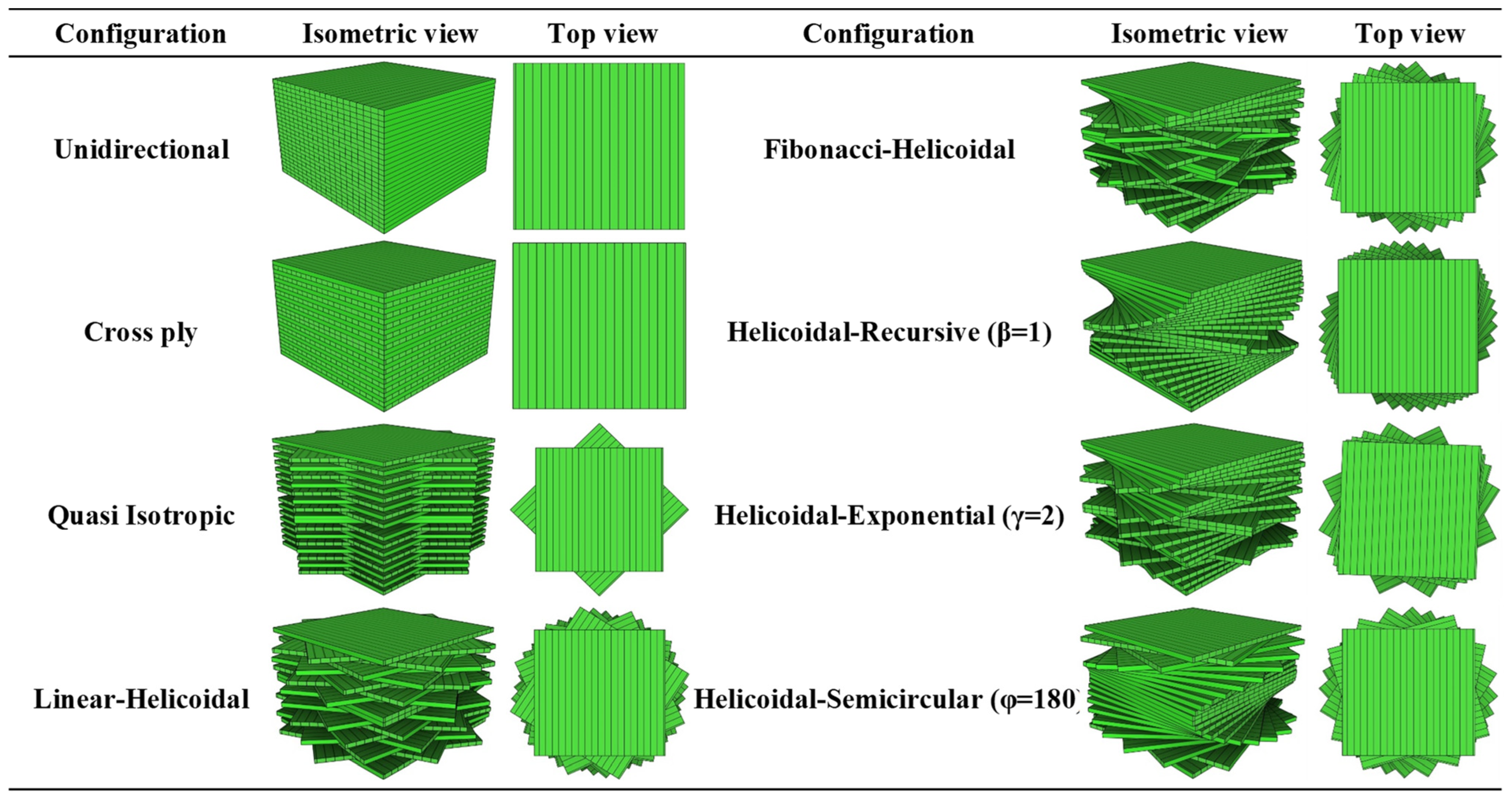


| Configuration | Abbreviation | Stacking Sequence | 16 | 24 | 32 |
|---|---|---|---|---|---|
| Unidirectional | UD | [(0)] | [(0)16] | [(0)24] | [(0)32] |
| Cross-Ply | CP | [(0/90)()]s | [(0/90)4]s | [(0/90)6]s | [(0/90)8]s |
| Quasi-Isotropic | QI | [(0/45/90/−45)()]s | [(0/45/90/−45)2]s | [(0/45/90/−45)3]s | [(0/45/90/−45)4]s |
| Linear Helicoidal | LH | , ; | [(0/51.43/…/360)]s | [(0/32.72/…/360)]s | [(0/24/…/360)]s |
| Fibonacci Helicoidal | FH | , ; | [(0/10/10/20/…/130)]s | [(0/10/10/20/…/890)]s | [(0/10/10/20/…/6100)]s |
| Helicoidal Recursive | HR (β = 1) | [(0/1/3/6/10/15/21/28)]s | [(0/1/3/6/10/15/21/28/36/45/55/66)]s | [(0/1/3/6/10/15/21/28/36/45/ 55/66/78/91/105/120)]s | |
| Helicoidal Exponential | HE (γ = 2) | [(2/4/8/16)2]s | [(2/4/8/16/32/64)2]s | [(2/4/8/16/32/64/128/256)2]s | |
| Helicoidal Semicircular | HS (φ = 180) | (); [(0/93.2/126.6/148.3/163.2/ 172.9/178.4/180)]s | (); [(0/74.2/102.4/122.4/137.6/149.7/159.2/ 166.7/172.3/176.4/178.9/180)]s | (); [(0/64.6/89.8/108.0/122.4/134.2/ 144.0/152.3/159.2/165.0/169.7/ 173.5/176.4/178.4/179.6/180)]s |
| Property Name | Value |
|---|---|
| Density (kg/m3) | 1540 |
| E11 (GPa) | 132.5 |
| E22 = E33 (GPa) | 10.8 |
| ν12 = ν13 | 0.24 |
| ν23 | 0.49 |
| G12 = G13 (GPa) | 5.7 |
| G23 (GPa) | 3.4 |
| Zhang et al. [42] | Zhang et al. [42] | Zhang et al. [42] | Present | Present |
|---|---|---|---|---|
| Ptest | Pelastic–perfectly plastic | Pelastic–plastic | Pcritical | Pcritical |
| Experimental | FEM—ABAQUS | FEM—ABAQUS | 3D Elasticity Theory and FEM | FEM—ANSYS |
| 5.445 | 5.270 | 5.412 | 5.172 | 5.251 |
| Polar Angle | Ref. | ω1 | ω2 | ω3 | ω4 |
|---|---|---|---|---|---|
| 180° | Zhou et al. [41] (ANSYS) | 2.890 | 2.901 | 2.990 | 3.001 |
| Zhou et al. [41] | 2.908 | 2.924 | 3.008 | 3.021 | |
| Present Study | 3.070 | 2.860 | 3.120 | 2.910 | |
| 90° | Zhou et al. [41] (ANSYS) | 1.861 | 1.867 | 2.110 | 2.101 |
| Zhou et al. [41] | 1.873 | 1.875 | 2.180 | 2.211 | |
| Present Study | 1.820 | 1.910 | 2.290 | 2.040 |
| Load Type | Ranking of First Mode for Ease of Comparison | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Normal | Torsional | |||||||||||
| Pattern | Parameter | Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 1 | Mode 2 | Mode 3 | Mode 4 | Rank (Lowest to Highest) | Normal Buckling | Torsional Buckling |
| UD | 56.51 | 56.72 | 60.03 | 61.72 | 87.54 | 91.80 | 91.87 | 92.39 | 1 (lowest Load) | UD | CP | |
| CP | 85.85 | 85.93 | 85.98 | 86.14 | 76.73 | 90.68 | 101.48 | 106.13 | 2 | HR (β = 1) | UD | |
| QI | 128.95 | 128.97 | 130.62 | 130.66 | 185.06 | 185.09 | 185.35 | 185.36 | 3 | HS (φ = 45°) | HR (β = 2) | |
| LH | 125.61 | 125.63 | 128.07 | 128.13 | 179.97 | 179.98 | 180.21 | 180.22 | 4 | HE (γ = 2) | HR (β = 1) | |
| FH | 102.45 | 103.46 | 104.65 | 105.11 | 137.04 | 137.07 | 137.24 | 137.31 | 5 | HE (γ = 3) | HE (γ = 3) | |
| HR | 63.24 | 63.95 | 64.21 | 64.89 | 120.25 | 120.66 | 123.02 | 123.47 | 6 | HS (φ = 90°) | HE (γ = 2) | |
| 92.47 | 92.49 | 94.12 | 94.25 | 117.70 | 117.85 | 117.89 | 118.01 | 7 | CP | HS (φ = 45°) | ||
| 110.71 | 110.81 | 111.74 | 111.81 | 131.04 | 131.07 | 131.12 | 131.37 | 8 | HE (γ = 2.5) | HR (β = 3) | ||
| HE | 71.14 | 72.00 | 73.16 | 73.71 | 128.04 | 128.95 | 131.05 | 131.35 | 9 | HR (β = 2) | FH | |
| 89.88 | 90.09 | 92.45 | 92.88 | 141.67 | 142.39 | 142.55 | 142.82 | 10 | HS (φ = 180°) | HE (γ = 2.5) | ||
| 79.83 | 80.13 | 84.74 | 84.77 | 125.37 | 127.04 | 128.63 | 130.55 | 11 | FH | HS (φ = 90°) | ||
| HS | , | 70.64 | 71.05 | 73.32 | 73.57 | 130.13 | 130.26 | 130.30 | 130.34 | 12 | HR (β = 3) | HS (φ = 180°) |
| , | 84.44 | 84.49 | 85.03 | 85.07 | 145.65 | 145.69 | 146.33 | 146.48 | 13 | LH | LH | |
| , | 95.24 | 95.46 | 98.83 | 99.16 | 152.42 | 152.50 | 152.80 | 156.41 | 14 (highest load) | QI | QI | |
| Load Type | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Normal | Torsional | ||||||||
| Pattern | Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 1 | Mode 2 | Mode 3 | Mode 4 | |
| 16 | UD | 56.51 | 56.72 | 60.03 | 61.72 | 87.54 | 91.80 | 91.87 | 92.39 |
| CP | 85.46 | 85.56 | 85.59 | 85.76 | 78.72 | 91.76 | 106.54 | 106.85 | |
| QI | 122.28 | 122.32 | 124.60 | 124.62 | 175.88 | 175.92 | 176.02 | 176.07 | |
| LH | 126.35 | 126.38 | 128.91 | 129.03 | 178.17 | 178.25 | 178.47 | 178.68 | |
| FH | 90.26 | 90.38 | 91.31 | 91.71 | 115.63 | 115.90 | 115.91 | 115.96 | |
| HR () | 59.20 | 60.72 | 61.22 | 63.43 | 109.27 | 109.90 | 110.05 | 110.30 | |
| HE () | 57.91 | 59.68 | 60.20 | 63.78 | 96.58 | 96.74 | 97.01 | 97.73 | |
| HS () | 88.24 | 88.59 | 93.56 | 93.87 | 143.95 | 144.17 | 145.14 | 151.82 | |
| 24 | UD | 56.51 | 56.72 | 60.03 | 61.72 | 87.54 | 91.80 | 91.87 | 92.39 |
| CP | 85.85 | 85.93 | 85.98 | 86.14 | 76.73 | 90.68 | 101.48 | 106.13 | |
| QI | 128.95 | 128.97 | 130.62 | 130.66 | 185.06 | 185.09 | 185.35 | 185.36 | |
| LH | 125.61 | 125.63 | 128.07 | 128.13 | 179.97 | 179.98 | 180.21 | 180.22 | |
| FH | 102.45 | 103.46 | 104.65 | 105.11 | 137.04 | 137.07 | 137.24 | 137.31 | |
| HR () | 63.24 | 63.95 | 64.21 | 64.89 | 120.25 | 120.66 | 123.02 | 123.47 | |
| HE () | 71.14 | 72.00 | 73.16 | 73.71 | 128.04 | 128.95 | 131.05 | 131.35 | |
| HS () | 95.24 | 95.46 | 98.83 | 99.16 | 152.42 | 152.50 | 152.80 | 156.41 | |
| 32 | UD | 56.51 | 56.72 | 60.03 | 61.72 | 87.54 | 91.80 | 91.87 | 92.39 |
| CP | 86.01 | 86.07 | 86.13 | 86.25 | 78.36 | 91.16 | 105.26 | 106.08 | |
| QI | 132.06 | 132.10 | 133.31 | 133.35 | 189.13 | 189.15 | 189.47 | 189.49 | |
| LH | 125.37 | 125.38 | 127.66 | 127.73 | 180.40 | 180.43 | 180.66 | 180.73 | |
| FH | 94.35 | 94.82 | 95.40 | 95.52 | 144.14 | 144.16 | 144.44 | 144.52 | |
| HR () | 84.10 | 84.27 | 85.30 | 85.76 | 113.63 | 113.91 | 113.97 | 113.99 | |
| HE () | 104.97 | 105.35 | 106.33 | 106.93 | 147.33 | 147.48 | 147.64 | 147.76 | |
| HS () | 96.78 | 96.91 | 99.22 | 99.35 | 153.42 | 154.18 | 154.22 | 155.95 | |
| Load Type | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Normal | Torsional | ||||||||
| Pattern | Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 1 | Mode 2 | Mode 3 | Mode 4 | |
| 10 | UD | 129.18 | 132.81 | 136.69 | 157.45 | 158.08 | 194.20 | 221.25 | 225.65 |
| CP | 313.64 | 313.89 | 316.42 | 316.61 | 171.02 | 205.97 | 237.38 | 238.65 | |
| QI | 436.87 | 436.94 | 443.20 | 443.29 | 631.00 | 633.39 | 633.84 | 635.99 | |
| LH | 430.24 | 430.38 | 440.25 | 440.50 | 602.66 | 605.17 | 605.57 | 608.89 | |
| FH | 248.28 | 251.81 | 272.15 | 274.72 | 492.22 | 503.60 | 511.56 | 512.25 | |
| HR () | 206.80 | 217.76 | 226.93 | 232.65 | 324.47 | 332.87 | 333.45 | 338.98 | |
| HE () | 192.20 | 205.59 | 212.64 | 236.16 | 300.57 | 311.07 | 314.66 | 331.80 | |
| HS () | 303.99 | 322.73 | 324.43 | 333.04 | 360.90 | 393.65 | 413.34 | 419.31 | |
| 20 | UD | 56.51 | 56.72 | 60.03 | 61.72 | 87.54 | 91.80 | 91.87 | 92.39 |
| CP | 85.85 | 85.93 | 85.98 | 86.14 | 76.73 | 90.68 | 101.48 | 106.13 | |
| QI | 128.95 | 128.97 | 130.62 | 130.66 | 185.06 | 185.09 | 185.35 | 185.36 | |
| LH | 125.61 | 125.63 | 128.07 | 128.13 | 179.97 | 179.98 | 180.21 | 180.22 | |
| FH | 102.45 | 103.46 | 104.65 | 105.11 | 137.04 | 137.07 | 137.24 | 137.31 | |
| HR () | 63.24 | 63.95 | 64.21 | 64.89 | 120.25 | 120.66 | 123.02 | 123.47 | |
| HE () | 71.14 | 72.00 | 73.16 | 73.71 | 128.04 | 128.95 | 131.05 | 131.35 | |
| HS () | 95.24 | 95.46 | 98.83 | 99.16 | 152.42 | 152.50 | 152.80 | 156.41 | |
| 40 | UD | 16.06 | 16.17 | 17.00 | 17.34 | 20.58 | 20.76 | 20.78 | 21.19 |
| CP | 22.19 | 22.20 | 22.20 | 22.21 | 26.85 | 28.09 | 30.88 | 31.24 | |
| QI | 35.01 | 35.03 | 35.41 | 35.42 | 44.76 | 44.76 | 44.81 | 44.83 | |
| LH | 33.94 | 33.96 | 34.38 | 34.40 | 43.55 | 43.55 | 43.62 | 43.65 | |
| FH | 27.68 | 27.78 | 28.13 | 28.25 | 32.62 | 32.63 | 32.71 | 32.75 | |
| HR () | 15.60 | 15.67 | 15.88 | 15.96 | 27.54 | 27.72 | 27.87 | 27.94 | |
| HE () | 18.15 | 18.30 | 18.39 | 18.51 | 30.25 | 30.46 | 30.67 | 30.72 | |
| HS () | 25.10 | 25.19 | 25.47 | 25.63 | 38.57 | 38.69 | 39.15 | 39.37 | |
| Load Type | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Normal | Torsional | |||||||||
| BC | Pattern | Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 1 | Mode 2 | Mode 3 | Mode 4 | |
| Clamped supported | 90° | UD | 78.09 | 79.11 | 85.00 | 87.77 | 134.35 | 134.49 | 153.60 | 155.27 |
| CP | 112.45 | 112.60 | 113.69 | 113.80 | 156.48 | 163.80 | 173.71 | 184.51 | ||
| QI | 159.19 | 159.21 | 163.29 | 163.46 | 241.05 | 241.29 | 257.16 | 257.17 | ||
| LH | 150.54 | 150.57 | 158.55 | 158.58 | 232.48 | 232.77 | 258.07 | 258.09 | ||
| FH | 122.57 | 122.79 | 128.90 | 129.19 | 193.79 | 194.23 | 210.38 | 210.39 | ||
| HR () | 76.92 | 77.55 | 87.88 | 88.83 | 145.80 | 145.83 | 181.68 | 181.74 | ||
| HE () | 86.91 | 87.22 | 100.98 | 102.18 | 173.41 | 173.51 | 189.18 | 189.47 | ||
| HS () | 110.73 | 110.73 | 120.23 | 120.31 | 230.75 | 230.87 | 248.14 | 248.17 | ||
| 180° | UD | 56.51 | 56.72 | 60.03 | 61.72 | 87.54 | 91.80 | 91.87 | 92.39 | |
| CP | 85.85 | 85.93 | 85.98 | 86.14 | 76.73 | 90.68 | 101.48 | 106.13 | ||
| QI | 128.95 | 128.97 | 130.62 | 130.66 | 185.06 | 185.09 | 185.35 | 185.36 | ||
| LH | 125.61 | 125.63 | 128.07 | 128.13 | 179.97 | 179.98 | 180.21 | 180.22 | ||
| FH | 102.45 | 103.46 | 104.65 | 105.11 | 137.04 | 137.07 | 137.24 | 137.31 | ||
| HR () | 63.24 | 63.95 | 64.21 | 64.89 | 120.25 | 120.66 | 123.02 | 123.47 | ||
| HE () | 71.14 | 72.00 | 73.16 | 73.71 | 128.04 | 128.95 | 131.05 | 131.35 | ||
| HS () | 95.24 | 95.46 | 98.83 | 99.16 | 152.42 | 152.50 | 152.80 | 156.41 | ||
| Simply supported | 90° | UD | 47.73 | 47.98 | 63.91 | 64.30 | 88.51 | 88.97 | 90.01 | 93.31 |
| CP | 81.40 | 82.67 | 87.51 | 87.78 | 101.22 | 140.12 | 142.81 | 145.32 | ||
| QI | 107.60 | 107.91 | 114.55 | 115.84 | 143.76 | 150.71 | 167.63 | 171.81 | ||
| LH | 103.91 | 104.12 | 113.24 | 114.22 | 143.83 | 149.13 | 169.85 | 172.64 | ||
| FH | 79.55 | 79.60 | 95.50 | 97.20 | 119.75 | 123.03 | 128.15 | 131.54 | ||
| HR () | 58.51 | 58.88 | 71.89 | 73.16 | 91.52 | 94.93 | 102.02 | 104.84 | ||
| HE () | 64.59 | 65.13 | 77.42 | 78.89 | 104.05 | 107.49 | 108.97 | 110.57 | ||
| HS () | 84.82 | 85.49 | 91.57 | 93.95 | 149.32 | 156.24 | 173.64 | 175.99 | ||
| 180° | UD | 45.69 | 48.57 | 52.24 | 52.44 | 72.21 | 80.32 | 83.49 | 85.04 | |
| CP | 64.22 | 64.30 | 64.33 | 64.33 | 76.38 | 86.42 | 96.00 | 98.96 | ||
| QI | 96.31 | 96.75 | 97.94 | 97.94 | 143.35 | 146.48 | 152.92 | 176.39 | ||
| LH | 93.96 | 94.17 | 95.82 | 96.00 | 143.75 | 147.33 | 154.31 | 173.87 | ||
| FH | 74.94 | 78.12 | 82.48 | 82.51 | 114.30 | 116.22 | 121.13 | 131.05 | ||
| HR () | 48.21 | 49.92 | 51.96 | 52.19 | 85.10 | 92.52 | 95.51 | 107.87 | ||
| HE () | 54.87 | 56.55 | 58.34 | 58.99 | 89.17 | 98.87 | 110.99 | 114.75 | ||
| HS () | 76.43 | 76.56 | 80.07 | 80.54 | 133.57 | 147.87 | 145.95 | 155.68 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayat, M.J.; Kalhori, A.; Babaei, M.; Asemi, K. Buckling Characteristics of Bio-Inspired Helicoidal Laminated Composite Spherical Shells Under External Normal and Torsional Loads Subjected to Elastic Support. Buildings 2025, 15, 3165. https://doi.org/10.3390/buildings15173165
Bayat MJ, Kalhori A, Babaei M, Asemi K. Buckling Characteristics of Bio-Inspired Helicoidal Laminated Composite Spherical Shells Under External Normal and Torsional Loads Subjected to Elastic Support. Buildings. 2025; 15(17):3165. https://doi.org/10.3390/buildings15173165
Chicago/Turabian StyleBayat, Mohammad Javad, Amin Kalhori, Masoud Babaei, and Kamran Asemi. 2025. "Buckling Characteristics of Bio-Inspired Helicoidal Laminated Composite Spherical Shells Under External Normal and Torsional Loads Subjected to Elastic Support" Buildings 15, no. 17: 3165. https://doi.org/10.3390/buildings15173165
APA StyleBayat, M. J., Kalhori, A., Babaei, M., & Asemi, K. (2025). Buckling Characteristics of Bio-Inspired Helicoidal Laminated Composite Spherical Shells Under External Normal and Torsional Loads Subjected to Elastic Support. Buildings, 15(17), 3165. https://doi.org/10.3390/buildings15173165








