Abstract
Artifact style is still assessed primarily visually/descriptively, and much less morphologically/parametrically—by processing latent geometric peculiarities. This research aims to explore how the morphology of artifacts can be represented and quantitatively compared in order to validate their stylistic affiliation cost-efficiently. Since the term “style” herein refers to orders of classical architecture, (Roman) capitals of the oldest, Doric order, were chosen for such a validation-oriented assessment. The methodology included the following: (1) scaling capital 3D models to a uniform height to make the number of equidistant crosscuts invariant, (2) substituting contours thereof with circles (by retaining area values) to marginalize ornamentation factors, (3) determining stepwise dynamics of perimeter change across circles to ensure relative comparisons, (4) generating diagrammatic representatives by revolving dynamics-wise trendlines, and (5) comparing them quantitatively. To make the latter valid in a statistical sense, three groups of capitals were foreseen: Control (of indisputable Doric), 1st Experimental (of assumed Doric), and 2nd Experimental (of non-Doric, i.e., Ionic). Distances between the vertices of every compared representative (from defined groups) and their nearest neighbors on the reference (a representative obtained by “averaging” control ones) were computed. Distributions of such distances induced normal probabilities capable of “inferring” whether the analyzed capital could likely be a member of the assumed order.
1. Introduction
Even today, artifacts are differentiated in terms of style they belong to—mainly visually/descriptively, and to a much lesser extent morphologically/parametrically—by processing their latent geometric peculiarities. However, the problem arises when a machine is to be hired for the aforementioned, since it processes and interprets the relevant data in a way different from that of humans, relying on software that can be very expensive nowadays.
To stylistically verify any artifact based on its morphology, it has to be compared quantitatively to an adequate reference. Additionally, to perform any comparison scientifically, entities being mutually compared have to be “comparable”, namely, must satisfy certain requirements to ensure the “sufficient” reliability of that process. Whether the reference entity that the “stylistically unknown artifact” is being compared to is another artifact or a somewhat different representative of the assumed style, such requirements ought to be carefully defined (see Section 2.2.2). While some previous research that were aimed at improving style similarity metrics or matching with shape distributions dealt with vehicles, furniture, and cutlery predominantly [1,2], other research that explored various ways of geometry processing in favor of expressing an entity’s morphology was predominantly focused on characterizing the human shape, 3D description of the human body, etc. [3,4].
In the domains of architecture and urbanism, whereas previous subject-related research that concerns style identification is predominantly focused on the stylistic classification of BIM products [5,6], cultural heritage buildings [7], and historic city districts [8], investigations that deal with style recognition of building facades are also performed [9].
If the term “style” is understood as referring to the classical orders of architecture (as is the case herein), the focus then shifts to the set of the five major orders wherein—despite significant advances in the digital modeling, digitization and visualization [10,11]—the study of columns and their capitals remains largely qualitative [12], accordingly. Namely, current practices often rely on manual and descriptive interpretation, artistic convention, or canonical templates rooted in Vitruvian or Palladian ideals [13,14,15].
1.1. Historical Background of Architectural Orders
The architectural orders, which originated in ancient Greece, were primarily developed to establish a set of rules for constructing ancient temples and other buildings. These orders served as a guide for architects, ensuring consistency and harmony in their designs. Marcus Vitruvius Pollio was the first architectural theoretician from the 1st century BC [16] (p. I) who systematically presented the development of architectural orders and defined a set of construction rules that are specific to them.
1.1.1. The Architectural Orders: Origins and Development
The first and oldest architectural order obtained the name from its creator—Dorus, the mythical ancestor of the Dorians and Hellen’s son, who built a temple in Juno’s sanctuary in Argos in an architectural order later defined as Doric [14] (p. 124). As observed by Vitruvius, the proportions applied within the Doric order are ergonomic, based on the proportions of the male body [14] (p. 124). In this way, the proportional relations between the elements of the Doric column (the base, stem, and capital) were defined. The second architectural order, the Ionic one, was named after the Ionians and developed from the need to visually lengthen the Doric column whose proportional ratio between the diameter of its base and the entire height, including the capital, was 1:6. Also, the Ionic column is characterized by the appearance of volutes in the capital’s zone and the grooves in the shaft’s zone, symbolizing the ideal of female beauty [14] (pp. 124–125). The third, Corinthian order, represents a further development of the Ionic order [14] (p. 125), as it continues to imitate the ideal of female beauty through its slenderness and decorativeness.
The special contribution of Vitruvius’s work is reflected in the definition of the module—the primary measure that determines all other proportional relationships while building within the Doric, Ionic, or Corinthian order [14] (p. 128). However, the importance of Vitruvius’s work was particularly highlighted after historical events that changed global political power relations and cultural influences, replacing Greek construction methods and aesthetic ideals with Roman ones. In this context, the Roman Doric, Ionic, Corinthian, Tuscan, and Composite architectural orders were developed. A systematic review of all the architectural orders and their historical development, either Greek or Roman, with particular reference to their comparative analysis, was provided by Robert Chitham [17]. On the other hand, Christof Thoenes suggests that the development of architectural orders (from the Tuscan to the Roman Composite) is not based on ancient models but rather the result of the progressive Italian Renaissance school and authors [18]. Moreover, Thoenes points out that Vitruvius did not define the term “order” itself but rather Brunelleschi and Alberti in their research [18] (p. 299).
Although Renaissance theorists sought to define their own construction methods and architectural orders, their primary source from the classical period was the book “De Architectura Libri Decem” and its author, Vitruvius, who directly witnessed ancient construction methods [16] (p. XVI). By translating it into Italian, French, German, and Spanish during the 15th and 16th centuries, Vitruvius’s text greatly influenced the further development and definition of construction methods and architectural orders [16] (p. XII). On the other hand, although Renaissance theorists initially based their analysis on the work of Vitruvius, there were inconsistencies in the definition of architectural orders. As a result, between three and six orders were recognized, as Thoenes also indicated in his research [18] (p. 303). The division into five recognizable orders—Doric, Ionic, Corinthian, Tuscan, and Composite—first appeared as an independent theory in Book IV of Sebastiano Serlio [19]. Following his work, Giacomo Barozzi da Vignola also recognized five orders as follows: “There are five Orders of Architecture, of which three are Greek,—the Doric, Ionic, and Corinthian; and two Italian,—the Tuscan and the Composite” [20] (p. 5).
The inconsistency in defining the orders of classical architecture and their characteristics is also reflected in determining the proportional ratio between the column’s base diameter and the column’s height [14,17,18], explained in detail below, in Table 1.

Table 1.
Proportional ratios of column’s base diameter to column’s height for the five major classical orders, according to various authors.
The previously highlighted inconsistencies in determining architectural orders’ characteristics, especially the continuous reinterpretation of the Doric column—from ancient Greek and Roman architecture, through the Renaissance, all the way to neoclassical and postmodernist architecture—have led to the need for a new examination of the Doric order’s characteristics and the elements that influence its distinction from other architectural orders. Accordingly, for conducting an intended stylistic assessment and developing an approach, the Doric order—with the adopted column proportion of 1:7, firstly defined by Vitruvius and supported by Alberti and Serlio—was chosen from the set of five major orders. More specifically, its capitals—the uppermost column members crowning the column shafts—were chosen as the subject of our study, but only those of the Roman type, not Greek-type ones either.
A compelling argument for choosing the Doric order lies in its historical significance. It is the first and oldest of all the architectural orders that developed later in response to its shortcomings or as a result of further development. On the other hand, arguments for taking the Roman over the Greek Doric order into account refer to the extensiveness of the relevant literature, sources, and archival material as well as their availability. Focusing on the column’s capital as the subject of the study stems from the fact that it represents the most visually distinctive part of the column and plays a significant role in distinguishing different architectural orders. The proportional relations between the inner zones of the capital are taken over from Vitruvius, who defines three such zones (neck, abacus, and echinus) as perfectly equal to each other, whereas the height of the capital is equal to ½ the diameter of the column’s base [14] (p. 128).
1.1.2. The Roman Doric Architectural Order
Two subtypes are recognized within the Roman Doric order: the Mutulary and the Denticulated one. The main differences between these subtypes are reflected in the design of the cornice—the zone that is located above the column’s capital. These distinctions are explained in detail by Frank Halstead [21] (p. 45) and William Ware [22] (pp. 11–13). When it comes to capitals of those two subtypes, their proportions are mutually identical, with their height being ½ of the column’s base diameter [21] (p. 45). However, despite the mutually identical proportions, Mutulary and Denticulated Roman Doric capitals morphologically differ from each other where the neck transitions into the abacus, as well as in the capital’s echinus as the highest inner zone.
1.2. Recent Advances and Limitations in Digital Heritage Analysis
A growing convergence is observed between advanced 3D data acquisition, geometric analysis, and computational classification methods in the study of cultural heritage, morphology, and artifact interpretation. Digital tools such as CAD (Computer Aided Design) and recently HBIM (Heritage Building Information Modeling) [23,24,25], and techniques such as laser scanning, photogrammetry, and parametric modeling have enabled more detailed representations of classical elements [26,27,28].
Moreover, workflows that integrate the aforementioned techniques capture quite dense and accurate artifact models [29,30,31,32,33]. These non-destructive, remote-sensing methods preserve the integrity of the target object [29,34] while yielding rich point clouds, enhancing the fidelity of subsequent simulations and interpretations. Although the integration of point cloud data into HBIM and its operability were previously uncertain [35], recent advances have helped to resolve these challenges.
However, while the detail is advantageous, it comes at the expense of processing speed and resource requirements, limiting real-time use and scalability (very large datasets often require simplification or powerful hardware, thus causing high cost). Nevertheless, in some works it is demonstrated that software optimizations alone can improve results cost-effectively [30], avoiding the need for extra hardware.
The identification and analysis of classical orders seldom address the underlying morphological variation across time, geography, and cultural adaptation. As a result, they continue to lack methodological rigor and reproducibility in digital heritage and architectural scholarship [36,37,38]. In other words, heritage-specific classification needs are still insufficiently addressed through computational analysis. Nevertheless, workflows that enable translation from raw spatial data into analytical formats—ranging from Scan-to-FEM structural modeling [29] to point cloud segmentation [39] and geometric feature interpretation [31], as well as ones that combine multiple sensing techniques within a systematic methodology [32,33], underscore applicability to fields such as heritage conservation.
Some methods support damage detection and deformation mapping [33], but they stop short of establishing typological or stylistic taxonomies, thereby limiting their utility for comparative heritage studies. On the other hand, although the use of region-growing, octree partitioning, and shape descriptors [1,2,39] demonstrates progress in unsupervised segmentation and global shape matching, these computational approaches often neglect semantic, functional, or symbolic attributes of architecture. AI-based methods have begun to bridge this gap in other domains—such as style recognition in design repositories—but few of the papers reviewed attempt to implement machine learning-based classification in a heritage context due to the fact that style similarity models can struggle outside their training domain, i.e., may not generalize to new categories without retraining [1].
Therefore, regarding the generalizability, many methods are tailored to specific scenarios and may not transfer easily. For example, optimizations designed for linear features [30] do not necessarily apply to arbitrary geometry. Findings drawn from a single sample or species [40] cannot be assumed to hold across other cases. Some studies focus on static or linear analyses [29] and do not account for dynamic changes or material degradation over time. In general, adaptation of these techniques to new contexts often demands additional calibration or data, reducing their out-of-the-box applicability.
In addition to key limitations such as high computational demands [29,31,33], sensitivity to environmental conditions [30,34], and dependence on expert interpretation [29,33,39], affordability and scalability remain open challenges. Very few approaches offer integrated pipelines that are cost-effective and broadly comparable across different cultural contexts. In this regard, methodological innovation must also address systemic accessibility—an area where a diagrammatic, rule-based classification scheme may offer an alternative to data-hungry AI models or proprietary BIM systems.
1.3. Study Objectives and Outline
This paper identifies a critical gap in quantitative distinction of digitized or modeled artifacts of classical architecture: the absence of systematic, data-driven methods for classifying and analyzing classical column capitals. Without statistical techniques, large-scale datasets of scanned, documented, or modeled capitals—spanning different periods and regions—remain underutilized [41,42]. A statistical framework could extract and correlate features such as curvature profiles, leaf patterns, or volute geometry, enabling the discovery of regional styles, undocumented variants, or evolutionary trends that are difficult to detect through traditional means [40,43,44].
These collections could present an untapped opportunity for quantitative classification, comparative typology, and probabilistic attribution of even incomplete or fragmentary artifacts [34,45,46]. The methodological gap, highlighted in Section 1.2, presents an opportunity for new approaches—particularly those capable of encoding both morphological structure and stylistic syntax. The diagrammatic–morphological approach proposed herein may offer such a synthesis by formalizing visual logic and spatial proportions beyond the pixel- or mesh-based analyses found in most current studies.
To address these gaps, we propose the integration of different methods—including feature extraction, parametric analysis, morphology diagramming, and supervised classification based on statistical techniques—into the study of classical orders. By applying these methods to curated digital models and historical datasets, we aim to develop a robust analytical toolset for classifying and interpreting column capitals. Accordingly, some previously conducted subject-related works—focusing on columns and capitals of classical architectural orders [47,48]—were used herein as the starting points.
Unlike analyzing 2D images, which has generally become a widespread trend in the context of artificial intelligence, this investigation started from a 3D approach to solving problems, which is essential for investigating architectural heritage from the morphological point of view (hereinafter referred to as POV) and obtaining the corresponding encoding-oriented spatial information. The fundamental weakness of that (2D) Image Analysis approach, in this context, lies in the fact that it is very sensitive to any destructive factor the AI algorithm is not trained to properly answer to, either the mentioned factor is morphologically insignificant or not (e.g., graffiti- or damage-related one) [49,50,51].
Therefore, this research aims to establish a methodologically reliable approach for assessing artifact stylistic affiliation and validating architectural heritage in a widely affordable and “machine-friendly” way. Such an approach should not only enhance the objectivity and scalability of architectural analysis but also support conservation, education, and digital heritage documentation by offering a reproducible, evidence-based framework for understanding the formal complexity of classical architectural language. Additionally, in order for the mentioned approach to be as cost-efficient and broadly applicable as possible in the domain of architectural heritage, the usage of freeware is mainly foreseen.
In line with the aforementioned, the research question is as follows:
How can the morphology of classical architectural artifacts be represented and quantitatively compared to cost-efficiently validate their stylistic affiliation, particularly within the Doric order?
In accordance with the research question defined, the foundational framework of this study is established, based on the following premises: (a) all the capital stylistic regularities (peculiarities) regarding the order identity can be faithfully expressed by diagramming its morphology; (b) the comparison of such diagrammatic representatives of physical entities, instead of literal ones, overcomes the bottlenecks regarding the initial “incomparability”, enabling order-belonging assessment to be scientifically feasible as well as general and broadly applicable.
Consequently, it is implied that specifically created diagrammatic expressions of artifact morphology and their computational processing—by using widely affordable software only—could answer the research question scientifically satisfying.
2. Materials and Methods
As introduced in Section 1.3, the architectural heritage validation approach proposed herein integrates multiple methods into the study of classical orders, developing a robust analytical toolset for classifying and interpreting column capitals.
The overall workflow involves the following five key steps: (i) input preparation → (ii) feature extraction → (iii) morphology diagramming → (iv) quantitative comparison → (v) stylistic assessment.
Each of these steps includes corresponding substeps, collectively outlining the classification pipeline, which is visually represented in the flowchart below (Figure 1).
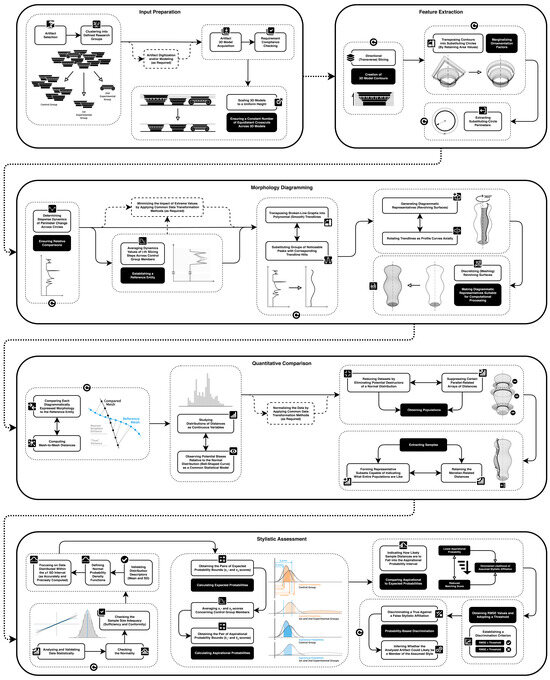
Figure 1.
Workflow of the methodological process. A high-resolution figure is reported in the Supplementary Materials (Figure S1).
2.1. Equipment and Software Employed
The following equipment and widely affordable software (predominantly freeware ones) were used:
- Dell Vostro 15 3580 Laptop, 15.6-inch FHD Display, Intel(R) Core(TM) i7-8565U CPU, 8 GB DDR4 SODIMM RAM, SSD M.2 PCLe NVMe 256 GB, AMD(R) Radeon(TM) 520 2 GB GDDR5;
- Robert McNeel & Associates (TLM, Inc.) Rhino 7 SR 9 (7.9.21222.15001) along with Grasshopper 1.0.0007 (hereinafter referred to as GH) as an already built-in visual programming tool (bearing in mind that an adequate freeware alternative to Rhino could be the latest version of Blender, including the Sverchok add-on, as the most appropriate substitute for Grasshopper, and/or Geometry Nodes as an already built-in visual programming tool—all of which we are not familiar with, wherefore we have not used them), for generating capital 3D models and making their sizes uniform; for extracting latent features (Section 2.3) and diagramming morphologies (Section 2.4); and for obtaining populations (hereinafter referred to as POPs) and extracting samples (hereinafter referred to as SMPs) of the relevant comparison-wise numerical outputs (Section 2.5.2);
- CloudCompare 2.13.2 freeware (hereinafter referred to as CC), for comparing previously paired up diagrammatic representatives quantitatively, i.e., for computing, within such pairs, how far the vertices of the one representative are from the nearest ones of the other, as well as for defining scalar fields (hereinafter referred to as SFs) based on those comparison-wise distance datasets and deriving the relevant statistical parameters from (Section 2.5.1 and Section 3.1.1);
- Microsoft Excel for the Web as a free spreadsheet software available online at https://excel.cloud.microsoft/ (accessed on 25 July 2025), for creating relevant dynamics-wise graphs with associated trendlines (Section 2.4.1); obtaining range bounds of SFs, of their absolute and transformed forms as well as of POPs and SMPs derived from (all together previously imported into); organizing such ranges into a tabular format (Section 3.1.2); and for obtaining the remaining relevant statistical parameters, besides importing the certain subsequently obtained outputs related to the other software used (Section 3.1.4 and Section 3.2);
- Matplotlib (3.10.0) as a comprehensive Python (3.13.1) library within Microsoft Visual Studio Code 1.96.4 (hereinafter referred to as VS Code), for visualizing relevant frequency- and density-wise histograms, where the latter ensured the normal probability density functions (hereinafter referred to as PDFs) are fitted in (Section 3.1.2 and Section 3.1.3);
- Sample Size Calculator (Raosoft, Inc., 2009) as a free tool available online at http://www.raosoft.com/samplesize.html (accessed on 25 July 2025), for checking the adequacy (sufficiency) of defined SMPs (in terms of size) relative to sizes of corresponding POPs (Section 3.1.3);
- Statisty freeware, available online at https://statisty.app/ (accessed on 25 July 2025), for creating relevant normal quantile–quantile (hereinafter referred to as Q–Q) plots in the role of indicators of normality of SMP-related distance distributions (Section 3.1.3);
- Statistics Kingdom (launched in November 2017) as a freeware available online at https://www.statskingdom.com/ (accessed on 25 July 2025), for applying simple linear regression (hereinafter referred to as SLR) models in the role of estimators of the amount of correlation between SMP-related distances and their corresponding normal/theoretical z-scores (Section 3.1.3), as well as for defining normal PDFs of distributions of such distances and calculating relevant areas under, equal to aim-directed probabilities (Section 3.1.4).
2.2. Input Preparation
2.2.1. Artifact Selection and Clustering
Regarding Section 1, column capitals of five major orders of classical architecture were taken into account as artifacts to which the architectural heritage validation approach could be applied. It was assumed that they faithfully reflect characteristics of their own orders (as the most distinctive column parts), representing thereby elements that reliably substitute the whole building whose order affiliation is being assessed.
As explained in Section 1.1.1, from that set of five major orders, the Doric one was chosen for the approach development, or more specifically, its capitals as ones of a medium-complex morphology in relation to the remaining orders (they are a little bit more complex than those of the Tuscan order, but a bit simpler compared to the Ionic, Corinthian and Composite orders). Additionally, bearing in mind the extensiveness of the relevant literature, sources, and archival material as well as their availability, it should be noted that only Roman-type Doric capitals were taken into account, while those of the Greek type were excluded.
For assessment purposes, the column zone which theoretically defines capital [13,14,15,17], was taken into account. Accordingly, in the case of the Doric order, the aforementioned zone was considered as a part of the column between the astragal (positioned on the top of the column shaft) and the architrave (epistyle), whereas, in the case of the Ionic order, that zone included the astragal (see Figure 2).
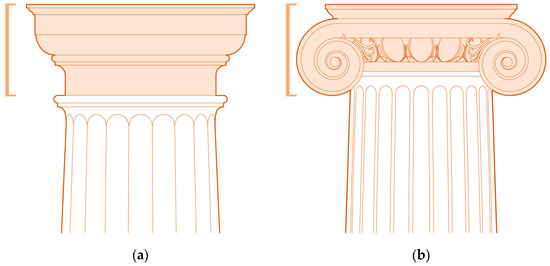
Figure 2.
Column zone theoretically defining the capital: (a) the Doric order; (b) the Ionic order.
To draw scientifically and statistically sound conclusions, selected artifacts were clustered into three research groups: Control, 1st Experimental, and 2nd Experimental, relative to the reason they were chosen as such and in such quantities, i.e., relative to predefined group roles.
The Control group—whose roles were (a) to establish a reference entity and “constant” probability bounds and (b) to provide expected results of the stylistic assessment—included eight indisputable Roman Doric (hereinafter referred to as IRD) capitals of columns differing in height and of both subtypes (Mutulary and Denticulated). The first four, namely IRD(1–4) capitals, were chosen so as to represent the Denticulated subtype—either with or without ornamentation, whereas the remaining four, namely IRD(5–8) capitals, were chosen to represent the Mutulary subtype—either with or without ornamentation, as well.
The 1st Experimental group—whose role was to confirm the assumed order affiliation—included two assumed Roman Doric (hereinafter referred to as ARD) capitals of columns of different heights.
The 2nd Experimental group was introduced to prove the reliability of the proposed architectural heritage validation approach by containing capitals that are not of the assumed order. Although this group should include at least one capital from each of the four remaining major orders, that was not the case in this study due to its purpose (establishing methodology only). Accordingly, the 2nd Experimental group included herein only one non-Doric capital: an Ionic (hereinafter referred to as ION) capital, adopted regardless of the Greek/Roman dichotomy. The research groups constituted as described are shown in Figure 3.
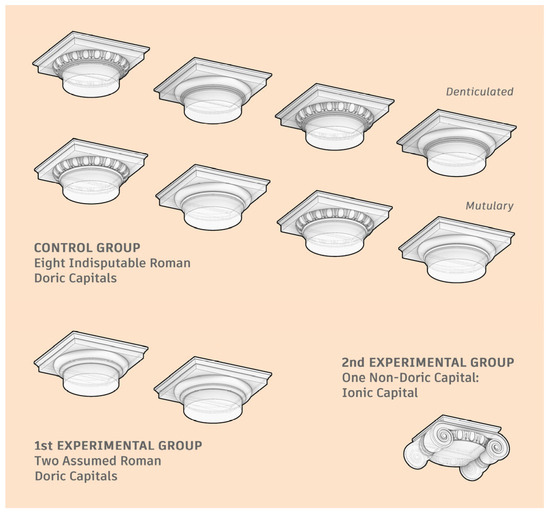
Figure 3.
Three-dimensional models of the eleven chosen capitals, clustered into the three defined research groups.
The mentioned roles of the research groups, along with a more detailed specification of their members—regarding order and type/subtype distinction, order affiliation status, and ornamentation possession—are tabularly provided below, in Table 2.

Table 2.
Overview of the roles of the research groups and attributes of their members.
2.2.2. Acquisition and Requirement-Based Validation
One should note that, for operational/practical reasons and consistently with the proposed approach, solely 3D models (as representatives) of real capitals (originals) are intended to be morphologically processed instead of physical entities. Therefore, they were previously generated parametrically as in [48], according to the annotated drawings, proportional rules, and ornamentation details extracted from both the relevant literature and available archival material. Namely, although capital 3D models could be obtained by digitizing the originals—e.g., contactlessly, using the photogrammetry (image-based) and/or 3D laser scanning (range-based) techniques—they were generated herein by applying the descriptive interpretation method (3D modeling), based on profile extracting and geometrical primitives defining, consistently with the certain recent works [52,53]. The modeling units were centimeters. Considering the aim of this research, the procedure of generating capital 3D models as digital representatives of physical entities is not explained in more detail.
The necessary and sufficient conditions—i.e., the requirements that comparing entities must meet to ensure reliable research outcomes—are as follows: (a) chosen capitals’ originals must conform to known canonical proportions [13,14,15,17], (b) digital 3D models have to represent originals as accurately as possible, and (c) their “digital masses” must be unified—represented in the form of closed B-Reps/meshes (in order for the corresponding contours to be closed as well). Therefore, for all 3D models used, special care was taken to check manually whether they satisfy those requirements and, consequently, can be declared appropriate digital representatives from the theoretical POV—having a typical/canonical configuration without any “excessive” ornamentation.
2.2.3. Scaling 3D Models to a Uniform Height
Each of the previously generated 3D models of capitals was uniformly scaled to the same height so as to ensure the number of equidistant crosscuts is constant across 3D models. In fact, sizes of capital 3D models were mutually uniformed by scaling lower diameters of related column shafts (to reach the value of 2 theoretical modules). Thus, capitals’ heights also became proportionally/canonically mutually complied, despite the general fact that the upper shaft’s diameter (dimensionally related to the diameter of the lower capital’s base) diminishes proportionally as the shaft’s height increases [13,14,15,17,47]. Such “adjustment” provided more sustainable cross-comparison of intra- and inter-order relations.
However, despite ensuring that capital 3D models are of the same height, i.e., their lower/upper bases are aligned, the bottleneck regarding the mutual morphological comparison of any two capitals (even of the same order) remained unsurpassed. Namely, 3D models still were significantly (either partially or entirely) inside/outside each other along the perimeter as a result of (a) the presence/absence of more or less lavish ornamentation and (b) the canonical “flexibility” in terms of applying the different proportional rules depending on the column height, i.e., thus allowed diversity of capitals (which therefore, after being conformed in height, might be nonconforming radially).
Accordingly, instead of comparing the literal 3D representatives of capital morphology (which are, in most cases, metrically incomparable from the research aim POV), comparing their specific diagrammatic expressions was assumed more sustainable and adopted as a method herein (Section 2.5). In order for such expressions to be entities equally as capable of being compared with (e.g., in CC) as the conventional 3D entities are, dynamics-wise trendlines—i.e., planar graphical equivalents of the capital 3D models’ profile curves—were spatialized. In a particular case, they formed the corresponding revolving surfaces by rotating around the common axial axis (Section 2.4.2).
2.3. Feature Extraction
To provide an adequate input for the forthcoming morphology diagramming, capital 3D models were to be “morphologically encoded”, i.e., the relevant latent features were to be extracted from. The main methodology principles concerning the directional slicing were retrieved from our previous research [54] in order to acquire a desired set of contours of 3D model masses herein as well. Nevertheless, to shorten the processing time, without minimizing the validity of the results obtained, the inherited protocol was modified by reducing the number of kinds of contour features the mentioned research [54] dealt with. Therefore, consistently with the findings of that research, only the Euclidean areas of the acquired contours were computed herein, not their fractal dimensions either (since fractal dimensions did not turn out to be sensitive enough to slight morphological changes).
2.3.1. Creating 3D Model Contours
Directional (transverse) slicing was performed on each of the acquired capital 3D models by using a set of equidistant section planes (a total of 97 ones) perpendicular to the column’s axis and distributed along the entire capital’s height, as shown in Figure 4.

Figure 4.
Set of transverse equidistant section planes distributed along the entire capital’s height.
Besides the fact that the smaller the transverse-slicing step (hereinafter referred to as TSS) is, the less approximated the morphological encoding will be—the optimal size of such a step generally depends on what is being sliced, particularly on the object’s size and shape. After testing several TSS values as input parameters (ranging from 1 cm to 0.1 cm), half a centimeter (0.5 cm) was empirically found to best capture latent features within this study in order for the consequent dynamics-wise trendlines to be informative enough morphologically.
Accordingly, the value adopted for the TSS size herein (as 1⁄96 of the total capital’s height) was also deemed adequate from the research aim POV, although one should be aware that when establishing methodology, the values adopted for certain parameters are not themselves crucial. Due to a large number of section planes foreseen, the creation of the corresponding contours was automated, namely, performed by employing a visually coded GH algorithm shown in Figure 5.
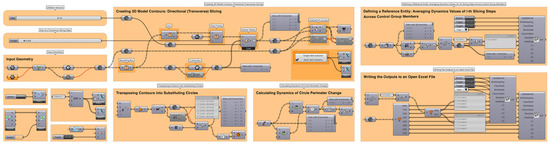
Figure 5.
Visually coded GH algorithm employed for automating repetitive tasks. A high-resolution figure is reported in the Supplementary Materials (Figure S2).
2.3.2. Transposing Contours into Substituting Circles
Transposing created contours into substituting circles was introduced as a novelty with respect to another of our previous research [55], in order to minimize the impact of lavish ornamentation (as well as of any potential surface damage, which, however, was not present in this study) on the subject-related assessment. From the conceptual POV, by transposing the crosscut of the current outline into the ideal shape of a circle (as perfectly balanced and symmetrical from any position, with no corners and no weak points) while retaining the area value, all the information irrelevant for a reliable stylistic assessment of artifacts, i.e., order-belonging assessment of capitals, was marginalized (see Figure 6).
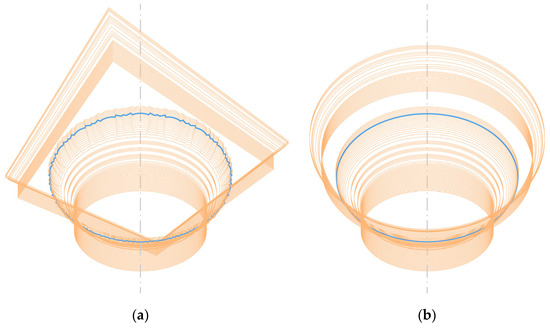
Figure 6.
Transposing contours into substituting circles: (a) the set of capital 3D model’s contours wherein the particular one is designated; (b) the set of substituting circles wherein the corresponding one is designated.
Whenever the particular section plane (from the set of transverse equidistant ones) created more than one closed contour, their areas were summed, and the corresponding circle accordingly substituted that summed-area value. Since substituting circle represents a shape of the shortest outline/smallest perimeter with the same area as the initial contour, the feature that imposed itself to be extracted from was the perimeter of substituting circle (hereinafter referred to as PSC)—representing thus the feature whereon the forthcoming acquisition of the values of dynamics was based (Section 2.4.1) within the broader, morphology diagramming step.
2.4. Morphology Diagramming
As announced above, the step of diagramming morphology is considered crucial for overcoming the bottlenecks associated with the recognized initial “incomparability” (inadequate comparability) of the literal representations of physical entities.
Namely, in accordance with [55] and the fundamental meaning of the term “dynamics”, intra-capital dynamics related to the change in a certain contour feature (i.e., in a PSC) was calculated—describing a variation level between every two neighboring values of that feature per the distance of their carriers, i.e., per the TSS value (determined by two consecutive section planes perpendicular to the column’s axis).
The values of such dynamics served afterward not only as indicators of how dynamically the perimeter changes across circles, but for obtaining the aforementioned planar graphical equivalents (dynamics-wise trendlines), and thus, the profile curves of the consequent revolving while generating diagrammatic representatives (Section 2.4.2).
2.4.1. Calculating Dynamics of Circle Perimeter Change
As implied, in order to ensure relative comparisons, it was determined how much the perimeter changes dynamically from circle to circle within the sets of intra-capital ones, or in other words, the stepwise dynamics of perimeter change across circles (hereinafter referred to as DPC) was calculated. Such a calculation was performed by using GH within Rhino, repeatedly—for each of the eleven capital 3D models processed (IRD(1–8), ARD(1), ARD(2), and ION), namely, for each of the associated sets of PSC values ninety-six times, according to the following equation:
for every i ∈ ℤ such that 1 ≤ i < n, where n is the total number of section planes.
As presented, only absolute values stood for ∆PSC, not signed ones either, in order for the corresponding DPC values to become capable of being scaled/normalized by applying some of the common data transformation methods if necessary.
To define a reference entity (hereinafter referred to as REF), mutually akin DPCs (in terms of the TSS ordinal number) related to 3D models of IRD(1–8) capitals were averaged. Despite the fact that the larger the number of IRD capitals used to create REF is, the more reliable comparison with it will be—the number of eight chosen ones (from the Control group) was declared adequate from the research aim POV (establishing methodology only), namely, suitable to reflect morphology-related order (Doric) properties faithfully. Accordingly, the mentioned averaging was performed by using GH within Rhino, for each of the ninety-six octets of DPC values (every group of DPCs related to the i-th TSS among IRD capital 3D models), separately, producing the corresponding values of an averaged DPC (hereinafter referred to as ) respecting the following equation:
for every i ∈ ℤ such that 1 ≤ i < n, where n is the total number of section planes, and for k such that k ∈ ℤ ∧ 1 ≤ k ≤ m, where m is the total number of chosen IRD capitals.
To minimize the significant impact of extreme values that, nevertheless, appeared within the obtained datasets, DPC values related to the processed capital 3D models, namely, values related to the REF, were transformed by applying a square root.
Additionally, an arbitrarily adopted value of a constant (c = 4) was added to every DPC, namely, value to move certain parts of derived graphical equivalents (those related to the lowest such values) away from the zero line as an axis of the forthcoming revolving, i.e., to avoid any possible self-intersection of corresponding surfaces.
Such operations compounded induced a transformed dynamics of subject-related change (hereinafter referred to as TDC), and were, according to the following equation, applied by using Excel, to each of the calculated sets of DPC values, namely, to the set of values, respectively:
for every i ∈ ℤ such that 1 ≤ i < n, where n is the total number of section planes, and for the constant c such that c ∈ ℝ ∧ c ≥ 0.
The distributions of calculated TDC values, graphically depicted in the form of broken-line graphs, caused noticeable peaks (see Figure 7). However, due to the certain shifts in the position of the peaks along the TSS-related axis (y-axis), which would have an unfavorable effect on the morphological comparison, i.e., on the distance computation in CC (by causing the biases), such broken-line expressions of TDC distributions were transposed into substituting trendlines by using Excel’s polynomial fit function. After testing all available polynomial degrees as input parameters (integers 2–6), sixth-degree polynomial trendlines were empirically found to best fit the initial behavior of the dynamics-wise distributions, particularly in terms of data fluctuations.
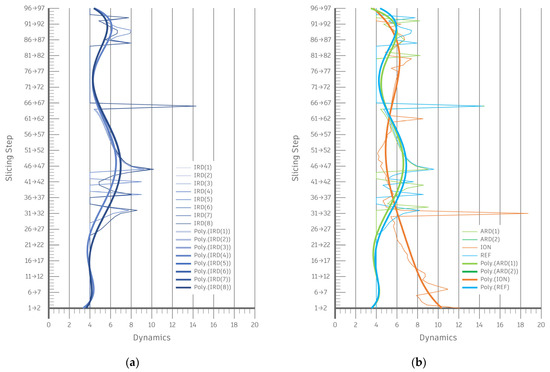
Figure 7.
Dynamics-wise distributions in the form of broken-line graphs with the associated sixth-degree polynomial (smooth) trendlines: (a) the TDC distributions/trends regarding IRD(1–8) capitals; (b) the TDC distributions/trends regarding ARD(1), ARD(2), and ION capitals as well as the REF.
Namely, the degree value (of six) adopted for the polynomial fit function ensured the best substitution of groups of the noticeable broken-line peaks with the corresponding trendline hills. Thus, TDC distributions became acceptably approximated by their trends, which were, from the morphological POV, found as more suitable for further cross-comparisons.
2.4.2. Generating Diagrammatic Representatives
For relevant reasons explained in Section 2.2.3, and retracing the substituting circles’ analogy, every sixth-degree polynomial trendline (as a counterpart of the capital 3D model’s profile curve) is given the role of generatrix of the corresponding “substituting revolving surface”. Namely, with the aim of finding a suitable substitute for the literal capital morphology, each of the twelve generatrices was rotated axially by using Rhino (around the zero line, i.e., TSS-related y-axis designated in Figure 7), forming thus the corresponding 3D entity, called diagrammatic representative, with the associated system of meridians and parallels.
Since either a point cloud or a mesh is the only type of entity the CC can handle, created revolving surfaces (open B-Reps) were converted into meshes, namely, were discretized (meshed)—by using GH within Rhino. Such newly generated 3D entities (open meshes) were reoriented afterward so that their longitudinal axis (y-axis) took the vertical (z-axis) direction. So, a total of twelve diagrammatic representatives—the eleven ones of IRD(1–8), ARD(1), ARD(2), and ION capital morphologies, including the REF (as one of “averaged” IRD(1–8) capital morphologies)—are, in the form of (quad-face) meshes, shown in Figure 8.
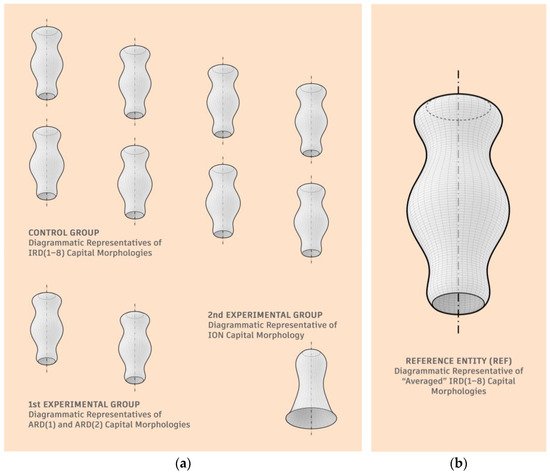
Figure 8.
Diagrammatically expressed capital morphologies: (a) the eleven diagrammatic representatives of IRD(1–8), ARD(1), ARD(2), and ION capital morphologies, clustered by research group; (b) the REF as a diagrammatic representative of “averaged” IRD(1–8) capital morphologies.
The research groups and associated members of the corresponding type, shown in Figure 8a, are arranged therein in the same way as those in Figure 3.
Discretization was performed consistently with the concept of transferring continuous models into discrete counterparts—so that the constant number of meridians (360) stood for all discretized entities, whereas the number of parallels varied from mesh to mesh as the meridian length varied as well (the division length tended to be uniform across meshes).
Despite the fact that for a given mesh resolution of a compared entity, the higher the mesh resolution of a REF is, the more accurate the mesh-to-mesh distances will be computed (as their directions will align more closely with the normal vectors), mesh resolutions were nevertheless made uniform across the diagrammatic representatives, regardless of the forthcoming comparing role, for the methodological reasons.
2.5. Quantitative Comparison
2.5.1. Mesh-to-Mesh Distance Computation
To achieve the aim of this research, each of the diagrammatic representatives clustered into defined research groups (Figure 8a) was compared to the REF (Figure 8b) quantitatively and under careful control, namely, distances between the vertices of compared meshes and the corresponding nearest neighbors on the REF mesh were computed in CC. So, a total of eleven comparisons were digitally conducted: eight IRD-to-REF comparisons, two ARD-to-REF comparisons, and one ION-to-REF comparison—requiring that the associated pairs of diagrammatic representatives (meshes) had previously been imported therein in a specific way.
Namely, every two meshes paired up for the mentioned comparisons were imported into CC separately as .obj files, ensuring that they are of the mutually overlapped axes and base planes only (having the same height, as they represent the capitals already conformed in height). Since each of such comparison-wise pairs, as indicated, consisted of the REF mesh and the mesh needed to be compared with, the “Reference role” was naturally assigned to the REF mesh in CC, whereas the “Compared role” was assigned to the remaining one (see Figure 9).
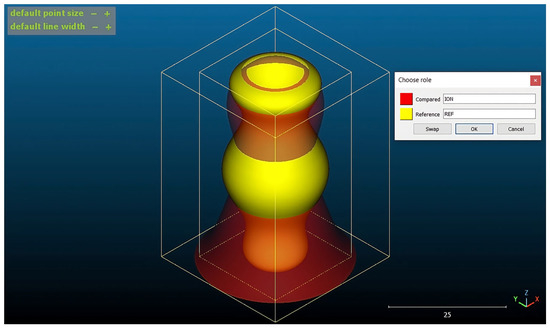
Figure 9.
Assigning the “Reference” and “Compared” roles to the meshes paired up: the example of the ION-to-REF comparison.
To make the overall processing technically possible due to the limited performances of the computer used, mesh-to-mesh distance computing (comparison) was repeatedly (for each of the pairs separately) performed by using the following preset of the “General parameters”: (a) “octree level” set to 8, being aware that this value, as default, can be declared adequate from the research aim POV (establishing methodology only); (b) checked “signed distances” to enable the deviations inward and outward from the REF mesh to be differentiated; (c) checked “robust” computing option; (d) checked “multi-threaded” option; and (e) “max thread count” set to 7/8 (14/16) in order that the automatic adjustment be avoided (i.e., so that the constant value is ensured across all the comparisons intended). The results of such distance computations (comparisons) are presented in Section 3.1.1 and discussed afterward.
The “Blue > White > Red” color scale (cool–warm diverging) as one of the CC default color scales—ranging smoothly from pure blue to pure red, symmetrically in relation to the unsaturated white in between—was associated with previously computed (signed) distances (hereinafter referred to as CDs) for each of the eleven comparisons separately. It was performed by aligning the mentioned color range with the particular range of CDs, so that an existing extreme value of the distance was assigned the corresponding pure cool/warm hue (in accordance with the minus/plus sign), whereas such a symmetrically inverse (imaginary) extreme was assigned the opposite pure hue.
Accordingly, each of the SFs defined by mesh-to-mesh comparisons (i.e., based on the corresponding dataset of CDs) was separately color-coded by mapping color tints in accordance with the principle that the more inward the (negative) deviation from the REF is, the more saturated blue is to be assigned to, and vice versa, the more outward the (positive) deviation from the REF is, the more saturated red is to be assigned to—thus forming a 3D color map. Consequently, CDs were assigned either bluish or reddish tints whose dependence on distance value varies from comparison to comparison, representing thus (only relatively), how far the values of CDs are above or below their targeted (close-to-zero) values.
2.5.2. Obtaining Populations and Extracting Samples
In a formational sense, each of the obtained SFs referred to the own dataset of CDs bounded below by the corresponding greatest value of the negatively signed CDs as lower bound (hereinafter referred to as LB), namely, above by the associated greatest value of the positively signed CDs as upper bound (hereinafter referred to as UB), and somehow ranged in between. Therefore, intra-SF distributions of CDs, along with their main descriptors (statistical CC outputs) represented by the values of mean and standard deviation (hereinafter referred to as SD), were considered important for the further analysis and validation, from the statistical POV. Normal distribution was chosen as a common and widely affordable statistical model, particularly applicable in the domain of examining continuous variables such as distance.
However, despite the fact that continuous variation was noticeable in CDs, their intra-SF distributions were not predominantly of a normal/Gaussian type. Consequently, the solution was sought in normalizing the data by applying a certain data transformation method. To ensure that the common transformations (logarithmic, square-root, etc.) are feasible, the absolute values of CDs (hereinafter referred to as s) had to be obtained beforehand. In the particular case, the square-root transformation empirically turned out to be the most suitable one as it made the data less skewed and the variation more uniform.
Although distributions of such transformed values of s (hereinafter referred to as TDs) became much closer to the normal ones, derived datasets were still not acceptable enough because of (a) their enormous sizes (in terms of number of TDs), which made them difficult to deal with, and (b) the existence of certain biases relative to the known bell-shaped curve. Therefore, the eleven datasets of TDs, related to the eleven comparisons performed, required further processing. The bounds of ranges concerning - and TD-related datasets, including the associated values of mean and SD (as main descriptors) of those datasets, were previously determined by using Excel.
In the first stage, the announced further processing implied a reduction in TD-related datasets by suppressing certain arrays of identical TDs (subsets defined by vertices of the same mesh parallel), for each of the datasets separately. Actually, those of such arrays that were considered potential destructors of a normal distribution, were eliminated by using a “Graph Mapper” GH component (with a Gaussian graph type chosen)—in a way to ensure that: (a) the bounds of ranges as well as the values of mean and SD are preserved as close as possible to the initial ones (i.e., to the bounds of TDRanges, namely, to the values of TDMeans and TDSDs, respectively); (b) the reduction rates (hereinafter referred to as RRs) are as similar as possible to each other. However, although being reduced and without so noticeable biases anymore, such newly formed subsets (consisted of retained arrays of TDs) still were too large from the operational/practical POV, which induced us to proclaim them POPs—consistently with the definition that POP is an entire group that one wants to draw conclusions about, whereas SMP is a subset used to represent it practically.
The resulting POPRanges, POPMeans, and POPSDs thus became further orienters. Also, it is important to note that, methodologically—by performing actions inverse to the applied data transformation, namely, by squaring distance values—all the POP-related distances could easily be returned to their actual (measured) values, i.e., any of the POPs defined could easily became datasets capable of being meaningfully discussed in terms of frequency. The results of the steps taken to achieve the derivation and reduction described above are presented in the corresponding tables and figures (histograms) in Section 3.1.2.
Following the reducing analogy, in the second stage, i-th (meridian-related) TDs, i.e., one TD for each of the retained (parallel-related) arrays of TDs, were extracted from POPs—consistently with the fact that, in the particular case, TDs concerning the meridian turned out to be the only carriers of normal distribution properties. Consequently, not only optimal or small enough, but possibly representative subsets were formed (of totally preserved range bounds and values of mean as well as of almost preserved values of SD), capable of reliably indicating what entire POPs are like (from the statistical POV), which induced us to proclaim them SMPs rightly.
2.6. Stylistic Assessment
2.6.1. Statistical Data Analysis and Validation
The normality checking was performed afterward to confirm whether the extracted segments of POPs represent the valid SMPs from a statistical POV. Methodologically, it was based on the so-called goodness-of-fit checking, whose outputs were evaluated at the following two levels:
- Graphical—by observing how well (a) heights of SMP-related bins, defined within density histograms, follow the corresponding normal PDF, i.e., (smooth) bell-shaped curve, fitted relative to the associated SMPMean and SMPSD values; (b) data points of SMP-related quantiles, plotted against the normal/theoretical quantiles within normal Q–Q plots, follow the corresponding identity line, i.e., (straight) line of equality; (c) data points of SMP-related normal/theoretical z-scores (as possibly dependent variable), plotted against the SMP-related distances (as independent variable) within the SLR model-based line fit plots, follow the corresponding regression line, i.e., (straight) line of best fit—in accordance with the principle that the better the data fit the certain model, the more normally distributed they are;
- Numerical—by considering how close the values of the coefficient of determination (hereinafter referred to as r2), calculated based on the line fit plots created, are to their targeted values, namely, by indicating how large the portions of the variances in the dependent variable (SMP-related normal/theoretical z-scores) are such that can be explained by the independent variable (SMP-related distances)—in accordance with the principle that the higher the value of r2 (in the range between 0 and 1) is, or in other words, the better the SLR model fits the data, the more strongly correlated the variables are to each other and the data, consequently, more normally distributed.
The mentioned density histograms were created in VS Code (by using Python Matplotlib) in a way to ensure that the bin width is proportionally constant relative to the corresponding overall range, i.e., it represents a predefined n-th part of that range. Consequently, the inter-capital relations concerning the deviation from normal PDFs (fitted in as mentioned above) became distinguishable. On the other side, the creation of normal Q–Q plots was performed by using Statisty freeware, repeatedly for the confidence interval defined at a 95% confidence level (hereinafter referred to as CL), adhering to the commonly used level of significance of 0.05 (5%), and thus, meeting the conventional statistical significance. Consequently, identity lines of normal Q–Q plots ended up between the 95% confidence bands (hereinafter referred to as CBs), i.e., outlines of corresponding fat pencils. To allow the assessment of how well each SMP-related dataset fits the corresponding SLR model to become feasible at both the graphical and numerical level, i.e., to produce the eleven lines of best fit with the associated values of r2, Statistics Kingdom freeware was employed. The outcomes of verifying the normality of SMP-related distance distributions are presented in Section 3.1.3.
Besides the normality checking, the adequacy (sufficiency and conformity) of defined SMPs (in terms of size) with respect to the sizes of corresponding POPs was also checked. Therefore, the total number of TDs retained within the particular POP was proclaimed POPSize, whereas the number of such TDs extracted from (forming the corresponding SMP) was proclaimed SMPSize accordingly.
The statistically acceptable sufficiency of SMPSizes became verifiable thanks to recommended SMPSizes obtained by using Sample Size Calculator—specifically, relying on the associated POPSizes and typical, statistically common presets (“margin of error” of 5%, CL of 95%, and “response distribution” of 50%), namely, in accordance with the principle that as the POPSize approaches infinity, the recommended SMPSize approaches the value of 385. So, by providing the comparison between existing SMPSizes and the corresponding recommended ones, it was ensured that targeted sufficiency could be quantitatively easily checked. It is important to note that, according to the mentioned calculator, the recommended SMPSize does not change significantly for POPSizes larger than 20,000; moreover, for POPSizes larger than 128,062, it amounts to 384 until POPSize even exceeds the value of 1,008,502.
On the other hand, to ensure that mutual conformity of SMPSizes (in terms of balance of their “weight”) became verifiable, it was determined what portions of POPSizes relate to SMPs, or in other words, SMPPercentages were calculated using Excel. By confirming whether each “Gaussian” SMP is of statistically adequate size, all the obtained values of statistical parameters, such as SMPMean and SMPSD, could be proclaimed valid from a statistical POV. The outcomes of verifying both the sufficiency and mutual consistency of SMPSizes, or in one word, their adequacy, are presented in Section 3.1.3.
2.6.2. Probability-Based Discrimination
Based on the previously obtained SMPMeans and SMPSDs, normal PDFs of SMP-related distance distributions were defined for each of the eleven comparisons using Statistics Kingdom freeware. In accordance with the general fact that the data distributed within the ±1 SD interval (defined relative to the associated mean) can be declared accurately and precisely computed, SMPMeans and SMPSDs ensured that the bounds (as x-scores) of under-bell areas proclaimed expected probabilities (hereinafter referred to as EPs) and the corresponding interval lengths (hereinafter referred to as ILs) in between are defined.
More precisely, by subtracting/adding SMPSDs from/to the corresponding SMPMeans, EP-related bounds, i.e., EPLBs/EPUBs, were obtained, respectively, thus forming the pairs of the corresponding x1- and x2-scores. Consequently, EPILs (bounded below and above by such bounds) were obtained as the values equal to the two corresponding SMPSDs, namely, by subtracting x1-scores from the corresponding x2-scores.
Having the eleven normal PDFs previously defined and pairs of EP-related bounds (as their x1- and x2-scores that vary from PDF to PDF), the eleven EPs in between were calculated using Statistics Kingdom freeware, repeatedly. Afterward, it was checked whether each of the EPs is equal to the value of 0.682690 (as the value of theoretical probability related to every ±1 SD interval, which is a “product” of the normal distribution). The normal PDFs and EP-related bounds, including the probabilities calculated for the ILs in between (EPs), are presented in Section 3.1.4.
Based on a subset of EP-related bounds concerning the eight IRD-to-REF comparisons (as control ones), “constant” LB/UB of aspirational probabilities (hereinafter referred to as APs) was calculated by averaging the eight EPLBs/EPUBs, respectively, thus forming the pair of x̅1- and x̅2-scores. Accordingly, the value of APIL (bounded below and above by such bounds) was obtained by subtracting x̅1-score from the associated x̅2-score. The values of APLB/APUB and APIL are presented in Section 3.2.
Having the same normal PDFs previously defined as well as the pair of AP-related bounds (as their “constant” x1- and x2-scores, invariant to the PDF properties), namely, x̅1- and x̅2-scores, the eleven APs in between were calculated using Statistics Kingdom freeware, repeatedly. The values of AP are presented in Section 3.2, too.
Each of the APs was calculated to indicate how likely SMP-related distances of the particular comparison are to fall into the APIL (defined between APLB and APUB), or in other words, to “infer” whether the analyzed capital is likely to belong to the assumed order, namely, to the Doric order. Consequently, the smaller the value of AP is, the smaller the possibility that a diagrammatic representative of the corresponding capital 3D model, namely, the source capital itself, can be declared a member of the classical architectural order represented by REF.
The visual explanation of a principle aimed at finding the AP is shown in Figure 10, wherein the blue-colored area under a certain normal PDF (bell-shaped curve), bounded between the specified x̅1- and x̅2-scores (APLB and APUB), graphically represents the corresponding value of AP.
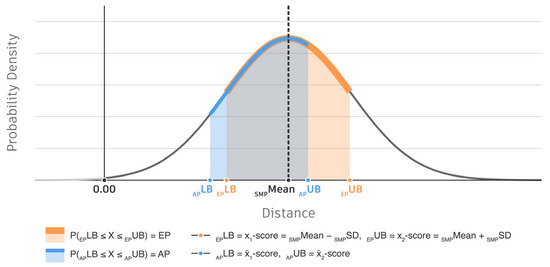
Figure 10.
Value of AP, graphically represented by blue-colored area under the normal PDF and bounded between the specified x̅1- and x̅2-scores, in comparison with the value of EP, graphically represented by orange-colored such area and bounded between the specified x1- and x2-scores.
To achieve a strict discrimination criterion capable of validating capitals in terms of their order affiliation unambiguously, the root-mean-square error (hereinafter referred to as RMSE) was introduced as an additional parameter. Based on probabilistic outputs (EPs and APs), RMSE was calculated for each of the eleven mesh-to-mesh comparisons using Excel and compared with an adopted value of threshold (0.2). Being aware of the fact that the RMSE value of zero (which indicates that the meshes being mutually compared are congruent, i.e., perfectly matched) is typically unattainable, RMSEs were just obtained to tell of how far each of the EP values (of 0.682690) is from the corresponding value of AP and whether that deviation exceeds a threshold or not. The outcomes of the discrimination performed according to the explained criterion are presented in Section 3.2.
3. Results
The research results are in the form of intermediate and final ones. The intermediate results include comparison-wise (CC) outputs as well as the outputs related to data derivation/reduction, goodness-of-fit checking, and probability densities defining, obtained by using all the other freeware (except CC) listed in Section 2.1. The final results imply outputs of a probability-based discrimination (stylistic assessment), along with the probabilistic outputs it relied on, obtained by purposefully using the corresponding freeware from those listed in the same Section 2.1.
3.1. Intermediate Results
3.1.1. Comparison-Wise Outputs
The CC outputs of a graphical nature are color-coded SFs (consisting of CDs), i.e., 3D color maps with the associated color scales as representations of color tints assigned to CDs relative to their magnitudes and signs.
So, the results of comparing each of the IRD(1–8) diagrammatic representatives to the REF quantitatively (as mentioned in Section 2.5.1), namely, the color-coded SFs regarding the eight IRD-to-REF comparisons, are shown in Figure 11.
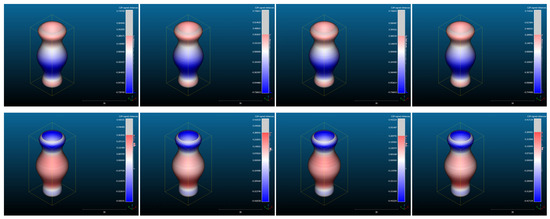
Figure 11.
Color-coded SFs regarding the eight IRD-to-REF comparisons: 3D color maps with the associated color scales beside (left–right, top–bottom).
Accordingly, the results of comparing ARD(1), ARD(2), and ION diagrammatic representatives to the REF separately, namely, the color-coded SFs regarding the two ARD-to-REF comparisons and one ION-to-REF comparison, are shown in Figure 12.
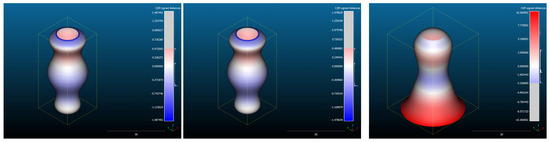
Figure 12.
Color-coded SFs regarding the two ARD-to-REF comparisons and one ION-to-REF comparison: 3D color maps with the associated color scales beside (left–right).
3.1.2. Derivation- and Reduction-Wise Outputs
The statistical CC outputs (of a numerical nature), as mentioned in Section 2.5.2, imply ranges, means, and SDs concerning the datasets of CDs whose values (for reasons stated in the same Section 2.5.2) needed to be absolutized—affecting, in turn, such a triplet of parameters indispensably. So, the values concerning such outputs, including ranges, means, and SDs that relate to the derivatives of CDs, i.e., to the datasets of s are listed for each mesh-to-mesh comparison in Table 3.

Table 3.
Per-comparison ranges, means, and SDs concerning CD- and -related datasets, clustered by research group.
As explained in Section 2.5.1, since the “signed distances” option was checked during the CC computation, the CDs whose endpoints (vertices) that belong to the compared mesh occurred inside the REF were assigned the minus (−) sign, and vice versa, the CDs whose such endpoints occurred outside the REF were assigned the plus (+) sign.
The relationships (in terms of frequency) between the distributions of distance values were, as mentioned in Section 2.5.2, visualized by the corresponding frequency histograms (created in VS Code). More specifically, each of such histograms contains the corresponding pair of distributions and clearly provides an insight into the relationship between them, relying on the following principle: the histogram bins concerning the one of distributions paired-up are to be assigned a blue hue, whereas the remaining one, related to the other, are to be assigned an orange hue.
Additionally, thanks to a certain level of transparency employed, the heights of the bins that ended up in the histograms’ overlapping zones remained readable.
Those of such histograms that show the relationships between the distributions of CDs and those of s, and that relate to the eight IRD-to-REF comparisons, are presented in Figure 13.
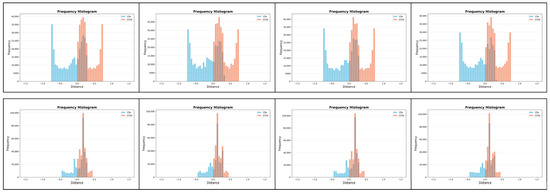
Figure 13.
Relationships between the distributions of CDs and those of s: frequency histograms regarding the eight IRD-to-REF comparisons (left–right, top–bottom).
The remaining frequency histograms that show the relationships between the distributions of CDs and those of s, but concerning the two ARD-to-REF comparisons and one ION-to-REF comparison, are presented in Figure 14.
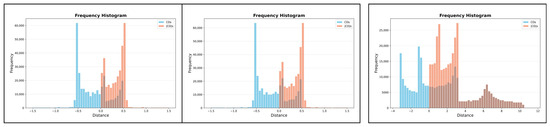
Figure 14.
Relationships between the distributions of CDs and those of s: frequency histograms regarding the two ARD-to-REF comparisons and one ION-to-REF comparison (left–right).
The ranges, means, and SDs related to the datasets derived from those of s (by square-root transformation), namely, concerning the datasets of TDs, are listed for each mesh-to-mesh comparison in Table 4. Additionally, the values that relate to such a triplet of parameters, but concerning the POPs (defined by reducing TD-related datasets, i.e., retaining certain parallel-related arrays of TDs for each of those datasets separately), are listed in the same Table 4, respectively.

Table 4.
Per-comparison ranges, means, and SDs concerning TD- and POP-related datasets, clustered by research group.
The frequency histograms that show the relationships between the distributions of s and those of TDs, and that relate to the eight IRD-to-REF comparisons, are presented in Figure 15a.
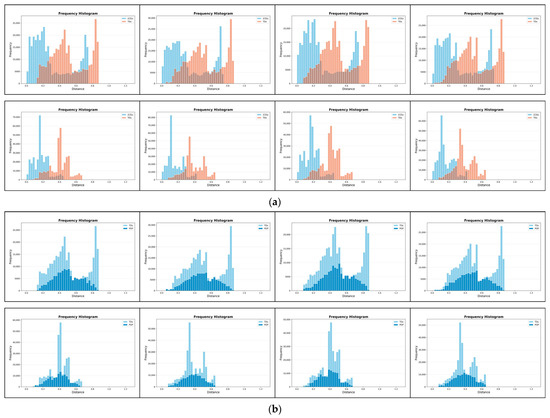
Figure 15.
Frequency histograms regarding the eight IRD-to-REF comparisons (left–right, top–bottom): (a) the relationships between the distributions of s and those of TDs; (b) the relationships between the distributions of TDs and POP-related ones.
Following the analogy, the relationships between the distributions of TDs and POP-related ones were visualized in the same way, except in terms of color-coding. Namely, although the only hue assigned is bluish (without any transparency), the histogram bins related to TDs are light blue, whereas the remaining ones, concerning the POP-related distances, are dark blue. Those of such frequency histograms that relate to the eight IRD-to-REF comparisons are presented in Figure 15b, respectively.
The remaining frequency histograms that show the relationships between the distributions of s and those of TDs, but concerning the two ARD-to-REF comparisons and one ION-to-REF comparison, are presented in Figure 16a.
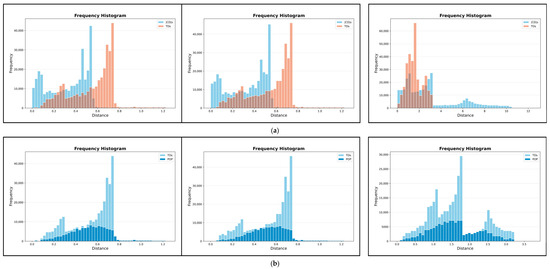
Figure 16.
Frequency histograms regarding the two ARD-to-REF comparisons and one ION-to-REF comparison (left–right): (a) the relationships between the distributions of s and those of TDs; (b) the relationships between the distributions of TDs and POP-related ones.
Accordingly, the remaining frequency histograms that show the relationships between the distributions of TDs and POP-related ones, but concerning the two ARD-to-REF comparisons and one ION-to-REF comparison, are presented in Figure 16b.
It is important to note that Figure 13, Figure 14, Figure 15 and Figure 16 presented above will not be discussed further as they do not convey the quantitative information about the actual (non-transformed) values of measured mesh-to-mesh distances. Their content was already implied through the explanation of the steps taken to achieve the derivation and reduction (Section 2.5.2).
The frequency histograms that show the relationships between the distributions of POP-related distances and those of squared such distances (i.e., of actual values thereof), and that relate to the eight IRD-to-REF comparisons, are presented in Figure 17.
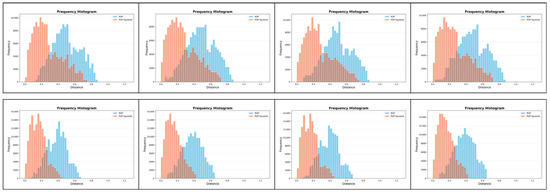
Figure 17.
Relationships between the distributions of POP-related distances and those of squared POP-related distances: frequency histograms regarding the eight IRD-to-REF comparisons (left–right, top–bottom).
And the only remaining but not least frequency histograms are the histograms that show the relationships between the distributions of POP-related distances and those of squared such distances, and concerning the two ARD-to-REF comparisons and one ION-to-REF comparison (see Figure 18).
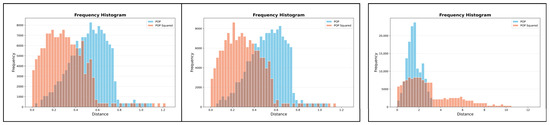
Figure 18.
Relationships between the distributions of POP-related distances and those of squared POP-related distances: frequency histograms regarding the two ARD-to-REF comparisons and one ION-to-REF comparison (left–right).
3.1.3. Goodness-of-Fit Outputs
Consistent with Section 2.6.1, the goodness-of-fit outputs concerning the extent of conformity of the SMP-related distribution densities with normal PDFs (defined by SMPMeans and SMPSDs) were visualized by the corresponding density histograms (created in VS Code).
Accordingly, the goodness-of-fit outputs concerning the extent of alignment of the data points of SMP-related quantiles (plotted against the normal/theoretical quantiles) with identity lines surrounded by 95% CBs, i.e., “covered” with fat pencils determined in between, were visualized by the corresponding normal Q–Q plots (created by Statisty freeware), as mentioned in the same Section 2.6.1.
Any of the deviations from such a straight line (or even from the fat-pencil region) within the normal Q–Q plots relates to the corresponding less or more noticeable biases in density histograms, and vice versa.
Those of such histograms, namely, of such plots that relate to the eight IRD-to-REF comparisons, are presented in Figure 19a and Figure 19b, respectively.
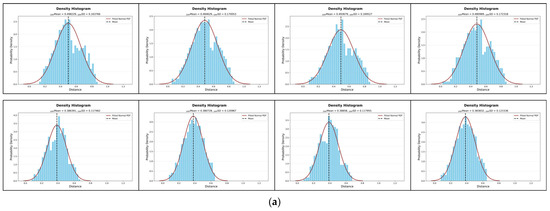
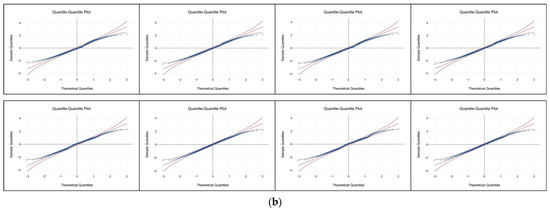
Figure 19.
Goodness-of-fit outputs regarding the eight IRD-to-REF comparisons (left–right, top–bottom): (a) the density histograms concerning the extent of conformity of the SMP-related distribution densities with normal PDFs; (b) the normal Q–Q plots concerning the extent of alignment of the data points of SMP-related quantiles with identity lines surrounded by 95% CBs.
The remaining density histograms, namely, normal Q–Q plots, as goodness-of-fit outputs concerning the two ARD-to-REF comparisons and one ION-to-REF comparison, are presented in Figure 20a and Figure 20b, respectively.
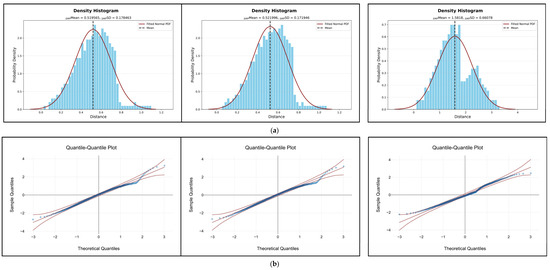
Figure 20.
Goodness-of-fit outputs regarding the two ARD-to-REF comparisons and one ION-to-REF comparison (left–right): (a) the density histograms concerning the extent of conformity of the SMP-related distribution densities with normal PDFs; (b) the normal Q–Q plots concerning the extent of alignment of the data points of SMP-related quantiles with identity lines surrounded by 95% CBs.
As aforementioned in Section 2.6.1, the goodness-of-fit outputs concerning the extent of alignment of the data points of SMP-related normal/theoretical z-scores (plotted against the SMP-related distances) with regression lines were visualized by the corresponding SLR model-based line fit plots (created by Statistics Kingdom freeware). Those of such plots that relate to the eight IRD-to-REF comparisons are presented in Figure 21.
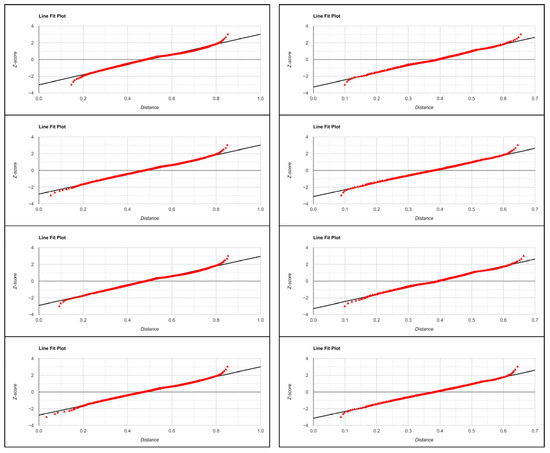
Figure 21.
SLR model-based line fit plots concerning the extent of alignment of the data points of SMP-related normal/theoretical z-scores with regression lines: goodness-of-fit outputs regarding the eight IRD-to-REF comparisons (top–bottom, left–right).
The remaining SLR model-based line fit plots, as goodness-of-fit outputs concerning the two ARD-to-REF comparisons and one ION-to-REF comparison, are presented in Figure 22.

Figure 22.
SLR model-based line fit plots concerning the extent of alignment of the data points of SMP-related normal/theoretical z-scores with regression lines: goodness-of-fit outputs regarding the two ARD-to-REF comparisons and one ION-to-REF comparison (left–right).
Besides TDCounts and RRs, which—relying on Section 2.5.2—indicate how balanced TD-related datasets are to each other, namely, how consistently they were reduced, SMPPercentages (stemmed from SMPSize-to-POPSize relationships), SMPSizes (relative to the value of 384 as the recommended SMPSize for all the POPs such that POPSize > 128,062), and POPSizes (relative to the value of 128,062 as the mentioned threshold) are, as the indicators of size adequacy, listed for each mesh-to-mesh comparison in Table 5.

Table 5.
Per-comparison indicators of reduction consistency, size adequacy, and goodness-of-fit concerning TD-, POP-, and SMP-related datasets, clustered by research group.
The same Table 5 also includes the goodness-of-fit numerical outputs in the form of values of r2, which—relying on Section 2.6.1—quantitatively tell of how strongly the SLR model fits the SMP-related data for each of the comparisons separately.
3.1.4. Probability Density Outputs
The ranges, means, and SDs concerning the SMPs (defined by extracting meridian-related TDs from corresponding POPs) are listed for each mesh-to-mesh comparison in Table 6. Additionally, the EP-related bounds, i.e., EPLBs (x1-scores) and EPUBs (x2-scores), as well as ILs between them—obtained consistently with Section 2.6.2—are listed in the same Table 6, respectively.

Table 6.
Per-comparison ranges, means, and SDs concerning SMP-related datasets, including the EP-related bounds and in-between ILs, clustered by research group.
The normal PDFs (bell-shaped curves) of SMP-related distance distributions—as probability density outputs defined consistently with Section 2.6.2 and based on the values of mean and SD from Table 6 (by using Statistics Kingdom freeware, repeatedly)—are presented in Figure 23 and Figure 24.
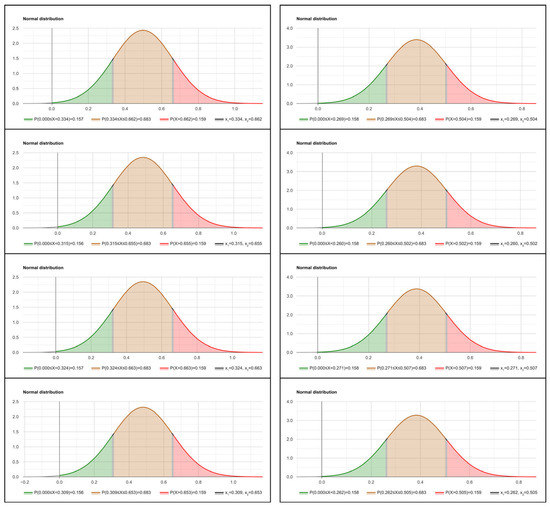
Figure 23.
Probabilistic outputs, graphically represented by brownish-colored areas under the corresponding normal PDFs: the EPs regarding the eight IRD-to-REF comparisons (top–bottom, left–right).

Figure 24.
Probabilistic outputs, graphically represented by brownish-colored areas under the corresponding normal PDFs: the EPs regarding the two ARD-to-REF comparisons and one ION-to-REF comparison (left–right).
Accordingly, the probabilistic outputs concerning the EP—calculated consistently with the same Section 2.6.2, or more specifically, with the principle demonstrated in Figure 10 and relying on the pairs of EP-related bounds from Table 6—are graphically represented by corresponding brownish-colored areas under these normal PDFs. The EPs represented in this way and concerning the eight IRD-to-REF comparisons are shown in Figure 23.
The remaining EPs represented so, but concerning the two ARD-to-REF comparisons and one ION-to-REF comparison, are shown in Figure 24.
3.2. Final Results
The pair of AP-related bounds, i.e., APLB (x̅1-score) and APUB (x̅2-score), as well as IL between them—obtained based on the set of eight IRD-to-REF comparisons consistently with Section 2.6.2—are listed in Table 7.

Table 7.
Pair of AP-related bounds and in-between IL relying on the set of eight IRD-to-REF comparisons.
The probabilistic outputs concerning the AP—calculated consistently with Section 2.6.2, or more specifically, with the principle demonstrated in Figure 10 and relying on the pair of AP-related bounds from Table 7 (by using Statistics Kingdom freeware, repeatedly)—are graphically represented by brownish-colored areas under the corresponding normal PDFs among those already defined and presented in Section 3.1.4. The APs represented like so under the corresponding normal PDFs taken from Figure 23, relating thus to the eight IRD-to-REF comparisons, are shown in Figure 25.
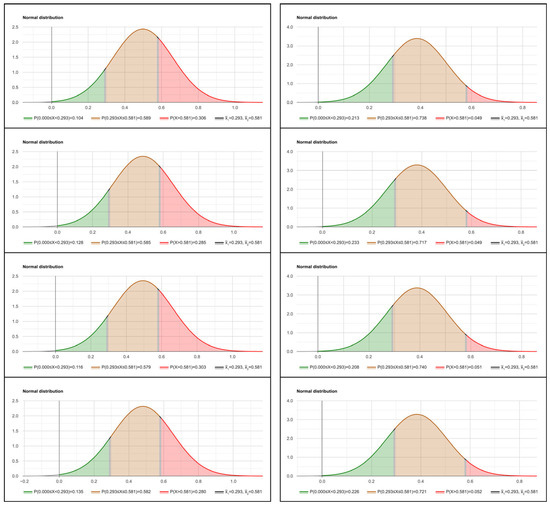
Figure 25.
Probabilistic outputs, graphically represented by brownish-colored areas under the corresponding normal PDFs: the APs regarding the eight IRD-to-REF comparisons (top–bottom, left–right).
The remaining APs represented so, but under the corresponding normal PDFs taken from Figure 24, relating thus to the two ARD-to-REF comparisons and one ION-to-REF comparison, are shown in Figure 26.

Figure 26.
Probabilistic outputs, graphically represented by brownish-colored areas under the corresponding normal PDFs: the APs regarding the two ARD-to-REF comparisons and one ION-to-REF comparison (left–right).
When it comes to the outputs of a probability-based discrimination, i.e., an indirect stylistic assessment, the eleven values of EP, namely, of AP—taken from Figure 23 and Figure 24, namely, from Figure 25 and Figure 26, wherein they were initially disclosed—are listed for each mesh-to-mesh comparison in Table 8, along with the associated RMSEs (calculated consistently with Section 2.6.2—by using Excel), given relative to the value of 0.2 as adopted threshold.

Table 8.
Per-comparison values of EP, AP, and RMSE, clustered by research group.
4. Discussion
4.1. Interpreting and Valorizing Intermediate Results
4.1.1. Comparison-Based Color-Coding
By observing the eight SFs represented by 3D color maps in Figure 11 (related to the eight IRD-to-REF comparisons), a certain similarity between the ways corresponding SFs are color-coded becomes noticeable with respect to the subtype of which the capital being compared is. Namely, among the IRD(1–4) diagrammatic representatives on one side, and among the IRD(5–8) diagrammatic representatives on the other, it is evident that corresponding SF parts share hue besides being properly assigned the associated tints (relative to the magnitudes of CDs), which is a consequence of choosing IRD capitals to be of the Denticulated/Mutulary subtype, respectively.
Moreover, the bluish SF parts from the first quartet of IRD diagrammatic representatives (1–4) mainly correspond to the reddish ones from the second quartet of IRD diagrammatic representatives (5–8), and vice versa (see Figure 11). Additionally, for each of the eight SFs, a more saturated color was applied in favor of the blue hue (regardless of the Denticulated/Mutulary dichotomy), indicating that the deviations inward from the REF (regarding the Control group members) are characterized by greater magnitudes of CDs in comparison with the outward such deviations. As expected, the IRD representatives deviate more significantly from the REF individually since the capitals which they represent were chosen as polarized entities in terms of Denticulated/Mutulary dichotomy—in order that the REF, obtained by “averaging” them, faithfully depicts Doric characteristics, including the entire range of morphologies in between.
Following the analogy, besides the eight SFs discussed above, by observing both SFs that relate to the ARD-to-REF comparisons (from the 1st Experimental group), the similarity by means of way corresponding SF parts are color-coded becomes noticeable between them as well (see Figure 12). Moreover, in accordance with the fact that the more congruent the compared diagrammatic representative with the REF is, the less saturated the color mapped to the corresponding SF will be—both of them are pretty whitish. The significantly acceptable matching of both ARD diagrammatic representatives to the REF, besides indicating that the members of the 1st Experimental group are likely to belong to the Doric order, confirms that the REF faithfully represents that order, i.e., that the eight IRD capitals used for its creation constitute a representative SMP of capitals.
On the other hand, it is noticeable that the ION diagrammatic representative (from the 2nd Experimental group) significantly differ from both the IRD and the ARD representatives by means of subject-related color-coding (see Figure 11, namely, Figure 12, respectively), which confirms that the approach is sensitive to style variation, or in other words, that it is unlikely that the claim that something belongs to the Doric order can be confirmed by representatives of other architectural orders, i.e., styles. Also, whereas gradual gradients reflect smooth transitions in magnitudes of CDs, telling of consistent variations, sharp contrasts in coloring indicate abrupt morphological differences, potentially pointing out key inconsistencies.
4.1.2. Reduction-Wise Outputs and Distance Frequencies
When it comes to the reduction-wise outputs presented in Section 3.1.2, the ranges, means, and SDs concerning the POPs (i.e., the reduced datasets of TDs) turned out to be quite well preserved for each mesh-to-mesh comparison with respect to the initial such values concerning the corresponding datasets of TDs (see Table 4). Moreover, as presented in Section 3.1.3, or more specifically, in Table 5, RRs, all being about 55% (ranging from 55.02% to 55.86%), indicate that the datasets of TDs are quite consistently reduced.
The histograms presented in Figure 17 and Figure 18 are the only frequency histograms being discussed herein since they, by showing the relationships between the distributions of POP-related distances and those of squared such distances, solitarily convey the quantitative information about the actual (non-transformed) values of measured mesh-to-mesh distances.
Based on the aforementioned histograms, an extreme value of squared POP-related distances can be identified for each of the eight IRD-to-REF comparisons, namely, for both of the ARD-to-REF comparisons as well as the ION-to-REF one. So, for the first quartet of IRD-to-REF comparisons (1–4), such an extreme value ranges from 0.723 cm to 0.728 cm, whereas for the second quartet of IRD-to-REF comparisons (5–8), it ranges from 0.416 cm to 0.441 cm (see Figure 17), pointing out that by being compared to the REF, diagrammatic representatives of the Control group induce a set of preferred such extremes (ranging from 0.416 cm to 0.728 cm).
Accordingly, the fact that for ARD-to-REF comparisons, such a value ranges from 1.147 cm to 1.207 cm (see Figure 18) indicates that the diagrammatic representatives of the 1st Experimental group (and thus, the source capitals which they represent) could not likely be of the Roman Doric order. Nevertheless, it turns out to be the opposite if an extreme distance value related to the ION-to-REF comparison is taken into account, since it is much more significantly outside the mentioned range of preferred extremes (10.309 cm >> 0.728 cm), even more than fourteenfold.
Following the analogy, similar specificities arise when it comes to an interval of frequently occurring distances. Specifically, as Figure 17 shows, for the first quartet of IRD-to-REF comparisons (1–4), such an interval ranges from 0.025 cm, namely, from 0.050 cm, to 0.300 cm (wherein an extreme frequency reaches the value between 9500 and 10,500). In contrast, for the second quartet of IRD-to-REF comparisons (5–8), it ranges from 0.025 cm to 0.275 cm (wherein an extreme frequency reaches the value between 15,000 and 15,500), pointing out that by being compared to the REF, diagrammatic representatives of the Control group induce a preferred such interval (ranging from 0.025 cm to 0.300 cm).
Accordingly, the fact that for ARD-to-REF comparisons such an interval, as shown in Figure 18, ranges from 0.000 cm to 0.575 cm (wherein an extreme frequency reaches the value between 7500 and 8000), indicates again that the diagrammatic representatives of the 1st Experimental group (and thus, the source capitals which they represent) could not likely be of the Roman Doric order. Nevertheless, it turns out to be the opposite again if an interval of frequently occurring distances related to the ION-to-REF comparison is taken into account, since it is much more significantly larger than the mentioned preferred interval, even more than elevenfold (ranging from 0.000 cm to 3.250 cm and reaching the extreme frequency of about 8000).
4.1.3. Distribution Normality and Size Adequacy
The normal Q–Q plots, presented in Figure 19b and Figure 20b, show that the data points of SMP-related quantiles (plotted against the normal/theoretical quantiles) are quite well aligned with the associated identity lines surrounded by 95% CBs. In other words, compared sets of estimated/actual quantiles (defined for each of the eleven comparisons) form approximate lines that are roughly straight, proving that the corresponding distance distributions (actual ones) are of the normal/Gaussian type. Some minor deviations from these lines, visible at their ends, are not significant, because they exist mainly inside and to a much lesser extent slightly outside the corresponding fat-pencil regions.
The same applies to biases present in the form of less or more noticeable deviations from normal PDFs fitted in the corresponding density histograms presented in Figure 19a and Figure 20a. Neglecting these biases, the mentioned histograms show that the SMP-related distribution densities are mainly conformed with the associated normal PDFs—additionally proving that the subject-related distributions are of the desired type.
Accordingly, SLR model-based line fit plots, presented in Figure 21 and Figure 22, show that the data points of SMP-related normal/theoretical z-scores (plotted against the SMP-related distances) are also quite well aligned with the associated regression lines. Moreover, distribution normality of SMP-related distances is confirmed by the values of r2 as well, all of which exceed even 0.98 (ranging from 0.9850 to 0.9938), as listed in Table 5, indicating thus that the mentioned regression lines approximate actual distance data very well, so that outputs can be stated statistically reliable (conventionally, r2 > 0.8 tells of very strong correlation between the variables, i.e., strong goodness-of-fit).
When it comes to the size adequacy (sufficiency and conformity), Table 5 also shows that POPSizes are all greater than the value of 128,062, which ensured that the corresponding recommended SMPSizes amount to 384. Accordingly, since all of the real SMPSizes are greater than the recommended (ranging from 385 to 388), the subject-related sufficiency is confirmed. Additionally, SMPPercentage, stemming from the SMPSize-to-POPSize relationship, amounts to 0.28% across all eleven comparisons (see Table 5), proving the subject-related conformity, i.e., indicating that the SMPSizes are perfectly balanced to each other, so that they can be considered equitable and treated equally from the statistical POV. Thereby, the “rigid” statistical adequacy (in terms of size) of the extracted SMPs is also proved.
4.1.4. Statistical Parameters of “Gaussian” Datasets
Regarding the values of SMPSDs listed in Table 6, it is obvious that they are for all the eight IRD-to-REF comparisons, as well as both ARD-to-REF ones, pretty balanced and much lower than 0.5 cm, even than 0.25 cm (ranging from 0.117 cm to 0.178 cm), whereas the only one excessive SD value of 0.661 cm evidently refers to the ION-to-REF comparison, indicating significantly greater dispersion of the associated distances in relation to the corresponding SMPMean. Because that value is greater than 0.5 cm, the ION-to-REF comparison shows that the vertices of the ION diagrammatic representative (mesh) are significantly more distant from the REF than they should be from the statistical POV (based on the mentioned pretty balanced values of the remaining SDs).
According to the values of SMPMeans, listed in the same Table 6, for all the eight IRD-to-REF comparisons, including both ARD-to-REF ones, it is obvious that those values are small, i.e., relatively close to zero (ranging from 0.381 cm to 0.522 cm), thus indicating the large subject-related closeness/compatibility of the IRD and the ARD diagrammatic representatives to/with the REF (in terms of the investigated distances), unlike the ION diagrammatic representative, whose comparison-wise SMPMean is more than threefold further, or more specifically, even 1.582 cm away from the unattainable zero value (i.e., from the perfect matching).
Additionally, the values of EPILs, listed in the same Table 6, strongly support all the preceding considerations: they are less than 0.5 cm for all eight IRD-to-REF comparisons, including both ARD-to-REF ones (ranging from 0.235 cm to 0.357 cm), whereas that value for the ION-to-REF comparison is much higher (1.322 cm). Consequently, about 68.27% of its SMP-related distances are, from the statistical POV, distributed along the much more “lengthy” ±1 SD interval, or in other words, are significantly dispersed (in contrast to the remaining comparisons whose associated distances are “condensed”). This expresses the significant level of discrepancy between the ION diagrammatic representative and the REF in another way.
All the aforementioned are depicted by the eleven normal PDFs (see Figure 23 and Figure 24) under which the corresponding EPs are graphically represented by brownish-colored areas. One should be aware of the fact that their mutual comparison and interpretation are a little bit difficult since x-scaling differs from case to case.
4.2. Interpreting and Valorizing Final Results
With regard to all the mentioned above, it can be underlined that for any comparison of two diagrammatic representatives, based on processing the SMP of their distances that are normally distributed, each of the previously investigated parameters of morphology-wise and statistics-wise nature can be declared specific qualifier/quantifier usable for the general stylistic discrimination (“on first sight”). Namely, according to their values, it is obvious that such parameters concerning the ARD(1)-to-REF and ARD(2)-to-REF comparisons are (as it was expected) similar to those that relate to all eight IRD-to-REF comparisons, whereas the ones concerning the ION-to-REF comparison are significantly excessive.
The outcomes of the probability-based discrimination (stylistic assessment), based on the “strict” discrimination criterion and the associated values that are in the form of relevant RMSEs (as described in Section 2.6.2), are summarized in Table 8. It is obvious that RMSEs concerning both of the ARD-to-REF comparisons are smaller than 0.2 (0.15 and 0.14), as is the case with all eight IRD-to-REF comparisons, whereas that value regarding the ION-to-REF comparison significantly exceeds the mentioned threshold (0.64 > 0.2). Thereby, this criterion discriminated the ION-to-REF comparison—as an “improper” or “unacceptable” one from the subject-related POV—in favor of comparisons of the 1st Experimental group (ARD(1)-to-REF and ARD(2)-to-REF).
Finally, by utilizing the demonstrated RMSE parameter, it became possible to assess how likely the concrete capital (expressed by its diagrammatic representation), whose stylistic affiliation is being validated (based on the known REF and its relating parameters introduced herein), is of the assumed order (represented by that REF). Because a CL of 95% was used for probabilistic calculations, one can be 95% sure of the validity of the assessment performed by implementing the proposed methodology.
In accordance with the fact that the smaller the value of AP is, the smaller the possibility that the corresponding capital (3D model) can be declared a member of the assumed order, the same conclusions could be drawn while observing the eleven normal PDFs under which the corresponding APs are graphically represented by brownish-colored areas (see Figure 25 and Figure 26).
Nevertheless, regardless of the effective discrimination criteria defined, some limitations of the presented approach still exist. Namely, by comparing a diagrammatic representative of a particular capital, assumed to belong to the specific architectural order, with the one which represents that order entirely—the degree of adherence to the corresponding canon cannot be assessed (despite that only the capitals that strictly follow the canon ought to be used for generating such diagrammatic representative of the entire order). Thus, one should be careful during the subject-related analysis in order to avoid consequent (possible) conclusion biases: if the examined capital adheres to the canon of the assumed architectural order, it does not necessarily mean that it belongs to that order, and vice versa, if it is confirmed that the examined capital belongs to the assumed architectural order, it does not imply its full adherence to the prescribed canon.
The mentioned reasoning assertion in the form of implication (not equivalence) can be explained by taking into account the nature of the applied methodology-wise logic of transposing the dynamics-wise distribution’s broken-line expressions (whose predominant peaks correspond to the boundaries of the inner capital zones) into the corresponding substituting trendlines (as explained in Section 2.4.1), resulting in a loss of sensitivity to canon adherence. Consequently, one might declare examined capital a member of the assumed order, although it locally slightly deviates from the canon of that order, as long as it globally (morphologically) reflects characteristics of the capitals thereof. However, the mentioned transposing was performed herein on purpose—being aware of the fact that (according to the aim of this study) its effect described could not have any unexpected influence on the reliability of the results obtained.
5. Conclusions
This research set out to develop a cost-efficient and statistically grounded methodology for the stylistic assessment and validation of architectural heritage artifacts, with a focus on column capitals of the Roman Doric order. Recognizing the limitations of traditional visual or descriptive assessments, the study proposed an innovative, morphology-based approach that leverages digital processing of diagrammatic representations derived from 3D models. By utilizing widely affordable software, it was ensured that the proposed workflow is broadly applicable.
The methodology involved generating parametric models of capitals based on canonical proportional rules and morphologically significant features, followed by the extraction of substituting-circle perimeters across transverse sections. These perimeter dynamics were then used to generate diagrammatic representatives—revolving surfaces (meshes) that captured the essential morphological characteristics of capitals. Moreover, by diagrammatically expressing capital’s morphology, it turned out to be possible not only to numerically encode particular capital’s stylistic regularities (peculiarities), but to compare them to those of order’s representatives, estimating thus intra- or inter-order relations.
Mesh-to-mesh comparisons enabled quantitative (statistical) assessments through analyses of in-between distances. Distributions of such distances induced normal probabilities capable of “inferring” whether the analyzed capital could likely be a member of the assumed order. Additionally, each of the comparisons employed a 3D color map to represent the magnitudes of computed distances, effectively visualizing discrepancies between diagrammatic representatives, in terms of morphology. Those maps ensured that both the geometrical cross-analyses and the associated metrics behind them are easily interpreted. Such interpretations facilitate the identification of regions in the models where geometric alignment is strong or weak, informing both the degree and the spatial localization of morphological discrepancies.
The results confirmed the validity of the proposed approach. Moreover, the diagrammatic representatives enabled reliable statistical assessments of stylistic affiliation, even among capitals that differed in ornamentation and proportion. The eight indisputable Doric capitals displayed strong statistical alignment with the reference entity. Additionally, the two assumed Doric capitals (1st Experimental group) also demonstrated a high degree of morphological congruence, suggesting their likely stylistic affiliation.
Conversely, the Ionic capital used as a non-Doric example (2nd Experimental group) deviated significantly in both geometric and statistical terms, reinforcing the method’s sensitivity to stylistic variation. Such a non-affiliation of the Ionic capital to the assumed Doric order proved that the methodology was correctly set up, as well as the fact that a style-belonging assessment can be performed confidently.
The scientific contributions of this research can be divided into three groups:
- Theoretical;
- Methodological;
- Practical.
The theoretical contribution—in addition to the systematic presentation and use of the relevant literature and sources—refers to the possibility of architectural heritage digitization and digital archiving, which is of great importance for future research in protecting and preserving architectural heritage.
The methodological contribution is reflected in the newly defined methodology for determining the affiliation of a specific and, in practice, existing column capital to a particular architectural order. The defined methodology has the potential to be applied to other architectural orders, representing the direction of further research.
The practical contribution of this research paper is about more than just comparing the current state of the column in situ with its ideal and canonically defined characteristics. It is about using this comparison to guide future measures of technical protection in situ (revitalization, conservation, restoration, and anastylosis) that align with the diagrammatically defined canon. This approach ensures the preservation of the principles of authenticity, integrity, and value of the original, which are the fundamental principles in the field of protection and preservation of architectural heritage, contributing to cultural heritage praxis.
When it comes to the benefits of the approach presented herein, its universality ensures analyzing various artifact styles and kinds, whereas its applicability enables cost-efficient comparison and stylistic validation of diagrammatic expressions of artifact morphology. However, despite being effective for assessing overall morphological similarity and likely stylistic affiliation, the approach does not directly evaluate strict adherence to the canonical rules of an architectural order. Additionally, a broader validation, involving capitals from all five classical orders, is necessary to generalize the approach further.
In conclusion, the research successfully establishes a novel, reproducible, and cost-efficient methodology for digital stylistic assessment in architectural heritage, while advancing the discourse in computational heritage studies and digital humanities more broadly. The study is inventive in three key ways: (1) it transitions from traditional visual assessments to a computationally verifiable process grounded in geometry and statistics, (2) it offers a cost-efficient technique for generating and comparing morphological diagrams of artifacts, and (3) it demonstrates the viability of stylistic inference based on probabilities derived from normal distributions of mesh-to-mesh distances. The promising results suggest that the approach can be expanded for wider use in heritage documentation, conservation decision-making, and academic study. Future work should aim to extend the methodology to other classical orders, refine sensitivity to canonical variation, investigate how surface damage affects the reliability of the proposed approach, and explore automation potentials as well as opportunities for integrating alternative statistical models into the established workflow.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/buildings15173147/s1, Figure S1: Workflow of the methodological process. Figure S2: Visually coded GH algorithm employed for automating repetitive tasks.
Author Contributions
Conceptualization, D.M. and D.D.; methodology, D.M., D.D., M.D., M.N., J.Š. and J.I.; software, D.M., M.D. and J.I.; validation, M.D., M.N. and J.I.; formal analysis, D.M., D.D. and J.I.; investigation, D.M., D.D., M.N. and J.Š.; resources, D.M. and J.Š.; data curation, D.M. and J.Š.; writing—original draft preparation, D.M., D.D. and J.Š.; writing—review and editing, M.D., M.N. and J.I.; visualization, D.M.; supervision, D.D. and M.N.; project administration, D.M. and D.D.; funding acquisition, M.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia, grant number 200090.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
This investigation was performed at the University of Belgrade, Faculty of Architecture, within the research unit for research, valorization, protection, and revitalization of cultural heritage (PVZR).
Conflicts of Interest
The authors declare no conflicts of interest. The funder had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| AP | Aspirational probability |
| ARD | Assumed Roman Doric |
| CB | Confidence band |
| CC | CloudCompare |
| CD | Computed distance |
| Absolute value of computed distance | |
| CL | Confidence level |
| DPC | Dynamics of perimeter change |
| Dynamics of averaged perimeter change | |
| EP | Expected probability |
| GH | Grasshopper |
| IL | Interval length |
| ION | Ionic |
| IRD | Indisputable Roman Doric |
| LB | Lower bound |
| Probability density function | |
| POP | Population |
| POV | Point of view |
| PSC | Perimeter of substituting circle |
| Q–Q | Quantile–quantile |
| r2 | Coefficient of determination |
| REF | Reference entity |
| RMSE | Root-mean-square error |
| RR | Reduction rate |
| SD | Standard deviation |
| SF | Scalar field |
| SLR | Simple linear regression |
| SMP | Sample |
| TDC | Transformed dynamics of (averaged) perimeter change |
| TD | Transformed absolute value of computed distance |
| TSS | Transverse-slicing step |
| UB | Upper bound |
| VS Code | Visual Studio Code |
References
- Dev, K.; Kim, K.; Villar, N.; Lau, M. Improving Style Similarity Metrics of 3D Shapes. In Proceedings of the 42nd Graphics Interface Conference, Graphics Interface 2016, Victoria, BC, Canada, 1–3 June 2016; pp. 175–182. Available online: https://graphicsinterface.org/proceedings/gi2016/gi2016-22/ (accessed on 25 July 2025).
- Osada, R.; Funkhouser, T.; Chazelle, B.; Dobkin, D. Matching 3D Models with Shape Distributions. In Proceedings of the International Conference on Shape Modeling and Applications, Genova, Italy, 7–11 May 2001; pp. 154–166. Available online: https://ieeexplore.ieee.org/document/923386/ (accessed on 25 July 2025).
- Azouz, Z.B.; Rioux, M.; Shu, C.; Lepage, R. Characterizing Human Shape Variation Using 3D Anthropometric Data. Vis. Comput. 2006, 22, 302–314. [Google Scholar] [CrossRef]
- Azouz, Z.B.; Rioux, M.; Lepage, R. 3D Description of the Human Body Shape: Application of Karhunen-Loève Expansion to the CAESAR Database. In CARS 2002 Computer Assisted Radiology and Surgery; Lemke, H.U., Inamura, K., Doi, K., Vannier, M.W., Farman, A.G., Reiber, J.H.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 571–576. [Google Scholar]
- Cui, J.; Zang, M.; Liu, Z.; Qi, M.; Luo, R.; Gu, Z.; Lu, H. BIM Product Style Classification and Retrieval Based on Long-Range Style Dependencies. Buildings 2023, 13, 2280. [Google Scholar] [CrossRef]
- Austern, G.; Bloch, T.; Abulafia, Y. Incorporating Context into BIM-Derived Data—Leveraging Graph Neural Networks for Building Element Classification. Buildings 2024, 14, 527. [Google Scholar] [CrossRef]
- Siountri, K.; Anagnostopoulos, C.-N. The Classification of Cultural Heritage Buildings in Athens Using Deep Learning Techniques. Heritage 2023, 6, 3673–3705. [Google Scholar] [CrossRef]
- Luo, S.; Shang, W.; Yan, Z.; Bi, S. Research on Factors Influencing the Style of Chinese Historic Districts Based on the Mask R-CNN Deep Learning Model. Buildings 2024, 14, 420. [Google Scholar] [CrossRef]
- Shan, L.; Zhang, L. Application of Intelligent Technology in Facade Style Recognition of Harbin Modern Architecture. Sustainability 2022, 14, 7073. [Google Scholar] [CrossRef]
- Lian, Y.; Xie, J. The Evolution of Digital Cultural Heritage Research: Identifying Key Trends, Hotspots, and Challenges through Bibliometric Analysis. Sustainability 2024, 16, 7125. [Google Scholar] [CrossRef]
- Barrios Hernandez, C.R. Thinking Parametric Design: Introducing Parametric Gaudi. Des. Stud. 2006, 27, 309–324. [Google Scholar] [CrossRef]
- Katifori, A.; Antoniou, A.; Damala, A.; Raftopoulou, P. Editorial for the Special Issue “Advanced Technologies in Digitizing Cultural Heritage”. Appl. Sci. 2023, 13, 5873. [Google Scholar] [CrossRef]
- Vitruvius Pollio, M. The Ten Books on Architecture (De Architectura Libri Decem); Morgan, M.H., Translator; Warren, H.L., Ed.; Harvard University Press: Cambridge, MA, USA, 1914. [Google Scholar]
- Vitruvius Pollio, M. On Architecture (De architectura); Bojić, Z., Translator; Bojić, Z., Ed.; Textbook Institute, Dosije Studio: Belgrade, Serbia, 2009. (In Serbian) [Google Scholar]
- Vitruvius Pollio, M. The Ten Books on Architecture (De Architectura Libri Decem); Lopac, M., Translator; Jadrešin-Milić, R., Ed.; Orion Art: Belgrade, Serbia, 2014. (In Serbian) [Google Scholar]
- Jadrešin-Milić, R. Aktuelnost Vitruvijeve teorije arhitekture. In The Ten Books on Architecture (De Architectura Libri Decem); Lopac, M., Translator; Jadrešin-Milić, R., Ed.; Orion Art: Belgrade, Serbia, 2014; pp. I–XXVII. (In Serbian) [Google Scholar]
- Chitham, R. The Classical Orders of Architecture, 2nd ed.; Architectural Press: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Thoenes, C.; Byatt, L. Architectural Orders: Rebirth or Invention? Art Transl. 2017, 9, 296–311. [Google Scholar] [CrossRef]
- Serlio, S. General Rules of Architecture; Francesco Marcolini da Forli: Venice, Italy, 1537. (In Italian) [Google Scholar]
- Vignola, G.B. The Five Orders of Architecture (Regola Delli Cinque Ordini d’architettura); Juglaris, T.; Locke, W.S., Translators; Press of Berwick & Smith: Boston, MA, USA, 1889. [Google Scholar]
- Halstead, F. The Orders of Architecture; John Wiley & Sons: New York, NY, USA, 1927. [Google Scholar]
- Ware, W.R. The American Vignola: The Five Orders, 5th ed.; International Textbook Company: Scranton, PA, USA, 1925; Volume 1. [Google Scholar]
- Penjor, T.; Banihashemi, S.; Hajirasouli, A.; Golzad, H. Heritage Building Information Modeling (HBIM) for Heritage Conservation: Framework of Challenges, Gaps, and Existing Limitations of HBIM. Digit. Appl. Archaeol. Cult. Herit. 2024, 35, e00366. [Google Scholar] [CrossRef]
- Aubin, P.F. Renaissance Revit: Creating Classical Architecture with Modern Software; G3B Press: Oak Lawn, IL, USA, 2013. [Google Scholar]
- Spallone, R.; Vitali, M. Parametric Thinking: Recognizing the “Architectural Formulas” in Cultural Built Heritage by Parametric Digital Modelling. In Proceedings of the 2018 Metrology for Archaeology and Cultural Heritage (MetroArchaeo), Cassino, Italy, 22–24 October 2018; pp. 102–106. Available online: https://ieeexplore.ieee.org/document/9089745/ (accessed on 25 July 2025).
- Pepe, M.; Garofalo, A.R.; Costantino, D.; Tana, F.F.; Palumbo, D.; Alfio, V.S.; Spacone, E. From Point Cloud to BIM: A New Method Based on Efficient Point Cloud Simplification by Geometric Feature Analysis and Building Parametric Objects in Rhinoceros/Grasshopper Software. Remote Sens. 2024, 16, 1630. [Google Scholar] [CrossRef]
- Diara, F.; Rinaudo, F. Building Archaeology Documentation and Analysis through Open Source HBIM Solutions via NURBS Modelling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B2-2020, 1381–1388. [Google Scholar] [CrossRef]
- Zhang, K.; Fassi, F. Transforming Architectural Digitisation: Advancements in Ai-Driven 3D Reality-Based Modelling. Heritage 2025, 8, 81. [Google Scholar] [CrossRef]
- Alfio, V.S.; Costantino, D.; Pepe, M.; Restuccia Garofalo, A. A Geomatics Approach in Scan to FEM Process Applied to Cultural Heritage Structure: The Case Study of the “Colossus of Barletta”. Remote Sens. 2022, 14, 664. [Google Scholar] [CrossRef]
- Đorđević, Đ.; Đukanović, G.; Duta, A.; Devetaković-Radojević, M.; Popović, N. Point-Clouds as Photogrammetric Representations of Linear Objects Surfaces: The Impact of Extrinsic Shooting Parameters on the Change of Roughness-Quality of Their Textures. FME Trans. 2019, 47, 316–325. [Google Scholar] [CrossRef]
- Harshit, H.; Kushwaha, S.K.P.; Jain, K. Geometric Features Interpretation of Photogrammetric Point Cloud from Unmanned Aerial Vehicle. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, X-4/W2-2022, 83–88. [Google Scholar] [CrossRef]
- Milosz, M.; Kęsik, J.; Montusiewicz, J. Three-Dimensional Digitization of Documentation and Perpetual Preservation of Cultural Heritage Buildings at Risk of Liquidation and Loss—The Methodology and Case Study of St Adalbert’s Church in Chicago. Electronics 2024, 13, 561. [Google Scholar] [CrossRef]
- Sánchez-Aparicio, L.J.; Santamaría-Maestro, R.; Sanz-Honrado, P.; Villanueva-Llauradó, P.; Aira-Zunzunegui, J.R.; González-Aguilera, D. A Holistic Solution for Supporting the Diagnosis of Historic Constructions from 3D Point Clouds. Remote Sens. 2025, 17, 2018. [Google Scholar] [CrossRef]
- Spreafico, M.C.; Franci, F.; Bitelli, G.; Borgatti, L.; Ghirotti, M. Intact Rock Bridge Breakage and Rock Mass Fragmentation upon Failure: Quantification Using Remote Sensing Techniques. Photogramm. Rec. 2017, 32, 513–536. [Google Scholar] [CrossRef]
- Moyano, J.; Nieto-Julián, J.E.; Lenin, L.M.; Bruno, S. Operability of Point Cloud Data in an Architectural Heritage Information Model. Int. J. Archit. Herit. 2022, 16, 1588–1607. [Google Scholar] [CrossRef]
- Fattore, C.; Buldo, M.; Priore, A.; Porcari, S.; Porcari, V.D.; De Fino, M. A Comprehensive Overview of Heritage BIM Frameworks: Platforms and Technologies Integrating Multi-Scale Analyses, Data Repositories, and Sensor Systems. Heritage 2025, 8, 247. [Google Scholar] [CrossRef]
- Silva, C.; Oliveira, L. Artificial Intelligence at the Interface between Cultural Heritage and Photography: A Systematic Literature Review. Heritage 2024, 7, 3799–3820. [Google Scholar] [CrossRef]
- Gîrbacia, F. An Analysis of Research Trends for Using Artificial Intelligence in Cultural Heritage. Electronics 2024, 13, 3738. [Google Scholar] [CrossRef]
- Vo, A.-V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-Based Region Growing for Point Cloud Segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Cerio, D.G.; Witmer, L.M. Intraspecific Variation and Symmetry of the Inner-Ear Labyrinth in a Population of Wild Turkeys: Implications for Paleontological Reconstructions. PeerJ 2019, 7, e7355. [Google Scholar] [CrossRef]
- Loiotine, L.; Andriani, G.F.; Jaboyedoff, M.; Parise, M.; Derron, M.-H. Comparison of Remote Sensing Techniques for Geostructural Analysis and Cliff Monitoring in Coastal Areas of High Tourist Attraction: The Case Study of Polignano a Mare (Southern Italy). Remote Sens. 2021, 13, 5045. [Google Scholar] [CrossRef]
- Buldo, M.; Agustín-Hernández, L.; Verdoscia, C. Semantic Enrichment of Architectural Heritage Point Clouds Using Artificial Intelligence: The Palacio de Sástago in Zaragoza, Spain. Heritage 2024, 7, 6938–6965. [Google Scholar] [CrossRef]
- Janković Babić, R. A Comparison of Methods for Image Classification of Cultural Heritage Using Transfer Learning for Feature Extraction. Neural Comput. Appl. 2024, 36, 11699–11709. [Google Scholar] [CrossRef]
- Rashid, S.; Qasha, R. Cloud-Based Data Classification Framework for Cultural Heritage Conservation. In Proceedings of the GI-Edition: Lecture Notes in Informatics (LNI), INFORMATIK 2024, Wiesbaden, Germany, 24–26 September 2024; Volume P-352, pp. 973–983. Available online: https://dl.gi.de/handle/20.500.12116/45251 (accessed on 25 July 2025).
- Chen, B.; Wang, X. Artificial Intelligence for Cultural Heritage: Digital Image Processing-Based Techniques and Research Challenges. Int. J. Inf. Commun. Technol. 2025, 26, 37–60. [Google Scholar] [CrossRef]
- Hwang, H.; Park, C.-W.; Kim, H.-K.; Lee, J.-H. CATS: Cultural-Heritage Classification Using LLMs and Distribute Model. Npj Herit. Sci. 2025, 13, 76. [Google Scholar] [CrossRef]
- Vila Domini, D.A. The Diminution of the Classical Column: Visual Sensibility in Antiquity and the Renaissance. Nexus Netw. J. 2003, 5, 99–124. [Google Scholar] [CrossRef][Green Version]
- Frazer, J. Parametric Computation: History and Future. Archit. Des. 2016, 86, 18–23. [Google Scholar] [CrossRef]
- Khanzode, C.; Sarode, R. Advantages and Disadvantages of Artificial Intelligence and Machine Learning: A Literature Review. Int. J. Libr. Inf. Sci. IJLIS 2022, 9, 30–36. [Google Scholar] [CrossRef]
- Moshayedi, A.J.; Roy, A.S.; Kolahdooz, A.; Shuxin, Y. Deep Learning Application Pros and Cons Over Algorithm. EAI Endorsed Trans. AI Robot. 2022, 1, e7. [Google Scholar] [CrossRef]
- Tsimenidis, S. Limitations of Deep Neural Networks: A Discussion of G. Marcus’ Critical Appraisal of Deep Learning. arXiv 2020, arXiv:2012.15754. [Google Scholar] [CrossRef]
- De Luca, L.; Veron, P.; Florenzano, M. Reverse Engineering of Architectural Buildings Based on a Hybrid Modeling Approach. Comput. Graph. 2006, 30, 160–176. [Google Scholar] [CrossRef]
- De Luca, L.; Véron, P.; Florenzano, M. A Generic Formalism for the Semantic Modeling and Representation of Architectural Elements. Vis. Comput. 2007, 23, 181–205. [Google Scholar] [CrossRef]
- Mitrovic, D.; Djordjevic, D.; Devetakovic, M.; Djukanovic, G. Encoding/Decoding Capitals of Classical Architectural Orders by Using Fractal Geometry: Establishing Methodology. In Proceedings of the 9th International Scientific Conference on Geometry, Graphics and Design in the Digital Age, MoNGeometrija 2023, Novi Sad, Serbia, 7–10 June 2023; pp. 153–167. Available online: https://raf.arh.bg.ac.rs/handle/123456789/1628 (accessed on 25 July 2025).
- Mitrović, D.; Djordjević, D.; Devetaković, M.; Djukanović, G. Towards Numerical Architectural Order Identification: Expressing Capital Morphology by Using Dynamics of Its Parameters. In Proceedings of the International Conference Synergy of Architecture & Civil Engineering, SINARG 2023, Niš, Serbia, 14–15 September 2023; Volume 2, pp. 886–897. Available online: https://raf.arh.bg.ac.rs/handle/123456789/1639 (accessed on 25 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).