Experimental and Numerical Bearing Capacity Analysis of Locally Corroded K-Shaped Circular Joints
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Design
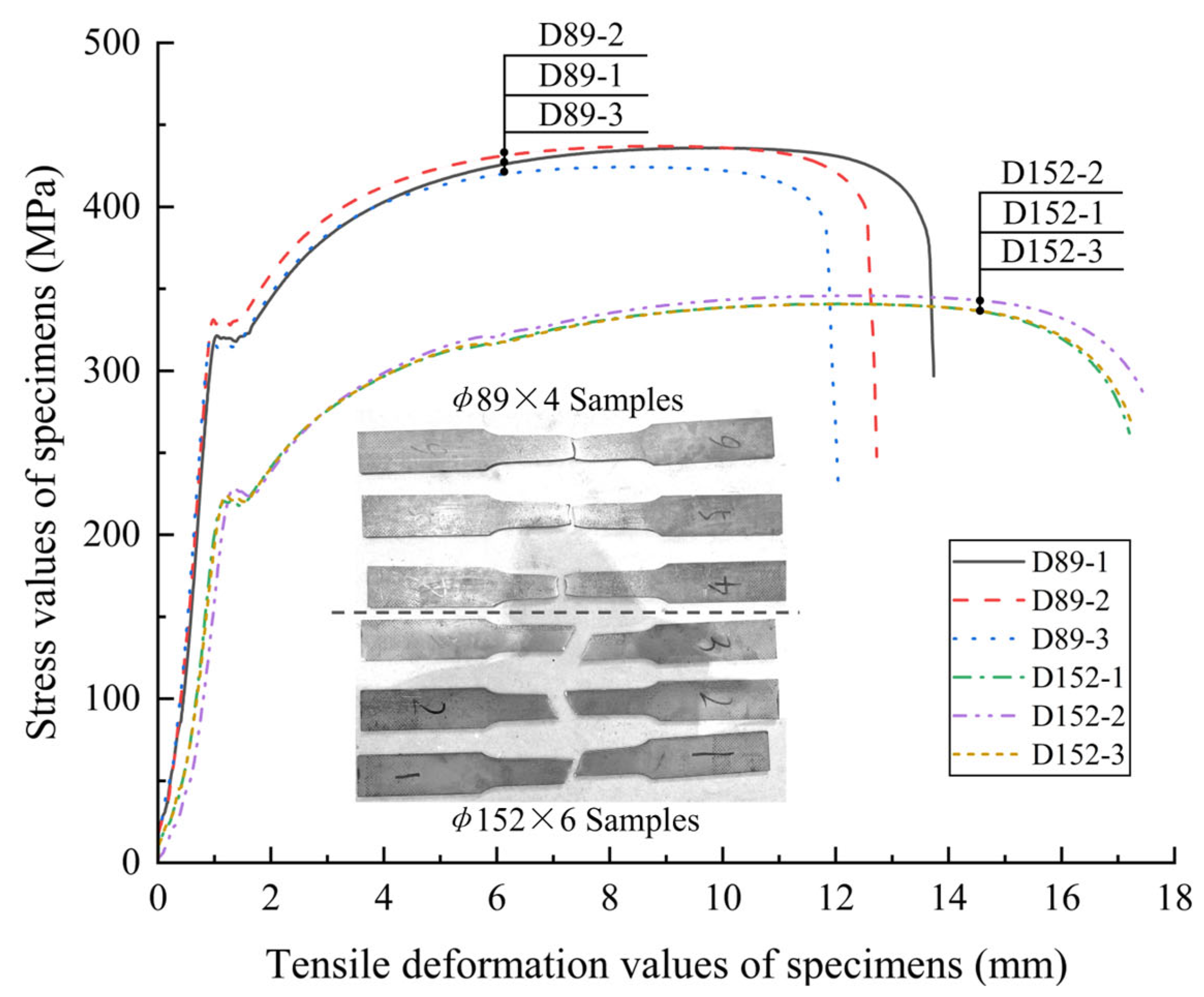
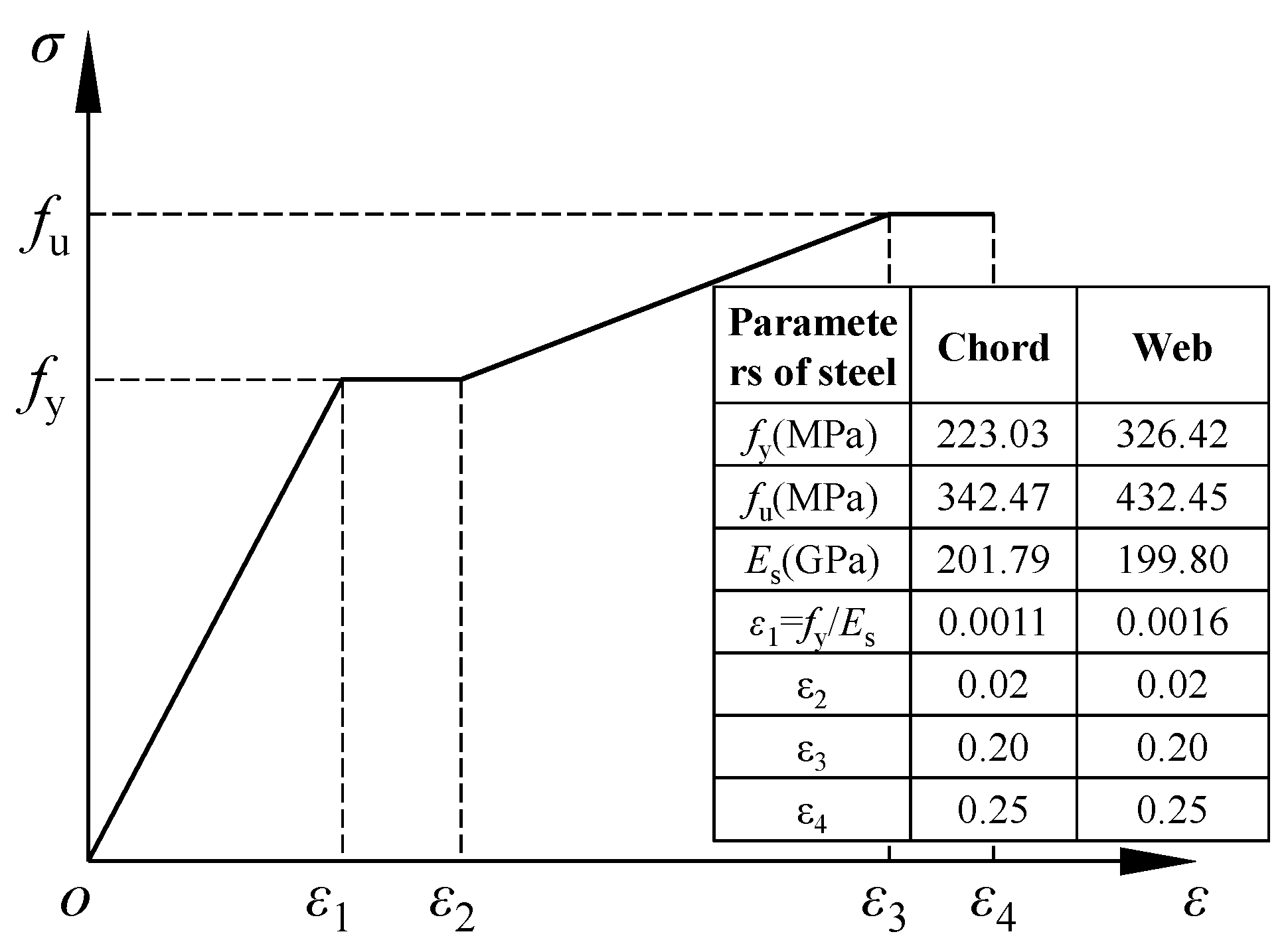
2.2. Material Performance Tests
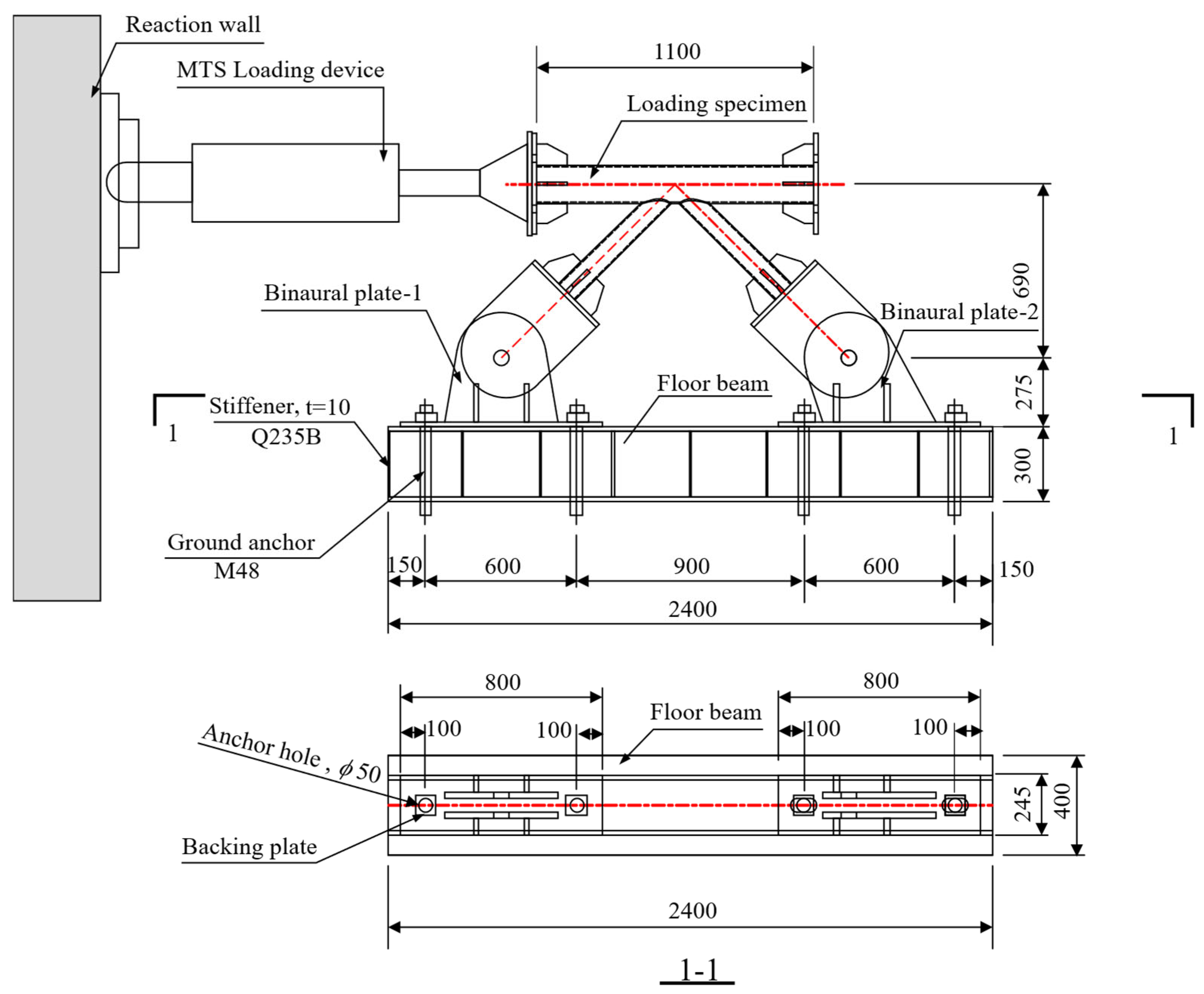
2.3. Test Setup and Loading Scheme
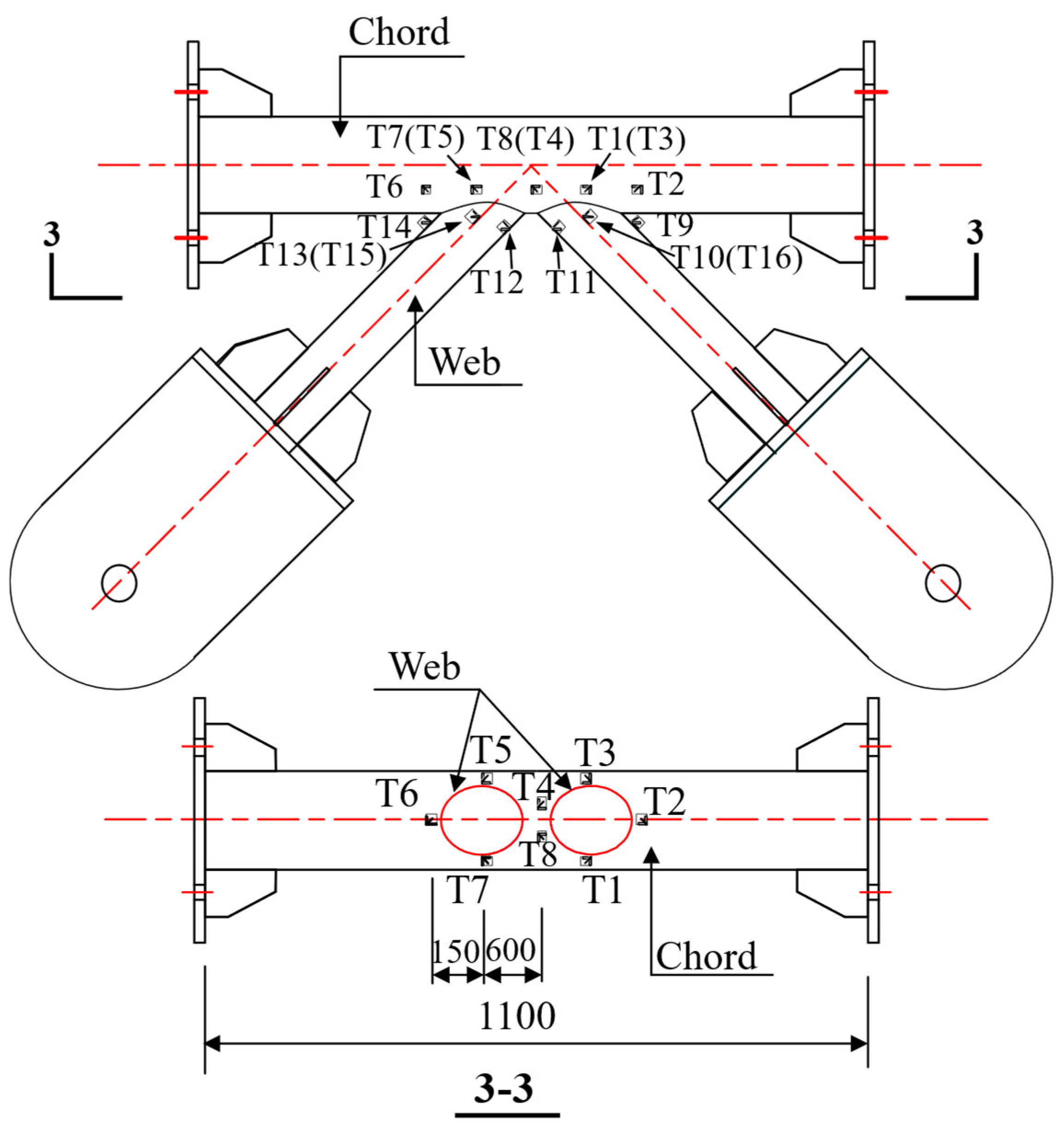
2.4. Nodal Zone Measurement Program
3. Results and Analysis of the Tests
3.1. Node Destruction Model
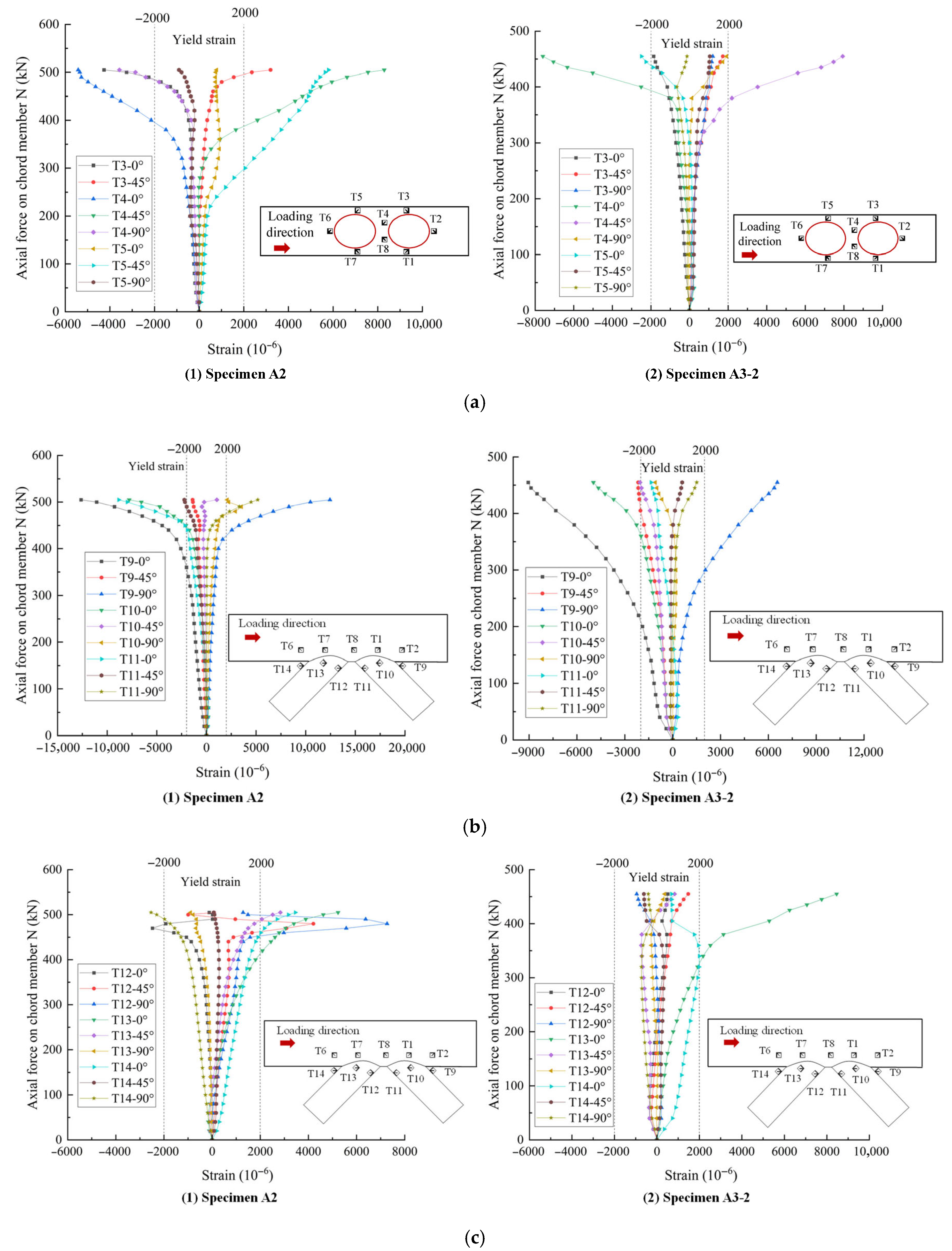
3.2. Strain Data for Joints
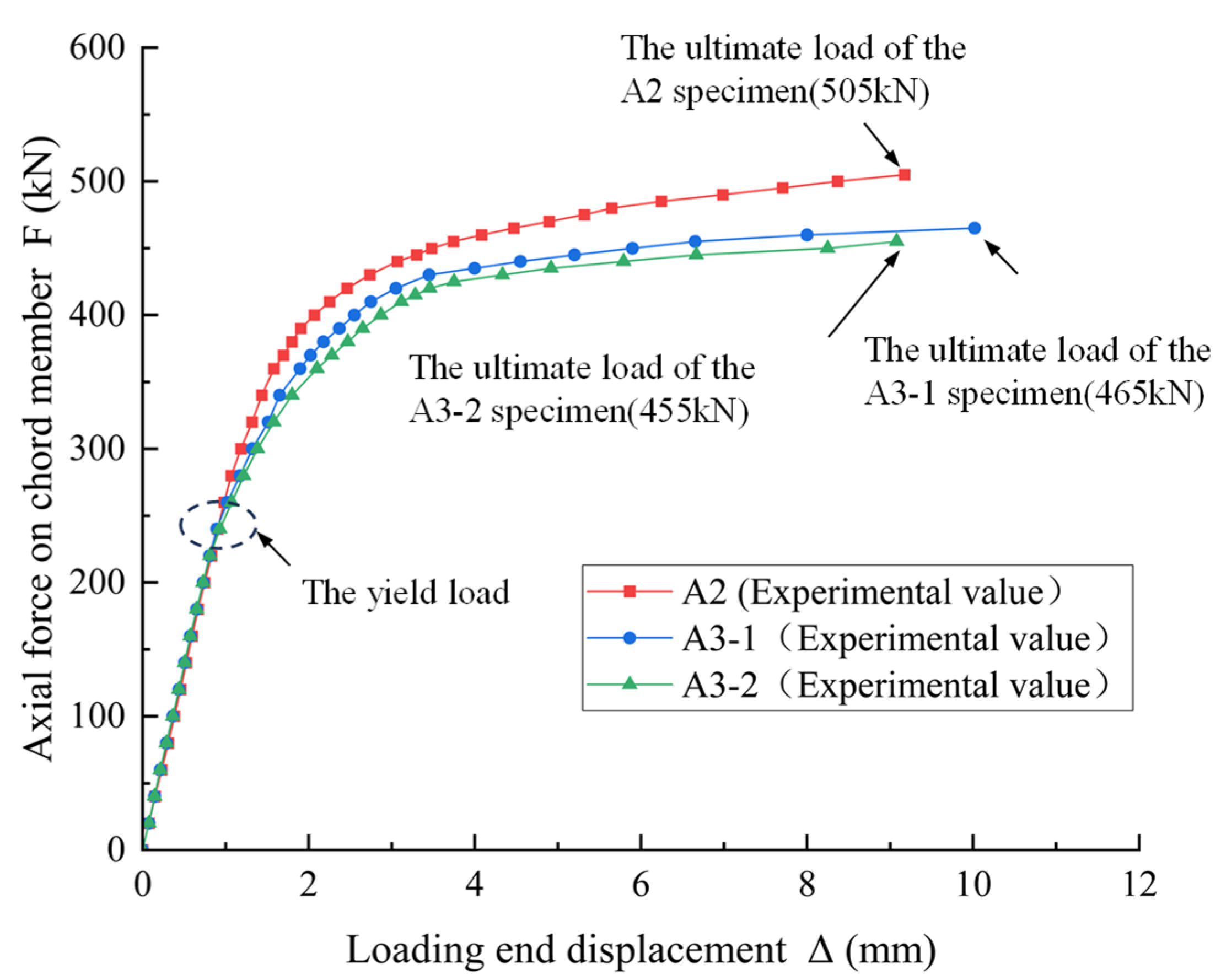
3.3. Load-Deflection Relationship of Nodes
4. Finite Element Analysis and Discussion
4.1. Finite Element Model
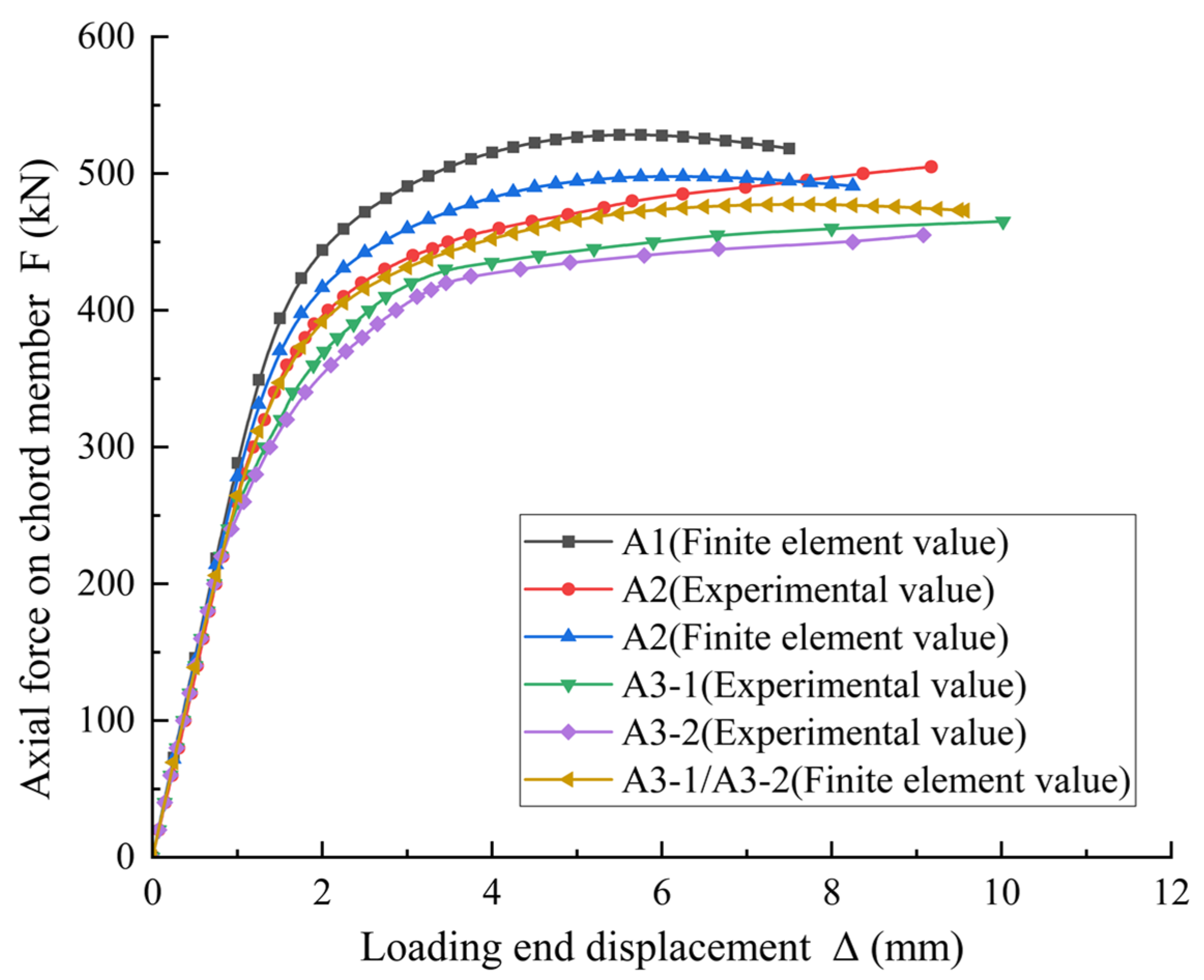
4.2. Finite Element Simulation Verification
4.3. Finite Element Parametric Analysis
- (1)
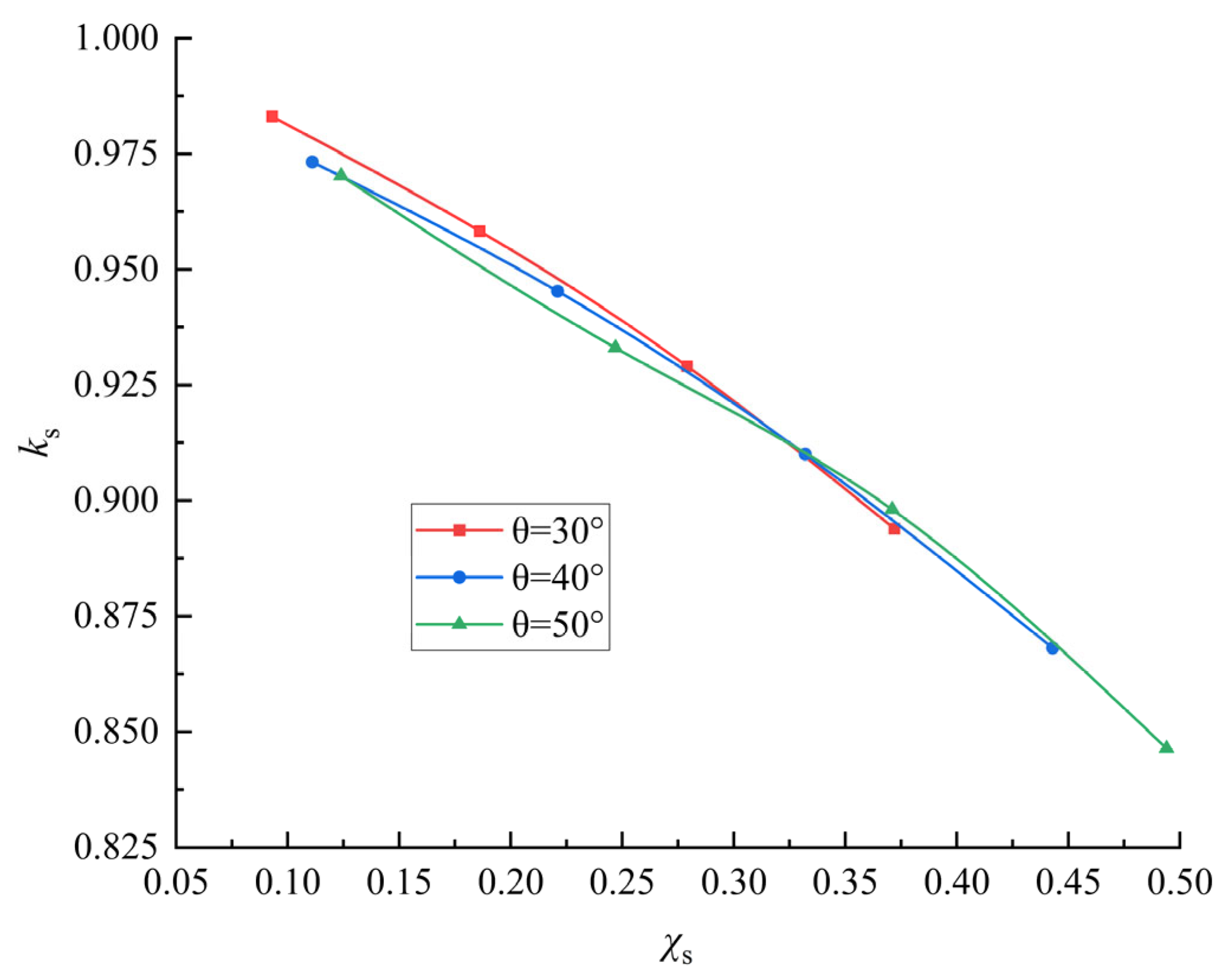
- The effect of the angle θ of the ventral chord clip
- (2)
- Influence of the diameter-to-thickness ratio γ of the stringers
- (3)
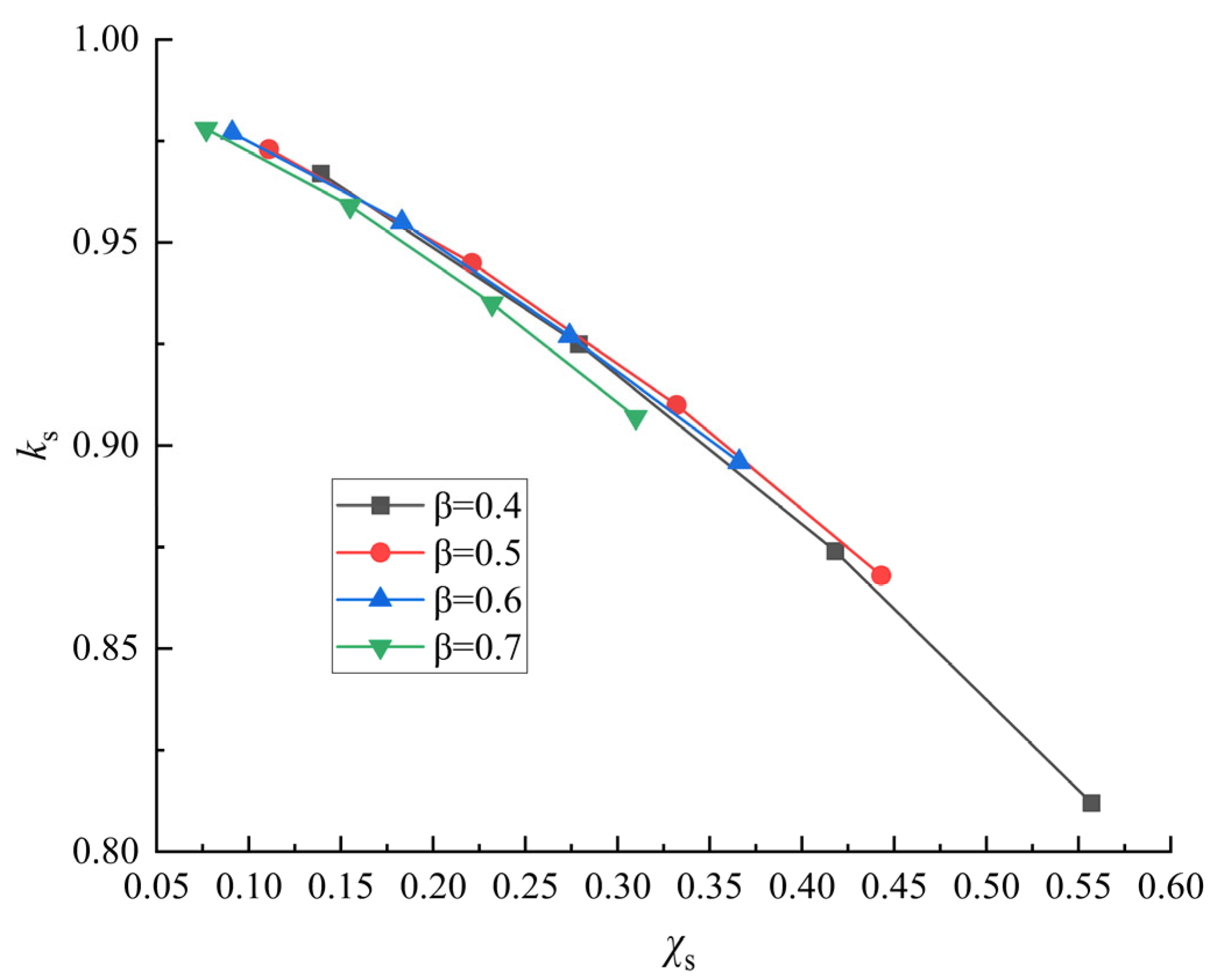
- Influence of the pipe diameter ratio β of the ventral chord bar
- (4)
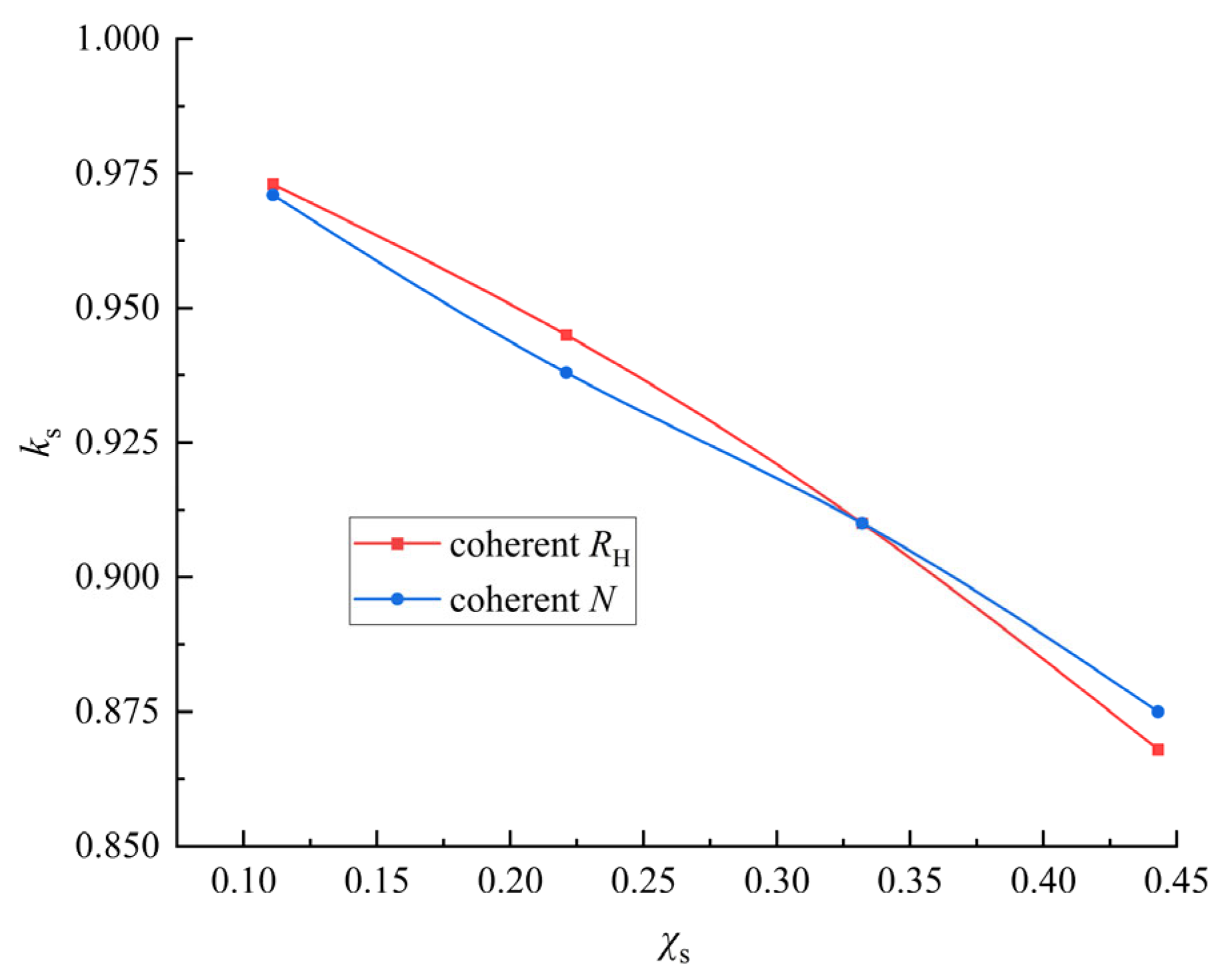
- Effect of the number and diameter of corrosion pits
5. Conclusions
- (1)
- Failure mode and corrosion impact. For the locally corroded nodes, the corrosion of the steel at the coherent line (simulated openings) reduced the effective bearing area and exacerbated the stress concentration. During the loading process, the node went through elastic and elasto-plastic stages. Finally, the weld at the connection between the chord and the tensile web fractured in a brittle manner, characterized by both tensile and shear failure, and the web dislodged, leading to node failure. This indicated that corrosion had caused significant damage to the mechanical properties of the node.
- (2)
- As the diameter of the corrosion pit increases, the node stiffness decreases, and the dispersion trend of the load-strain curve becomes increasingly pronounced. The stress concentration occurs at the crown point of the distal end of the compressed web bar, and the axial strain is the first to reach the yield limit. The strain development at different measurement points of the tensile web varies significantly.
- (3)
- Mechanical property degradation. When the load was less than 50% of the ultimate load capacity, the node was in the elastic stage, and a linear relationship existed between displacement and load. When the load reached 80%, the growth rate of displacement accelerated. Further, when the load reached the ultimate value, the weld between the chord and the tensile web fractured. Comparing the experimental results with the model calculation results, the average ratio is approximately 1.00, with a standard deviation of 0.06. The damage pattern and load–displacement curves are in high agreement, indicating that the model accurately predicts the load-bearing capacity of the coherent nodes in locally corroded K-shaped round tubes.
- (4)
- The results indicate that localized rusting significantly impacts the residual strength of the K-shaped circular pipe’s coherent nodes. The corrosion discount factor, ks, decreases with an increase in the coherent corrosion rate χs, indicating that a higher corrosion rate leads to greater loss of bearing capacity of the node. The resistance of the nodes to corrosion is weaker at smaller web chord angles θ, larger chord diameter-to-thickness ratios γ, and larger web chord tube diameter ratios β. Furthermore, an increase in the corrosion area, through an increase in the number or diameter of corrosion pits, also leads to a decrease in ks. The effect of a few large corrosion pits is usually greater than that of many small ones for the same total corrosion area.
- (5)
- Due to space limitations, this article only explores the impact of concentrated rust pits in the intersection area of K-shaped steel pipe joints on the degradation of their bearing capacity. However, in actual engineering, the distribution of rust pits typically exhibits significant randomness. In subsequent research, the author plans to perform an in-depth analysis of the degradation pattern of the bearing capacity of steel pipe joints caused by random pitting corrosion. Systematic research will establish a foundation for bearing capacity correction in existing standards and promote the improvement of relevant design theories and the optimization of engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shu, G.; Yu, G. Experimental study on the progressive collapse of spatial pipe truss structures. Prog. Steel Build. Struct. 2015, 17, 7. [Google Scholar]
- Koch, G.H.; Thompson, N.G.; Moghissi, O.; Payer, J.H.; Varney, J. IMPACT (International Measures of Prevention, Application, and Economics of Corrosion Technologies Study); Report No. OAPUS310GKOCH (AP110272); NACE International: Houston, TX, USA, 2016. [Google Scholar]
- Kaita, T.; Appuhamy, J.; Itogawa, K.; Ohga, M.; Fujii, K. Experimental study on remaining strength estimation of corroded wide steel plates under tensile force. Procedia Eng. 2011, 14, 2707–2713. [Google Scholar] [CrossRef][Green Version]
- Appuhamy, J.M.R.S.; Kaita, T.; Ohga, M.; Fujii, K. Prediction of residual strength of corroded tensile steel plates. Int. J. Steel Struct. 2011, 11, 65–79. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, X.; Zhao, X.; Liu, Y. Experimental and restoring force model research on the seismic behavior of corroded steel frame beams in offshore atmospheric environment. Eng. Mech. 2018, 35, 98–106, 115. [Google Scholar]
- Bai, Y. Experimental Study and Theoretical Analysis on the Bending Behavior of Corroded Channel Steel. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2009. [Google Scholar]
- Sheng, J. Study on Surface Characteristics and Mechanical Properties of Corroded H Steel Beam Under Coupling Action of Load and Underground Environment. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2017. [Google Scholar]
- Yang, S.; Zheng, S.; Tian, Z.; Ming, M.; Xu, Y.; Wang, T. Mechanical properties test and cyclic constitutive model of corroded Q345B steel. Eng. Mech. 2025, 42, 206–215, 252. [Google Scholar]
- Liu, Y. Effect of Corrosion on Mechanical Properties of Q355 and Q390 Steel with its Application. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2023. [Google Scholar]
- Sheng, J.; Xia, J. Effect of simulated pitting corrosion on the tensile properties of steel. Constr. Build. Mater. 2017, 131, 90–100. [Google Scholar] [CrossRef]
- Yao, Y.; Yang, Y.; He, Z.; Wang, Y. Experimental study on generalized constitutive model of hull structural plate with multi-parameter pitting corrosion. Ocean Eng. 2018, 170, 407–415. [Google Scholar] [CrossRef]
- Wang, R.; Shenoi, R.A. Experimental and numerical study on ultimate strength of steel tubular members with pitting corrosion damage. Mar. Struct. 2019, 64, 124–137. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, N.; Liu, H.; Zhao, Z.; Fan, X.; Zhang, H. Influence of random pit corrosion on axial stiffness of thin-walled circular tubes. Structures 2020, 28, 2596–2604. [Google Scholar] [CrossRef]
- Zhao, Z.; Zheng, C.; Zhang, J.; Liang, B.; Zhang, H. Influence of random pitting corrosion on moment capacity of thin-walled circular tubes subjected to compression force. Int. J. Press. Vessel. Pip. 2021, 189, 104260. [Google Scholar] [CrossRef]
- Chen, M.; Luo, S.; Huang, H.; Fang, W.; Xu, K.; Qian, W. Experimental studies on axial compressive bearing capacity of circular CFST stub columns with localized corrosion. J. Cent. South Univ. Sci. Technol. 2024, 55, 317–329. [Google Scholar]
- Wang, Y.; Zhang, F.; Xu, Q. Research progress of the effect of corrosion on the properties of existing steel structures. Constr. Technol. 2020, 49, 7. [Google Scholar]
- Guo, L.; Huang, H.; Jia, C.; Romanov, K. Axial behavior of square CFST with local corrosion simulated by artificial notch. J. Constr. Steel Res. 2020, 174, 106314. [Google Scholar] [CrossRef]
- Huang, H.; Guo, L.; Qu, B.; Jia, C.; Elchalakani, M. Tests of circular concrete-filled steel tubular stub columns with artificial notches representing local corrosions. Eng. Struct. 2021, 242, 112598. [Google Scholar] [CrossRef]
- Hou, C.; Liu, X.; Zhao, W. SCF analysis for CFST K-joints subjected to combined long-term loading and random localized corrosion. J. Build. Struct. 2023, 44, 209–219. [Google Scholar]
- Xu, S.; Wang, Y. Estimating the effects of corrosion pits on the fatigue life of steel plate based on the 3D profile. Int. J. Fatigue 2015, 72, 27–41. [Google Scholar] [CrossRef]
- Ren, S. Study on Evolutionary Process of Corrosion Pit and its Effect on the Fatigue Property of Corroded Steel. Ph.D. Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2016. [Google Scholar]
- Liang, X.; Sheng, J.; Wang, K. Investigation of the mechanical properties of steel plates with artificial pitting and the effects of mutual pitting on the stress concentration factor. Results Phys. 2019, 14, 102520. [Google Scholar] [CrossRef]
- GB/T 228.1-2021; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Standards Press of China: Beijing, China, 2022.
- Zhou, L. Degradation Law and Evaluation of Axial Compression Performance of Locally Corroded X-Joints. Master’s Thesis, China University of Mining & Technology, Xuzhou, China, 2020. [Google Scholar]
- Zhao, W.; Zhang, J.; Hou, C. Mechanical performance analysis of concrete filled steel tubular K-joints subjected to random local corrosion. Steel Constr. 2022, 37, 10–19. [Google Scholar]
- Zheng, B.; Wu, B.; Zhang, K.; Wang, J.; Shu, G.; Jiang, Q. Investigations on capacity of stainless steel T- and Y-joints in circular hollow sections with axial tension in brace. J. Xi’an Univ. Arch. Technol. 2022, 54, 508–516. [Google Scholar]
- Gao, C.; Wang, J. Experimental study and numerical simulation for the concrete-filled steel tubular K-joint. Chin. J. Appl. Mech. 2021, 38, 38. [Google Scholar]
- Zhu, S.N. Analysis and Full-Scale Test Research on Ultimate Bearing Capacity of Circular Steel Pipe Intersecting Joints. Master’s Thesis, Hunan University, Changsha, China, 2003. [Google Scholar]
- Song, S.; Chen, J.; Xu, F.; Wang, Y. Mechanical behavior of concrete-filled K- and KK-type CHS connections. J. Build. Struct. 2021, 42, 133–142. [Google Scholar]
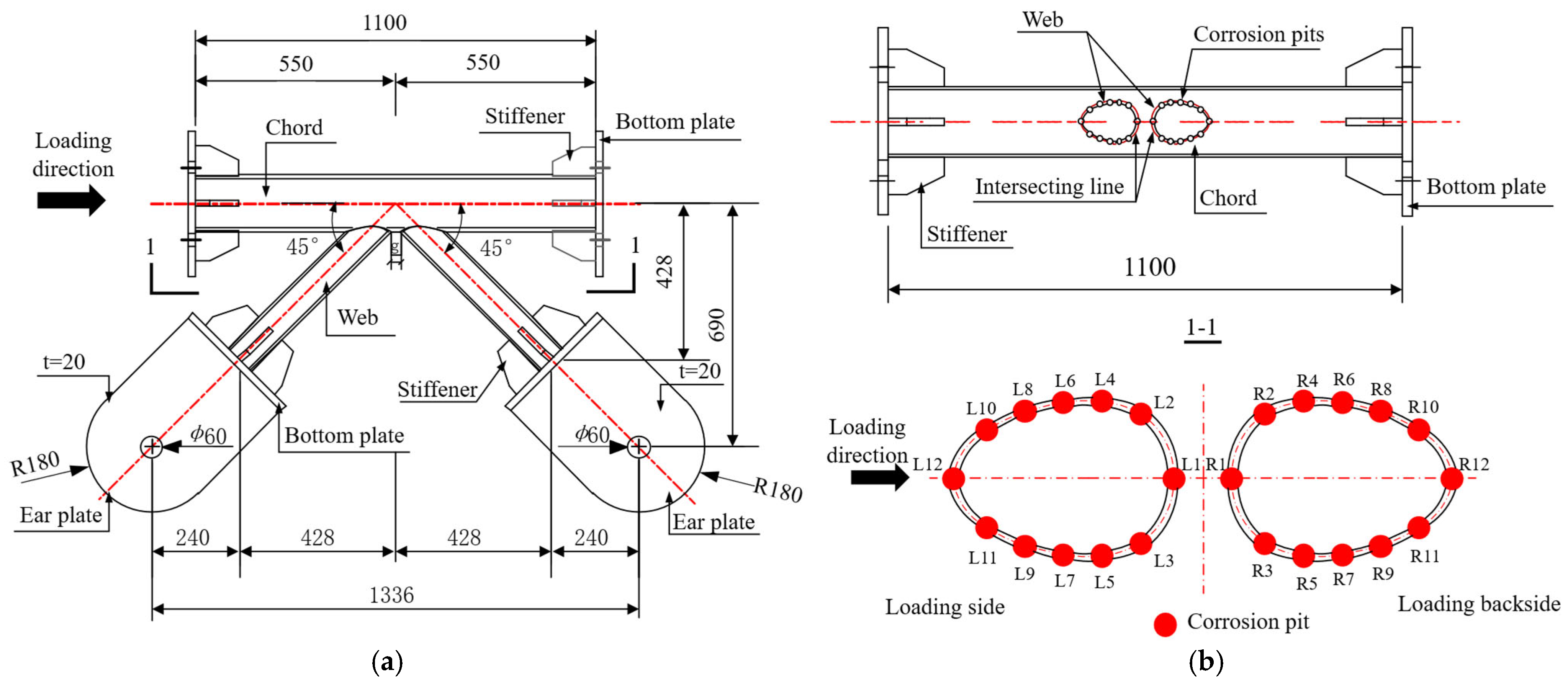








| Specimen Number | Chord Specification | Web Specification | Gap g/mm | Diameter of Corrosion Pit d/mm | Depth of Corrosion Pit H/mm | Number of Corrosion Pits N | Material |
|---|---|---|---|---|---|---|---|
| A1 | Ф152 × 6 | Ф89 × 4 | 27 | - | - | - | Q235B |
| A2 | Ф152 × 6 | Ф89 × 4 | 27 | 8 | 6 | 24 | Q235B |
| A3-1 | Ф152 × 6 | Ф89 × 4 | 27 | 12 | 6 | 24 | Q235B |
| A3-2 | Ф152 × 6 | Ф89 × 4 | 27 | 12 | 6 | 24 | Q235B |
| Specimen Number | Loading Side (E) Corrosion Pit Diameter Measured Value (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| L1 | L2/L3 | L4/L5 | L6/L7 | L8/L9 | L10/L11 | L12 | Average Value | Standard Deviation | |
| A2 | 7.30 | 7.8/7.6 | 7.3/7.4 | 8/7.2 | 7.9/7.6 | 7.2/7.6 | 8.0 | 7.58 | 0.29 |
| A3-1 | 10.50 | 11.1/11.5 | 10.8/10.8 | 10.9/13.1 | 11.9/10.8 | 11.1/12 | 10.9 | 11.28 | 0.70 |
| A3-2 | 10.20 | 11.8/11 | 11/10.5 | 10/11.5 | 11.6/11.7 | 11.5/11.9 | 10.0 | 11.06 | 0.69 |
| Specimen Number | Loading Backside (W) Corrosion Pit Diameter Measured Value (mm) | ||||||||
| R1 | R2/R3 | R4/R5 | R6/R7 | R8/R9 | R10/R11 | R12 | Average Value | Standard Deviation | |
| A2 | 7.60 | 7.6/6.9 | 7.8/6.8 | 6.9/7.3 | 8/7.2 | 8.6/8.6 | 7.8 | 7.59 | 0.59 |
| A3-1 | 10.30 | 10.9/12.2 | 10.8/11.2 | 11.8/10.9 | 11.9/11 | 11.6/10.7 | 10.1 | 11.12 | 0.62 |
| A3-2 | 10.90 | 12.6/13.1 | 10.8/10.9 | 11.7/10.6 | 12/12 | 10.6/11.5 | 10.90 | 11.47 | 0.79 |
| Specimen Number | T/mm | fy/MPa | fu/MPa | Es/GPa | δ/(%) |
|---|---|---|---|---|---|
| D89-1 | 3.74 | 322.92 | 435.96 | 193.84 | 23 |
| D89-2 | 3.76 | 331.47 | 437.03 | 199.70 | 22 |
| D89-3 | 3.76 | 324.88 | 424.37 | 205.85 | 21 |
| Average value | 3.75 | 326.42 | 432.45 | 199.80 | 22 |
| D152-1 | 5.80 | 220.38 | 340.84 | 207.25 | 29 |
| D152-2 | 5.80 | 226.44 | 345.89 | 192.43 | 30 |
| D152-3 | 5.78 | 222.26 | 340.68 | 205.68 | 28 |
| Average value | 5.79 | 223.03 | 342.47 | 201.79 | 29 |
| Nodal Specimen Number | NT /kN | NF /kN | NT/NF | NF/NF0 | Corrosion Rate XSL | Corrosion Pits’ Data Quantity/Diameter |
|---|---|---|---|---|---|---|
| A1 | — | 528.29 | — | 1.0 | 0.0 | — |
| A2 | 505 | 497.85 | 1.01 | 0.94 | 26.18% | 24/8 mm |
| A3-1 | 465 | 477.43 | 0.97 | 0.90 | 38.59% | 24/12 mm |
| A3-2 | 455 | 477.43 | 0.95 | 0.90 | 38.59% | 24/12 mm |
| Average value | 0.98 | 0.92 | ||||
| Standard deviation | 0.03 | 0.02 |
| Model Name | t0 /mm | t1 /mm | θ | γ | β | RH /mm | N | Lp /mm | χs | Nup or Nu/kN | ks |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P210p105-30-14-0.5-HAR0N0 | 7.5 | 6 | 30 | 14 | 0.5 | 0 | 0 | 515.95 | 0 | 1073.02 | — |
| P210p105-40-14-0.5-HAR0N0 | 7.5 | 6 | 40 | 0 | 0 | 433.45 | 0 | 741.70 | — | ||
| P210p105-50-14-0.5-HAR0N0 | 7.5 | 6 | 50 | 0 | 0 | 388.46 | 0 | 526.75 | — | ||
| P210p105-30-14-0.5-HAR2N12 | 7.5 | 6 | 30 | 14 | 0.5 | 2 | 12 | 515.95 | 0.093 | 1054.89 | 0.983 |
| P210p105-30-14-0.5-HAR4N12 | 7.5 | 6 | 4 | 12 | 515.95 | 0.186 | 1028.30 | 0.958 | |||
| P210p105-30-14-0.5-HAR6N12 | 7.5 | 6 | 6 | 12 | 515.95 | 0.279 | 996.93 | 0.929 | |||
| P210p105-30-14-0.5-HAR8N12 | 7.5 | 6 | 8 | 12 | 515.95 | 0.372 | 959.20 | 0.894 | |||
| P210p105-40-14-0.5-HAR2N12 | 7.5 | 6 | 40 | 14 | 0.5 | 2 | 12 | 433.45 | 0.111 | 721.88 | 0.973 |
| P210p105-40-14-0.5-HAR4N12 | 7.5 | 6 | 4 | 12 | 433.45 | 0.221 | 701.10 | 0.945 | |||
| P210p105-40-14-0.5-HAR6N12 | 7.5 | 6 | 6 | 12 | 433.45 | 0.332 | 674.96 | 0.910 | |||
| P210p105-40-14-0.5-HAR8N12 | 7.5 | 6 | 8 | 12 | 433.45 | 0.443 | 643.89 | 0.868 | |||
| P210p105-50-14-0.5-HAR2N12 | 7.5 | 6 | 50 | 14 | 0.5 | 2 | 12 | 388.46 | 0.124 | 511.08 | 0.970 |
| P210p105-50-14-0.5-HAR4N12 | 7.5 | 6 | 4 | 12 | 388.46 | 0.247 | 491.49 | 0.933 | |||
| P210p105-50-14-0.5-HAR6N12 | 7.5 | 6 | 6 | 12 | 388.46 | 0.371 | 473.06 | 0.898 | |||
| P210p105-50-14-0.5-HAR8N12 | 7.5 | 6 | 8 | 12 | 388.46 | 0.494 | 445.85 | 0.846 |
| Model Name | t0/mm | t1/mm | θ | γ | β | RH/mm | N | Lp/mm | χs | Nup or Nu/kN | ks |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P210p105-40-10-0.5-HAR0N0 | 10.5 | 8.4 | 40 | 10 | 0.5 | 0 | 0 | 433.45 | 0 | 1268.99 | — |
| P210p105-40-12.5-0.5-HAR0N0 | 8.4 | 6.72 | 12.5 | 0 | 0 | 433.45 | 0 | 889.28 | — | ||
| P210p105-40-15-0.5-HAR0N0 | 7 | 5.6 | 15 | 0 | 0 | 433.45 | 0 | 663.90 | — | ||
| P210p105-40-17.5-0.5-HAR0N0 | 6 | 4.8 | 17.5 | 0 | 0 | 433.45 | 0 | 517.25 | — | ||
| P210p105-40-20-0.5-HAR0N0 | 5.25 | 4.2 | 20 | 0 | 0 | 433.45 | 0 | 416.49 | — | ||
| P210p105-40-10-0.5-HAR2N12 | 10.5 | 8.4 | 40 | 10 | 0.5 | 2 | 12 | 433.45 | 0.111 | 1241.61 | 0.978 |
| P210p105-40-10-0.5-HAR4N12 | 10.5 | 8.4 | 4 | 12 | 433.45 | 0.221 | 1210.27 | 0.954 | |||
| P210p105-40-10-0.5-HAR6N12 | 10.5 | 8.4 | 6 | 12 | 433.45 | 0.332 | 1168.15 | 0.921 | |||
| P210p105-40-10-0.5-HAR8N12 | 10.5 | 8.4 | 8 | 12 | 433.45 | 0.443 | 1105.25 | 0.871 | |||
| P210p105-40-12.5-0.5-HAR2N12 | 8.4 | 6.72 | 40 | 12.5 | 0.5 | 2 | 12 | 433.45 | 0.111 | 866.62 | 0.975 |
| P210p105-40-12.5-0.5-HAR4N12 | 8.4 | 6.72 | 4 | 12 | 433.45 | 0.221 | 842.74 | 0.948 | |||
| P210p105-40-12.5-0.5-HAR6N12 | 8.4 | 6.72 | 6 | 12 | 433.45 | 0.332 | 812.38 | 0.914 | |||
| P210p105-40-12.5-0.5-HAR8N12 | 8.4 | 6.72 | 8 | 12 | 433.45 | 0.443 | 774.23 | 0.871 | |||
| P210p105-40-15-0.5-HAR2N12 | 7 | 5.6 | 40 | 15 | 0.5 | 2 | 12 | 433.45 | 0.111 | 645.91 | 0.973 |
| P210p105-40-15-0.5-HAR4N12 | 7 | 5.6 | 4 | 12 | 433.45 | 0.221 | 626.84 | 0.944 | |||
| P210p105-40-15-0.5-HAR6N12 | 7 | 5.6 | 6 | 12 | 433.45 | 0.332 | 603.10 | 0.908 | |||
| P210p105-40-15-0.5-HAR8N12 | 7 | 5.6 | 8 | 12 | 433.45 | 0.443 | 575.42 | 0.867 | |||
| P210p105-40-17.5-0.5-HAR2N12 | 6 | 4.8 | 40 | 17.5 | 0.5 | 2 | 12 | 433.45 | 0.111 | 503.27 | 0.973 |
| P210p105-40-17.5-0.5-HAR4N12 | 6 | 4.8 | 4 | 12 | 433.45 | 0.221 | 488.03 | 0.944 | |||
| P210p105-40-17.5-0.5-HAR6N12 | 6 | 4.8 | 6 | 12 | 433.45 | 0.332 | 468.99 | 0.907 | |||
| P210p105-40-17.5-0.5-HAR8N12 | 6 | 4.8 | 8 | 12 | 433.45 | 0.443 | 447.54 | 0.865 | |||
| P210p105-40-20-0.5-HAR2N12 | 5.25 | 4.2 | 40 | 20 | 0.5 | 2 | 12 | 433.45 | 0.111 | 405.00 | 0.972 |
| P210p105-40-20-0.5-HAR4N12 | 5.25 | 4.2 | 4 | 12 | 433.45 | 0.221 | 392.28 | 0.942 | |||
| P210p105-40-20-0.5-HAR6N12 | 5.25 | 4.2 | 6 | 12 | 433.45 | 0.332 | 382.27 | 0.918 | |||
| P210p105-40-20-0.5-HAR8N12 | 5.25 | 4.2 | 8 | 12 | 433.45 | 0.443 | 359.74 | 0.864 |
| Model Name | t0 /mm | t1 /mm | θ | γ | β | RH /mm | N | Lp /mm | χs | Nup or Nu/kN | ks |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P210p105-40-14-0.5-HAR0N0 | 7.5 | 6 | 40 | 14 | 0.4 | 0 | 0 | 0 | 0 | 602.33 | — |
| P210p105-40-14-0.5-HAR12N2 | 7.5 | 6 | 40 | 14 | 0.5 | 0 | 0 | 0 | 0 | 741.7 | — |
| P210p105-40-14-0.5-HAR12N4 | 7.5 | 6 | 40 | 14 | 0.6 | 0 | 0 | 0 | 0 | 892.57 | — |
| P210p105-40-14-0.5-HAR12N6 | 7.5 | 6 | 40 | 14 | 0.7 | 0 | 0 | 0 | 0 | 1103.21 | — |
| P210p105-40-14-0.5-HAR12N8 | 7.5 | 6 | 40 | 14 | 0.4 | 2 | 12 | 344.59 | 0.139 | 582.36 | 0.967 |
| P210p105-40-14-0.5-HAR4N6 | 7.5 | 6 | 40 | 14 | 0.4 | 4 | 12 | 344.59 | 0.279 | 557.11 | 0.925 |
| P210p105-40-14-0.5-HAR8N6 | 7.5 | 6 | 40 | 14 | 0.4 | 6 | 12 | 344.59 | 0.418 | 526.47 | 0.874 |
| P210p105-40-14-0.5-HAR12N6 | 7.5 | 6 | 40 | 14 | 0.4 | 8 | 12 | 344.59 | 0.557 | 489.36 | 0.812 |
| P210p105-40-14-0.5-HAR16N6 | 7.5 | 6 | 40 | 14 | 0.5 | 2 | 12 | 433.45 | 0.111 | 721.88 | 0.973 |
| P210p105-40-14-0.5-HAR0N0 | 7.5 | 6 | 40 | 14 | 0.5 | 4 | 12 | 433.45 | 0.221 | 701.1 | 0.945 |
| P210p105-40-14-0.5-HAR12N2 | 7.5 | 6 | 40 | 14 | 0.5 | 6 | 12 | 433.45 | 0.332 | 674.96 | 0.910 |
| P210p105-40-14-0.5-HAR12N4 | 7.5 | 6 | 40 | 14 | 0.5 | 8 | 12 | 433.45 | 0.443 | 643.89 | 0.868 |
| P210p105-40-14-0.5-HAR12N6 | 7.5 | 6 | 40 | 14 | 0.6 | 2 | 12 | 524.64 | 0.091 | 871.87 | 0.977 |
| P210p105-40-14-0.5-HAR12N8 | 7.5 | 6 | 40 | 14 | 0.6 | 4 | 12 | 524.64 | 0.183 | 852.71 | 0.955 |
| P210p105-40-14-0.5-HAR4N6 | 7.5 | 6 | 40 | 14 | 0.6 | 6 | 12 | 524.64 | 0.274 | 827.83 | 0.927 |
| P210p105-40-14-0.5-HAR8N6 | 7.5 | 6 | 40 | 14 | 0.6 | 8 | 12 | 524.64 | 0.366 | 799.51 | 0.896 |
| P210p105-40-14-0.5-HAR12N6 | 7.5 | 6 | 40 | 14 | 0.7 | 2 | 12 | 619.41 | 0.077 | 752.06 | 0.978 |
| P210p105-40-14-0.5-HAR16N6 | 7.5 | 6 | 40 | 14 | 0.7 | 4 | 12 | 619.41 | 0.155 | 1036.32 | 0.959 |
| P210p105-40-14-0.5-HAR0N0 | 7.5 | 6 | 40 | 14 | 0.7 | 6 | 12 | 619.41 | 0.232 | 1031.4 | 0.935 |
| P210p105-40-14-0.5-HAR12N2 | 7.5 | 6 | 40 | 14 | 0.7 | 8 | 12 | 619.41 | 0.310 | 1000.15 | 0.907 |
| Model Name | t0/mm | t1/mm | θ | γ | β | RH/mm | N | Lp/mm | χs | Nup or Nu/kN | ks |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P210p105-40-14-0.5-HAR0N0 | 7.5 | 6 | 40 | 14 | 0.5 | 0 | 0 | — | — | 741.70 | — |
| P210p105-40-14-0.5-HAR12N2 | 7.5 | 6 | 40 | 14 | 0.5 | 12 | 2 | 433.45 | 0.111 | 721.88 | 0.973 |
| P210p105-40-14-0.5-HAR12N4 | 7.5 | 6 | 40 | 14 | 0.5 | 12 | 4 | 433.45 | 0.221 | 701.10 | 0.945 |
| P210p105-40-14-0.5-HAR12N6 | 7.5 | 6 | 40 | 14 | 0.5 | 12 | 6 | 433.45 | 0.332 | 674.96 | 0.910 |
| P210p105-40-14-0.5-HAR12N8 | 7.5 | 6 | 40 | 14 | 0.5 | 12 | 8 | 433.45 | 0.443 | 643.89 | 0.868 |
| P210p105-40-14-0.5-HAR4N6 | 7.5 | 6 | 40 | 14 | 0.5 | 4 | 6 | 433.45 | 0.111 | 719.84 | 0.971 |
| P210p105-40-14-0.5-HAR8N6 | 7.5 | 6 | 40 | 14 | 0.5 | 8 | 6 | 433.45 | 0.221 | 696.00 | 0.938 |
| P210p105-40-14-0.5-HAR12N6 | 7.5 | 6 | 40 | 14 | 0.5 | 12 | 6 | 433.45 | 0.332 | 674.96 | 0.910 |
| P210p105-40-14-0.5-HAR16N6 | 7.5 | 6 | 40 | 14 | 0.5 | 16 | 6 | 433.45 | 0.443 | 649.29 | 0.875 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.-Q.; Tong, S.-J.; Jiang, H.-L.; Feng, X.-D.; Li, J.-H.; Xu, J.-K. Experimental and Numerical Bearing Capacity Analysis of Locally Corroded K-Shaped Circular Joints. Buildings 2025, 15, 3111. https://doi.org/10.3390/buildings15173111
Su Y-Q, Tong S-J, Jiang H-L, Feng X-D, Li J-H, Xu J-K. Experimental and Numerical Bearing Capacity Analysis of Locally Corroded K-Shaped Circular Joints. Buildings. 2025; 15(17):3111. https://doi.org/10.3390/buildings15173111
Chicago/Turabian StyleSu, Ying-Qiang, Shu-Jing Tong, Hai-Lou Jiang, Xiao-Dong Feng, Jian-Hua Li, and Jian-Kun Xu. 2025. "Experimental and Numerical Bearing Capacity Analysis of Locally Corroded K-Shaped Circular Joints" Buildings 15, no. 17: 3111. https://doi.org/10.3390/buildings15173111
APA StyleSu, Y.-Q., Tong, S.-J., Jiang, H.-L., Feng, X.-D., Li, J.-H., & Xu, J.-K. (2025). Experimental and Numerical Bearing Capacity Analysis of Locally Corroded K-Shaped Circular Joints. Buildings, 15(17), 3111. https://doi.org/10.3390/buildings15173111





