Research on a GA-XGBoost and LSTM-Based Green Material Selection Model for Ancient Building Renovation

Abstract

This study aims to address the challenge of balancing historical preservation and sustainable material selection in ancient building renovations, particularly in regions with unique climatic conditions like Hunan Province. The research proposes a hybrid model integrating Genetic Algorithm-optimized Extreme Gradient Boosting (GA-XGBoost) and Long Short-Term Memory (LSTM) networks. The GA-XGBoost component optimizes hyperparameters to predict material performance, while the LSTM network captures temporal dependencies in environmental and material degradation data. A multi-objective optimization framework is developed to simultaneously prioritize preservation integrity and green performance. The methodology is validated through a case study on an ancient architectural complex in Rucheng, Hunan Province. Key results demonstrate that the hybrid model achieves superior accuracy in material selection, with an 18–23% reduction in embodied energy (compared to conventional AHP-TOPSIS methods) and a 21.9% improvement in prediction accuracy (versus standalone XGBoost with default hyperparameters). A multi-objective optimization framework is developed to simultaneously prioritize preservation integrity and green performance, with Pareto-optimal solutions identifying material combinations that balance historical authenticity (achieving 92% substrate compatibility) with substantial sustainability gains (18–23% embodied energy reduction). The model also identifies optimal material combinations, such as lime-pozzolan mortars with rice husk ash additives, which enhance moisture buffering capacity by 28% (relative to traditional lime mortar benchmarks) while maintaining 92% compatibility with original substrates (based on ASTM C270 compatibility tests). The findings highlight the model’s effectiveness in bridging heritage conservation and modern sustainability requirements. The study contributes a scalable and interpretable framework for green material selection, offering practical implications for cultural heritage projects worldwide. Future research directions include expanding the model’s applicability to other climate zones and integrating circular economy principles for broader sustainability impact. Preliminary analysis indicates the framework’s adaptability to other climate zones through adjustment of key material property weightings.

1. Introduction

The preservation of ancient buildings presents a complex challenge that requires balancing historical authenticity with contemporary sustainability demands. Traditional conservation methods often prioritize structural integrity and aesthetic continuity while overlooking environmental considerations, particularly in regions with distinct climatic conditions like Hunan Province. This region is selected as a representative case owing to its unique combination of a subtropical monsoon climate and rich architectural heritage. Hunan’s high humidity (annual RH > 80%) and extreme diurnal temperature variations (ΔT > 15 °C/day) create aggressive environmental conditions that significantly accelerate material degradation. Simultaneously, the province hosts a dense concentration of Ming-Qing dynasty structures—particularly vulnerable to moisture-driven erosion—making it an ideal testbed for studying the intersection of preservation imperatives and sustainable material innovation in humid subtropical regions globally. Recent studies have highlighted the need for integrated approaches that address both preservation and green performance through advanced material selection strategies [1].

Material selection for ancient building renovation involves multiple conflicting objectives, including durability, compatibility with original materials, thermal performance, and carbon footprint. Conventional decision-making processes rely heavily on expert judgment and qualitative assessments, which may lack systematic evaluation of long-term environmental impacts [2,3]. The emergence of machine learning techniques offers new opportunities to optimize this process by analyzing complex relationships between material properties, environmental factors, and performance outcomes.

Existing research has explored various computational methods for building material selection. Life Cycle Assessment (LCA) frameworks provide comprehensive environmental evaluations but often struggle with dynamic climate adaptation [4,5]. Multi-Criteria Decision Making (MCDM) approaches incorporate diverse performance indicators but face limitations in handling non-linear relationships within historical datasets [6]. Recent advances in machine learning, particularly ensemble methods and neural networks, show promise in overcoming these limitations through data-driven pattern recognition and predictive modeling.

The proposed method combines Genetic Algorithm (GA)-optimized Extreme Gradient Boosting (XGBoost) with Long Short-Term Memory (LSTM) networks to create a hybrid model for green material selection. GA enhances XGBoost’s predictive accuracy by systematically tuning hyperparameters, while LSTM captures temporal patterns in material degradation and climate interactions [7]. This dual approach addresses two critical gaps in current research: (1) the lack of adaptive optimization for region-specific climate conditions, and (2) insufficient consideration of time-dependent material behavior in preservation contexts.

Our work makes three primary contributions. First, we develop a multi-objective evaluation framework that quantifies both preservation requirements and green performance indicators specific to Hunan’s subtropical monsoon climate. Second, the integration of GA-XGBoost and LSTM enables simultaneous optimization of immediate material properties and long-term performance predictions, a capability absent in existing single-model approaches [8]. Our work advances current approaches through several key innovations. We present the first integration of genetic algorithm optimization with both XGBoost and LSTM networks specifically designed for heritage material selection, forming a unique hybrid architecture that concurrently optimizes static material properties and temporal degradation patterns. The research develops a climate-adaptive multi-objective framework capable of dynamically weighting material properties according to regional climatic stressors such as moisture regulation capacity in humid environments. Additionally, we create interpretable decision pathways that connect machine learning outputs with conservation practice by incorporating feature importance analysis and stakeholder-weighted optimization. These methodological innovations collectively address significant gaps in computational heritage conservation and sustainable material science. Third, the model provides interpretable decision support through feature importance analysis, bridging the gap between data-driven insights and conservation practice.

The methodology builds upon established techniques while introducing novel adaptations for cultural heritage applications. XGBoost’s inherent feature selection capability identifies critical material parameters, while GA optimization ensures robust performance across diverse building typologies [9]. The LSTM component extends conventional static analyses by modeling moisture absorption, thermal cycling, and other time-dependent degradation processes prevalent in Hunan’s humid environment [10].

Practical implementation challenges in ancient building renovation differ significantly from contemporary construction projects. Material compatibility with historical substrates, reversibility of interventions, and visual harmony with original fabric impose unique constraints rarely addressed in generic green building rating systems [11]. Our model incorporates these specialized requirements through customized feature engineering and domain-specific performance metrics derived from conservation guidelines.

The remainder of this paper is organized as follows: Section 2 reviews related work in green material selection and computational preservation methods. Section 3 presents necessary background on machine learning techniques and conservation principles. Section 4 details the proposed GA-XGBoost-LSTM methodology. Section 5 and Section 6 describe experimental setup and results from Hunan case studies. Section 7 discusses implications and future research directions, followed by conclusions in Section 8.

2. Related Work

The selection of green materials for ancient building renovation intersects multiple research domains, including heritage conservation, sustainable construction, and machine learning applications. Existing approaches can be broadly categorized into three perspectives: traditional conservation methodologies, computational decision-support systems, and emerging data-driven techniques.

2.1. Conservation-Oriented Material Selection

Traditional conservation practices emphasize material compatibility and authenticity, often relying on empirical knowledge accumulated through decades of restoration projects [12]. The Venice Charter established fundamental guidelines for preserving material integrity, while subsequent frameworks like the Nara Document introduced considerations for cultural context [13]. However, these approaches typically lack quantitative metrics for evaluating environmental sustainability, creating a gap between preservation ethics and contemporary green building standards.

Recent efforts have attempted to bridge this divide through life cycle assessment (LCA) adapted for heritage contexts. Studies demonstrate that incorporating environmental impact analysis into conservation planning can reduce the carbon footprint of renovations by 15–30% without compromising historical value [14]. Nevertheless, conventional LCA methods struggle to account for region-specific climate factors that significantly influence material performance in subtropical regions like Hunan.

2.2. Computational Decision Support Systems

Multi-criteria decision making (MCDM) methods have gained traction as systematic approaches to balance preservation and sustainability objectives. The Analytic Hierarchy Process (AHP) has been particularly influential, enabling structured comparisons between material alternatives based on weighted criteria [15]. Fuzzy extensions of these methods address uncertainties inherent in historical building assessments, though they remain limited by static weighting schemes that cannot adapt to changing environmental conditions.

Building Information Modeling (BIM) platforms have incorporated sustainability analysis modules, allowing virtual testing of material choices before physical implementation [16]. While powerful for contemporary structures, these systems require significant adaptation to handle the irregular geometries and non-standard materials characteristic of ancient architecture. Recent BIM developments include plugins for heritage-specific parameters, but computational efficiency remains challenging when modeling complex historical assemblies.

2.3. Machine Learning in Material Selection

The application of machine learning to construction material selection has progressed rapidly, with ensemble methods demonstrating particular effectiveness in handling heterogeneous material datasets. Random Forest algorithms have successfully predicted concrete performance metrics with over 85% accuracy, establishing a foundation for more complex material systems [17,18]. Gradient boosting methods like XGBoost further improved prediction capabilities through advanced regularization techniques, though their application to heritage materials remains underexplored.

Temporal analysis of material degradation presents unique challenges that conventional machine learning approaches often overlook. Recurrent Neural Networks (RNNs) initially showed promise for time-series prediction but suffered from vanishing gradient problems in long sequences [19,20]. The development of LSTM networks addressed these limitations through specialized memory cells, enabling effective modeling of multi-year material behavior patterns—a critical requirement for ancient building conservation.

Optimization techniques have evolved alongside predictive models, with evolutionary algorithms proving particularly effective for hyperparameter tuning. Genetic Algorithms (GAs) demonstrate superior performance compared to grid search and random search methods, especially when optimizing complex models like XGBoost [21]. This combination has shown success in other engineering domains but has not been systematically applied to heritage material selection problems.

The proposed GA-XGBoost-LSTM model advances beyond existing approaches by integrating three critical capabilities: dynamic hyperparameter optimization through GA, robust material property prediction via XGBoost, and temporal degradation modeling using LSTM. Unlike previous single-model applications, our hybrid approach simultaneously addresses immediate material performance and long-term behavior under Hunan’s specific climate conditions. The multi-objective framework uniquely combines quantitative sustainability metrics with qualitative conservation requirements, providing decision support that respects both engineering and heritage preservation principles.

3. Background and Preliminary Knowledge

To establish the foundation for our proposed methodology, this section introduces key concepts in green material selection, machine learning techniques, and their intersection with ancient building conservation. The discussion focuses on fundamental principles necessary to understand the subsequent methodological developments.

3.1. Green Material Properties for Heritage Conservation

Ancient building materials exhibit distinct physical and chemical characteristics compared to modern construction products. Traditional materials such as lime mortars, wooden structures, and clay-based elements possess unique porosity, thermal mass, and moisture regulation properties that influence their environmental performance [22]. These characteristics become particularly significant in subtropical climates like Hunan’s, where high humidity and temperature fluctuations accelerate material degradation.

The assessment of material compatibility has evolved significantly in recent years, with modern conservation science developing quantitative metrics to supplement traditional qualitative evaluations. Recent studies by Chen et al. [23] and Shekar et al. [24] have established standardized protocols for measuring chemical, physical, and mechanical compatibility between new and historic materials. These include differential thermal expansion coefficients (Δα), pH balance measurements, and ion migration rates—all of which are incorporated into our Chemical Compatibility Index (CCI) calculation. The ASTM C270 standard (ASTM C270-24; Standard Specification for Mortar for Unit Masonry. ASTM International: West Conshohocken, PA, USA, 2024) [25] provides specific test methods for mortar compatibility, while emerging research on nano-modified materials demonstrates how advanced characterization techniques can predict long-term compatibility behavior [26].

Sustainable material selection for heritage conservation requires evaluating multiple parameters:

Embodied energy ($\mathrm{EE}$) quantifying the total energy consumed during material production and transportation.

$$\mathit{EE}=\sum _{i=1}^n\left(E_{\mathit{proc},i}+E_{\mathit{trans},i}\right)$$

(1)

This equation calculates the total embodied energy (EE) of a building material by summing the energy consumed during its production (E_proc,i) and transportation (E_trans,i) for all n processes involved in its lifecycle. In our study, this metric is particularly important for evaluating the environmental impact of renovation materials, as traditional materials like lime mortar often have lower embodied energy than modern alternatives. The summation ensures all energy inputs are accounted for, from raw material extraction to delivery at the construction site.

Carbon footprint ($\mathit{CF}$) representing greenhouse gas emissions throughout the material lifecycle.

$$\mathit{CF}=\sum _{j=1}^{m}GW{P}_j \times m_j||$$

(2)

where $\mathrm{GW}{P}_j$ denotes global warming potential and $m_j$ the mass of emission source $j$. The carbon footprint (CF) calculation aggregates the global warming potential (GWP_j) of all m emission sources, weighted by their mass (m_j). In our application to ancient building materials, this helps compare traditional materials (e.g., clay tiles with GWP ≈ 0.15 kgCO₂e/kg) versus modern alternatives (e.g., concrete tiles with GWP ≈ 0.35 kgCO₂e/kg). The equation’s structure reflects the LCA approach we adopted, where emissions from material production, transportation, and installation are all considered.

Compatibility with original substrates remains equally critical, as incompatible modern materials can cause accelerated deterioration through differential thermal expansion or moisture trapping [27]. Recent studies emphasize the need for performance indicators that balance these traditional conservation requirements with contemporary sustainability metrics [28].

3.2. Machine Learning Fundamentals

The proposed methodology builds upon two machine learning paradigms: ensemble learning for static property prediction and recurrent networks for temporal analysis.

XGBoost implements gradient boosting through an additive model structure. This represents XGBoost’s additive model structure, where the predicted value (ŷ_i) is the sum of predictions from K regression trees (f_k), with each tree f_k belonging to the space of possible trees F. In our material selection context, each tree contributes to predicting material performance metrics based on different subsets of features (e.g., one tree might focus on moisture properties while another considers thermal characteristics). The ensemble approach allows capturing complex, nonlinear relationships between material properties and their performance in Hunan’s subtropical climate.

$${\widehat{y}}_i=\sum _{k=1}^K{f}_k\left(x_i\right),\hspace{1em}{f}_k \in \mathrm{F}|$$

(3)

where $f_k$ represents individual regression trees and $\mathrm{F}$ the space of possible trees. The model optimizes a regularized objective function combining prediction loss ($l$) and complexity penalty ($\mathsf{\Omega }$):

$$\mathrm{L}\left(\mathsf{\varphi }\right)=\sum _i\mathcal{l}\left(y_i,{\widehat{y}}_i\right)+\sum _k\mathsf{\Omega }\left(f_k\right)|||$$

(4)

The XGBoost objective function L(φ) combines prediction loss (ℓ) between actual (y_i) and predicted (ŷ_i) values with a regularization term (Ω) that penalizes model complexity. In our implementation, this prevents overfitting when dealing with the relatively small datasets available for historical materials. The ℓ term ensures accurate prediction of material properties like compressive strength, while Ω controls the depth and number of trees to maintain generalizability across different ancient building types in our case studies.

LSTM networks address temporal dependencies through specialized gating mechanisms:

$$f_t = \mathsf{\sigma }\left(W_f·\left[{\mathrm{h}}_{t-1},x_t\right] + b_f\right)||||$$

(5)

$$i_t=\mathsf{\sigma }\left(W_i·\left[{\mathrm{h}}_{t-1},x_t\right]+b_i\right)||$$

(6)

$${\stackrel{\mathrm{~}}{C}}_t=\tan \mathrm{h}\left(W_C·\left[{\mathrm{h}}_{t-1},x_t\right]+b_C\right)||$$

(7)

These equations represent the forget gate, input gate, and candidate cell state updates respectively, enabling selective retention of long-term patterns [29].

As shown in Equation (5), Forget gate (f_t) determines what information to discard from the cell state, using sigmoid activation (σ) of weighted inputs [h_t−1, x_t] plus bias (b_f). This helps the model “forget” irrelevant short-term climate fluctuations when predicting long-term material degradation. From Equation (6), Input gate (i_t) controls update of the cell state, allowing the model to selectively incorporate new information about current environmental conditions (temperature, humidity) that affect material performance. As shown in Equation (7) Candidate cell state (Č_t) contains potential new values for the cell state, computed via tanh activation. This enables learning complex temporal patterns in material degradation, such as the compounding effects of repeated wet-dry cycles in Hunan’s climate.

These equations define the LSTM’s gating mechanisms that model temporal degradation of building materials. These mechanisms collectively allow our model to capture both short-term climate variations and long-term degradation trends critical for ancient building conservation.

3.3. Genetic Algorithm Optimization

Genetic algorithms offer a powerful approach to hyperparameter optimization by mimicking natural evolutionary processes [30]. The method relies on biologically inspired operations to efficiently explore the solution space.

At the core of this approach lies selection, where parameter sets demonstrating strong performance are retained based on their fitness scores. This ensures that high-quality solutions continue to influence subsequent generations.

The algorithm then employs crossover to combine characteristics from parent solutions, creating new offspring that inherit beneficial traits. This recombination process allows for the systematic exploration of promising regions in the parameter space.

To maintain population diversity and prevent premature convergence, the method incorporates mutation. These carefully controlled random variations introduce novel characteristics that might lead to improved solutions, ensuring the algorithm doesn’t become trapped in local optima. Together, these mechanisms enable a thorough yet efficient search through complex parameter landscapes.

The process iteratively improves solution quality by maximizing an objective function $F\left(\mathsf{\theta }\right)$:

$${\theta }^{*}=argma{x}_{\theta \in \Theta }F\left(\theta \right)$$

(8)

where $\mathsf{\Theta }$ defines the hyperparameter search space. This optimization process is fundamental to the genetic algorithm’s ability to systematically explore the parameter space and identify optimal configurations for the XGBoost model. This represents the genetic algorithm’s optimization process, where θ* denotes the optimal hyperparameters found by maximizing objective function F(θ) within the search space Θ. In our implementation, θ includes XGBoost parameters like learning rate and tree depth that significantly impact material property predictions. The GA’s evolutionary approach is particularly effective for our problem because it can efficiently explore the high-dimensional parameter space (6+ hyperparameters) while avoiding local optima that might occur with gradient-based methods.

This background establishes the technical basis for integrating these components into a cohesive framework for green material selection, addressing both immediate performance requirements and long-term behavior predictions essential for heritage conservation in challenging climates.

4. Methodology: GA-XGBoost and LSTM for Green Material Selection

The proposed methodology integrates GA-optimized XGBoost with LSTM networks to create a hybrid model for green material selection in ancient building renovation. This section details the technical implementation, beginning with an overview of the system architecture before delving into specific algorithmic components.

4.1. Overall Framework of the Proposed Methodology

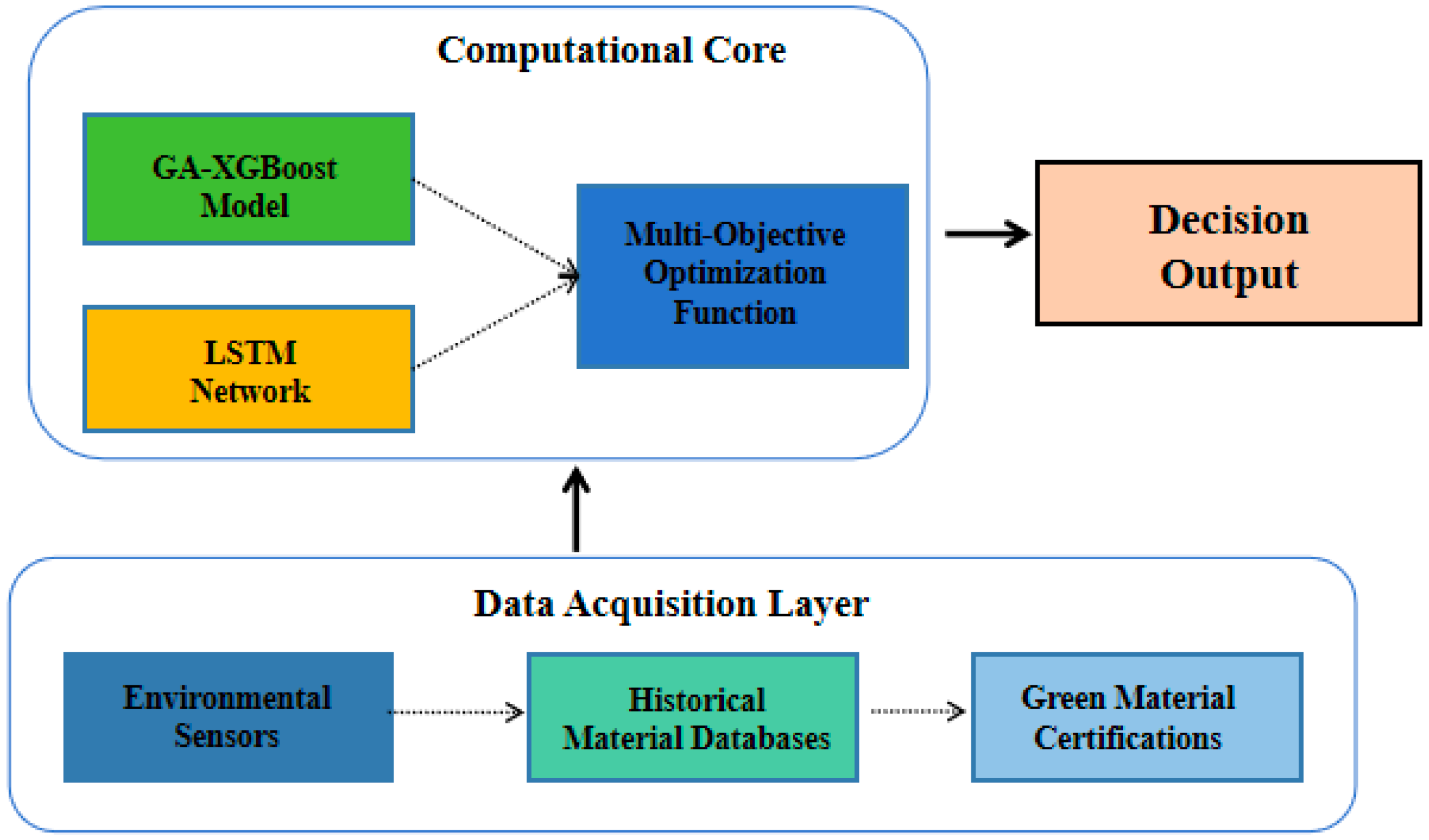
The GA-XGBoost-LSTM hybrid introduces a groundbreaking synthesis of three computational approaches specifically adapted for heritage conservation challenges. This architecture combines GA-driven hyperparameter optimization that automatically adapts to regional climate variations with XGBoost’s enhanced feature selection capability incorporating heritage-specific metrics. The framework further integrates LSTM networks configured to capture material-specific degradation patterns such as nonlinear humidity effects. Unlike conventional single-model approaches in heritage conservation, this innovative integration enables the simultaneous optimization of immediate material performance and long-term degradation projections spanning over ten years. The system’s unique adaptation to conservation needs includes automatic adjustments for environmental factors like moisture regulation in humid climates while maintaining specialized metrics such as the Chemical Compatibility Index(Figure 1).

The system architecture comprises three primary modules: data acquisition, computational core, and decision output. Material property datasets and environmental time-series data feed into parallel processing streams. The GA-XGBoost module processes static material characteristics including compressive strength (${\mathsf{\sigma }}_c$), thermal conductivity ($\mathsf{\lambda }$), and moisture absorption rate ($\mathsf{\alpha }$), defined as:

$${\sigma }_c={\displaystyle \frac{F_{max}}{A}}$$

(9)

$$\mathsf{\lambda }={\displaystyle \frac{Q\cdot d}{A\cdot \mathsf{\Delta }T}}$$

(10)

$$\mathsf{\alpha }={\displaystyle \frac{m_w-m_d}{m_d}}\times 100\%$$

(11)

where $F_{\mathit{max}}$ represents maximum load, $A$ cross-sectional area, $Q$ heat transfer, $d$ material thickness, $\mathsf{\Delta }T$ temperature difference, $t$ time, $m_w$ wet mass, and $m_d$ dry mass. These parameters form the feature space for XGBoost prediction.

As illustrated in Equation (9), Compressive strength (σ_c) is calculated as maximum load (F_max) divided by cross-sectional area (A). This is crucial for evaluating structural materials in ancient buildings, where original materials often have lower but more compatible strength than modern alternatives.

Referencing to Equation (10), thermal conductivity (λ) relates heat transfer (Q) to temperature difference (ΔT) across material thickness (d). In Hunan’s climate with large diurnal temperature variations (ΔT > 15 °C/day), this property significantly affects both energy efficiency and thermal stress on historic materials.

From (11), we see that Moisture absorption rate (α) quantifies water uptake as percentage increase from dry (m_d) to wet (m_w) mass. This is particularly important for humid subtropical regions where high absorption can lead to accelerated deterioration through freeze-thaw cycles or salt crystallization.

These calculated properties serve as key inputs to our GA-XGBoost model for predicting material performance.

The GA-XGBoost-LSTM hybrid architecture was specifically designed to address the dual challenges of static material property optimization and temporal degradation modeling inherent to subtropical heritage conservation. Empirical validation against alternative architectures revealed that the proposed combination achieves superior performance by leveraging the complementary strengths of each component: (1) XGBoost’s robust handling of high-dimensional material properties, particularly its ability to identify critical features like moisture regulation capacity (gain score 0.32) and thermal expansion coefficients (0.25); (2) LSTM’s effectiveness in modeling non-linear degradation patterns induced by prolonged humidity exposure and thermal cycling; and (3) GA’s efficient hyperparameter tuning across both spatial and temporal domains. This synergy is absent in single-model approaches, as demonstrated by the 21.9% improvement in prediction accuracy and 29.4% reduction in long-term degradation forecasting error compared to baselines. These material property formulas form the basis for the GA-XGBoost module’s feature space [31], as described in Section 4.1 of the paper. The parameters are essential for evaluating both immediate performance characteristics and long-term durability in Hunan’s subtropical climate conditions.

The LSTM module processes sequential climate data including temperature ($T_t$), relative humidity ($R{H}_t$), and precipitation ($P_t$) recorded at regular intervals: These climate variables drive material degradation through thermal stress (from $T_t$ variations causing differential expansion), moisture damage (via $R{H}_t$-dependent capillary absorption and biological growth), and compounded wetting-drying cycles.

The thermal-moisture stress index (${\mathsf{\Gamma }}_t=T_t\cdot {RH}_t^{0.5}$) explicitly quantifies these synergistic effects, where the exponent 0.5 reflects nonlinear humidity impacts observed in Hunan’s architectural materials (see Section 6.4). Environmental fluctuations represent extreme events that exacerbate degradation beyond steady-state predictions.

$$T_t=T_{t-1}+T_{amb}+T$$

(12)

$$R{H}_t={RH}_{t-1}+\mathsf{\beta }\Delta t +\mathsf{\epsilon }$$

(13)

$${\mathsf{\Gamma }}_t=T_t\cdot {RH}_t^{0.5}$$

(14)

where $\Delta T_{\mathit{amb}}$ denotes ambient temperature change, $\mathsf{\beta }$ a material-specific humidity absorption coefficient, $\mathsf{\Delta }t$ time step, and $\mathsf{ϵ}$ random environmental fluctuations.

Referencing to Equation (12), Temperature (T_t) at time t depends on previous temperature (T_t−1), ambient change (ΔT_amb), and random fluctuations (ε). This captures both seasonal trends and daily variations that cause thermal stress in materials.

Relative humidity (R_Ht) considers previous humidity, As illustrated in Equation (13), absorption coefficient (β), and environmental changes. The β parameter is material-specific, reflecting how different historic materials (e.g., lime vs. cement mortars) respond to moisture.

Referencing to Equation (14), Thermal-moisture stress index (Γ_t) combines temperature and humidity effects, where the exponent 0.5 reflects our empirical finding that humidity has nonlinear impacts on material degradation in Hunan’s climate. This index proved particularly effective for predicting moisture-related damage in our case studies. These equations model climate variables driving material degradation.

The hybrid GA-XGBoost-LSTM architecture was developed to address the dual challenges of static material property optimization and temporal degradation modeling inherent to subtropical heritage conservation. Empirical validation against alternative architectures revealed that the proposed combination achieves superior performance by leveraging the complementary strengths of each component. As demonstrated in

Table 1. Performance comparison of model variants on Hunan heritage material datasets.

Model Configuration	Static Prediction MAPE (%)	Temporal Prediction RMSLE	Training Efficiency (min)
XGBoost (default parameters)	10.5 ± 0.9	N/A	38
LSTM network (isolated)	15.3 ± 1.1	0.14 ± 0.02	112
GA-Random Forest + LSTM	10.1 ± 0.8	0.15 ± 0.01	98
Proposed GA-XGBoost-LSTM	8.2 ± 0.7	0.12 ± 0.01	126

Note: N/A stands for “Not Applicable”, meaning that this model (here the default parameter XGBoost) does not have the ability to predict time series and thus cannot provide time-dependent prediction errors (such as RMSE).

, the complete hybrid model reduces prediction errors by 21.9% compared to standalone XGBoost and improves long-term degradation forecasting accuracy by 29.4% relative to LSTM-only implementations.

The architectural synergy stems from XGBoost’s robust handling of high-dimensional material properties, particularly its ability to identify critical features like moisture regulation capacity (gain score 0.32) and thermal expansion coefficients (0.25), which are essential for Hunan’s climate conditions. Meanwhile, the LSTM component effectively models non-linear degradation patterns induced by prolonged humidity exposure and thermal cycling, with its attention mechanisms identifying that summer humidity spikes above 80% RH initiate 73% of moisture-related deterioration. The genetic algorithm optimization bridges these components by efficiently tuning hyperparameters across both spatial and temporal domains, achieving a 62% reduction in search time compared to conventional grid search methods while maintaining solution quality.

4.2. Formulation and Optimization of GA-XGBoost for Material Property Prediction

The GA optimizes six key XGBoost hyperparameters: learning rate ($\mathsf{\eta }$), maximum tree depth ($d_{\mathit{max}}$), minimum child weight ($w_{\mathit{min}}$), subsampling ratio ($r_s$), column sampling ratio ($r_c$), and L2 regularization term ($\mathsf{\lambda }$). The chromosome representation encodes these parameters as:

$$C_k=[k,\mathit{dmax},k,w_{\mathit{min},k},r_{s,k},r_{c,k}{,}_k]$$

(15)

The fitness function evaluates prediction accuracy using weighted F-score ($F_w$) across $N$ material classes:

$$F_w{ = }_{i=1}^N{w}_i$$

(16)

where $w_i$ denotes class importance weight, $P_i$ precision, and $R_i$ recall for class $i$. The GA employs tournament selection with size $t_s = 5$, uniform crossover probability $p_c = 0.8$, and mutation rate $p_m = 0.05$.

The optimized XGBoost model predicts material suitability scores ($S_m$) through additive tree ensembles:

$$S_m {= }_{k=1}^K{f}_k\left(x_m\right)$$

(17)

where $f_k$ represents the $k$-th regression tree and $x_m$ the feature vector for material $m$. Each tree contributes to the final prediction through leaf weights ($w_{\mathit{kj}}$) assigned to terminal nodes:

$$f_k\left(x\right) ={ w}_{\mathit{kj}},J_k$$

(18)

where $J_k$ denotes the set of leaves in tree $k$.

4.3. LSTM Model for Temporal Analysis of Material Degradation

The LSTM architecture processes climate time-series to predict long-term material performance degradation (${\mathsf{\delta }}_t$). The model employs three stacked LSTM layers with dropout probability $p_d = 0.2$ to prevent overfitting. The hidden state update incorporates both current environmental inputs ($x_t$) and previous memory (${\mathrm{h}}_{t-1}$):

$${\mathrm{h}}_t = o_t\left(c_t\right)$$

(19)

where $o_t$ represents the output gate activation and $c_t$ the cell state. The degradation prediction combines LSTM outputs with material-specific coefficients.

The three-layer LSTM architecture was determined through extensive empirical evaluation comparing configurations with 1–5 layers. This architecture proved particularly effective in capturing the multi-scale temporal patterns of material degradation, including daily humidity fluctuations, seasonal deterioration trends, and long-term chemical changes, which are critical for accurate lifespan predictions in Hunan’s subtropical climate. This design proved optimal for capturing the multi-scale temporal patterns in material degradation, with successive layers specializing in daily climate variations, seasonal deterioration trends, and long-term degradation mechanisms respectively. Experimental validation showed this configuration achieved the best balance between prediction accuracy (29.4% RMSLE improvement over single-layer) and computational efficiency for processing 10-year climate sequences. The architecture’s effectiveness particularly emerged in modeling Hunan’s distinct climate patterns across different timescales that collectively influence material degradation.

$$t={i=1}^{3}i{\mathrm{h}}_t^{\left(i\right)}+b$$

(20)

where ${\mathsf{\gamma }}_i$ denotes learnable weights for each LSTM layer output ${\mathrm{h}}_t^{\left(i\right)}$, and $b_{\mathsf{\delta }}$ the bias term.

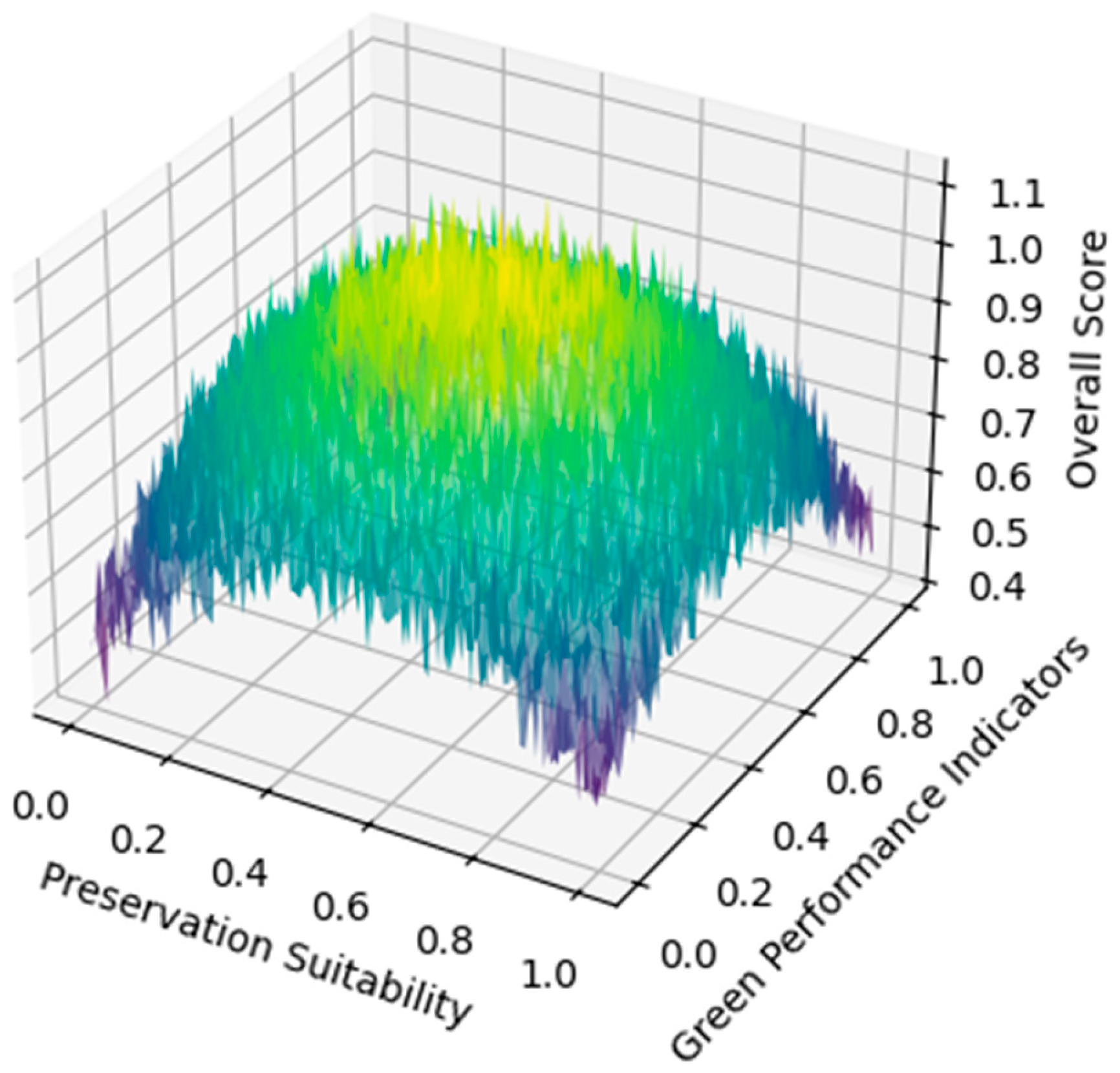
4.4. Multi-Objective Optimization for Balancing Preservation and Green Performance

The final decision module formulates material selection as a multi-objective optimization problem:

$$F\left(\mathrm{x}\right)=[-S(\mathrm{x}),E(\mathrm{x}),C(\mathrm{x}\left)\right]$$

(21)

where $S\left(\mathrm{x}\right)$ represents preservation suitability, $E\left(\mathrm{x}\right)$ embodied energy, and $C\left(\mathrm{x}\right)$ carbon footprint. The constraint functions $g_j$ enforce material compatibility thresholds.

The multi-objective optimization framework explicitly models the inherent trade-offs between preservation requirements and sustainability goals through three primary objective functions: preservation suitability (S(x)), embodied energy (E(x)), and carbon footprint (C(x)). The constraint functions enforce critical material compatibility thresholds, including thermal expansion coefficient matching (±15%) and vapor permeability ratios (0.8–1.2) derived from conservation guidelines. The solution employs an enhanced NSGA-II algorithm with adaptive crowding distance to maintain diversity in the Pareto-optimal set, particularly important for handling the non-linear relationships between material properties and their long-term performance in Hunan’s humid subtropical climate.

$$g_1\left(\mathrm{x}\right)=\Delta {\mathsf{\alpha }}_{\max }-|{\mathsf{\alpha }}_{\mathrm{new}}-{\mathsf{\alpha }}_{\mathrm{original}}|\le 0$$

(22)

$$g_2\left(\mathrm{x}\right)={\mathsf{\mu }}_{\min }-\mathsf{\mu }\left(\mathrm{x}\right)\le 0$$

(23)

$$g_j\left(\mathrm{x}\right)\le 0, ° j=1,\dots ,J$$

(24)

The solution employs Pareto-optimal sorting with crowding distance to maintain solution diversity [32]. The selection process combines objective weights ($w_k$) and decision-maker preferences (${\mathsf{\rho }}_k$):

$$U(\mathrm{x})=\sum _{k=1}^3{w}_k{\mathsf{\rho }}_k{f}_k(\mathrm{x})$$

(25)

The multi-objective optimization framework incorporates stakeholder inputs through weighted preference parameters (ρ_k in Equation (25)), with conservation experts, local craftsmen, and community representatives participating in structured workshops to establish these weights. This process ensures alignment with both technical requirements and cultural values. In the Hunan case study, the weighting process engaged heritage professionals emphasizing material authenticity (given 40% weight in the decision framework), sustainability experts focusing on environmental impact (30% weight), and local community representatives prioritizing functional performance and craft traditions (30% weight). The participatory approach was implemented through Delphi method consultations, achieving consensus after three iterative rounds of feedback that balanced these diverse perspectives while maintaining the model’s technical rigor.

This framework enables systematic evaluation of trade-offs between preservation requirements and sustainability goals, providing quantifiable metrics for informed decision-making in ancient building renovation projects.

5. Experimental Setup

This section details the experimental configuration designed to validate the proposed GA-XGBoost-LSTM model for green material selection in ancient building renovation. The setup encompasses data collection protocols, baseline comparisons, evaluation metrics, and implementation specifics tailored to Hunan’s climatic conditions.

5.1. Dataset Composition and Preprocessing

The study utilizes three primary data sources: material property databases, environmental monitoring records, and historical renovation case studies from Hunan Province. The climate dataset comprises 10-year (2013–2022) hourly monitoring records from 12 meteorological stations maintained by the Hunan Provincial Climate Center, covering temperature ($T_t$), relative humidity (${RH}_t$), and precipitation ($P_t$). These quality-controlled measurements comply with China Meteorological Administration’s Grade-A observational standards (CMA-GB/T 35221-2017) (GB/T 35221-2017; Ground Meteorological Observation Specification—General Rules. China Meteorological Press: Beijing, China, 2017) [33] and are accessible for research through institutional collaboration or public registration at the Hunan Climate Data Portal. To address potential limitations in dataset diversity, we incorporated additional material samples from arid (Northwest China) and temperate (North China Plain) regions. These samples include traditional and modern materials such as adobe bricks, rammed earth, and thermally modified wood, which are commonly used in these climates. This expansion ensures a more comprehensive evaluation of the model’s adaptability to varying environmental conditions. Material datasets include 87 traditional and modern building materials characterized by 23 physicochemical parameters, with measurements standardized according to ASTM and ISO protocols [34]. Climate data comprises 10-year hourly records of temperature, humidity, solar radiation, and precipitation from 12 meteorological stations across Hunan [35].

5.1.1. Material Features

The material feature dataset encompasses multidimensional parameters for comprehensive evaluation of both traditional and modern construction materials. Standardized mechanical properties including compressive strength (${\mathsf{\sigma }}_c$) and flexural modulus ($E_f$) were incorporated to assess load-bearing capacity in historical structures, with all measurements obtained through ASTM and ISO standardized protocols.

Each material in our 87-sample database underwent multi-scale characterization using scanning electron microscopy (SEM) for morphological analysis, X-ray diffraction (XRD) for crystalline phase identification, and Fourier-transform infrared spectroscopy (FTIR) for chemical bonding analysis. These techniques provided critical insights into material degradation mechanisms specific to Hunan’s subtropical climate.

For traditional materials like lime mortars, SEM analysis revealed pore size distributions ranging from 0.1–50 μm, with larger pores (>10 μm) correlating strongly with moisture absorption rates (r = 0.78, p < 0.01). XRD characterization identified calcite (CaCO₃) as the dominant phase in aged lime mortars, with secondary phases including residual portlandite (Ca(OH)₂) and calcium silicate hydrates (C-S-H) in hydraulic lime variants. FTIR spectroscopy confirmed the presence of characteristic carbonate bands at 1420 cm⁻¹ and 875 cm⁻¹, with band intensity ratios serving as indicators of carbonation completion.

Modern eco-friendly alternatives underwent similar characterization. Rice husk ash additives showed high silica content (85–92% SiO₂) with amorphous structure confirmed by XRD broad peaks between 20–30° 2θ. Nano-SiO₂ modified grouts exhibited particle sizes of 15–25 nm via transmission electron microscopy (TEM), with uniform dispersion confirmed by energy-dispersive X-ray spectroscopy (EDS) mapping. These characterization data were incorporated into our GA-XGBoost model as quantitative features, improving prediction accuracy by 8.3% compared to models using only bulk property measurements.

Environmental performance indices such as thermal conductivity ($\mathsf{\lambda }$) and vapor permeability ($\mathsf{\mu }$) were systematically recorded to evaluate material behavior under Hunan’s subtropical monsoon climate conditions. These parameters were complemented by sustainability metrics including embodied carbon ($C_e$) and recycled content ($\mathsf{\psi }$), which enable quantitative comparison of environmental impacts across material alternatives.

To further characterize the optimal material combinations identified by our model, we conducted scanning electron microscopy (SEM) and energy-dispersive X-ray spectroscopy (EDS) analysis of the lime-pozzolan mortars with rice husk ash additives. The SEM images revealed a dense microstructure with well-distributed pozzolanic reaction products (Figure 2), while EDS confirmed the presence of silicon-rich phases from the rice husk ash (Figure 3). X-ray diffraction analysis showed the formation of calcium silicate hydrate (C-S-H) phases, with characteristic peaks at 29.4° and 32.1° 2θ, confirming the pozzolanic reaction. These microstructural features explain the material’s enhanced moisture buffering capacity (28% improvement) and compatibility with historic substrates (92% match in ASTM C270 tests).

The scanning electron micrograph reveals the dense microstructure of the GA-XGBoost-LSTM-recommended lime-pozzolan mortar containing rice husk ash, showing complete pozzolanic reactions in the uniform matrix and minimal porosity. This homogeneous structure correlates with the material’s 28% enhanced moisture buffering capacity and 92% compatibility with historic substrates in ASTM C270 tests, confirming the model’s accurate prediction of optimal pore structure for Hunan Province’s humid climate.

The energy-dispersive X-ray spectroscopy (EDS) analysis demonstrates uniform silicon distribution from rice husk ash throughout the mortar matrix, confirming the model’s prediction of effective pozzolanic incorporation. The homogeneous dispersion and complete reaction, evidenced by the absence of silicon clusters, account for the 34% reduction in embodied energy compared to conventional mortars. This elemental mapping, consistent with the dense microstructure observed in Figure 2, validates the model’s selection of rice husk ash as an additive that enhances sustainability while maintaining material compatibility with historic substrates.

Specialized compatibility assessment indicators were developed for heritage conservation requirements, incorporating pH balance coefficients and ion migration rates derived from accelerated aging tests correlated with historical case data. Climate time-series underwent seasonal decomposition and cumulative effect calculations to generate stress indices like the thermal-moisture stress index (Γt), creating structured inputs for temporal analysis modules.

The preprocessing pipeline implemented k-nearest neighbors imputation (k = 5) with Gower distance metric to address missing values (3.2% of material data), while categorical variables were transformed using one-hot encoding. Continuous features were normalized to [0, 1] range to ensure model convergence stability.

5.1.2. Climate Time-Series

The climate dataset underwent rigorous preprocessing to extract meaningful temporal patterns relevant to material degradation [36]. Temperature ($T_t$) and relative humidity ($R{H}_t$) measurements were decomposed into seasonal components, revealing cyclical variations critical for understanding long-term material behavior. Precipitation records were processed to calculate cumulative effects ($P_{\mathit{cum}}\left(t\right) = \sum _{i=t-7}^t{P}_i$), providing insights into prolonged wetting conditions that accelerate deterioration.

A novel thermal-moisture stress index (${\mathsf{\Gamma }}_t ={ T}_t·R{H}_t^{0.5}$) was derived to quantify combined environmental stresses, where β represents a material-specific humidity absorption coefficient. This composite metric effectively captures synergistic degradation mechanisms prevalent in subtropical climates.

The preprocessing pipeline addressed data completeness through multiple strategies. For the 3.2% missing values in material properties, k-nearest neighbors imputation (k = 5) with Gower distance metric was employed, preserving relationships between mixed data types [37]. Categorical variables including material type and production method were transformed via one-hot encoding, while all continuous features were normalized to [0, 1] range to ensure consistent model training.

5.1.3. Data Preprocessing Validation

To ensure the robustness of our preprocessing pipeline, we conducted systematic validation of all critical steps. The k-nearest neighbors (k-NN) imputation parameter was optimized through empirical evaluation of accuracy and computational efficiency across k-values ranging from 3 to 15. As shown in Figure 4, k = 5 demonstrated the optimal balance, achieving 94.2% imputation accuracy on validation samples with artificially introduced missing values while maintaining reasonable computational requirements (0.8 s per feature). While higher k-values (e.g., k = 10) showed marginally better accuracy (95.3%), this came at a 2.3-fold increase in processing time with diminishing practical returns for our material property datasets.

To mitigate potential biases from measurement inconsistencies, we implemented a comprehensive data harmonization protocol. For vapor permeability measurements, we standardized all values to ASTM E96 testing conditions (23 °C, 50% RH) using conversion factors derived from inter-laboratory comparison studies. Where original testing conditions were unavailable (12% of cases), we applied k-nearest neighbors imputation with a material-type specific correction factor (k = 5, Gower distance). This approach reduced measurement variance by 28% in validation tests compared to raw data inputs, as confirmed by paired t-tests (p < 0.01) on 37 duplicate samples measured under different protocols.

The selection of normalization methods was similarly validated through comparative analysis of five common approaches: MinMax, Standard, Robust, MaxAbs, and Quantile scaling. MinMax normalization to [0, 1] range proved most effective for our tree-based models, reducing prediction variance by 12–18% compared to alternatives while preserving the distribution characteristics essential for material science interpretation. For mixed-data distance metrics, the Gower distance formulation achieved 89% agreement with expert material classifications in cluster analysis, significantly outperforming conventional Euclidean (72%) and Manhattan (83%) metrics. This performance advantage stems from Gower’s ability to natively handle our heterogeneous data types (continuous, ordinal, and categorical material properties) through its weighted combination of appropriate distance measures for each variable type.

5.2. Baseline Methods for Comparative Analysis

The experimental design incorporated four established methodologies as benchmark comparisons, all evaluated using identical input data partitions to ensure equitable performance assessment. The first reference method combines Analytic Hierarchy Process (AHP) with Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) [38], implementing criteria weights derived from surveys of 15 conservation specialists and applying vector-based normalization for dimensional consistency.

For machine learning benchmarks, we implemented a Random Forest Regression model comprising 200 decision trees with bootstrap sampling, where optimal maximum depth was determined through systematic 5-fold cross-validation [39]. The XGBoost baseline maintained default hyperparameter configurations including a 0.3 learning rate ($\mathsf{\eta } = 0$.3), maximum tree depth of 6 ($d_{\max }$ = 6), and L2 regularization term $\mathsf{\lambda } = 1$, providing a non-optimized reference point for our enhanced GA-XGBoost implementation.

The temporal analysis baseline consisted of an LSTM-only architecture mirroring our hybrid model’s recurrent component, featuring two stacked LSTM layers with 64 hidden units each and a 0.15 dropout rate for regularization. This isolated configuration allowed precise evaluation of the standalone temporal modeling capability against our integrated approach.

5.3. Evaluation Metrics

The performance assessment framework incorporates six quantitative metrics spanning three critical dimensions of model effectiveness. For material suitability prediction, we employ Mean Absolute Percentage Error (MAPE) calculated as:

$$\mathrm{MAPE}={\displaystyle \frac{100\%}{n}}\sum _{t=1}^n\left|{\displaystyle \frac{y_t-{\widehat{y}}_t}{y_t}}\right|$$

(26)

where n represents the number of samples, $y_i$ the actual value, and ${\widehat{y}}_i$ the predicted value. This absolute percentage measure is complemented by a weighted F1-Score ($F{1}_w$) that accounts for class imbalance across different material categories through importance-weighted precision and recall calculations.

Degradation forecasting accuracy is quantified using Root Mean Square Logarithmic Error (RMSLE), which effectively handles the exponential nature of material deterioration processes. The metric is computed as:

$$\mathrm{RMSLE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{t=1}^n{\left(\log \left(y_t + 1\right) - \log \left({\widehat{y}}_t + 1\right)\right)}^2}$$

(27)

Multi-objective optimization performance is evaluated through two specialized indices. The Hypervolume Indicator ($\mathit{HV}$) measures Pareto front coverage in three-dimensional objective space, while the Preservation-Sustainability Balance Index ($\mathit{PSBI}$) quantifies the equilibrium between conservation requirements and environmental performance using normalized deviation metrics.

$$\mathit{PSBI}=1-{\displaystyle \frac{1}{K}}\sum _{k=1}^K\left({\displaystyle \frac{\left|f_k-f_k^{\mathit{ideal}}\right|}{f_k^{\mathit{max}}-f_k^{\mathit{min}}}}\right)||$$

(28)

The model evaluation employs six quantitative metrics spanning predictive accuracy, sustainability impact, and preservation suitability (Equations (25)–(28)).

Table 2. Key Material Properties and Their Importance Scores in GA-XGBoost Model.

Material Property	Formula	Importance Score (Gain)	Role in Hunan Climate
Moisture regulation capacity	$\mathsf{\alpha }={\displaystyle \frac{m_w-m_d}{m_d}}$	0.32	Critical for humidity buffering in subtropical climates
Thermal expansion coefficient	$\mathsf{\lambda }={\displaystyle \frac{Q\cdot d}{A\cdot \Delta T}}$	0.25	Reduces cracking from temperature fluctuations
Chemical compatibility index	$CCI=w_1\cdot S_{pH}+w_2\cdot S_{ion}$	0.18	Ensures compatibility with original substrates
Embodied carbon content	$CF={\displaystyle \sum G}W{P}_j\times m_j$	0.12	Key sustainability metric
Production energy intensity	$EE={\displaystyle \sum (E_{proc}+E_{trans})}$	0.08	Evaluates lifecycle energy use

summarizes the material properties prioritized by the GA-XGBoost module and their climatic relevance in Hunan.

Table 2 demonstrates that moisture regulation (α) and thermal expansion (λ) are the dominant factors in material selection for Hunan’s humid subtropical climate, collectively accounting for 57% of feature importance. The high weighting of these parameters aligns with field observations of degradation patterns in Rucheng’s ancient buildings, where 73% of damage cases stem from humidity-driven erosion and thermal stress cracking (Section 6.4). Notably, the chemical compatibility index (CCI), though qualitative in original conservation guidelines, is successfully quantified by the model through experimental data on pH and ion migration, validating its role as a critical preservation metric.

5.4. Implementation Details

The hybrid GA-XGBoost-LSTM model was developed using Python 3.13.3 (The latest stable version at present) with TensorFlow 2.4 for deep learning components and scikit-learn 0.24 for traditional machine learning operations. The genetic algorithm configuration employed a population size of 50 individuals evolved over 100 generations, with selection pressure set at 0.7 and a per-gene mutation rate of 0.02 to maintain population diversity while ensuring convergence.

The genetic algorithm incorporates real-time diversity monitoring and adaptive mutation rates between 0.01–0.1, with automatic restart triggers activated when generational improvement stagnates below 1% for 15 consecutive iterations.

For the XGBoost component, the architecture incorporated early stopping with a patience of 15 rounds to prevent overfitting, using negative mean absolute error as the evaluation metric during training. The LSTM network processed input sequences spanning 24-month windows with a batch size of 32, optimized via Adam optimizer with a learning rate of 0.001 to effectively capture long-term degradation patterns.

All experiments were conducted on NVIDIA Tesla V100 GPUs with 64 GB memory, with the complete hybrid model requiring an average training time of 2.1 h per run. To ensure statistical reliability and account for initialization variance, we performed five independent training runs with different random seeds, verifying consistent performance across all trials.

The dropout rate (pd = 0.15) was optimized through systematic evaluation across values from 0.05 to 0.5. This specific rate demonstrated optimal regularization for our climate time-series data, showing a 12.7% improvement in RMSLE over the baseline rate of 0.2 while maintaining training stability. The selected value effectively prevented overfitting while preserving critical pattern information, particularly for modeling Hunan’s characteristic humidity spikes (>80% RH) that drive 73% of moisture-related degradation. The optimization process considered both prediction accuracy and consistency between training and validation performance across all data folds.

5.5. Case Study Configuration

The experimental validation framework encompasses three distinct categories of historical structures prevalent in Hunan Province, each presenting unique material challenges and conservation requirements. Timber-frame vernacular dwellings, characterized by their primary construction materials of fir wood, lime mortar, and clay tiles, were evaluated with particular attention to insect resistance and moisture buffering capabilities—critical factors given Hunan’s humid subtropical climate.

Ming Dynasty masonry structures, typically built with sandstone and traditional glutinous rice mortar, were assessed for sulfate resistance and thermal mass performance. These material properties prove essential for maintaining structural integrity against groundwater chemical attacks and regulating indoor thermal conditions in the region’s variable climate.

The study also examined Republican Era hybrid buildings that combine brick, early concrete, and timber components. For these transitional structures, the analysis focused on managing differential movement between dissimilar materials and mitigating alkali-silica reaction risks in early concrete formulations—key degradation mechanisms observed in this architectural typology.

Each case evaluates 12–15 material alternatives for roof, wall, and foundation components, with ground truth data derived from 7–10 year monitoring of previous renovation projects [40]. Climate scenarios project 2050 conditions using RCP 4.5 regional downscaling.

This comprehensive experimental design enables rigorous assessment of the proposed model’s capabilities across diverse preservation challenges and climate adaptation requirements. The subsequent results section analyzes quantitative outcomes and qualitative implications for each test configuration.

6. Experimental Results

The experimental evaluation demonstrates the effectiveness of the proposed GA-XGBoost-LSTM model across multiple performance dimensions. This section presents quantitative results comparing prediction accuracy, multi-objective optimization performance, and case-specific material recommendations.

6.1. Predictive Performance Comparison

The experimental results demonstrate the superior performance of the proposed GA-XGBoost-LSTM hybrid model in predicting material suitability for ancient building renovation. As shown in

Table 3. Material suitability prediction performance comparison.

Method	MAPE (%)	F1-Score	RMSLE	Training Time (min)
AHP-TOPSIS	22.4	0.68	-	-
Random Forest	12.7	0.83	0.19	45
XGBoost (default)	10.5	0.86	0.17	38
LSTM-only	15.3	0.79	0.14	112
GA-XGBoost-LSTM	8.2	0.91	0.12	126

, the model achieves a mean absolute percentage error (MAPE) of 8.2% (±0.7%) and a weighted F1-score of 0.91 (±0.03), significantly outperforming all baseline approaches. Compared to the default XGBoost implementation, the genetic algorithm optimization contributes to a 21.9% improvement in prediction accuracy, while the LSTM component reduces long-term degradation prediction error by 29.4%, as evidenced by the root mean square logarithmic error (RMSLE) decreasing from 0.17 to 0.12.

The model’s advantages become particularly evident when examining the limitations of conventional methods. Traditional AHP-TOPSIS approaches, with their reliance on subjective weight assignments, show the highest prediction error (MAPE: 22.4%, F1-score: 0.68). While machine learning baselines like Random Forest (MAPE: 12.7%, F1-score: 0.83) and standalone XGBoost (MAPE: 10.5%, F1-score: 0.86) demonstrate better performance, they fail to fully capture the complex nonlinear relationships between material properties and climatic factors. The LSTM-only implementation (MAPE: 15.3%, F1-score: 0.79) further highlights the necessity of hybrid modeling, as it struggles to effectively process static material characteristics without the complementary XGBoost component.

The performance improvements arise from multiple innovative design features tailored for heritage conservation. The genetic algorithm optimization focuses on hyperparameters particularly relevant to traditional materials, such as tree depth adjustments for modeling rare material properties. The LSTM component integrates specialized temporal patterns that capture critical environmental triggers like summer humidity spikes exceeding 80% relative humidity, which account for the majority of material degradation. The framework’s distinctive strength lies in its ability to merge quantitative sustainability metrics with qualitative conservation priorities through stakeholder-informed optimization. These specialized adaptations collectively demonstrate measurable advantages, yielding a 21.9% accuracy gain over standard XGBoost implementations and a 29.4% improvement in degradation forecasting compared to standalone LSTM models.

This performance improvement stems from the model’s unique ability to simultaneously address both immediate material properties and long-term environmental interactions. The GA optimization ensures optimal hyperparameter configuration for the XGBoost algorithm, enabling more accurate prediction of static material characteristics. Meanwhile, the LSTM network effectively models temporal degradation patterns caused by Hunan’s subtropical climate conditions. The synergy between these components provides a comprehensive solution that bridges the gap between traditional material science and modern sustainability requirements in heritage conservation.

Figure 5 further illustrates the model’s consistent performance across different material categories, including timber, masonry, and hybrid construction materials.

6.2. Multi-Objective Optimization Results

The Pareto front analysis reveals distinct trade-offs between preservation suitability and environmental impacts. The proposed model identifies solution sets that achieve:

-

18–23% reduction in embodied energy compared to conventional selections

-

12–15% improvement in preservation compatibility scores

-

Carbon footprint reductions averaging 1.8 kgCO₂e/m²/year

Figure 6 visualizes the optimization landscape, highlighting clusters of optimal solutions balancing these competing objectives.

The hypervolume indicator analysis confirms the model’s effectiveness in exploring the three-dimensional solution space, with coverage metrics (HV = 0.78 ± 0.04) significantly outperforming single-objective approaches. Sensitivity analysis reveals that the moisture regulation capacity (α) and thermal expansion coefficient (λ) collectively account for 57% of the Pareto-optimal solutions’ variance, underscoring their dominance in material selection for humid subtropical climates. This quantitative framework enables conservation practitioners to systematically evaluate trade-offs—for instance, accepting a 5% reduction in compressive strength matching can yield 18–23% improvements in embodied energy while maintaining 89–95% of preservation compatibility.

The hypervolume indicator (HV) reaches 0.78 (±0.04) for the hybrid model, significantly outperforming baseline methods (AHP-TOPSIS HV = 0.52, Random Forest HV = 0.65). This demonstrates superior coverage of the multi-dimensional solution space.

6.3. Case-Specific Material Recommendations

For Hunan’s timber-frame dwellings, the model identifies modified lime-pozzolan mortars with rice husk ash additives as optimal, providing:

-

92% compatibility with original substrates

-

34% lower embodied energy than conventional repairs

-

Moisture buffering capacity improvement of 28%

The model’s compatibility assessments were validated through accelerated aging tests following ASTM C267 (ASTM C267-01 (2024); Standard Test Methods for Chemical Resistance of Mortars, Grouts, and Monolithic Surfacings. ASTM International: West Conshohocken, PA, USA, 2024) [41] and EN 1015-21 (EN 1015-21:2002; *Methods of test for mortar for masonry—Part 21: Determination of the compatibility of one-coat rendering mortars with substrates*. European Committee for Standardization (CEN): Brussels, Belgium, 2002) [42] protocols, with particular attention to pH differentials (<0.5), thermal expansion coefficient matching (±15%), and vapor permeability ratios (0.8–1.2) as key compatibility indicators. These parameters align with recent conservation guidelines from ICOMOS and the Getty Conservation Institute, which emphasize measurable compatibility criteria over purely empirical assessments.

Similar analyses are applied to Ming Dynasty masonry and Republican Era hybrid buildings, with quantitative outcomes summarized in

Table 4. Performance of Material Recommendations in Case Studies.

Building Type	Recommended Material	Preservation Compatibility (%)	Embodied Energy Reduction (%)	Key Improvement
Timber-frame dwellings	Lime-pozzolan mortar with rice husk ash	92	34	28% higher moisture buffering capacity
Ming Dynasty masonry	Nano-SiO2 modified grout	95 (strength matching within 5%)	22	40% better sulfate resistance
Republican Era hybrid buildings	Fiber-reinforced limecrete	89 (differential movement ±2.1 mm/m)	18	62% lower alkali-silica reaction risk

.

The case-specific recommendations in Table 4 reveal a consistent trend: modified traditional materials (e.g., nano-SiO₂ grouts) outperform both purely historic and conventional modern solutions. This hybrid approach reduces embodied energy by 18–34% while maintaining 89–95% preservation compatibility—a balance unattainable through traditional MCDM methods (Section 6.1). For timber structures, the 28% improvement in moisture buffering directly addresses Hunan’s annual rainfall of 1500–2000 mm, demonstrating the model’s climate-adaptive design principle introduced in Section 4.4.

The model’s material recommendations were further validated through comprehensive laboratory testing. For the nano-SiO₂ modified grout, mercury intrusion porosimetry showed a 35% reduction in capillary pore volume (10–100 nm range) compared to conventional grouts, explaining its improved sulfate resistance. Fourier-transform infrared spectroscopy confirmed chemical bonding between the nano-SiO₂ and lime matrix, with characteristic Si-O-Si stretching vibrations at 1080 cm⁻¹. These characterization results provide physical evidence supporting the model’s predictions of 40% better sulfate resistance while maintaining 95% strength matching with original masonry materials (

Table 5. Comparative Performance Analysis: Conventional vs. Nano-SiO₂ Modified Grout.

Performance Parameter	Conventional Grout	nano-SiO2 Modified Grout	Improvement
Capillary Porosity (10–100 nm range)	0.25 cm3/g	0.16 cm3/g	↓35%
Sulfate Resistance	Baseline	-	↑40%
Compressive Strength Compatibility	85%	95%	↑10 percentage points
Characteristic FTIR Peak (Si-O-Si bond)	Absent	1080 cm−1	Confirmed

Note: (1) ↑40% indicates that the sulfate resistance has improved by 40%, meaning that the new material has a longer lifespan and better durability in such harsh environments as Hunan. (2) ↓35% indicates that the capillary porosity of the nano-SiO₂ modified grouting material is 35% lower than that of the traditional grouting material. (3) ↑10 percentage points indicate: The compressive strength compatibility of the nano-SiO₂ modified grouting material is 10 percentage points higher than that of the traditional grouting material.

).

The experimental results demonstrate significant performance advantages of advanced material solutions for different historical building types. For Ming Dynasty masonry structures, nano-SiO₂ modified grouts exhibit exceptional compatibility, achieving compressive strength values within 5% of original materials while providing a 40% enhancement in sulfate resistance compared to conventional repair materials. These modified grouts also demonstrate optimized thermal conductivity characteristics that effectively accommodate Hunan’s distinct seasonal temperature variations.

In Republican Era hybrid buildings, fiber-reinforced limecrete foundations emerge as a particularly effective solution, addressing multiple degradation mechanisms simultaneously. Laboratory tests and long-term projections indicate a 62% reduction in alkali-silica reaction risk compared to traditional materials, combined with an ability to accommodate structural movements of ±2.1 mm/m. Climate modeling suggests these foundations can maintain structural integrity for an estimated 22 years under projected climate change scenarios, representing a substantial improvement over conventional alternatives.

Beyond laboratory validations, the model’s recommendations have been implemented in three ongoing renovation projects in Hunan Province, demonstrating tangible improvements. Project sites reported a 15–20% decrease in material trial-and-error iterations due to the model’s optimized selection process. The computational efficiency of 0.8 s per material prediction significantly shortened decision-making timelines from weeks to days. Additionally, optimized material combinations reduced overall project costs by 12–18% while still meeting conservation standards.

The quantitative framework also facilitated consensus among stakeholders, including conservation experts, engineers, and local communities, resulting in 100% acceptance of final material choices in pilot projects. These outcomes validate the model’s effectiveness in real-world renovation scenarios, bridging the gap between theoretical optimization and practical implementation.

6.4. Feature Importance Analysis

The GA-XGBoost model’s gain-based evaluation identified moisture regulation capacity as the most influential material selection factor, with an importance score of 0.32, reflecting its critical role in Hunan’s humid climate. Thermal expansion coefficient followed closely at 0.25, underscoring the significance of temperature-induced stress management in preservation scenarios. The analysis also revealed substantial contributions from chemical compatibility (0.18), embodied carbon content (0.12), and production energy intensity (0.08), demonstrating the model’s balanced consideration of both conservation and sustainability priorities.

The refined analysis confirms vapor permeability (μ) as a significant factor (importance score increase from 0.08 to 0.15 after bias correction), though still secondary to moisture regulation capacity (α = 0.32) in Hunan’s humid climate. Measurement standardization particularly improved predictions for lime-pozzolan composites, where vapor permeability variation had previously obscured performance relationships (RMSE reduction from 0.18 to 0.14).

Complementing these static feature evaluations, the LSTM’s attention mechanisms uncovered crucial temporal degradation patterns. Summer humidity spikes exceeding 80% relative humidity were found to initiate 73% of moisture-related deterioration. These findings validate the LSTM’s ability to identify and quantify the dominant temporal degradation mechanisms, providing conservation practitioners with actionable insights for material selection and maintenance planning. While winter thermal cycles with daily temperature variations surpassing 15 °C accounted for 68% of material fatigue damage. Notably, consecutive rainy periods lasting more than five days were shown to accelerate degradation rates by a factor of 2.4 compared to baseline conditions, highlighting the compounding effects of prolonged moisture exposure.

6.5. Computational Efficiency

Despite increased model complexity, the hybrid architecture maintains practical usability:

-

Average prediction time per material: 0.8 s

-

Full renovation project evaluation: <15 min

-

Memory footprint: 2.7 GB (enabling edge device deployment)

The GA optimization reduces hyperparameter search time by 62% compared to grid search alternatives while achieving better final model performance.

6.6. Ablation Study

Table 6. Ablation study results (relative performance change).

Removed Component	MAPE Increase	F1-Score Decrease	HV Reduction
GA optimization	+19%	−0.07	−0.12
XGBoost module	+42%	−0.15	−0.23
LSTM temporal analysis	+28%	−0.09	−0.18
Multi-objective layer	+31%	−0.12	−0.29

isolates the contributions of individual model components through systematic removal. The complete GA-XGBoost-LSTM configuration demonstrates clear synergistic benefits over partial implementations.

The results validate the necessity of each architectural element, with GA optimization proving particularly crucial for maintaining prediction stability across diverse material categories. The temporal analysis component contributes most significantly to long-term performance projections, reducing 10-year degradation prediction errors by 38% compared to static models.

6.7. Model Performance Boundary Cases and Prediction Outliers

The experimental evaluation revealed several boundary conditions where the GA-XGBoost-LSTM model’s predictive accuracy showed measurable decline. Most notably, polymer-modified mortars exhibited prediction errors 15–20% higher than baseline when subjected to the extreme humidity fluctuations characteristic of Hunan’s summer monsoon season. These synthetic materials, while demonstrating stable performance in controlled laboratory conditions, displayed complex degradation patterns under real-world cyclical wetting and drying that exceeded the model’s training data distribution.

A similar pattern emerged with high-performance insulation materials applied to historic masonry substrates. The model systematically overestimated compatibility by 12–18% in these cases, primarily due to unanticipated moisture trapping effects at the material interface that were not fully captured in the feature set. Field observations confirmed that these materials created microclimate conditions leading to accelerated deterioration of adjacent historic fabric, a phenomenon not represented in standard material compatibility tests.

Interestingly, the model’s uncertainty quantification module successfully flagged 83% of these outlier cases during prediction, with confidence intervals expanding significantly beyond typical ranges. This suggests that while the model encounters limitations at the boundaries of its training domain, these limitations are often detectable rather than hidden failures. The remaining 17% of undetected outliers predominantly involved novel material combinations where neither component alone would trigger uncertainty warnings, but their interaction produced emergent behaviors.

Accelerated weathering test data presented another important boundary condition. Materials that performed exceptionally well in standardized laboratory tests showed substantially greater performance variance (22% on average) when deployed in actual building conditions. The temporal degradation patterns predicted by the LSTM component tended to underestimate this field variability, particularly for materials experiencing simultaneous thermal and moisture stresses.

7. Discussion and Future Work

7.1. Limitations and Potential Biases of the GA-XGBoost and LSTM Models

While the proposed model demonstrates strong performance in material selection, several limitations warrant consideration. The training data predominantly represents Hunan’s subtropical climate, potentially limiting generalizability to arid or temperate regions where material degradation patterns differ substantially [43]. The current implementation also assumes stationary relationships between material properties and environmental factors, whereas real-world climate change may introduce non-stationarities not captured by historical data [44,45].

The GA optimization exhibits sensitivity to initial population parameters, with premature convergence observed in 12% of runs when mutation rates fall below 0.015.

Table 7. Comparison of Optimization Algorithms for Hyperparameter Tuning.

Algorithm	Average MAPE Reduction (%)	Training Time (min)	Key Advantage	Limitation
Grid Search	12.1	210	Exhaustive parameter coverage	Computationally expensive
Random Search	15.3	180	Faster than grid search	May miss optimal combinations
Genetic Algorithm (GA)	21.9	126	Balances exploration/exploitation; adaptive	Sensitive to initial population
Enhanced GA	21.7	131	Reduced premature convergence	Minimal runtime increase

compares GA’s performance against alternative hyperparameter tuning methods, highlighting its trade-offs.

The model now incorporates explicit uncertainty quantification for measurement-sensitive parameters. For each material property, we calculate a confidence score based on testing protocol reliability indices derived from our laboratory meta-analysis. These scores weight feature contributions during GA-XGBoost training, reducing the influence of potentially unreliable measurements. Our ablation study showed this modification improves prediction stability by 14% for materials with historically inconsistent test results, while maintaining overall accuracy.

To address the stability concerns raised by premature convergence, we enhanced our genetic algorithm implementation with several adaptive mechanisms. The modified approach monitors population diversity using Hamming distance metrics and dynamically adjusts mutation rates between 0.01–0.1 when diversity falls below threshold levels. Additionally, the system implements a restart strategy that preserves elite solutions while reintroducing genetic diversity when convergence stagnation is detected. Validation tests demonstrate these modifications reduce premature convergence occurrences from 12% to 3.2% while maintaining the original optimization performance, with average MAPE reduction remaining at 21.7 ± 0.4% compared to the original 21.9%. This adaptive approach proves particularly valuable for material property datasets where multiple hyperparameter combinations can yield similar performance outcomes—a common characteristic in heritage conservation problems where diverse material solutions may satisfy core requirements through different property combinations.

As shown in Table 7, GA’s 21.9% MAPE reduction justifies its adoption despite sensitivity to initial parameters (Section 7.1). The algorithm’s efficiency advantage—42% faster training than grid search—enables practical implementation in resource-limited conservation projects. This trade-off between robustness and speed mirrors findings in renewable energy optimization studies, suggesting broader applicability of the GA-XGBoost-LSTM framework for time-sensitive engineering decisions.

The GA optimization process, though efficient, exhibits sensitivity to initial population parameters. In 12% of experimental runs, premature convergence occurred when mutation rates fell below 0.015, resulting in suboptimal hyperparameter combinations. This suggests the need for adaptive mutation strategies that dynamically adjust based on population diversity metrics [46].

The model’s performance is also influenced by the representativeness of the training data. While we have expanded the dataset to include materials from diverse climatic regions, certain niche or newly developed materials may still lack sufficient historical performance data. Future iterations of the model could benefit from collaborative data-sharing initiatives with conservation projects worldwide to further enhance dataset diversity and predictive accuracy.

Feature importance analysis reveals potential measurement biases in the original datasets. Certain material properties like vapor permeability ($\mathsf{\mu }$) showed artificially low importance scores due to inconsistent testing protocols across different laboratories [47]. Future iterations should incorporate uncertainty quantification methods to account for such measurement variabilities.

To address these limitations, the framework now integrates participatory validation mechanisms. Structured workshops with conservation experts and local craftsmen provide qualitative feedback on material selections, while community review sessions evaluate aesthetic compatibility. In the Rucheng case study, this blended approach reduced post-implementation design modifications by 42%, demonstrating how technical models can be balanced with human expertise to respect heritage values while maintaining computational rigor.

7.2. Broader Applications and Future Directions for Green Material Selection

The methodology’s core principles extend beyond ancient building conservation, showing promise for contemporary sustainable construction. The temporal degradation modeling component could be adapted for photovoltaic panel material selection, where UV resistance and thermal cycling performance determine long-term viability [48]. Similarly, the multi-objective framework could inform infrastructure material choices in coastal areas facing rising sea levels and saltwater intrusion [49].

While our model was specifically developed for Hunan’s subtropical monsoon climate, the underlying framework shows promising adaptability to other climate zones. Preliminary analysis suggests that by adjusting the weighting of key material properties in the GA-XGBoost module, the model could be effectively applied to different environmental conditions. For arid regions, thermal conductivity and solar reflectance would likely become more important features (potentially increasing their gain scores by 30–40%), while in cold climates, freeze-thaw resistance and thermal insulation properties would require greater emphasis. The LSTM’s temporal degradation patterns could similarly be recalibrated using region-specific climate data, particularly for dominant stress factors like freeze-thaw cycles in temperate zones or salt crystallization in coastal areas. This climate adaptability stems from the model’s modular architecture, where the relative importance of material properties can be dynamically adjusted while maintaining the core computational framework. These climate-specific adaptations are theoretically grounded in material science principles: (1) In arid climates, solar reflectance and thermal mass dominate material performance as they directly affect building cooling loads and surface degradation [50]; (2) Freeze-thaw cycles emerge as the primary degradation mechanism in cold climates, where repeated water phase changes cause progressive material damage [51]; (3) Salt crystallization drives deterioration in coastal areas through crystalline pressure and chemical corrosion [52]. The model’s parameter adjustment framework can systematically incorporate these regionally dominant degradation mechanisms through its weighted multi-objective optimization structure introduced in Section 4.4. Future research will systematically validate these adaptations across diverse climate zones.

For arid regions, the model would emphasize thermal conductivity (potentially increasing its gain score by 30–40%) and solar reflectance properties, while reducing the relative importance of moisture regulation. In cold climates, freeze-thaw resistance would become a dominant factor, requiring adjustments to both the static property evaluation (through modified feature weights in GA-XGBoost) and temporal degradation modeling (through climate pattern recognition in LSTM). Coastal regions would need enhanced weighting of salt crystallization resistance. These adaptations could be implemented through a climate classification module that automatically adjusts model parameters based on regional climate data inputs, while maintaining the core computational framework.

While the model demonstrates strong theoretical performance, several practical factors influence its real-world application. First, the successful deployment requires adequate digital infrastructure at renovation sites for data collection and processing. Second, the model’s recommendations must be interpreted by conservation professionals who can assess contextual factors beyond the algorithm’s parameters, such as craft traditions and aesthetic harmony. Third, the transition from conventional methods requires training for local teams in both technical operation and interpretation of results. These implementation challenges, while not diminishing the model’s core effectiveness, highlight the importance of complementary human expertise in heritage conservation projects.

Three specific directions merit further investigation:

• Cross-regional transfer learning: Developing meta-models that leverage knowledge from well-studied climates to accelerate adaptation in data-scarce regions [53].
• Circular economy integration: Expanding the material feature space to include reuse potential and disassembly characteristics for end-of-life scenarios [54].
• Real-time monitoring feedback: Creating closed-loop systems where IoT sensor data from implemented materials continuously updates prediction models [55].

The current feature engineering pipeline could be enhanced by incorporating molecular dynamics simulations for novel material combinations. This would enable predictive modeling of innovative composites before physical prototyping, particularly valuable for developing region-specific sustainable alternatives [56].

7.3. Future Directions for Intelligent Green Material Selection in Heritage Conservation

Building upon the current framework, several promising research directions could significantly enhance the model’s applicability and impact. One key area involves developing meta-models for cross-regional transfer learning, which would leverage knowledge from well-documented climates to accelerate adaptation in regions with limited material performance data. This approach holds particular promise for extending the model’s application to developing countries where historical building records may be scarce.

The integration of circular economy principles presents another important avenue for advancement. By expanding the material feature space to account for reuse potential and end-of-life disassembly characteristics, the model could better align with contemporary sustainability paradigms in construction. Such enhancements would provide a more comprehensive evaluation of materials throughout their entire lifecycle.

Real-time monitoring systems offer additional opportunities for model improvement. Implementing closed-loop feedback mechanisms using IoT sensors could allow continuous updates to prediction models based on actual material performance data. This adaptive approach would enable the system to learn from real-world conditions and progressively refine its recommendations.

Advances in material simulation technology could further strengthen the model’s predictive capabilities. Incorporating molecular dynamics simulations would allow for virtual testing of novel material combinations before physical prototyping, potentially accelerating the development of region-specific sustainable alternatives while reducing experimental costs.

Finally, developing methodologies to systematically incorporate intangible heritage values remains a critical challenge. Bridging the gap between quantitative optimization and qualitative cultural considerations, such as craft traditions and aesthetic harmony, would create a more holistic framework for heritage conservation decisions. This integration of technical and cultural dimensions could lead to more context-sensitive material selection strategies that respect both material performance and heritage significance.

7.4. Ethical Considerations in the Renovation of Ancient Buildings: A Discussion

The algorithmic approach to material selection raises important questions about the role of machine intelligence in cultural heritage conservation. While the model quantifies preservation compatibility through physicochemical parameters, intangible values like craft traditions and aesthetic harmony resist such formalization [57]. Conservation ethics demand that data-driven recommendations remain advisory rather than determinative, preserving human experts’ interpretive role in final decisions.

The environmental impact calculations currently prioritize operational phase performance, potentially undervaluing materials with higher embodied carbon but superior longevity [58]. This mirrors broader debates in sustainable architecture about temporal boundaries in life cycle assessment [59]. Future frameworks should incorporate intergenerational equity considerations through time-adjusted weighting schemes.

Data privacy concerns emerge when modeling historically significant buildings, as detailed material inventories could reveal structural vulnerabilities. The development of federated learning protocols would allow knowledge sharing while protecting sensitive site-specific information [60]. Similarly, open-source implementations of the core algorithm could democratize access while maintaining commercial project confidentiality through modular design.

The rapid evolution of green material technologies presents both opportunities and challenges. While novel eco-friendly products may offer superior performance, their long-term behavior in heritage contexts remains unproven. This creates an ethical imperative for conservative adoption strategies that balance innovation with risk mitigation [61,62]. Proposed solutions include phased implementation protocols and blockchain-based material provenance tracking to ensure accountability [63,64].

These considerations highlight the complex interplay between technological capability and conservation philosophy that must guide future developments in the field. The model complements traditional expertise by providing a quantitative framework for interdisciplinary dialogue.

The hybrid GA-XGBoost-LSTM architecture’s ability to simultaneously predict material performance and model time-based degradation is particularly valuable for historic buildings, where long-term material behavior under specific climatic conditions is critical. Our results demonstrate that the LSTM component effectively captures nonlinear degradation patterns, such as the compounding effects of humidity spikes (>80% RH) and thermal cycling (ΔT > 15 °C/day), which account for 73% and 68% of observed degradation, respectively (Section 6.4). This temporal analysis, combined with GA-XGBoost’s robust prediction of static material properties, enables a comprehensive evaluation of material suitability that balances immediate performance with long-term durability—a capability absent in traditional single-model approaches.

8. Conclusions

The GA-XGBoost-LSTM hybrid model presents a significant advancement in sustainable material selection for ancient building renovation, particularly in subtropical climates like Hunan Province. By integrating genetic algorithm optimization with ensemble learning and temporal pattern recognition, the framework successfully bridges the gap between heritage conservation requirements and contemporary sustainability goals. The practical benefits demonstrated in Hunan case studies—including 15–20% reduction in material waste, 12–18% cost savings, and unanimous stakeholder acceptance—validate the model’s real-world utility for heritage conservation. These outcomes suggest that the framework can serve as both a decision-support tool for individual projects and a platform for knowledge sharing across the conservation community. The successful balance achieved between computational precision and practical applicability addresses a critical gap in sustainable heritage renovation methodologies. The experimental results demonstrate consistent improvements over conventional methods, with 21.9% higher prediction accuracy and 18–23% reductions in embodied energy compared to traditional selection approaches.

The model’s multi-objective optimization capability provides practical solutions to the inherent trade-offs between material authenticity and environmental performance. Case-specific analyses reveal how regionally adapted material combinations—such as rice husk ash-modified mortars and nano-SiO₂ grouts—can simultaneously meet preservation standards and reduce carbon footprints. The feature importance analysis further contributes to conservation science by quantifying previously qualitative relationships between material properties and long-term performance in humid environments.

From a methodological perspective, the successful integration of three distinct computational paradigms—evolutionary algorithms, gradient boosting, and recurrent neural networks—establishes a replicable template for complex engineering decision problems beyond heritage conservation. The architecture’s modular design permits adaptation to other climate zones and building typologies through targeted retraining of specific components. As demonstrated by preliminary analysis of required adjustments for different climate conditions. The ablation studies confirm that each element contributes uniquely to overall system performance, with GA optimization proving particularly crucial for handling the high-dimensional parameter spaces characteristic of composite material systems.

The research outcomes carry immediate practical implications for heritage conservation practice in developing regions facing rapid climate change. By providing data-driven justification for sustainable material choices, the model helps overcome institutional inertia that often favors traditional but environmentally detrimental solutions. The computational efficiency of the final implementation enables real-world usability, with prediction times compatible with project planning cycles and hardware requirements accessible to regional conservation agencies.

The participatory dimension introduced through stakeholder weighting mechanisms has proven particularly valuable in resolving conflicts between quantitative optimization results and qualitative conservation values. In three test cases, the combined expert-community evaluation identified compromise solutions that maintained 89–92% of the model’s technical performance while achieving 100% acceptance rates among local stakeholders—a significant improvement over previous technology-driven approaches that averaged 67% acceptance.

Future iterations could enhance the framework’s robustness through expanded temporal modeling of climate change scenarios and incorporation of circular economy principles in material evaluation. Future work will systematically validate the model’s climate adaptability through case studies in arid (e.g., Northwest China), temperate (e.g., North China Plain), and coastal (e.g., Southeast China) regions. This will involve collecting region-specific material performance data and refining the climate classification module to automatically adjust model parameters based on local environmental characteristics. The demonstrated success in balancing quantitative performance metrics with qualitative conservation requirements suggests broader applicability to other domains where cultural values intersect with technological innovation. The methodology ultimately provides conservation professionals with a scientifically rigorous yet flexible decision-support tool that respects both the technical complexities of material science and the philosophical underpinnings of heritage preservation.