Research on Seismic Performance of Assembled Steel–Concrete Composite Joints in the Top Layer of Subway Station Under High Axial Compression Ratio
Abstract
1. Introduction
2. Materials and Methods Experimental Programs
2.1. Specimen Design
2.2. Material Properties
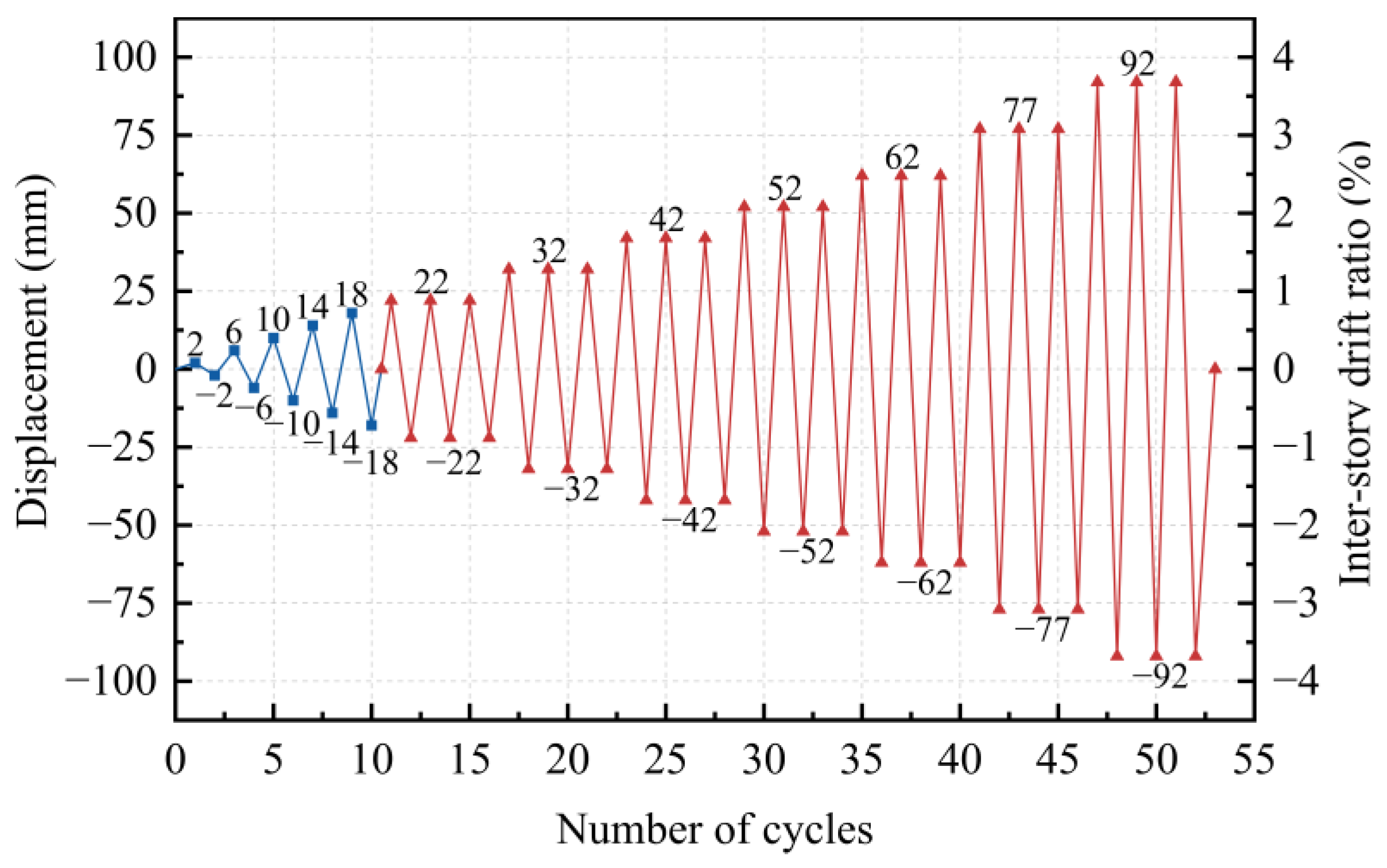
2.3. Experimental Device and Loading Scheme
3. Experimental Results
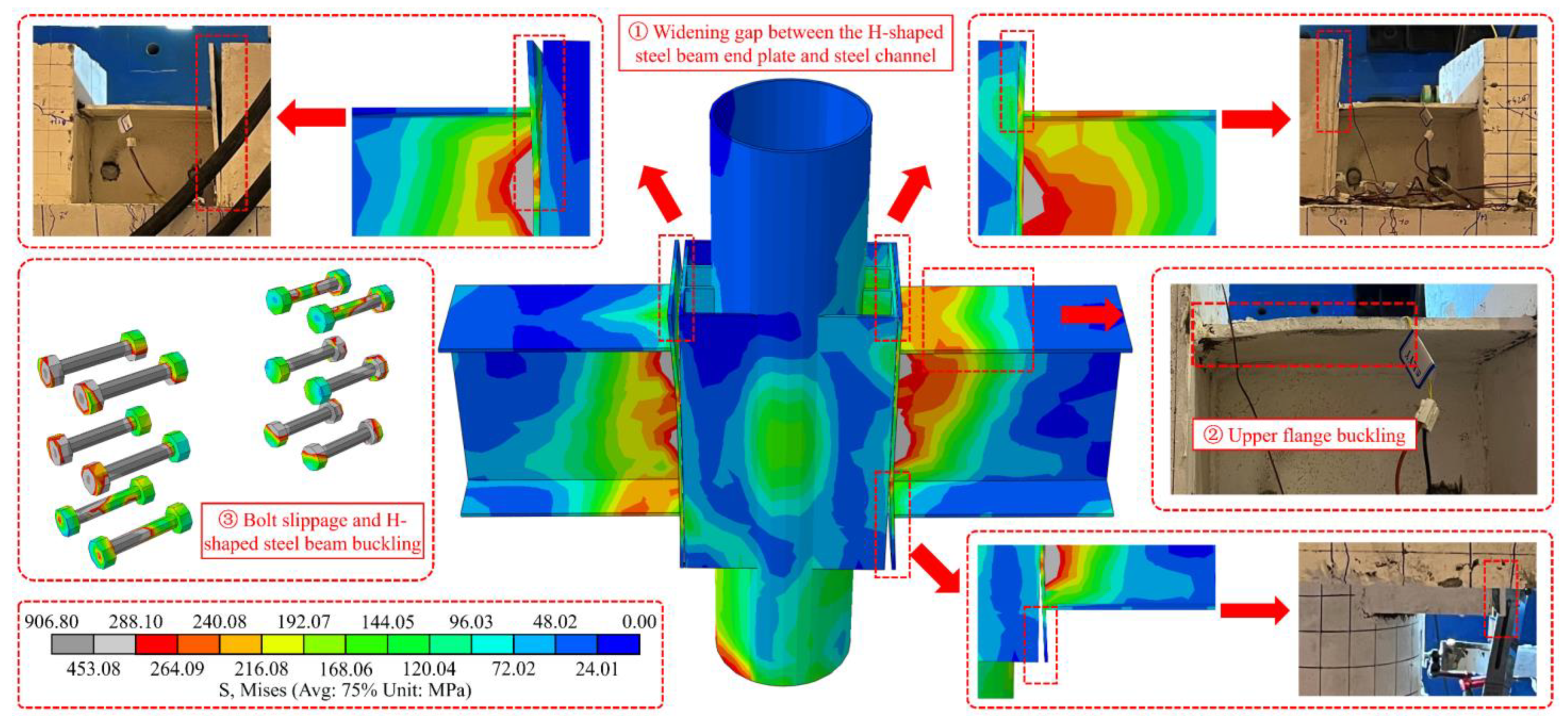
3.1. Experimental Phenomena
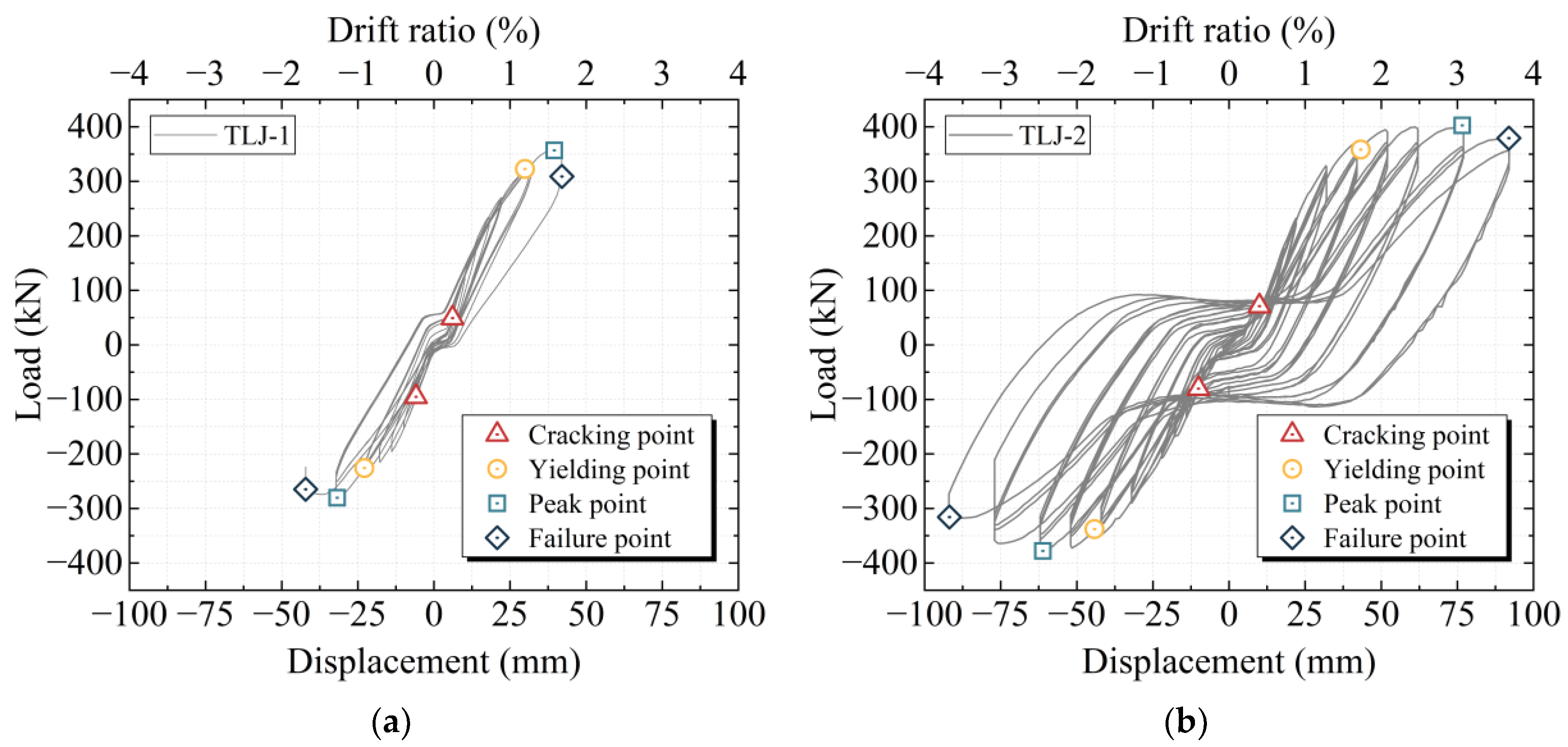
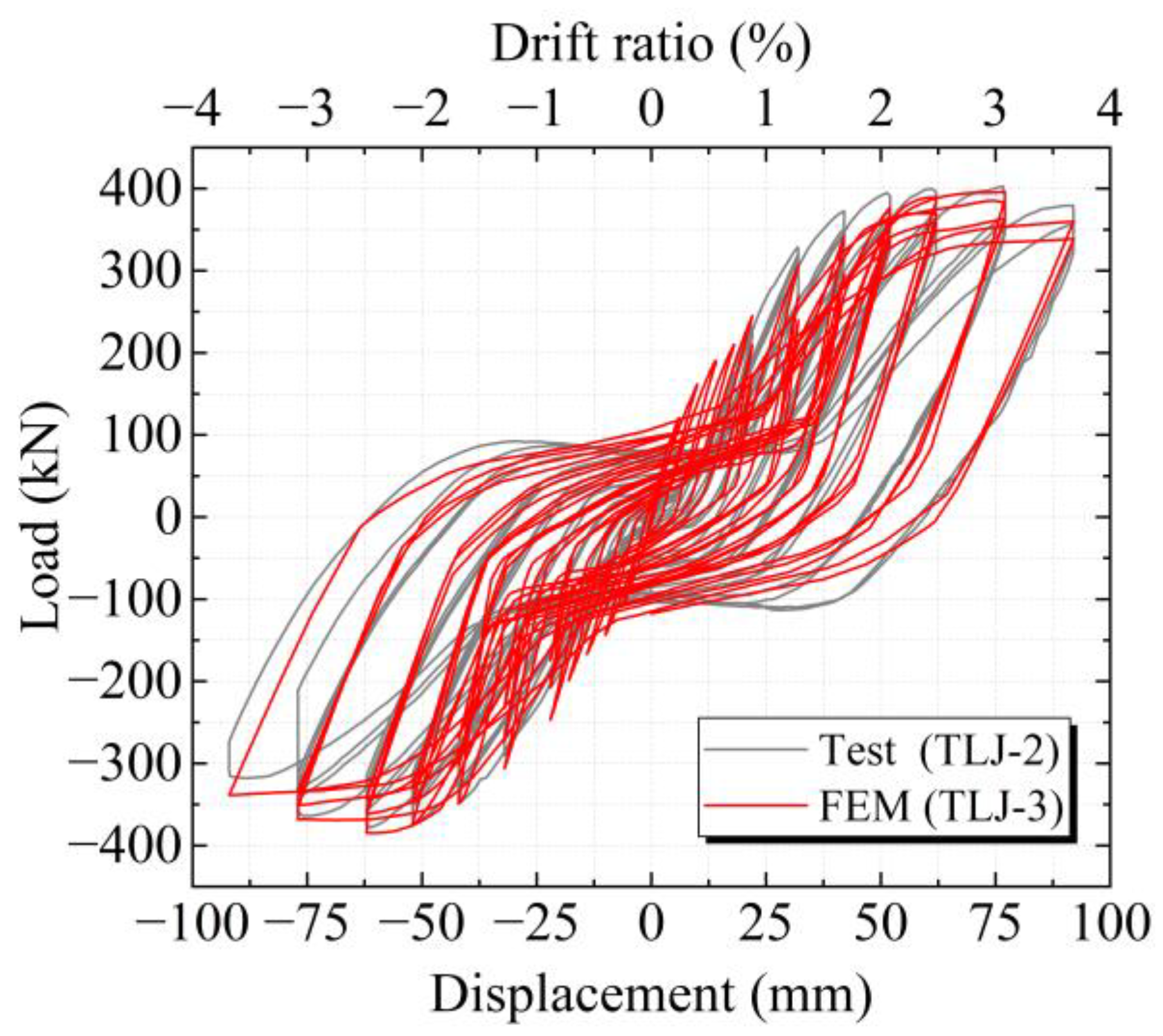
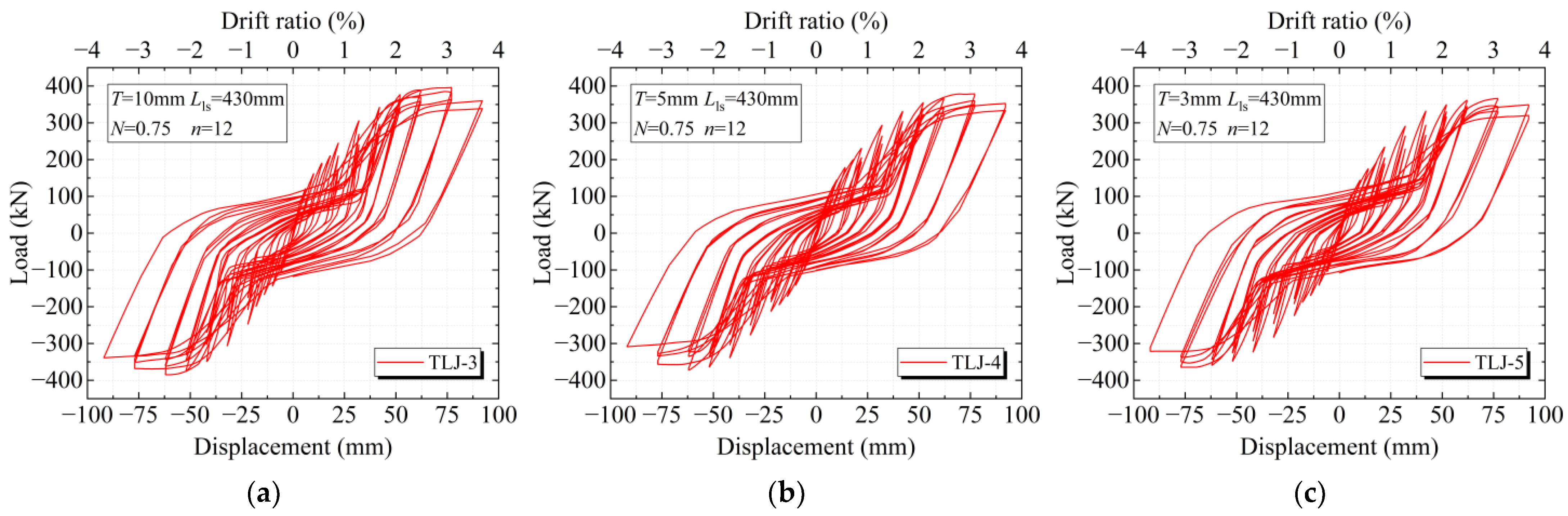
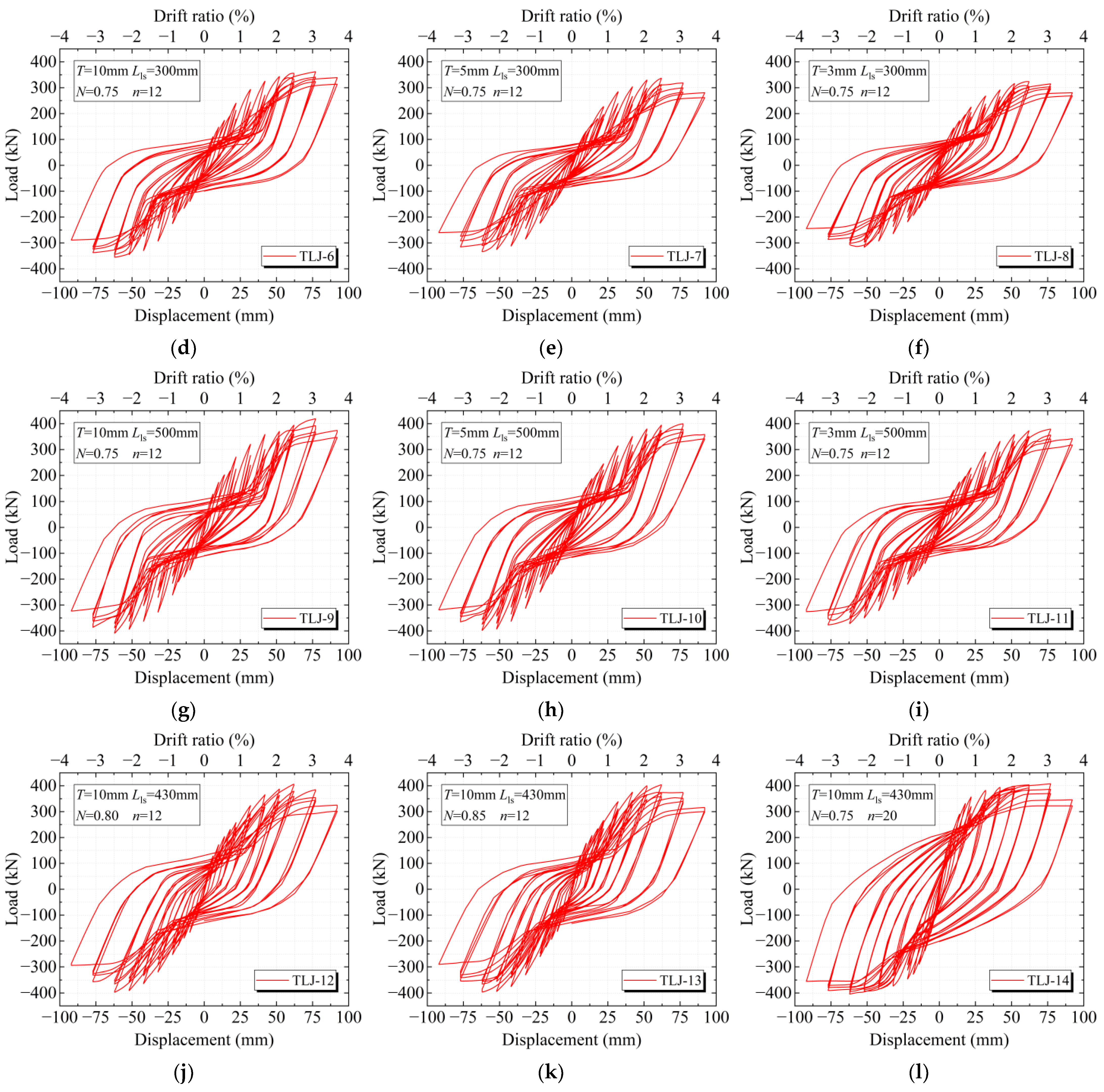
3.2. Hysteresis Curve
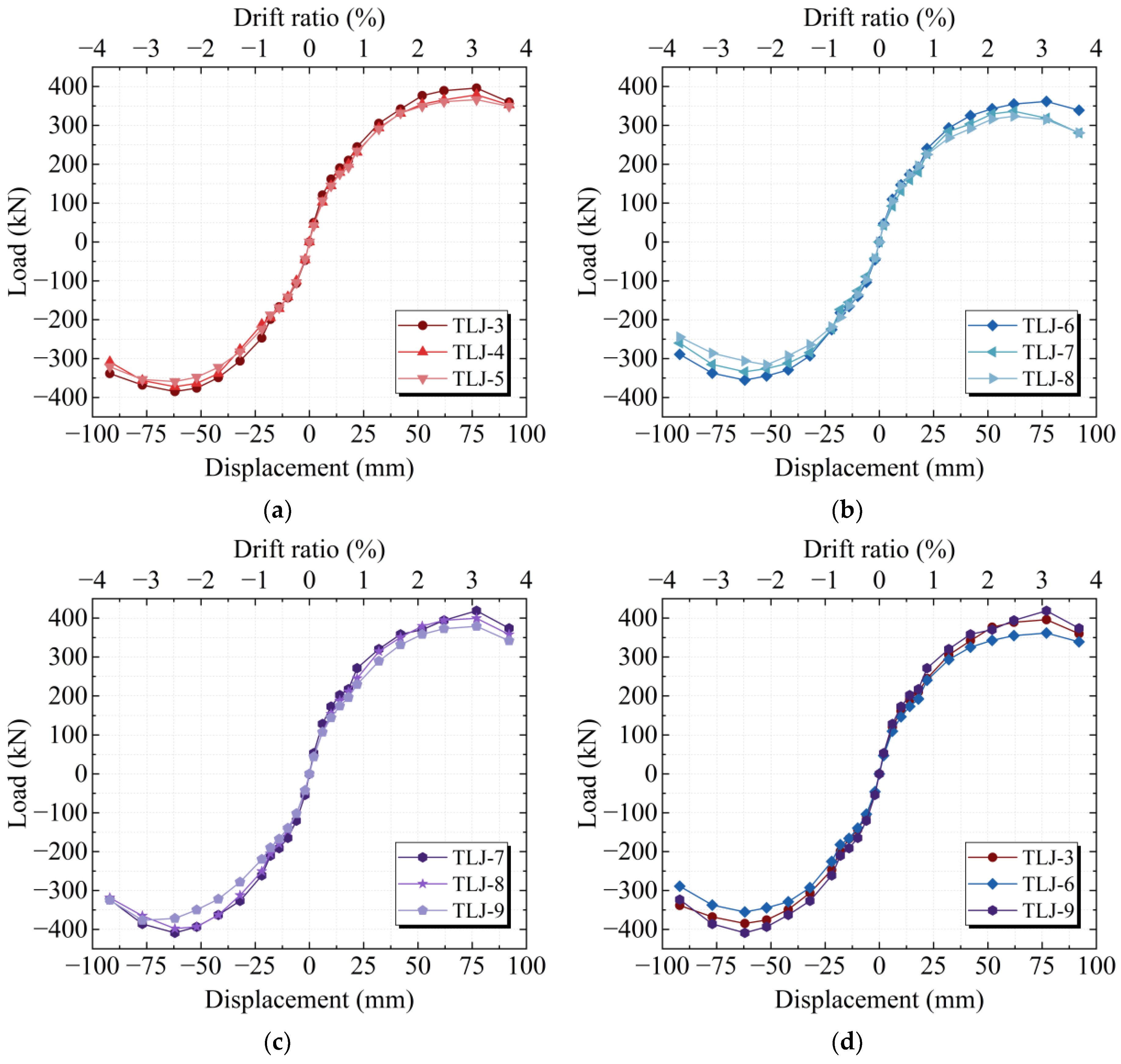
3.3. Skeleton Curve
3.4. Ductility
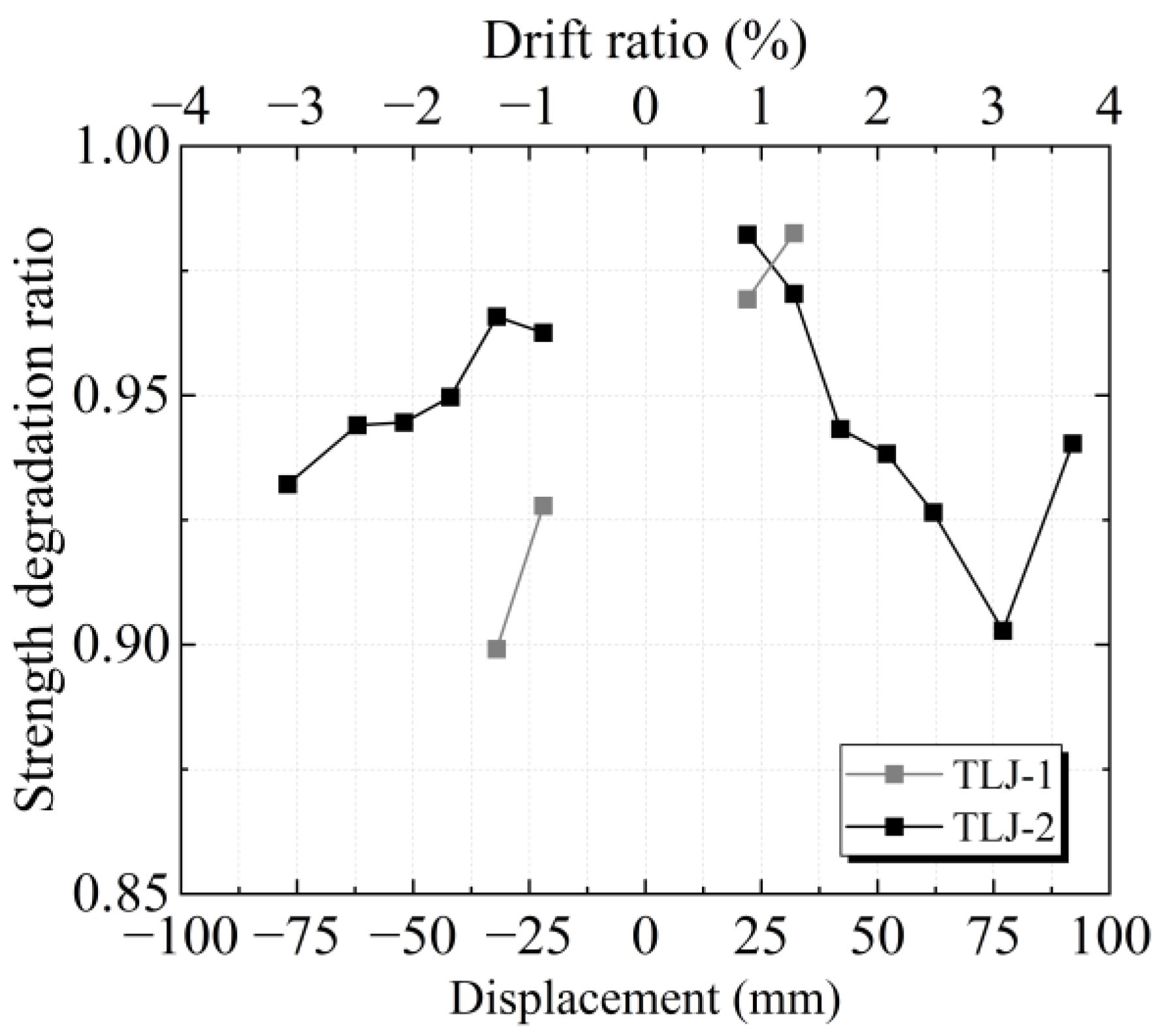
3.5. Strength Degradation
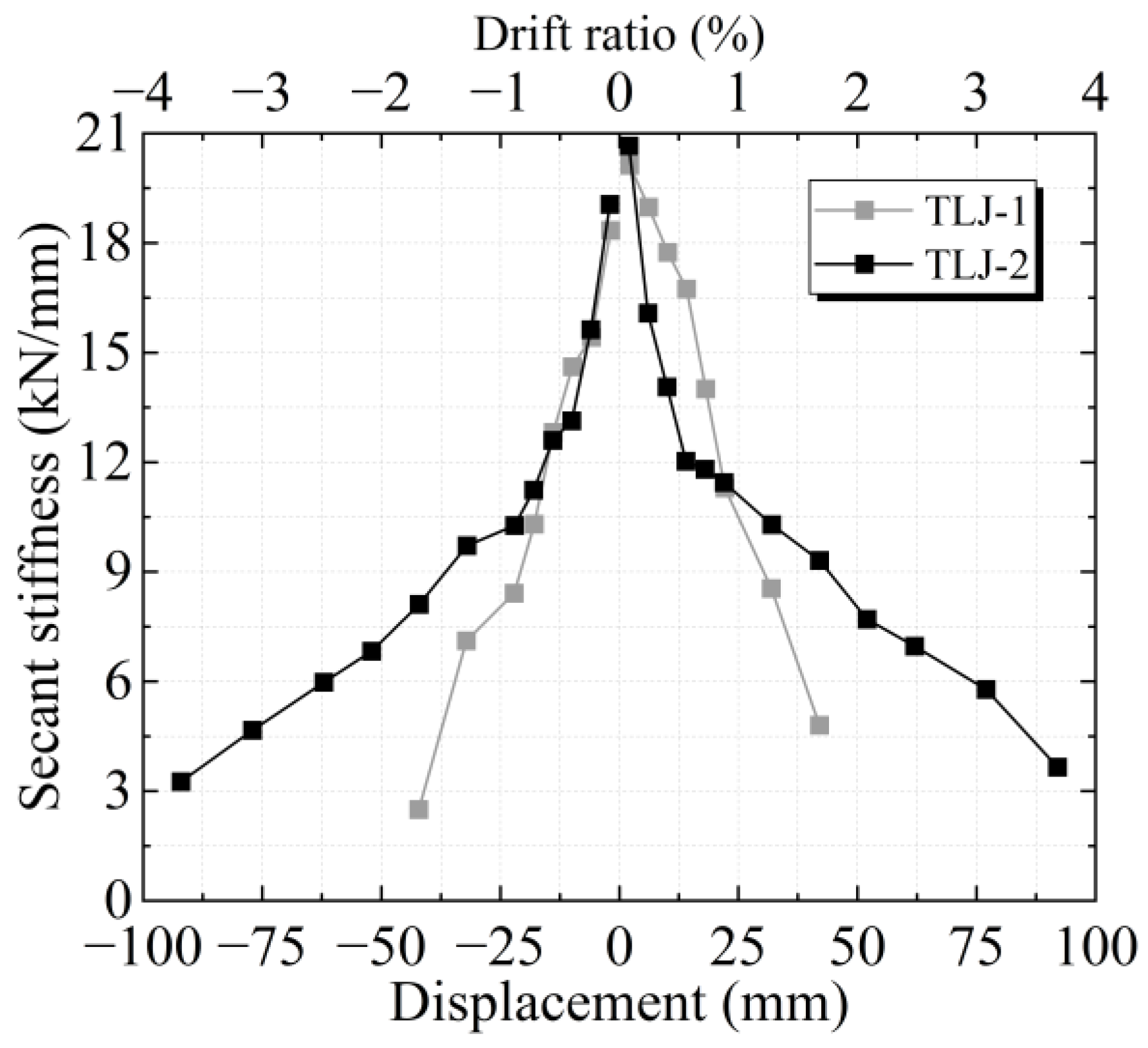
3.6. Stiffness Degradation
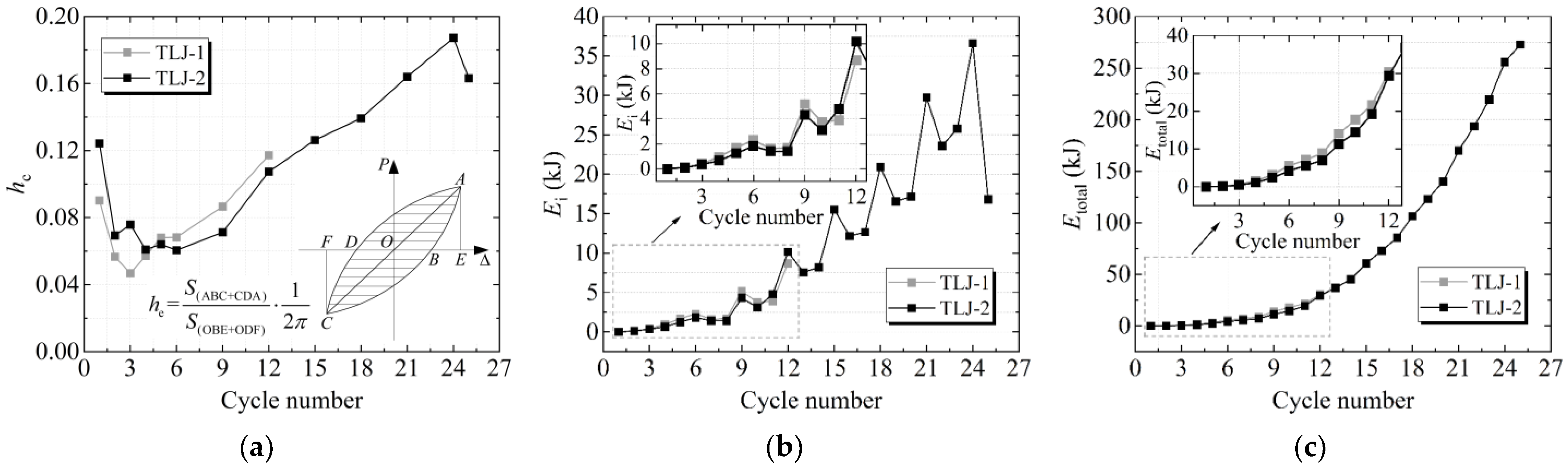
3.7. Energy Dissipation Capacity
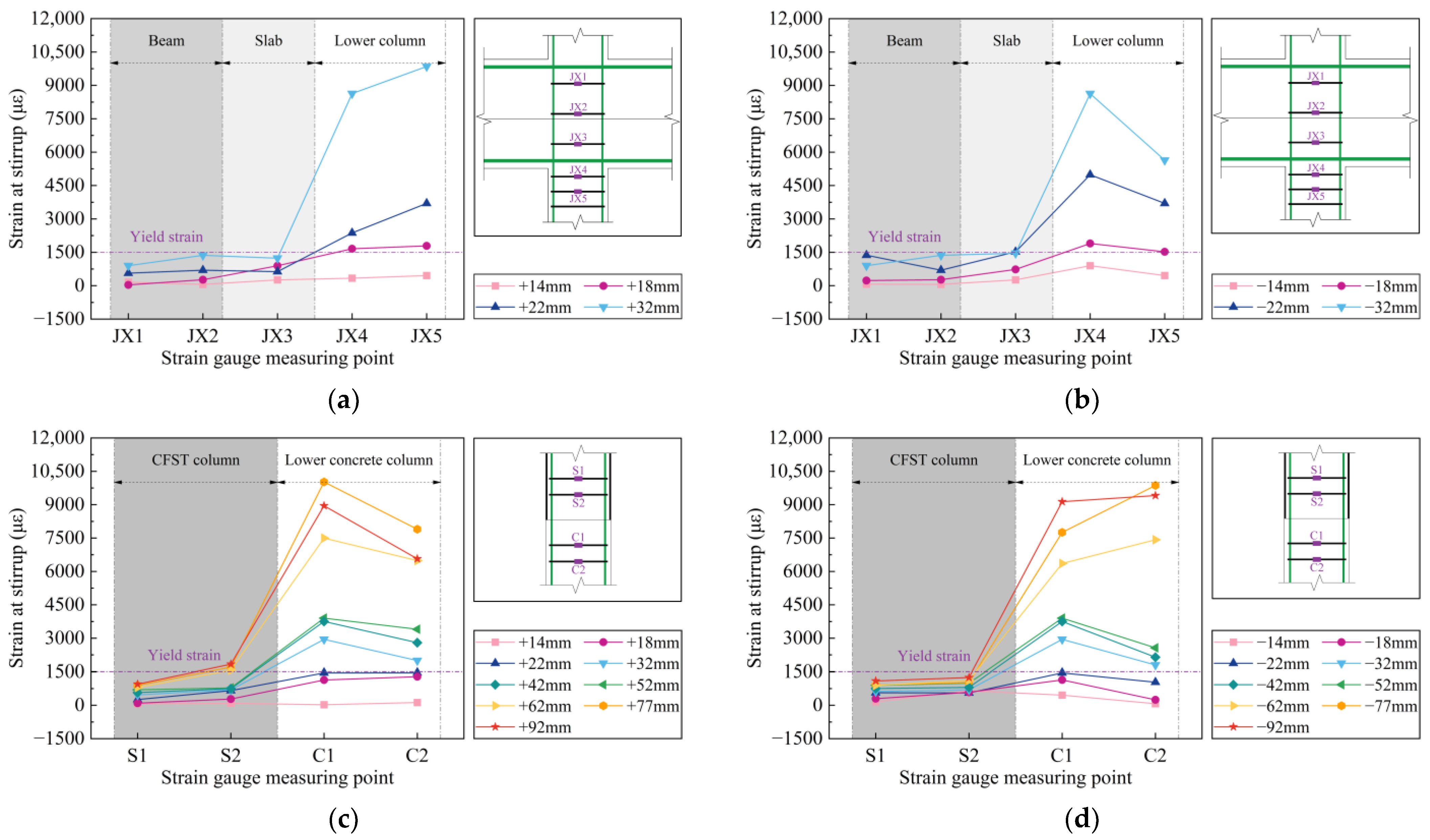
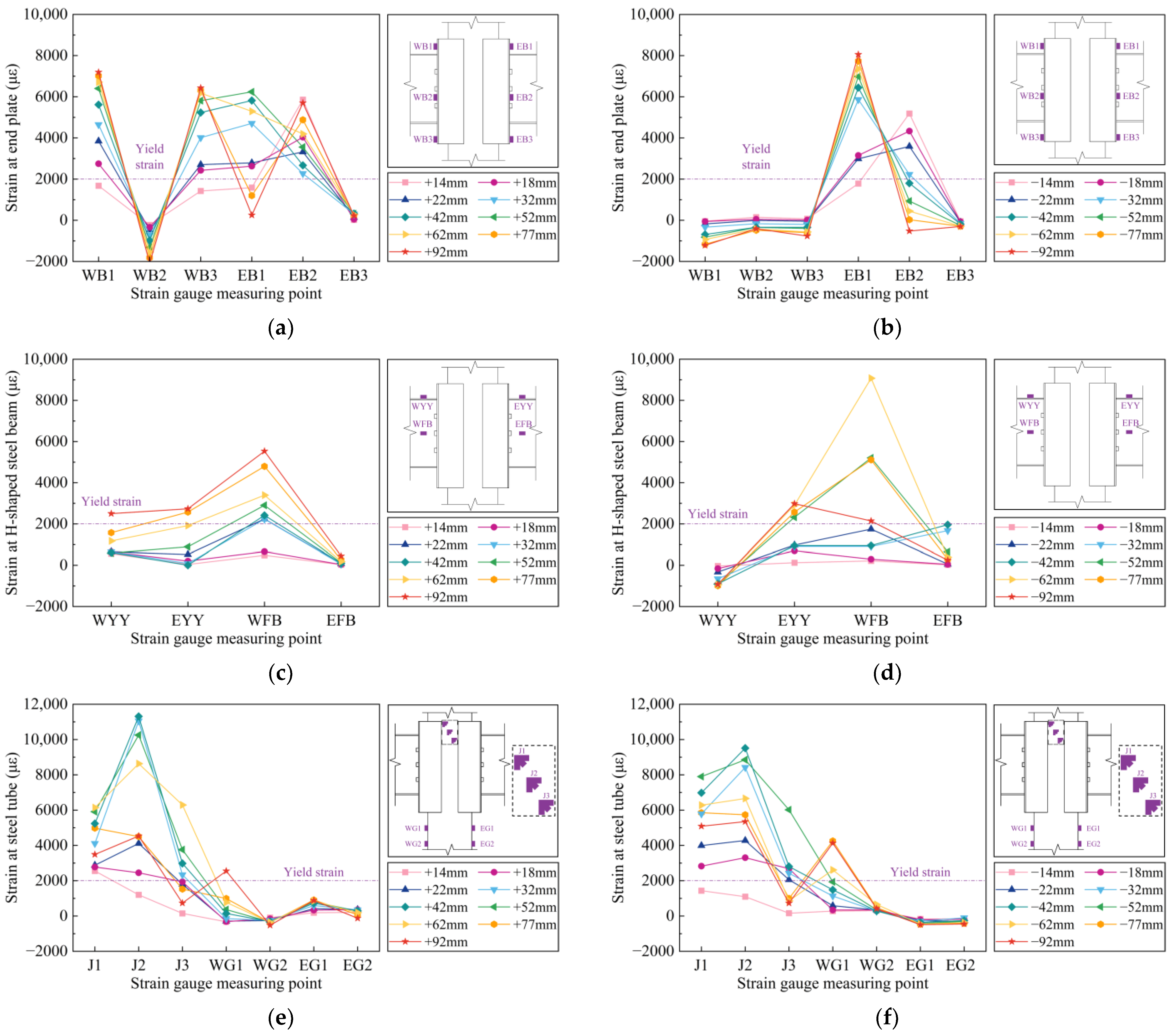
3.8. Strain Analysis
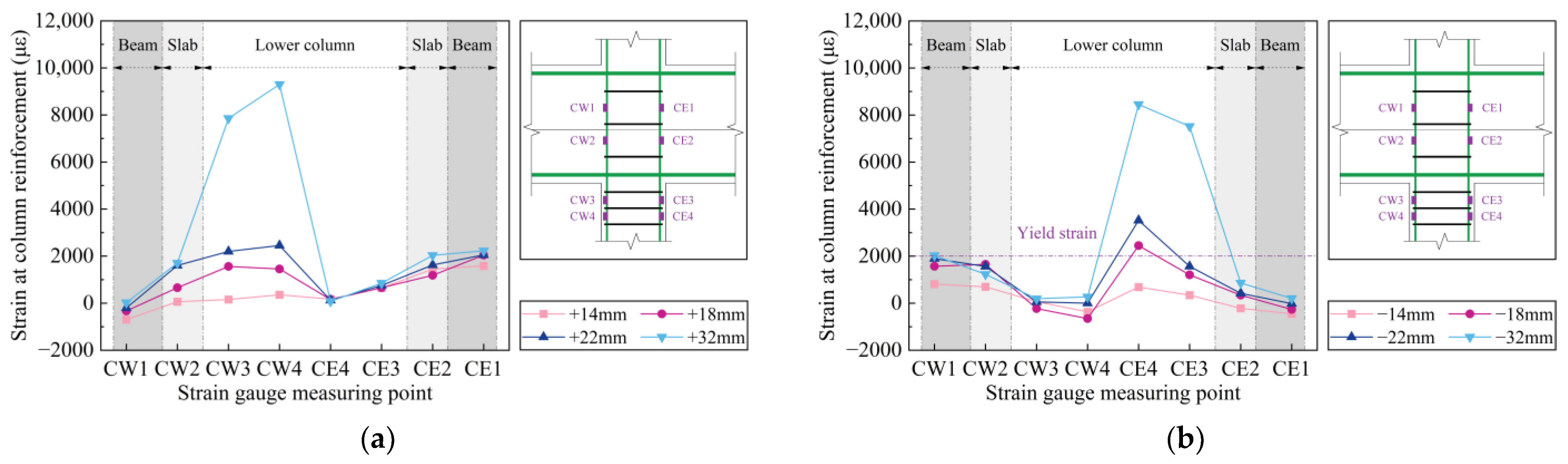
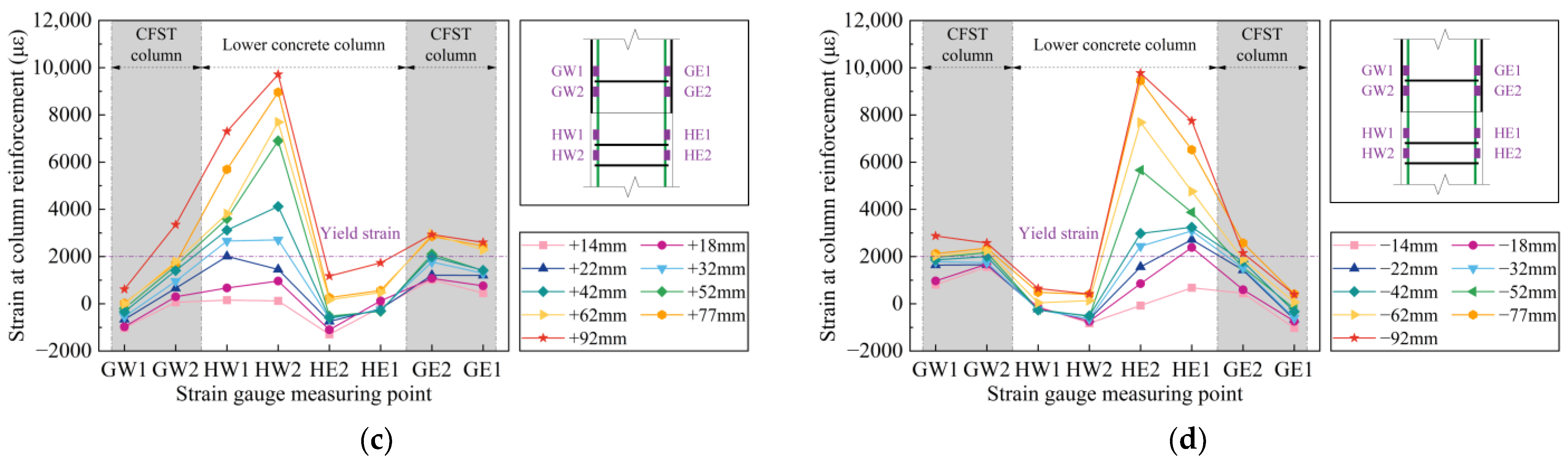
3.8.1. Column Longitudinal Reinforcement Strain Distribution
3.8.2. Column Stirrup Strain Distribution
3.8.3. Steel Member Strain Distribution
4. Finite Element Analysis
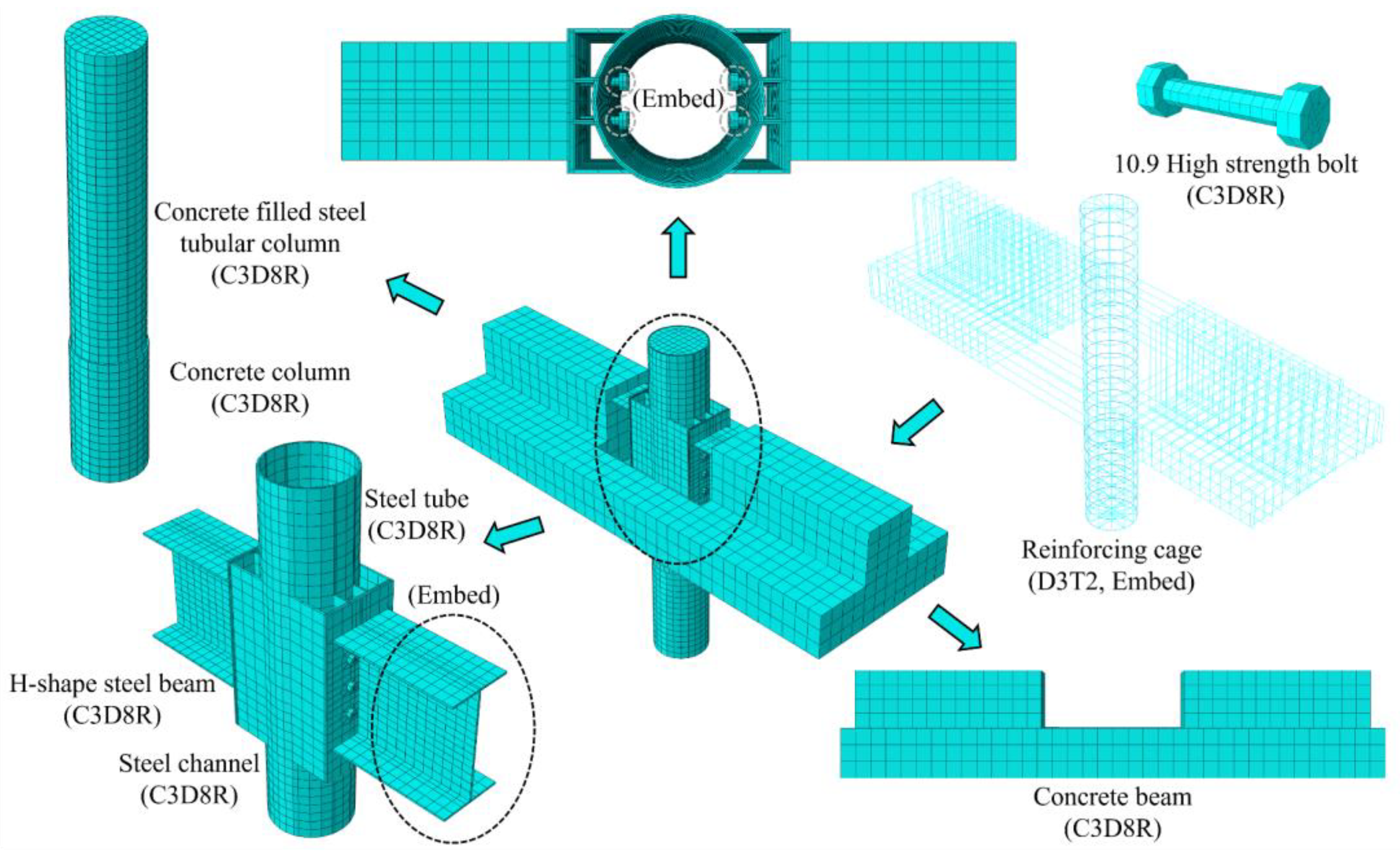
4.1. Finite Element Analysis Models
4.2. Material Properties
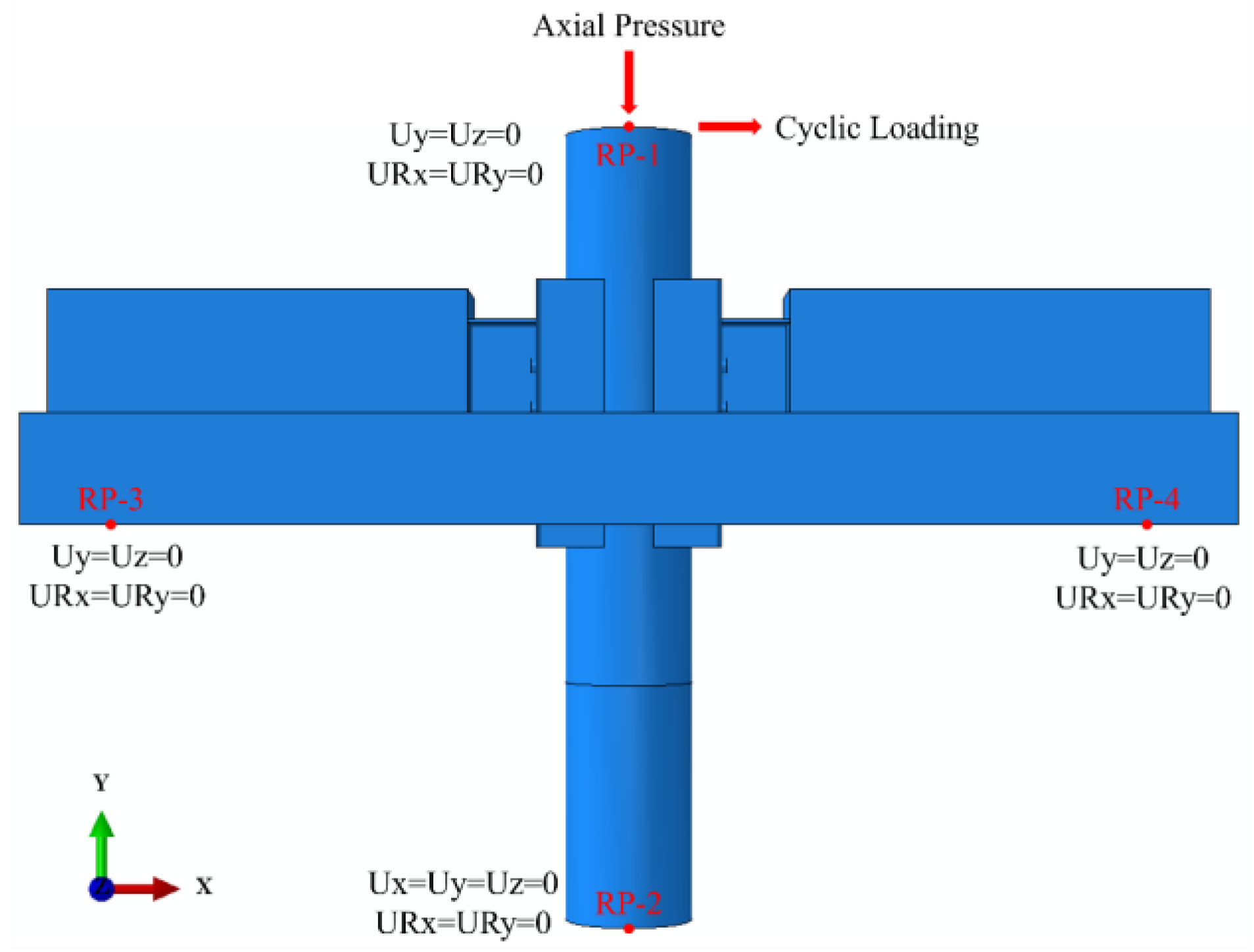
4.3. Boundary Conditions and Load Loading
4.4. Verification of Finite Element Results
4.4.1. Hysteresis Curve
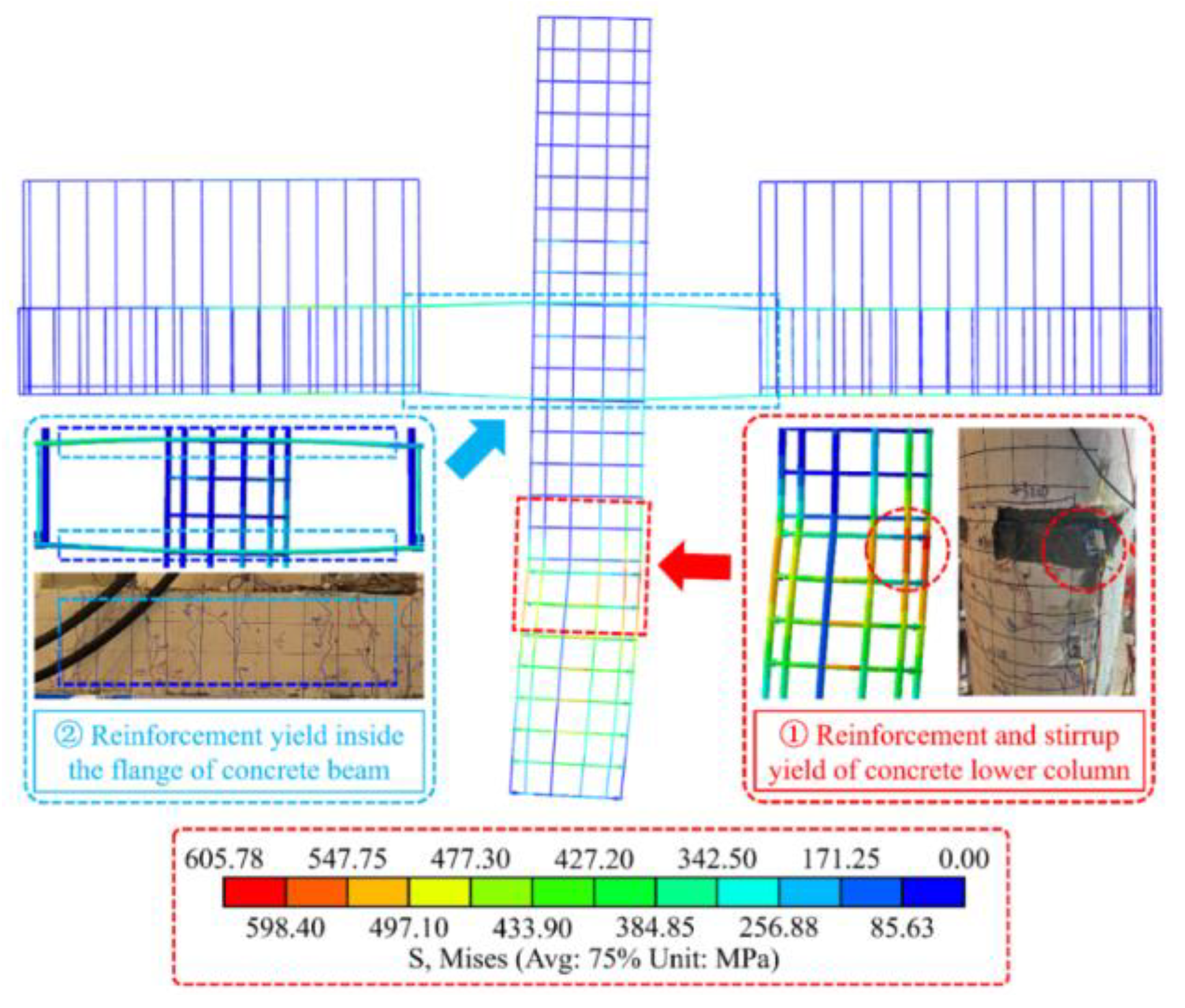
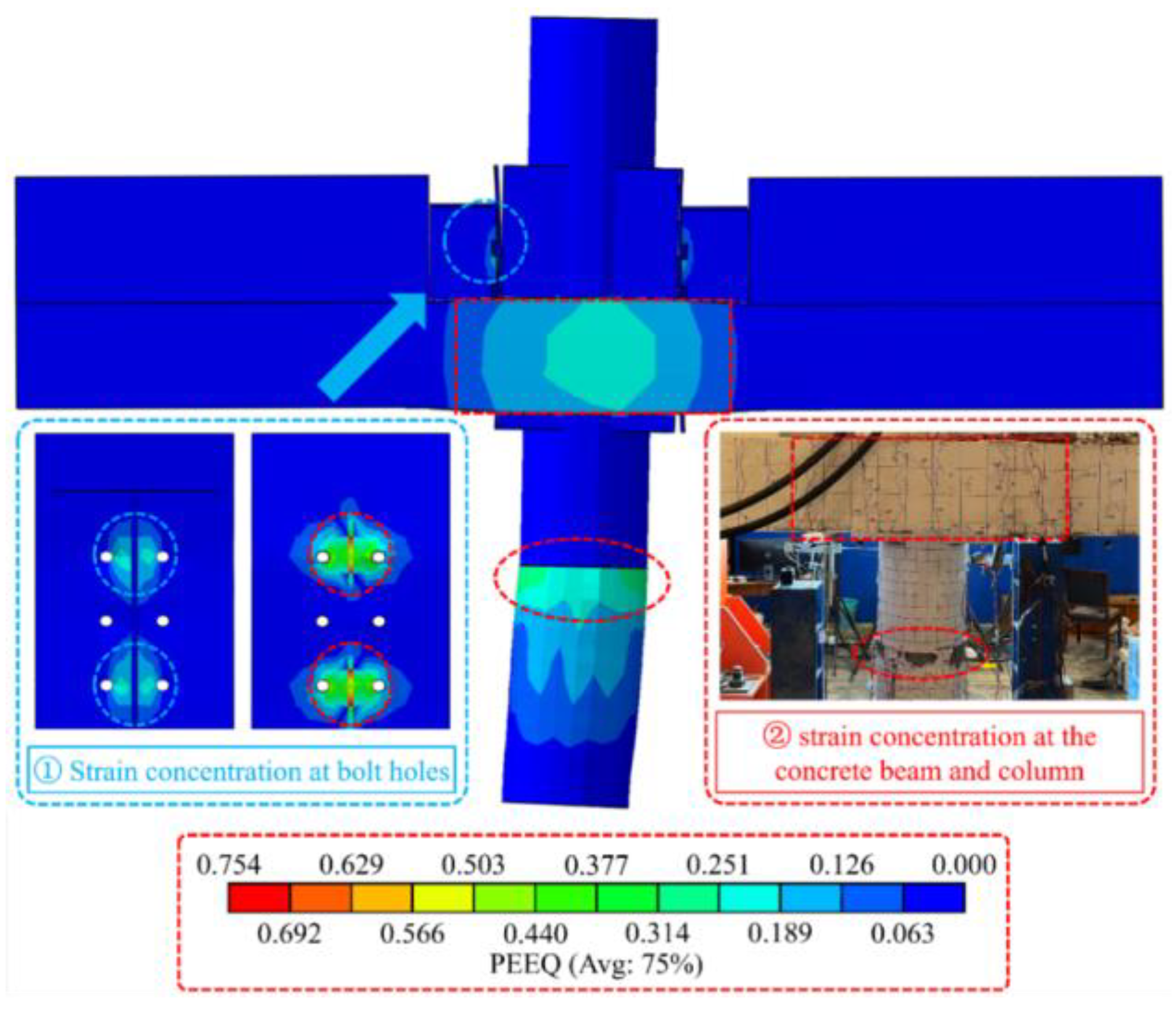
4.4.2. Crack Patterns
4.4.3. Failure Mode
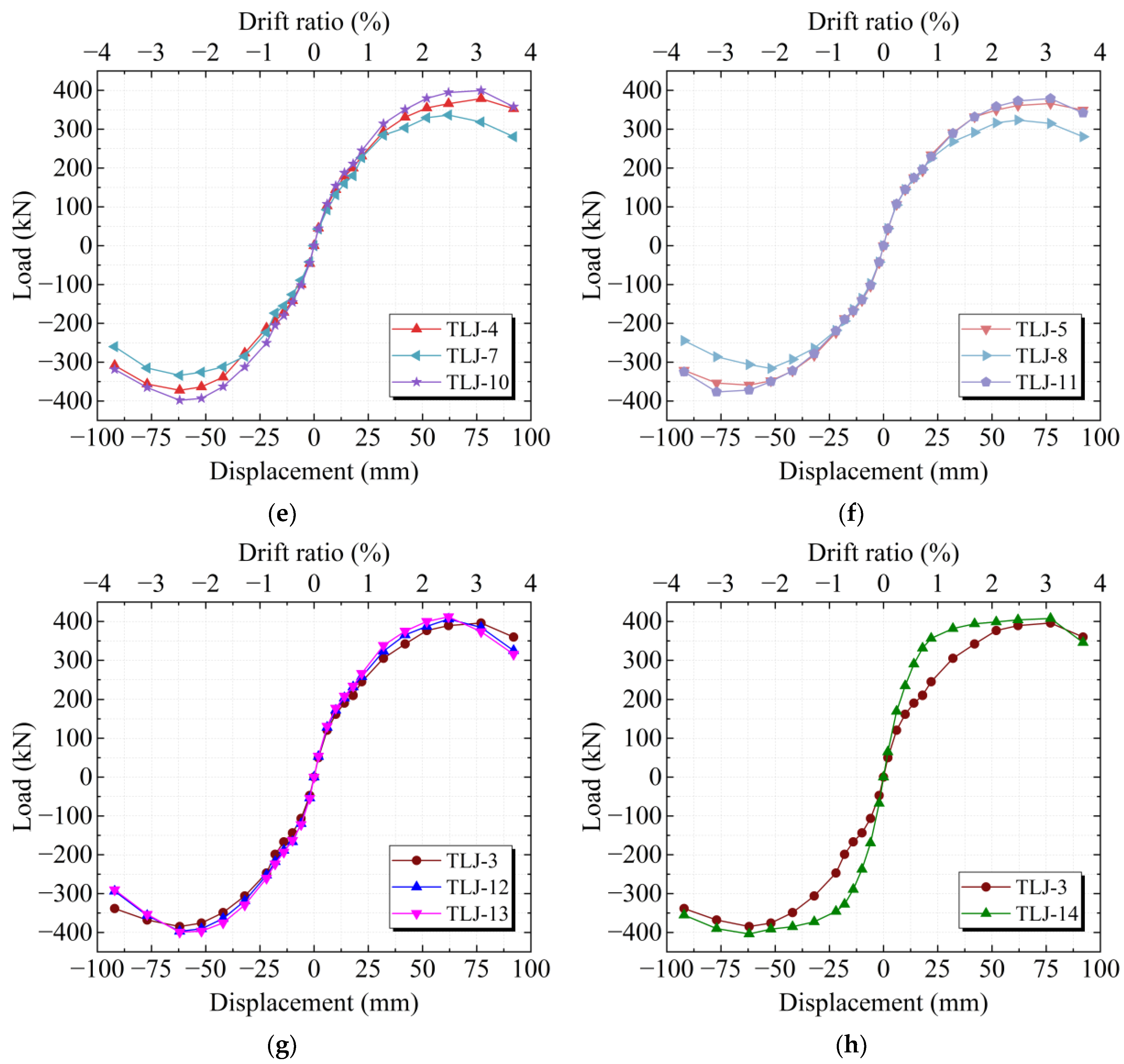
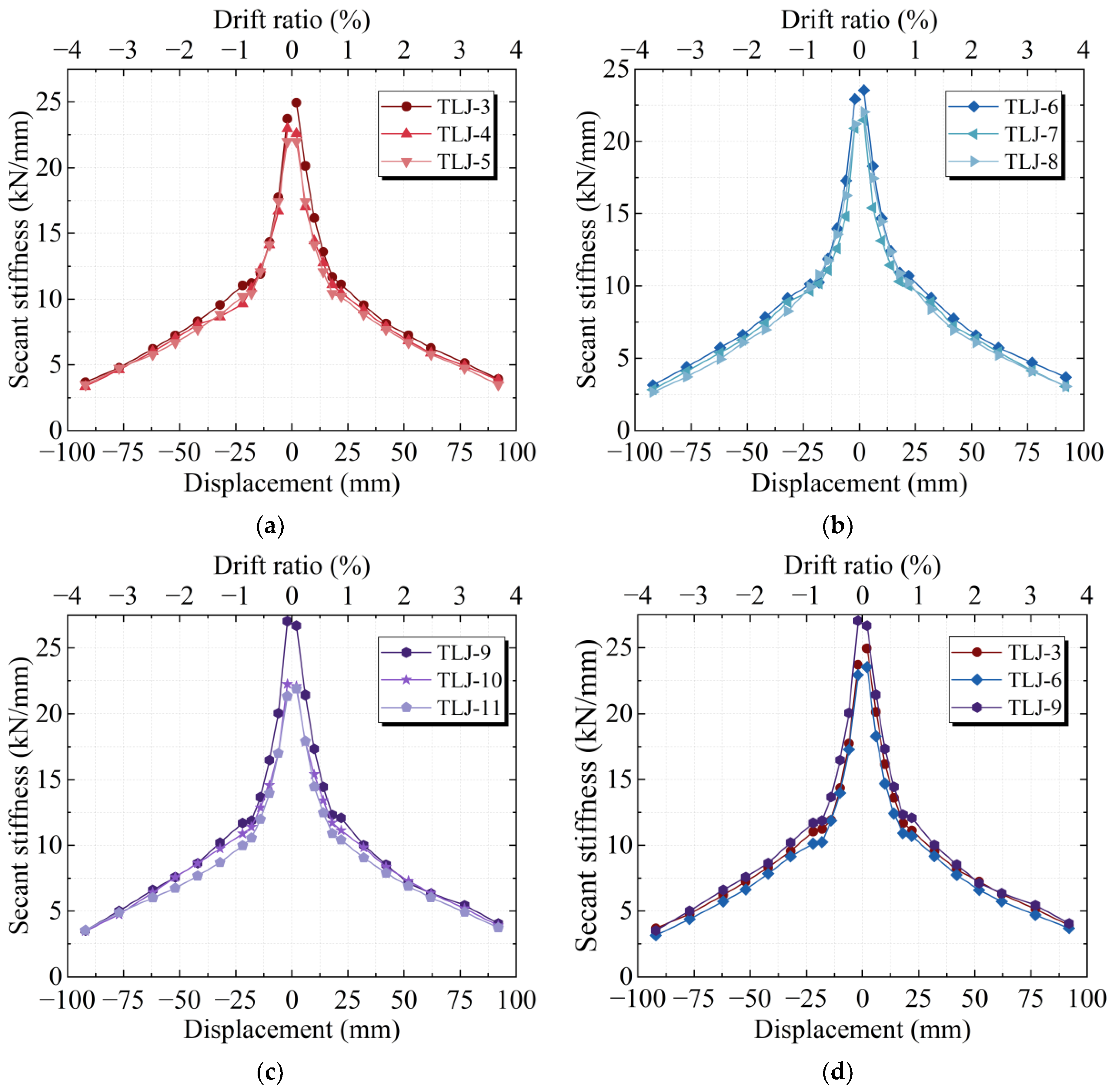
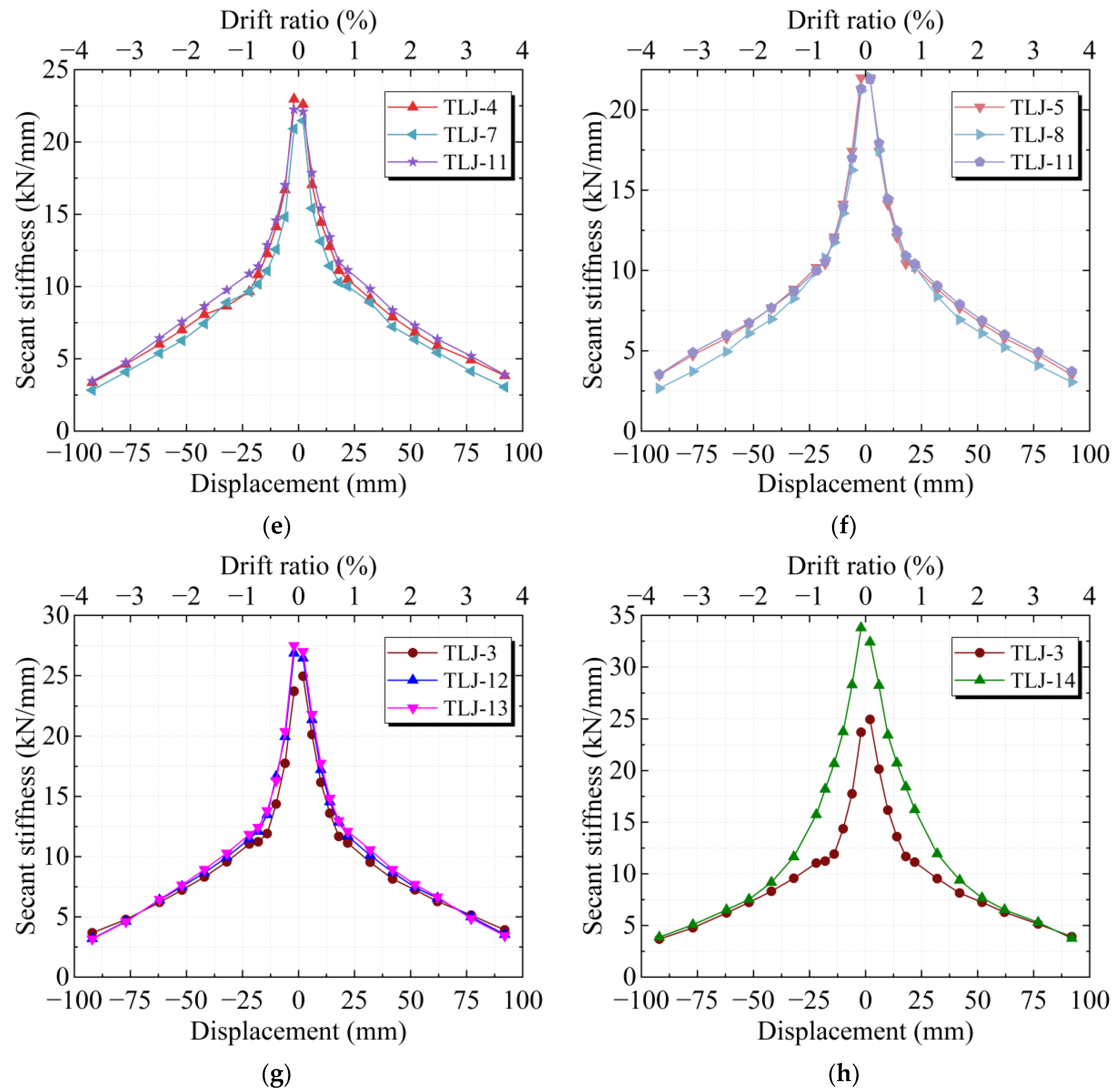
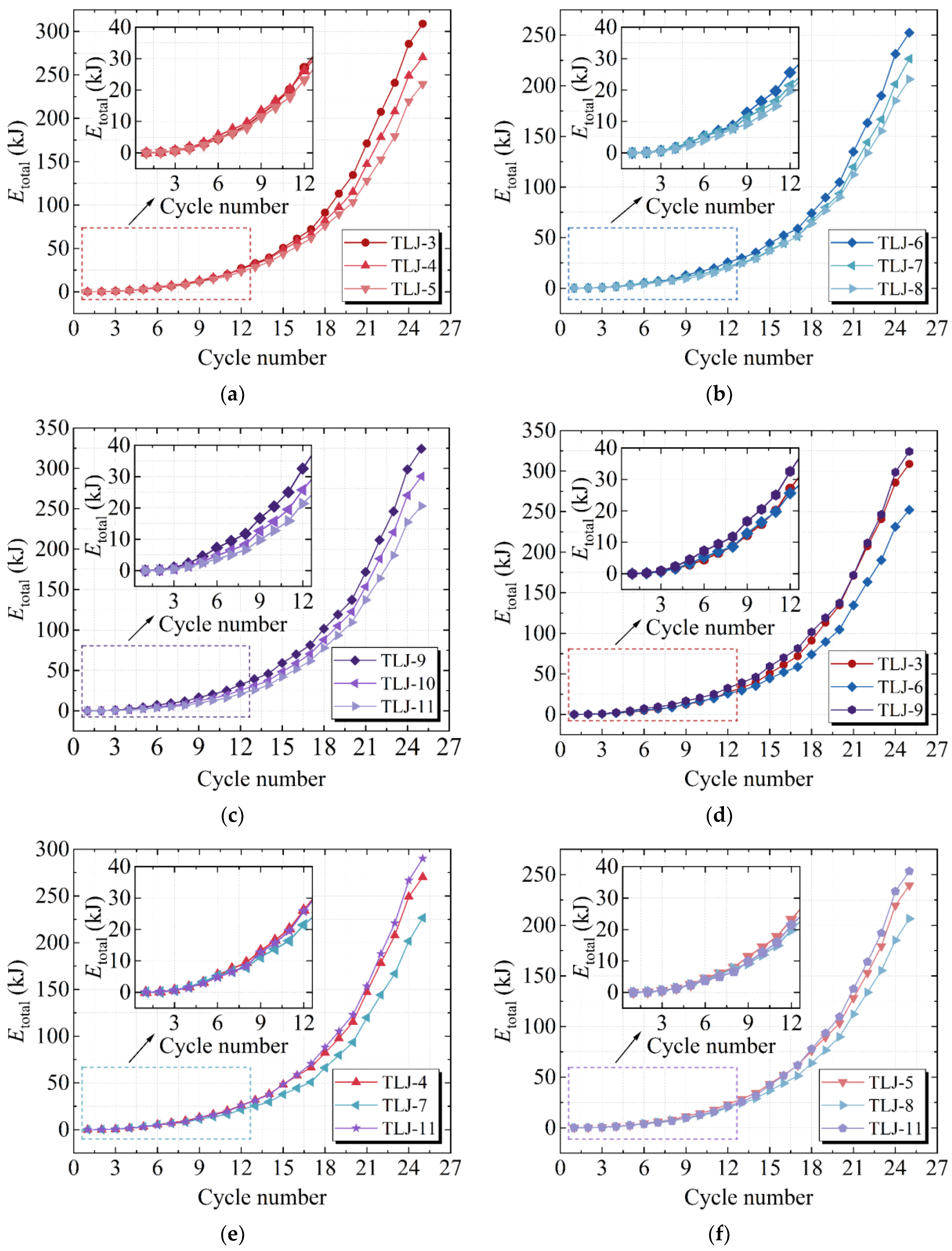
5. Seismic Performance Analysis
5.1. Hysteresis Curve
5.2. Skeleton Curve and Ductility Analysis
5.3. Stiffness Degradation
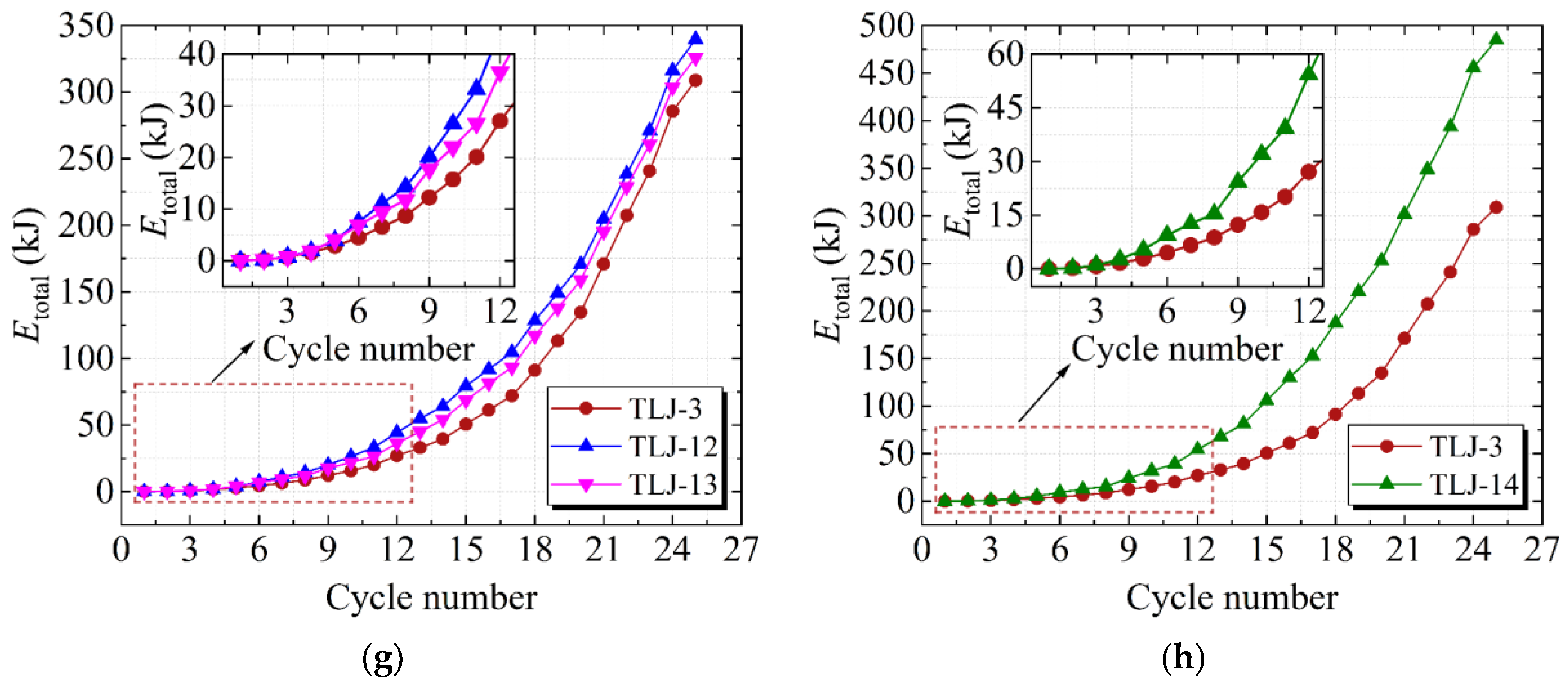
5.4. Energy Dissipation Capacity
6. Conclusions
- (1)
- Compared to reinforced concrete joint exhibited “strong beam and weak column” characteristics, the ASCC joint demonstrated superior seismic performance and “strong column and weak beam” failure mode, with improvements of approximately 46%, 13%, and 40% in yield bearing capacity, peak bearing capacity, and ductility, respectively.
- (2)
- During low cyclic loading tests, both joints showed comparable energy dissipation characteristics in the initial loading phase. The implementation of steel member connections enhanced the energy dissipation capacity of the top-layer joint. The finite element analysis results showed good agreement with experimental findings, providing a foundation for subsequent parametric studies of ASCC top-layer joints.
- (3)
- Parametric analysis was conducted through finite element modeling to investigate the influence of steel tube thicknesses (T), lower steel tube lengths (Lls), axial compression ratios (N), and bolt quantity (n) on the mechanical behavior of ASCC joints. The numerical simulations reveal that under the condition of 0.80 as the upper limit of high axial compression ratio, specimens with increased steel tube thickness, extended lower steel tube length, and bolt quantity demonstrate significant improvements in load-bearing capacity, lateral displacement resistance, and energy dissipation capacity.
- (4)
- For practical engineering applications, the optimal joint parameters were determined to be steel tube thickness at 1–2% of the column diameter and lower steel tube length at 1/3 of the lower column length, with more bolts restricting the deformation of the extended plates. The value of 0.80 can be recommended as the new high axial compression ratio upper limit of the current code.
- (5)
- The results presented in this study can be used in the design and construction of top-layer beam–column joints in subway stations. Furthermore, future research can be conducted to derive the theoretical model and bearing capacity formula of this new structure.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.N.; Xu, C.S.; El Naggar, H.M.; Du, X.L. Seismic response analysis of rectangular prefabricated subway station structure. Tunn. Undergr. Sp. Tech. 2023, 131, 104795. [Google Scholar] [CrossRef]
- Chen, J.N.; Xu, C.S.; Du, X.L.; Han, R.B.; El Naggar, H.M. Physical and numerical modeling of seismic soil-structure interaction of prefabricated subway station structure. Eng. Struct. 2023, 290, 116364. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Chen, Z.Y.; Huang, Y.; Fan, Y.F. Seismic performance evaluation of a metro station structure under multi-source random conditions based on probability density evolution method. Soil. Dyn. Earthq. Eng. 2024, 179, 108509. [Google Scholar] [CrossRef]
- Ma, C.; Zhao, Y.Q.; Dong, H.H.; Lu, D.C.; Du, X.L. Comparative study on the seismic performance of subway stations using reinforced concrete cast-in-place columns and truncated columns. Soil. Dyn. Earthq. Eng. 2023, 169, 107862. [Google Scholar] [CrossRef]
- Ma, C.; Lu, D.C.; Gao, H.; Du, X.L.; Qi, C.Q. Seismic performance improvement of underground frame structures by changing connection type between sidewalls and slab. Soil. Dyn. Earthq. Eng. 2021, 149, 106851. [Google Scholar] [CrossRef]
- Iida, H.; Hiroto, T.; Yoshida, N.; Iwafuji, M. Damage to Daikai subway station. Soils. Found. 1996, 36, 283–300. [Google Scholar] [CrossRef]
- Zhuang, H.Y.; Cheng, S.G.; Chen, G.X. Numerical simulation and analysis of earthquake damages of Dakai metro station caused by Kobe earthquake. Rock. Soil. Mech. 2008, 29, 245–250. [Google Scholar] [CrossRef]
- Bird, J.F.; Bommer, J.J. Earthquake losses due to ground failure. Eng. Geol. 2004, 75, 147–179. [Google Scholar] [CrossRef]
- Van de Lindt, J.W.; Goh, G.H. Effect of earthquake duration on structural reliability. Eng. Struct. 2004, 26, 1585–1597. [Google Scholar] [CrossRef]
- Liu, H.T.; Xu, C.S.; Du, X.L. Seismic response analysis of assembled monolithic subway station in the transverse direction. Eng. Struct. 2020, 219, 110970. [Google Scholar] [CrossRef]
- Liu, H.T.; Wang, Z.Y.; Du, X.L.; Shen, G.Q. The seismic behaviour of precast concrete interior joints with different connection methods in assembled monolithic subway station. Eng. Struct. 2021, 232, 111799. [Google Scholar] [CrossRef]
- Belleri, A.; Brunesi, E.; Nascimbene, R.; Pagani, M.; Riva, P. Seismic performance of precast Industrial facilities following major earthquakes in the Italian territory. J. Perform. Constr. Fac. 2015, 29, 04014135. [Google Scholar] [CrossRef]
- Brunesi, E.; Nascimbene, R.; Bolognini, D.; Bellotti, D. Experimental investigation of the cyclic response of reinforced precast concrete framed structures. PCI J. 2015, 60, 57–79. [Google Scholar] [CrossRef]
- Guerrero, H.; Rodriguez, V.; Escobar, J.A.; Alcocer, S.M.; Bennetts, F.; Suarez, M. Experimental tests of precast reinforced concrete beam-column connections. Soil. Dyn. Earthq. Eng. 2019, 125, 105743. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, P.; Shi, J.Q. Flexural behavior of precast UHPC beam with prestressed bolted hybrid joint. Eng. Struct. 2020, 206, 110100. [Google Scholar] [CrossRef]
- Liu, J.; Xue, Y.T.; Wang, C.K.; Nie, J.G.; Wu, Z.H. Experimental investigation on seismic performance of mechanical joints with bolted flange plate for precast concrete column. Eng. Struct. 2021, 216, 110729. [Google Scholar] [CrossRef]
- Jiang, H.B.; Qiu, H.X.; Sun, J.; Yang, Y. Behavior of steel–concrete composite bolted connector in precast reinforced concrete shear wall. Adv. Struct. Eng. 2019, 22, 2572–2582. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Ghanbari-Ghazijahani, T.; Jankowski, R. Ensemble machine learning models for estimating mechanical curves of concrete-timber-filled steel tubes. Eng. Appl. Artif. Intel. 2025, 156, 111234. [Google Scholar] [CrossRef]
- Koloo, F.A.; Badakhshan, A.; Fallahnejad, H.; Jamkhaneh, M.E.; Ahmadi, M. Investigation of proposed concrete filled steel tube connections under reversed cyclic loading. Int. J. Steel. Struct. 2018, 18, 163–177. [Google Scholar] [CrossRef]
- Ding, K.W.; Liu, J.H.; Ma, W.; Liu, Y.L. Experimental study on seismic performances of a new type of fabricated semi-rigid beam-to-column connection. China Civ. Eng. J. 2021, 54, 1–7+56. [Google Scholar] [CrossRef]
- Ding, K.W.; Liu, J.H.; Ren, J.W.; Ma, W. Dynamic Responses of Cellular Metal-Filled Steel Beam-Column Joint Under Impact Loading. J. Shanghai Jiaotong Univ. (Sci.) 2020, 25, 384–393. [Google Scholar] [CrossRef]
- Ding, K.W.; Ye, Y.; Ma, W. Seismic performance of precast concrete beam-column joint based on the bolt connection. Eng. Struct. 2021, 232, 111884. [Google Scholar] [CrossRef]
- Ding, K.W.; Chen, D.; Liu, Y.L.; Xia, S. Theoretical and experimental study on mechanical behavior of laminated slabs with new type joints. China Civ. Eng. J. 2015, 48, 64–69. [Google Scholar] [CrossRef]
- Liu, J.H.; Liu, Y.L.; Yu, D.H. Experimental and Numerical Studies on the Seismic Performance of New Assembled Concrete Frame Beam–Column Joints. Buildings 2023, 13, 329. [Google Scholar] [CrossRef]
- Qu, X.S.; Xie, Y.N.; Sun, G.J.; Liu, Q.W.; Wang, H. Seismic Behavior of Assembly Joint with CFST Column and H-shaped Steel Beam. KSCE J. Civ. Eng. 2022, 27, 670–683. [Google Scholar] [CrossRef]
- Rong, X.; Zhang, X.W.; Li, Y.Y.; Du, Y.S.; Zhang, J.X.; Shi, X. Seismic Behavior of Top-Weld Bottom-Bolt Joints Between CFST Columns and H-Beams. Arabian. J. Sci. Eng. 2022, 47, 12585–12603. [Google Scholar] [CrossRef]
- Khador, M.; Chan, T.M. Cyclic behaviour of external diaphragm joint to CHS column with built-in replaceable links. Steel. Constr. 2016, 9, 331–338. [Google Scholar] [CrossRef]
- Li, W.; Han, L.H. Seismic performance of CFST column to steel beam joint with RC slab: Joint model. J. Constr. Steel. Res. 2012, 73, 66–79. [Google Scholar] [CrossRef]
- Li, W.; Han, L.H. Seismic performance of CFST column to steel beam joints with RC slab: Analysis. J. Constr. Steel. Res. 2011, 67, 127–139. [Google Scholar] [CrossRef]
- Han, L.H.; Li, W. Seismic performance of CFST column to steel beam joint with RC slab: Experiments. J. Constr. Steel. Res. 2010, 66, 1374–1386. [Google Scholar] [CrossRef]
- Zhu, L.H.; Ning, Q.J.; Zhao, C.; Ji, C.R.; Pan, X.B.; Han, W. Seismic performance of self-centering circular concrete-filled steel tubular column to steel beam connection with web friction device. Structures 2021, 34, 1843–1857. [Google Scholar] [CrossRef]
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010.
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. China Architecture & Building Press: Beijing, China, 2019.
- GB 55008-2021; General Code for Concrete Structures. China Architecture & Building Press: Beijing, China, 2021.
- GB/T 228.1-2021; Metallicmaterials-Tensiletesting-Part1: Method of Test at Room Temperature. State Administration for Market Regulation: Beijing, China, 2021.
- JGJ/T 101-2015; Specification for Seismic Test of Buildings. China Architecture & Building Press: Beijing, China, 2015.
- Stoakes, C.D.; Fahnestock, L.A. Cyclic Flexural Testing of Concentrically Braced Frame Beam-Column Connections. J. Struct. Eng. 2011, 137, 739–747. [Google Scholar] [CrossRef]
- GB/T 51336-2018; Standard for Seismic Design of Underground Structures. China Architecture & Building Press: Beijing, China, 2018.
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015.
- Han, L.H. Theory of Concrete-Filled Steel Tubular Structures; Springer Nature Singapore: Singapore, 2024. [Google Scholar]
- GB 50017-2017; Steel Structure Design Standards. China Architecture & Building Press: Beijing, China, 2017.

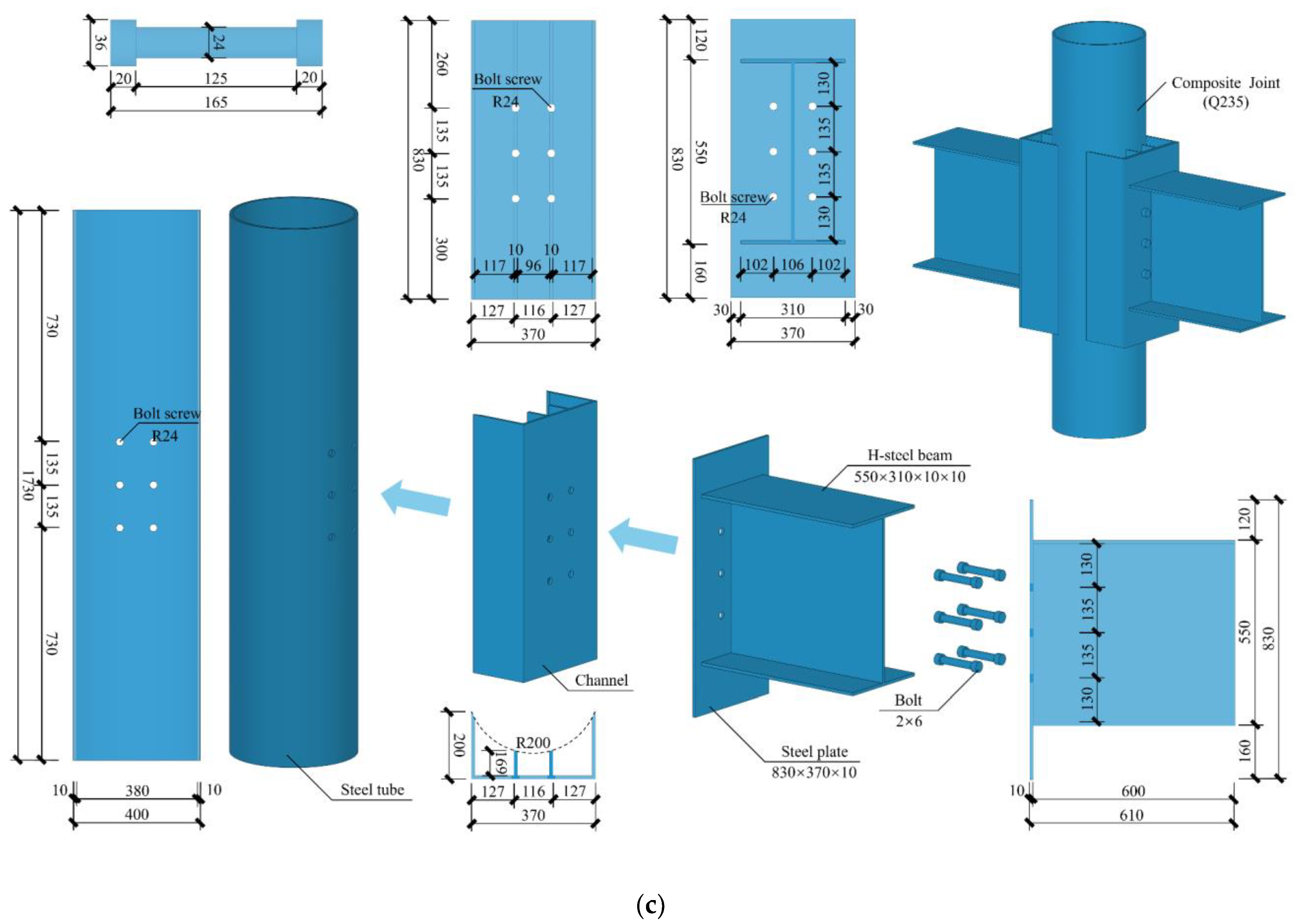
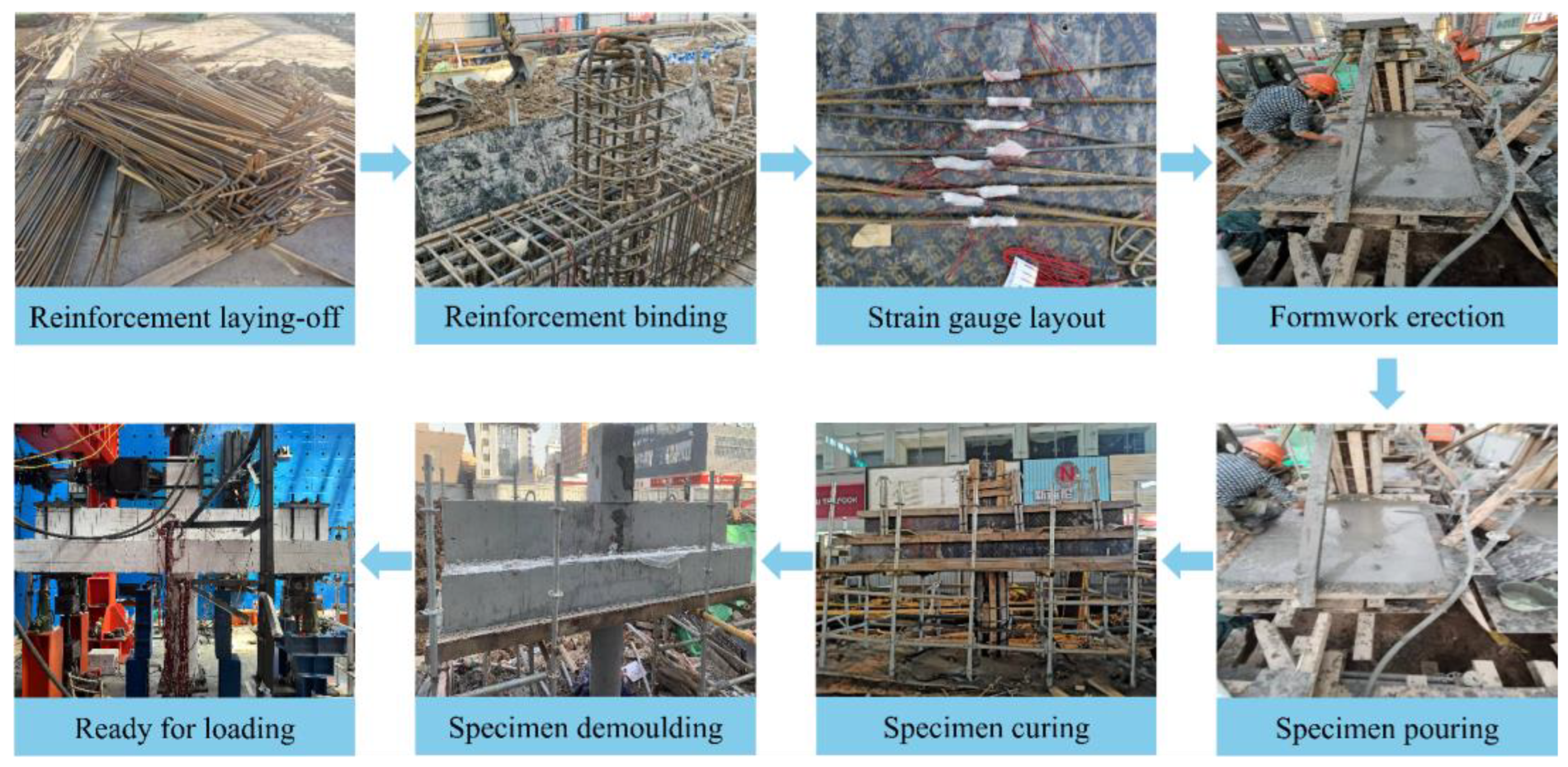
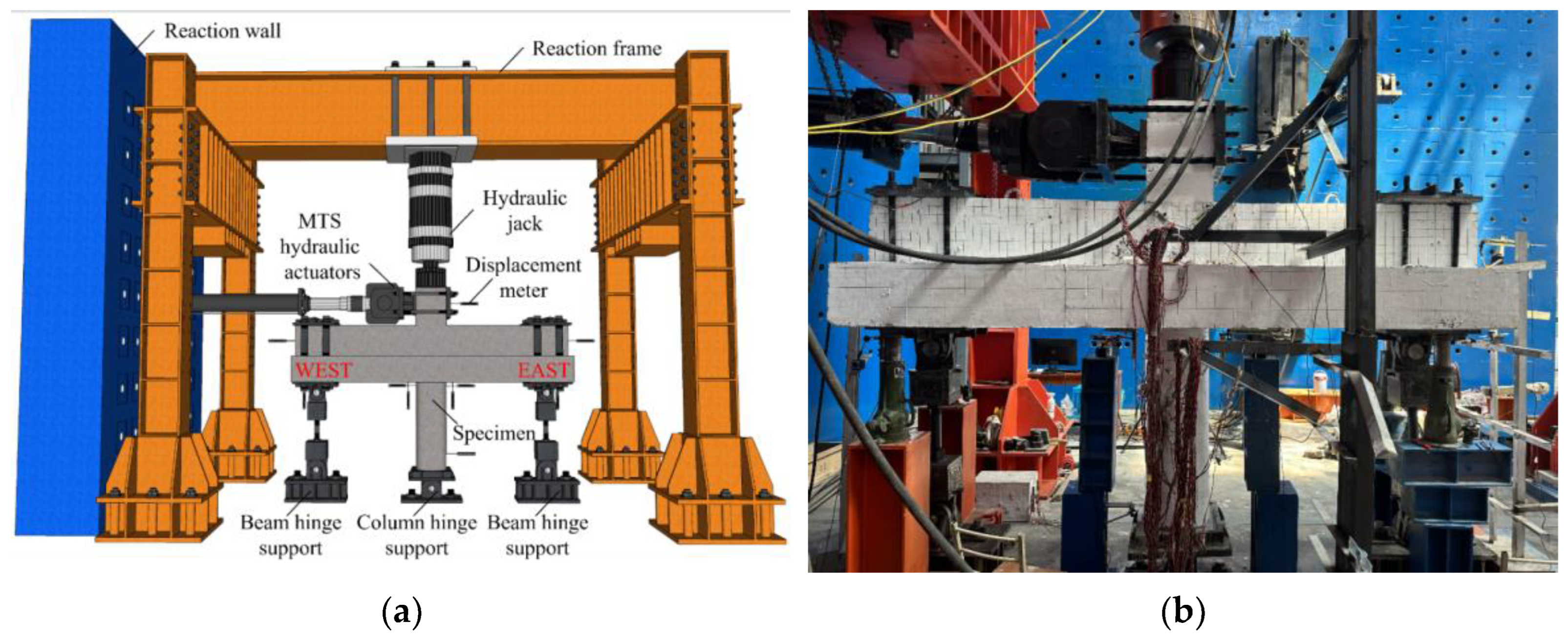
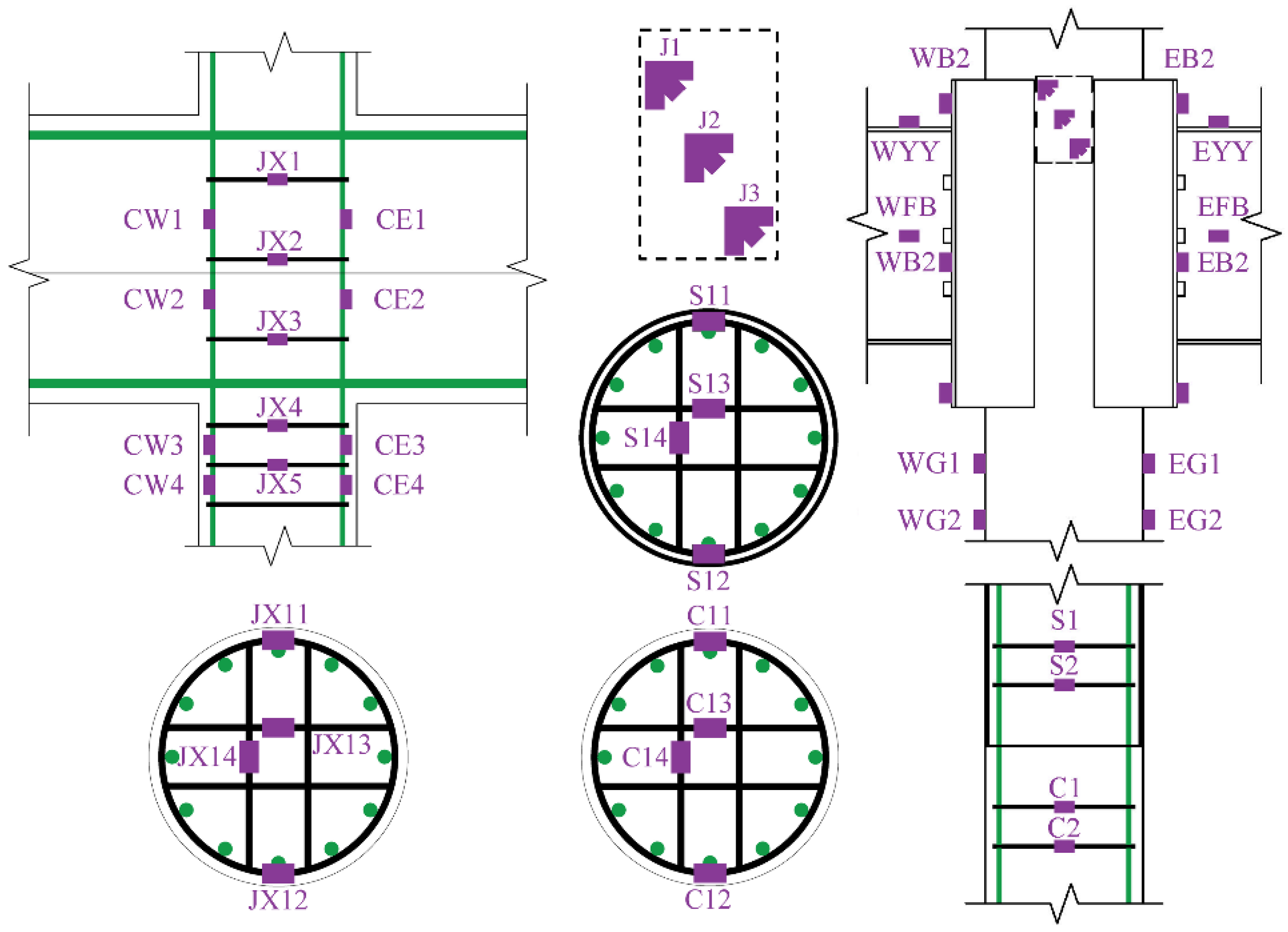


| Specimen | Element | Section Size/mm | Longitudinal Reinforcement | Longitudinal Reinforcement Ratio/% | Transverse Reinforcement | Transverse Reinforcement Ratio/% | Stirrup | Stirrup Reinforcement Ratio | Axial Compression Ratio | Mcu/Mbu | Boundary Conditions |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TLJ-1 | Beam | 400 × 730 | 6C22(4 + 2) /4C22 | 1.30 | A12@80 | 1.28 | A12@80 | 0.86 | 0.75 | 0.326 | Hinge support |
| Slab | 300 × 1200 | A12@80 | 0.86 | A12@80 | 1.35 | ||||||
| Column | Ø400 | 12C18 | 2.43 | \ | \ | A10@100 | 1.95 | Sliding (top) /Fix hinge (bottom) support | |||
| TLJ-2 | Beam | 400 × 730 | 6C22(4 + 2) /4C22 | 1.30 | A12@80 | 1.28 | A12@80 | 0.86 | 0.75 | 0.326 | Hinge support |
| Slab | 300 × 1200 | A12@80 | 0.86 | A12@80 | 1.35 | ||||||
| Column | Ø400 | 12C18 | 2.43 | \ | \ | A10@100 /200 | 0.28 | Sliding (top) /Fix hinge (bottom) support |
| Materials | Strength | fcu/MPa | fc/MPa | Ec/MPa | υ |
|---|---|---|---|---|---|
| Concrete | C35 | 35.71 | 27.11 | 3.11 × 104 | 0.2 |
| C50 | 50.90 | 38.69 | 3.39 × 104 | 0.2 |
| Materials | Grade | Diameter or Thickness/mm | fy/MPa | fu/MPa | Ec/MPa |
|---|---|---|---|---|---|
| Reinforcement | HRB400 | 12 | 427.2 | 603.1 | 2.03 × 105 |
| 18 | 477.3 | 655.0 | 2.08 × 105 | ||
| 22 | 433.9 | 598.4 | 2.12 × 105 | ||
| HPB300 | 10 | 342.5 | 497.1 | 2.10 × 105 | |
| Steel | Q235 | 10 | 288.1 | 453.7 | 2.14 × 105 |
| Bolt | 10.9 | 24 | 903.4 | 1010.2 | 2.11 × 105 |
| Specimen Number | Direction | Fy/kN | ∆y/mm | Fp/kN | ∆p/mm | Fu/kN | ∆u/mm | Etotal/kJ | Stiffness Degradation Rate Rsd | |
|---|---|---|---|---|---|---|---|---|---|---|
| TLJ-1 | Positive | 318.476 | 29.697 | 356.864 | 39.526 | 356.864 | 39.526 | 1.478 | 30.395 | 0.239 |
| Negative | −235.643 | −22.832 | −280.315 | −31.787 | −274.375 | −37.081 | 0.136 | |||
| TLJ-2 | Positive | 375.683 | 43.354 | 402.564 | 76.624 | 370.019 | 92.025 | 2.067 | 272.646 | 0.280 |
| Negative | −352.785 | −43.529 | −377.865 | −61.138 | −321.185 | −87.552 | 0.314 |
| Dilation Angle | Eccentricity | fb0/fc0 | K | Viscosity Parameter |
|---|---|---|---|---|
| 30 | 0.1 | 1.16 | 0.66667 | 0.0005 |
| Finite Element Model | Parameter | |||
|---|---|---|---|---|
| Steel Tube Thickness T (mm) | Lower Steel Tube Length Lls (mm) | Axial Compression Ratio N | Bolt Quantity n | |
| TLJ-3 | 10 | 430 | 0.75 | 12 (3 rows) |
| TLJ-4 | 5 | 430 | 0.75 | 12 (3 rows) |
| TLJ-5 | 3 | 430 | 0.75 | 12 (3 rows) |
| TLJ-6 | 10 | 300 | 0.75 | 12 (3 rows) |
| TLJ-7 | 5 | 300 | 0.75 | 12 (3 rows) |
| TLJ-8 | 3 | 300 | 0.75 | 12 (3 rows) |
| TLJ-9 | 10 | 500 | 0.75 | 12 (3 rows) |
| TLJ-10 | 5 | 500 | 0.75 | 12 (3 rows) |
| TLJ-11 | 3 | 500 | 0.75 | 12 (3 rows) |
| TLJ-12 | 10 | 430 | 0.80 | 12 (3 rows) |
| TLJ-13 | 10 | 430 | 0.85 | 12 (3 rows) |
| TLJ-14 | 10 | 430 | 0.75 | 20 (5 rows) |
| Specimen Number | Direction | Fy/kN | ∆y/mm | Fp/kN | ∆p/mm | Fu/kN | ∆u/mm | Etotal/kJ | Stiffness Degradation Rate Rsd | |
|---|---|---|---|---|---|---|---|---|---|---|
| TLJ-3 | Positive | 332.818 | 39.477 | 396.026 | 77 | 359.836 | 92 | 2.363 | 308.876 | 0.206 |
| Negative | −331.419 | −37.915 | −384.898 | −68.955 | −338.464 | −90.832 | 0.262 | |||
| TLJ-4 | Positive | 326.192 | 40.702 | 378.792 | 76.984 | 352.719 | 91.922 | 2.241 | 270.180 | 0.218 |
| Negative | −323.914 | −39.651 | −372.412 | −62 | −308.515 | −91.420 | 0.262 | |||
| TLJ-5 | Positive | 315.789 | 38.106 | 366.140 | 77 | 349.239 | 92 | 2.372 | 239.334 | 0.226 |
| Negative | −312.874 | −39.483 | −364.545 | −77 | −320.980 | −91.996 | 0.215 | |||
| TLJ-6 | Positive | 310.241 | 37.293 | 361.694 | 76.654 | 339.063 | 91.817 | 2.435 | 252.237 | 0.200 |
| Negative | −309.579 | −36.516 | −355.157 | −62 | −289.055 | −91.987 | 0.250 | |||
| TLJ-7 | Positive | 291.936 | 36.863 | 336.595 | 61.959 | 280.742 | 89.010 | 2.390 | 226.509 | 0.253 |
| Negative | −294.709 | −35.573 | −333.915 | −62 | −283.828 | −85.450 | 0.258 | |||
| TLJ-8 | Positive | 273.024 | 34.142 | 324.008 | 61.903 | 280.731 | 91.987 | 2.594 | 206.397 | 0.237 |
| Negative | −268.234 | −33.372 | −316.494 | −51.988 | −269.020 | −83.214 | 0.287 | |||
| TLJ-9 | Positive | 357.694 | 41.840 | 419.151 | 76.997 | 374.027 | 91.979 | 2.240 | 324.239 | 0.204 |
| Negative | −348.070 | −37.797 | −408.910 | −62 | −347.574 | −86.223 | 0.244 | |||
| TLJ-10 | Positive | 346.157 | 40.705 | 404.196 | 76.996 | 373.790 | 91.883 | 2.236 | 289.933 | 0.235 |
| Negative | −343.258 | −38.582 | −398.093 | −62 | −318.518 | −85.255 | 0.289 | |||
| TLJ-11 | Positive | 324.931 | 40.374 | 378.967 | 61.966 | 342.249 | 91.996 | 2.268 | 253.349 | 0.225 |
| Negative | −323.013 | −40.766 | −376.650 | −76.880 | −325.678 | −91.991 | 0.229 | |||
| TLJ-12 | Positive | 343.920 | 36.885 | 406.241 | 62 | 345.304 | 86.905 | 2.303 | 334.619 | 0.238 |
| Negative | −338.063 | −36.253 | −397.104 | −62 | −337.539 | −81.549 | 0.248 | |||
| TLJ-13 | Positive | 357.671 | 37.282 | 404.112 | 62 | 350.295 | 83.022 | 2.102 | 342.861 | 0.234 |
| Negative | −351.874 | −36.885 | −396.341 | −62 | −339.440 | −80.343 | 0.246 | |||
| TLJ-14 | Positive | 337.505 | 18.973 | 407.756 | 77 | 346.563 | 91.795 | 4.924 | 484.866 | 0.193 |
| Negative | −329.120 | −18.367 | −403.802 | −62 | −355.197 | −92 | 0.163 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Qiu, J.; Li, L.; Qin, Q.; Zhang, Y.; Xiong, G.; Wang, S. Research on Seismic Performance of Assembled Steel–Concrete Composite Joints in the Top Layer of Subway Station Under High Axial Compression Ratio. Buildings 2025, 15, 3083. https://doi.org/10.3390/buildings15173083
Li H, Qiu J, Li L, Qin Q, Zhang Y, Xiong G, Wang S. Research on Seismic Performance of Assembled Steel–Concrete Composite Joints in the Top Layer of Subway Station Under High Axial Compression Ratio. Buildings. 2025; 15(17):3083. https://doi.org/10.3390/buildings15173083
Chicago/Turabian StyleLi, Haoxuan, Jisheng Qiu, Leilei Li, Qing Qin, Yuqing Zhang, Guanghong Xiong, and Shurui Wang. 2025. "Research on Seismic Performance of Assembled Steel–Concrete Composite Joints in the Top Layer of Subway Station Under High Axial Compression Ratio" Buildings 15, no. 17: 3083. https://doi.org/10.3390/buildings15173083
APA StyleLi, H., Qiu, J., Li, L., Qin, Q., Zhang, Y., Xiong, G., & Wang, S. (2025). Research on Seismic Performance of Assembled Steel–Concrete Composite Joints in the Top Layer of Subway Station Under High Axial Compression Ratio. Buildings, 15(17), 3083. https://doi.org/10.3390/buildings15173083







