Optimizing Subway HVAC Control Strategies for Energy Savings Using Dymola Simulation
Abstract
1. Introduction
2. Methodology
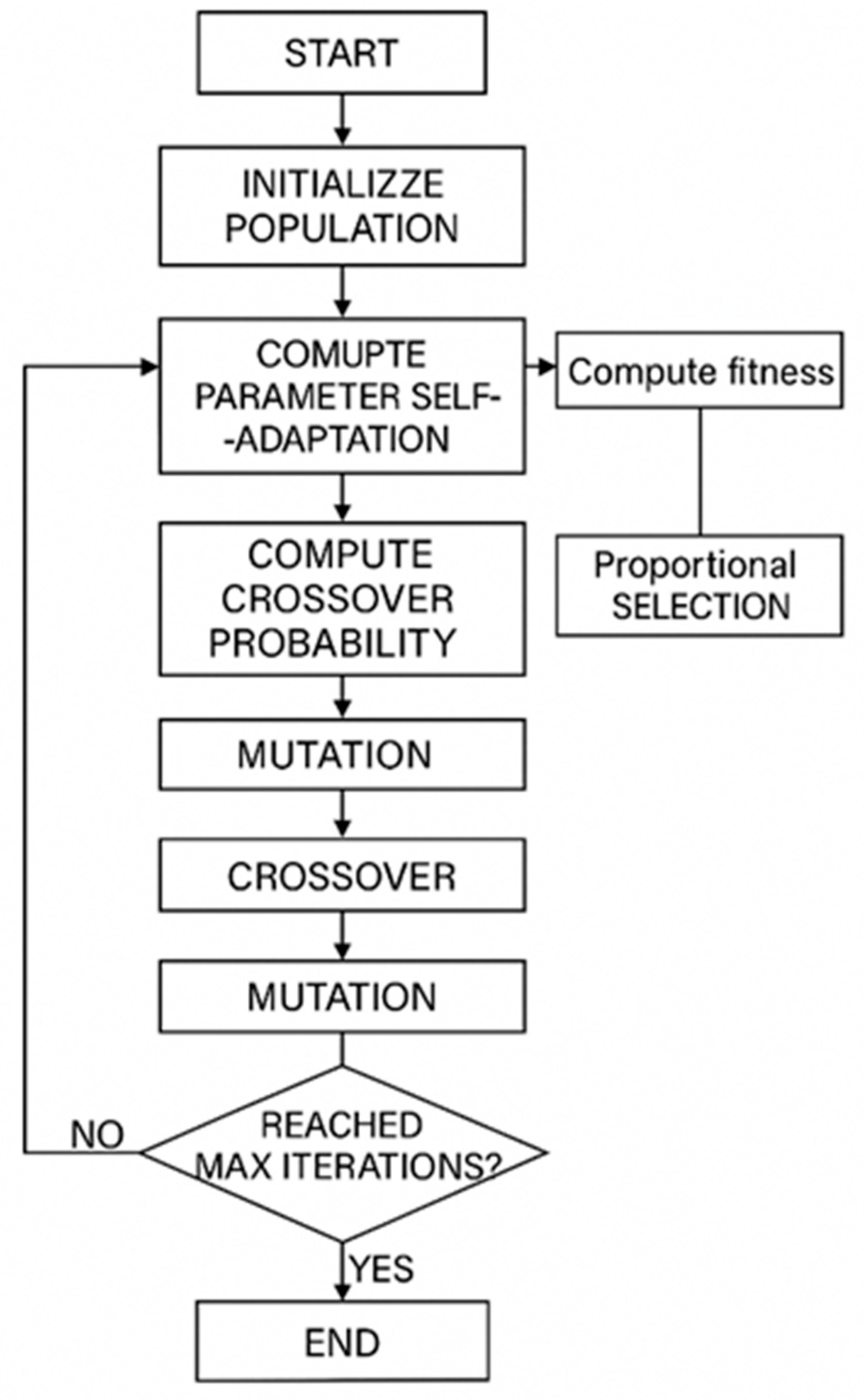
2.1. Genetic Algorithm Optimization
- cooling pump flow rate;
- chiller load-switching point;
- chilled water outlet temperature;
- cooling tower outlet temperature.
2.2. Mathematical Modeling of Water System Equipment
- Chiller
- Pump
- Cooling towers
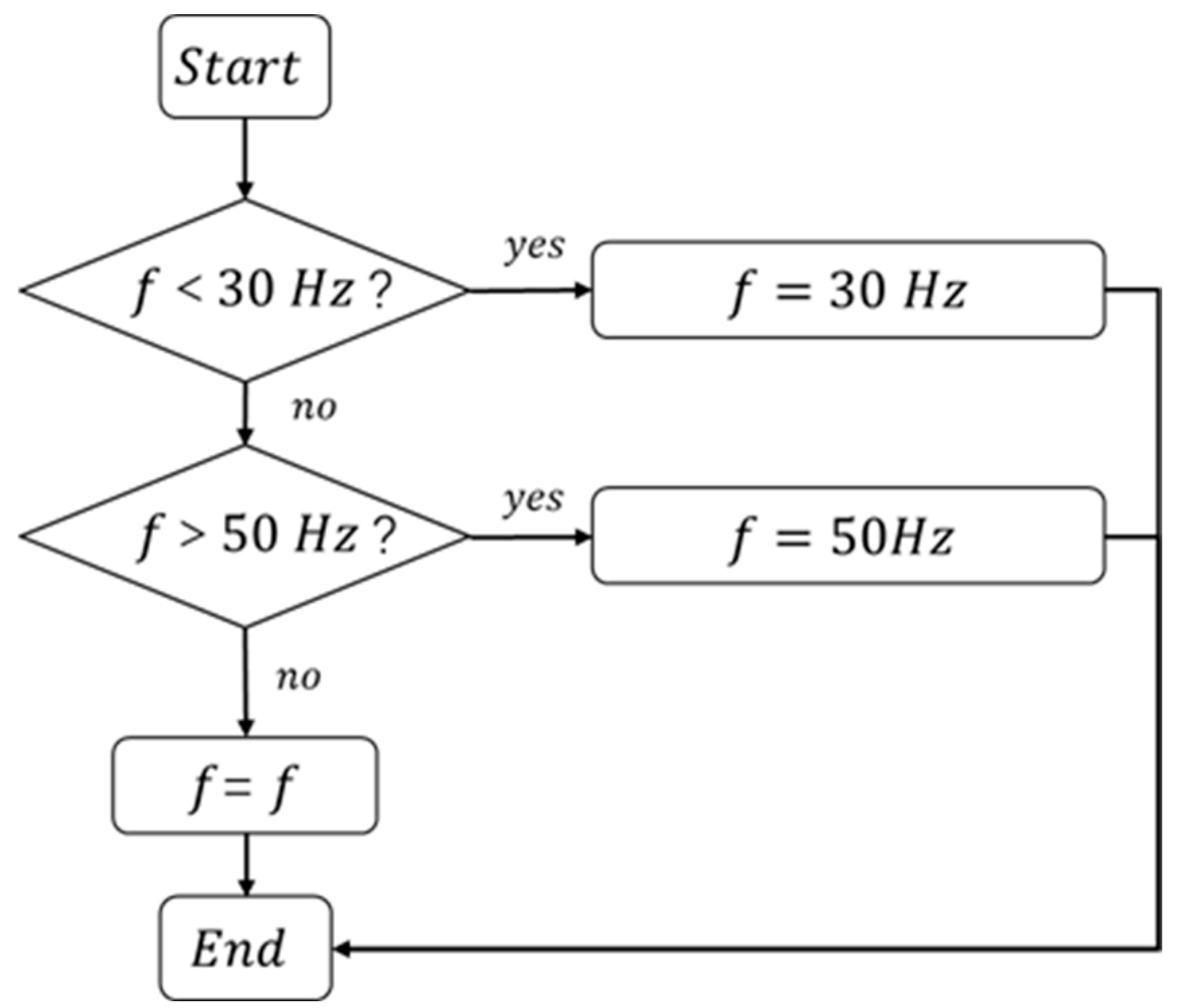
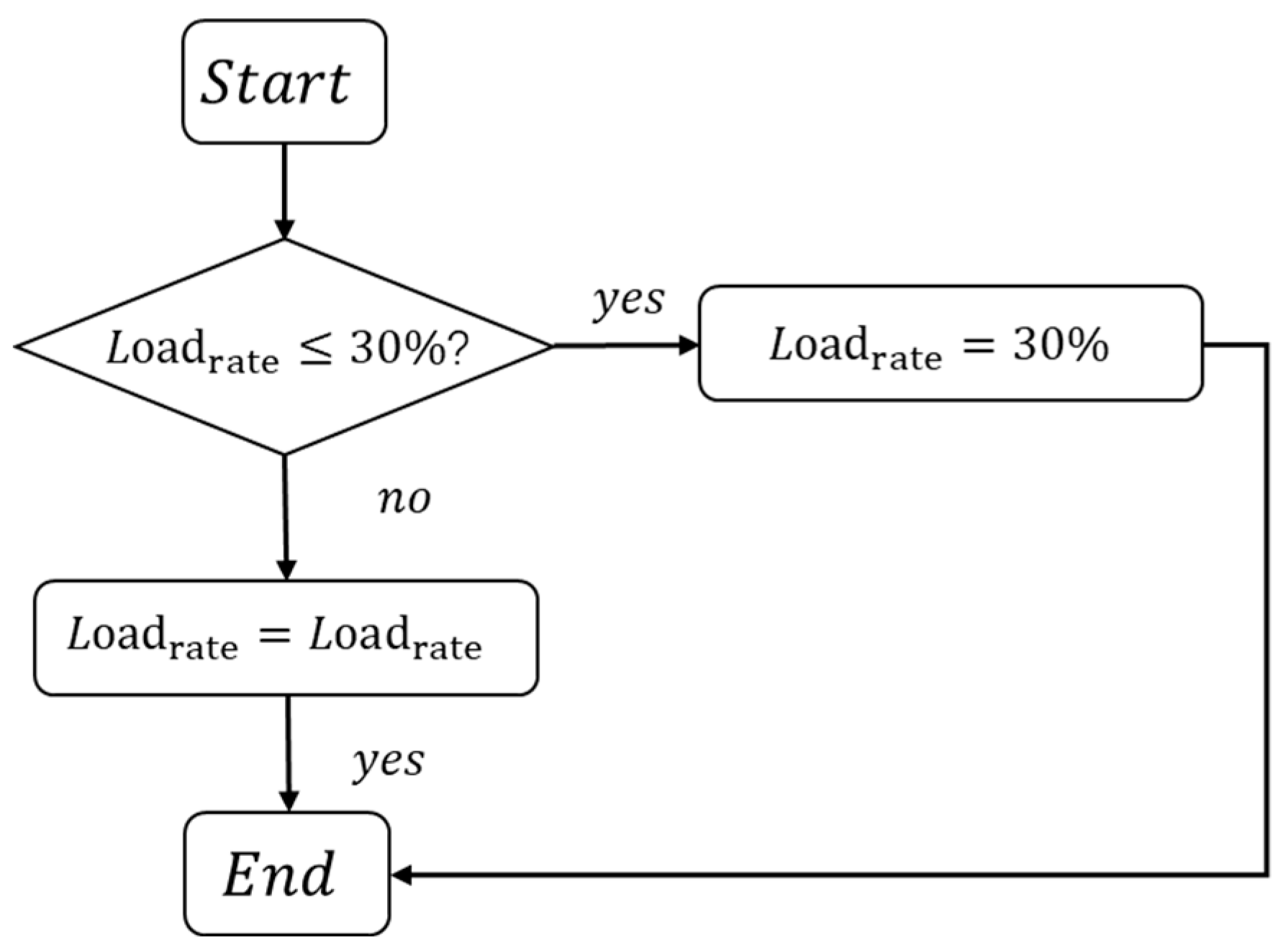
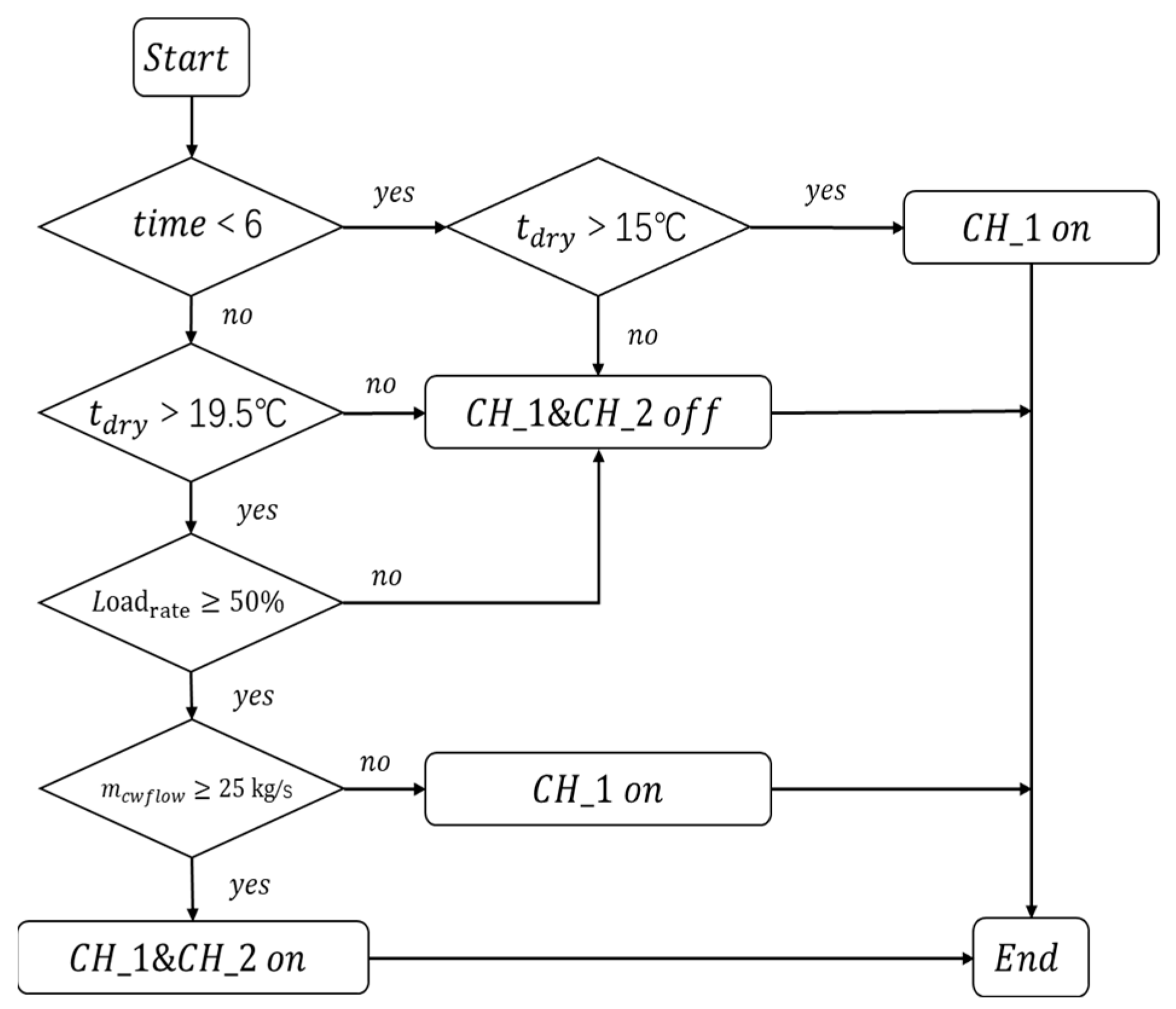
2.3. Establishment of a Simulation Scheme for Practice-Based Control Strategies
2.4. Dynamic Simulation Modeling of Water Systems Based on Dymola
3. Results and Analysis
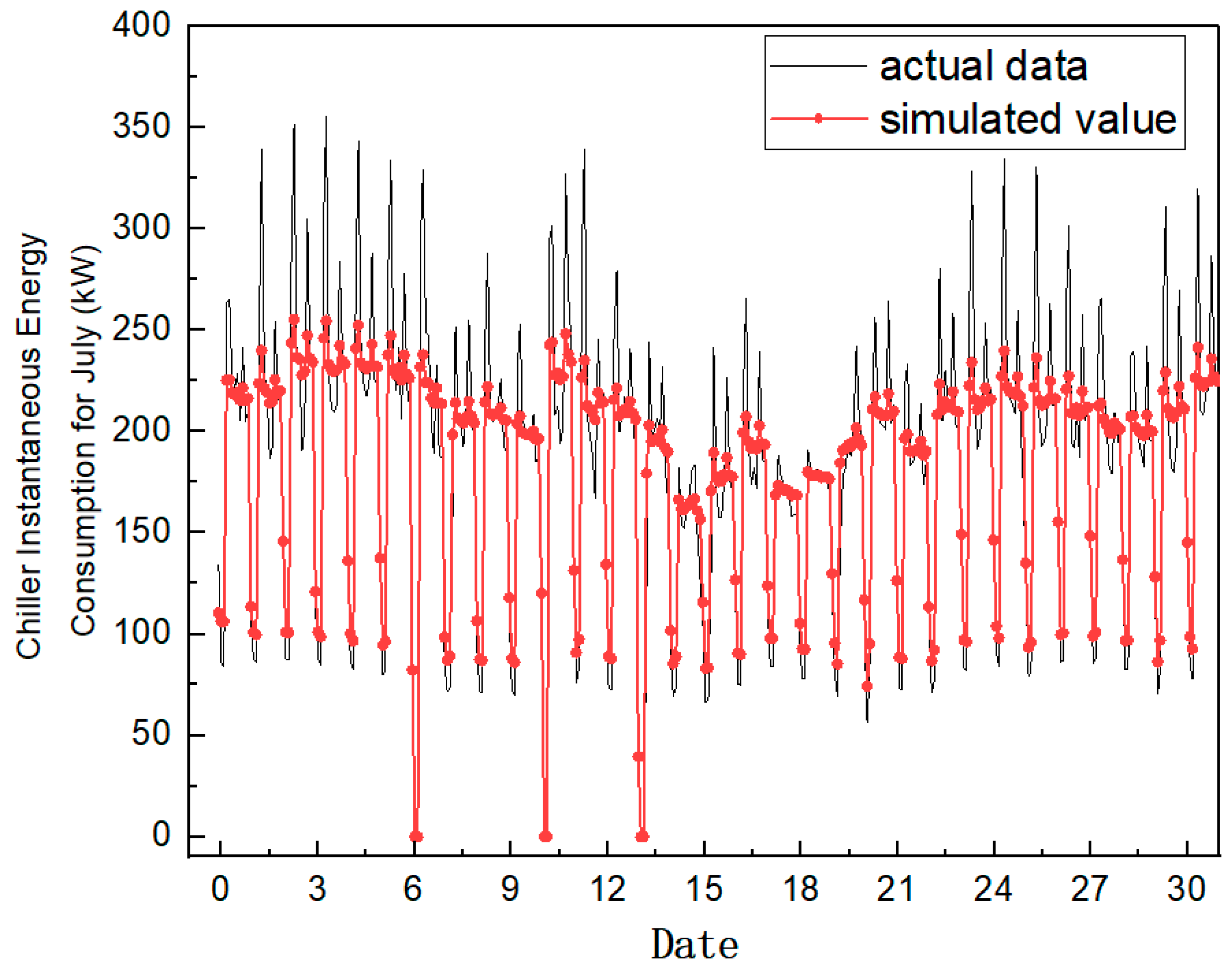
3.1. Simulation Validation and Error Analysis
- First, the control strategy assumes ideal conditions. It does not account for common real-world factors such as actuator delays, control hysteresis, or sensor noise. These factors may compromise control stability and responsiveness, particularly under variable load conditions.
- Second, the model relies on standard weather datasets rather than high-resolution or site-specific environmental data. This may reduce the accuracy of short-term load forecasts, especially during transitional seasons when outdoor conditions can change rapidly.
- Third, while the baseline model was validated against measured data from a representative month—with the simulation error kept below 5%—it has not yet been tested across a full year or under a wider range of operating scenarios. As a result, the generalizability of the findings remains limited.
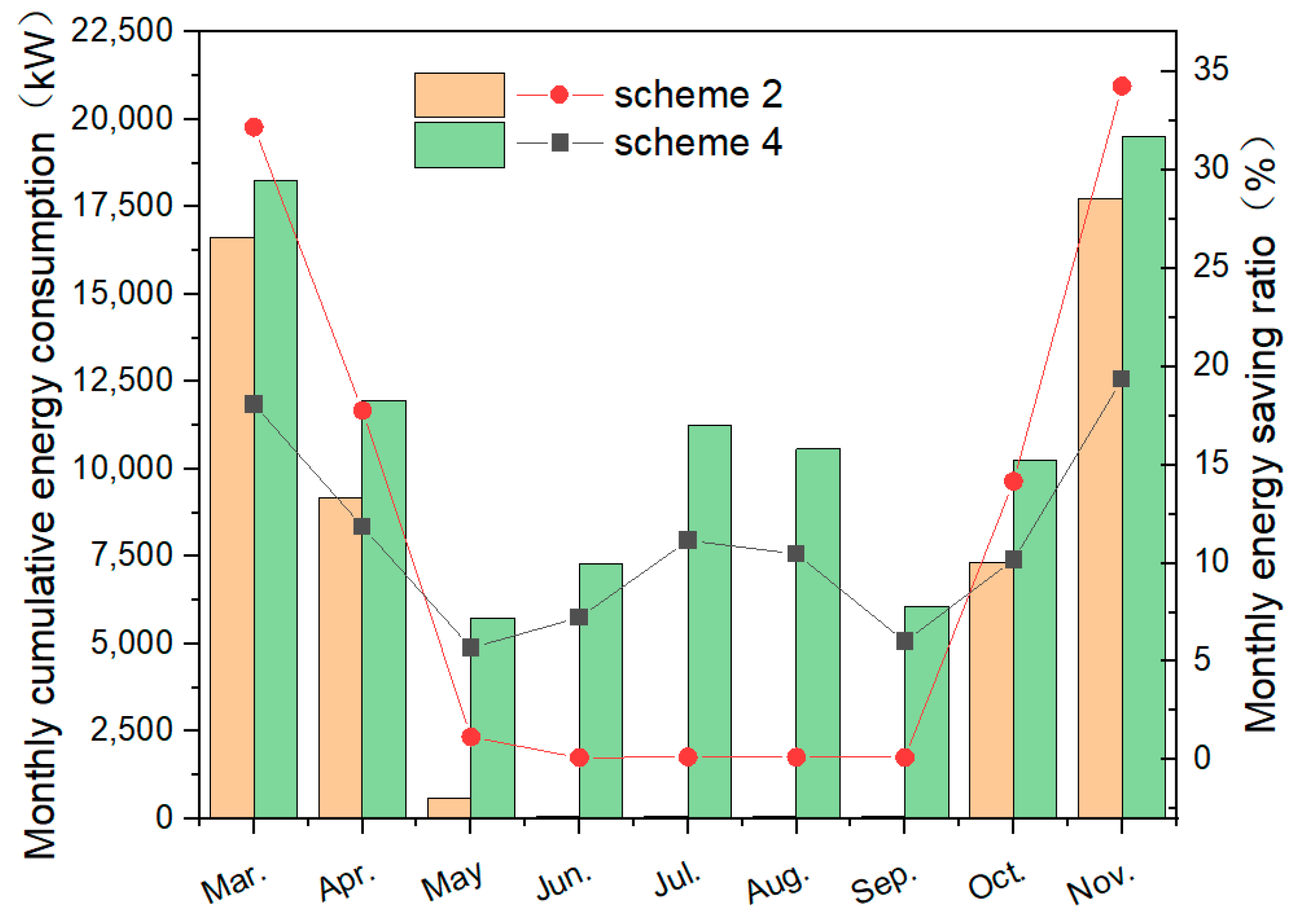
3.2. Analysis of Cumulative Energy Consumption of Systems and Equipment
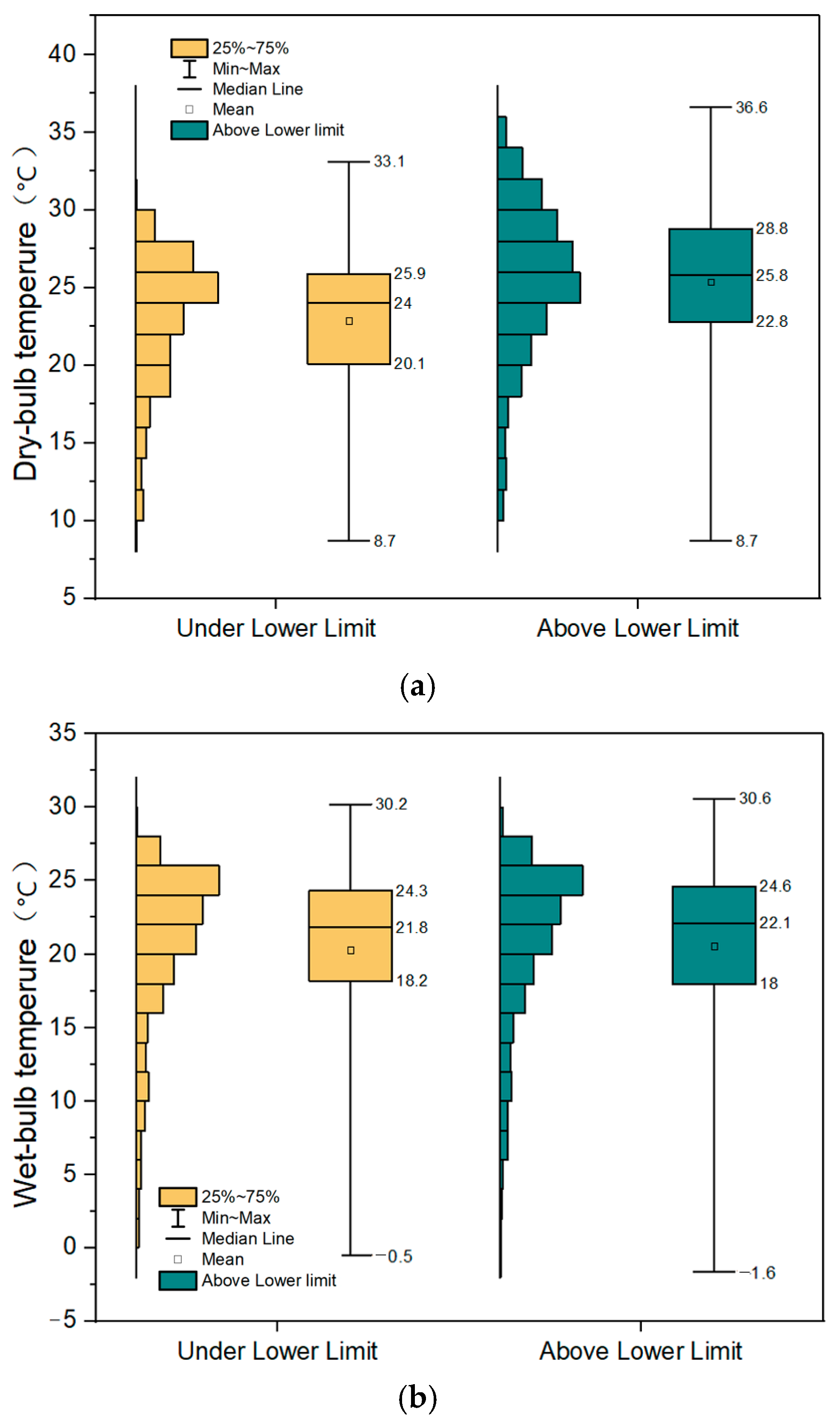
3.3. Impact of Equipment Frequency Upper and Lower Control Limits
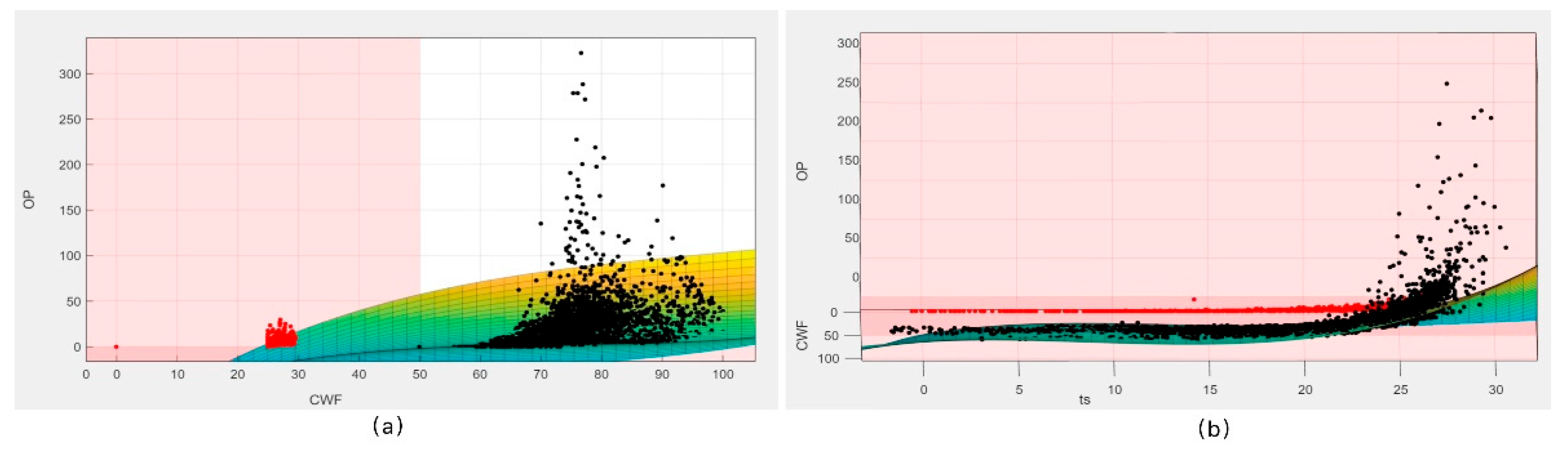
3.4. Quantitative Relationship Between Cooling Water Flow Rate, Outdoor Wet-Bulb Temperature, and Cooling Tower Energy Consumption
4. Conclusions
- (1)
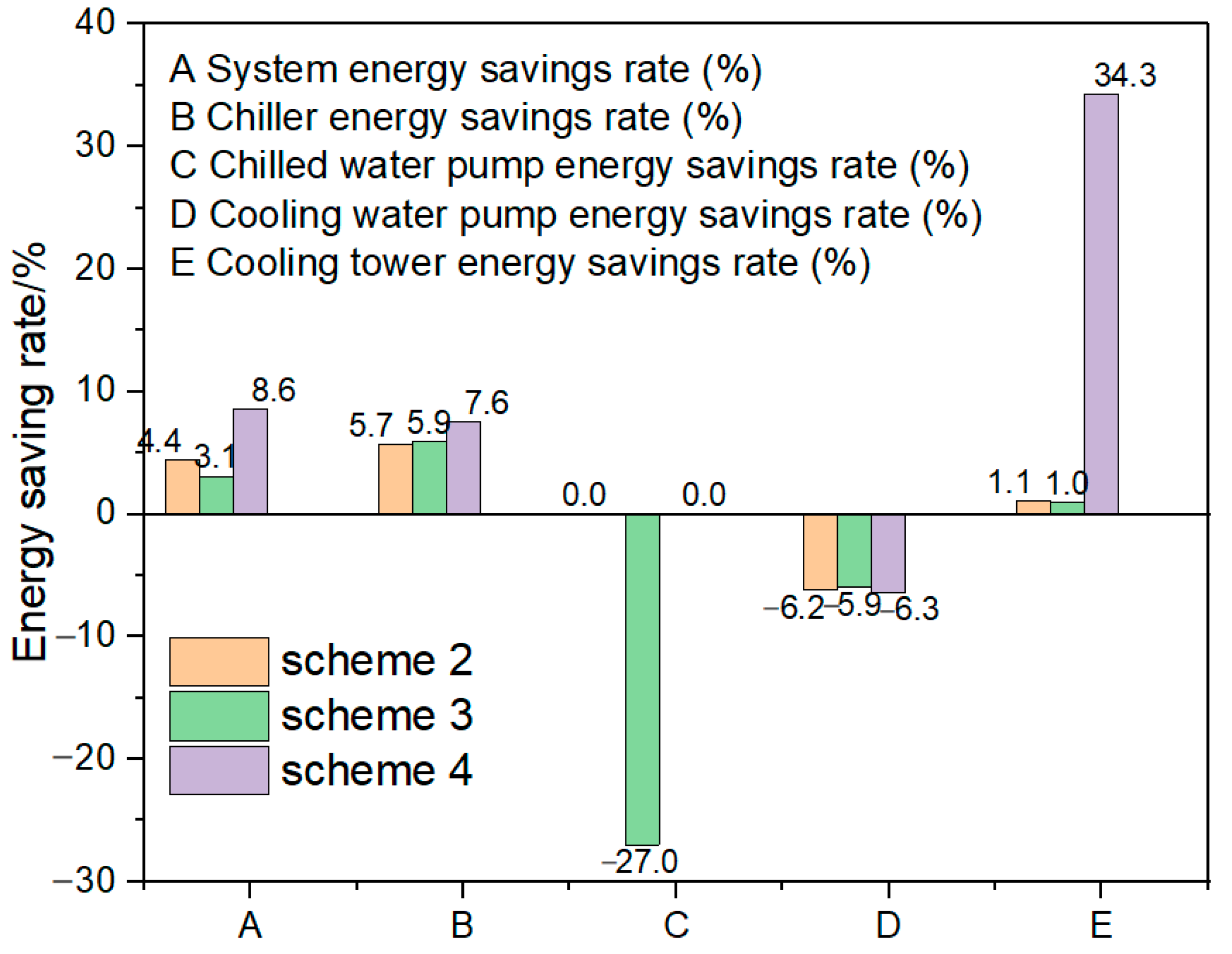
- Energy-saving performance: Schemes 2, 3, and 4 reduced total system energy use by 4.42%, 3.10%, and 8.62%, respectively, compared to the baseline. Scheme 2 integrated real-time outdoor weather data into frequency control logic, improving both efficiency and system stability. Scheme 4 went a step further. It used a genetic algorithm to optimize pump flow, load-switching points, and water outlet temperatures. This coordinated control delivered the greatest energy savings, underscoring the advantages of intelligent, multi-parameter optimization.
- (2)
- Equipment energy profiles: Chillers were responsible for nearly 80% of total system consumption, confirming their central role in HVAC energy use. Cooling tower demand varied with outdoor wet-bulb temperature, dropping sharply in cooler conditions. Cooling water pump loads fluctuated with seasonal weather, reflecting the system’s sensitivity to ambient conditions.
- (3)
- Implications for system control: These results highlight the value of digital, twin–based adaptive control. Unlike fixed-rule strategies, intelligent models can respond to changing environmental conditions in real time. The findings support a broader shift toward data-informed, model-supported control approaches, critical for improving operational resilience and advancing the decarbonization of metro HVAC systems.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, F.; Liang, S.; Feng, A. Statistics and development analysis of urban rail transit in China in 2023. Tunn. Constr. 2024, 44, 393–400. [Google Scholar]
- Su, X.; Huang, Y.; Wang, L.; Tian, S.; Luo, Y. Operating optimization of air-conditioning water system in a subway station using data mining and dynamic system models. J. Build. Eng. 2021, 44, 103379. [Google Scholar] [CrossRef]
- Yu, Y.; You, S.; Zhang, H.; Ye, T.; Wang, Y.; Wei, S. A review on available energy saving strategies for heating, ventilation and air conditioning in underground metro stations. Renew. Sustain. Energy Rev. 2021, 141, 110788. [Google Scholar] [CrossRef]
- Lee, G.-Y.; Noh, Y.; Kang, Y.-J.; Kim, N.; Park, N.; Oh, B.; Choi, G. Digital twin model calibration of HVAC system using adaptive domain Nelder-Mead method. Energy Build. 2025, 330, 115340. [Google Scholar] [CrossRef]
- Schicktanz, M.; Nunez, T. Modelling of an adsorption chiller for dynamic system simulation. Int. J. Refrig. 2009, 32, 588–595. [Google Scholar] [CrossRef]
- Huang, S.; Zuo, W.; Sohn, M.D. Improved cooling tower control of legacy chiller plants by optimizing the condenser water set point. Build. Environ. 2017, 111, 33–46. [Google Scholar] [CrossRef]
- Vering, C.; Mehrfeld, P.; Nurenberg, M. Unlocking Potentials of Building Energy Systems’ Operational Efficiency: Application of Digital Twin Design for HVAC systems. In Proceedings of the 16th International Building Performance Simulation Association (IBPSA), Rome, Italy, 2–4 September 2019. [Google Scholar]
- Kusiak, A.; Li, M.; Tang, F. Modeling and optimization of HVAC energy consumption. Appl. Energy 2010, 87, 3092–3102. [Google Scholar] [CrossRef]
- Wang, L. Energy-Saving Control Method of Building Central Air Conditioning Based on Genetic Algorithm. Adv. Multimed. 2022, 2022, 8738871. [Google Scholar] [CrossRef]
- Garcès-Jimènez, A.; Gómez Pulido, J.M.; Gallego-Salvador, N.; García-Tejedor, Á.J. Genetic and swarm algorithms for optimizing the control of building hvac systems using real data: A comparative study. Mathematics 2021, 9, 2181. [Google Scholar] [CrossRef]
- Hu, Y.; Qin, L.; Li, S.; Li, X.; Li, Y.; Sheng, W. A novel energy saving framework based on optimal chiller loading and parameter optimization for HVAC: A case study for subway station. J. Build. Eng. 2025, 101, 111887. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, J.; Xiao, F.; Xu, K.; Chen, Y. Physically consistent data-driven optimal sequencing strategy for variable speed pumps in large building chiller plants. Build. Environ. 2025, 281, 113177. [Google Scholar] [CrossRef]
- Zhang, Q.; Long, W.; Wang, R.; Cao, Z.; Wang, Z.; Yan, Y.; Wen, Y. CAPER: Dual-level physics-data fusion with modular metamodels for reliable generalization in predictive digital twins. Appl. Energy 2025, 398, 126393. [Google Scholar] [CrossRef]
- Borja-Conde, J.A.; Nadales, J.M.; Ordonez, J.G.; Fele, F.; Limon, D. Efficient management of HVAC systems through coordinated operation of parallel chiller units: An economic predictive control approach. Energy Build. 2024, 304, 113879. [Google Scholar] [CrossRef]
- Guan, B.; Liu, X.; Zhang, T.; Xia, J. Energy consumption of subway stations in China: Data and influencing factors. Sustain. Cities Soc. 2018, 43, 451–461. [Google Scholar] [CrossRef]
- Seo, B.M.; Lee, K.H. Detailed analysis on part load ratio characteristics and cooling energy saving of chiller staging in an office building. Energy Build. 2016, 119, 309–322. [Google Scholar] [CrossRef]
- Abou-Ziyan, H.Z.; Alajmi, A.F. Effect of load-sharing operation strategy on the aggregate performance of existed multiple-chiller systems. Appl. Energy 2014, 135, 329–338. [Google Scholar] [CrossRef]
- Huang, S.; Zuo, W.; Sohn, M.D. Amelioration of the cooling load based chiller sequencing control. Appl. Energy 2016, 168, 204–215. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, H.; Xi, X. Monitoring and autonomous control of Beijing Subway HVAC system for energy sustainability. Energy Sustain. Dev. 2017, 39, 1–12. [Google Scholar] [CrossRef]
- Sun, K.; Hong, T.; Taylor-Lange, S.C.; Piette, M.A. A pattern-based automated approach to building energy model calibration. Appl. Energy 2016, 165, 214–224. [Google Scholar] [CrossRef]
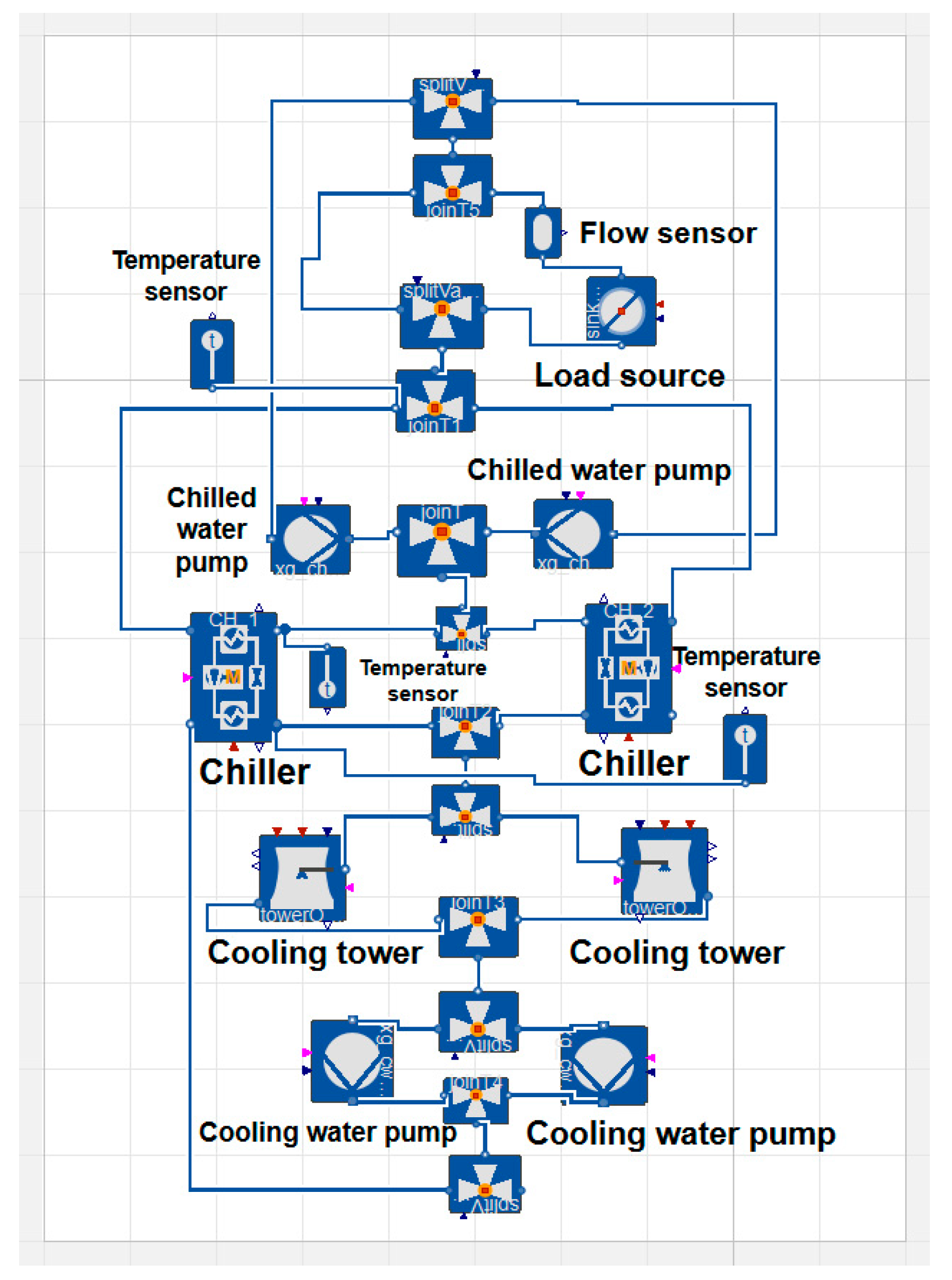




| Equipment | Quantities | Key Parameters |
|---|---|---|
| Chiller | 2 | Cooling capacity: 1233 kW; Power: 211 kW; Chilled water temperature: 14/7 °C; Cooling water temperature: 32/37 °C |
| Cooling water pumps | 2 | Flow rate: 243.7 m3/h; Head: 24 m; Power: 22 kW |
| Chilled water pump | 2 | Flow rate: 151.3 m3/h; Head: 23 m; Power: 15 kW |
| Cooling tower | 2 | Water flow rate: 370 m3/h; Power: 11 kW |
| Parametric | Source |
|---|---|
| Hourly loads during metro operation | EnergyPlus |
| Equipment parameters | Actual project |
| Indoor dry-bulb temperature | |
| Timetable for the operation of the system | |
| Outdoor dry- and wet-bulb temperature |
| Parametric | Lower Limit | Upper Limit | Step Size |
|---|---|---|---|
| Cooling water pump flow (kg/s) | 10 | 50 | 5 |
| Load-switching point (%) | 50 | 75 | 5 |
| Chiller cold end outlet set temperature (°C) | 5 | 9 | 1 |
| Cooling tower outlet set temperature (°C) | 27 | 31 | 1 |
| Cumulative Energy Consumption | Scheme 1 | Scheme 2 | Scheme 3 | Scheme 4 |
|---|---|---|---|---|
| Chiller energy consumption (kW) | 949,438 | 893,415 | 894,974 | 877,654 |
| Chilled water pump energy consumption (kW) | 63,075 | 80,082 | 63,067 | 63,077 |
| Cooling water (kW) | 61,455 | 65,102 | 65,250 | 65,350 |
| Cooling towers (kW) | 96,489 | 95,564 | 95,412 | 63,438 |
| Total system energy consumption (kW) | 1,170,456 | 1,118,704 | 1,134,163 | 1,069,519 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Luo, Y.; Wang, D.; Luo, H.; Zhong, X.; Qin, X.; Zhu, H. Optimizing Subway HVAC Control Strategies for Energy Savings Using Dymola Simulation. Buildings 2025, 15, 3064. https://doi.org/10.3390/buildings15173064
Zhu Y, Luo Y, Wang D, Luo H, Zhong X, Qin X, Zhu H. Optimizing Subway HVAC Control Strategies for Energy Savings Using Dymola Simulation. Buildings. 2025; 15(17):3064. https://doi.org/10.3390/buildings15173064
Chicago/Turabian StyleZhu, Yihao, Yanping Luo, Dijun Wang, Hui Luo, Xiaoqing Zhong, Xu Qin, and Han Zhu. 2025. "Optimizing Subway HVAC Control Strategies for Energy Savings Using Dymola Simulation" Buildings 15, no. 17: 3064. https://doi.org/10.3390/buildings15173064
APA StyleZhu, Y., Luo, Y., Wang, D., Luo, H., Zhong, X., Qin, X., & Zhu, H. (2025). Optimizing Subway HVAC Control Strategies for Energy Savings Using Dymola Simulation. Buildings, 15(17), 3064. https://doi.org/10.3390/buildings15173064





