Calculation Method and Experimental Study of Stress Loss in T-Beam External Prestressed Tendon Based on the Variation Principle
Abstract
1. Introduction
2. The Theory of Effective Stress Detection of External Prestressed Tendon
2.1. Assumption
- 1.
- Ignore the influence of the bending stiffness of the prestressed tendon. The span-to-diameter ratio of the prestressed tendon far exceeds 20, which leads to relatively small self-bending stiffness, which has a negligible impact on the result. Moreover, the lateral displacement of the prestressed tendon is mainly caused by the lateral force during the test.
- 2.
- The stress of the prestressed tendon between any two adjacent constraints varies linearly. The prestressed tendon is made by twisting multiple steel wires, and their microscopic stress distribution is non-uniform. However, on a macro level, when the prestressed tendon is used as an integral material, the uniform stress assumption can effectively characterize average mechanical properties.
- 3.
- The anchoring zones at both ends of the prestressed tendon are simplified to articulated constraints. In actual engineering, anchoring structures are usually designed to only constrain translational degrees of freedom while allowing a certain degree of rotation. The articulated constraints assumption would slightly overestimate the deflection of the prestressed tendon whose error is usually within the allowable range of the project and is biased towards safety.
- 4.
- Consider the lateral displacement of the restrictor under transverse tension.
- 5.
- Ignore the displacement of the boundary point position under transverse tension.
2.2. Calculation Method
- (1)
- Without restrictor
- (2)
- Single restrictor
- (3)
- Double restrictors
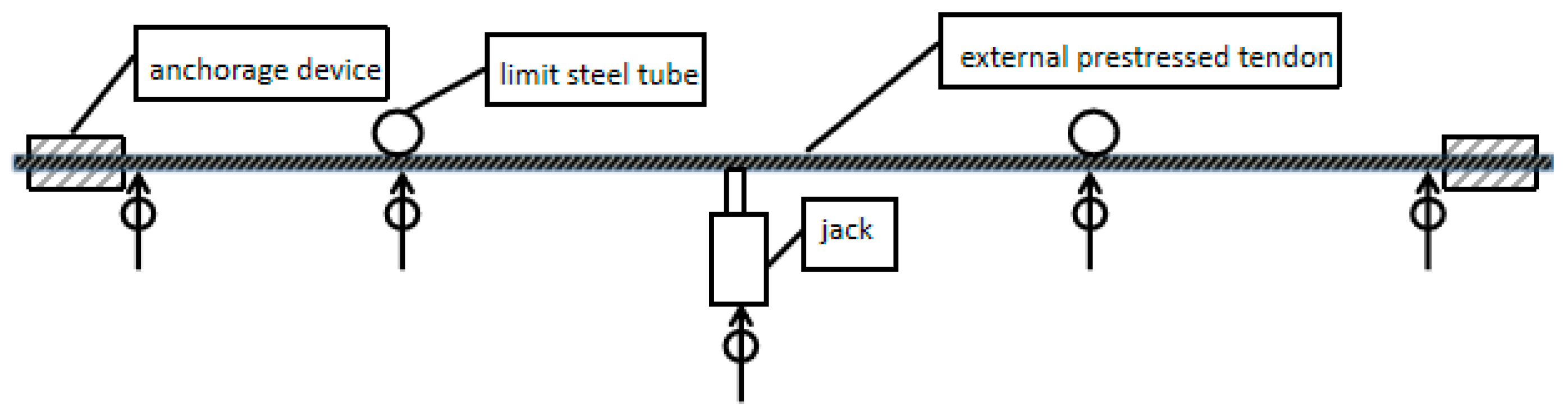
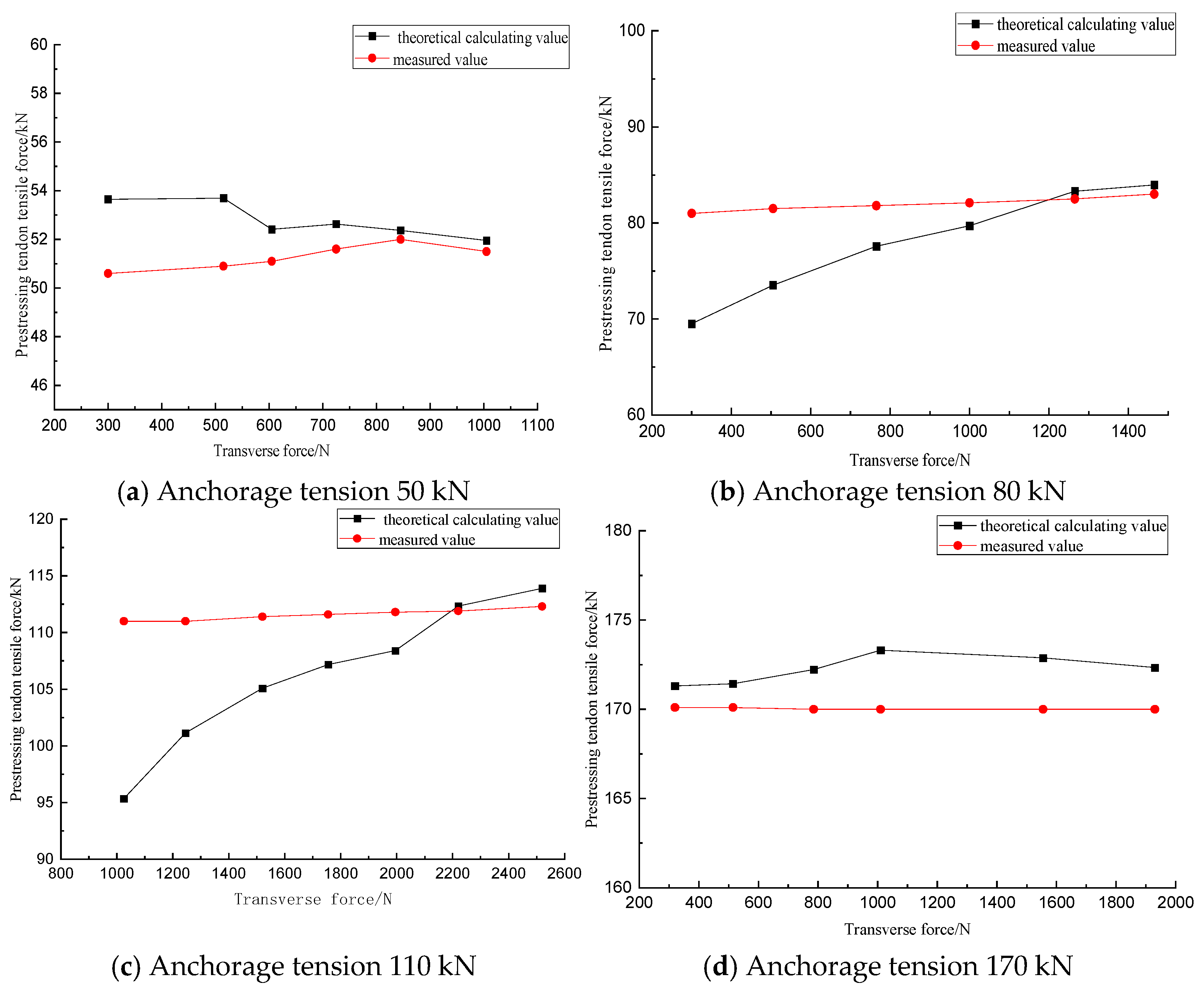
2.3. Experimental Verification
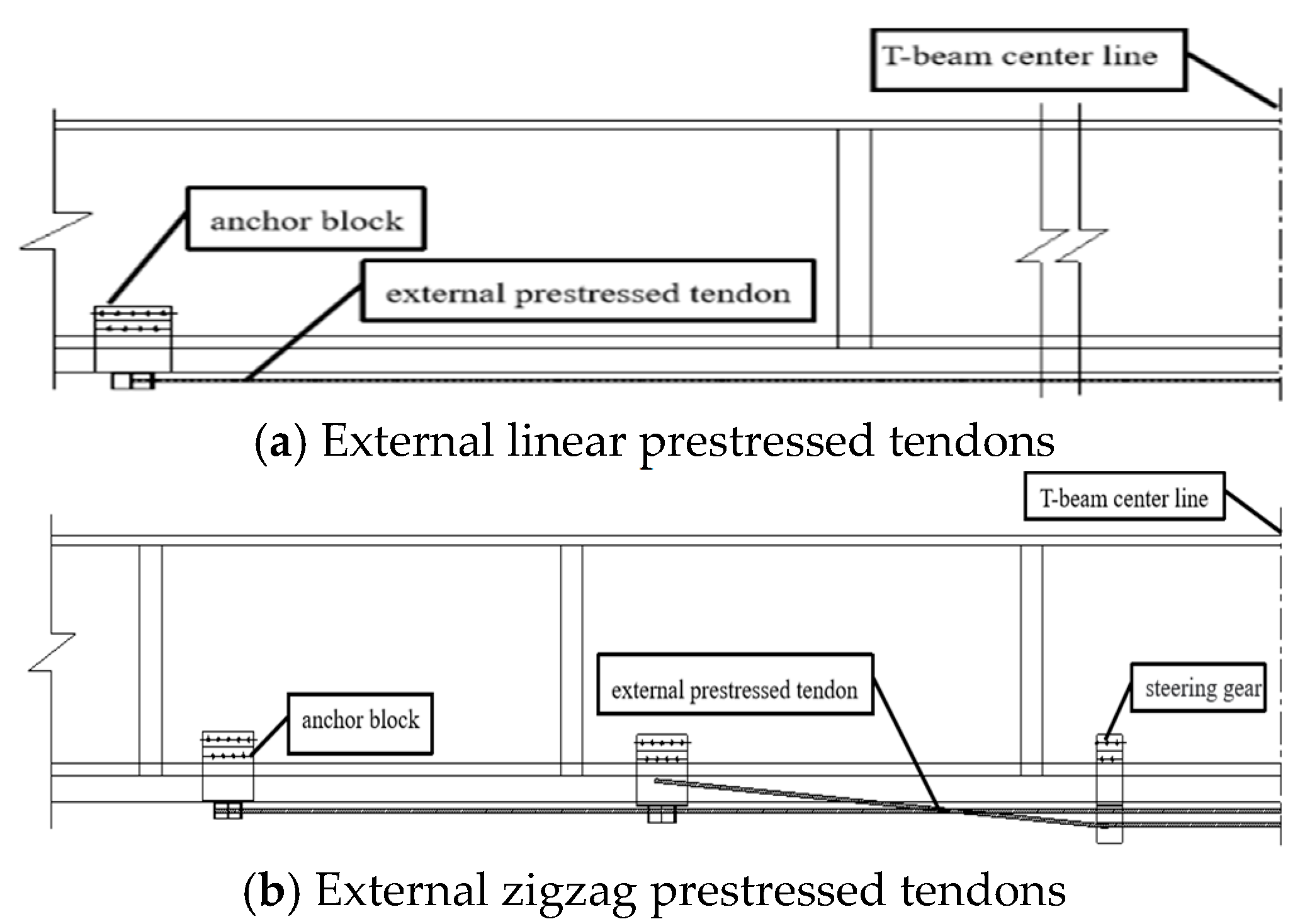
3. Detection of Stress Loss of External Prestressed Tendons for Existing Bridge
3.1. Measuring Method
3.2. Detection Procedure
3.3. Measured Data and Calculations
4. Results and Analysis
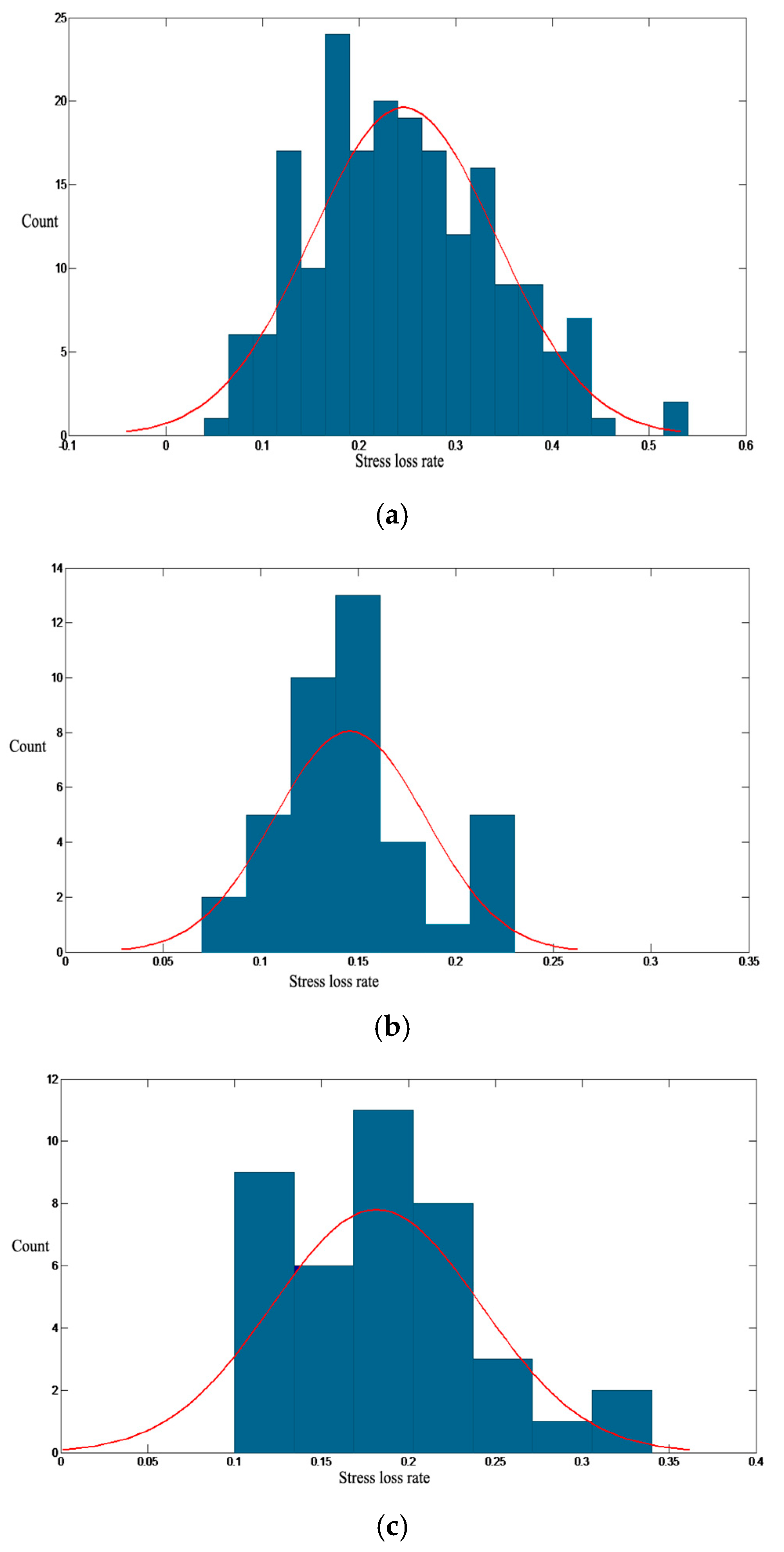
4.1. Statistic Analysis of Data
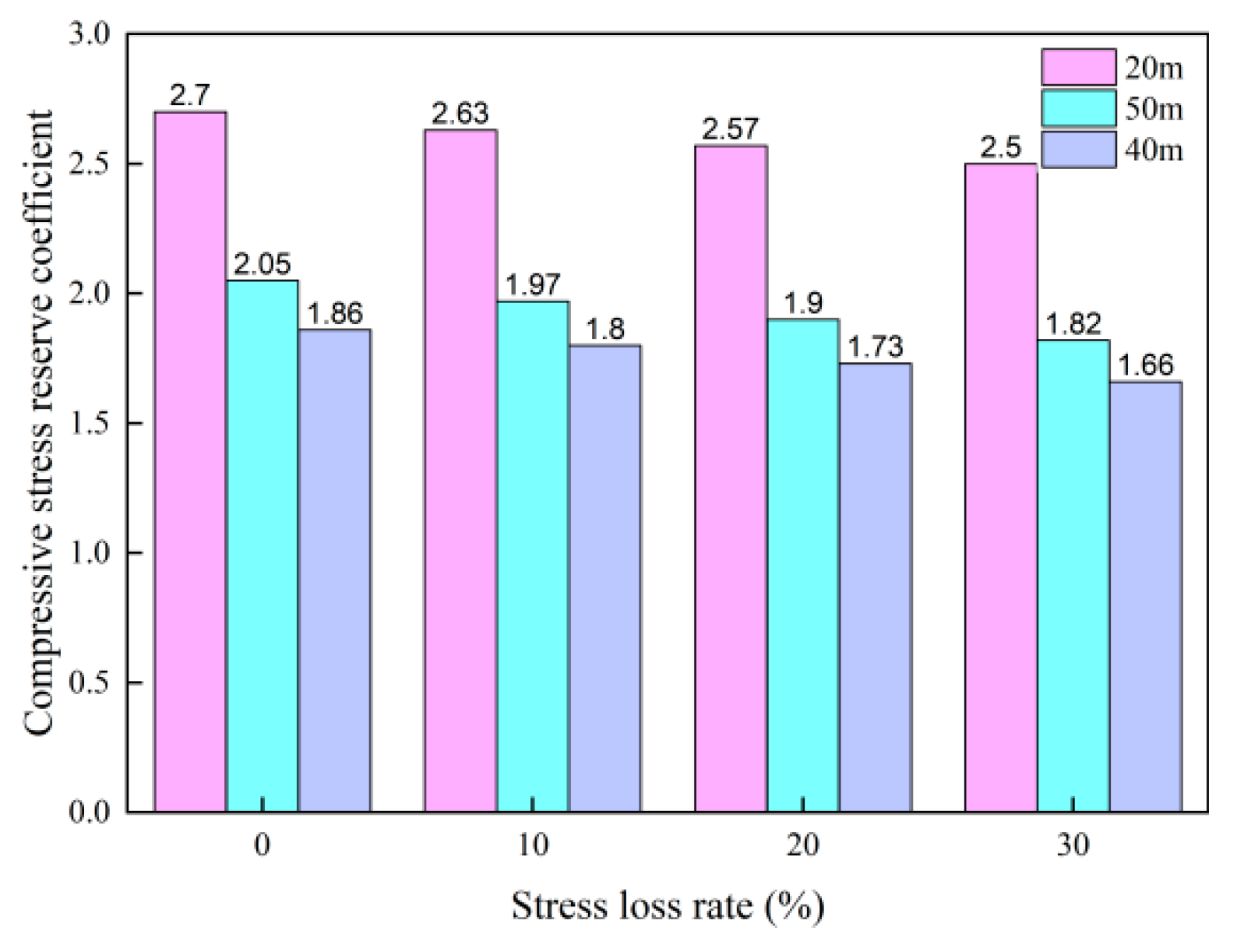
4.2. Analysis of the Influence of Stress Loss on the Reinforcement Effect of Bridges
5. Conclusions
- 1.
- The calculation formulas for different arrangements of prestressed tendons were derived based on the variational principle. The results of the transverse tensioning test show that as the transverse tension increases, the theoretically calculated value will gradually approach the measured value and tend to be stable. Eventually, the error between them can be controlled within 5%, indicating that this method is accurate and feasible.
- 2.
- The stress loss of the external prestressed tendons of 40 m and 50 m T-beams was detected and calculated using the proposed method. Both their stress loss rates and quantities conformed to the normal distribution after counting, and the hypothesis test fitting curves also conformed to the assumption. Taking environmental factors into account in actual measurement is an area that deserves investigation.
- 3.
- The ratio of the compressive stress at the bottom edge of the T-beam under self-weight and prestressed load to the tensile stress under vehicle load was proposed as the compressive stress reserve coefficient of the bridge. It was found that the decreased value of the compressive stress reserve coefficient was linearly proportional to the additional stress loss of the external prestressed tendon through calculating the coefficient at pre-strengthening, post-strengthening and post-prestress-loss scenarios. The compressive stress reserve coefficient could be used as an evaluation index for the influence of stress damage on the reinforcement effect and the supplementary tensioning of prestressed tendons.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| The compressive stress reserve coefficient of the bridge | |
| Bridge bearing capacity check factor | |
| The stress of the beam bottom plate under the stress of self-weight and internal prestressed tendon | |
| The stress of the beam bottom plate under the function of external prestressed tendon | |
| The design of the beam bottom plate stress under the super-20 load | |
| Live load influence correction factor |
References
- Zanini, M.A.; Toska, K.; Faleschini, F.; Pellegrino, C. Seismic Reliability of Reinforced Concrete Bridges Subject to Environmental Deterioration and Strengthened with FRCM Composites. Soil Dyn. Earthq. Eng. 2020, 136, 106224. [Google Scholar] [CrossRef]
- Park, Y.H.; Park, C.; Park, Y.G. The Behavior of an In-Service Plate Girder Bridge Strengthened with External Prestressing Tendons. Eng. Struct. 2005, 27, 379–386. [Google Scholar] [CrossRef]
- Panigrahi, S.K.; Salunke, P.J.; Gore, N.G. Rehabilitation, Monitoring and Strengthening of Bridges. Int. Res. J. Eng. Technol. 2015, 4. [Google Scholar]
- Miyamoto, A.; Tei, K.; Nakamura, H.; Bull, J.W. Behavior of Prestressed Beam Strengthened with External Tendons. J. Struct. Eng. 2000, 126, 1033–1044. [Google Scholar] [CrossRef]
- Straninger, W.; Wicke, M. Bridge Strengthening with Additional Prestressing. Struct. Eng. Int. 1995, 5, 78–80. [Google Scholar] [CrossRef]
- Madaj, A.; Mossor, K. Evaluation of External Prestressing as a Strengthening Method for Existing Concrete Bridges. Struct. Eng. Int. 2019, 29, 412–416. [Google Scholar] [CrossRef]
- Seręga, S.; Faustmann, D.H. Flexural Strengthening of Reinforced Concrete Beams Using External Tendons. Eng. Struct. 2022, 252, 113277. [Google Scholar] [CrossRef]
- Zou, J.; Huang, Y.; Feng, W.; Chen, Y.; Huang, Y. Experimental Study on Flexural Behavior of Concrete T-Beams Strengthened with Externally Prestressed Tendons. Math. Biosci. Eng. 2019, 16, 6962–6974. [Google Scholar] [CrossRef]
- Omar, A.H.; Gullu, M.F.; Ahmed, G.H. Experimental and Analytical Investigation of T-Beams Retrofitted through the External Post-Tensioning Using Steel and Various FRP Strands. Structures 2024, 68, 107129. [Google Scholar] [CrossRef]
- Mo, D.; Zhang, L.; Wang, L.; Wu, X. A PZT Active Sensing Method for Monitoring Prestressing Force Based on the Ultrasonic Reflection Coefficient. Measurement 2024, 228, 114348. [Google Scholar] [CrossRef]
- Chen, S.-Z.; Wu, G.; Xing, T.; Feng, D.-C. Prestressing Force Monitoring Method for a Box Girder through Distributed Long-Gauge FBG Sensors. Smart Mater. Struct. 2017, 27, 015015. [Google Scholar] [CrossRef]
- Shi, L.; He, H.; Yan, W. Prestress Force Identification for Externally Prestressed Concrete Beam Based on Frequency Equation and Measured Frequencies. Math. Probl. Eng. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Nejati, H.R.; Nazerigivi, A.; Imani, M.; Karrech, A. Monitoring of Fracture Propagation in Brittle Materials Using Acoustic Emission Techniques-A Review. Comput. Concr. 2020, 25, 15–27. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.-W.; Park, S. Investigation of Applicability of an Embedded EM Sensor to Measure the Tension of a PSC Girder. J. Sens. 2019, 2019, 2469647. [Google Scholar] [CrossRef]
- Identification of Prestress-Loss in PSC Beams Using Modal Information | Request PDF. Struct. Eng. Mech. 2004, 17, 467–482. [CrossRef]
- Huynh, T.-C.; Kim, J.-T. RBFN-Based Temperature Compensation Method for Impedance Monitoring in Prestressed Tendon Anchorage. Struct. Control Health Monit. 2018, 25, e2173. [Google Scholar] [CrossRef]
- Nguyen, K.-D.; Kim, J.-T. Smart PZT-Interface for Wireless Impedance-Based Prestress-Loss Monitoring in Tendon-Anchorage Connection. Smart Struct. Syst. 2012, 9, 489–504. [Google Scholar] [CrossRef]
- Ahlborn, T.M.; Shield, C.K.; French, C.W. Full-Scale Testing of Prestressed Concrete Bridge Girders. Exp. Tech. 1997, 21, 33–35. [Google Scholar] [CrossRef]
- Li, S.; Chang, S.; Li, P.; Zhang, X.; Jiang, N. Optimization of Concrete Surface Sensor Arrangement for Acoustic Emission Monitoring of Prestressed Steel Strand Damage in T-Beams. Appl. Acoust. 2024, 223, 110082. [Google Scholar] [CrossRef]
- Chen, R.H.L. An Ultrasonic Method for Measuring Tensile Forces in a Seven-Wire Prestressing Strand. AIP Conf. Proc. 2002, 615, 1295–1302. [Google Scholar] [CrossRef]
- Ghorbanpoor, A. Magnetic-Based NDE of Steel in Prestressed and Post-Tensioned Concrete Bridges. In Proceedings of the Structural Materials Technology III: An NDT Conference, San Antonio, TX, USA, 31 March–3 April 1998; SPIE: Bellingham, WA, USA, 1998. [Google Scholar]
- Kwahk, I.; Park, K.-Y.; Choi, J.-Y.; Kwon, H.; Joh, C. Non-Destructive Evaluation for Sectional Loss of External Tendon of Prestressed Concrete Structures Using Total Flux Leakage. Appl. Sci. 2020, 10, 7398. [Google Scholar] [CrossRef]
- Guo, H.; Yang, J.; Tang, R.; Yang, C.; Xu, F. Monitoring and Analysis of Prestress Loss in Prestressed Box Girder Bridges Strengthened with External Prestressing. Sensors 2024, 24, 4549. [Google Scholar] [CrossRef]
- Kim, J.-T.; Ryu, Y.-S.; Yun, C.-B. Vibration-Based Method to Detect Prestress Loss in Beam-Type Bridges. In Smart Structures and Materials 2003: Smart Systems and Nondestructive Evaluation for Civil Infrastructures; SPIE: Bellingham, WA, USA, 2003. [Google Scholar]
- Xu, J.L.; Sun, Z. Prestress Force Identification Based on Forced Vibration Tests of Eccentrically Prestressed Concrete Beam. AMR 2012, 479–481, 733–738. [Google Scholar] [CrossRef]
- Ye, C.; Butler, L.J.; Elshafie, M.Z.E.B.; Middleton, C.R. Evaluating Prestress Losses in a Prestressed Concrete Girder Railway Bridge Using Distributed and Discrete Fibre Optic Sensors. Constr. Build. Mater. 2020, 247, 118518. [Google Scholar] [CrossRef]
- Webb, G.T.; Vardanega, P.J.; Middleton, C.R. Categories of SHM Deployments: Technologies and Capabilities. J. Bridge Eng. 2015, 20, 04014118. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, J.; Zhang, C.; Xu, Q.; Chen, Y.; Wang, Z. Identification of Effective Prestress of Steel Strand Based on Blind-Hole Method. Tiedao Xuebao 2023, 45, 166–175. [Google Scholar]
- Wu, W.; Chen, S.; Dong, C.; Peng, W.; Yun, J.; Nie, L. Numerical Simulation and Experimental Study on Detecting Effective Prestress of 1860-Grade Strands Based on the Drilling Method. Coatings 2023, 13, 1869. [Google Scholar] [CrossRef]
- Mathar, J. Determination of Initial Stresses by Measuring the Deformations Around Drilled Holes. Trans. Am. Soc. Mech. Eng. 2023, 56, 249–254. [Google Scholar] [CrossRef]
- Schajer, G.S. Advances in Hole-Drilling Residual Stress Measurements. Exp. Mech. 2010, 50, 159–168. [Google Scholar] [CrossRef]
- Vimalanandam, V.; Babu, S.; Sreenath, H.G.; Rao, G.; Rao, A.S. Estimation of Residual Prestress in Uninstrumented Prestressed Concrete Structures Using SSRHT in Wires. Indian Concr. J. 2000, 74, 631–636. [Google Scholar]
- Blödorn, R.; Viotti, M.R.; Schroeter, R.B.; Albertazzi, A. Analysis of Blind-Holes Applied in the Hole-Drilling Method for Residual Stress Measurements. Exp. Mech. 2015, 55, 1745–1756. [Google Scholar] [CrossRef]
- Yun, J.; Chen, S.; Dong, C.; Wu, W.; Nie, L.; He, M. Detection of Effective Prestressing of 1860-Grade Strands Based on the Microporous Method. Sci. Rep. 2024, 14, 26084. [Google Scholar] [CrossRef] [PubMed]
- Schajer, G.S. Measurement of Non-Uniform Residual Stresses Using the Hole-Drilling Method. Part II—Practical Application of the Integral Method. J. Eng. Mater. Technol. 1988, 110, 344–349. [Google Scholar] [CrossRef]
- Schajer, G.S. Application of Finite Element Calculations to Residual Stress Measurements. J. Eng. Mater. Technol. 1981, 103, 157–163. [Google Scholar] [CrossRef]
- Mainjot, A.K.; Schajer, G.S.; Vanheusden, A.J.; Sadoun, M.J. Influence of Veneer Thickness on Residual Stress Profile in Veneering Ceramic: Measurement by Hole-Drilling. Dent. Mater. 2012, 28, 160–167. [Google Scholar] [CrossRef]
- Osborn, G.P.; Barr, P.J.; Petty, D.A.; Halling, M.W.; Brackus, T.R. Residual Prestress Forces and Shear Capacity of Salvaged Prestressed Concrete Bridge Girders. J. Bridge Eng. 2012, 17, 302–309. [Google Scholar] [CrossRef]




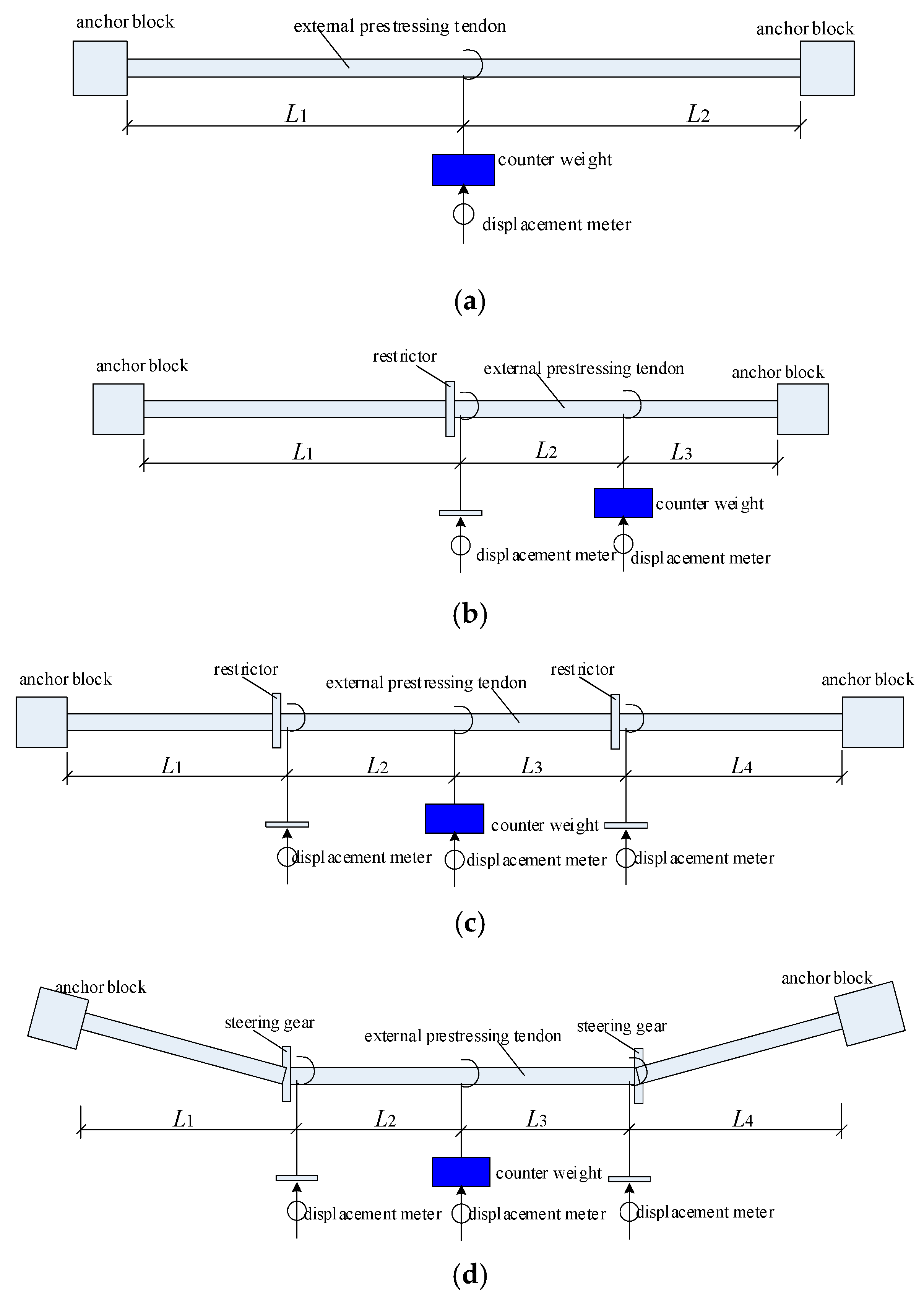

| Number of restrictors | The effective internal force calculation formula of the prestressed tendon |
| Without restrictor | |
| Single restrictor | |
| Double restrictors |
| Object | H | P | J | CV |
|---|---|---|---|---|
| 40 m straight external prestressed tendon | 0 | 0.0613 | 5.1334 | 5.6756 |
| 50 m zigzag external prestressed tendon | 0 | 0.1767 | 2.1438 | 4.7481 |
| 50 m straight external prestressed tendon | 0 | 0.0596 | 4.2316 | 4.7481 |
| Object | Average Value | Standard Deviation | Variable Coefficient |
|---|---|---|---|
| 40 m straight external prestressed tendon | 0.2461 | 0.0956 | 0.39 |
| 50 m zigzag external prestressed tendon | 0.1458 | 0.0389 | 0.27 |
| 50 m straight external prestressed tendon | 0.1818 | 0.0601 | 0.33 |
| Bridge Span | (Unreinforcement) | (Reinforcement) | Increase Rate | |||
|---|---|---|---|---|---|---|
| 20 m | −14.1 | 6.88 | −4.45 | 2.05 | 2.70 | 31.59% |
| 50 m | −9.23 | 7.22 | −5.58 | 1.28 | 2.05 | 60.50% |
| 40 m | −9.03 | 7.51 | −4.95 | 1.20 | 1.86 | 54.82% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, B.; Zhang, X.; Tang, G.; Yu, J.; Diao, X. Calculation Method and Experimental Study of Stress Loss in T-Beam External Prestressed Tendon Based on the Variation Principle. Buildings 2025, 15, 3056. https://doi.org/10.3390/buildings15173056
Tang B, Zhang X, Tang G, Yu J, Diao X. Calculation Method and Experimental Study of Stress Loss in T-Beam External Prestressed Tendon Based on the Variation Principle. Buildings. 2025; 15(17):3056. https://doi.org/10.3390/buildings15173056
Chicago/Turabian StyleTang, Binpeng, Xiedong Zhang, Guobin Tang, Jianhua Yu, and Xigang Diao. 2025. "Calculation Method and Experimental Study of Stress Loss in T-Beam External Prestressed Tendon Based on the Variation Principle" Buildings 15, no. 17: 3056. https://doi.org/10.3390/buildings15173056
APA StyleTang, B., Zhang, X., Tang, G., Yu, J., & Diao, X. (2025). Calculation Method and Experimental Study of Stress Loss in T-Beam External Prestressed Tendon Based on the Variation Principle. Buildings, 15(17), 3056. https://doi.org/10.3390/buildings15173056







