Advanced Hybrid Modeling of Cementitious Composites Using Machine Learning and Finite Element Analysis Based on the CDP Model
Abstract
1. Introduction
2. Data Description
3. Methods
3.1. Support Vector Machine
3.2. Multilayer Perceptron Neural Network
3.3. Statistical Parameters for Model Evaluation
3.4. Finite Element Model Development
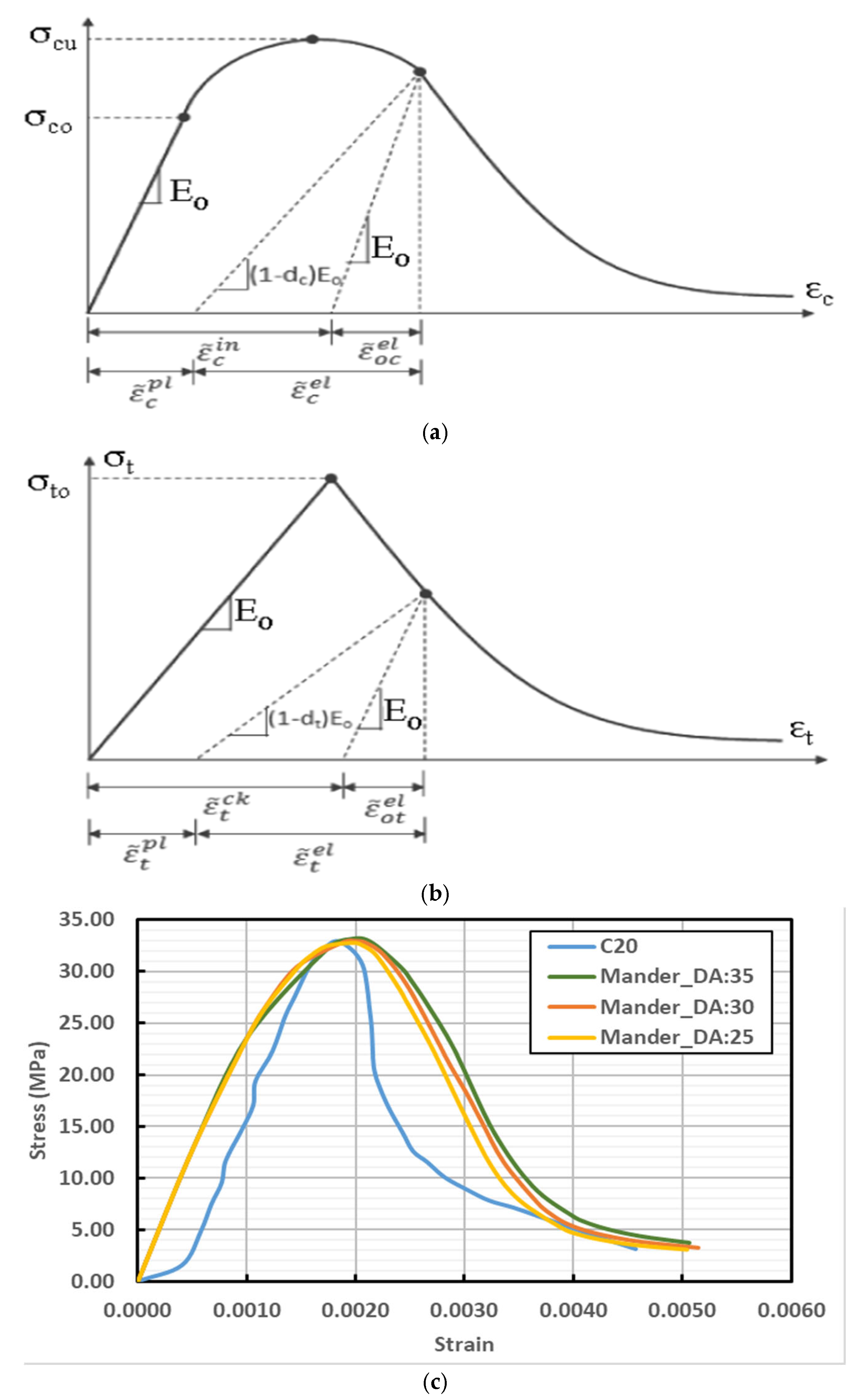
3.4.1. Implementation of the CDP Model
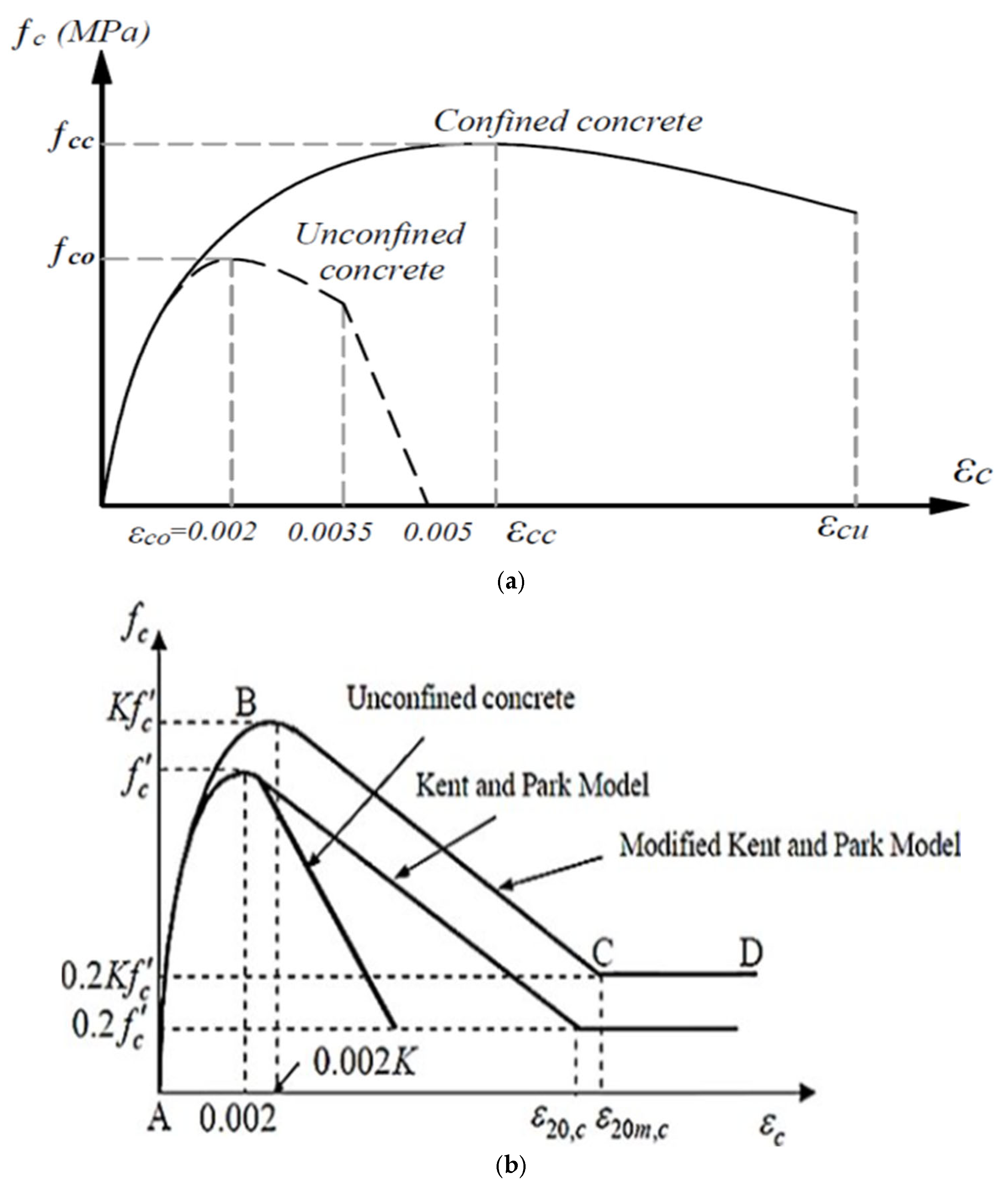
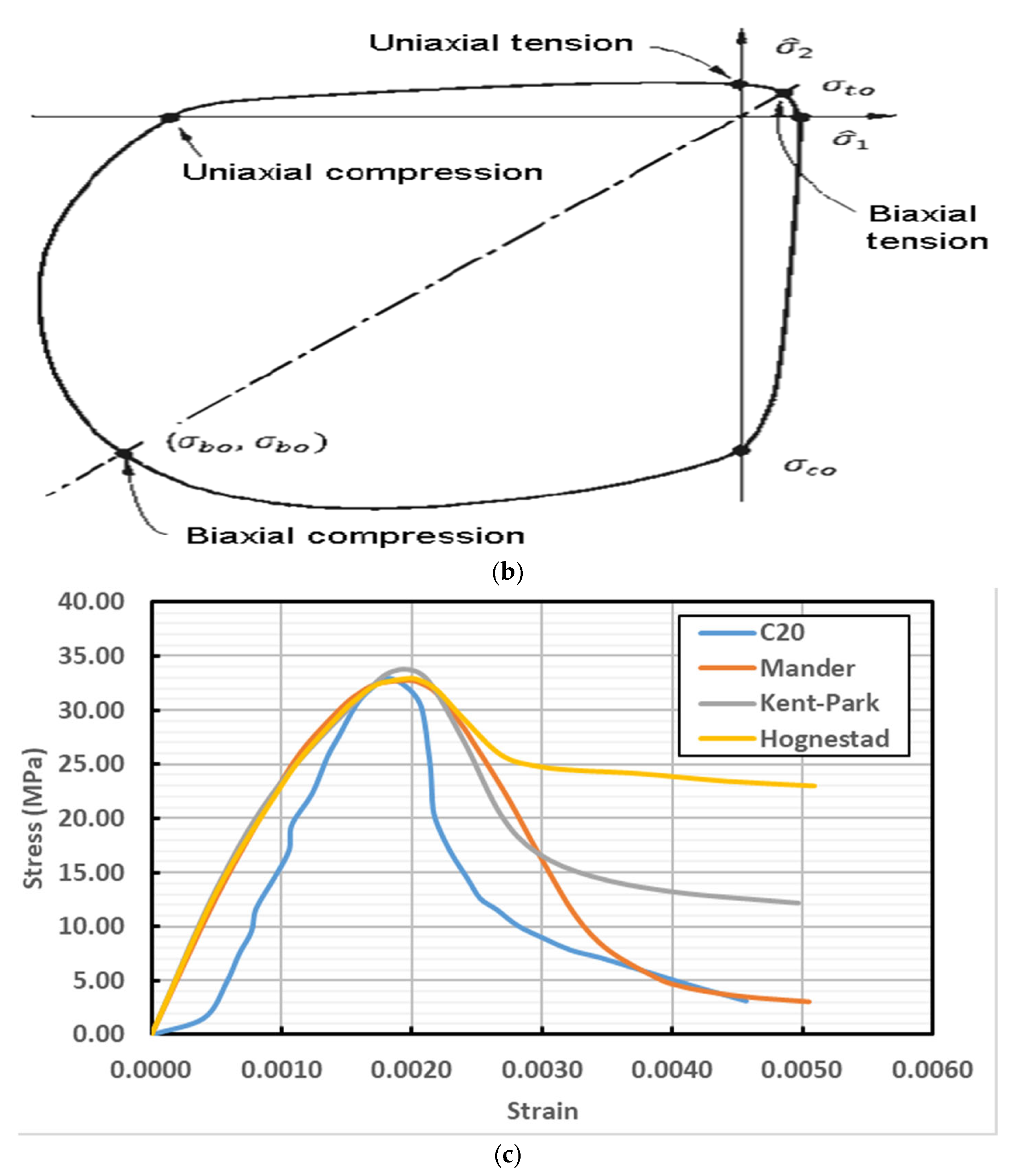
3.4.2. Key Parameters of the CDP Model
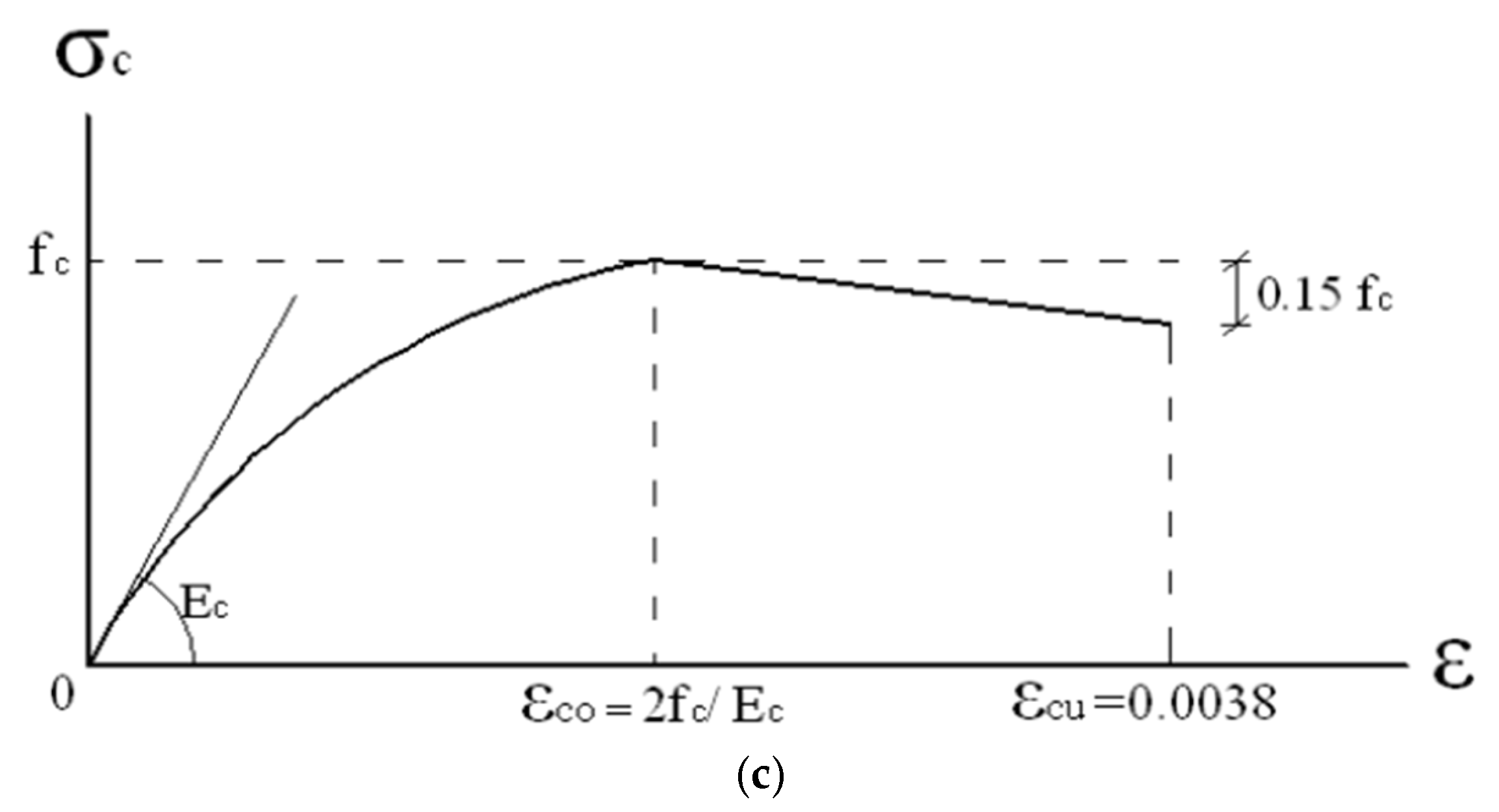
3.4.3. Uniaxial Material Characteristics of Concrete
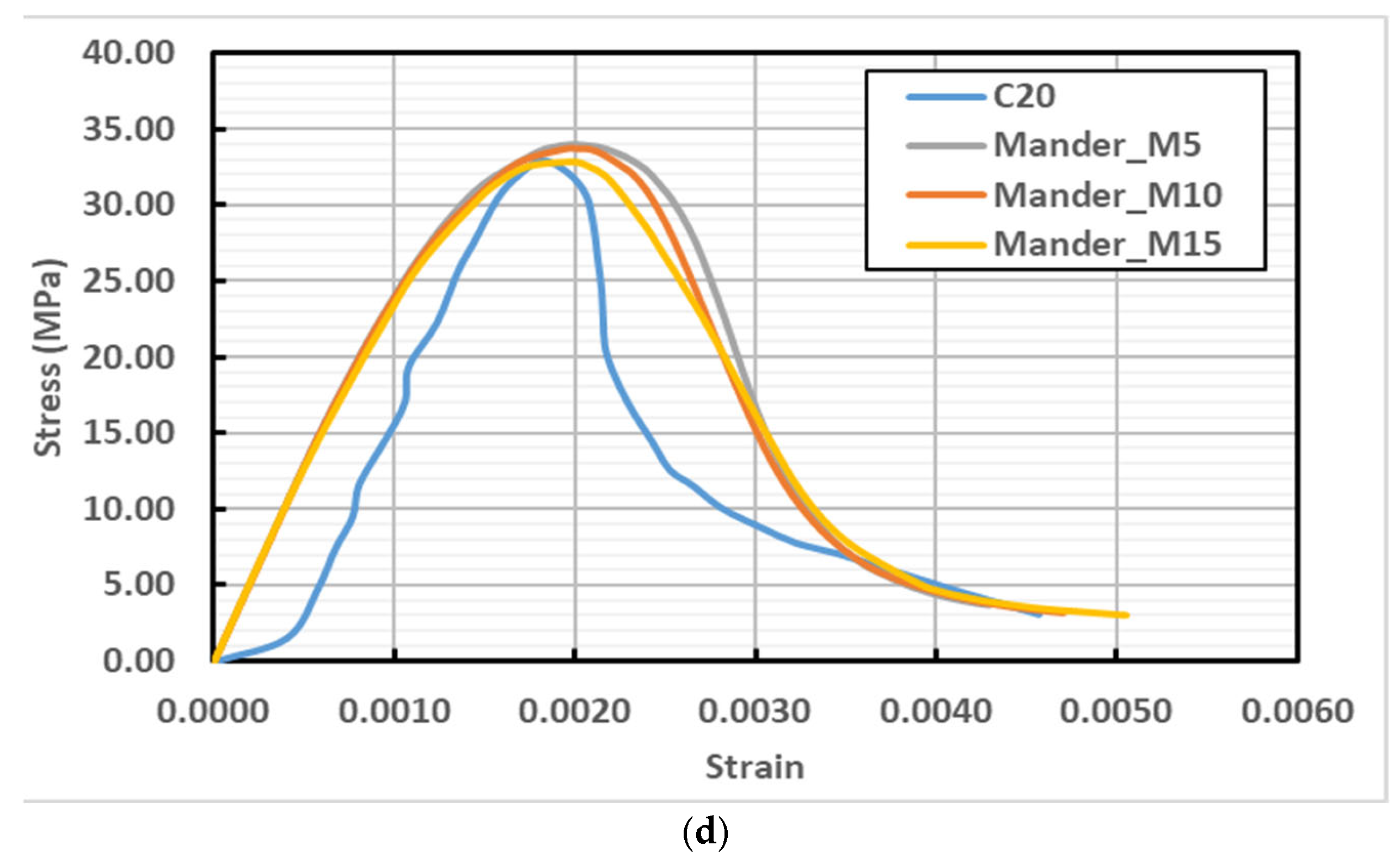
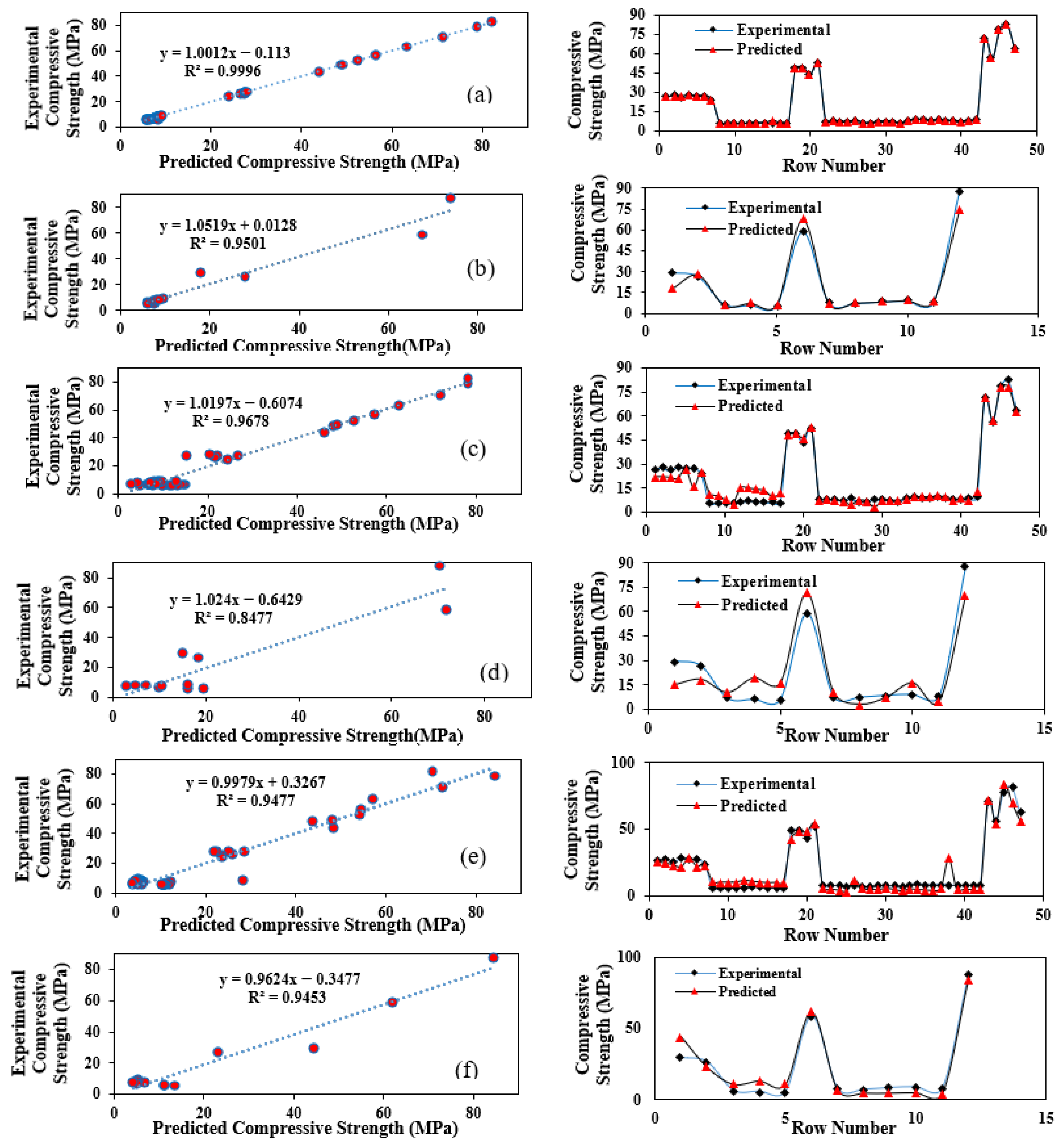
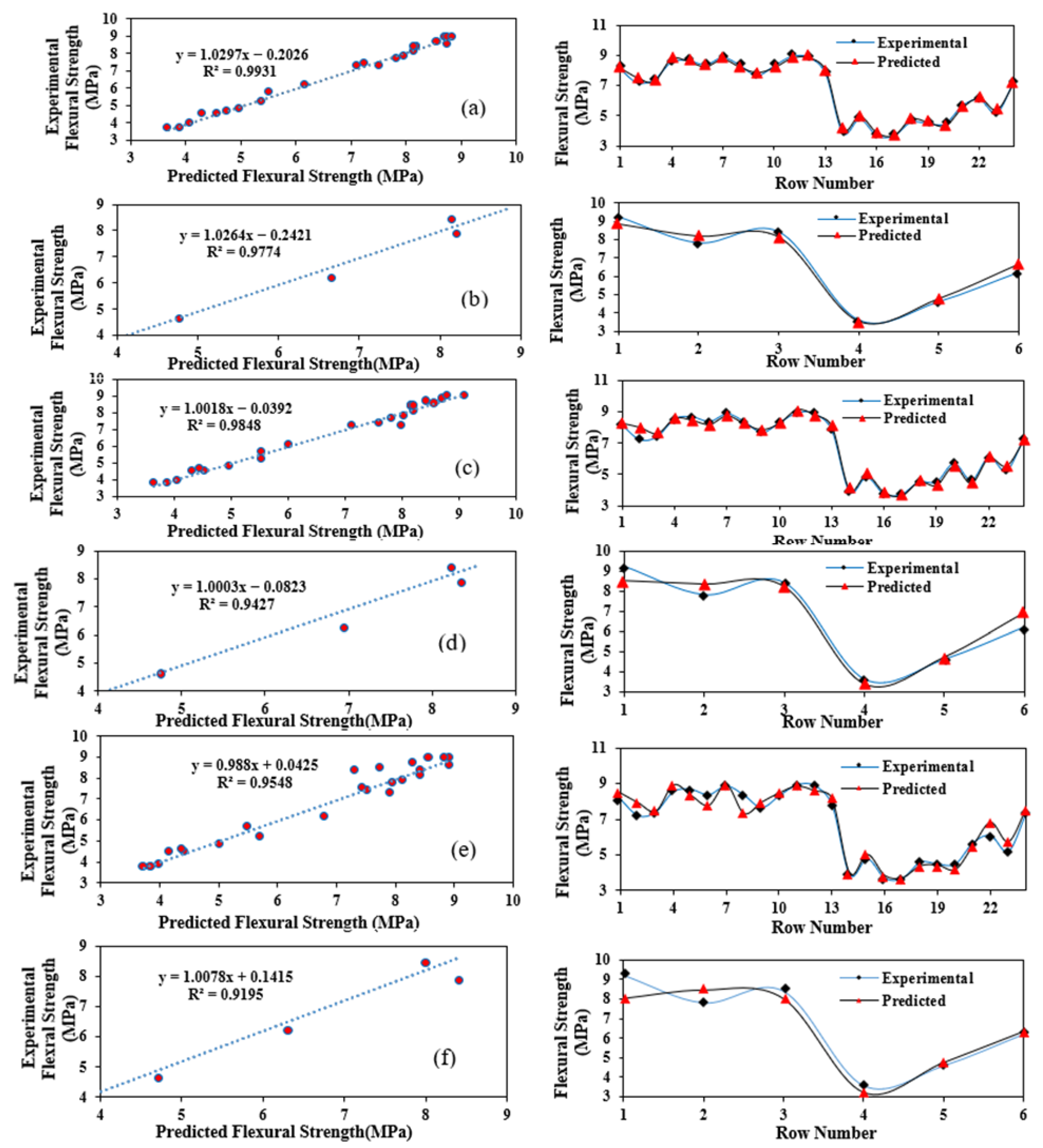
4. Results and Discussion
5. Conclusions
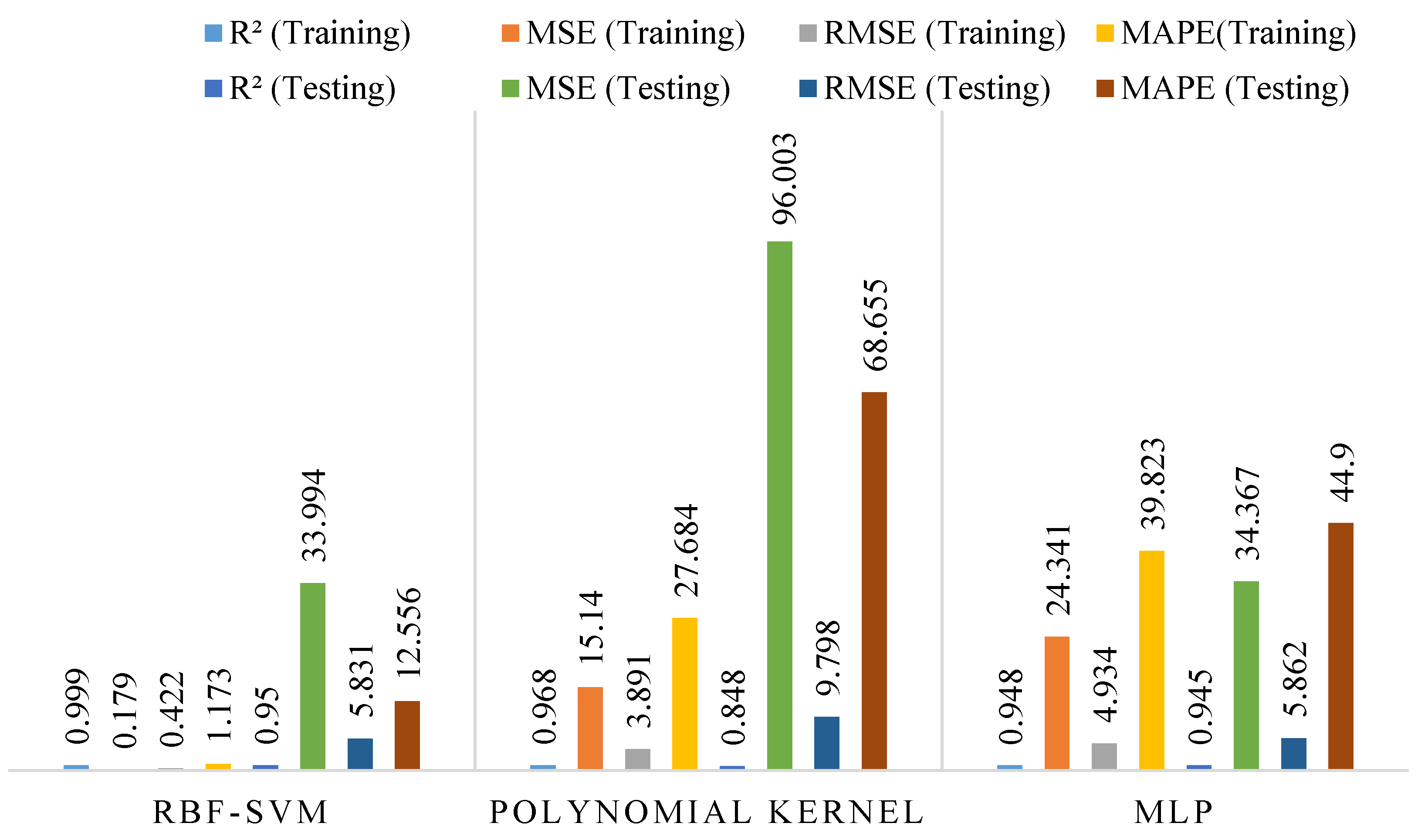
- The SVM model with the RBF kernel demonstrated superior accuracy in predicting the Fc and Fs of cement mortars containing NS and MS, outperforming both the SVM–polynomial kernel and MLP models. This highlights SVM-RBF as a robust and efficient alternative to conventional experimental testing, offering potential for cost- and time-effective material design.
- The Mander model within the CDP framework most accurately simulated the compressive behavior of concrete, effectively capturing peak strength, post-peak softening, and ductile damage distribution. In contrast, the Kent–Park and Hognestad models exhibited limitations in representing post-peak ductility and ultimate strain capacity, underscoring the importance of model selection in finite element analysis.
- Integrating AI-driven prediction with mechanics-based FEM provides complementary strengths: AI enables rapid, accurate property estimation across mixture designs, while FEM offers mechanistic insights into damage evolution and stress distribution. This hybrid approach enhances interpretability and supports multi-scale evaluation of cementitious composites.
- The proposed framework has practical applications in accelerating the development and optimization of cement mortar formulations, potentially reducing reliance on costly and labor-intensive experimental procedures.
- A notable limitation of this study is the relatively small experimental dataset, which constrains the generalizability of the predictive models. To address this, future research should focus on expanding dataset size and diversity, including external validation with independent experimental data to improve robustness.
- Further advancement could be achieved by refining FEM constitutive models and incorporating advanced AI techniques such as deep learning or transfer learning, aiming to improve predictive accuracy and broaden applicability to a wider range of cementitious materials.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Emamian, S.A.; Eskandari-Naddaf, H. Effect of porosity on predicting compressive and flexural strength of cement mortar containing micro and nano-silica by ANN and GEP. Constr. Build. Mater. 2019, 218, 8–27. [Google Scholar] [CrossRef]
- Singh, S.B.; Munjal, P.; Thammishetti, N. Role of water/cement ratio on strength development of cement mortar. J. Build. Eng. 2015, 4, 94–100. [Google Scholar] [CrossRef]
- Moses, O.; Samson, D.; Waila, O. Compressive strength characteristics of kenaf fibre reinforced cement mortar. Adv. Mater. 2015, 4, 6–10. [Google Scholar] [CrossRef]
- Mohamed, A.M. Influence of nano materials on flexural behavior and compressive strength of concrete. HBRC J. 2016, 12, 212–225. [Google Scholar] [CrossRef]
- Berra, M.; Carassiti, F.; Mangialardi, T.; Paolini, A.E.; Sebastiani, M. Effects of nanosilica addition on workability and compressive strength of Portland cement pastes. Constr. Build. Mater. 2012, 35, 666–675. [Google Scholar] [CrossRef]
- Li, L.; Zhu, J.; Huang, Z.; Kwan, A.; Li, L. Combined effects of micro-silica and nano-silica on durability of mortar. Constr. Build. Mater. 2017, 157, 337–347. [Google Scholar] [CrossRef]
- Seifan, M.; Mendoza, S.; Berenjian, A. Mechanical properties and durability performance of fly ash based mortar containing nano-and micro-silica additives. Constr. Build. Mater. 2020, 252, 119121. [Google Scholar] [CrossRef]
- Massana, J.; Reyes, E.; Bernal, J.; León, N.; Sánchez-Espinosa, E. Influence of nano-and micro-silica additions on the durability of a high-performance self-compacting concrete. Constr. Build. Mater. 2018, 165, 93–103. [Google Scholar] [CrossRef]
- Raheem, A.; Ikotun, B.; Oyebisi, S.; Ede, A. Machine learning algorithms in wood ash-cement-Nano TiO2-based mortar subjected to elevated temperatures. Results Eng. 2023, 18, 101077. [Google Scholar] [CrossRef]
- Garcia, J.; Villavicencio, G.; Altimiras, F.; Crawford, B.; Soto, R.; Minatogawa, V.; Franco, M.; Martínez-Muñoz, D.; Yepes, V. Machine learning techniques applied to construction: A hybrid bibliometric analysis of advances and future directions. Autom. Constr. 2022, 142, 104532. [Google Scholar] [CrossRef]
- Dong, C. Compressive strength prediction of high-performance concrete using MLP model. Smart Sci. 2024, 13, 137–166. [Google Scholar] [CrossRef]
- Gayathri, R.; Rani, S.U.; Čepová, L.; Rajesh, M.; Kalita, K. A comparative analysis of machine learning models in prediction of mortar compressive strength. Processes 2022, 10, 1387. [Google Scholar] [CrossRef]
- Jueyendah, S.; Lezgy-Nazargah, M.; Eskandari-Naddaf, H.; Emamian, S.A. Predicting the mechanical properties of cement mortar using the support vector machine approach. Constr. Build. Mater. 2021, 291, 123396. [Google Scholar] [CrossRef]
- Jueyendah, S.; Martins, C.H. Optimal Design of Welded Structure Using SVM. Comput. Eng. Phys. Model. 2024, 7, 84–107. [Google Scholar]
- Jueyendah, S.; Yaman, Z.; Dere, T.; Çavuş, T.F. Comparative Study of Linear and Non-Linear ML Algorithms for Cement Mortar Strength Estimation. Buildings 2025, 15, 2932. [Google Scholar] [CrossRef]
- Ombres, L.; Aiello, M.A.; Cascardi, A.; Verre, S. Modeling of steel-reinforced grout composite system-to-concrete bond capacity using artificial neural networks. J. Compos. Constr. 2024, 28, 04024034. [Google Scholar] [CrossRef]
- Bayram, S.; Ocal, M.E.; Laptali Oral, E.; Atis, C.D. Comparison of multi layer perceptron (MLP) and radial basis function (RBF) for construction cost estimation: The case of Turkey. J. Civ. Eng. Manag. 2016, 22, 480–490. [Google Scholar] [CrossRef]
- Ghazanfari, N.; Gholami, S.; Emad, A.; Shekarchi, M. Evaluation of GMDH and MLP networks for prediction of compressive strength and workability of concrete. Bull. Soc. R. Sci. Liège 2017, 86, 855–868. [Google Scholar] [CrossRef]
- Eskandari-Naddaf, H.; Kazemi, R. ANN prediction of cement mortar compressive strength, influence of cement strength class. Constr. Build. Mater. 2017, 138, 1–11. [Google Scholar] [CrossRef]
- Amin, M.N.; Alkadhim, H.A.; Ahmad, W.; Khan, K.; Alabduljabbar, H.; Mohamed, A. Experimental and machine learning approaches to investigate the effect of waste glass powder on the flexural strength of cement mortar. PLoS ONE 2023, 18, e0280761. [Google Scholar] [CrossRef]
- Sarıdemir, M. Predicting the compressive strength of mortars containing metakaolin by artificial neural networks and fuzzy logic. Adv. Eng. Softw. 2009, 40, 920–927. [Google Scholar] [CrossRef]
- Siddique, R.; Aggarwal, P.; Aggarwal, Y. Prediction of compressive strength of self-compacting concrete containing bottom ash using artificial neural networks. Adv. Eng. Softw. 2011, 42, 780–786. [Google Scholar] [CrossRef]
- Alahmari, T.S.; Ashraf, J.; Sobuz, M.H.R.; Uddin, M.A. Predicting the compressive strength of fiber-reinforced self-consolidating concrete using a hybrid machine learning approach. Innov. Infrastruct. Solut. 2024, 9, 446. [Google Scholar] [CrossRef]
- Maabreh, M.; Almasabha, G. Machine Learning Regression Algorithms for Shear Strength Prediction of SFRC-DBs: Performance Evaluation and Comparisons. Arab. J. Sci. Eng. 2024, 49, 4711–4727. [Google Scholar] [CrossRef]
- Jamal, A.S.; Ahmed, A.N. Estimating compressive strength of high-performance concrete using different machine learning approaches. Alex. Eng. J. 2025, 114, 256–265. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Ly, H.-B. Development of machine learning methods to predict the compressive strength of fiber-reinforced self-compacting concrete and sensitivity analysis. Constr. Build. Mater. 2023, 367, 130339. [Google Scholar]
- Kashem, A.; Karim, R.; Malo, S.C.; Das, P.; Datta, S.D.; Alharthai, M. Hybrid data-driven approaches to predicting the compressive strength of ultra-high-performance concrete using SHAP and PDP analyses. Case Stud. Constr. Mater. 2024, 20, e02991. [Google Scholar] [CrossRef]
- Kashem, A.; Karim, R.; Das, P.; Datta, S.D.; Alharthai, M. Compressive strength prediction of sustainable concrete incorporating rice husk ash (RHA) using hybrid machine learning algorithms and parametric analyses. Case Stud. Constr. Mater. 2024, 20, e03030. [Google Scholar] [CrossRef]
- Shafighfard, T.; Kazemi, F.; Bagherzadeh, F.; Mieloszyk, M.; Yoo, D.Y. Chained machine learning model for predicting load capacity and ductility of steel fiber–reinforced concrete beams. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 3573–3594. [Google Scholar] [CrossRef]
- Isleem, H.F.; Qiong, T.; Chukka, N.D.K.R.; Kumar, R.; Nagaraju, T.V.; Hamed, A.Y. Machine learning and nonlinear finite element analysis of fiber-reinforced polymer-confined concrete-steel double-skin tubular columns under axial compression. Struct. Concr. 2025, 26, 248–292. [Google Scholar] [CrossRef]
- Raju, M.R.; Rahman, M.; Islam, M.M.; Hasan, N.M.S.; Hasan, M.M.; Sharmily, T.; Hosen, M.S. A Comparative Analysis of Machine Learning Approaches for Evaluating the Compressive Strength of Pozzolanic Concrete. IUBAT Rev. 2024, 7, 90–122. [Google Scholar] [CrossRef]
- Altuncı, Y.T. A Comprehensive Study on the Estimation of Concrete Compressive Strength Using Machine Learning Models. Buildings 2024, 14, 3851. [Google Scholar] [CrossRef]
- Ali, I.; Suthar, M. Comparison between Random forest and M5P to predict the compressive strength of concrete modified with solid wastes. IOP Conf. Ser. Earth Environ. Sci. 2023, 1110, 012085. [Google Scholar] [CrossRef]
- Jain, D.; Bhadauria, S.S.; Kushwah, S.S. Analysis and prediction of plastic waste composite construction material properties using machine learning techniques. Environ. Prog. Sustain. Energy 2023, 42, e14094. [Google Scholar] [CrossRef]
- Guan, Q.T.; Tong, Z.L.; Amin, M.N.; Iftikhar, B.; Qadir, M.T.; Khan, K. Analyzing the efficacy of waste marble and glass powder for the compressive strength of self-compacting concrete using machine learning strategies. Rev. Adv. Mater. Sci. 2024, 63, 20240043. [Google Scholar] [CrossRef]
- Iannuzzo, A.; Musone, V.; Ruocco, E. A neural network-based automated methodology to identify the crack causes in masonry structures. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 3769–3785. [Google Scholar] [CrossRef]
- Megahed, K.; Mahmoud, N.S.; Abd-Rabou, S.E.M. Application of machine learning models in the capacity prediction of RCFST columns. Sci. Rep. 2023, 13, 20878. [Google Scholar] [CrossRef]
- Biswas, R.; Kumar, M.; Kumar, D.R.; Samui, P.; Rajak, M.K.; Armaghani, D.J.; Singh, S. Application of novel deep neural network on prediction of compressive strength of fly ash based concrete. Nondestruct. Test. Eval. 2024, 1, 1–31. [Google Scholar] [CrossRef]
- Alghrairi, N.S.; Aziz, F.N.; Rashid, S.A.; Mohamed, M.Z.; Ibrahim, A.M. Machine learning-based compressive strength estimation in nanomaterial-modified lightweight concrete. Open Eng. 2024, 14, 20220604. [Google Scholar] [CrossRef]
- Bahaa, T. Effect of utilizing nano and micro silica on early properties of cement mortar. World Appl. Sci. J. 2014, 29, 370–382. [Google Scholar]
- Sherrod, P. DTREG Predictive Modeling Software. Manual for Software. 2008. Available online: www.dtreg.com (accessed on 21 August 2025).
- Moguerza, J.M.; Muñoz, A. Support vector machines with applications. Stat. Sci. 2006, 21, 322–336. [Google Scholar] [CrossRef]
- Joachims, T. Text categorization with support vector machines: Learning with many relevant features. In Proceedings of the European Conference on Machine Learning, Chemnitz, Germany, 21–23 April 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 137–142. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; ACM: New York, NY, USA, 1992; pp. 144–152. [Google Scholar]
- Sonebi, M.; Cevik, A.; Grünewald, S.; Walraven, J. Modelling the fresh properties of self-compacting concrete using support vector machine approach. Constr. Build. Mater. 2016, 106, 55–64. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Salcedo-Sanz, S.; Rojo-Álvarez, J.L.; Martínez-Ramón, M.; Camps-Valls, G. Support vector machines in engineering: An overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 234–267. [Google Scholar] [CrossRef]
- Sopelsa Neto, N.F.; Stefenon, S.F.; Meyer, L.H.; Bruns, R.; Nied, A.; Seman, L.O.; Gonzalez, G.V.; Leithardt, V.R.Q.; Yow, K.-C. A study of multilayer perceptron networks applied to classification of ceramic insulators using ultrasound. Appl. Sci. 2021, 11, 1592. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Kent, D.C.; Park, R. Flexural members with confined concrete. J. Struct. Div. 1971, 97, 1969–1990. [Google Scholar] [CrossRef]
- Yang, L.; Gao, Y.; Chen, H.; Jiao, H.; Dong, M.; Bier, T.A.; Kim, M. Three-dimensional concrete printing technology from a rheology perspective: A review. Adv. Cem. Res. 2024, 36, 567–586. [Google Scholar] [CrossRef]
- Wang, K.; Cao, J.; Ye, J.; Qiu, Z.; Wang, X. Discrete element analysis of geosynthetic-reinforced pile-supported embankments. Constr. Build. Mater. 2024, 449, 138448. [Google Scholar] [CrossRef]
- Wei, M.; Chen, L.; Lei, N.; Li, H.; Huang, L. Mechanical properties and microstructures of thermally activated ultrafine recycled fine powder cementitious materials. Constr. Build. Mater. 2025, 475, 141195. [Google Scholar] [CrossRef]
- Liu, F.; Tang, R.; Li, Q.; Wang, H.; Zou, Y.; Yuan, X. Improved thermal performance, frost resistance, and pore structure of cement–based composites by binary modification with mPCMs/nano–SiO2. Energy 2025, 332, 137166. [Google Scholar] [CrossRef]
- Zheng, M.; Zhang, Y.; Yan, S.; Wu, Z.; Li, X.; Wu, D.; Xiong, L. Effect of carrier-encapsulated microbial calcium carbonate on the performance of cement mortar. Constr. Build. Mater. 2025, 483, 141579. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, W.; Su, Y.; Jia, F.; Long, X. Plastic damage prediction of concrete under compression based on deep learning. Acta Mech. 2024, 235, 255–266. [Google Scholar] [CrossRef]
- Huang, Z.; Luo, Y.; Zhang, W.; Ye, Z.; Li, Z.; Liang, Y. Thermal insulation and high-temperature resistant cement-based materials with different pore structure characteristics: Performance and high-temperature testing. J. Build. Eng. 2025, 101, 111839. [Google Scholar] [CrossRef]
- Sun, L.; Wang, X.; Zhang, C. Three-dimensional high fidelity mesoscale rapid modelling algorithm for concrete. Structures 2024, 70, 107561. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, J.; Huang, Y.; Lin, B.; Liu, X. State of the art regarding interface bond behavior between FRP and concrete based on cohesive zone model. Structures 2025, 74, 108528. [Google Scholar] [CrossRef]
- Huang, H.; Guo, M.; Zhang, W.; Huang, M. Seismic behavior of strengthened RC columns under combined loadings. J. Bridge Eng. 2022, 27, 05022005. [Google Scholar] [CrossRef]
- Huang, H.; Li, M.; Yuan, Y.; Bai, H. Theoretical analysis on the lateral drift of precast concrete frame with replaceable artificial controllable plastic hinges. J. Build. Eng. 2022, 62, 105386. [Google Scholar] [CrossRef]
- Yaman, Z.; Sümer, Y.; Ağcakoca, E.; Maali, M.; Aydın, A.C. Behavioral analysis of steel I-beams under repeated dynamic loads: Impact of various impactor head types. Dev. Built Environ. 2025, 21, 100620. [Google Scholar] [CrossRef]
- Dikmen Coşkun, K.; Yaman, Z.; Maali, M.; Ağcakoca, E.; Sadid, M.S. The effects of corrosion damage on the square hollow steel section (SHSS) profiles: An experimental and numerical investigation. Arab. J. Sci. Eng. 2024, 49, 6125–6144. [Google Scholar] [CrossRef]
- Nasery, M.M.; Ağcakoca, E.; Yaman, Z. Experimental and numerical analysis of impactor geometric shape effects on steel beams under impact loading. Structures 2020, 27, 1118–1138. [Google Scholar] [CrossRef]
- Maali, M.; Ağcakoca, E.; Nasery, M.M.; Macit, F.; Aydin, A.C. Post fire performance of galvanized cylindrical shells for buckling failure. Arch. Civ. Mech. Eng. 2024, 24, 125. [Google Scholar] [CrossRef]
- Aydin, A.C.; Yaman, Z.; Ağcakoca, E.; Kiliç, M.; Maali, M.; Aghazadeh Dizaji, A. CFRP effect on the buckling behavior of dented cylindrical shells. Int. J. Steel Struct. 2020, 20, 425–435. [Google Scholar] [CrossRef]


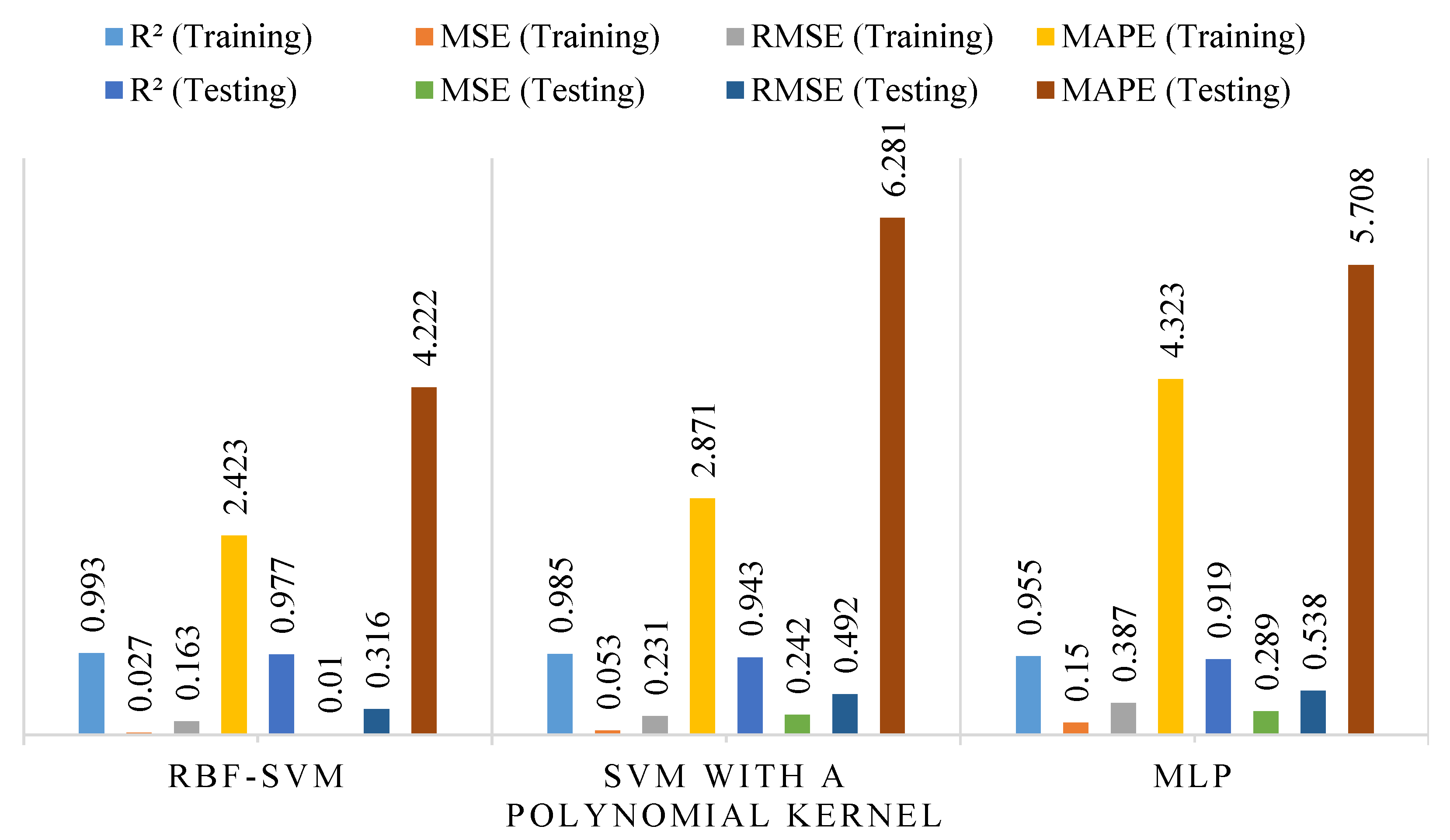

| Variable | Compressive Data | Flexural Data | ||||||
|---|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Mean | Std. Dev. | Minimum | Maximum | Mean | Std. Dev. | |
| W/C | 0.396 | 0.632 | 0.532 | 0.053 | 0.380 | 0.632 | 0.487 | 0.082 |
| S/C | 2.220 | 4.492 | 3.291 | 0.485 | 2.222 | 4.650 | 3.496 | 0.534 |
| NS/C (%) | 0 | 0.110 | 0.042 | 0.028 | 0 | 0.111 | 0.033 | 0.032 |
| MS/C (%) | 0 | 0.388 | 0.075 | 0.097 | 0 | 0.388 | 0.058 | 0.102 |
| Age (day) | 3 | 28 | 14.695 | 9.800 | ||||
| Fc28 (MPa) | 5.650 | 87.900 | 20.684 | 22.307 | ||||
| Fs28 (MPa) | 3.600 | 9.210 | 6.705 | 1.894 | ||||
| Methods | RBF Kernel | Polynomial Kernel | MLP | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model parameters | C | γ | ε | C | γ | d | Layer | Neurons | Activation |
| Fc | 7230.42 | 0.83 | 0.001 | 487.09 | 0.224 | 3 | input | 5 | Passthru |
| hidden | 4 | Logistic | |||||||
| output | 1 | Logistic | |||||||
| Fs | 49.94 | 1.06 | 0.001 | 6.47 | 0.224 | 3 | input | 4 | Passthru |
| hidden | 3 | Logistic | |||||||
| output | 1 | Logistic | |||||||
| Methods | Training Results | Testing Results | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | MSE | RMSE | MAPE (%) | R2 | MSE | RMSE | MAPE (%) | ||
| SVM | RBF | 0.999 | 0.179 | 0.422 | 1.173 | 0.950 | 33.994 | 5.831 | 12.556 |
| Polynomial | 0.968 | 15.140 | 3.891 | 27.684 | 0.848 | 96.003 | 9.798 | 68.655 | |
| MLP | 0.948 | 24.341 | 4.934 | 39.823 | 0.945 | 34.367 | 5.862 | 44.900 | |
| Methods | Training Results | Testing Results | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | MSE | RMSE | MAPE (%) | R2 | MSE | RMSE | MAPE (%) | ||
| SVM | RBF | 0.993 | 0.027 | 0.163 | 2.423 | 0.977 | 0.010 | 0.316 | 4.222 |
| Polynomial | 0.985 | 0.053 | 0.231 | 2.871 | 0.943 | 0.242 | 0.492 | 6.281 | |
| MLP | 0.955 | 0.150 | 0.387 | 4.323 | 0.919 | 0.289 | 0.538 | 5.708 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ağcakoca, E.; Jueyendah, S.; Yaman, Z.; Sümer, Y.; Maali, M. Advanced Hybrid Modeling of Cementitious Composites Using Machine Learning and Finite Element Analysis Based on the CDP Model. Buildings 2025, 15, 3026. https://doi.org/10.3390/buildings15173026
Ağcakoca E, Jueyendah S, Yaman Z, Sümer Y, Maali M. Advanced Hybrid Modeling of Cementitious Composites Using Machine Learning and Finite Element Analysis Based on the CDP Model. Buildings. 2025; 15(17):3026. https://doi.org/10.3390/buildings15173026
Chicago/Turabian StyleAğcakoca, Elif, Sebghatullah Jueyendah, Zeynep Yaman, Yusuf Sümer, and Mahyar Maali. 2025. "Advanced Hybrid Modeling of Cementitious Composites Using Machine Learning and Finite Element Analysis Based on the CDP Model" Buildings 15, no. 17: 3026. https://doi.org/10.3390/buildings15173026
APA StyleAğcakoca, E., Jueyendah, S., Yaman, Z., Sümer, Y., & Maali, M. (2025). Advanced Hybrid Modeling of Cementitious Composites Using Machine Learning and Finite Element Analysis Based on the CDP Model. Buildings, 15(17), 3026. https://doi.org/10.3390/buildings15173026







