Constitutive Modeling of Coal Gangue Concrete with Integrated Global–Local Explainable AI and Finite Element Validation

Abstract

Coal gangue concrete (CGC), a recycled cementitious material derived from industrial solid waste, presents both opportunities and challenges for structural applications due to its heterogeneous composition and variable mechanical behavior. This study develops an ensemble learning framework—incorporating XGBoost, LightGBM, and CatBoost—to predict four key constitutive parameters based on experimental data. The predicted parameters are subsequently incorporated into an ABAQUS finite element model to simulate the compressive–bending response of CGC columns, with simulation results aligning well with experimental observations in terms of failure mode, load development, and deformation characteristics. To enhance model interpretability, a hybrid approach is adopted, combining permutation-based global feature importance analysis with SHAP (SHapley Additive exPlanations)-derived local explanations. This joint framework captures both the overall influence of each feature and its context-dependent effects, revealing a three-stage stiffness evolution pattern—brittle, quasi-ductile, and re-brittle—governed by gangue replacement levels and consistent with micromechanical mechanisms and numerical responses. Coupled feature interactions, such as between gangue content and crush index, are shown to exacerbate stiffness loss through interfacial weakening and pore development. This integrated approach delivers both predictive accuracy and mechanistic transparency, providing a reference for developing physically interpretable, data-driven constitutive models and offering guidance for tailoring CGC toward ductile, energy-absorbing structural materials in seismic and sustainability-focused engineering.

1. Introduction

Coal remains a principal energy source worldwide, with a particularly strong reliance observed across the Asia-Pacific region, where its share has consistently remained elevated. Among the primary by-products of coal mining, coal gangue (CG) represents roughly 10% to 25% of annual coal production, resulting in accumulated stockpiles surpassing 4.5 billion tons—constituting over 40% of China’s total industrial solid waste [1]. At present, open-air dumping remains the predominant disposal method, causing extensive land occupation and triggering secondary geological hazards, such as landslides and debris flows. Moreover, prolonged exposure leads to the leaching of heavy metals (e.g., Pb²⁺, Zn²⁺, and Cu²⁺) into the surrounding ecosystems, contaminating soil and water bodies. The spontaneous combustion of residual coal and pyrite further aggravates environmental risks by releasing harmful gases (SO₂, NOₓ, CO), intensifying regional air quality concerns [2].

Existing research on CGC has coalesced into three principal strands. First, controlled experiments establish a pronounced non-monotonic dependence of mechanical performance on the gangue-aggregate replacement ratio: moderate substitution (30% coarse aggregate) tends to maximize strength, whereas excessive incorporation induces marked reductions in both elastic modulus and compressive strength [3]. Second, mixture-design optimization—via proportioning strategies and targeted material modifications, such as partial substitution of quartz powder with activated gangue or the inclusion of discrete fibers—has yielded improvements in strength, durability, and fatigue resistance [4,5]. Third, thermal mechanical activation protocols demonstrate that calcination at approximately 800 °C followed by fine grinding produces pozzolanic gangue powders that promote secondary hydration, densify the cementitious matrix, and refine pore structure, thereby enhancing strength development in alkali-activated binders. Collectively, this literature delineates the coupled influences of replacement level, mix design, and activation treatment, while elucidating the microstructural mechanisms governing performance enhancement in CGC [6].

The lack of robust mechanical modeling remains a central impediment to the widespread structural application of CGC. Although numerous constitutive formulations have been advanced across disparate experimental regimes, including uniaxial compression, varying replacement ratios, and freeze–thaw cycles [5,7], persistent deficiencies in generalizability, adaptability, and physical transparency are evident. A critical appraisal isolates three limitations: (1) minimal adoption of machine learning, only a small subset applies ML to CGC [8], with a prevailing reliance on linear regression to calibrate isolated parameters [6,9], a paradigm unable to capture the nonlinear, hierarchical interactions of heterogeneous cementitious systems; (2) reliance on restrictive statistical premises, normality, homoscedasticity, and feature independence—misaligned with CGC’s variability and skewed distributions, degrading robustness across loading and curing regimes [9,10]; and (3) weak interpretability, models rarely identify dominant predictors or coupled mechanisms, limiting engineering deployment and mechanistic insight into CGC’s behavior [10,11].

In contrast, recent advances in machine learning, particularly in geotechnics, fracture mechanics, and structural health monitoring, have addressed the limitations of conventional constitutive models [12,13,14,15]. Building on this, we develop a Gradient Boosted Tree (GBT) framework for predicting CGC constitutive parameters. By iteratively fitting the residuals, the model captures nonlinear interactions without prespecified functional forms and operates effectively in high-dimensional, heterogeneous feature spaces. To reconcile accuracy with physical interpretability, we couple permutation-based global importance with SHAP to quantify both aggregate influence and context-dependent effects. The framework yields three advances: (1) a unified, scalable pipeline linking feature attribution, multi-parameter prediction, stress–strain reconstruction, and finite element validation; (2) a data-driven yet interpretable alternative to regression formulations that identifies critical mix and curing variables—gangue replacement ratio, water–binder ratio, and age governing peak stress and fracture toughness; and (3) identification of a three-stage stiffness evolution—brittle, quasi-ductile, re-brittle—modulated by gangue content and consistent with micromechanical observations and numerical simulations. Collectively, these results establish a robust basis for embedding explainable AI into constitutive modeling and the engineering application of sustainable concrete.

2. Explainable Modeling of CGC Constitutive Parameters

2.1. Constitutive Foundations and Explainable-AI Problem Framing

Rigorous characterization of the compressive stress–strain response is fundamental to evaluating the CGC strength and deformability [16,17]. Convergent evidence shows that increasing gangue-aggregate replacement precipitates substantial capacity attenuation— peak stress reductions of 12.1 to 49.2%—while the macroscopic stress–strain morphology remains broadly consonant with conventional concrete [18,19]. However, CGC exhibits heightened parametric susceptibility of constitutive descriptors to gangue content, as corroborated by normative modeling [20]. Accordingly, we adopt the uniaxial compressive damage model codified in the Code for Design of Concrete Structures (GB50010-2010) as the baseline constitutive schema [21].

This stress–strain curve (Figure 1) is controlled by four key parameters: the elastic modulus $E_{\mathfrak{c}}$ dictates the initial stiffness; the uniaxial compressive strength $f_{\mathrm{c},\mathrm{r}}$ and peak strain ${\epsilon }_{\mathrm{c},\mathrm{r}}$ define the location of the curve’s apex; and the post-peak parameter ${\alpha }_{\mathrm{c}}$ characterizes the steepness of the descending branch. These parameters collectively influence the damage evolution function $d_{\mathfrak{c}}$, which in turn governs the slope transitions and geometric shape of the stress–strain trajectory. Accordingly, this study constructs a predictive modeling framework based on three machine learning algorithms, with these four constitutive parameters as the target variables. By learning the complex mapping between input features (material composition and curing conditions) and the key model parameters, this approach aims to provide a robust quantitative basis for developing accurate constitutive models of CGC.

Within this modeling context, XAI has materially advanced the transparency of civil engineering by integrating local, global, and deep learning interpretability. Locally, SHAP and LIME delineate salient predictors and material idiosyncrasies in structural retrofitting [22] and subgrade-strength prediction [23]; system-level frameworks fuse FEM-generated datasets with SHAP and a coherence model to robustly infer failure mechanisms and critical accelerations of flexible retaining walls under seismic loading [24]; globally, permutation importance and partial-dependence (PDP) analyses coupled with Auto ML prognosticate the capacity of ultra-high-performance concrete members [25]; for strengthening, experimental bond tests, literature synthesis, and ANN modeling yield a physically grounded analytical formula for SRG–concrete bond capacity, bridging data-driven inference with mechanics [26]; in deep learning, LIME and Grad-CAM render CNN decision pathways legible for ground-penetrating-radar inversion, exposing hierarchical subsurface features [27]. Collectively, these exemplars consolidate XAI’s remit as an interpretable, domain-consonant paradigm across civil engineering applications.

Figure 1. Schematic representation of the uniaxial stress–strain curve in concrete. Adapted from the Chinese Code for Design of Concrete Structures (GB50010-2015) [28].

Figure 1. Schematic representation of the uniaxial stress–strain curve in concrete. Adapted from the Chinese Code for Design of Concrete Structures (GB50010-2015) [28].

2.2. Dataset Assembly and Feature Characterization

2.2.1. Experimental Data Integration and Predictor Selection

This study leverages a curated corpus of 262 representative CGC samples synthesized from diverse experimental programs spanning gangue typologies, replacement ratios, and curing regimens (Figure 2) [7,9,21,29,30,31,32,33,34]. The dataset comprises ten predictors and four response variables indexing salient mechanical properties. To foreground feature effects on model outputs, the six most prognostic variables were selected for statistical visualization in Figure 2.

To comprehensively delineate the structural characteristics of the dataset, descriptive statistics, including the minimum, maximum, mean, standard deviation, and number of unique values, were computed for each variable. The mean and interquartile range (Qi) capture the central tendency of the data distribution, whereas the standard deviation and extrema reflect the degree of variability and potential outliers. The summary statistics are listed in

Table 1. Descriptive statistics of key features and target parameters in the CGC dataset.

Parameter	Mean	Std	Min	Q1	Q2	Q3	Max
content (%)	66.3	35.11	0	40.0	70.0	100.0	100
age(day)	27.87	8.5	7	28.0	28.0	28.0	60
Bulk density (kg/m3)	1205.78	124.29	1044	1100.0	1160.0	1350.0	1590
Cement kg×m−3	395.19	104.19	210.0	325.0	361.0	457.0	640.0
crush index%	17.12	4.73	9.8	12.6	18.6	21.0	24.38
ratio	0.46	0.13	0.25	0.35	0.45	0.55	0.75
water kg×m−3	173.36	23.32	136.5	160.0	160.0	195.0	268.0
water absorption	4.81	1.78	0.7	4.4	5.1	5.7	8.4
water reducer kg×m−3	2.52	1.56	0.0	1.46	2.37	3.41	8.64
$E_{\mathfrak{c}}$	17,562.57	9881.03	1730	10,520.0	13,566.5	26,650.0	40,630
${\epsilon }_{\mathrm{c},\mathrm{r}}$	2992.76	830.22	1564.67	2439.5	2808.85	3361.75	5153.32
$f_{\mathrm{c},\mathrm{r}}$	29.14	8.86	10.97	22.58	29.04	34.98	56.2
${\alpha }_{\mathrm{c}}$	1.29	1.42	0.67	0.35	0.99	1.69	7.01

. Notably, variables such as elastic modulus and bulk density exhibit broad value ranges and high standard deviations, indicating pronounced variability in material composition and mechanical performance under diverse experimental conditions.

The final dataset was constructed through a rigorous selection and normalization process, consolidating approximately 500 raw data entries extracted from 16 core publications. Given the inconsistencies in testing standards, variable nomenclature, and measurement units across sources, all samples were manually reviewed, cleaned, and harmonized to ensure coherence. After careful screening, 262 high-quality entries were retained, most of which originated from the same laboratory and followed a consistent testing protocol. This standardized dataset effectively captures the representative parameter space of CGC and provides a robust foundation for subsequent machine learning modeling, particularly in validating model stability and generalizability across varied input domains.

2.2.2. Stratified Augmentation for Replacement-Level Balancing

To mitigate distributional sparsity while ensuring physical plausibility, we employed a physics-guided covariance-aware data augmentation strategy [35,36] applied exclusively to the training set. For each stratification tier of coal gangue replacement (0–40%, 50–80%, and 100%), synthetic samples were generated by drawing multivariate Gaussian perturbations as follows:

$$\Delta \mathrm{x}\sim \mathcal{N}(0,{\eta }^2\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(\sigma \left)R\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\right(\sigma \left)\right)$$

(1)

where $R$ is the empirical correlation matrix of the training features and $\sigma$ is the vector of their standard deviations (heteroscedastic scaling), perturbed samples were projected back into feasible domains by clipping each feature to its 1st–99th percentile range, enforcing the mix-design constraint ratio, and bounding gangue replacement between 0% and 100%. This procedure preserves observed inter-feature dependencies and mix-design constraints while increasing the effective sample density in each tier without contaminating the validation or test sets.

2.3. Predictive Performance Evaluation and Model Optimization

2.3.1. Metrics for Regression Accuracy and Robustness

To ensure a rigorous, generalizable evaluation across all constitutive targets, we conjointly employed five canonical regression metrics—R², MAE, MSE, RMSE, and MAPE (Equations (2)–(7)), per established practice [37,38]. This battery spans complementary error modalities, including absolute deviation, dispersion, relative bias, and explanatory power. Given scale and variance heterogeneity across outputs (elastic modulus and post-peak parameter α), single-metric appraisal is intrinsically susceptible to bias. Accordingly, we define a Composite Performance Index (CPI) that min–max normalizes and aggregates the five indicators, rendering them commensurate and enabling equitable comparison across multiscale responses. A lower CPI denotes a uniformly strong accuracy, whereas higher values indicate metric-specific weaknesses or imbalances, permitting a direct, objective ranking of predictive efficacy across heterogeneous constitutive parameters.

$$R^2=1-{\displaystyle \frac{{\displaystyle {\sum }_{i=1}^m} {\left({\widehat{y}}_i-y_i\right)}^2}{{\displaystyle {\sum }_{i=1}^m} {\left(\overline{y}-y_i\right)}^2}}$$

(2)

$$MAPE={\displaystyle \frac{100\mathrm{\%}}{m}}{\displaystyle {\sum }_{i=1}^m} {\displaystyle \frac{\left|\right(y_i-{\widehat{y}}_i\left)\right|}{y_i}}$$

(3)

$$MAE={\displaystyle \frac{1}{m}}{\displaystyle {\sum }_{i=1}^m} \left|\right(y_i-{\widehat{y}}_i\left)\right|$$

(4)

$$MSE={\displaystyle \frac{1}{m}}{\displaystyle {\sum }_{i=1}^m} {\left(y_i-{\widehat{y}}_i\right)}^2$$

(5)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{m}}{\displaystyle {\sum }_{i=1}^m} {\left(y_i-{\widehat{y}}_i\right)}^2}$$

(6)

$$\mathrm{C}\mathrm{P}\mathrm{I}={\displaystyle \frac{1}{\mathrm{N}}}{\displaystyle {\sum }_{\mathrm{j}=1}^{\mathrm{N}}} {\displaystyle \frac{{\mathrm{P}}_{\mathrm{j}}-{\mathrm{P}}_{\mathrm{j},\mathrm{m}\mathrm{i}\mathrm{n}}}{{\mathrm{P}}_{\mathrm{j},\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{P}}_{\mathrm{j},\mathrm{m}\mathrm{i}\mathrm{n}}}}$$

(7)

Let $y_i$, ${\widehat{y}}_i$ and $\overline{y}$ represent the observed value, predicted value, and mean of the observed values, respectively, across a dataset comprising m samples. In Equation (7), $P_j$ denotes the j-th evaluation indicator used to quantify model performance, with $P_{j,\mathrm{m}\mathrm{i}\mathrm{n}}$ and $P_{j,\mathrm{m}\mathrm{a}\mathrm{x}}$ corresponding to its lower and upper bounds. The total number of metrics employed, denoted as N, is predefined as 5 in this study.

2.3.2. Cross-Model Comparison Under Unified Conditions

To ensure the rigor and comparability of algorithmic performance evaluation, the following methodological safeguards were implemented:

(1)

A suite of complementary performance metrics was employed to capture predictive error from multiple perspectives, including absolute deviation, outlier sensitivity, and relative accuracy, thereby enabling a comprehensive and balanced assessment across models.

(2)

To eliminate randomness-induced variance, a fixed random seed was used to partition the dataset into training (64%), validation (16%), and test (20%) subsets [39]. This ensured that all models were trained and evaluated on identical data splits, enhancing the reliability of inter-model comparisons.

(3)

Hyperparameter optimization was conducted uniformly across algorithms using the Optuna framework, with the population size and iteration count held constant. A total of 40 independent trials were performed within a unified search space encompassing five key hyperparameters (

Table 2. Hyperparameter search space and ranges for ensemble models.

Hyperparameter	Type	Range
n_estimators	Integer	50–300
max_depth	Integer	2–6
learning_rate	Float	0.01–0.2
subsample	Float	0.6–1.0
colsample_bytree	Float	0.6–1.0

). Model performance in each trial was evaluated on the validation set using multiple indicators, and the optimal configuration was selected based on the lowest Composite Performance Index (CPI), ensuring convergence toward high-performing, generalizable solutions.

2.3.3. Hyperparameter Tuning Guided by Composite Performance Index

To identify the optimal hyperparameter configurations for each ensemble model, CPI-based heatmap visualizations were constructed using a unified Optuna optimization framework (Figure 3). In the heatmaps, darker color indicates lower CPI and thus better overall model performance. These visual gradients highlight sensitive regions in the hyperparameter space, where predictive accuracy is maximized. As shown in

Table 3. Optimal hyperparameters and CPI values across models and targets.

Model	Target	Max Depth	Learning Rate	CPI
XGBoost	$E_{\mathfrak{c}}$	6	0.0781	0.003
LightGBM	$f_{\mathrm{c},\mathrm{r}}$	6	0.1294	0.04
LightGBM	${\alpha }_{\mathrm{c}}$	6	0.0751	0.008
CatBoost	${\epsilon }_{\mathrm{c},\mathrm{r}}$	6	0.1376	0.068

, the search space spanned tree depth and learning rate, with the Composite Performance Index (CPI) serving as the unified evaluation metric. These heatmaps not only facilitated cross-model performance comparison but also guided the selection of final model parameters used in subsequent predictive tasks. For XGBoost, CPI steadily decreased with increasing depth, reaching 0.003 for elasticity modulus at a learning rate of 0.078. LightGBM exhibited similar trends, with optimal performance on UCS and descent section parameters at learning rates of 0.129 and 0.075, and CPI values of 0.040 and 0.008, respectively. CatBoost showed a more scattered behavior but still achieved its best CPI (0.068) for the peak strain at a depth of 6 and a learning rate of 0.138 (Table 3).

These CPI heatmaps directly informed the selection of final model configurations, ensuring both methodological consistency and improved generalization in the subsequent prediction tasks. As summarized in Figure 4, after database establishment and sample stratification, the dataset was partitioned into training (64%), validation (16%), and testing (20%) datasets. Augmentation was restricted to the training split; no synthetic samples were entered for validation or testing. Standardization was estimated on the augmented training data and transported to the other splits to prevent leakage. XGBoost, LightGBM, and CatBoost were fitted to the training split, with hyperparameters optimized via Optuna on validation (selection landscapes in Figure 3). With selection fixed, the held-out test split alone underpinned downstream reporting: (1) predictive accuracy and stress–strain reconstructions (Figure 5); (2) global attribution via permutation importance (Figure 6); and (3) interaction diagnostics via SHAP dependence plots for key parameters (Figure 7 and Figure 8). Interpretability was strictly out-of-sample; training and validation data were not used.

3. Interpretability and Validation of Predictive Models for CGC Constitutive Behavior

3.1. Predictive Accuracy and Multi-Model Performance Comparison

To fairly assess the predictive performance of the three ensemble models—XGBoost, LightGBM, and CatBoost [40], this setup was designed to reflect realistic prediction scenarios and avoid bias from repeated data exposure. Performance was measured using a set of standard regression metrics, including co and the Composite Performance Index (CPI). Visual validation was also carried out using ±15% error-band scatter plots.

As summarized in

Table 4. Statistics of training model information for descending segment parameters.

Model	R2	MAPE	MAE	MSE	RMSE	CPI
XGBoost	0.96	3.21	90.74	26,645.40	163.29	0.11
LightGBM	0.96	3.06	88.39	26,108.22	161.58	0.01
CatBoost	0.96	3.62	98.99	22,967.33	151.55	0.03

,

Table 5. Statistics of peak strain training model information.

Model	R2	MAPE	MAE	MSE	RMSE	CPI
XGBoost	0.98	7.34	850.48	1,997,496.00	1413.33	0.58
LightGBM	0.98	7.75	880.75	2,099,099.00	1448.83	0.02
CatBoost	0.97	9.78	1141.07	2,792,556.00	1671.09	0.03

,

Table 6. Information statistics of the uniaxial compressive strength training model.

Model	R2	MAPE	MAE	MSE	RMSE	CPI
XGBoost	0.96	4.72	1.26	2.95	1.72	0.34
LightGBM	0.96	4.62	1.23	2.86	1.69	0.03
CatBoost	0.95	5.80	1.57	4.21	2.05	0.03

and

Table 7. Statistics of the elastic modulus training model information.

Model	R2	MAPE	MAE	MSE	RMSE	CPI
XGBoost	0.93	77.80	0.25	0.14	0.37	0.57
LightGBM	0.93	75.39	0.26	0.15	0.38	0.03
CatBoost	0.91	87.43	0.30	0.18	0.43	0.04

, all models showed reasonable predictive accuracy across the four target parameters, with R² values above 0.91 in all instances. Notably, LightGBM maintained low CPI values on the test set—consistently below 0.04—which closely matched its performance on the validation set (Table 3). This level of consistency suggests that the model generalized well without clear signs of overfitting. For XGBoost and CatBoost, the gap between the validation and test CPI was more variable, especially for targets like the peak strain and elastic modulus, indicating some sensitivity to data distribution shifts.

Each model exhibited distinct strengths. LightGBM performed reliably across all targets, particularly for high-variance outputs like the elasticity modulus and compressive strength (Figure 5b). XGBoost effectively captured the structural patterns, which is reflected in the close clustering of the prediction points along the diagonal in Figure 5a. Although slightly less stable overall, CatBoost handled sample dispersion well; its predictions remained within the ±15% error band, even when the data became sparse or unevenly distributed.

3.2. Global–Local Feature Attribution and Mechanistic Interpretation

To further elucidate the feature response mechanisms within the predictive models for different mechanical parameters, this section presents a systematic interpretability analysis using the SHAP method based on the best-performing LightGBM model. As a representative of gradient-boosted tree models, LightGBM offers a refined structure, high training stability, and superior error control, making its interpretability results a reliable reflection of the true feature contribution mechanisms.

A permutation-based global importance audit (Figure 6) quantifies the aggregate predictor influence across all targets. The salience hierarchy isolates coal gangue content, crush index, and cement content as dominant—governing, respectively, for replacement level, particle integrity, and binder proportion within the composite matrix. This system-level attribution provides a synoptic map of the feature–response landscape and a principled sieve for variables prioritized for deeper diagnostics.

3.2.1. Feature Attribution and Mechanistic Interpretation for Elasticity Modulus

As shown in the SHAP summary plot (Figure 7a), coal gangue content and crush index are the most influential features for predicting elasticity modulus, with both the highest mean SHAP values and the broadest dispersion. Figure 8a shows a nonlinear inverse relationship between gangue content and its marginal effect, partitioning three mechanical regimes (brittle → quasi-ductile → re-brittle). Below 28% replacement, the SHAP values are predominantly positive, indicating stiffness preservation via enhanced particle interlock, matrix continuity, and intact ITZ; angular gangue elevates internal friction, consistent with a brittle-dominated response [41,42]. Between 28% and 56%, SHAP precipitously crosses into negative territory at an inflection point where porosity-driven weakening supersedes the initial benefits. Microcracking, ITZ debonding, and flaw-controlled inclusions impede stress transmission, with fractography corroborating shear-slip and defect accrual [43,44]. Beyond ~56%, the SHAP stabilizes in the negative band (−4000 to −6000 MPa), indicating a re-brittle regime governed by a friable, low-strength aggregate skeleton, rapid crack coalescence, and localized interfacial failure with minimal strain accommodation [45,46]. A pronounced interaction with the crush index is also observed: jointly high values produce the SHAP nadir and compounded stiffness attrition, consistent with the premature fracture of friable particles, local densification, microvoid nucleation, and accelerated interfacial cracking that nonlinearly amplifies stiffness loss [47].

3.2.2. Feature Attribution and Mechanistic Interpretation for Uniaxial Compressive Strength (UCS)

As shown in the SHAP summary plot for UCS (Figure 7b), coal gangue content and water–cement ratio are the dominant features, followed by crush index and cement dosage. These variables display wide SHAP value dispersion, reflecting pronounced nonlinear and coupled effects. For gangue content, the SHAP values ranged from approximately +10 MPa to –7.5 MPa, indicating a bidirectional influence dependent on the replacement level.

Figure 8b shows the tripartite regime. For replacement < 26%, SHAP values are predominantly positive, indicating maintained or slightly augmented UCS via improved packing and interparticle friction from moderately angular gangue [48]. Across 26–54%, SHAP descends precipitously, an inflection where deleterious effects supersede initial gains, driven by proliferating weak ITZs, heightened capillary porosity, and matrix discontinuities that vitiate stress transmission and precipitate incipient cracking, in concordance with microstructural deterioration in prior studies [41,43]. Beyond 60%, the SHAP plateaus in a negative asymptote, evidencing saturation: additional gangue scarcely worsens UCS as failure is governed by a friable, low-strength aggregate skeleton, consistent with granular framework–collapse models [41]. The color gradient further evinces a strong interaction with the water–cement ratio: elevated ratios exacerbate the negative SHAP effect between 40% and 70% replacement via dual interfacial debilitation, matrix cohesion loss, and ITZ degradation from porous gangue (water uptake, shrinkage mismatch), accelerating microcrack coalescence and attenuating effective stress transfer, in line with observations on porosity- and moisture-induced interfacial weakening [49].

3.2.3. Prediction Mechanism and Feature Attribution for Peak Strain

As revealed in the SHAP summary plots (Figure 7c,d), water–cement ratio and coal gangue content are consistently identified as the principal drivers of both peak strain (εₚ) and the descending parameter α, reflecting their pivotal roles in regulating inelastic deformation and post-peak dissipation characteristics. These variables exhibit strongly monotonic SHAP trends, suggesting that their effects are scale-consistent across the composition spectrum. Additional contributors—such as packing density for εₚ and cement dosage for α—act as localized modulators, fine-tuning fracture progression and residual ductility.

The corresponding SHAP dependence plots (Figure 8c,d) indicate a clear positive shift in SHAP values as gangue content increases beyond approximately 47–60% (standardized values of −0.2 to +0.4), quantitatively supporting the ductility enhancement trend previously observed in the stiffness-related response (see Section 3.2.1). This upward transition reflects the cumulative effects of interfacial degradation, increased pore connectivity, and disrupted aggregate interlocks, which together promote greater strain accommodation capacity and retard stress collapse during the post-peak phase.

Taken together, these results suggest that elevated gangue incorporation induces progressive plasticization and energy dissipation, thereby reshaping the post-peak failure envelope through the coupled evolution of stiffness degradation and strain delocalization mechanisms. These insights reinforce the view that gangue not only alters strength capacity but also fundamentally transforms failure morphology in hybrid cementitious systems.

3.3. Constitutive Curve Prediction and Validation Based on Machine Learning

Building upon the SHAP-based interpretation of individual constitutive parameters, this section reconstructs the full stress–strain trajectories of coal gangue concrete under varying material conditions using LightGBM-predicted inputs(Figure 9 and Figure 10). The generated curves not only replicate the declining trends in stiffness and strength associated with increased gangue content but also reveal the progressive enhancement of ductility, as reflected in elevated peak strains and smoother post-peak descent. These emergent behaviors are consistent with the feature-wise mechanisms previously identified—particularly the interplay between coal gangue content, water–cement ratio, and aggregate integrity.

Notably, the predicted curves capture both the degradation and toughening effects induced by gangue replacement, with the former driven by microstructural weakening of the interfacial zones and the latter associated with crack deflection and energy absorption mechanisms. This model-driven constitutive reconstruction validates the internal consistency of the proposed framework by bridging parameter-level learning with holistic mechanical behavior. These predictive curves further serve as transferable inputs for the finite element simulations that follow, enabling structural-scale validation under coupled loading conditions.

4. Finite Element Simulation of Coal Gangue Concrete Columns Under Combined Loading in ABAQUS

4.1. Finite Element Modeling Strategy and Material Parameter Input

We employed the ABAQUS Concrete Damage Plasticity (CDP) model to simulate the nonlinear response of CGC columns under combined axial–bending, calibrating and validating against the small-eccentric compression tests of [30]. Specimens were 300 × 300 × 1800 mm RC columns with gangue-coarse-aggregate replacement of 40, 70, and 100% (w/c = 0.40; cement = 475 kg·m⁻³; mix proportions adjusted accordingly). Axial loading with e₀/h = 0.25 was applied under displacement control on a hydraulic frame, and LVDTs and strain gauges were instrumented on both the compression and tension faces. Failures manifested as flexural–compression: incipient horizontal cracking on the tension face, progressive crack coalescence, and compression face spalling near ultimate. Four key material parameters were subsequently rectified via Gradient-Boosted-Tree predictions in accordance with the experimental conditions. (

Table 8. Constitutive parameters of coal gangue concrete predicted by the LightGBM model.

Content of Coal Gangue	${\mathit{f}}_{\mathbf{c},\mathbf{r}}$(MPa)	${\mathit{\epsilon }}_{\mathbf{c},\mathbf{r}}$(10−6)	${\mathit{E}}_{\mathfrak{c}}$(MPa)	${\mathit{\alpha }}_{\mathbf{c}}$
40	29.67	2489.80	21,653	1.36
70	24.80	2794.01	19,412	4.15
100	20.53	2894.05	13,368	7.21

). Reinforcement was modeled as ideal elastic–plastic using T3D2 truss elements, while concrete was discretized with C3D8R solid elements. The steel–concrete system was assembled into a complete reinforced model, and the overall mesh sizes of the concrete member and the reinforced cage were set as 30 mm and 20 mm, respectively, to consider the calculation efficiency and accuracy, as illustrated in Figure 11a,b.

Table 9. Key parameter settings for the Concrete Damage Plasticity (CDP) model in ABAQUS.

Expansion Angle (°)	Eccentricity	fb0/fc0	K	Viscosity Parameter
40	0.1	1.16	0.6667	0.011

demonstrates the values of dilation angle (φ), eccentricity (ε), flow stress ratio (fb0/fc0), deviatoric shape factor (K), and viscosity coefficient were determined through a combination of literature references [50,51] and extensive numerical calibration. The final configuration was selected based on its ability to ensure numerical stability and accurately reproduce the post-peak softening behavior of coal-gangue concrete under combined loading conditions.

4.2. Numerical Simulation Analysis and Experimental Validation

Due to the inherent high porosity and crush value of coal gangue concrete, early-stage testing (displacement < 2.8 mm) tends to induce localized contact nonlinearity, which may compromise the accuracy of the constitutive response in the primary control zone. Therefore, initial instability data were excluded during numerical validation to ensure the focus remained on evaluating intrinsic constitutive behavior [7].

4.2.1. Validation of Failure Patterns and Crack Propagation Pathways

For the 40% coal gangue replacement specimen, Figure 12 illustrates the simulated tensile and compressive damage distributions at the final loading stage. The simulation indicates that tensile cracks initiate at the tension face and propagate vertically, while compressive crushing develops near the mid-low of the compression face. Figure 13 presents the corresponding experimental failure patterns. A direct comparison shows that the simulated crack initiation locations and damage severity are generally consistent with the experimental observations, indicating that the finite element model provides a reasonable representation of the failure process of the specimen under combined loading.

4.2.2. Comparative Analysis of Characteristic Loads

Table 10. Comparison of numerical simulation and test load parameters.

Content of Coal Gangue%		Cracking Load (KN)			Ultimate Load (KN)
	TEST	NUM	NUM/TEST	TEST	NUM	NUM/TEST
40%	670	692	1.03	1438	1445	1.01
70%	540	549	1.02	1397	1372	0.98
100%	460	482	1.05	1254	1319	1.05

TEST: the test record data. NUM: shows the numerical simulation data.

summarizes the comparison between predicted and measured characteristic loads. Overall, the simulation-to-test ratios fall within 0.98–1.05, encompassing the expected variability due to material heterogeneity and experimental error. Although the model slightly overpredicts peak loads, this deviation is within acceptable bounds given the intrinsic differences between the heterogeneous nature of coal gangue aggregates and the isotropic assumptions in the simulation. These findings confirm that the machine learning–enhanced constitutive framework effectively supports strength development simulations under uniaxial stress, meeting practical engineering accuracy requirements.

4.2.3. Load–Midspan Deflection Response Evolution

Figure 14a–c illustrates the comparative load–midspan deflection curves for specimens with 40%, 70%, and 100% replacement ratios. The finite element model successfully captures the full response trajectory, including the elastic phase, crack initiation, stiffness degradation, reinforcement yielding, and ultimate failure. The simulations showed high fidelity to the experiments at both inflection points and overall deformation trends.

The evolution of load–displacement responses under varying coal gangue replacement levels offers direct mechanical corroboration for the structural transition mechanisms previously inferred through SHAP-based feature attribution. As illustrated in Figure 10, specimens incorporating 40% and 70% gangue demonstrate a progressive attenuation of post-peak load, manifested in extended softening branches and delayed force degradation. These experimental and simulated responses reflect a notable increase in energy dissipation capacity and deformation tolerance, indicative of quasi-ductile behavior. The underlying mechanisms—such as frictional interlock among angular gangue particles, crack deflection, and matrix–aggregate interfacial plasticity—promote strain redistribution and delay catastrophic failure. In contrast, specimens with 100% gangue replacement exhibit a distinctly brittle response profile, characterized by a precipitous post-peak decline in load-bearing capacity and minimal inelastic accommodation. This abrupt structural collapse aligns with the SHAP-derived identification of a terminal degradation regime, wherein excessive porosity, weak interfacial bonding, and skeletal discontinuity coalesce to suppress any residual ductility.

Notably, these observed mechanical trajectories conform closely to the three-stage structural response model (brittle → quasi-ductile → re-brittle) proposed earlier in Section 3.2.1. The finite element results thus serve as an independent validation of the model sensitivity in capturing nonlinear mechanical transitions within coal gangue concrete. More importantly, the pronounced energy absorption behavior identified within the intermediate (saturation) regime suggests a tangible potential for engineering applications requiring seismic resilience and impact mitigation. Given the growing interest in sustainable and high-performance damping materials [52], the SHAP-enhanced interpretability framework established in this study may offer a new paradigm for the data-driven development of energy-dissipative concrete systems based on physical realism and verifiable design logic.

5. Conclusions and Future Directions

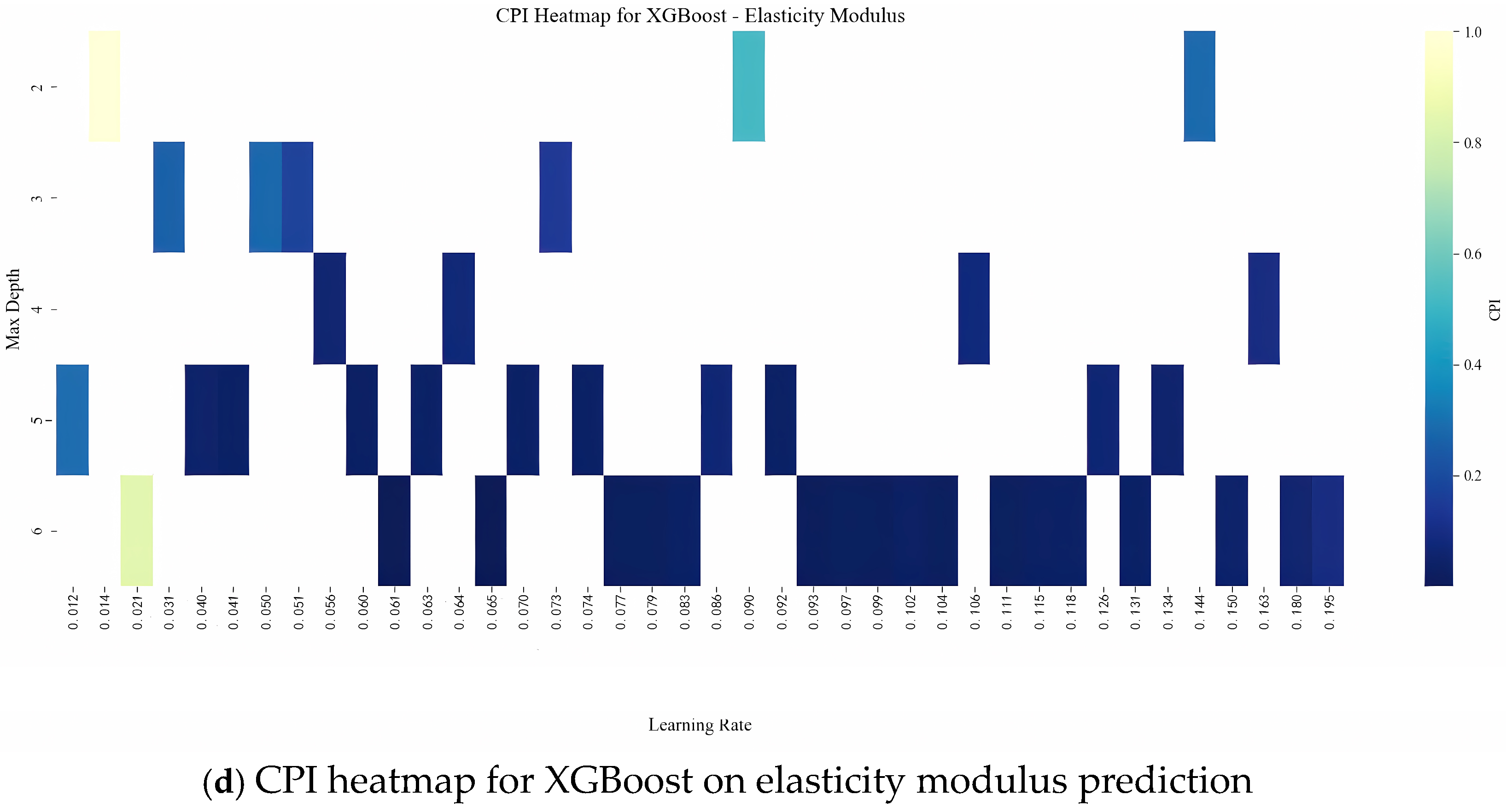
(1) The CPI-based heatmap analysis suggests that ensemble models perform best on coal gangue concrete data when trained with moderately low learning rates (around 0.07–0.13) and relatively shallow tree depths (no more than 6). This combination offers a good trade-off between capturing nonlinear patterns and avoiding overfitting, making it well-suited for modeling the complex and heterogeneous behavior of CGC materials.

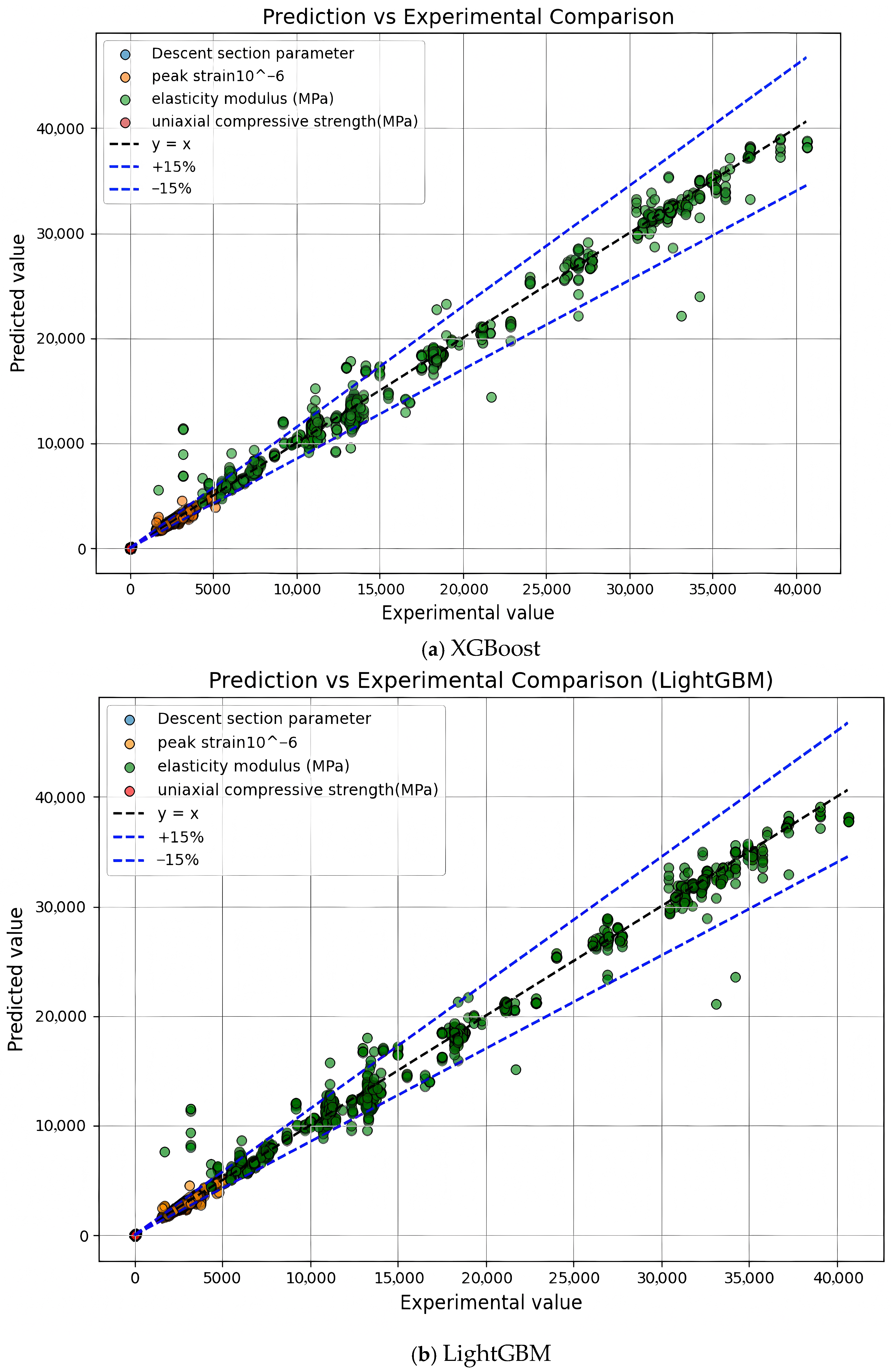
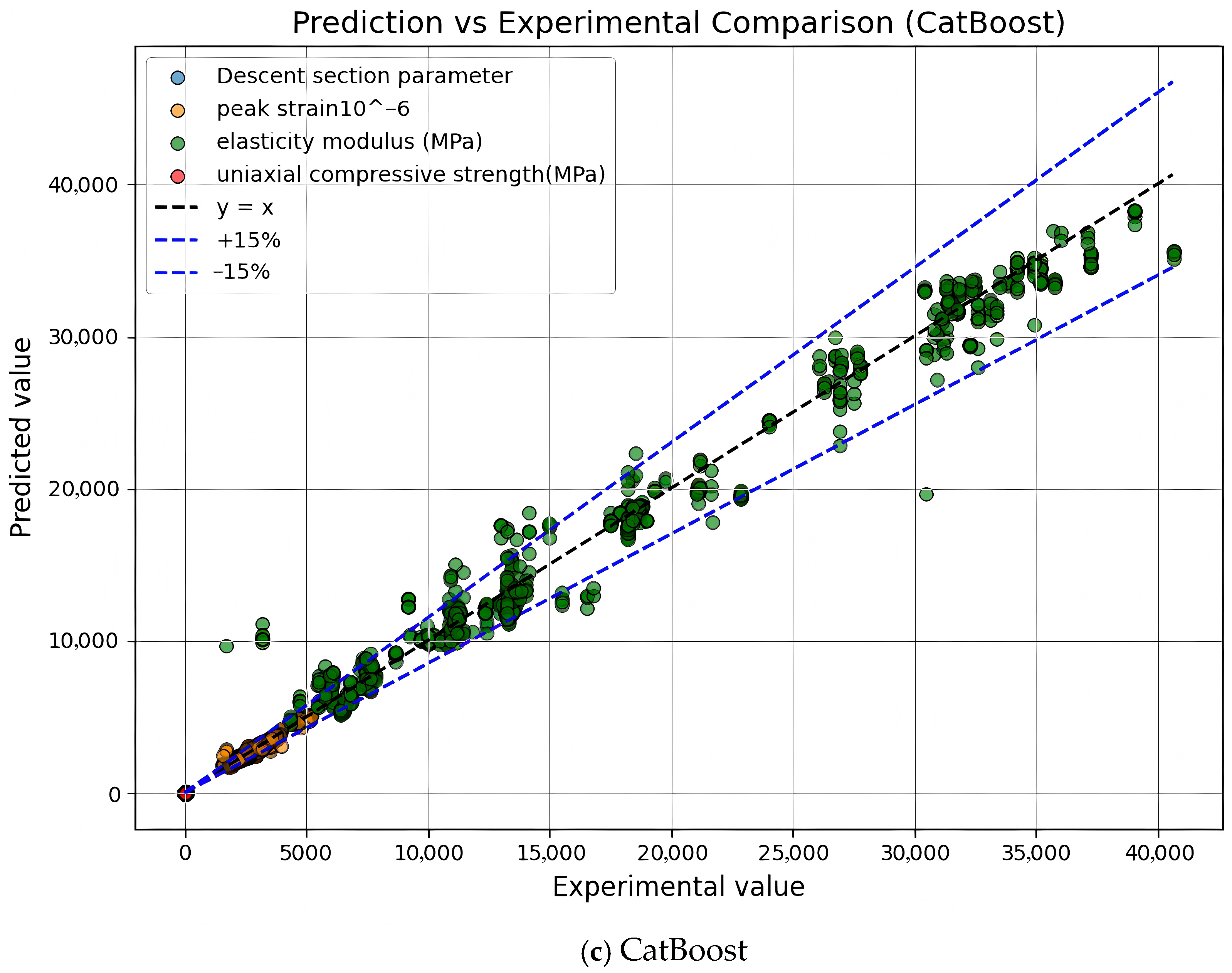
(2) Among the evaluated models, LightGBM outperforms in terms of accuracy, robustness, and error mitigation, particularly excelling in predicting high-dimensional targets such as the elasticity modulus and uniaxial compressive strength. CatBoost demonstrates superior adaptability in small-sample, discrete datasets, while XGBoost offers strong boundary detection and local fitting capabilities, making it ideal for scenarios with well-defined structural patterns.

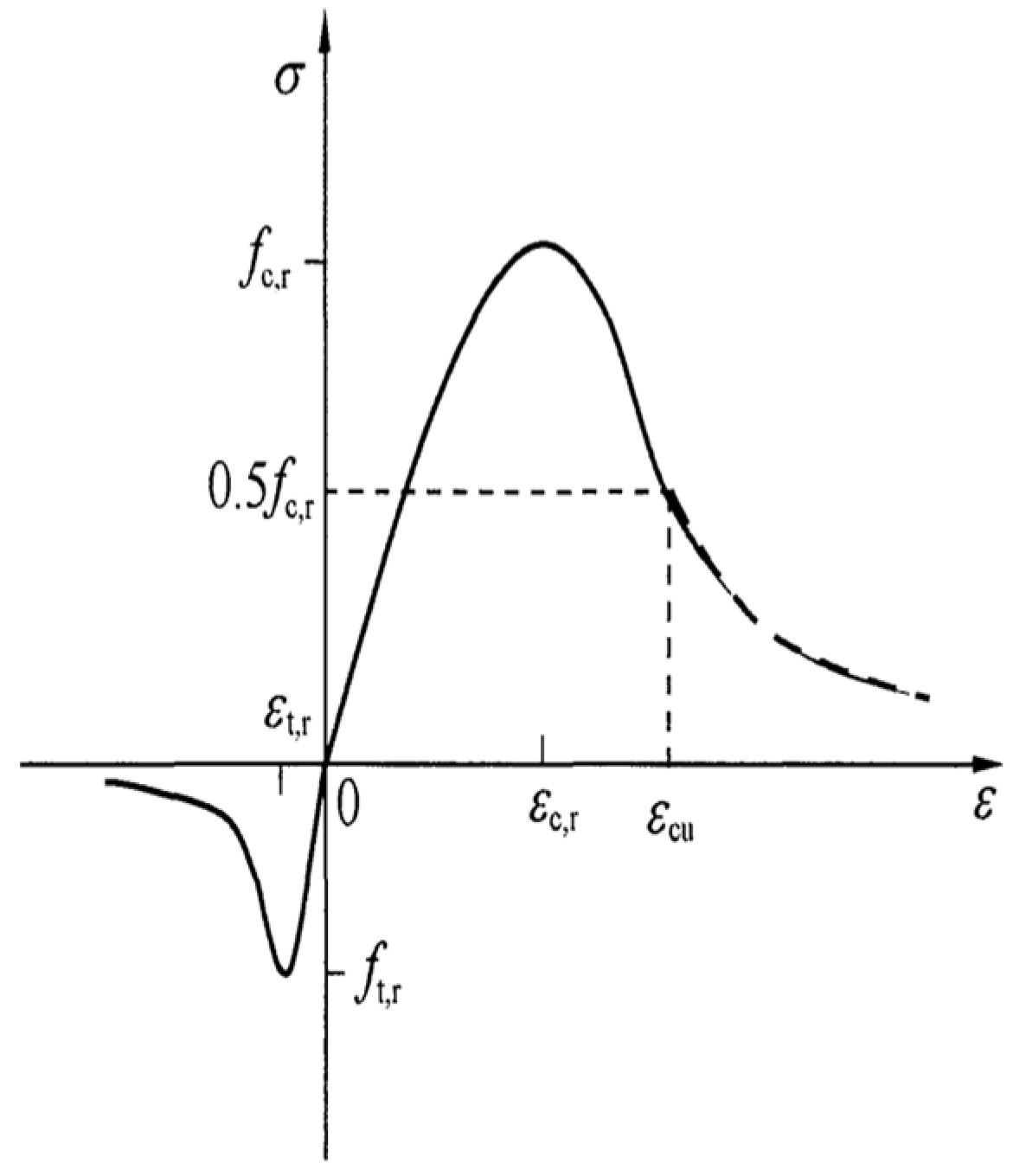
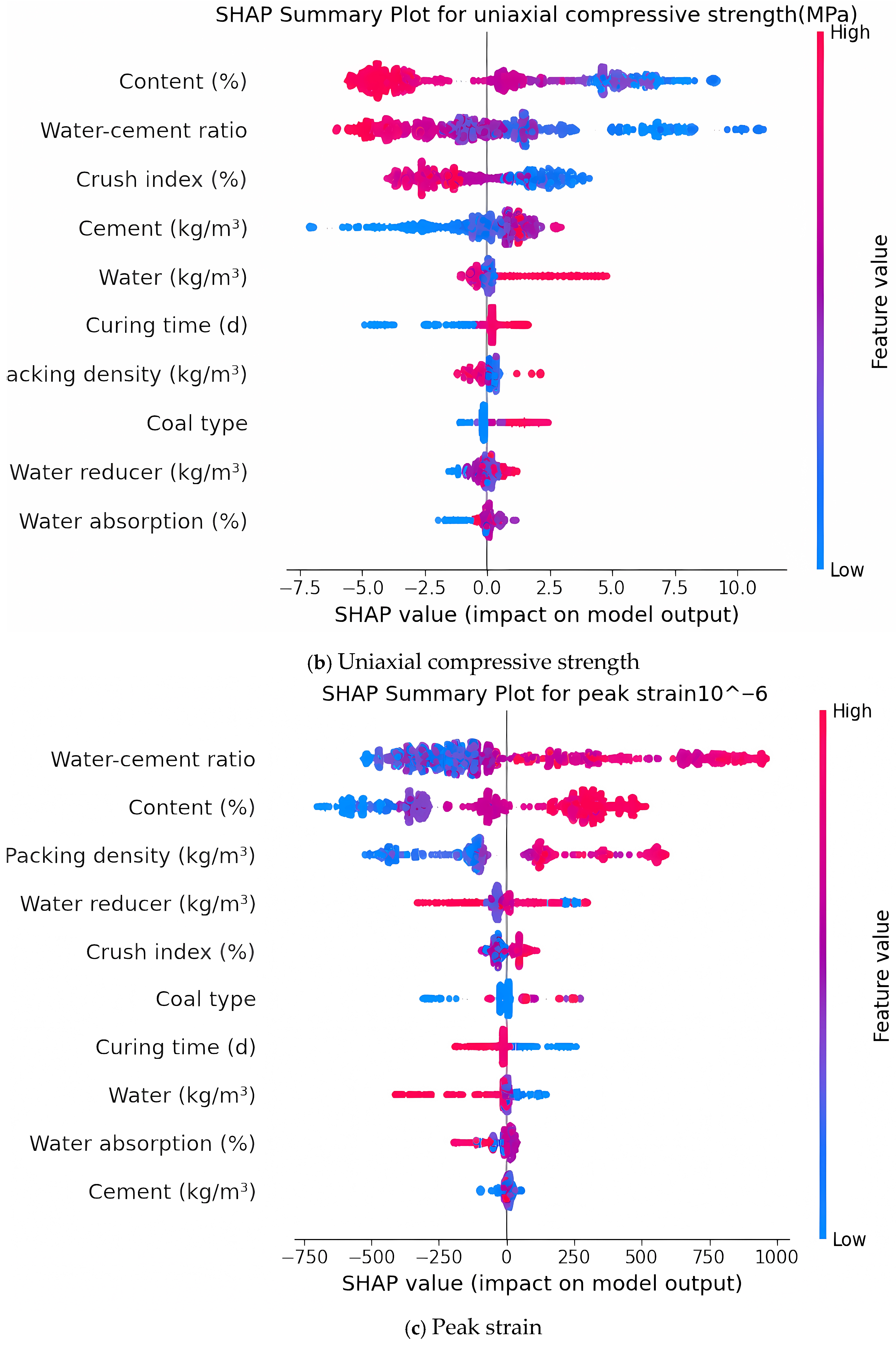
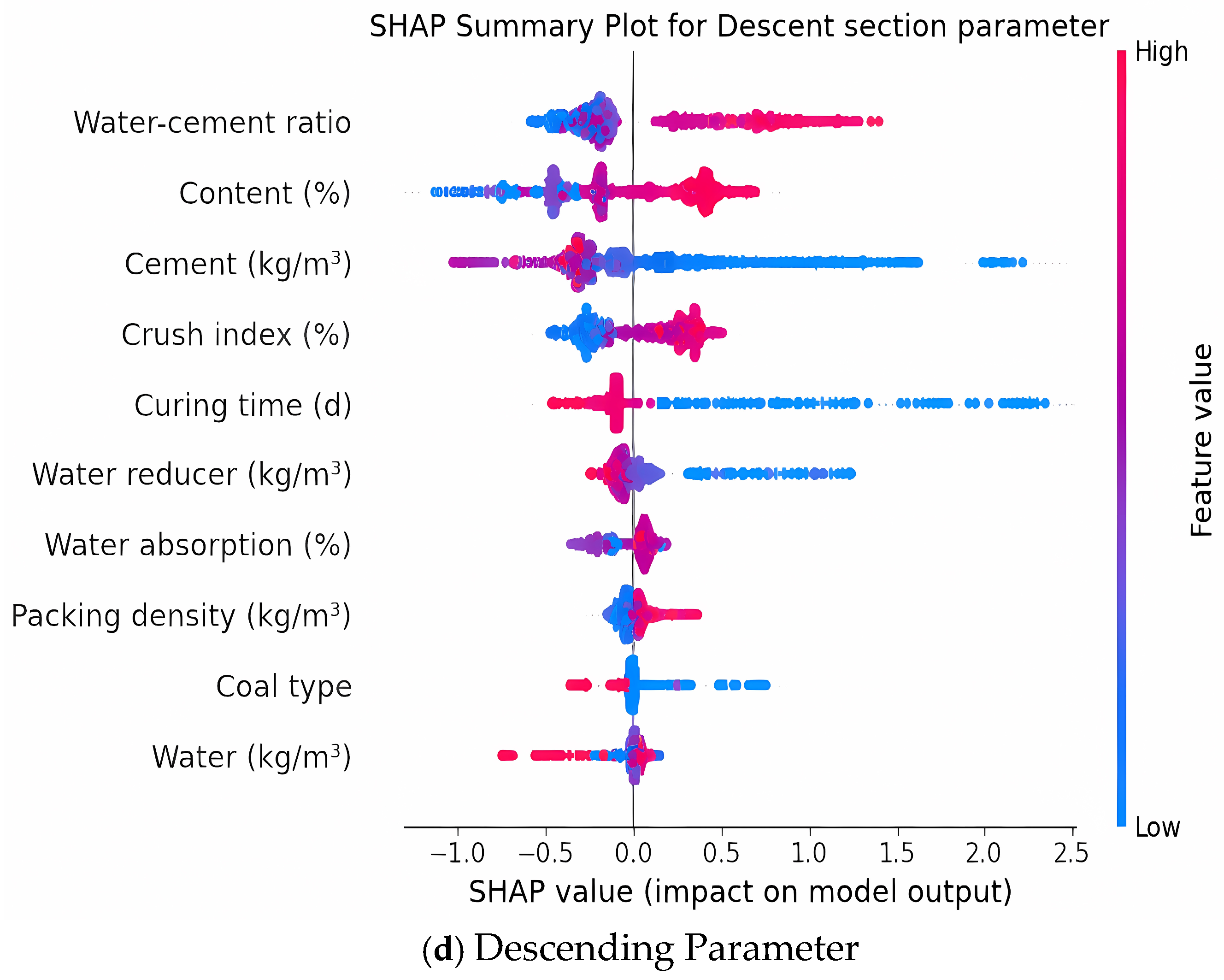
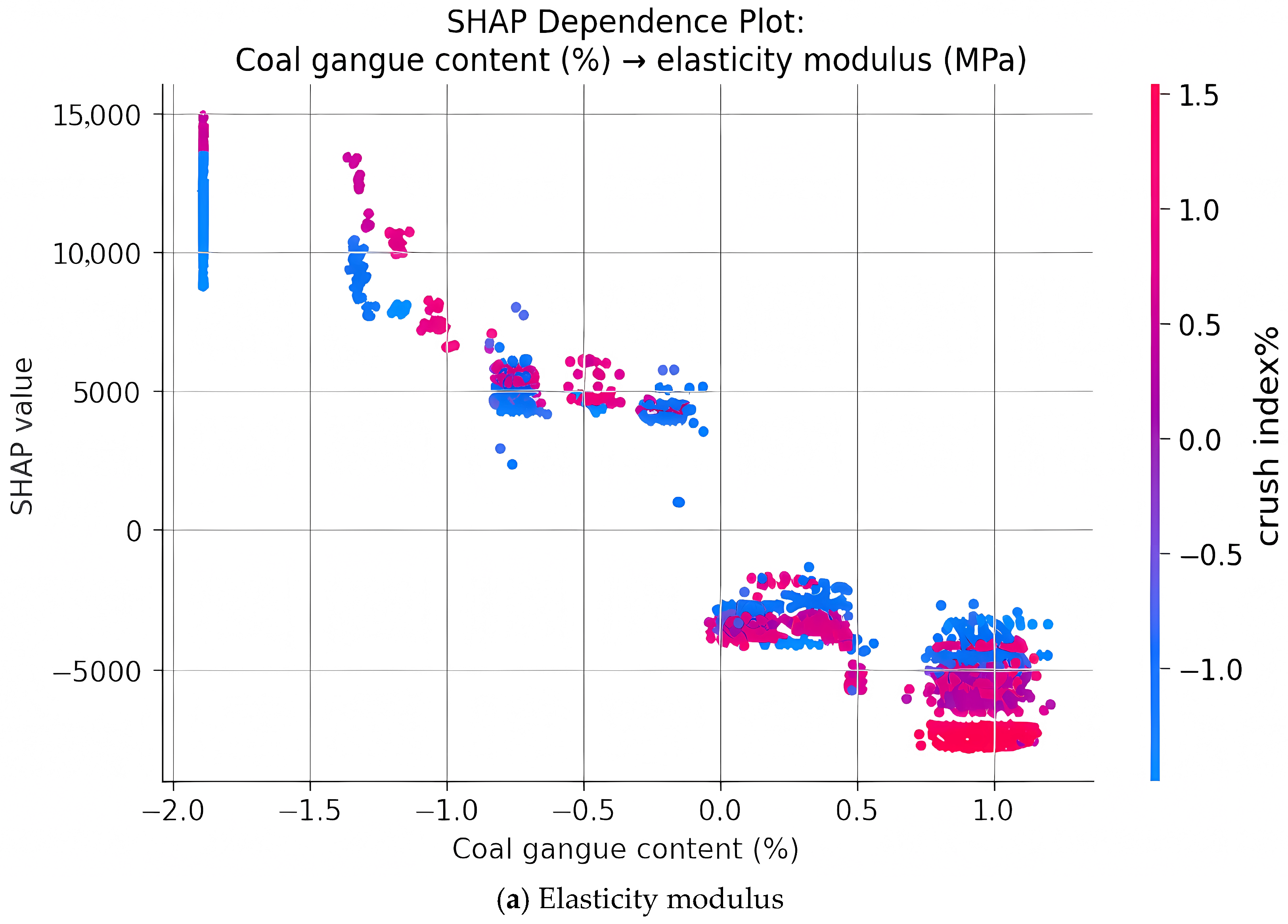
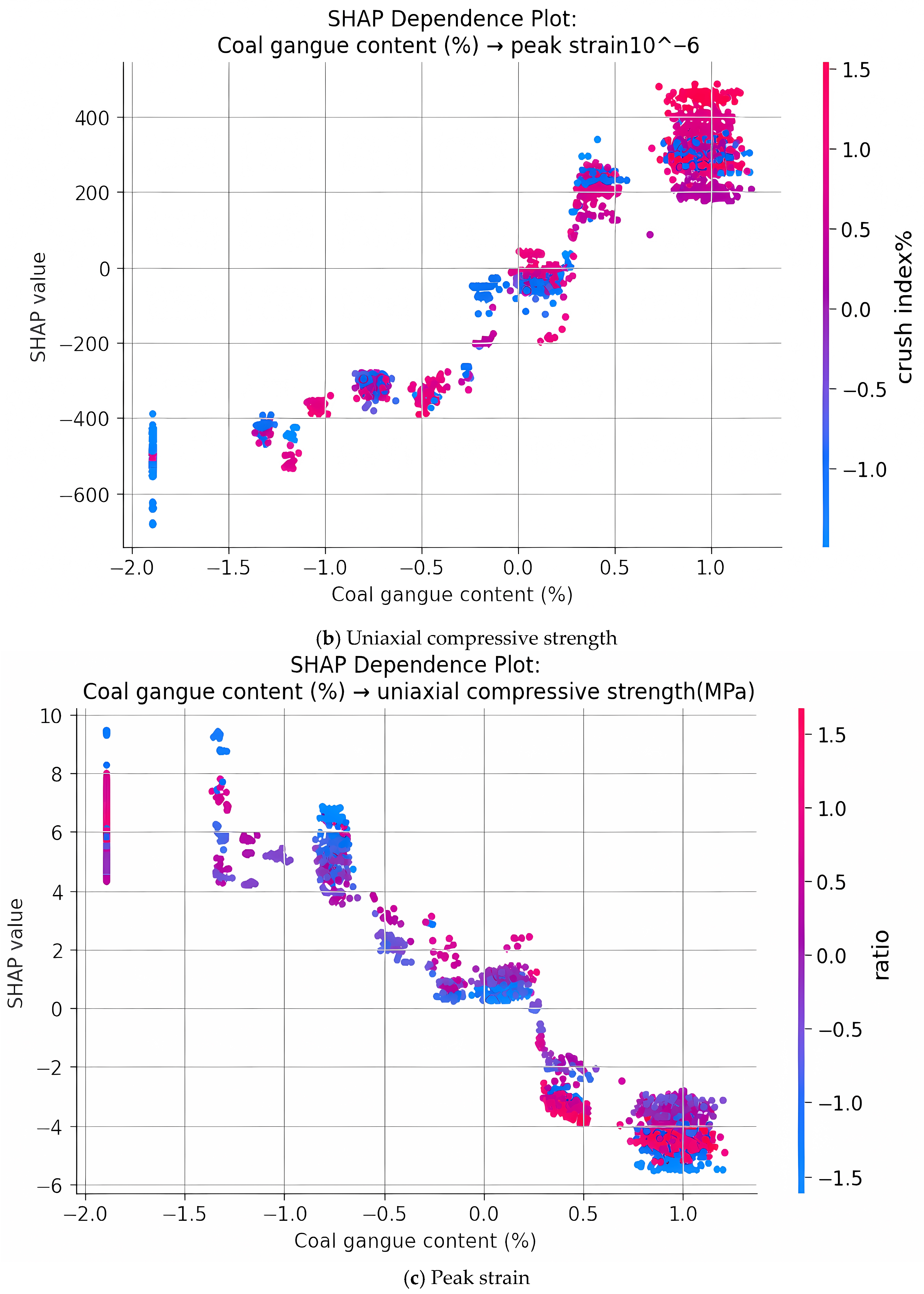
(3) SHAP-based interpretability analysis elucidated a three-stage mechanical response trajectory—brittle, quasi-ductile, and re-brittle—governing the stiffness evolution of CGC with increasing gangue incorporation. This phase-structured framework, grounded in feature–response attribution patterns, was corroborated through micromechanical evidence and deformation morphologies, thereby affirming the model’s capacity to capture nonlinear degradation thresholds and interfacial instability regimes intrinsic to hybrid aggregate systems.

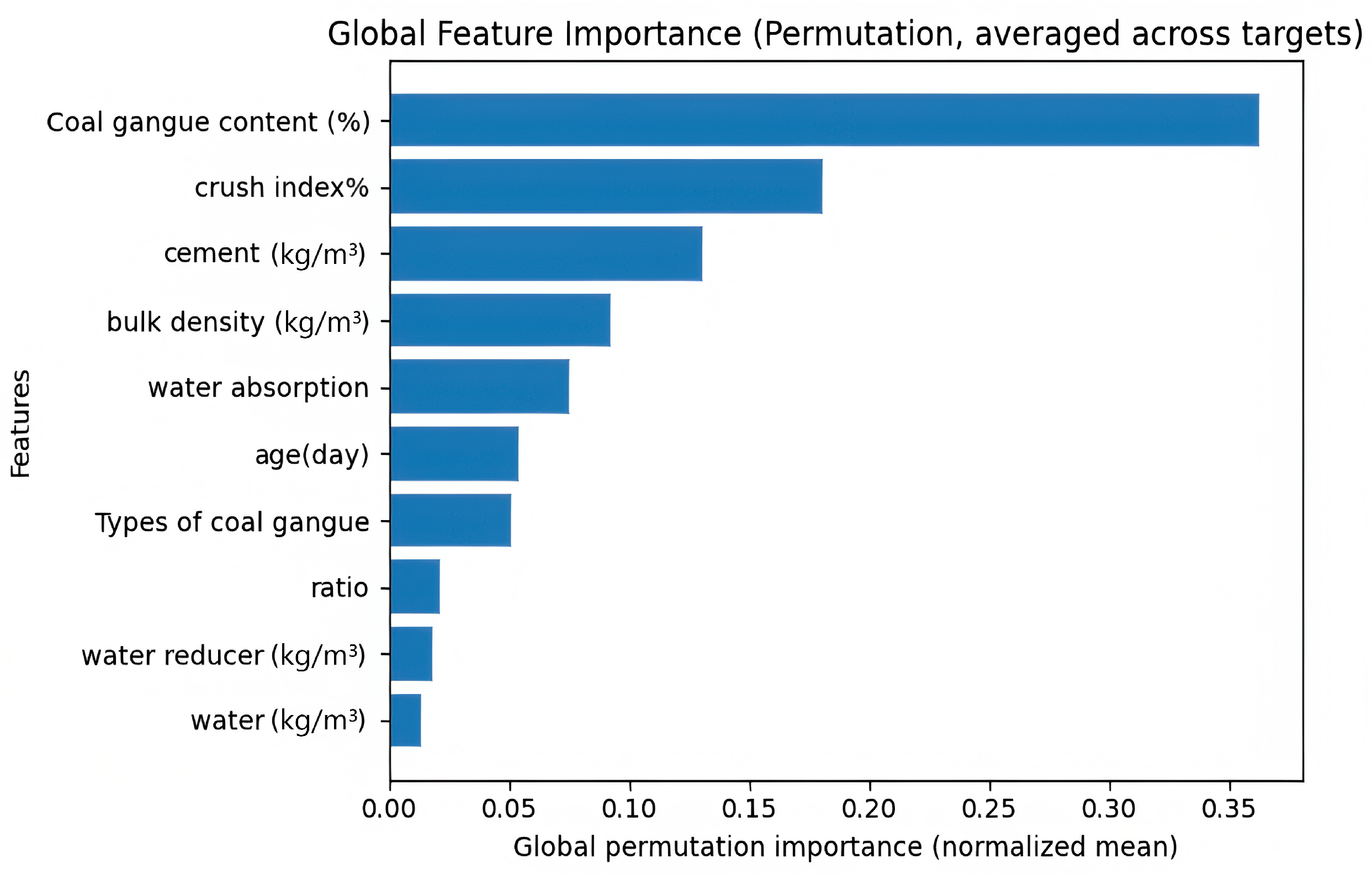
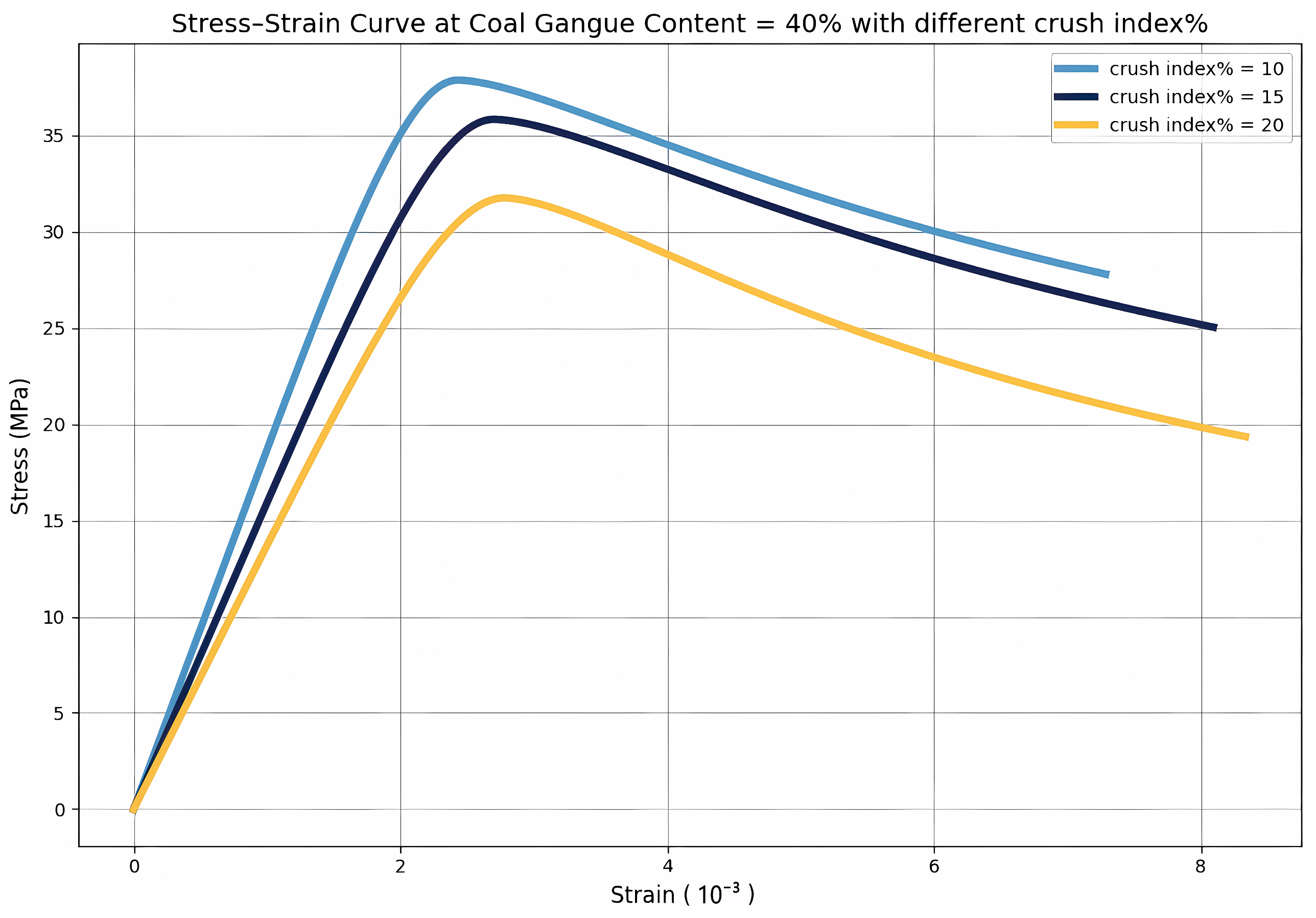
(4) Hybrid explainability analysis revealed compounded degradation effects arising from the coupled influence of coal gangue content with both crush index and water–cement ratio. The permutation-based global ranking established these variables as jointly dominant across all targets, while SHAP-based local visualizations elucidated nonlinear synergistic weakening mechanisms—wherein friable gangue particles and elevated moisture levels collectively destabilize the matrix–aggregate interface—thereby intensifying stiffness loss and precipitating compressive failure. These findings align with prior micromechanical observations linking interfacial debonding, pore coalescence, and moisture-induced damage to hybrid aggregate deterioration.

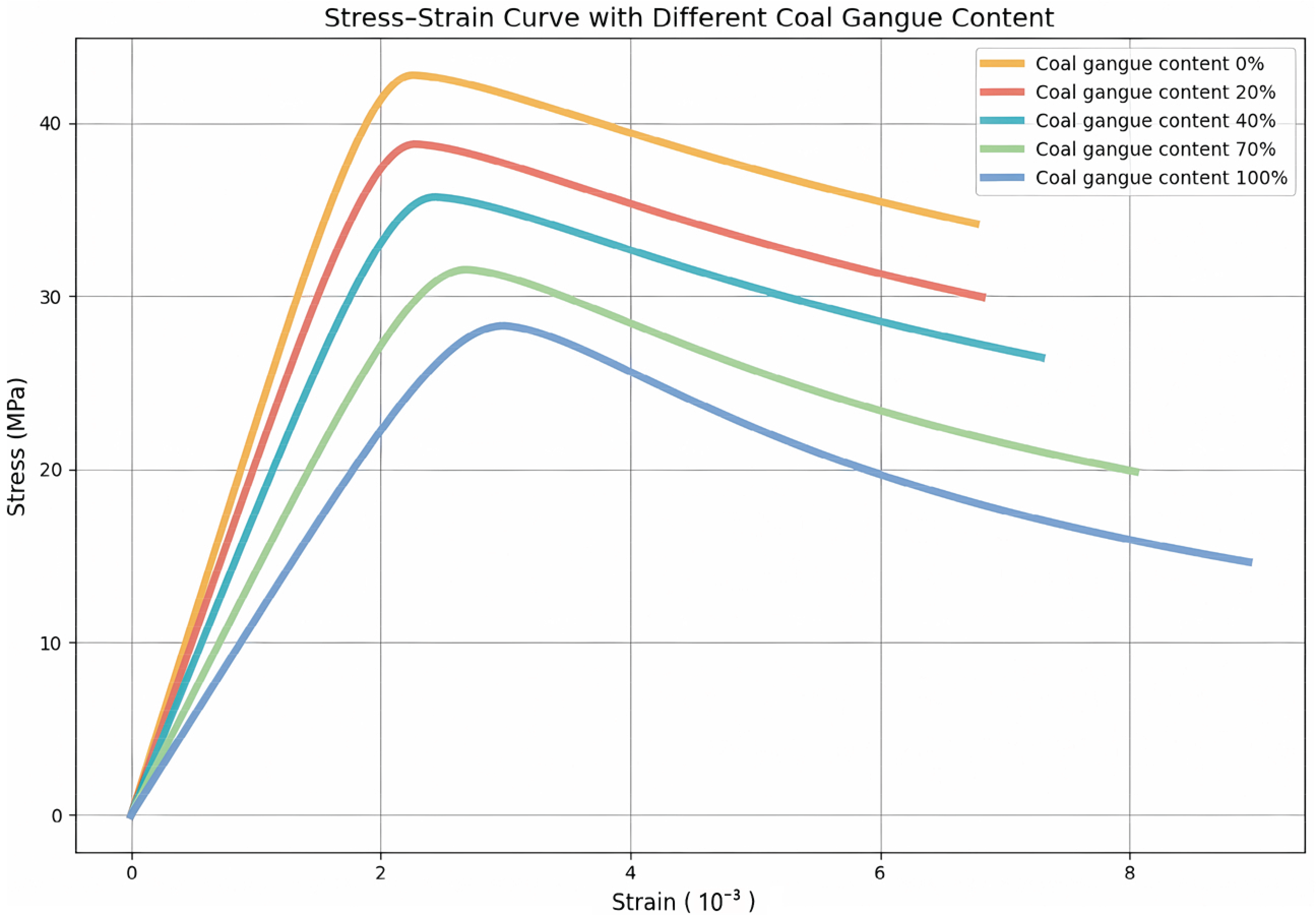
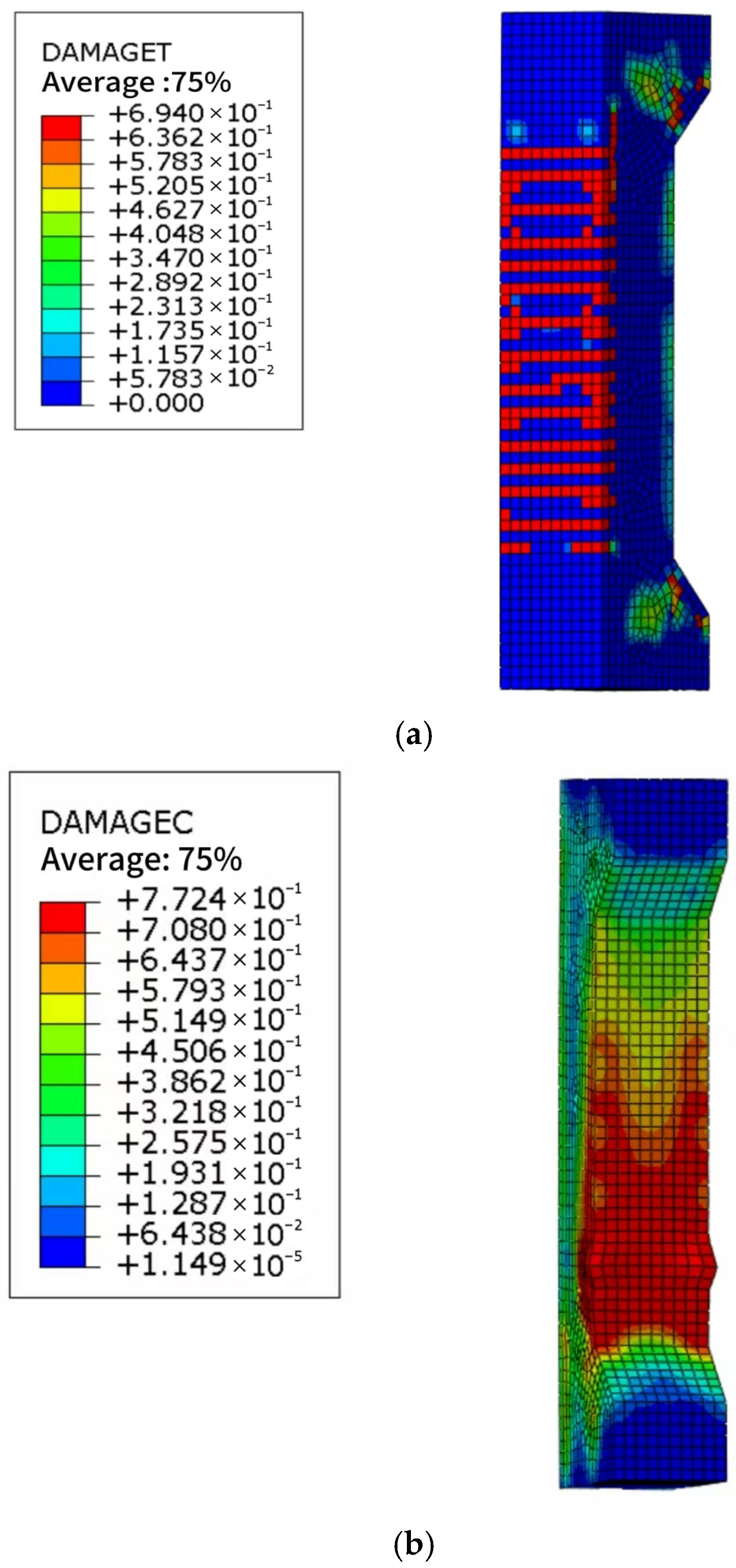
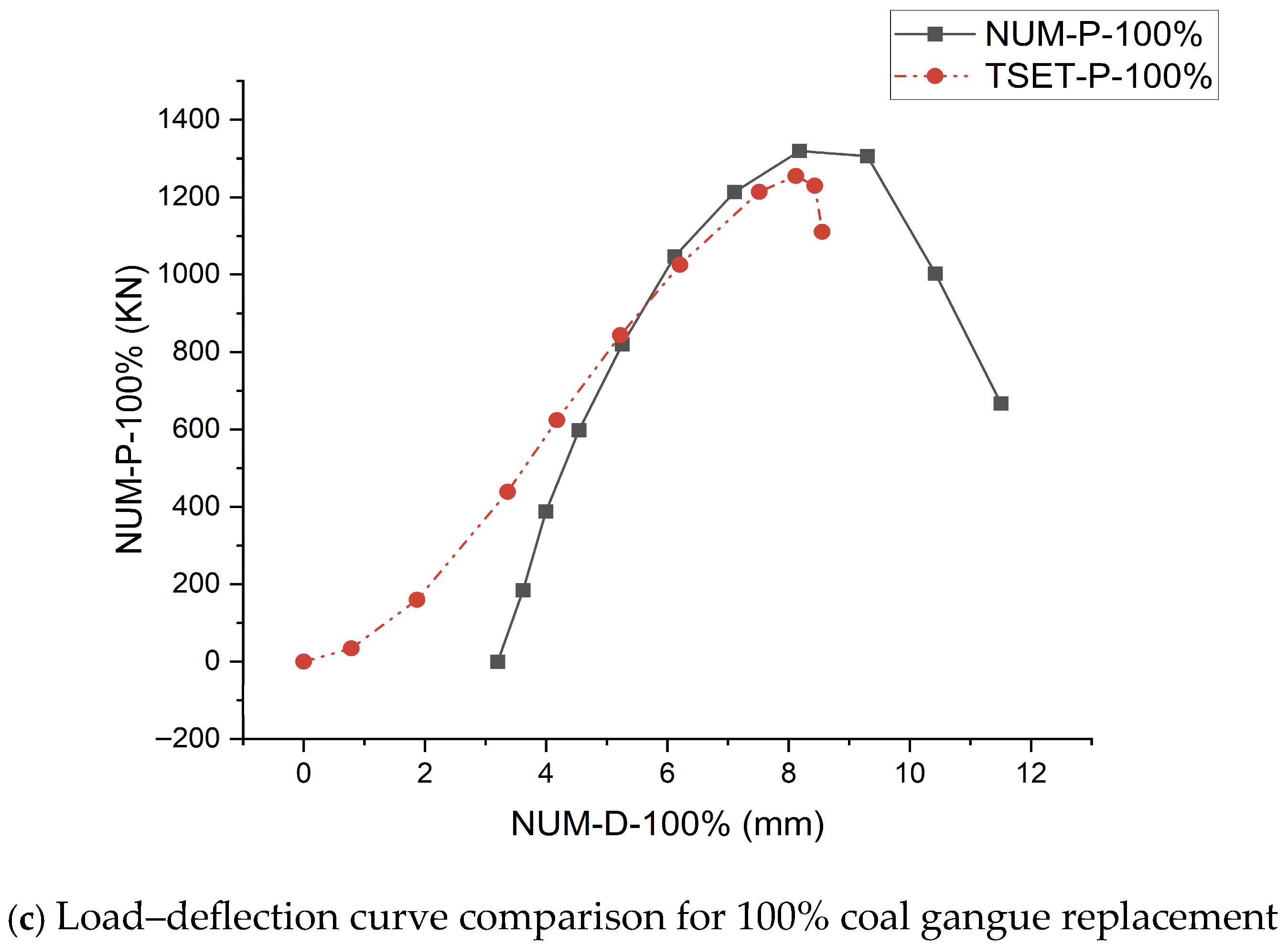
(5) Finite element validation, calibrated through fracture energy–based softening curves, independently substantiated the reliability of the SHAP-informed constitutive model in reproducing key structural responses across failure modes, load trajectories, and post-peak behavior. Notably, the model accurately captured the brittle → quasi-ductile → re-brittle evolution path of CGC, aligning simulation outcomes with SHAP-predicted transitions. The pronounced energy dissipation observed in the intermediate regime highlights the potential of coal gangue concrete as a ductile and damage-tolerant material for seismic applications. These findings establish a mechanistically interpretable and numerically verifiable framework for guiding the development of performance-based, data-driven structural materials. Building on the generalizability of the proposed modeling framework, there is significant potential for cross-domain extension. Future research should focus on the following key directions:

(1)

Enhancement of dataset scale and representativeness for advanced interaction modeling.

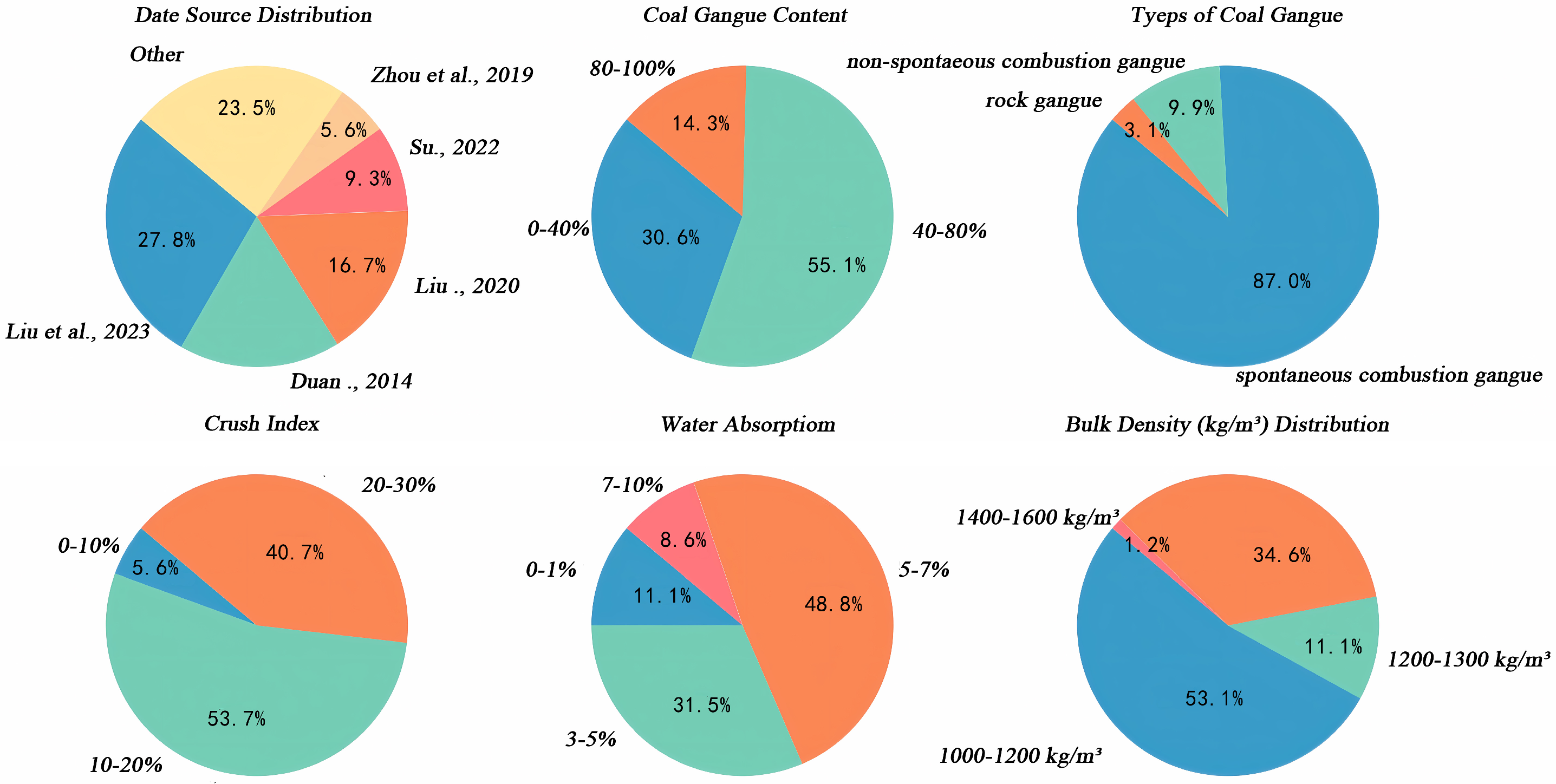
The present study, while based on a systematically curated dataset, remains constrained by the limited number and diversity of available samples. Future investigations should incorporate more extensive and heterogeneous datasets encompassing broader variations in material composition, curing regimes, and testing protocols. Such expansions would not only strengthen the statistical robustness of machine learning models but also enable a more rigorous identification of nonlinear feature interactions and latent coupling mechanisms that govern the mechanical behavior of coal gangue concrete.

(2)

Integration of inter-material coupling mechanisms into numerical simulations.

Although the current finite element modeling framework successfully captures the macroscopic response of CGC components, it inherently simplifies the material system by neglecting the meso-structural interactions among distinct phases, such as aggregates, cement paste, and interfacial transition zones. To enhance the physical fidelity of simulation outcomes, future work should aim to incorporate multi-phase constitutive relationships or cohesive interface models that account for inter-material bonding, slip, and damage evolution. This would facilitate a more comprehensive representation of the hybrid nature of CGC and improve the generalizability of the simulation results for complex structural scenarios.

(3)

Integration of advanced machine learning algorithms.

The accelerating convergence of artificial intelligence and materials science is ushering in a new era of modeling paradigms that transcend traditional input–output mappings. Future research may leverage architecture-aware frameworks—such as graph-based learning or physics-informed networks—to capture spatially distributed interactions, multiscale heterogeneity, and path-dependent responses under complex loading regimes. Such approaches hold promise for embedding structural priors and mechanistic constraints directly into learning processes, thereby enabling more robust and generalizable constitutive formulations for sustainable concrete systems.