The Magnitude of Stress in the Prop Depending on Its Manual Tightening

Abstract

Ensuring the stability of monolithic concrete slabs during construction represents a crucial safety challenge in monolithic reinforced concrete buildings. Theoretical models and structural analyses often assume ideal conditions of supporting props. However, significant deviations occur in practice due to variations in technical condition and installation methods. This study investigates the magnitude of prestressing forces generated in adjustable telescopic steel props depending on manual tightening and hammer blows. Experimental measurements were conducted on different types of props compliant with EN 1065, including both new and worn specimens, to simulate real on-site conditions. The influence of worker body weight was also analyzed. The results confirmed that the technical condition of the prop is the decisive factor affecting the level of prestress. Props in poor condition achieved substantially lower and inconsistent prestressing forces, while new props subjected to five hammer blows reached maximum values up to 13.16 kN. This difference can significantly influence static calculations for slab construction. Contrary to expectations, the influence of worker body weight was not statistically significant; instead, the dominant role was played by installation technique and the accuracy of hammer blows. The findings contribute to the optimization of safety guidelines and the improvement of calculation models for temporary support systems in monolithic construction.

1. Introduction

Research and studies have shown that many structural failures or even complete collapses originate from errors made during the construction phase of monolithic reinforced concrete structures, particularly related to the failure of formwork or inadequate structural stabilization during construction [1,2,3,4,5,6,7]. The causes of building collapse can be categorized into failures due to poor design and failures resulting from improper execution of the structure [7].

Today, there are numerous theories, calculations, analyses, experimental tests, and theoretical models on the topic of ensuring the stability of reinforced concrete slabs during construction. These enable a more specific and in-depth understanding of the subject. Initial research on this issue began as early as the 1950s [8] and continues to this day. Over time, theories and calculations have been modified and simplified to better align with values observed in practice [9,10,11]. Later research introduced complex mathematical models in 2D and 3D, attempting to capture various variables that influence the construction process [10,12,13,14,15,16].

Subsequent experimental research, using instrumentation to monitor buildings during construction, focused on analyzing the load distribution between props and ceiling slabs [15,17,18,19]. However, it is important to note that most studies have demonstrated the need for more experimental data and new field measurements to help identify additional factors affecting load transfer during construction [18].

So far, research and calculations have mostly focused on a single varying parameter, which is understandable given the wide range of possible variations—for example, slab dimensions, arrangement of props on one floor, arrangement of props on lower floors, and so on. Each of these variables affects load transfer and the stress acting on the props between the slabs. An additional variable also enters this system—stress induced by the installation of props.

Regarding the formwork removal process, the ceiling formwork may either be left in place simultaneously on several floors or it may be removed and the ceiling structure may be subsequently re-propped. When re-propping, several variations are possible. For example, the props can be placed in the same vertical positions across multiple floors. However, this may cause issues with the incorrect positioning of props, especially in the case of irregularly shaped slabs. Another option is to remove some props on the lower floors while keeping the remaining ones in place or relocating them to new positions, which, however, may not align with the axes of the props on the upper floor [20].

It is also necessary to consider the correct physical behavior of the props and reinforced concrete slabs [21]. According to a survey conducted in 2023 in Slovakia and neighboring countries, construction projects typically do not include detailed documentation specifying the exact positions of props, and decisions regarding their placement are often left to the construction crew. As a result, the placement of props is frequently random, particularly on smaller projects [22].

An additional and often overlooked factor in this complex topic is the stress in the props caused by their installation, specifically by the extension (fixation) of telescopic props between ceiling slabs. The extension is achieved by tightening a nut. Since it is not possible to install props with zero prestress—due to their technical condition, cleanliness, and the risk of loss of stability—workers must overcome resistance in the thread using force, typically delivered through hammer blows. However, due to the flexibility of the slab and high prestress in the props, this process may lead to the loosening of surrounding props during installation [20,21]. Field observations show that this usually involves 2 to 5 hammer strikes. This additional load on the prop is generally neglected in most calculations.

The aim of the experiment is to more precisely determine the prestress level in props within the structure across different types of props available on the Slovak market, to define the additional stress that should be considered in calculations, to verify the impact of the props’ technical condition on the degree of fixation, and to assess whether the worker’s weight influences the force of the hammer strike and, thus, the degree of fixation.

2. Experimental Measurements

All tested props complied with EN 1065 but included a combination of different classes (e.g., B, C, and D), which differ primarily in maximum load capacity, material thickness, and geometric parameters. This factor was managed as follows:

• For each prop, its type and class were recorded according to the manufacturer’s label or available technical documentation.
• Each “prop type” in the experiment represented a homogeneous group in which the EN 1065 class did not vary.
• Statistical analysis was performed separately for each prop type/class. Results from different classes were not directly compared to avoid the influence of differences in design and load capacity.

This approach minimized the effect of EN 1065 class differences on the results. The primary focus was on evaluating fixation behavior and achieving prestress under identical testing conditions, with class-specific parameters not serving as the main comparison criterion.

The aim of the experiment was to evaluate the mechanical properties and fixation of various types of construction props under controlled laboratory conditions. The primary focus was to examine the influence of the type of prop, its wear condition, and the weight of the worker on the stress induced during fixation. These data are essential for increasing the safety and efficiency of prop use on construction sites. Ten workers were selected for each prop type to achieve a balance between practical feasibility and statistical robustness. The number of participants allowed the study to capture inter-individual variability in technique, grip strength, and approach while avoiding excessive testing time or potential fatigue effects that could occur with larger groups. From a statistical perspective, ten measurements per prop type provided a sufficient sample size for correlation and regression analyses while keeping the experimental campaign within realistic time and cost constraints for construction site conditions.

Only props compliant with EN 1065 were used in the experiment. The European standard EN 1065 specifies materials, design requirements, and corrosion protection alternatives for adjustable telescopic steel props with covered or uncovered threads [23]. EN 1065 relates to telescopic steel props and defines requirements for their design, production, inspection, testing, and marking. It is a European standard used in the construction industry to ensure the safety and quality of steel props. The quality of props used on construction sites is verified by a certificate confirming that the properties of the props meet this standard. This standard sets the strictest global requirements for materials, structural specifications, and corrosion protection measures [24].

Materials must comply with existing European standards, and all components must be protected against corrosion. EN 1065 considers five protection methods, classified according to the manufacturing process. The applied method is marked on the prop label. The main parameter for props is their load-bearing capacity. According to the standard, the load-bearing capacity is defined as the minimum external load capable of initiating collapse mechanisms through tube bending failure [25]. The nominal thickness of any pipe (including tolerances) must not be less than 2.6 mm for props of classes B, C, D, and E. For class A props, it must be at least 2.3 mm. The inner and outer tubes must overlap by at least 300 mm when the prop is fully extended [23].

Measurements were conducted on a special steel structure (a testing table) with dimensions of 0.5 × 0.5 m, on which the prop was placed. Calibrated pressure-sensitive strain gauges were installed at its bottom (Figure 1). These sensors enabled precise recording of the stress induced during the fixation of the prop between the testing table and the ceiling slab. The experiment was carried out under laboratory conditions to ensure consistency of measurements and eliminate external interfering factors.

The props used in the experiment were sourced from the most commonly used manufacturers on the Slovak construction market. One used prop was randomly selected from each type. An exception was made for two types of props, for which new props were also tested. This selection was motivated by their widespread use on the Slovak market and allowed for a comparison of the effect of wear on the level of prestress induced during fixation.

Workers with different physical characteristics, experience levels, and weight categories participated in the experiment. This aspect was included to simulate real working conditions on construction sites where props are fixed by individuals with varying strength and technique. The data collected allow for the evaluation not only of the mechanical properties of the props but also of the impact of the human factor on fixation quality.

The fixation of props was carried out using three different methods:

• Manual tightening—simulating standard tightening without using tools;
• Fixation with three hammer blows—simulating quick prop fixation;
• Fixation with five hammer blows—simulating maximum prop fixation.

The choice of three and five hammer blows was based on common construction practice and pre-experimental field observations. Three blows are typically used on-site as a quick fixation method for temporary stability, whereas five blows are applied when a higher prestress is desired or when the prop is intended to remain in place for an extended period. These two fixation levels were selected to reflect realistic working habits while ensuring repeatability and comparability of results under controlled laboratory conditions.

Each method yielded different stress values, which were recorded and analyzed. Emphasis was placed on identifying the impact of physical wear on fixation strength and verifying whether the weight of the individual influences the force applied during prop fixation. The results of these measurements provide valuable insights for engineers, construction material suppliers, and contractors involved in the structural design of props, their implementation in construction processes, and the execution of monolithic structures.

3. Props

• Doka Eurex 20 top-300
  • Manufacturer: Doka (Amstetten, Austria)
  • Description: Adjustable steel prop with integrated overload protection, ensuring high stability and safety on the construction site [26].
• ULMA EP + D30 20-35/180-300
  • Manufacturer: ULMA Construction (Oñati, Spain)
  • Description: As specified in [27].
• SPANISH TYPE OF SUPPORT
  • Manufacturer: Unspecified (unbranded, purchased in Slovakia)
  • Description: Standard Spanish telescopic prop, commonly used in construction for ceiling structure support.
• ALIPIPROP ST B30-175/300
  • Manufacturer: Alpi (Nüziders, Austria)
  • Description: Lightweight aluminum prop with adjustable height, designed for easy handling and quick installation [28].
• PANALEX B35-200/350
  • Manufacturer: Panalex (Olang, Taliansko)
  • Description: Steel prop with high load capacity and adjustable height, ideal for various construction applications [29].
• MUBA Euro Baustützen der class B/D35-196/350
  • Manufacturer: MUBA (Müller & Baum GmbH & Co. KG, Sundern, Germany)
  • Description: Class B telescopic steel prop offering high load capacity and reliability for various construction projects [30].
• Scafom-rux EP20-300 D30
  • Manufacturer: Scafom-rux (Hagen, Germany)
  • Description: Adjustable steel prop with robust construction, designed for safe support of ceiling structures [31].
• CONCOR CEP 20/150-250
  • Manufacturer: Concor (Conza della Campania, Italy)
  • Description: Telescopic prop with a compact design, suitable for use in confined spaces [32].
• Peri Alpha-2 D300
  • Manufacturer: Peri (Weißenhorn, Germany)
  • Description: As specified in [33].

The listed props were selected due to their widespread use in construction practice. Two types of props will be tested in two conditions—new and used. The props will then be randomly labeled with numbers from 1 to 11 to ensure anonymity of the individual prop types.

4. Technical Condition of Props

The technical condition of props is one of the most important factors influencing their safety and efficiency on construction sites. Properly functioning props must ensure structural stability, even load distribution, and safe handling for workers. If props are in poor technical condition, they can pose a risk that may lead to premature failure, inconsistent force transmission, or even accidents on-site.

In this study, the “worn” condition of a prop was defined based on a combined visual and functional inspection conducted prior to testing, following common on-site acceptance criteria and EN 1065 requirements. The assessment included the following:

• Visible wear or contamination of threads (flattening, corrosion, deformation, dirt or paint residues);
• Surface corrosion covering more than 10% of load-bearing areas;
• Dents or bends exceeding 2 mm over a 300 mm length;
• Increased torque required for manual adjustment of the thread;
• Uneven or difficult nut movement during rotation;
• Deformations or irregularities on contact surfaces that could affect even force transfer.

Props exhibiting at least two of these indicators were classified as “worn.” This classification was applied consistently across all tested types to reflect realistic deterioration levels observed on construction sites. The evaluation was performed by two independent technicians with hands-on construction experience.

Among the tested samples, four props exhibited an unsuitable technical condition:

• Type no. 5;
• Type no. 6 (thread contamination visible in Figure 2);
• Type no. 7;
• Type no. 11.

These props had issues with mechanical functionality, which manifested in various ways:

• Jammed or difficult-to-move threads, preventing smooth extension and adjustment of the prop;
• Corrosion and wear on connection parts, reducing fixation strength and potentially lowering load capacity;
• Deformations in the telescopic section of the prop, causing instability under load.

In contrast, the remaining tested props did not show any technical deficiencies. Their mechanisms functioned without complications, threads were smooth and continuous, and extension and locking were carried out without excessive resistance. This indicates that these props were in good condition and provided consistent results during experimental testing.

The results highlight the importance of regular inspection and maintenance of props in construction practice. Props showing signs of wear or mechanical damage should be promptly repaired or taken out of service to prevent safety risks and structural failures. Regular maintenance can extend the service life of props and ensure their reliable performance throughout their usage period. In Figure 2, you can see a prop with a heavily contaminated thread.

5. Measurement Results

The experimental measurements aimed to determine the point load from the props depending on the fixation force, for each examined prop type and for different fixation methods performed by various workers.

The individual props were labeled with numbers using a random selection.

5.1. Type No. 1

Table 1. Measured data from prop type no. 1.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 1	14	1	112.5	1.02		1.83		2.37
		2	117.5	1.22		2.18		2.34
		3	102	0.93		1.39		1.79
		4	120	0.54		0.81		2.65
		5	108	0.98		1.42		2.56
		6	79	0.66		1.39		1.34
		7	83	0.71		1.32		2.01
		8	70.5	1.22		2.35		3.27
		9	82	1.77		2.32		3.60
		10	91.5	0.97	1.00	1.73	1.67	2.51	2.44

presents the results of prestress for three methods of fixation of prop no. 1—manual tightening, fixation with three hammer blows, and fixation with five hammer blows—for ten workers.

With manual tightening, the prestress values were lower, mostly ranging between 0.5 and 1.8 kN, with the highest value recorded by worker 9 (1.77 kN) and the lowest by worker 4 (0.54 kN). Fixation with three hammer blows increased the prestress for all workers, with the highest values reached by workers 2 and 8 (around 2.3 kN). Fixation with five hammer blows resulted in a further significant increase, with the highest prestress recorded by worker 9 (3.60 kN) and worker 8 (3.27 kN).

5.2. Type No. 2

Table 2. Measured data from prop type no. 2.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 2	14	1	112.5	1.49		2.84		4.04
		2	117.5	1.23		2.45		3.94
		3	102	0.82		2.22		2.40
		4	120	1.27		2.62		3.24
		5	108	1.45		2.13		3.05
		6	79	1.16		1.97		5.26
		7	83	1.65		3.88		6.06
		8	70.5	1.27		2.78		5.63
		9	82	1.41		2.93		5.88
		10	91.5	1.09	1.28	2.40	2.62	4.15	4.36

shows the prestress results for prop no. 2 under manual tightening, fixation with three hammer blows, and fixation with five hammer blows for ten workers.

The values for manual tightening ranged from 0.8 to 1.65 kN, with the highest value recorded by worker 7. Fixation with three hammer blows increased the prestress to values between 1.97 and 3.88 kN, again with the highest result from worker 7. After five hammer blows, the prestress increased even further, with workers 7, 8, and 9 reaching values above 5.5 kN.

5.3. Type No. 3

Table 3. Measured data from prop type no. 3.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 3 (New)	14	1	112.5	1.29		4.82		8.48
		2	117.5	1.22		4.60		5.88
		3	102	3.75		3.87		4.53
		4	120	2.21		4.40		6.41
		5	108	2.37		4.91		6.39
		6	79	1.18		6.81		11.22
		7	83	1.32		6.87		10.63
		8	70.5	2.40		5.91		9.81
		9	82	1.94		4.79		7.60
		10	91.5	2.00	1.97	5.29	5.23	6.33	7.73

shows the prestress results for prop no. 3 under manual tightening, fixation with three hammer blows, and fixation with five hammer blows for ten workers.

With manual tightening, the prestress ranged from 1.18 to 3.75 kN, with the highest value recorded by worker 3. Fixation with three hammer blows significantly increased the prestress, reaching levels between 3.87 and 6.87 kN, with the highest value from worker 7. After five hammer blows, the prestress increased even further, with several workers (especially workers 6, 7, and 8) reaching values above 9 kN, and a maximum of 11.22 kN recorded by worker 6.

5.4. Type No. 4

Table 4. Measured data from prop type no. 4.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 4	14	1	112.5	2.49		5.48		11.08
		2	117.5	2.49		4.45		13.16
		3	102	4.44		5.07		6.88
		4	120	3.03		5.69		9.00
		5	108	3.16		5.59		9.68
		6	79	1.01		5.53		9.27
		7	83	0.91		5.17		9.91
		8	70.5	2.92		6.93		11.95
		9	82	3.19		7.35		11.16
		10	91.5	1.95	2.56	6.65	5.79	11.75	10.38

shows that the values under manual tightening ranged from 0.91 to 4.44 kN, with the highest prestress recorded by worker 3. Fixation with three hammer blows improved the prestress to values ranging from 4.45 to 7.35 kN, with the highest value recorded by worker 9. With fixation using five hammer blows, all workers achieved very high prestress levels, ranging from 6.88 to 13.16 kN.

5.5. Type No. 5

Table 5. Measured data from prop type no. 5.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 5	17	1	112.5	2.43		2.36		7.15
		2	117.5	2.55		3.08		6.74
		3	102	3.50		3.10		7.43
		4	120	2.95		3.14		7.65
		5	108	2.83		2.93		6.95
		6	79	1.11		4.39		8.17
		7	83	2.93		5.57		8.10
		8	70.5	1.86		3.27		7.96
		9	82	2.26		2.92		7.24
		10	91.5	2.28	2.47	2.95	3.37	6.76	7.42

illustrates the prestress results for prop no. 5 under manual tightening, fixation with three hammer blows, and fixation with five hammer blows, performed by ten workers. The values for manual tightening ranged from 1.11 to 3.50 kN, with the highest prestress achieved by worker 3. Fixation with three hammer blows led to an increase in prestress, reaching values between 2.36 and 5.57 kN, with the highest value recorded by worker 7. When using five hammer blows, the prestress increased further, reaching values from 6.74 to 8.17 kN

5.6. Type No. 6

Table 6. Measured data from prop type no. 6.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 6	14.5	1	112.5	N		0.95		1.08
		2	117.5	N		0.54		1.29
		3	102	N		0.53		1.23
		4	120	N		0.87		1.29
		5	108	N		0.57		0.97
		6	79	N		0.74		2.76
		7	83	N		0.87		5.17
		8	70.5	N		0.82		1.94
		9	82	N		0.65		2.18
		10	91.5	N	N	0.75	0.73	1.94	1.99

presents the prestress results for prop no. 6 under fixation with three and five hammer blows as manual tightening could not be performed due to the technical condition of the prop. The values for fixation with three hammer blows ranged from 0.53 to 0.95 kN, with the highest prestress achieved by worker 1. Fixation with five hammer blows increased the prestress to values ranging from 0.97 to 5.17 kN.

5.7. Type No. 7

Table 7. Measured data from prop type no. 7.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 7	19	1	112.5	1.50		2.71		3.91
		2	117.5	0.27		1.58		2.60
		3	102	0.72		0.93		2.03
		4	120	0.64		1.09		2.81
		5	108	1.00		1.41		2.35
		6	79	1.06		2.79		5.28
		7	83	1.07		2.29		5.45
		8	70.5	0.53		1.21		4.25
		9	82	0.95		0.98		3.71
		10	91.5	0.99	0.87	1.94	1.69	4.89	3.73

illustrates the prestress results for prop no. 7 under manual tightening, fixation with three hammer blows, and fixation with five hammer blows, as performed by ten workers. The values for manual tightening ranged from 0.27 to 1.50 kN, with the highest prestress achieved by worker 1. Fixation with three hammer blows increased the prestress to values from 0.93 to 2.79 kN, with the highest value recorded by worker 6. Fixation with five hammer blows resulted in a further significant increase in prestress, reaching values from 2.03 to 5.45 kN.

5.8. Type No. 8

Table 8. Measured data from prop type no. 8.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 8	15	1	112.5	1.66		2.41		3.78
		2	117.5	0.91		1.65		4.31
		3	102	1.01		1.59		5.38
		4	120	1.09		1.97		4.12
		5	108	0.87		1.94		5.76
		6	79	0.27		3.22		6.44
		7	83	0.64		3.49		7.70
		8	70.5	1.37		2.97		5.21
		9	82	1.33		2.82		4.80
		10	91.5	0.98	1.01	1.94	2.40	4.92	5.24

shows that the values for manual tightening ranged from 0.27 to 1.66 kN, with the highest value achieved by worker 1. Fixation with three hammer blows increased the prestress to values from 1.59 to 3.49 kN. Fixation with five hammer blows led to a further significant increase, with prestress reaching values from 3.71 to 7.70 kN.

5.9. Type No. 9

Table 9. Measured data from prop type no. 9.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 9	13	1	112.5	1.82		1.43		5.43
		2	117.5	2.06		1.06		5.99
		3	102	4.14		4.48		4.67
		4	120	2.83		4.80		5.23
		5	108	3.04		4.94		5.86
		6	79	2.12		4.05		7.02
		7	83	4.91		6.42		8.57
		8	70.5	4.04		5.97		7.73
		9	82	2.71		3.72		4.58
		10	91.5	3.16	3.08	4.43	4.13	5.44	6.05

shows that the values for manual tightening ranged from 1.82 to 4.91 kN, with the highest prestress achieved by worker 7. Fixation with three hammer blows increased the prestress to values from 1.06 to 6.42 kN. Fixation with five hammer blows resulted in a significant increase in prestress, with values ranging from 4.58 to 8.57 kN.

5.10. Type No. 10

The values for manual tightening in

Table 10. Measured data from prop type no. 10.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 10	19	1	112.5	1.25		2.59		4.38
		2	117.5	1.26		1.99		3.93
		3	102	2.15		2.34		3.55
		4	120	0.76		2.94		4.90
		5	108	0.98		2.83		3.69
		6	79	0.45		4.41		7.50
		7	83	1.09		3.32		8.40
		8	70.5	0.26		1.95		4.25
		9	82	1.09		3.09		5.65
		10	91.5	1.86	1.12	2.53	2.80	4.94	5.12

ranged from 0.26 to 2.15 kN, with the highest value achieved by worker 3. Fixation with three hammer blows increased the prestress to values from 1.95 to 4.41 kN, with the highest prestress recorded by worker 6. After five hammer blows, the prestress further increased to values between 3.55 and 8.40 kN.

5.11. Type No. 11

The values for manual tightening in

Table 11. Measured data from prop type no. 11.

Type of Props	Support Weight [kg]	Workers	Worker Weight [kg]	Manual Tightening [kN]	Diameter—Hand Tightening [kN]	Fix—3× Hammer Blow [kN]	Diameter—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]	Diameter—5× Hammer Blow [kN]
Type No. 11	8.5	1	112.5	0.26		1.07		1.95
		2	117.5	0.36		0.51		1.35
		3	102	1.47		1.55		1.78
		4	120	0.43		1.06		1.96
		5	108	1.00		1.97		2.28
		6	79	1.89		3.13		5.70
		7	83	1.58		4.40		6.35
		8	70.5	0.31		0.77		3.70
		9	82	0.85		1.02		2.96
		10	91.5	0.75	0.89	1.27	1.68	4.30	3.23

ranged from 0.26 to 1.89 kN, with the highest prestress achieved by worker 6. Fixation with three hammer blows increased the prestress to values from 0.51 to 4.40 kN, with the highest value again achieved by worker 7. After five hammer blows, the prestress increased significantly to values from 1.35 to 6.35 kN.

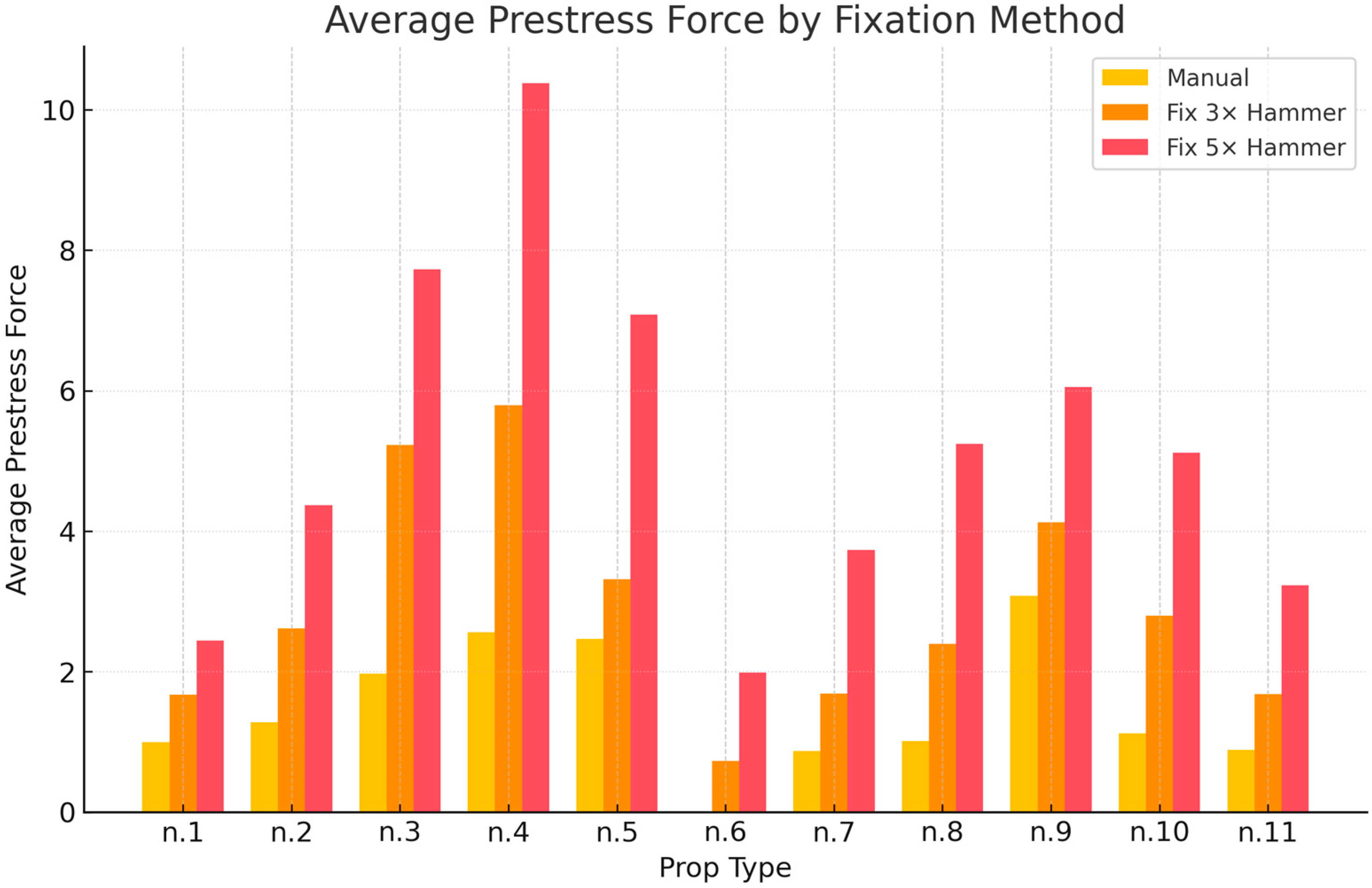
Based on all measured data for each type of prop, the average prestress force was calculated separately for manual tightening, fixation with three hammer blows, and fixation with five hammer blows. All measurements were included in the analysis, except in cases where it was not possible to obtain a value (e.g., for manual tightening of prop type no. 6 due to its technical condition), which were excluded from the average calculation.

The results shown in

Table 12. Average prestress forces for each prop type by fixation method.

Prop	Manual_avg [kN]	Fix3_avg [kN]	Fix5_avg [kN]
no. 1	1.00	1.67	2.44
no. 2	1.28	2.62	4.37
no. 3	1.97	5.23	7.73
no. 4	2.56	5.79	10.38
no. 5	2.47	3.32	7.08
no. 6	N	0.73	1.99
no. 7	0.87	1.69	3.73
no. 8	1.01	2.40	5.24
no. 9	3.08	4.13	6.05
no. 10	1.12	2.80	5.12
no. 11	0.89	1.68	3.23

indicate significant differences between the individual fixation methods. The average prestress values for manual tightening ranged from 0.87 kN (no. 7) to 3.08 kN (no. 9), excluding prop no. 6 where measurement was not possible. For fixation with three hammer blows, averages ranged from 0.72 kN (no. 6) to 5.79 kN (no. 4), while five hammer blows produced the highest prestress values—from 1.99 kN (no. 6) to 10.38 kN (no. 4).

These results are graphically illustrated in Figure 3, which clearly shows the increase in prestress force with the number of hammer blows across all prop types.

6. Influence of Worker Weight on Fixation Force

To determine the influence of worker weight on the fixation force of the props, we used the method of regression analysis. The analysis procedure was as follows:

• Data collection—values for worker weight and the measured fixation forces (five hammer blows) for each prop were extracted from the experimental measurement tables.
• Pearson correlation—for each prop, the correlation coefficient (r) and the p-value were calculated in order to determine whether there was a statistically significant relationship between worker weight and prop fixation.
• Linear regression analysis—for each prop, a regression equation was established in the following form:

where is the fixation force (five hammer blows), is the worker’s weight, is the slope of the regression line, and is the intercept.

• Calculation of the coefficient of determination—this coefficient expresses what percentage of the variability in prop fixation can be explained by worker weight.
• Evaluation of results—comparison of correlation coefficients and p-values is performed for all props to identify relationships and their statistical significance.

Results of Regression Analysis

The aim of the regression analysis was to determine the effect of a worker’s body weight on the achieved pre-tension of supports. Three fixation methods were evaluated: manual tightening, fixation with three hammer blows, and fixation with five hammer blows. The data were analyzed separately for each type of support (no. 1–no. 11) to identify possible differences related to technical condition or thread type.

The statistical analysis was based on two indicators: Pearson’s correlation coefficient (r) and the coefficient of determination (R²) obtained from simple linear regression. Pearson’s r was calculated using the standard formula:

$$r={\displaystyle \frac{\sum _{i=1}^n(x_i-x)(y_i-\stackrel{-}{\mathrm{y}})}{\sqrt{{\sum }_{i=1}^n{(x_i-x)}^2}\ast \sqrt{{\sum }_{i=1}^n{(y-\stackrel{-}{\mathrm{y}})}^2}}}$$

(1)

where

• $x_i$—body weight of the iii-th worker;
• $y_i$—measured pre-tension value;
• $x$—mean body weight;
• $\stackrel{-}{\mathrm{y}}$—mean pre-tension value.

To determine the proportion of pre-tension variability that can be explained by the worker’s body weight, a simple linear regression model was used:

y_i = β₀ + β_{1x_1} + ϵ_i

(2)

where

• ${\beta }_0$—intercept;
• ${\beta }_{1x_1}$i—slope of the regression line (change in pre-tension per unit change in body weight);
• ${ϵ}_i$—residual error.

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-ŷ)}^2}{{\sum }_{i=i}^n{(y_i-\stackrel{-}{\mathrm{y}})}^2}}$$

(3)

In the case of a single predictor, $R^2$ is equal to the square of the correlation coefficient:

$$R^2=r^2$$

(4)

Missing values (e.g., in cases where manual tightening could not be measured due to excessive wear of the support) were excluded from the analysis. Statistical significance was evaluated at the p < 0.05 level.

The results showed substantial variability among the individual supports. In some cases, the correlation between worker body weight and pre-tension was very weak (e.g., type no. 1: r = 0.13, $R^2=0.018$ with five hammer blows), indicating virtually no relationship. Conversely, some supports exhibited moderate to strong correlations, particularly negative ones, suggesting that higher worker body weight was associated with lower final pre-tension (e.g., type no. 10: r = 0.75, $R^2=0.57$ with five hammer blows). Positive correlations occurred more frequently with manual tightening—for instance, in support no. 9 (r = 0.88, $R^2=0.77$)—indicating that in these cases, worker body weight had a direct positive effect.

In general, manual tightening showed weaker correlations (often $R^2$ < 0.2), whereas three and five hammer blows produced more varied results, including several cases with $R^2$ > 0.4, particularly for supports in poorer technical condition. These results suggest that the relationship between worker body weight and pre-tension is not consistent and is significantly influenced by the technical condition of the support, thread cleanliness, and the chosen fixation method.

In conclusion, worker body weight may, in some cases, have a measurable effect, but it is not a reliable predictor for all types of supports and fixation methods. The findings highlight the need to focus more on regular inspection, maintenance, and cleaning of threads, as well as training in proper fixation technique, rather than relying on worker body weight as the primary factor for achieving sufficient pre-tension.

Table 13. Correlation coefficients (r) and coefficients of determination ($R^2$) between worker body weight and achieved pre-tension for different fixation methods and support types.

Prop	Manual_r	$\mathbf{Manual}\_{\mathit{R}}^2$	Fix3_r	$\mathbf{Fix}3\_{\mathit{R}}^2$	Fix5_r	$\mathbf{Fix}5\_{\mathit{R}}^2$
no. 1	0.239	0.057	0.193	0.037	0.134	0.018
no. 2	0.292	0.085	0.185	0.034	−0.257	0.066
no. 3	0.347	0.12	−0.079	0.006	0.203	0.041
no. 4	−0.158	0.025	−0.303	0.092	0.108	0.012
no. 5	−0.006	0	−0.084	0.007	−0.130	0.017
no. 6	N	N	−0.684	0.468	−0.659	0.434
no. 7	−0.194	0.038	−0.547	0.299	−0.676	0.457
no. 8	−0.110	0.012	−0.206	0.042	−0.268	0.072
no. 9	0.880	0.774	−0.671	0.450	−0.522	0.273
no. 10	0.418	0.175	−0.618	0.382	−0.755	0.57
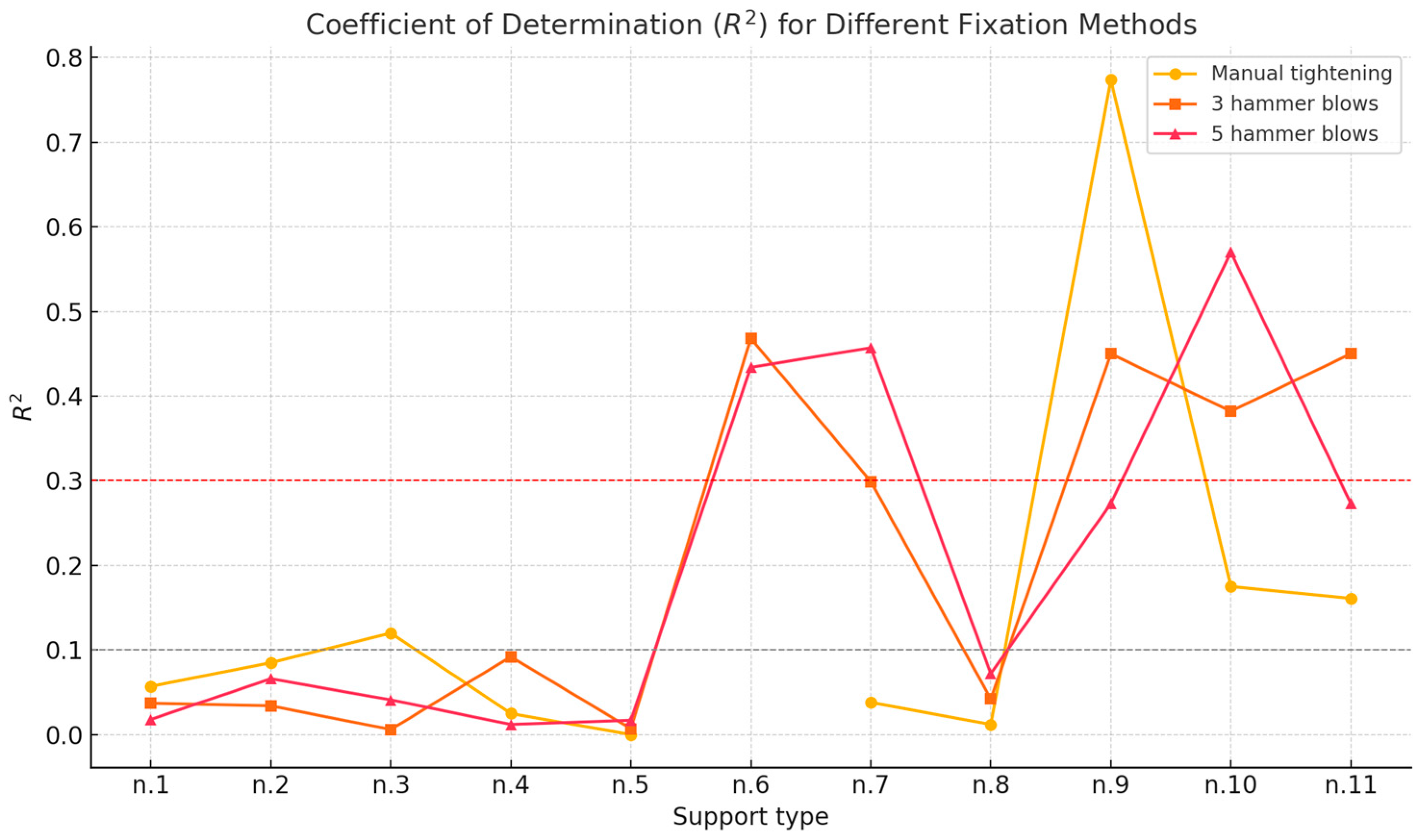
no. 11	0.401	0.161	−0.671	0.450	−0.522	0.273

presents Pearson’s correlation coefficient (r) and coefficient of determination ($R^2$) between worker body weight and support pre-tension for three fixation methods: manual tightening, three hammer blows, and five hammer blows.

The table summarizes the results of linear regression analyses conducted separately for each support type. The correlation coefficient (r) indicates both the direction and the strength of the linear relationship: positive values suggest that higher worker body weight is associated with higher pre-tension, whereas negative values indicate the opposite trend. The coefficient of determination ($R^2$) represents the proportion of pre-tension variability explained solely by worker body weight.

Overall, $R^2$ values were generally low (below 0.1), indicating very weak or negligible predictive power. Notable exceptions were observed for certain supports (e.g., no. 9 with manual tightening, and no. 6, no. 7, and no. 8 with three or five hammer blows), where $R^2$ exceeded 0.3, potentially reflecting the influence of the support’s technical condition or other unobserved factors.

For support no. 6, manual tightening values could not be measured due to excessive wear; these cells are marked as “N” and left blank in the table.

As shown in Figure 4, the coefficient of determination ($R^2$) between worker body weight and support pre-tension varies considerably across fixation methods and support types. Most supports exhibit low $R^2$ values (below 0.1), indicating negligible predictive power of body weight. In contrast, several supports—particularly no. 6, no. 7, no. 9, and no. 10—show higher $R^2$ values (above 0.3) for the three- and five-hammer-blow methods. This pattern suggests that factors such as the technical condition of the support, thread cleanliness, or other unmeasured variables may have a more significant influence on the achieved pre-tension than worker body weight alone.

7. Influence of the Technical Condition of the Prop on Fixation Force

The technical condition of props represents a key factor influencing the quality and safety of their installation during the construction of monolithic reinforced concrete structures. During construction, props are used repeatedly, which leads to wear of mechanical parts, especially thread systems, telescopic segments, and locking mechanisms. These defects can significantly affect the prop’s ability to provide sufficient prestressing between ceiling slabs during installation.

In practice, when implementing temporary support for monolithic slabs, it is common to encounter a heterogeneous arrangement of props—that is, the use of props from different manufacturers, of various types, and most importantly, in different technical conditions. This phenomenon may result from a lack of technical resources on-site or from an effort to reduce costs by reusing older props. Although individual props may appear functional at first glance, differences in their actual fixation capacity can significantly influence the final force distribution within the support system.

In the experiment, four props in visibly deteriorated technical condition were compared with a new prop of type no. 3, which can be seen in

Table 14. Comparison of the average measured values of props in poor technical condition with props in good condition.

Type of Props	Manual Tightening [kN]	Fix—3× Hammer Blow [kN]	Fix—5× Hammer Blow [kN]
Type no. 5	2.47	3.37	7.42
Type no. 6	N	0.73	1.99
Type no. 7	0.87	1.69	3.73
Type no. 11	0.89	1.68	3.23
Type no. 3 (new)	1.97	5.23	7.73

. The evaluation focused primarily on the prestressing achieved during installation using three and five hammer blows, which simulate common on-site working procedures. The results demonstrated dramatic differences. While the new Doka prop already reached a prestress value of 5.23 kN with three hammer blows and up to 7.73 kN with five blows, the worn props, for example, type no. 6, did not even reach 1 kN with three blows and only 1.99 kN with five blows. Similarly, poor results were observed for type no. 7 and type no. 11, where values ranged between 1.68 and 3.73 kN, which is significantly lower than for the new prop.

The most serious finding was that, for some props in poor technical condition, it was not possible to perform effective fixation using manual tightening at all (type no. 6). The threads were so contaminated that it was physically impossible to fix the prop between the ceiling slabs. This directly indicates a failure of the prop’s function as a load-bearing system already in the initial stage of installation. These differences are critical, especially in cases where calculation models and FEM simulations assume ideal conditions without taking into account the technical condition of the props.

For this reason, it is necessary either to significantly improve the quality control of props before use on-site or to introduce correction coefficients that reflect the actual technical condition of specific prop types. Props with technical defects transmit installation prestressing much less effectively, which can lead to uneven force distribution in the structure, greater deformations, and potential risk of local failure.

From the comparison, it is clear that the new prop (in this case, type no. 3) showed a high level of reliability, consistent prestress values, and full functionality of the threaded mechanism. In contrast, props with damaged or poorly maintained fixation mechanisms should be subject to regular inspection or excluded from use.

8. Discussion

The results of the experiment showed that the technical condition of the props has a significant influence on the resulting fixation force. In general, used props exhibited higher fixation values, suggesting that their threads were smoothed and allowed easier handling. On the other hand, props in deteriorated technical condition had inconsistent results, and in some cases, manual fixation was not possible at all. Corrosion, thread wear, and mechanical deformations can significantly affect the achievable prestress in the prop, thereby increasing the risk of failure.

A comparison of new and used props showed that new props provided uniform and predictable results, although they did not always reach the highest prestress values. Used props, when in good technical condition, were fixed more effectively, suggesting that slight wear can actually be beneficial for their functionality. The most noticeable differences between new and used props were observed for type no. 3 and type no. 4, where the used version achieved significantly higher fixation values.

The highest measured stress in the experiment reached 13.16 kN. High forces generated in the prop can pose risks when transferring load to the ceiling slabs. If the slab is weak or incorrectly designed, local overloading at the contact point with the prop can occur, potentially leading to deformation or damage. This is particularly risky in structures with thinner slabs, balconies, precast slabs, or areas with high load concentrations.

Regression analysis demonstrated that worker weight does not have a significant influence on the quality of prop fixation. The results showed that only a small percentage of variability in fixation can be explained by worker weight, with the main factors affecting fixation being the technical condition of the prop, thread type, and installation method. This suggests that during the selection and inspection of props, emphasis should be placed not on worker weight but rather on the technical condition of the prop and the correct fixation technique.

Based on the obtained results, it is recommended to carry out regular maintenance of props to ensure consistent fixation and reduce the risk of mechanical failure. Used props should be regularly inspected for potential damage and deformation. In addition, the analysis showed that the number of hammer blows has a greater influence on fixation than manual tightening, which highlights the importance of correct installation procedures.

The overall evaluation of the experiment indicates that prop fixation depends primarily on their technical condition and installation method. By using the correct fixation technique, it is possible to improve structural stability even when working with less experienced workers. The necessity of prop inspection before use is shown to be a key safety factor on construction sites. This research provides a basis for further experimental studies that could focus on dynamic loading of props, the influence of different thread types, and the optimization of installation techniques.

9. Conclusions

The results of the experiment clearly demonstrated that the technical condition of props is a key factor influencing fixation quality and overall structural safety during construction. Props in good technical condition, whether new or slightly used, showed consistent and reliable prestress values. In contrast, props in deteriorated condition achieved significantly lower and more variable fixation values, and in some cases, manual tightening could not be performed at all.

The influence of worker weight proved to be statistically insignificant. The effectiveness of fixation depended primarily on the technical condition of the prop, the thread type, and the installation technique used. Props with damaged or corroded threads transmitted loads less effectively, increasing the risk of uneven force distribution, deformations, and local structural failures.

The findings emphasize the need for regular inspection and maintenance of props before use. It was also shown that the fixation method, particularly the number of hammer blows, has a greater influence than manual tightening alone, highlighting the importance of correct on-site installation procedures.

This research provides a foundation for further experimental studies focused on dynamic loading of props, optimization of thread systems, and the development of practical recommendations for quality control and the safe use of temporary support systems in the construction of monolithic reinforced concrete structures.