Design and Numerical Analysis of a Combined Pile–Raft Foundation for a High-Rise in a Sensitive Urban Environment
Abstract
1. Introduction
2. Materials and Methods
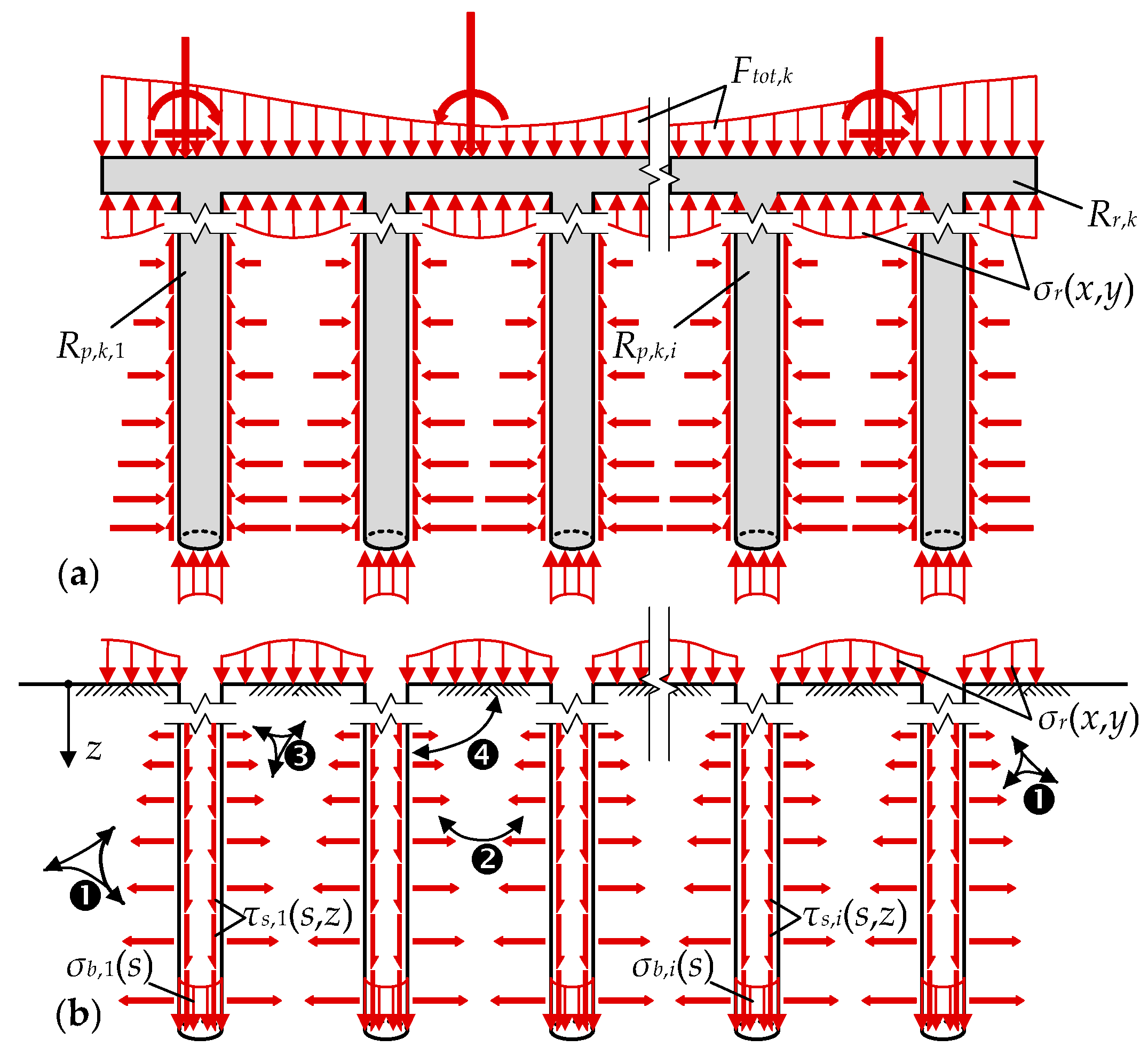
2.1. Design Principles and Load–Deformation Behavior
2.2. Design and Safety Concept
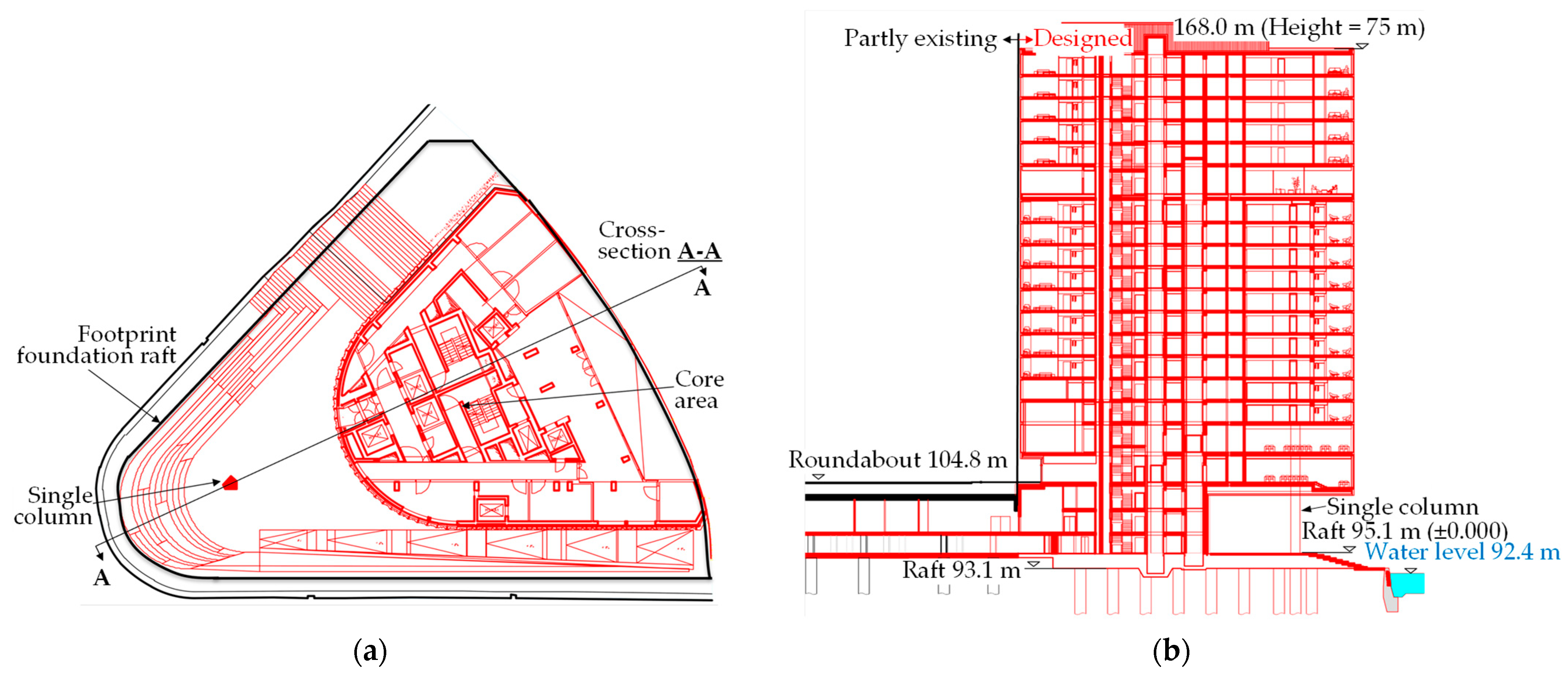
2.3. Description of the Project
3. Numerical Modeling
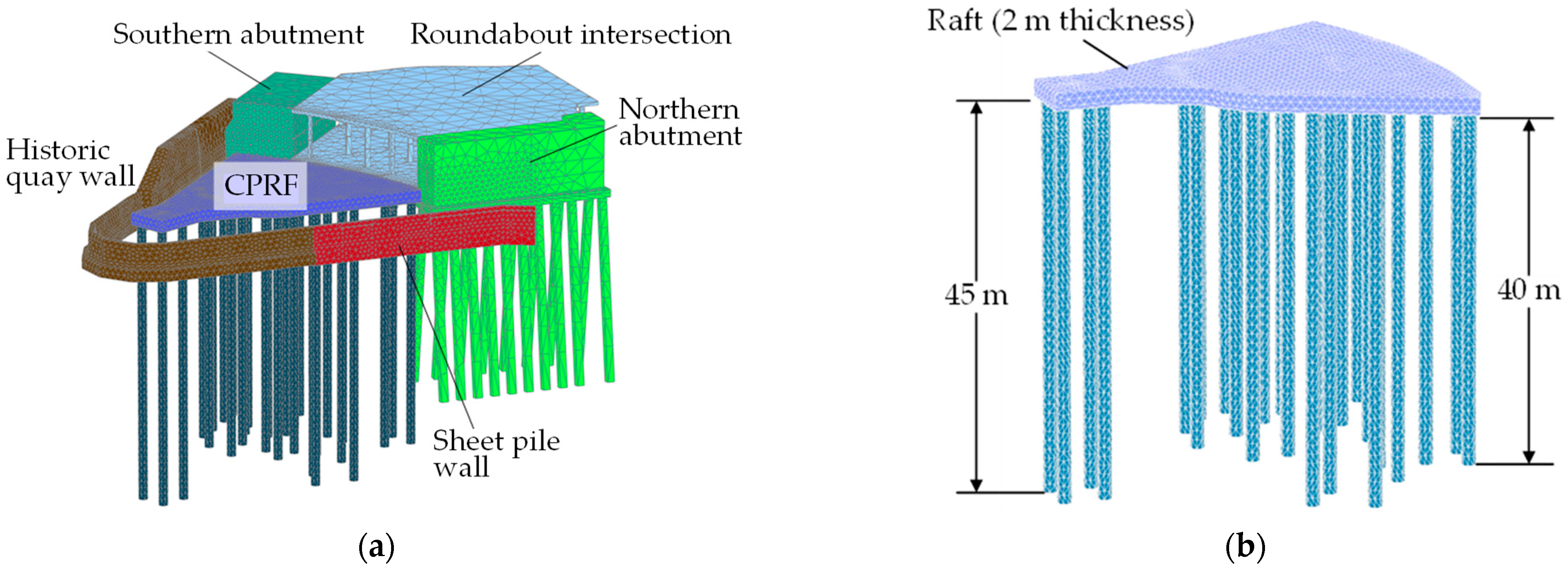
3.1. Numerical Model Setup and Material Properties
- Mohr–Coulomb (MC) for the artificial fill;
- Hardening soil (HS) for natural layers, including quaternary alluvial deposits and tertiary marl.
3.2. Simulation Strategy and Parameter Extraction
- Pile spring stiffness extracted from the load–settlement response at pile heads;
- Subgrade reaction modulus, derived from the stress–settlement behavior beneath the raft.
4. Results and Discussion
4.1. Load Sharing and Foundation Performance
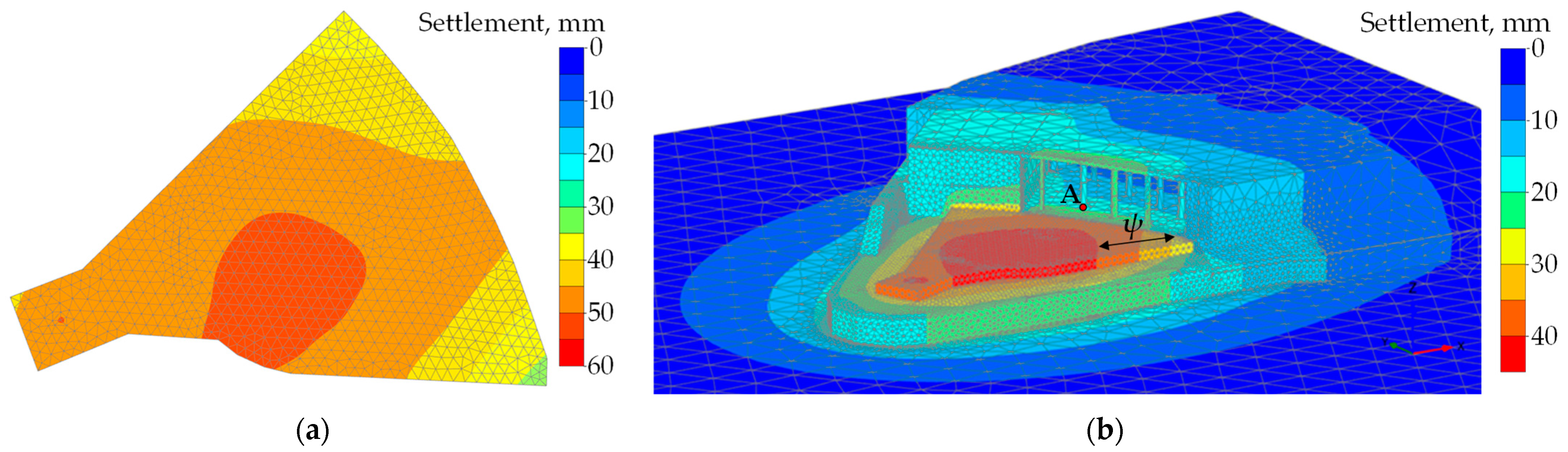
4.2. Settlement Predictions and Structural Implications
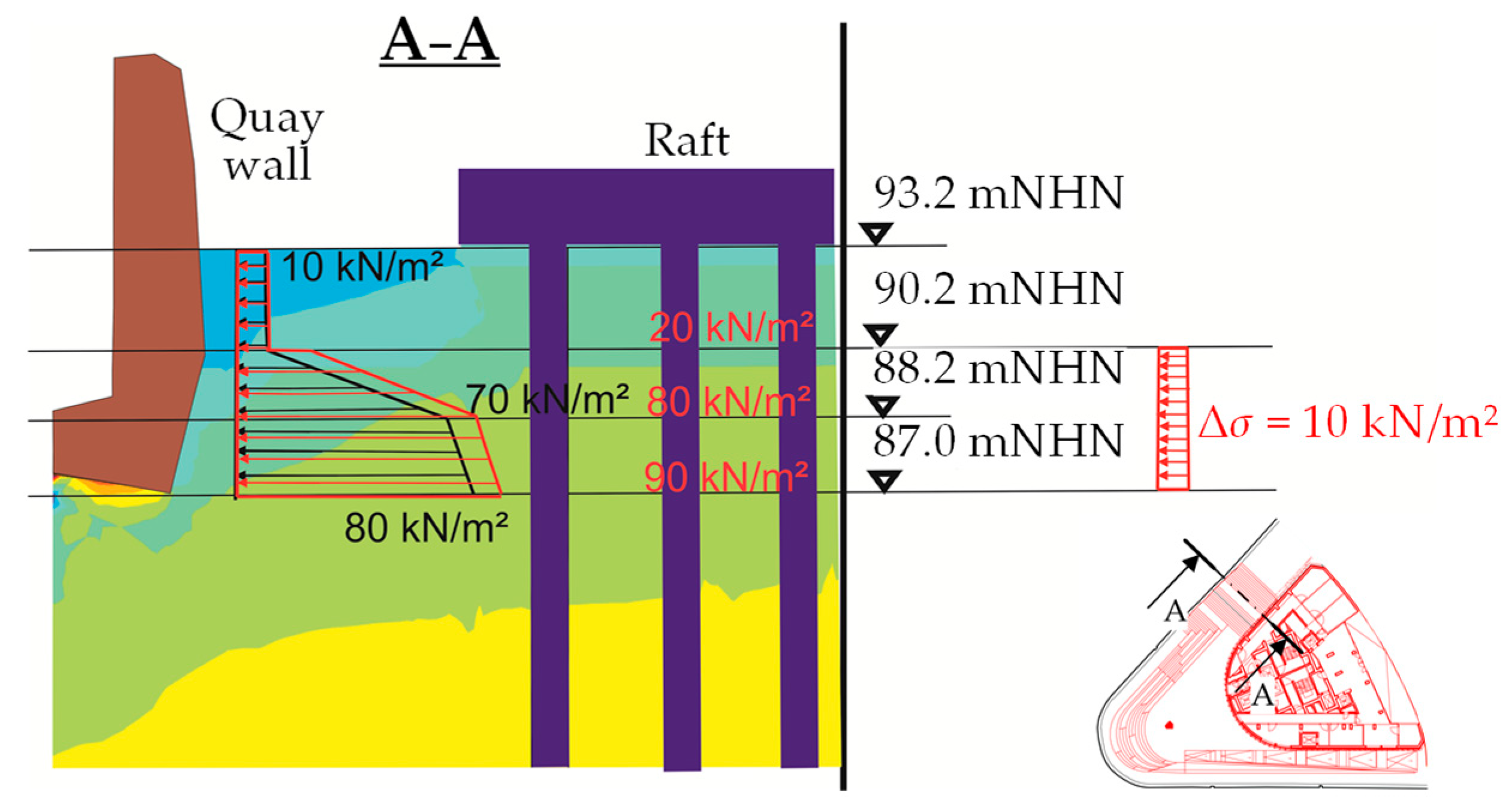
4.3. Impact on the Historic Quay Wall
- The additional lateral stresses on the quay wall, induced by the building loads in cross-section A−A shown in Figure 8. The extra stresses begin at a depth of 3 m below the raft and are approximately 10 kN/m2. Although they are not significant, the impact of these additional stresses on the stability of the quay wall must be considered.
4.4. Broader Implications, Innovation, and Research Outlook
- Probabilistic modeling can address uncertainties in soil properties and construction sequences, improving the robustness of CPRF design under variable conditions [22].
- Field validation through instrumentation and long-term monitoring will provide empirical evidence for numerical predictions and improve the modeling approach.
5. Concluding Remarks
- It applies a fully staged construction simulation to a multi-structure urban context, capturing the sequential development of interacting elements.
- It integrates heritage preservation criteria (e.g., angular rotation limits) into the numerical modeling framework, which is rarely addressed in CPRF studies.
- It provides a stiffness extraction methodology for use in structural modeling, enhancing compatibility between geotechnical and structural design domains.
- Parametric studies to evaluate the influence of pile configuration, raft thickness, and soil variability on load-sharing behavior and settlement control.
- Integration of digital twin technologies for real-time geotechnical monitoring and adaptive foundation design, particularly in heritage-sensitive zones.
- Probabilistic modeling to quantify the impact of soil variability and construction uncertainties on CPRF performance.
- Experimental validation through field instrumentation and long-term monitoring of the constructed foundation system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Poulos, H.G. Foundation Design for Tall Buildings. In Proceedings of the Geotechnical Engineering State of the Art and Practice: Keynote Lectures from GeoCongress, Oakland, CA, USA, 25–29 March 2012; pp. 786–809. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhu, S.; Que, X.; Ge, X. Deformation effects of deep foundation pit excavation on retaining structures and adjacent subway stations. Buildings 2024, 14, 2521. [Google Scholar] [CrossRef]
- Norkus, A.; Martinkus, V.; Mandolini, A.; Gribniak, V. Experimental study of ground resistance of short displacement piles and pile groups in artificial deposition of natural sand. Eur. J. Environ. Civ. Eng. 2025, 1–24. [Google Scholar] [CrossRef]
- Tian, J.; Xia, Y.; Zhang, J.; Liu, H.; Zhang, M.; Gao, Y.; Liu, J.; Han, B.; Huang, S. Urban underground space geological suitability—A theoretical framework, index system, and evaluation method. Appl. Sci. 2025, 15, 4326. [Google Scholar] [CrossRef]
- Franke, E.; Lutz, B.; El-Mossallamy, Y. Measurements and numerical modelling of high-rise building foundations on Frankfurt Clay. Vert. Horiz. Deform. Found. Embankments ASCE Geotech. Spec. Publ. 1994, 40, 1325–1336. [Google Scholar]
- Katzenbach, R.; Leppla, S.; Seip, M. Das Verformungsverhalten des Frankfurter Tons infolge Baugrundentlastung. Bauingenieur 2011, 86, 233–240. (In German) [Google Scholar]
- Katzenbach, R.; Leppla, S. Deformation behavior of clay due to unloading and the consequences on construction projects in inner cities. In Proceedings of the 18th Conference of the International Society for Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; Volume 3, pp. 2023–2026. [Google Scholar]
- Abdel-Azim, O.A.; Abdel-Rahman, K.; El-Mossallamy, Y.M. Numerical investigation of optimized piled raft foundation for high-rise building in Germany. Innov. Infrastruct. Solut. 2020, 5, 11. [Google Scholar] [CrossRef]
- Davis, E.H.; Poulos, H.G. The analysis of piled raft systems. Aust. Geotech. J. 1972, 2, 21–27. [Google Scholar]
- Clancy, P.; Randolph, M.F. Simple design tools for piled raft foundations. Geotechnique 1996, 46, 313–328. [Google Scholar] [CrossRef]
- Bhaduri, A.; Choudhury, D. Steady-state response of flexible combined pile-raft foundation under dynamic loading. Soil Dyn. Earthq. Eng. 2021, 145, 106664. [Google Scholar] [CrossRef]
- Tarenia, K.; Patra, N.R. Long-term effect of vertical and lateral loads on piled raft foundations: A case study. Proc. Inst. Civ. Eng.-Geotech. Eng. 2024, 177, 337–349. [Google Scholar] [CrossRef]
- Pandey, G.; Mourya, V.K.; Patel, D.; Kumar, R.; Kumar, S. Load sharing behaviour in piled-raft foundations over sand and clay: An experimental investigation. Res. Eng. Struct. Mater. 2024, 10, 917–942. [Google Scholar] [CrossRef]
- Gunawan, H.; Flessati, L.; Marveggio, P. Optimizing foundation performance: The impact of raft on piled raft foundation in sand. Géotechnique Lett. 2025, 1–5. Available online: https://www.sciencedirect.com/org/science/article/abs/pii/S2045254325000239 (accessed on 13 August 2025).
- Akbari, A.; Eslami, A. Performance of composite piled raft foundations with long and short piles under static and seismic loading. Geotech. Geol. Eng. 2025, 43, 188. [Google Scholar] [CrossRef]
- Mahata, K.; Bera, A.K. Load settlement and load sharing characteristics of a combined pile-raft foundation in granular soil deposits: A numerical simulation approach. Transp. Infrastruct. Geotechnol. 2025, 12, 88. [Google Scholar] [CrossRef]
- Wang, J.; Xie, Y.; Guo, T.; Du, Z. Predicting the influence of soil–structure interaction on seismic responses of reinforced concrete frame buildings using convolutional neural network. Buildings 2023, 13, 564. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, S. Settlement based load-bearing in a combined pile–raft foundation. Geotech. Geol. Eng. 2024, 42, 1405–1421. [Google Scholar] [CrossRef]
- Chimdesa, F.F.; Chimdesa, F.F.; Jilo, N.Z.; Hulagabali, A.; Babalola, O.E.; Tiyasha, T.; Ramaswamy, K.; Kumar, A.; Bhagat, S.K. Numerical analysis of pile group, piled raft, and footing using finite element software PLAXIS 2D and GEO5. Sci. Rep. 2023, 13, 15875. [Google Scholar] [CrossRef]
- Islam, M.R.; Turja, S.D.; Van Nguyen, D.; Forcellini, D.; Kim, D. Seismic soil-structure interaction in nuclear power plants: An extensive review. Results Eng. 2024, 23, 102694. [Google Scholar] [CrossRef]
- Singh, G.G.; Tiwari, R.P.; Kumar, V. Insights into the behaviour of piled raft foundations under vertical-horizontal-moment loading conditions. Transp. Infrastruct. Geotechnol. 2025, 12, 60. [Google Scholar] [CrossRef]
- Deb, P.; Pal, S.K. Evolution of piled raft foundation at static loading condition and application of numerical modelling: A state-of-the-art review. Arch. Comput. Methods Eng. 2025, 32, 1097–1133. [Google Scholar] [CrossRef]
- Reul, O.; Randolph, M. Combined Pile-Raft Foundations: Design and Practice; CRC Press: Boca Raton, FL, USA, 2025; 270p. [Google Scholar]
- Bolborea, B.; Baeră, C.; Gruin, A.; Vasile, A.; Barbu, A. A review of non-destructive testing methods for structural health monitoring of earthen constructions. Alex. Eng. J. 2025, 114, 55–81. [Google Scholar] [CrossRef]
- Qasim Derhem Dammag, B.; Jian, D.; Dammag, A.Q. Cultural heritage sites risk assessment and management using a hybridized technique based on GIS and SWOT-AHP in the Ancient City of Ibb, Yemen. Int. J. Archit. Herit. 2024, 1–36. [Google Scholar] [CrossRef]
- Vandelli, V.; Selmi, L.; Faccini, F.; Ferrando, A.; Coratza, P. Geoheritage degradation risk assessment: Methodologies and insights. Sustainability 2024, 16, 10336. [Google Scholar] [CrossRef]
- Song, J.; Munyinda, M.; Adu Sarfo, P. Examining the impact of risk management practices on sustainable project performance in the construction industry: The role of stakeholder engagement. Front. Built Environ. 2025, 11, 1575827. [Google Scholar] [CrossRef]
- EN 1997-1:2004; Eurocode 7: Geotechnical Design—Part 1: General Rules. CEN: Brussels, Belgium, 2004.
- German Geotechnical Society (GGS). Empfehlungen für Verformungen des Baugrunds bei Baulichen Anlagen; Ernst & Sohn: Berlin, Germany, 1993. (In German) [Google Scholar]
- International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE). Combined Pile-Raft Foundation Guideline; ISSMGE: Darmstadt, Germany, 2013. [Google Scholar]
- Mandolini, A.; Russo, G.; Viggiani, C. Pile Foundations: Experimental Investigations, Analysis and Design. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering (ICSMGE 2005), Osaka, Japan, 12–16 September 2005; Volume 1, pp. 177–216. [Google Scholar] [CrossRef]
- Viggiani, C.; Mandolini, A.; Russo, G. Piles and Pile Foundations, 1st ed.; Spon Press: London, UK, 2012; 296p. [Google Scholar]
- Randolph, M.F. Design methods for pile groups and piled rafts. In Proceedings of the XIII Conference on Soil Mechanics and Geotechnical Engineering, New Delhi, India, 5–10 January 1994; Volume 5, pp. 61–82. [Google Scholar]
- Katzenbach, R.; Leppla, S.; Choudhury, D. Foundation Systems for High-Rise Structures, 1st ed.; CRC Press: Boca Raton, FL, USA, 2016; 314p. [Google Scholar]
- Horikoshi, K.; Randolph, M.F. A contribution to optimal design of piled rafts. Geotechnique 1998, 48, 301–317. [Google Scholar] [CrossRef]
- Poulos, H.G.; Carter, J.P.; Small, J.C. Foundations and Retaining Structures: Research and Practice. In Proceedings of the 15th International Conference on Soil Mechanics and Geotechnical Engineering, Istanbul, Turkey, 27–31 August 2001; Volume 4, pp. 2527–2606. [Google Scholar]
- Merino, C.; González, J.; Prados, A. Advanced numerical modelling using the hardening soil small strain material model for sensitive excavations adjacent to a metro station. In Geotechnical Engineering Challenges to Meet Current and Emerging Needs of Society, 1st ed.; Guerra, N., Fernandes, M.M., Ferreira, C., Correia, A.G., Pinto, A., Pinto, P.S., Eds.; CRC Press: Boca Raton, FL, USA, 2024; pp. 660–663. [Google Scholar] [CrossRef]
- Bahramipour, O.; Moezzi, R.; Jalali, F.M.; Khaksar, R.Y.; Gheibi, M. Parametric evaluation of soil nail configurations for sustainable excavation stability using finite element analysis. Inventions 2025, 10, 45. [Google Scholar] [CrossRef]
- Beltrán-Vargas, D.; García-Páez, F.; Martínez-Morales, M.; Rentería-Guevara, S.A. Novel numerical modeling of a groundwater level-lowering approach implemented in the construction of high-rise/complex buildings. Water 2025, 17, 732. [Google Scholar] [CrossRef]



| Settlement, mm | Rotation | ||
|---|---|---|---|
| High-Rise | Adjacent Structures | Raft | Quay Wall 1 |
| 45 | 25 | 1/500 | 1/1000 |
| Part | Dead Load, MN | Traffic Load, MN |
|---|---|---|
| Walls and columns | 325 | 60 |
| Highly loaded column | 65 | 15 |
| Parameter | Mohr–Coulomb | Hardening Soil 1 | ||
|---|---|---|---|---|
| Filling | QAC | QS | TM | |
| γsat [kN/m3] | 19 | 19 | 19.5 | 19 |
| γunsat [kN/m3] | 19 | 19 | 19.5 | 19 |
| φ’ [°] | 20 | 25 | 35 | 22.5 |
| c’ [kN/m2] | 5 | 5 | 0 | 20 |
| Ψ [°] | 0 | 0 | 5 | 0 |
| E/E50,ref [GPa] | – | 4 | 70 | 60 |
| Eoed,ref [GPa] | – | 4 | 70 | 60 |
| Eur,ref [GPa] | – | 8 | 140 | 120 |
| ν/νur [–] | – | 0.3 | 0.3 | 0.25 |
| K0 [–] | – | 0.5774 | 0.4264 | 0.6173 |
| Rf [–] | – | 0.9 | 0.9 | 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leppla, S.; Norkus, A.; Karbočius, M.; Gribniak, V. Design and Numerical Analysis of a Combined Pile–Raft Foundation for a High-Rise in a Sensitive Urban Environment. Buildings 2025, 15, 2933. https://doi.org/10.3390/buildings15162933
Leppla S, Norkus A, Karbočius M, Gribniak V. Design and Numerical Analysis of a Combined Pile–Raft Foundation for a High-Rise in a Sensitive Urban Environment. Buildings. 2025; 15(16):2933. https://doi.org/10.3390/buildings15162933
Chicago/Turabian StyleLeppla, Steffen, Arnoldas Norkus, Martynas Karbočius, and Viktor Gribniak. 2025. "Design and Numerical Analysis of a Combined Pile–Raft Foundation for a High-Rise in a Sensitive Urban Environment" Buildings 15, no. 16: 2933. https://doi.org/10.3390/buildings15162933
APA StyleLeppla, S., Norkus, A., Karbočius, M., & Gribniak, V. (2025). Design and Numerical Analysis of a Combined Pile–Raft Foundation for a High-Rise in a Sensitive Urban Environment. Buildings, 15(16), 2933. https://doi.org/10.3390/buildings15162933







