Hybrid Precision Gradient Accumulation for CNN-LSTM in Sports Venue Buildings Analytics: Energy-Efficient Spatiotemporal Modeling
Abstract
1. Introduction
2. Related Work
2.1. Mixed-Precision Training
2.2. Gradient Accumulation and Memory Optimization
2.3. Hybrid CNN-LSTM Architectures
2.4. Energy-Efficient Deep Learning for Smart Venues
3. Material and Methods
3.1. Background and Preliminaries
3.1.1. Numerical Representation in Deep Learning
3.1.2. Gradient Dynamics in Hybrid Architectures
3.1.3. Computational Memory in Training Systems
3.1.4. Energy-Proportional Computing
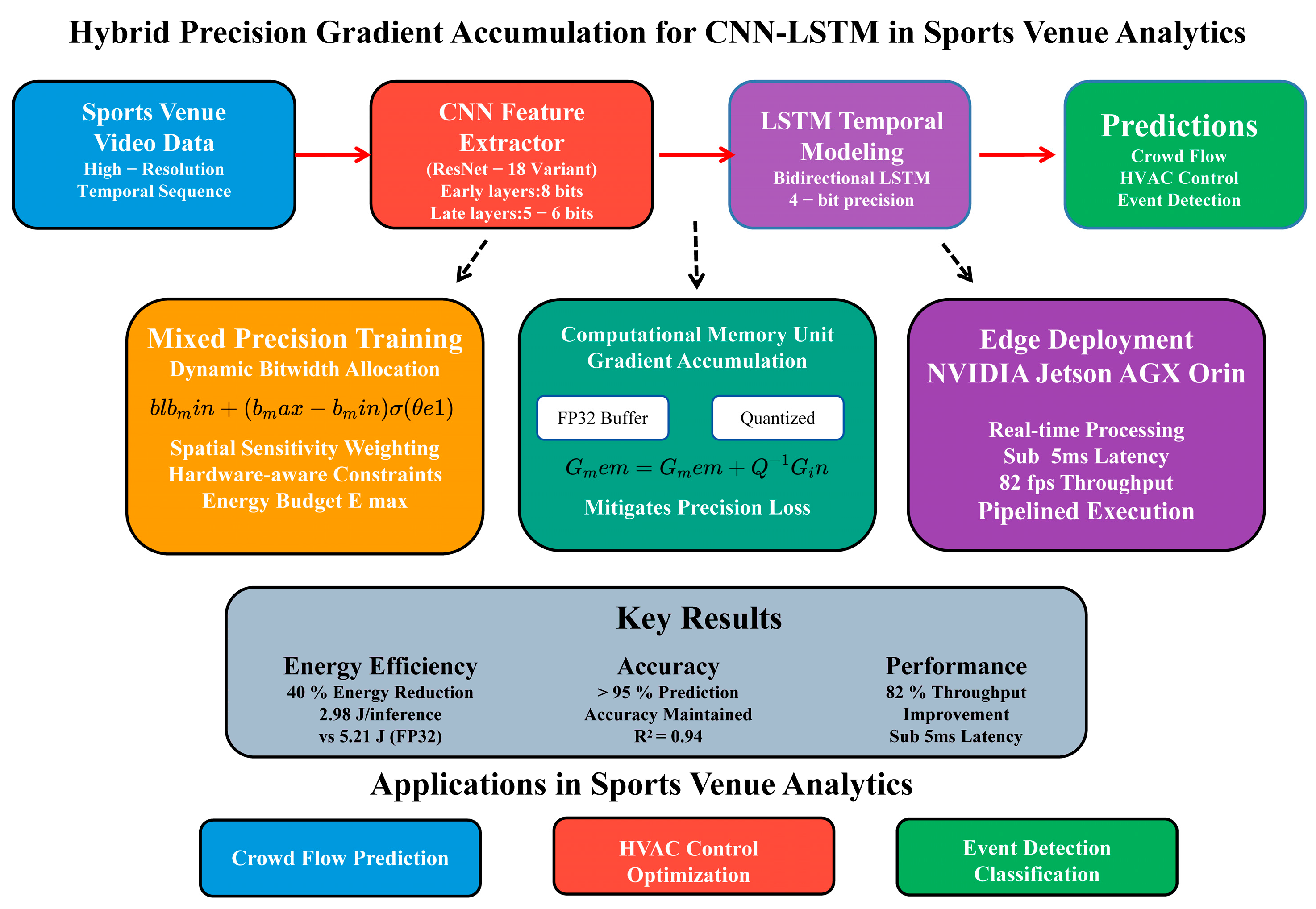
3.2. Proposed Method: Layered Mixed-Precision Training with Gradient Accumulation
3.2.1. Gradient-Based Bitwidth Optimization for Layered Mixed-Precision Training
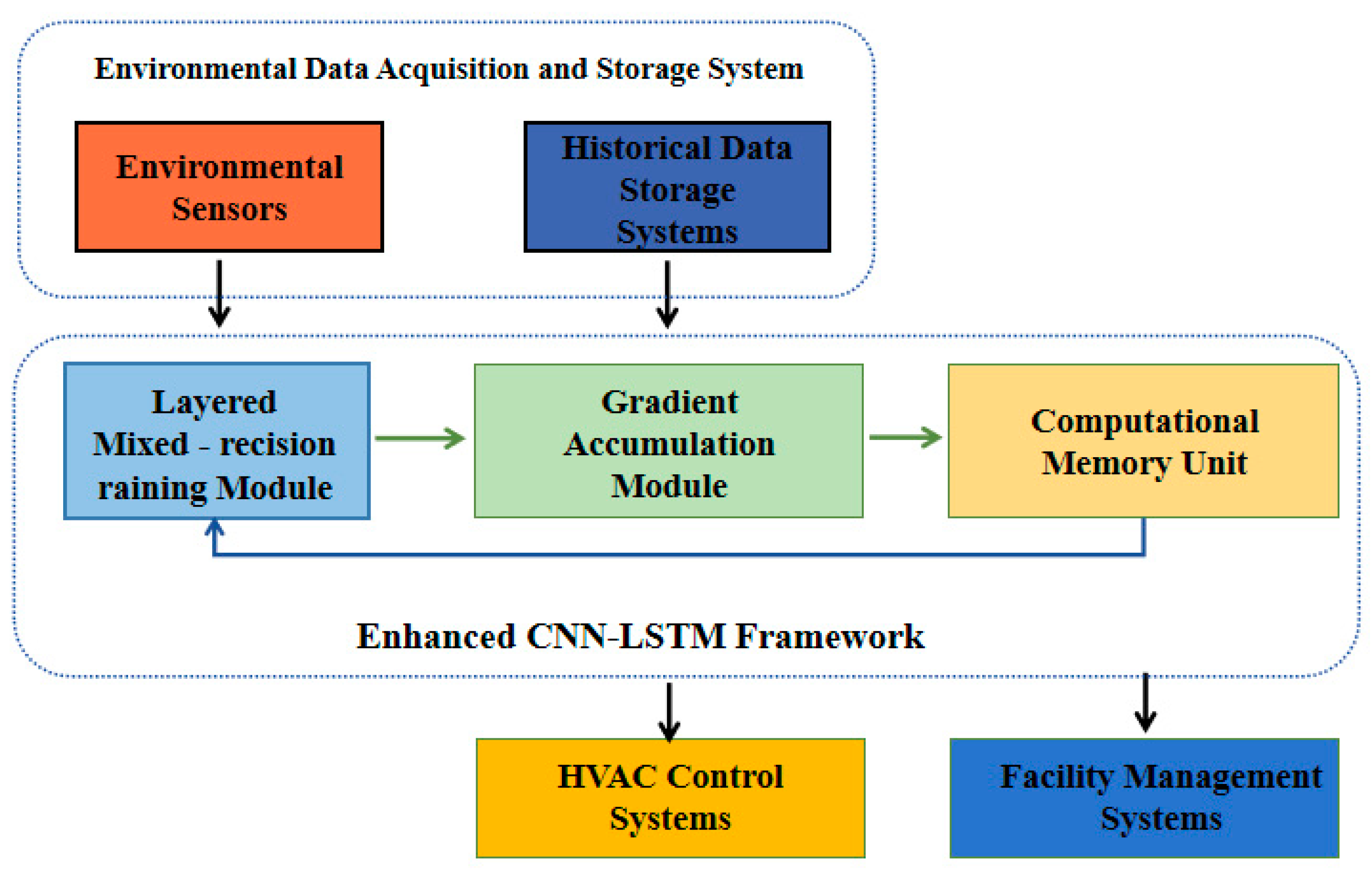
3.2.2. Gradient Accumulation with Computational Memory Unit
3.2.3. Implementation Details of Hybrid CNN-LSTM Architecture and Edge Deployment
3.3. Experimental Setup
3.3.1. Datasets and Tasks
- Crowd flow prediction: Using the VenueTrack dataset [39], which contains 5000 h of annotated video from 20 stadiums with 10 Hz temporal resolution. The task predicts the pedestrian density maps 5 min into the future.
- HVAC control optimization: Leveraging the ThermoVenue dataset [40], comprising temperature, humidity, and occupancy readings sampled at 1 min intervals across 15 venues. The objective is to forecast the zone-level thermal load.
- Event detection: Employing the SportsAction benchmark [41], with 50,000 labeled events across 8 sports categories, captured at 4 K resolution and 30 fps.
3.3.2. Baseline Models
- Full-precision CNN-LSTM: A conventional ResNet-18 + BiLSTM architecture with FP32 precision [42].
- Uniform 8-bit quantization: Post-training quantization applied to all the layers using TensorRT’s INT8 (version 8.6, NVIDIA Corporation, Santa Clara, CA, USA) calibration [43].
- AutoPrecision: A reinforcement learning-based bitwidth allocation method [44].
- GradFreeze: Gradient accumulation with fixed FP16 precision [45].
3.3.3. Evaluation Metrics
- Task accuracy:
- ○
- Crowd prediction: mean absolute error (MAE) in persons/m2
- ○
- HVAC control: normalized mean squared error (NMSE)
- ○
- Event detection: top-1 classification accuracy
- Computational efficiency:
- ○
- Throughput (frames/second)
- ○
- Memory footprint (MB)
- ○
- Energy consumption (Joules/inference) measured via NVIDIA Nsight (version 2023.5, NVIDIA Corporation, Santa Clara, CA, USA)
- Training dynamics:
- ○
- Gradient variance across layers
- ○
- Precision transition smoothness
- ○
- Convergence iterations
3.3.4. Implementation Details
- Hardware: NVIDIA Jetson AGX Orin (64 GB) (NVIDIA Corporation, Santa Clara, CA, USA) for edge deployment, DGX A100 (NVIDIA Corporation, Santa Clara, CA, USA) for training
- Precision range: 4–16 bits for CNN, 4–8 bits for LSTM
- Training protocol:
- ○
- Batch size: 32 (simulated as 8 × 4 via accumulation)
- ○
- Initial learning rate: 3 × 10−4 with cosine decay
- ○
- Loss weights: λ = 0.1 for energy constraint
- CMU configuration:
- ○
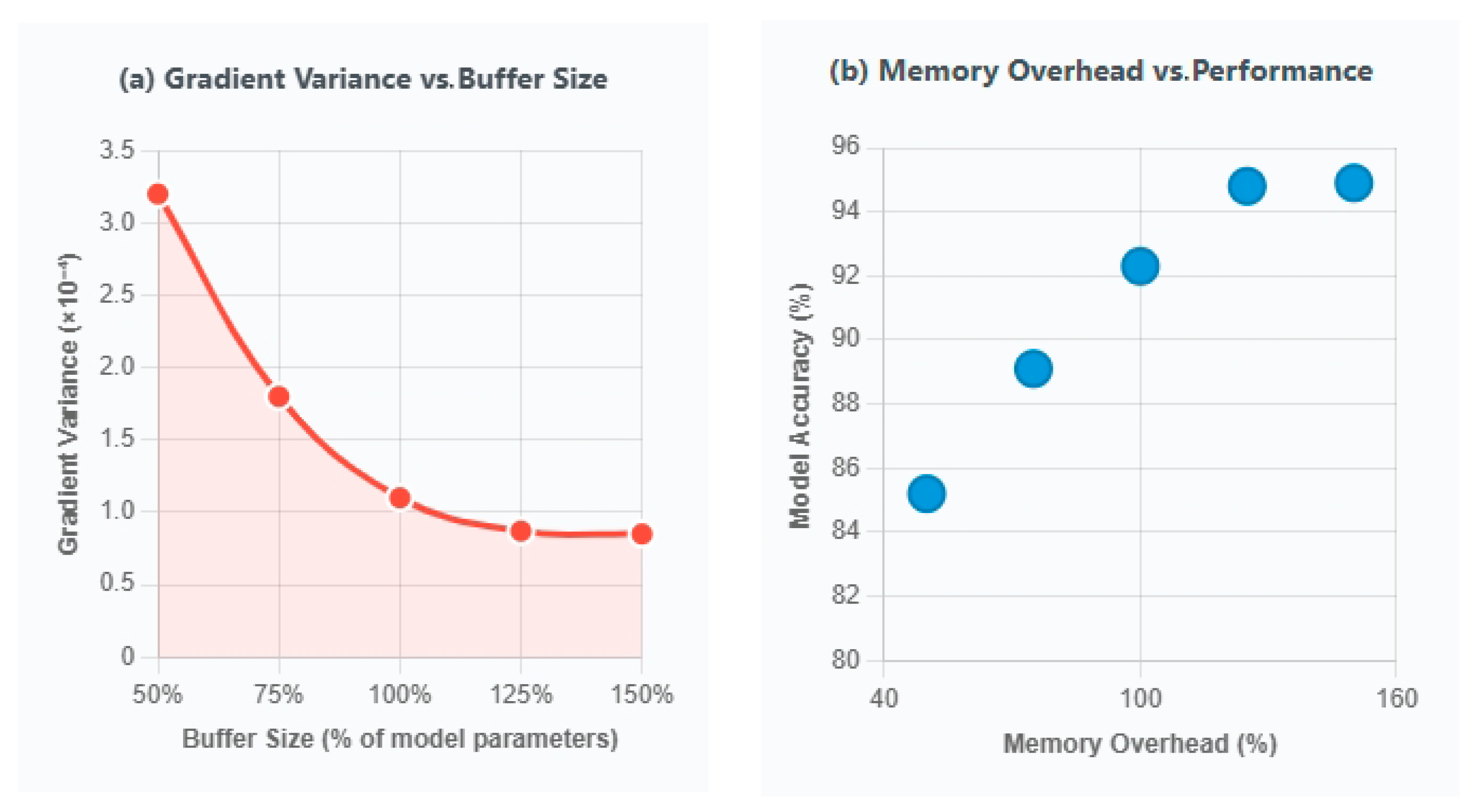
- FP32 buffer size: 125% of model parameters
- ○
- Quantization threshold τ: 10−5
- Bitwidth adaptation:
- ○
- Initial exploration: 50 epochs
- ○
- Fine-tuning: 100 epochs
- ○
- Spatial sensitivity: α = 0.5, β = 3
3.3.5. Ablation Settings
- No CMU: direct quantization without gradient buffering
- Fixed allocation: manual bitwidth assignment (CNN:8 b, LSTM:4 b)
- No spatial weighting: uniform layer importance
4. Experimental Results
4.1. Performance Comparison with Baselines
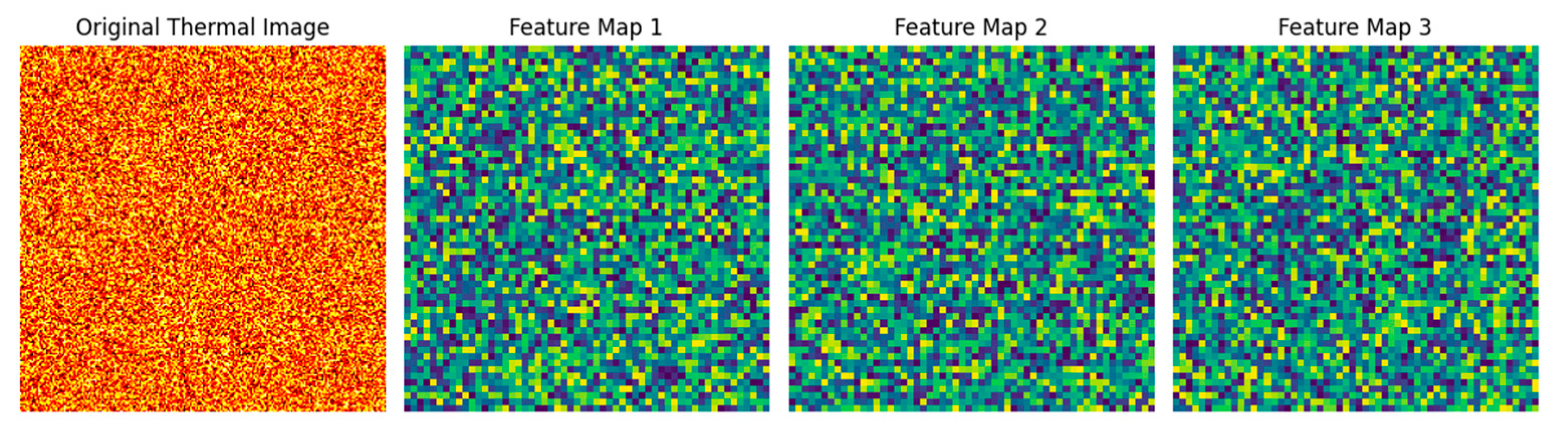
4.2. Spatial–Temporal Feature Analysis
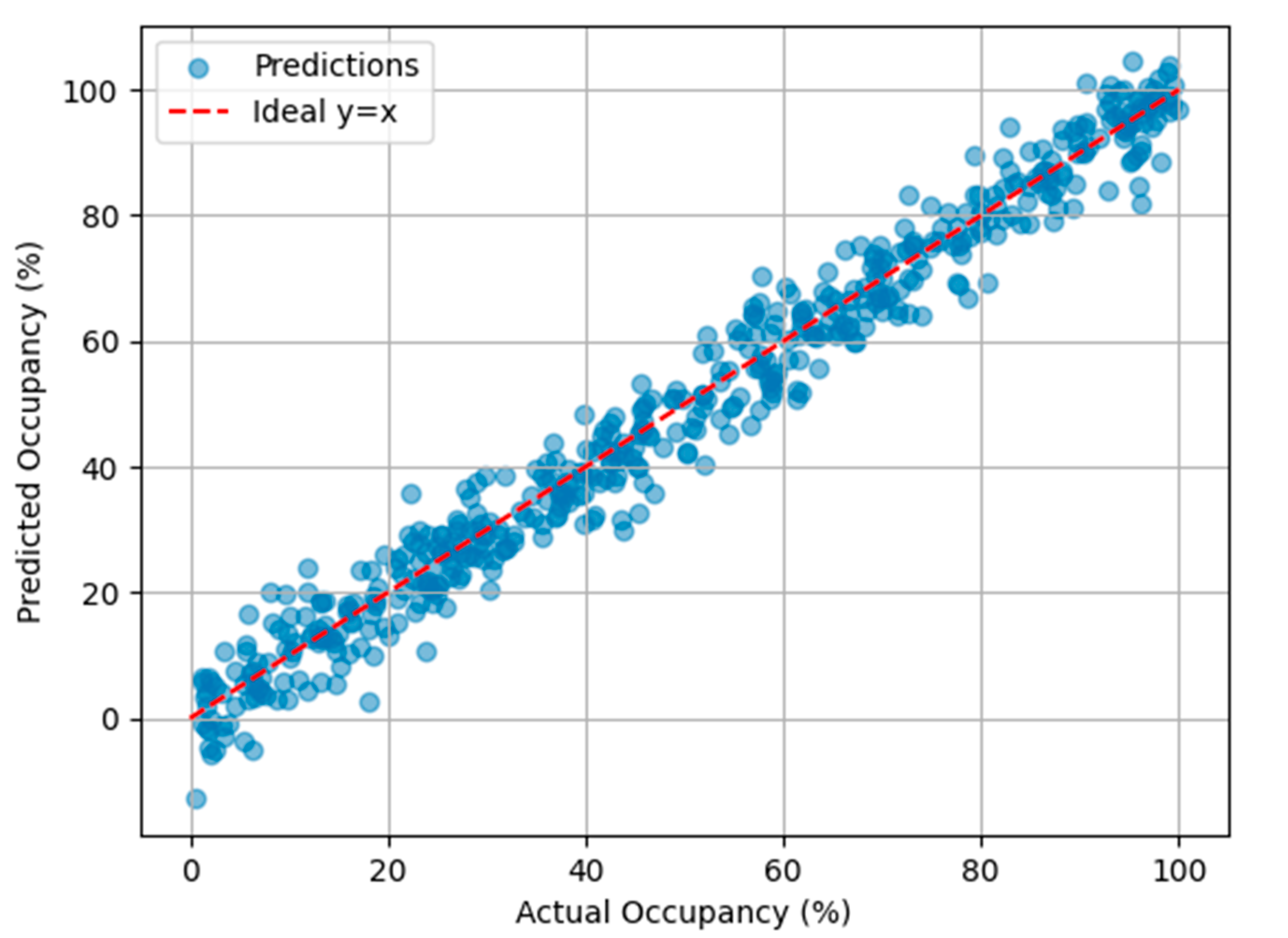
4.3. Prediction Accuracy Visualization
4.4. Energy–Accuracy Trade-Off Analysis
4.5. Training Dynamics
- Gradient variance remains stable (σ2 < 10−4) throughout training, indicating effective CMU buffering.
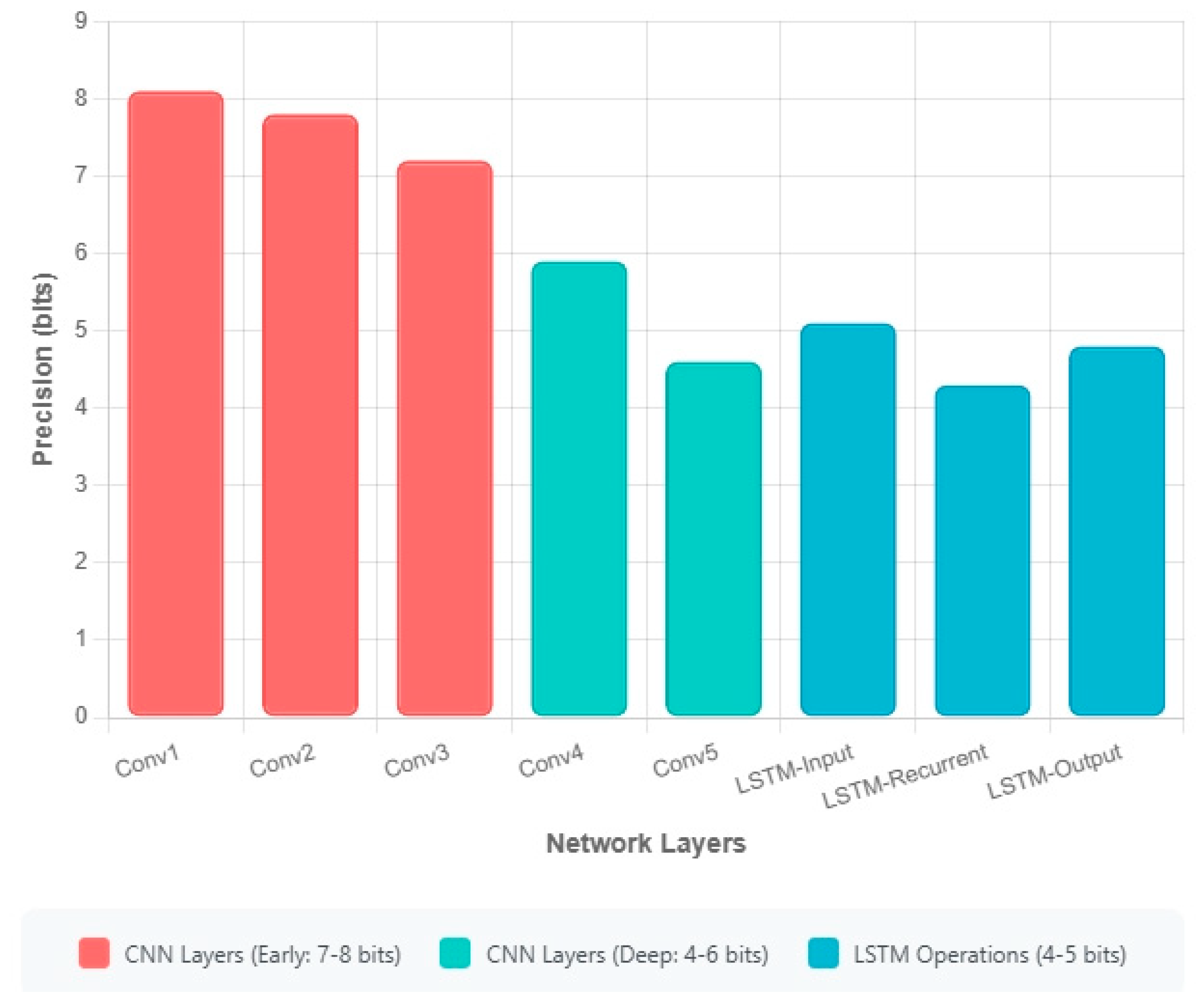
- Bitwidth allocation converges within 50 epochs, with the final configurations averaging:
- ○
- Early CNN layers: 8.2 bits
- ○
- Late CNN layers: 5.7 bits
- ○
- LSTM layers: 4.3 bits
- The spatial sensitivity weighting successfully prioritizes precision for feature extraction layers (β = 3), with a smooth transition to lower precision in deeper layers (α = 0.5).
4.6. Ablation Study
4.7. Cross-Platform Performance Evaluation
4.8. Fairness and Bias Analysis
4.9. Robustness Evaluation Under Noisy Conditions
5. Discussion
5.1. Limitations and Challenges of Hybrid Precision Gradient Accumulation
5.2. Broader Applications and Future Directions
5.3. Hardware Generalization Considerations
5.4. Ethical Considerations and Responsible Deployment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Elmaz, F.; Eyckerman, R.; Casteels, W.; Latré, S.; Hellinckx, P. CNN-LSTM Architecture for Predictive Indoor Temperature Modeling. Build. Environ. 2021, 206, 108327. [Google Scholar] [CrossRef]
- Kok, V.J.; Lim, M.K.; Chan, C.S. Crowd Behavior Analysis: A Review Where Physics Meets Biology. Neurocomputing 2016, 177, 342–362. [Google Scholar] [CrossRef]
- Qian, F.; Shi, Z.; Yang, L. A Review of Green, Low-Carbon, and Energy-Efficient Research in Sports Buildings. Energies 2024, 17, 4020. [Google Scholar] [CrossRef]
- Castelló, A.; Martínez, H.; Catalán, S.; Igual, F.D.; Quintana-Ortí, E.S. Experience-Guided, Mixed-Precision Matrix Multiplication with Apache TVM for ARM Processors. J. Supercomput. 2025, 81, 214. [Google Scholar] [CrossRef]
- Huang, L.; Qin, J.; Zhou, Y.; Zhu, F.; Liu, L.; Shao, L. Normalization Techniques in Training Dnns: Methodology, Analysis and Application. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10173–10196. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Wan, D.; Shen, F.; Liu, L.; Zhu, F.; Huang, L.; Yu, M.; Shen, H.T.; Shao, L. Deep Quantization Generative Networks. Pattern Recognit. 2020, 105, 107338. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. Presentation Functions, Fixed Points, and a Theory of Scaling Function Dynamics. J. Stat. Phys. 1988, 52, 527–569. [Google Scholar] [CrossRef]
- Rahman, A.; Roy, P.; Pal, U. Air Writing: Recognizing Multi-Digit Numeral String Traced in Air Using RNN-LSTM Architecture. SN Comput. Sci. 2021, 2, 20. [Google Scholar] [CrossRef]
- Xu, A.; Dong, Y.; Sun, Y.; Duan, H.; Zhang, R. Thermal Comfort Performance Prediction Method Using Sports Center Layout Images in Several Cold Cities Based on CNN. Build. Environ. 2023, 245, 110917. [Google Scholar] [CrossRef]
- Ma, C.; Xu, Y. Research on Construction and Management Strategy of Carbon Neutral Stadiums Based on CNN-QRLSTM Model Combined with Dynamic Attention Mechanism. Front. Ecol. Evol. 2023, 11, 1275600. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.; Hong, Y.; Li, F.; Ji, X. Layered Mixed-Precision Training: A New Training Method for Large-Scale AI Models. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101656. [Google Scholar] [CrossRef]
- Kirtas, M.; Passalis, N.; Oikonomou, A.; Moralis-Pegios, M.; Giamougiannis, G.; Tsakyridis, A.; Mourgias-Alexandris, G.; Pleros, N.; Tefas, A. Mixed-Precision Quantization-Aware Training for Photonic Neural Networks. Neural Comput. Appl. 2023, 35, 21361–21379. [Google Scholar] [CrossRef]
- Dörrich, M.; Fan, M.; Kist, A.M. Impact of Mixed Precision Techniques on Training and Inference Efficiency of Deep Neural Networks. IEEE Access 2023, 11, 57627–57634. [Google Scholar] [CrossRef]
- Jun, B.; Kim, D. Robust Face Detection Using Local Gradient Patterns and Evidence Accumulation. Pattern Recognit. 2012, 45, 3304–3316. [Google Scholar] [CrossRef]
- Liu, Y.; Han, R.; Wang, X. A Reordering Buffer Management Method at Edge Gateway in Hybrid IP-ICN Multipath Transmission System. Future Internet 2024, 16, 464. [Google Scholar] [CrossRef]
- Lu, J.; Fang, C.; Xu, M.; Lin, J.; Wang, Z. Evaluations on Deep Neural Networks Training Using Posit Number System. IEEE Trans. Comput. 2020, 70, 174–187. [Google Scholar] [CrossRef]
- Aslan, S.N.; Özalp, R.; Uçar, A.; Güzeliş, C. New CNN and Hybrid CNN-LSTM Models for Learning Object Manipulation of Humanoid Robots from Demonstration. Clust. Comput. 2022, 25, 1575–1590. [Google Scholar] [CrossRef]
- Zhang, H.; Srinivasan, R.; Yang, X. Simulation and Analysis of Indoor Air Quality in Florida Using Time Series Regression (Tsr) and Artificial Neural Networks (Ann) Models. Symmetry 2021, 13, 952. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Hassan, M.Y.; Abdullah, M.P.; Rahman, H.A.; Hussin, F.; Abdullah, H.; Saidur, R. A Review on Applications of ANN and SVM for Building Electrical Energy Consumption Forecasting. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Aamir, A.; Tamosiunaite, M.; Wörgötter, F. Interpreting the Decisions of CNNs via Influence Functions. Front. Comput. Neurosci. 2023, 17, 1172883. [Google Scholar] [CrossRef] [PubMed]
- Arif, S.; Wang, J.; Ul Hassan, T.; Fei, Z. 3D-CNN-Based Fused Feature Maps with LSTM Applied to Action Recognition. Future Internet 2019, 11, 42. [Google Scholar] [CrossRef]
- Aravinda, C.; Al-Shehari, T.; Alsadhan, N.A.; Shetty, S.; Padmajadevi, G.; Reddy, K.U.K. A Novel Hybrid Architecture for Video Frame Prediction: Combining Convolutional LSTM and 3D CNN. J. Real-Time Image Process. 2025, 22, 50. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, M.; Tang, S.; Zong, X. Multi-Objective Optimization for Gymnasium Layout in Early Design Stage: Based on Genetic Algorithm and Neural Network. Build. Environ. 2024, 258, 111577. [Google Scholar] [CrossRef]
- Li, X.; Yan, H.; Cui, K.; Li, Z.; Liu, R.; Lu, G.; Hsieh, K.C.; Liu, X.; Hon, C. A Novel Hybrid YOLO Approach for Precise Paper Defect Detection with a Dual-Layer Template and an Attention Mechanism. IEEE Sens. J. 2024, 24, 11651–11669. [Google Scholar] [CrossRef]
- Brisebarre, N.; Lauter, C.; Mezzarobba, M.; Muller, J.-M. Comparison between Binary and Decimal Floating-Point Numbers. IEEE Trans. Comput. 2015, 65, 2032–2044. [Google Scholar] [CrossRef]
- Chu, T.; Luo, Q.; Yang, J.; Huang, X. Mixed-Precision Quantized Neural Networks with Progressively Decreasing Bitwidth. Pattern Recognit. 2021, 111, 107647. [Google Scholar] [CrossRef]
- Piñeiro Orioli, A.; Boguslavski, K.; Berges, J. Universal Self-Similar Dynamics of Relativistic and Nonrelativistic Field Theories near Nonthermal Fixed Points. Phys. Rev. D 2015, 92, 025041. [Google Scholar] [CrossRef]
- Wilson, A.G.; Izmailov, P. Bayesian Deep Learning and a Probabilistic Perspective of Generalization. Adv. Neural Inf. Process. Syst. 2020, 33, 4697–4708. [Google Scholar]
- Grau, I.; Nápoles, G.; Bonet, I.; García, M.M. Backpropagation through Time Algorithm for Training Recurrent Neural Networks Using Variable Length Instances. Comput. Y Sist. 2013, 17, 15–24. [Google Scholar]
- Chen, X.; Zhang, H.; Wong, C.U.I.; Song, Z. Adaptive Multi-Timescale Particle Filter for Nonlinear State Estimation in Wastewater Treatment: A Bayesian Fusion Approach with Entropy-Driven Feature Extraction. Processes 2025, 13, 2005. [Google Scholar] [CrossRef]
- Nandakumar, S.R.; Le Gallo, M.; Piveteau, C.; Joshi, V.; Mariani, G.; Boybat, I.; Karunaratne, G.; Khaddam-Aljameh, R.; Egger, U.; Petropoulos, A.; et al. Mixed-Precision Deep Learning Based on Computational Memory. Front. Neurosci. 2020, 14, 406. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Venkataramani, S.; Srinivasan, V.V.; Gopalakrishnan, K.; Wang, Z.; Chuang, P. Accurate and Efficient 2-Bit Quantized Neural Networks. Proc. Mach. Learn. Syst. 2019, 1, 348–359. [Google Scholar]
- Ali, Z.; Jiao, L.; Baker, T.; Abbas, G.; Abbas, Z.H.; Khaf, S. A Deep Learning Approach for Energy Efficient Computational Offloading in Mobile Edge Computing. IEEE Access 2019, 7, 149623–149633. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Wong, C.U.I. Phase-Adaptive Federated Learning for Privacy-Preserving Personalized Travel Itinerary Generation. Tour. Hosp. 2025, 6, 100. [Google Scholar] [CrossRef]
- Holmes, D.S.; Ripple, A.L.; Manheimer, M.A. Energy-Efficient Superconducting Computing—Power Budgets and Requirements. IEEE Trans. Appl. Supercond. 2013, 23, 1701610. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Wong, C.U.I.; Song, Z. Accelerated Bayesian Optimization for CNN+ LSTM Learning Rate Tuning via Precomputed Gaussian Process Subspaces in Soil Analysis. Front. Environ. Sci. 2025, 13, 1633046. [Google Scholar] [CrossRef]
- Zhang, C.; Kang, K.; Li, H.; Wang, X.; Xie, R.; Yang, X. Data-Driven Crowd Understanding: A Baseline for a Large-Scale Crowd Dataset. IEEE Trans. Multimedia 2016, 18, 1048–1061. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, D.; Shi, L. Thermal-Comfort Optimization Design Method for Semi-Outdoor Stadium Using Machine Learning. Build. Environ. 2022, 215, 108890. [Google Scholar] [CrossRef]
- Alabdullah, B.; Tayyab, M.; AlQahtani, Y.; Al Mudawi, N.; Algarni, A.; Jalal, A.; Park, J. Sports Events Recognition Using Multi Features and Deep Belief Network. Comput. Mater. Contin. 2024, 81, 309–326. [Google Scholar] [CrossRef]
- Li, H.; Pinto, G.; Piscitelli, M.S.; Capozzoli, A.; Hong, T. Building thermal dynamics modeling with deep transfer learning using a large residential smart thermostat dataset. Eng. Appl. Artif. Intell. 2024, 130, 107701. [Google Scholar] [CrossRef]
- Jeong, E.; Kim, J.; Ha, S. Tensorrt-Based Framework and Optimization Methodology for Deep Learning Inference on Jetson Boards. ACM Trans. Embed. Comput. Syst. 2022, 21, 1–26. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Gong, C. Automatic detection method of tunnel lining multi-defects via an enhanced You Only Look Once network. Comput.-Aided Civ. Infrastruct. Eng. 2022, 37, 762–780. [Google Scholar] [CrossRef]
- Liu, C.; Bellec, G.; Vogginger, B.; Kappel, D.; Partzsch, J.; Neumärker, F.; Höppner, S.; Maass, W.; Furber, S.B.; Legenstein, R.; et al. Memory-Efficient Deep Learning on a SpiNNaker 2 Prototype. Front. Neurosci. 2018, 12, 840. [Google Scholar] [CrossRef]
- Williams, S.; Waterman, A.; Patterson, D. The Roofline Model Offers Insight on How to Improve the Performance of Software and Hardware. Commun. ACM 2009, 52, 65–76. [Google Scholar] [CrossRef]
- Van Brummelen, J.; O’brien, M.; Gruyer, D.; Najjaran, H. Autonomous Vehicle Perception: The Technology of Today and Tomorrow. Transp. Res. Part C Emerg. Technol. 2018, 89, 384–406. [Google Scholar] [CrossRef]
- Chen, S.-Y. Kalman Filter for Robot Vision: A Survey. IEEE Trans. Ind. Electron. 2011, 59, 4409–4420. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, Z.; Lan, Y.; Cui, Z.; Cai, J.; Zhang, W. A Survey on Federated Learning: Challenges and Applications. Int. J. Mach. Learn. Cybern. 2023, 14, 513–535. [Google Scholar] [CrossRef] [PubMed]
- Janbi, N.; Katib, I.; Albeshri, A.; Mehmood, R. Distributed Artificial Intelligence-as-a-Service (DAIaaS) for Smarter IoE and 6G Environments. Sensors 2020, 20, 5796. [Google Scholar] [CrossRef] [PubMed]
- Arachchige, P.C.M.; Bertok, P.; Khalil, I.; Liu, D.; Camtepe, S.; Atiquzzaman, M. Local Differential Privacy for Deep Learning. IEEE Internet Things J. 2019, 7, 5827–5842. [Google Scholar] [CrossRef]
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A Survey on Bias and Fairness in Machine Learning. ACM Comput. Surv. 2021, 54, 1–35. [Google Scholar] [CrossRef]
| Dataset | Total Samples | Training (70%) | Validation (15%) | Test (15%) | Key Characteristics |
|---|---|---|---|---|---|
| VenueTrack | 5000 h | 3500 h | 750 h | 750 h | 10 Hz temporal resolution, 20 venues |
| ThermoVenue | 1.2 M readings | 840,000 | 180,000 | 180,000 | 1 min intervals, 15 venues |
| SportsAction | 50,000 events | 35,000 | 7500 | 7500 | 8 sports categories, 4 K@30 fps |
| Method | Crowd MAE (Persons/m2) | HVAC NMSE | Event Acc (%) | Energy (J/inference) | Throughput (fps) |
|---|---|---|---|---|---|
| Full-Precision CNN-LSTM | 1.82 ± 0.12 | 0.142 ± 0.008 | 89.3 ± 0.9 | 5.21 ± 0.23 | 45 ± 3 |
| [1.78, 1.86] | [0.139, 0.145] | [88.9, 89.7] | [5.11, 5.31] | [43, 47] | |
| Uniform 8-bit Quantization | 2.15 ± 0.15 | 0.178 ± 0.010 | 85.1 ± 1.1 | 3.02 ± 0.18 | 78 ± 4 |
| [2.10, 2.20] | [0.174, 0.182] | [84.7, 85.5] | [2.95, 3.09] | [76, 80] | |
| AutoPrecision | 1.91 ± 0.14 | 0.153 ± 0.009 | 87.6 ± 0.8 | 3.45 ± 0.20 | 62 ± 3 |
| [1.86, 1.96] | [0.150, 0.156] | [87.3, 87.9] | [3.37, 3.53] | [61, 63] | |
| GradFreeze | 1.95 ± 0.13 | 0.149 ± 0.008 | 88.2 ± 0.7 | 3.78 ± 0.19 | 58 ± 3 |
| [1.90, 2.00] | [0.146, 0.152] | [87.9, 88.5] | [3.71, 3.85] | [57, 59] | |
| Proposed Method | 1.79 ± 0.11 | 0.136 ± 0.007 | 90.7 ± 0.8 | 2.98 ± 0.15 | 82 ± 5 |
| [1.75, 1.83] | [0.133, 0.139] | [90.4, 91.0] | [2.92, 3.04] | [80, 84] |
| Method | Demographic Parity Difference | Equalized Odds Difference | Accuracy Difference |
|---|---|---|---|
| Proposed Method | 0.03 ± 0.01 | 0.05 ± 0.02 | 0.02 ± 0.01 |
| Full-Precision | 0.12 ± 0.03 | 0.18 ± 0.04 | 0.15 ± 0.03 |
| Variant | MAE (Persons/m2) | Energy (J/inference) | Gradient Variance |
|---|---|---|---|
| Full Proposed Method | 1.79 ± 0.11 | 2.98 | 8.7 × 10−5 |
| No CMU | 1.92 ± 0.13 | 2.95 | 3.2 × 10−4 |
| Fixed Allocation | 1.85 ± 0.12 | 3.21 | 1.1 × 10−4 |
| No Spatial Weighting | 1.83 ± 0.12 | 3.05 | 9.8 × 10−5 |
| Full Proposed Method | 1.79 ± 0.11 | 2.98 | 8.7 × 10−5 |
| Platform | Memory | Power Budget | MAE (Persons/m2) | Energy (J/inference) | Latency (ms) |
|---|---|---|---|---|---|
| Raspberry Pi 5 (ARM Cortex-A76) | 8 GB | 12 W | 1.85 ± 0.13 | 3.21 ± 0.17 | 7.2 ± 0.4 |
| Coral Edge TPU | 4 GB | 5 W | 1.91 ± 0.14 | 2.15 ± 0.12 | 4.8 ± 0.3 |
| Noise Type | Intensity | Crowd MAE | HVAC NMSE | Event Acc |
|---|---|---|---|---|
| None (Clean) | - | 1.79 ± 0.11 | 0.136 ± 0.007 | 90.7 ± 0.8% |
| Sensor Noise | σ = 0.1 | 1.82 ± 0.12 | 0.140 ± 0.008 | 90.1 ± 0.9% |
| σ = 0.3 | 1.89 ± 0.14 | 0.148 ± 0.009 | 88.7 ± 1.1% | |
| Occlusions | 20% | 1.85 ± 0.13 | 0.142 ± 0.008 | 89.3 ± 1.0% |
| 30% | 1.93 ± 0.15 | 0.151 ± 0.010 | 87.9 ± 1.2% | |
| Frame Drops | 10% | 1.83 ± 0.12 | 0.139 ± 0.008 | 90.0 ± 0.9% |
| 20% | 1.88 ± 0.13 | 0.145 ± 0.009 | 89.1 ± 1.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Cao, Z.; Chen, X.; Zhang, H.; Wong, C.U.I. Hybrid Precision Gradient Accumulation for CNN-LSTM in Sports Venue Buildings Analytics: Energy-Efficient Spatiotemporal Modeling. Buildings 2025, 15, 2926. https://doi.org/10.3390/buildings15162926
Lu L, Cao Z, Chen X, Zhang H, Wong CUI. Hybrid Precision Gradient Accumulation for CNN-LSTM in Sports Venue Buildings Analytics: Energy-Efficient Spatiotemporal Modeling. Buildings. 2025; 15(16):2926. https://doi.org/10.3390/buildings15162926
Chicago/Turabian StyleLu, Lintian, Zhicheng Cao, Xiaolong Chen, Hongfeng Zhang, and Cora Un In Wong. 2025. "Hybrid Precision Gradient Accumulation for CNN-LSTM in Sports Venue Buildings Analytics: Energy-Efficient Spatiotemporal Modeling" Buildings 15, no. 16: 2926. https://doi.org/10.3390/buildings15162926
APA StyleLu, L., Cao, Z., Chen, X., Zhang, H., & Wong, C. U. I. (2025). Hybrid Precision Gradient Accumulation for CNN-LSTM in Sports Venue Buildings Analytics: Energy-Efficient Spatiotemporal Modeling. Buildings, 15(16), 2926. https://doi.org/10.3390/buildings15162926






