Automated Arch Profile Extraction from Point Clouds and Its Application in Arch Bridge Construction Monitoring
Abstract
1. Introduction
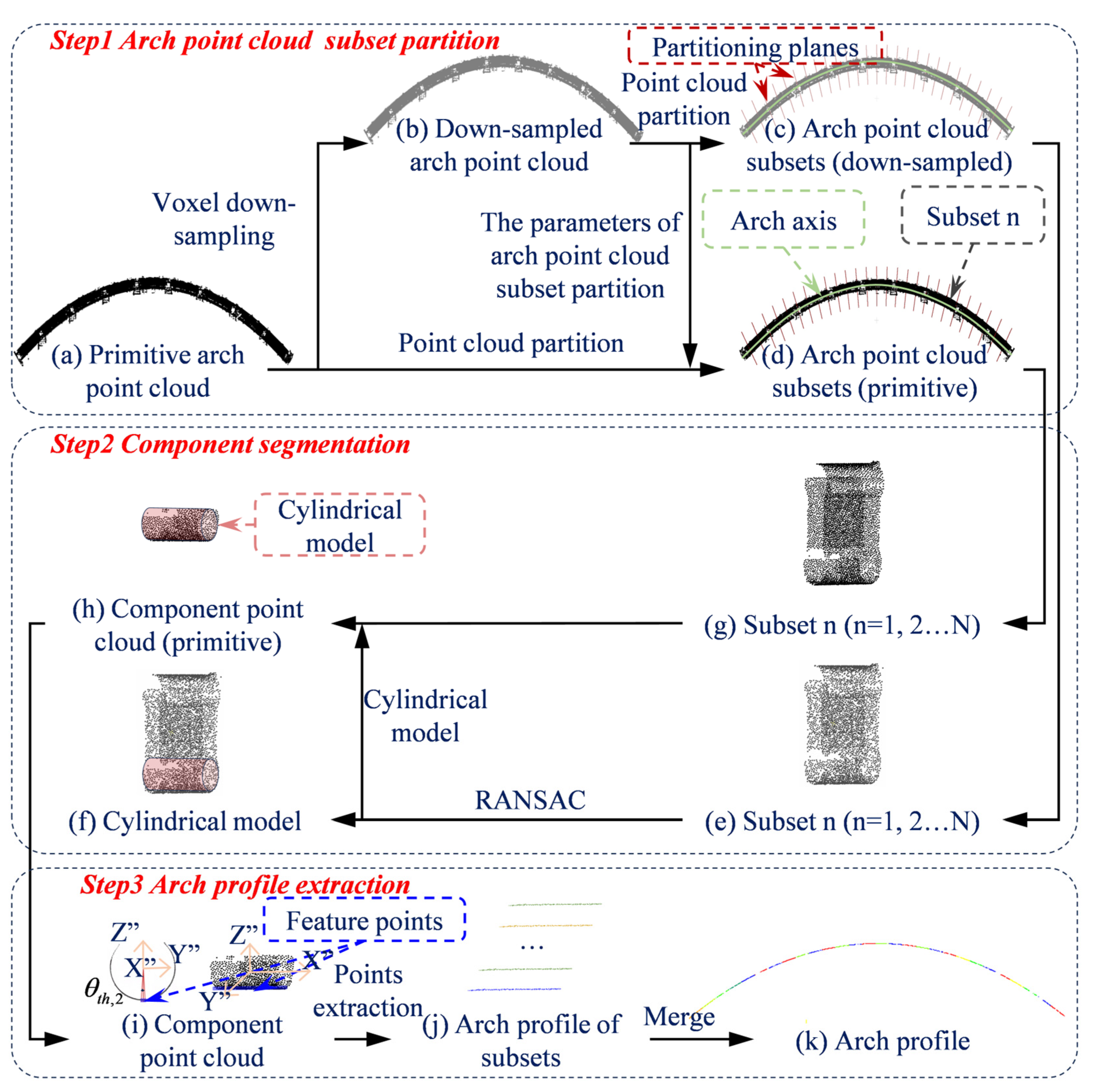
2. Methods
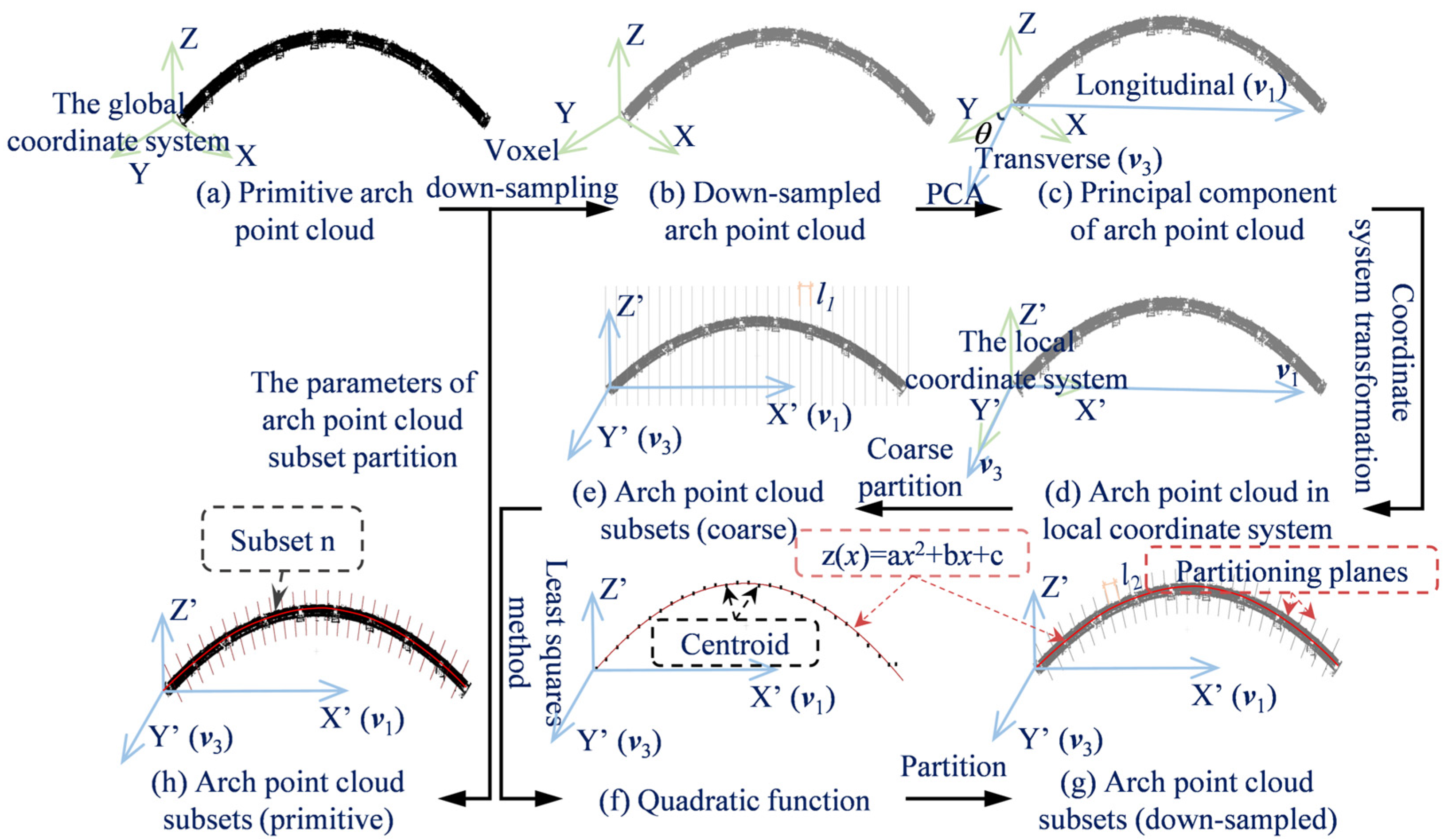
2.1. Arch Point Cloud Subset Partition
| Algorithm 1. Arch point cloud subset partition. |
| Inputs: Primitive arch point cloud P_arch, voxel size , coarse partition length l1, curve partition length l2 Output: Primitive arch points cloud subsets S = {subset 1, subset 2, …, subset n} 1: P_down ← VoxelDownsample (P_arch, voxel size) 2: cov_matrix ← ComputeCovariance (P_down) 3: eigenvalues, eigenvectors ← EigenDecompose (cov_matrix) 4: v1, v2, v3 ← eigenvectors [:, 0], eigenvectors [:, 1], eigenvectors [:, 2] 5: T_rot ← RotationMatrixFromVectors (v1, v3) 6: P_down’ ← TransformPoints (P_down, T_rot) 7: min_x, max_x ← MinMaxX (P_down’) 8: For x from min_x to max_x step l1 do 9: S’_i ← ExtractPointsInRange (P_down’, x, x + l1) 10: centroid_i ← ComputeCentroid (S’_i) 11: end for 12: centroids ← [centroid 1, centroid 2, …, centroid m] 13: curve_params ← LeastSquaresFit(centroids, degree = 2) 14: partition_planes ← GeneratePerpendicularPlanes (curve_params, spacing = l2) 15: S ← ApplyPartitionToPrimitiveArchPointCloud (P_arch, partition_planes) 16: return S |
2.2. Component Segmentation
- The orthogonality between axis and arch transverse direction, as defined in Equation (1).
- The radius tolerance constraint, as defined in Equation (2).
- The elevation constraint, as defined in Equation (3).
| Algorithm 2. Constrained RANSAC cylinder fitting. |
| Inputs:, minimum number of internal points MinPts1, expected probability p, Maximum number of iterations k, eigenvectors v3 Output: Optimal cylinder model C_opt 1: max_inliers ← Ø 2: w_est ← 0.5 3: k_max ← (log (1 − p)/log (1 − w_est^2)) 4: j ← 05: while j < min (k_max, k) do: 6: sample_points ← RandomSample (Si, 2) 7: n1, n2 ← ComputeNormals (sample_points)8: axis_dir ← n1 × n2 9: radius, centroid ← EstimateCylParams (sample_points, n1, n2) 10: h_subset ← ComputeSubsetCentroid (Si).z 11: : 12: continue 13: if |radius − R| >= t: 14: continue 15: if centroid.z <= h_subset: 16: continue 17: inliers ← [] 18: for p in Si: 19: dist ← DistanceToCylinder (p, axis_dir, radius) 20: 21: inliers. append(p) 22: if len(inliers) > max_inliers and len (inliers) >= MinPts1 23: continue 24: w_current ← |inliers|/|S_i| 25: if w_current > w_est: 26: w_est ← w_current 27: k_max ← log (1 − p)/log (1 − w_est^2) 28: max_inliers ← len (inliers) 29: C_opt ← (axis_dir, radius, centroid, inliers) 30: return C_opt |
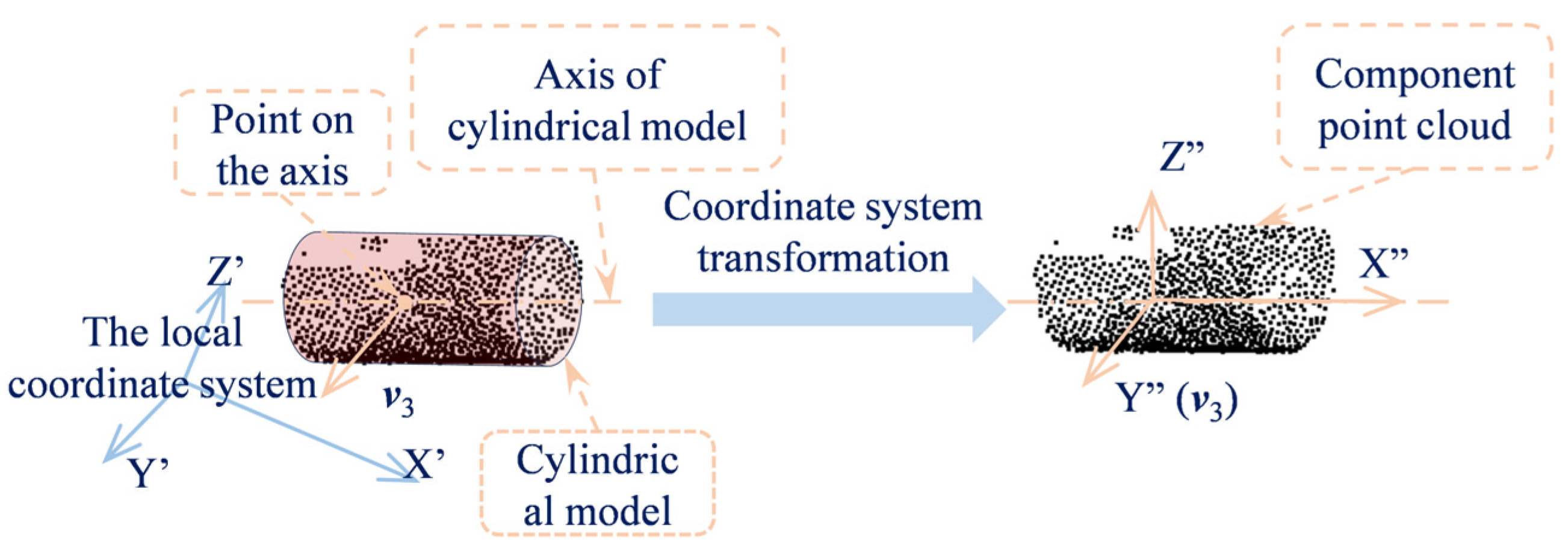
2.3. Arch Profile Extraction
| Algorithm 3. Profile point extraction. |
| Inputs:, eigenvectors v3 Output: Optimal cylinder model C_opt 1: X” ← C.axis_dir 2: Y” ← v3 3: Z” ← X” × Y” 4: origin ← C.centroid 5: T ← ConstructTransformMatrix (X”, Y”, Z”, origin) 6: P_comp” ← TransformPoints (P_comp, T) 7: P_profile ← [] 8: for p” in P_comp”: 9: y = p”.y; z = p”.z 10: angle = atan2(z, y) 11: : 12: P_profile.append (OriginalPosition (p”)) 13: return P_profile |
3. Method Validation
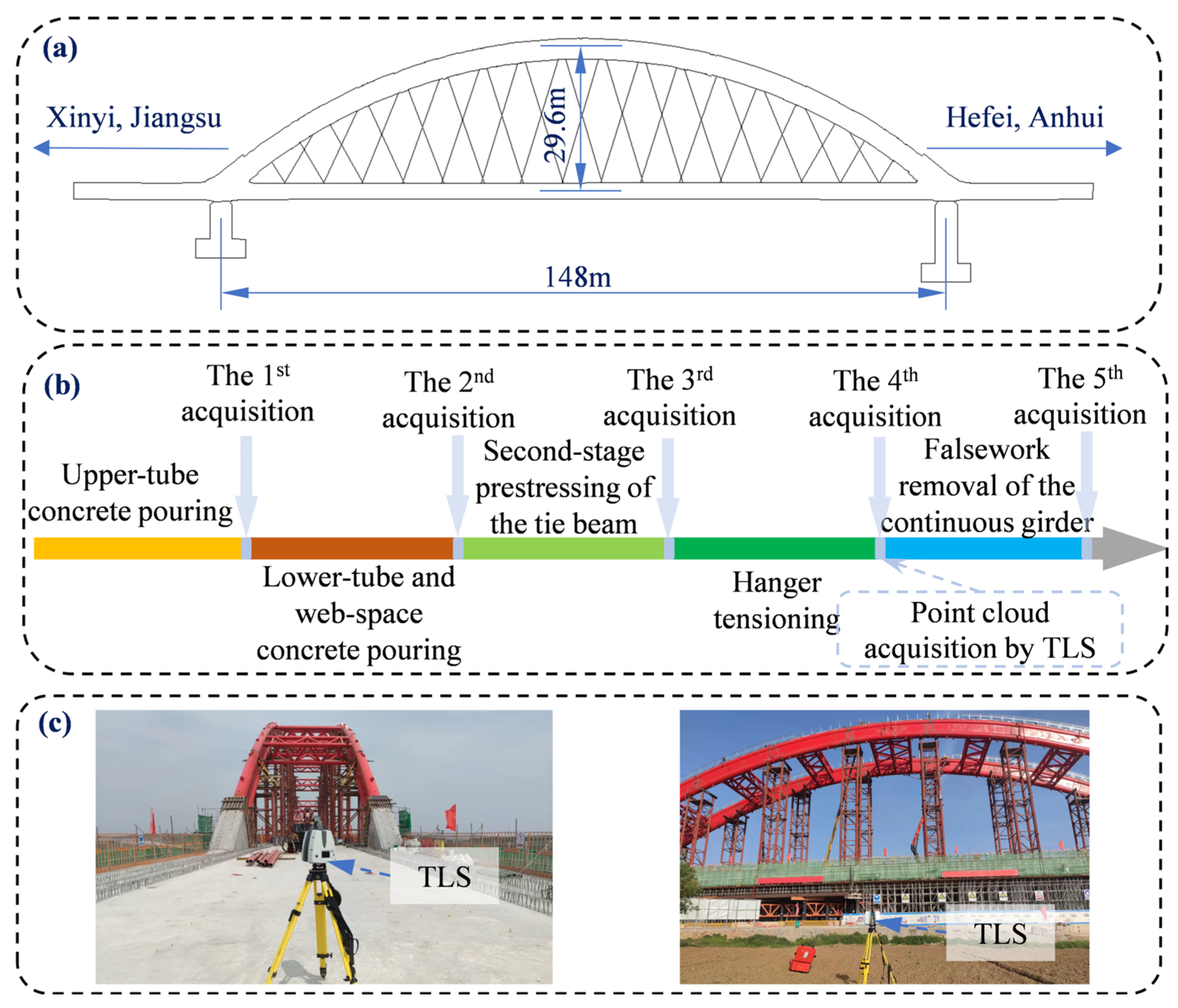
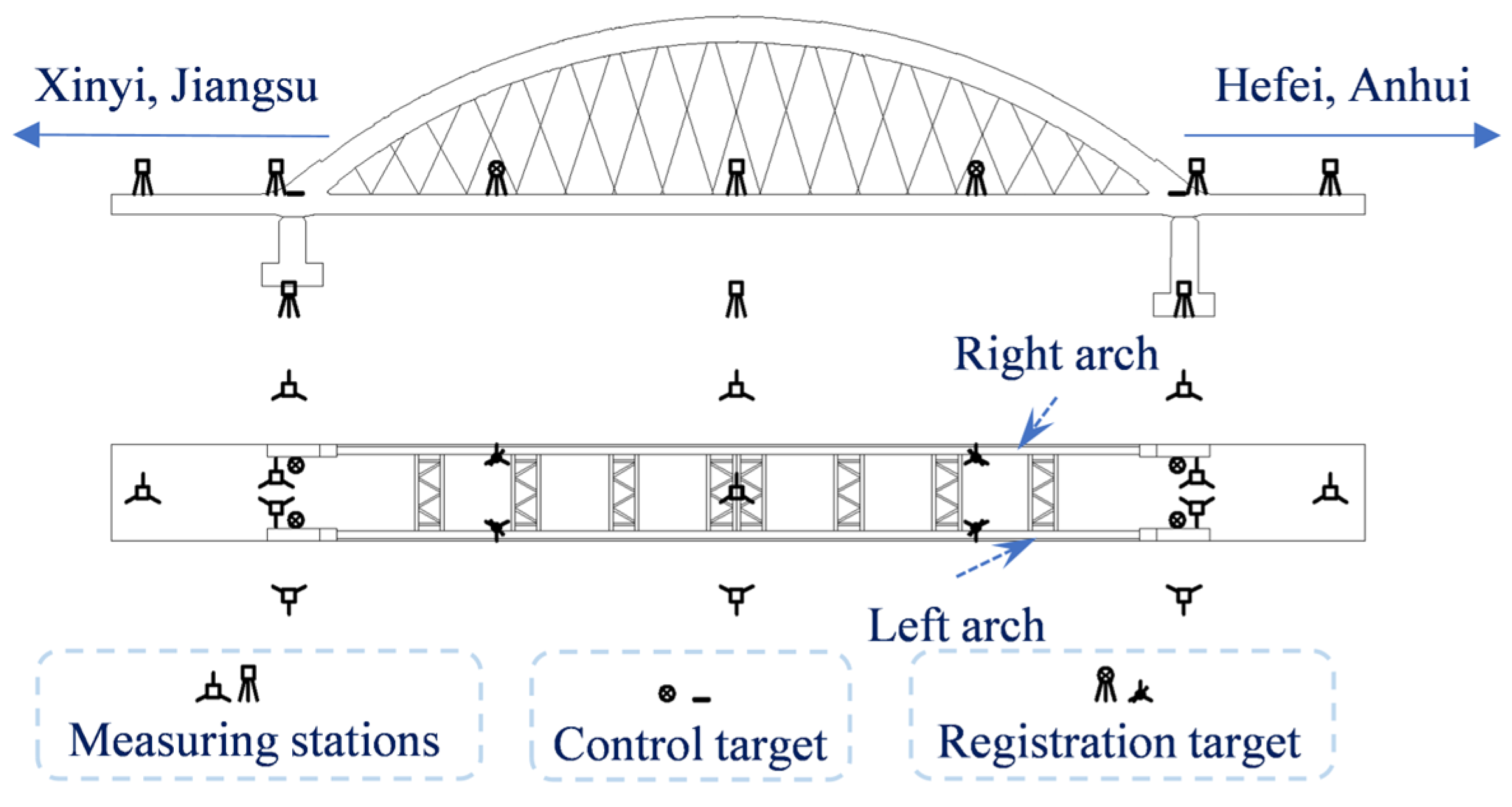
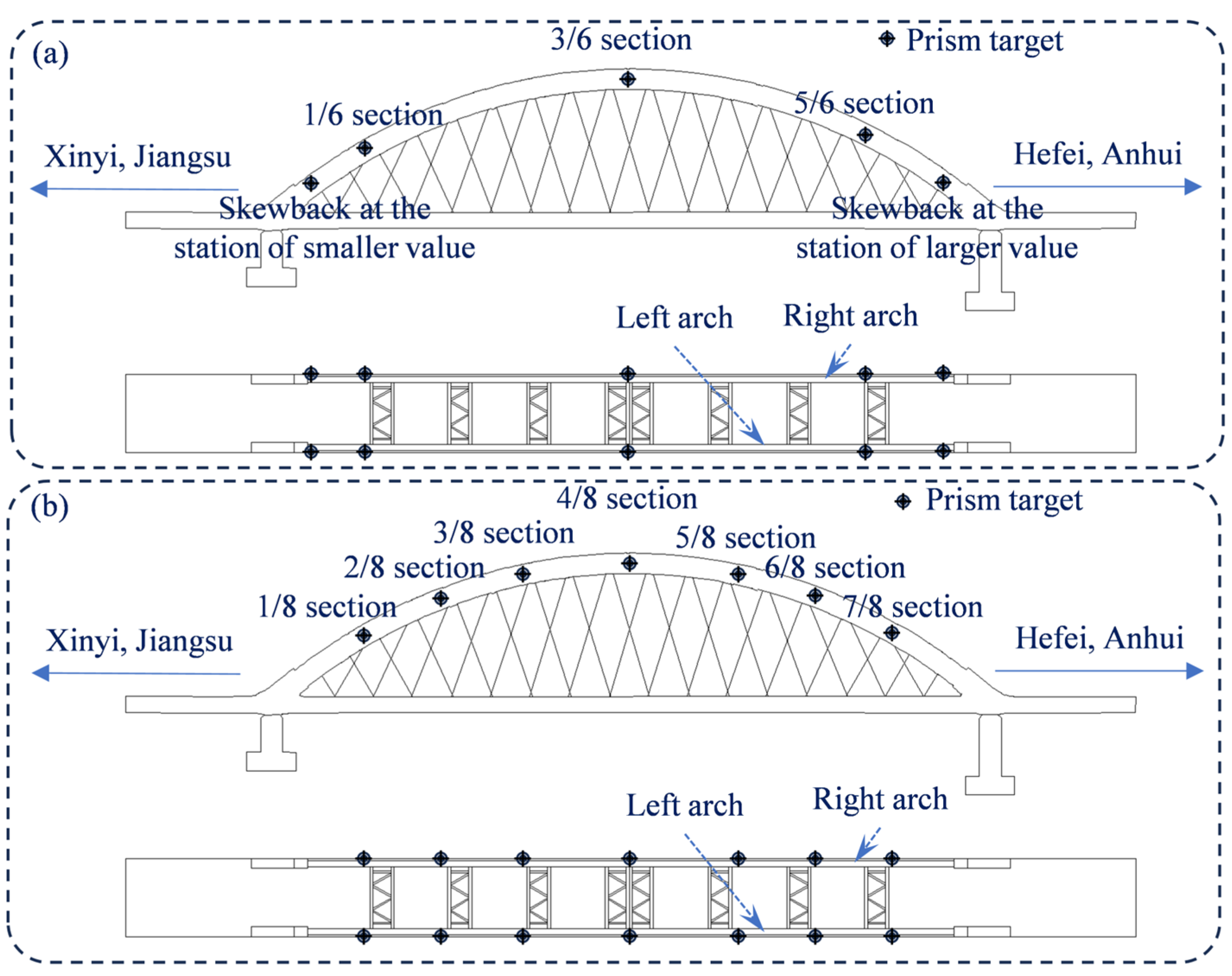
3.1. Description of the CFST Arch Bridge
3.2. Arch Point Clouds Acquisition
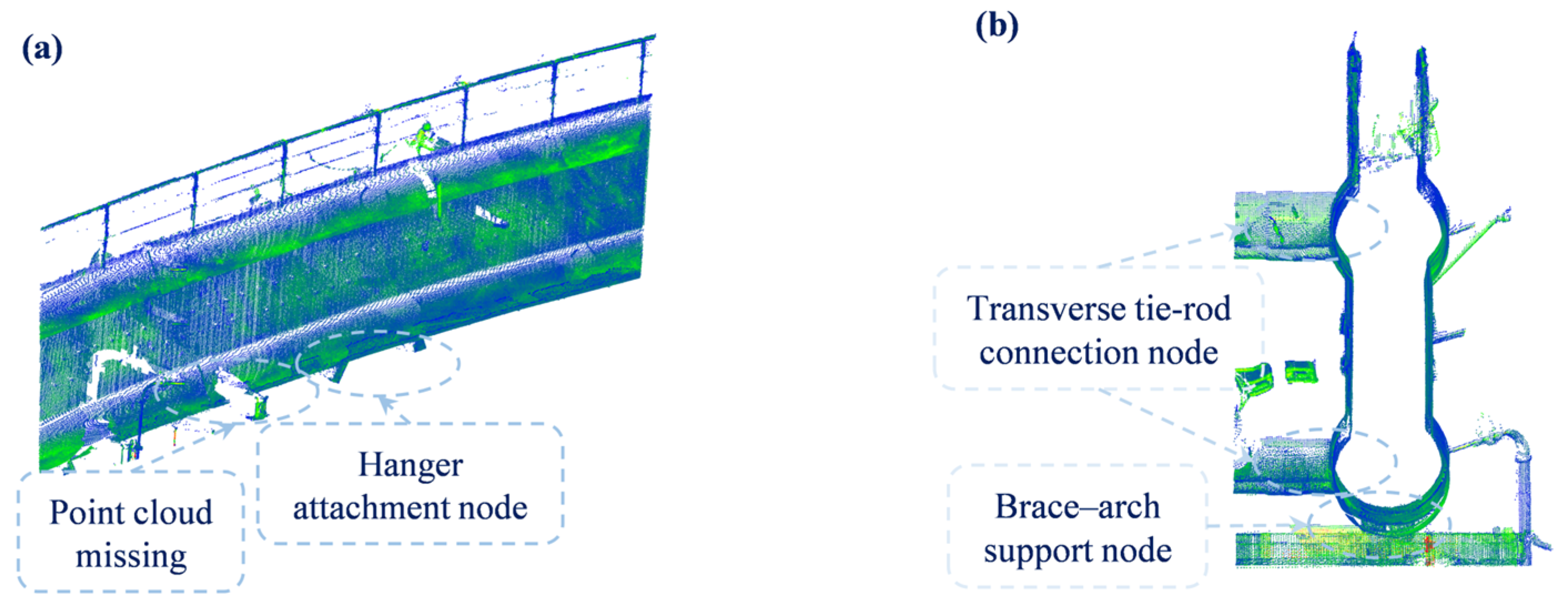
3.3. Arch Profile Automatic Extraction
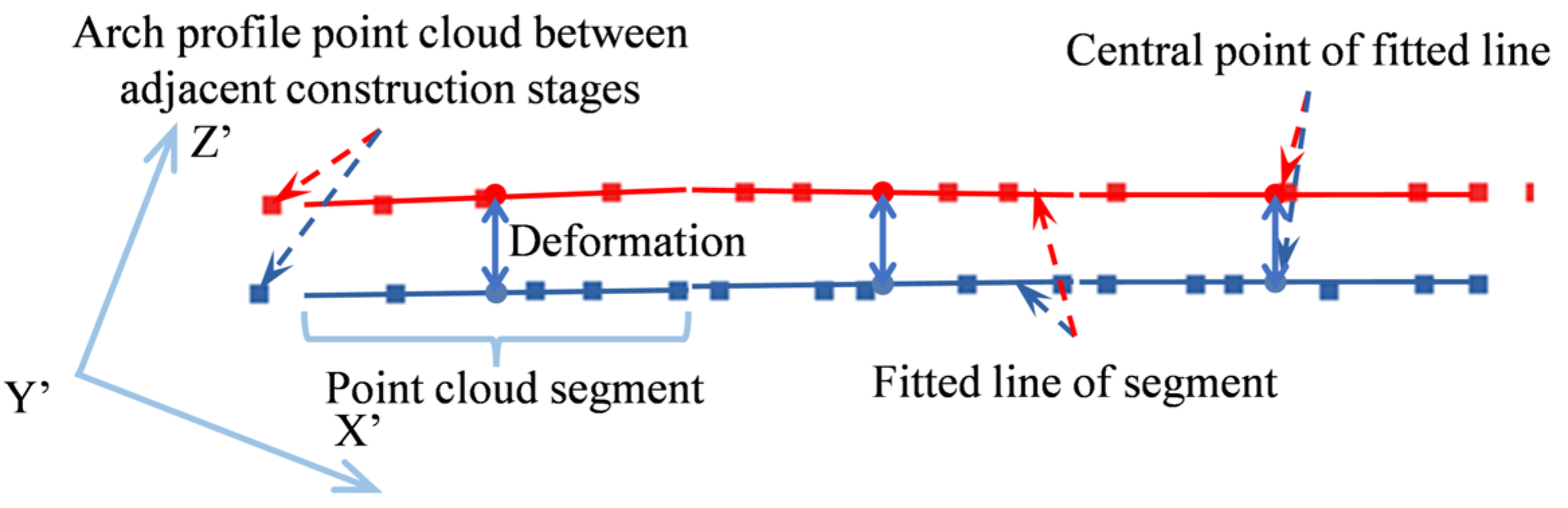
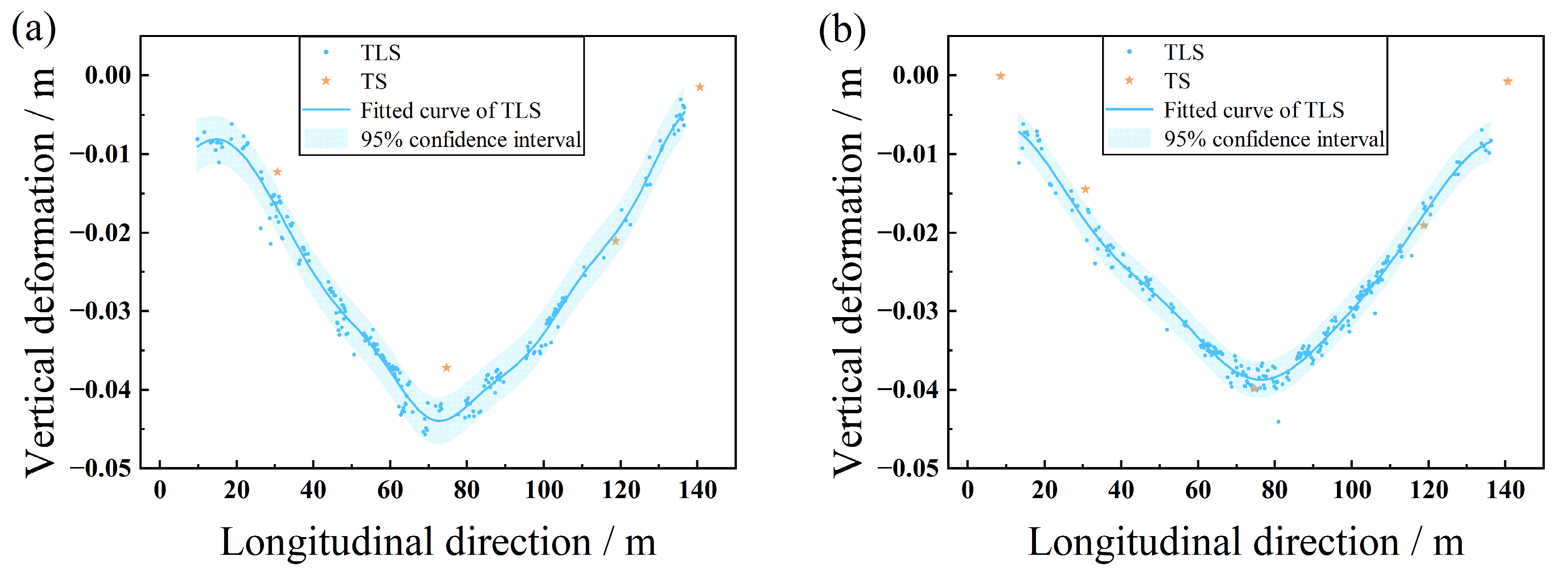
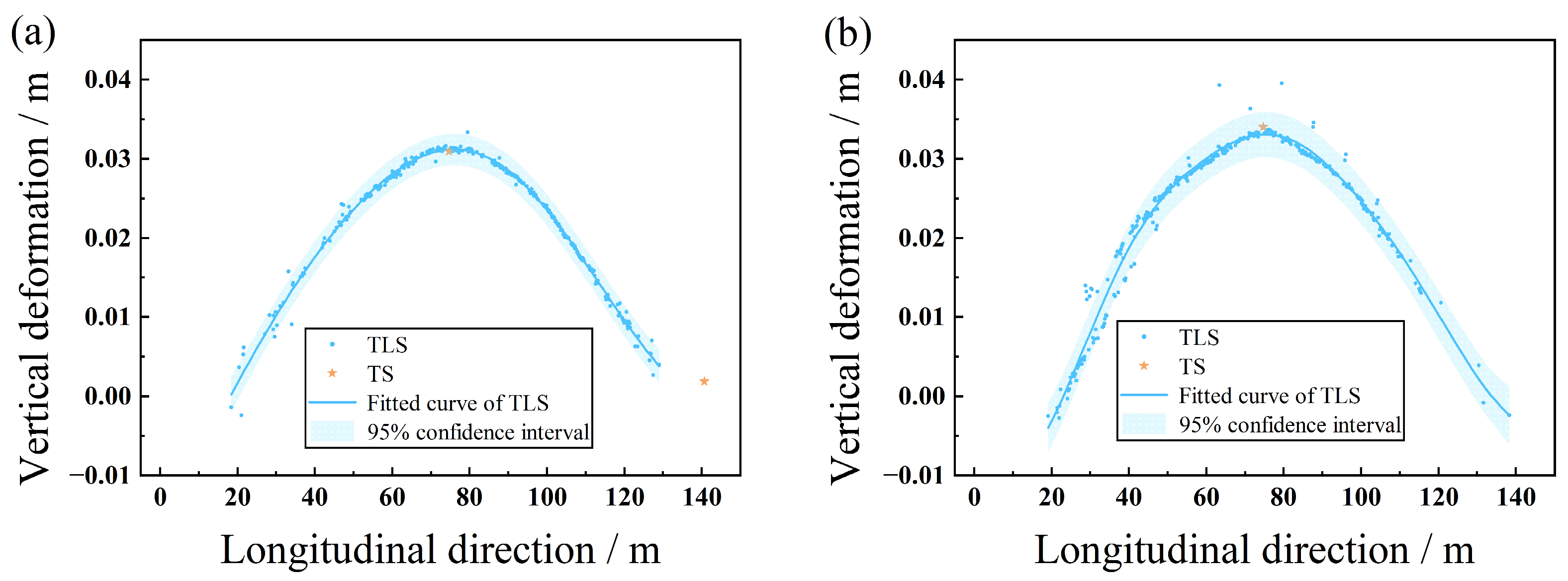
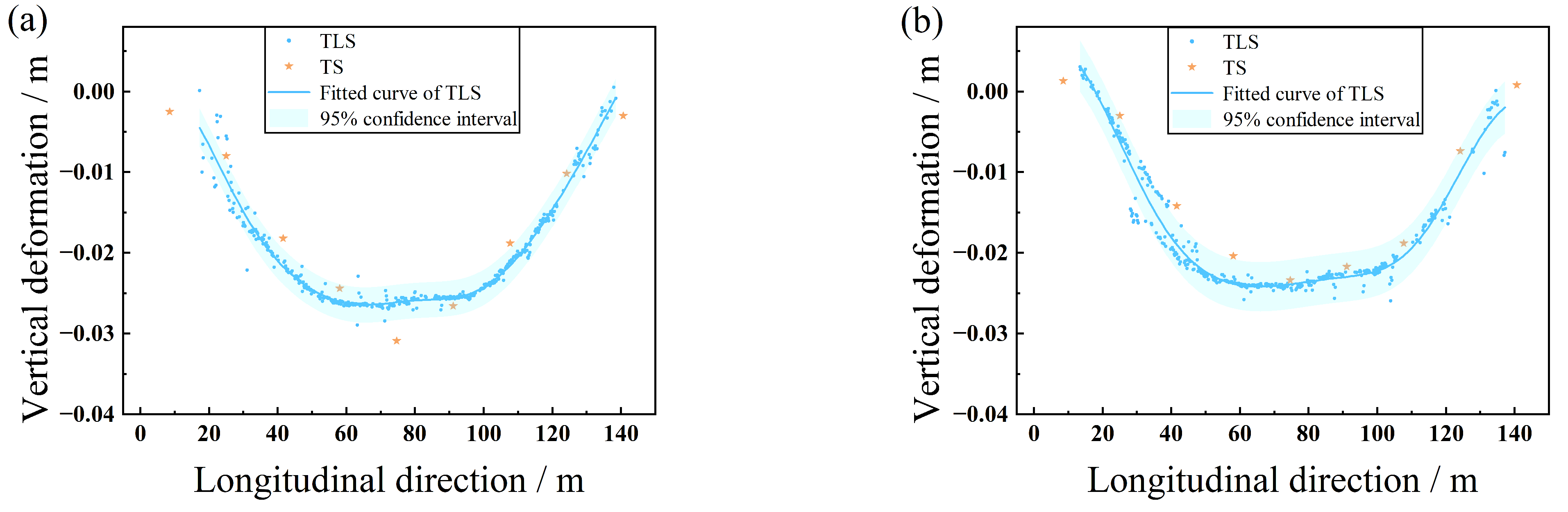
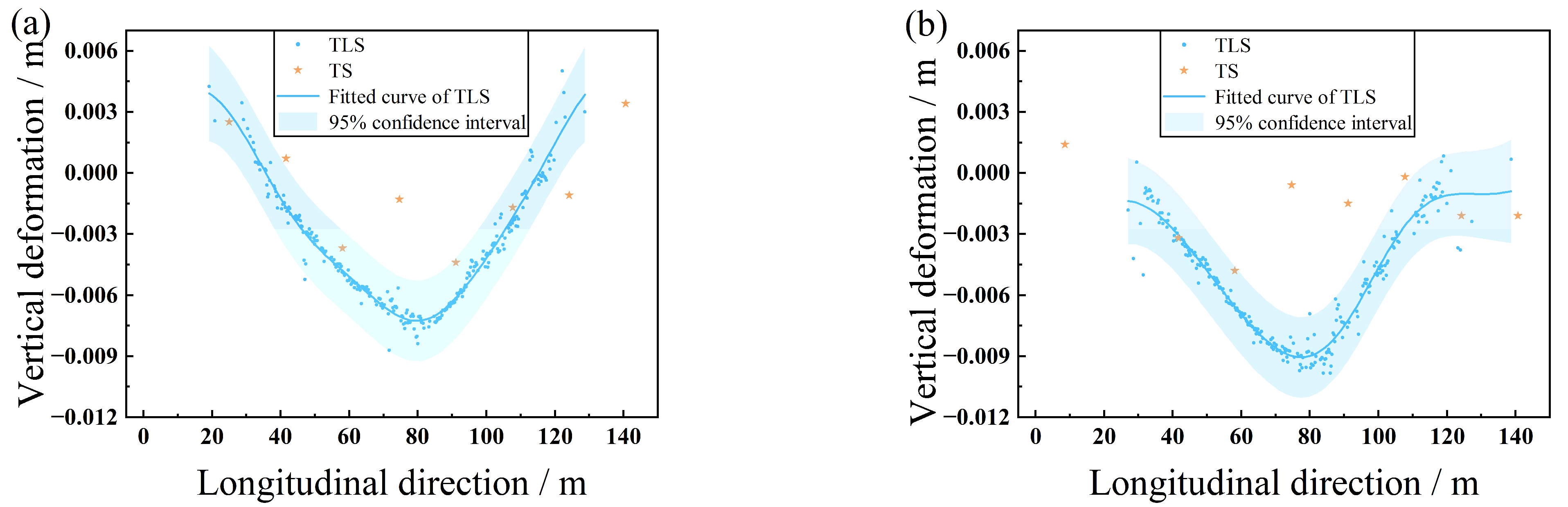
3.4. Arch Vertical Deformation Calculation
3.5. Comparison with TS
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, X.L.; Deng, T.X.; Chen, L.; Chen, J.; Li, A.; Yuan, Q.J.; Fang, W.; Gu, J.F. Application of Bayesian update method in the construction control of continuous rigid frame bridge girders with high piers and large spans. Buildings 2023, 13, 1556. [Google Scholar] [CrossRef]
- Au, F.T.F.; Wang, J.J.; Liu, G.D. Construction control of reinforced concrete arch bridges. J. Bridge Eng. 2003, 8, 39–45. [Google Scholar] [CrossRef]
- Gou, H.G.; Liu, C.; Bao, Y.; Han, B.; Pu, Q.H. Construction monitoring of self-anchored suspension bridge with inclined tower. J. Bridge Eng. 2021, 26, 05021011. [Google Scholar] [CrossRef]
- Li, Z.P.; Dong, X.T.; Chen, H.R.; Chi, L.J.; Zhang, Z.C. Overall lifting construction control method for large-segment steel arch bridges based on unstressed state control theory. Buildings 2025, 15, 523. [Google Scholar] [CrossRef]
- Pan, J.; Wang, X.R.; Huang, K.N.; Wang, W.S. Symmetrically construction monitoring analysis and completed state evaluation of a tied steel box arch bridge based on finite element method. Symmetry 2023, 15, 932. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Wang, L.L.; Nong, Y.; Wang, W.S. Construction-monitoring analysis of a symmetrical rigid frame tied steel box arch bridge in southwest China based on segmental assembly technique. Symmetry 2023, 15, 1437. [Google Scholar] [CrossRef]
- Yin, Y.H.; Liu, X.L.; Hu, B.; Chen, W.J.; Guo, X.; Ma, D.Y.; Ding, X.H.; Han, L.H.; Yu, Q.F. A displacement measurement methodology for deformation monitoring of long-span arch bridges during construction based on scalable multi-camera system. Comput. Aided Civil Infrastruct. Eng. 2025, 40, 1871–1885. [Google Scholar] [CrossRef]
- Nguyen, A.C.; Weinand, Y. Displacement study of a large-scale freeform timber plate structure using a total station and a terrestrial laser scanner. Sensors 2020, 20, 413. [Google Scholar] [CrossRef]
- Psimoulis, P.A.; Stiros, S.C. Measuring deflections of a short-span railway bridge using a robotic total station. J. Bridge Eng. 2013, 18, 182–185. [Google Scholar] [CrossRef]
- Han, Y.T.; Feng, D.M.; Wu, W.W.; Yu, X.Y.; Wu, G.; Liu, J.X. Geometric shape measurement and its application in bridge construction based on UAV and terrestrial laser scanner. Autom. Constr. 2023, 151, 104880. [Google Scholar] [CrossRef]
- Yang, T.; Zou, Y.; Yang, X.F.; Del Rey Castillo, E. Domain knowledge-enhanced region growing framework for semantic segmentation of bridge point clouds. Autom. Constr. 2024, 165, 105572. [Google Scholar] [CrossRef]
- Yang, X.F.; Del Rey Castillo, E.; Zou, Y.; Wotherspoon, L.; Tan, Y. Automated semantic segmentation of bridge components from large-scale point clouds using a weighted superpoint graph. Autom. Constr. 2022, 142, 104519. [Google Scholar] [CrossRef]
- Jing, Y.X.; Sheil, B.; Acikgoz, S. A lightweight Transformer-based neural network for large-scale masonry arch bridge point cloud segmentation. Comput. Aided Civil Infrastruct. Eng. 2024, 39, 2427–2438. [Google Scholar] [CrossRef]
- Lamas, D.; Justo, A.; Soilán, M.; Riveiro, B. Automated production of synthetic point clouds of truss bridges for semantic and instance segmentation using deep learning models. Autom. Constr. 2024, 158, 105176. [Google Scholar] [CrossRef]
- Jing, Y.X.; Zhong, J.X.; Sheil, B.; Acikgoz, S. Anomaly detection of cracks in synthetic masonry arch bridge point clouds using fast point feature histograms and PatchCore. Autom. Constr. 2024, 168, 105766. [Google Scholar] [CrossRef]
- Valença, J.; Puente, I.; Júlio, E.; González-Jorge, H.; Arias-Sánchez, P. Assessment of cracks on concrete bridges using image processing supported by laser scanning survey. Constr. Build. Mater. 2017, 146, 668–678. [Google Scholar] [CrossRef]
- Puri, N.; Turkan, Y. Bridge construction progress monitoring using lidar and 4D design models. Autom. Constr. 2020, 109, 102961. [Google Scholar] [CrossRef]
- Cha, G.C.; Park, S.; Oh, T. A terrestrial LiDAR-based detection of shape deformation for maintenance of bridge structures. J. Constr. Eng. Manag. 2019, 145, 04019075. [Google Scholar] [CrossRef]
- Gawronek, P.; Makuch, M. TLS measurement during static load testing of a railway bridge. ISPRS Int. J. Geo-Inf. 2019, 8, 44. [Google Scholar] [CrossRef]
- Lõhmus, H.; Ellmann, A.; Märdla, S.; Idnurm, S. Terrestrial laser scanning for the monitoring of bridge load tests–two case studies. Surv. Rev. 2018, 50, 270–284. [Google Scholar] [CrossRef]
- Mahphood, A.; Arefi, H. Grid-based building outline extraction from ready-made building points. Autom. Constr. 2022, 139, 104321. [Google Scholar] [CrossRef]
- Erdélyi, J.; Kopáčik, A.; Lipták, I.; Kyrinovič, P. Automation of point cloud processing to increase the deformation monitoring accuracy. Appl. Geomat. 2017, 9, 105–113. [Google Scholar] [CrossRef]
- Xiong, W.; Diaw, I.; Zhu, Y.J.; Zhang, H.W.; Cai, C.S. Spatial shape identification of long-span suspension bridges using 3d laser scanning technology. J. Civ. Struct. Health Monit. 2024, 14, 383–400. [Google Scholar] [CrossRef]
- Li, X.X.; Deng, E.; Wang, Y.W.; Ni, Y.Q. 3D laser scanning for predicting the alignment of large-span segmental precast assembled concrete cable-stayed bridges. Autom. Constr. 2023, 155, 105056. [Google Scholar] [CrossRef]
- Derpanis, K.G. Overview of the RANSAC algorithm. Image Rochester NY 2010, 4, 2–3. [Google Scholar]
- Xu, Y.S.; Tong, X.H.; Stilla, U. Voxel-based representation of 3D point clouds: Methods, applications, and its potential use in the construction industry. Autom. Constr. 2021, 126, 103675. [Google Scholar] [CrossRef]
- Greenacre, M.; Groenen, P.J.F.; Hastie, T.; D’Enza, A.L.; Markos, A.; Tuzhilina, E. Principal component analysis. Nat. Rev. Method. Prim. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Hansen, P.C.; Pereyra, V.; Scherer, G. Least Squares Data Fitting with Applications; JHU Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Suhulz, E.; Speekenbrink, M.; Krause, A. Atutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Williams, C.K.I.; Rasmussen, C.E. Gaussian processes for regression. Adv. Neural Inf. Process. Syst. 1995, 8. Available online: https://proceedings.neurips.cc/paper/1995/hash/7cce53cf90577442771720a370c3c723-Abstract.html (accessed on 11 July 2025).
| Point Cloud Acquisition by TLS | Arch Bridge Point Cloud | Arch Point Cloud | Arch Profile |
|---|---|---|---|
| The 1st acquisition |  (point count = 933,590,837) |  (point count = 24,078,996) |  (point count = 141,038) |
| The 2nd acquisition |  (point count = 633,536,300) |  (point count = 39,415,439) |  (point count = 85,369) |
| The 3rd acquisition |  (point count = 537,051,279) |  (point count = 38,937,110) |  (point count = 167,111) |
| The 4th acquisition |  (point count = 770,959,076) |  (point count = 47,674,762) |  (point count = 538,979) |
| The 5th acquisition |  (point count = 758,519,093) |  (point count = 46,700,482) |  (point count = 667,235) |
| Sub Step | Parameter | Value | Rationale | |
|---|---|---|---|---|
| Step 1 | Voxel down-sampling | Voxel size | 0.05 m | Matches the minimum cross-sectional dimension of component. |
| Coarse partition | Partition length l1 | 1 m | Approximates the width of arch cross-sections. | |
| Partition along the curve | Partition length l2 | 0.25 m | One quarter of the cross-section width. | |
| Step 2 | RANSAC | Angle threshold | 7.5° | Reflects maximum allowable deviation between cylindrical axis and arch transverse direction (v3). |
| Radius deviation t | 0.01 m | Ensures extracted cylinders match design radius R. | ||
| Distance threshold | 0.05 m | Matches voxel size to filter noise while retaining points within typical surface roughness. | ||
| Minimum number of internal points MinPts1 | 10 | Threshold derived empirically. Reject spurious cylinders. | ||
| Expected probability p | 0.99 | Ensures >99% probability of finding valid cylinders within iterations. | ||
| Maximum number of iterations k | Conservative upper bound for complex scenes. | |||
| Coarse extraction | Distance threshold | 0.05 m | Consistent with RANSAC inlier threshold to maintain data coherence. | |
| Fine Extraction | Angle threshold | 5° | Filters non-radial points. Tolerance set below typical noise levels in TLS normal estimation. | |
| Step 3 | Lower profile extraction | Angle threshold | 1° | Small value chosen for high accuracy in profile feature identification. |
| Construction Stage | Left Arch (mm) | Right Arch (mm) |
|---|---|---|
| Lower-tube and web-space concrete pouring | 4.13 | 2.22 |
| Second-stage prestressing of the tie beam | 0.24 | 0.93 |
| Hanger tensioning | 2.60 | 2.48 |
| Falsework removal of the continuous girder | 2.24 | 3.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Liu, Y.; Zuo, X.; Zhong, J.; Yuan, Y.; Wang, Y.; Li, C.; Zou, Y. Automated Arch Profile Extraction from Point Clouds and Its Application in Arch Bridge Construction Monitoring. Buildings 2025, 15, 2912. https://doi.org/10.3390/buildings15162912
Wei X, Liu Y, Zuo X, Zhong J, Yuan Y, Wang Y, Li C, Zou Y. Automated Arch Profile Extraction from Point Clouds and Its Application in Arch Bridge Construction Monitoring. Buildings. 2025; 15(16):2912. https://doi.org/10.3390/buildings15162912
Chicago/Turabian StyleWei, Xiaojun, Yang Liu, Xianglong Zuo, Jiwei Zhong, Yihua Yuan, Yafei Wang, Cheng Li, and Yang Zou. 2025. "Automated Arch Profile Extraction from Point Clouds and Its Application in Arch Bridge Construction Monitoring" Buildings 15, no. 16: 2912. https://doi.org/10.3390/buildings15162912
APA StyleWei, X., Liu, Y., Zuo, X., Zhong, J., Yuan, Y., Wang, Y., Li, C., & Zou, Y. (2025). Automated Arch Profile Extraction from Point Clouds and Its Application in Arch Bridge Construction Monitoring. Buildings, 15(16), 2912. https://doi.org/10.3390/buildings15162912







