A SketchUp-Based Optimal Design Tool for PV Systems in Zero-Energy Buildings During the Early Design Stage
Abstract
1. Introduction
2. Algorithm and Tool Development
2.1. Energy Performance Calculation Algorithm
2.2. PSO-Based PV Preliminary Sizing Algorithm for Achieving Target ESR
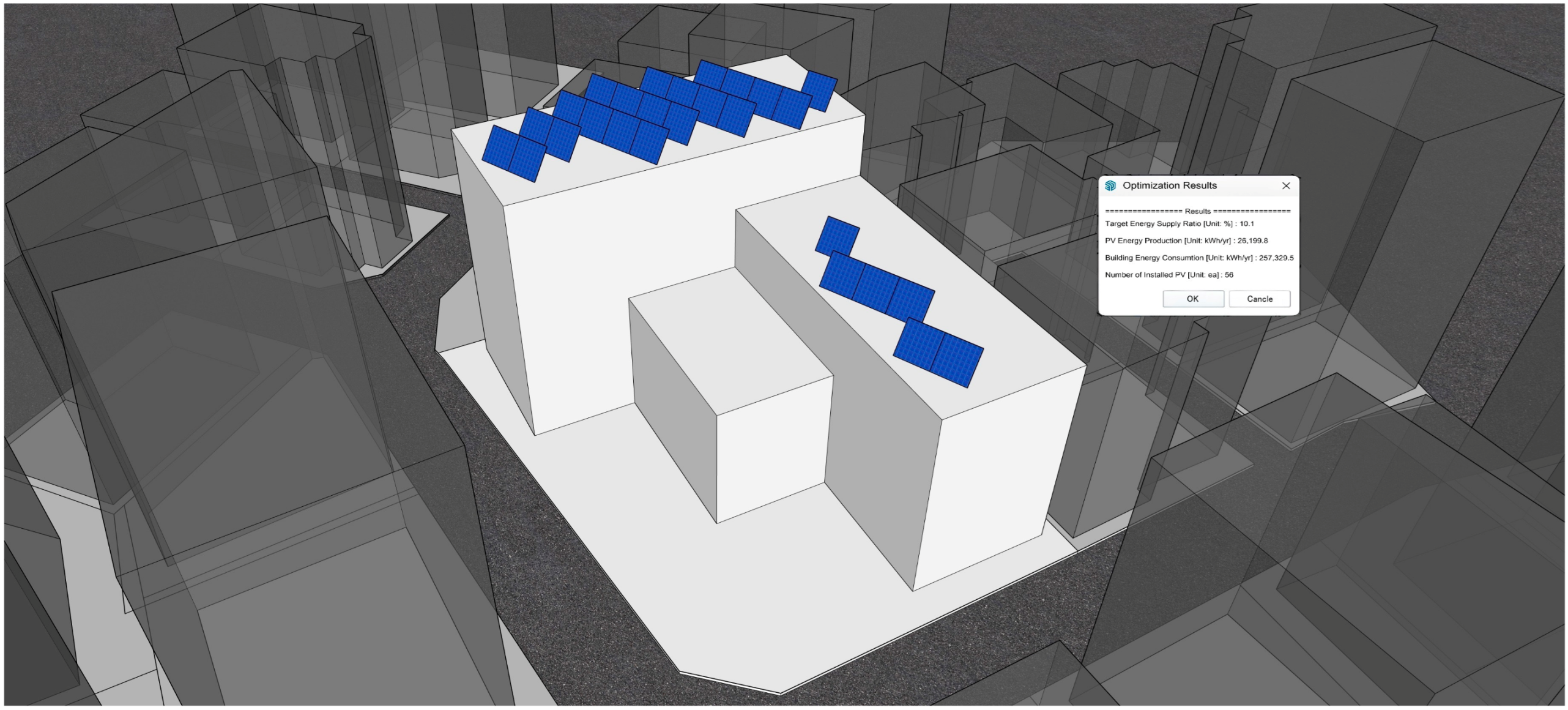
2.3. Implementation in SketchUp
3. Verification of PV Performance Evaluation Module
3.1. Verification Method
3.2. Verification Results
4. Case Studies on Diverse Building Masses
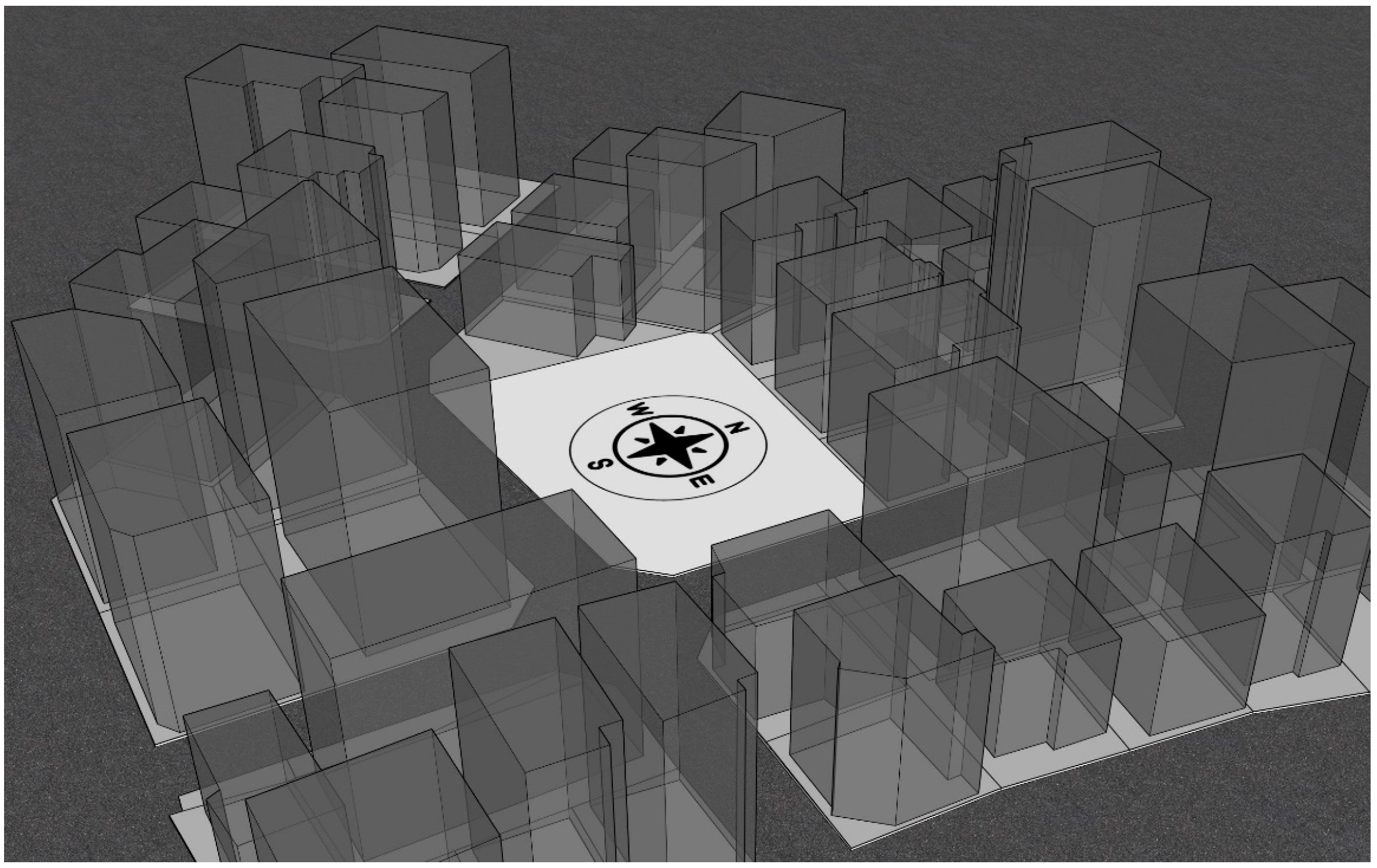
4.1. Test Overview
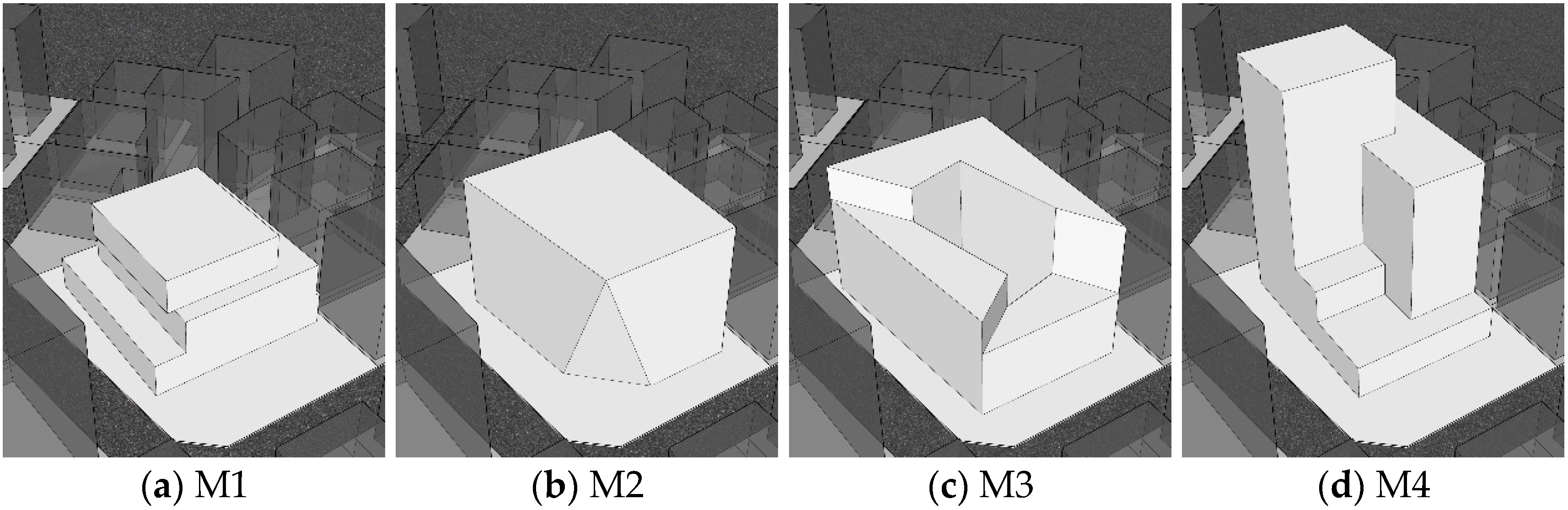
4.2. Results of Determined Building Masses
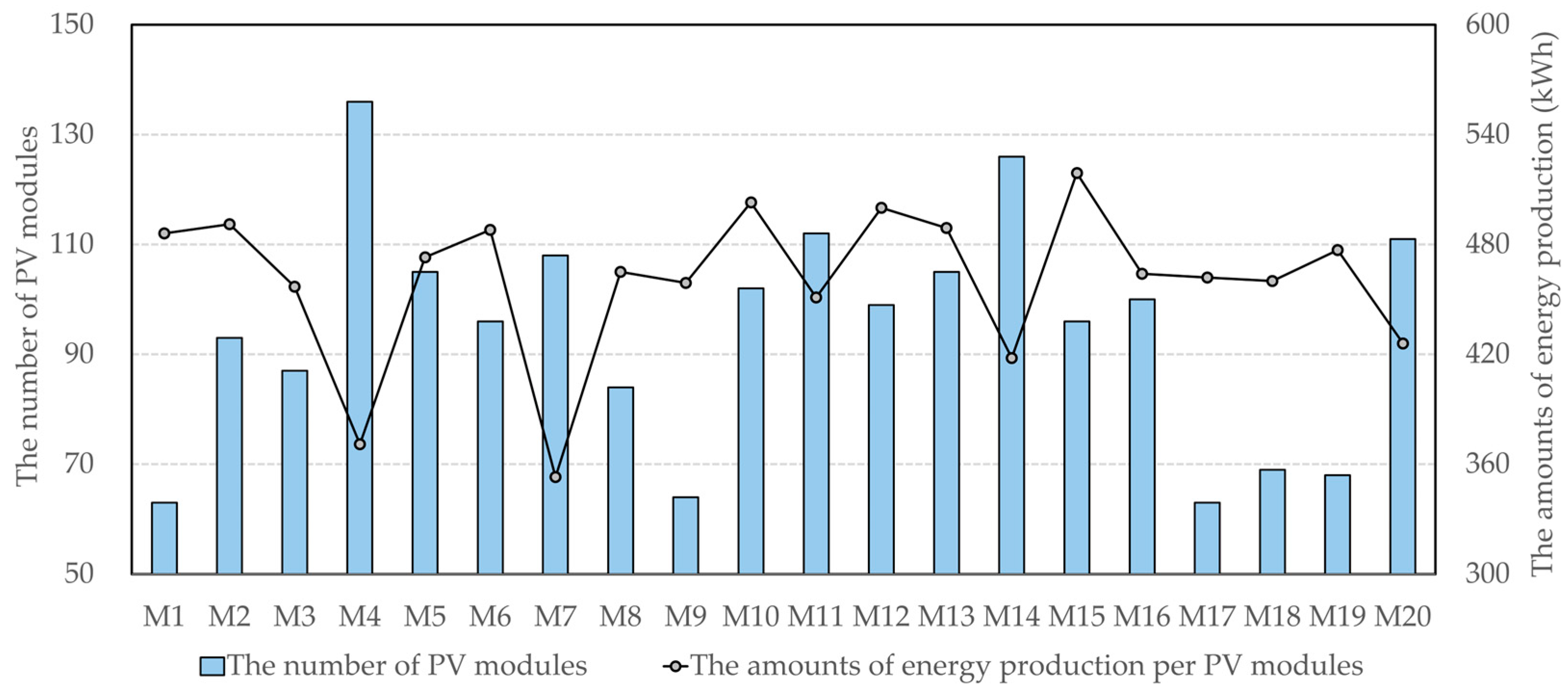
4.3. Results of Optimal Design Alternatives for Each Building Mass
5. Discussion
5.1. Capabilities
5.2. Integrating Mass Studies and PV Performance in Early Design Stage
5.3. Limitations and Future Research
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ambient temperature [°C] | |
| PV module rear surface temperature [°C] | |
| PV cell temperature [°C] | |
| PV module STC temperature [°C] | |
| Total irradiance incident on the PV module surface [W/m2] | |
| PV module area [m2] | |
| PV module DC power generation loss rate [%] | |
| Loss rate excluding inverter AC conversion efficiency [%] | |
| Vertical length of the PV module [m] | |
| DC power output of the PV module [W] | |
| AC power converted by the inverter [W] | |
| Required number of PV modules meeting the target ESR [-] | |
| Energy self-sufficiency rate [-] | |
| Annual energy supply from the RES [Wh] | |
| Annual building energy consumption [Wh] | |
| PV module efficiency as a function of cell temperature [°C] | |
| Sun altitude angle [°] | |
| Tilt angle of the PV module [°] | |
| PV module nominal efficiency [%] | |
| Inverter conversion efficiency [%] | |
| PV module temperature coefficient [%/°C] | |
| Temperature coefficient [°C] | |
| Temperature coefficient [-] | |
| Temperature coefficient [-] | |
| Wind speed [m/s] |
References
- Attia, S.; Gratia, E.; De Herde, A.; Hensen, J.L. Simulation-Based Decision Support Tool for Early Stages of Zero-Energy Building Design. Energy Build. 2012, 49, 2–15. [Google Scholar] [CrossRef]
- Bogenstätter, U. Prediction and Optimization of Life-Cycle Costs in Early Design. Build. Res. Inf. 2000, 28, 376–386. [Google Scholar] [CrossRef]
- Li, D.H.; Yang, L.; Lam, J.C. Zero Energy Buildings and Sustainable Development Implications—A Review. Energy 2013, 54, 1–10. [Google Scholar] [CrossRef]
- Araji, M.T. Surface-to-Volume Ratio: How Building Geometry Impacts Solar Energy Production and Heat Gain through Envelopes. IOP Conf. Ser. Earth Environ. Sci. 2019, 323, 012034. [Google Scholar] [CrossRef]
- Liang, H.; Shen, J.; Yip, H.-L.; Fang, M.M.; Dong, L. Unleashing the Green Potential: Assessing Hong Kong’s Building Solar PV Capacity. Appl. Energy 2024, 369, 123567. [Google Scholar] [CrossRef]
- Sánchez-Pantoja, N.; Vidal, R.; Pastor, M.C. Aesthetic Perception of Photovoltaic Integration within New Proposals for Ecological Architecture. Sustain. Cities Soc. 2018, 39, 203–214. [Google Scholar] [CrossRef]
- Zhou, A.; Thomaschke, R.; Wessels, A.; Glunz, S.; Speck, T.; Kiesel, A. (Not) in My City: An Explorative Study on Social Acceptance of Photovoltaic Installations on Buildings. Technol. Soc. 2024, 79, 102725. [Google Scholar] [CrossRef]
- Haghighi, Z.; Dehnavi, M.A.; Konstantinou, T.; van den Dobbelsteen, A.; Klein, T. Architectural Photovoltaic Applications: Lessons Learnt and Perceptions from Architects. Buildings 2021, 11, 62. [Google Scholar] [CrossRef]
- Jakica, N. State-of-the-Art Review of Solar Design Tools and Methods for Assessing Daylighting and Solar Potential for Building-Integrated Photovoltaics. Renew. Sustain. Energy Rev. 2018, 81, 1296–1328. [Google Scholar] [CrossRef]
- Kanters, J.; Horvat, M.; Dubois, M.-C. Tools and Methods Used by Architects for Solar Design. Energy Build. 2014, 68, 721–731. [Google Scholar] [CrossRef]
- Panicker, K.; Anand, P.; George, A. Assessment of Building Energy Performance Integrated with Solar PV: Towards a Net Zero Energy Residential Campus in India. Energy Build. 2023, 281, 112736. [Google Scholar] [CrossRef]
- Imalka, S.T.; Yang, R.J.; Zhao, Y. Machine Learning Driven Building Integrated Photovoltaic (BIPV) Envelope Design Optimization. Energy Build. 2024, 324, 114882. [Google Scholar] [CrossRef]
- Vahdatikhaki, F.; Salimzadeh, N.; Hammad, A. Optimization of PV Modules Layout on High-Rise Building Skins Using a BIM-Based Generative Design Approach. Energy Build. 2022, 258, 111787. [Google Scholar] [CrossRef]
- Wijeratne, W.P.U.; Samarasinghalage, T.I.; Yang, R.J.; Wakefield, R. Multi-Objective Optimisation for Building Integrated Photovoltaics (BIPV) Roof Projects in Early Design Phase. Appl. Energy 2022, 309, 118476. [Google Scholar] [CrossRef]
- Muthumanickam, N.K.; Duarte, J.P.; Simpson, T.W. Multidisciplinary Concurrent Optimization Framework for Multi-Phase Building Design Process. Artif. Intell. Eng. Des. Anal. Manuf. 2023, 37, e3. [Google Scholar] [CrossRef]
- Freitas, J.d.S.; Cronemberger, J.; Soares, R.M.; Amorim, C.N.D. Modeling and Assessing BIPV Envelopes Using Parametric Rhinoceros Plugins Grasshopper and Ladybug. Renew. Energy 2020, 160, 1468–1479. [Google Scholar] [CrossRef]
- Ning, G.; Kan, H.; Zhifeng, Q.; Weihua, G.; Geert, D. E-BIM: A BIM-Centric Design and Analysis Software for Building Integrated Photovoltaics. Autom. Constr. 2018, 87, 127–137. [Google Scholar] [CrossRef]
- El Sayary, S.; Omar, O. Designing a BIM Energy-Consumption Template to Calculate and Achieve a Net-Zero-Energy House. Sol. Energy 2021, 216, 315–320. [Google Scholar] [CrossRef]
- Salimzadeh, N.; Vahdatikhaki, F.; Hammad, A. Parametric Modeling and Surface-Specific Sensitivity Analysis of PV Module Layout on Building Skin Using BIM. Energy Build. 2020, 216, 109953. [Google Scholar] [CrossRef]
- Lin, Q.; Kensek, K.; Schiler, M.; Choi, J. Streamlining Sustainable Design in Building Information Modeling BIM-Based PV Design and Analysis Tools. Archit. Sci. Rev. 2021, 64, 467–477. [Google Scholar] [CrossRef]
- Xiang, Y.; Mahamadu, A.-M.; Florez-Perez, L. Engineering Information Format Utilisation across Building Design Stages: An Exploration of BIM Applicability in China. J. Build. Eng. 2024, 95, 110030. [Google Scholar] [CrossRef]
- da Silva, T.F.L.; Vieira, D.R.; de Carvalho, M.M. Exploring the Challenges in Building Information Modeling (BIM) during the Design Phase: Evidence from Cross-Country Studies. IEEE Trans. Eng. Manag. 2024, 71, 14846–14860. [Google Scholar] [CrossRef]
- Bazafkan, E.; Pont, U.; Mahdavi, A. Usability and Usefulness of Non-Conventional Building Performance Simulation Tools in Architectural Design Processes. Appl. Mech. Mater. 2019, 887, 219–226. [Google Scholar] [CrossRef]
- Chopra, A.; Laura, T. Introduction to Google Sketchup, 1st ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Tang, H.; Wang, C.X. Discussing Sketchup Software in the Application of Architectural Design Teaching. J. Theor. Appl. Inf. Technol. 2013, 48, 1319–1323. [Google Scholar]
- American Society of Heating Refrigerating and Air-Conditioning Engineers. 2013 ASHRAE Handbook—Fundamentals; American Society of Heating Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2013. [Google Scholar]
- Gilman, P. SAM Photovoltaic Model Technical Reference Update; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2018. Available online: https://sam.nrel.gov/images/web_page_files/sam-help-2018-11-11-r4.pdf (accessed on 15 May 2025).
- CETC. Clean Energy Project Analysis: RetScreen® Engineering & Cases Textbook—Photovoltaic Project Analysis Chapter; CANMET Energy Technology Centre—Varennes (CETC): Varennes, QC, Canada, 2004. [Google Scholar]
- Reindl, D.T. Estimating Diffuse Radiation on Horizontal Surfaces and Total Radiation on Tilted Surfaces. Ph.D. Thesis, University of Wisconsin, Madison, WI, USA, 1988. [Google Scholar]
- Liu, B.Y.; Jordan, R.C. The Long-Term Average Performance of Flat-Plate Solar-Energy Collectors: With Design Data for the US, Its Outlying Possessions and Canada. Sol. Energy 1963, 7, 53–74. [Google Scholar] [CrossRef]
- King, D.L.; Kratochvil, J.A.; Boyson, W.E. Photovoltaic Array Performance Model; Sandia National Laboratories: Albuquerque, NM, USA, 2004; Volume 8. [Google Scholar]
- Evans, D.L. Simplified Method for Predicting Photovoltaic Array Output. Sol. Energy 1981, 27, 555–560. [Google Scholar] [CrossRef]
- Barber, K.A.; Krarti, M. A Review of Optimization Based Tools for Design and Control of Building Energy Systems. Renew. Sustain. Energy Rev. 2022, 160, 112359. [Google Scholar] [CrossRef]
- Bichiou, Y.; Krarti, M. Optimization of Envelope and HVAC Systems Selection for Residential Buildings. Energy Build. 2011, 43, 3373–3382. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Clerc, M.; Kennedy, J. The Particle Swarm-Explosion, Stability, and Convergence in a Multidimensional Complex Space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Blair, N.; DiOrio, N.; Freeman, J.; Gilman, P.; Janzou, S.; Neises, T.; Wagner, M. System Advisor Model (SAM) General Description (Version 2017.9.5); NREL: Golden, CO, USA, 2018. Available online: https://www.nrel.gov/docs/fy18osti/70414.pdf (accessed on 15 May 2025).
- Freeman, J.; Whitmore, J.; Blair, N.; Dobos, A.P. Validation of Multiple Tools for Flat Plate Photovoltaic Modeling against Measured Data. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014; pp. 1932–1937. [Google Scholar]
- Soo-Yeon, H. Statistical Analysis of Energy Use Intensity by End Use in Sample Office Buildings Based on Measurement Data; Ewha Womans University: Seoul, Republic of Korea, 2019. [Google Scholar]
- Attia, S.; De Herde, A.; Gratia, E.; Hensen, J.L.M. Achieving Informed Decision-Making for Net Zero Energy Buildings Design Using Building Performance Simulation Tools. Build. Simul. 2013, 6, 3–21. [Google Scholar] [CrossRef]
- Østergård, T.; Jensen, R.L.; Maagaard, S.E. Early Building Design: Informed Decision-Making by Exploring Multidimensional Design Space Using Sensitivity Analysis. Energy Build. 2017, 142, 8–22. [Google Scholar] [CrossRef]
- White, T.; Dec, M.; Troy, D.; Thornton, B. Effective Early Collaboration Between Engineers and Architects for Successful Energy-Efficient Design. In Proceedings of the SimBuild Conference 2008: 3rd Conference of IBPSA-USA, Berkeley, CA, USA, 30 July–1 August 2008; pp. 182–189. [Google Scholar]
- Akin, O.; Moustapha, H. Strategic Use of Representation in Architectural Massing. Des. Stud. 2004, 25, 31–50. [Google Scholar] [CrossRef]
- Huang, Y.-S.; Chang, W.-S.; Shih, S.-G. Building Massing Optimization in the Conceptual Design Phase. Comput.-Aided Des. Appl. 2015, 12, 344–354. [Google Scholar] [CrossRef]
- Villaggi, L.; Nagy, D. Generative Design for Architectural Space Planning: The Case of the Autodesk University 2017 Layout. 2019. Available online: https://static.au-uw2-prd.autodesk.com/Class_Handout_AS124721_Generative_Design_for_Architectural_Space_Planning_The_Case_of_the_Autodesk_University_2017_Layout_Lorenzo_Villaggi.pdf (accessed on 10 June 2025).
- Wang, L.; Janssen, P.; Ji, G. Optimization-Based Design Exploration of Building Massing Typologies—EvoMass and a Typology-Oriented Computational Design Optimization Method for Early-Stage Performance-Based Building Massing Design. Front. Archit. Res. 2024, 13, 1400–1422. [Google Scholar] [CrossRef]
- Catalina, T.; Virgone, J.; Iordache, V. Study on the Impact of the Building Form on the Energy Consumption. In Proceedings of the Building Simulation 2011, Sydney, Australia, 14–16 November 2011; pp. 1726–1729. [Google Scholar]






| PV Type | Structure and Mounting | a | b | |
|---|---|---|---|---|
| Mono and poly | Glass/Cell/Glass—Open Rack | −3.47 | −0.0594 | 3 |
| Glass/Cell/Glass—Close Roof Mount | −2.98 | −0.0471 | 1 | |
| Thin film | Polymer/Thin Film/Steel—Open Rack | −3.58 | −0.113 | 3 |
| Variable Name | Unit | Range | Step Value |
|---|---|---|---|
| PV array tilt | ° | 0–90 | 5 |
| PV array azimuth | ° | −180–+180 | 5 |
| PV modules per array (Horizontal count) | - | 1–20 | 1 |
| PV modules per array (Vertical count) | - | 1–20 | 1 |
| Roof PV coverage ratio | % | 0–100 | 1 |
| Exterior wall PV coverage ratio | % | 0–100 | 1 |
| Inter-PV array spacing | m | 0.5 |
| Variable Name | Values |
|---|---|
| Number of particles | 100 |
| Maximum iterations | 100 |
| Inertia weight (w) | 0.9–0.4 |
| Cognitive coefficient (c1) | 2.45 |
| Social coefficient (c2) | 1.65 |
| Case No. | Region | Location of PV | Installation Method | Number of PV Modules |
|---|---|---|---|---|
| Case1 | Seoul | Roof | Flush-mounting | 228 |
| Case2 | Roof | Optimally tilted | 108 | |
| Case3 | Exterior wall facing south | Flush-mounting | 48 | |
| Case4 | Exterior wall facing east | Flush-mounting | 36 | |
| Case5 | Exterior wall facing west | Flush-mounting | 36 | |
| Case6 | Daejeon | Roof | Flush-mounting | 228 |
| Case7 | Roof | Optimally tilted | 99 | |
| Case8 | Exterior wall facing south | Flush-mounting | 48 | |
| Case9 | Exterior wall facing east | Flush-mounting | 36 | |
| Case10 | Exterior wall facing west | Flush-mounting | 36 | |
| Case11 | Busan | Roof | Flush-mounting | 228 |
| Case12 | Roof | Optimally tilted | 99 | |
| Case13 | Exterior wall facing south | Flush-mounting | 48 | |
| Case14 | Exterior wall facing east | Flush-mounting | 36 | |
| Case15 | Exterior wall facing west | Flush-mounting | 36 |
| Parameters | Unit | Value |
|---|---|---|
| PV module type | - | Mono |
| Area of PV module | m2 | 0.74 |
| Efficiency of PV module | % | 19.0 |
| Temperature coefficient of PV cell | %/°C | 0.4 |
| Maximum power of PV module | kW | 0.14 |
| Efficiency of inverter | % | 95.777 |
| Parameters | Description | Value [%] |
|---|---|---|
| PV mismatch | PV module mismatch losses | 0.5 |
| Diodes and connections | Diode and interconnection losses | 2.0 |
| DC wiring | DC cabling losses between PV modules | 2.0 |
| AC wiring | Inverter-to-grid AC wiring losses | 1.0 |
| Case No. | Amount of Yearly Generated Energy from PV System | Error in The Yearly Energy Production | Absolute Error-to-PV Module Yield Ratio [-] | ||
|---|---|---|---|---|---|
| SAM [kWh/yr] | PV Design Tool [kWh/yr] | Relative Error [%] | Absolute Error [kWh/yr] | ||
| Case1 | 65,314 | 65,159 | 0.24 | 155 | 0.54 |
| Case2 | 42,505 | 42,124 | 0.90 | 381 | 0.97 |
| Case3 | 10,080 | 10,153 | 0.72 | 73 | 0.35 |
| Case4 | 7120 | 7162 | 0.59 | 42 | 0.21 |
| Case5 | 5302 | 5386 | 1.60 | 85 | 0.58 |
| Case6 | 67,366 | 67,268 | 0.15 | 98 | 0.33 |
| Case7 | 42,071 | 41,839 | 0.55 | 231 | 0.54 |
| Case8 | 10,598 | 10,679 | 0.77 | 81 | 0.37 |
| Case9 | 7467 | 7530 | 0.84 | 63 | 0.30 |
| Case10 | 5831 | 5921 | 1.54 | 90 | 0.56 |
| Case11 | 67,521 | 67,384 | 0.20 | 137 | 0.46 |
| Case12 | 42,394 | 42,085 | 0.73 | 310 | 0.72 |
| Case13 | 8979 | 9061 | 0.91 | 82 | 0.44 |
| Case14 | 6025 | 6085 | 1.00 | 60 | 0.36 |
| Case15 | 4318 | 4415 | 2.25 | 97 | 0.81 |
| Total Floor Area Range (m2) | Annual Energy Consumption Per Unit Area (kWh/m2·yr) |
|---|---|
| Less than 3000 | 115.3 |
| 3000–9999 | 126.4 |
| More than 10,000 | 171.9 |
| Design No. | Number of Floors [-] | Total Floor Area [m2] | Roof Surface Area [m2] | Exterior Wall Surface Area [m2] | Estimated Yearly Energy Consumption [kWh] |
|---|---|---|---|---|---|
| M1 | 3 | 883 | 412 | 816 | 151,787 |
| M2 | 4 | 1323 | 336 | 1168 | 227,388 |
| M3 | 4 | 1155 | 341 | 1761 | 198,625 |
| M4 | 7 | 1465 | 340 | 1728 | 251,838 |
| M5 | 5 | 1444 | 211 | 1805 | 248,224 |
| M6 | 5 | 1358 | 304 | 1705 | 233,355 |
| M7 | 5 | 1073 | 302 | 1763 | 184,363 |
| M8 | 4 | 1136 | 351 | 1462 | 195,193 |
| M9 | 3 | 851 | 413 | 1115 | 146,263 |
| M10 | 4 | 1492 | 452 | 1504 | 256,476 |
| M11 | 4 | 1468 | 452 | 1344 | 252,349 |
| M12 | 5 | 1437 | 390 | 1546 | 246,964 |
| M13 | 5 | 1488 | 410 | 1728 | 255,787 |
| M14 | 5 | 1532 | 453 | 1600 | 263,377 |
| M15 | 5 | 1434 | 400 | 2008 | 246,454 |
| M16 | 4 | 1342 | 420 | 1324 | 230,655 |
| M17 | 3 | 842 | 349 | 854 | 144,820 |
| M18 | 4 | 924 | 324 | 1065 | 158,913 |
| M19 | 3 | 943 | 369 | 1525 | 162,147 |
| M20 | 5 | 1372 | 435 | 1387 | 235,898 |
| Design No. | ESR | Amount of Energy Production Per PV Module [kWh] | Number of PV Modules | Specifics of PV Modules Installation | |||
|---|---|---|---|---|---|---|---|
| At Roof | At Exterior Walls | Tilt Angle | Azimuth Angle | Inter-PV Array Spacing | |||
| M1 | 20.2% | 486 | 63 | 0 | 40 | 0 | - |
| M2 | 20.1% | 491 | 93 | 0 | 20 | 0 | 2 |
| M3 | 20.0% | 457 | 87 | 0 | 35 | −15 | 0.5 |
| M4 | 20.0% | 371 | 88 | 48 | 0 | 0 | 0 |
| M5 | 20.0% | 473 | 105 | 0 | 35 | 0 | 1.5 |
| M6 | 20.1% | 488 | 96 | 0 | 35 | 0 | 3 |
| M7 | 20.7% | 353 | 108 | 0 | 30 | 0 | 3 |
| M8 | 20.0% | 465 | 84 | 0 | 30 | 0 | 2.5 |
| M9 | 20.1% | 459 | 64 | 0 | 40 | 25 | - |
| M10 | 20.0% | 503 | 102 | 0 | 35 | 0 | - |
| M11 | 20.0% | 451 | 112 | 0 | 20 | −20 | 0.5 |
| M12 | 20.1% | 500 | 99 | 0 | 40 | 0 | - |
| M13 | 20.1% | 489 | 105 | 0 | 45 | 0 | - |
| M14 | 20.0% | 418 | 126 | 0 | 10 | 0 | 0.5 |
| M15 | 20.2% | 519 | 96 | 0 | 40 | 0 | - |
| M16 | 20.1% | 464 | 100 | 0 | 40 | 0 | 1.5 |
| M17 | 20.1% | 462 | 63 | 0 | 35 | −5 | 3 |
| M18 | 20.0% | 460 | 69 | 0 | 40 | −35 | - |
| M19 | 20.0% | 477 | 68 | 0 | 30 | −10 | 1 |
| M20 | 20.0% | 426 | 111 | 0 | 30 | 0 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.H.; Baek, S.H. A SketchUp-Based Optimal Design Tool for PV Systems in Zero-Energy Buildings During the Early Design Stage. Buildings 2025, 15, 2863. https://doi.org/10.3390/buildings15162863
Park JH, Baek SH. A SketchUp-Based Optimal Design Tool for PV Systems in Zero-Energy Buildings During the Early Design Stage. Buildings. 2025; 15(16):2863. https://doi.org/10.3390/buildings15162863
Chicago/Turabian StylePark, Jun Hwan, and Seung Hyo Baek. 2025. "A SketchUp-Based Optimal Design Tool for PV Systems in Zero-Energy Buildings During the Early Design Stage" Buildings 15, no. 16: 2863. https://doi.org/10.3390/buildings15162863
APA StylePark, J. H., & Baek, S. H. (2025). A SketchUp-Based Optimal Design Tool for PV Systems in Zero-Energy Buildings During the Early Design Stage. Buildings, 15(16), 2863. https://doi.org/10.3390/buildings15162863





