Pricing Decisions in a Dual-Channel Construction and Demolition Waste Recycling Supply Chain with Bilateral Free-Riding Behavior

Abstract

The dramatic increase in global construction and demolition waste (CDW) is a considerable environmental challenge, but recycled building materials face serious marketing bottlenecks. Although existing studies have focused on the technological path and policy regulation of CDW management, they have not yet considered the impact of sales effort level under the dual-channel sales model. Considering the coexistence of price competition and bidirectional free-riding behavior, this paper constructs a Stackelberg game model, which includes a construction waste remanufacturer with both online and offline sales channels and a building materials retailer, to reveal the pricing decision-making mechanism under bidirectional free-riding behavior. The results of the study show that (1) in the decentralized decision-making model, offline free-riding has a negative effect on the online channel, and when the effort cost coefficient is high, it increases the retail price of recycled cement in the offline channel; at the same time, under high cross-price sensitivity, both the manufacturer and the retailer are negatively affected by online free-riding behaviors; (2) in contrast to decentralized decision-making, centralized decision-making motivates the supply chain as a whole to significantly increase sales effort investment and develop a better pricing strategy under the condition of satisfying the threshold cross-price sensitivity, which ultimately improves the overall efficiency of the supply chain. The findings provide an important theoretical basis and management insights for the coordination of dual-channel supply chains, the governance of free-riding behavior, and the promotion of recycled building materials in the recycling economy.

1. Introduction

Construction and demolition waste (CDW) is generally defined as abandoned substances generated during construction, renovation, and demolition activities and accounts for approximately 30–40% of the total solid waste worldwide [1,2]. The amount generated has continued to rise in recent years, with annual global production exceeding 10 billion tons [3]. In terms of geographical distribution, the problem of CDW is prevalent in countries with different levels of development. Statistics from developed countries show that the amount of CDW generated in the United States reached 600 million tons in 2018 [4]; in 2022, the total amount of waste generated by all economic activities and households in the European Union increased to 2233 million tons, with construction activities accounting for 38.4% of the total [5]. As the world’s largest developing country, China generated approximately 2.4 billion tons of CDW in 2020, more than 10 times the amount of domestic waste generated in the same year [6]. This figure is expected to grow rapidly to 3.2 billion tons, accounting for more than 40% of the total amount of municipal waste [7], which makes the situation of management grim. Recycling has long been recognized as an effective strategy for solving the CDW problem [8], with significant advantages in terms of resource recovery and environmental protection, and has therefore received increasing attention from more countries [9].

The process of recycling CDW involves three main stages: first, the generation and collection of waste; second, recycling and manufacturing; and finally, the sale of the product [9]. For a long time, researchers and construction practitioners have focused on technological methods for recycling CDW and have achieved relatively fruitful research results. Technical issues are no longer the key cause of low CDW recycling rates. In Singapore, for example, it is possible to achieve 100% recycling of steel slag, asphalt wear layers, and CDW aggregates with existing technology [10]. The real problem with the continuation of recycled building materials lies on the demand side. Taking Sichuan U Renewables Resources Co., Ltd., in China as an example, although it has enormous market advantages such as neat factories, complete equipment, and rich products, the sales of recycled building materials are far lower than expected [11]. Among the complex reasons behind this situation, the lack of effective sales strategies is undoubtedly important. This implies that even excellent products, without proper sales efforts, may be overlooked [12].

Because consumer acceptance of recycled building materials is lower than that of traditional building materials [13], sales efforts are critical to increasing market awareness and consumer acceptance. For example, manufacturers of remanufactured building materials can attract customers through advertising to increase brand awareness. For retailers, promotions, display optimization, and professional guidance are considered effective strategies to stimulate purchasing desires and expand market demand [14]. Research has shown that sales efforts such as advertising, promises, and promotions are effective in improving consumers’ perceptions of remanufactured products, helping them recognize environmental values and thus increasing demand. In practice, companies often adopt a combination of online and offline strategies [15]. For example, Shaanxi Building Materials Technology Group Co., Ltd. promotes its brand through its corporate website and social media and participates in industry exhibitions and seminars to increase the exposure of its entities [16]; Huaxin Cement Co., Ltd. has set up an e-commerce platform, Huaxin Mall, which has led to a significant increase in online turnover from 535 million yuan in 2017 to 709 million yuan in 2018 [17]. Offline retailers have also focused on channel construction and service optimization. For example, the retailer of Huangsha Cement emphasized product knowledge training so that its sales staff had an in-depth understanding of the quality, specifications, and uses of cement to provide professional advice [18]. Moreover, enterprises can increase sales of products by keeping storefronts tidy, implementing flexible pricing, such as wholesale offers and membership discounts, and combining online and offline promotions, such as leafleting at construction sites and social media campaigns. The use of a combination of these sales efforts is especially important for recycled building materials from CDW, a market that requires consumer education.

However, the use of combinations of sales efforts, such as the dual-channel strategy online and offline, results in synergies while also stimulating competition for consumer demand between online and offline [19]. This approach allows consumers to alternate their purchases between these channels, taking advantage of the unique conveniences offered by each, but it is precisely this versatility that leads to free-riding behavior [20]. On the one hand, although recycled building materials are promoted through online and offline promotional activities by remanufacturers, consumers may turn to brick-and-mortar retailers due to pricing strategies or perceived convenience. On the other hand, brick-and-mortar retailers are also involved in promotional and marketing activities during the sales process, and some consumers who receive services and explanations at brick-and-mortar stores may choose to purchase products online, thus causing the manufacturer to ride on the brick-and-mortar retailer’s coattails [21]. This means that bidirectional free riding in today’s dual channels is no longer a one-way street but rather a two-way street. As a result, remanufacturers with online direct sales channels may not be the only ones with bidirectional free-riding, and brick-and-mortar retailers can also benefit from free-riding [19]. In addition, the issue of bidirectional free-riding in the recycled building materials industry has its own peculiarities, as the environmental attributes of recycled materials require more consumer education and market cultivation, which makes the marginal cost of sales efforts higher than that of traditional building materials, a situation that prompts companies to adopt more prudent channel strategies and pricing tactics.

Bidirectional free-riding behavior affects sales efforts in both online and offline channels, which in turn affects the efforts of members of the entire supply chain in terms of pricing and profitability [21]. For the field of CDW resourcing, this study is devoted to constructing a supply chain decision-making model that takes into account the bidirectional free-riding effect and responds to two key questions: (1) How does bidirectional free-riding behavior affect the optimal level of pricing decisions and sales efforts invested by refinishers in a dual-channel supply chain with retailers’ optimal pricing decisions and sales effort investment levels in a dual-channel supply chain? (2) Can a centralized decision-making model improve sales effort and achieve a better pricing strategy than decentralized decision-making does, which ultimately improves the overall efficiency of the supply chain? Therefore, the purpose of this paper is to reveal the mechanism of the effect of bidirectional free-riding behavior on the optimal pricing and selling effort of supply chain entities.

The novelty of this study is reflected in three main aspects: (1) For the first time, free-riding theory is systematically introduced into the research framework of the CDW recycled building material supply chain. Unlike previous studies that focused on ordinary commodities or relatively simple remanufacturing situations [19,22], this study reveals the unique theoretical complexity and management coordination challenges induced by bidirectional free-riding behavior in such a cost-sensitive environment, targeting the core attributes of the recycled building materials market, namely, high consumer education requirements (low acceptance) and high marginal costs of sales efforts. (2) A “remanufacturer of self-built platforms-offline retailer” bilateral game-theoretic framework was constructed, highly aligned with the strategic objectives of resource-recycling enterprises establishing their own direct-sales platforms [17]. This model overcomes the paradigm limitations of traditional bidirectional free-riding research, such as “online retailers-physical retailers” [21,22,23] or “manufacturers-EPC-retailers” [19,20]. By stripping away exogenous variables such as policy subsidies and platform commissions, it accurately depicts the core bidirectional free-riding dynamics driven by the inherent characteristics of CDW (such as high education costs) and the channel structure itself, solving the problem of the disconnect between theory and industry practice. (3) Sales efforts are internalized as continuous decision variables, and quadratic cost function modeling is used. In response to the industry reality of intensive and continuous education in the recycled building materials market, this design breaks through the traditional two-party game paradigm of treating sales efforts as static or discrete [23], enabling the model to dynamically capture the sensitive response of channel competition to high-cost sales efforts. To highlight the differences and innovations between this study and the literature, we comprehensively summarize the various studies related to bidirectional free-riding in

Table 1. A comparison of relevant studies.

References	Free-Riding in CDW	Remanufactured Products	Game Subject		Stackelberg Game	Sales Effort
			Remanufacturer of Self-Built Platforms	Offline Retailer
[19]	×	×	×	√	√	√
[20]	×	√	×	√	√	√
[21]	×	×	×	√	×	×
[24]	×	×	√	√	√	×
[22]	×	×	×	√	√	√
[23]	×	×	×	√	√	×
[25]	×	×	√	√	√	×
This study	√	√	√	√	√	√

Note: “√” indicates that the reference is relevant to the aspect, and “×” indicates that the reference is not relevant to the aspect.

.

The structure of the rest of this study is summarized as follows: in Section 2, we review the relevant literature. In Section 3, we develop the modeling framework. In Section 4, using a decentralized decision model and a centralized decision model, we investigate the impact of free-riding behavior on pricing decisions and selling efforts in dual channels. In Section 5, we conduct a comparative analysis. We perform numerical simulations in Section 6. Finally, Section 7 summarizes the conclusions and implications of this paper.

2. Literature Review and Theory

2.1. Market Promotion Challenges in CDW Recycling

CDW is the main source of solid waste, with an annual production of more than 10 billion tons, and its recycling is crucial to sustainable construction. Although countries such as the Netherlands and Japan have achieved recycling rates of over 90% [6], there remains a significant imbalance globally. For example, even in developed countries such as Portugal, the recycling rate is only 9% [9]. This disparity highlights structural bottlenecks in market promotion: consumers’ willingness to pay for recycled building materials is significantly lower than that for traditional materials [26], even though their technical performance has been validated through engineering testing.

Current research focuses on two main pathways: first, engineering feasibility verification of technologies and the enhancement of material performance, such as studies on the feasibility of recycled aggregate technology [27] and investigations into processes to reduce clinker factors and raw material substitution [28,29]; second, modeling and analysis of policy regulatory mechanisms, such as using evolutionary game models to examine the decision-making incentives of recycling units [30], and exploring the incentive mechanisms of subsidies on supply chains through differential games [9] or Stackelberg games [31,32]. However, these two mainstream paradigms have failed to address the key issues underlying the failure of market promotion effectively, leading to academic models struggling to explain the gaps in the market acceptance of recycled building materials in reality.

Specifically, existing research has two core limitations. First, although scholars have recognized that the lack of sales strategies such as advertising, channel building, and consumer education is a key obstacle to the popularization of remanufactured products [12,33], existing supply chain models are still limited to the indirect game framework of government-recycler-remanufacturer [34,35], ignoring the collaborative sales effort mechanism between remanufacturers and retailers to eliminate consumer quality perception bias in the direct-to-consumer link. Second, in terms of distribution model response, in the context of digital transformation, e-commerce live streaming and social media marketing have not only changed the form of promotion but also reshaped the consumer decision-making path, exacerbating the complexity of channel free-riding [36]. Research on CDW resource utilization has failed to adequately respond to the unique promotional value of the dual-channel distribution model formed by the deep integration of online direct sales and offline retail and the complex channel interactions it triggers, such as the free-riding effect [37].

In summary, existing studies have neglected the collaborative mechanism between remanufacturers and retailers in their sales efforts toward consumers [34], as well as the complexity of free riding in dual channels under digital transformation, making it difficult to break through the bottleneck of ineffective promotion in the recycled building materials market [12]. Therefore, unlike existing policy regulation models, this study reveals the optimal pricing strategy and dynamic investment mechanism for sales efforts under bidirectional free-riding constraints by constructing a manufacturer-led, dual-channel supply chain Stackelberg game model that includes online direct sales and offline retail, providing new theoretical support for CDW market promotion.

2.2. Dual-Channel Supply Chains and Sales Effort Dynamics

A dual-channel market strategy expands coverage by integrating manufacturers’ online direct sales with offline retail, but while improving accessibility, it also intensifies competition between channels [19]. It has become normal for consumers to search for information across channels, which directly leads to a core contradiction in actual operations: the free-riding effect [37]. Under the influence of this effect, the sales effort resources (such as product education and technical services) invested by one party to stimulate demand are easily appropriated by the other channel without compensation [38], which not only weakens the motivation for collaboration among supply chain members but also causes overall efficiency losses [39,40].

Research on dual-channel supply chains has significant theoretical limitations in regard to promoting recycled building materials from CDW. The primary problem lies in the disconnect between model construction and industry practice: most of the literature derives decision-making mechanisms on the basis of standardized commodity sales scenarios [19,23], whose assumed low sales effort costs are fundamentally at odds with the high consumer education costs and strong channel externalities characteristic of recycled building materials, thereby weakening the model’s guidance value. More importantly, the existing model’s setting of game subjects lags behind the industry’s digital transformation process: although the model of manufacturers building their own online platforms to connect directly with end consumers has become the mainstream choice of leading enterprises [17], it has been marginalized in research on the transition from unidirectional free-riding to bidirectional free-riding [21,37]. The existing bidirectional free-riding literature focuses on a three-party game framework (e.g., manufacturer-EPC-retailer), which essentially defaults to the control of third-party platforms over direct sales channels and fails to respond to the industrial reality of resource-based enterprises independently building direct sales channels [19,20].

In addition, the literature systematically simplifies the treatment of sales effort variables. Although some studies involve manufacturer-led models, sales effort is generally set as an exogenous parameter or simplified to a discrete distribution [23], making it difficult to characterize the dynamic decision-making process of supply chain entities continuously adjusting their sales efforts. Although recent modeling methods have begun to internalize continuous variables to improve accuracy [21,24], such breakthroughs have not been effectively applied in the field of CDW recycling supply chains, making it difficult for models to capture the special patterns of sales resource investment in the promotion of recycled building materials.

In summary, existing models ignore the high education costs of recycled building materials and the changes in direct sales models brought about by digital transformation [20,21], making it difficult to capture the dynamics of sales efforts under bidirectional free-riding constraints [22,23]. Therefore, this study focuses on the market characteristics of CDW recycled products and constructs a manufacturer-led, dual-channel Stackelberg game model that includes online direct sales and offline retail. It clearly internalizes sales efforts as continuous decision variables, aiming to reveal the optimal pricing strategy and dynamic coordination mechanism for sales efforts under bidirectional free-riding scenarios.

2.3. Developments in Free-Riding Theory Under Digital Transformation

The core contradiction of free-riding theory lies in the structural separation between value creators and value capturers. Early research focused on the non-excludability of public goods consumption, which led individuals to avoid cost investments [41]. However, the digital channel revolution has restructured traditional value flow paths through immersive content dissemination through live-stream e-commerce and cross-platform information spillover derived from social media [42]. This transformation has given rise to a bidirectional value encroachment phenomenon between physical and digital channels: offline retailers can freely convert the consumption demand stimulated by online technical demonstrations, whereas online platforms can capture the experiential value created by the professional consulting services of physical stores [21]. For example, consumers may verify product performance in-store before shifting to online channels to seek price advantages. This mechanism innovation exposes the explanatory limitations of traditional theory—although the weak free-riding theory corrects the absolute assumption of “completely free occupation”, it fails to analyze the micro pathways of the dynamic transfer of sales effort resources in cross-channel interactions [43].

Existing research has two theoretical limitations in the context of digital transformation. On the one hand, the mainstream three-party game framework presumes that third-party platforms control manufacturers’ direct sales channels [19,20], ignoring the universal practice of remanufacturers building their own direct sales platforms in the CDW recycling industry, such as Huaxin Cement Co., Ltd.’s online mall channel autonomy [17]. When the model architecture is fixed in the “manufacturer-e-commerce platform-retailer” paradigm, it cannot accommodate the dual-channel game situation dominated by recycling enterprises, resulting in a disconnect between theory and practice. On the other hand, when considering the two-party game of manufacturers’ self-built platforms, only unidirectional free-riding is often considered, or the handling of channel conflicts caused by bidirectional free-riding is too static: either the sales effort costs are simplified to exogenous parameters [23] or using discrete decision distributions [22], it is difficult to characterize the dynamic response of remanufacturers and retailers in continuously adjusting resource inputs when faced with consumer perception bias. This simplification further weakens the applicability of the model in the promotion of recycled building materials—the high sales effort costs in this industry cause the marginal utility of sales efforts to show a significant diminishing return, making dynamic coordination mechanisms particularly important.

This study addresses digital challenges through three theoretical breakthroughs: first, by embedding free-riding theory into the unique characteristics of the regenerated product supply chain, a manufacturer-dominated Stackelberg game model is constructed to avoid structural mismatches caused by the intervention of third-party platforms [19,20]; second, it internalizes sales efforts such as physical technical services, marketing, and promotional activities as continuous decision variables, breaking through the shackles of traditional discrete processing [22,23]. Finally, an analysis of the coordination effectiveness of centralized decision-making models on two-way value appropriation reveals the governance logic of internalizing channel externalities within the supply chain to increase the intensity of sales efforts. This provides a theoretical framework for the dilemma of “technological feasibility but market barriers” in the recycled building materials market that is in line with the mechanisms of the digital age.

3. Problem Description and Associated Assumptions

Consider a dual-channel supply chain consisting of an online channel and an offline channel, where the supply chain members consist of a recycled cement manufacturer and a retailer. The manufacturer uses both the traditional channel retailer and its own online channel to sell its products. The retailer buys the product from the manufacturer at a wholesale price and then sells the product to consumers. Both the manufacturer and the retailer conduct sales efforts during this period.

In this study, the recycled cement manufacturer is assumed to act as a leader, and the retailer is assumed to act as a follower. First, the manufacturer and the retailer set their respective sales efforts simultaneously [44]. After observing the sales effort of the retailer, the recycled cement manufacturer determines the wholesale price and the online direct selling price. Finally, the retailer sets the offline channel retail price to maximize profit [37]. In a two-channel supply chain for recycled cement, the sale of recycled cement faces problems such as customers’ doubts about its strength and low market awareness. To open the market, recycled cement manufacturers hold technical seminars and conduct site demonstrations, and retailers train salespeople and optimize displays. These sales efforts are time-consuming, require investment in advance, and are the basis for market development. Therefore, both parties need to determine the optimal sales effort strategy first and then make pricing decisions after the market has initially matured to balance the benefits and maximize the supply chain [19]. The formed game model is shown in Figure 1.

The parameters of this paper are shown in

Table 2. Definition of parameters.

Parameter	Description	Source Papers
$S_i$	The sales effort of the recycled cement manufacturer/retailer in the channel, such as sales and marketing efforts, including advertising and other promotional efforts (decision variable), $i\in \left\{d,r\right\}$	[19,45]
$w$	Wholesale price (decision variable)	[46]
$P_d$	Online direct selling price (decision variable)	[47]
$P_r$	Offline retail price (decision variable)	[48]
$C_p$	The cost of building the recycled cement manufacturer’s self-built platform, $C_p>0$	[49]
${\lambda }_d$	Free-riding coefficient of the online channel, $0<{\lambda }_d<0.5$	[20,45]
${\lambda }_r$	Free-riding coefficient of the offline channel, $0<{\lambda }_r<0.5$	[19,20]
$\gamma$	The cross-price sensitivity coefficient, $0<\gamma <1$	[50,51]
${\eta }_d$	Sales effort cost coefficient for the recycled cement manufacturer in the online channel, ${\eta }_d>0$	[20,52]
${\eta }_r$	Sales effort cost coefficient for the retailer in the offline channel, ${\eta }_r>0$	[19,53]
$D_i$	Expected demand in channel $i$, $i\in \left\{d,r\right\}$	[46]
${\pi }_d$	The recycled cement manufacturer’s profit	[54]
${\pi }_r$	The retailer’s profit	[50]

.

3.1. Model Assumptions

This subsection clearly defines the key theoretical premises of the decision-making model for bidirectional free-riding in the dual-channel supply chain supporting CDW recycling. These basic assumptions jointly define the boundaries of the model, the fundamental relationships between the main entities, and the interactive logic of key variables, forming the basis for subsequent model construction and solution:

(1)

Product homogeneity: Recycled cement products supplied through online sales channels operated directly by manufacturers and offline physical sales channels operated by retailers are completely consistent in terms of core functions, performance quality, and physical characteristics. This setting is the basic premise for the model to depict the essence of competition in a dual-channel structure. This effectively eliminates the interference of product differences on consumer channel preferences and ensures that the model can focus purely on the combined impact of price competition and free-riding behavior on demand.

(2)

Zero production costs and zero basic operating costs: Referring to [25,37], to focus the research on the complex decision-making conflicts caused by the interaction between the dual-channel structure, free-riding behavior, and subject strategies, the model sets the unit production cost of recycled cement manufacturing to zero. Moreover, the model ignores the basic unit sales or fulfillment costs involved in the operation of online direct sales channels and offline channels (such as basic packaging and standardized short-distance logistics).

(3)

Parametric constraints on bidirectional free-riding behavior: The core parameters depicting cross-channel sales service externalities in the model, namely, the free-riding coefficient (${\lambda }_r$) of offline channel members on online channel efforts and the free-riding coefficient (${\lambda }_d$) of online channels on offline channel efforts, are strictly defined to have theoretical values ranging from 0 to 0.5 ($0<{\lambda }_r<0.5$, $0<{\lambda }_d<0.5$). This is because although the sales efforts provided by one channel increase the demand of the other channel, the increase in demand of the other channel will not exceed the increase in the channel’s own market demand [23].

(4)

Specific simplification of sales effort costs: To further control the model parameter dimensions and computational complexity and facilitate a more intuitive analysis of the core mechanisms (free riding and competition), the model sets the sales effort cost coefficient of the retailer’s offline channel to a fixed unit value (${\eta }_r=1$) and sets the sales effort cost coefficient of the online channel to ${\eta }_d=\eta$. This simplification is an important variable normalization technique. By setting ${\eta }_r$ as the benchmark, we can more clearly explore the impact of the relative relationship between the manufacturer’s online sales effort cost coefficient $\eta$ and other parameters (${\lambda }_d$, ${\lambda }_r$) on decision-making [25].

(5)

Intrinsic conditions for model solubility and feasibility: To ensure that subsequent analysis based on the Stackelberg game framework can smoothly obtain meaningful and realistic equilibrium solutions (e.g., nonnegative sales effort values and the existence of a unique internal equilibrium), the model parameters must satisfy a set of specific technical constraints with clear mathematical guarantees: $0<\gamma <{\gamma }_1$ and $\eta >\max \left\{{\eta }_1,{\eta }_2\right\}$. The mathematical basis for this constraint lies in ensuring the strict concavity of the profit functions of manufacturers and retailers within their respective decision spaces (negative Hessian matrix), which is a fundamental requirement for solving interior-point equilibria via first- and second-order optimization conditions. The ultimate goal is to eliminate unreasonable solutions caused by the model form (such as negative effort levels) and ensure the practical significance and economic interpretability of the final solution set. The proof of its mathematical necessity is provided in Appendix A, along with the subsequent derivation process for solving the model.

3.2. Demand Function

In the bidirectional free-riding scenario, the dynamics of cross-channel transactions can significantly affect demand in both the online and offline channels. Referring to previous studies [19], this study assumes that the total initial market demand is normalized to 1. The market demand is jointly affected by the sales price and sales effort, and any supply chain participant making a sales effort will result in an increase in the market demand for both itself and the other party. The demand functions for the recycled cement manufacturer and the retailer are represented in Equations (1) and (2), respectively [22]:

$$D_d=1-P_d+\gamma P_r+{\lambda }_d{S}_r+\left(1-{\lambda }_r\right)S_d$$

(1)

$$D_r=1-P_r+\gamma P_d+{\lambda }_r{S}_d+\left(1-{\lambda }_d\right)S_r$$

(2)

In addition, with reference to previous studies [19,37], this study uses quadratic equations to model the costs associated with sales effort inputs, and the costs of sales effort inputs for recycled cement manufacturers and retailers are represented in Equations (3) and (4), respectively:

$$c\left(S_d\right)={\displaystyle \frac{1}{2}}{\eta }_d{S_d}^2$$

(3)

$$c\left(S_r\right)={\displaystyle \frac{1}{2}}{\eta }_r{S_r}^2$$

(4)

4. Model Building and Solving

4.1. Decentralized Decision Model (D Model)

Under the decentralized decision model, the profit function of the recycled cement manufacturer is shown in Equation (5).

$${\pi }_d^D=w{D}_r+D_d{P}_d-{\displaystyle \frac{1}{2}}\eta {S_{d1}}^2-C_p$$

(5)

The retailer’s profit function is shown in Equation (6).

$${\pi }_r^D=\left(P_r-w\right)D_r-{\displaystyle \frac{1}{2}}{S_r}^2$$

(6)

4.1.1. Optimal Price Response for Retailer

By standard backward induction, we can easily derive the retailer’s optimal price response strategy $P_r^D$.

$$P_r^D={\displaystyle \frac{1}{2}}\left(1+\gamma P_d+w-S_r\left(-1+{\lambda }_d\right)+S_d{\lambda }_r\right)$$

(7)

4.1.2. Pricing Decisions of Recycled Cement Manufacturers

After simultaneously setting sales effort levels $S_d^D$ and $S_r^D$, the manufacturer determines the wholesale price $w^D$ and the direct selling price $P_d^D$ in the online channel to maximize its profit function, easily obtaining ${\pi }_d^D$ as a strictly concave function with respect to $w^D$ and $P_d^D$: ${\displaystyle \frac{{\partial }^2{\pi }_d^D}{\partial w^2}}=-1$, ${\displaystyle \frac{{\partial }^2{\pi }_d^D}{\partial P_d^2}}=-2+{\gamma }^2<0$, ${\displaystyle \frac{{\partial }^2{\pi }_d^D}{\partial w\partial P_d}}={\displaystyle \frac{{\partial }^2{\pi }_d^D}{\partial P_d\partial w}}=\gamma$.

As a result, the optimal wholesale price $w^D$ and direct selling price $P_d^D$ of the recycled cement manufacturer can be obtained.

$$\left\{\begin{array}{l}{w}^D={\displaystyle \frac{-1-\gamma +S_r\left(-1-{\chi }_1{\lambda }_d\right)+S_d\left(-\gamma +{\chi }_1{\lambda }_r\right)}{2{\chi }_2}}\\ P_d^D={\displaystyle \frac{-1-\gamma +S_r\left(-\gamma +{\chi }_1{\lambda }_d\right)+S_d\left(-1-{\chi }_1{\lambda }_r\right)}{2{\chi }_2}}\end{array}\right.$$

(8)

Note: ${\chi }_1=-1+\gamma$ and ${\chi }_2=-1+{\gamma }^2$.

The optimal equilibrium pricing strategy of the retailer can be obtained by substituting the recycled cement manufacturer’s optimal wholesale price $w^D$ and the direct selling price $P_d^D$ in the online channel.

$$P_r^D={\displaystyle \frac{\left(-3+\gamma \right)\left(1+\gamma \right)+S_r\left(-3+{\gamma }^2-\left(3+\gamma \right){\chi }_1{\lambda }_d\right)+S_d\left(-2\gamma +\left(3+\gamma \right){\chi }_1{\lambda }_r\right)}{4{\chi }_2}}$$

(9)

4.1.3. Best Effort Level of Model D

Recycled cement manufacturers and retailers set both sales effort levels $S_d^D$ and $S_r^D$ to ensure concavity and that there is no pathology of negative sales effort; the requirements are shown below [44].

$$\left(1+2{\chi }_2\eta \right){\mathrm{B}}_1+\left(14-15\gamma +{\lambda }_d\left(3-2\gamma +{\chi }_1{\lambda }_d\right)\right){\lambda }_r-{\mathrm{A}}_1{\chi }_1{\lambda }_r^2>0$$

Note: ${\mathrm{A}}_1=\left(-11+4\gamma -{\lambda }_d\right){\lambda }_r$ and ${\mathrm{B}}_1=\left(-7+\left(-2+{\lambda }_d\right){\lambda }_d\right)$.

The optimal sales effort $S_d^{D*}$ for recycled cement manufacturers and $S_r^{D*}$ for retailers can be obtained.

$$\left\{\begin{array}{l}{S}_d^{D*}={\displaystyle \frac{7+8\gamma +{\chi }_1\left(3+4\gamma \right){\lambda }_r-{\lambda }_d\left(-3+2{\lambda }_d\right)\left(1+{\chi }_1{\lambda }_r\right)}{\left(1+2{\chi }_2\eta \right){\mathrm{B}}_1+\left(14-15\gamma +{\lambda }_d\left(3-2\gamma +{\chi }_1{\lambda }_d\right)\right){\lambda }_r-{\mathrm{A}}_1{\chi }_1{\lambda }_r^2}}\\ S_r^{D*}={\displaystyle \frac{\left(-1+{\lambda }_d\right)\left(1+2{\chi }_2\eta +{\lambda }_r\left(-3+\gamma -2{\chi }_1{\lambda }_r\right)\right)}{\left(1+2{\chi }_2\eta \right){\mathrm{B}}_1+\left(14-15\gamma +{\lambda }_d\left(3-2\gamma +{\chi }_1{\lambda }_d\right)\right){\lambda }_r-{\mathrm{A}}_1{\chi }_1{\lambda }_r^2}}\end{array}\right.$$

(10)

The optimal equilibrium pricing strategies of the manufacturer and retailer can be obtained by substituting the optimal sales effort $S_d^{D*}$ of the recycled cement manufacturer and the optimal sales effort $S_r^{D*}$ of the retailer.

$$\left\{\begin{array}{l}{w}^{D*}={\displaystyle \frac{-4+\left(8+7\gamma \right)\eta +3\gamma \eta {\lambda }_d-2\gamma \eta {\lambda }_d^2+2{\lambda }_r\left(6-\gamma +2{\chi }_3{\lambda }_r\right)}{\left(1+2{\chi }_2\eta \right){\mathrm{B}}_1+\left(14-15\gamma +{\lambda }_d\left(3-2\gamma +{\chi }_1{\lambda }_d\right)\right){\lambda }_r-{\mathrm{A}}_1{\chi }_1{\lambda }_r^2}}\\ P_d^{D*}={\displaystyle \frac{\eta \left(7+8\gamma +\left(3-2{\lambda }_d\right){\lambda }_d\right)+2{\lambda }_r-4{\lambda }_r^2}{\left(1+2{\chi }_2\eta \right){\mathrm{B}}_1+\left(14-15\gamma +{\lambda }_d\left(3-2\gamma +{\chi }_1{\lambda }_d\right)\right){\lambda }_r-{\mathrm{A}}_1{\chi }_1{\lambda }_r^2}}\\ P_r^{D*}={\displaystyle \frac{-6+\left(12+\left(7-4\gamma \right)\gamma \right)\eta +3\gamma \eta {\lambda }_d-2\gamma \eta {\lambda }_d^2+2{\lambda }_r\left(9-2\gamma +\left(-6+4\gamma \right){\lambda }_r\right)}{\left(1+2{\chi }_2\eta \right){\mathrm{B}}_1+\left(14-15\gamma +{\lambda }_d\left(3-2\gamma +{\chi }_1{\lambda }_d\right)\right){\lambda }_r-{\mathrm{A}}_1{\chi }_1{\lambda }_r^2}}\end{array}\right.$$

(11)

Note: ${\chi }_3=-2+\gamma$.

Further analysis of the impact trends of relevant parameters on the decisions of supply chain members under the decentralized decision-making model is shown in

Table 3. Relationships between the optimal decisions of supply chain members under a decentralized decision-making model and changes in various parameters.

	$\mathit{\eta }>\mathbf{m}\mathbf{a}\mathbf{x}\left\{{\mathit{\eta }}_3,{\mathit{\eta }}_4\right\}$			$\frac{7}{16}<\mathit{\gamma }<\frac{\sqrt{2}}{2}$
	${\mathit{w}}^{\mathit{D}\mathbf{*}}$	${\mathit{P}}_{\mathit{r}}^{\mathit{D}\mathbf{*}}$	${\mathit{S}}_{\mathit{r}}^{\mathit{D}\mathbf{*}}$	${\mathit{P}}_{\mathit{d}}^{\mathit{D}\mathbf{*}}$	${\mathit{S}}_{\mathit{d}}^{\mathit{D}\mathbf{*}}$
${\lambda }_d$	$\searrow$	$\searrow$	$\searrow$	$\searrow$	$\searrow$
${\lambda }_r$	$\nearrow$	$\nearrow$	$\nearrow$	$\searrow$	$\searrow$

Note: “$\nearrow$” indicates a positive correlation, “$\searrow$” indicates a negative correlation.

.

Proposition 1.

The impact of the free-riding coefficient of the online channel on the decision-making of the supply chain participants in the decentralized decision model is as follows.

(1)

When $\eta >{\eta }_3$, that is, ${\displaystyle \frac{\partial w^{D*}}{\partial {\lambda }_d}}<0$, ${\displaystyle \frac{\partial P_r^{D*}}{\partial {\lambda }_d}}<0$, and ${\displaystyle \frac{\partial S_r^{D*}}{\partial {\lambda }_d}}<0$.

(2)

When ${\displaystyle \frac{7}{16}}<\gamma <{\displaystyle \frac{\sqrt{2}}{2}}$, that is, ${\displaystyle \frac{\partial P_d^{D*}}{\partial {\lambda }_d}}<0$, ${\displaystyle \frac{\partial S_d^{D*}}{\partial {\lambda }_d}}<0$.

Proposition 1 shows that, in the presence of online free-riding for recycled cement products, when $\eta$ is greater than some threshold value, the selling price and the level of sales effort of cement products in the retail channel decrease with the degree of online free-riding for cement products. There is a similar change in the wholesale price of cement products, which decreases with the degree of online free-riding for cement products. This suggests that as the degree of online free-riding increases, more customers who prefer the services of the offline channel migrate to the online channel. To maintain demand, offline retailers may reduce their prices [24], while at the same time, to avoid losses from free-riding behavior, offline retailers may reduce the level of sales effort. Following a similar logic, at a large value of $\gamma$ (${\displaystyle \frac{7}{16}}<\gamma <{\displaystyle \frac{\sqrt{2}}{2}}$), both the selling price and the level of sales effort of the cement product in the direct channel are reduced. This suggests that in an environment of high cross-price sensitivity, manufacturers may still choose to reduce direct selling prices in the online channel to maintain their attraction to consumers, even as more customers who prefer the services of the offline channel migrate to the online channel as the degree of free riding increases. Moreover, manufacturers may choose to reduce the level of sales effort to reduce the cost of goods sold. As a result, both manufacturers and retailers are negatively impacted by online free-riding in an environment of high cross-price sensitivity.

Proposition 2.

The impact effect of the free-riding coefficient of the offline channel on the decision-making of the supply chain participants in the decentralized decision model is as follows.

(1)

${\displaystyle \frac{\partial P_d^{D*}}{\partial {\lambda }_r}}<0$, ${\displaystyle \frac{\partial S_d^{D*}}{\partial {\lambda }_r}}<0$, ${\displaystyle \frac{\partial S_r^{D*}}{\partial {\lambda }_r}}>0$.

(2)

When $\eta >{\eta }_4$, that is, ${\displaystyle \frac{\partial w^{D*}}{\partial {\lambda }_r}}>0$, ${\displaystyle \frac{\partial P_r^{D*}}{\partial {\lambda }_r}}>0$.

Proposition 2 shows that when there is offline free-riding of recycled cement products, the direct selling price and the level of sales effort of cement products in the online channel decrease with the degree of offline free-riding of cement products, in contrast to the level of sales effort of offline retailers, which increases with the degree of offline free-riding of cement products. Similarly, when $\eta$ is greater than some threshold, both the retail and wholesale prices of cement products in the offline channel increase with the degree of offline free-riding of cement products. Offline free-riding will inevitably have a negative effect on the online channel, but when certain conditions are met, offline free-riding can have positive benefits for the offline channel.

4.2. Centralized Decision Model (C Model)

Under centralized decision-making, where the manufacturer and the retailer are considered as a whole for decision-making, the system profit function of the dual-channel supply chain of cement products is as follows:

$${\pi }^C=D_d{P}_d-{\displaystyle \frac{1}{2}}\eta {S_d}^2-C_p+P_r{D}_r-{\displaystyle \frac{1}{2}}{S_r}^2$$

(12)

4.2.1. Optimal Price Response for Recycled Cement Manufacturers and Retailers

After the level of sales effort is set, the recycled cement manufacturer and the retailer determine the direct selling price $P_d^C$ in the online channel and the retail price $P_r^C$ in the offline channel to maximize the system profit function Π, respectively, and it is easy to determine that ${\pi }^C$ is a strictly concave function with respect to $P_d^C$ and $P_r^C$: ${\displaystyle \frac{{\partial }^2{\pi }^C}{\partial P_d^2}}=-2$, ${\displaystyle \frac{{\partial }^2{\pi }^C}{\partial P_r^2}}=-2$, ${\displaystyle \frac{{\partial }^2{\pi }^C}{\partial P_d\partial P_r}}={\displaystyle \frac{{\partial }^2{\pi }^C}{\partial P_r\partial P_d}}=2\gamma$.

The optimal direct selling price $P_d^C$ in the online channel and the retail price $P_r^C$ in the offline channel for the manufacturer and the retailer are as follows:

$$\left\{\begin{array}{l}{P}_d^C={\displaystyle \frac{-1-\gamma +S_r\left(-\gamma +{\chi }_1{\lambda }_d\right)+S_d\left(-1-{\chi }_1{\lambda }_r\right)}{2{\chi }_2}}\\ P_r^C={\displaystyle \frac{-1-\gamma +S_r\left(-1-{\chi }_1{\lambda }_d\right)+S_d\left(-\gamma +{\chi }_1{\lambda }_r\right)}{2{\chi }_2}}\end{array}\right.$$

(13)

This suggests that under a dual-channel supply chain, if the recycled cement manufacturer and the retailer are the first to determine their sales effort, the formulas for the optimal wholesale price and the online direct selling price are the same as the formulas for the optimal offline retail price and the online direct selling price in the centralized decision model. This is reasonable because the recycled cement manufacturer is the leader in setting the pricing strategy in both the decentralized and centralized decision models, and therefore treats the retailer in the decentralized decision model as the final consumer, just as in the centralized decision model. Therefore, the recycled cement manufacturer sets the wholesale price equal to the offline retail price and retains the online price [38].

4.2.2. Best Effort Level of Model C

The recycled cement manufacturer and the retailer determine the level of sales effort $S_d^C$ in the online channel and $S_r^C$ in the offline channel, respectively, and it is easy to determine that ${\pi }^C$ is a binary concave function with respect to $S_d^C$ and $S_r^C$, which is obtained by solving the Hessian matrix.

$$H_c=\left[\begin{array}{cc}{\displaystyle \frac{-1-2\left(-1+{\gamma }^2\right)\eta +2{\chi }_1\left(-1+{\lambda }_r\right){\lambda }_r}{2{\chi }_2}}& -{\displaystyle \frac{\gamma -{\chi }_1{\lambda }_r+{\chi }_1{\lambda }_d\left(-1+2{\lambda }_r\right)}{2{\chi }_2}}\\ -{\displaystyle \frac{\gamma -{\chi }_1{\lambda }_r+{\chi }_1{\lambda }_d\left(-1+2{\lambda }_r\right)}{2{\chi }_2}}& {\displaystyle \frac{1-2{\gamma }^2+2{\chi }_1\left(-1+{\lambda }_d\right){\lambda }_d}{2{\chi }_2}}\end{array}\right]$$

Since $\left|H_c\right|={\displaystyle \frac{\left(1+\left(-2+4{\gamma }^2\right)\eta +\left(-1-4{\chi }_1\eta \right){\lambda }_d^2+2{\lambda }_d\left(2{\chi }_1\eta -{\psi }_1\right)+{\lambda }_r\left(-2+4\gamma -{\chi }_8{\lambda }_r\right)\right)}{4{\chi }_2}}>0$, ${\displaystyle \frac{{\partial }^2{\pi }^C}{\partial S_d^2}}<0$, ${\displaystyle \frac{{\partial }^2{\pi }^C}{\partial S_r^2}}<0$, concavity can be ensured, and there is no pathological situation of negative sales effort; thus, the optimum sales effort $S_d^{C*}$ for recycled cement manufacturers and $S_r^{C*}$ for retailers are derived as follows:

$$\left\{\begin{array}{l}{S}_d^{C*}=-{\displaystyle \frac{1+2\gamma +{\lambda }_d\left(3-2{\lambda }_d-2{\lambda }_r\right)+{\lambda }_r}{\left(1+\left(-2+4{\gamma }^2\right)\eta +\left(-1-4{\chi }_1\eta \right){\lambda }_d^2+2{\lambda }_d\left(2{\chi }_1\eta -{\psi }_1\right)+{\lambda }_r\left(-2+4\gamma -{\chi }_8{\lambda }_r\right)\right)}}\\ S_r^{C*}={\displaystyle \frac{1-2\left(1+\gamma \right)\eta +{\lambda }_r\left(-3+2{\lambda }_r\right)+{\lambda }_d\left(-1+2{\lambda }_r\right)}{\left(1+\left(-2+4{\gamma }^2\right)\eta +\left(-1-4{\chi }_1\eta \right){\lambda }_d^2+2{\lambda }_d\left(2{\chi }_1\eta -{\psi }_1\right)+{\lambda }_r\left(-2+4\gamma -{\chi }_8{\lambda }_r\right)\right)}}\end{array}\right.$$

(14)

Note: ${\chi }_8=-3+4\gamma$ and ${\psi }_1=-1+{\lambda }_r$.

The optimal equilibrium pricing strategies of the manufacturer and the retailer can be obtained by substituting the optimal sales effort $S_d^{C*}$ for the recycled cement manufacturer and the optimal sales effort $S_r^{C*}$ for the retailer.

$$\left\{\begin{array}{l}{P}_d^{C*}=-{\displaystyle \frac{\eta +2\gamma \eta +\eta \left(3-2{\lambda }_d\right){\lambda }_d+{\lambda }_r-2{\lambda }_r^2}{\left(1+\left(-2+4{\gamma }^2\right)\eta +\left(-1-4{\chi }_1\eta \right){\lambda }_d^2+2{\lambda }_d\left(2{\chi }_1\eta -{\psi }_1\right)+{\lambda }_r\left(-2+4\gamma -{\chi }_8{\lambda }_r\right)\right)}}\\ P_r^{C*}={\displaystyle \frac{1-2\left(1+\gamma \right)\eta +\eta {\lambda }_d\left(-1+2{\lambda }_d\right)+{\lambda }_r\left(-3+2{\lambda }_r\right)}{\left(1+\left(-2+4{\gamma }^2\right)\eta +\left(-1-4{\chi }_1\eta \right){\lambda }_d^2+2{\lambda }_d\left(2{\chi }_1\eta -{\psi }_1\right)+{\lambda }_r\left(-2+4\gamma -{\chi }_8{\lambda }_r\right)\right)}}\end{array}\right.$$

(15)

A further analysis of the impact trends of relevant parameters on the decisions of supply chain members under the centralized decision-making model is shown in

Table 4. Relationships between the optimal decisions of supply chain members under a centralized decision-making model and changes in various parameters.

	$\mathit{\eta }>\mathbf{m}\mathbf{a}\mathbf{x}\left\{{\mathit{\eta }}_5,{\mathit{\eta }}_6,{\mathit{\eta }}_8\right\}$		$0<\mathit{\gamma }<\mathbf{m}\mathbf{i}\mathbf{n}\left\{\frac{1}{2}\left(-1+\sqrt{3}\right),{\mathit{\gamma }}_2\right\}$ and $\mathit{\eta }>{\mathit{\eta }}_6$
	${\mathit{P}}_{\mathit{r}}^{\mathit{C}\mathbf{*}}$	${\mathit{S}}_{\mathit{r}}^{\mathit{C}\mathbf{*}}$	${\mathit{P}}_{\mathit{d}}^{\mathit{C}\mathbf{*}}$	${\mathit{S}}_{\mathit{d}}^{\mathit{C}\mathbf{*}}$
${\lambda }_d$	$\searrow$	$-$	$\nearrow$	$-$
${\lambda }_r$	$\nearrow$	$\nearrow$	$\searrow$	$-$

Note: “$\nearrow$” indicates a positive correlation, “$\searrow$” indicates a negative correlation, and “$-$” indicates an uncertain correlation.

.

Proposition 3.

The impact of the free-riding coefficient of the online channel on the decision-making of the supply chain participants in the centralized decision model is as follows.

(1)

When $\eta >{\eta }_5$, that is, ${\displaystyle \frac{\partial P_r^{D*}}{\partial {\lambda }_d}}<0$.

(2)

When $0<\gamma <{\displaystyle \frac{1}{2}}\left(-1+\sqrt{3}\right)$, that is, ${\displaystyle \frac{\partial P_d^{D*}}{\partial {\lambda }_d}}>0$.

Proposition 3 shows that, in the presence of online free-riding for recycled cement products, when $\eta$ is greater than some threshold value, the retail price of the cement product in the offline channel decreases with the degree of online free-riding for the cement product. Following a similar logic, the opposite nature of the online direct selling price can be noted for a smaller value of $\gamma$ ($0<\gamma <{\displaystyle \frac{1}{2}}\left(-1+\sqrt{3}\right)$), i.e., as the degree of online free-riding increases, the direct selling price of cement products in the online channel increases. This suggests that in an environment of low cross-price sensitivity, more customers who prefer the services of the offline channel migrate to the online channel, and the manufacturer may choose to increase the selling price to increase profits.

Proposition 4.

The impact of the free-riding coefficient of the offline channel on the decision-making of the supply chain participants in the centralized decision model is as follows.

(1)

When $\eta >{\eta }_6$, that is, ${\displaystyle \frac{\partial P_r^{C*}}{\partial {\lambda }_r}}>0$.

(2)

When $0<\gamma <{\gamma }_2$ and $\eta >{\eta }_7$, that is, ${\displaystyle \frac{\partial P_d^{C*}}{\partial {\lambda }_r}}<0$.

(3)

When $\eta >{\eta }_8$, that is, ${\displaystyle \frac{\partial S_r^{C*}}{\partial {\lambda }_r}}>0$.

Proposition 4 shows that in the presence of offline free-riding for recycled cement products, the level of sales effort increases with the degree of offline free-riding for a certain threshold. When the conditions are met, retail prices in the offline channel are positively related to the degree of offline free-riding, and direct selling prices in the online channel are negatively related to the degree of offline free-riding. The free-riding phenomenon prompts consumers to alternate their purchases between online and offline channels, forcing online and offline channels to readjust their pricing strategies and sales effort strategies to counteract consumer free-riding in competing channels [20].

5. Model Analysis

In this paper, the optimal pricing and effort levels of supply chain agents under the decentralized and centralized decision models are solved in Section 4. To investigate whether the centralized decision-making model can improve sales effort and achieve a better pricing strategy than decentralized decision-making can achieve, the relationships between the magnitude of optimal pricing and effort levels under the decentralized decision-making and centralized decision-making models are compared in Propositions 5 and 6, respectively, in this section. The results are shown in

Table 5. Comparison of balanced results.

Decentralized Decision Model	Centralized Decision Model	Comparison Results
$P_d^{D*}$	$P_d^{C*}$	$P_d^{D*}<P_d^{C*}$
$P_r^{D*}$	$P_r^{C*}$	$P_r^{D*}<P_r^{C*}$$\left(\gamma >0.193\right)$
$S_d^{D*}$	$S_d^{C*}$	$S_d^{D*}<S_d^{C*}$
$S_r^{D*}$	$S_r^{C*}$	$S_r^{D*}<S_r^{C*}$

.

Proposition 5.

This can be obtained by comparing the optimal pricing of the decentralized and centralized decision-making models:

(1)

$P_d^{D*}<P_d^{C*}$.

(2)

When $\gamma >0.193$, that is, $P_r^{D*}<P_r^{C*}$.

Proposition 5 shows that when certain conditions are satisfied ($\gamma >0.193$), the centralized decision model leads to higher selling prices due to its systematic nature. Since an increase in sales effort requires an increase in service cost, both recycled cement manufacturers and retailers should increase the online direct selling price and the offline retail price, respectively, to cover the cost of sales effort [38]. Under the decentralized decision, to maximize their own profits, both recycled cement manufacturers and retailers choose to lower their selling prices to increase channel demand.

Proposition 6.

$S_d^{D*}<S_d^{C*}$, $S_r^{D*}<S_r^{C*}$.

Proposition 6 suggests that the centralized decision model leads to a higher level of effort due to its systematic nature. This is a good indication of the important role of centralized decision-making in mitigating competitive conflicts in different channels, whereas under decentralized decision-making, to maximize their own profits, recycled cement manufacturers and retailers reduce their costs by lowering the level of sales effort.

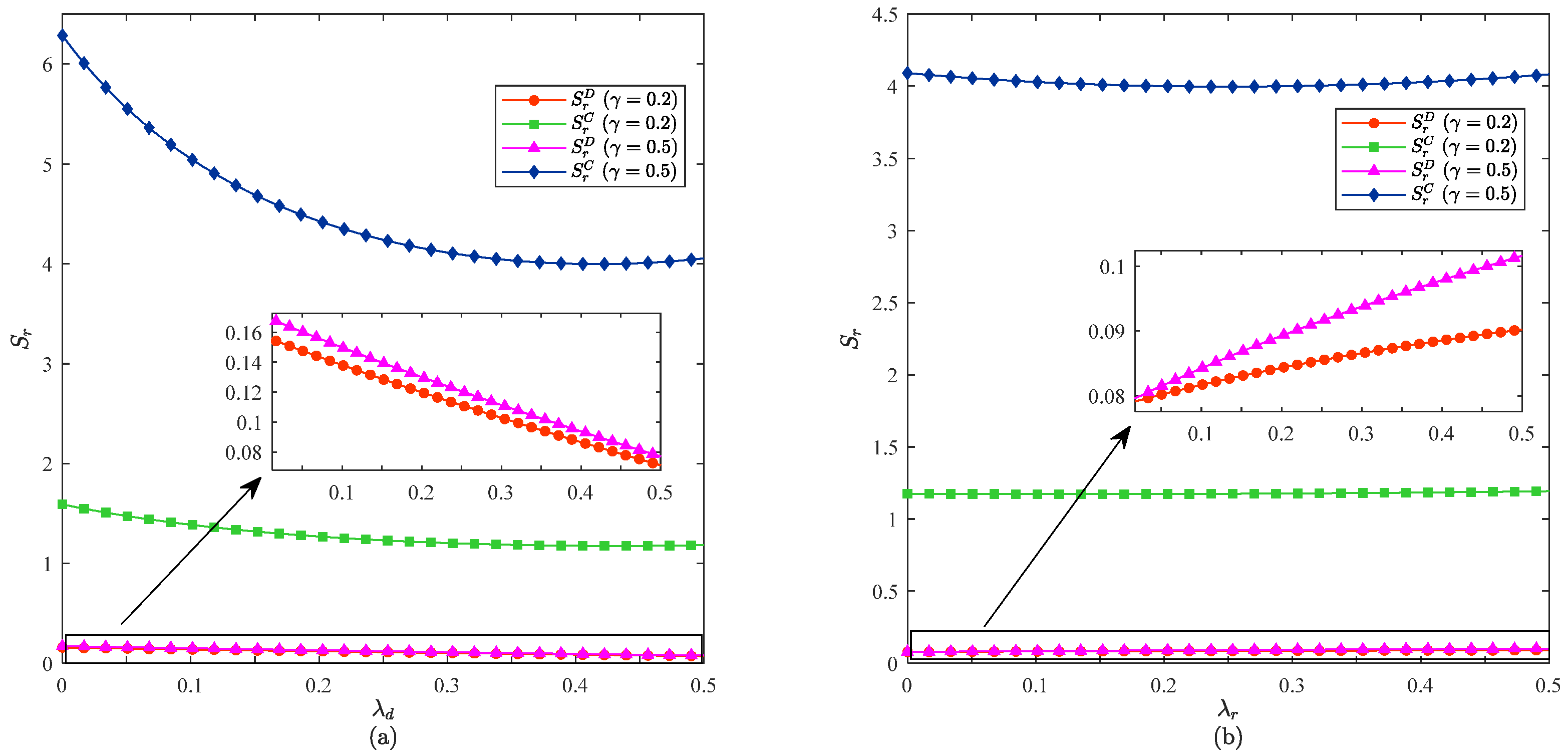
6. Numerical Simulation

This section describes the simulation and analysis of the game model using MATLAB 2024b to illustrate more visually the impact of free-riding behavior on the CDW recycling supply chain. For this purpose, the basic parameters $\eta =2$, ${\lambda }_r=0.3$ and ${\lambda }_d=0.4$ were set in this study with reference to [25,55].

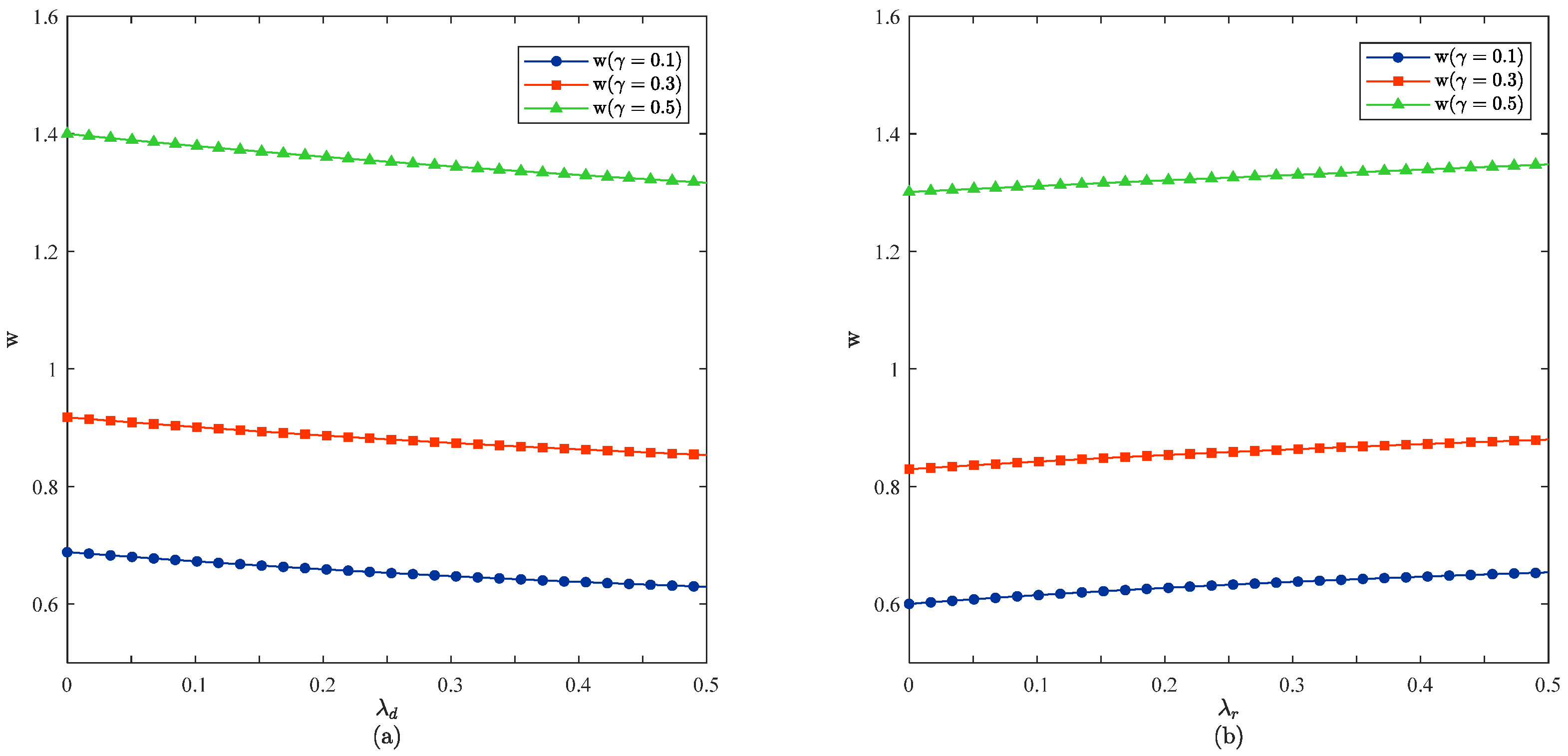
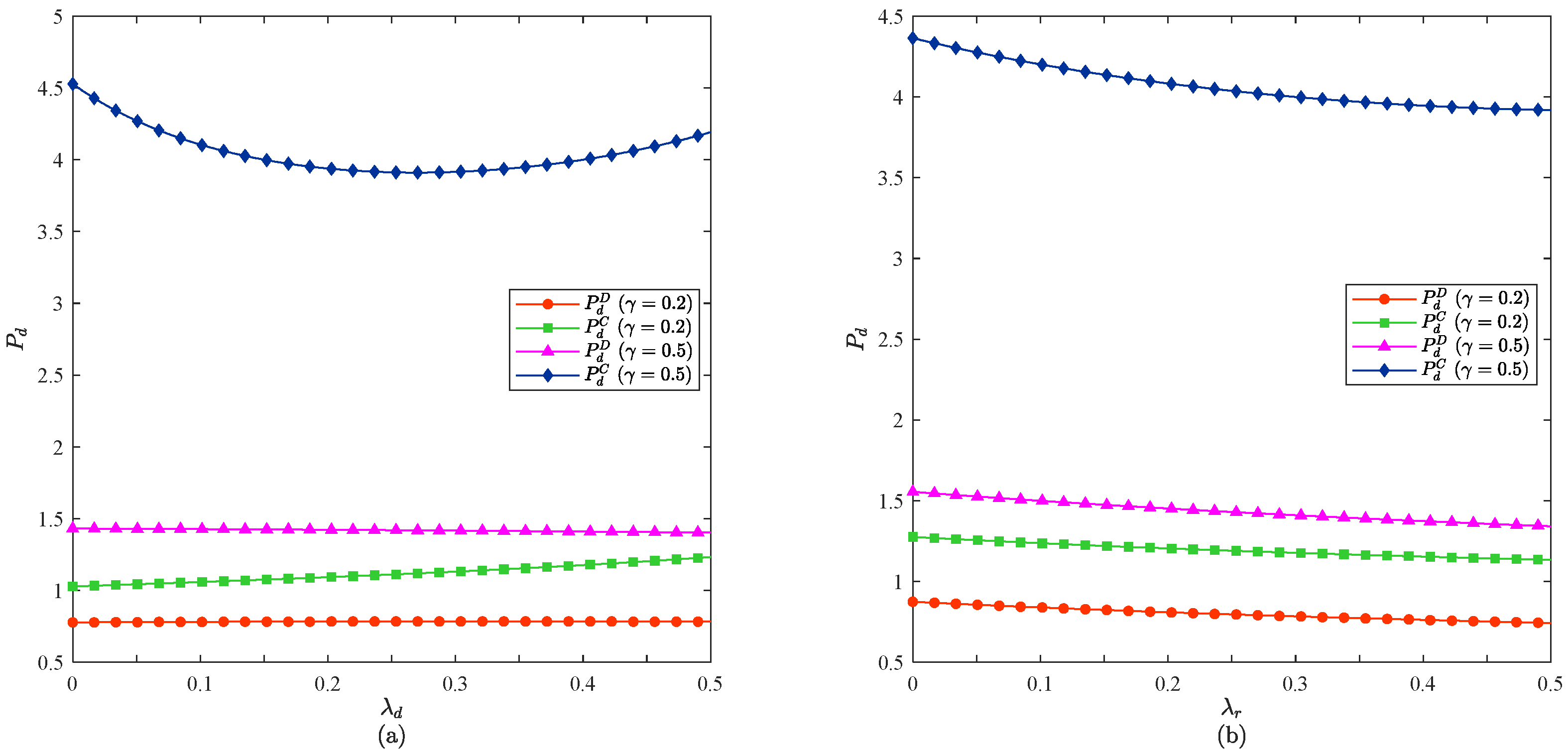
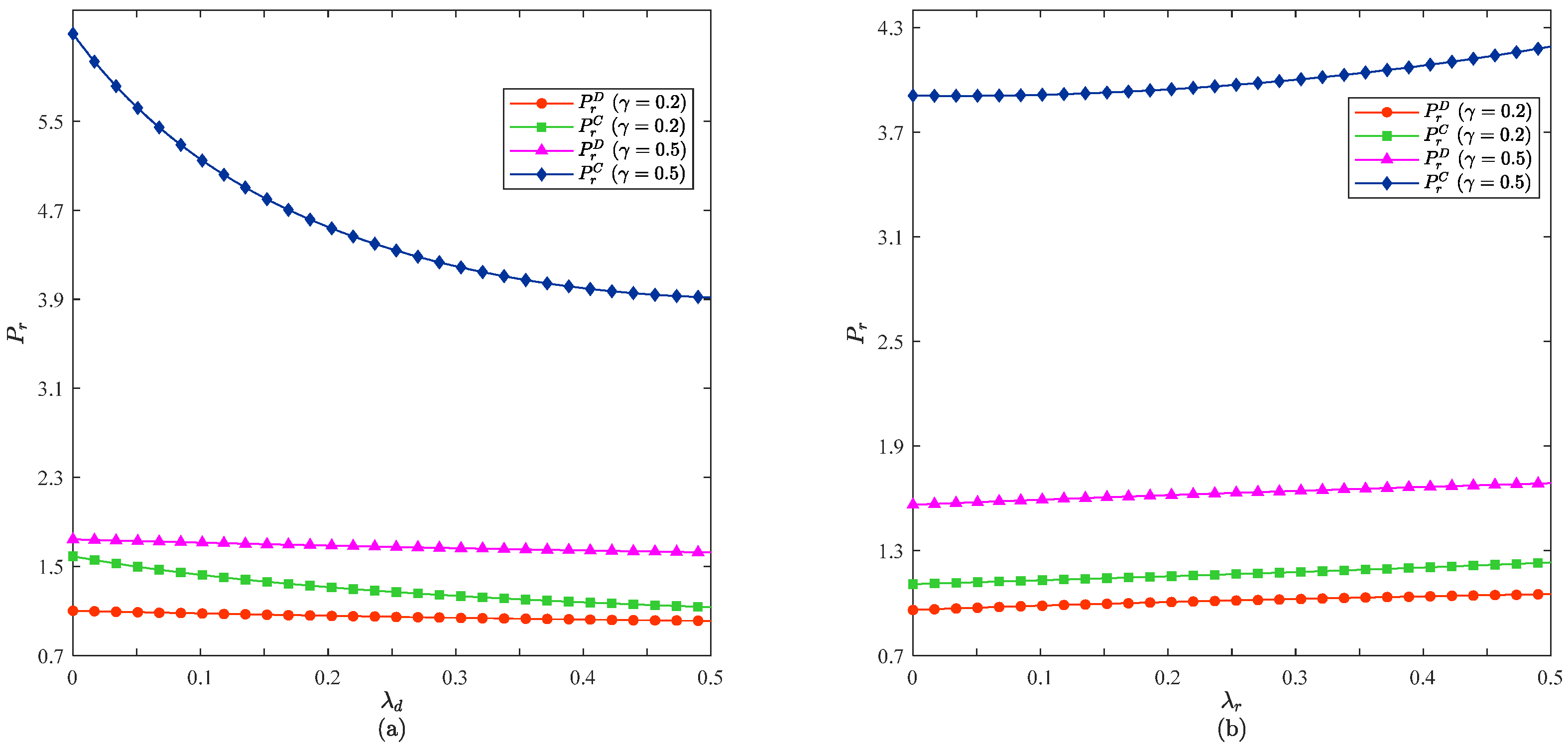
6.1. Impact of the Free-Riding Coefficient on the Wholesale Price

In addition to the basic parameters mentioned above, with reference to [47,50], three cases of $\gamma =0.1$, $\gamma =0.3$ and $\gamma =0.5$ are also set in this section, and the results are shown in Figure 2.

As shown in Figure 2, the wholesale price strategy of recycled cement manufacturers is influenced by the cross-price sensitivity coefficient and the free-riding coefficient. The higher the cross-price sensitivity coefficient is, the higher the wholesale price set by the manufacturer. Figure 2a shows that when $\eta$ is given such that it satisfies certain conditions, the wholesale price always decreases as the free-riding coefficient of the online channel increases, regardless of whether the cross-price sensitivity of the two channels is relatively small or large. This implies that as the degree of online free-riding increases, more customers who prefer offline channel services migrate to the online channel, and the manufacturer can utilize the online channel to gain more benefits and choose to reduce the wholesale price to maintain equilibrium with the retailer. Figure 2b shows that when $\eta$ is given such that it satisfies certain conditions, the wholesale price always increases with increasing offline free-riding coefficient, regardless of whether the cross-price sensitivities of the two channels are relatively small or large. This means that as the degree of offline free-riding increases, more consumers who have accepted the efforts of the online channel choose to make purchases in the offline channel, the manufacturer loses some of the consumers in the online channel, the profit gained in the online channel decreases, and the manufacturer takes to increase the wholesale price to increase its profit.

6.2. Impact of the Free-Riding Coefficient on the Online Direct Selling Price

In addition to the basic parameters mentioned above, with reference to [47,56], this section also sets $\gamma =0.2$ and $\gamma =0.5$, and the results are shown in Figure 3.

As shown in Figure 3, the direct selling price strategy of recycled cement manufacturers is jointly influenced by the price sensitivity between channels and the free-riding coefficient. The higher the cross-price sensitivity coefficient is, the higher the direct selling price set by the manufacturer. Moreover, Figure 3 shows that even if the cross-price sensitivity coefficient and free-riding coefficient change, the direct selling price set by recycled cement manufacturers is always higher in the centralized decision model than in the decentralized decision model.

Figure 3a shows that under the decentralized decision model, when the price sensitivity between channels is relatively high, the direct selling price decreases as the free-riding coefficient of the online channel increases. This is because, in an environment of high cross-price sensitivity, recycled cement manufacturers may still choose to reduce their direct selling price to maintain their attraction to consumers, even if more customers who prefer the services of the offline channel migrate to the online channel as the free-rider coefficient of the online channel increases. Under the centralized decision model, the direct selling price increases with the free-riding coefficient of the online channel when the cross-price sensitivity of the two channels is within a small range. This suggests that in an environment of low cross-price sensitivity, more customers who prefer the services of the offline channel migrate to the online channel, and the recycled cement manufacturer may choose to increase the direct selling price to obtain higher profits.

Figure 3b shows that under the decentralized decision model, the direct selling price always decreases with increasing offline free-riding coefficient, regardless of whether the cross-price sensitivity coefficient is relatively small or large. This means that as the degree of offline free-riding increases, consumers in the online channel migrate to the offline channel, the manufacturer loses some of the consumers in the online channel, and the manufacturer adopts to reduce the direct selling price to expand the demand in the online channel and increase competitiveness in the market to improve its profit. Under the centralized decision model, when $\eta$, which satisfies certain conditions and the cross-price sensitivity coefficient is also in the corresponding range, the results are similar to those obtained from the decentralized decision model.

6.3. Impact of the Free-Riding Coefficient on the Offline Retail Price

This section examines the impact of the free-riding coefficient on retailers’ retail prices under different cross-price sensitivity coefficients, and the results are shown in Figure 4.

As shown in Figure 4, retailers’ retail price strategies are jointly influenced by the cross-price sensitivity coefficient and the free-riding coefficient. The higher the cross-price sensitivity coefficient is, the higher the retail price set by the retailer. Moreover, Figure 4 shows that when certain conditions are satisfied, even if the cross-price sensitivity coefficient and the free-riding coefficient change, the offline retail price set by the retailer is always higher in the centralized decision model than in the decentralized decision model.

Figure 4a shows that under the decentralized decision model, when $\eta$ is given such that it satisfies certain conditions, the retail price always decreases with increasing free-riding coefficient in the online channel, regardless of whether the channel cross-price sensitivity is relatively small or large. The current cement market is characterized by the existence of online and offline dual-channel sales, and to attract online customers, a retailer (distributor) in Changzhou has lowered the price of bagged cement from 15 yuan/bag to 10 yuan/bag [57]. Offline retailers (dealers) found that some customers first learned about cement products offline and then chose to buy them online because of the low online price. To maintain sales, offline retailers (dealers) had to lower their prices. This suggests that as the degree of online free-riding increases and more customers who prefer the services of the offline channel migrate to the online channel, the offline retailer may choose to reduce prices to maintain demand. A similar situation is found in the centralized decision model.

Figure 4b shows that under the decentralized decision model, when $\eta$ is given such that it satisfies certain conditions, the retail price always increases as the offline free-riding coefficient increases, regardless of whether the cross-price sensitivity coefficient is relatively small or large. This suggests that as the degree of offline free-riding increases and more consumers who have embraced the sales effort of the online channel migrate to the offline channel, the offline retailer may choose to increase the retail price to capture higher profits. A similar situation is found in the centralized decision model.

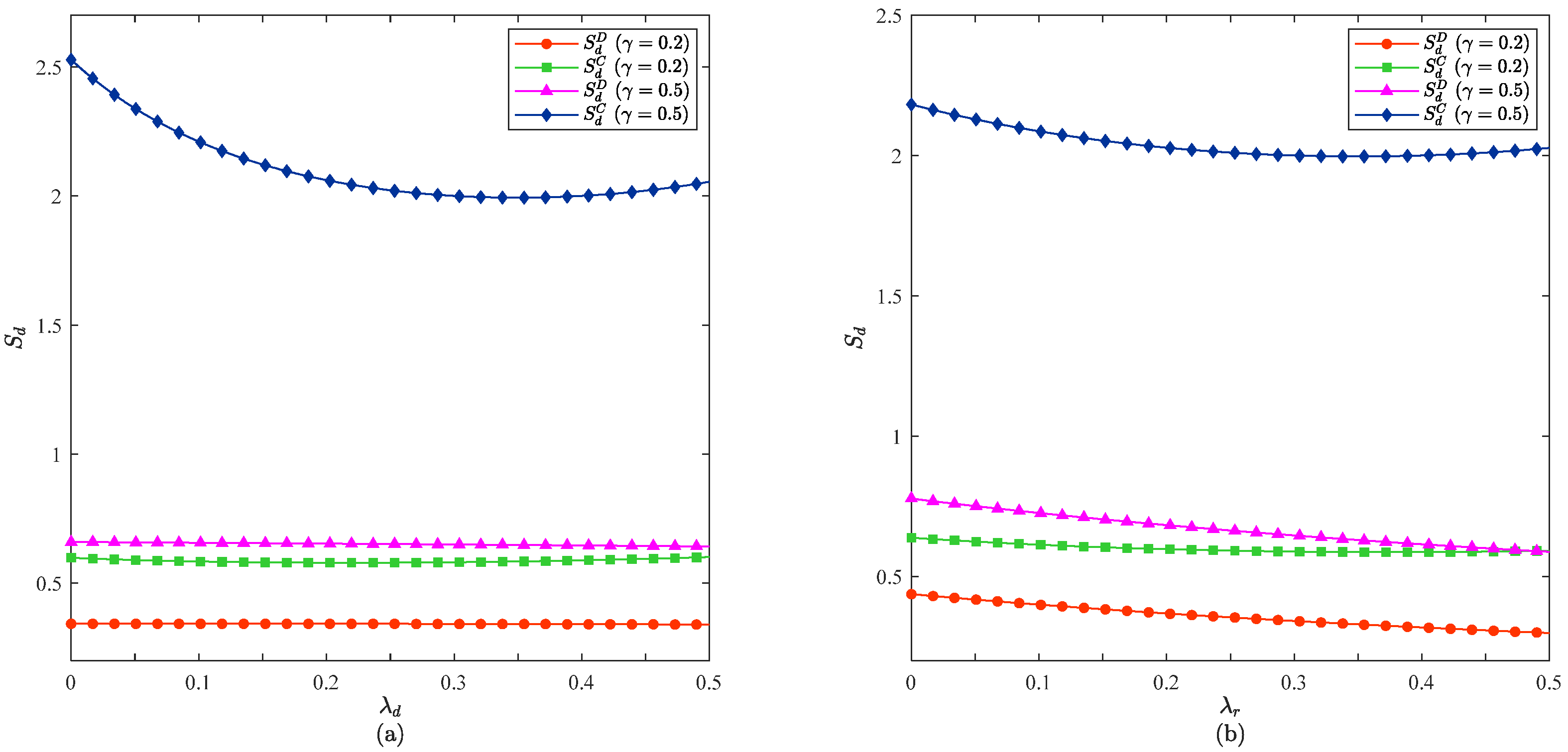
6.4. Impact of the Free-Riding Coefficient on Sales Effort in the Online Channel

This section focuses on the impact of the free-riding coefficient on the effort of the recycled cement manufacturer in the online channel under different price sensitivity coefficients between channels, and the results are shown in Figure 5.

As shown in Figure 5, the sales effort strategy of recycled cement manufacturers is influenced by the combination of the cross-price sensitivity coefficient and the free-riding coefficient. The higher the cross-price sensitivity coefficient is, the greater the sales effort formulated by the manufacturer. Moreover, Figure 5 shows that the level of sales effort formulated by recycled cement manufacturers is always greater in the centralized decision model than in the decentralized decision model, even if the cross-price sensitivity coefficient, the free-riding coefficient, and the free-riding coefficient change.

Specifically, as shown in Figure 5a, under the decentralized decision model, the level of sales effort in the online channel is less affected by the degree of free-riding in the online channel, and the level of sales effort in the online channel decreases with increasing free-riding coefficient in the online channel when the cross-price sensitivity coefficient is large. This suggests that in an environment with a high price sensitivity coefficient between channels, as the degree of free-riding increases and more customers who prefer the services of the offline channel migrate to the online channel, recycled cement manufacturers may choose to lower the level of sales effort to reduce the cost of goods sold to obtain higher profits.

Figure 5b shows that under the decentralized decision model, the sales effort in the online channel always decreases as the free-riding coefficient of the offline channel increases, regardless of whether the price sensitivity coefficients between channels are relatively small or large. This means that as the degree of offline free-riding increases, consumers in the online channel migrate to the offline channel, and the recycled cement manufacturer loses some of the consumers in the online channel. The recycled cement manufacturer may choose to reduce its investment in sales efforts to ensure that the amount of loss is not too high. For example, Yatai Group Harbin Cement Co., Ltd. promoted cement through online sales efforts such as webcasts and posters [58], but the sale of recycled cement in townships still has practical problems such as “difficulty in purchasing cement online, difficulty in delivering cement to the home, and difficulty in purchasing cement in a single bag” [59], and some consumers still choose to purchase it offline after learning about the product online. This real-life dilemma has prompted manufacturers to reduce the number of online purchases. This dilemma has prompted recycled cement manufacturers to reduce their investment in online sales to minimize the economic losses caused by customer loss.

6.5. Impact of the Free-Riding Coefficient on Sales Effort in the Offline Channel

This section focuses on the impact of the free-riding coefficient on retailers’ sales efforts in the offline channel under different price sensitivity coefficients between channels, and the results are shown in Figure 6.

As shown in Figure 6, the retailer’s sales effort strategy is jointly influenced by the cross-price sensitivity coefficient and the free-riding coefficient. The higher the cross-price sensitivity coefficient is, the greater the sales effort formulated by retailers. Moreover, Figure 6 shows that even if the cross-price sensitivity coefficient and the free-riding coefficient change, the level of sales effort formulated by retailers is always greater in the centralized decision model than in the decentralized decision model.

Specifically, as shown in Figure 6a, under the decentralized decision model, when $\eta$ is given such that it satisfies certain conditions, the level of sales effort in the offline channel decreases as the free-riding coefficient of the online channel increases, regardless of whether the cross-price sensitivity coefficient is relatively small or large. This suggests that to avoid losses from free-riding behavior, offline retailers may reduce the level of sales effort. This phenomenon reflects the real-life free-riding problem: In the cement market, for example, due to the existence of counterfeit products (e.g., the counterfeit “Conch brand” cement detected in Suixi County in 2024) [60], some consumers choose to buy the genuine product online after learning about the product information in the offline channel. In this case, offline retailers bear the cost of services such as product display and technical explanations but have difficulty obtaining a corresponding sales return, which ultimately results in them having to reduce their sales effort to minimize their losses.

In another scenario, Figure 6b shows that under the decentralized decision model, the sales effort in the offline channel always increases with increasing offline free-riding coefficient, regardless of whether the cross-price sensitivity coefficient is relatively small or large. This implies that as the degree of offline free-riding increases and consumers in the online channel migrate to the offline channel, the retailer may choose to invest more in sales efforts to solidify consumers and increase market competitiveness. In the case of cement sales in townships [59], for example, even if consumers learn about the product online, they will still choose to buy offline owing to practical constraints. Faced with this situation, offline retailers are more willing to increase sales investment and consolidate customer resources by increasing sales effort. Under the centralized decision model, the situation is similar to that of the decentralized decision model when $\eta$ is given such that it satisfies certain conditions.

7. Conclusions and Implications

7.1. Conclusions

This study addresses the challenges of promoting recycled cement made from CDW by constructing a two-party game model that includes manufacturers’ self-built direct sales platforms and offline retailers. It uses continuous sales effort variables to reveal the impact of bidirectional free-riding behavior on supply chain pricing and sales effort investment. The model overcomes the limitations of traditional research, which relies on third-party platforms or discrete processing of effort variables. The main conclusions are as follows:

First, under a decentralized decision-making model, bidirectional free-riding behavior has differentiated and interrelated impacts on supply chain members. Unlike studies that analyze heterogeneous products [24] or structures involving third parties (EPC or digital retailers) [19,21,22], this paper finds that, under the combined influence of homogeneous products, a manufacturer-dominated dual-channel architecture, and high cross-price sensitivity, both online and offline free-riding behavior erodes the competitiveness of online channels, causing manufacturers to reduce direct sales prices and sales efforts. More critically, when the market exhibits high cross-price sensitivity coupled with high effort costs, online free-riding not only prompts retailers to lower prices and effort levels but also forces manufacturers to reduce their online strategies simultaneously, triggering a “two-channel synchronous suppression effect”. This finding reveals the risk that bidirectional free-riding may cause the supply chain to fall into a vicious cycle of efficiency decline, breaking through the traditional understanding in the literature that free-riding weakens only specific channels in one direction [20]. The underlying reason is that this study accurately captures the dynamic process of bidirectional effort feedback through endogenous continuous sales effort variables and a main structure that fits industry practices.

Second, the centralized decision-making model significantly improves system efficiency by internalizing the externalities generated by free-riding behavior [22,23]. Consistent with the consensus on supply chain coordination theory, this paper clarifies its mechanism of action: on the one hand, by eliminating the investment inhibition caused by “bearing the cost of effort alone while reaping the benefits,” sales efforts under centralized decision-making are always greater than those in a decentralized scenario; on the other hand, under the condition of satisfying the cross-price sensitivity threshold, overall profits can be increased by optimizing pricing strategies. This provides a key theoretical basis for building strategic alliances or in-depth collaboration agreements to achieve intensive investment in sales resources and improved marketing efficiency [20].

In summary, this study not only reveals the complex decision-making mechanism of the CDW recycling supply chain in the context of bidirectional free-riding but also identifies the risk of systemic efficiency decline under highly competitive pressure. Furthermore, it clarifies the core role of internalizing channel externalities in overcoming the dilemmas of technological feasibility and market weakness in this field.

7.2. Implications

The management takeaways from this paper are as follows:

(1)

For recycled cement manufacturers, when cross-price sensitivity is high, both online and offline free-riding weaken the competitiveness of online channels, so it is necessary to establish a systematic strategy to prevent bidirectional free-riding. In response to the risk of offline consumer migration due to offline free-riding, the online experience should be optimized through technological innovation, such as establishing an omni-channel membership points system or learning from Conch Cement’s use of 3D+VR technology tools to transform traditional education costs into customer loyalty advantages [61]. At the same time, it is necessary to work with retailers to build a cross-channel investment measurement mechanism, such as a revenue sharing scheme based on the proportion of sales efforts, to resolve the contradiction of unilateral investment and multiparty benefits through contract design.

(2)

Retailers should take a dialectical view of the free-riding effect. Faced with the shift in demand caused by offline free-riding, they should seize the opportunities brought about by offline free-riding and invest more sales efforts, such as equipping themselves with professional technical teams in the engineering field and providing customized solutions and other nonprice means to lock in core customer groups. Regarding the phenomenon where the service value of offline channels is absorbed by online channels due to online free-riding, retailers can proactively collaborate with manufacturers to enhance supply chain synergy—jointly organizing technical seminars in offline settings to integrate brand resources, breaking down data barriers between supply and demand on the digital front, and establishing a joint decision-making mechanism to mitigate channel conflicts.

(3)

Government departments should adopt a combination of policies. The first priority is to set mandatory procurement quotas for recycled building materials in municipal engineering tenders, using large-scale demand to break through market bottlenecks. The second priority is to accelerate the establishment of a product certification standard system to increase public trust in recycled building materials. Policy resources should be prioritized for companies implementing end-to-end traceability technology, particularly supply chain consortia adopting a manufacturer–retailer decision-making collaboration model. This approach can reduce the intensity of market competition while amplifying collaborative advantages through incentive mechanisms, effectively transforming free-riding behavior from a threat into a catalyst for channel integration.

7.3. Limitations

Despite the valuable findings of this study, there are still limitations that need to be pointed out, and these limitations point the way to future research:

(1)

The model structure of this study focuses on the dual-subject game between recycled cement manufacturers’ self-built platforms and offline retailers. Although this approach is consistent with the practices of leading companies in the industry, it does not include multichannel competition scenarios involving third-party digital retailers (such as EPC). In reality, it is difficult for manufacturers to completely monopolize online channels, and the intervention of digital retailers may reshape the role of bidirectional free-riding behavior. Future research can construct a dynamic game model involving three parties, self-built platform manufacturers, digital retailers, and physical retailers, to explore the enabling mechanism of platform data advantages for free-riding governance.

(2)

At the theoretical level, the study is based solely on the free-riding theory framework and has not yet incorporated new perspectives from behavioral economics. The risk preferences and trust-building of consumers of recycled building materials exhibit significant characteristics of prospect theory, such as loss aversion toward the uncertainty of recycled aggregate strength. Future research should combine social exchange theory with consumer experiments to investigate the moderating role of quality trust gaps and service commitments in cross-channel free-riding, thereby optimizing the demand function assumption.

(3)

The conclusions rely on pure mathematical reasoning and lack empirical calibration in industry. Although case studies from companies such as Huaxin Cement Co., Ltd. are cited to support the explanation, there is a risk of a disconnect between the model parameters and actual market feedback. It is recommended that subsequent scholars collaborate with resource recycling companies to conduct experiments to identify the price sensitivity thresholds and free-riding factors of contractors in different regions, thereby improving the practicality of management recommendations.