Study on Residual Load-Bearing Capacity of Composite Steel Truss Bridge Girders After Vehicle Fire

Abstract

To investigate the residual load-bearing capacity of composite steel truss bridge girders after vehicle fire, a 100 m simple supported composite steel truss bridge girder was selected as the research object, and a typical oil tanker fire was taken as the fire scenario. This study identifies the most critical conditions associated with an oil tanker fire and outlines the degradation pattern of the residual load-bearing capacity of composite steel truss bridge girders after a vehicle fire. It also proposes a damage classification standard and an evaluation method for the load-bearing capacity based on the structural failure path and load-displacement curve. The results indicate that the most critical scenario during a vehicle fire occurs when the fire is located on the bridge deck, particularly in the middle section of the longitudinal bridge and the outermost lane of the transverse bridge. During a vehicle fire, the top chord is the component most affected by the thermal history. Under immersion cooling conditions, the remaining load-bearing capacity of the girder decreases more significantly compared with natural cooling. After the fire, the upper chord first reaches the yield strength, causing load transfer to adjacent horizontal inclined members. The stress of the horizontal inclined rod will develop rapidly, leading to structural instability and eventual failure. Four grades of load-bearing capacity damage for composite steel truss bridge girders after vehicle fire are defined to serve as references for practical engineering applications.

1. Introduction

In accordance with the national strategic objectives for “dual carbon” and the imperative for sustainable transportation development, there is a growing emphasis on steel structures in bridge construction. Composite steel truss bridge girders, in particular, have become prevalent in bridge engineering due to their benefits, such as ease of fabrication and adaptability in assembly. Despite these advantages, the material’s relatively low fire resistance has persistently raised concerns regarding its safety [1,2,3,4,5]. Local instability within composite steel truss bridge girders can markedly reduce the residual load-bearing capacity of the structure, thereby posing significant risks to safety performance. In the most severe scenarios, this could result in catastrophic safety incidents, including bridge collapses and fatalities. After emergency incidents such as vehicle fires, although some steel structures do not show obvious structural damage, local components may have yielded and lost their load-bearing capacity. Therefore, the ability to quickly and accurately assess the safety status of bridge structures affected by fire directly affects the implementation of emergency rescue and the rapid recovery of traffic flow.

Zhang et al. [6,7] proposed methods for fire scene inversion and high-temperature field estimation to evaluate the load-bearing capacity of steel-concrete composite beams post-fire, establishing a safety evaluation process for these beams. Through fire resistance tests on two-span continuous double-chamber steel box structure model beams, they investigated the degradation of the bearing performance of plate rubber bearings during fire and elucidated the evolution mechanism of continuous steel box beams’ fire resistance performance. Tang et al. [8] analyzed the deflection variation of key sections and failure modes of model beams through hydrocarbon fire tests on three simply supported bottom-bearing steel truss–concrete composite model beams, revealing structural responses and failure mechanisms under heat-force coupling. Li et al. [9] examined the failure mechanisms of steel–concrete composite continuous box girders under different conditions based on fire tests and proposed methods to enhance their fire resistance toughness. Wan et al. [10] studied a new method to evaluate the thermal behavior of wind-driven rectangular fires through three stages, linking the flame morphology to key thermal aspects. Zhao et al. [11,12] proposed a numerical method for predicting the fire response of steel truss–concrete composite bridges under semi-open fire conditions and studied the damage mechanism of steel truss bridges under HC fires through experiments and numerical simulations. Egle et al. [13] employed mobile fire analysis to study the structural responses of steel frame structures in various fire scenarios. Tang et al. [14] analyzed the degradation of mechanical properties in steel structures under fire, calculating the residual strength of complex steel truss bridges after fire. Zhang et al. [15] studied the high-temperature performance of Q345 structural steel considering two cooling methods: natural and water cooling. Maraveas et al. [16] investigated the mechanical properties of structural steel and components post-fire, establishing assessment and repair specifications for fire-damaged structures. Piroglu et al. [17] conducted tensile tests on fire-affected components in a factory, inferring fire exposure temperatures based on residual mechanical properties to evaluate component serviceability and safety. Aziz et al. [18] developed a residual strength evaluation method for steel structural bridges, covering analysis in three stages: natural conditions, fire, and post-fire cooling. Hosseini et al. [19] constructed a three-dimensional finite element model using ABAQUS to study I-shaped beam-column joints’ mechanical properties post-fire. He et al. [20] conducted experiments and finite element simulations on circular hollow cross-section stainless steel short columns, analyzing material responses and structural behaviors post-high temperature exposure. The aforementioned studies indicate a lack of research focused on post-fire mechanical properties of bridge structures, with most existing studies concentrated on building structures. To thoroughly analyze the residual load-bearing capacity of steel structural bridges after fire, further experimental research and theoretical analyses are required. Flodr J et al. [21] conducted a numerical simulation study on cold-formed thin-walled Ω-shaped fixtures under temperature and force loads, and found that thermal loads play a dominant role in the load-bearing capacity and behavior of the fixtures.

Currently, research on temperature fields in bridge fires primarily employs numerical simulation methods, typically simplifying the fire as a uniform temperature field that varies with the temperature rise curve [22]. However, for bridge structures in open environments, the fire temperature field exhibits strong gradient characteristics and non-uniformity. Consequently, existing simplification methods can lead to distortions in the temperature field of bridge fires, resulting in errors in predicting bridge fire responses. Some studies utilize Computational Fluid Dynamics (CFD) to achieve a more accurate simulation of fire scenarios. Emre et al. [23] analyzed the potential causes of a fire incident in a fabric finishing factory (including washing and drying units) using the CFD method, and pointed out that the numerical simulation method is a powerful tool for analyzing fire scenes. Alos-Moya et al. [24] used the CFD method to develop a fire model for the oil tanker fire incident at the I-65 overpass in Birmingham, Alabama. They arranged measurement points to obtain the structure’s adiabatic surface temperature and analyzed the standard temperature rise curve and the thermal structural response of the bridge in CFD fires. Choi et al. [25] conducted fire dynamics analysis, nonlinear transient heat transfer analysis of the fire temperature field, and coupled thermal–structural analysis using FDS 6.9.1 software. Peris-Sayol et al. [26] calculated the adiabatic surface temperature of a 12.2 m simply supported beam bridge using FDS software and applied it as the thermal boundary condition in the finite element model of the thermal structure. The existing studies focus on specific fire scenarios and do not consider composite steel truss bridge girders in open environments. Therefore, for structures like composite steel truss bridge girders in open environments, more accurate simulations of fire temperature fields are essential.

Acknowledging the gaps in existing research, this paper dedicates its focus to composite steel truss bridge girders, scrutinizing their residual load-bearing capacity post-vehicle fire incidents. Initially, Computational Fluid Dynamics (CFD) will be utilized to simulate the temperature field of the vehicle fire and to assess the temperature distribution patterns within the fire-impacted regions of the composite steel truss bridge girder. Following this, this study will evaluate the residual load-bearing capacity of the bridge’s truss system, accounting for deformations induced by the vehicle fire, and pinpoint the truss members that are most severely impacted. Ultimately, this paper will calculate the remaining load-bearing capacity of the composite steel truss bridge girder after a vehicle fire, analyzing the reduction in load-bearing capacity, and propose a classification criterion for the damage grades of load-bearing capacity in the aftermath of a vehicle fire.

2. Vehicle Fire Temperature Field of Composite Steel Truss Bridge Girder

2.1. Selection of Research Subjects

This paper takes the simply supported bottom-supported composite steel truss bridge girder in Shaanxi, China as the research object. The span of the bridge is 100 m, and the width of the bridge deck is 12.5 m. The main truss adopts a triangular truss composed of upper and lower chord members and web members, with a center spacing of 14 m, a truss height of 11 m, and a joint length of 10 m. All components are made of Q355 [27] grade structural steel (nominal yield strength equals 355 MPa), the mechanical properties of this structural steel after fire are based on the existing test data [28,29], the bridge deck is made of C50 [30] concrete (characteristic compressive strength = 50 MPa), and the plate thickness is 250 mm. The structural layout of the composite steel truss bridge girder is shown in Figure 1. The cross-sections of the composite steel truss bridge components are shown in

Table 1. Section table of composite steel truss bridge components.

Location	Cross-Sectional Form	Width	Height	Vertical Version		Top Plate
		mm	mm	mm	mm	mm	mm
Winding bar		600	960	960	36	600	32
Lower chord		600	1200	1200	36	600	32
Web member		600	960	960	32	600	28
		600	960	960	32	600	24
Horizontal bracing		400	960	928	10	400	16
End transverse bracing		400	960	912	16	400	24
Horizontal diagonal bar		400	350	318	10	400	16
Longitudinal beam		600	300	272	12	600	16
Middle crossbeam		700	400	1168	14	700	16
End crossbeam		960	1200	1144	20	960	24

.

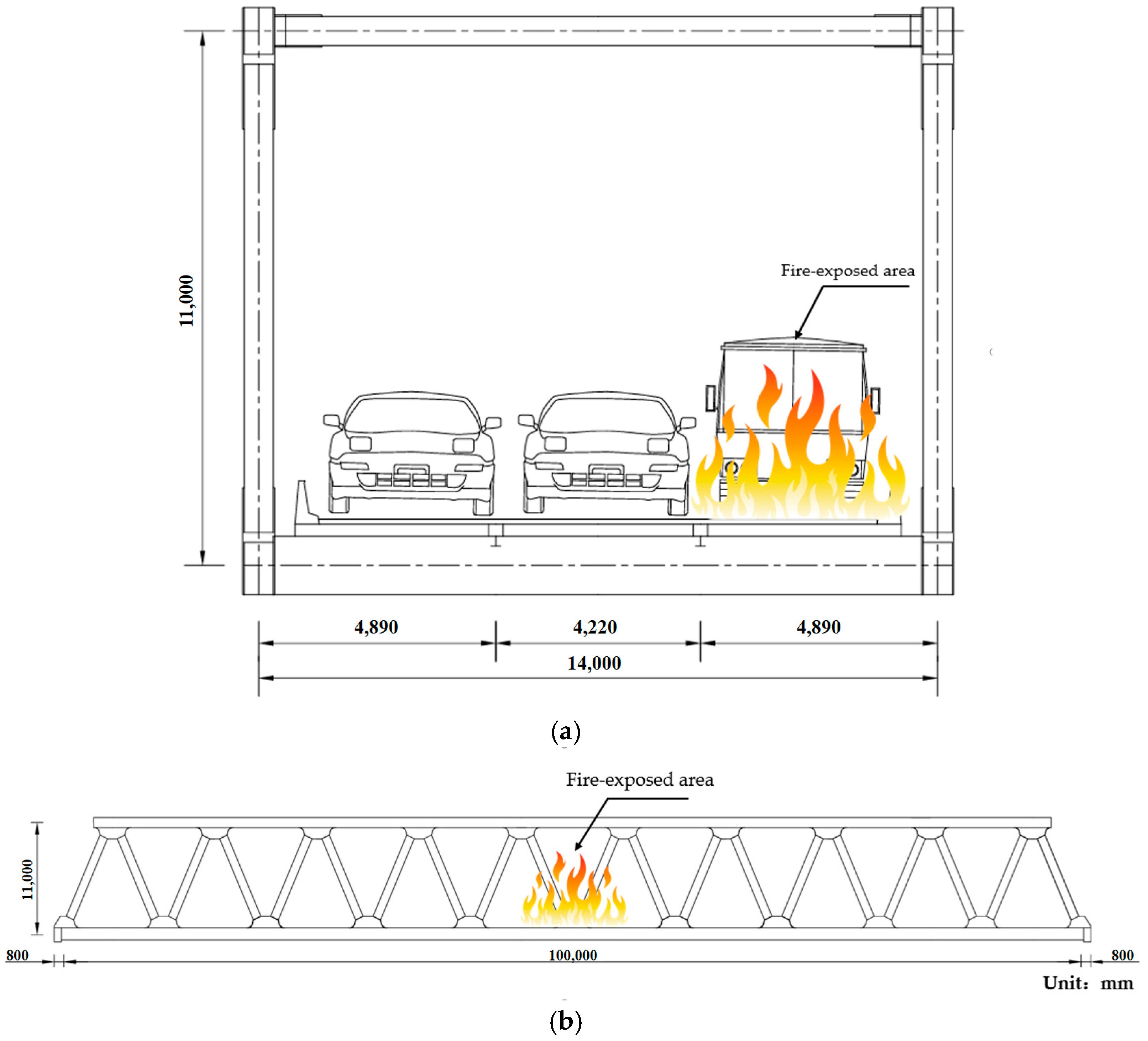
2.2. The Most Unfavorable Location for Fire

Since the load-bearing performance of the bridge within 15 min after the bridge deck and the underside are exposed to fire under the same conditions is 70% and 95% of the original structure, respectively [31], the fire location is set above the bridge deck. Meanwhile, due to the buckling effect caused by the fire history, the structural stiffness and load-bearing capacity of the main truss diagonal members and the upper chord members have undergone severe degradation [31]. Therefore, the fire position is set on the outermost lane in the transverse bridge direction, which makes the temperature of the upper chord members and web members close to the fire source higher, having the greatest impact on the composite steel truss bridge girder.

Utilizing MIDAS 2021 software, we perform a static analysis of the bridge structures. The composite steel truss bridge girder exhibits maximum tensile stress in the web members and maximum compressive stress in the upper chord members. Figure 2 depicts the maximum compressive stress in the upper chord at mid-span as 133.62 MPa, and the maximum tensile stress in the web at the fulcrum as 127.73 MPa. Since the upper chord members are the bridge’s primary load-bearing elements, any fire-induced impact can drastically diminish the overall load-bearing capacity. Thus, the fire is hypothesized to occur in the mid-span region, as depicted in Figure 3.

2.3. Temperature Field of Oil Tanker Fire

2.3.1. Model Verification

To verify the effectiveness of the fire simulation using Pyrosim 2023 software, this paper compares the fire test results with those of Alos-Moya et al. [32]. In the test, the main beam adopts a double I-beam–concrete composite beam, which is formed by connecting a concrete slab with two steel beams through shear nails. The main beam is supported on the abutment by two unreinforced rubber bearings with dimensions of 200 × 200 × 20 mm. The two abutments place the lower surface of the main beam at a height of 1.9 m above the ground. Two auxiliary steel frames are installed on the bridge deck to fix the LVDT sensor for recording the vertical deflection of the bridge deck. Reference [32] conducted eight fire tests under the bridge in four fire scenarios for the test beam. The layout of the fire test scenarios is shown in

Table 2. Fire test scene.

Fire Scene	Oil Pool Size (m)	Location of the Fire	HRR (kW)	Test Serial Number	Location of the Oil Pool
					x (m)	z (m)
Scene 1	0.5	mid-span	415	1	3.00	0.2
				2
Scene 2	0.75	mid-span	1131	3	3.00	0.2
				4
Scene 3	0.5	bearing	415	5	5.27	0.5
				6	5.59
				7	5.59
Scene 4	0.75	mid-span	1131	8	3.00	0.8

. The fire thermal analysis model of double I-beam–concrete composite beam was established by using the fire dynamics simulation software Pyrosim. In the model, five thermocouples (V1–V5) are arranged along the central axis of the flame to record the flame temperature at different heights. On the lower surface of the beam, six thermocouples (GC1–GC6) are arranged along the central axis of the bridge span to record the air temperature at different positions from the beam end. The comparison results of the flame temperatures measured by thermocouples at different heights of the oil pool fire with the calculated values of the model are shown in

Table 3. Test values and calculated values of temperature at measurement points in various fire scenarios.

Measuring Point			Test Value/°C					Calculated Value/°C
	Text 1	Text 2	Text 3	Text 4	Text 7	Text 8	Text 1–2	Text 3–4	Text 7	Text 8
V1	786	765	796	863	847	908	751	989	857	1026
V2	597	535	873	873	649	885	633	945	724	970
V3	431	455	813	840	675	901	444	841	637	970
V4	282	315	745	743	527	908	368	770	577	940
V5	280	308	758	702	589	926	349	726	544	914
GC1	141	164	264	279	133	422	142	314	128	408
GC2	175	205	362	389	151	639	177	376	143	515
GC3	268	326	607	707	184	941	270	646	165	841
GC4	288	288	644	737	234	921	263	634	204	914
GC5	166	172	378	431	289	594	181	414	272	526
GC6	139	148	279	323	546	504	138	307	558	414

.

It can be found from Table 3 that due to the deviation between the theoretical and experimental heat release rates of the oil pool, as well as the failure to take into account the influence of wind speed, there may be a certain degree of error in the simulation results. In addition, the influence of environmental factors in the test leads to certain differences in the temperatures at the measurement points obtained from two repeated tests under the same conditions. Overall, the calculated temperature values of the measurement points in the numerical simulation in this paper are in good agreement with the test results. The finite element calculation method used can predict the temperature distribution of vehicle fires relatively accurately.

2.3.2. Simulation of Fire Temperature Field

This paper adopts Pyrosim software for FDS preprocessing in combination with SmokeView 6.7.18 visualization post-processing software to establish a CFD model of vehicle fire in a composite steel truss bridge in an open environment. The grid size is 0.5 m × 0.5 m × 0.5 m, with a total of 135,000 grids. In the CFD model, it is assumed that the surface of the bridge structure is adiabatic. The combustion model adopts the heptane combustion reaction. The maximum heat release rate of the tanker fire is defined as 300 MW, with a stable burning duration of 900 s. The fire simulation in the CFD model is conducted for 1800 s. Figure 4 presents the cloud diagrams of slice temperatures set along the longitudinal and transverse directions of the bridge during stable burning of the fire source. When the fire broke out in the oil tanker, the highest temperature of the fire source reached 1350 °C. The flame height significantly exceeds that of the main truss, rising to approximately 15 m.

To facilitate the subsequent discussion of temperature field changes in each truss member, this paper assigns numbers and sequences to select truss members in the mid-span area. Using the central axis of the bridge as a dividing line, the truss member closer to the fire source is designated as the near-fire side truss member, while the one farther from the fire source is the far-fire side truss member. In this context, “S” represents the upper chord member, “F” denotes the web member, “H” stands for the horizontal transverse brace, and “X” indicates the horizontal diagonal member. The specific numbering can be found in Figure 5.

Figure 6 depicts the temporal variation in surface temperatures of select truss members. The analysis indicates that trusses on the far-fire side experience significantly lower temperatures compared with those on the near-fire side. Within the same side, truss members closer to the fire source’s center exhibit a more rapid increase in surface temperature, culminating in higher temperatures.

Table 4. Maximum surface temperature of each truss member under tanker truck fire.

Number	Temperature	Number	Temperature	Number	Temperature	Number	Temperature	Number	Temperature
F1	1000.5 °C	F9	356.2 °C	S1	826.8 °C	X1	1015.0 °C	H1	1015.0 °C
F2	987.5 °C	F10	360.5 °C	S2	803.2 °C	X2	1015.0 °C	H2	1015.0 °C
F3	803.2 °C	F11	352.3 °C	S3	226.9 °C	X3	261.1 °C	H3	529.07 °C
F4	818.9 °C	F12	358.3 °C	S4	230.7 °C	X4	254.3 °C	H4	488.5 °C
F5	286.8 °C	F13	270.2 °C	S5	222.6 °C	X5	1015.0 °C	H5	488.2 °C
F6	290.2 °C	F14	266.0 °C	S6	222.0 °C	X6	1015.0 °C	-	-
F7	166.5 °C	F15	180.4 °C	S7	73.6 °C	X7	244.1 °C	-	-
F8	165.0 °C	F16	192.3 °C	S8	77.8 °C	X8	210.9 °C	-	-

presents the maximum surface temperatures recorded for each truss member in the local model of the composite steel truss bridge girder throughout the entire combustion process. The surface temperatures of the horizontally connected diagonal members (X1, X2, X5, X6) and transverse braces (H1, H2) on the side truss adjacent to the fire can peak at 1015.0 °C. Upper chord rods (S1, S2), shielded from direct flame by cross braces, are heated by high-temperature flue gas, resulting in slightly lower temperatures than those of directly exposed chord rods, with a maximum recorded at 826.8 °C. The maximum temperatures of upper chord members (S5, S6, S7, S8) in the truss far from the fire do not exceed 300 °C. Immediately following the fire outbreak, the transverse brace H1, positioned directly above the fire source’s center, reached its peak temperature within 10 min of fire exposure, demonstrating the most rapid heating rate. Web members F1 and F3, which are in direct contact with the flame, heat up more quickly than other truss members, with the exception of cross brace H1. After 15 min of fire exposure, as the heat release rate reached its peak, the surface temperatures of all truss members approached their maximum values. Thereafter, the combustion process stabilized, leading to minor fluctuations in the surface temperatures of the truss members.

3. Residual Load-Bearing Capacity

3.1. Model Establishment

The finite element model was developed with the large deformation switch enabled and the large strain effect activated within the ANSYS 2021 program to account for geometric nonlinearity. The structural steel employed is of Q355 grade, and the bilinear kinematic hardening model BKIN is utilized as the material constitutive model in ANSYS. The material’s stress–strain relationship is characterized by two straight lines, aligning with the Von Mises yield criterion. The bridge deck, composed of C50 concrete, employs the multilinear kinematic hardening model KINH as its material constitutive model, described by a general formulation. This study takes into account both geometric and material nonlinearities’ impact on the structure. The concrete bridge deck is modeled using the Solid65 eight-node three-dimensional reinforced concrete solid element, capable of simulating concrete cracking and crushing. The steel beam is represented by the Shell181 four-node shell element. Both element types are suitable for nonlinear calculations and analyses. To enhance the model’s computational efficiency and manage its volume, the simulation of shear connectors has been streamlined. The TARGE170 and CONTA175 contact elements are employed to model the contact interaction between longitudinal and transverse beams and the concrete slab, ensuring compatibility between shell and solid elements, as well as meeting the demands for force transmission and heat transfer. In this study, the bolted connections and gusset plate connections between truss members in the actual bridge are simplified to common node connections. Reflecting the actual bridge conditions, the simply supported bridge bearings are simplified as multi-directional node constraints to emulate the fixed bearings, transverse movable bearings, multi-directional movable bearings, and longitudinal movable bearings present in the actual bridge. The finite element model is depicted in Figure 7.

3.2. The Remaining Load-Bearing Capacity of the Truss After a Vehicle Fire

When a bridge is exposed to fire, the mechanical properties of its fire-damaged truss members deteriorate, making them susceptible to plastic deformation during load-bearing. Consequently, this study posits that truss members most adversely affected by fire, displaying significant declines in mechanical properties, are the least favorable for load-bearing. Based on the vehicle fire temperature field detailed in Section 2.3 and the truss numbering system, truss members experiencing temperatures exceeding 600 °C during a fire are identified as the least favorable load-bearing components.

The mechanical properties of structural steel after a fire are significantly influenced by the cooling method. In examining the residual load-bearing capacity of trusses post-fire, this study considers the effects of two cooling methods: natural cooling (CIA) and immersion cooling (CIW). Additionally, residual deformation can affect the truss’s load-bearing capacity to some extent. In the subsequent analysis, the influence of truss deformation due to fire is incorporated using the Upgeom command in ANSYS 2021 software.

The method of surface loading based on the axial force of the truss was adopted to determine the most unfavorable load arrangement of the truss in the composite steel truss bridge girder. For the critical load-bearing members of the composite steel truss bridge girder, we utilized axial force influence surface loading, and the resulting load-displacement curve is depicted in Figure 8. Owing to the extensive number of fire-exposed truss members in the composite steel truss bridge girder, we present only a selection of these load-displacement curves. In the figure, the vertical axis represents the load-bearing capacity coefficient, with $\lambda$ symbolizing the load-bearing capacity coefficient of the truss member under normal temperature conditions. ${\lambda }_1$ denotes the load-bearing capacity coefficient of the truss after cooling naturally (CIA) post-fire, and ${\lambda }_2$ signifies the load-bearing capacity coefficient following water immersion cooling (CIW) post-fire. The horizontal axis represents the vertical displacement at the mid-span of the structure. From Figure 7, it is evident that prior to reaching the yield stress, the mid-span displacement increases linearly with increasing load. Upon reaching the yield stress, the load-displacement curve exhibits an inflection point. At this juncture, even if the load remains constant, the vertical displacement continues to increase, indicating that the truss is approaching its limit state. The live load factor at this point is referred to as the residual load-bearing capacity coefficient of the truss.

The ultimate load-bearing capacity of the upper chord bar S1 and the horizontal crossbar H1 after a vehicle fire was further investigated, as illustrated in Figure 9. Following the cooling of the oil tanker, different load arrangement methods lead to variations in the stress distribution within the structure. For the most unfavorable load configuration of the upper chord S1 under natural cooling conditions, when the fire temperature for the horizontally connected inclined member exceeds 1000 °C, there is approximately a 43.2% reduction in yield strength. The upper chord S1, exposed to fire temperatures above 800 °C, experiences a strength reduction of approximately 29.2% under natural cooling. Referring to Figure 9a, the longitudinal and transverse beams of these inclined members undergo buckling, with the maximum stress of 352.99 MPa occurring at the same section as the upper chord bar S1. Under water immersion cooling, the yield strength of the horizontally connected inclined members recovers to about 99% of its original value. However, the strength loss of the upper chord under water immersion is 1.9% greater than under natural cooling conditions. Both the horizontal diagonal members and the upper chord members exhibit some degree of buckling. Referring to Figure 9b, the maximum stress of the structure under these conditions is 354.82 MPa, occurring at the horizontal connection.

In accordance with the most unfavorable load arrangement for the transverse brace H1 under natural cooling conditions, referring to Figure 9c, the horizontal coupling initially undergoes buckling, with a maximum stress of 351.68 MPa occurring at the lower chord bar, which aligns with the longitudinal bridge position of the transverse brace H1. Under water immersion cooling, referring to Figure 9c, structural failure similarly results from the buckling of the flat joint; however, the stress levels at which the truss yields differ. Specifically, the stress under natural cooling is 201.64 MPa, while under water immersion cooling, it reaches 354.84 MPa.

From Figure 10, it is evident that under various fire conditions, when the bridge structure reaches its limit state, significant buckling occurs in the truss members on the fire-exposed side. This buckling is accompanied by increased plastic deformation, which leads to an overall increase in the vertical deflection of the structure. The maximum vertical displacement of the bridge deck consistently occurs at mid-span on the fire-exposed side. Nonetheless, under different fire conditions, the force transmission paths vary, resulting in differences in the magnitude of ultimate state displacement. Additionally, the cooling method employed post-fire also exerts an influence.

The calculation results indicate that the upper chord rod S2 exhibits the lowest load-bearing capacity coefficients of 6.48 and 6.35 under natural cooling and water immersion cooling, respectively, following a vehicle fire. Similarly, the load-bearing capacity of the upper chord rod S1 is also relatively low under these same cooling conditions. This suggests that after a vehicle fire in a composite steel truss bridge girder, the upper chord members are the most significantly impacted by the fire history when subjected to load. The findings demonstrate that the residual load-bearing capacity of the truss is influenced by the cooling method applied to the oil tanker post-fire. The decline in load-bearing capacity for the upper chord members S1 and S2 and the web member F1 is more pronounced under water immersion cooling compared with natural cooling.

3.3. The Remaining Load-Bearing Capacity of the Composite Steel Truss Bridge Girder

3.3.1. Bridge Structural Failure Path

Through the evaluation of the remaining load-bearing capacity of a truss following a vehicle fire, it is evident that the upper chord is the most severely impacted component, with the lowest remaining capacity coefficient. The upper chord is crucial for maintaining the structural integrity. Before assessing the post-fire residual load-bearing capacity of a composite steel truss bridge girder, it is imperative to analyze the structural failure pathway resulting from damage to the upper chord members. The failure pathway, particularly for the upper chord members, is detailed with the load–stress curve of the truss members shown in Figure 11. Initially, under external loads, the upper chord members yield first, undergoing plastic deformation. As the load increases further, it is redistributed to other components, such as the diagonally connected members. At this point, the plastic deformation of the upper chord members, coupled with the escalating load, triggers rapid stress development in adjacent truss members. This leads to structural instability and eventual failure.

3.3.2. Structural Load-Displacement Curve

Factors such as burning duration, traffic volume, and fire cooling methods can significantly influence the remaining load-bearing capacity of a bridge post-fire. Therefore, this study focuses on a composite steel truss bridge girder and develops a scenario database that considers three critical factors: the fire characteristic temperature, the load level during the fire, and the fire cooling method. The database is established for the most unfavorable fire location identified in this study concerning an oil tanker fire affecting the composite steel truss bridge girder.

• Fire characteristic temperature;

The fire characteristic temperature refers to the maximum temperature to which a structure is exposed during a fire. This temperature level significantly affects the mechanical properties of structural steel, making its determination crucial. As noted in Section 3.1, the critical truss component in the structure is the upper chord member. Consequently, the historical temperature of the mid-span upper chord S2 during the fire is used as the fire characteristic temperature for the composite steel truss bridge girder, with the range set between 600 °C and 800 °C.

2.

Load level;

Under identical characteristic temperature conditions, varying load levels will result in differing degrees of structural deformation, thereby influencing the remaining load-bearing capacity of the composite steel truss bridge girder. Additionally, factors such as traffic disruptions during a fire can cause variations in the number of vehicles on the bridge, thereby altering the load level. Consequently, this study considers three load levels: 20%, 60%, and 100% of the lane load.

3.

Cooling method;

The mechanical properties of structural steel post-fire are notably influenced by the cooling method employed. This study examines the effects of two cooling methods—natural cooling (CIA) and immersion cooling (CIW)—on the residual load-bearing capacity of composite steel truss bridge girders after a fire.

Figure 12 presents structural load-bearing capacity-displacement curves under 24 different fire scenarios for oil tankers, taking into account varying fire characteristic temperatures, load levels, and cooling methods. The results indicate that as the fire temperature experienced by the critical truss increases, the residual load-bearing capacity of the composite steel truss bridge girder decreases post-vehicle fire. The cooling method has a relatively minor impact on the elastic modulus of structural steel during the initial loading phase, resulting in similar bearing stiffness across methods. However, higher load levels significantly shorten the elastic bearing phase of the structure.

For instance, in the fire scenario O-800-CIW-100, the minimum residual load-bearing capacity after high temperature is significantly reduced, showing a 58.68% decrease compared with the normal temperature load-bearing capacity. In the scenario naming convention, “O” denotes oil tanker, “800” refers to the temperature, “CIW” indicates immersion cooling (with “CIA” for natural cooling), and “100” represents the load level.

3.3.3. Assessment Methods of Residual Load-Bearing Capacity

The decline rate R is introduced to quantify the change in the load-bearing capacity of a composite steel truss bridge girder following a vehicle fire. This rate reflects the relationship between the structure’s residual load-bearing capacity post-fire and its original capacity at normal temperature. R is calculated as a percentage, representing the ratio of the post-fire residual load-bearing capacity to the normal temperature load-bearing capacity. The formula is expressed as follows:

$$R={Q_T/Q}_0\times 100\%$$

(1)

The remaining load-bearing capacity of the structure is compared with the load multiples of three lanes, and the damage grades of four grades of load-bearing capacity in a composite steel truss bridge girder following a vehicle fire are defined. Figure 13 illustrates the degradation curve of the bridge’s load-bearing capacity post-fire.

When the remaining load-bearing capacity of the composite steel truss bridge girder is less than 5 times the lane load ($R\le 52.97\mathrm{\%}$), the damage grade is defined as Grade IV. At this stage, the bridge structure is prone to instability and failure. Even if the bridge is repaired and reinforced, it may still fail to meet the normal usage requirements. Bridges at this grade are recommended to be demolished and rebuilt.

When the remaining load-bearing capacity of the composite steel truss bridge girder is less than 6 times the lane load but greater than 5 times the lane load ($52.97\mathrm{\%}<R\le 64.17\mathrm{\%}$), the damage grade is defined as Grade III. At this stage, there are many truss members with deformation values greater than the limit values stipulated in the code. The bridge needs to be repaired to a large extent, and all the truss members with abnormal deformation should be replaced to ensure the stability and safety of the structure.

When the remaining load-bearing capacity of the composite steel truss bridge girder is less than 7 times the lane load but greater than 6 times the lane load ($64.17\mathrm{\%}<R\le 75.37\mathrm{\%}$), the damage grade is defined as Grade II. At this stage, abnormal deformation occurs in some of the truss rods of the structure. The bridge needs to be repaired to a lesser extent, and the abnormal truss rods should be replaced and reinforced.

When the remaining load-bearing capacity of the composite steel truss bridge girder is greater than 7 times the lane load ($75.37\%<R$), the damage grade is Grade I. At this stage, some individual truss members of the structure have abnormal deformation, and replacing the key load-bearing truss members can meet the normal use of the structure.

The analysis presented in Figure 13 indicates that, when a composite steel truss bridge experiences a vehicle fire, the structural load-bearing capacity falls within Grade II damage as long as the characteristic temperature of the fire remains below 700 °C. Once the temperature exceeds 800 °C, the damage escalates to Grade IV. It is notable that when the temperature surpasses 700 °C, the damage incurred is greater following water immersion cooling compared with natural cooling. At the fire scenario O-750-CIW-100, the structural damage is classified as Grade IV. A higher load level results in a decreased residual load-bearing capacity of the composite steel truss bridge girder post-fire. For instance, under the fire scenario O-700-CIA-100, the bridge sustains Grade II damage, whereas under scenario O-700-CIA-20, it incurs only grade I damage.

4. Conclusions

(1)

This study develops a realistic temperature field model for the girders of composite steel truss bridges subjected to oil tanker fires. Utilizing Computational Fluid Dynamics (CFD), a numerical model was established to simulate various fire scenarios in an open environment. The analysis focused on the temperature variations and maximum temperatures attained by individual truss members during these events. The results indicate that the most critical scenario involves a fire on the outermost lane of the bridge deck at the mid-span. Specifically, truss members situated directly above the fire’s epicenter reached the highest temperatures, with thermal values diminishing as the distance from the fire source increased.

(2)

By considering the deformation of the truss during the fire event, the analysis identified the most critically affected members and subsequently evaluated their residual load-bearing capacity. The findings demonstrate that the upper chord members are the most vulnerable to fire-induced damage. Furthermore, it was determined that the choice of post-fire cooling method significantly influences the final residual load-bearing capacity.

(3)

An evaluation method was established to assess the residual load-bearing capacity of composite steel truss bridge girders, which comprehensively considers truss deformation effects and structural steel strength degradation. This study analyzed the decline in residual load-bearing capacity following a vehicle fire and discovered that higher fire exposure temperatures and increased load levels shorten the elastic stage, reducing residual capacity. At characteristic fire temperatures below 700 °C, the load-bearing capacity damage is classified as Grade II, whereas temperatures above 800 °C escalate the damage to Grade IV. Post-fire, when characteristic temperatures exceed 700 °C, water immersion cooling results in greater load-bearing capacity loss.

(4)

The proposed methodology and classification standards provide a robust scientific foundation for the post-fire safety assessment of composite steel truss bridges. This framework enables the rapid and accurate determination of damage levels, which can guide systematic emergency response efforts and mitigate the risk of secondary disasters from sudden structural collapse. Moreover, it offers theoretical support for decisions regarding traffic restoration, thereby minimizing economic losses and social disruption. The findings also serve as a crucial reference for design optimization, the formulation of fire prevention strategies, and post-disaster repair and reinforcement protocols, ultimately contributing to the enhanced safety and fire resilience of steel bridge structures.

(5)

While this study provides valuable insights into the post-fire residual capacity of composite steel truss bridges, several limitations should be acknowledged as avenues for future research. Firstly, the investigation was confined to a single fire scenario; future work should therefore explore a broader range of fire types and locations to enhance the generalizability of the findings. Secondly, fire scenario data were generated exclusively through CFD simulations, with model validation relying on a limited set of the existing literature. Consequently, further research would greatly benefit from validation against large-scale experimental data obtained from physical bridge fire tests. Such empirical data are essential for improving the model’s accuracy and practical applicability.