Efficient Hyperparameter Optimization Using Metaheuristics for Machine Learning in Truss Steel Structure Cross-Section Prediction
Abstract
1. Introduction
- Reducing human effort: HPO minimizes the manual labor required to apply machine learning effectively [15].
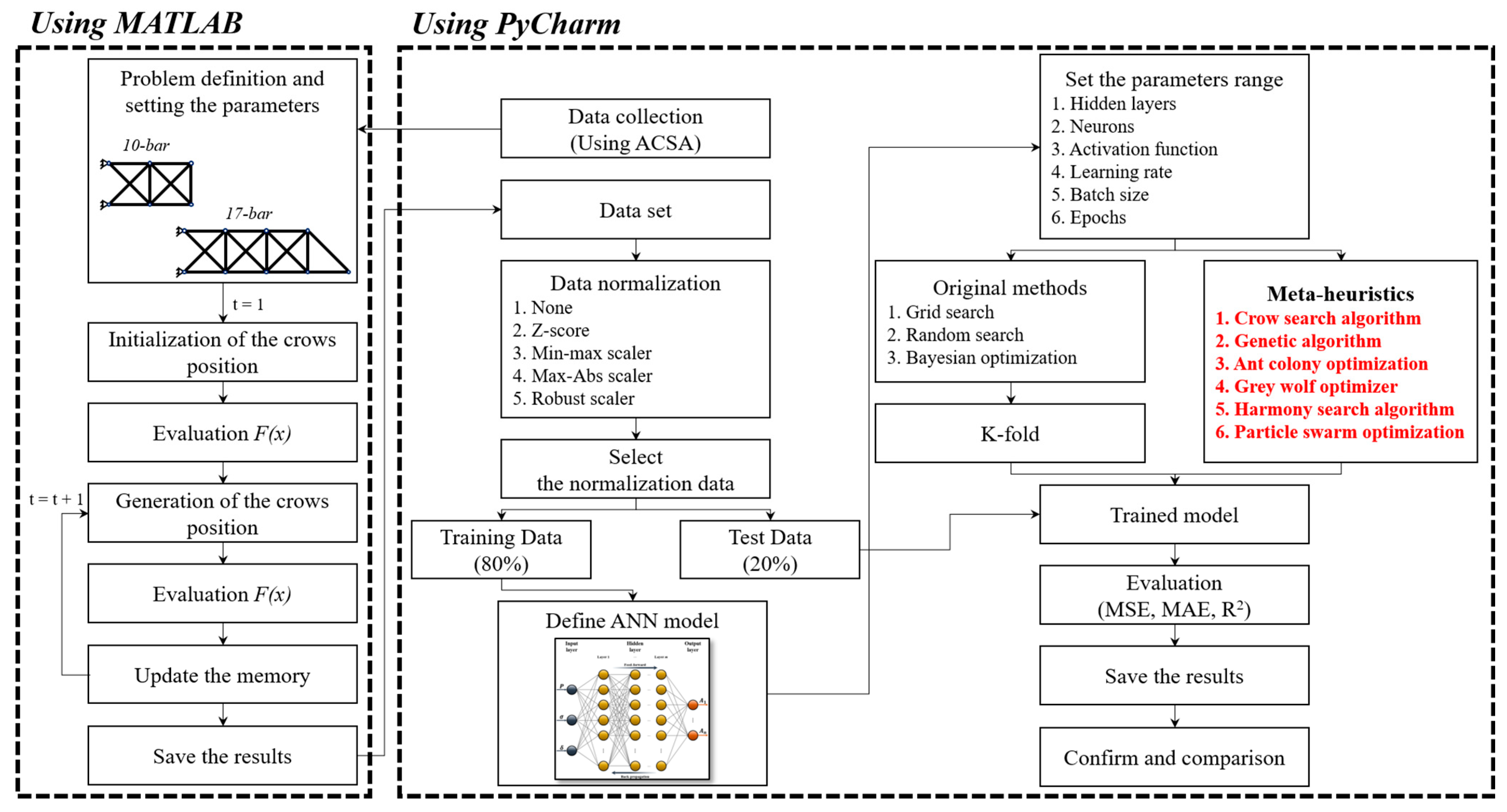
2. Methodology
2.1. Data Collection
2.2. Hyperparameter Optimization
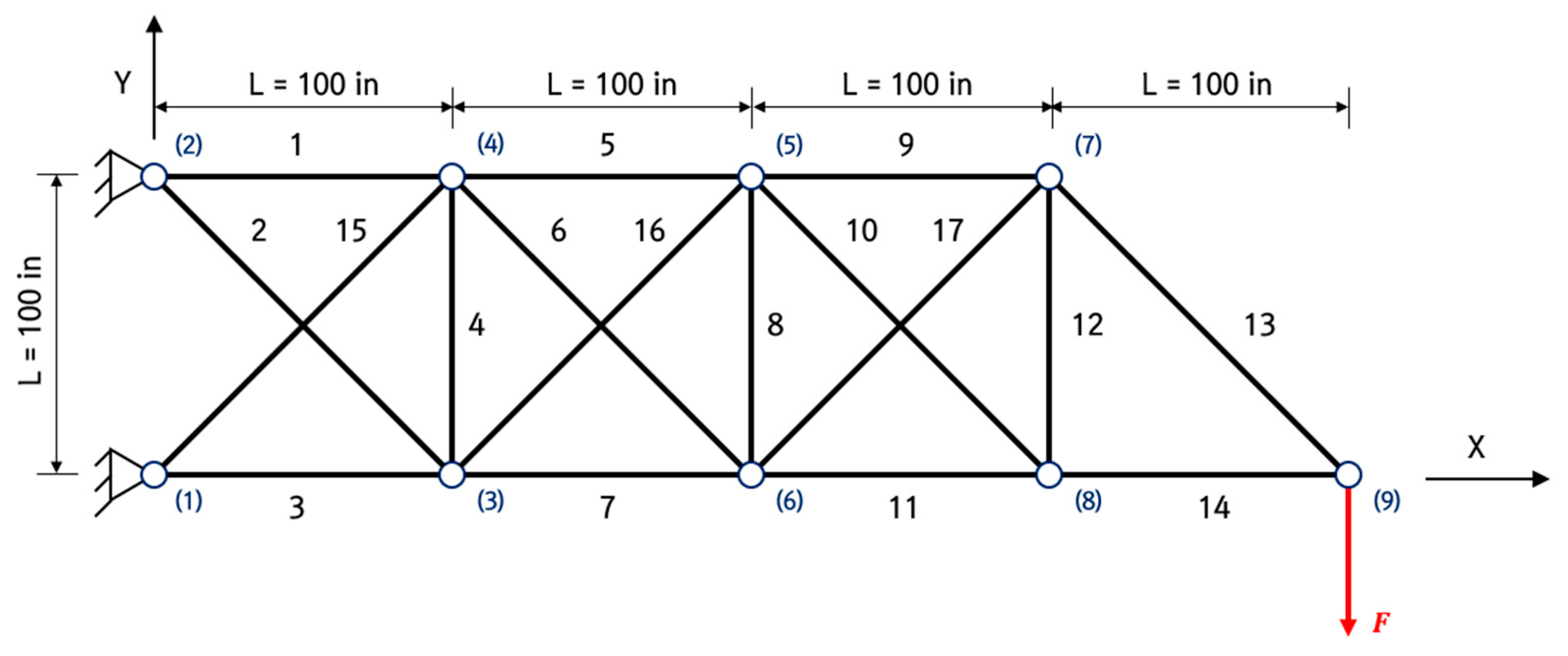
3. Definition of 2D Truss Structures
3.1. The 10-Bar Truss Structure
3.2. The 17-Bar Truss Structure
4. Comparison of Prediction Performance by Hyperparameters Optimization Methods
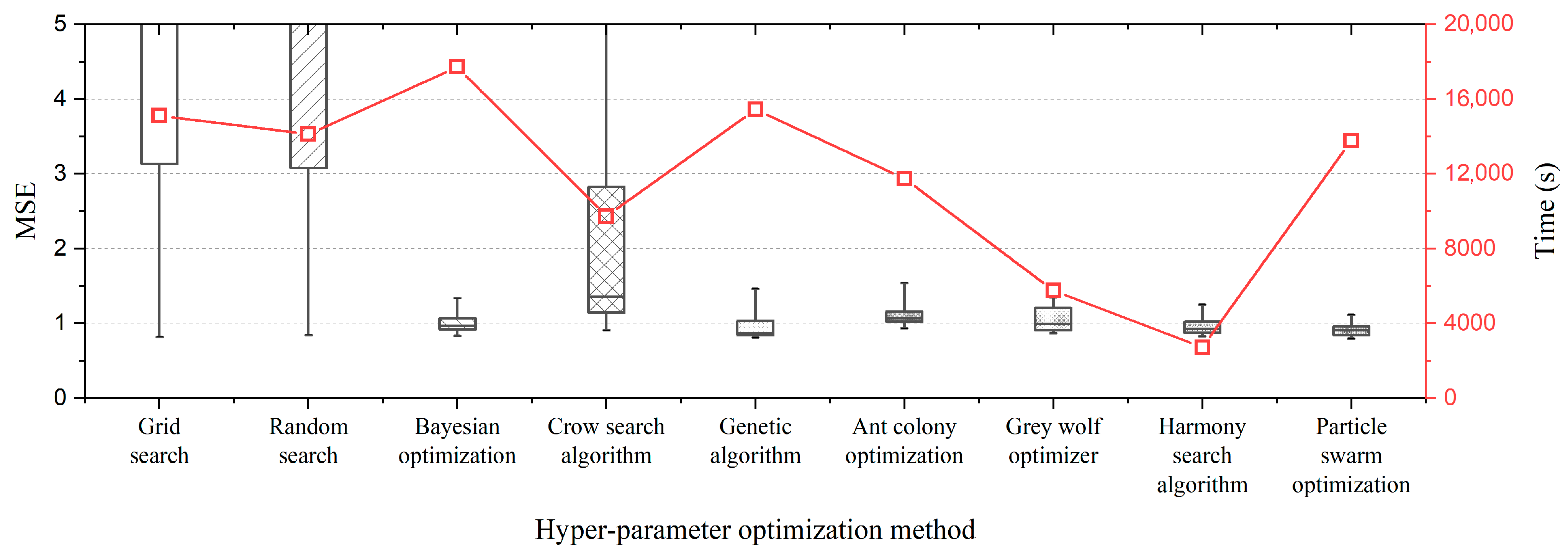
4.1. The 10-Bar Truss Structure
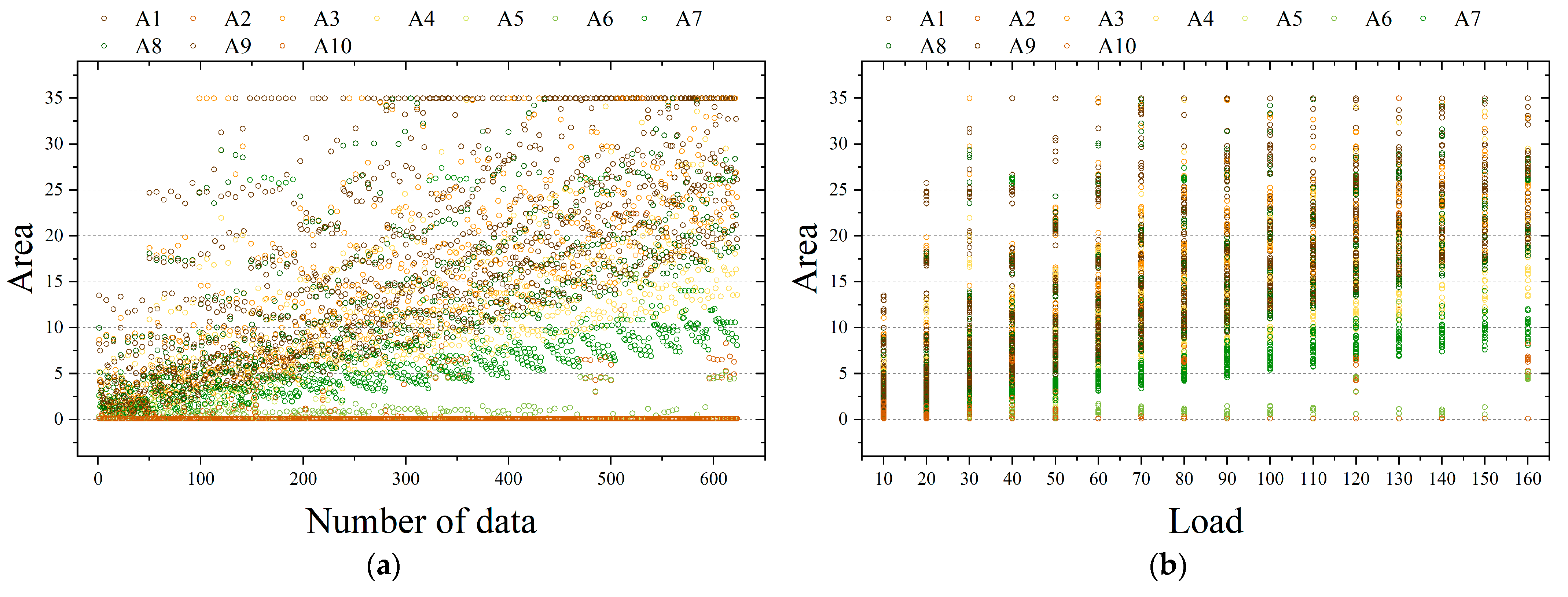
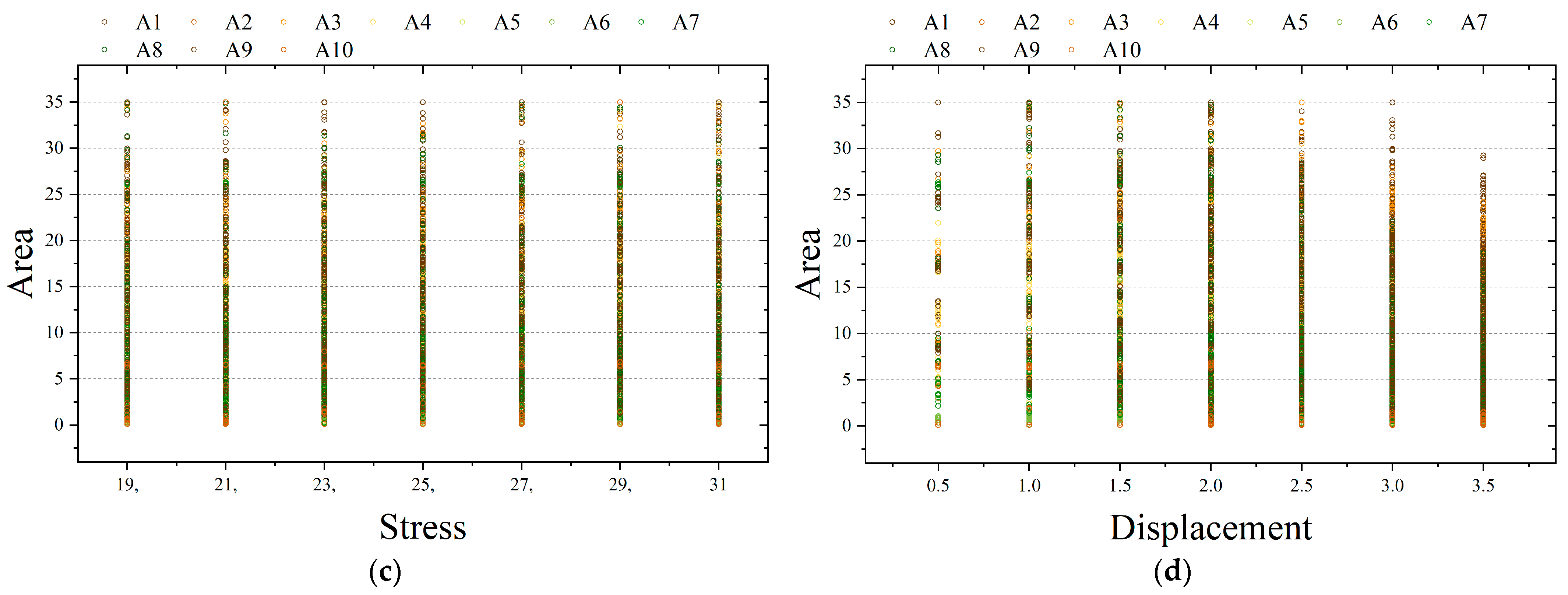
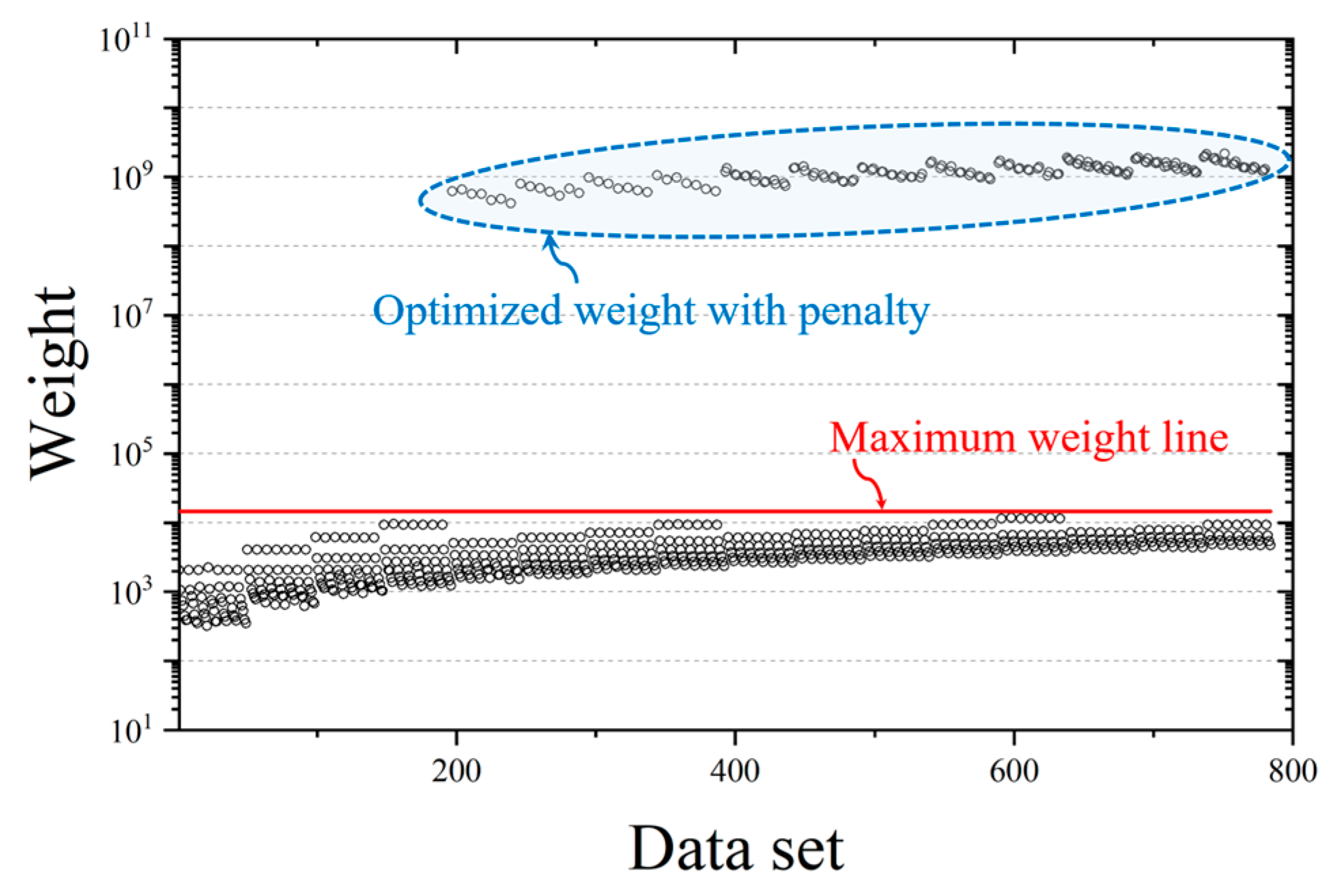
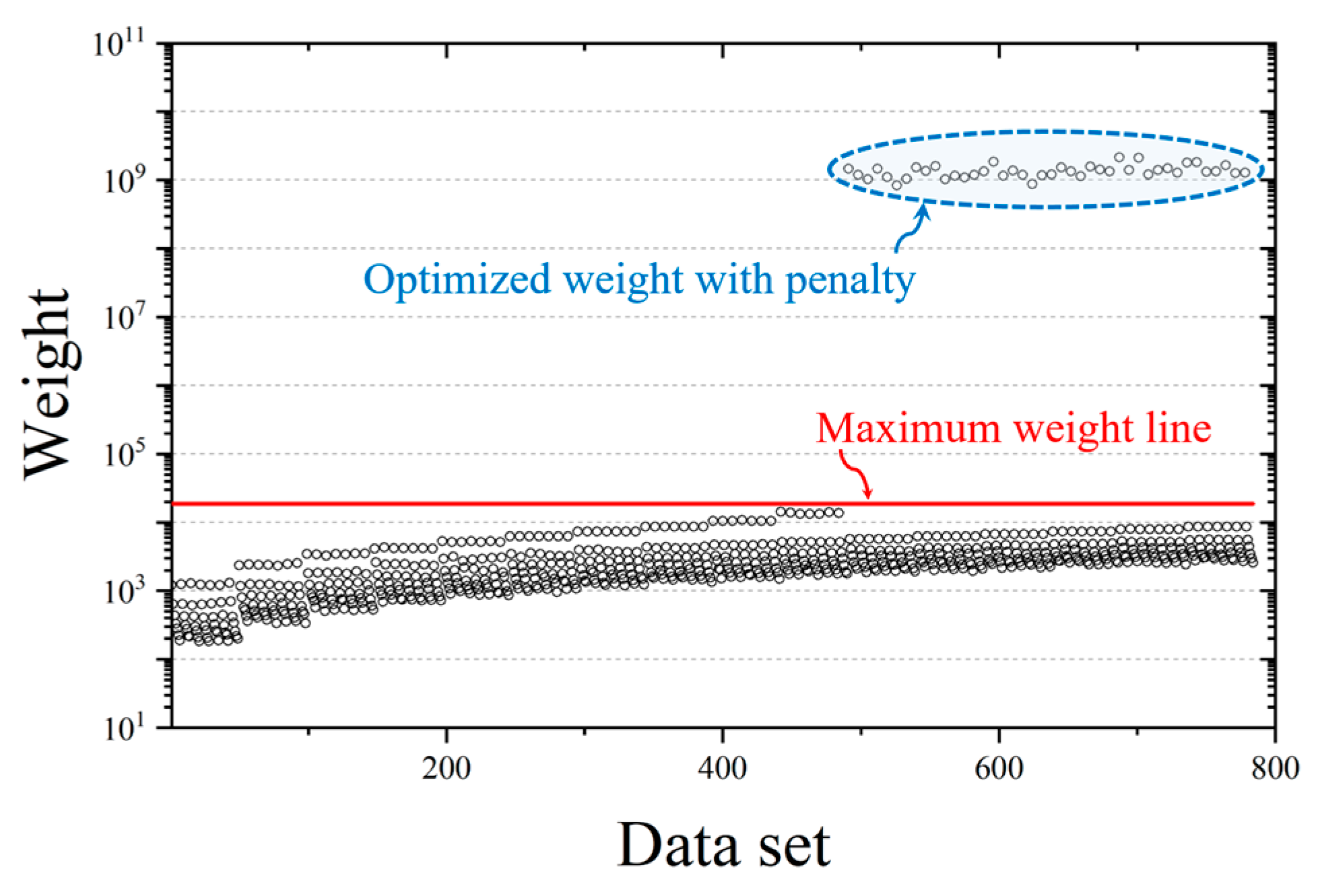
4.1.1. Datasets
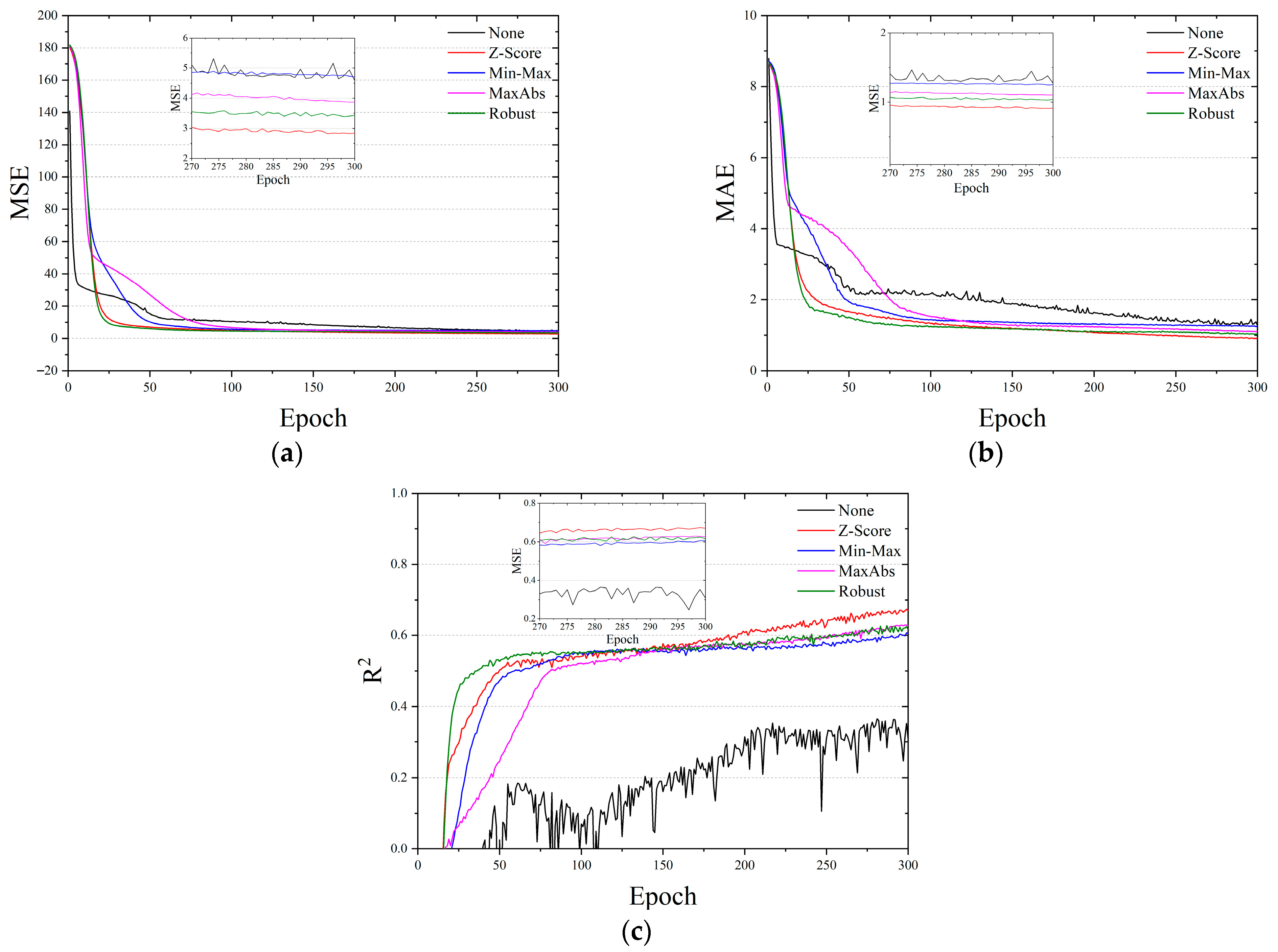
4.1.2. Data Normalization
4.1.3. Hyperparameter Optimization
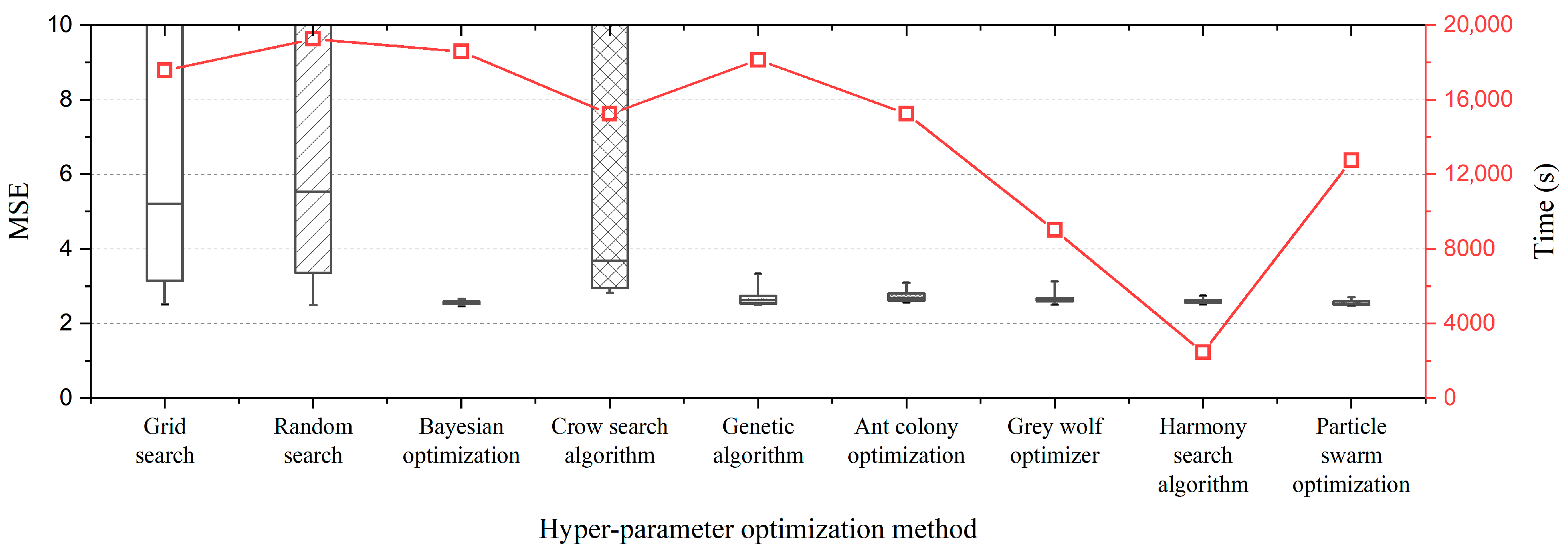
4.2. The 17-Bar Truss Structure
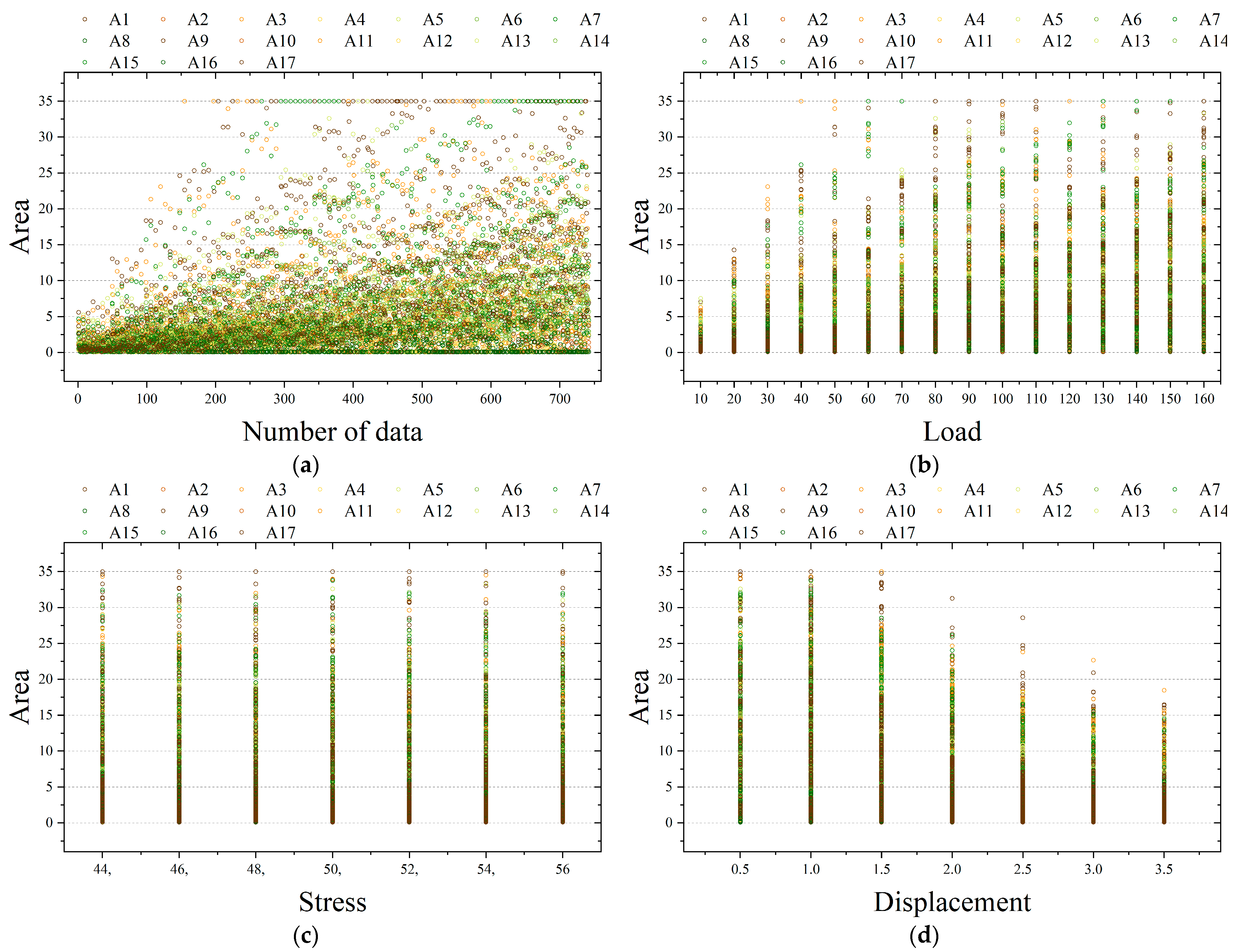
4.2.1. Datasets
4.2.2. Data Normalization
4.2.3. Hyperparameter Optimization
4.3. Summary and Comparative Analysis of HPO Results
5. Conclusions
- First, we systematically applied HPO to the machine learning-based prediction of truss cross-sections—a topic that has received limited attention in prior research—and demonstrated its effectiveness using data derived from structural analysis.
- Second, we conducted a fair and comprehensive comparison of nine HPO methods under consistent conditions, thereby providing practical guidelines for selecting suitable algorithms in structural design problems.
- Third, we empirically analyzed the impact of various data normalization techniques on prediction performance and confirmed that Z-score normalization yields the most accurate results. This finding provides practical insight into the importance of data preprocessing in machine learning applications to structural optimization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lee, D.; Shon, S.; Lee, S.; Ha, J. Size and Topology Optimization of Truss Structures Using Quantum-Based HS Algorithm. Buildings 2023, 13, 1436. [Google Scholar] [CrossRef]
- Lee, S.; Ha, J.; Shon, S.; Lee, D. Weight Optimization of Discrete Truss Structures Using Quantum-Based HS Algorithm. Buildings 2023, 13, 2132. [Google Scholar] [CrossRef]
- El-Kassas, E.; Mackie, R.; El-Sheikh, A. Using neural networks in cold-formed steel design. Comput. Struct. 2001, 79, 1687–1696. [Google Scholar] [CrossRef]
- Cheng, J.; Li, Q.S. A hybrid artificial neural network method with uniform design for structural optimization. Comput. Mech. 2009, 44, 61–71. [Google Scholar] [CrossRef]
- Yin, T.; Zhu, H.-P. Probabilistic damage detection of a steel truss bridge model by optimally designed Bayesian neural network. Sensors 2018, 18, 3371. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, A.; Shao, W.; Zhang, A.; Du, X. Artificial-neural-network-based mechanical simulation prediction method for wheel-spoke cable truss construction. Int. J. Steel Struct. 2021, 21, 1032–1052. [Google Scholar] [CrossRef]
- Mai, H.T.; Lee, S.; Kim, D.; Lee, J.; Kang, J.; Lee, J. Optimum design of nonlinear structures via deep neural network-based parameterization framework. Eur. J. Mech.-A/Solids 2023, 98, 104869. [Google Scholar] [CrossRef]
- Nguyen, L.C.; Nguyen-Xuan, H. Deep learning for computational structural optimization. ISA Trans. 2020, 103, 177–191. [Google Scholar] [CrossRef]
- Yu, Z. Frequency prediction and optimization of truss structure based on BP neural network. In Proceedings of the 2021 3rd International Conference on Artificial Intelligence and Advanced Manufacture, Manchester, UK, 23–25 October 2021; pp. 354–358. [Google Scholar]
- Liu, J.; Xia, Y. A hybrid intelligent genetic algorithm for truss optimization based on deep neutral network. Swarm Evol. Comput. 2022, 73, 101120. [Google Scholar] [CrossRef]
- Mai, H.T.; Lieu, Q.X.; Kang, J.; Lee, J. A novel deep unsupervised learning-based framework for optimization of truss structures. Eng. Comput. 2023, 39, 2585–2608. [Google Scholar] [CrossRef]
- Tran, M.Q.; Sousa, H.S.; Ngo, T.V.; Nguyen, B.D.; Nguyen, Q.T.; Nguyen, H.X.; Baron, E.; Matos, J.; Dang, S.N. Structural assessment based on vibration measurement test combined with an artificial neural network for the steel truss bridge. Appl. Sci. 2023, 13, 7484. [Google Scholar] [CrossRef]
- King, R.D.; Feng, C.; Sutherland, A. Statlog: Comparison of classification algorithms on large real-world problems. Appl. Artif. Intell. 1995, 9, 289–333. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Automatic parameter selection by minimizing estimated error. In Proceedings of the Machine Learning Proceedings 1995 Morgan Kaufmann, Tahoe, CA, USA; 1995; pp. 304–312. [Google Scholar]
- Feurer, M.; Hutter, F. Hyperparameter optimization. In Automated Machine Learning: Methods, Systems, Challenges; Springer International Publishing: Cham, Switzerland, 2019; pp. 3–33. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the International conference on machine learning, Atlanta, GA, USA, 16–21 June 2013; pp. 115–123. [Google Scholar]
- Sculley, D.; Snoek, J.; Wiltschko, A.; Rahimi, A. Winner’s curse? On pace, progress, and empirical rigor. In Proceedings of the International Conference on Learning Representations 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Jerebic, J.; Mernik, M.; Liu, S.-H.; Ravber, M.; Baketarić, M.; Mernik, L.; Črepinšek, M. A novel direct measure of exploration and exploitation based on attraction basins. Expert Syst. Appl. 2021, 167, 114353. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, H.; Zhan, Z.-H.; Li, J.; Zhang, H. Growth Optimizer: A powerful metaheuristic algorithm for solving continuous and discrete global optimization problems. Knowl. Based Syst. 2023, 261, 110206. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Nematzadeh, S.; Kiani, F.; Torkamanian-Afshar, M.; Aydin, N. Tuning hyperparameters of machine learning algorithms and deep neural networks using metaheuristics: A bioinformatics study on biomedical and biological cases. Comput. Biol. Chem. 2022, 97, 107619. [Google Scholar] [CrossRef] [PubMed]
- Bacanin, N.; Stoean, C.; Zivkovic, M.; Rakic, M.; Strulak-Wójcikiewicz, R.; Stoean, R. On the benefits of using metaheuristics in the hyperparameter tuning of deep learning models for energy load forecasting. Energies 2023, 16, 1434. [Google Scholar] [CrossRef]
- Nair, A.T.; Arivazhagan, M. Industrial activated sludge model identification using hyperparameter-tuned metaheuristics. Swarm Evol. Comput. 2024, 91, 101733. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Dahou, A.; Abualigah, L.; Yu, L.; Alshinwan, M.; Khasawneh, A.M.; Lu, S. Advanced metaheuristic optimization techniques in applications of deep neural networks: A review. Neural Comput. Appl. 2021, 33, 14079–14099. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Jankowski, R. Optimization-based stacked machine-learning method for seismic probability and risk assessment of reinforced concrete shear walls. Expert Syst. Appl. 2025, 255, 124897. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Lee, D.; Kim, J.; Shon, S.; Lee, S. An Advanced Crow Search Algorithm for Solving Global Optimization Problem. Appl. Sci. 2023, 13, 6628. [Google Scholar] [CrossRef]
- Andonie, R. Hyperparameter optimization in learning systems. J. Membr. Comput. 2019, 1, 279–291. [Google Scholar] [CrossRef]
- Shankar, K.; Zhang, Y.; Liu, Y.; Wu, L.; Chen, C.-H. Hyperparameter tuning deep learning for diabetic retinopathy fundus image classification. IEEE Access 2020, 8, 118164–118173. [Google Scholar] [CrossRef]
- Claesen, M.; Simm, J.; Popovic, D.; Moreau, Y.; De Moor, B. Easy hyperparameter search using optunity. arXiv 2014, arXiv:1412.1114. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Lindauer, M. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2023, 13, e1484. [Google Scholar]
- Hussien, A.G.; Amin, M.; Wang, M.; Liang, G.; Alsanad, A.; Gumaei, A.; Chen, H. Crow search algorithm: Theory, recent advances, and applications. IEEE Access 2020, 8, 173548–173565. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 1992. [Google Scholar]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. Ant colony optimization: Overview and recent advances. Springer Int. Public 2019, 272, 311–351. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Al-Betar, M.A.; Abu Doush, I.; Awadallah, M.A.; Kassaymeh, S.; Mirjalili, S.; Abu Zitar, R. Recent advances in Grey Wolf Optimizer, its versions and applications. IEEE Access 2023, 12, 22991–23028. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Alia, O.M.; Mandava, R. The variants of the harmony search algorithm: An overview. Artif. Intell. Rev. 2011, 36, 49–68. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory, MHS’95. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 4 November 1995; pp. 1942–1948. [Google Scholar]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar]
- Lee, K.S.; Geem, Z.W. A new structural optimization method based on the harmony search algorithm. Comput. Struct. 2004, 82, 781–798. [Google Scholar] [CrossRef]
- Hasançebi, O.; Azad, S.K.; Azad, S.K. Automated sizing of truss structures using a computationally improved SOPT algorithm. Int. J. Optim. Civ. Eng. 2013, 3, 209–221. [Google Scholar]
- Massah, S.R.; Ahmadi, H. Weight Optimization of Truss Structures by the Biogeography-Based Optimization Algorithms. Civ. Eng. Infrastruct. J. 2021, 54, 129–144. [Google Scholar]
- Smith, L.N. A disciplined approach to neural network hyper-parameters: Part 1—learning rate, batch size, momentum, and weight decay. arXiv 2018, arXiv:1803.09820. [Google Scholar]
- Fridrich, M. Hyperparameter optimization of artificial neural network in customer churn prediction using genetic algorithm. Trendy Ekon. Manag. 2017, 11, 9. [Google Scholar]
- Kalliola, J.; Kapočiūtė-Dzikienė, J.; Damaševičius, R. Neural network hyperparameter optimization for prediction of real estate prices in Helsinki. PeerJ Comput. Sci. 2021, 7, e444. [Google Scholar] [CrossRef]
- Keskar, N.S.; Mudigere, D.; Nocedal, J.; Smelyanskiy, M.; Tang, P.T.P. On large-batch training for deep learning: Generalization gap and sharp minima. arXiv 2016, arXiv:1609.04836. [Google Scholar]


| Type | Parameters |
|---|---|
| 10-bar truss structure | D = 10, tmax = 3000, N = 10, fl = 2.0, APmax = 0.4, APmin = 0.01, FAR = 0.4 |
| 17-bar truss structure | D = 17, tmax = 5000, N = 10, fl = 2.0, APmax = 0.4, APmin = 0.01, FAR = 0.4 |
| Type | Range |
|---|---|
| Load (kips) | 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160 |
| Maximum stress (ksi) | 19, 21, 23, 25, 27, 29, 31 |
| Maximum displacement (in) | 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5 |
| Type | Range |
|---|---|
| Load (kips) | 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160 |
| Maximum stress (ksi) | 44, 46, 48, 50, 52, 54, 56 |
| Maximum displacement (in) | 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5 |
| Methods | Range |
|---|---|
| GS | Hidden layers = [1, 3, 5] Neurons = [8, 64, 128] Activation function = [1: ReLU, 2: Sigmoid, 3: Tan-Sigmoid] Learning rates = [0.001, 0.05, 0.1] Batch size = [16, 64, 128] Epochs = [10, 150, 300] |
| RS, BO, CSA, GA, ACO, GWO, HAS, and PSO | Hidden layers = [1, 5] Neurons = [8, 128] Activation function = [1: ReLU, 2: Sigmoid, 3: Tan-Sigmoid] Learning rates = [0.001, 0.1] Batch size = [16, 128] Epochs = [10, 300] |
| Methods | Parameters | nEva |
|---|---|---|
| GS | K-fold = 3 | 2187 |
| RS | nLoop = 729, K-fold = 3 | 2187 |
| BS | nIter = 20, nLoop = 35, K-fold = 3 | 2100 |
| CSA | nLoop = 20, n = 5, nGen = 20, AP = 0.2, fl = 2 | 2000 |
| GA | nLoop = 20, n = 5, nGen = 20, mutation = 0.1, crossover = 0.7 | 2000 |
| ACO | nLoop = 20, n = 5, nGen = 20, evaporation = 0.5, pheromone = 1.0 | 2000 |
| GWO | nLoop = 20, n = 5, nGen = 20, a_initial = 2.0, a_final = 0 | 2000 |
| HSA | nLoop = 20, n = 5, nGen = 20, HMCR = 0.9, PAR = 0.3, Pitch = 0.05 | 2000 |
| PSO | nLoop = 20, n = 5, nGen = 20, w = 0.5, c1 = 1.5, c2 = 1.5 | 2000 |
| Index | Min | Max | Mean | Std. |
|---|---|---|---|---|
| A1 | 1.420 | 35.000 | 20.703 | 10.864 |
| A2 | 0.100 | 15.856 | 0.540 | 1.829 |
| A3 | 0.790 | 35.000 | 17.256 | 10.263 |
| A4 | 0.435 | 35.000 | 11.748 | 8.097 |
| A5 | 0.100 | 2.616 | 0.170 | 0.305 |
| A6 | 0.100 | 15.901 | 0.680 | 1.830 |
| A7 | 0.100 | 35.000 | 7.026 | 6.191 |
| A8 | 0.100 | 35.000 | 15.514 | 9.457 |
| A9 | 0.675 | 35.000 | 15.830 | 9.567 |
| A10 | 0.100 | 35.000 | 0.738 | 3.071 |
| Index | None | Z-Score | Min-Max | Max-Abs | Robust |
|---|---|---|---|---|---|
| MSE | 4.5817 | 2.8355 | 4.7072 | 3.8717 | 3.4296 |
| MAE | 1.2738 | 0.9119 | 1.2500 | 1.1040 | 1.0382 |
| R2 | 0.3083 | 0.6704 | 0.6063 | 0.6267 | 0.6166 |
| Index | Min | Max | Mean | Std. |
|---|---|---|---|---|
| A1 | 0.626 | 35.000 | 14.436 | 10.725 |
| A2 | 0.100 | 35.000 | 1.814 | 2.467 |
| A3 | 0.484 | 35.000 | 12.884 | 9.725 |
| A4 | 0.100 | 9.299 | 1.128 | 1.471 |
| A5 | 0.441 | 35.000 | 9.532 | 7.612 |
| A6 | 0.100 | 35.000 | 5.284 | 5.641 |
| A7 | 0.231 | 35.000 | 11.389 | 9.719 |
| A8 | 0.100 | 35.000 | 1.145 | 1.910 |
| A9 | 0.272 | 35.000 | 8.232 | 7.572 |
| A10 | 0.100 | 35.000 | 1.325 | 2.126 |
| A11 | 0.130 | 35.000 | 5.237 | 4.927 |
| A12 | 0.100 | 35.000 | 1.380 | 2.039 |
| A13 | 0.296 | 35.000 | 6.450 | 5.808 |
| A14 | 0.100 | 35.000 | 4.756 | 4.574 |
| A15 | 0.100 | 35.000 | 5.007 | 5.626 |
| A16 | 0.100 | 35.000 | 1.561 | 2.564 |
| A17 | 0.100 | 35.000 | 5.631 | 5.913 |
| Index | None | Z-Score | Min-Max | Max-Abs | Robust |
|---|---|---|---|---|---|
| MSE | 5.4184 | 3.2937 | 4.2894 | 4.0807 | 3.1174 |
| MAE | 1.4760 | 1.1830 | 1.3622 | 1.3223 | 1.1820 |
| R2 | 0.5636 | 0.6781 | 0.6058 | 0.6117 | 0.7017 |
| Method | MSE | MAE | R2 | Time (s) | |||
|---|---|---|---|---|---|---|---|
| Mean | Best | Mean | Best | Mean | Best | ||
| GS | 45.668 | 0.817 | 3.210 | 0.5244 | 0.016 | 0.850 | 15,109.48 |
| RS | 18.828 | 0.843 | 2.038 | 0.547 | 0.423 | 0.806 | 14,120.52 |
| BO | 1.011 | 0.830 | 0.586 | 0.543 | 0.829 | 0.850 | 17,726.25 |
| CSA | 4.499 | 0.908 | 1.022 | 0.568 | 0.704 | 0.833 | 9730.93 |
| GA | 0.951 | 0.810 | 0.658 | 0.529 | 0.797 | 0.844 | 15,446.18 |
| ACO | 1.101 | 0.935 | 0.743 | 0.630 | 0.781 | 0.830 | 11,742.17 |
| GWO | 1.055 | 0.869 | 0.707 | 0.610 | 0.785 | 0.835 | 5761.11 |
| HSA | 0.968 | 0.826 | 0.670 | 0.632 | 0.783 | 0.791 | 2716.88 |
| PSO | 0.913 | 0.799 | 0.729 | 0.566 | 0.773 | 0.834 | 13,771.43 |
| Method | MSE | MAE | R2 | Time (s) | |||
|---|---|---|---|---|---|---|---|
| Mean | Best | Mean | Best | Mean | Best | ||
| GS | 15.517 | 2.510 | 2.105 | 1.074 | 0.343 | 0.745 | 17,574.93 |
| RS | 9.685 | 2.498 | 1.743 | 1.054 | 0.509 | 0.750 | 19,265.74 |
| BO | 2.559 | 2.464 | 1.071 | 1.055 | 0.744 | 0.749 | 18,586.78 |
| CSA | 9.792 | 2.814 | 1.835 | 1.170 | 0.516 | 0.728 | 15,244.83 |
| GA | 2.659 | 2.496 | 1.248 | 1.070 | 0.691 | 0.742 | 18,135.92 |
| ACO | 2.721 | 2.567 | 1.317 | 1.086 | 0.668 | 0.734 | 15,253.99 |
| GWO | 2.676 | 2.507 | 1.173 | 1.075 | 0.701 | 0.733 | 9011.93 |
| HSA | 2.599 | 2.509 | 1.269 | 1.082 | 0.675 | 0.745 | 2450.20 |
| PSO | 2.549 | 2.469 | 1.237 | 1.055 | 0.689 | 0.745 | 12,747.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.; Noh, S.; Kim, J.; Lee, S. Efficient Hyperparameter Optimization Using Metaheuristics for Machine Learning in Truss Steel Structure Cross-Section Prediction. Buildings 2025, 15, 2791. https://doi.org/10.3390/buildings15152791
Lee D, Noh S, Kim J, Lee S. Efficient Hyperparameter Optimization Using Metaheuristics for Machine Learning in Truss Steel Structure Cross-Section Prediction. Buildings. 2025; 15(15):2791. https://doi.org/10.3390/buildings15152791
Chicago/Turabian StyleLee, Donwoo, Seunghyeon Noh, Jeonghyun Kim, and Seungjae Lee. 2025. "Efficient Hyperparameter Optimization Using Metaheuristics for Machine Learning in Truss Steel Structure Cross-Section Prediction" Buildings 15, no. 15: 2791. https://doi.org/10.3390/buildings15152791
APA StyleLee, D., Noh, S., Kim, J., & Lee, S. (2025). Efficient Hyperparameter Optimization Using Metaheuristics for Machine Learning in Truss Steel Structure Cross-Section Prediction. Buildings, 15(15), 2791. https://doi.org/10.3390/buildings15152791







