Flexural Behavior of Lap Splice Connection Between Steel-Plate Composite Wall and Reinforced Concrete Foundation Subjected to Impact Loading
Abstract
1. Introduction
2. Experimental Study
2.1. Test Specimens and Materials
2.2. Test Set-Up and Data Measurements
3. Test Results and Discussion
3.1. Damage Analysis and Failure Modes
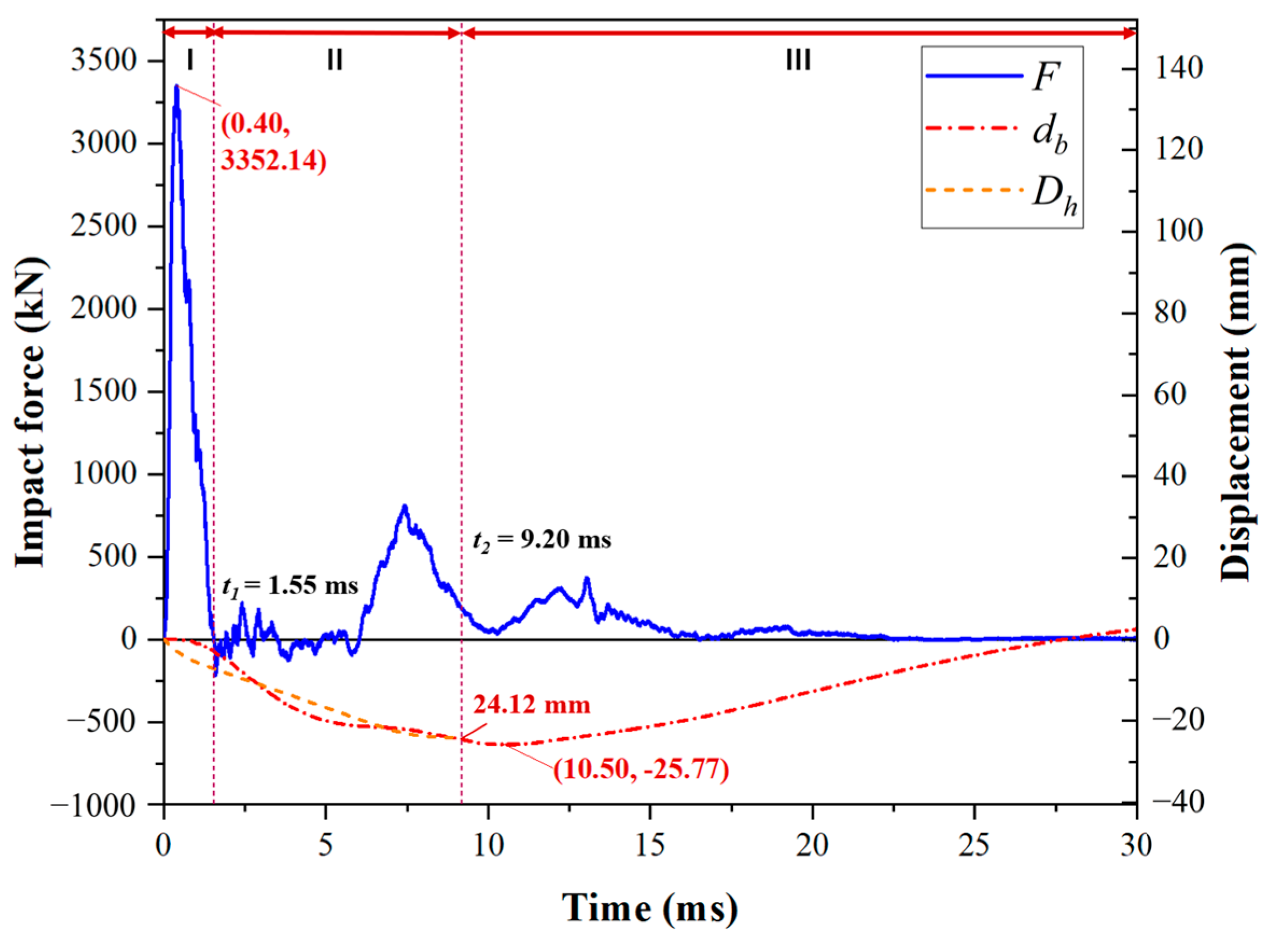
3.2. Impact Force and Deflection Responses
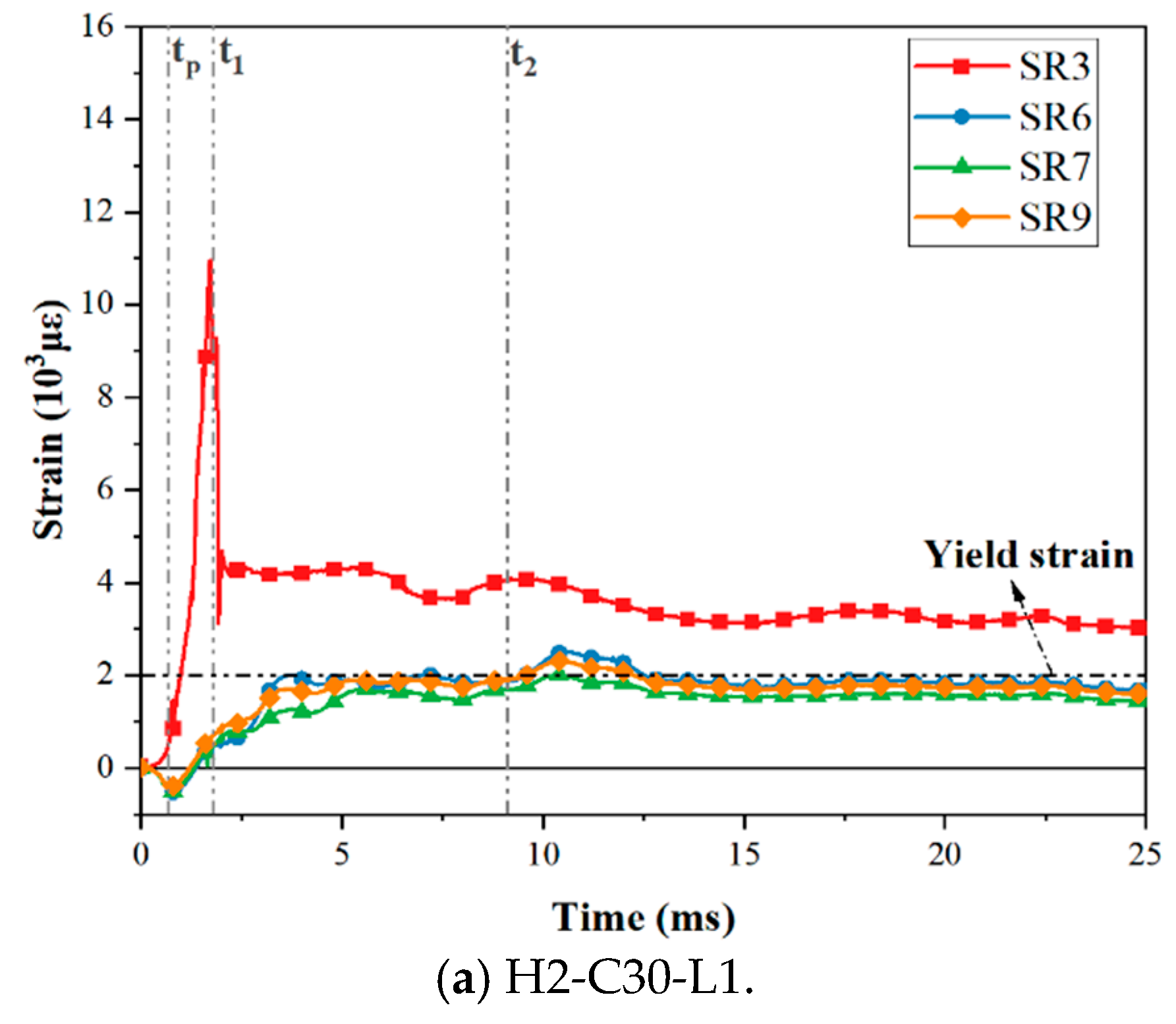
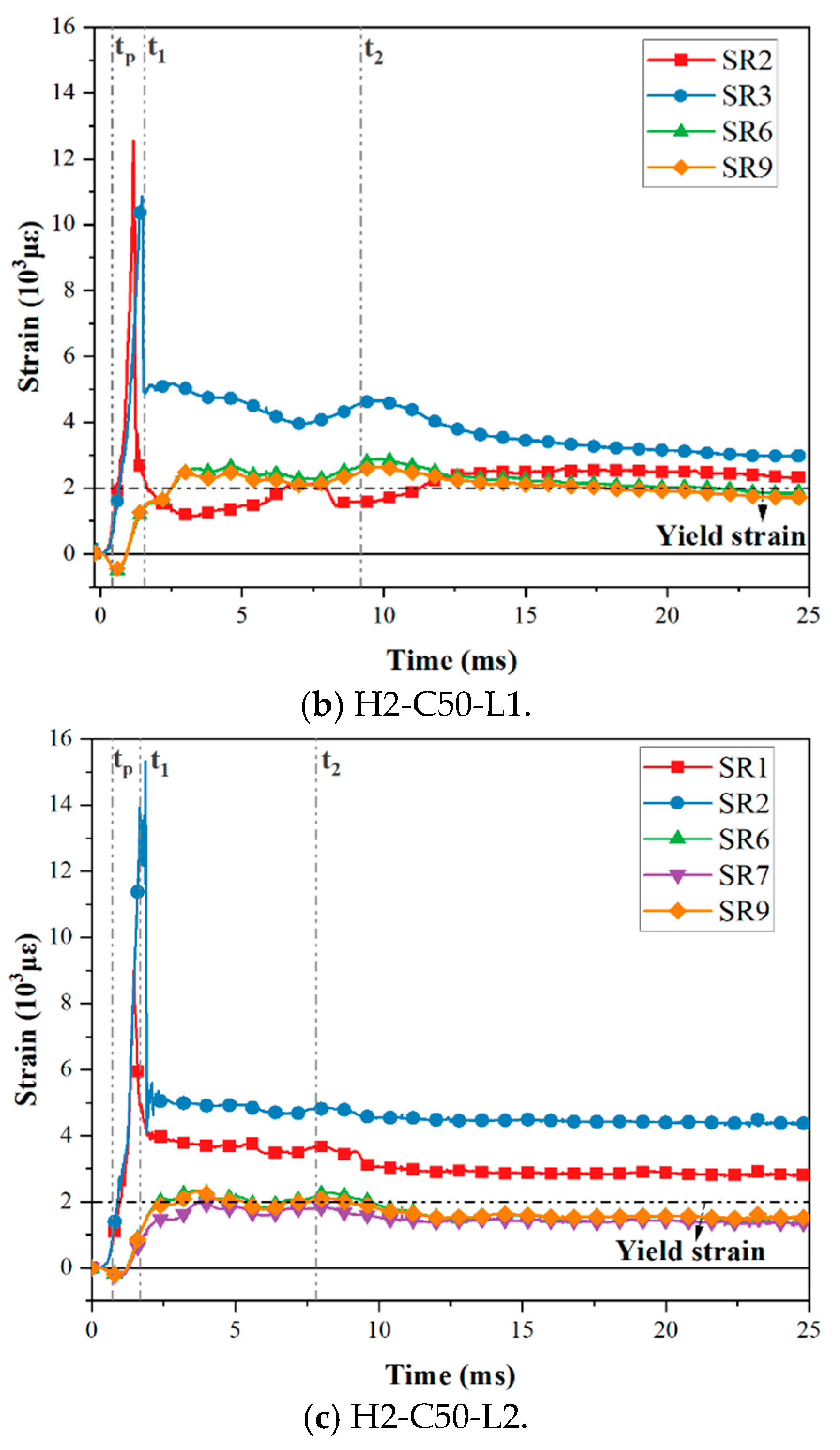
3.3. Strain Response
3.4. Impact Dynamic Response Mechanism
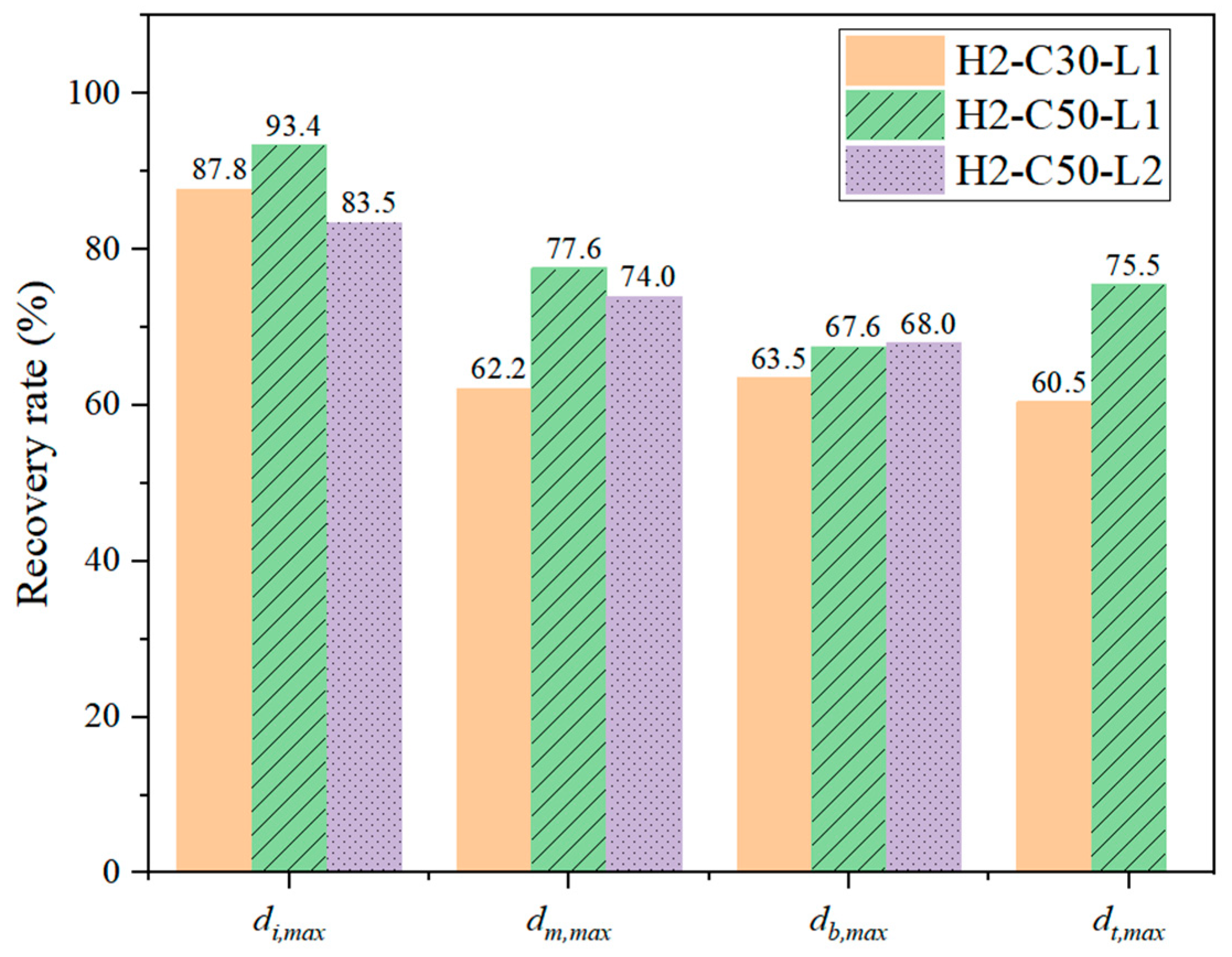
3.5. Influence of Design Parameters
3.5.1. Influence of Concrete Strength Grade
3.5.2. Influence of Impact Energy
4. Numerical Study
4.1. FE Model Establishment
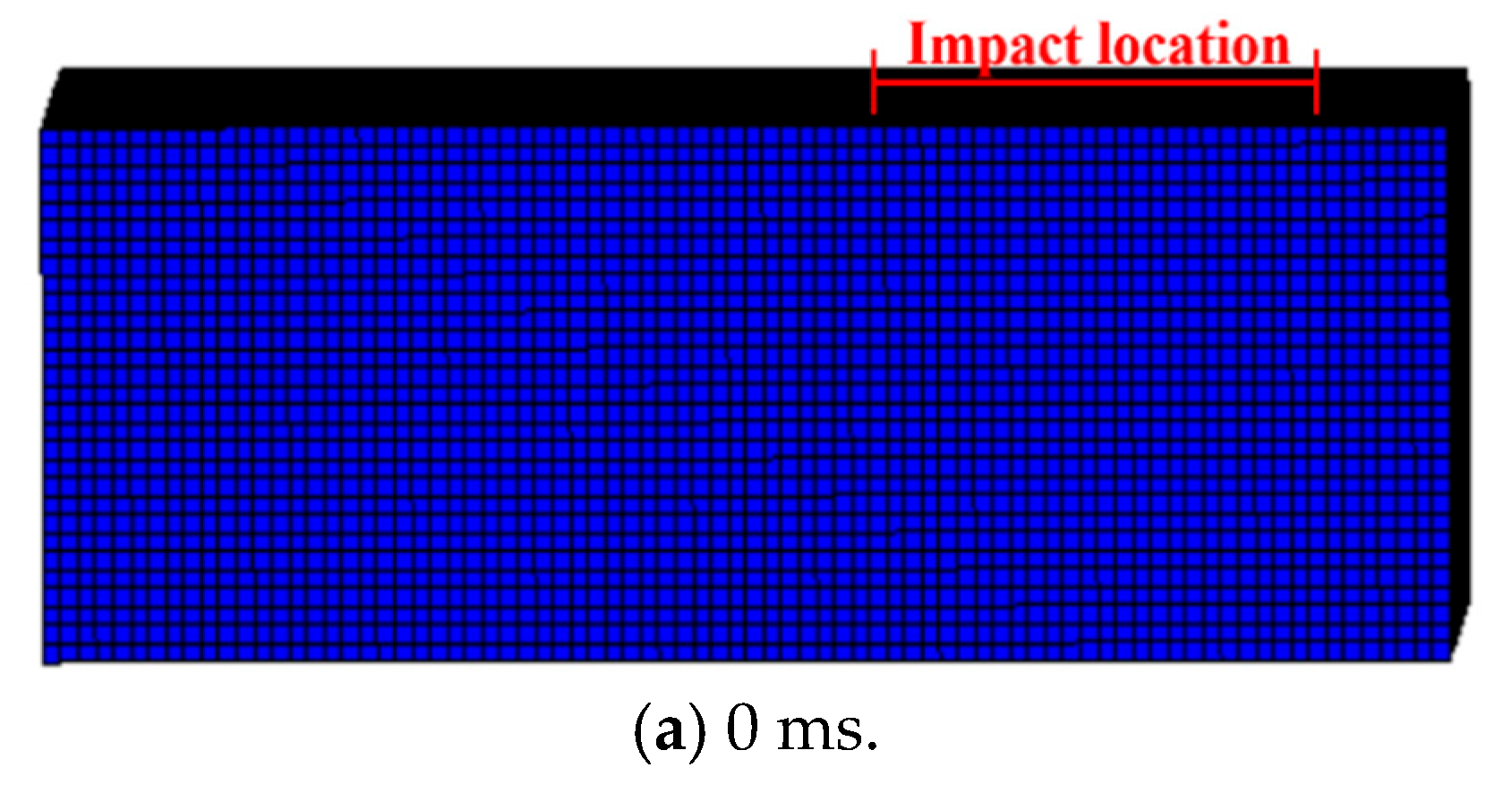
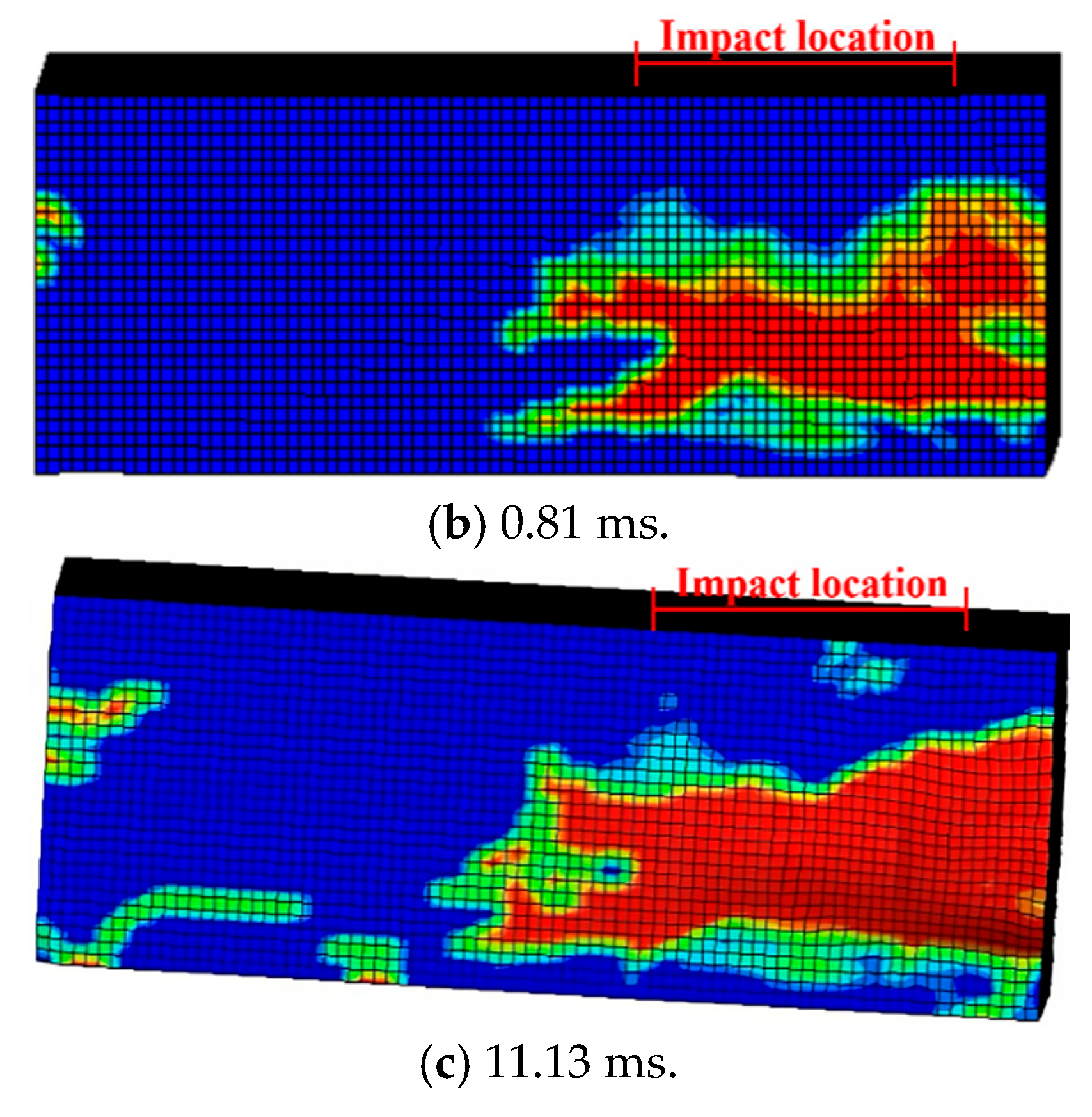
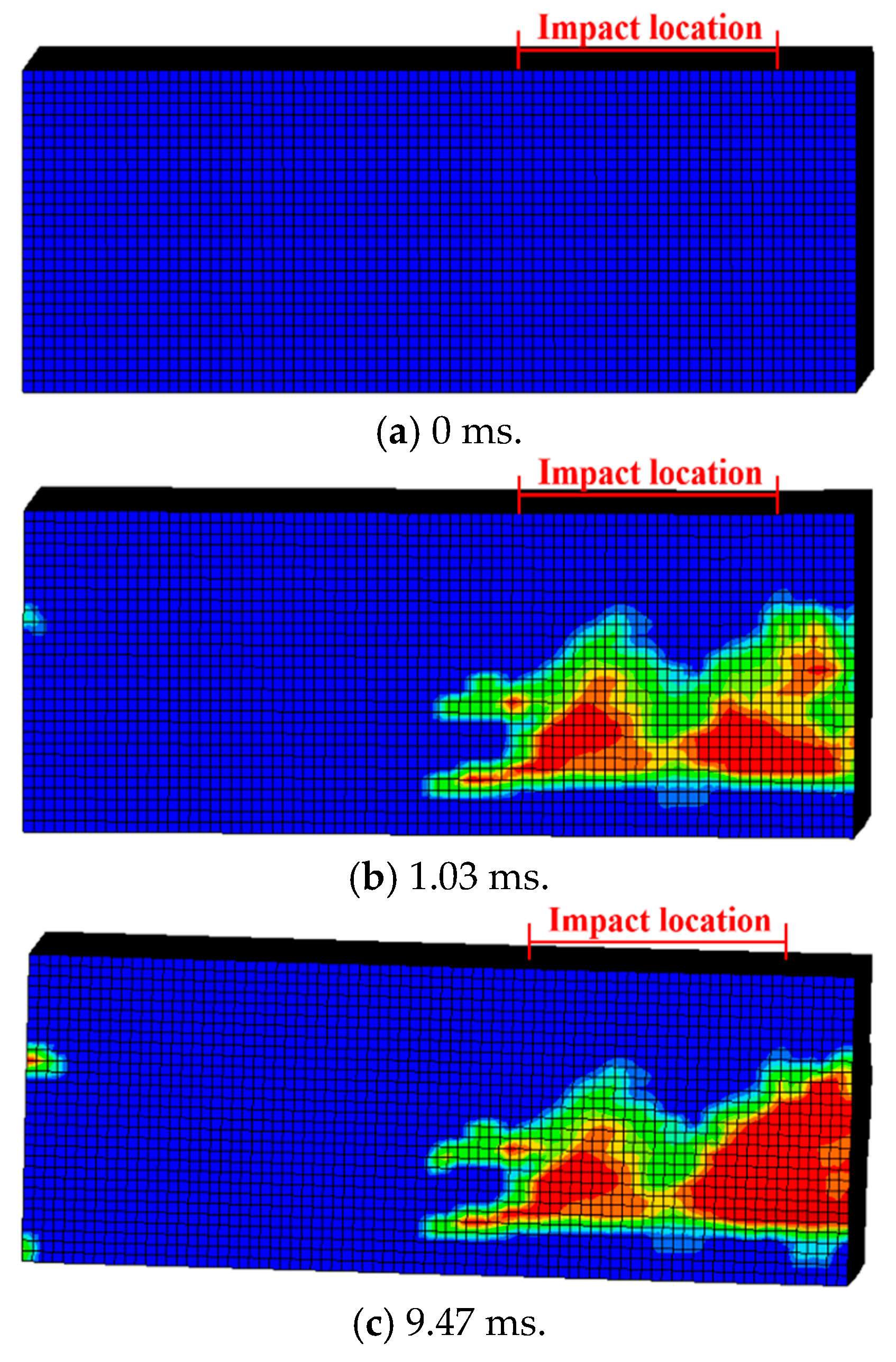
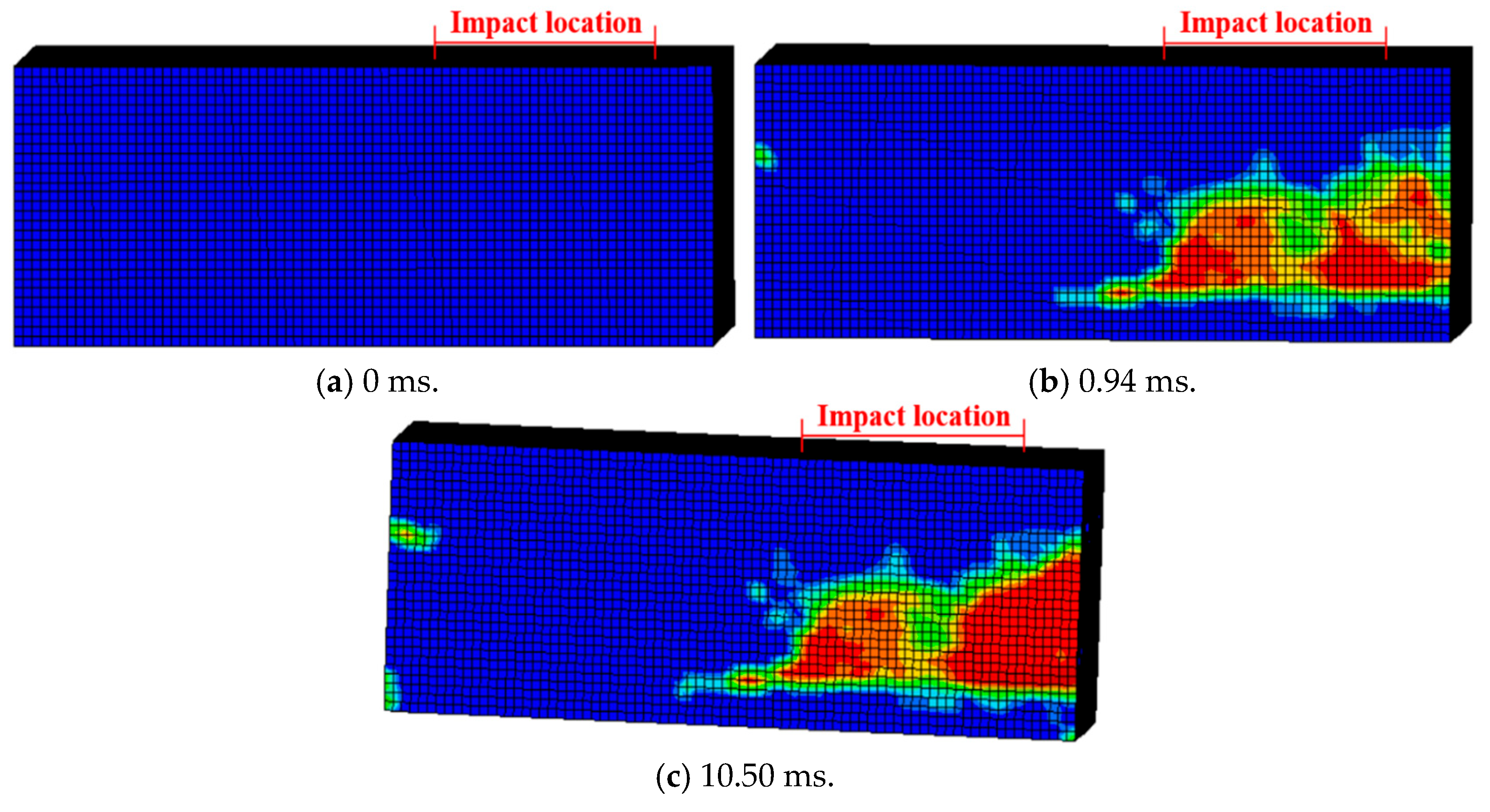
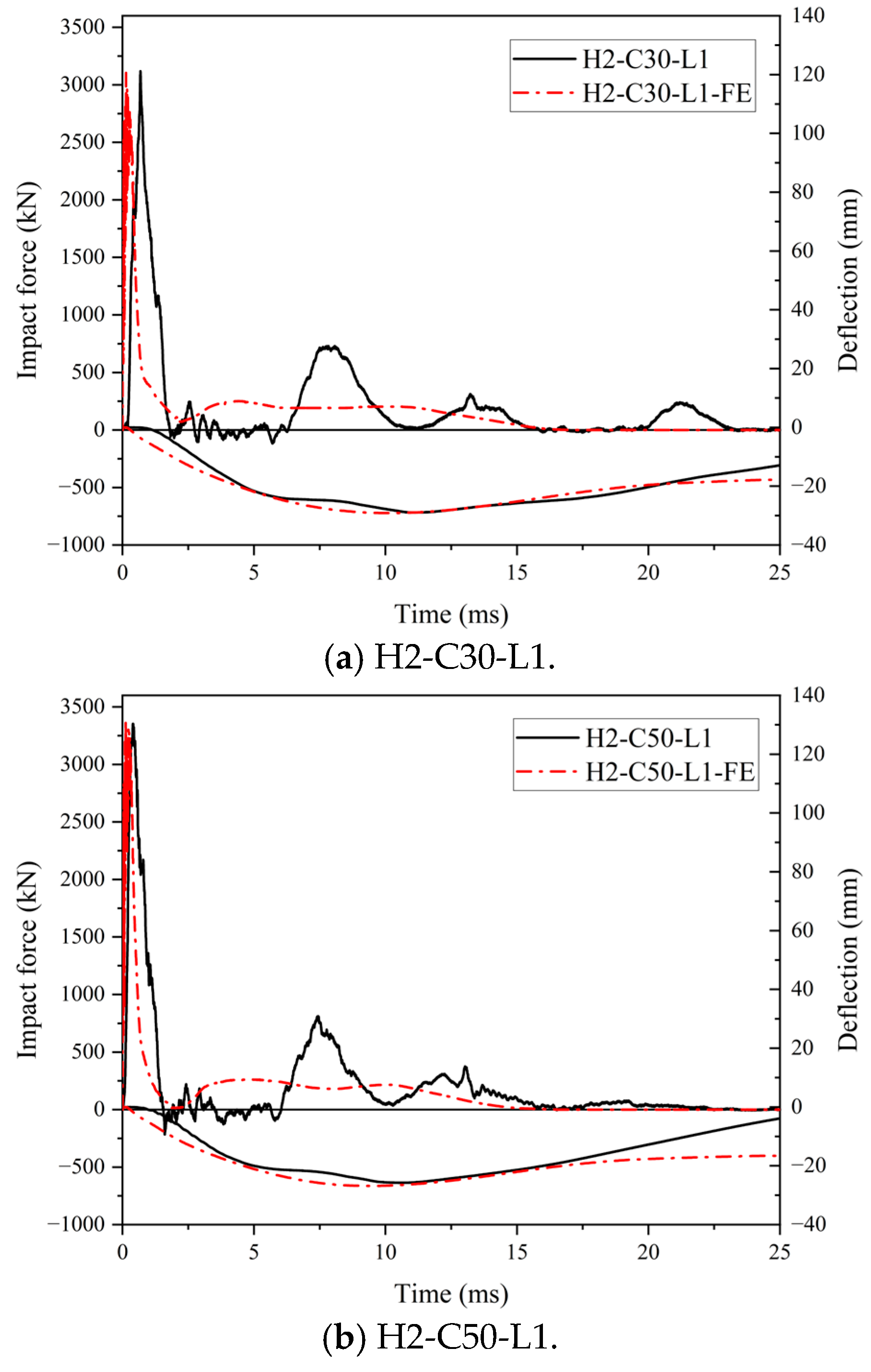
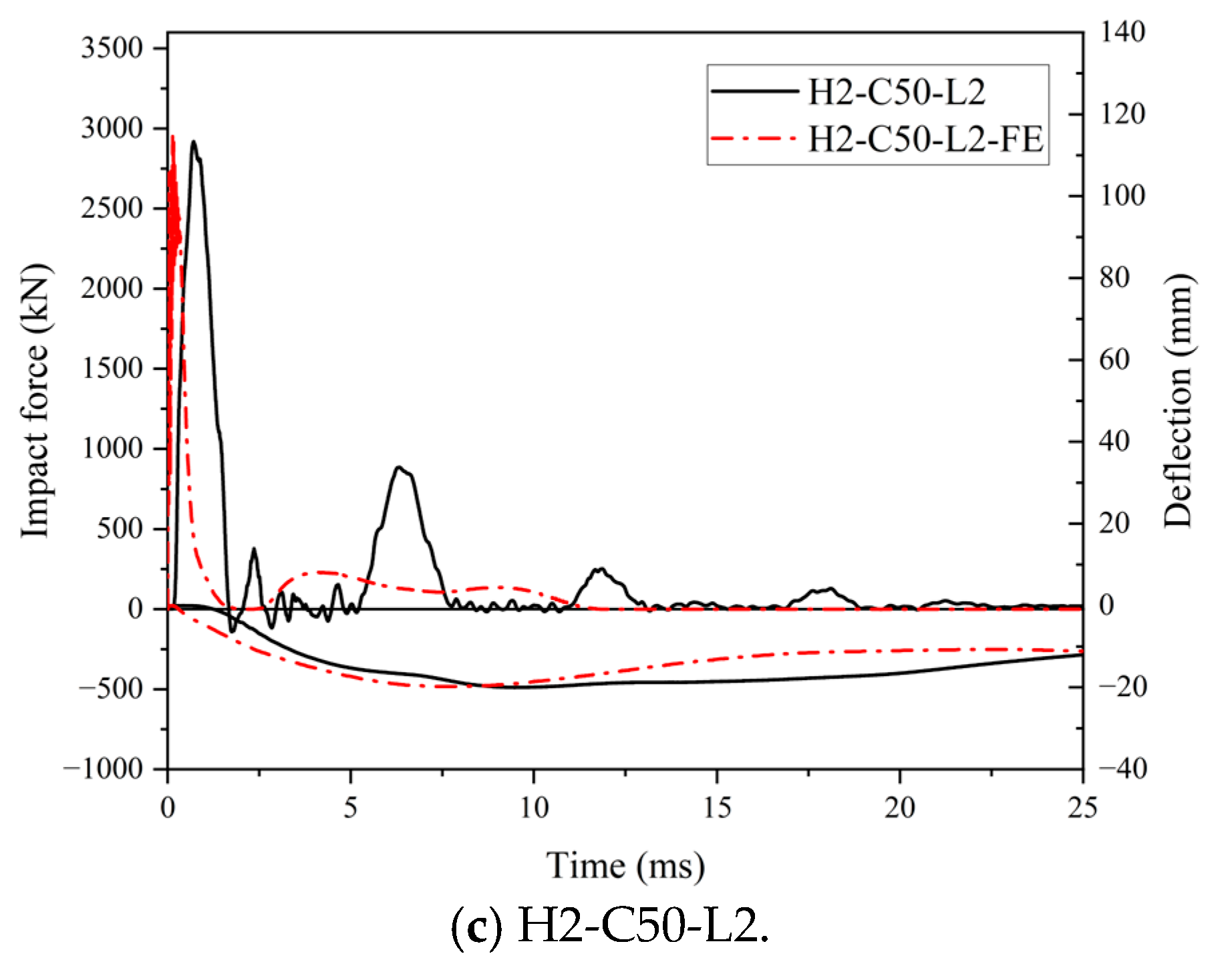
4.2. FE Results and Discussions
4.3. Parametric Studies
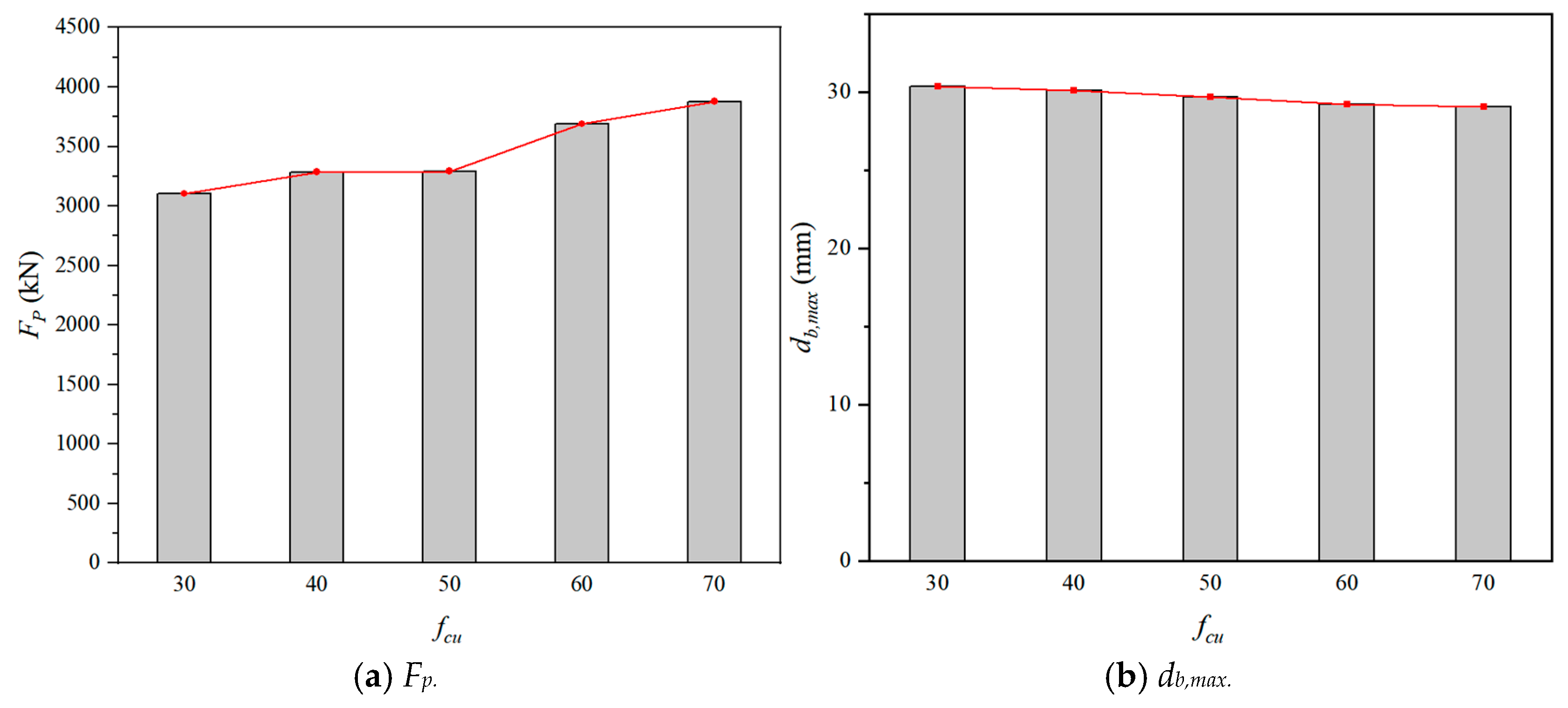
4.3.1. Effect of Concrete Compressive Strength
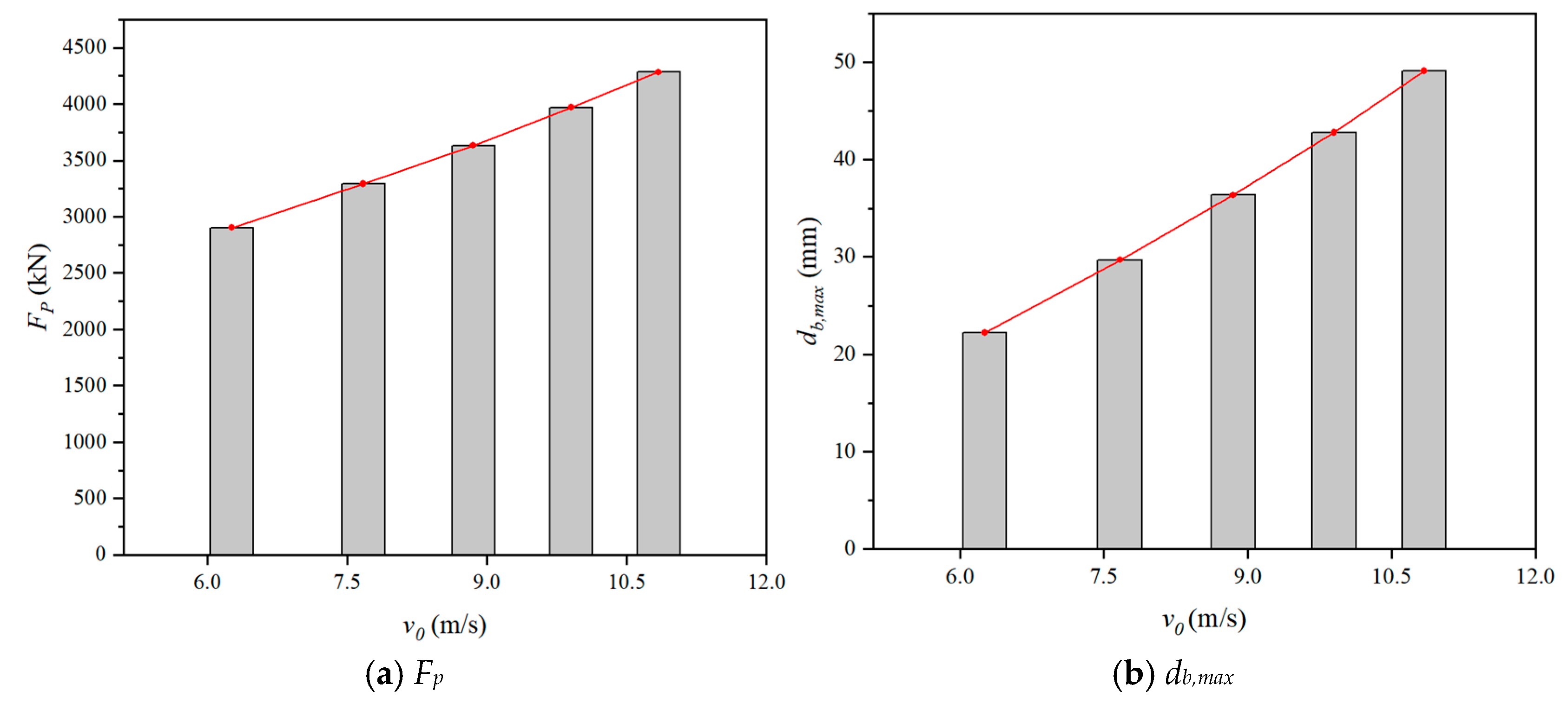
4.3.2. Effect of Impact Velocity
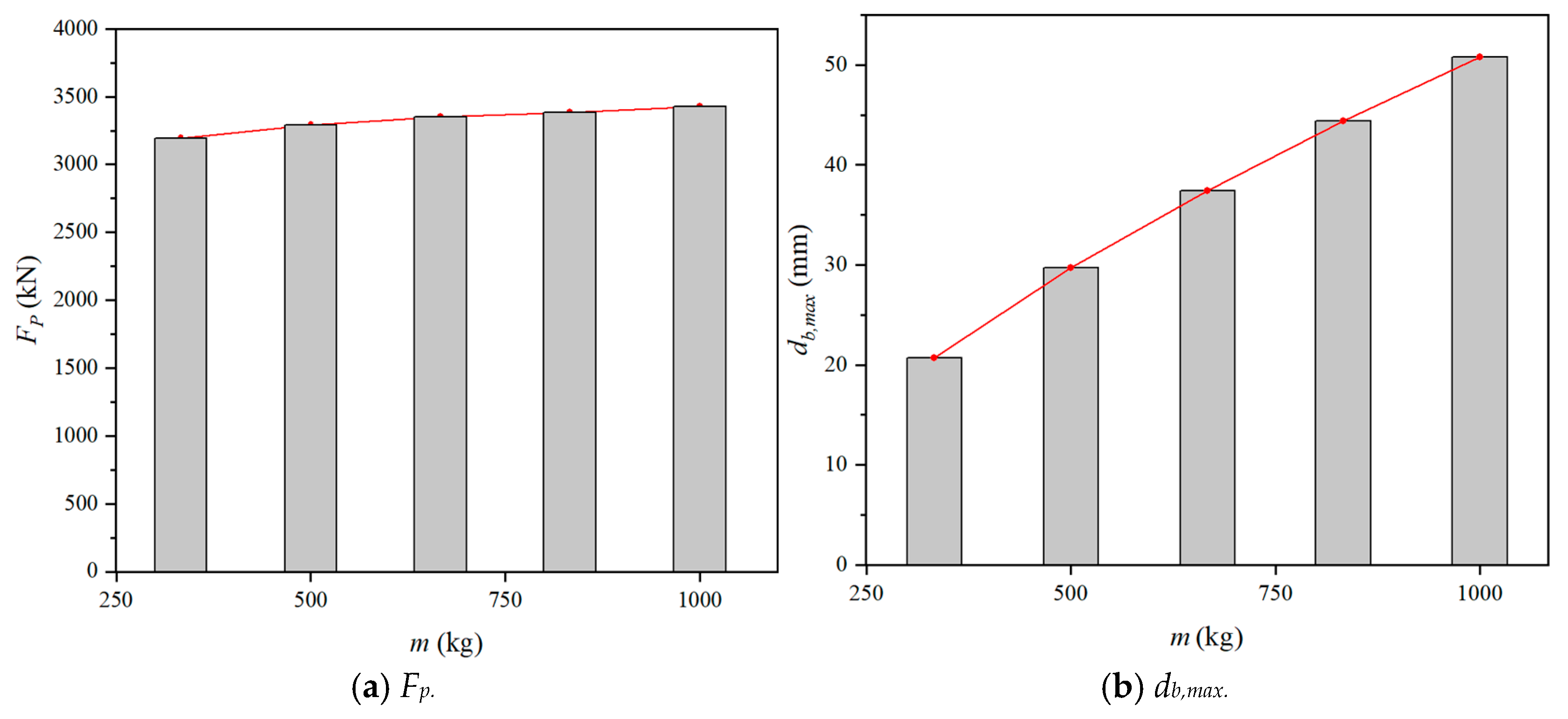
4.3.3. Effect of Impact Mass
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, N.; Zhou, F.; Qu, Y.; Xu, Z.; Li, Z.; Wang, F. Flexural behavior of curved steel-plate composite (SC) walls under combined axial compression and cyclic lateral force. Eng. Struct. 2021, 245, 112919. [Google Scholar] [CrossRef]
- Xie, M.; Chapman, J.C. Static and fatigue tensile strength of friction-welded bar-plate connections embedded in concrete. J. Constr. Steel Res. 2005, 61, 651–673. [Google Scholar] [CrossRef]
- Huang, Z.; Liew, J.Y.R. Compressive resistance of steel-concrete-steel sandwich composite walls with J-hook connectors. J. Constr. Steel Res. 2016, 124, 142–162. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, X.; Chen, J.; Zhai, X.; Zhi, X.; Zhou, H.; Zhong, J. Experimental and analytical studies on impact behaviours of a steel–concrete–steel sandwich beam with novel interlocked angle connectors. Thin-Walled Struct. 2022, 181, 110089. [Google Scholar] [CrossRef]
- Mo, J.; Uy, B.; Li, D.; Thai, H.T.; Tran, H. A review of the behaviour and design of steel–concrete composite shear walls. Structures 2021, 31, 1230–1253. [Google Scholar] [CrossRef]
- Do, T.V.; Pham, T.M.; Hao, H. Impact force profile and failure classification of reinforced concrete bridge columns against vehicle impact. Eng. Struct. 2019, 183, 443–458. [Google Scholar] [CrossRef]
- Meng, L.; Wang, Y.; Zhai, X. Modeling and Dynamic Response of Curved Steel–Concrete–Steel Sandwich Shells Under Blast Loading. Int. J. Steel Struct. 2020, 20, 1663–1681. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, Y.; Wang, R.; Chen, W.; Wang, Y.; Lam, D. Performance of steel–concrete composite walls with recycled aggregate concrete under low-velocity lateral impact loading. Eng. Struct. 2023, 296, 116899. [Google Scholar] [CrossRef]
- Huang, Z.; So, C.S.; Chen, W.; Htet, P.M.; Li, D.; Hao, H. Impact performance of fibre reinforced geopolymer concrete beams with steel-FRP composite bars. Eng. Struct. 2025, 329, 119880. [Google Scholar] [CrossRef]
- Mizuno, J.; Koshika, N.; Sawamoto, Y.; Niwa, N.; Yamashita, T.; Suzuki, A. Investigation on impact resistance of steel plate reinforced concrete barriers against aircraft impact. Part 1: Test program and results. In Proceedings of the 8th International Conference on Structural Mechanics in Reactor Technology (SMiRT 18), Beijing, China, 7–12 August 2005; pp. 2566–2579. [Google Scholar]
- Mizuno, J.; Koshika, N.; Mrikawa, H.; Wakimoto, K.; Kobayashi, K.; Fukuda, R. Investigation on impact resistance of steel plate reinforced concrete barriers against aircraft impact. Part 2: Simulation analyses of scale model impact tests. In Proceedings of the 8th International Conference on Structural Mechanics in Reactor Technology (SMiRT 18), Beijing, China, 7–12 August 2005; pp. 2566–2579. [Google Scholar]
- Sohel, K.M.A.; Liew, J.Y.R. Behavior of steel-concrete-steel sandwich slabs subject to impact load. J. Constr. Steel Res. 2014, 100, 163–175. [Google Scholar] [CrossRef]
- Liew, J.Y.R.; Sohel, K.M.A.; Koh, C.G. Impact tests on steel–concrete–steel sandwich beams with lightweight concrete core. Eng. Struct. 2009, 31, 2045–2059. [Google Scholar] [CrossRef]
- Remennikov, A.M.; Kong, S.Y.; Uy, B. The response of axially restrained non-composite steel-concrete-steel sandwich panels due to large impact loading. Eng. Struct. 2013, 49, 806–818. [Google Scholar] [CrossRef]
- Zhao, W.; Guo, Q.; Dou, X.; Zhou, Y.; Ye, Y. Impact response of steel-concrete composite panels: Experiments and FE analyses. Steel Compos. Struct. 2018, 26, 255–263. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, W. Displacement response analysis of steel-concrete composite panels subjected to impact loadings. Int. J. Impact Eng. 2019, 131, 272–281. [Google Scholar] [CrossRef]
- JEAG 4618-2005; Technical Guidelines for Seismic Design of Steel Plate Concrete Structures: For Buildings and Structures. Architectural Institute of Japan: Tokyo, Japan, 2005.
- Seo, J.; Varma, A.H. Experimental Behavior and Design of Steel Plate Composite-to-Reinforced Concrete Lap Splice Connections. J. Struct. Eng. 2017, 143, 04017011. [Google Scholar] [CrossRef]
- Kurt, E.G. Steel-Plate Composite (SC) Walls and Their Basemat Connections: Seismic Behavior, Analysis and Design. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2015. [Google Scholar]
- Wang, N.; Zhou, F.; Xu, H.; Xu, Z. Experimental study on steel-plate composite wall-to-foundation connections subjected to combined axial compression and cyclic lateral-force. Eng. Struct. 2020, 207, 110205. [Google Scholar] [CrossRef]
- Wang, T.; Yan, J.B. Developments of steel-concrete-steel sandwich composite structures with novel EC connectors: Members. J. Constr. Steel Res. 2020, 175, 106335. [Google Scholar] [CrossRef]
- Lin, Y.; Yan, J.; Cao, Z.; Zeng, X.; Fan, F.; Zou, C. Ultimate strength behaviour of S-UHPC-S and SCS sandwich beams under shear loads. J. Constr. Steel Res. 2018, 149, 195–206. [Google Scholar] [CrossRef]
- Huang, Z.; Liew, J.Y.R.; Xiong, M.; Wang, J. Structural behaviour of double skin composite system using ultra-lightweight cement composite. Constr. Build. Mater. 2015, 86, 51–63. [Google Scholar] [CrossRef]
- Sener, K.C.; Varma, A.H. Steel-plate composite walls: Experimental database and design for out-of-plane shear. J. Constr. Steel Res. 2014, 100, 197–210. [Google Scholar] [CrossRef]
- Kim, M.; Park, H.; Han, M.; Choi, B.J. Experimental evaluation of bending-moment performance about steel plate-concrete structures with mechanical splice. J. Constr. Steel Res. 2017, 128, 362–370. [Google Scholar] [CrossRef]
- Sener, K.C.; Varma, A.H.; Ayhan, D. Steel-plate composite (SC) walls: Out-of-plane flexural behavior, database, and design. J. Constr. Steel Res. 2015, 108, 46–59. [Google Scholar] [CrossRef]
- GB/T 228.1-2010; Metallic Materials Tensile Testing—Part 1 Method of Test at Room Temperature. Ministry of Communications of the Peoples Republic of China: Beijing, China, 2010.
- GB/T 50081-2002; Standard for Test Method of Mechanical Properties on Ordinary Concrete. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China: Beijing, China, 2003.
- Sener, K.C.; Varma, A.H.; Seo, J. Experimental and numerical investigation of the shear behavior of steel-plate composite (SC) beams without shear reinforcement. Eng. Struct. 2016, 127, 495–509. [Google Scholar] [CrossRef]
- He, Q.; Yue, L.; Mao, J. An experimental study on dynamic performance of CFRP-repaired RC composite beams under impact. J. Vib. Shock 2021, 40, 171–178. [Google Scholar]
- Wang, Y.; Sah, T.P.; Liu, S.; Zhai, X. Experimental and numerical studies on novel stiffener-enhanced steel-concrete-steel sandwich panels subjected to impact loading. J. Build. Eng. 2022, 45, 103479. [Google Scholar] [CrossRef]
- Yan, C.; Wang, Y.; Zhai, X. Low velocity impact performance of curved steel-concrete-steel sandwich shells with bolt connectors. Thin-Walled Struct. 2020, 150, 106672. [Google Scholar] [CrossRef]
- Livermore Technology Software Corporation. LS-DYNA Keyword User’s Manual Version 971; Livermore Technology Software Corporation: Livermore, CA, USA, 2012. [Google Scholar]
- Remennikov, A.M.; Kong, S.Y. Numerical simulation and validation of impact response of axially-restrained steel–concrete–steel sandwich panels. Compos. Struct. 2012, 94, 3546–3555. [Google Scholar] [CrossRef]
- Yan, C.; Wang, Y.; Zhai, X.; Meng, L.; Zhou, H. Experimental study on curved steel-concrete-steel sandwich shells under concentrated load by a hemi-spherical head. Thin-Walled Struct. 2019, 137, 117–128. [Google Scholar] [CrossRef]
- Jones, N. Structural Impact; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar] [CrossRef]
- An, G.; Wang, R.; Zhao, H.; Chen, W.; Li, T.; Liu, Y. Response of axial-loaded steel-concrete composite walls under low-velocity impact. J. Constr. Steel Res. 2023, 203, 107829. [Google Scholar] [CrossRef]

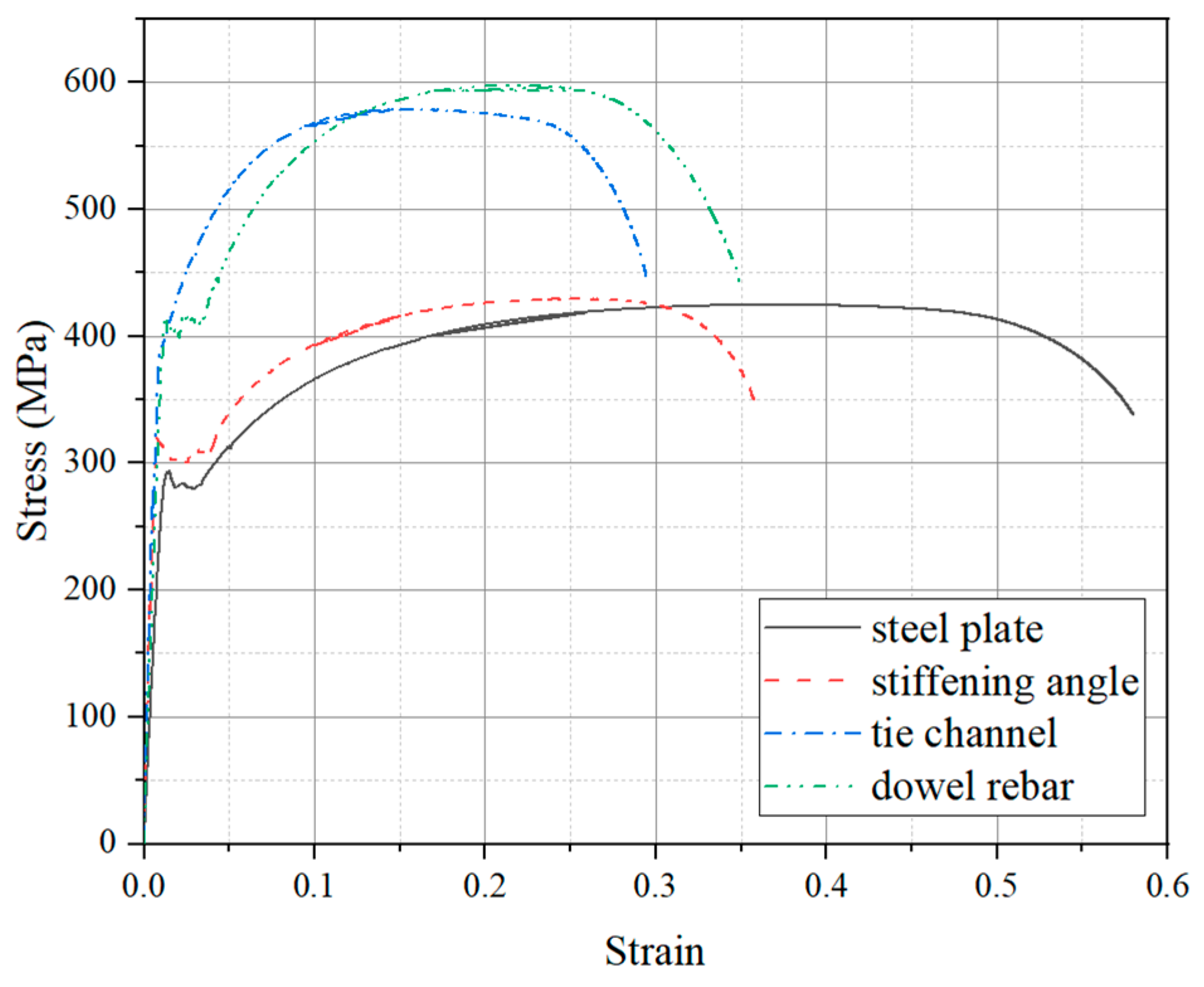
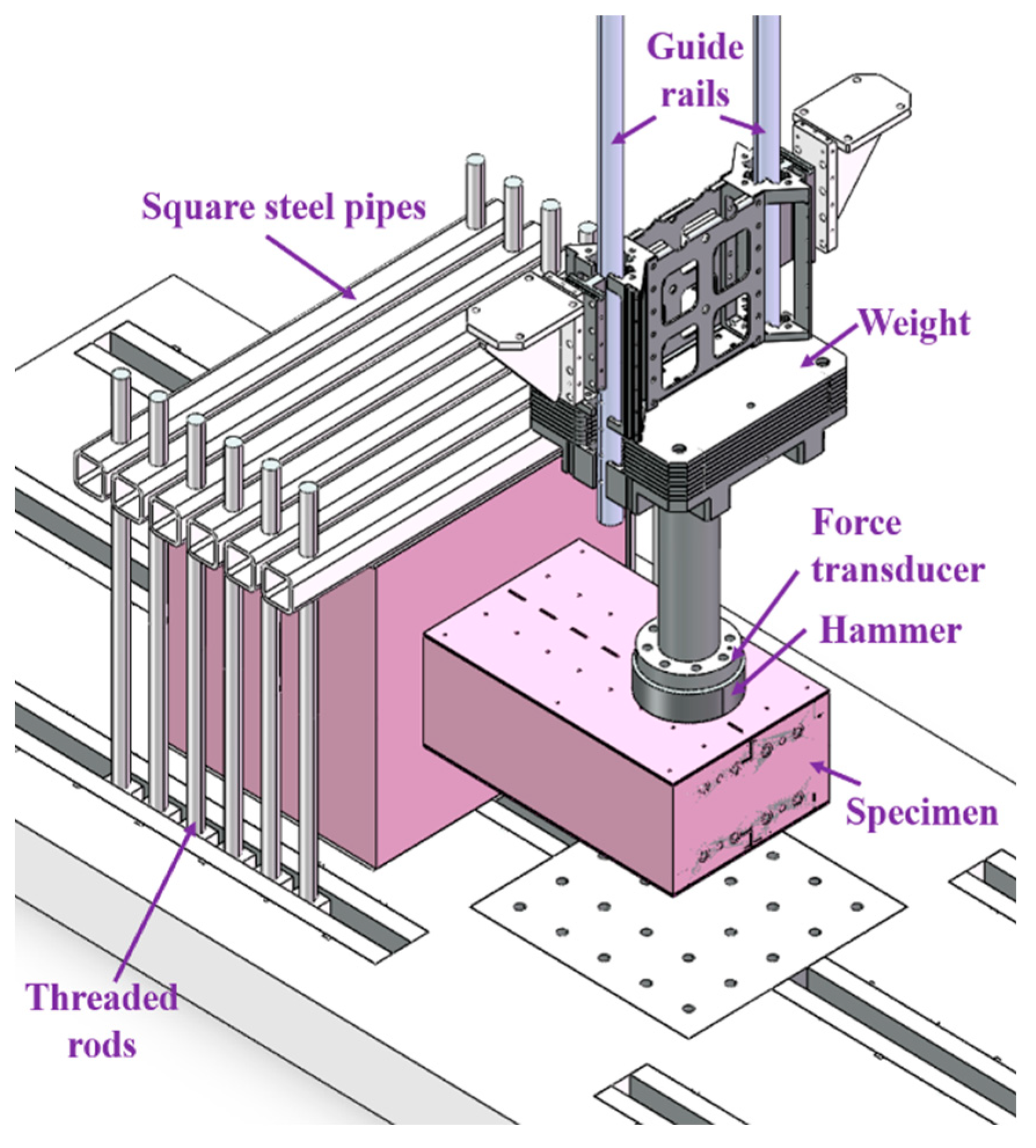
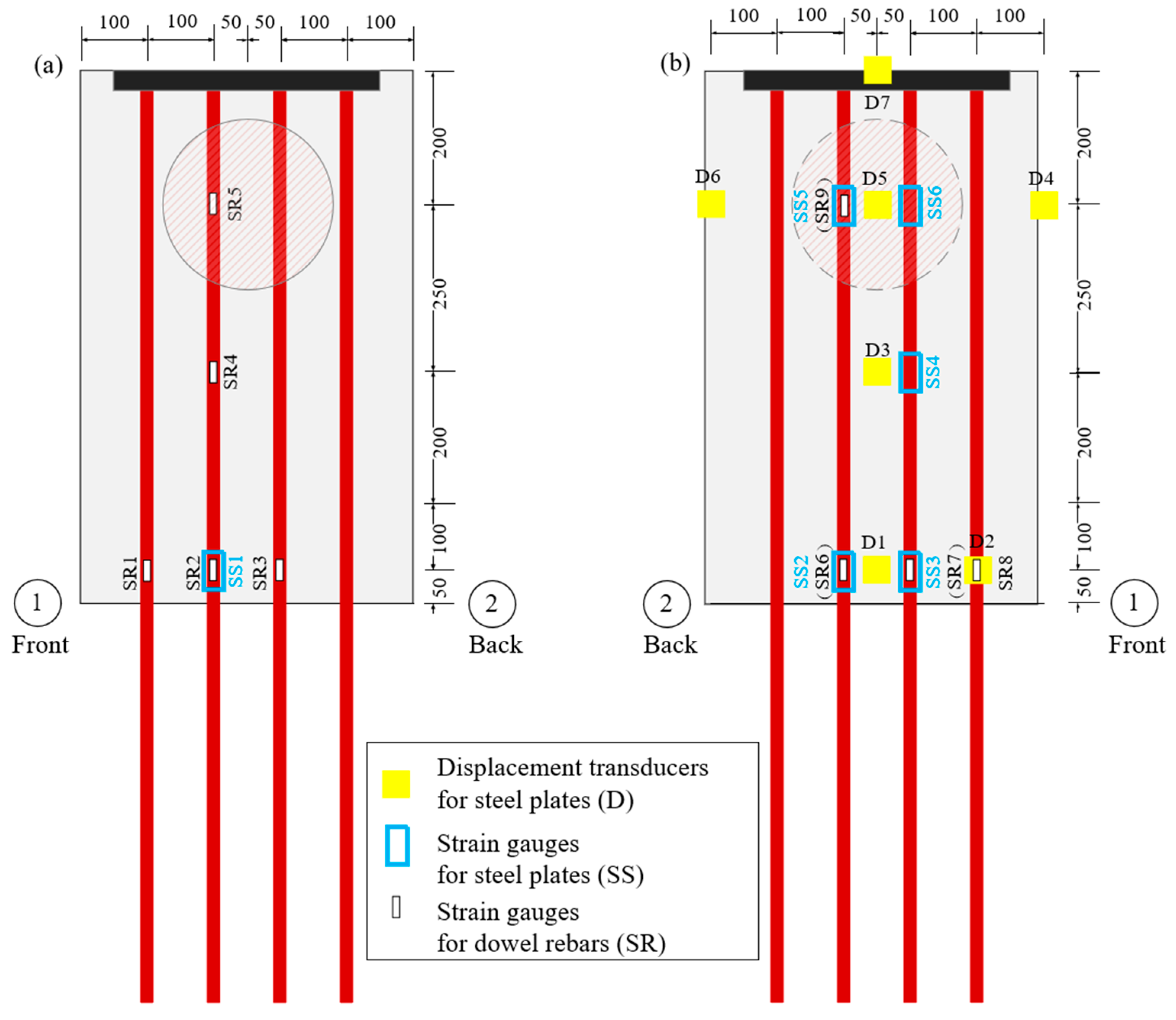




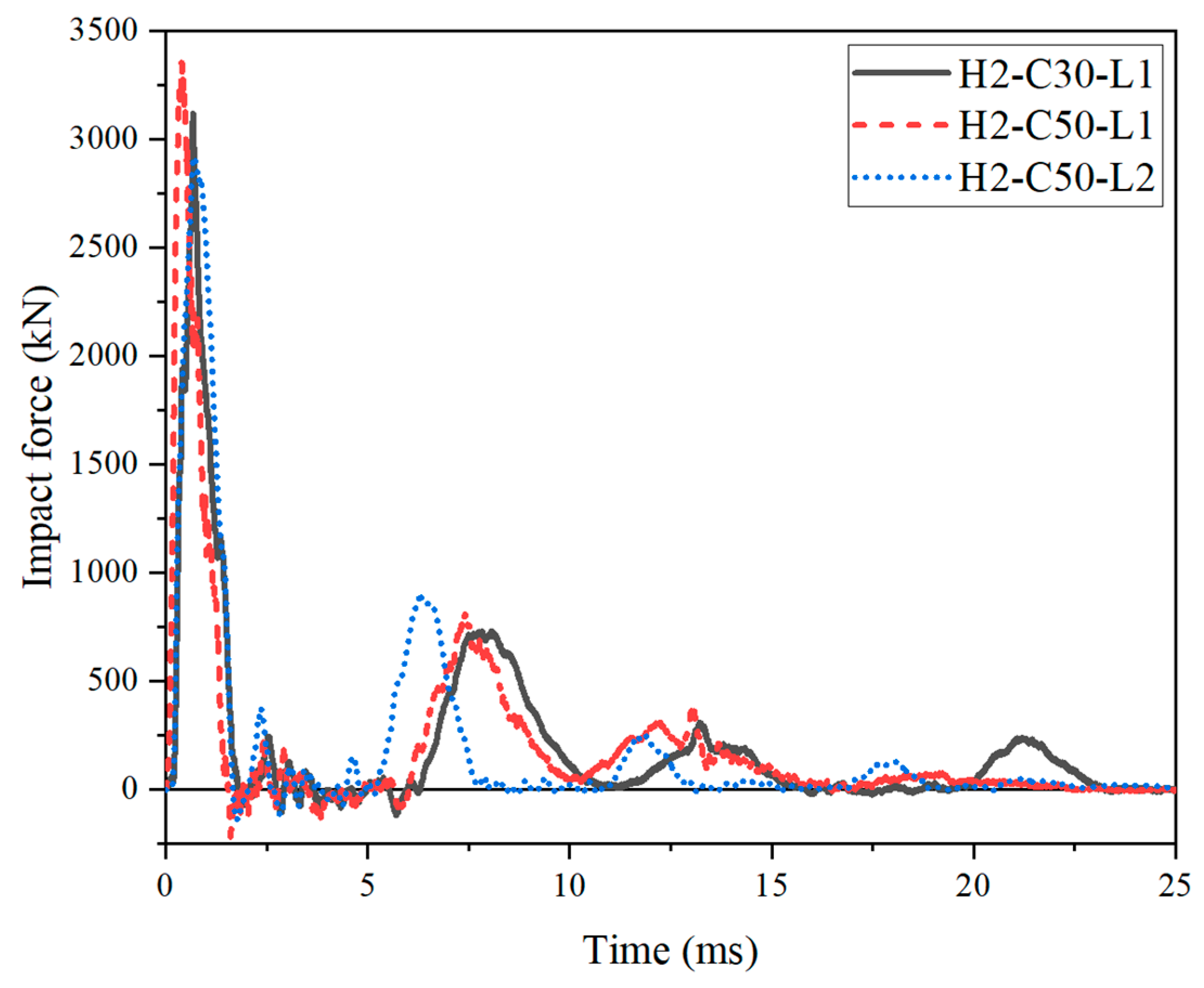




| Components | Material Grade | E | fy | fu | fcu |
|---|---|---|---|---|---|
| (GPa) | (MPa) | (MPa) | (MPa) | ||
| Concrete of SC walls | C50 | - | - | - | 54.8 |
| C30 | - | - | - | 27.5 | |
| Steel plates of SC walls | Q235B | 197 | 287 | 572 | - |
| Stiffening angles | Q235B | 190 | 308 | 546 | - |
| Tie channels | Q235B | 197 | 395 | 667 | - |
| Dowel rebars | HRB400 | 203 | 409 | 773 | - |
| Specimen | Concrete Strength Grade of SC Wall | H0 | ts | m | Hh | vd | P | E |
|---|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (kg) | (m) | (m/s) | (kg·m/s) | (kJ) | ||
| H2-C30-L1 | C30 | 600 | 6 | 500 | 3.00 | 7.67 | 3835 | 14.7 |
| H2-C50-L1 | C50 | 600 | 6 | 500 | 3.00 | 7.67 | 3835 | 14.7 |
| H2-C50-L2 | C50 | 600 | 6 | 300 | 3.33 | 8.08 | 2424 | 9.8 |
| Specimen | v | P | Cl | Cu | Cr | Failure Mode |
|---|---|---|---|---|---|---|
| (m/s) | (kg·m/s) | (mm) | (mm) | (mm) | ||
| H2-C30-L1 | 7.41 | 3705 | 2.90 | 4.46 | 8.75 | Flexure failure |
| H2-C50-L1 | 7.45 | 3725 | 2.12 | 4.33 | 2.43 | Flexure failure |
| H2-C50-L2 | 7.90 | 2370 | 1.60 | 2.25 | 1.89 | Flexure failure |
| Specimen | Fp | db,max | dbr | di,max | dir | dm,max | dmr | dt,max | dtr |
|---|---|---|---|---|---|---|---|---|---|
| (kN) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | |
| H2-C30-L1 | 3118 | 28.94 | 10.56 | 6.38 | 0.78 | 18.73 | 7.09 | 38.01 | 15.02 |
| H2-C50-L1 | 3352 | 25.77 | 8.36 | 3.94 | 0.26 | 17.43 | 3.90 | 51.71 | 12.68 |
| H2-C50-L2 | 2919 | 20.01 | 6.40 | 5.86 | 0.97 | 13.41 | 3.49 | 26.83 | - |
| Specimen | Fp | Fp,FE | Fp,FE/Fp | db,max | db,maxFE | db,maxFE/db,max |
|---|---|---|---|---|---|---|
| (kN) | (kN) | (mm) | (mm) | |||
| H2-C30-L1 | 3118 | 3104 | 1.00 | 28.94 | 29.12 | 1.01 |
| H2-C50-L1 | 3352 | 3395 | 1.01 | 25.77 | 26.83 | 1.04 |
| H2-C50-L2 | 2919 | 2948 | 1.01 | 20.01 | 19.81 | 0.99 |
| Average | 1.01 | 1.01 |
| fcu | Hh | v0 | m | E | Fp | db,max |
|---|---|---|---|---|---|---|
| (MPa) | (m) | (m/s) | (kg) | (kJ) | (kN) | (mm) |
| 50 | 3 | 7.67 | 500 | 14.7 | 3292 | 29.70 |
| 30 | 3 | 7.67 | 500 | 14.7 | 3104 | 30.35 |
| 40 | 3 | 7.67 | 500 | 14.7 | 3286 | 30.12 |
| 60 | 3 | 7.67 | 500 | 14.7 | 3689 | 29.20 |
| 70 | 3 | 7.67 | 500 | 14.7 | 3878 | 29.08 |
| 50 | 2 | 6.26 | 500 | 9.8 | 2903 | 22.22 |
| 50 | 4 | 8.85 | 500 | 19.6 | 3632 | 36.35 |
| 50 | 5 | 9.90 | 500 | 24.5 | 3971 | 42.80 |
| 50 | 6 | 10.84 | 500 | 29.4 | 4285 | 49.10 |
| 50 | 3 | 7.67 | 333 | 9.8 | 3192 | 20.69 |
| 50 | 3 | 7.67 | 667 | 19.6 | 3351 | 37.44 |
| 50 | 3 | 7.67 | 833 | 24.5 | 3385 | 44.43 |
| 50 | 3 | 7.67 | 1000 | 29.4 | 3426 | 50.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, W.; Hua, J.; Wang, N.; Li, S.; Chang, Y.; Wang, F.; Xue, X. Flexural Behavior of Lap Splice Connection Between Steel-Plate Composite Wall and Reinforced Concrete Foundation Subjected to Impact Loading. Buildings 2025, 15, 2707. https://doi.org/10.3390/buildings15152707
Deng W, Hua J, Wang N, Li S, Chang Y, Wang F, Xue X. Flexural Behavior of Lap Splice Connection Between Steel-Plate Composite Wall and Reinforced Concrete Foundation Subjected to Impact Loading. Buildings. 2025; 15(15):2707. https://doi.org/10.3390/buildings15152707
Chicago/Turabian StyleDeng, Wenjie, Jianmin Hua, Neng Wang, Shuai Li, Yuruo Chang, Fei Wang, and Xuanyi Xue. 2025. "Flexural Behavior of Lap Splice Connection Between Steel-Plate Composite Wall and Reinforced Concrete Foundation Subjected to Impact Loading" Buildings 15, no. 15: 2707. https://doi.org/10.3390/buildings15152707
APA StyleDeng, W., Hua, J., Wang, N., Li, S., Chang, Y., Wang, F., & Xue, X. (2025). Flexural Behavior of Lap Splice Connection Between Steel-Plate Composite Wall and Reinforced Concrete Foundation Subjected to Impact Loading. Buildings, 15(15), 2707. https://doi.org/10.3390/buildings15152707









