Analysis of Heat Exchange Efficiency and Influencing Factors of Energy Tunnels: A Case Study of the Torino Metro in Italy
Abstract
1. Introduction
- (1)
- To develop and validate a thermal–hydraulic (TH) coupled finite element model of a tunnel ring segment from the Torino Metro Line using COMSOL Multiphysics.
- (2)
- To conduct an environmental sensitivity analysis on key parameters affecting heat transfer efficiency.
- (3)
- To perform a comparative analysis of the heat transfer efficiency between energy-tunnel-lining heat-exchange segments and traditional GSHPs.
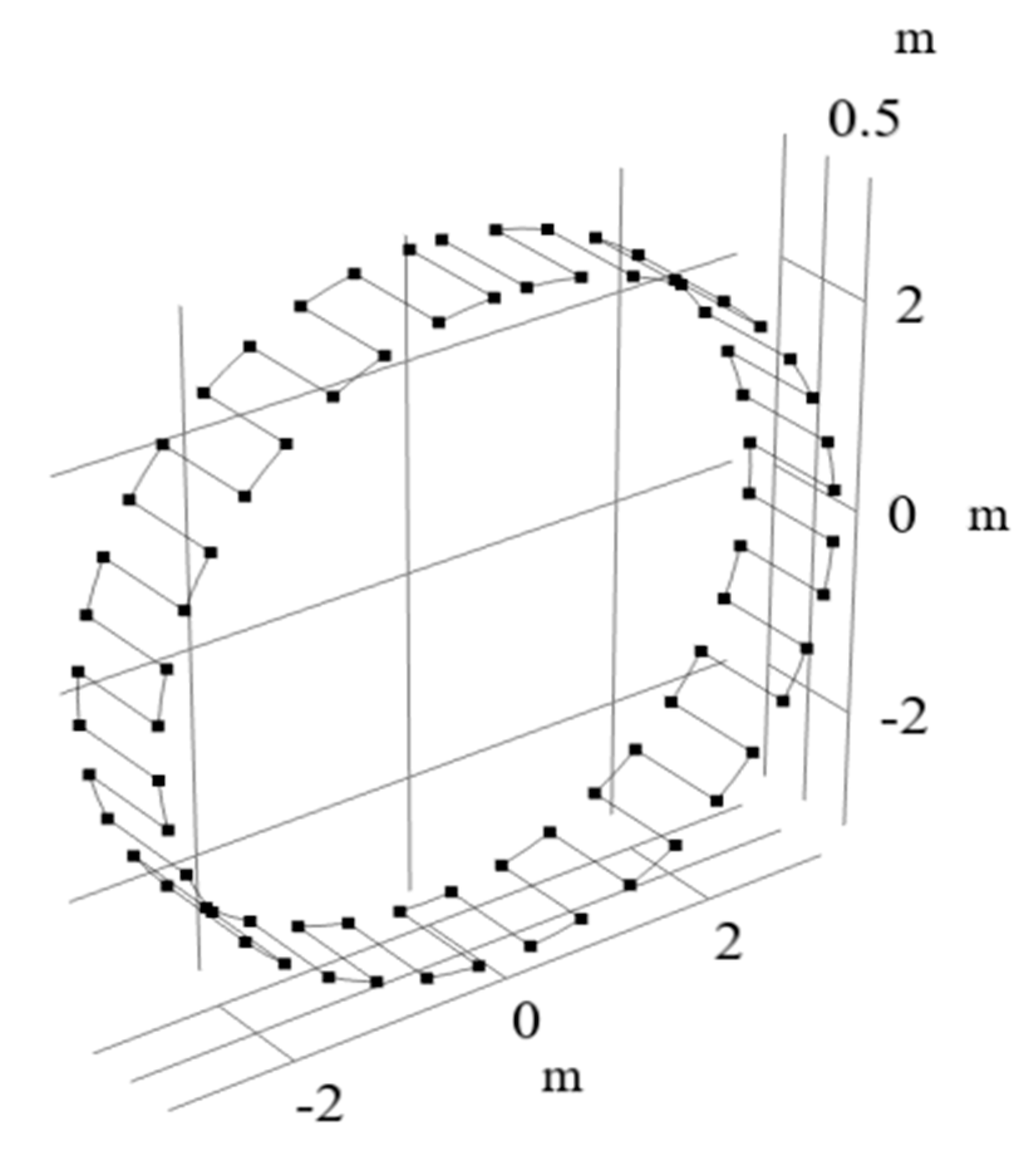
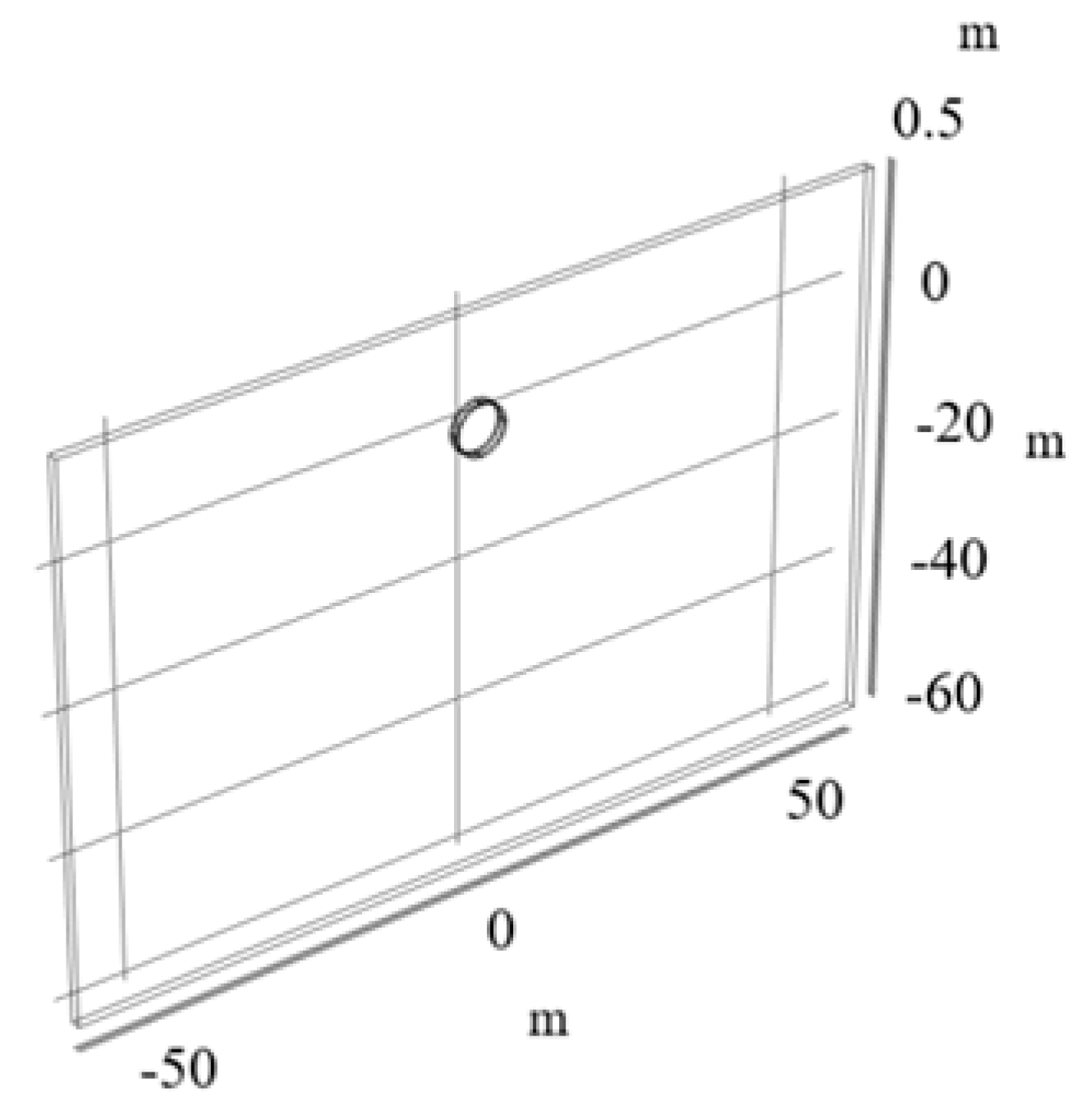
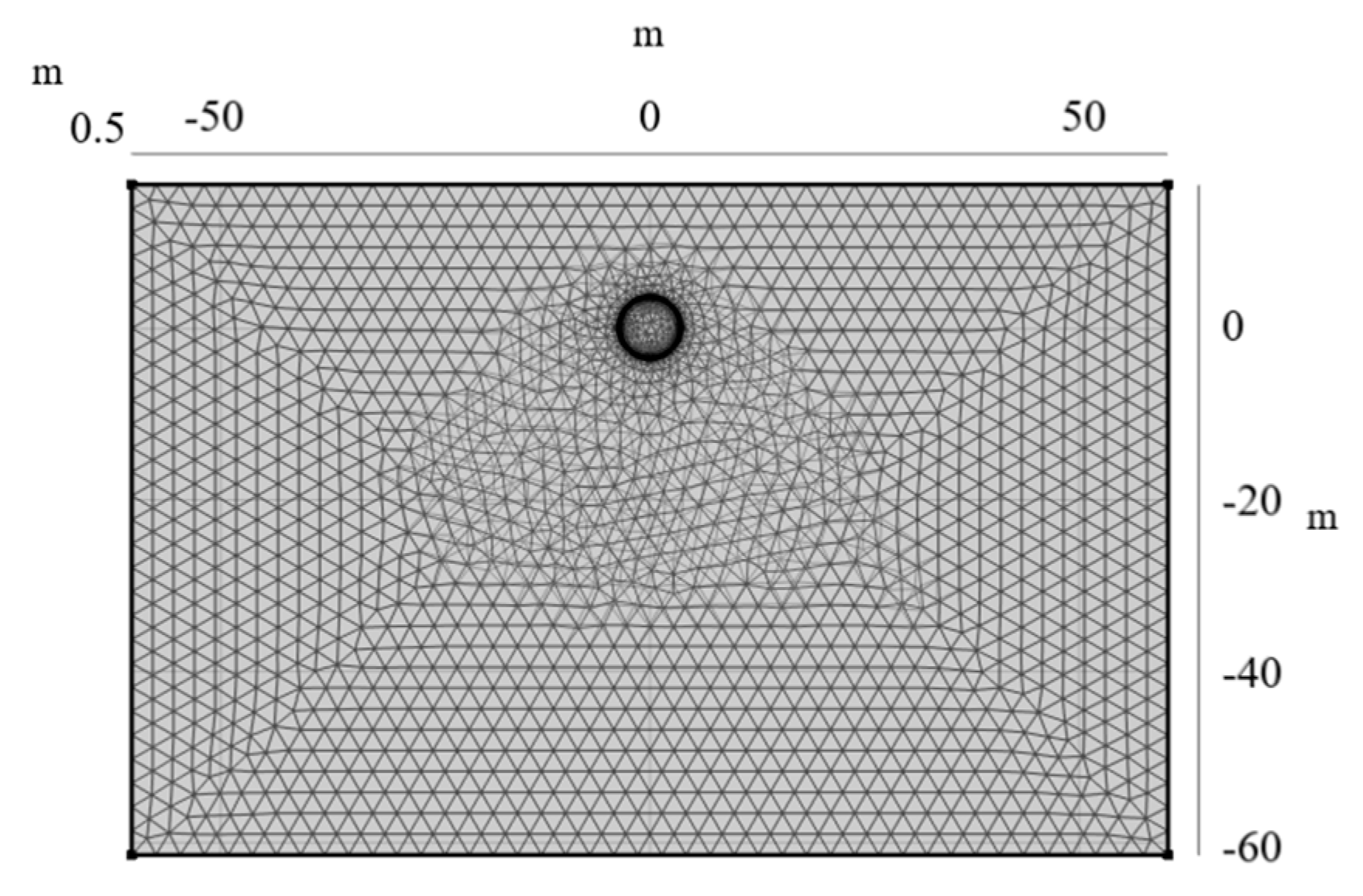
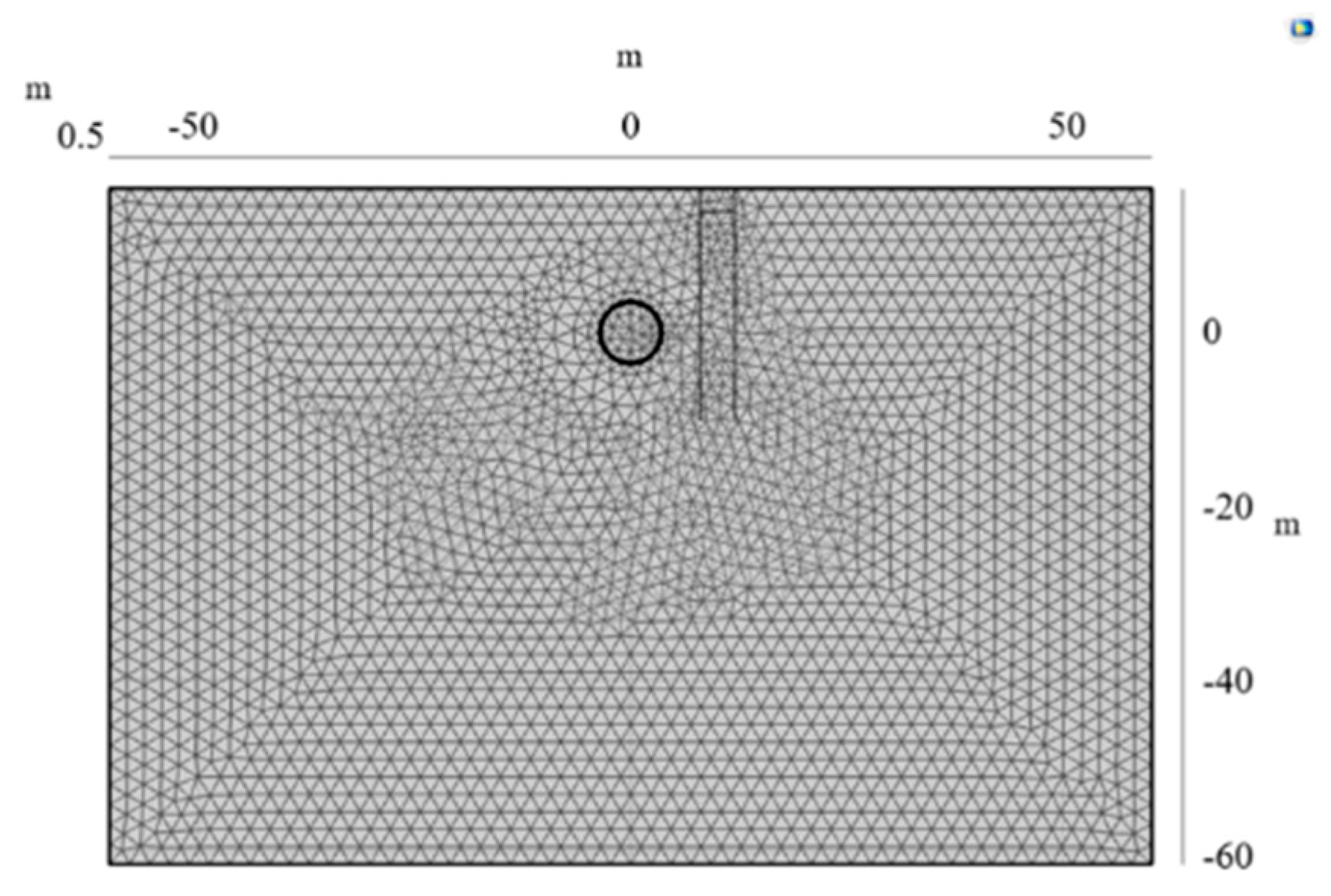
2. Establishment of a 3D Thermal–Hydraulic Coupled FEM Model
3. Methodology and Validation of the Model
3.1. Equation for Heat Transfer
- Darcy’s Law
- 2.
- Pipe Heat Transfer
- 3.
- Total Heat Transfer and Unit-Area Heat Transfer
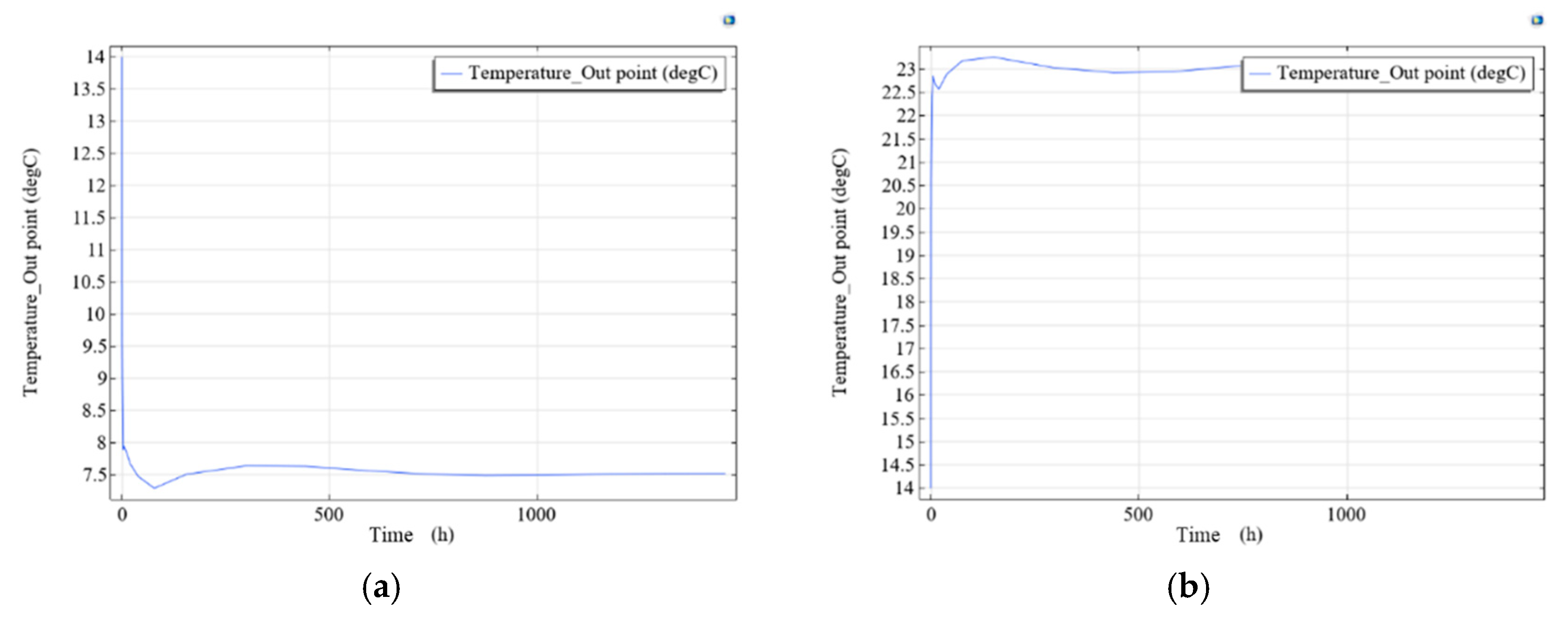
3.2. Model Validation
4. Results and Discussion
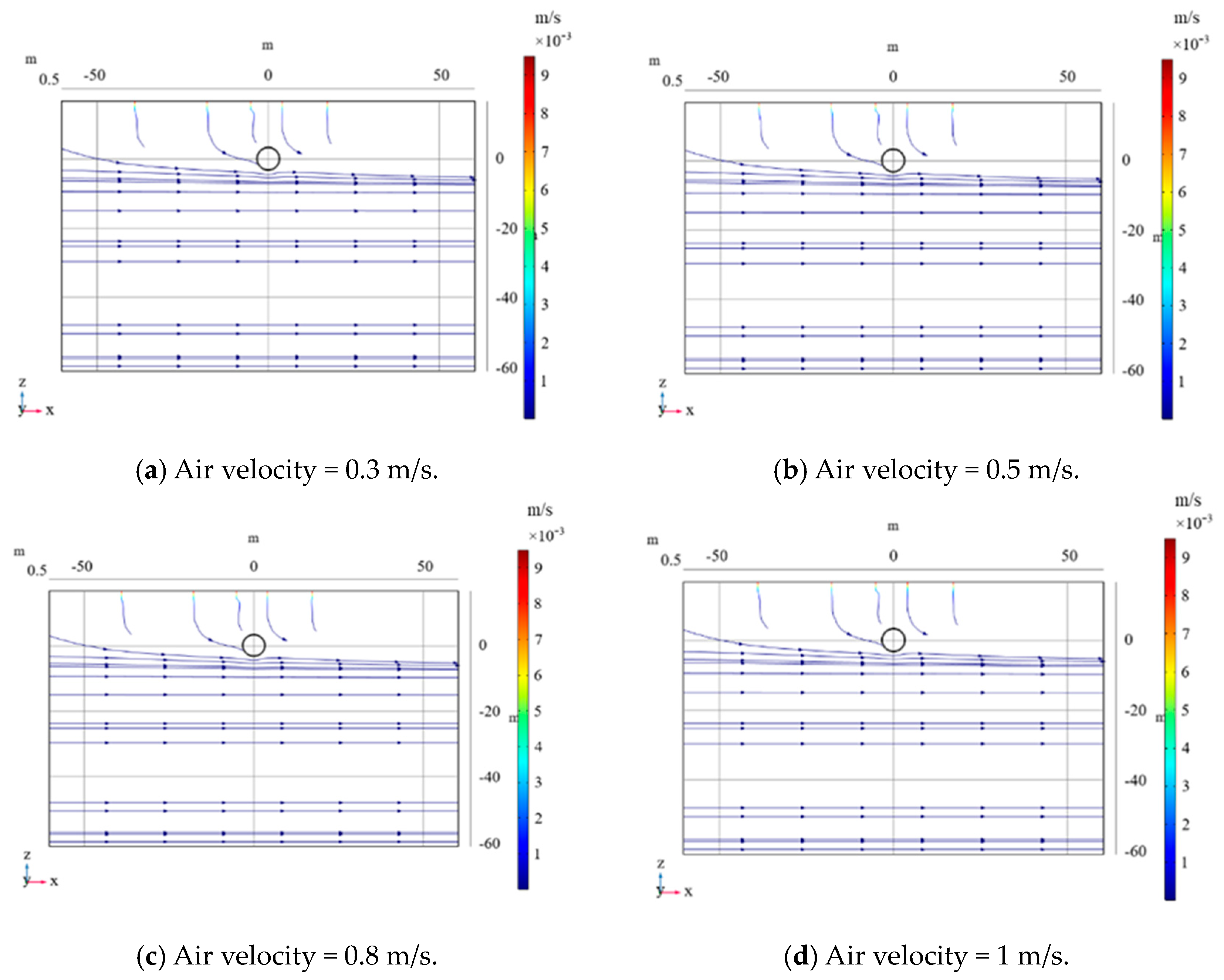
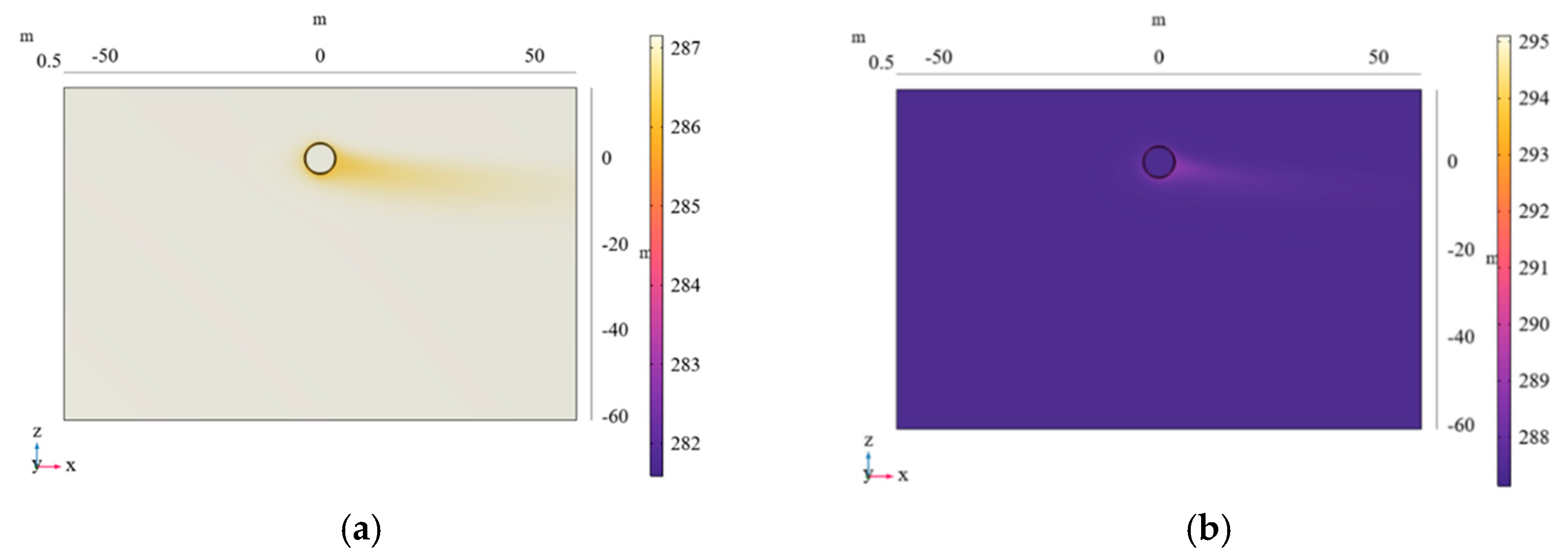
4.1. Analysis of the Influence of Air Velocity in the Tunnel
4.2. Comparative Analysis of Heat Transfer Efficiency Between Energy Tunnels and GSHPs
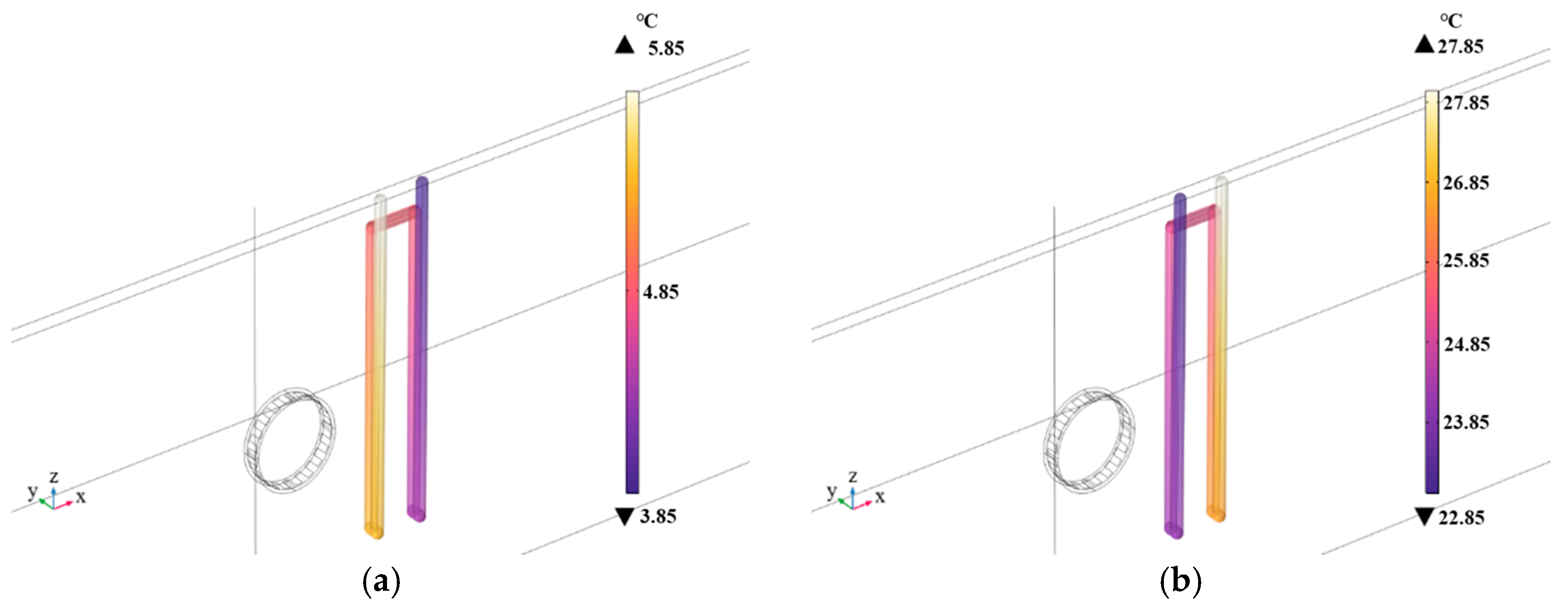
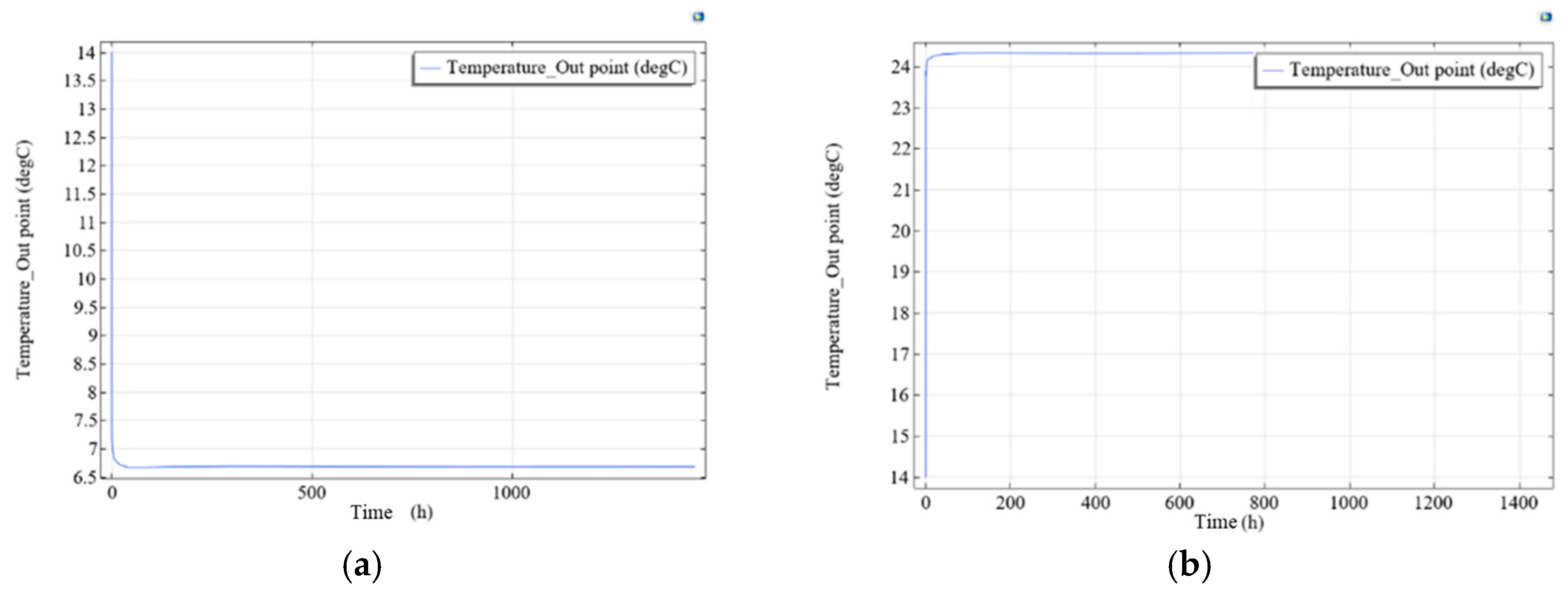
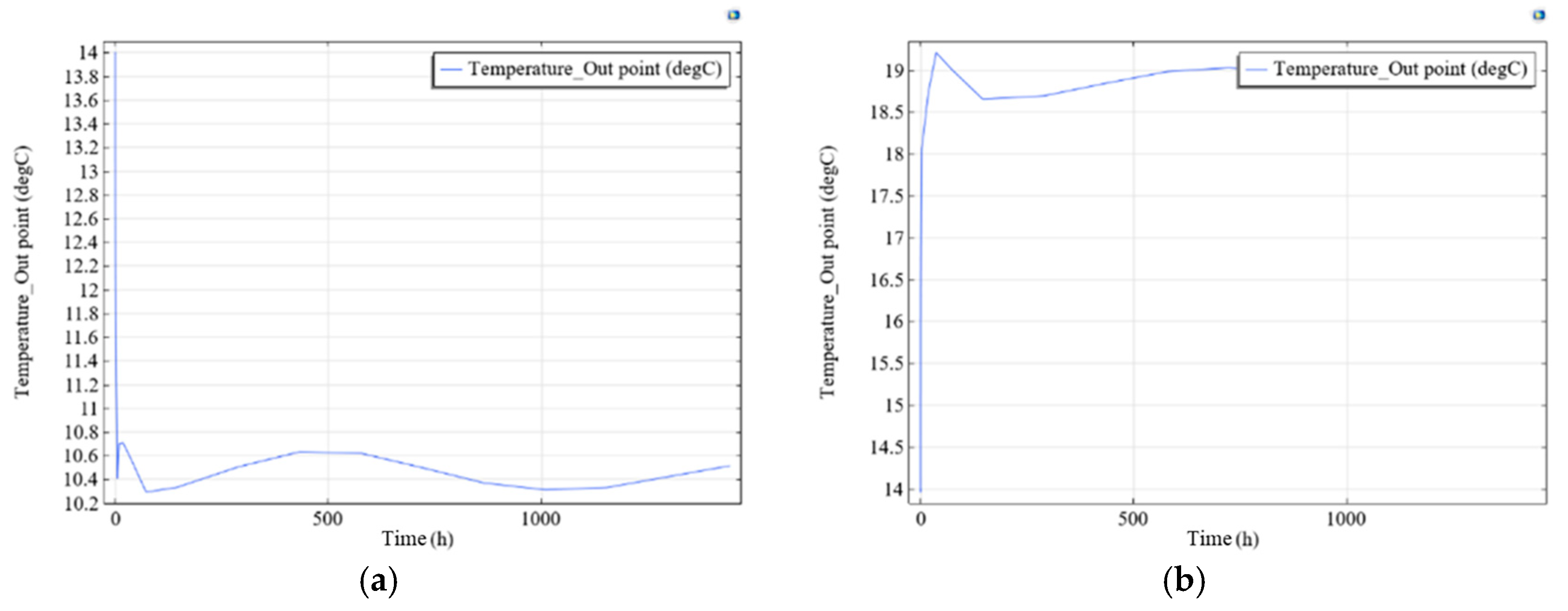
4.2.1. Analysis of Energy Tunnel Heat Transfer Efficiency
4.2.2. Analysis of GSHP Heat Transfer Efficiency
4.3. Analysis of Heat Carrier Fluids in Energy Tunnels and GSHPs
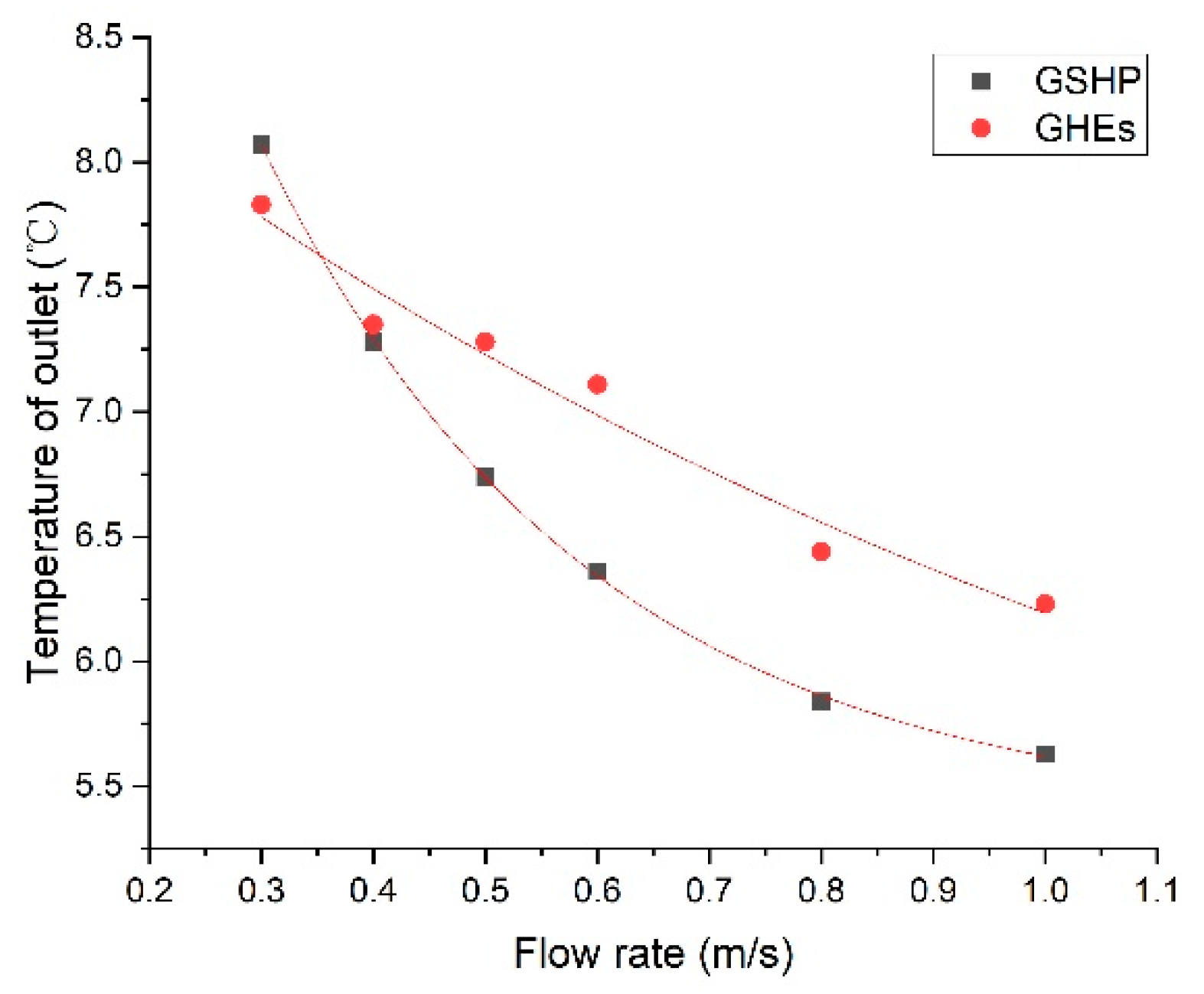
4.3.1. Analysis of Heat Carrier Fluid Flow Rate
4.3.2. Analysis of Heat Carrier Fluid Medium
5. Conclusions
- (1)
- A thermal–hydraulic coupled finite element model was successfully established and validated.
- (2)
- Under the same conditions, the heat transfer performance of energy tunnels is superior to that of conventional GSHP systems.
- (3)
- The type of heat carrier fluid significantly affects heat transfer performance, with R-134a showing the best overall results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rui, Y.; Yin, M. Finite element modeling of thermo-active diaphragm walls. Front. Struct. Civ. Eng. 2020, 14, 646–663. [Google Scholar] [CrossRef]
- Yin, M.; Rui, Y. Investigation of long-term behaviour of thermal wall by finite element analysis. Soils Found. 2019, 59, 1182–1192. [Google Scholar] [CrossRef]
- Rui, Y.; Soga, K. Thermo-hydro-mechanical coupling analysis of a thermal pile. Proc. Inst. Civ. Eng.-Geotech. Eng. 2019, 172, 155–173. [Google Scholar] [CrossRef]
- Rui, Y.; Yin, M. Investigations of pile–soil interaction under thermo-mechanical loading. Can. Geotech. J. 2018, 55, 1016–1028. [Google Scholar] [CrossRef]
- Rui, Y.; Yin, M. Thermo-hydro-mechanical coupling analysis of a thermo-active diaphragm wall. Can. Geotech. J. 2018, 55, 720–735. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, K.; Lu, X.; Huang, X.; Liu, K.; Wu, X. A review of geothermal energy resources, development, and applications in China: Current status and prospects. Energy 2015, 93, 466–483. [Google Scholar] [CrossRef]
- Haehnlein, S.; Bayer, P.; Blum, P. International legal status of the use of shallow geothermal energy. Renew. Sustain. Energy Rev. 2010, 14, 2611–2625. [Google Scholar] [CrossRef]
- Xu, Y.-S.; Wang, X.-W.; Shen, S.-L.; Zhou, A. Distribution characteristics and utilization of shallow geothermal energy in China. Energy Build. 2020, 229, 110479. [Google Scholar] [CrossRef]
- Hou, J.; Cao, M.; Liu, P. Development and utilization of geothermal energy in China: Current practices and future strategies. Renew. Energy 2018, 125, 401–412. [Google Scholar] [CrossRef]
- Rui, Y.; Garber, D.; Yin, M. Modelling ground source heat pump system by an integrated simulation programme. Appl. Therm. Eng. 2018, 134, 450–459. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. General review of ground-source heat pump systems for heating and cooling of buildings. Energy Build. 2014, 70, 441–454. [Google Scholar] [CrossRef]
- Luo, J.; Rohn, J.; Xiang, W.; Bertermann, D.; Blum, P. A review of ground investigations for ground source heat pump (GSHP) systems. Energy Build. 2016, 117, 160–175. [Google Scholar] [CrossRef]
- Brandl, H. Geothermal geotechnics for urban undergrounds. Procedia Eng. 2016, 165, 747–764. [Google Scholar] [CrossRef]
- Brandl, H. Energy foundations and other thermo-active ground structures. Géotechnique 2006, 56, 81–122. [Google Scholar] [CrossRef]
- Adam, D.; Markiewicz, R. Energy from earth-coupled structures, foundations, tunnels and sewers. Géotechnique 2009, 59, 229–236. [Google Scholar] [CrossRef]
- Zhang, G.; Xia, C.; Sun, M.; Zou, Y.; Xiao, S. A new model and analytical solution for the heat conduction of tunnel lining ground heat exchangers. Cold Reg. Sci. Technol. 2013, 88, 59–66. [Google Scholar] [CrossRef]
- Makasis, N.; Narsilio, G.A. A case study on the application of energy tunnels in Sydney, Australia. In Challenges and Innovations in Geomechanics: Proceedings of the 16th International Conference of IACMAG-Volume 2; Springer: Cham, Switzerland, 2021; pp. 1077–1084. [Google Scholar]
- Buhmann, P.; Moormann, C.; Westrich, B.; Pralle, N.; Friedemann, W. Tunnel geothermics—A German experience with renewable energy concepts in tunnel projects. Geomech. Energy Environ. 2016, 8, 1–7. [Google Scholar] [CrossRef]
- Lee, C.; Park, S.; Choi, H.-J.; Lee, I.-M.; Choi, H. Development of energy textile to use geothermal energy in tunnels. Tunn. Undergr. Space Technol. 2016, 59, 105–113. [Google Scholar] [CrossRef]
- Islam, M.S.; Fukuhara, T.; Watanabe, H.; Nakamura, A. Horizontal U-tube road heating system using tunnel ground heat. J. Snow Eng. Jpn. 2006, 22, 229–234. [Google Scholar] [CrossRef]
- Franzius, J.N.; Pralle, N. Turning segmental tunnels into sources of renewable energy. In Proceedings of the Institution of Civil Engineers-Civil Engineering, 2011; Thomas Telford Ltd.: London, UK, 2011; pp. 35–40. [Google Scholar]
- Barla, M.; Baralis, M.; Insana, A.; Aiassa, S.; Antolini, F.; Vigna, F.; Azzarone, F.; Marchetti, P. On the thermal activation of Turin metro Line 2 tunnels. In Challenges and Innovations in Geomechanics: Proceedings of the 16th International Conference of IACMAG-Volume 2; Springer: Cham, Switzerland, 2021; pp. 1069–1076. [Google Scholar]
- Carteni, A.; Cascetta, F. Particulate matter concentrations in a high-quality rubber-tyred metro system: The case study of Turin in Italy. Int. J. Environ. Sci. Technol. 2018, 15, 1921–1930. [Google Scholar] [CrossRef]
- Baralis, M.; Barla, M.; Bogusz, W.; Di Donna, A.; Ryżyński, G.; Żeruń, M. Geothermal potential of the NE extension Warsaw (Poland) metro tunnels. Environ. Geotech. 2018, 7, 282–294. [Google Scholar] [CrossRef]
- Zhang, G.; Xia, C.; Yang, Y.; Sun, M.; Zou, Y. Experimental study on the thermal performance of tunnel lining ground heat exchangers. Energy Build. 2014, 77, 149–157. [Google Scholar] [CrossRef]
- Barla, M.; Di Donna, A.; Perino, A. Application of energy tunnels to an urban environment. Geothermics 2016, 61, 104–113. [Google Scholar] [CrossRef]
- Di Donna, A.; Barla, M. The role of ground conditions on energy tunnels’ heat exchange. Environ. Geotech. 2016, 3, 214–224. [Google Scholar] [CrossRef]
- Magdy, A.; Ogunleye, O.; Mroueh, H.; Di Donna, A.; Singh, R.M. A review of exploiting shallow geothermal energy through tunnels: Current status and future prospects. Renew. Energy 2024, 238, 121958. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, Z.; Xiao, S.; Guo, Y.; Li, C. A promising technology of cold energy storage using phase change materials to cool tunnels with geothermal hazards. Renew. Sustain. Energy Rev. 2022, 163, 112509. [Google Scholar] [CrossRef]
- Shafagh, I.; Rees, S.; Loveridge, F. Investigations into thermal resistance of tunnel lining heat exchangers. In E3S Web of Conferences, 2020; EDP Open: Paris, France, 2020. [Google Scholar]
- Barla, M.; Di Donna, A.; Insana, A. A novel real-scale experimental prototype of energy tunnel. Tunn. Undergr. Space Technol. 2019, 87, 1–14. [Google Scholar] [CrossRef]
- Rasti, M.; Aghamiri, S.; Hatamipour, M.-S. Energy efficiency enhancement of a domestic refrigerator using R436A and R600a as alternative refrigerants to R134a. Int. J. Therm. Sci. 2013, 74, 86–94. [Google Scholar] [CrossRef]
- Lee, J.; Bae, S.; Bang, K.; Kim, M. Experimental and numerical research on condenser performance for R-22 and R-407C refrigerants. Int. J. Refrig. 2002, 25, 372–382. [Google Scholar] [CrossRef]
- Atwood, T.; Hughes, H.M. Refrigerants and energy efficiency. Int. J. Refrig. 1990, 13, 270–273. [Google Scholar] [CrossRef]
| Parameter | Symbol | Unit | Size |
|---|---|---|---|
| Diameter | mm | 24 | |
| Thickness | t | mm | 2 |
| Velocity of Flow | v | 0.4 | |
| Thermal Conductivity of Flow | kf | 0.58 | |
| Thermal Conductivity of Concrete | 0.38 | ||
| Thermal Capacity of Flow | 4.2 |
| Material | Property | Unit | Size |
|---|---|---|---|
| Soil | Porosity | 1 | 0.25 |
| Density | 2202.6 | ||
| Thermal Conductivity of Soil | 2.8 | ||
| Thermal Conductivity of Flow | 0.65 | ||
| Thermal Capacity of Soil | 2.0 | ||
| Thermal Capacity of Flow | 4.2 | ||
| Transverse Heat Dispersion Coefficient | m | 3.1 | |
| Longitudinal Heat Dispersion Coefficient | m | 0.3 | |
| Concrete | Thermal Conductivity of Concrete | 2.3 | |
| Thermal Capacity of Concrete | 2.19 | ||
| Density | 2300 |
| Name | Season | Q (W) | Qs (W/m2) |
|---|---|---|---|
| Results of Barla [20] | Winter | 1.67 | 52.76 |
| Summer | 2.34 | 73.87 | |
| Results of this study | Winter | 1.66 | 55.56 |
| Summer | 2.12 | 70.95 |
| Name | Season | Outlet Temperature (°C) | Q (W) |
|---|---|---|---|
| GHEs | Winter | 7.55 | 0.05 |
| Summer | 23.00 | 0.07 | |
| GSHP | Winter | 6.25 | 0.06 |
| Summer | 23.16 | 0.07 |
| Fluid Medium | Season | Outlet Temperature (°C) | Q (KW) |
|---|---|---|---|
| Water | Winter | 7.55 | 1.66 |
| Summer | 23.00 | 2.12 | |
| Ethylene glycol | Winter | 6.68 | 1.25 |
| Summer | 24.32 | 1.56 | |
| R-134a | Winter | 10.51 | 3.85 |
| Summer | 18.91 | 3.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, M.; Liu, P.; Wu, Z. Analysis of Heat Exchange Efficiency and Influencing Factors of Energy Tunnels: A Case Study of the Torino Metro in Italy. Buildings 2025, 15, 2704. https://doi.org/10.3390/buildings15152704
Yin M, Liu P, Wu Z. Analysis of Heat Exchange Efficiency and Influencing Factors of Energy Tunnels: A Case Study of the Torino Metro in Italy. Buildings. 2025; 15(15):2704. https://doi.org/10.3390/buildings15152704
Chicago/Turabian StyleYin, Mei, Pengcheng Liu, and Zhenhuang Wu. 2025. "Analysis of Heat Exchange Efficiency and Influencing Factors of Energy Tunnels: A Case Study of the Torino Metro in Italy" Buildings 15, no. 15: 2704. https://doi.org/10.3390/buildings15152704
APA StyleYin, M., Liu, P., & Wu, Z. (2025). Analysis of Heat Exchange Efficiency and Influencing Factors of Energy Tunnels: A Case Study of the Torino Metro in Italy. Buildings, 15(15), 2704. https://doi.org/10.3390/buildings15152704







