Cable Force Optimization of Circular Ring Pylon Cable-Stayed Bridges Based on Response Surface Methodology and Multi-Objective Particle Swarm Optimization

Abstract

Cable force distribution in cable-stayed bridges critically impacts structural safety and efficiency, yet traditional optimization methods struggle with unconventional designs due to nonlinear mechanics and computational inefficiency. This study proposes a hybrid approach combining Response Surface Methodology (RSM) and Multi-Objective Particle Swarm Optimization (MOPSO) to overcome these challenges. RSM constructs surrogate models for strain energy and mid-span displacement, reducing reliance on finite element analysis, while MOPSO optimizes Pareto solution sets for rapid cable force adjustment. Validated through an engineering case, the method reduces the main girder’s max bending moment by 8.7%, mid-span displacement by 31.2%, and strain energy by 7.1%, improving stiffness and mitigating stress concentrations. The response surface model demonstrates prediction errors of 0.35% for strain energy and 5.1% for maximum vertical mid-span deflection. By synergizing explicit modeling with intelligent algorithms, this methodology effectively resolves the longstanding efficiency–accuracy trade-off in cable force optimization for cable-stayed bridges. It achieves over 80% reduction in computational costs while enhancing critical structural performance metrics. Engineers are thereby equipped with a rapid and reliable optimization framework for geometrically complex cable-stayed bridges, delivering significant improvements in structural safety and construction feasibility. Ultimately, this approach establishes both theoretical substantiation and practical engineering benchmarks for designing non-conventional cable-stayed bridge configurations.

1. Introduction

As a modern bridge structural form, cable-stayed bridges have been widely adopted in contemporary bridge engineering due to their superior spanning capacity, lightweight design, and aesthetic appeal, particularly meeting the demands of long-span bridge construction. The stay cables—the core load-transferring components that transmit deck loads to the pylons—constitute the primary structural system of the bridge. The distribution of cable forces not only directly affects the internal forces and deformation states of the girder and pylon but also determines the overall mechanical performance, structural safety, economy, and durability of the bridge. This makes cable force optimization a critical factor in the design, construction, and maintenance of cable-stayed bridges. For unconventional cable-stayed bridges with complex geometric configurations and mechanical behaviors, rational determination of cable forces becomes especially crucial, as it directly impacts static and dynamic performance, fatigue life, and constructability [1]. Systematic research on cable force optimization not only enhances structural safety and economy but also provides scientific foundations for bridge design, offering significant theoretical and practical value [2]. Optimizing cable force distribution can markedly improve stress states, reduce material usage, extend service life, and provide technical support for innovative designs of complex bridge structures.

In recent years, with the rapid development of computational technology and optimization theory, intelligent optimization algorithms have gained widespread application in cable force optimization for cable-stayed bridges due to their robust global search capabilities and adaptability to complex problems [3]. These algorithms, inspired by human intelligence, biological group behaviors, and natural phenomena, are novel mathematical optimization methods. Their core idea lies in simulating evolutionary processes, collaborative mechanisms, or adaptive behaviors in nature to efficiently explore optimal solutions within complex search spaces. Characterized by simplicity, versatility, and parallel processing capabilities, these algorithms have become essential tools for solving engineering optimization challenges. In the field of cable force optimization for cable-stayed bridges, intelligent algorithms are widely used for determining and adjusting cable force distributions, as they effectively handle multi-objective, multi-constraint optimization problems.

Extensive research has been conducted on intelligent optimization algorithms for cable force adjustment. Among these, Particle Swarm Optimization (PSO) and Genetic Algorithms (GAs) are the most widely adopted methods [4]. PSO, with its low requirements for objective functions, high optimization efficiency, and computational simplicity, is a highly promising intelligent algorithm. Wang [5] integrated influence matrices into a multi-objective PSO algorithm with mutation operations, establishing a mathematical model for cable force optimization. This approach refines initial solutions obtained from traditional methods to generate Pareto front solution sets. Chu [6] proposed a novel optimization method combining BP neural networks, Gaussian process prediction, and simulated annealing-optimized PSO to determine allowable ranges for construction cable forces. Chen Zhijun et al. [7] applied PSO combined with ANSYS finite element software to optimize cable forces for single-pylon cable-stayed bridges, achieving uniform stress distributions and meeting design requirements. Wei [8] introduced an improved PSO (IPSO) with adaptive inertia weights to efficiently solve the complete curve of main cables. Zhang Yuping et al. [9] developed a cable force optimization method based on MOPSO, enhancing traditional PSO by incorporating external archives and improved update strategies to better address multi-objective, multi-constraint challenges. Compared to single-objective methods that yield limited solutions, MOPSO provides comprehensive Pareto-optimal solutions by considering multiple factors. Cai Jing et al. [10] enhanced PSO by adaptively adjusting inertia weights based on cable force performance, improving convergence rates and computational accuracy in cable force optimization.

Genetic Algorithms are widely applied to various complex optimization problems. In cable force optimization, GAs have become an effective tool due to their strong global search capability and ability to handle multiple constraints. Compared to traditional optimization methods, GAs exhibit robust self-adaptability, efficiently exploring the solution space to identify global optima [11]. To address the drawbacks of conventional cable force optimization methods—such as high computational load, long processing time, low efficiency, and slow convergence—Zhu [12] integrated the influence matrix and an elite retention strategy into GAs for optimizing cable forces during bridge formation. Hu et al. [13] applied an improved GA to the structural calculation of steel-truss arch bridge installation, transforming a multivariable, multi-constraint minimization problem into an unconstrained one and constructing a tailored GA optimization model. Tian [14] enhanced the nondominated sorting genetic algorithm II by refining crowding distance, mutation rate, elite retention, and selection operators, proposing an initial cable force optimization method for cast-in situ cantilever-constructed arch bridges. Arellano [15] developed a multi-objective optimization approach to determine optimal overlapping lengths for crisscrossing cables in multi-span cable-stayed bridges, deriving Pareto-optimal solutions via GAs. Feng [16] coupled the influence matrix method with GAs to optimize stay cables, while Wang [17] embedded GAs into finite element analysis, using beam and truss elements to model a long-span rail-road cable-stayed bridge. Hu [18] employed GAs for cable force optimization, leveraging Pareto theory for multi-objective trade-offs, particularly when balancing competing design goals. The optimization results and limitations of the various methods mentioned above are shown in

Table 1. Comparison table of optimization algorithms.

Reference	Key Objectives	Optimization Results	Limitations
Wang [5]	Generate Pareto solution sets; optimize cable force distribution	Refined initial solutions from traditional methods; enabled multi-objective trade-offs	Dependency on frequent FEA calls; high computational costs
Chu [6]	Determine allowable ranges for construction cable forces	Enhanced prediction accuracy; optimized tension ranges	Hybrid framework (BP neural network + simulated annealing) increased complexity
Chen et al. [7]	Achieve uniform stress distribution in single-pylon cable-stayed bridges	Met design requirements; reduced stress concentrations	Only applicable to simple geometries
Wei [8]	Efficiently solve the complete curve of main cables	Adaptive inertia weights improved convergence efficiency	Focused solely on cable subsystems; ignored full-structural behavior
Zhang et al. [9]	Handle multi-objective, multi-constrained cable force optimization	Enhanced update strategies; improved Pareto solution quality	No reduction in FEA calls; low optimization efficiency
Cai et al. [10]	Adjust cable forces for performance optimization	Adaptive inertia weights increased convergence rates (up to 20%)	Limited to specific cable types; poor generalizability
Zhu [12]	Optimize cable forces during bridge formation	Achieved uniform force distribution via elite strategy	Computationally intensive for long-span bridges; time-consuming
Hu et al. [13]	Optimize structural installation of steel-truss arch bridges	Transformed multi-variable, multi-constraint minimization into unconstrained problem	Poor scalability to nonlinear systems (e.g., large geometric deformations)
Tian [14]	Optimize initial cable forces for cast-in-situ arch bridges	Improved NSGA-II with refined crowding distance; diversified solution sets	Required high iteration counts (>1000); impractical for real-time optimization
Arellano [15]	Determine optimal overlapping lengths for crisscrossing cables	Derived Pareto-optimal solutions for multi-span bridges	Ignored impacts of complex geometries
Feng [16]	Optimize stay cables	Coupled influence matrix method; stabilized convergence	Fully dependent on FEA; no surrogate models; heavy computational load
Wang [17]	Optimize completed-bridge cable forces using GA	Integrated finite element models (beam/truss elements)	Failed to address FEA dependency; no significant efficiency gain
Hu [18]	Balance competing objectives (e.g., safety vs. cost)	Leveraged Pareto theory for multi-objective trade-offs	Required excessive FEA iterations in practice; low engineering feasibility

.

Although intelligent optimization algorithms have made significant strides and are maturing in the field of cable force optimization for cable-stayed bridges, these methods still face critical constraints in practical applications: their iterative optimization process requires over-reliance on finite element analysis (FEA), resulting in prohibitively excessive computational costs—particularly acute for cable-stayed bridges featuring complex geometric configurations and nonlinear mechanical behavior. This process not only substantially increases computational costs but also severely reduces optimization efficiency—particularly for cable-stayed bridges with complex geometries and nonlinear mechanical behaviors, where computational demands become prohibitive. For instance, in cable-stayed bridges with circular ring pylons, the unique geometric configuration and load-bearing characteristics make traditional optimization methods inefficient in handling complex cable force distributions. To bridge this critical gap, this paper proposes a hybrid intelligent optimization algorithm. Specifically, by synergistically integrating the Response Surface Method (RSM) with Multi-Objective Particle Swarm Optimization (MOPSO), this approach fundamentally eradicates the efficiency–accuracy trade-off dilemma. The approach first identifies critical optimization objectives based on structural mechanics, then employs RSM to construct explicit quadratic surrogate models that map cable forces to objectives (e.g., global strain energy and mid-span displacement), thereby replacing computationally expensive FEA simulations. Subsequently, MOPSO rapidly explores Pareto-optimal solutions using these surrogate models, ensuring high precision while drastically reducing FEA iterations. Validation via a real-world case study confirms the method’s effectiveness, demonstrating its capability to enhance structural stiffness, minimize deformations, and improve energy efficiency with negligible prediction errors. This methodology not only overcomes the computational inefficiency of conventional intelligent algorithms but also provides a novel paradigm for cable force optimization in geometrically complex cable-stayed bridges.

2. Cable Force Optimization Method Based on Response Surface Methodology and Multi-Objective Particle Swarm Optimization

Particle Swarm Optimization, as an efficient intelligent optimization algorithm, has been widely applied in structural force optimization of cable-stayed bridges due to its low requirements for objective functions, strong optimization capability, simple computation, and good convergence [19]. The algorithm can flexibly adapt to the structural characteristics of cable-stayed bridges and achieve efficient optimization of cable force distribution through reasonable selection of objective functions and constraints. However, in previous structural optimization methods, most algorithms require frequent calls to finite element calculations to evaluate objective function values during the optimization process, which not only increases computational costs but also significantly reduces optimization efficiency. Especially for unconventional cable-stayed bridges, due to their complex structural forms and nonlinear force characteristics, traditional optimization methods often require enormous computational resources, resulting in poor economic efficiency. To address this issue, this paper introduces Response Surface Methodology, which fits the relationship between optimization variables (such as cable forces) and objective functions, transforming the originally implicit objective functions into explicit ones and constructing response surface equations. On this basis, the particle swarm algorithm is combined to efficiently optimize the explicit objective functions, thereby significantly reducing the number of calls to finite element calculations while ensuring optimization accuracy and markedly improving the efficiency of cable force optimization. This method not only solves the problem of high computational costs in traditional optimization methods but also provides an efficient and economical technical approach for cable force optimization in complex cable-stayed bridges.

2.1. Explicit Formulation of Objective Functions

In the optimization process based on Response Surface Methodology (RSM), sample data of the objective functions are first obtained through finite element model computations. Specifically, for the cable force optimization problem of cable-stayed bridges, the design variables are adjusted and numerical simulations of the bridge structure are performed using finite element analysis software. The optimized objective function values after each adjustment are recorded to generate a set of sample point data. Subsequently, regression fitting is performed on the sample points using RSM to establish an explicit mathematical relationship between the responses (i.e., the optimization objective functions) and design variables, replacing the original complex implicit functional relationships [20]. The commonly used response surface fitting function is a quadratic polynomial, expressed as follows:

$$f\left(x_1,x_2,x_3,\dots ,x_n\right)={\alpha }_0+\sum _{i=1}^n\left({\alpha }_i{x}_i+{\alpha }_{ii}{x}_i^2\right)$$

(1)

where f represents the structural response function; x₁, x₂, …, x_n denote n variables; and α₀, α_i, α_ii are response surface coefficients. After performing m (m = 2n + 1) sampling points for these n variables, the response surface coefficient vector α can be calculated as follows:

$$\mathit{\alpha }={\mathit{X}}^{-1}\mathit{f}$$

(2)

where X represents the sample point matrix of the variables; and f denotes the response vector corresponding to the m sample points.

2.2. Multi-Objective Particle Swarm Optimization

Particle Swarm Optimization is a swarm intelligence-based optimization algorithm that has gained widespread application in engineering optimization due to its conceptual simplicity, low requirements for objective functions, and ease of programming implementation. The fundamental principle of PSO simulates the cooperative behavior observed in biological groups such as bird flocks or fish schools, where information sharing and collaboration among individuals enables efficient search for optimal solutions in the solution space.

In practical implementation, within a D-dimensional search space, the PSO algorithm initializes n particles, with each particle representing a potential solution to the problem. The position of the i-th particle is defined by vector x_i = [x_i1, x_i2, …, x_in], while its velocity is characterized by vector v_i = [v_i1, v_i2, …, v_in]. During each iteration cycle, the algorithm evaluates the fitness value of each particle through objective function computation. Based on comparative analysis of these fitness values, the system updates both the personal best position for individual particles and the global best position for the entire swarm. The personal best position of the i-th particle, denoted as p_{best 1} = [p_{best i1}, p_{best i2}, …, p_{best id}], records the optimal solution discovered by that particular particle throughout its search history. Conversely, the global best position, expressed as g_{best 1} = [g_{best 1}, g_{best 2}, …, g_{best d}], represents the best solution identified by the collective swarm during the optimization process. The algorithm’s core mechanism involves dynamic adjustment of particle velocities and positions during each iteration, incorporating both individual experience (personal best position) and collective experience (global best position). This adjustment follows specific update rules:

$${\upsilon }_{id}^k=\omega {\upsilon }_{id}^{k-1}+c_1{r}_1\left({\mathit{p}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t} id}^{k-1}-x_{id}^{k-1}\right)+c_2{r}_2\left({\mathit{g}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t} d}^{k-1}-x_{id}^{k-1}\right)$$

(3)

$$x_{id}^k=x_{id}^{k-1}+{\upsilon }_{id}^{k-1}$$

(4)

$$\left\{\begin{array}{c}{\upsilon }_{dmin}\le {\upsilon }_{id}^k\le {\upsilon }_{dmax}\\ x_{dmin}\le x_{id}^k\le x_{dmax}\end{array}\right.$$

(5)

where ${\upsilon }_{id}^k$ represents the d-th dimensional velocity component of particle i during the k-th iteration, with ${\upsilon }_{dmin}$ and ${\upsilon }_{dmax}$ defining its minimum and maximum limits. $x_{id}^k$ corresponds to the d-th dimensional position component of particle i at the k-th iteration, also bounded by $x_{dmin}$ and $x_{dmax}$. ${\mathit{p}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t} d}^{k-1}$ indicates the d-th dimensional component of particle i’s personal best position from the (k−1)-th iteration, while ${\mathit{g}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t} d}^{k-1}$ represents the d-th dimensional component of the swarm’s global best position at the (k−1)-th iteration. The inertia weight ω, a non-negative parameter, controls the exploration range within the solution space. Acceleration constants c₁ and c₂, in the range of [0, 2], regulate the maximum step size. Random numbers r₁ and r₂, uniformly distributed in (0, 1), introduce stochastic elements to enhance search randomness.

The Multi-Objective Particle Swarm Optimization algorithm represents an extension of the classical PSO algorithm, specifically designed as an efficient solution for multi-objective optimization problems. Building upon the strengths of PSO—including conceptual simplicity, rapid convergence, and ease of implementation—MOPSO overcomes PSO’s limitation to single-objective optimization by simultaneously handling multiple conflicting optimization objectives. Unlike traditional optimization methods, MOPSO imposes no strict requirements on the continuity or differentiability of objective functions, granting it broad applicability in engineering optimization and establishing it as one of the most promising approaches for multi-objective problem-solving.

The algorithm’s core innovation lies in its introduction of an external repository for storing non-dominated solutions (Pareto-optimal solutions) generated during iterations. MOPSO employs sophisticated update strategies to dynamically adjust each particle’s pbest (personal guide) and gbest (global guide) while maintaining diversity and distribution quality of non-dominated solutions within the repository. The algorithm achieves multi-objective optimization through three key mechanisms:

First, non-dominated solution screening compares current population solutions against repository members during each iteration, continuously updating the repository. Second, global guide selection strategically chooses repository solutions as global guides to balance convergence and diversity. Third, personal guide updating modifies individual guides based on each particle’s historical best positions and current fitness values.

The optimization outcome of MOPSO consists of a Pareto-optimal solution set rather than a single solution, providing decision-makers with multiple trade-off alternatives. The algorithm’s workflow clearly illustrates the complete process from initialization through non-dominated solution screening, velocity and position updates, to repository maintenance. These enhancements enable MOPSO to excel in complex multi-objective optimization scenarios, solidifying its position as an essential tool in engineering optimization. The visual representation of the algorithm’s workflow effectively demonstrates this comprehensive procedure from initialization to final solution output.

3. Engineering Case Study of Cable Force Optimization for a Ring-Shaped Pylon Cable-Stayed Bridge

3.1. Project Overview

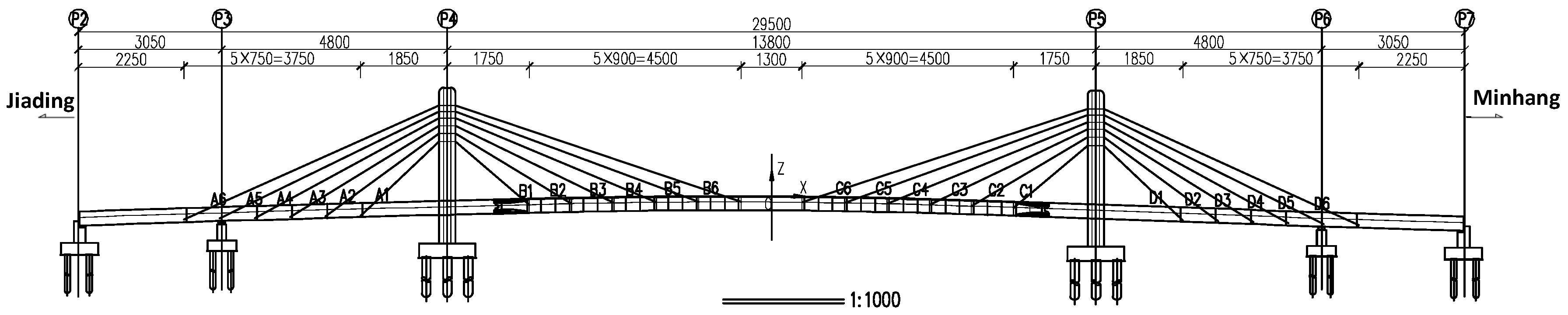
This study employs the Jinyun Road–Shenkun Road Connection Project (from Aite Road to North Zhai Road) as its engineering context, with the specific location of the bridge structure illustrated in Figure 1.

The total length of the bridge within the project scope is 415 m. The main bridge adopts a double-ring low-pylon cable-stayed bridge form with a span combination of 30.5 m + 48 m + 138 m + 30.5 m + 48 m, resulting in a total span of 295 m. The main pylon is designed as an arched cable tower, with a total height of 33.695 m from the top of the pile cap to the top of the tower, of which the height above the bridge deck is 25.965 m. The pylon is vertically positioned at the main pier location, with a steel–concrete composite cross-section design at the tower base to ensure overall structural stability and load-bearing capacity.

The girder adopts a hybrid structure with a height of 3 m and an overall length of 295 m, including a main span of 138 m and side spans of 78.5 m each. The total length of concrete girder segments is 88 m, comprising the 78.5 m side spans and the 9.5 m segment extending from the main pier into the main span. The steel–concrete transition segment is 7 m long, while the remaining main span section uses a steel girder structure with a total length of 105 m. The substructure consists of prestressed concrete rectangular cap beams, twin-column piers and rectangular pile caps. The foundation employs bored piles with diameters of 800 mm and 1500 mm, with grouting technology applied at pile tips to enhance bearing capacity and durability.

The cable-stayed system features a spatial double-cable-plane fan arrangement, with cable spacing of 9.0 m on the steel box girder side, 7.5 m on the concrete side, and 1.0 m at the tower top. Six pairs of stay cables are installed on each side, totaling 24 pairs for the entire bridge. The stay cables are made of unbonded steel strands with wedge-type anchors to ensure anchoring performance and long-term reliability. The construction method involves single-strand installation, individual tensioning and overall cable adjustment, equipped with computer-controlled intelligent tensioning equipment to achieve precise control of cable forces, ensuring construction quality and structural safety. Figure 2 shows the elevation layout of this ring-shaped pylon cable-stayed bridge.

The numerical analysis model of the cable-stayed bridge was established using Midas Civil NX finite element software to accurately simulate the structural behavior and mechanical response of the bridge. The main girder, pylon, and piers were modeled using beam elements to precisely represent their bending, shear, and axial force characteristics. Given the relatively short length of the stay cables in this bridge, their sag effect can be considered negligible. To quantitatively verify the rationality of this assumption, this paper conducts sensitivity analysis using the Ernst equivalent modulus method:

$$E_{eq}={\displaystyle \frac{E}{1+\frac{{\left(\gamma L\right)}^{2}EA}{12T^3}}}$$

(6)

where E denotes the elastic modulus, γ the material unit weight, A the cross-sectional area of the stay cable, T the design tension force, and L the horizontal projected length of the stay cable. Computational results confirm that the equivalent stiffness reduction rate for all stay cables remains below 1.2%, satisfying the accuracy requirements for global static analysis. Consequently, stay cables in the numerical model are simulated using truss elements, considering only axial tensile-compressive stiffness while neglecting bending and shear effects.

Rigid connections were adopted between the main girder, pylon, and piers to ensure proper force transfer and deformation coordination among structural components. The model base was fixed with rigid constraints to simulate the rigid connection between bridge foundations and ground, restricting all directional displacements and rotations.

According to the actual loading conditions of the bridge, external loads are added to the model, including the constant load on the bridge, secondary loads on the steel strands, as well as creep secondary loads and shrinkage secondary loads. The cable forces were introduced through initial tension loads to simulate the prestressing forces of stay cables in the completed bridge state, ensuring the mechanical behavior of the bridge model accurately reflects real working conditions. The established finite element model of the entire bridge is shown in Figure 3.

3.2. Objectives of Cable Force Optimization

Although the dynamic performance of bridges (such as vibration modes and fatigue under live loads) is crucial to long-term structural integrity, this study ultimately selected only static response indicators for optimization when determining cable force optimization objectives. This decision was based on comprehensive consideration of phase-specific relevance and computational efficiency. Specifically, the optimization targets the dead load state after structural completion—a critical condition where initial structural safety and service performance are predominated by static mechanical distributions.

To scientifically determine appropriate objectives for cable force optimization, it is essential to thoroughly consider the structural characteristics and mechanical behavior of single-pylon cable-stayed bridges. The initial step involves conducting numerical analysis on the ring-shaped pylon cable-stayed bridge before optimization using finite element simulation methods to obtain its stress state and deformation characteristics. Through finite element modeling calculations, the bending moment distribution of the entire bridge under dead load was obtained, as shown in Figure 4.

The finite element analysis results reveal significant non-uniformity in the internal force distribution of the main girder under self-weight and dead loads, with the bending moment reaching a maximum value of 259,206 kN·m. This phenomenon indicates an unfavorable stress state in the girder at this location, presenting considerable stress concentration risks that may adversely affect the structure’s long-term performance and fatigue life. Additionally, the maximum vertical displacement at the mid-span measures 116.694 mm. While this deformation remains within code-permissible limits, it suggests room for improvement in the bridge’s overall stiffness to ensure safer load-bearing performance.

The ring-shaped pylon cable-stayed bridge’s unique structural configuration and complex mechanical behavior make cable force optimization crucial for ensuring structural safety and service performance. The primary optimization objectives involve rationally adjusting stay cable force distribution to improve global stress states, thereby guaranteeing structural safety, durability, and cost effectiveness. The observed non-uniform bending moment distribution and excessive maximum moment values may lead to localized stress concentrations, increasing fatigue failure risks while compromising deformation performance under loads. Consequently, the optimization focuses on achieving balanced stress distribution through appropriate cable force adjustments to mitigate stress concentrations, reduce fatigue risks, and maintain deformation within allowable limits to prevent functional failure.

Based on the above analysis, the total strain energy of the bridge and the maximum vertical displacement at mid-span are selected as optimization objectives. The total strain energy of the bridge reflects the overall structural stress state and energy distribution. Minimizing this parameter helps improve the uniformity of internal force distribution and reduces stress concentrations. Meanwhile, the maximum vertical displacement at mid-span directly indicates the bridge’s global stiffness and deformation performance. Controlling this parameter ensures structural safety and serviceability under loading conditions.

The strain energy formula for discrete structures is as follows:

$$U=\sum _{i=1}^m{\displaystyle \frac{L_i}{4E_i{I}_i}}\left(M_{L_i}^2+M_{R_i}^2\right)+\sum _{i=1}^m{\displaystyle \frac{L_i}{4E_i{A}_i}}(N_{L_i}^2+N_{R_i}^2)$$

(7)

where m represents the number of structural elements; L_i, E_i, I_i denote the length, elastic modulus, and moment of inertia of the i-th element respectively; M_Li and M_Ri represent the left and right end moments of the i-th element; A_i indicates the cross-sectional area of the i-th element; and N_L and N_Ri correspond to the left and right end axial forces of the i-th element respectively.

3.3. Response Surface Function Construction

After determining the optimization objectives as the total strain energy of the bridge and the maximum vertical displacement at mid-span of the main girder, and selecting the initial cable forces of stay cables as design variables, the response surface method is employed to establish the objective function for this ring-shaped pylon cable-stayed bridge. In this model, the initial cable forces serve as independent variables of the response surface, while the total strain energy and maximum vertical displacement at mid-span function as dependent variables.

To ensure the adjusted cable force values remain aligned with actual conditions, the initial design cable forces for the bridge-completed state are systematically modified by applying incremental adjustments of ±10% to each stay cable’s target force value, with the corresponding total strain energy and maximum vertical displacement recorded as sample points after each adjustment. These sample points are then used to construct an approximate functional relationship between the optimization objectives and cable force variables through the response surface method.

The initial cable forces of all stay cables in the cable-stayed bridge are selected as design variables for optimization calculation, denoted as X = (x₁, x₂, …, x_i, …, x_n), where x_i (I = 1, 2, …, n) represents the initial cable force of the i-th stay cable, and n is the total number of stay cables in the entire bridge, where n = 48. With the optimization objectives defined as the total strain energy U and maximum vertical displacement y at mid-span of the main girder, and the initial cable forces of stay cables selected as design variables, the response surface method is applied to establish the optimization objective function for the ring-shaped pylon cable-stayed bridge. In this formulation, the initial cable forces act as independent variables of the response surface, while the total strain energy and maximum vertical displacement at mid-span serve as dependent variables.

The specific implementation steps are as follows:

(1)

Sample point generation: Based on the original design of initial cable forces, adjust the initial cable force value of each stay cable sequentially within a variation range of ±10%. After each adjustment, calculate the total strain energy U of the bridge and the maximum vertical displacement y at mid-span of the main girder using the finite element model, and record these data as sample points.

(2)

Response surface fitting: Using the generated sample points, construct an approximate functional relationship between the optimization objective function and the initial cable force variables through the response surface method. The commonly used response surface fitting function is a quadratic polynomial with the following form:

$$U=a_0+\sum _{i=1}^n\left(a_i{x}_i+a_{ii}{x}_i^2\right)$$

(8)

$$y=b_0+\sum _{i=1}^n\left(b_i{x}_i+b_{ii}{x}_i^2\right)$$

(9)

In the equation, U and y represent the total strain energy of the bridge and the maximum vertical displacement at mid-span of the main girder under specific initial cable forces, respectively; x_i represents the initial cable force of stay cables; a₀ and b₀ are constant terms in the response surface function; a_i and b_i are coefficients of the first-order terms in the corresponding response surface function; and a_ii and b_ii are coefficients of the second-order terms in the corresponding response surface function. As illustrated in Figure 5, this diagram depicts the step-by-step flow from finite element analysis sampling to response surface function fitting procedures.

3.4. Cable Force Optimization Based on MOPSO Algorithm

Based on the Particle Swarm Optimization framework and considering the special requirements of multi-objective optimization, the multi-objective search is achieved by maintaining a non-dominated solution set (Pareto front) and balancing solution diversity. The specific steps are as follows:

(1)

Set the MOPSO algorithm parameters, including acceleration constants, inertia coefficients, population size, position and velocity limits, and maximum algorithm iterations.

(2)

Use the design cable force values as initial cable forces, and randomly generate an initial population where each particle’s position x_i represents a set of cable force values X = (x₁, x₂, …, x_i, …, x_n).

(3)

Calculate the fitness value (total bridge strain energy U and mid-span displacement y) for each particle using the response surface equation (as a substitute for finite element models). Initialize the personal best position p_best as the current particle position, and initialize the external archive set as an empty set.

(4)

Adjust particle states according to the MOPSO velocity and position update formulas.

(5)

Substitute the updated cable force values into the response surface equation to directly calculate the total bridge strain energy and mid-span displacement, avoiding calls to finite element models.

(6)

Compare the current particle swarm solutions with those in the external archive set to screen for Pareto-optimal solutions.

(7)

If the current particle position is better than the historical optimum, update p_best and select a global guide g_best from the external archive set to balance convergence and diversity.

(8)

Terminate iterations when reaching maximum iterations or solution set convergence. Output the Pareto-optimal solution set and select the final optimal solution through normalized weighted scoring method.

The main parameter settings of the algorithm are shown in

Table 2. Main parameters of the MOPSO algorithm.

ω	c1	c2	n	υdmax	υdmin
0.7298	1.49618	1.49618	14	400	−400

. The inertia weight coefficient and acceleration constants c₁ and c₂ adopt the recommended values from the work of Vandenbergh et al. [21]. The population size n is set to 14, which ensures algorithm performance while maintaining computational efficiency. The particle velocity υ_id is constrained within the range of [−400, 400] to prevent particles from deviating from the feasible region due to excessive velocity during the search process, thereby ensuring optimization stability. The specific algorithm process is shown in Figure 6.

The maximum number of iterations is set to 800, which guarantees algorithm convergence within a reasonable timeframe while avoiding unnecessary computational resource consumption caused by excessive iterations. The cable force optimization of the cable-stayed bridge is performed based on the designed initial cable forces. To ensure that the optimized cable forces do not deviate significantly from the design values, the initial cable forces are allowed to fluctuate within ±10%, meaning the optimized cable forces are constrained to the range of [0.9T_i, 1.1T_i]. This constraint condition ensures the optimization results remain within engineering-acceptable limits while preventing excessive cable force adjustments that could compromise structural safety.

4. Optimization Results and Analysis

The proposed cable force optimization method was implemented using MATLAB 2021a to program the multi-objective particle swarm algorithm, which was combined with the established response surface function to optimize the bridge’s initial cable forces. The resulting Pareto front solution set is shown in Figure 7.

The Pareto solution set shown in the figure exhibits typical nonlinear distribution characteristics. In the strain energy–vertical displacement coordinate system, the solution set forms a continuous and smooth convex frontier curve, clearly demonstrating a significant trade-off relationship between the two optimization objectives.

Specifically, when the strain energy decreases to a certain critical value, further optimization of strain energy (i.e., further reduction) will cause a sharp increase in mid-span vertical displacement. This indicates that in this region, the optimization process achieves significant strain energy reduction at the cost of increased mid-span displacement. Conversely, when the mid-span vertical displacement decreases to a certain critical value, further optimization of vertical displacement (i.e., further reduction) will lead to a sharp increase in strain energy. This shows that in this region, the optimization process obtains significant improvement in mid-span displacement at the expense of increased strain energy. This trade-off relationship reflects the essential complexity of multi-objective optimization problems.

4.1. Optimal Solution Selection

In multi-objective optimization problems, since different objective functions may have significant differences in dimensions, value ranges, or importance, directly applying simple weighting to the objectives would bias the optimization process toward certain specific objectives, thereby affecting the rationality and practicality of the optimization results. To solve this problem, this paper normalizes the obtained Pareto front solution set. First, using the strain energy U and mid-span vertical displacement y under design cable forces as benchmarks, each solution in the Pareto front solution set is normalized to achieve dimensional consistency. Then, each objective is assigned a weight, with the weight values determined based on the importance of the objectives. Finally, Select the solution with the lowest score as the optimal solution [22], the score S_i of each Pareto front solution is calculated according to the following equation:

$$S_i={\omega }_1{\displaystyle \frac{U_{pi}}{U_0}}+{\omega }_2{\displaystyle \frac{y_{pi}}{y_0}}$$

(10)

where S_i is the score of each Pareto front solution; ω₁ and ω₂ are weighting coefficients, with ω₁ + ω₂ = 1; U_pi and y_pi are the strain energy and maximum mid-span vertical displacement calculated for each Pareto front solution; and U₀ and y₀ are the strain energy and maximum mid-span vertical displacement under design cable forces.

Under the design cable forces, the internal force distribution of the main girder shows significant non-uniformity, with large bending moment values (maximum reaching 259,206 kN·m). This stress state may lead to local stress concentrations, increasing the risk of structural fatigue failure while affecting the bridge’s overall performance and safety. Therefore, the total bridge strain energy is taken as the primary optimization objective to improve the uniformity of internal force distribution, reduce stress concentrations, and enhance the structure’s overall stiffness. To properly balance the relationship between strain energy and mid-span vertical displacement in multi-objective optimization, the weighting coefficients are selected as ω₁ = 0.7 (corresponding to total bridge strain energy) and ω₂ = 0.3 (corresponding to mid-span vertical displacement). The calculation results are shown in Figure 8, where the solution with the smallest weighted score is selected as the final optimal solution.

4.2. Analysis of Optimization Results

The cable force values of the optimal solution were input into Midas Civil NX finite element software for operational analysis. The initial cable forces before and after optimization are shown in Figure 9.

Analysis of the optimized cable force adjustment characteristics reveals that the post-optimization cable forces fluctuate within the range of [0.92T_i, 1.08T_i], strictly complying with the ±10% constraint relative to the design cable forces, thereby ensuring engineering feasibility and safety of the optimization results. Specifically, the cable forces in shorter cables proximal to the pylon exhibit intensified magnitudes, with increases in the range of 5% to 8%. Conversely, longer cables in the mid-span region show moderated reductions in cable forces, decreasing by 6% to 9%.

This adjustment pattern demonstrates strong consistency with structural mechanical principles: The enhanced forces in short cables significantly improve the restraint stiffness at the pylon–girder connections, effectively controlling mid-span vertical displacements and consequently improving the bridge’s overall deformation performance. Meanwhile, the moderate force reduction in long cables decreases axial compression in the main-span steel segments, preventing local stress exceedance and reducing stress concentration phenomena, which collectively enhance the structure’s fatigue resistance.

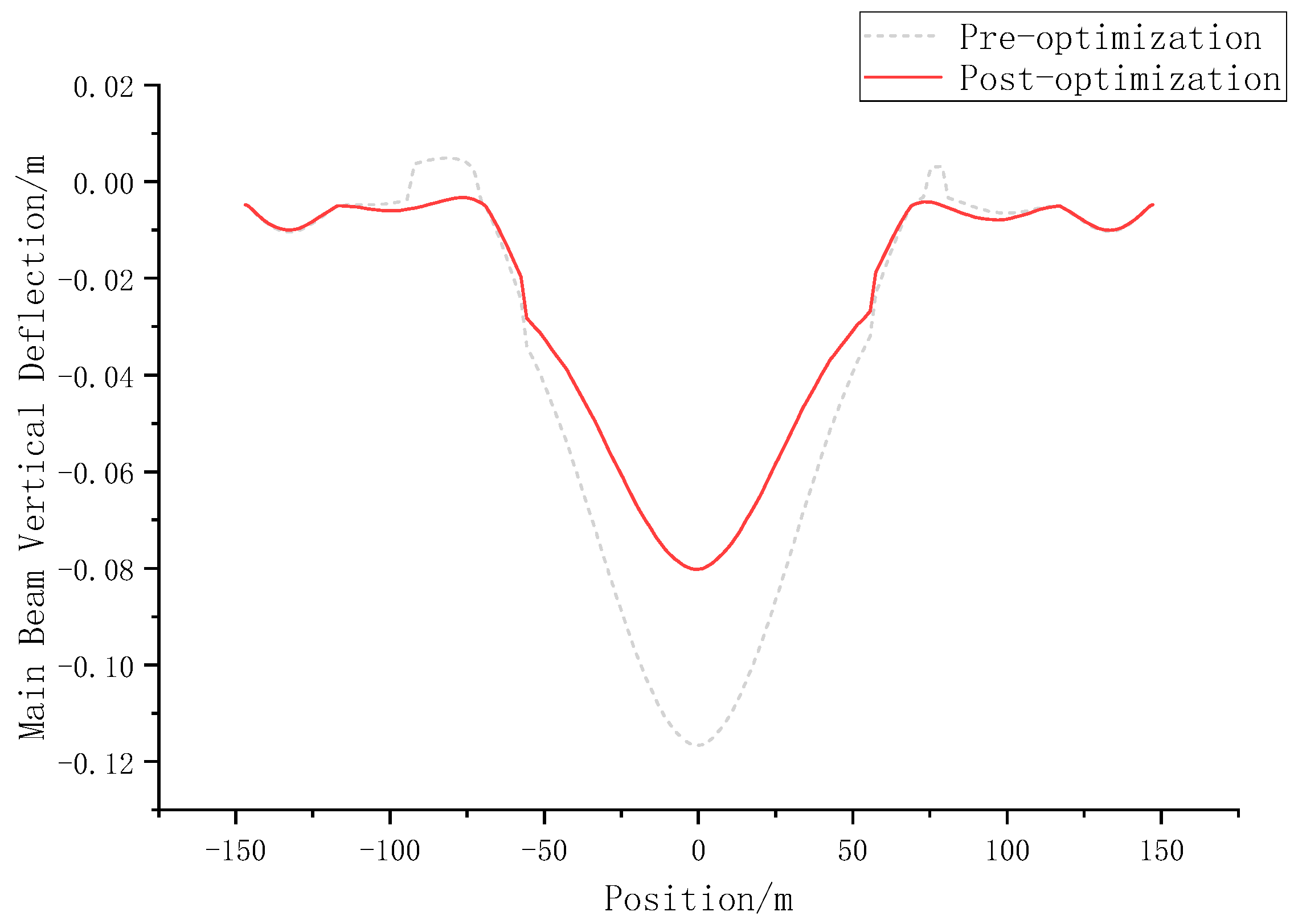
Figure 10 and Figure 11 show the comparison of bending moments and vertical displacements before and after optimization obtained through finite element analysis. The verification results show that the maximum bending moment of the optimized main girder decreased from 259,205 kN·m to 236,647 kN·m, a reduction of 8.7%, with more uniform moment distribution, indicating significantly improved fatigue resistance of the structure. In addition, calculations using the strain energy formula show that the total strain energy of the bridge decreased from 1600.7388 kJ to 1487.4116 kJ, a reduction of 7.1%, while the maximum vertical displacement at mid-span decreased from 0.11669 m to 0.08030 m, a reduction of 31.2%. These data indicate that the optimized structure has achieved significant improvements in both strain energy and deformation performance. By optimizing the cable force distribution, the bending moment distribution of the main girder becomes more uniform, reducing local stress concentrations and thereby improving the fatigue resistance and service life of the structure. The significant reduction in vertical displacement at mid-span after optimization indicates that the overall stiffness of the bridge has been enhanced, enabling it to better resist deformation under external loads and ensuring structural safety and service performance.

4.3. Comparison of Response Surface Model Prediction Results

The optimal solution was input into the response surface function to calculate the total bridge strain energy and maximum mid-span vertical displacement. These calculated results were then compared with those obtained from actual finite element analysis, as shown in the

Table 3. Comparison of response surface function and finite element analysis results.

	Response Surface Function Calculation	Finite Element Analysis Calculation	Error
Total bridge strain energy/KJ	1482.2116	1487.4116	0.35%
Maximum vertical displacement at mid-span/m	0.08463	0.08030	5.1%

.

The comparison results show that the response surface model’s prediction error for total bridge strain energy is only 0.35%, indicating that the explicit surrogate model based on strain energy has extremely high fitting accuracy and can accurately reflect the bridge’s stress state. However, the prediction error for maximum mid-span vertical displacement is 5.1%, slightly higher than the strain energy error. This difference is mainly due to the nonlinear sensitivity of the displacement field to cable force adjustments, where the response relationship is more complex, resulting in relatively larger prediction errors.

According to China’s Bridge Design Code JTG D60-2015 [23], the allowable vertical deflection at mid-span under dead load is strictly limited to one-five-hundredth of the span length (for this bridge with a 138 m span, corresponding to a limit of 0.276 m). The mid-span deflection predicted by the response surface method is 0.08463 m, showing a mere 5.1% relative deviation from the high-fidelity finite element analysis result of 0.08030 m, with an absolute error of 0.00433 m. This absolute error constitutes only 1.57% of the code-specified limit—significantly below the required engineering safety margin. While minor local deviations exist in the prediction, the response surface model achieves substantial computational efficiency gains by reducing finite element iterations, and the required number of finite element analyses was slashed from 800 invocations to 97 computations, thus validating its practicality and reliability for static performance optimization.

By explicitly formulating the objective function, the response surface model greatly reduces single-optimization computation time, avoiding the high computational costs associated with frequent finite element model calls in traditional methods. The comparative data prove that this approach can meet the engineering accuracy requirements for multi-objective optimization of special-shaped cable-stayed bridges while ensuring computational efficiency.

5. Conclusions

This paper proposes an efficient optimization method based on Response Surface Methodology and a multi-objective particle swarm algorithm for cable force optimization of circular pylon cable-stayed bridges, and verifies its feasibility and superiority through practical engineering cases. The main conclusions are summarized as follows:

(1)

To address the inefficiency of traditional intelligent optimization algorithms that require frequent finite element calculations in complex cable-stayed bridge optimization, this study introduces Response Surface Methodology to explicitly express the implicit relationship between optimization objectives and cable forces using quadratic polynomials. Combined with Multi-Objective Particle Swarm Optimization (MOPSO), this approach achieves efficient optimization of design variables while significantly reducing computational costs. The synergistic application preserves MOPSO’s global optimization capability for multi-objective problems while reducing finite element calls through the response surface model, providing an efficient and reliable new approach for cable force optimization.

(2)

Practical engineering case verification demonstrates the effectiveness of the proposed method. The optimized maximum girder bending moment decreased from 259,205 kN·m to 236,647 kN·m (8.7% reduction), while the maximum mid-span vertical displacement decreased from 116.6940 mm to 80.3024 mm (31.2% reduction). The optimal solution shows this collaborative optimization not only improves moment distribution uniformity and reduces local stress concentrations, but also significantly enhances overall structural stiffness, ensuring bridge safety and durability.

(3)

The response surface surrogate model achieves a remarkably low prediction error of 0.35% for full-bridge strain energy, validating its exceptional engineering practicality in structural design. By establishing explicit mathematical relationships, this model efficiently maps the intricate correlations between cable forces and strain energy, thereby supplanting computation-intensive resources traditionally required for finite element analysis. Leveraging this surrogate framework, engineers can rapidly optimize cable forces while ensuring safety reliability, substantially advancing design efficiency for complex bridge projects.

(4)

The 5.1% displacement prediction error, slightly higher than strain energy error, relates directly to displacement field’s nonlinear sensitivity to cable force adjustments. Despite localized errors, the model demonstrates remarkable computational efficiency by substantially reducing single optimization time. Comparative data confirm the method meets engineering accuracy requirements for multi-objective cable-stayed bridge optimization while maintaining computational efficiency, providing reliable technical support for complex bridge optimization design.

Future research will extend this methodology to diverse pylon structural configurations, rigorously examining its adaptability across varying geometries. Concurrently, by integrating construction phase optimization strategies, the approach ensures seamless mechanical continuity between distinct construction phases and permanent service states, thereby enhancing the engineering utility of this design framework. These extensions will propel the Response Surface Methodology–Multi-objective Particle Swarm Optimization framework toward evolution as a versatile powerful toolkit for next-generation cable-stayed bridge design and analysis.