Effect of Systematic Errors on Building Component Sound Insulation Measurements Using Near-Field Acoustic Holography

Abstract

Near-field acoustic holography (NAH) provides an effective way to achieve wide-band, high-resolution visualization measurement of the sound insulation performance of building components. However, based on Green’s function, the microphone array’s inherent amplitude and phase mismatch errors will exponentially amplify the sound field inversion process, significantly reducing the measurement accuracy. To systematically evaluate this problem, this study combines numerical simulation with actual measurements in a soundproof room that complies with the ISO 10140 standard, quantitatively analyzes the influence of array system errors on NAH reconstructed sound insulation and acoustic images, and proposes an error correction strategy based on channel transfer function normalization. The research results show that when the array amplitude and phase mismatch mean values are controlled within 5% and 5°, respectively, the deviation of the weighted sound insulation measured by NAH can be controlled within 1 dB, and the error in the key frequency band of building sound insulation (200–1.6k Hz) does not exceed 1.5 dB; when the mismatch mean value increases to 10% and 10°, the deviation of the weighted sound insulation can reach 2 dB, and the error in the high-frequency band (≥1.6k Hz) significantly increases to more than 2.0 dB. The sound image shows noticeable spatial distortion in the frequency band above 250 Hz. After applying the proposed correction method, the NAH measurement results of the domestic microphone array are highly consistent with the weighted sound insulation measured by the standard method, and the measurement difference in the key frequency band is less than 1.0 dB, which significantly improves the reliability and applicability of low-cost equipment in engineering applications. In addition, the study reveals the inherent mechanism of differential amplification of system errors in the propagating wave and evanescent wave channels. It provides quantitative thresholds and operational guidance for instrument selection, array calibration, and error compensation of NAH technology in building sound insulation detection.

1. Introduction

Lee and Williams proposed near-field acoustic holography (NAH) in the 1980s [1]. Its core idea is to obtain complex sound pressure or particle velocity distribution in the near field of the sound source and reconstruct the three-dimensional sound field through wavenumber domain spatial transformation to realize the visualization of sound pressure, velocity, sound intensity, and radiation power [2]. After more than 40 years of development, NAH has formed a relatively mature technical system for diagnosing noise in automobiles [3], aerospace [4], and electromechanical equipment [5], especially in the localization of noise sources [6] and mechanical fault warnings [7], showing the unique advantages of high spatial resolution and wide bandwidth. However, systematic research is still relatively scarce in architectural acoustics, especially in measuring airborne sound insulation and defect location of building components.

Traditional sound insulation measurement mainly adopts the sound pressure difference method [8] and the sound intensity method [9]. The former evaluates the sound insulation by comparing the average sound pressure level difference between the source room and the receiving room. Although the equipment is universal and easy to operate, it is sensitive to reverberation conditions and background noise, and it is difficult to reflect local defects [10,11,12]. The latter uses point-by-point scanning sound intensity to infer the radiation power, which can suppress background noise to a certain extent. However, the test cycle is long, and real-time imaging is not possible [13,14,15]. Asadi Jafari et al. [16] Conducted a wide-band sound insulation study on the composite shell of the double curvature truss core, which showed that the promotion of new lightweight composite components further highlighted the need for rapid and accurate evaluation of sound insulation performance in complex sound fields. At the same time, the widespread application of composite components in green buildings has put forward higher requirements for the measured sound environment indicators in the green building evaluation system. In this context, the NAH sound insulation measurement method, which can achieve rapid on-site evaluation, has shown significant engineering value and application potential. NAH relies on an array to collect the radiated near-field complex sound pressure at one time and reconstructs the surface normal sound intensity field through wavenumber domain inversion [17,18]. It can not only obtain the full-band sound insulation but also output high-resolution two-dimensional sound images in real time, thereby simultaneously completing the sound insulation level assessment and defect location in one measurement [19,20,21].

However, the measurement accuracy of NAH is highly sensitive to the array aperture, sampling spacing, and measurement signal-to-noise ratio [22,23,24]. Especially in the test scenario of building components with large aperture and dense sampling, due to the manufacturing tolerance of microphones, installation errors, and inconsistency of electronic links, the channels of the holographic array inevitably have amplitude and phase mismatches [25]. This type of system error will be exponentially amplified in Green’s function inversion. It will have a cumulative effect on the reconstruction results, far exceeding the influence of random noise [26,27,28]. Existing studies have shown that system errors will distort the complex sound pressure angular spectrum, causing the reconstruction of normal sound intensity to have different degrees of deviation in the high-frequency band dominated by propagating waves and the low-frequency band dominated by evanescent waves [29]; however, there is still a lack of quantitative analysis of the frequency domain characteristics and threshold laws of the dual indicators of sound insulation (reconstruction of average normal sound intensity level) and acoustic image (reconstruction of normal sound intensity level distribution).

In response to the above problems, the academic community has proposed various error suppression methods, such as transfer function normalization, array posture adaptive correction, and Bayesian regularization [30]. Among them, the amplitude and phase normalization strategy based on the channel transfer function has attracted widespread attention due to its low implementation cost and strong online operability [31,32,33]. However, most existing results focus on noise source identification and mechanical fault diagnosis. For the measurement scenarios of building components with wide bandwidth, large size, and intense reflection, there is still no unified understanding of their scope of application and residual error.

This paper discusses the influence mechanism of array system error on measurement accuracy at three levels: theory, simulation, and measurement. It also proposes targeted correction strategies to improve the reliability of NAH sound insulation measurement technology in engineering applications. First, a large-aperture NAH measurement framework suitable for building components is constructed, and the complete process of signal acquisition, complex sound pressure calculation, sound field reconstruction, and sound insulation index extraction is given; secondly, through the simulation of the ideal point sound source model in the 1/3 octave band of 100–3.15k Hz, the frequency domain evolution law of amplitude and phase mismatch on the average normal sound intensity level and sound image error is analyzed; thirdly, comparative experiments are carried out in a soundproof room that meets the ISO 10140 standard to verify the system error threshold and correction effect, and evaluate the applicability of domestic low-cost arrays; finally, the linear amplification of system error with frequency and the differentiated sensitivity of propagating waves and evanescent waves are discussed, and array calibration and error compensation suggestions for field applications are given. The research conclusions can provide a theoretical basis and operational specifications for the engineering promotion of NAH in building sound insulation testing.

2. NAH Sound Insulation Measurement Principle

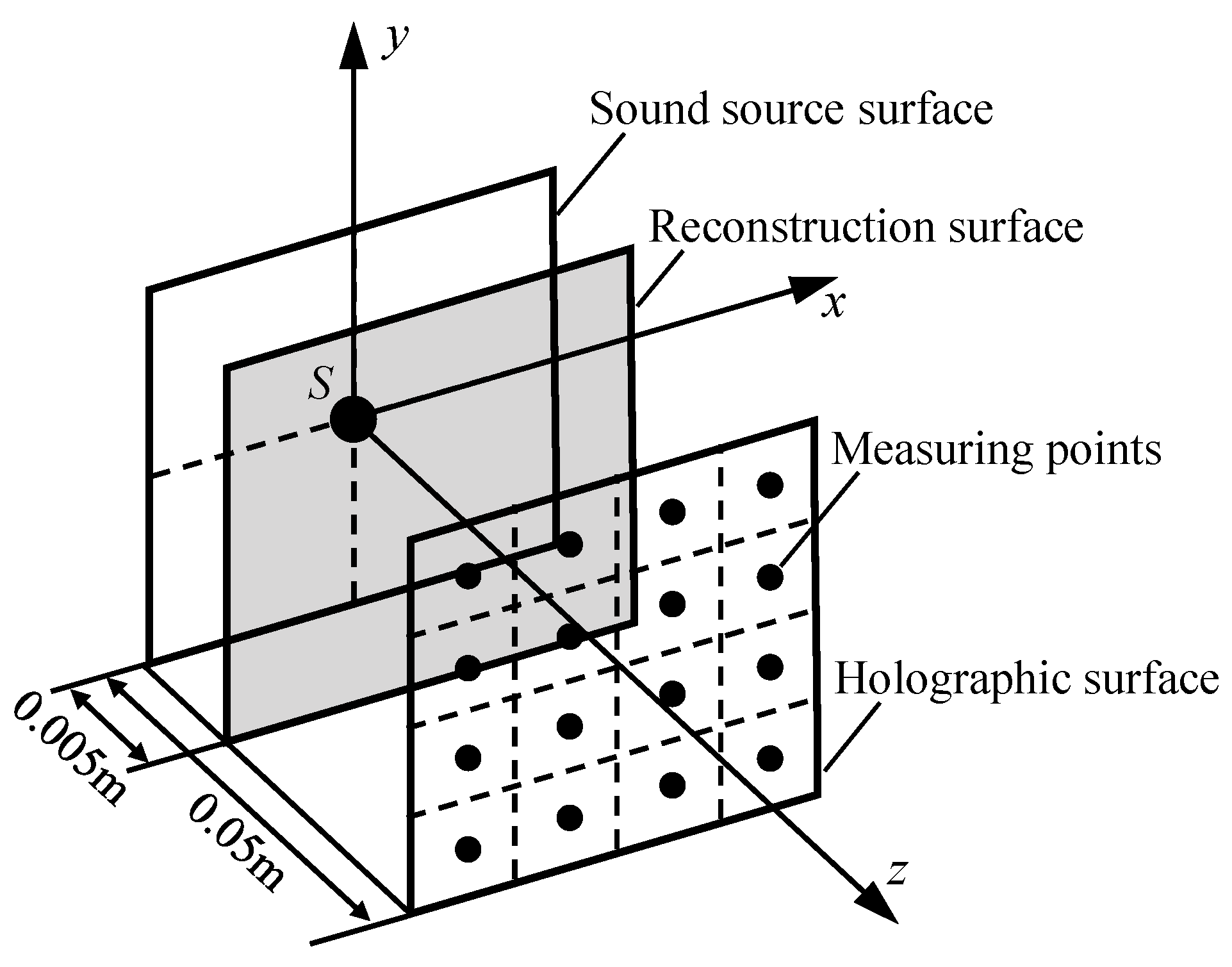
Figure 1 shows the basic NAH measurement of building component sound insulation. First, a microphone array is arranged in the near field of component radiation to directly obtain the complex sound pressure distribution of the holographic surface; then, the sound field is reversed in the wave number domain to reconstruct the normal active sound intensity field on the component surface, and the overall sound insulation and the location of sound insulation defects are obtained at the same time. The process can be divided into four steps: “signal acquisition, complex sound pressure determination, sound field reconstruction, and sound insulation evaluation”. It not only retains the full-frequency monitoring of incident sound energy by the sound pressure method but also inherits the direct measurement of radiation energy flow by the sound intensity method, realizing the integration of quantitative evaluation and visual diagnosis.

(1)

Signal acquisition

The measurement signal consists of two parts: the time domain sound pressure $P_N\left(t\right)$ at several representative points in the sound source room, which is obtained by fast Fourier transform (FFT) and energy averaging to obtain the indoor average sound pressure level $L_{\mathrm{P}}\left(f_{\mathrm{m}}\right)$, which is used to estimate the incident sound power; the sound pressure $P_{\mathrm{H}}\left(l_1,l_2,t\right)$ recorded by the microphone array on the holographic surface of the receiving room and the reference channel sound pressure $P_{\mathrm{C}}\left(t\right)$. The holographic hole diameter must completely cover the projected area of the component, and the test distance and the distance between the test points should meet the spatial Nyquist condition of $\Delta x=\Delta y={\lambda }_{\min }/2$ to ensure that the propagating wave and the evanescent wave at the highest analysis frequency are fully sampled.

(2)

Solution of holographic surface complex sound pressure

In the frequency domain, the holographic surface complex sound pressure can be expressed as:

$$P_{\mathrm{H}}\left(l_1,l_2,f\right)=\left|P_{\mathrm{H}}\left(l_1,l_2,f\right)\right|e^{j\phi (l_1,l_2,f)},$$

(1)

$\left|P_{\mathrm{H}}\left(l_1,l_2,f\right)\right|$ and $\phi \left(l_1,l_2,f\right)$ are the amplitude distribution and phase distribution of the holographic surface complex sound pressure, respectively; $l_1,l_2$ = 1, 2, …, n represent the serial numbers of the holographic measurement points and the sound field reconstruction points in the $x$ and $y$ directions of the real number domain. The amplitude is obtained by the auto-power spectrum of the time domain signal of each measurement point on the holographic surface, and the cross-power spectrum of the time domain signal of each measurement point and the reference signal calculates the phase:

$$\left|P_{\mathrm{H}}\left(l_1,l_2,f\right)\right|=\sqrt{S_x\left(l_1,l_2,f\right)},$$

(2)

$$\phi \left(l_1,l_2,f\right)=\arctan \left\{{\displaystyle \frac{\mathrm{Im}\left[S_{xy}\left(l_1,l_2,f\right)\right]}{\mathrm{Re}\left[S_{xy}\left(l_1,l_2,f\right)\right]}}\right\},$$

(3)

“Re” and “Im” represent the real part and imaginary part of the complex function, respectively; $S_x$ is the unilateral auto-power spectrum density function of the sound pressure of each channel of the holographic surface; $S_{xy}$ is the unilateral cross-power spectrum density function of the sound pressure of each channel and the reference sound pressure.

(3)

Sound field reconstruction

First, the complex sound pressure matrix is zero-filled to avoid convolution aliasing. Then, a two-dimensional discrete Fourier transform (DFT) is performed to obtain the angular spectrum ${\widehat{P}}_{\mathrm{H}}\left(k_1,k_2,f\right)$. In the wavenumber domain, the Rayleigh first integral can be used to establish the transfer relationship between the angular spectrum of the complex sound pressure on the holographic surface and the component surface:

$$P_{\mathrm{S}}\left(l_1,l_2,f\right)=\mathrm{IDFT}\left\{\mathrm{DFT}\left[P_{\mathrm{H}}\left(l_1,l_2,f\right)\right]·{\widehat{G}}^{-1}\left(k_1,k_2,f\right)·W\left(k_1,k_2,f\right)\right\},$$

(4)

“DFT” {·} and “IDFT” {·} represent two-dimensional Fourier transform and inverse transform, respectively; ${\widehat{G}}^{-1}$ is the Green function. $W$ is a constrained least squares window that suppresses high wave number noise and retains practical evanescent wave information. The normal velocity angular spectrum ${\widehat{U}}_{\mathrm{S}}$ is obtained through the Euler equation. Then, the two-dimensional inverse DFT restores the spatial domain complex sound pressure $P_{\mathrm{S}}$ and velocity $U_{\mathrm{S}}$. The coupling of the two can obtain the normal active sound intensity distribution on the component surface:

$$U_{\mathrm{S}}\left(l_1,l_2,f\right)=\mathrm{IDFT}\left\{{\displaystyle \frac{k_{\mathrm{z}}}{{\rho }_0{c}_{0}k}}·\mathrm{DFT}\left[P_{\mathrm{S}}\left(l_1,l_2,f\right)\right]\right\},$$

(5)

$$I_{\mathrm{S}}\left(l_1,l_2,f\right)={\displaystyle \frac{1}{2}}\mathrm{Re}\left[P_{\mathrm{S}}\left(l_1,l_2,f\right)·{U_{\mathrm{S}}}^{\ast }\left(l_1,l_2,f\right)\right],$$

(6)

where ${\rho }_0$ is the air density; $c_0$ is the sound speed in the air; $k_{\mathrm{z}}$ is the standard component of the sound wave number $k$; “*” represents the complex conjugate operator. The expression of $W$ is:

$$W\left(k_1,k_2\right)=\left\{\begin{array}{ll}\begin{array}{c}\left\{\begin{array}{cc}1-0.5\exp \left[\left(k_r/k_c-1\right)/\alpha \right]\hfill & k_r\le k_c\hfill \\ 0.5\exp \left[\left(1-k_r/k_c\right)/\alpha \right]\hfill & k_r>k_c\hfill \end{array}\right.\end{array}& z_h\le {\displaystyle \frac{\lambda }{3}}\hfill \\ \begin{array}{l}\left\{\begin{array}{ll}1& k_r\le k_c\\ 0& k_r>k_c\end{array}\right.\end{array}\hfill & z_h\le {\displaystyle \frac{\lambda }{3}}\hfill \end{array}\right.,$$

(7)

where the radius of the radiation circle $k_r=\sqrt{{\left(k_1\Delta k_x\right)}^2+{\left(k_2\Delta k_y\right)}^2}$, $k_1$ and $k_2$ represent the sampling numbers in the $x$ and $y$ directions in the wave number domain, respectively, $\Delta k_x$ and $\Delta k_y$ are the sampling intervals in the $x$ and $y$ directions in the wave number domain, respectively, where $\Delta k_x=\pi /L_x,\Delta k_y=\pi /L_y$, $L_x$ and $L_y$ are the measurement apertures in the $x$ and $y$ directions of the holographic surface, respectively; $k_{\mathrm{c}}=0.6\pi /\Delta \mathrm{x}$, where $\Delta \mathrm{x}$ is the sampling interval; the steepness coefficient $\alpha$ is 0.2; $z_h$ is the distance between the holographic surface and the component surface; $\lambda$ is the wavelength of the sound wave.

Since the holographic surface measures complex sound pressure data, the ${\widehat{G}}^{-1}$ used for sound field reconstruction is based on Green’s function under the Dirichlet boundary condition. ${\widehat{G}}^{-1}$ is obtained by the wavenumber domain spatial sampling method:

$${\widehat{G}}^{-1}\left(k_1,k_2,f\right)=\left\{\begin{array}{cc}\exp \left(-jd\sqrt{k^2-k_r^2}\right)& k_r\le k\\ \exp \left(d\sqrt{k_r{}^2-k^2}\right)& k_r>k\end{array}\right.,$$

(8)

$d$ is the sound field reconstruction distance.

(4)

Sound insulation evaluation and defect diagnosis

The narrowband sound intensity is integrated according to the 1/3 octave to obtain the normal sound intensity level distribution $I_{\mathrm{S}}\left(l_1,l_2,f_m\right)$. Its two-dimensional mapping is the sound image, and the energy hot spots correspond to the sound leakage path and weak parts. The surface average normal sound intensity level $L_I\left(f_m\right)$ is obtained by spatial averaging $I_{\mathrm{S}}\left(l_1,l_2,f_m\right)$ and then combined with the sound source side $L_{\mathrm{P}}\left(f_{\mathrm{m}}\right)$ according to the ISO 15186 sound intensity method formula to obtain the sound insulation curve $R\left(f_{\mathrm{m}}\right)$, and calculate the weighted sound insulation $R_{\mathrm{W}}$ and spectrum correction $C$, $C_{\mathrm{tr}}$

$$R\left(f_{\mathrm{m}}\right)=L_P\left(f_{\mathrm{m}}\right)-L_I\left(f_{\mathrm{m}}\right)+10\lg \left({\displaystyle \frac{S_{\mathrm{m}}}{S}}\right)-6,$$

(9)

where $f_{\mathrm{m}}$ is the 1/3 octave center frequency; $S_m$ is the reconstruction surface area; $S$ is the component area.

Compared with the traditional sound pressure method, the NAH method of sound insulation measurement not only eliminates the strict restrictions on the uniformity of reverberation and background noise in the receiving room but also can output the full-frequency sound insulation and high-resolution sound image synchronously in a single measurement; compared with the point scanning sound intensity method, its array sampling significantly shortens the test time and avoids the accumulation of scanning errors. It should be noted that the array amplitude and phase mismatch will be exponentially amplified in the wavenumber domain inversion link, so it is necessary to study the impact of system errors to ensure the reliability of sound insulation measurement and defect location.

3. Numerical Simulations

3.1. Simulation Settings

In order to quantitatively reveal the influence of system errors on the accuracy of NAH sound insulation measurement, this section constructs an ideal point sound source model on the MATLAB (v2022) platform. It performs sound field reconstruction calculations in the range of 100–3.15k Hz according to the 1/3 octave division recommended by ISO 10140. The simulation parameters and geometric relationships are shown in Figure 2: the point sound source $S$ with a radius of 0.001 m and a normal vibration velocity of 2.5 m/s is located at the origin of the coordinate system; the holographic surface is set at $z_{\mathrm{h}}$ = 0.05 m, the sampling grid $N_1$ × $N_2$ = 40 × 40, and the spacing $\Delta \mathrm{x}$ = $\Delta y$ = 0.045 m; the reconstruction surface is set at $z_{\mathrm{S}}$ = 0.005 m, and the grid is consistent with the holographic surface. The reconstruction distance and sampling spacing are less than the half-wavelength of the highest frequency ${\lambda }_{\min }/2$ ≈ 0.048 m. This can effectively avoid spatial aliasing and ensure that the evanescent wave information is not distorted.

To simulate the array amplitude and phase mismatch, the amplitude mismatch errors ${\epsilon }_a\sim N\left({\mu }_a,{\sigma }_a^2\right)$ and phase mismatch errors ${\epsilon }_{\phi }\sim N\left({\mu }_{\phi },{\sigma }_{\phi }^2\right)$ are randomly extracted from the normal distribution and kept constant in the whole frequency band. Three groups of means $\left({\mu }_a,{\mu }_{\phi }\right)$ = (0%, 0°), (5%, 5°), (10%, 10°) are selected, and the standard deviations $\left({\sigma }_a,{\sigma }_{\phi }\right)$ are unified as (5%, 5°), corresponding to working conditions I, II, and III, respectively, and consistent with subsequent experiments. The complex sound pressure of the holographic surface with systematic error is:

$${\tilde{P}}_{\mathrm{H}}\left(l_1,l_2,f\right)=P_H\left(l_1,l_2,f\right)\left[1+{\epsilon }_a\left(l_1,l_2,f\right)\right]\exp \left[j{\epsilon }_{\phi }\left(l_1,l_2,f\right)\right],$$

(10)

where $P_{\mathrm{H}}$ is the theoretical value, ${\tilde{P}}_{\mathrm{H}}$ and $P_{\mathrm{H}}$ are input into the wavenumber domain inversion algorithm to obtain two groups of normal sound intensity fields; ${\tilde{I}}_{\mathrm{S}}$ and $I_{\mathrm{S}}$, with and without systematic errors. The evaluation index is:

$$err{L}_I\left(f_{\mathrm{m}}\right)=\left|L_I{}^R\left(f_{\mathrm{m}}\right)-L_I{}^T\left(f_{\mathrm{m}}\right)\right|,$$

(11)

$$err{I}_S\left(f_{\mathrm{m}}\right)={\displaystyle \frac{1}{N_1\times N_2}}{\displaystyle \sum _{l_1=1}^{N_1}{\displaystyle \sum _{l_2=1}^{N_2}\left|I_S{}^R\left(l_1,l_2,f_{\mathrm{m}}\right)-I_S{}^T\left(l_1,l_2,f_{\mathrm{m}}\right)\right|}},$$

(12)

where $err{L}_I$ and $err{I}_{\mathrm{S}}$ correspond to the average normal sound intensity level error and sound intensity distribution error, respectively. To ensure statistical robustness, each group of working conditions is repeated 50 times independently, and the average is taken.

3.2. Simulation Results and Analysis

Figure 3 shows the curves of $err{L}_I$ and $err{I}_{\mathrm{S}}$ changing with frequency under three working conditions. Through quantitative analysis, it is found that when the mean values of amplitude and phase mismatch are reduced from 10% and 10° to 5% and 5°, the $err{L}_I$ in the whole frequency band (100–3.15k Hz) is significantly reduced by 0.40–0.41 dB (mean value is 0.40 dB), and $err{I}_{\mathrm{S}}$ is reduced by 0.10–0.26 dB (mean value is 0.16 dB); when the ideal state (0%, 0°) is further achieved, the two errors are further reduced by 0.30–0.31 dB (mean value is 0.31 dB) and 0.03–0.19 dB (mean value is 0.10 dB), respectively. This law not only confirms that there is an approximately linear negative correlation between system error and measurement accuracy, but more importantly, it reveals that the amplitude-phase mismatch has a synchronous inhibitory effect on the energy-type index ($err{L}_I$) and the spatial distribution index ($err{I}_{\mathrm{S}}$).

In-depth research shows that $err{L}_I$ and $err{I}_{\mathrm{S}}$ present opposite frequency-varying characteristics: the former increases monotonically with increasing frequency, while the latter gradually decreases. This phenomenon originates from the differentiated action mechanism of propagation waves and evanescent waves in the process of sound field inversion. For $err{L}_I$, the amplitude of the error transfer function of its dominant factor propagation wave component increases linearly with frequency during the Green function inversion process, resulting in the amplification of high-frequency reconstruction errors. While $err{I}_{\mathrm{S}}$ is mainly affected by the evanescent wave, its energy decays exponentially with increasing frequency, which naturally reduces the distribution error in the high-frequency band. This complementary characteristic of “high-frequency energy sensitivity and low-frequency distribution sensitivity” provides important inspiration for the optimization of the NAH system. In engineering applications, the amplitude-phase consistency of different frequency bands needs to be optimized in a targeted manner according to specific measurement requirements (overall sound insulation evaluation or local defect diagnosis).

4. Experimental Study

To verify the conclusions of the numerical simulation and evaluate the engineering applicability of the error correction strategy, the double-layer hollow glass curtain wall (2.9 m × 2.7 m) was measured by the sound pressure method and the NAH method in parallel in the soundproof room of the National Key Laboratory of Subtropical Architecture and Urban Science of South China University of Technology (by ISO 10140 requirements). The measurement results of the sound pressure method were used as a reference to quantify the measurement deviation of the NAH method under actual system error conditions.

4.1. Experimental Setup

The experimental system and equipment layout are shown in Figure 4, respectively. The sound source room uses a 4296 regular dodecahedron loudspeaker (Brüel & Kjær, Hørsholm, Denmark) driven by a 2716 amplifier (Brüel & Kjær, Hørsholm, Denmark); the acoustic excitation signal uses a broadband white noise generated by Adobe Audition (v2022), which is input into the amplifier after D/A conversion by the sound card. The sound pressure level and reverberation time in the sound source room were measured by a 2270 sound level meter (Brüel & Kjær, Hørsholm, Denmark) and a 4189 microphone (Brüel & Kjær, Hørsholm, Denmark), respectively, and their uniformity and background noise meet the requirements of ISO 10140.

On one side of the receiving room, a 2.9 m × 2.7 m holographic measurement surface was arranged at 0.045 m from the outer surface of the specimen, with a grid spacing of $\Delta x$ = $\Delta y$ = 0.045 m, and a total of 64 × 60 measurement points. The reference channel selected a fixed point 0.1 m away from the curtain wall surface to ensure the stability of the holographic surface phase reference. The measurement system is based on the PXIe 1062Q chassis (NI, Austin, Texas, USA), equipped with a PXIe-8102 embedded controller (NI, Austin, Texas, USA) and equipped with PXIe-4497 (16 channels, 204.8 kS/s) and PXI-4461 (4 channels, 204.8 kS/s) data acquisition cards (NI, Austin, Texas, USA); the holographic surface signal acquisition uses a 16-channel linear array composed of MPA201 free-field microphones (BSWA, Beijing, China), and the reference signal acquisition uses a 46AE standard microphone (GRAS, Holstebro, Denmark). All channels synchronously collect 10 s time domain signals, and the LabVIEW program (v2022) completes FFT, complex sound pressure calculation, sound field reconstruction, and result visualization and outputs the sound insulation spectrum and two-dimensional sound image in real-time.

4.2. System Error Setting

Four working conditions are set to investigate the influence and correction effect of system error: Working conditions I–III are three groups of standard distribution mismatch matrices consistent with the simulation in Section 2 (mean 0%, 0°, 5%, 5°, 10%, 10°), with standard deviations of 5% and 5°; working condition IV is the actual mismatch matrix of the domestic MPA201 line array (BSWA, Beijing, China).

The transfer function method is used to calibrate the amplitude and phase in the full anechoic room (see Figure 5): GRAS 46AE is used as the reference channel, and each channel of the line array is placed in the same sound field as the reference in turn. The loudspeaker radiates steady-state white noise for 10 s, and the signal is synchronously collected. The amplitude and phase calibration factors are calculated using Equations (13) and (14).

$${\epsilon }_a\left(l_1,l_2,f\right)={\displaystyle \frac{\left|P_C\left(f\right)\right|}{\left|{\tilde{P}}_H\left(l_1,l_2,f\right)\right|}}-1,$$

(13)

$${\epsilon }_{\phi }\left(l_1,l_2,f\right)={\phi }_C\left(f\right)-\tilde{\phi }\left(l_1,l_2,f\right)$$

(14)

The amplitude and phase mismatch correction matrices of the microphone array obtained after calibration are shown in Figure 6 and Figure 7, respectively. In the range of 89–3.55k Hz (corresponding to 100–3.15k Hz 1/3 octave), the mean amplitude mismatch is −4 to 3%, the standard deviation is 2–7%, and the mean phase mismatch is −4 to 3°, and the standard deviation is 0–3°. The experiment uses the complex sound pressure before and after calibration for sound intensity reconstruction. It uses the calibration result as a reference without systematic error to calculate the measurement deviation of the sound insulation and the sound image, further verifying the effectiveness of the numerical simulation conclusion and calibration compensation. The calibration expression is as follows:

$$P_H\left(l_1,l_2,f\right)={\tilde{P}}_H\left(l_1,l_2,f\right)\left[1+{\epsilon }_a\left(l_1,l_2,f\right)\right]e^{j{\epsilon }_{\phi }(l_1,l_2,f)}.$$

(15)

4.3. Experimental Results

Figure 8 shows the $err{L}_I$ measured by NAH under four working conditions based on the calibration results. The analysis shows that when the mean amplitude and phase mismatch gradually decrease from 10% and 10° to 5% and 5°, the error in the 100–3.15k Hz test frequency band is significantly reduced by 0.37–0.44 dB (mean value is 0.41 dB); after the mean mismatch is further reduced to 0% and 0°, the error is further reduced by 0.35–0.38 dB (mean value is 0.36 dB). This linear decrease in error with the degree of mismatch indicates that the system error has a consistent effect on the measurement results of the entire frequency band, and this trend is consistent with the numerical simulation results. It is worth noting that although the error curve of the domestic microphone array (condition IV) is relatively close to that of working condition I, it shows a unique spectral characteristic: the measurement error in the high-frequency band ($f_{\mathrm{m}}$ ≥ 1.6 kHz) is significantly higher than that in the low-frequency band. This is directly related to the characteristic of the system error increasing with frequency revealed by the calibration data.

Figure 9 shows the deviation of the sound insulation frequency curve measured by NAH under different working conditions based on the ISO 10140 method. The weighted sound insulation $R_{\mathrm{W}}$ and spectrum correction $C$ and $C_{\mathrm{tr}}$ measured by the two methods are detailed in

Table 1. Comparison of weighted sound insulation measured by ISO 10140 and NAH.

Method	${\mathit{R}}_{\mathbf{W}}$ (dB)	$\mathit{C}$ (dB)	${\mathit{C}}_{\mathbf{tr}}$ (dB)
ISO 10140 method	41	−2	−6
NAH (calibrated)	41	−2	−6
NAH (Condition I)	41	−2	−6
NAH (Condition II)	42	−1	−6
NAH (Condition III)	43	−1	−5
NAH (Condition IV)	41	−1	−6

. The strictly calibrated line array maintains excellent consistency with the benchmark results in 100–3.15k Hz. The maximum deviation in the key frequency band (200–1.6k Hz) is only 1.0 dB, and the difference between $R_{\mathrm{W}}$, $C$, and $C_{\mathrm{tr}}$ is 0 dB, which fully meets the engineering accuracy requirements. However, when the mean amplitude and phase mismatch increases to 5% and 5° (condition II), the sound insulation error in the high-frequency band ($f_{\mathrm{m}}$ ≥ 1.6 kHz) is significantly magnified to more than 1.5 dB, resulting in a 1 dB deviation in $R_{\mathrm{W}}$; when the mismatch further increases to 10% and 10° (condition III), the error in the high-frequency band exceeds 2.0 dB, and the $R_{\mathrm{W}}$ deviation reaches 2 dB. The measurement accuracy of the uncalibrated domestic linear array (condition IV) is between working conditions I and II, which strongly confirms that the channel consistency of the microphone array is a key factor in ensuring the measurement accuracy of NAH.

Figure 10 shows the variation of $err{I}_{\mathrm{S}}$ with frequency under different mismatch conditions. As the mean value of amplitude and phase mismatch decreases from 10% and 10° to 5% and 5°, the error in the 100–3.15k Hz frequency band decreases by 0.38–0.42 dB (mean value is 0.40 dB); after the mean value of mismatch decreases to 0% and 0°, the error further decreases by 0.21–0.31 dB (mean value is 0.26 dB). It is worth noting that under the same system error level, $err{I}_{\mathrm{S}}$ shows a trend of slowly decreasing with increasing frequency, consistent with the numerical simulation results.

Figure 11 compares the effects of acoustic image reconstruction under different working conditions. The results show that the error-corrected acoustic image can accurately reflect the real sound field distribution of the component. In contrast, when there is a systematic error (conditions II, III, and IV), the quality of the acoustic image significantly deteriorates. Specifically, the uncalibrated domestic array (condition IV), condition II, and condition III show noticeable spatial distortion in the frequency bands above 1k Hz, 500 Hz, and 250 Hz, respectively, resulting in a significant decrease in the recognition accuracy of component sound insulation defects. In-depth analysis shows that high-frequency acoustic images are more sensitive to systematic errors. The main reason is that the absolute value of the normal sound intensity in the high-frequency band is relatively low, which will produce a larger relative error at the same absolute error level. These findings reveal that the influence of systematic errors on the quality of acoustic images has dual characteristics: the degree of influence depends not only on the amplitude and phase mismatch level of the measurement system itself but also on the energy distribution characteristics of the reconstructed sound field (especially the normal sound intensity amplitude). This profound understanding provides an important theoretical basis for optimizing the design of NAH measurement systems and improving the accuracy of sound insulation defect detection.

5. Discussion

(1)

Frequency-selective amplification mechanism of system errors

In the first Rayleigh integral in the wavenumber domain, the amplitude of the propagating wave remains unchanged during the inverse reconstruction process. In contrast, the amplitude of the evanescent wave increases exponentially in the z-direction at the rate of $e^{\left(z_{\mathrm{h}}-z_{\mathrm{S}}\right)\sqrt{k_x^2+k_y^2-k^2}}$ during the inverse reconstruction process [34]. When the complex sound pressure contains amplitude and phase mismatch errors, the influence of the propagating wave on the average normal sound intensity level is linearly amplified with frequency [35]. In contrast, the influence of the evanescent wave on the local sound intensity distribution is particularly significant in the low-frequency band, thus forming the differentiated characteristics of “high-frequency average index sensitivity and low-frequency image index sensitivity”, indicating that the error amplification law of Green’s function inversion has cross-domain commonality.

(2)

Differences in sensitivity between energy-based and distribution-based indicators

The sound insulation is an energy-type indicator that is averaged over a surface. It is highly robust to random noise due to the statistical averaging effect. The acoustic image is based on the spatial distribution of normal sound intensity, which can intuitively reveal the weak links in sound insulation but is particularly sensitive to the distortion of the evanescent wave amplitude. The experimental results show that when the amplitude and phase mismatch mean values of the microphone array are controlled at 5% and 5°, the sound insulation deviation between the NAH method and the ISO 10140 method in the 200–1.6k Hz frequency band does not exceed 1.5 dB, which meets the engineering tolerance. However, the acoustic image reconstructed by the NAH method is distorted above 500 Hz, resulting in a significant decrease in defect location accuracy. This comparison highlights the advantages of NAH technology over traditional methods in detecting sound insulation defects. On the other hand, it also suggests that the different accuracy requirements of “quantitative evaluation” and “visual diagnosis” should be distinguished in engineering practice. The acoustic image index can be moderately relaxed if only the sound insulation level needs to be assessed.

(3)

Research limitations

The current research still has three limitations: First, the random errors introduced by background noise, wall scattering and boundary reflection of the measurement area are not systematically considered, and the superposition effect of them and the system error needs to build an overall uncertainty model; second, only the mean of the amplitude and phase mismatch is changed, and the standard deviation is not analyzed; there is also a lack of verification of the non-normal distribution of system errors; for the case of ultra-high sound insulation ($R_{\mathrm{W}}$ > 60 dB), whether the system error amplification will produce nonlinear deviations due to the decrease in signal-to-noise ratio still needs to be verified by a stronger excitation source and a longer integration time.

6. Conclusions

This study systematically explored the application potential of NAH technology in the sound insulation measurement of building components and its sensitivity to system errors by combining numerical simulation with actual measurements in a soundproof room. The research results show that the sound insulation curve of the component obtained by the NAH measurement method of the domestic microphone array calibrated by the transfer function method in the full frequency range of 100 Hz to 3.15k Hz is highly consistent with the ISO 10140 standard method; at the same time, the NAH technology can synchronously output high-resolution sound images to intuitively reveal the weak links of the sound insulation of the component, providing strong technical support for the realization of the integrated sound insulation diagnosis process of “assessment, positioning, and repair”.

Further error sensitivity analysis reveals that the amplitude and phase mismatch of the array channel are the dominant factors restricting the NAH measurement accuracy, and their influence tends to increase with the increase of the mean mismatch. Specifically, when the mean value of amplitude and phase mismatch is controlled within the threshold of 5% and 5°, the sound insulation measurement error in the key frequency band (200–1.6k Hz) can be kept within 1.5 dB, and the sound image measurement error is less than 0.5 dB, which meets the error tolerance requirements of engineering practice; however, when the mean value of mismatch rises to 10% and 10°, the sound insulation measurement error in the key frequency band increases significantly to 2.0 dB. The error in the frequency band above 2.5k Hz exceeds 2.5 dB. At the same time, the sound image shows apparent artifact aggravation in the frequency band above 250 Hz, which will significantly increase the risk of misjudgment of component sound insulation level and misdetection of defects.

Based on the above key findings, this study proposes the following application suggestions: First, in engineering practice, the measurement array must be strictly calibrated in amplitude and phase, and the mismatch mean must be strictly controlled within the thresholds of 5% and 5°; second, given the characteristics of domestic equipment, it is recommended to adopt a frequency-related dynamic compensation strategy; third, it is necessary to focus on optimizing the error correction algorithm in the mid- and high-frequency bands (especially $f_{\mathrm{m}}$ ≥ 1.6 kHz). The results of this study provide a theoretical basis and practical specifications for applying NAH technology in the on-site detection of architectural acoustics. Subsequent research will focus on developing systems, random error coupling modeling, and intelligent correction technology to expand the applicability of this method in complex environments on engineering sites.