Mechanical Characterization and Theoretical Study of Friction Pile Groups in Coastal Areas Based on Finite Element Analysis
Abstract
1. Introduction
2. Field Test of Foundation Pile
2.1. Geological Conditions Overview
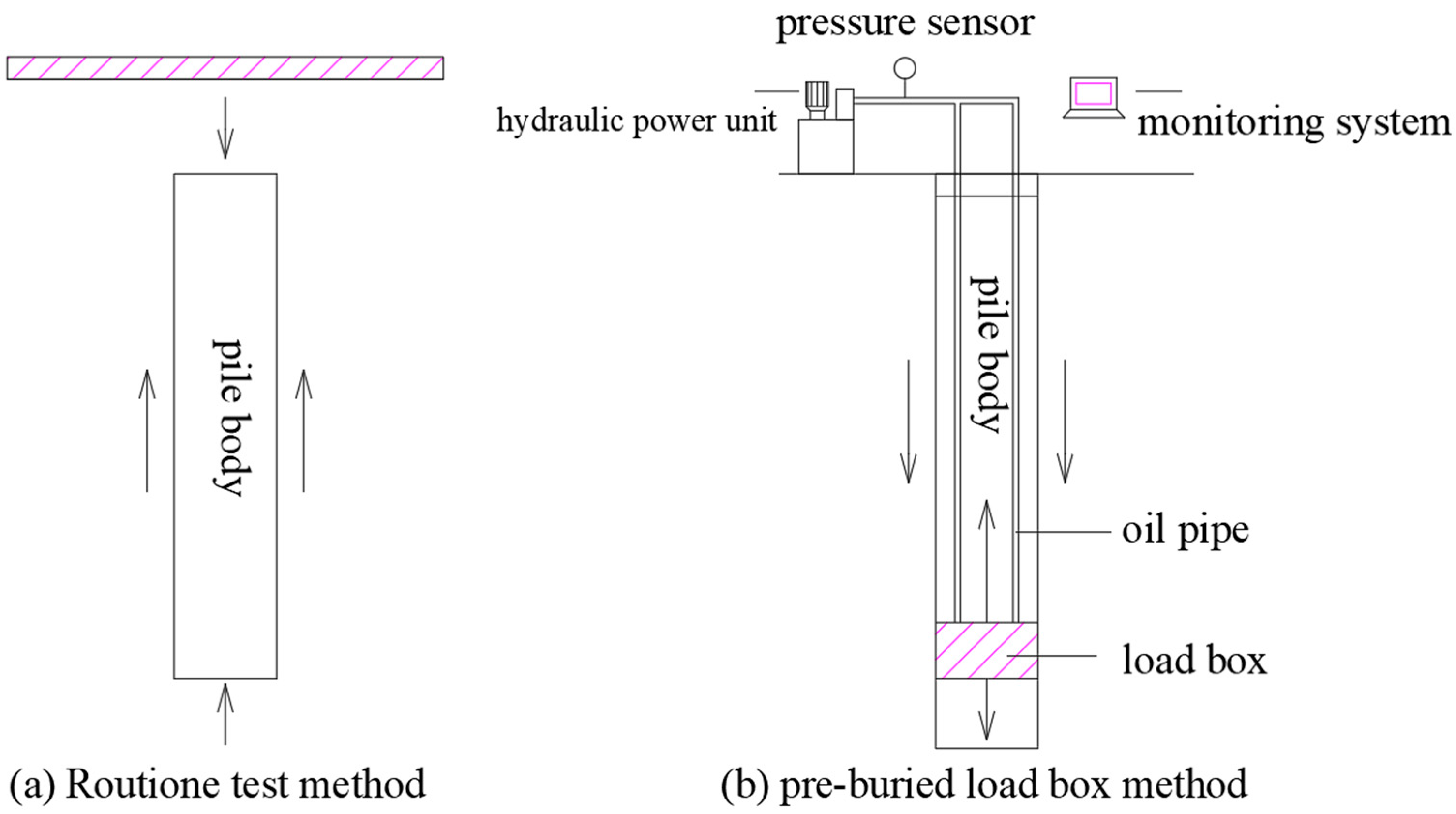
2.2. Choice of Experimental Methods
2.3. Test Program
2.3.1. Loading Method
2.3.2. Unloading-Stage Settlement Monitoring
2.3.3. Install Monitoring Instruments
2.3.4. Data Collection
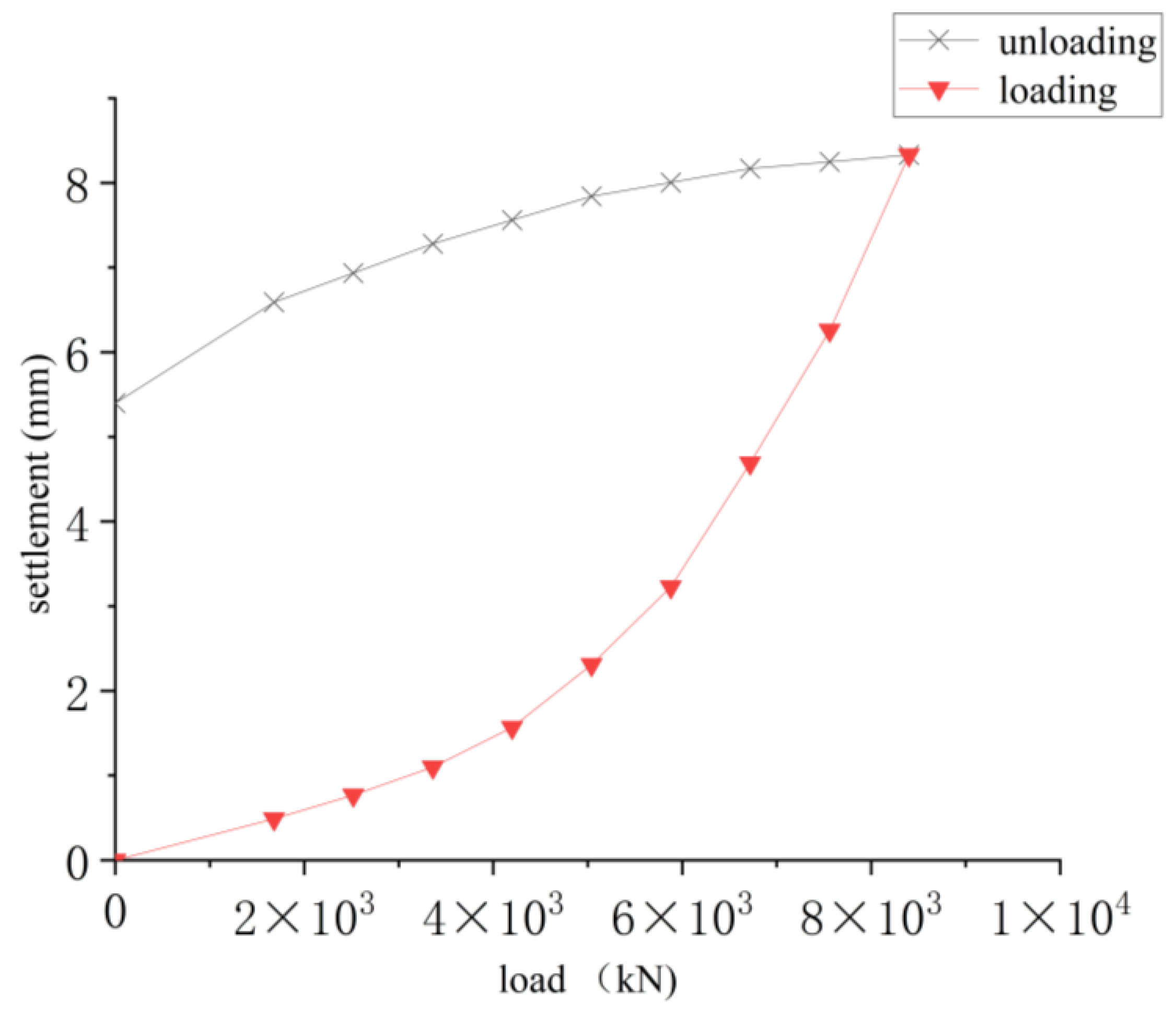
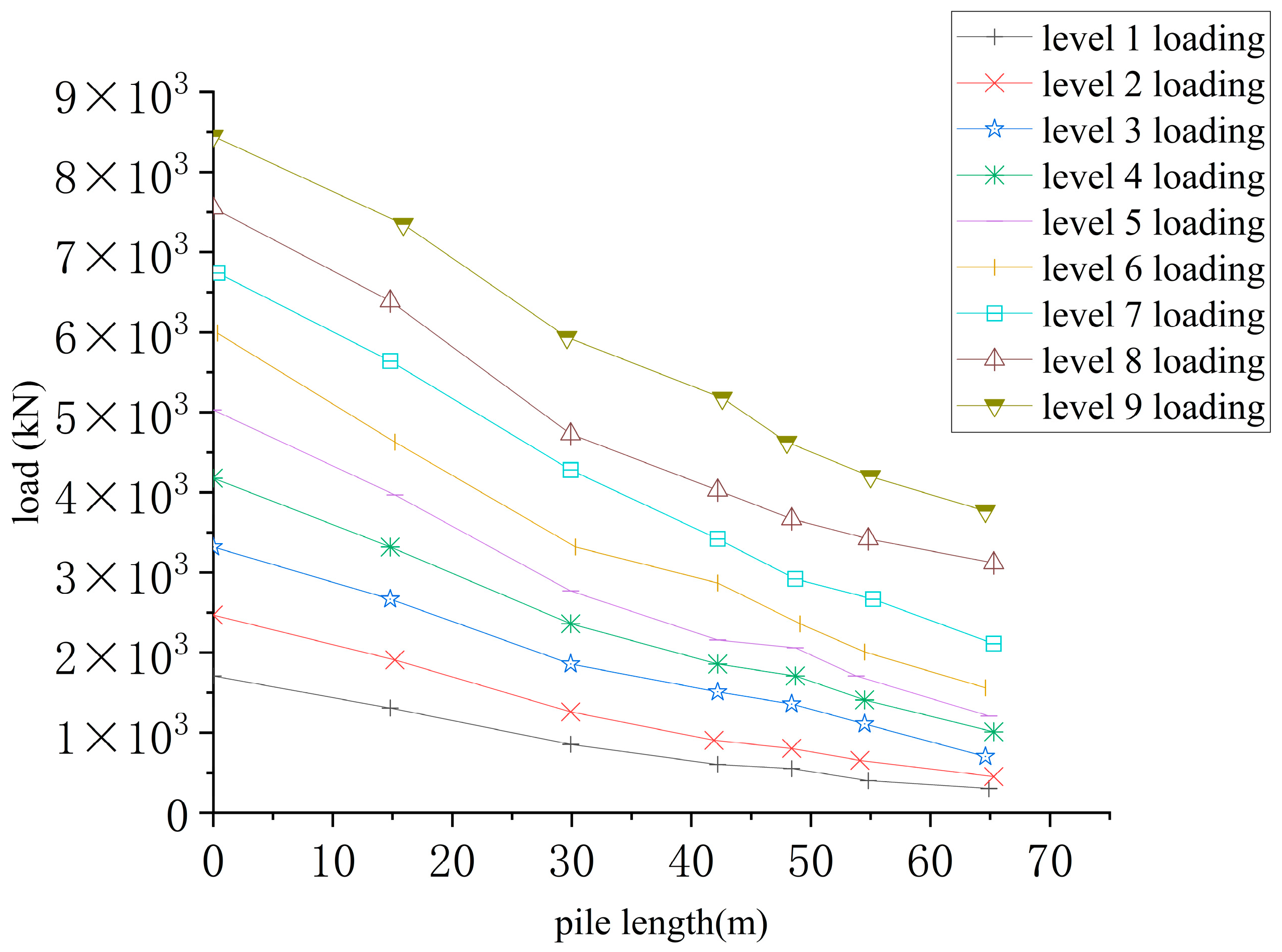
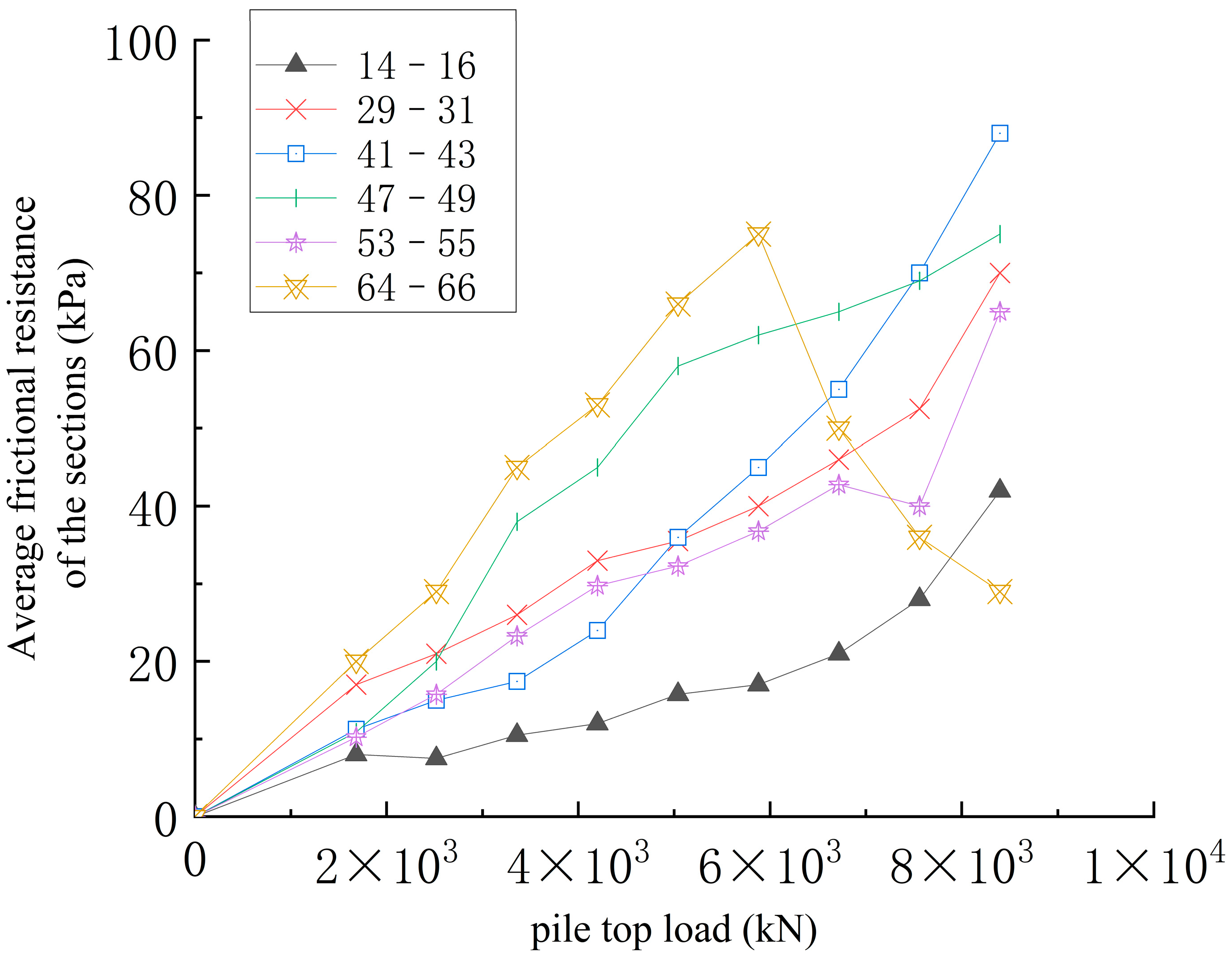
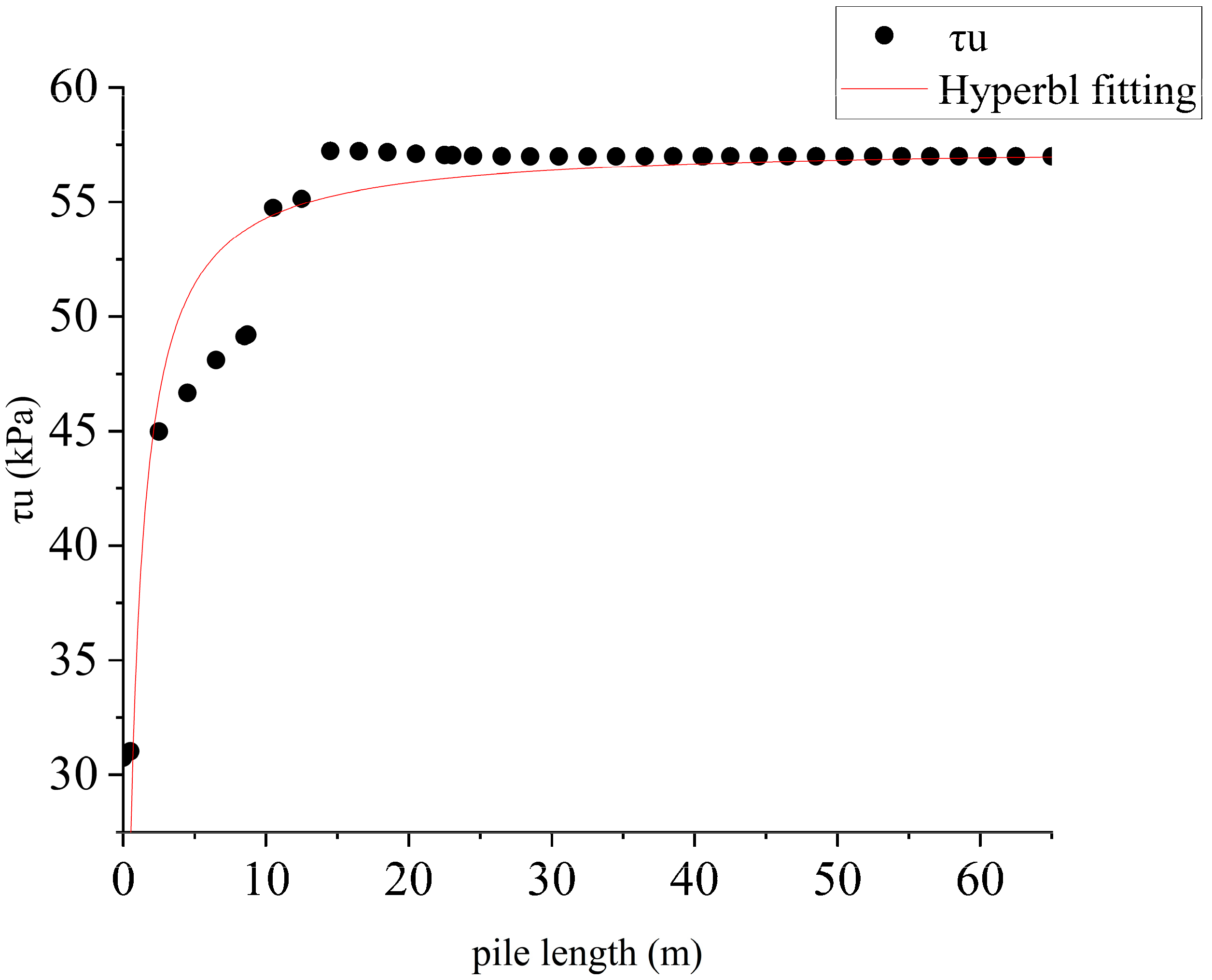
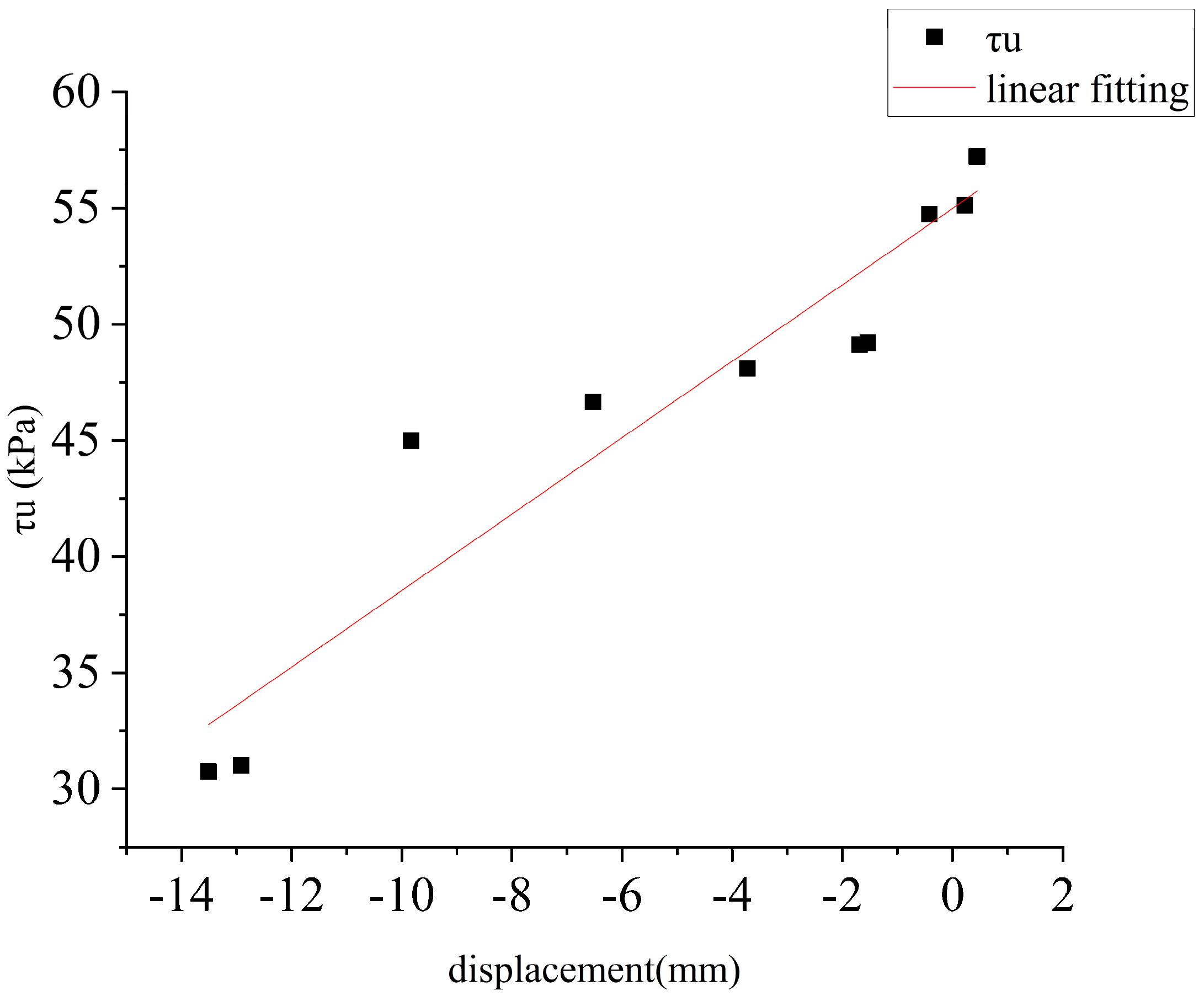
2.4. Analysis of Test Results
3. Finite Element Analysis of Friction Base Pile Force Characteristics
3.1. Establishment of a Base Pile Finite Element Model
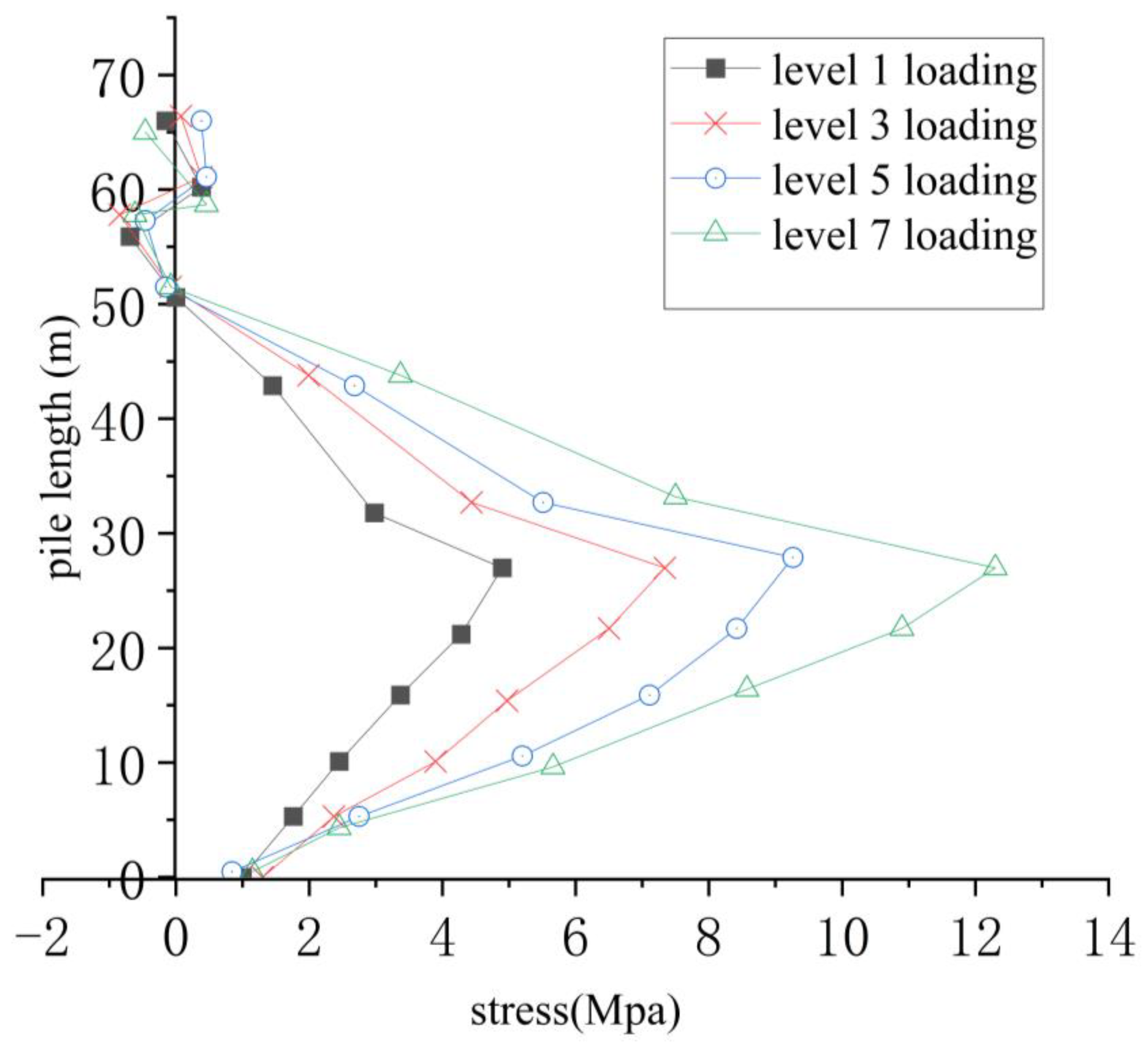
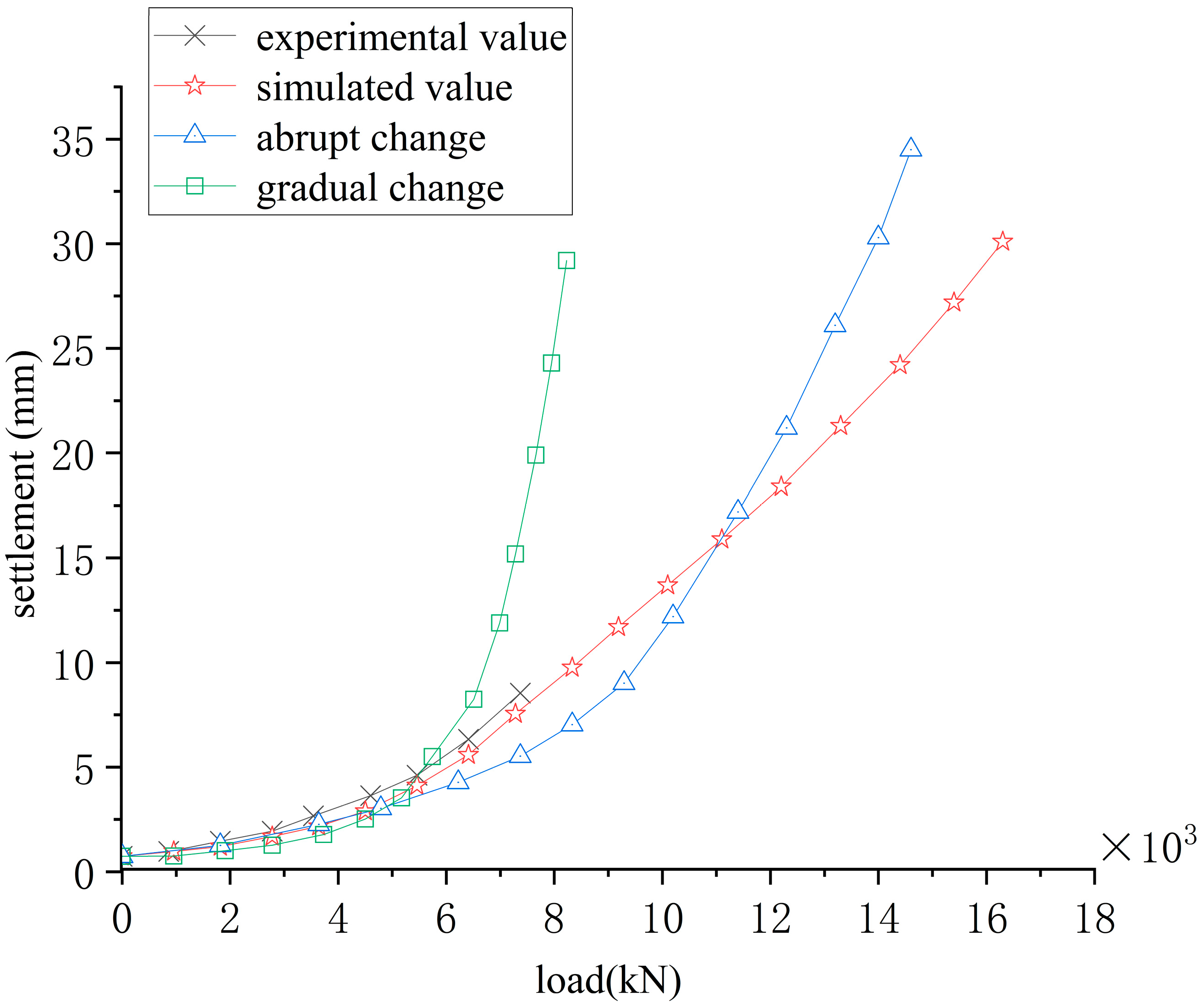
3.2. Analysis of Finite Element Calculation Results
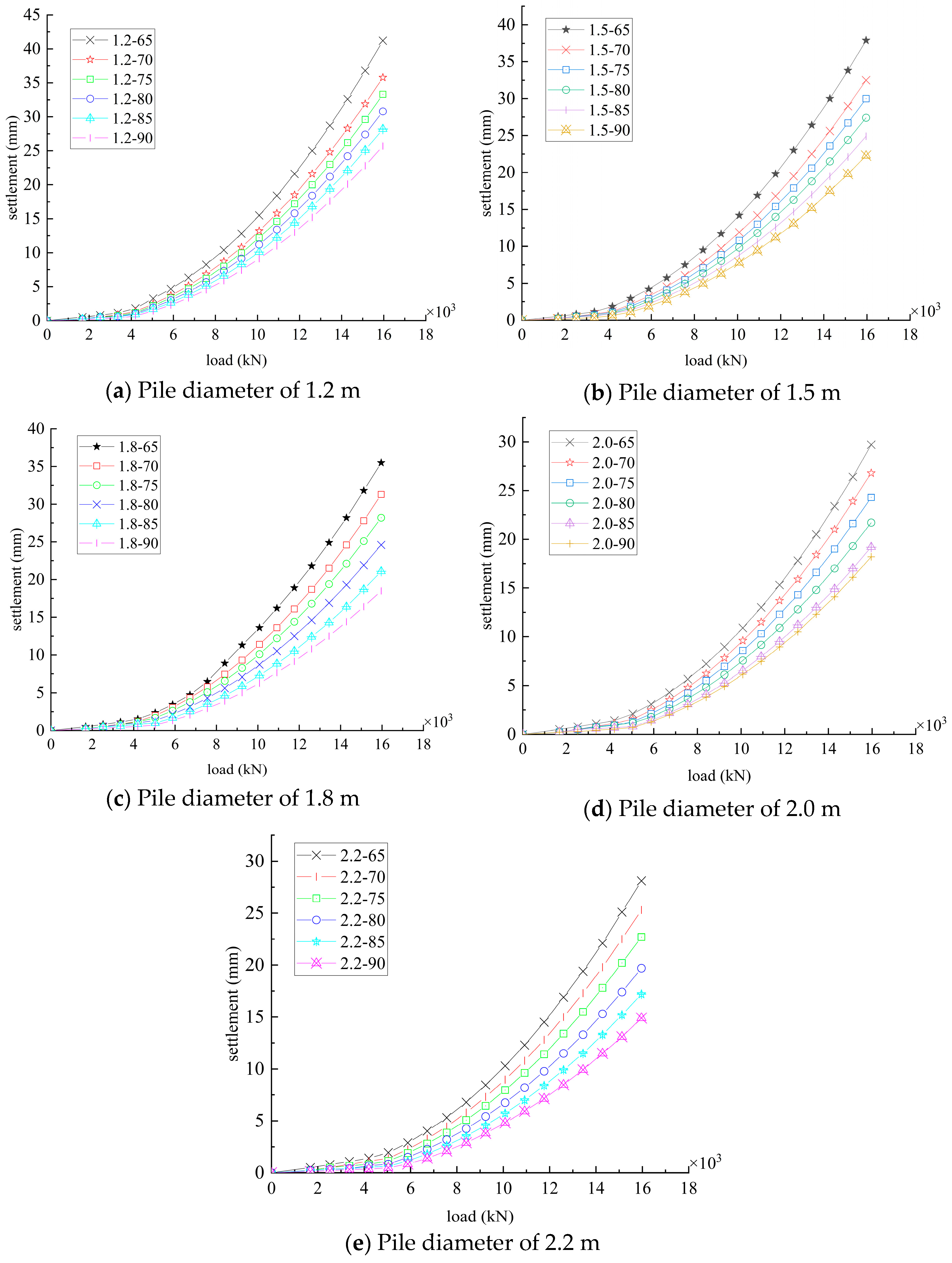
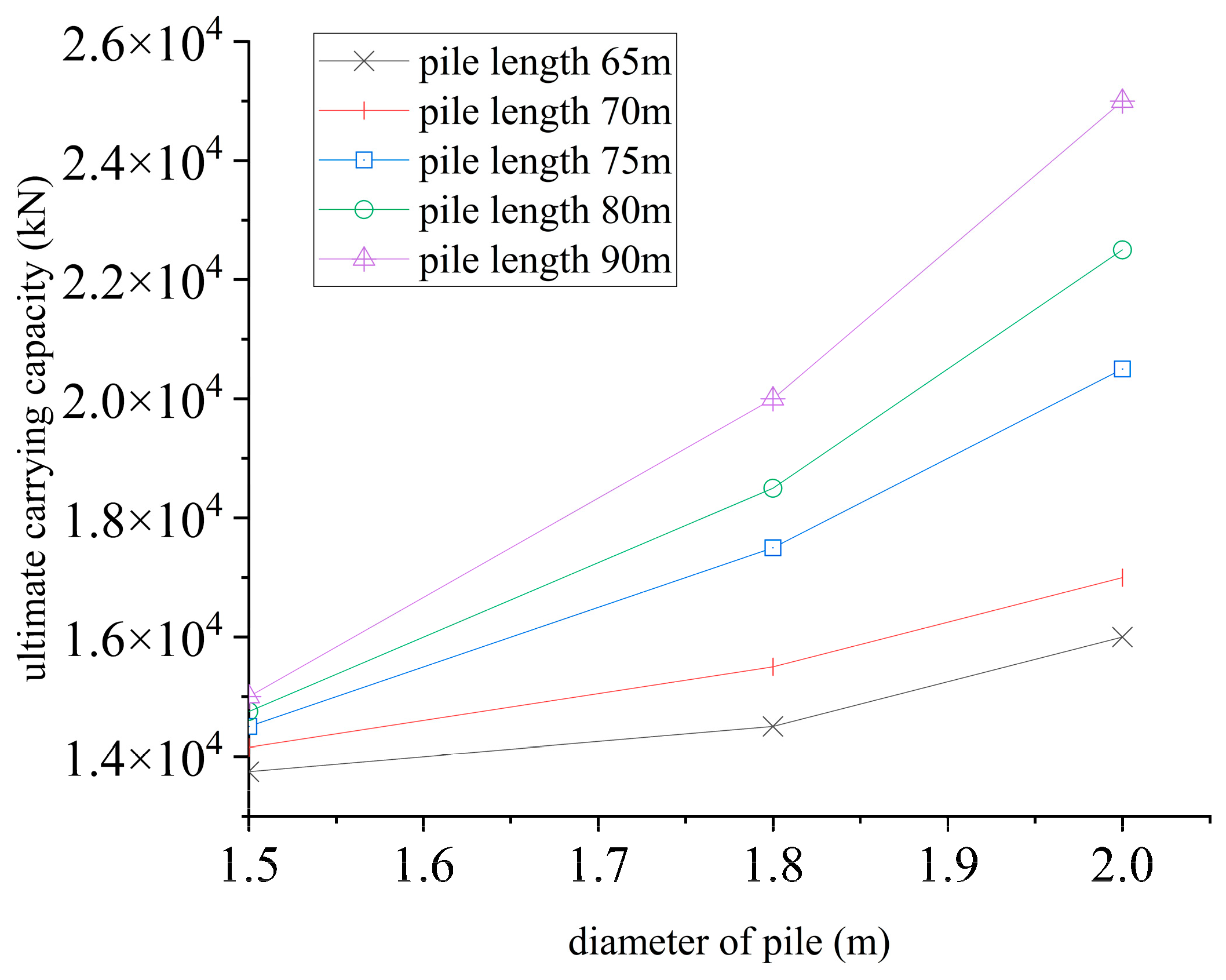
3.3. Analysis of Influencing Factors of Foundation Pile Settlement
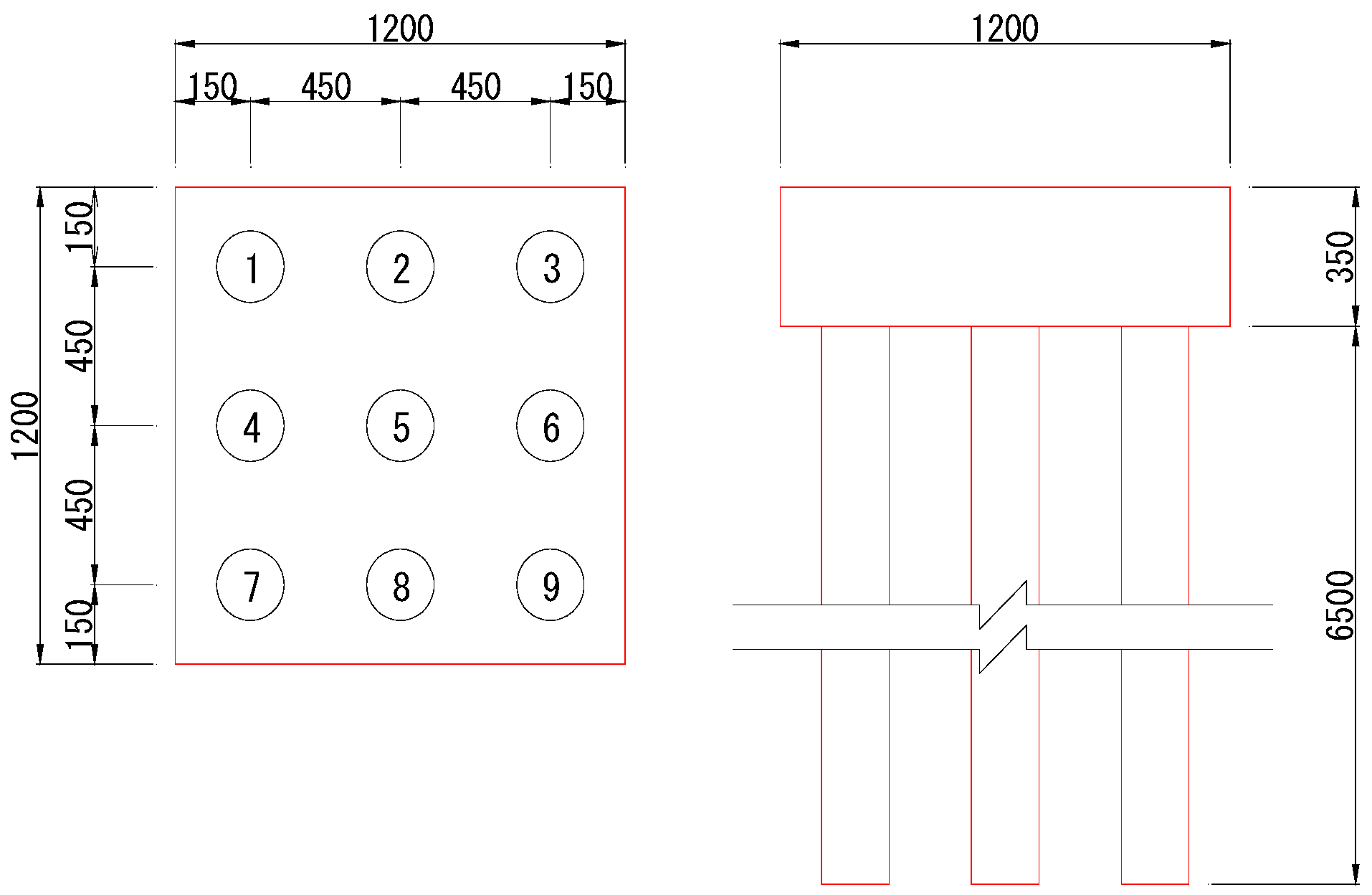
4. Example Analysis of a Coastal Area Friction Pile Group Foundation Project
4.1. Finite Element Model of a Pile Group
4.1.1. Model Dimensions and Parameter Selection
4.1.2. Boundary Conditions
4.1.3. Finite Element Modeling
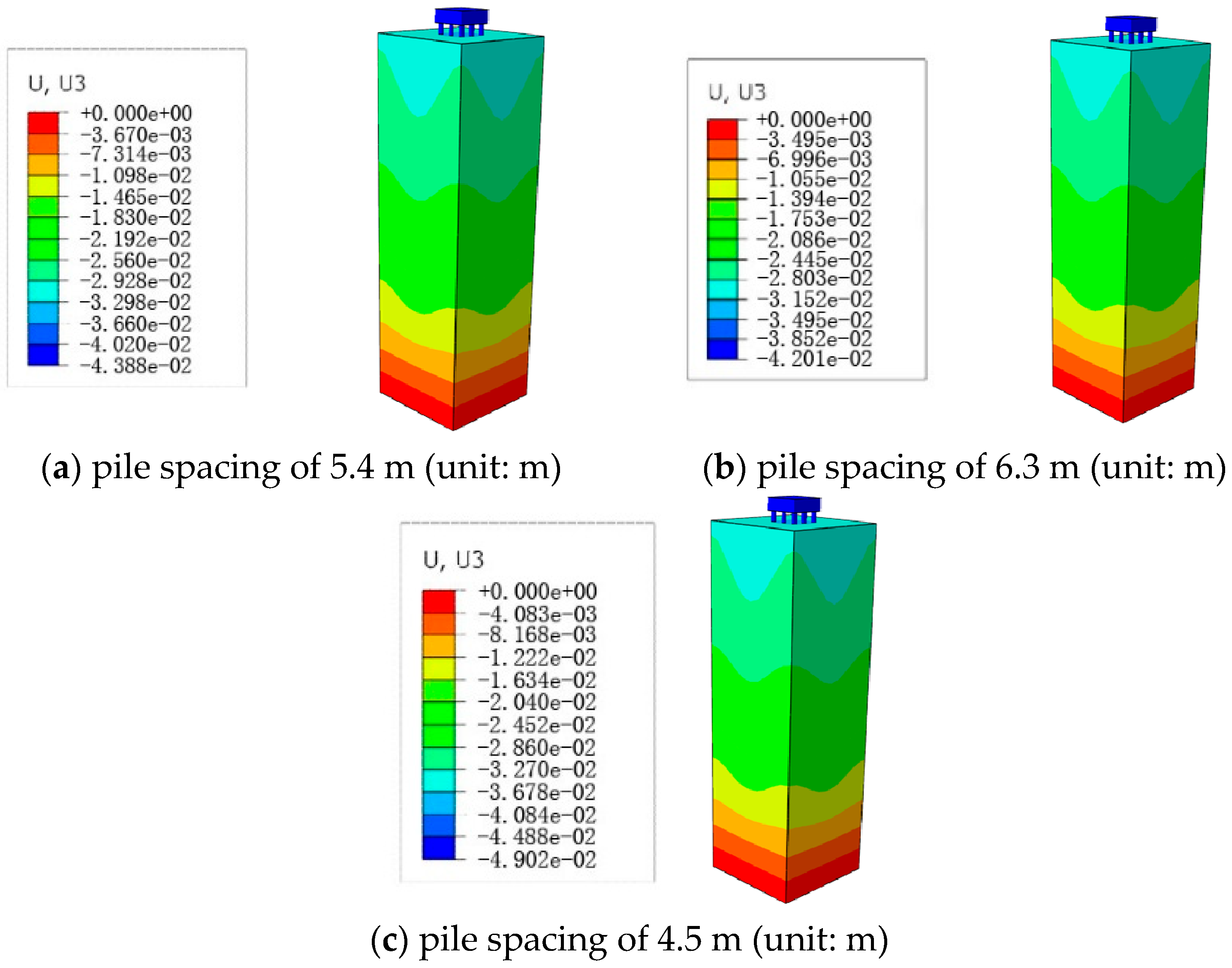
4.2. Comparative Analysis of Models with Different Pile Spacing
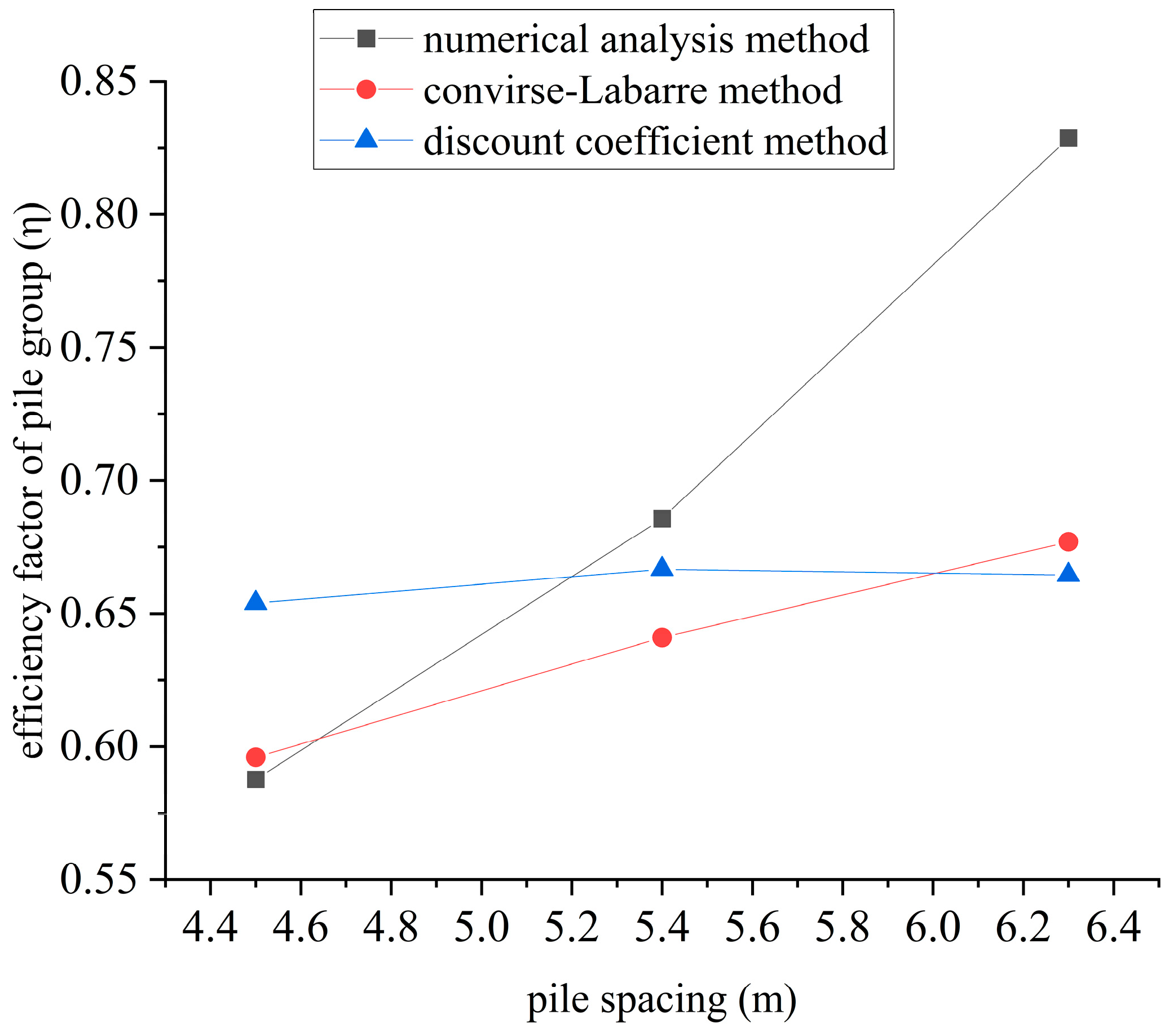
4.3. Calculating the Efficiency Factor of Pile Group Bridges
4.4. Structural Dynamic Characterization
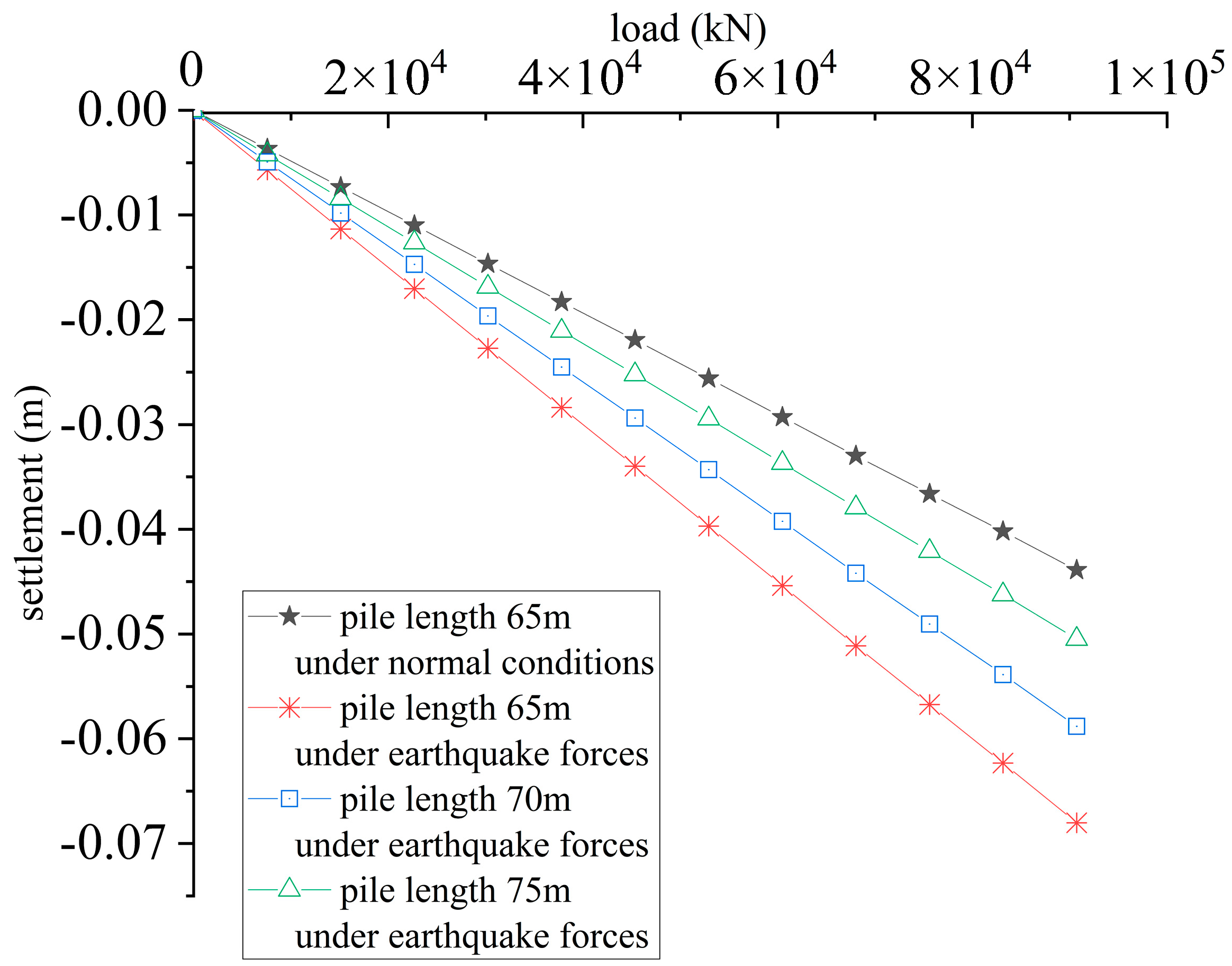
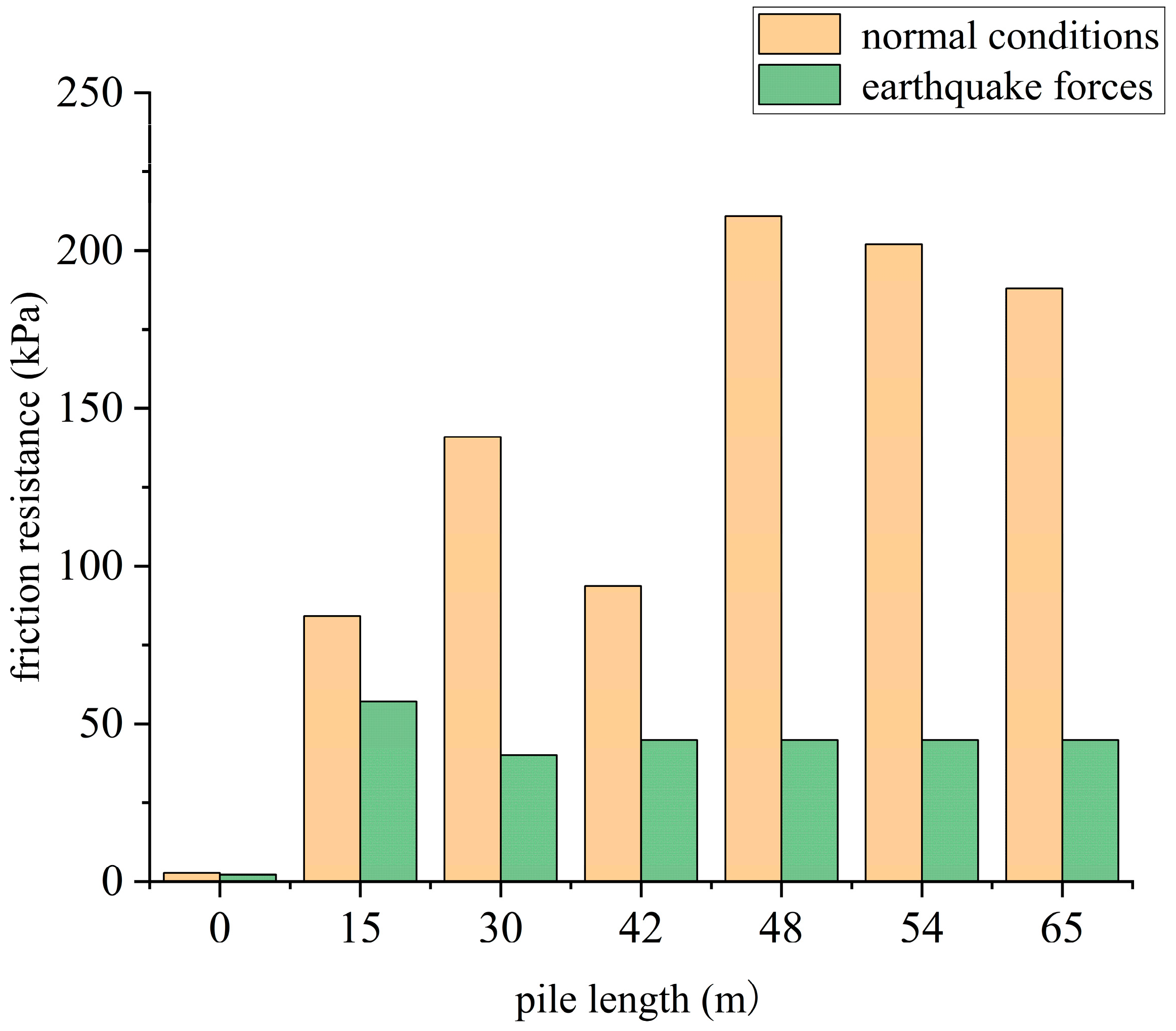
4.5. Comparative Analysis of Structures Under Static and Seismic Actions
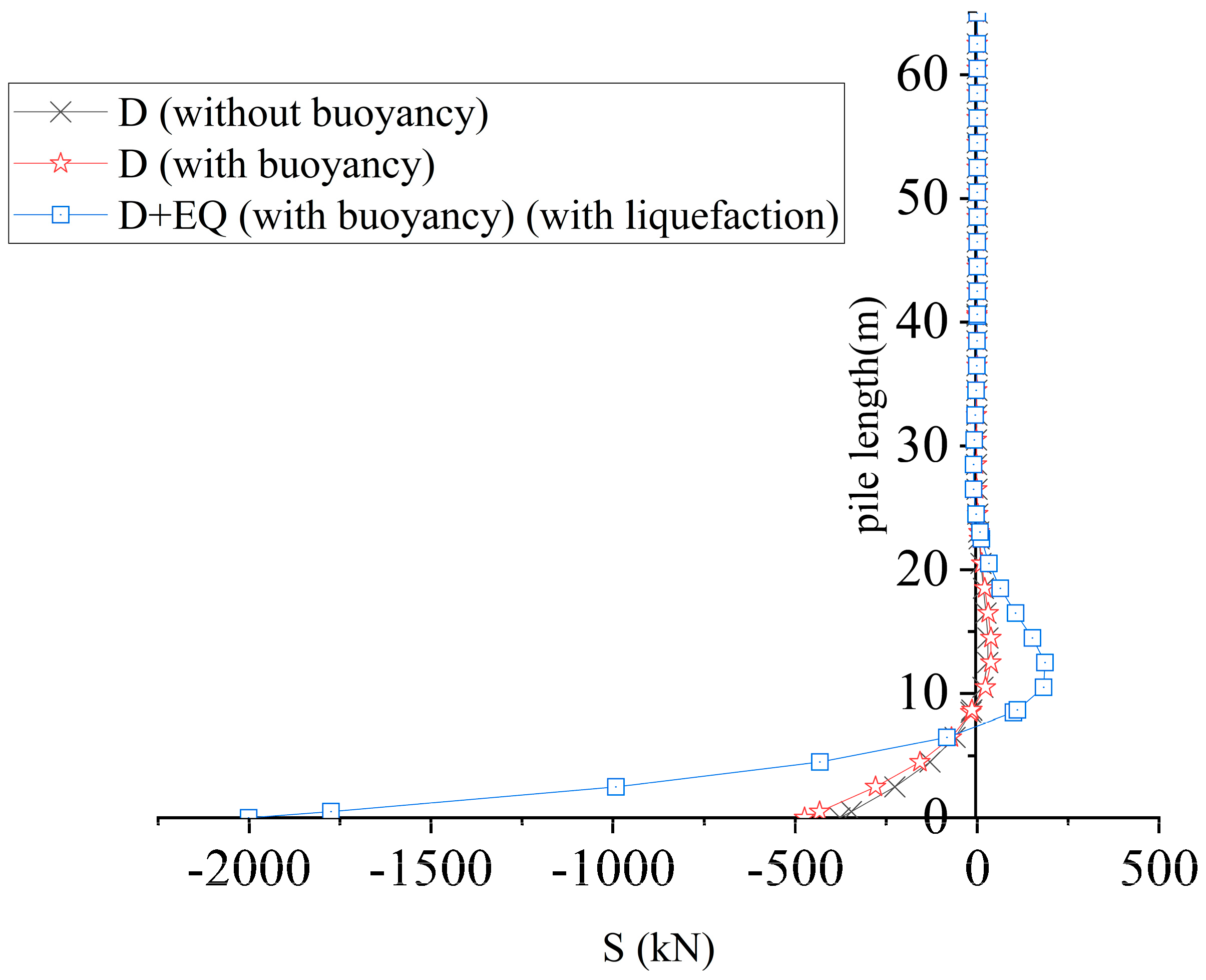
4.5.1. Comparison of Horizontal Displacement Distributions
4.5.2. Comparison of Bending Moment Distribution
4.5.3. Comparison of Shear Distributions
4.6. Settlement Correction Formula for Pile Group Foundations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, W.; Li, W.; Zhang, F. Parsing and application of the tri-linear model of single pile load transfer method. Build. Struct. 2017, 47, 1059–1066. [Google Scholar]
- Wang, F.; Miao, L.; Shi, M. Analysis of Single Pile’s Load Transfer Improvement Method. J. Highw. Transp. Res. Dev. 2007, 24, 53–57. [Google Scholar]
- Coyle, H.M.; Reese, L.C. Load transfer for axially loaded piles in clay. J. Soil Mech. Found. Div. 1966, 92, 1–26. [Google Scholar] [CrossRef]
- Seed, H.B.; Reese, L.C. The action of soft clay along friction piles. Trans. Am. Soc. Civ. Eng. 1957, 122, 731–754. [Google Scholar] [CrossRef]
- Fei, Q.; Ma, H. The Application of the Method of Layered Summation to Nonlinear Analyses of Pile Group. Shanghai J. Mech. 1997, 18, 78–83. [Google Scholar]
- Yang, M.; Zhan, X. An Approach for a Single Pile in Layered Soil. J. Tongji Univ. 1992, 20, 421–428. [Google Scholar]
- Zhang, Y. Numerical Research on the Load and Settlement of Single Pile in Layered Soil Using Load Transmission Method. J. Lanzhou Jiaotong Univ. 2009, 28, 15–17. [Google Scholar]
- Liu, F.; Zheng, J. Immersion tests on PHC piles in collapsible loess. Chin. J. Geotech. Eng. 2011, 33, 362–363. [Google Scholar]
- Yang, Y.; Dai, Z. Monitoring negative skin frictions on PHC pipe piles using FBG sensors. Chin. J. Rock Mech. Eng. 2017, 36, 3111–3120. [Google Scholar]
- Fang, Y. Study on Distribution Characteristics of Negative Friction of Pile Foundation in Fast Reclamation Site; Anhui University of Science and Technology: Huainan, China, 2019. [Google Scholar]
- Fellenius, B.H. Negative Skin Friction on Long Piles Driven in Clay; Statens Geotekniska Institut: Linköping, Sweden, 1971. [Google Scholar]
- Endo, M.; Minou, A.; Kawasaki, I.; Shibata, T. Negative skin friction acting on steel pipe pile in clay. In Proceedings of the International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 25–29 August 1969. [Google Scholar]
- Sheil, B.B.; McCabe, B.A. An analytical approach for the prediction of single pile and pile group behaviour in clay. Comput. Geotech. 2016, 75, 145–158. [Google Scholar] [CrossRef]
- Liu, Y.; Wan, Z.; Luo, P.; Chen, C. Analysis of ultra-long friction pile of wharf under condition of ultra-thick soft soil. Port Waterw. Eng. 2019, 188–192. [Google Scholar] [CrossRef]
- Yuan, Z.; Liang, B.; Song, C. Analysis of vertical bearing capacity of super-long pile foundation of main tower of cable-stayed bridge in offshore silt area. J. Henan Univ. Sci. Technol. 2019, 40, 62–68. [Google Scholar]
- Guo, Z.; Yuan, F.; Wang, H.; Liang, B. Self-balancing method-based experimental study on bearing capacity of super-long pile foundation for cable-stayed bridge in marine silt area. Water Resour. Hydropower Eng. 2020, 51, 181–190. [Google Scholar]
- Jiang, Y.; Yang, D. Seismic design of pile moment control under the mudline for vertically piled wharf under strong earthquakes. China Harb. Eng. 2014, 36–40. [Google Scholar] [CrossRef]
- Guixuan, W.; Rui, Z.; Jie, Z. Analysis on Seismic Bearing Capacity of Natural and Pile Foundations about a Coastal Nuclear Power Plant in Soft Ground. J. Seismol. Res. 2016, 39, 15–21+179–180. [Google Scholar]
- Xu, L.-Y.; Song, C.-X.; Chen, W.-Y.; Cai, F.; Li, Y.-Y.; Chen, G.-X. Liquefaction-induced settlement of the pile group under vertical and horizontal ground motions. Soil Dyn. Earthq. Eng. 2021, 144, 106709. [Google Scholar] [CrossRef]
- Karimi, Z.; Dashti, S.; Bullock, Z.; Porter, K.; Liel, A. Key predictors of structure settlement on liquefiable ground: A numerical parametric study. Soil Dyn. Earthq. Eng. 2018, 113, 286–308. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Z.; Fu, H.; Dong, Q.; Cai, Y.; Hu, X. Influence of vacuum preloading on vertical bearing capacities of piles installed on coastal soft soil. Mar. Georesources Geotechnol. 2019, 37, 870–879. [Google Scholar] [CrossRef]
- Hussein, A.F.; El Naggar, M.H. Seismic axial behaviour of pile groups in non-liquefiable and liquefiable soils. Soil Dyn. Earthq. Eng. 2021, 149, 106853. [Google Scholar] [CrossRef]
- Bagheri, M.; Jamkhaneh, M.E.; Samali, B. Effect of Seismic Soil–Pile–Structure Interaction on Mid- and High-Rise Steel Buildings Resting on a Group of Pile Foundations. Int. J. Geomech. 2018, 18, 04018103. [Google Scholar] [CrossRef]
- Asgari, A.; Bagheri, M.; Hadizadeh, M. Advanced seismic analysis of soil-foundation-structure interaction for shallow and pile foundations in saturated and dry deposits: Insights from 3D parallel finite element modeling. Structures 2024, 69, 107503. [Google Scholar] [CrossRef]
- Wang, X. Basic Engineering; China Communications Press: Beijing, China, 2010. [Google Scholar]
- Technical Code for Building Pile Foundations; China Architecture ang Building Press: Beijing, China, 2008.
- Dai, G.; Dai, Y.; Mao, Y.; Gong, W.; Li, X. Full scale in-situ static loading tests on pile groups in soft soils. Chin. J. Geotech. Eng. 2015, 37, 158–163. [Google Scholar]
- Deng, Y.; Gong, W.; Li, Z. Research on Effect Coefficient of Piles Group Based on Stress Superposition. J. Wuhan Univ. Technol. 2007, 29, 108–110. [Google Scholar]
- Jiang, C.; Yin, J.; Feng, B.; Lu, P.; Wei, D. A New Prediction Method of Settlement of Extra-Long Large Diameter Pile Groups Foundation at Super-Deep Soft Soil District. In Proceedings of the Thirteenth Annual Meeting of the Chinese Association for Science and Technology, Session 19-Seminar on the Position and Role of Highways in the Comprehensive Transportation System; China Academic Department of China Association for Science and Technology, Tianjin Municipal People’s Government: Tianjian, China, 2011; p. 6. [Google Scholar]







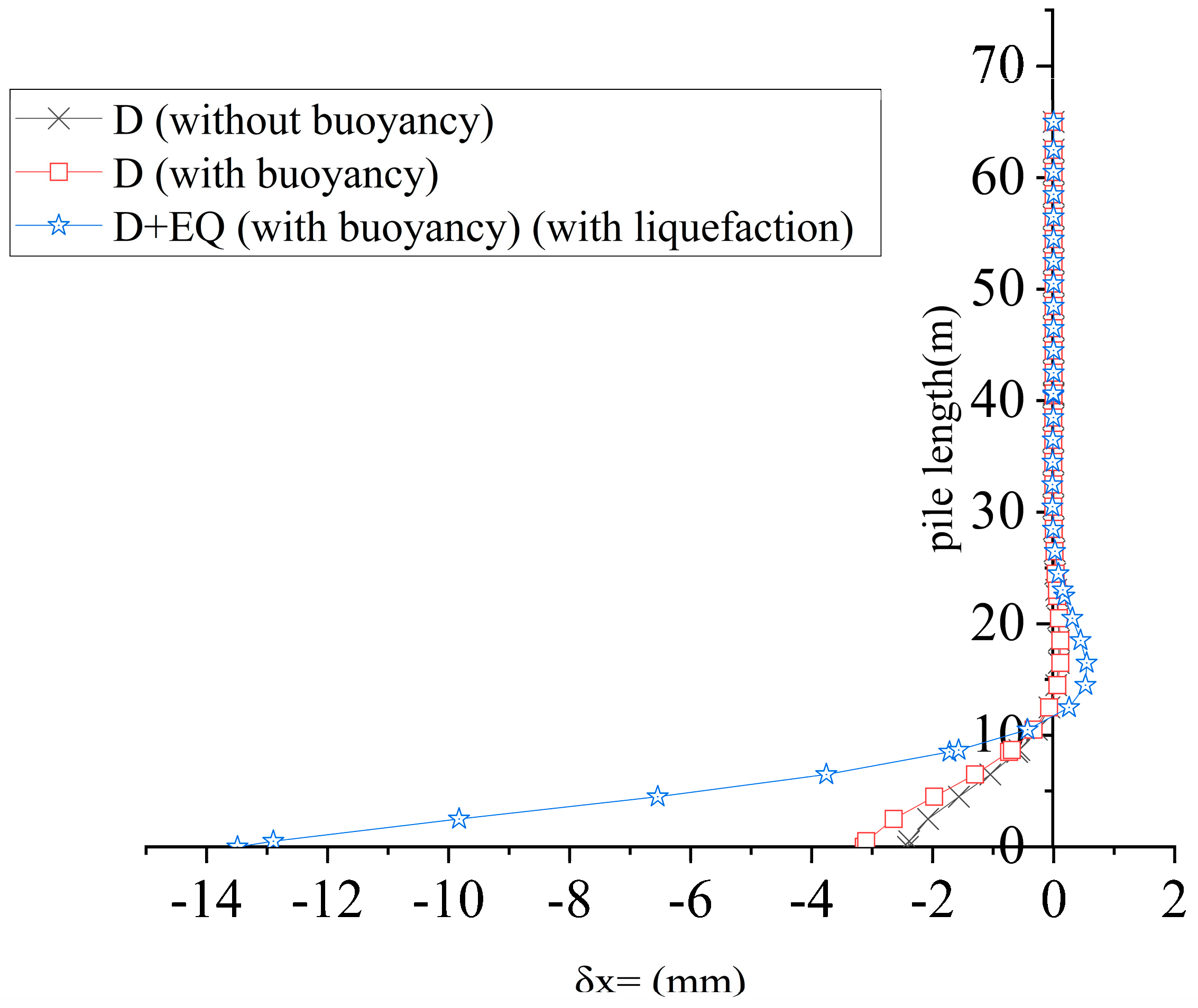
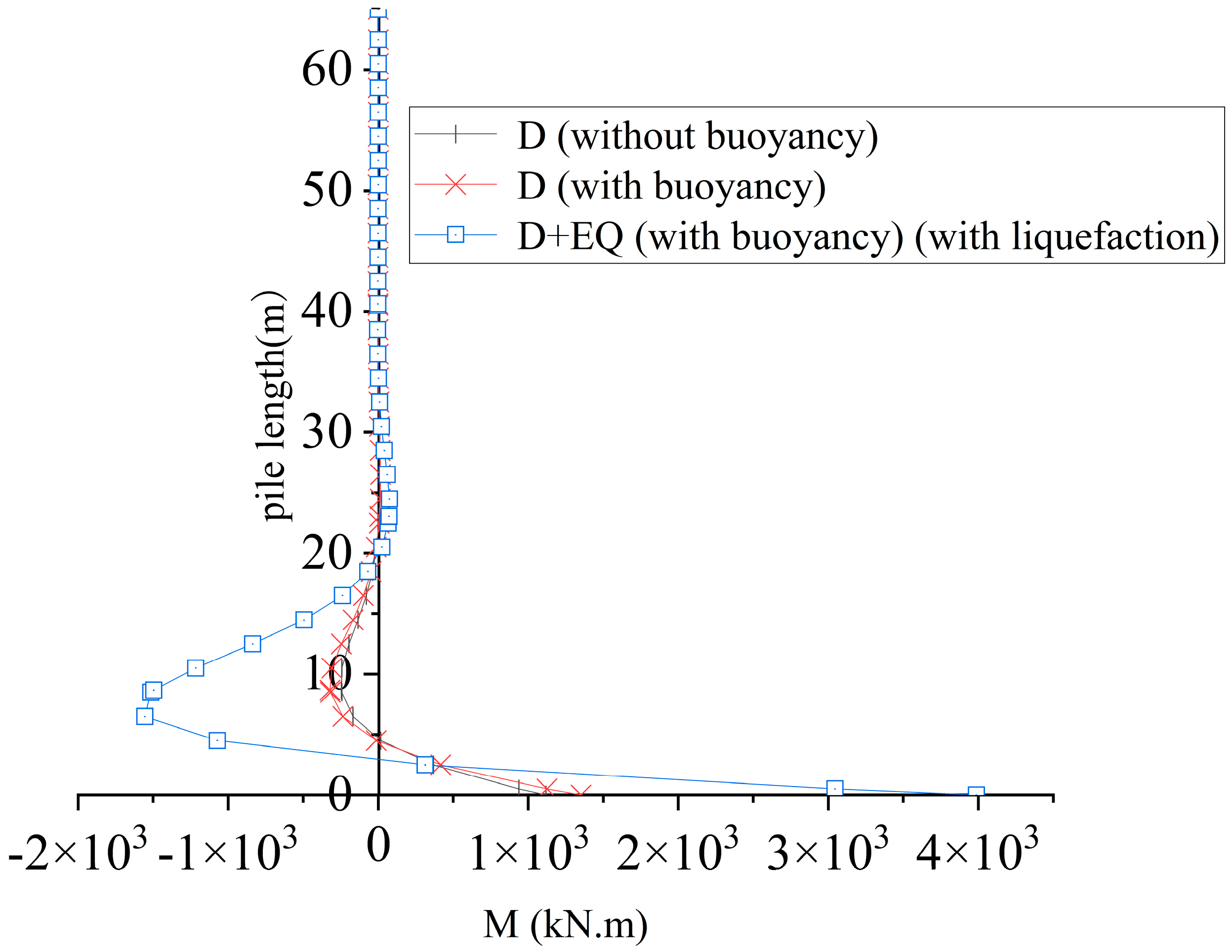
| Soil Layer Type | Plain Fill | Silty Clay | Coarse Sand | Completely Weathered Mudstone | ||
|---|---|---|---|---|---|---|
| Soil Profile | Layer 1 Soil | Layer 2 Soil | Layer 3 Soil | Layer 4 Soil | Layer 5 Soil | Layer 6 Soil |
| Pile Shaft Length (m) | 0.50 | 8.50 | 4.70 | 15.40 | 2.70 | 33.20 |
| Soil Profile | Cohesion (c) | Internal Friction Angle (°) | Compression Modulus (MPa) | Poisson’s Ratio μ |
|---|---|---|---|---|
| 1 | 37.0 | 24.8 | 20.0 | 0.28 |
| 2 | 50.0 | 27.0 | 20.0 | 0.25 |
| 3 | 55.0 | 31.2 | 20.0 | 0.28 |
| 4 | 57.0 | 27.0 | 23 | 0.30 |
| 5 | 40.0 | 25.0 | 23 | 0.26 |
| 6 | 45.0 | 23.5 | 23 | 0.30 |
| Material | Densities (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Yield Strength (MPa) | Yield Strain (με) |
|---|---|---|---|---|---|
| Sandy soil | 2000 | 0.08 | 0.35 | 2 | 0 |
| Concrete reinforcing bar | 7800 | 210 | 0.3 | 300 | 0.002 |
| Concrete | 2500 | 33.5 | 0.2 | 32.4 | 0 |
| Structural Parts | Bridge Formation State | |||||
|---|---|---|---|---|---|---|
| △x | △y | △z | θx | θy | θz | |
| Interface between the brake pier and the pile cap | 1 | 1 | 1 | 1 | 0 | 0 |
| Interface between the pile and the pile cap | 0 | 1 | 1 | 1 | 0 | 0 |
| Pile toe | 1 | 1 | 1 | 1 | 1 | 1 |
| Pile spacing | 4.5 m | 5.4 m | 6.3 m |
| Efficiency factor of pile group | 0.5877 | 0.6857 | 0.8228 |
| Pile spacing | 4.5 m | 5.4 m | 6.3 m |
| Efficiency factor of pile group | 0.5960 | 0.6410 | 0.6770 |
| Pile spacing | 4.5 m | 5.4 m | 6.3 m |
| Efficiency factor of pile group | 0.6540 | 0.6667 | 0.6645 |
| Working Conditions | Static Force | Static Force | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Pile Diameter 1.8 m, Pile Length 65 m | Pile Diameter 1.8 m, Pile Spacing 4.5 m | Pile Length 60 m, Pile Spacing 4.5 m | |||||||
| Subside (mm) | Distance Between Piles 4.5 m | Distance Between Piles 5.4 m | Distance Between Piles 6.3 m | Pile Length 65 m | Pile Length 70 m | Pile Length 75 m | Pile Length 1.5 m | Pile Length 2.0 m | |
| Finite element | 49.02 | 43.88 | 42.01 | 68.00 | 58.63 | 50.46 | 87.08 | 55.77 | |
| Revised formula | 49.01 | 44.62 | 38.81 | 67.64 | 56.24 | 48.06 | 90.02 | 56.90 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Li, Y.; Zhao, J.; Feng, G.; Li, Y.; Li, J.; Jin, J. Mechanical Characterization and Theoretical Study of Friction Pile Groups in Coastal Areas Based on Finite Element Analysis. Buildings 2025, 15, 2556. https://doi.org/10.3390/buildings15142556
Wu J, Li Y, Zhao J, Feng G, Li Y, Li J, Jin J. Mechanical Characterization and Theoretical Study of Friction Pile Groups in Coastal Areas Based on Finite Element Analysis. Buildings. 2025; 15(14):2556. https://doi.org/10.3390/buildings15142556
Chicago/Turabian StyleWu, Jun, Yanfeng Li, Jia Zhao, Guangzuo Feng, Yuanhui Li, Jialong Li, and Jiaxu Jin. 2025. "Mechanical Characterization and Theoretical Study of Friction Pile Groups in Coastal Areas Based on Finite Element Analysis" Buildings 15, no. 14: 2556. https://doi.org/10.3390/buildings15142556
APA StyleWu, J., Li, Y., Zhao, J., Feng, G., Li, Y., Li, J., & Jin, J. (2025). Mechanical Characterization and Theoretical Study of Friction Pile Groups in Coastal Areas Based on Finite Element Analysis. Buildings, 15(14), 2556. https://doi.org/10.3390/buildings15142556





