Robustness of Steel Moment-Resisting Frames Under Column Loss Scenarios with and without Prior Seismic Damage
Abstract
1. Introduction
- To evaluate the robustness of steel MRFs by using a refined model strategy (3D model accounting for the contribution of joints and claddings).
- To focus on the eventual impact of seismic damage on the ability of MRFs to resist progressive collapse.
- To identify key structural parameters influencing post-seismic robustness, including the number of storeys, span lengths, column loss scenario, etc.
- To assess the contribution of secondary structural elements and non-structural components, such as façade claddings, in preventing collapse propagation.
2. Parametric Study
2.1. Parameters of Variation
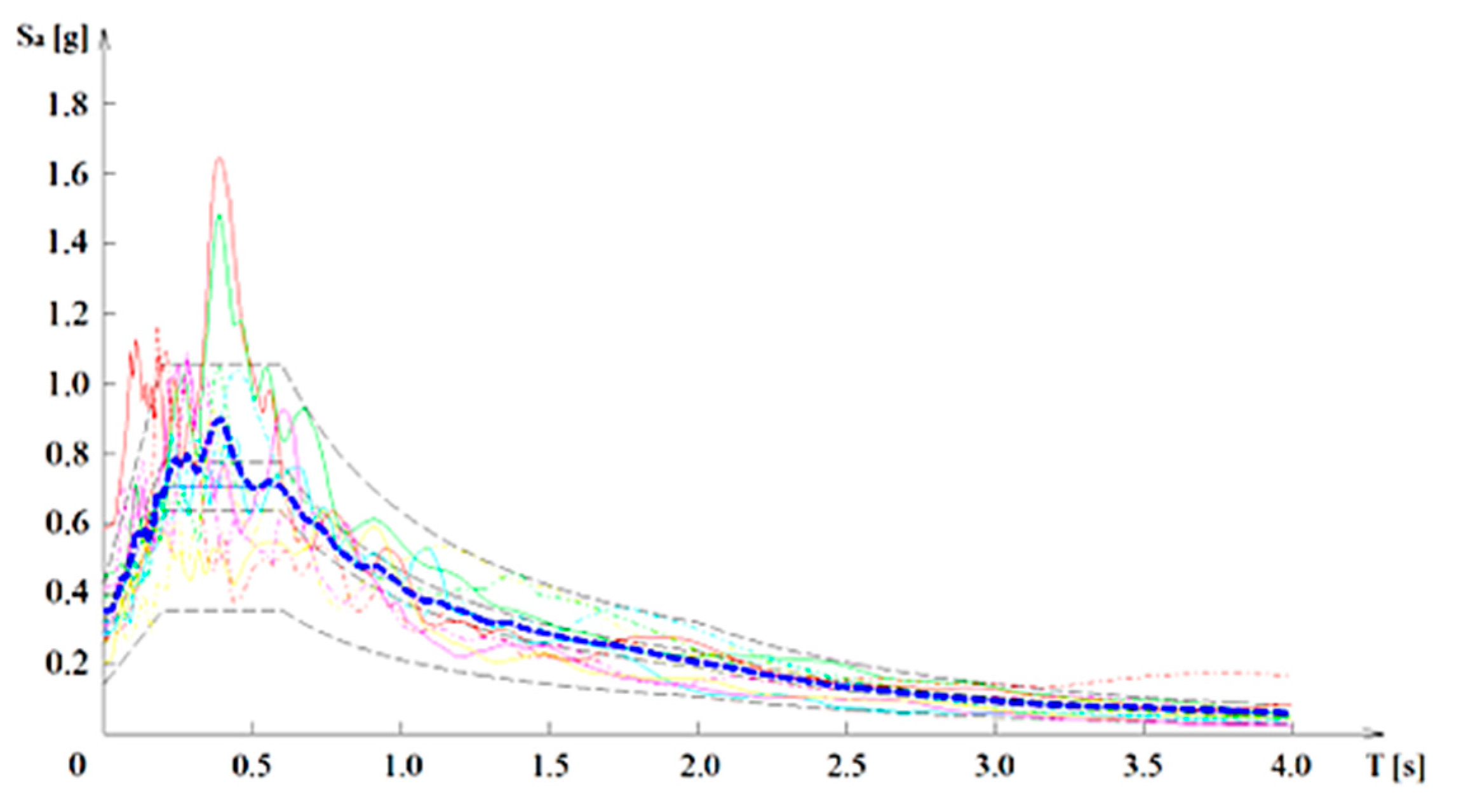
2.2. Design Assumptions
- Seismic action Type 1 (agR = 2.45 ms2) and Type 2 (agR = 2.45 ms2);
- Soil type C;
- Importance class II;
- Ductility class DCH;
- Behaviour factor q = 5 × (au/a1) = 5 × 1.3 = 6.5.
3. Robustness Performance Evaluation
3.1. Analysis Methodology
3.2. Modelling Assumptions

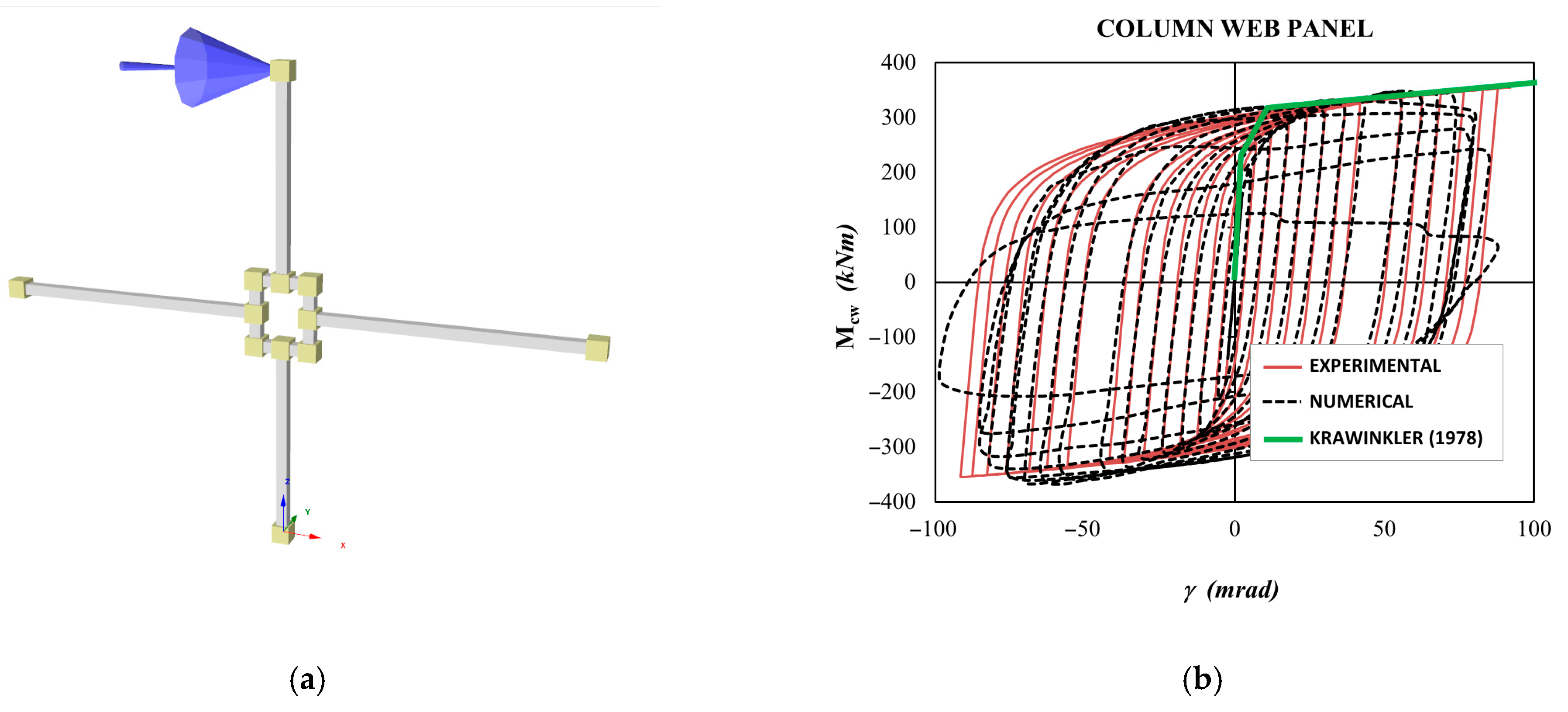
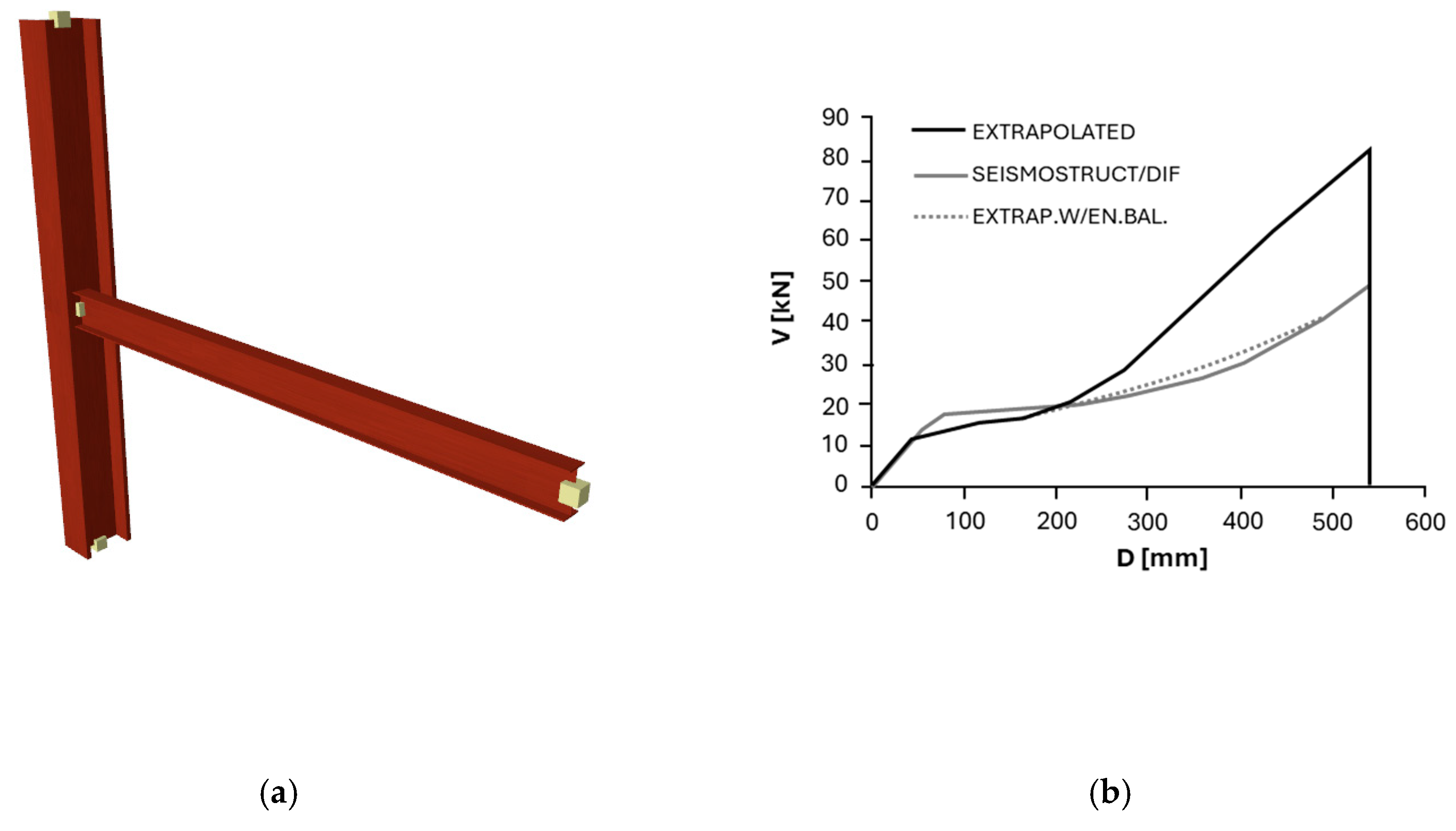

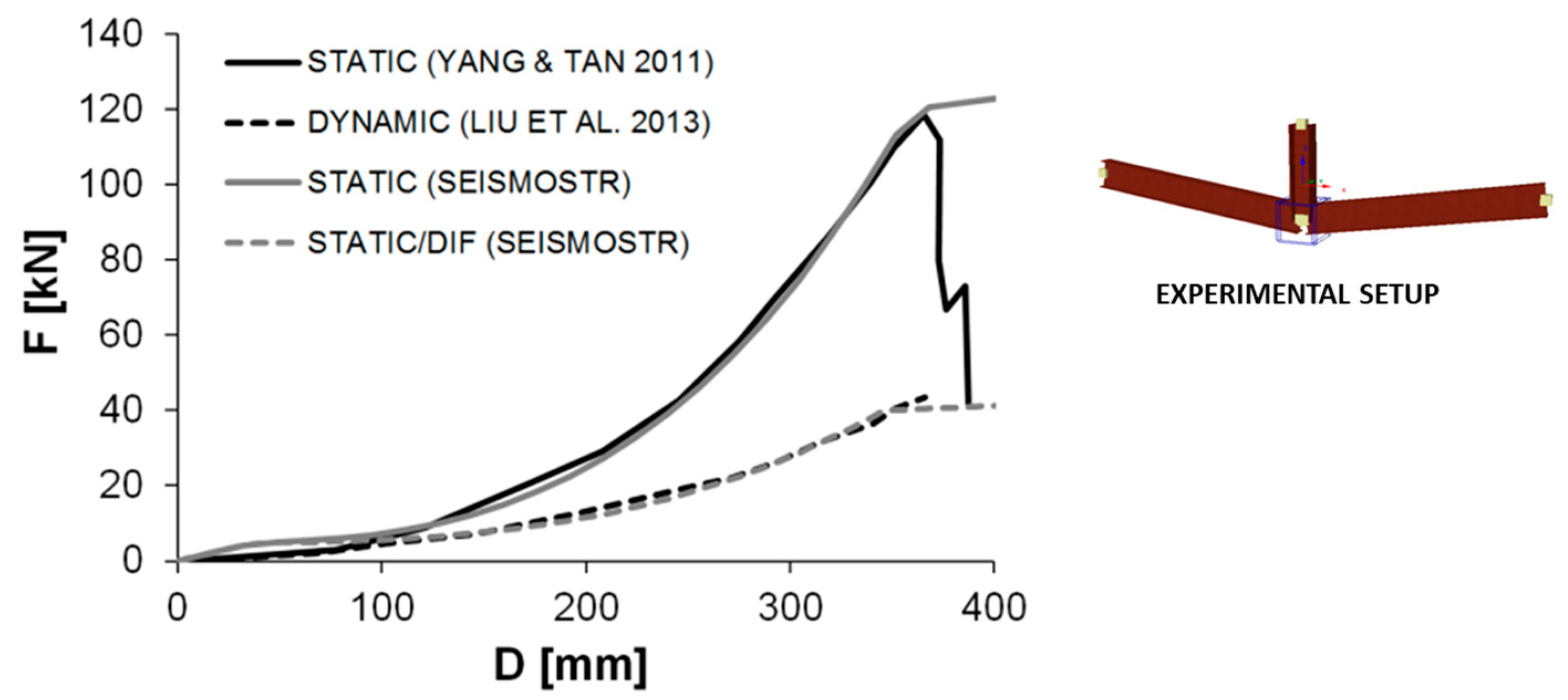
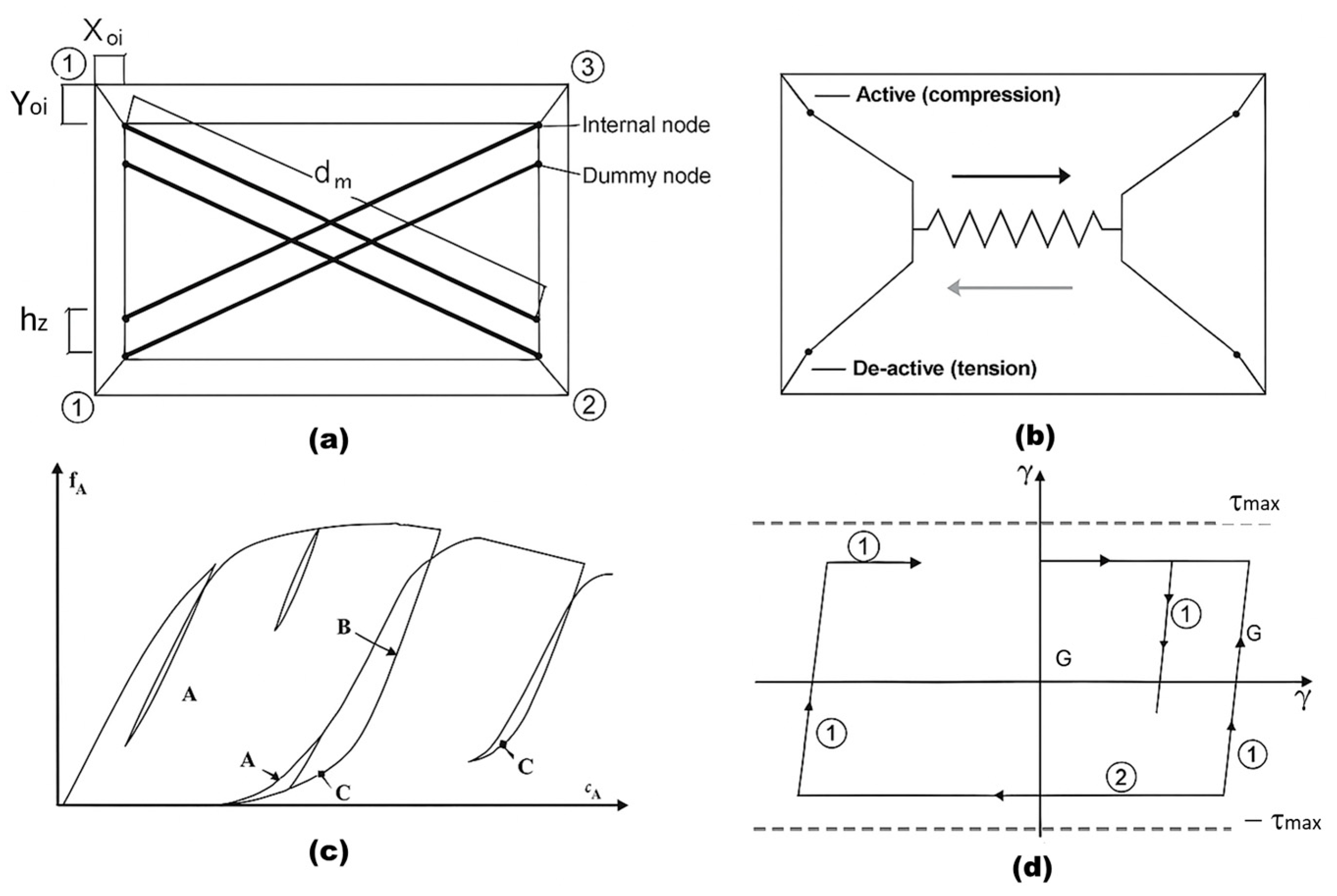
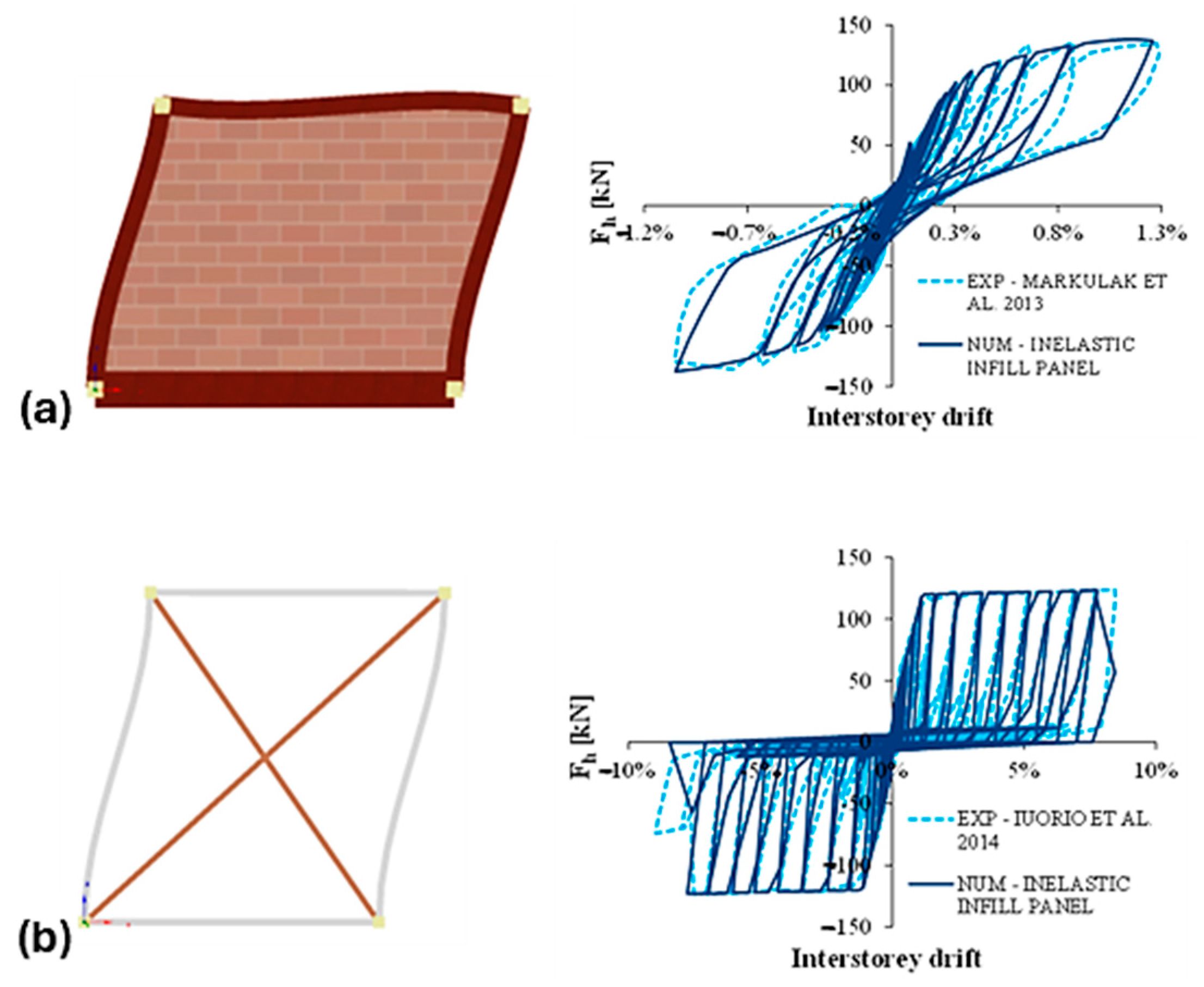
3.3. Monitored Parameters
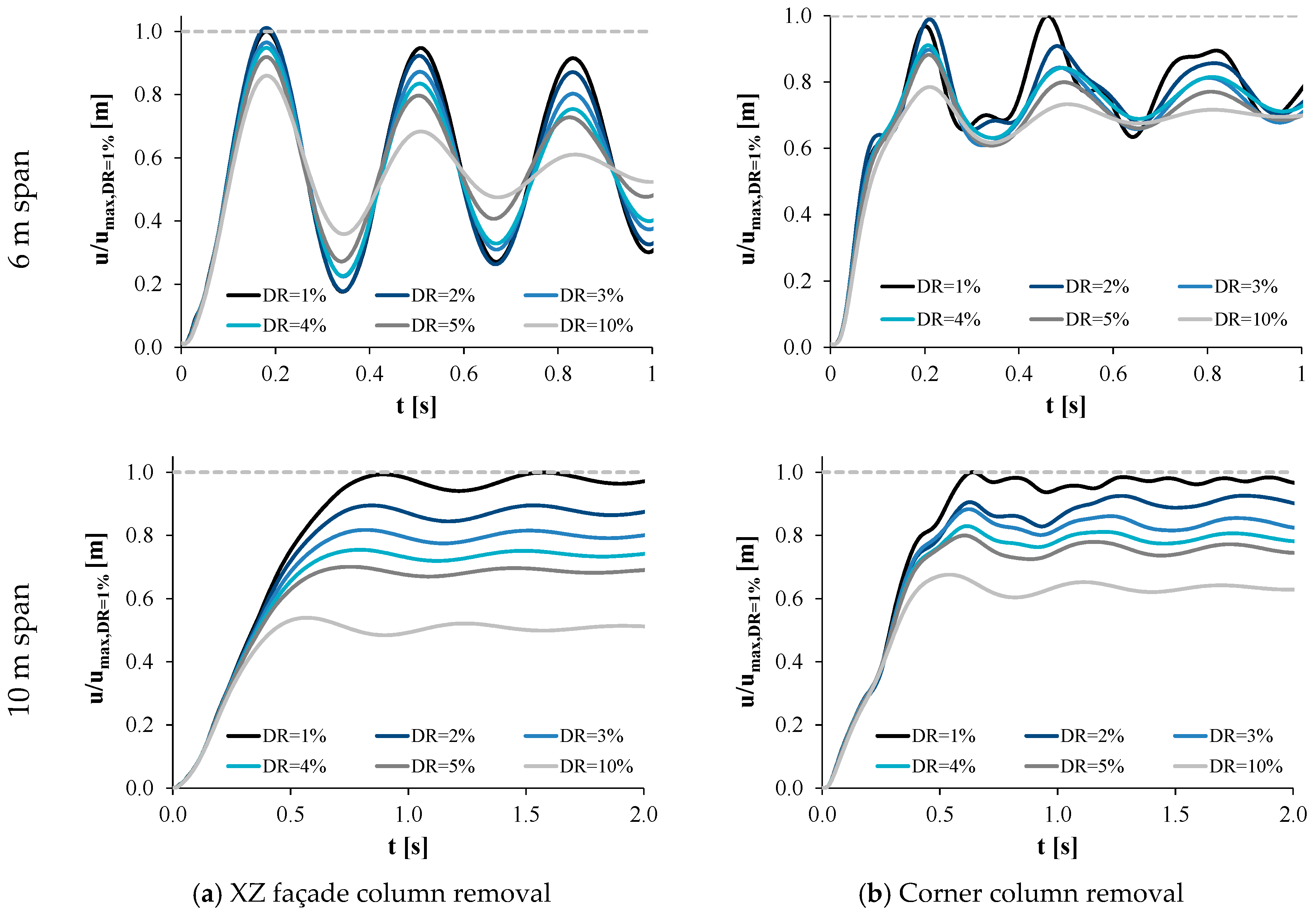
- The damping ratio (DR): This parameter was found to significantly affect the dynamic response under column loss [46]; a sensitivity analysis was performed to investigate the influence of the damping ratio, by varying it between 1% and 10%, and to determine the value to be assumed during the NDA.
- Vertical displacement under column loss was monitored.
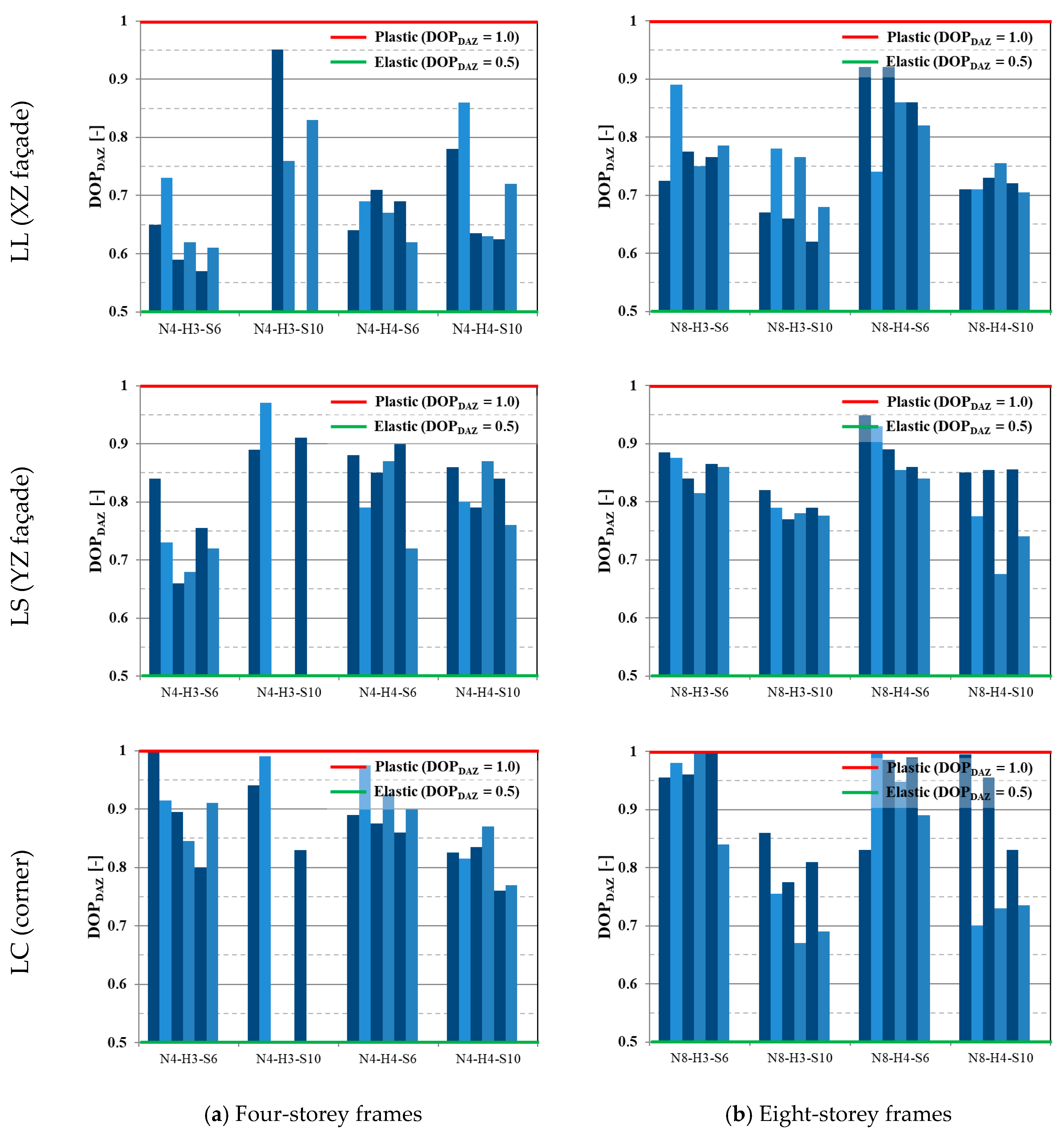
- To quantify the capacity of the system to mobilise plasticity for arresting the progressive collapse, the degree of plasticity (DOP) in the directly affected zones (DAZs) (DOPDAZ) was computed as follows:The DOPDAZ can vary between 0.5 for a fully elastic DAZ response and 1 for perfectly plastic behaviour. This ratio enables the quantification of the capacity of different structural typologies to mobilise plasticity for arresting the progressive collapse.
- Rotational demand: The total chord rotational demand ϕ was computed as the arctangent of the ratio between the maximum dynamic vertical displacement udyn,max,damaged and the span L.
- To quantify the system’s reserve displacement capacity, the Residual Ductility Ratio (RDR) was computed as follows:where (uu,damaged) is the system’s displacement immediately prior to global collapse and (udyn,damaged) is the maximum dynamic displacement evaluated through NDA.
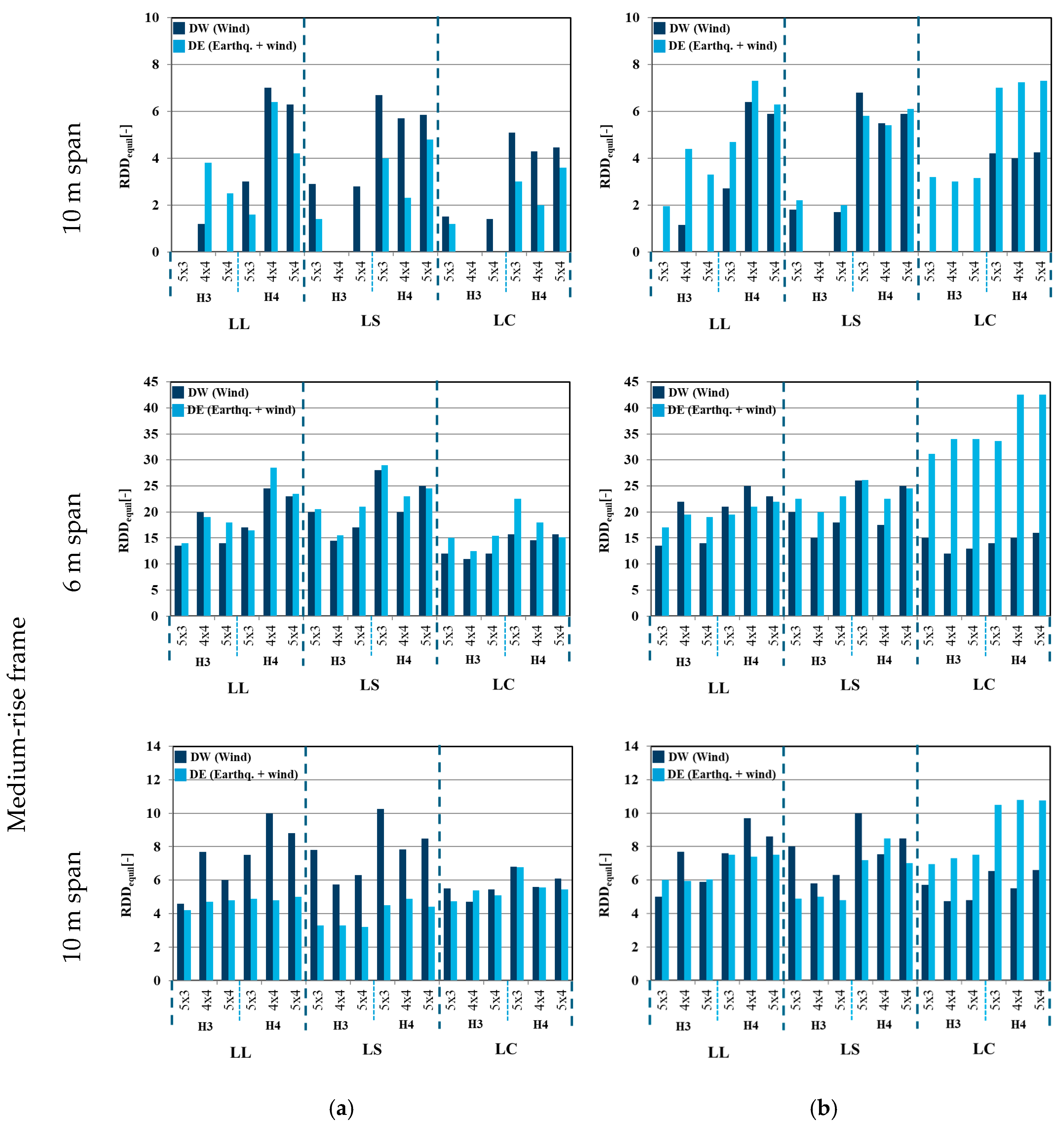
- To assess the structural safety in post-seismic scenarios involving column loss, the system’s residual ductility was evaluated through the RDDequil ratio, defined as the ratio between the ultimate displacement capacity uu,damaged and the stabilised dynamic equilibrium displacement after damage, udyn,equil,damaged (see Equation (6)). This parameter provides a more realistic measure of the reserve capacity at the time of potential rescue interventions, compared to ratios based on the peak dynamic response.
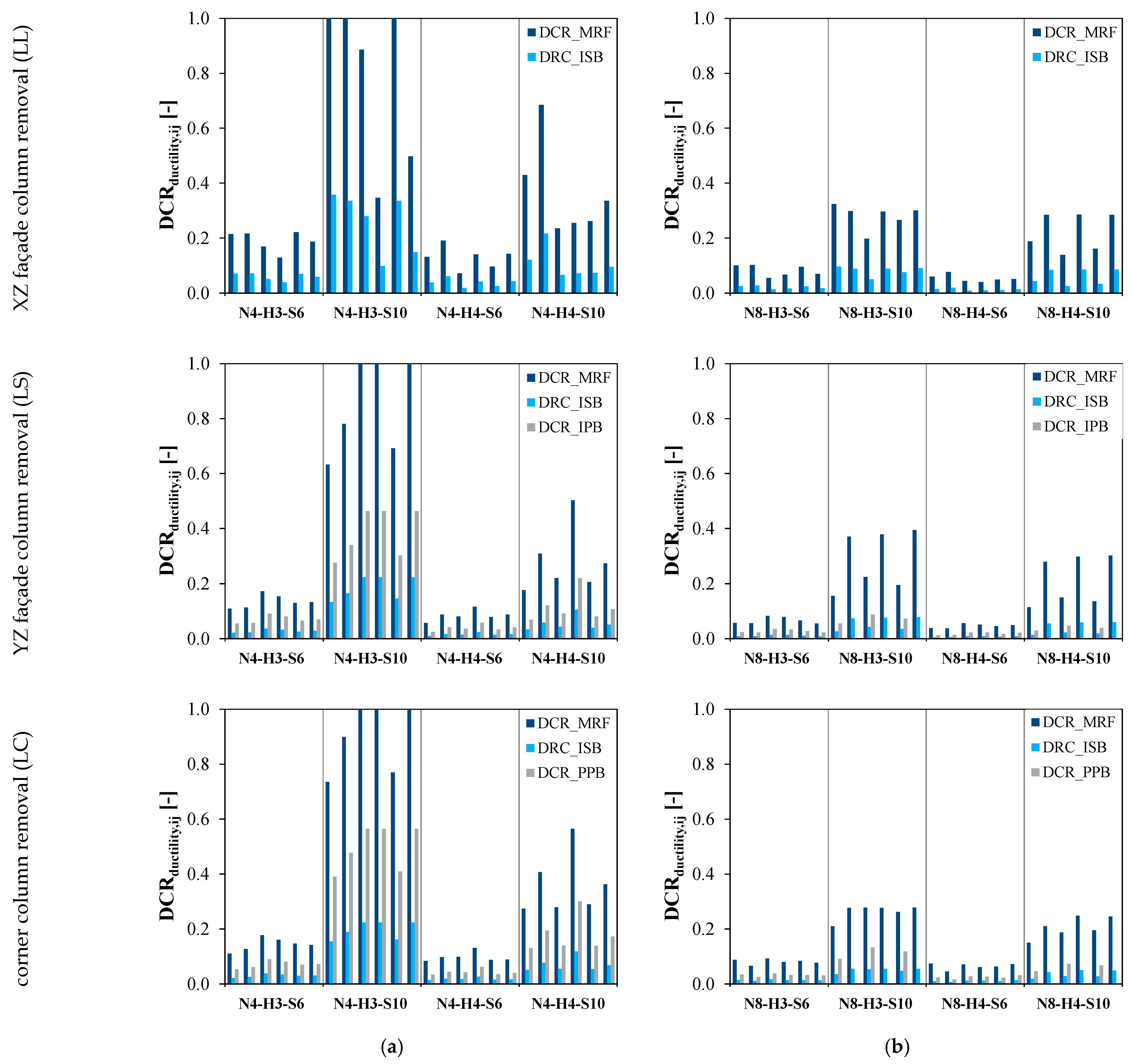
- Additionally, ductility demand-to-capacity ratios (DCRductility) were computed for moment-resisting frame (MRF) members and secondary gravity frame components to identify the structural elements most susceptible to ductility demands exceeding their capacity, thus clarifying retrofit priorities and contributing to the development of design recommendations aimed at enhancing global structural robustness. The ductility DCR ratio for member i in structure j was computed according to the following expression:where (udyn,damaged,j) is the maximum dynamic displacement (or rotation) subsequent to column removal in structure j (depends on the characteristics of structure j and all members i), i.e., the ductility demand, whereas (uu,damaged,i) is the ultimate displacement (or rotation) capacity of member i when subjected to column loss action (is independent of the characteristics of structure j), i.e., the member ductility capacity.
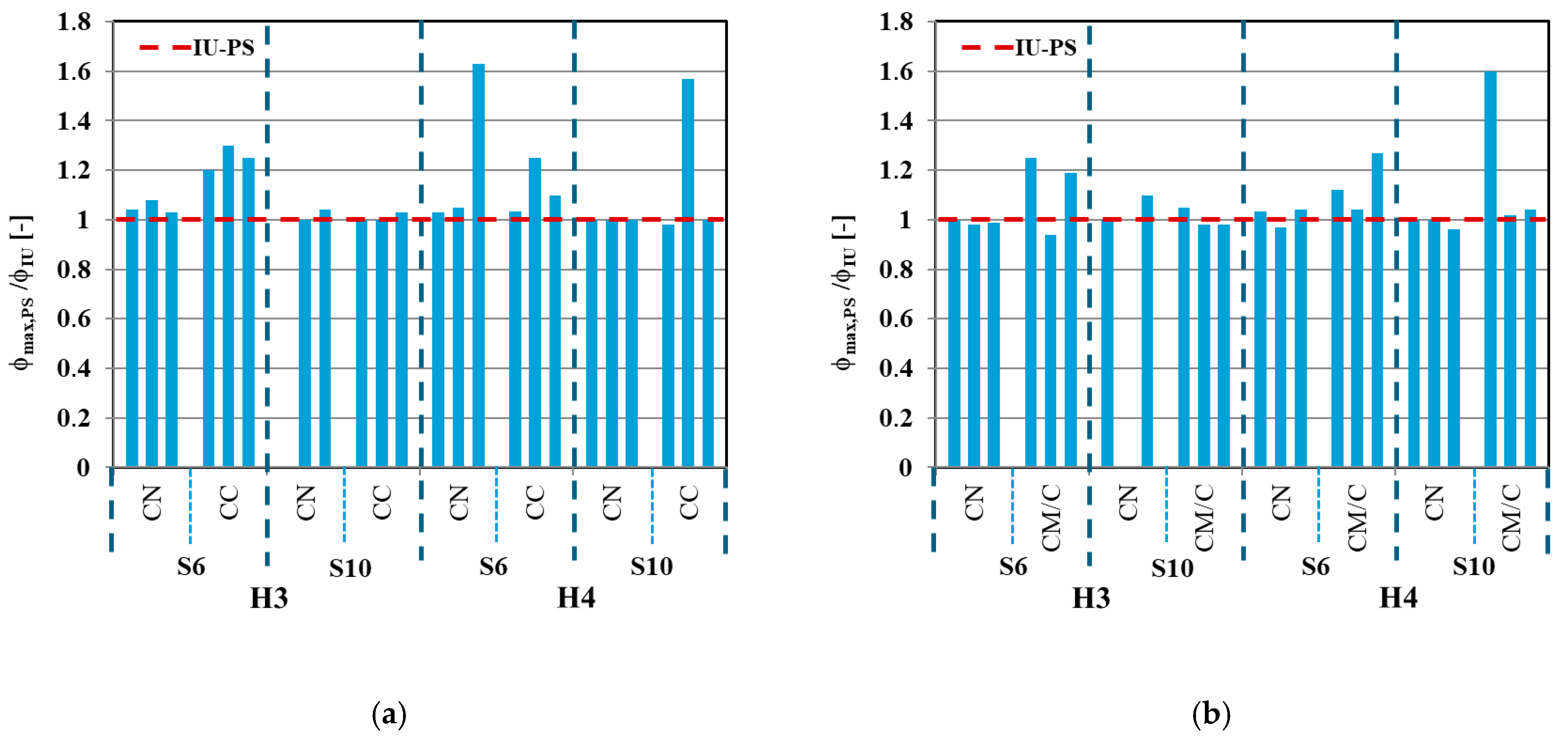
4. Results
4.1. Baseline Robustness
4.1.1. Sensitivity to Damping Ratio
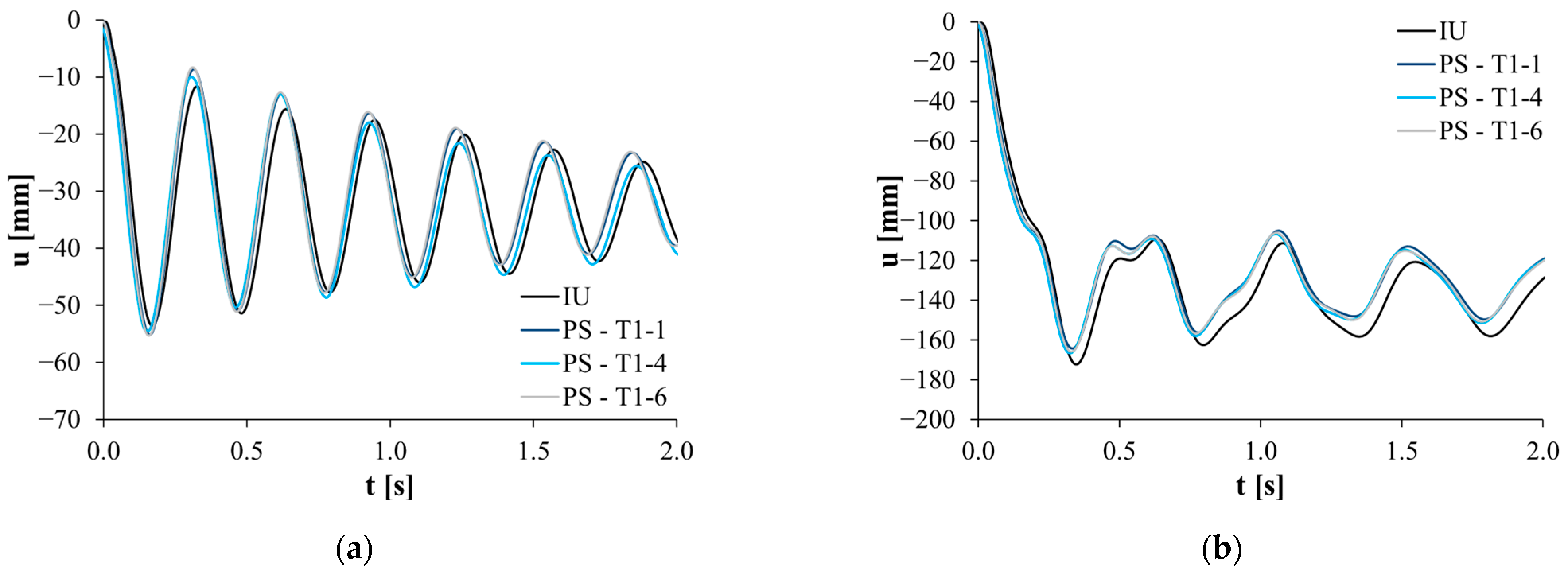
4.1.2. Displacement Time History Under Column Loss
4.1.3. Degree of Plasticity of Directly Affected Zones
4.1.4. Reserve Displacement Ductility (RDDequil)
4.1.5. Demand-to-Capacity Ratios (DCRductility,ij)
4.2. Post-Seismic Robustness
5. Concluding Remarks
- The initial sensitivity tests show maximum dynamic displacements to be sensitive to the damping ratio.
- The analysis revealed that long-span, low-rise frames (e.g., four-storey frames with 10 m spans) proved to be particularly vulnerable to progressive collapse, exhibiting displacement demands roughly ten times higher than those of shorter-span frames. Conversely, higher-rise frames demonstrated enhanced internal redistribution capabilities due to increased Vierendeel action, yielding approximately 3–4 times higher (around 21.5 versus roughly 6.3) Reserve Displacement Ductility (RDD) values.
- The reserve ductility ratio (RDD) was used to assess the safety margin after stabilisation. While medium-span frames showed robust behaviour (RDD ≈ 6.3), several long-span configurations had RDD values close to 1.0, indicating imminent collapse.
- The role of non-structural claddings was also analysed. Cold-formed steel (CFS) claddings contributed effectively to robustness by reducing joint rotation demands and increasing energy dissipation. In contrast, masonry claddings were less effective, often failing to mobilise tensile resistance due to early fracture or detachment. The cladding contribution was particularly relevant in corner column loss scenarios.
- Prior seismic damage introduced in the simulations had only a limited effect, increasing the rotational demands by roughly 5–10% compared with the undamaged state. Displacement histories and maximum rotations remained largely unchanged, suggesting that moderate earthquake damage may not significantly compromise the structure’s resistance to progressive collapse.
- These results imply that for the analysed structural type, the design for progressive collapse in post-seismic scenarios can be made analogously to the initially undamaged structure scenario.
- Further experimental studies are needed to characterise the overall robustness of steel moment frames, including the influence of non-structural elements.
- The importance of maintaining joint integrity and catenary capacity in perimeter beams;
- The vulnerability of frames with long spans and unbraced layouts to the loss of vertical support;
- The limited contribution of non-structural claddings to post-seismic robustness unless properly anchored.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cassiano, D.; D’Aniello, M.; Rebelo, C.; Landolfo, R.; da Silva, L.S. Influence of seismic design rules on the robustness of steel moment resisting frames. Steel Compos. Struct. 2015, 21, 479–500. [Google Scholar] [CrossRef]
- Marchand, K.; McKay, A.; Stevens, D.J. Development and application of linear and nonlinear static approaches in UFC 4-023-03. In Proceedings of the Structures Congress 2009: Don’t Mess with Structural Engineers: Expanding Our Role, Austin, TX, USA, 30 April 2009. [Google Scholar] [CrossRef]
- Sadek, F.; Main, J.A.; Lew, H.S.; Bao, Y. Testing and Analysis of Steel and Concrete Beam-Column Assemblies under a Column Removal Scenario. J. Struct. Eng. 2011, 137, 881–892. [Google Scholar] [CrossRef]
- Krawinkler, H. System performance of steel moment resisting frame structures. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland: New Zealand Society for Earthquake Engineering, Salt Lake City, UT, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Comeliau, L.; Demonceau, J.F.; Jaspart, J.P. Robustness of steel and composite buildings under impact loading. In Proceedings of the SDSS’Rio 2010 Stability and Ductility of Steel Structures, Rio de Janeiro, Brazil, 8–10 September 2010. [Google Scholar]
- Guo, L.; Zhang, S.; Shen, S. Numerical investigation on progressive collapse resistance of steel moment frames under column loss scenario. Eng. Struct. 2015, 86, 95–104. [Google Scholar] [CrossRef]
- Augusto, H.; Silva, L.S.; Rebelo, C.; Castro, J.M. Cyclic behaviour characterisation of web panel components in bolted end-plate steel joints. J. Constr. Steel Res. 2016, 160, 101–108. [Google Scholar] [CrossRef][Green Version]
- Pandikkadavath, M.S.; Nair, A.K.M.; Menon, A. Seismic Robustness Assessment of Steel Moment-Resisting Frames Employing Material Uncertainty Incorporated Incremental Dynamic Analysis. J. Constr. Steel Res. 2022, 191, 107200. [Google Scholar] [CrossRef]
- André, J.; Anghileri, M.; Belletti, B.; Biondini, F.; Caspeele, R.; Demonceau, J.; Izzuddin, B.; Martinelli, P.; Molkens, T.; O’Connor, A.; et al. Guidance on the Design for Structural Robustness; JRC Technical Report EUR 32018; Publications Office of the European Union: Luxembourg, 2024; ISBN 978-92-68-19818-6. [Google Scholar] [CrossRef]
- Masoero, E.; Wittel, F.K.; Herrmann, H.J.; Chiaia, B.M. Hierarchical Structures for a Robustness-Oriented Capacity Design. In Proceedings of the 12th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP12), Vancouver, BC, Canada, 12–15 July 2015. [Google Scholar]
- Zhang, Y.; Wang, J.; Gao, S.; Wang, S.; Fu, F. Tensile resistance of bolted angle connections in the beam-column joint against progressive collapse. Eng. Struct. 2021, 236, 112106. [Google Scholar] [CrossRef]
- Myers, A.T.; Kanvinde, A.M.; Deierlein, G.G. Calibration of the SMCS Criterion for Ductile Fracture in Steels: Specimen Size Dependence and Parameter Assessment. J. Eng. Mech. 2010, 136, 1401–1410. [Google Scholar] [CrossRef]
- Parisi, F.; Augenti, N. Influence of seismic design criteria on blast resistance of RC framed buildings: A case study. Eng. Struct. 2012, 44, 78–93. [Google Scholar] [CrossRef]
- Khandelwal, K.; El-Tawil, S.; Kunnath, S.; Lew, H. Macromodel-Based Simulation of Progressive Collapse: Steel Frame Structures. J. Struct. Eng. 2008, 137, 1070–1078. [Google Scholar] [CrossRef]
- EN 1998-1; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. CEN: Brussels, Belgium, 2004.
- United States of America Department of Defense. Unified Facilities Criteria: Design of Buildings to Resist Progressive Collapse; U.S. Department of Defense: Washington, DC, USA, 2013.
- Wang, Y.; Yang, J.; Tian, Y. Seismic performance of steel moment and hinged frames with rocking shear walls. J. Build. Eng. 2021, 50, 104121. [Google Scholar] [CrossRef]
- Farazman, S.; Izzudin, B.; Cormie, D. Influence of unreinforced masonry infill panels on the robustness of multi-story buildings. J. Perform. Constr. Facil. 2012, 27, 392. [Google Scholar] [CrossRef]
- Fiorino, L.; Macillo, V.; Terracciano, G.; Iuorio, O.; Landolfo, R. The influence of masonry infill panels on the robustness of steel frames. J. Constr. Steel Res. 2014, 98, 209–221. [Google Scholar]
- United States of America Department of Defense. United Facilities Criteria (UFC)—Design of Buildings to Resist Progressive Collapse; United States of America Department of Defense: Washington, DC, USA, 2009.
- EN 1991-1-7; Eurocode 1—Actions on Structures—Part 1–7: General Actions—Accidental Actions. CEN: Brussels, Belgium, 2006.
- EN 1993-1-1; Eurocode 3—Design of Steel Structures—Part 1: General Rules and Rules for Buildings. CEN: Brussels, Belgium, 2005.
- EN 1991-1-4; Eurocode 1—Actions on Structures—Part 1–4: General Actions—Wind Actions. CEN: Brussels, Belgium, 2005.
- D’Aniello, M.; Tartaglia, R.; Costanzo, S.; Landolfo, R. Seismic design of extended stiffened end-plate joints in the framework of Eurocodes. J. Constr. Steel Res. 2017, 128, 512–527. [Google Scholar] [CrossRef]
- Safaei, S.; Erfani, S. Developing energy-based loading protocols for seismic evaluation of steel moment frames’ components. J. Constr. Steel Res. 2020, 174, 106306. [Google Scholar] [CrossRef]
- Dias, J.; Castro, J.M.; Romão, X.; Gonçalves, M.; Lopes, J.C. SelEQ: A web-based application for the selection of earthquake ground motions for structural analysis. In Proceedings of the 14th European Conference on Earthquake Engineering, Ohrid, North Macedonia, 30 August–3 September 2010. [Google Scholar]
- Seismosoft. SeismoStruct v2025—Release 2—A Computer Program for Static and Dynamic Nonlinear Analysis of Framed Structures. 2011. Available online: www.seismosoft.com (accessed on 12 October 2022).
- Alashker, Y.; Li, H.; El-Tawil, S. Approximations in Progressive Collapse Modeling. J. Struct. Eng. 2011, 137, 914–924. [Google Scholar] [CrossRef]
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded R.C. plane frames including changes in geometry and non-elastic behaviour of elements under combined normal force and bending. In Proceedings of the Symposium on the Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads, Lisbon, Portugal, 13–14 September 1973. [Google Scholar]
- Xu, C.; Zhang, L.; Su, Q.; Abbas, S. Mechanical behavior of a novel steel–concrete joint in concrete-composited hybrid continuous bridges. Structures 2022, 36, 291–302. [Google Scholar] [CrossRef]
- Dubina, D.; Ciutina, A.; Stratan, A. Cyclic Tests of Double-Sided Beam-to-Column Joints. J. Struct. Eng. 2001, 127, 129–136. [Google Scholar] [CrossRef]
- Schneider, S.P.; Amidi, S. Influence of Panel Zone Behavior on Seismic Performance of Steel Moment Connections. Eng. J. 1998, 35, 114–125. [Google Scholar]
- Krawinkler, H. Shear in Beam-Column Joints in Seismic Design of Steel Frames. Eng. J. 1978, 15, 82–91. [Google Scholar] [CrossRef]
- Gupta, A.; Krawinkler, H. Influence of Column Web Stiffening on the Seismic Behaviour of Beam-to-Column Joints; Stanford University: Stanford, CA, USA, 1999. [Google Scholar]
- Kim, K.; Engelhardt, M.D. Development of Analytical Models for Earthquake Analysis of Steel Moment Frames; Report No. PMFSEL 95-2; Departiment of Civil Engineering, University of Texas at Austin: Austin, TX, USA, 1995. [Google Scholar]
- Cassiano, D.; D’Aniello, M.; Rebelo, C. Parametric finite element analyses on flush end-plate joints under column removal. J. Constr. Steel Res. 2017, 137, 77–92. [Google Scholar] [CrossRef]
- Cassiano, D.; D’Aniello, M.; Rebelo, C. Seismic behaviour of gravity load designed flush end-plate joints. Steel Compos. Struct. 2018, 26, 621–634. [Google Scholar] [CrossRef]
- Liu, C.; Tan, K.H.; Fung, T.C. Dynamic behaviour of web cleat connections subjected to sudden column removal scenario. J. Constr. Steel Res. 2013, 86, 92–106. [Google Scholar] [CrossRef]
- Yang, B.; Tan, K.H. Component-based model of bolted-angle connections subjected to catenary action. In Proceedings of the 10th International Conference on Advances in Steel Concrete Composite and Hybrid Structures, Singapore, 2–4 July 2012; pp. 654–661. [Google Scholar]
- Yang, B.; Tan, K. Experimental tests of different types of bolted steel beam-column joints under a central-column removal scenario. Eng. Struct. 2013, 54, 112–130. [Google Scholar] [CrossRef]
- Polyakov, S.V. On the Interaction Between Masonry Filler Walls and Enclosing Frame When Loaded in the Plane of the Wall; Translations in Earthquake Engineering; Earthquake Engineering Research Institute: San Francisco, CA, USA, 1960; pp. 36–42. [Google Scholar]
- Holmes, M. Steel frames with brickwork and concrete infilling. Proc. Inst. Civ. Eng. 1961, 19, 473–478. [Google Scholar] [CrossRef]
- Markulak, D.; Radic, J.; Sigmund, V. Experimental investigation of the behavior of steel frames with infill masonry panels. Eng. Struct. 2013, 51, 278–286. [Google Scholar]
- Iuorio, O.; Macillo, V.; Terracciano, M.T.; Pali, T.; Fiorino, L.; Landolfo, R. Seismic response of CFS strap-braced stud walls: Experimental investigation. Thin-Walled Struct. 2014, 85, 466–480. [Google Scholar] [CrossRef]
- Centre for the Protection of National Infrastructure. Review of International Research on Structural Robustness and Disproportionate Collapse; Department for Communities and Local Government: London, UK, 2011.
- Kim, J.; Park, J.-H.; Lee, T.-H. Sensitivity analysis of steel buildings subjected to column loss. Eng. Struct. 2011, 33, 421–432. [Google Scholar] [CrossRef]
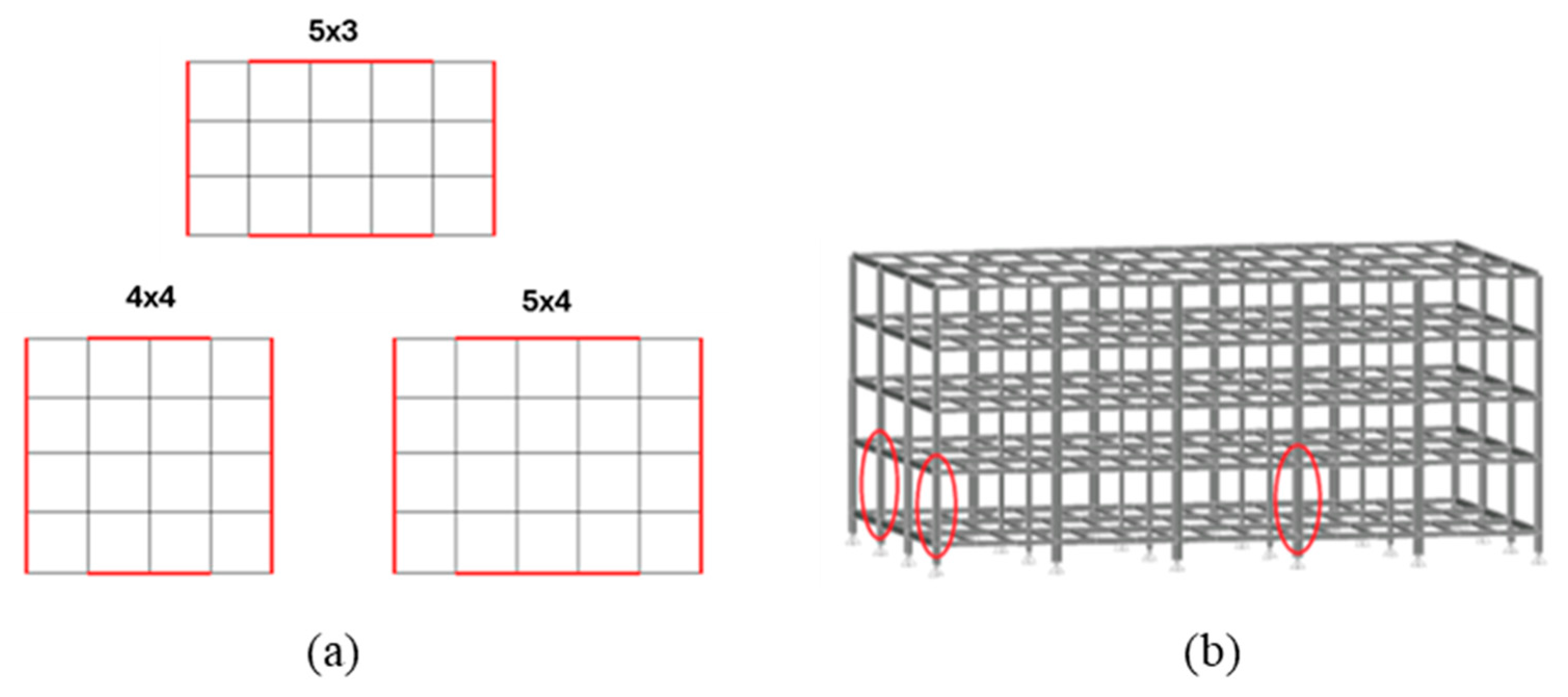



| Parametric Variable | Admissible Values |
|---|---|
| (N) Number of storeys | 4; 8 |
| (H) Interstorey height | 3 m (3.5 m between gr. and 1st floor); 4 m (4.5 m between gr. and 1st floor) |
| (S) Bay span | 6 m; 10 m |
| (C) Façade claddings | None (N); brick masonry (M—for wind-designed frames); Cold-formed steel “X” bracing (C—for seismically designed frames) |
| (T) Bay plan layout | 3 × 5; 4 × 4; 5 × 4 |
| (D) Lateral force design scenario | Wind-designed (W); seismic- + wind-designed (E) |
| (L) Column removal scenario | XZ façade (L); XY façade (S); corner (C) |
| Type of Load | Location | Value |
|---|---|---|
| Permanent structural load | All storeys | 1.7 kN/m2 |
| Permanent non-structural load | Ground floor | 1.2 kN/m2 |
| i-th floor | 1.4 kN/m2 | |
| Roof | 1.2 kN/m2 | |
| Live loads | Ground floor | 4.0 kN/m2 |
| i-th floor | 3.0 kN/m2 | |
| Roof | 0.4 kN/m2 |
| Signal Designation | Earthquake Name | Year | Magnitude | Station Name | Station Soilvs,30 [m/s] |
|---|---|---|---|---|---|
| T1-1 | Tabas, Iran | 1978 | 7.35 | Dayhook | 659.6 |
| T1-2 | Loma Prieta | 1989 | 6.93 | SF—Diamond Heights | 582.9 |
| T1-3 | Chi-Chi, Taiwan | 1999 | 7.62 | ILA064 | 375.3 |
| T1-4 | Coyote Lake | 1979 | 5.74 | San Juan Bautista, 24 Polk St | 370.8 |
| T1-5 | Chi-Chi, Taiwan | 1999 | 7.62 | TCU072 | 468.1 |
| T1-6 | Coalinga-01 | 1983 | 6.36 | Parkfield—Gold Hill 2W | 376.1 |
| T1-7 | Chi-Chi, Taiwan | 1999 | 7.62 | TCU046 | 465.6 |
| T1-8 | Chi-Chi, Taiwan-06 | 1999 | 6.30 | CHY035 | 473.9 |
| T1-9— | Chi-Chi, Taiwan-03 | 1999 | 6.20 | TCU138 | 652.9 |
| T1-10 | Chi-Chi, Taiwan | 1999 | 7.62 | HWA035 | 473.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costanzo, S.; Cassiano, D.; D’Aniello, M. Robustness of Steel Moment-Resisting Frames Under Column Loss Scenarios with and without Prior Seismic Damage. Buildings 2025, 15, 2490. https://doi.org/10.3390/buildings15142490
Costanzo S, Cassiano D, D’Aniello M. Robustness of Steel Moment-Resisting Frames Under Column Loss Scenarios with and without Prior Seismic Damage. Buildings. 2025; 15(14):2490. https://doi.org/10.3390/buildings15142490
Chicago/Turabian StyleCostanzo, Silvia, David Cassiano, and Mario D’Aniello. 2025. "Robustness of Steel Moment-Resisting Frames Under Column Loss Scenarios with and without Prior Seismic Damage" Buildings 15, no. 14: 2490. https://doi.org/10.3390/buildings15142490
APA StyleCostanzo, S., Cassiano, D., & D’Aniello, M. (2025). Robustness of Steel Moment-Resisting Frames Under Column Loss Scenarios with and without Prior Seismic Damage. Buildings, 15(14), 2490. https://doi.org/10.3390/buildings15142490