1. Introduction
In recent years, China’s large-scale infrastructure construction is developing in the direction of more professional, more standardized, and more green environmental protection, which indicates that in the construction process of engineering projects, we can no longer blindly compress the construction period or reduce the cost but need to seek the optimal balance of multiple main control objectives. The Yellow River Grand Bridge passes through the Yellow River floodplain. It is difficult to construct since it has a long construction period, consumes a lot of resources, and has a special construction environment. So it is difficult to achieve multi-objective balance [
1]. Therefore, it is of great practical significance to conduct multi-objective equilibrium optimization research on the construction of the Yellow River Grand Bridge.
At present, many scholars have conducted research on the multi-objective optimization problems of engineering projects. Zhang Fengli [
2] took the maintenance of emergency diesel engines in a nuclear power plant as the research object and established a multi-objective optimization model with the objective of execution cost and maintenance duration under the premise of considering multi-dimensional maintenance resources. A. Afshar [
3] proposed a heuristic optimal scheduling model by taking the trade-off analysis of time and cost as an important aspect of construction project planning and control, which focuses on the two key objectives of time and cost. Then, Khaled El-Rayes [
4] transformed the traditional two-dimensional time-cost trade-off analysis into an advanced three-dimensional time-cost-quality trade-off analysis, minimizing the cost and time spent in the construction process while ensuring the highest level of building quality. Zhang Lianying [
5] aimed at the uncertain factors existing in actual engineering projects. Through the fuzzy description of the interrelationships among the three objective functions of project duration, cost, and quality, a fuzzy equilibrium optimization model based on these three was established. Liu Jia [
6] conducted a systematic study on the multi-objective trade-off optimization of construction project duration, cost, and quality based on the fuzzy set theory and established a multi-objective trade-off optimization model of construction duration, cost, and quality under uncertain conditions. Xundi [
7] pointed out that previous studies mainly focused on project planning and control, focusing only on cost-time trade-offs, while project quality research based on mathematical methods was very limited. Therefore, a trade-off model for time-cost-quality performance was proposed. In order to maximize the comprehensive benefits of municipal road construction and reduce the impact of construction on the surrounding residents, Tao Jingyu [
8] introduced the environmental protection objective and constructed a multi-objective optimization model that includes construction period, quality, cost, and environmental protection. In order to solve the quality and safety issues in the planning stage, Abhilasha [
9] constructed a decision-making model involving construction period, cost, quality, and safety factors and verified the effectiveness of the model using specific engineering projects. In order to solve the time, cost, quality, and resource trade-off issues, Duc-HocTran [
10] integrated a scheduling module (M1) to determine all project goals, including time, cost, quality, and resources, and verified the performance of the model. Zeng Qiang [
11] proposed a multi-objective optimization scheduling method for tasks in large-scale engineering projects. On the basis of the three major objectives of project duration; cost; and quality, safety, and environmental issues were added, and an optimization model based on the five major objectives was obtained. Li Xuelin [
12], based on the multi-objective optimization theory, established a multi-objective optimization model for engineering projects covering project duration, cost, quality, resources, environment, and safety.
In solving multi-objective problems, intelligent optimization algorithms are gradually replacing traditional optimization methods. L. A. Zadeh [
13] was the first to use the linear weighting method to solve this type of problem. Next, Y. Y. Haime [
14] proposed a method to simplify multi-objective problems into single-objective problems by setting constraints and named it the constraint method. J. Schaffer [
15] took the lead in introducing genetic algorithms into the research of multi-objective optimization and innovatively proposed a vector-evaluated genetic algorithm. Liu Ling [
16] explored the non-linear relationship between the cost and function of engineering projects that change over time. On this basis, a multi-objective optimization model was constructed using the linear weighting method, and the optimal solution of the model was obtained through the genetic algorithm. Huo Yuyu [
17], based on the NSGA-II algorithm, established a multi-objective equilibrium optimization model of duration-robustness-resources of technical interfaces in an uncertain environment, obtained a series of Pareto optimal solution sets, and achieved coordinated optimization of various objectives. Zhuo Jinsong [
18] and others constructed a linear model of duration, cost, and quality for a certain construction engineering project and optimized it using the standard particle swarm algorithm, verifying the practicality of the particle swarm algorithm in solving multi-objective optimization problems. Gao Ying [
19] integrated the idea of the simulated annealing algorithm into the standard particle swarm algorithm and introduced the sudden jump mechanism in this algorithm, which greatly enhanced the rapid convergence ability of the particle swarm algorithm in the search space. Ukoima Kelvin Nkalo [
20] proposed and utilized an improved multi-objective particle swarm optimization algorithm by integrating the ant colony algorithm into the particle swarm algorithm to optimize the solar–wind–battery hybrid renewable energy system in rural communities of Rivers State, Nigeria. Wu Yuefeng [
21] combined the traditional grey wolf optimization algorithm with the shuffled frog leaping algorithm to conduct multi-objective optimization for micro-service container scheduling. Most of the abovementioned studies adopted a single algorithm for solution, which has certain limitations. Although some scholars have already attempted to combine two different intelligent algorithms, they failed to achieve practical application in the multi-objective optimization of bridge construction projects.
In summary, it can be seen that domestic and foreign scholars have continuously applied new technologies and methods to the solution of multi-objective optimization problems based on in-depth studies of multi-objective optimization theory for engineering projects and have extended their research scope to engineering construction. The research on multi-objective optimization problems at home and abroad is undergoing important evolution, which is mainly reflected in two aspects as follows:
- (1)
In the study of multi-objective systems, research on multi-objectives has gradually expanded to comprehensive investigations, including multiple dimensions such as safety, resources, the environment, and carbon emissions. Additionally, methods for studying the relationships between objectives are shifting from traditional linear models to non-linear models, aiming to reveal the complex interactions among construction duration, cost, and quality and make them more consistent with engineering practices.
- (2)
In terms of solving multi-objective problems, intelligent optimization algorithms are gradually replacing traditional optimization methods. However, most studies only use a single algorithm for solving, which has certain limitations. Although some scholars have attempted to combine two different intelligent algorithms, this approach has not been practically applied in multi-objective optimization for bridge construction projects.
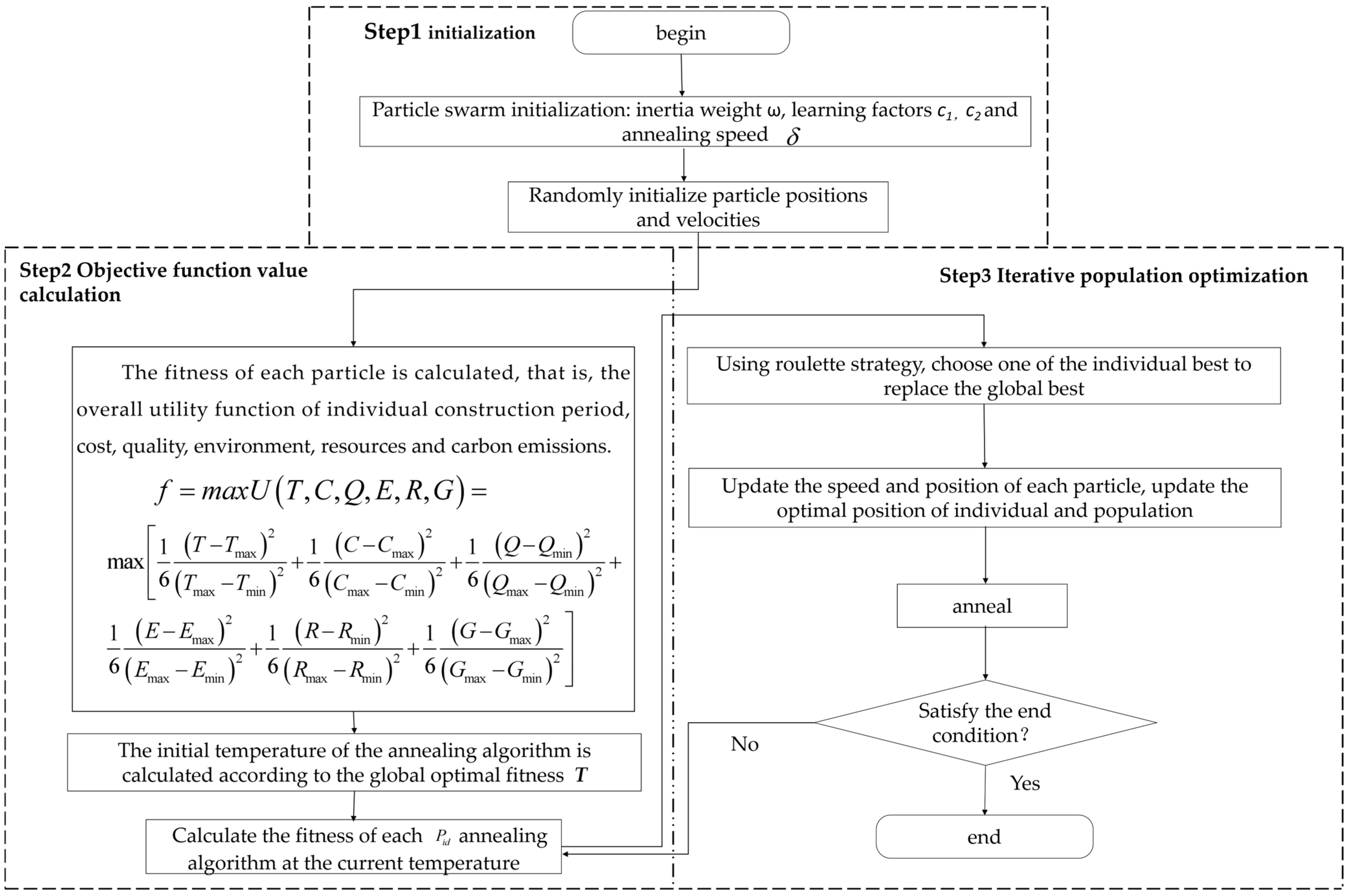
Therefore, in order to fill the gap in multi-objective optimization research for bridge construction and solve various problems caused by the complex terrain, changeable climate, high sediment content, and complicated construction procedures in the Yellow River Basin, including low quality, resource waste, and environmental pollution, so as to achieve the balance of multiple objectives. This article aims to combine the environment, resource, and carbon emission goals in green construction with the traditional three goals, conduct a comprehensive analysis, build a multi-objective balanced optimization model that is consistent with engineering reality, and combine the particle swarm algorithm and simulated annealing algorithm. Combined with this, the multi-objective optimization model for the construction of the Yellow River Grand Bridge is solved to find more ideal construction decisions.
5. Prospect
The multi-objective optimization problem in bridge engineering construction has always been a hot topic in the transportation industry. In recent years, with the deepening of the concept of sustainable development, the promotion of green construction technologies, and the implementation of the Dual Carbon policy, environment, resources, and carbon emissions have gradually become the main control objectives for multi-objective optimization. Based on this, this paper takes the Jiaoping Expressway Yellow River Super Large Bridge as a case study, establishes a multi-objective equilibrium optimization model for construction period-quality-cost-environment-resources-carbon emissions in its construction, and uses the Simulated Annealing Particle Swarm Optimization (SA-PSO) algorithm to solve the model. However, due to limitations in personal capabilities, data availability, and the complexity of the Yellow River Bridge project itself, there are still many shortcomings that need further improvement and in-depth research.
- (1)
Incomplete consideration in analyzing influencing factors and constructing objective models
When analyzing the influencing factors of each objective and constructing objective models in combination with the actual construction of the Yellow River Super Large Bridge, the consideration was not comprehensive enough, especially for the three objectives of quality, environment, and resources. Only a few representative influencing factors were selected, lacking consideration of other relevant influencing factors. Moreover, the established models are relatively idealized. It is necessary to deeply engage with engineering practices, consider multiple perspectives comprehensively, and ensure that the constructed models can better guide project construction.
- (2)
Inadequate accounting of carbon emissions
Due to conditional limitations, the research on carbon emissions only accounted for the carbon emissions from three parts of the construction process: building material production, material transportation, and mechanical construction. Carbon emissions from workers’ production and daily life, lighting facilities, and other aspects throughout the project construction process were ignored. In future research, it is necessary to further supplement and improve this aspect.