Pressure-Amplified Structural Superiority in Silty Clays: Dynamic Divergence Between Undisturbed and Remolded States

Abstract

Silty clay is extensively distributed in northern China. Numerous seismic events have demonstrated that underground structures embedded in silty clay strata are prone to severe damage during earthquakes. This study employs dynamic cyclic triaxial tests on undisturbed and remolded specimens (50–300 kPa confining pressures) to pioneer the quantification of pressure-amplified structural superiority. The experimental results reveal that: (1) Undisturbed soils exhibit 20–30% higher maximum shear stress (τ_dmax) and shear modulus (G_dmax) than remolded counterparts at 300 kPa, far exceeding the <5% deviation at 50 kPa due to enhanced particle-cementation synergy under pressure. (2) The normalized shear modulus ratio (G_d/G_dmax) exhibits low sensitivity to confining pressure, with G_d/G_dmax–γ_d relationship curves predominantly confined within a narrow band range. A triphasic evolutionary characteristic is manifested in the progressive reduction of G_d/G_dmax with increasing shear strain (γ_d), and quasi-linear attenuation is observed within the shear strain range of 1 × 10⁻⁴ ≤ γ_d ≤ 1 × 10⁻². (3) Remolded and undisturbed specimens demonstrate close correspondence in damping ratio (λ_d) across consolidation pressures. Under identical γ_d conditions, undisturbed specimens consistently exhibit lower λ_d values than remolded counterparts, attributable to enhanced energy dissipation resulting from structural homogenization in remolded soils, with λ_dmax magnitudes ranging between 0.2 and 0.3. The research provides mechanistic insights for seismic design of underground structures in silty clay terrains, particularly regarding disturbance sensitivity under deep burial conditions.

1. Introduction

The shear stress (τ_d), shear modulus (G_d) and damping ratio (λ_d) are recognized as the three core parameters in soil dynamics [1,2]. They serve as the key indices for assessing the seismic performance of the soil. The factors influencing soil dynamic characteristics can be categorized into three primary aspects: (1) the inherent physical-mechanical properties of soil, including unit weight, particle size distribution, void ratio, liquid and plastic limit, compression coefficient, water content, and sensitivity; (2) the initial in situ stress conditions of undisturbed soil, defined as the confining pressure acting on soil units in their natural state; (3) dynamic loading conditions encompassing amplitude, frequency, waveform, and drainage status. These dynamic parameters can be obtained by in situ tests and laboratory tests. In situ testing effectively mitigates soil disturbance effects during sampling and transportation processes, though practical implementation is constrained by operational complexity and elevated costs, while determining G_d and λ_d through laboratory testing is more mature. Globally, τ_d, G_d and λ_d parameters have been extensively investigated through dynamic cyclic triaxial tests and resonant column tests [3,4,5,6,7,8]. Dong et al. [9] investigated the dynamic characteristics of silt under varying moisture contents and compaction degrees by accounting for rainfall infiltration and groundwater effects, concluding that the critical dynamic stress decreases with increasing moisture content but increases with higher compaction levels. Li et al. [10] performed dynamic tests on remolded lacustrine soft clay, establishing the evolution patterns of dynamic shear modulus and damping ratio. Wang [11] and Ren et al. [12] examined the influence of cyclic stress ratio (CSR), revealing accelerated accumulation of plastic deformation at higher CSR values. They further classified dynamic behaviors under cyclic loading into three states—stable, metastable, and unstable—using a threshold cyclic stress ratio concept. However, these studies predominantly target remolded soils [13,14,15], while comparative investigations into the dynamic characteristics of undisturbed and remolded silty clays remain relatively limited.

The natural structure (particle arrangement, cementation networks, and stress history) is preserved in undisturbed soils [16,17,18], whose dynamic parameters closely approximate in situ soil behavior. However, due to the high operational costs, time-consuming procedures, and low success rates of deep sampling associated with undisturbed sampling techniques, most geotechnical investigations are conducted using remolded specimens to simulate the dynamic responses of in situ soils. Undisturbed and remolded soft clay specimens were employed in Chen et al. [19] investigation to evaluate stress-level dependencies of static-dynamic deformation characteristics in structured clays. The experimental program incorporated consolidated compression tests with shear wave velocity measurements coupled with cyclic triaxial testing. It was demonstrated that structural configurations of undisturbed soils critically govern their dynamic response mechanisms under cyclic loading regimes. The effects of soil state and consolidation pressure on G_d and λ_d were investigated through dynamic cyclic triaxial testing by Song et al. [20] using undisturbed alluvial silty clays from the Eastern Henan Plain. Revealing analogous evolutionary patterns in dynamic properties between widely distributed plastic silty clay (PSC) and soft plastic silty clay (SSC), the normalized shear modulus ratio was observed to decrease with increasing shear strain, while the damping ratio exhibited a corresponding escalation. Zhao et al. [21] conducted investigations on weathered mudstone soil under varying consolidation pressures. The maximum damping ratios of remolded specimens were found to be comparable to those of in situ samples. Furthermore, the intersecting convergence of damping ratio-shear strain curves was observed when the shear strain approached 1.0. The dynamic strength characteristics of undisturbed and remolded marine silty soil were comparatively investigated by Tong et al. [22] using dynamic cyclic triaxial tests and resonant column tests. Experimental measurements revealed that undisturbed marine silty soil exhibited significantly higher dynamic shear modulus and reference shear strain values compared to their remolded counterparts under identical testing conditions, while damping ratios demonstrated comparable magnitudes between the two specimen types.

Situated within the Yellow River alluvial plain, Zhengzhou has a widespread distribution of silty clay. While recent studies on sedimentary or alluvial silty clays in regions such as Central Jiangsu, Northern Jiangsu, and Northeast China have yielded regionally applicable findings, the silty clay in Zhengzhou—characteristic of Yellow River alluvial deposits—possesses unique formation histories [23,24]. Existing research remains limited and is inapplicable to extrapolation from other regions. Substantial evidence confirms marked regional variations in soil dynamic characteristics [25,26,27,28], and direct application of mechanical properties derived from non-local silty clays to Zhengzhou engineering projects would introduce significant safety hazards. Consequently, experimental investigation into the dynamic properties of Zhengzhou’s typical silty clay is imperative for guiding regional engineering practice.

Dynamic cyclic triaxial tests were conducted on both undisturbed and remolded silty clay specimens from Zhengzhou City under confining pressures ranging from 50 to 300 kPa, to evaluate structural degradation effects on soil dynamic characteristics. Significant disparities in dynamic behaviors between the two specimen types were observed. The findings provide theoretical references for characterizing the dynamic properties of Zhengzhou’s silty clay, offering critical insights for the seismic design of underground structures in this region.

2. Materials and Methods

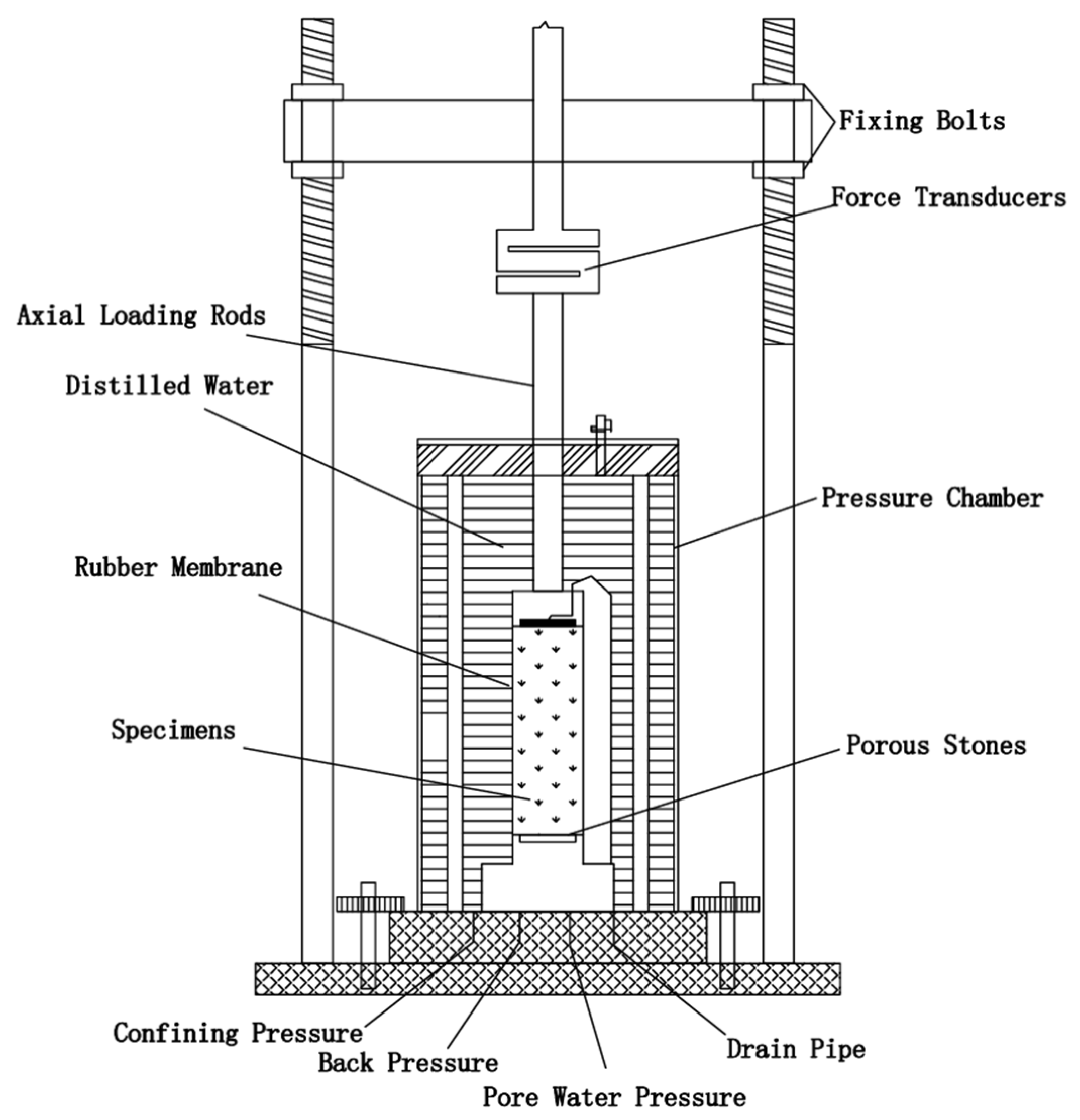
2.1. Test Apparatus

The dynamic triaxial apparatus with bidirectional control was employed in this study, with the pressure chamber capable of applying confining pressures and back pressures up to 2 MPa, as shown in Figure 1. The system operates at vibration frequencies ranging from 0 to 20 Hz, equipped with an axial displacement sensor (50 mm range, 0.01 mm accuracy), the load sensor range is ±22 KN, with an accuracy of 0.05%. This configuration facilitates advanced geotechnical investigations, including complex stress path testing, cyclic loading simulations, triaxial compression experiments, and consolidation analysis.

2.2. Specimen Preparation

Undisturbed specimens were prepared following Chinese National Standard GB/T 50123-2019 (Standard for geotechnical testing method) [29], using the standard ring cutter method for in situ cutting of a 50 mm × 100 mm cylinder to preserve the natural microstructure (cementation networks, particle arrangement) and stress state.

Table 1. Physical properties parameters of in situ.

Borehole	Depths (m)	Dry Density (g/cm3)	Liquid Limit (%)	Plastic Limit (%)	Water Content (%)
BH1	5	1.62	49.2	25.1	28.5
	10	1.73	37.3	19.3	23.6
	20	1.71	41.4	22.7	20.4
	30	1.69	45.6	28.1	21.7
BH2	6	1.65	40.3	24.7	24.6
	12	1.66	44.5	28.5	25.3
	20	1.64	37.9	21.2	22.4
	30	1.63	42.4	24.3	23.6

shows the physical property parameters of the in situ soil. The undisturbed specimen preparation process is shown in Figure 2.

Remolded specimens were prepared from remnants of soil during undisturbed specimens fabrication, dried at 105 °C for 24 h, mechanically pulverized using an agate mortar, and sieved through a 2 mm mesh. Deionized water was sprayed to achieve in situ natural moisture content, followed by 48 h of equilibrium curing in a humidity-controlled chamber. Five-layer compaction with equal energy was performed to match the in situ dry density. All layers underwent surface processing to ensure full particle interlocking by eliminating weak interfaces. Post-compaction, specimens were sealed and maintained for 48 h until suction equilibrium was achieved. The remolded specimens exhibited physical indices with ≤1.5% deviation from in situ soil, complying with the Chinese National Standard GB/T 50123-2019 requirements for homogeneity. The remolded specimen preparation process is shown in Figure 3.

2.3. Test Program

The sampling area for this study was located in a typical sedimentary silty clay site in Zhengzhou, Henan Province, China. Twenty boreholes were drilled with depths varying between 5 m and 30 m. To systematically analyze the depth-dependent dynamic properties, four groups of undisturbed soil were collected through stratified sampling from each borehole. The height and inner diameter of the soil sampling cylinder are 300 mm and 100 mm. To minimize transport-induced disturbances, specimens were secured in wire-reinforced thin-walled steel containers and subsequently encapsulated with protective membranes to prevent moisture variations caused by oxidative corrosion. Post-transportation procedures included wax-sealing all cylindrical interfaces to achieve airtight isolation, followed by storage in environmentally controlled curing chambers maintaining stable temperature and relative humidity.

BH1 and BH2, selected based on stratigraphic representativeness, underwent detailed analysis. Confining pressures (50, 100, 200, 300 kPa) were determined through the theoretical model of in situ stress field, following the depth equivalence principle where effective vertical stress (σ₃′ = γ′·h) was combined with the lateral earth pressure coefficient (K₀ = 0.5). The undisturbed and the remolded specimens were saturated by the vacuum saturation method for ≥24 h and B-value ≥ 0.95. Isotropic consolidation with a consolidation ratio of Kc = 1 was used, and the consolidation completion time was determined from the time settling curve.

A strain-controlled sinusoidal cyclic loading protocol was implemented with increasing amplitude, 10 load cycles per stage, and the loading frequency was set to 1 Hz. The undrained test conditions were maintained throughout dynamic loading to simulate seismic-induced pore water pressure accumulation during transient loading events. The test was terminated when the specimen axial strain exceeded 5% [30]. The technology roadmap is shown in Figure 4.

3. Results and Discussion

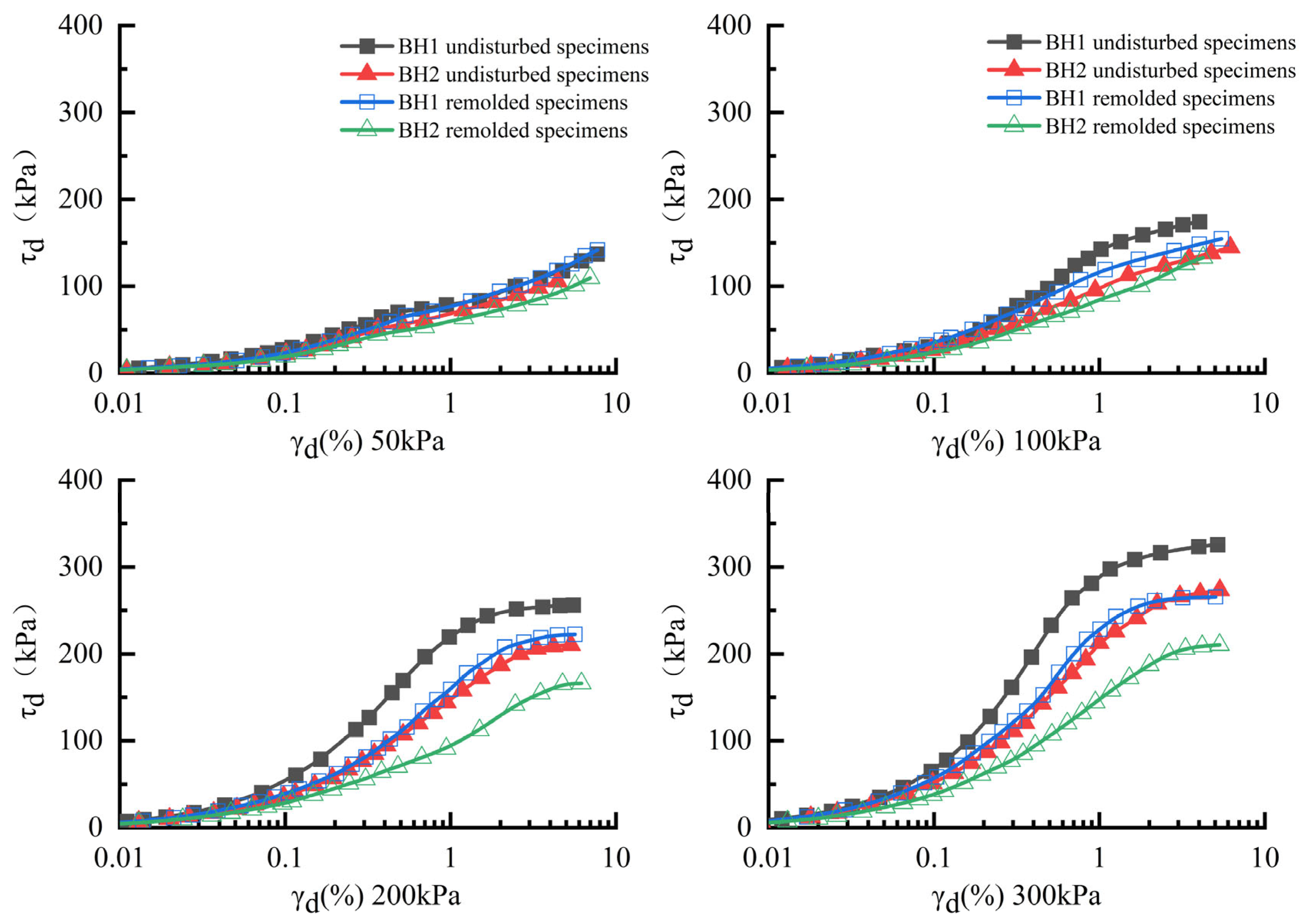
3.1. Shear Stress (τ_d)–Dynamic Strain (γ_d) Relationship

In cyclic loading analyses, the dynamic shear stress (τ_d) is operationally defined as the stress amplitude required to induce specified failure criteria at designated cyclic counts [31]. According to the principle of dynamic strength test, the equations of γ_d and τ_d can be obtained, as shown in (1)~(2) [32]. The τ_d–γ_d relationship is shown in Figure 5.

$${\tau }_d=\left({\sigma }_{1d}-{\sigma }_{3d}\right)/2$$

(1)

$${\gamma }_d={\epsilon }_d\left(1+\nu \right)$$

(2)

Formula:

• σ_1d—effective axial consolidation stress (kPa);
• σ_3d—effective lateral consolidation stress (kPa);
• ε_d—axial dynamic strain (%);
• ν—Poisson’s ratio.

As illustrated in Figure 5, the τ_d–γ_d curves of undisturbed and remolded specimens exhibit near-overlapping trajectories under low confining pressure (50 kPa), with deviation percentages remaining below 5%. With increasing confining pressure, the τ_d–γ_d curves became significantly separated, and the slope of the undisturbed specimens increased at a markedly faster rate compared to that of the remolded specimens. Undisturbed specimens retain deposition-induced particle orientation and cementation bonds, thus establishing enhanced frictional-interlocking synergy via preserved geological fabrics. In contrast, remolded specimens undergo structural homogenization during disturbance processes, with cementation bond fracturing reducing shear resistance to interparticle friction-dominated mechanisms. This structural degradation diminishes confinement sensitivity in remolded specimens compared to undisturbed counterparts, indicating that greater stiffness retention capacity is exhibited by soils with intact structure.

The maximum dynamic shear stress (τ_dmax) of undisturbed and remolded specimens under various confining pressures is summarized in

Table 2. Maximum dynamic shear stress under various confining pressures of undisturbed and remolded specimens.

Borehole	Specimen Type	Experimental State	Confining Pressure (kPa)	τdmax (kPa)	Borehole	Specimen Type	Experimental State	Confining Pressure (kPa)	τdmax (kPa)
BH1	Undisturbed specimens	Saturation	50	137	BH2	Undisturbed specimens	Saturation	50	106
			100	174				100	144
			200	256				200	210
			300	325				300	273
	Remolded specimens	Saturation	50	134		Remolded specimens	Saturation	50	101
			100	155				100	132
			200	222				200	166
			300	265				300	210

. A progressive enhancement in the discrepancy of τ_dmax between undisturbed and remolded specimens is demonstrated with increasing confining pressure under identical experimental conditions. For BH1, the percentage deviation of τ_dmax in remolded specimens relative to the undisturbed specimens exhibits a nonlinear rise from 2.2% to 22.6% as the confining pressure is increased from 50 kPa to 300 kPa. Similarly, for BH2, a sharp escalation in τ_dmax deviation is recorded, increasing from 4.9% at 50 kPa to 30% at 300 kPa. The reduction in τ_dmax of remolded specimens relative to undisturbed specimens under confining pressures ranging from 50 kPa to 300 kPa can be detailed as follows:

BH1: 50 kPa (−2.2%)→100 kPa (−12.2%)→200 kPa (−15.3%)→300 kPa (−22.6%)

BH2: 50 kPa (−4.9%)→100 kPa (−9.1%)→200 kPa (−26.5%)→300 kPa (−30%)

Experimental data indicate that the influence intensity of soil disturbance on the τ_dmax demonstrates a near-exponential increase with confining pressure elevation, while the structural superiority of undisturbed soil is amplified under high confining pressures.

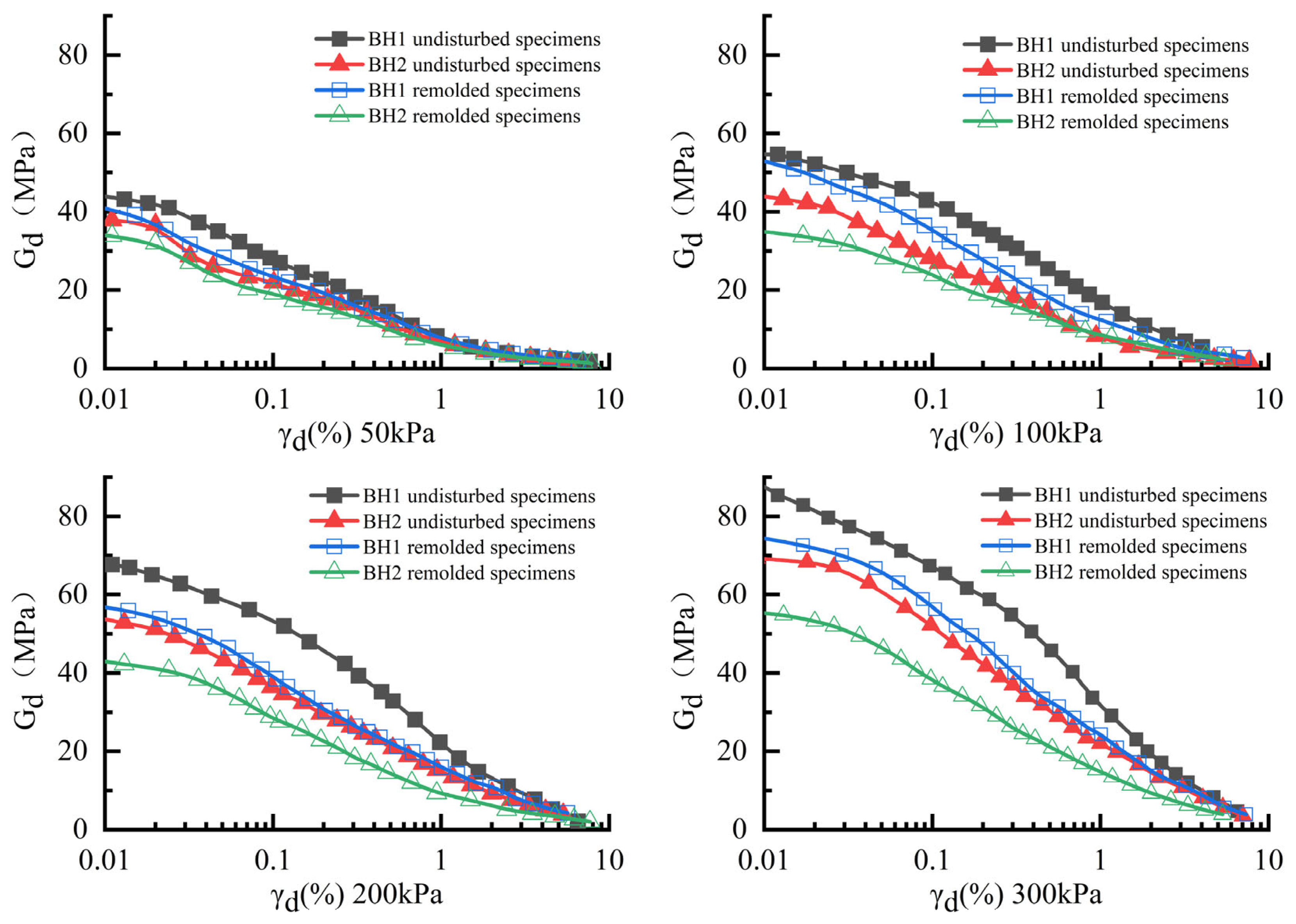
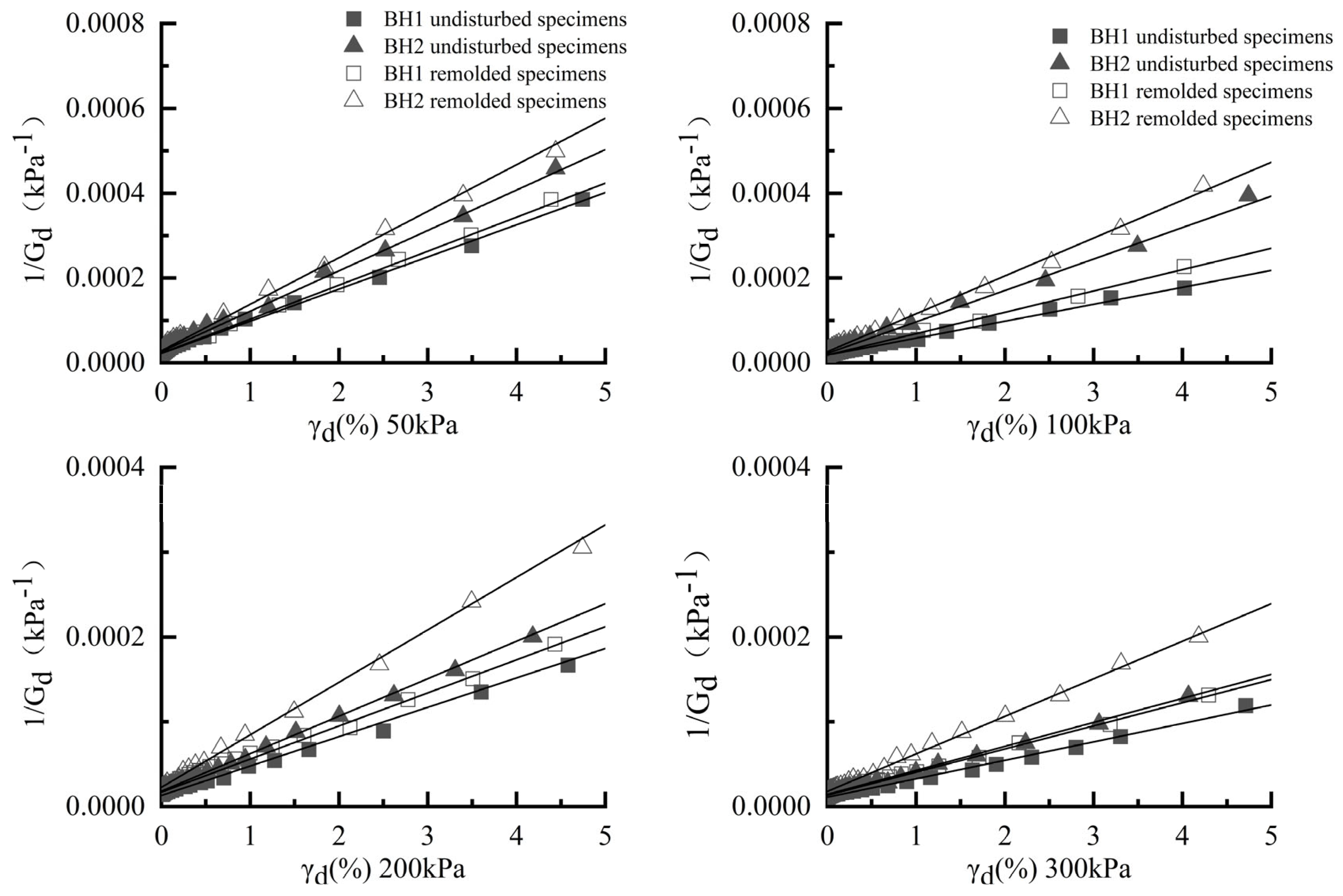
3.2. Shear Modulus (G_d)–Dynamic Strain (γ_d)

The G_d–γ_d relationship curves of undisturbed and remolded specimens under different confining pressures are shown in Figure 6. It can be observed that under identical experimental conditions, the G_d values of both undisturbed and remolded specimens gradually decrease with increasing γ_d, and the decreasing rate of G_d is progressively reduced as γ_d increases. When the confining pressure is relatively low, the discrepancy between the G_d–γ_d curves of undisturbed and remolded specimens is found to be less than 5%. As the confining pressure increases, a rapid divergence between the G_d–γ_d curves of undisturbed and remolded specimens is observed. The separation amplitude of the G_d–γ_d relationship curves is demonstrated to increase with ascending confining pressure, which confirms the amplifying effect of high confining pressure on soil structure destruction.

The hyperbolic relationship between G_d and γ_d is described by the Hardin–Drnevich model [33], where γ_d is taken as the horizontal coordinate and 1/G_d is plotted as the vertical coordinate, enabling the derivation of their mathematical relationship as follows (3):

$$1/G_d=a+b{\gamma }_d$$

(3)

within the formulation, parameters a and b correspond to the intercept and slope, respectively, of the linear regression.

It can be derived that the expression for the maximum dynamic shear modulus is formulated as G_dmax = 1/a. The fitted 1/G_d–γ_d curves of undisturbed and remolded specimens under various confining pressures are presented in Figure 7. Furthermore, the linear regression R² values of 1/G_d–γ_d for all specimens are maintained above 0.95, which provides further validation that the G_d–γ_d relationships in both undisturbed and remolded specimens are effectively described by the Hardin–Drnevich hyperbolic model.

The G_dmax of undisturbed and remolded specimens under various confining pressures was calculated based on its theoretical formulation, with the computational results systematically tabulated in

Table 3. Maximum shear modulus and parametric fitting values.

Borehole	Specimen Type	Experimental State	Confining Pressure (kPa)	Intercept a	Slope b	Gdmax (MPa)	R2
BH1	Undisturbed specimens	Saturation	50	2.22 × 10−5	7.58 × 10−5	45.05	0.9915
			100	1.88 × 10−5	3.99 × 10−5	53.15	0.9998
			200	1.39 × 10−5	3.46 × 10−5	71.76	0.9919
			300	1.10 × 10−5	2.17 × 10−5	90.91	0.9979
	Remolded specimens	Saturation	50	2.28 × 10−5	8.01 × 10−5	43.86	0.9878
			100	2.09 × 10−5	5.03 × 10−5	53.76	0.9932
			200	1.39 × 10−5	3.90 × 10−5	61.48	0.9964
			300	1.34 × 10−5	2.73 × 10−5	74.63	0.9940
BH2	Undisturbed specimens	Saturation	50	2.64 × 10−5	9.52 × 10−5	37.88	0.9960
			100	2.23 × 10−5	7.42 × 10−5	44.84	0.9863
			200	1.82 × 10−5	4.42 × 10−5	54.95	0.9979
			300	1.44 × 10−5	2.83 × 10−5	69.44	0.9964
	Remolded specimens	Saturation	50	2.76 × 10−5	9.62 × 10−5	36.21	0.9905
			100	2.51 × 10−5	8.94 × 10−5	39.92	0.9956
			200	2.18 × 10−5	6.19 × 10−5	45.86	0.9841
			300	1.85 × 10−5	6.26 × 10−5	53.87	0.9980

. Experimental data demonstrate that under identical confining pressures, the G_dmax of undisturbed specimens consistently exceeds that of remolded counterparts, while exhibiting an approximately linear ascending trend with increasing confining pressure. However, distinct nonlinear fluctuations are observed in this progression, attributed to microstructural deterioration induced by sample disturbance. For borehole BH1, the percentage deviation of G_dmax between remolded and undisturbed specimens is quantified to increase from 2.71% (50 kPa) to 21.81% (300 kPa). Comparatively, borehole BH2 exhibits greater sensitivity to structural disturbance, with its percentage deviation demonstrating gradient expansion from 4.61% (50 kPa) to 28.9% (300 kPa). The reduction in G_dmax of remolded specimens relative to undisturbed specimens under confining pressures ranging from 50 kPa to 300 kPa can be detailed as follows:

BH1: 50 kPa (−2.71%)→100 kPa (−11.28%)→200 kPa (−16.72%)→300 kPa (−21.81%)

BH2: 50 kPa (−4.61%)→100 kPa (−12.32%)→200 kPa (−19.82%)→300 kPa (−28.9%)

The discrepancy in G_dmax between undisturbed and remolded specimens is demonstrated to increase progressively with equivalent depth escalation, as evidenced by the foregoing analytical results

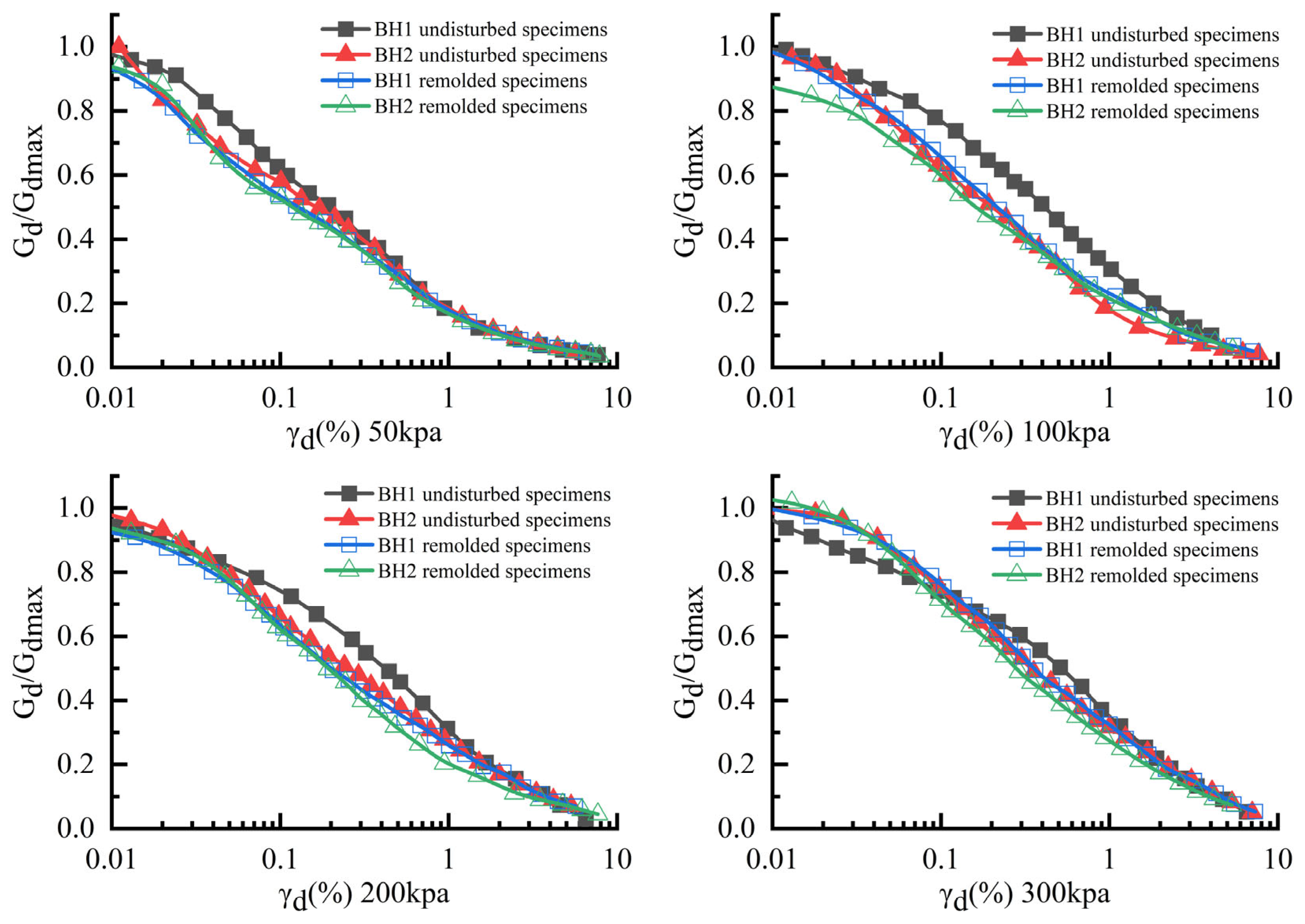
3.3. Normalized Modulus Ratio (G_d/G_dmax)–Dynamic Strain (γ_d)

In seismic site response analyses, the normalized shear modulus ratio (G_d/G_dmax) is recognized as a critical parameter exerting significant influence on computational outcomes of soil layer seismic responses [34]. A qualitative analysis was conducted focusing on the Zhengzhou region, Henan Province. The relationship curves (G_d/G_dmax–γ_d) for both undisturbed and remolded specimens under varying confining pressures are presented in Figure 8, demonstrating that these relationship curves for both specimens predominantly cluster within a narrow band distribution range, indicative of limited data dispersion.

The G_d/G_dmax–γ_d relationship curves of undisturbed and remolded specimens exhibit fundamentally similar shape across varying confining pressures, with the G_d/G_dmax demonstrating triphasic evolutionary characteristics during γ_d increment: (1) quasi-linear attenuation dominates when γ_d < 1 × 10⁻³; (2) accelerated nonlinear attenuation occurs within 1 × 10⁻³ ≤ γ_d ≤ 1 × 10⁻²; (3) residual stiffness stabilization is attained at γ_d > 1 × 10⁻². This triphasic behavior fundamentally reflects the intrinsic nonlinearity and hysteresis governing the soil’s G_d/G_dmax–γ_d relationships. Notably, undisturbed specimens demonstrate left-shifted curves under high confining pressure (300 kPa), sustaining 18–25% greater dynamic strains at equivalent modulus degradation levels—a phenomenon aligning with the Hardin–Drnevich reference strain amplification mechanism. This reflects preserved structural integrity, optimizing energy distribution during cyclic loading.

3.4. Damping Characteristics

The damping ratio (λ_d), characterizing energy dissipation during vibratory motion, is quantitatively determined through computation of hysteresis loop areas on the τ_d–γ_d constitutive curves [33], with the mathematical formulation explicitly provided in Equation (4):

$$\lambda ={\displaystyle \frac{1}{4\pi }}{\displaystyle \frac{A}{A_L}}$$

(4)

In equation: λ is the damping ratio; A is the total area of the hysteresis curve; A_L is the area of the triangle.

The λ_d–γ_d relationship curves for undisturbed and remolded specimens under different confining pressures were obtained through systematic computation of damping ratios at varying dynamic shear strain levels, as illustrated in Figure 9. Comparative analysis reveals that the λ_d values of both undisturbed and remolded specimens progressively increase with γ_d amplification, while demonstrating close proximity across all tested confining pressure conditions. And the maximum damping ratio (λ_dmax) ranges from 0.2 to 0.3.

The influence of confining pressure on λ_d is less pronounced than its effects on τ_d and G_d, and the λ_d–γ_d relationship curves exhibit crossover when γ_d < 10⁻³. Crucially, undisturbed specimens exhibit systematically 15–22% lower λ_d values than remolded counterparts at equivalent shear strains—a divergence attributable to preserved fabric integrity enhancing intergranular bonding forces, thereby inhibiting particle misalignment. This structural integrity inhibits particle misalignment during dynamic loading applications, coupled with reduced interparticle frictional dissipation that consequently diminishes energy consumption during deformation. Conversely, remolded specimens develop looser microstructures with increased randomness in particle contacts, leading to amplified sliding friction during vibratory conditions and thereby elevated damping ratios relative to undisturbed specimens.

3.5. Discussion

Comparative dynamic characterization of undisturbed and remolded silty clay specimens from Zhengzhou reveals the amplification effect of high confining pressures on structural superiority in undisturbed soils: under 300 kPa confining pressure, undisturbed specimens exhibit 20–30% enhancement in dynamic strength (τ_dmax) and stiffness (G_dmax) relative to remolded counterparts. This nonlinear escalation originates from high-pressure-induced enhancement in cementation bond stress-transfer efficiency and synergistic shear resistance within natural particle-oriented fabric. Consequently, for deeply embedded structures exceeding 20 m depth (effective confining pressure σ_c ≥ 200 kPa), such as metro tunnels and deep excavations, undisturbed soil parameters must be adopted in seismic design. Employing remolded soil parameters would systematically underestimate dynamic foundation strength by 30%.

The applicability of substituting remolded soils for undisturbed soils adheres to a dual “depth-parameter” criterion: Substitution is permissible for normalized modulus ratio (G_d/G_dmax) analysis in shallow foundations (σ_c ≤ 100 kPa), where this parameter exhibits low sensitivity to structural state. Remolded soil dynamic parameters may replace undisturbed soil properties for seismic design, significantly reducing evaluation costs for low-rise building seismic responses. However, strength design, damping characteristic prediction, and modulus attenuation threshold determination for deep-buried structures strictly prohibit substitution with remolded soil parameters. Under high confining pressures, τ_dmax differences reach 20–30%, with systematic λ_d deviations of 15–22%. In seismic design, using remolded soil parameters would cause severe safety hazards.

For exceptional deep-burial projects, a hybrid approach combining undisturbed soil data with a remolded soil correction factor (K = 1.25–1.30) may be adopted, while damping parameters must be derived exclusively from undisturbed soil tests. This criterion rectifies the structural state oversight in the conventional Hardin–Drnevich model, providing a safety-economy balance design reference for the deep underground space development in Zhengzhou.

4. Conclusions and Prospect

4.1. Conclusions

This investigation systematically examines the effects of structural degradation on soil dynamic characteristics through comparative analysis of undisturbed and remolded silty clay specimens under confining pressures spanning 50–300 kPa. The principal findings are delineated as follows:

(1)

Confining pressure exerts a significant influence on the dynamic parameters (τ_d, τ_dmax, G_d, G_dmax) of both undisturbed and remolded specimens; the τ_d–γ_d and G_d–γ_d relationship curves exhibit near-overlapping trajectories under low confining pressure (50 kPa), with deviation percentages remaining below 5%. However, with the confining pressure increasing to 300 kPa, the slope of τ_d and G_d with the increase of γ_d of the undisturbed soils is significantly higher than that of remolded soils, and the deviation percentage can reach 20–30%. This pressure-amplified discrepancy unequivocally confirms that high confining pressure activates and amplifies intrinsic structural superiority in undisturbed soils, through enhanced stress transfer efficiency within natural cementation networks and optimized particle interlocking, fundamentally altering soil dynamic behavior beyond 200 kPa threshold confining pressures.

(2)

The influence of confining pressure on the G_d/G_dmax is relatively minor for both undisturbed and remolded specimens, with their G_d/G_dmax–γ_d relationship curves confined within a narrow banded range exhibiting limited dispersion. A triphasic evolutionary characteristic is manifested in the progressive reduction of G_d/G_dmax with increasing γ_d: quasi-linear attenuation dominates within the 1 × 10⁻⁴ ≤ γ_d ≤ 1 × 10⁻² strain range, followed by accelerated G_d/G_dmax reduction rates when γ_d exceeds 10⁻³. It is noteworthy that under high confining pressure (300 kPa), undisturbed soil specimens exhibit a distinct leftward shift in their stress-strain curves and sustain dynamic strains of higher magnitudes at equivalent modulus degradation levels. This phenomenon confirms that during cyclic loading, the structural integrity of undisturbed soil is preserved, thereby optimizing the energy distribution mechanism.

(3)

This study establishes that confining pressure exerts significantly less influence on damping ratios (λ_d) than do shear stress and Shear modulus, with λ_d–γ_d relationship curves converging when γ_d < 10⁻³ across pressure conditions. Crucially, undisturbed specimens exhibit λ_d values systematically 15–22% lower than those of remolded counterparts at equivalent shear strains. The maximum damping ratio (λ_dmax) of all specimens is confined within the range of 0.2–0.3, reflecting the limiting effect of pore fluid viscosity within the microstructure of silty clay.

(4)

The applicability of substituting remolded soils for undisturbed soils obeys the “depth-parameter” criterion: Substitution is permissible for normalized modulus ratio (G_d/G_dmax) analysis in shallow foundations (σ_c ≤ 100 kPa), where this parameter exhibits low sensitivity to structural state. However, dynamic parameters for deep-buried structures strictly prohibit substitution with remolded soil parameters. Under high confining pressures, τ_dmax differences reach 20–30%, with systematic λ_d deviations of 15–22%. Using remolded soil parameters for seismic design would cause severe safety hazards.

4.2. Prospect

This study conducted dynamic cyclic triaxial tests on both undisturbed and remolded silty clays from Zhengzhou under varying confining pressures to evaluate the impact of structural degradation on soil dynamic properties. While significant behavioral differences between the two sample types were observed, the multifactorial nature of soil dynamics necessitates further investigation in the following directions:

(1)

The current comparison using only four discrete confining pressure levels may not fully represent the dynamic characteristics of undisturbed soils across different depths; future studies should correlate confining pressures with in situ burial depths of undisturbed samples.

(2)

The exclusive application of unidirectional cyclic loading fails to comprehensively simulate seismic loading conditions; subsequent research should incorporate cyclic stress ratio variations and multidirectional loading protocols to elucidate coupled stress-path effects.

(3)

Existing analyses primarily described phenomenological trends without theoretical quantification; advancing this requires integrating experimental outcomes with intrinsic soil properties—particularly mineral composition, particle size distribution, and microstructural features—to establish mechanistic linkages.