Abstract
In contrast to brittle normal-strength concrete (NSC), high-performance steel-fiber-reinforced concrete (HPSFRC) provides better tensile and shear resistance, enabling enhanced bridge girder design. To achieve a balance between cost efficiency and quality, reducing conventional reinforcement is a viable cost-saving strategy. This study focused on the flexural behavior of a type of pre-tensioned precast HPSFRC girder without longitudinal and shear reinforcement. This type of girder consists of HPSFRC and prestressed steel strands, balancing structural performance, fabrication convenience, and cost-effectiveness. A 30.0 m full-scale girder was randomly selected from the prefabrication factory and tested through a four-point bending test. The failure mode, load–deflection relationship, and strain distribution were investigated. The experimental results demonstrated that the girder exhibited ductile deflection-hardening behavior (47% progressive increase in load after the first crack), extensive cracking patterns, and large total deflection (1/86 of effective span length), meeting both the serviceability and ultimate limit state design requirements. To complement the experimental results, a nonlinear finite element model (FEM) was developed and validated against the test data. The flexural capacity predicted by the FEM had a marginal 0.8% difference from the test result, and the predicted load–deflection curve, crack distribution, and load–strain curve were in adequate agreement with the test outcomes, demonstrating reliability of the FEM in predicting the flexural behavior of the girder. Based on the FEM, parametric analysis was conducted to investigate the effects of key parameters, namely concrete tensile strength, concrete compressive strength, and prestress level, on the flexural responses of the girder. Eventually, design recommendations and future studies were suggested.
1. Introduction
The use of conventional steel reinforcement can mitigate cracking in brittle normal-strength concrete (NSC) and expand its applications. The emergence of high-performance concrete (HPC) has broadened the application of concrete, enabling progress towards higher-rise buildings or larger-span bridges. HPC is engineered with a relatively low water-to-binder ratio, supplementary cementitious materials (SCMs), and a superplasticizer to achieve a more densified matrix and exceptional compressive strength, commonly over 70 MPa at 28 days [1]. However, HPC appears to be more brittle than NSC. The addition of fibers is an effective way to increase concrete tensile strength, toughness, and ductility [2,3]. Steel-fiber-reinforced concrete (SFRC) is one of the most widely implemented solutions to improve the flexural and shear strength of structural members [2].
With improved tensile behavior and ductility, high-performance SFRC (HPSFRC) has become an increasingly adopted solution in bridge engineering. However, additional raw materials and more stringent quality control have driven an increase in the cost of SFRC/HPSFRC over NSC [1]. Several studies have explored cost-saving strategies through feasible structural design [4,5,6,7]. Mufti et al. [4] took advantage of transverse confinement and arching action in bridge deck slabs to eliminate conventional steel reinforcement within the slab. Kwak et al. [5] investigated the behaviors of beams without shear reinforcement under two-point loads, and found that increased steel fiber addition contributed to distinct increases in shear capacity, showing the possibility of removing the shear reinforcement in flexural members. For prestressed beams, Padmarajaiah and Ramaswamy [6] studied fully and partially prestressed HPSFRC beams with full-depth and partial-depth steel fiber reinforcement. Their experimental results indicated that partial-depth fiber inclusion limited to the tensile zone of fully prestressed beams provided cost efficiency without sacrificing performance. Dhonde et al. [7] also implemented HPSFRC in prestressed beams, showing that the prestressed beam with the addition of 1.5% steel fibers by volume was able to eliminate all transverse reinforcement, which proved the effectiveness of HPSFRC in prestressed beams for crack control and shear resistance.
Ultra-high-performance fiber-reinforced concrete (UHPFRC), which has superior compressive strength typically exceeding 130 MPa, is achieved through the integration of three fundamental concrete technologies: self-compacting concrete (SCC), FRC, and HPC [8,9]. Similarly, UHPFRC exhibits higher costs and greater manufacturing difficulties. In recent years, broad implementation of UHPFRC in real-scale bridge girders has been documented, demonstrating its utility in applications other than repairs [10,11,12,13,14,15,16,17,18,19]. The Mars Hill Bridge constructed in North America used 110 ft (33.5 m) long UHPC-modified 45 in (1.14 m) deep bulb-tee girders without shear reinforcement [10]. One span of the Route 624 bridge over Cat Point Creek in the US was built with 24.8 m long UHPC bulb-tee girders, which eliminated all non-prestressed shear reinforcement [15]. The Bourg-Les-Valence bridges in France consist of UHPC pi-shaped girders with lengths of 20.5 m and 22.5 m, utilizing reinforcement only at the longitudinal or transverse joints and the locations of attachments [16]. The first highway bridge constructed with UHPFRC in China had a relatively conservative design; it included 30 m precast UHPFRC box girders that had a thinner top flange and web, with 46% fewer prestressing strands and 8% less reinforcement [17]. However, due to the higher costs, complex manufacture, and lack of design specifications for UHPFRC, these girders have not yet achieved widespread applications.
Prior experimental studies concerning SFRC/HPSFRC/UHPFRC beams or girders with reduced or nearly negligible reinforcement are mostly limited to relatively small scales or short spans with simple rectangular sections (as listed in Table 1), leaving the scalability of conclusions uncertain [5,6,7,17,18,19,20,21,22,23]. A few studies have tested large-scale girders with negligible reinforcement. Graybeal [18] tested 23.9 m long pre-tensioned precast UHPFRC I-girders (compressive strength over 190 MPa) without mild steel reinforcement, whose fracture failure mode without concrete crushing in the top flange indicated under-utilizing the superior compressive strength of UHPFRC. Tu et al. [19] reported a 25.0 m long prestressed UHPFRC-NSC composite I-girder without stirrups, employing NSC in the top compression zone and UHPFRC in the bottom tensile zone, to take advantage of both concrete types. The large-scale tests indicated that unlike the enhanced tensile and shear performance, the superior compressive strength of UHPFRC was somewhat redundant.

Table 1.
Prior experimental studies concerning SFRC/HPSFRC/UHPFRC beams or girders.
This study focused on a 30.0 m long pre-tensioned precast HPSFRC girder from Sichuan, China, which eliminated conventional reinforcement, relying on HPSFRC and prestressed strands. The HPSFRC used in this study has a compressive strength less than 130 MPa, which is different from UHPFRC. Since the compressive strength is enough for the compression zone of a flexural member, HPSFRC with adequate steel fibers and sufficient strands is able to eliminate the need for reinforcement, as mentioned in [6,7]. In addition, the cost and manufacturing complexity of HPSFRC are lower than those of UHPFRC, allowing for easier implementation of the HPSFRC girder. Considering that few experimental studies have tested real-scale and relatively large-span pre-tensioned precast girders without conventional reinforcement, and HPSFRC has rarely been reported to be applied in similar girders, it is necessary to investigate the full-scale pre-tensioned precast HPSFRC girder to fill this gap. Moreover, a full-scale test is the most direct way to validate the performance and feasibility and instruct standard design.
Therefore, a 30.0 m long pre-tensioned precast HPSFRC girder was tested through a four-point bending test. This study centered on the full-process flexural behavior, presenting comprehensive data on deflection, strain, crack distribution, and flexural load-bearing capacity throughout stages of linear elasticity, cracking, post-cracking, and failure. To complement the experimental study on a single beam, based on the material strength test results, a nonlinear finite element model (FEM) was developed and validated against the bending test results. Parametric analysis was then conducted through FEM. The research concluded with actionable recommendations for practitioners and suggestions for future research directions.
2. Engineering Background
The 30.0 m full-scale pre-tensioned precast HPSFRC girder without conventional reinforcement bars investigated in this study was randomly selected from the prefabrication factory of Qingjiang Bridge, located in Sichuan Province, China. The Qingjiang Bridge is a ramp bridge, connecting the G0521 Hanrong Expressway and the Jintang North Toll Station. The bridge spans are 4 × 30.0 m, with a superstructure consisting of pre-tensioned precast I-shaped HPSFRC girders and cast-in-place composite bridge decks, as shown in Figure 1. The bridge design complied with China’s transport professional standards JTG D60-2015 [24] and JTG 3362-2018 [25]. Without longitudinal and shear reinforcement, the concrete stress condition becomes a critical indicator for the girders. The girders were designed as fully prestressed flexural members to account for the safety and durability considerations of the innovative bridge structure. By reserving adequate compressive stress for mid-span lower-edge concrete, no tension was allowed in any service load combination.
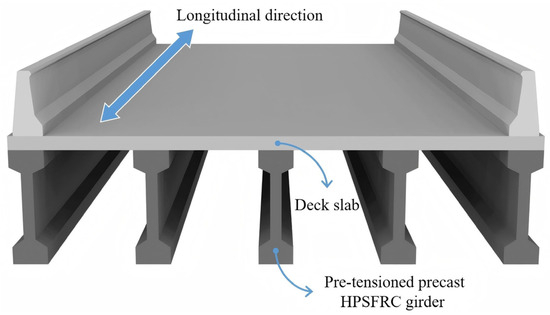
Figure 1.
Superstructure of Qingjiang Bridge.
When checking the normal stress in tension of a fully prestressed flexural member, JTG 3362-2018 requires that the load-induced maximum concrete extreme fiber stress in tension () and concrete prestress in compression () satisfy . In addition, the maximum concrete principal stress in tension () and concrete tensile strength () satisfy . According to Table 2, was calculated as 10.5 MPa under service load combinations, while was determined as 14.9 MPa under prestressing load, which satisfied the requirement. Meanwhile, under service load combinations, also satisfied the requirement, in comparison with the tested material properties of HPSFRC in Section 3.3. It is noteworthy that the maximum principal stress in compression remained below 15.0 MPa, indicating substantial residual capacity.

Table 2.
The concrete stress under prestressing load and service load combinations (unit: MPa).
According to JTG 3362-2018, the concrete tensile strength is neglected when calculating the ultimate bending resistance, and there is a reduction factor for the concrete compressive strength and ultimate strength of strands. The calculation method is based on the plane section assumption, and equilibrium equations of internal forces and moments. In addition, there is a conservative rectangular stress block consideration for concrete compressive behavior, a simplified and empirically validated method for predicting the nonlinear stress–strain behavior of NSC, which is widely adopted in reinforced concrete design codes for flexural analysis [16]. Under the strength limit state, the factored design load and ultimate bending resistance predicted by the current standard for a single girder were determined as 5512.9 kN·m and 9843.7 kN·m, respectively, with a safety factor () equal to 1.62. The structural configuration of the girder is detailed in Figure 2.
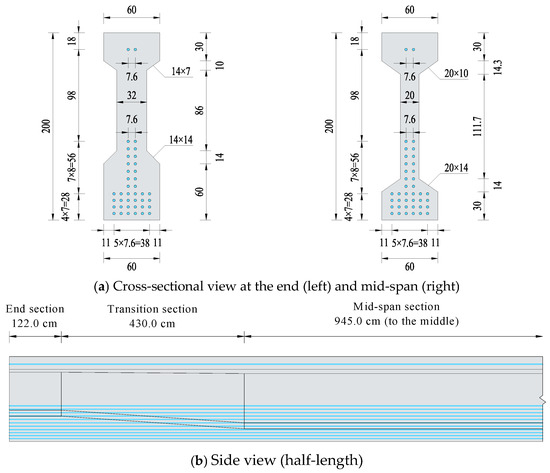
Figure 2.
Structural configuration and strand arrangement of pre-tensioned precast HPSFRC girder (unit: cm).
3. Four-Point Bending Test for Single Girder
3.1. Details of Tested Girder
The structural configuration and strand arrangement are depicted in Figure 2. The end-to-end full length and height of the selected I-shaped girder are 29.94 m and 2.0 m, respectively, while the nominal span is 30.0 m. The web thickness is 32 cm for the end section and 20 cm for the mid-span section. The flange width is 60 cm for all sections. According to the side view shown in Figure 2b, there are two 122 cm long end sections, two 430 cm long transition sections, and one 1890 cm long mid-span section along the longitudinal direction of the girder. In the transition section, all dimensions maintain a smooth linear shift along the longitudinal direction. Multiple pre-tensioned steel strands with a nominal diameter of 15.2 mm are positioned at the girder web and lower flanges, with two strands passing through the upper flange. The strands are horizontally straight, which is convenient for positioning, fixing, and pre-tensioning. To ensure smooth concrete flow between the strands, the minimum clear spacing of the strands was limited to 54.8 mm. The controlled pre-tensioned stress level for the strands was 1395.0 MPa. After the strands were pre-tensioned to the designed stress level, HPSFRC was poured in to fabricate the girders, followed by seven-day moisturized curing in natural condition. The pre-tensioned strands were released and cut off after the concrete strength requirements were satisfied.
The pre-tensioned precast HPSFRC girder has eliminated conventional reinforcement, thereby reducing the labor costs and construction time associated with steel manufacturing, placement, and tying. When compared to post-tensioned girders, pre-tensioned girders exhibit better bonding performance and more efficient direct prestress transfer between steel strands and concrete, resulting in enhanced durability. The elimination of components including the end-anchorage system, strand ducts, grouting materials, and end-zone reinforcement results in a simplified structural layout for pre-tensioned girders, which yields additional benefits in terms of production labor costs and overall project expenses. In addition, the straight-line design of the strand configuration decreases tensioning-induced risks, most notably the stress concentration at curvature points.
3.2. Girder Preparation
The prefabrication factory was 25 km away from the bridge location. It was one of the major prefabrication factories for the Chengmian Expressway Expansion Project. One temporary production line was established specifically for the HPSFRC girders of Qingjiang Bridge. The production process comprised the following sequential operations: (1) the preparation of the prestressing bed and abutments for pre-tensioning, Figure 3a; (2) the assembly and temporary anchorage of steel strands with sufficient initial stress to offset self-weight effects, Figure 3b; (3) the application of designed prestress to the steel strands using portable hydraulic jacks, Figure 3c; (4) closing and sealing of the stainless steel formwork, Figure 3d; (5) mixing, placement, and vibration of the HPSFRC, Figure 3e–h; (6) initial curing under natural conditions involving cling film coverage or polyethylene sheet encapsulation for a minimum duration of 16 h, Figure 3i; (7) formwork removal, followed by extended natural curing with supplemental water spraying for no less than 7 days, Figure 3j; and (8) the controlled release of steel strands employing symmetrical and staggered sequencing, Figure 3k,l. The specimen girder was stored alongside other HPSFRC girders under factory conditions for an average period of approximately 2.5 months prior to the bending test, which was conducted in advance of bridge construction.



Figure 3.
Production process for pre-tensioned precast HPSFRC girders.
3.3. Material Properties
In the factory, concrete fabrication complied with Chinese national standard GB/T 31387-2015 [26] and building professional standard JG/T 472-2015 [27], which are related to reactive powder concrete and SFRC, respectively. For design of the HPSFRC mix, the water-to-binder ratio and the volume fraction of steel fiber were strictly controlled at 0.2 and 1.9%, respectively. Proportions of the designed mix are listed in Table 3. The geometries and mechanical properties of the steel fiber are collected in Table 4. The HPSFRC used for girder fabrication was tested according to Chinese national standards GB/T 31387-2015 and GB/T 50081-2019 [28]. The mechanical properties of HPSFRC were obtained at 28 days and are listed in Table 5. The photographs in Figure 4 display the tested specimens and corresponding failure modes. The cubic compressive strength and direct tensile strength of HPSFRC reached 106.3 MPa and 8.7 MPa, respectively. Tensile tests were conducted for the 15.2 mm diameter steel strands according to China transport professional standard JT/T 329-2010 [29]. The yield and ultimate strengths were obtained as 1761.4 MPa and 1907.2 MPa, with the elastic modulus obtained as MPa.

Table 3.
Proportions of the HPSFRC mix.

Table 4.
Geometric and mechanical properties of steel fiber.

Table 5.
Mechanical properties of HPSFRC (at 28 days).

Figure 4.
Mechanical tests for HPSFRC. (a) Cubic compression test (specimen size: 100 mm × 100 mm × 100 mm), (b) Flexural tension test (specimen size: 150 mm × 150 mm × 550 mm), (c) Direct tension test (tested section size: 50 mm × 50 mm), (d) Elastic modulus test (specimen size: 150 mm × 150 mm × 300 mm).
3.4. Test Setup and Load Protocol
The test setup is shown in Figure 5a. The girder was tested under a pure bending span of 5.0 m, while the length between the centers of two rubber supports was 29.1 m. The load was applied using a hydraulic jack with a load cell, distributed to two points by a stiffened steel beam. From Figure 5a, it can be seen that one LVDT was installed at the middle of the pure bending span to measure the mid-span deflection, while two LVDTs were used to measure the vertical deformation of the rubber supports. As shown in Figure 5b, at the mid-point A-A section, strain gauges were mounted symmetrically on the top, bottom, and two lateral-side surfaces of the girder to monitor the concrete strains along the depth of girder. Continuous data acquisition for the load cell, LVDTs, and strain gauges was performed during all phases of the load protocol. As depicted in Figure 5c, the full-scale girder test was carried out in situ.

Figure 5.
Test setup of the girder.
As shown in Figure 6, the loading protocol consisted of preliminary and destructive stepwise loading. The preliminary stepwise loading was force-controlled, and designed to verify the normal operation of the loading equipment and sensors. At each step, the load was applied for 2 min followed by holding for 3 min for observation. Unloading was conducted after reaching the target load of 500 kN, approximately 20% of the predicted peak load. Destructive stepwise loading was initially applied in force control. Before the first crack was observed, load was applied for 2 min followed by holding for 3 min for observation, similarly to the preliminary steps. The loading mode was switched to displacement control upon detection of a 0.2 mm wide crack, which was considered as the serviceability limit in accordance with Chinese national standard GB 50010-2010 (2015) [30] and transport professional standard JTG 3362-2018. The total maximum load at the preliminary stage was 500 kN, with a 100 kN increment for each step. After confirming the instrument’s functionality through preliminary loading, the hydraulic jack was unloaded to its initial position. Then, formal loading was initiated. The initial load increment for each step was 100 kN, which then changed to 50 kN after observation of the first crack. Upon detection of a 0.2 mm wide crack, the loading mode was switched to displacement control and maintained until the occurrence of critical failure, at which point the test was terminated. As stipulated by Chinese national standard GB 50204-2015 [31], a flexural member is considered to have reached critical failure if any of the following criteria are met: (1) the maximum tensile crack width of the concrete reaches 1.5 mm; (2) the mid-span deflection exceeds 1/50 of the span length; (3) concrete crushing failure occurs in the compression zone; or (4) fracture of the primary tensile reinforcement is observed. Throughout the loading process, manual observation and marking of crack development were conducted.
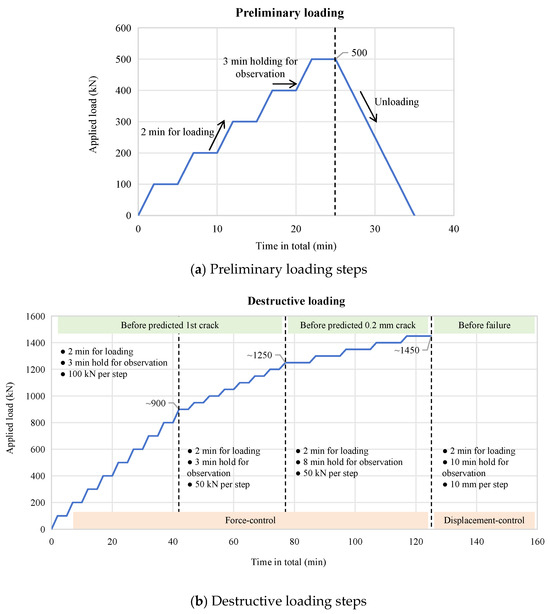
Figure 6.
Loading protocol.
4. Experimental Results
4.1. Failure Mode
Figure 7 illustrates the concrete crack distribution at four load steps to show the progressive development. The total force applied by the hydraulic jack is denoted as . When reached 1550.0 kN, it could be seen that tensile cracks were observed at the lower flange and exhibited a higher concentration directly under the load points. The progressive loading was accompanied by audible noises generated in the girder due to fiber pull-out, providing evidence of ongoing tensile crack propagation. Tensile cracks continued to extend to the girder web, and new cracks grew between the existing ones, which increased the crack density and caused a decline in the girder stiffness. When approaching the peak load, with the crack width increasing sharply, the steel strands started to yield. Subsequently, the rupture of the steel strands caused the girder to fracture into two separate parts, without obvious compressive cracks at the top flange. This phenomenon stemmed from a combined tensile failure of steel strands and HPSFRC. Generally, the cracks predominated in the pure bending section, with minor cracks developing in the shear-flexural region, and none detected elsewhere throughout the loading protocol. Photographs of the critical fracture are presented in Figure 8.
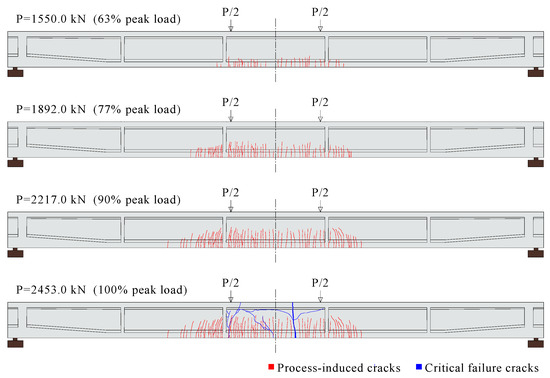
Figure 7.
Crack development of tested girder.


Figure 8.
Critical fracture of tested girder.
4.2. Crack Analysis
Figure 9 depicts the relationship between the applied load and the maximum crack width within the pure bending span. Crack monitoring was conducted intensively prior to the appearance of 0.2 mm wide cracks. Following the detection of these cracks, the recording frequency was gradually reduced due to safety considerations, and crack propagation observation was entirely suspended upon reaching a load of 2217.0 kN (90% peak load). Post-failure observation was then performed to document the characteristics of critical failure cracks. The plot in Figure 9 shows that the growth rate of the crack width remained nearly constant until the 0.29 mm wide cracks were detected. Due to the final fracture failure, the crack width at the ultimate stage exhibited a dramatic increase, resulting in an abrupt near-plateau segment in the curve. The results indicated that the critical cracks attained a width of 1.5 mm either immediately preceding or during the failure phase, with associated load close to 95% peak load.
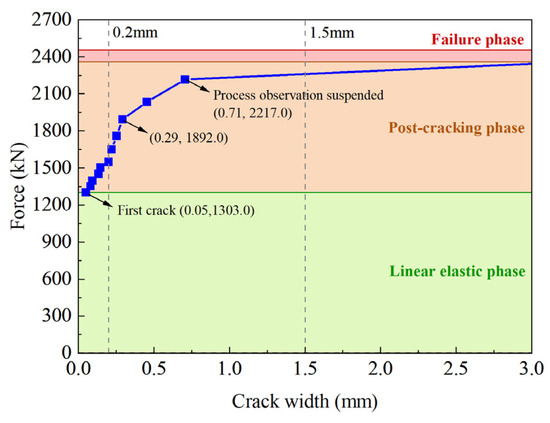
Figure 9.
Relationship between force and crack width in the tested girder.
4.3. Load–Deflection Curves
The load–deflection response curves for the tested girder are plotted in Figure 10, including force–deflection and moment–deflection curves. The load represents the total force applied by the hydraulic jack, or the induced normal section moment within the pure bending span, denoted as . The deflection is defined as the mid-point deflection of the tested girder subtracting the measured displacement of the rubber supports. Generally, the load–deflection curves exhibit three distinctive phases of response, namely (1) the linear elastic phase (segment OA), (2) the post-cracking phase (segment AC), and (3) the failure phase (segment CD). The curves indicate deflection-hardening behavior. Owing to the fiber bridging effect, this behavior is characterized by an ascending post-cracking load–deflection response and extensive cracking patterns [32].
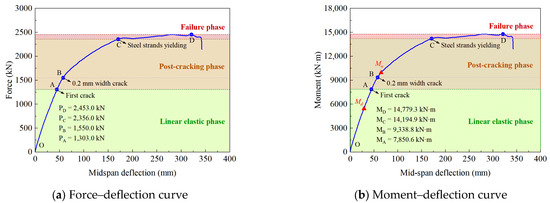
Figure 10.
Load–deflection response of tested girder.
In Figure 10, the mid-point deflection shows a linear relationship with the applied load prior to cracking. The first observable crack occurred in the pure bending span when the applied load reached 1303.0 kN (point A). Crack initiation does not induce an immediate or obvious change in the curve slope. Subsequent loading leads to more extensive cracking, with a notable stiffness degradation emerging once the crack width reaches 0.2 mm (point B). As shown in Figure 7, when the load continued to increase beyond 1550.0 kN, macro cracking developed with progressive densification, and crack heights surpassed half of the girder height. However, the curve shown in Figure 10 still displays an almost constant slope until progressive yielding of the steel strands commences (point C). When the load approaches 2356.0 kN, the curve slope reduced to almost zero upon the yielding of the steel strands. Upon fracture failure, the peak load was or , while the maximum deflection was around 340 mm. Since the girder consequently fractured, there was an abrupt load drop after the peak load was reached. As depicted in Figure 10b, the factored design load is still located within the linear elastic phase, while the factored ultimate bending resistance is near point B.
4.4. Plane Section Assumption
The concrete strain along the girder depth at the mid-point cross-section of the tested girder was continuously measured using the strain gauges shown in Figure 5. The strain distribution along the section depth at different load levels is plotted in Figure 11. The concrete strain represents the mean values of paired readings from strain gauges installed on the lateral-side surfaces. Before concrete cracking, the curves indicate a linear distribution of strain along the girder depth, and the neutral axis is approximately located at the center of the girder height, in agreement with the plane section assumption. The neutral axis of the tested girder remained in place until the first crack appeared. Due to the onset of a 0.2 mm wide crack, there was an obvious upward migration of the neutral axis when the load reached 1604.0 kN, and the strain distribution remained approximately linear before the cracks intersected the strain gauges. The measured strain gradually became nonlinear due to crack progression. When the load was approaching the peak load of 2453.0 kN, cracks extending through the strain gauges induced failure of several strain gauges.
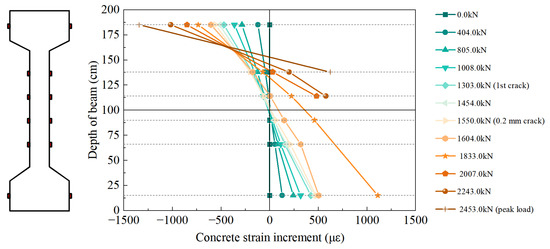
Figure 11.
Strain distribution along the depth of the girder.
4.5. Concrete Strain
The load–strain relationship of the girder concrete for the top and bottom edges at the mid-point cross-section is shown in Figure 12. Under pure bending, the top edge of the tested girder at the mid-point experienced compression, while the bottom edge was subjected to tensile stress. For the labels in the legend of Figure 12, the letters “T”, “B”, and “S” stand for top, bottom, and side surfaces, respectively. The curves of the bottom edge in tension were linear until the first crack occurred. When micro cracks formed, the curves of the bottom edge fluctuated. After a 0.2 mm wide crack was observed, turning points gradually appeared in the curves. Generally, the corresponding load for the first turning point was larger than that of the load–deflection curve. When the cracks passed through the strain gauges, the measured strain increased drastically with the increase in load, such as in B1-1. When approaching the failure phase, strain gauge SB1-6 was unable to accommodate further excessive deformation at the crack position, inducing a plateau in the curve. However, owing to the strain release of concrete blocks between the cracks, the concrete strain experienced a decrease with increasing load, such as in B1-2, B1-3, and SA1-6. For the top edge in compression, there was a similar linear shape before the first crack. A turning point gradually appeared due to the onset of 0.2 mm wide cracks. Upon the beginning of the failure phase, a second turning point appeared and led to a more extensive slope degradation.
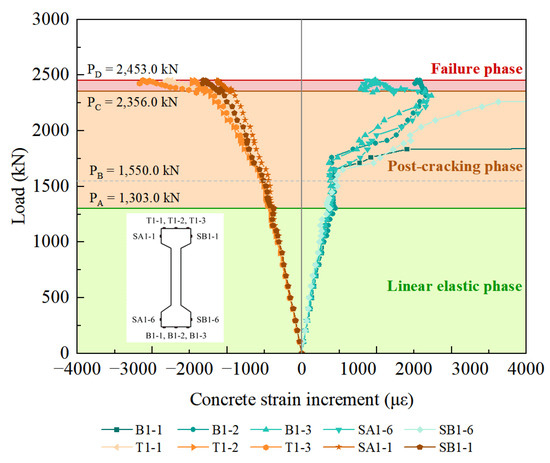
Figure 12.
Load–strain relationship of the girder concrete from the compressive and tensile edges.
5. Finite Element Analysis
5.1. General
A three-dimensional nonlinear finite element model (FEM) of the 30.0 m full-scale pre-tensioned precast HPSFRC girder was established, as shown in Figure 13. Loading pads and support blocks were utilized to prevent stress concentration at the loading points and supports, coupled with virtual reference nodes to facilitate vertical load application and reaction force output. Solid elements were employed in the FEM to model the HPSFRC, loading pads, and support blocks, while the steel strands were represented by truss elements. Based on the fact that there is no obvious slip between the concrete and the steel strands during the experiment, an “embedded region” interaction command, namely a perfect bond, was adopted between them. For the contact surfaces of other solid element components, “tie” interaction commands were executed. To simulate the prestressing process, a predefined temperature field was utilized to generate temperature load by “cooling down” the steel strands. The boundary condition was set as simply supported, which referred to pin support and roller support on each end, equivalent to the in situ experimental test. As shown in Figure 14, four models with different mesh sizes were established to carry out sensitivity analysis. Since a nominal element size of 200 mm induced results with satisfactory accuracy and a shorter running time than for 150 mm, the nominal element size was set to 200 mm for the 30.0 m full-scale girder and its parametric study.
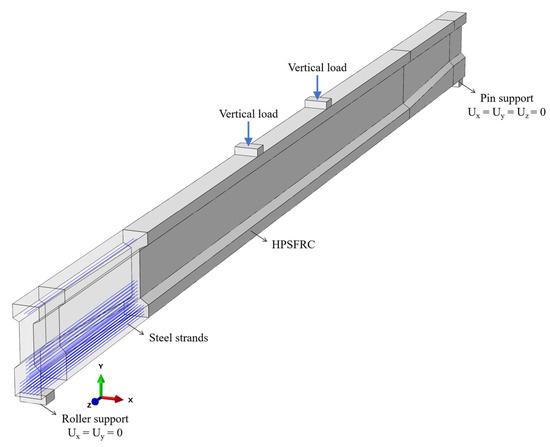
Figure 13.
Illustration of FEM for the tested girder.
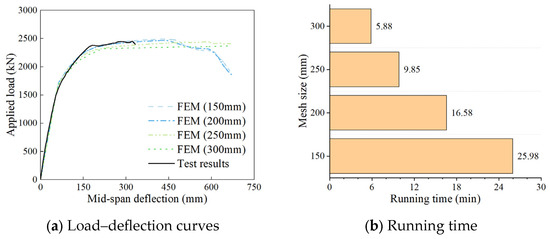
Figure 14.
Mesh sensitivity analysis.
5.2. Material Constitutive Models
To reflect the nonlinear behavior and cracking damage, a concrete damage plasticity (CDP) model was implemented to simulate both the tensile and compressive damages to the HPSFRC. According to prior studies [19,23,33], the CDP model replicated concrete compressive, tensile, and shear behaviors with relatively high confidence, even for UHPFRC. Five decisive parameters were defined for the CDP model: dilation angle (30°), eccentricity (0.1), the ratio of biaxial strength to uniaxial strength (1.16), the ratio between the magnitudes of deviatoric stress on tensile and compressive meridians (0.667), and the viscosity parameter (0.0005). The stress–strain relationships for HPSFRC used in the FEM were based on the mechanical test results in Section 3.2 and the constitutive prediction models further discussed below.
Previous research concerning the constitutive model of SFRC considered the fiber effect, including volume fraction and fiber properties [34,35,36,37]. The models successfully predicted the experimental responses reported in the corresponding studies. However, most studies covered SFRC with relatively lower strengths and lower volume fractions of fiber. Lv et al. [36] conducted an experimental study on high-strength SFRC with volume fractions ranging from 0% to 2.0% and cubic compressive strengths of 60 MPa and 80 MPa. The steel fibers used included hooked-end fibers. The proposed analytical model for compression considered the effects of fiber volume fraction on uniaxial compressive strength, strain corresponding to the peak stress, and the elasticity modulus, and agreed well with the experimental curves. Therefore, the model developed by Lv et al. [36] was adopted to determine the uniaxial compression stress–strain relationship of HPSFRC, the equations of which are provided through Equations (1)–(8). As shown in Figure 15a, the predicted compressive stress–strain curve was in good agreement with the test curve.
where and represent the concrete compressive stress and corresponding strain values from the curve; is the compressive strength of concrete (peak value of stress); is the strain at the peak stress; is the damage evolution parameters under uniaxial compression; is the elastic modulus of concrete; and , , and are fiber length, diameter, and volume fraction, respectively.
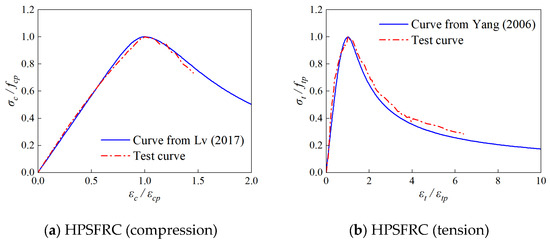
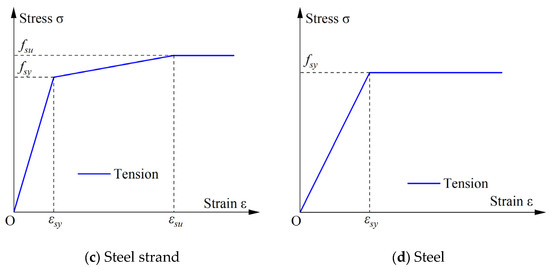
Figure 15.
Material constitutive models utilized in the FE simulation [36,38].
The analytical model proposed by Yang and Huang [38] was adopted to describe the uniaxial tensile stress–strain relationship of HPSFRC (Equations (9)–(11)), as shown in Figure 15b. Yang and Huang experimentally investigated the effects of four types of steel fibers, including hooked-end steel fiber, on the tensile strength of SFRC with compressive strengths of 30 MPa, 60 MPa, and 80 MPa. The values of key parameters in the model were determined by the mechanical tests in Section 3.2. Figure 15b also indicated that the predicted tensile stress–strain curve had satisfactory accuracy.
where and represent the concrete tensile stress and corresponding strain values from the curve; and are the tensile strength (peak value of stress) and the corresponding strain; and is the characteristic content parameter of steel fiber calculated through Equation (8).
As illustrated in Figure 15c, a bilinear tensile stress–strain relationship model is adopted for the steel strand, the equations of which are provided in Equation (12).
where and represent the tensile stress and corresponding strain values of the steel strand from the curve; is the elastic modulus of the steel strand; and are the yield strength and yield strain; and and are the ultimate strength and ultimate strain.
The steel material in the load pads and support blocks in the FEM was assigned an ideal elastoplastic model with a single yield point, as shown in Figure 15d. The elastic modulus and yield strength are taken as 200 GPa and 345 MPa.
5.3. Verification of Results
To validate the reliability of the FEM in predicting the overall flexural responses of the pre-tensioned precast HPSFRC girder, the load–deflection relationship obtained from this FEM was compared with the experimental outcomes presented in Section 4.3. As depicted in Figure 16, the reasonable consistency between the FEM predictions and experimental observations during the entire loading process supports the capability of this FEM when predicting the overall bending behavior. Notably, the FEM predicts a marginally higher (0.8%) load capacity (2473.4 kN) with larger corresponding deflection (437 mm) compared to the experimental results, which can be attributed to the idealized assumption for the steel strand constitutive model and perfect bond assumption between steel strands and HPSFRC. Figure 17 demonstrates the failure mode predicted by this FEM. The tensile and compressive damage patterns are monitored by DAMAGET and DAMAGEC values, respectively. The progressive tensile damage pattern shown in Figure 17a–d is in reasonable agreement with the actual crack development in Figure 7. The compressive damage pattern shown in Figure 17e indicates that no concrete crushing occurs at the top flange. Figure 17f demonstrates that all the steel strands in tension almost reach the ultimate strength condition upon peak load, which is in adequate agreement with the fracture failure observations in Section 4.1.
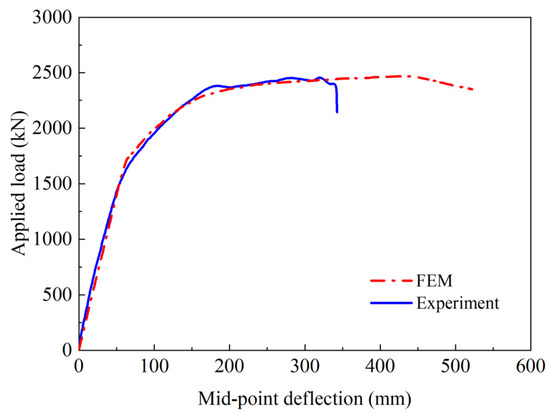
Figure 16.
Comparison of load–deflection relationship.
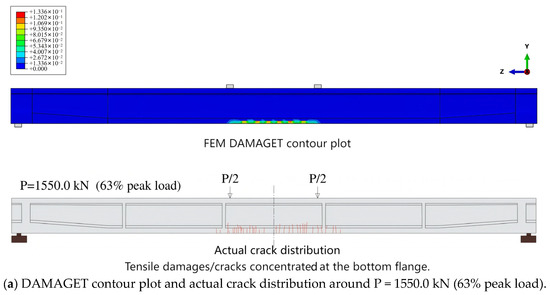

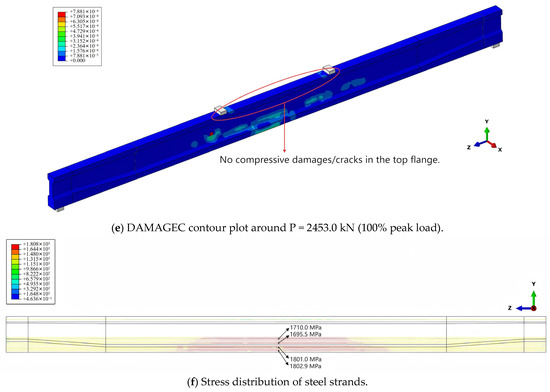
Figure 17.
Failure mode predicted by FEM.
The predicted tensile strain of the bottom surface and compressive strain of the top surface at the mid-point of the girder are compared with the experimental outcomes, as shown in Figure 18. For both the tensile and compressive conditions, the load–strain curves predicted by the FEM exhibit two distinct turning points, P = 1727.5 kN and 2240.3 kN, which adequately correspond to the experimental curves. Before the occurrence of the first turning point, the stiffness presented by the FEM curves matches that of the experimental curves well. Upon excessive yielding of the steel strands, the second turning point appeared for both the tensile and compressive FEM curves.
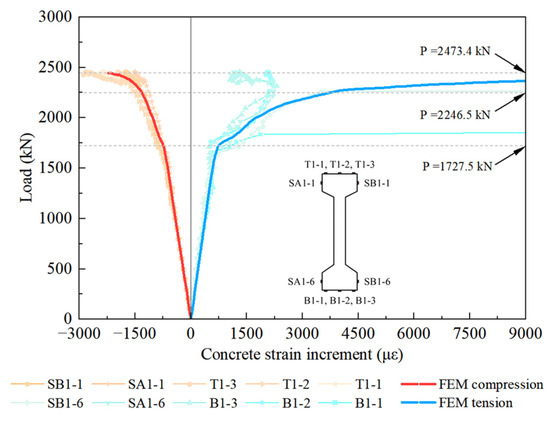
Figure 18.
Comparison of load–strain relationships.
5.4. Parametric Study
Experimental investigations of full-scale models with large spans are often costly because of demanding specimen preparation and loading requirements. Consequently, prior research mainly focused on scaled models, with limited parametric analysis conducted on full-scale systems. Since engineering practice prioritizes the performance of real-world structural members, comprehensive parametric analysis is essential for reliable design decisions. Thus, a parametric study was conducted for concrete tensile strength, concrete compressive strength, and the prestress level of the steel strands based on the validated full-scale FEM.
Three values of concrete tensile strength (6 MPa, 8 MPa, and 10 MPa) were selected without changing any of the other parameters. The corresponding load–deflection curves are plotted in Figure 19a. The figure indicates that enhancing the concrete tensile strength is beneficial to postponing the turning points and slightly enhancing the girder stiffness in the nonlinear post-cracking phase. The bending resistance is also improved, while there is no significant influence on girder ductility. As discussed in Section 5.2, several factors are closely related to the tensile strength of HPSFRC, namely the concrete matrix strength, fiber volume fraction, fiber geometries, and fabrication quality. To guarantee the post-cracking behavior of the girder, more attention should be paid to the quality control of raw materials and the mixing, pouring, and curing of HPSFRC in real-world construction contexts.
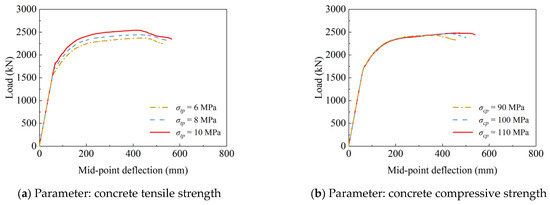
Figure 19.
Comparison of load–deflection response when varying concrete strength.
Figure 19b reveals that while solely increasing the concrete strength from 90 MPa to 110 MPa has a negligible effect on the linear elastic behavior, the post-cracking behavior, and the load capacity, it increases the deflection under the peak load by about 15% at each level, resulting in improvements in ductility. It is worth noting that, according to Equation (7), when the compressive strength increases, the corresponding peak strain also grows. Such changes in the concrete peak strain could exert an influence on the failure mode. In other words, variations in the peak compressive strain modify the timing of concrete crushing. Delayed concrete crushing relative to steel strand yielding could contribute to better structural ductility.
While maintaining the diameter, layout, and configuration of steel strands, the prestress was adjusted to three different levels, represented by varying proportions (relative to the standard ultimate strength of 1860 MPa). As depicted in Figure 20, although the prestress level of steel strands has no obvious effect on the load capacity, an elevated prestress level can suppress crack initiation and enhance post-crack stiffness, owing to a more sufficient reserve of compressive stress at the bottom edge of the girder. Additionally, the yielding of the steel strand is also accelerated when increasing the prestress of the steel strand, leading to an earlier occurrence of a plateau-like segment in the curve.
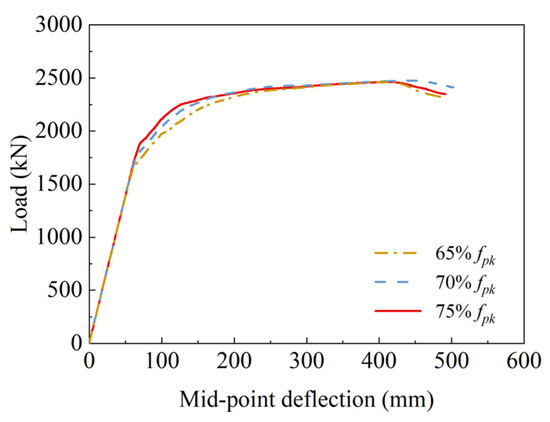
Figure 20.
Influence exerted by steel strand prestress level.
6. Discussions
For conventional prestressed precast girders using NSC, there is a requirement for a minimum reinforcement ratio according to current design specifications. Since NSC has a brittle nature, the minimum reinforcement ratio aims to prevent brittle failure, which means a sudden drop of load-carrying capacity. In addition, the steel reinforcement also ensures adequate visual signals, such as extensive cracking, and large deflection, before the final failure. Unlike NSC, HPSFRC or UHPFRC exhibit ductility, owing to the crack-bridging effect offered by steel fibers. Taking advantage of this material-level feature, HPSFRC or UHPFRC girders with prestressed strands are able to eliminate steel reinforcement.
The feasibility of reinforcement elimination is validated by the experimental outcomes. From Section 4.1 and Section 4.2, the HPSFRC girder tested in this study experienced a progressive and extensive cracking process before the final failure. The bending-induced cracks demonstrated small widths and closely spaced distributions. As described in Section 4.3, the load for the first crack () of the HPSFRC girder was approximately 53% of the peak load (), indicating a 47% increase in load-carrying capacity after cracking. The ratio of the deflection corresponding to the peak () to the effective span length () was approximately 1/86, showing a large deflection before the final failure. As shown in Table 6, the test results of Graybeal [18] and Tu et al. [19] demonstrated ductile behavior of the girders. It is worth noting that although utilizing HPSFRC instead of UHPFRC, the girder tested in this study exhibited no significant sacrifice of the deflection-hardening behavior and ductility.

Table 6.
Experimental results comparison with previous studies.
While scaled models provide preliminary insights [5,6,7,20,21,22,23], full-scale testing and validated simulation remain essential for reliable real-scale design decisions. Based on the comprehensive experimental and numerical investigations of the full-scale HPSFRC girder, several critical recommendations for construction practice have emerged. Construction quality control must rigorously address mixing, casting, and curing processes to ensure consistent post-cracking behavior. Based on the fabrication experience in this study, it is necessary to have trial batching and mixing in the mixing station to ensure continuous production of HPSFRC. Since the moisturized curing is important for HPSFRC, it is highly recommended that the girder should be sealed by films or sheets until the commencement of strand release. After the prestress transferring, curing through spraying water is suggested. As concrete with high strength is sensitive to temperature changes, it is crucial to mitigate the stress induced by temperature differences to prevent initial cracks. In simple words, before removing the covered sheets or formwork, checking the difference between the surface and environment temperature is strongly recommended. In addition, as the prestressing of steel strands can also affect the post-cracking behavior of the girder, the pre-tensioning process requires strict control. For instance, the tensioning reaction device must possess sufficient stiffness and strength to control non-tensioning deformations, and withstand the huge forces from the strands.
Regarding the flexural design of pre-tensioned precast HPSFRC girders without conventional reinforcement, since this type of girder satisfied the plane section assumption, the design methodology for prestressed concrete adopted by the current design codes remains partially applicable. The major distinction lies in the incorporation of the compressive and tensile stress–strain characteristics of HPSFRC. The core design consideration involves determining the utilization ratio of experimentally obtained capacities and establishing permissible crack criteria under service loads. Consequently, reduction factors or conservative approaches should be established for the uniaxial compressive and tensile behaviors of HPSFRC in accordance with these strength and serviceability limits. Current design specifications substantially underestimated actual flexural capacity of the HPSFRC girder by about 33%. Nevertheless, the development of calibrated design parameters requires extensive experimental validation to achieve both reliability and rationality in structural design. This validation requirement is not only for the material level, but also for the structural level [25]. Therefore, it is necessary to further conduct extensive material strength tests and girder experiments to establish comprehensive and accurate capacity calculation method and design methodology. If the scalability problem is appropriately addressed, the full-scale tests could be substituted by scaled tests, which are more cost- efficient. It is undeniable that while the enhanced shear resistance of SFRC is widely acknowledged, the validation of shear capacity of the HPSFRC girders with no steel reinforcement remains necessary. For such girders where shear reinforcement is omitted, the shear transfer mechanism becomes inherently complex, making it challenging to establish a definitive mechanism. Consequently, future research should systematically investigate the actual shear performance of such girders through experimental tests, analyze key influencing parameters, and develop comprehensive calculation methods integrating both theoretical and empirical approaches.
Cost efficiency remains a central focus in structural optimization. The HPSFRC girder proposed in this study has achieved elimination of conventional reinforcement while requiring only marginal increases in prestressing strands compared to standard girders. Although their concrete production is less demanding than UHPFRC, the geometric configuration of the section remains conventional. Recently, waste utilization has emerged as a critical research frontier. Developing HPC with equivalent strength and ductility using recycled aggregates, wasted plastics and glass, or electronic wastes not only yields cost reduction but also delivers environmental benefits, offering significant socioeconomic value [39,40,41]. Future research may investigate the mechanical behavior of girders incorporating these sustainable materials.
7. Conclusions
In this study, the flexural behavior of a 30.0 m full-scale pre-tensioned precast HPSFRC girder without longitudinal and shear reinforcement was experimentally investigated through a four-point bending test. To complement the experimental study, a three-dimensional nonlinear FEM was established to predict the flexural behavior of the tested girder. The key findings of the experimental test and FE analysis, and the recommendations are as follows:
(1) In the four-point bending test, the 30.0 m full-scale HPSFRC girder without steel reinforcement ultimately experienced a combined tensile failure of the steel strands and the concrete. The girder exhibited ductile deflection-hardening behavior (47% increase in load after the first crack), extensive cracking patterns, and large total deflection (1/86 of effective span length). Under the design load of the Qingjiang Bridge, the girder remained in the linear elastic phase, indicating a sufficient safety margin. Significant stiffness degradation of the load–deflection, load–strain, and load–crack width curves only occurred after the cracks exceeded the 0.2 mm serviceability limit specified in GB 50010-2010 (2015) and JTG 3362-2018.
(2) The failure mode, load–deflection relationship, and load–strain relationship simulated by the full-scale FEM were in good agreement with the experimental results. The ultimate bending resistance predicted by the FEM closely matched the experimental outcome (0.8% difference), while the load–deflection curve predicted by the FEM displayed a longer near-plateau segment due to idealized assumptions. Thus, the validated FEM is reliable for predicting flexural behavior.
(3) The parametric analysis revealed the effects of the mechanical properties and prestress level of HPSFRC on the girder’s load–deflection relationship. Higher tensile strength in HPSFRC can postpone the incipient cracking and moderately elevate the load-carrying capacity. An increase in the compressive strength of HPSFRC can improve ductility, characterized by a prolonged plateau-like segment in the load–deflection curve. An elevated prestress level can accelerate the yielding of steel strands and lead to earlier development of a plateau-like segment in the load–deflection curve.
(4) The parametric analysis results highlight the necessity for strict quality control in mixing, casting, and curing processes to ensure consistent post-cracking performance. Particular attention must be paid to the pre-tensioning process, requiring high-stiffness and high-strength reaction devices to control deformations and withstand huge forces.
(5) For flexural design of pre-tensioned HPSFRC girders without conventional reinforcement, the conventional prestressed concrete methodology applies but must incorporate HPSFRC stress–strain characteristics. Key considerations include the utilization ratio of experimentally obtained capacity and setting crack criteria, requiring conservative considerations for the uniaxial strengths of HPSFRC to meet strength and serviceability limit states. Current Chinese design codes significantly underestimate HPSFRC girders’ actual capacity, necessitating extensive material and structural testing to develop reliable, calibrated design methods. Shear capacity is also crucial for such girders. Future studies should experimentally investigate the shear capacity of the HPSFRC girder, and conduct parametric analysis to establish calculation methods.
(6) Future studies may pay attention to the sectional geometry optimization of the HPSFRC girder and concrete materials utilizing recycled wastes to achieve higher cost-efficiency without performance sacrifice.
Author Contributions
Conceptualization, L.K. and T.M.; methodology, T.M. and F.P.; software, H.B.; validation, L.K.; formal analysis, F.P. and H.B.; investigation, H.Z.; resources, T.M.; data curation, H.B.; writing—original draft preparation, H.B.; writing—review and editing, L.K.; visualization, F.P.; supervision, L.K.; project administration, H.Z.; funding acquisition, H.Z. and T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant no. U21A20149), the Sichuan Science and Technology Program of China (Grant no. 2023YFG0376), and the Sichuan Transportation Science and Technology Program of China (Grant no. 2022-ZL-05, and 2022-ZL-06).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
Authors Ling Kang, Tingmin Mu, and Haoyuan Bai are employed by the Sichuan Highway Planning, Survey, Design and Research Institute Ltd. Authors Haiyun Zou and Feifei Pei are employed by the Sichuan Chengmiancangba Expressway Construction & Development Group Co., Ltd. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NSC | Normal-strength concrete |
| HPC | High-performance concrete |
| SCMs | Supplementary cementitious materials |
| SFRC | Steel-fiber-reinforced concrete |
| HPSFRC | High-performance steel-fiber-reinforced concrete |
| UHPC | Ultra- high-performance concrete |
| FEM | Finite element model |
| CDP | Concrete damage plasticity |
References
- Leung, C.K.Y. Concrete as a Building Material. Encyclopedia of Materials: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2001; pp. 1471–1479. [Google Scholar] [CrossRef]
- Zheng, Y.; Lv, X.; Hu, S.; Zhuo, J.; Wan, C.; Liu, J. Mechanical properties and durability of steel fiber reinforced concrete: A review. J. Build. Eng. 2024, 82, 108025. [Google Scholar] [CrossRef]
- Naaman, A.E.; Reinhardt, H.W. Proposed classification of HPFRC composites based on their tensile response. Mater. Struct./Mater. Constr. 2006, 39, 547–555. [Google Scholar] [CrossRef]
- Mufti, A.A.; Leslie, G.J.; Baidar, B.; Leon, D.W. Experimental investigation of fibre-reinforced concrete deck slabs without internal steel reinforcement. Can. J. Civ. Eng. 1993, 20, 398–406. [Google Scholar] [CrossRef]
- Kwak, Y.; Eberhard, O.M.; Kim, W.; Kim, J. Shear strength of steel fiber-reinforced concrete beams without stirrups. ACI Struct. J. 2002, 99, 530–538. [Google Scholar] [CrossRef]
- Padmarajaiah, S.K.; Ramaswamy, A. Flexural strength predictions of steel fiber reinforced high-strength concrete in fully/partially prestressed beam specimens. Cem. Concr. Compos. 2004, 26, 275–290. [Google Scholar] [CrossRef]
- Dhonde, H.B.; Mo, Y.L.; Hsu, T.T.C. Fiber Reinforcement in Prestressed Concrete Beams; University of Houston: Houston, TX, USA, 2005. [Google Scholar]
- Azmee, N.M.; Shafiq, N. Ultra-high performance concrete: From fundamental to applications. Case Stud. Constr. Mater. 2018, 9, e00197. [Google Scholar] [CrossRef]
- Xue, J.; Briseghella, B.; Huang, F.; Nuti, C.; Tabatabai, H.; Chen, B. Review of ultra-high performance concrete and its application in bridge engineering. Constr. Build. Mater. 2002, 260, 119844. [Google Scholar] [CrossRef]
- Zhou, M.; Lu, W.; Song, J.; Lee, G.C. Application of Ultra-High Performance Concrete in bridge engineering. Constr. Build. Mater. 2018, 186, 1256–1267. [Google Scholar] [CrossRef]
- Blais, P.Y.; Couture, M. precast, prestressed pedestrian bridge-world’s first Reactive Powder Concrete structure. PCI J. 1999, 44, 60–71. [Google Scholar] [CrossRef]
- Fehling, E.; Bunje, K.; Schmidt, M.; Tue, N.V.; Schreiber, W.; Humburg, E. Design of first hybrid UHPC-steel bridge across River Fulda in Kassel, Germany. In Proceedings of the IABSE Symposium, Weimar 2007: Improving Infrastructure Worldwide, Weimar, Germany, 19–21 September 2007. [Google Scholar] [CrossRef]
- Chen, B.; An, M.; Huang, Q.; Wu, H.; Huang, W.; Zhao, Q. Application of Ultra-High Performance Concrete in Bridge Engineering in China. In Proceedings of the First International Interactive Symposium on UHPC 2016, Iowa State University, Des Moines, IA, USA, 27–30 October 2016. [Google Scholar] [CrossRef]
- Kasuga, A. Effects of butterfly web design on bridge construction. Struct. Concr. 2017, 18, 128–142. [Google Scholar] [CrossRef]
- Fan, D.; Tian, W.; Feng, D.; Cheng, J.; Yang, R.; Zhang, K. Development and Applications of Ultra-high Performance Concrete in Bridge Engineering. IOP Conf. Ser. Earth Environ. Sci. 2018, 189, 022038. [Google Scholar] [CrossRef]
- Graybeal, B.; Brühwiler, E.; Kim, B.-S.; Toutlemonde, F.; Voo, Y.L.; Zaghi, A. International Perspective on UHPC in Bridge Engineering. J. Bridge Eng. 2020, 25. [Google Scholar] [CrossRef]
- Su, J.Z.; Ma, X.L.; Chen, B.C.; Sennah, K. Full-scale bending test and parametric study on a 30-m span prestressed ultra-high performance concrete box girder. Adv. Struct. Eng. 2020, 23, 1276–1289. [Google Scholar] [CrossRef]
- Graybeal, B.A. Flexural Behavior of an Ultrahigh-Performance Concrete I-Girder. J. Bridge Eng. 2008, 13. [Google Scholar] [CrossRef]
- Tu, W.; Cheng, Q.; Zhang, L.; Li, P.; Jiang, H.; Tian, Y.; Fang, J. Shear performance of 25 m full-scale prestressed UHPC-NC composite I-beam without stirrups. Case Stud. Constr. Mater. 2024, 21, e03942. [Google Scholar] [CrossRef]
- Folino, P.; Ripani, M.; Xargay, H.; Rocca, N. Comprehensive analysis of Fiber Reinforced Concrete beams with conventional reinforcement. Eng. Struct. 2020, 202, 109862. [Google Scholar] [CrossRef]
- Wu, T.; Sun, Y.; Liu, X.; Cao, Y. Comparative study of the flexural behavior of steel fiber-reinforced lightweight aggregate concrete beams reinforced and prestressed with CFRP tendons. Eng. Struct. 2021, 233, 1119021. [Google Scholar] [CrossRef]
- Li, C.; Zhu, H.; Niu, G.; Cheng, S.; Gu, Z.; Yang, L. Flexural behavior and a new model for flexural design of concrete beams hybridly reinforced by continuous FRP bars and discrete steel fibers. Structures 2022, 38, 949–960. [Google Scholar] [CrossRef]
- Qasim, M.; Lee, C.K.; Zhang, Y.X. Flexural strengthening of reinforced concrete beams using hybrid fibre reinforced engineered cementitious composite. Eng. Struct. 2023, 284, 115992. [Google Scholar] [CrossRef]
- JTG D60-2015; General Code for Desigh of Highway Bridges and Culverts. China Communications Press: Beijing, China, 2015.
- JTG 3362-2018; Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts. China Communications Press: Beijing, China, 2018.
- GB/T 31387-2015; Reactive Powder Concrete. Standardization Administration of China: Beijing, China, 2015.
- JG/T 472-2015; Steel Fiber Reinforced Concrete. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2015.
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2019.
- JT/T 329-2010; Prestressing Strand Anchorage, Grip and Coupler for Highway Bridge. Ministry of Transport of China: Beijing, China, 2010.
- GB 50010-2010(2015); Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015.
- GB 50204-2015; Code for Acceptance of Constructional Quality of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015.
- Kim, D.-j.; Naaman, A.E.; El-Tawil, S. Comparative flexural behavior of four fiber reinforced cementitious composites. Cem. Concr. Compos. 2008, 30, 917–928. [Google Scholar] [CrossRef]
- Contento, A.; Aloisio, A.; Xue, J.; He, J.; Briseghella, B. Ultra-high performance concrete beam-to-beam connections in continuous bridges: Experimental full-scale tests, FE analyses and design. Eng. Struct. 2024, 316, 118594. [Google Scholar] [CrossRef]
- Ezeldin, A.S.; Balaguru, P.N. Normal-and High-Strength Fiber-Reinforced Concrete under Compression. J. Mater. Civ. Eng. 1992, 4, 415–429. [Google Scholar] [CrossRef]
- Nataraja, M.C.; Dhang, N.; Gupta, A.P. Stress–strain curves for steel-fiber reinforced concrete under compression. Cem. Concr. Compos. 1999, 21, 383–390. [Google Scholar] [CrossRef]
- Lu, X.L.; Zhang, Y.; Nian, X.C. Stress-strain behavior for high-strength steel fiber reinforced concrete under monotonic and repeated compressive loading. J. Build Struct. 2017, 38, 43–135. [Google Scholar]
- Lok, T.-S.; Pei, J.-S. Flexural Behavior of Steel Fiber Reinforced Concrete. J. Mater. Civ. Eng. 1998, 10, 86–97. [Google Scholar] [CrossRef]
- Yang, M.; Huang, C.; Wang, J. Characteristics of stress-strain curve of high strength steel fiber reinforced concrete under uniaxial tension. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2006, 21, 132–137. [Google Scholar] [CrossRef]
- Muhammad, F.; Harun, M.; Ahmed, A.; Kabir, N.; Khalid, H.R.; Hanif, A. Influence of bonded mortar on recycled aggregate concrete properties: A review. Constr. Build. Mater. 2024, 432, 136564. [Google Scholar] [CrossRef]
- de Assis, H.J.B.; da Silva Bezerra, A.C.; de Paula, J.N.; Moravia, W.G. Utilization of recycled synthetic fibers in concrete with a focus on structural properties enhancement: A critical literature review. Discov. Mater. 2024, 4, 77. [Google Scholar] [CrossRef]
- Ahmad, F.; Qureshi, M.I.; Rawat, S.; Alkharisi, M.K.; Alturki, M. E-waste in concrete construction: Recycling, applications, and impact on mechanical, durability, and thermal properties—A review. Innov. Infrastruct. Solut. 2025, 10, 246. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
