The Influence of Soft Soil, Pile–Raft Foundation and Bamboo on the Bearing Characteristics of Reinforced Concrete (RC) Structure
Abstract
1. Introduction
2. Model Parameters and Layout
2.1. Preparation of Similar Materials
Preparation of the Concrete in the Model
2.2. The Production of Models
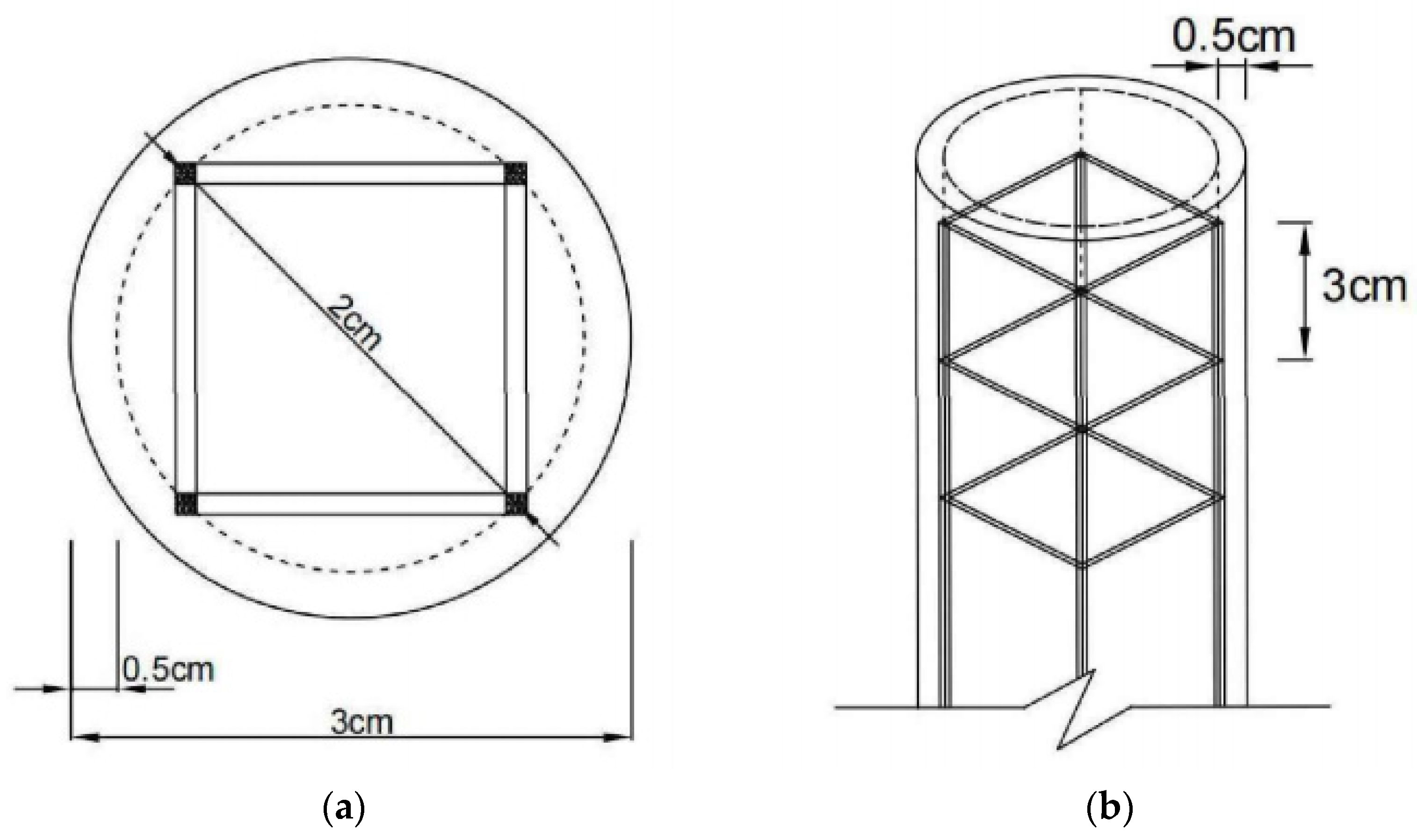
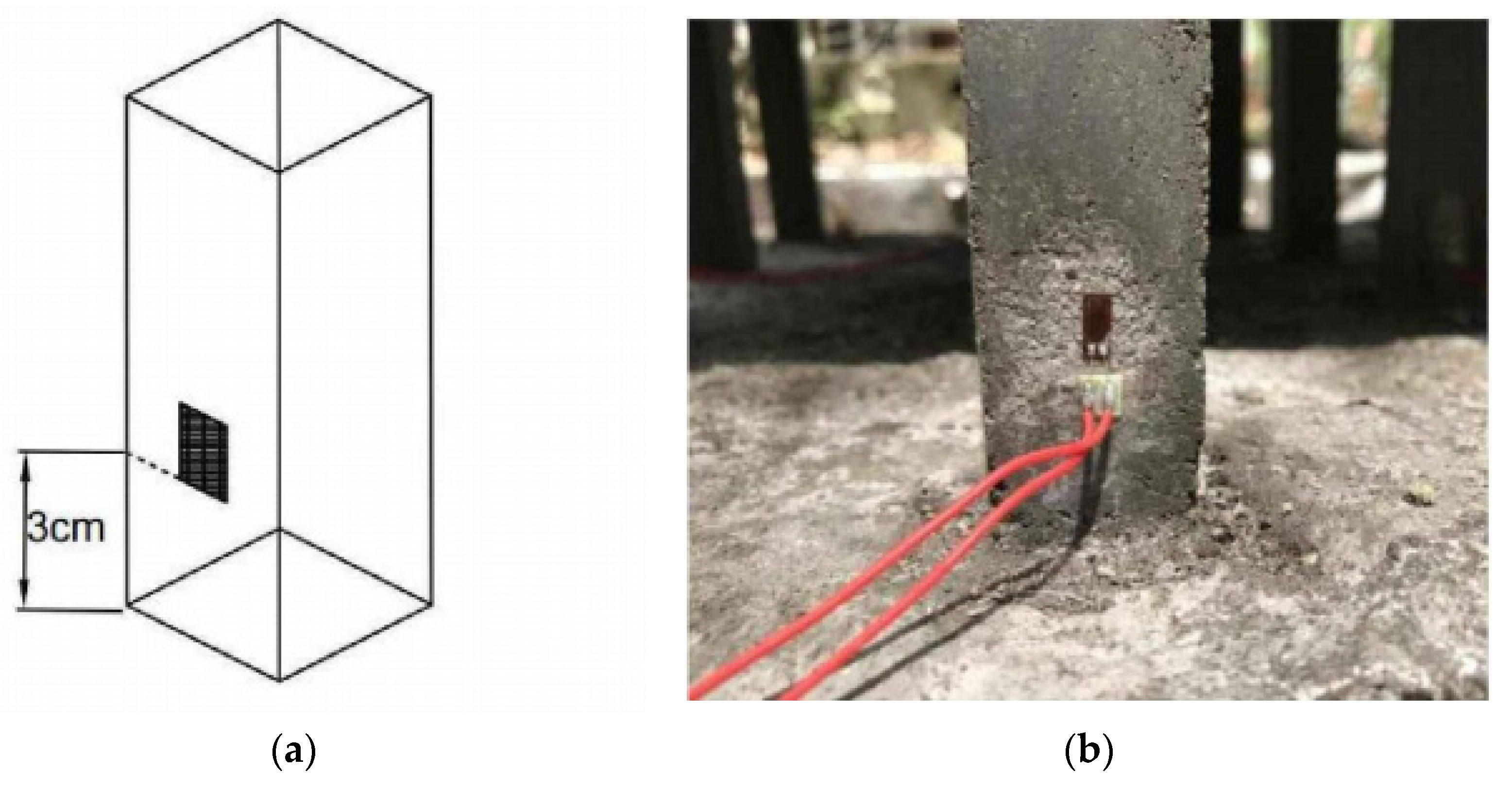
2.2.1. The Making of Pile
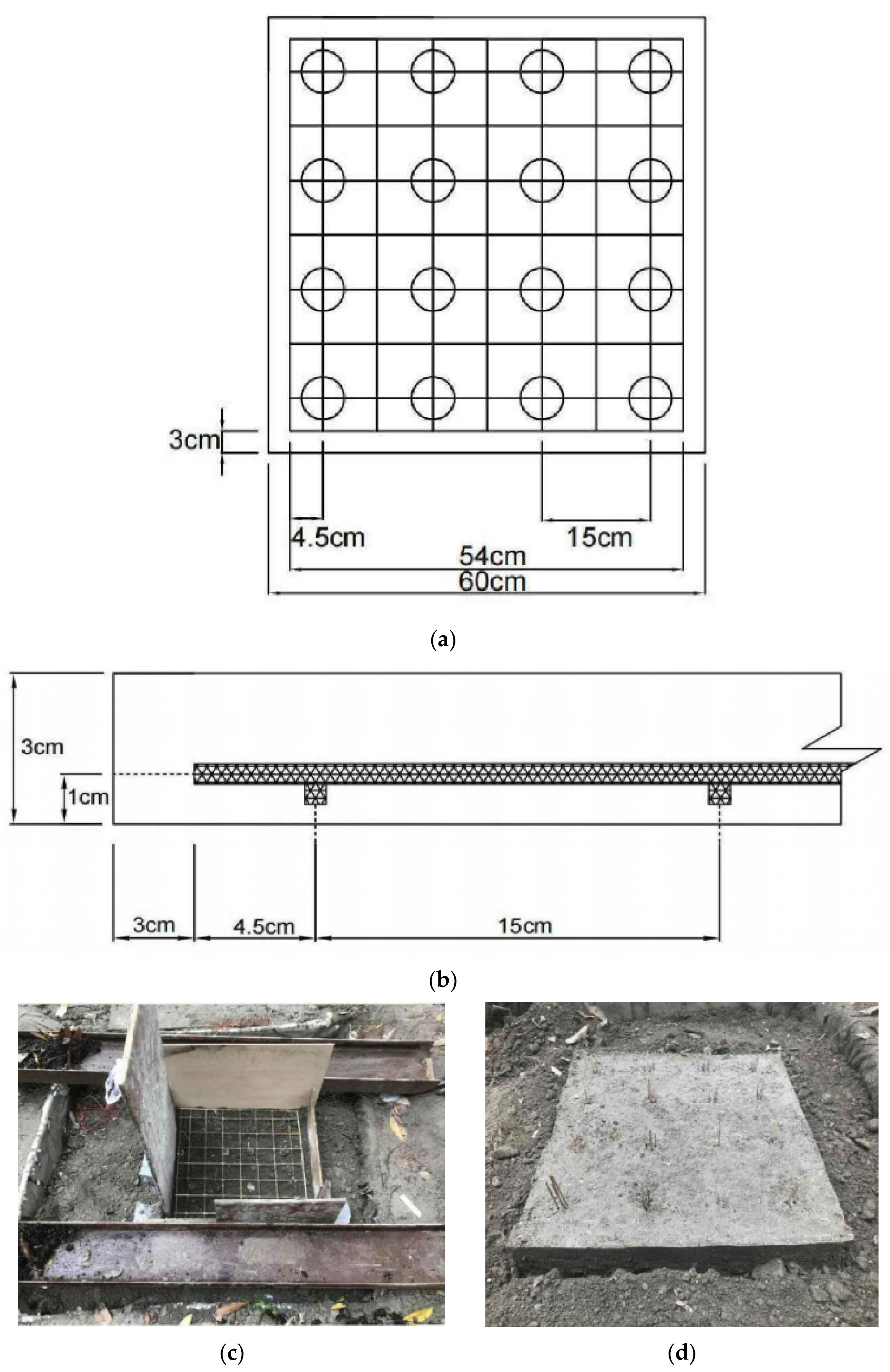
2.2.2. Raft Board Production
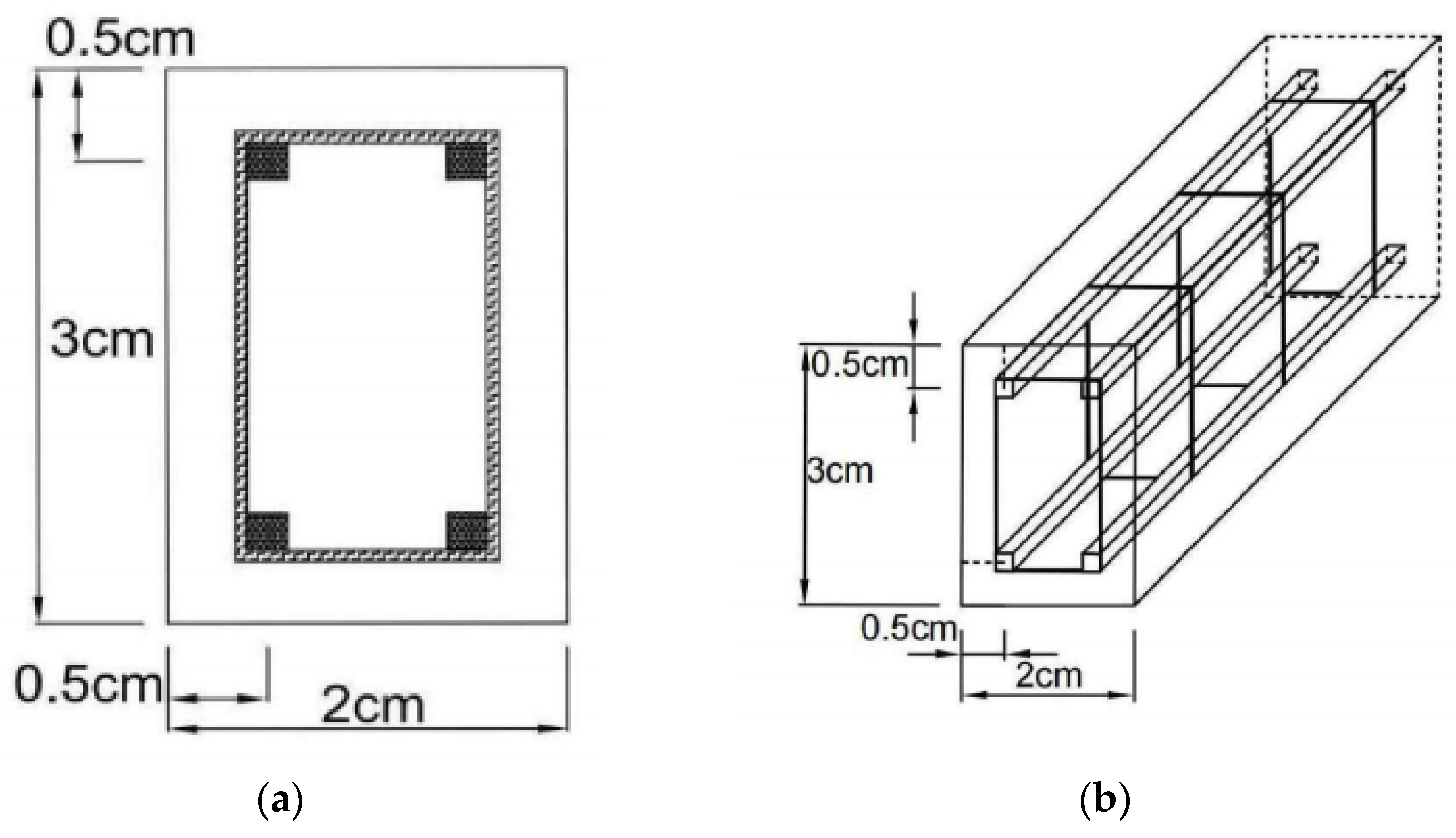
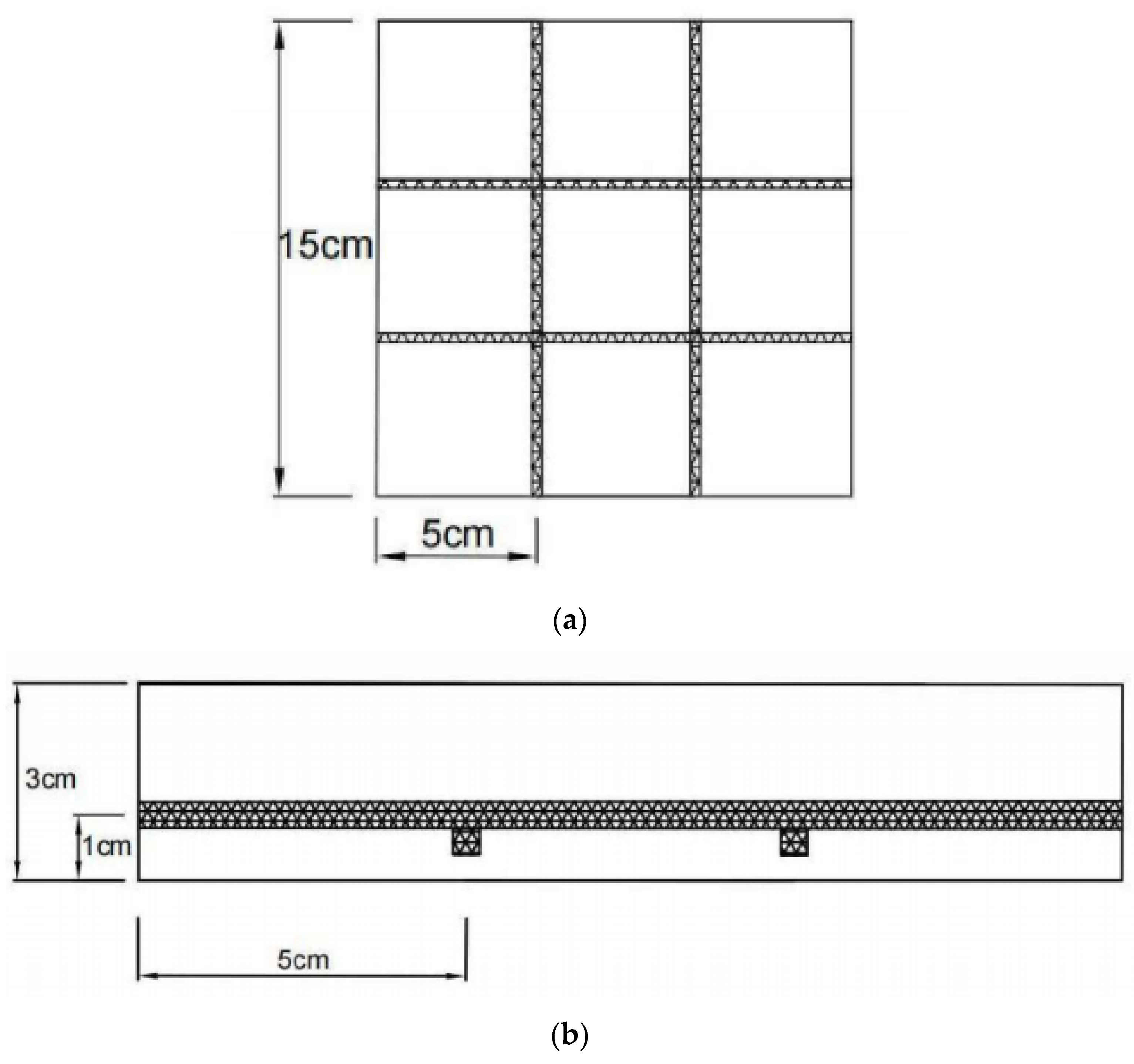
2.2.3. The Way in Which the Superstructure Is Made
2.2.4. Bamboo Tendon Link Way
2.3. Preparation of Soft Soil
2.3.1. Volume Weight Test of Soil
2.3.2. Water Content Test of Soil Body
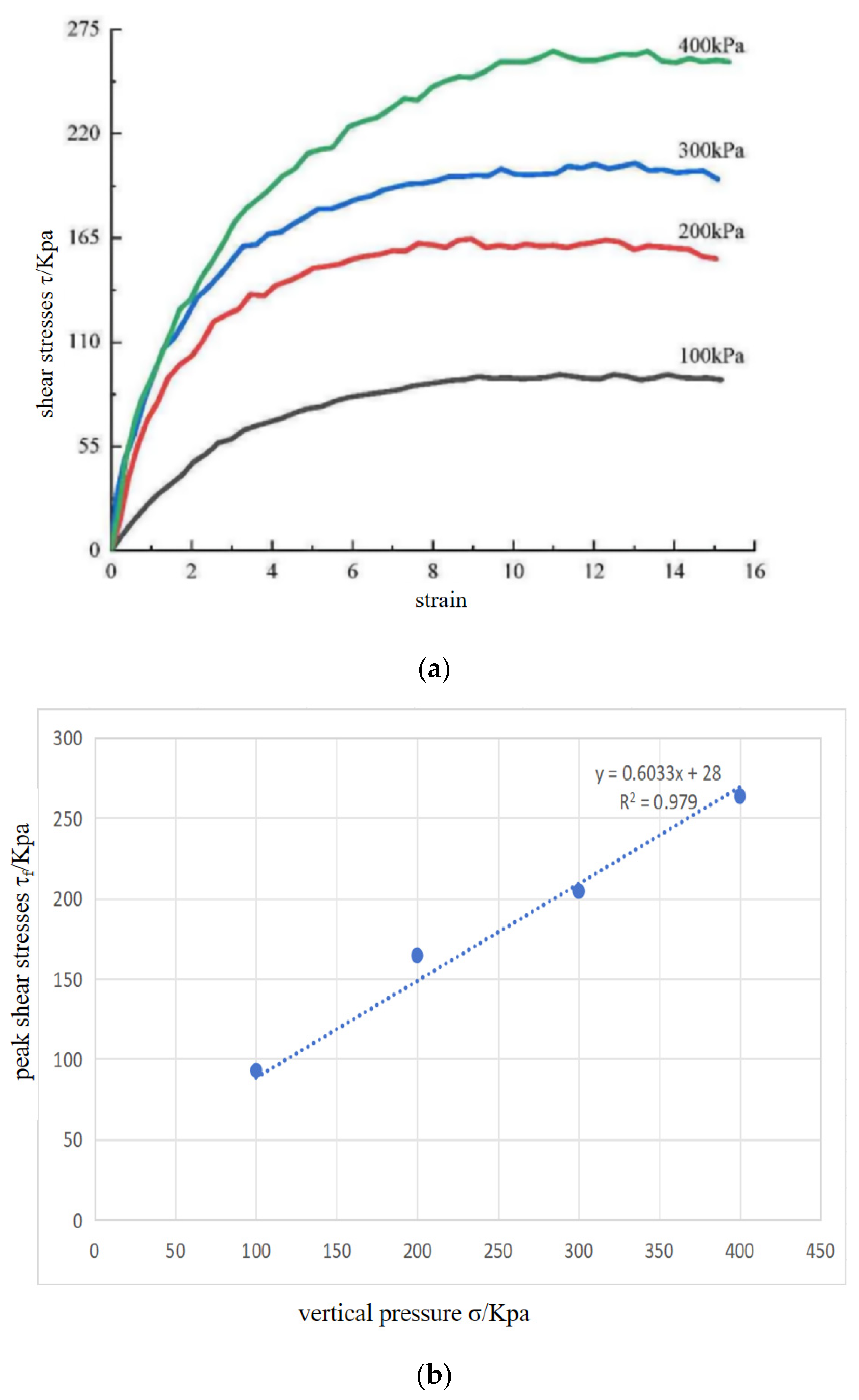
2.3.3. Direct Shear Test of Soil
2.4. Layout and Data Processing of the Test Components
2.4.1. The Disposal of Raft Plate
2.4.2. Treatment of the Superstructure
2.4.3. Loading Design
2.5. Test Process and Error Analysis
2.5.1. Experimental Flow
2.5.2. Analysis of Trial Error
3. Results and Discussion
3.1. Analysis of the Relative Stiffness of the Superstructure
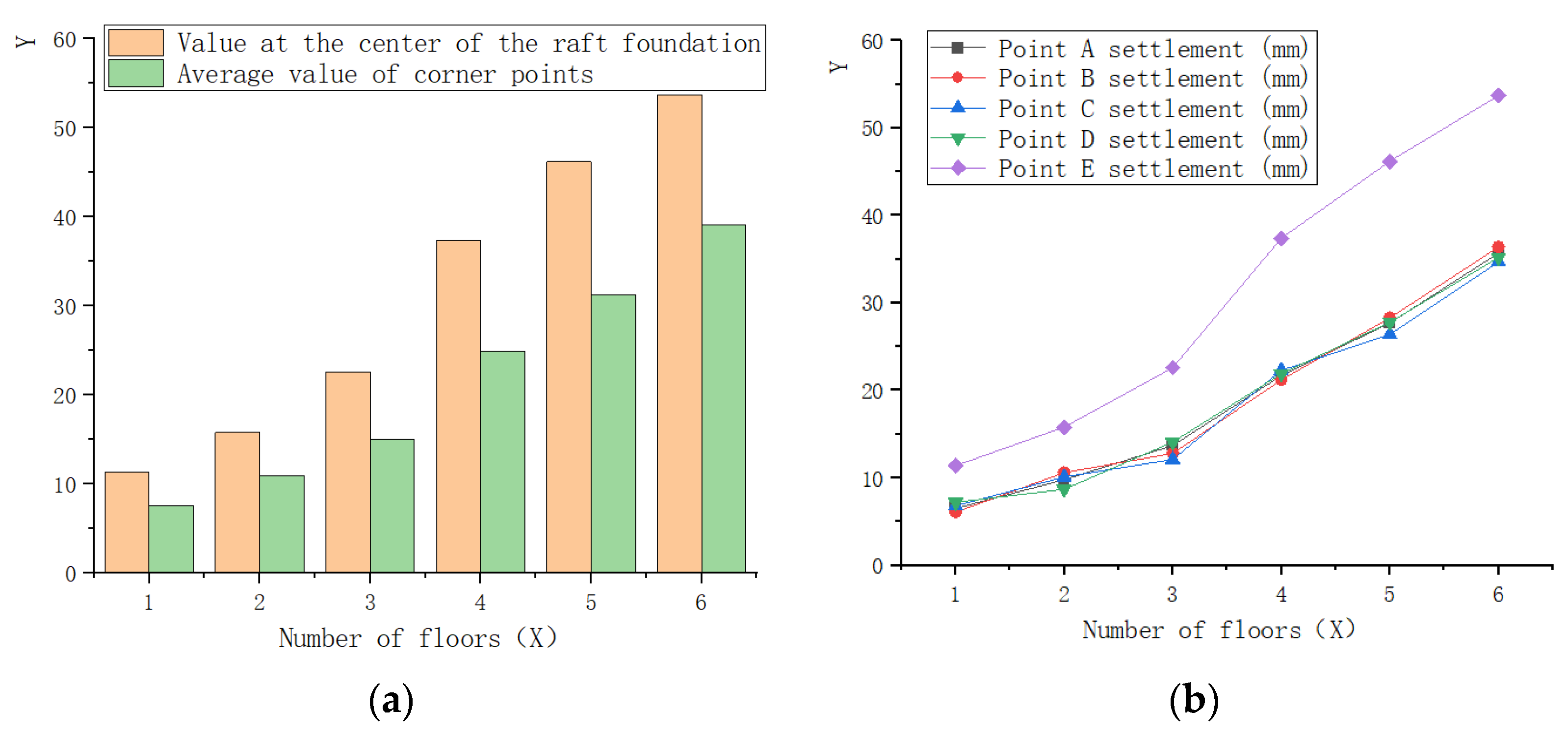
3.2. Load–Settlement Relationship
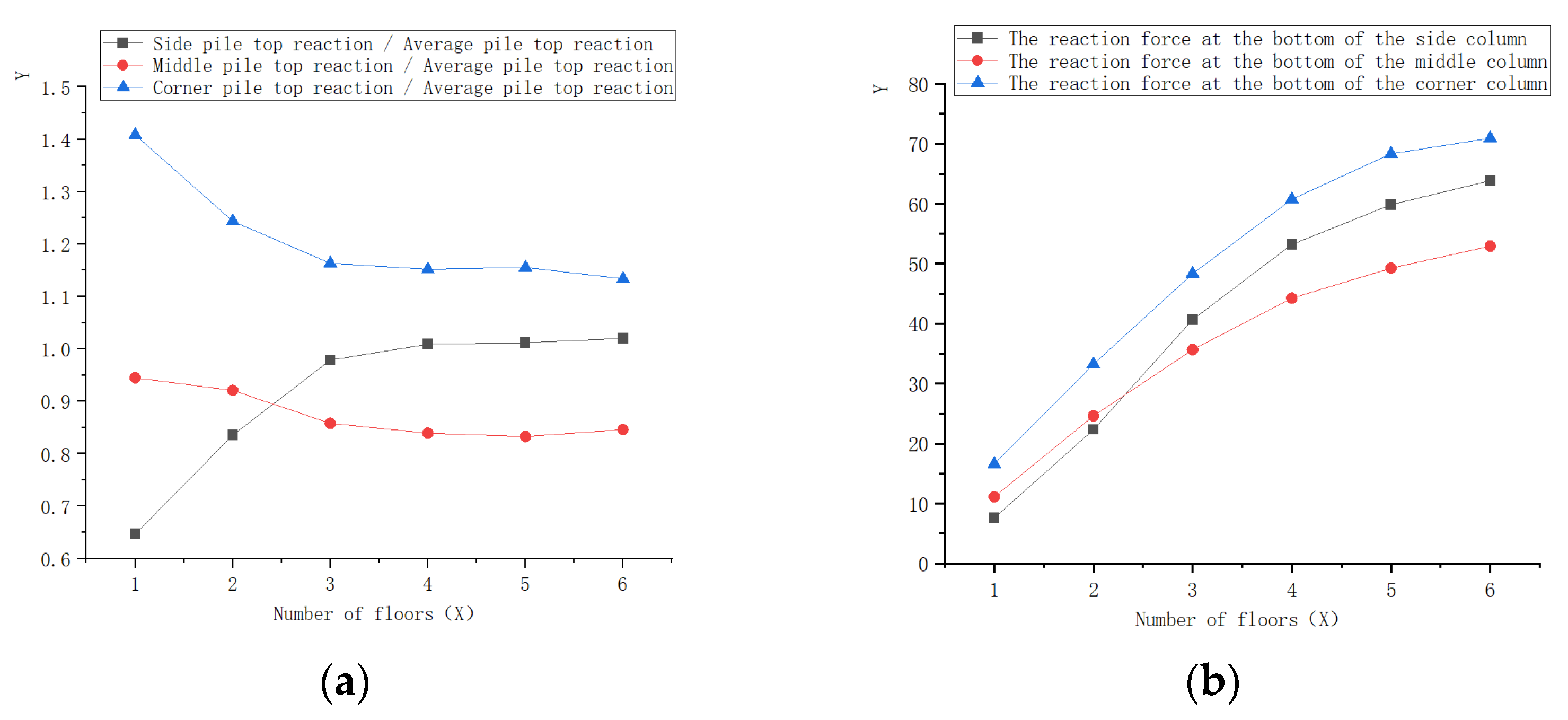
3.3. Load-Sharing Relationship of the Pile Body
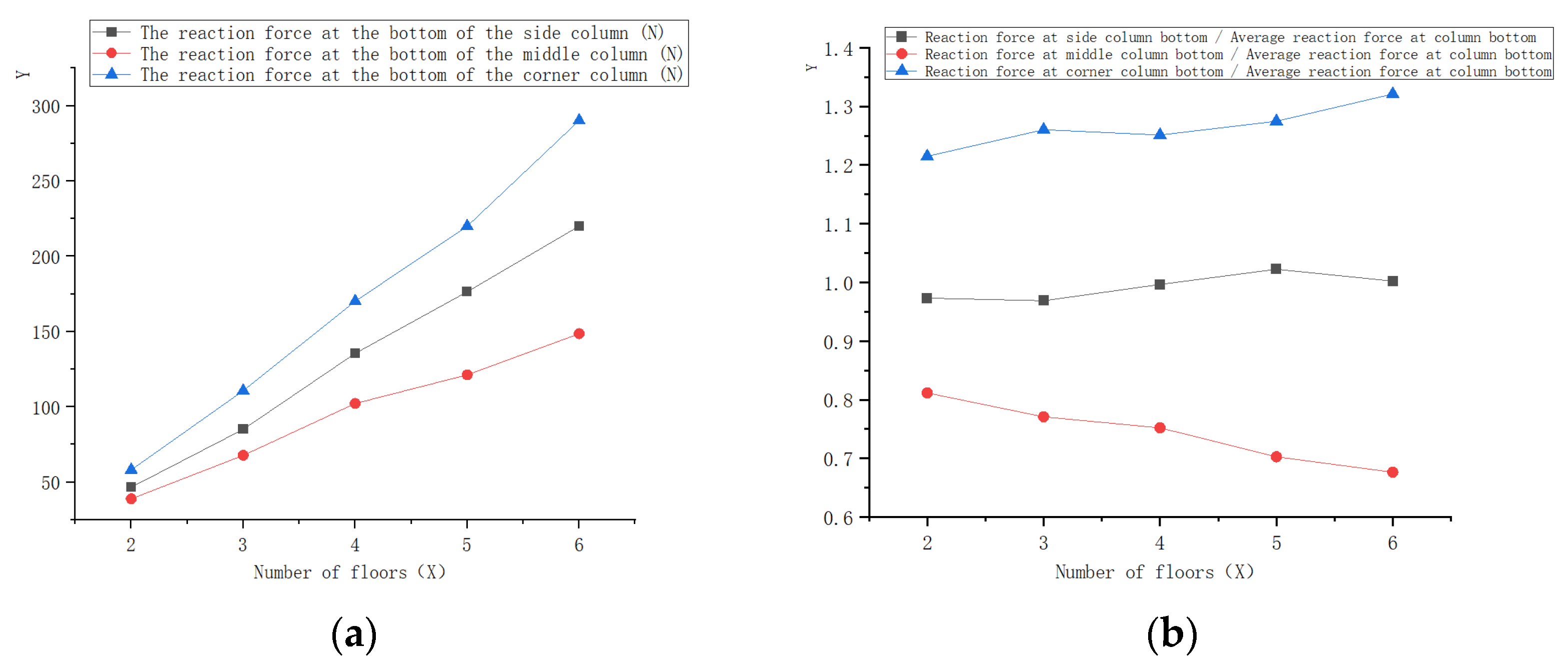
3.4. Working Characteristics of the Bottom Column of the Superstructure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, D.-W.; Lin, J.-H.; Cheng, S.-H.; Ge, L. Dimensionless Reaction Coefficients for Embedded Piled Raft Foundations in Soft Clays under Vertical Loads. Int. J. Géoméch. 2024, 24, 04024025. [Google Scholar] [CrossRef]
- Ahmed, D.; Taib, S.N.L.B.; Ayadat, T.; Hasan, A. Numerical Analysis of the Carrying Capacity of a Piled Raft Foundation in Soft Clayey Soils. Civ. Eng. J. 2022, 8, 622–636. [Google Scholar] [CrossRef]
- Van Cao, H.; Nguyen, T.A.; Le, V.A.N. 3D Finite Element Analysis of the Effect of Raft Thickness, Pile Spacing, and Pile Length on the Behavior of Piled Raft Foundation. Int. J. Geomate 2022, 23, 47–56. [Google Scholar] [CrossRef]
- Al-Zuhairi, A.H.; Abdualrahman, S.Q.; Hanoon, A.N.; Ali, A.I.T.; Abdulhameed, A.; Al Zand, A.W. Enhancing the Structural Analysis of RC Piled-Raft Foundation by Actual Behaviour of Supporting Piles. Civ. Environ. Eng. 2022, 18, 678–687. [Google Scholar] [CrossRef]
- Deb, P.; Debnath, B.; Reang, R.B.; Pal, S.K. Structural Analysis of Piled Raft Foundation in Soft Soil: An Experimental Simulation and Parametric Study with Numerical Method. Ocean. Eng. 2022, 261, 112139. [Google Scholar] [CrossRef]
- Harianto, T.; Yunus, M.; Walenna, M.A. Bearing Capacity of Raft-Pile Foundation Using Timber Pile on Soft Soil. Int. J. Geomate 2021, 21, 108–114. [Google Scholar] [CrossRef]
- Abdel-Azim, O.A.; Abdel-Rahman, K.; Ei-Mossallamy, Y.M. Numerical Investigation of Optimized Piled Raft Foundation for High-Rise Building in Germany. Innov. Infrastruct. Solut. 2020, 5, 11. [Google Scholar] [CrossRef]
- Lin, D.-G.; Liu, W.-T.; Chou, J.-C. Mechanical Behaviors of Piled-Raft Foundation and Diaphragm Wall in Deep Excavation of Taipei Metropolitan. J. Mar. Sci. Technol. 2016, 24, 980–991. [Google Scholar] [CrossRef]
- Watcharasawe, K.; Jongpradist, P.; Kitiyodom, P.; Matsumoto, T. Measurements and Analysis of Load Sharing Between Piles and Raft in a Pile Foundation in Clay. Geomech. Eng. 2021, 24, 559–572. [Google Scholar] [CrossRef]
- Visuvasam, J.; Chandrasekaran, S.S. Effect of Soil–Pile–Structure Interaction on Seismic Behaviour of RC Building Frames. Innov. Infrastruct. Solut. 2019, 4, 45. [Google Scholar] [CrossRef]
- Lee, S.; Moon, J.-S. Effect of Interactions between Piled Raft Components and Soil on Behavior of Piled Raft Foundation. KSCE J. Civ. Eng. 2017, 21, 243–252. [Google Scholar] [CrossRef]
- Bisht, R.S.; Juneja, A. Load Sharing Ratios and Interaction Effects for Piled Raft Foundations in Sands. Proc. Inst. Civ. Eng.-Geotech. Eng. 2021, 176, 105–117. [Google Scholar] [CrossRef]
- Patil, G.; Choudhury, D.; Mondal, A. Three-Dimensional Soil-Foundation-Superstructure Interaction Analysis of Nuclear Building Supported by Combined Piled-Raft System. Int. J. Géoméch. 2021, 21, 04021029. [Google Scholar] [CrossRef]
- Yang, Y.; Gong, W.; Cheng, Y.P.; Dai, G.; Zou, Y.; Liang, F. Effect of Soil-Pile-Structure Interaction on Seismic Behaviour of Nuclear Power Station via Shaking Table Tests. Structures 2021, 33, 2990–3001. [Google Scholar] [CrossRef]
- Hanna, A.M.; Vakili, R. Load-Sharing Mechanism of Non-Displacement Piled-Raft Foundation in Sand. Proc. Inst. Civ. Eng.-Ground Improv. 2021, 174, 105–115. [Google Scholar] [CrossRef]
- Chaudhuri, C.H.; Chanda, D.; Saha, R.; Haldar, S. Three-Dimensional Numerical Analysis on Seismic Behavior of Soil-Piled Raft-Structure System. Structures 2020, 28, 905–922. [Google Scholar] [CrossRef]
- Jayalekshmi, B.R.; Jisha, S.V.; Shivashankar, R. Response in Piled Raft Foundation of Tall Chimneys under Along-Wind Load Incorporating Flexibility of Soil. Front. Struct. Civ. Eng. 2015, 9, 307–322. [Google Scholar] [CrossRef]
- Mishra, A.; Venkatesh, K.; Karumanchi, S.R. 3D Numerical Analysis of Single Pile and Pile–Raft Subjected to Vertical Loading. Indian Geotech. J. 2023, 53, 686–697. [Google Scholar] [CrossRef]
- Sinha, A.; Hanna, A.M. 3D Numerical Model for Piled Raft Foundation. Int. J. Géoméch. 2017, 17, 04016055. [Google Scholar] [CrossRef]
- Singh, H.; Garg, P.; Jha, J.N. Modeling the Response of a Piled-Raft Footing: Ultimate Bearing Capacity. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 359–371. [Google Scholar] [CrossRef]
- Wang, C.; Gao, F.; Tan, X.; Xu, W. A Modified Method for Improving the Prediction Accuracy of the Tunnel Shaking Table Model Test Based on Non-Direct Similarity Technique. Syst. Sci. Control Eng. 2022, 10, 104–114. [Google Scholar] [CrossRef]
- GB 50016-2014; Code for Fire Protection Design of Buildings (2018 Edition). Ministry of Housing and Urban-Rural Development of the People’s Republic of China, China Planning Press: Beijing, China, 2018.
- Feng, Z.; Shen, D.; Zhang, J.; Tang, H.; Jiang, G. Effect of Crystalline Admixture on Early-Age Residual Stress and Cracking Potential of High-Strength Concrete. Struct. Concr. 2023, 24, 4243–4258. [Google Scholar] [CrossRef]
- Suryanita, R.; Maizir, H.; Zulapriansyah, R.; Subagiono, Y.; Arshad, M.F. The Effect of Silica Fume Admixture on the Compressive Strength of the Cellular Lightweight Concrete. Results Eng. 2022, 14, 100445. [Google Scholar] [CrossRef]
- Li, Z.; Gao, X.; Lu, D.; Dong, J. Early Hydration Properties and Reaction Kinetics of Multi-Composite Cement Pastes with Supplementary Cementitious Materials (SCMs). Thermochim. Acta 2022, 709, 179157. [Google Scholar] [CrossRef]
- Cheng, Y.-h.; Yang, S.-h.; Zhang, J.-y.; Sun, X.-h. Test Research on Hydration Process of Cement-Iron Tailings Powder Composite Cementitious Materials. Powder Technol. 2022, 399, 117215. [Google Scholar] [CrossRef]
- GB 55008-2021; Code for General Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, China Architecture & Building Press: Beijing, China, 2021.
- Coulomb, C.A. Essaí sur une application des règles de maximis & minimis à quelques problèmes de statique. Rev. Française Géotechnique 2023, 175, 1. [Google Scholar]











| Physical Quantity | Symbol | Similarity Relation | Similarity Constant |
|---|---|---|---|
| Geometric dimensions (control quantity) | L | CL = 10 | 10 |
| Elastic modulus (control quantity) | E | CE = CL Cγ | 20 |
| Compressive strength (control amount) | σ | Cσ = CL Cγ | 20 |
| Volume weight (control volume) | γ | Cγ = 2 | 2 |
| Internal friction angle | φ | Cφ = 1 | 1 |
| Cohesive strength | C | CC = CL Cγ | 20 |
| Meeting an emergency | ε | Cε = 1 | 1 |
| Acceleration of gravity | g | Cg = 1 | 1 |
| Time | t | Ct = CL0.5 | 3.2 |
| Project | Masonry Mortar | ||||
|---|---|---|---|---|---|
| M1.0 | M2.5 | M5.0 | M1.5 | ||
| material | unit | quantitative proportion | quantitative proportion | quantitative proportion | quantitative proportion |
| 32.5 MPa Cement | ton | 0.158 | 0.176 | 0.204 | 0.170 |
| lime | ton | 0.075 | 0.067 | 0.055 | / |
| medium sand | ton | 1.015 | 1.015 | 1.015 | 1.015 |
| water | cubic meter | 0.400 | 0.400 | 0.400 | 0.400 |
| Level Number (m) | X to Stiffness (kN/m) | Y Orientation Stiffness (kN/m) | Floor Height (m) | Upper Weight (kN) | X-Direction Stiffness-to-Weight Ratio | Y-Direction Stiffness-to-Weight Ratio |
|---|---|---|---|---|---|---|
| 6 | 61,893.19 | 61,893.17 | 3.00 | 734.40 | 252.83 | 252.83 |
| 5 | 61,014.11 | 61,014.09 | 3.00 | 1015.20 | 180.30 | 180.30 |
| 4 | 65,017.97 | 65,017.97 | 3.00 | 1749.60 | 111.48 | 111.48 |
| 3 | 64,588.52 | 64,588.49 | 3.00 | 2030.40 | 95.43 | 95.43 |
| 2 | 67,960.88 | 67,960.85 | 3.00 | 2764.80 | 73.74 | 73.74 |
| 1 | 87,309.00 | 87,308.99 | 3.00 | 3045.60 | 86.00 | 86.00 |
| Number of Floors | Point A Settlement (mm) | Point B Settlement (mm) | Point C Settlement (mm) | Point D Settlement (mm) | Point E Settlement (mm) |
|---|---|---|---|---|---|
| 1 | 6.5 | 6.1 | 6.8 | 7.2 | 11.4 |
| 2 | 9.8 | 10.6 | 10.1 | 8.7 | 15.8 |
| 3 | 13.7 | 12.8 | 12.1 | 14.1 | 22.6 |
| 4 | 21.7 | 21.2 | 22.3 | 21.9 | 37.4 |
| 5 | 27.7 | 28.3 | 26.4 | 27.8 | 46.2 |
| 6 | 35.7 | 36.4 | 34.7 | 35.2 | 53.7 |
| PT | Linear Fitting of the Expression | Correlation (R2) |
|---|---|---|
| A | y = 5.9343x − 1.5867 | 0.9772 |
| B | y = 6.0857x − 2.0667 | 0.9686 |
| C | y = 5.6743x − 1.1267 | 0.9593 |
| D | y = 5.8600x − 1.3600 | 0.9732 |
| E | y = 9.0714x − 0.5667 | 0.9778 |
| Number of Floors | Side Pile Top Thrust (N) | Middle Pile Crest Reaction (N) | Corner Pile Crest Reaction Force (N) |
|---|---|---|---|
| 1 | 7.62 | 11.13 | 16.59 |
| 2 | 22.35 | 24.63 | 33.26 |
| 3 | 40.69 | 35.67 | 48.36 |
| 4 | 53.21 | 44.26 | 60.75 |
| 5 | 59.85 | 49.26 | 68.35 |
| 6 | 63.85 | 52.95 | 70.95 |
| Number of Floors | Edge Column Base Reaction (N) | Interior Column Base Reaction (N) | Corner Column Base Reaction (N) |
|---|---|---|---|
| 2 | 46.65 | 38.90 | 58.23 |
| 3 | 85.13 | 67.75 | 110.75 |
| 4 | 135.52 | 102.27 | 170.14 |
| 5 | 176.44 | 121.26 | 220.01 |
| 6 | 220.09 | 148.59 | 290.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Z.; He, X.; Huang, S.; Ma, C.; Liu, B.; Shu, Z.; Wang, Y.; Cui, K.; Zheng, L. The Influence of Soft Soil, Pile–Raft Foundation and Bamboo on the Bearing Characteristics of Reinforced Concrete (RC) Structure. Buildings 2025, 15, 2302. https://doi.org/10.3390/buildings15132302
Zhong Z, He X, Huang S, Ma C, Liu B, Shu Z, Wang Y, Cui K, Zheng L. The Influence of Soft Soil, Pile–Raft Foundation and Bamboo on the Bearing Characteristics of Reinforced Concrete (RC) Structure. Buildings. 2025; 15(13):2302. https://doi.org/10.3390/buildings15132302
Chicago/Turabian StyleZhong, Zhibin, Xiaotong He, Shangheng Huang, Chao Ma, Baoxian Liu, Zhile Shu, Yineng Wang, Kai Cui, and Lining Zheng. 2025. "The Influence of Soft Soil, Pile–Raft Foundation and Bamboo on the Bearing Characteristics of Reinforced Concrete (RC) Structure" Buildings 15, no. 13: 2302. https://doi.org/10.3390/buildings15132302
APA StyleZhong, Z., He, X., Huang, S., Ma, C., Liu, B., Shu, Z., Wang, Y., Cui, K., & Zheng, L. (2025). The Influence of Soft Soil, Pile–Raft Foundation and Bamboo on the Bearing Characteristics of Reinforced Concrete (RC) Structure. Buildings, 15(13), 2302. https://doi.org/10.3390/buildings15132302





