A Novel Method for Comparing Building Height Hierarchies
Abstract
1. Introduction
2. Study Area and Data
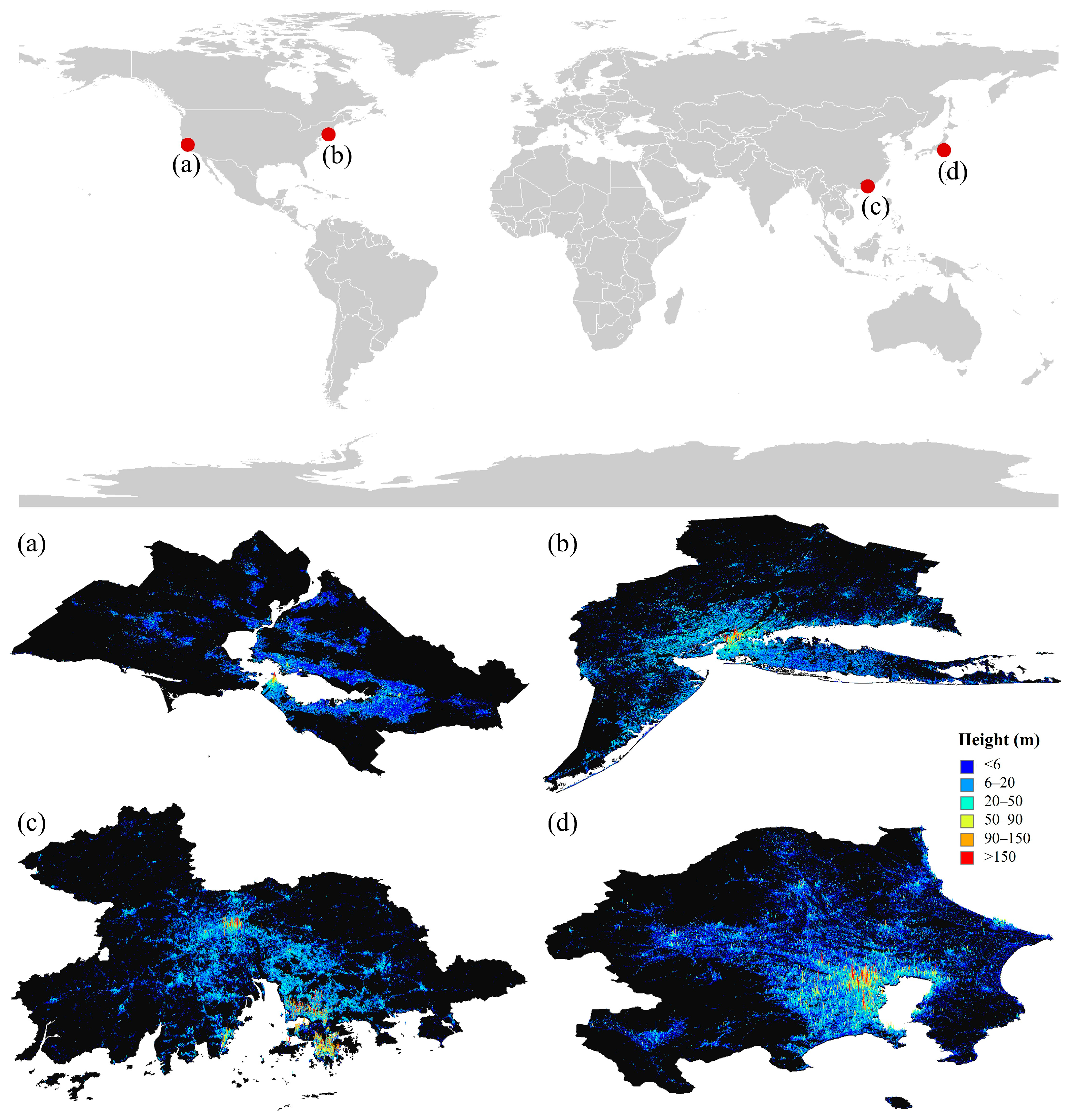
2.1. Study Area
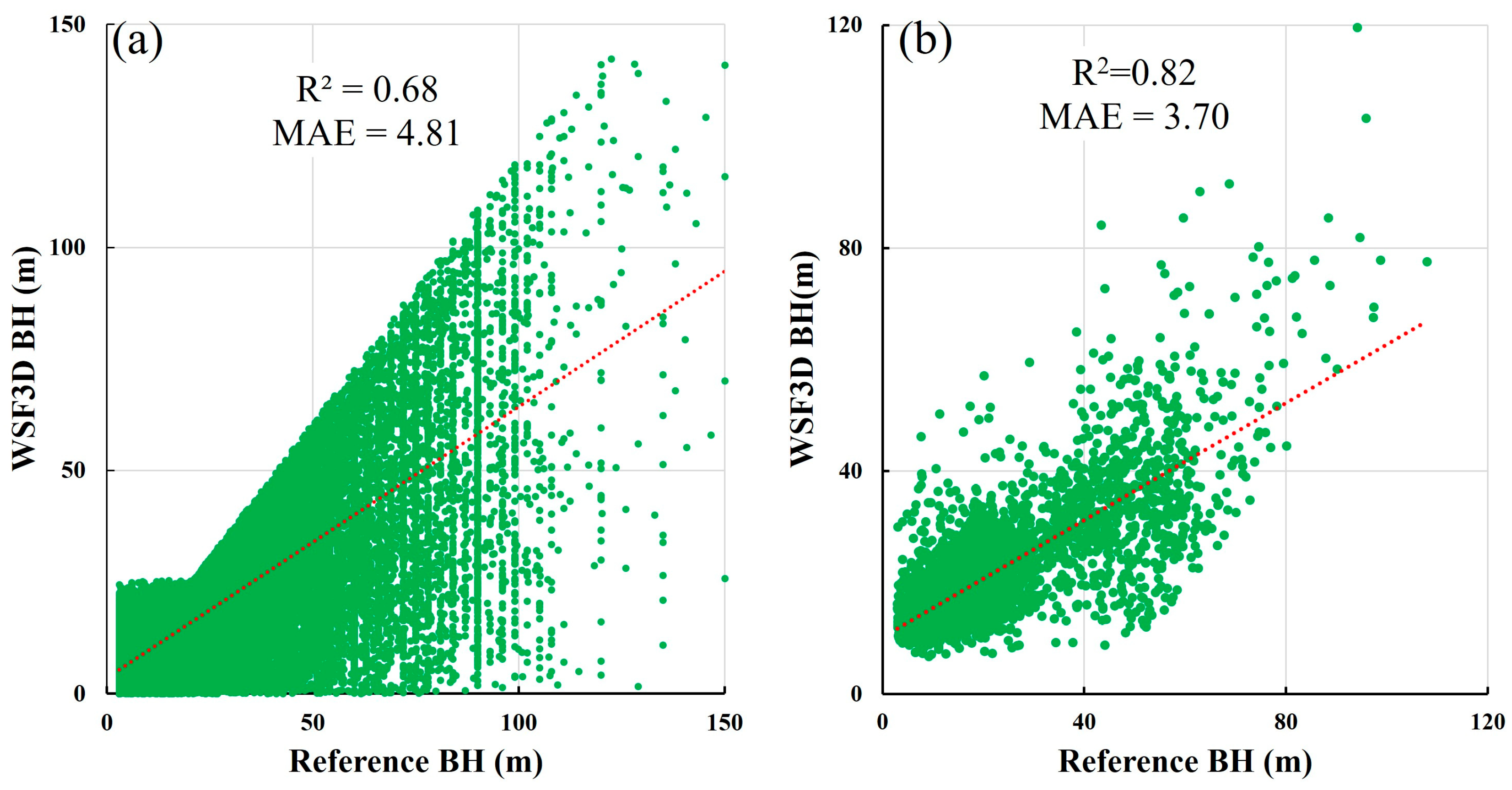
2.2. Data
3. Method
3.1. Theoretical Basis
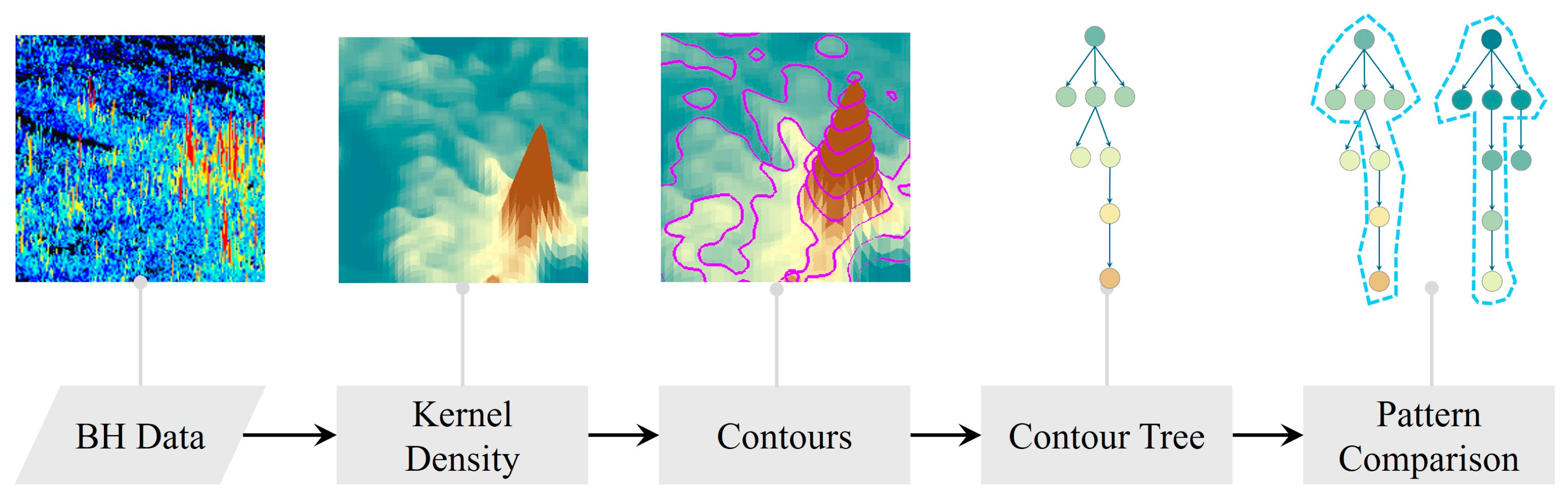
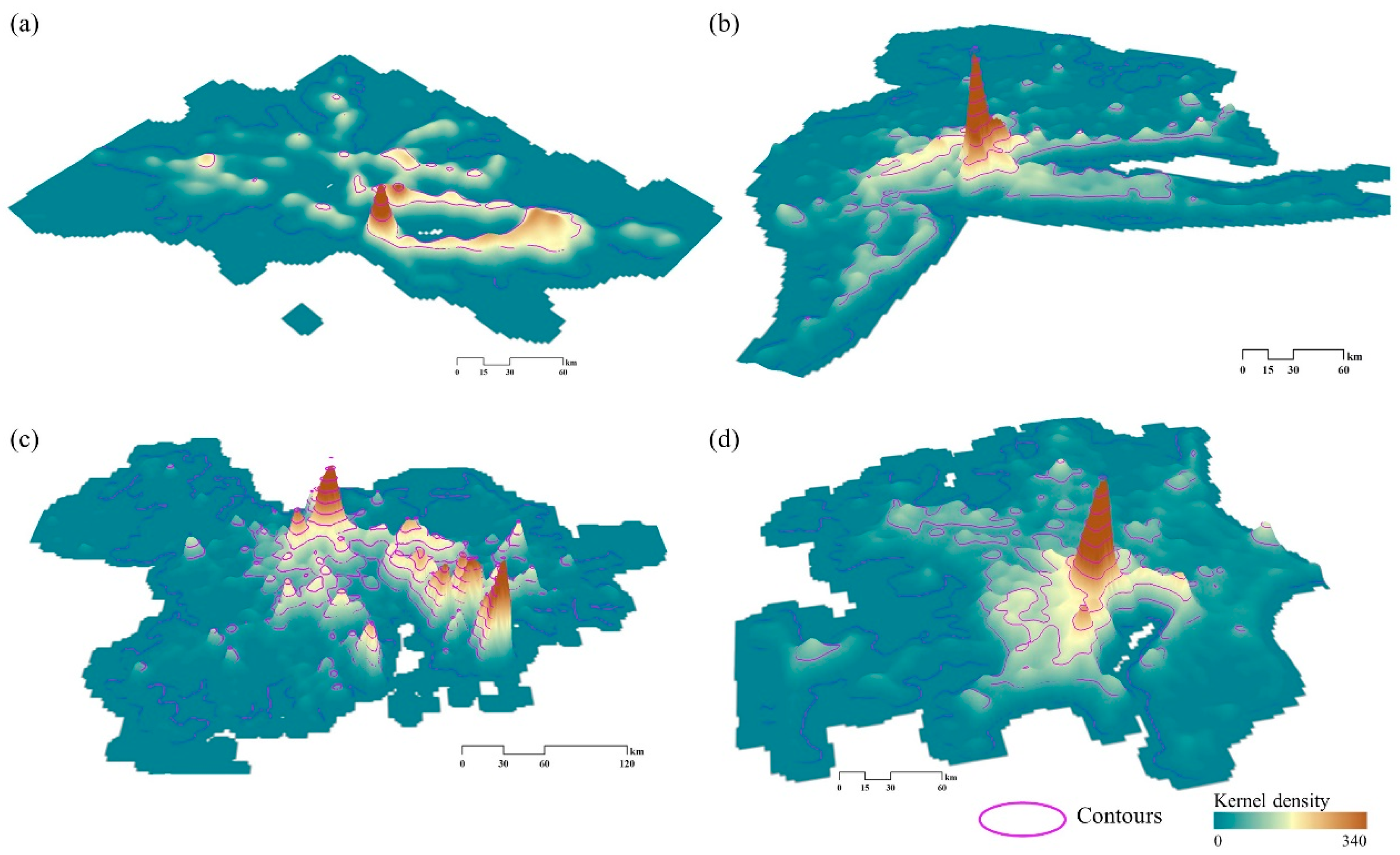
3.2. Kernel Density Estimation
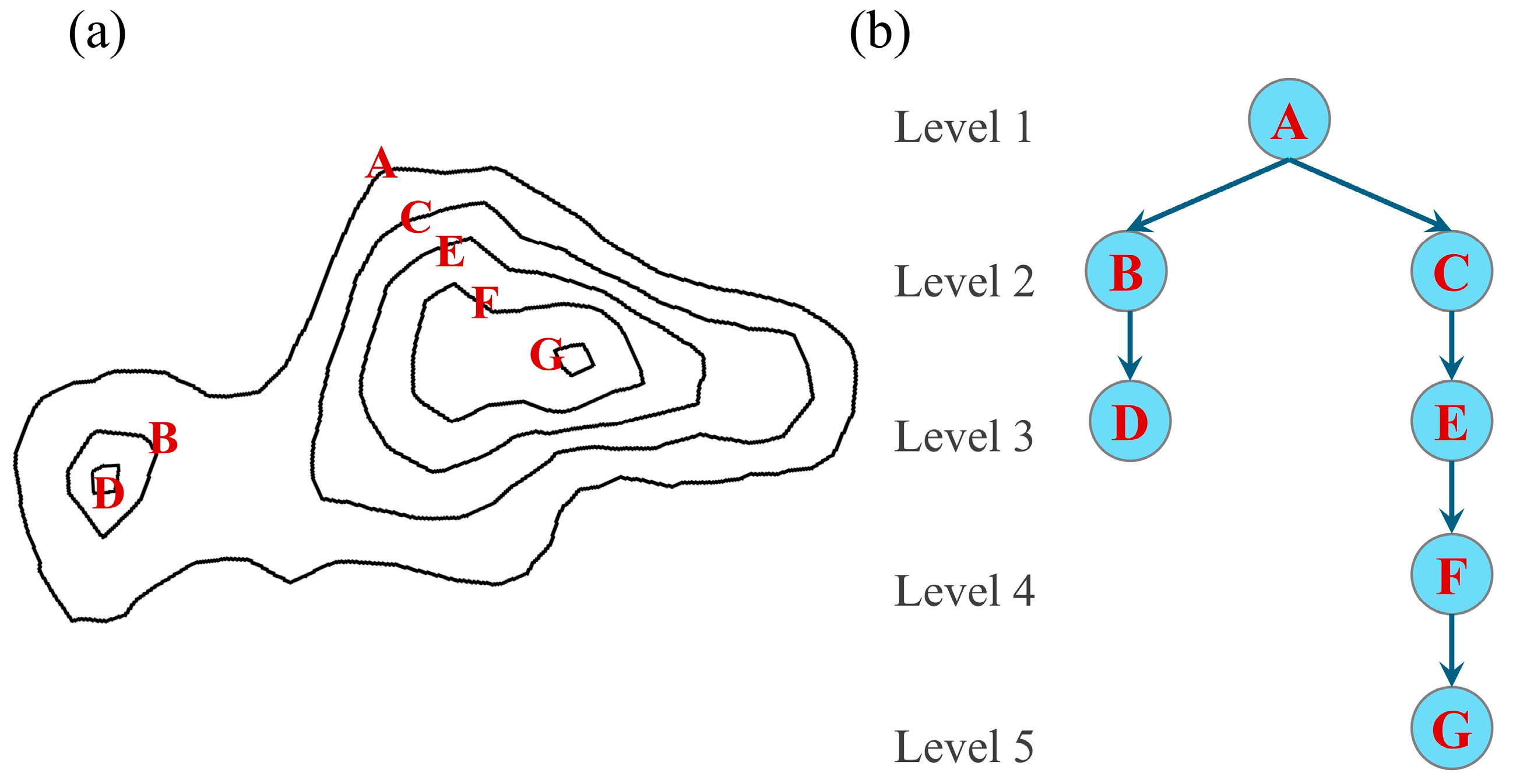
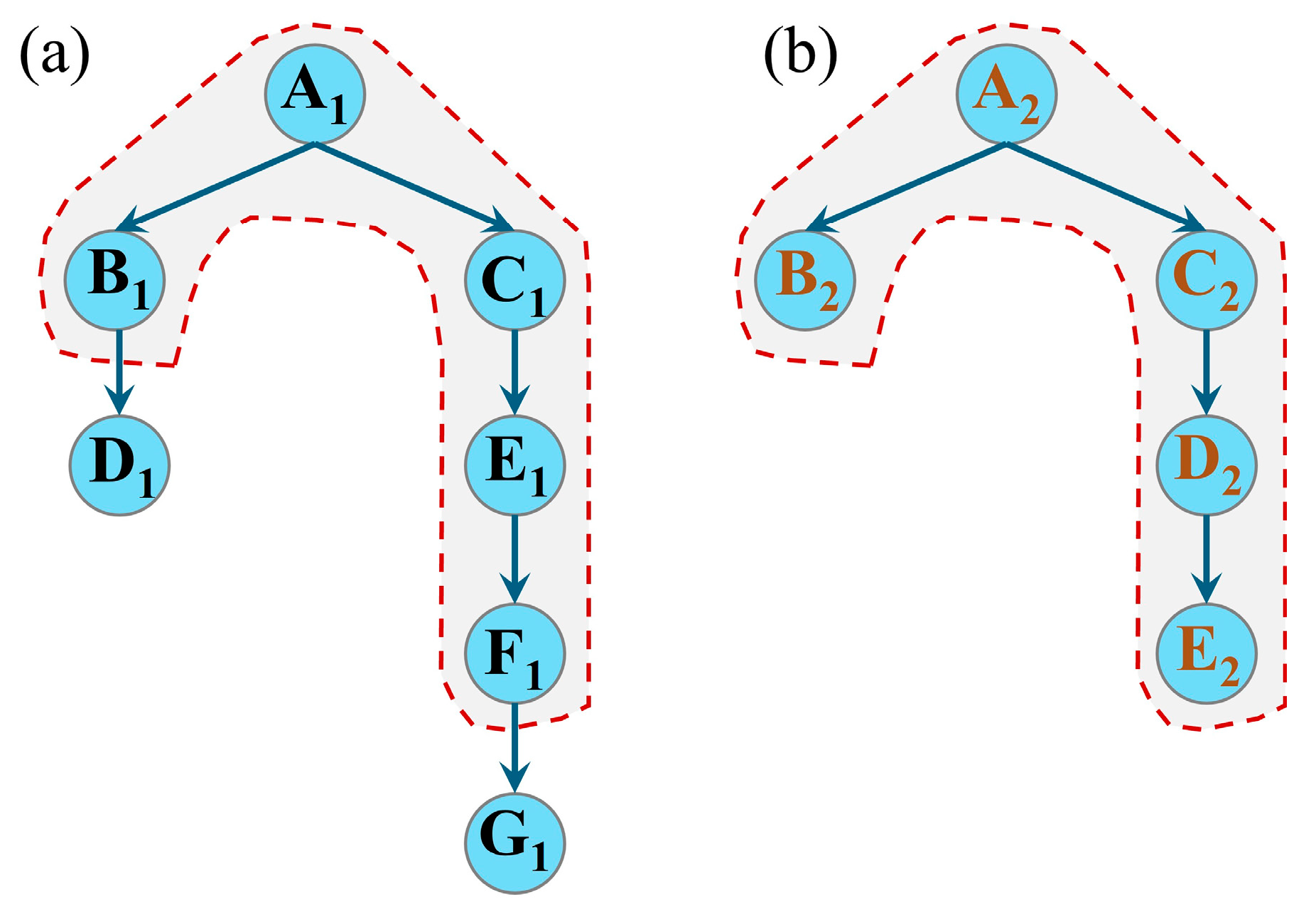
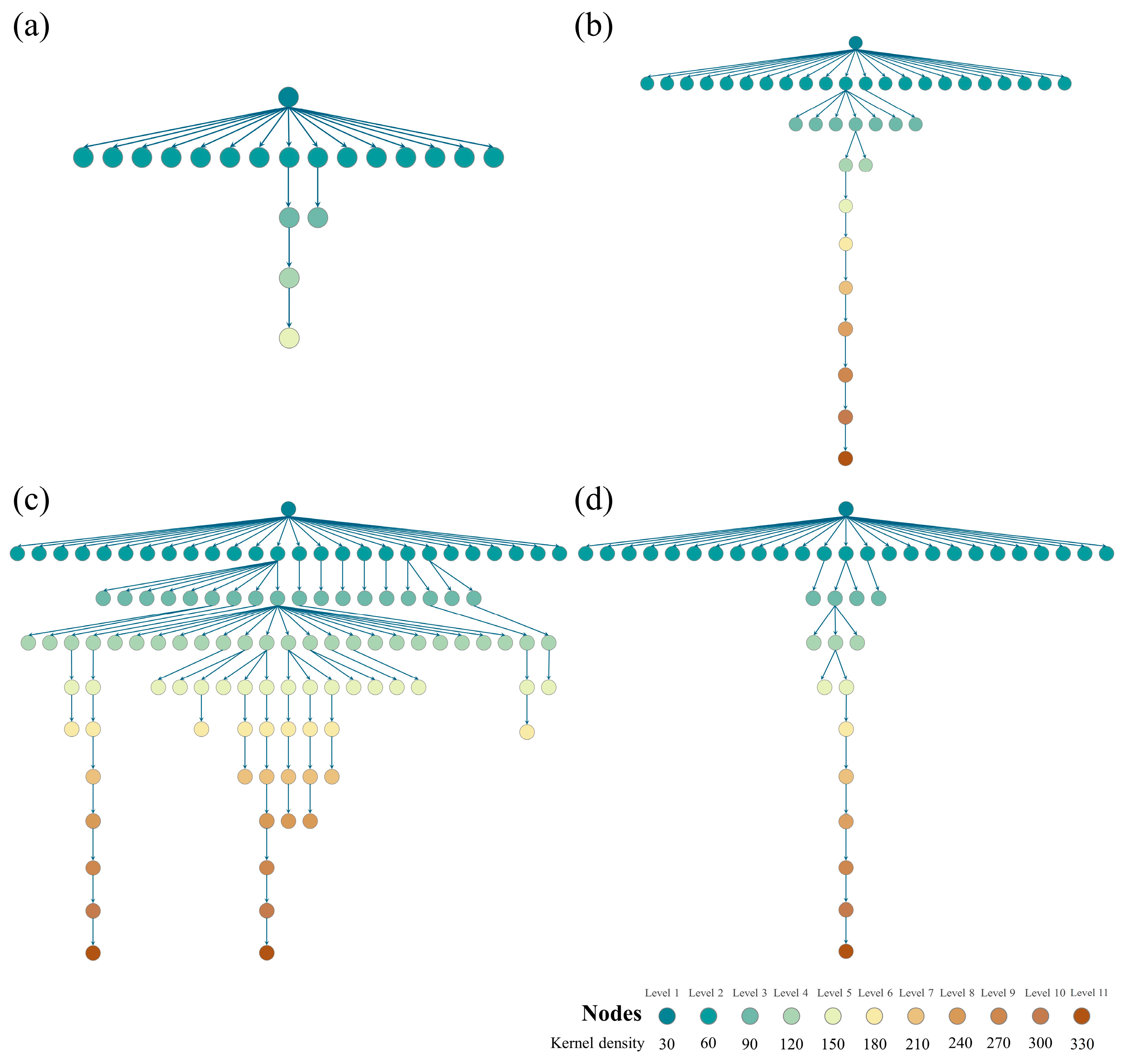
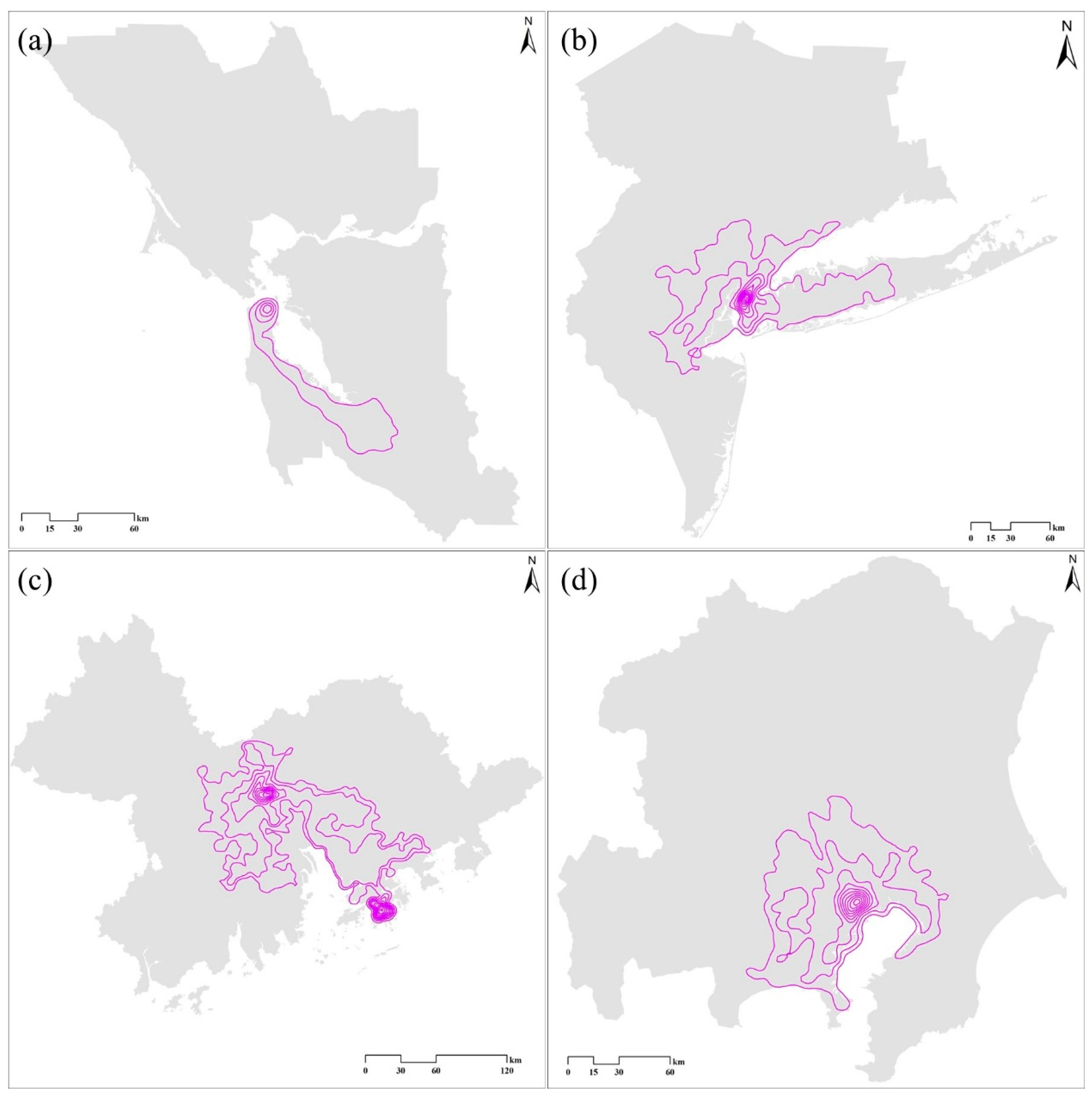
3.3. Contour Tree Representation
3.4. Contour Patterns’ Similarity Calculation
4. Results
4.1. The Similarity Between the Four Bay Areas
4.2. Enhancing Similarity Analysis with Building Metrics
4.3. Impacts of Contour Interval on Similarity Calculation
5. Discussion
5.1. The Use of Contour Tree
5.2. Implications for Urban System
5.3. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Frantz, D.; Schug, F.; Wiedenhofer, D.; Baumgart, A.; Virág, D.; Cooper, S.; Gómez-Medina, C.; Lehmann, F.; Udelhoven, T.; van der Linden, S.; et al. Unveiling patterns in human dominated landscapes through mapping the mass of US built structures. Nat. Commun. 2023, 14, 8014. [Google Scholar] [CrossRef]
- Esch, T.; Brzoska, E.; Dech, S.; Leutner, B.; Palacios-Lopez, D.; Metz-Marconcini, A.; Marconcini, M.; Roth, A.; Zeidler, J. World Settlement Footprint 3D—A first three-dimensional survey of the global building stock. Remote Sens. Environ. 2022, 270, 112877. [Google Scholar] [CrossRef]
- Chen, G.; Zhou, Y.; Voogt, J.A.; Stokes, E.C. Remote sensing of diverse urban environments: From the single city to multiple cities. Remote Sens. Environ. 2024, 305, 114108. [Google Scholar] [CrossRef]
- Xiao, W.; Ruan, L.; Wang, K.; Xu, S.; Yue, W.; He, T.; Chen, W.; Li, X.; Zhang, Y. Measuring three-dimension urban expansion using multi-source data and change detection algorithm: A case study of Shanghai. Cities 2025, 158, 105682. [Google Scholar] [CrossRef]
- Wu, B.; Huang, H.; Wang, Y.; Shi, S.; Wu, J.; Yu, B. Global spatial patterns between nighttime light intensity and urban building morphology. Int. J. Appl. Earth Obs. Geoinf. 2023, 124, 103495. [Google Scholar] [CrossRef]
- Biljecki, F.; Chow, Y.S. Global building morphology indicators. Comput. Environ. Urban Syst. 2022, 95, 101809. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, G.; Wu, Y.; Rosenberg, M.W. Urban 3D building morphology and energy consumption: Empirical evidence from 53 cities in China. Sci. Rep. 2024, 14, 12887. [Google Scholar] [CrossRef]
- Kamal, A.; Abidi, S.M.H.; Mahfouz, A.; Kadam, S.; Rahman, A.; Hassan, I.G.; Wang, L.L. Impact of urban morphology on urban microclimate and building energy loads. Energy Build. 2021, 253, 111499. [Google Scholar] [CrossRef]
- Chakraborty, S.; Maity, I.; Dadashpoor, H.; Novotnẏ, J.; Banerji, S. Building in or out? Examining urban expansion patterns and land use efficiency across the global sample of 466 cities with million+ inhabitants. Habitat Int. 2022, 120, 102503. [Google Scholar] [CrossRef]
- Ashik, F.R.; Sreezon, A.I.Z.; Rahman, M.H.; Zafri, N.M.; Labib, S.M. Built environment influences commute mode choice in a global south megacity context: Insights from explainable machine learning approach. J. Transp. Geogr. 2024, 116, 103828. [Google Scholar] [CrossRef]
- Wang, M.; Debbage, N. Urban morphology and traffic congestion: Longitudinal evidence from US cities. Comput. Environ. Urban Syst. 2021, 89, 101676. [Google Scholar] [CrossRef]
- Hui, E.C.M.; Li, X.; Chen, T.; Lang, W. Deciphering the spatial structure of China’s megacity region: A new bay area—The Guangdong-Hong Kong-Macao Greater Bay Area in the making. Cities 2020, 105, 102168. [Google Scholar] [CrossRef]
- Stokes, E.C.; Seto, K.C. Characterizing and measuring urban landscapes for sustainability. Environ. Res. Lett. 2019, 14, 045002. [Google Scholar] [CrossRef]
- Mouratidis, K. Urban planning and quality of life: A review of pathways linking the built environment to subjective well-being. Cities 2021, 115, 103229. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Shu, S.; Liang, H.; Zhao, Y.; Wu, J. Mapping fine-scale visual quality distribution inside urban streets using mobile LiDAR data. Build. Environ. 2021, 206, 108323. [Google Scholar] [CrossRef]
- Koumetio Tekouabou, S.C.; Diop, E.B.; Azmi, R.; Jaligot, R.; Chenal, J. Reviewing the application of machine learning methods to model urban form indicators in planning decision support systems: Potential, issues and challenges. J. King Saud. Univ.- Comput. Inf. Sci. 2022, 34, 5943–5967. [Google Scholar] [CrossRef]
- Liu, X.; Wu, X.; Li, X.; Xu, X.; Liao, W.; Jiao, L.; Zeng, Z.; Chen, G.; Li, X. Global mapping of three-dimensional (3D) urban structures reveals escalating utilization in the vertical dimension and pronounced building space inequality. Engineering 2024, 47, 86–99. [Google Scholar] [CrossRef]
- Lu, J.; Nazarian, N.; Hart, M.A.; Krayenhoff, E.S.; Martilli, A. Representing the effects of building height variability on urban canopy flow. Q. J. Roy. Meteorol. Soc. 2024, 150, 46–67. [Google Scholar] [CrossRef]
- Bruyns, G.J.; Higgins, C.D.; Nel, D.H. Urban volumetrics: From vertical to volumetric urbanisation and its extensions to empirical morphological analysis. Urban Stud. 2021, 58, 922–940. [Google Scholar] [CrossRef]
- Schröter, K.; Lüdtke, S.; Redweik, R.; Meier, J.; Bochow, M.; Ross, L.; Nagel, C.; Kreibich, H. Flood loss estimation using 3D city models and remote sensing data. Environ. Model. Softw. 2018, 105, 118–131. [Google Scholar] [CrossRef]
- Gao, J.; Zhong, X.; Cai, W.; Ren, H.; Huo, T.; Wang, X.; Mi, Z. Dilution effect of the building area on energy intensity in urban residential buildings. Nat. Commun. 2019, 10, 4944. [Google Scholar] [CrossRef]
- Geiß, C.; Schrade, H.; Aravena Pelizari, P.; Taubenböck, H. Multistrategy ensemble regression for mapping of built-up density and height with Sentinel-2 data. ISPRS J. Photogramm. Remote Sens. 2020, 170, 57–71. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Yin, P.; Yu, G.; Cao, W.; Liu, J.; Pei, L.; Hu, T.; Zhou, Y.; Liu, X.; et al. Characterizing annual dynamics of urban form at the horizontal and vertical dimensions using long-term Landsat time series data. ISPRS J. Photogramm. Remote Sens. 2023, 203, 199–210. [Google Scholar] [CrossRef]
- Grohmann, C.H. Evaluation of TanDEM-X DEMs on selected Brazilian sites: Comparison with SRTM, ASTER GDEM and ALOS AW3D30. Remote Sens. Environ. 2018, 212, 121–133. [Google Scholar] [CrossRef]
- Frantz, D.; Schug, F.; Okujeni, A.; Navacchi, C.; Wagner, W.; van der Linden, S.; Hostert, P. National-scale mapping of building height using Sentinel-1 and Sentinel-2 time series. Remote Sens. Environ. 2021, 252, 112128. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Wu, Q.; Yao, S.; Zhao, F.; Mao, W.; Wu, J. A graph-based approach for 3D building model reconstruction from airborne LiDAR point clouds. Remote Sens. 2017, 9, 92. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, B.; Li, Q.; Yang, L.; Fan, H.; Wu, J.; Yu, B. Combining ICESat-2 photons and Google Earth Satellite images for building height extraction. Int. J. Appl. Earth Obs. Geoinf. 2023, 117, 103213. [Google Scholar] [CrossRef]
- Wu, B.; Huang, H.; Zhao, Y. Utilizing building offset and shadow to retrieve urban building heights with ICESat-2 photons. Remote Sens. 2023, 15, 3786. [Google Scholar] [CrossRef]
- Huang, H.; Chen, P.; Xu, X.; Liu, C.; Wang, J.; Liu, C.; Clinton, N.; Gong, P. Estimating building height in China from ALOS AW3D30. ISPRS J. Photogramm. Remote Sens. 2022, 185, 146–157. [Google Scholar] [CrossRef]
- Choi, H.S.; Bruyns, G.; Zhang, W.; Cheng, T.; Sharma, S. Spatial cognition and three-dimensional vertical urban design guidelines—Cognitive measurement and modelling for human centre design. Urban Sci. 2023, 7, 125. [Google Scholar] [CrossRef]
- Zhang, H.; Andrade, B.; Wang, X.; Aburabee, I.; Yuan, S. A study of spatial cognition in the rural heritage based on VR 3D eye-tracking experiments. Herit. Sci. 2024, 12, 141. [Google Scholar] [CrossRef]
- Batty, M. The size, scale, and shape of cities. Science 2008, 319, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Georganos, S.; Kuffer, M.; Abascal, A.; Vanhuysse, S. On the knowledge gain of urban morphology from space. Comput. Environ. Urban Syst. 2022, 95, 101831. [Google Scholar] [CrossRef]
- Fleischmann, M.; Romice, O.; Porta, S. Measuring urban form: Overcoming terminological inconsistencies for a quantitative and comprehensive morphologic analysis of cities. Environ. Plan. B Urban Anal. City Sci. 2021, 48, 2133–2150. [Google Scholar] [CrossRef]
- Liqiang, Z.; Deng, H.; Chen, D.; Zhen, W. A spatial cognition-based urban building clustering approach and its applications. Int. J. Geogr. Inf. Sci. 2013, 27, 721–740. [Google Scholar] [CrossRef]
- Bonczak, B.; Kontokosta, C.E. Large-scale parameterization of 3D building morphology in complex urban landscapes using aerial LiDAR and city administrative data. Comput. Environ. Urban Syst. 2019, 73, 126–142. [Google Scholar] [CrossRef]
- Wu, B.; Huang, H.; Wang, Y. Quantifying spatial patterns of urban building morphology in the China’s Guangdong-Hong Kong-Marco greater bay area. Int. J. Digit. Earth 2024, 17, 2392832. [Google Scholar] [CrossRef]
- Labetski, A.; Vitalis, S.; Biljecki, F.; Arroyo Ohori, K.; Stoter, J. 3D building metrics for urban morphology. Int. J. Geogr. Inf. Sci. 2023, 37, 36–67. [Google Scholar] [CrossRef]
- Zhang, P.; Ghosh, D.; Park, S. Spatial measures and methods in sustainable urban morphology: A systematic review. Landsc. Urban Plan. 2023, 237, 104776. [Google Scholar] [CrossRef]
- Liu, M.; Hu, Y.-M.; Li, C.-L. Landscape metrics for three-dimensional urban building pattern recognition. Appl. Geog. 2017, 87, 66–72. [Google Scholar] [CrossRef]
- Plexida, S.G.; Sfougaris, A.I.; Ispikoudis, I.P.; Papanastasis, V.P. Selecting landscape metrics as indicators of spatial heterogeneity—A comparison among Greek landscapes. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 26–35. [Google Scholar] [CrossRef]
- Caruso, G.; Hilal, M.; Thomas, I. Measuring urban forms from inter-building distances: Combining MST graphs with a Local Index of Spatial Association. Landsc. Urban Plan. 2017, 163, 80–89. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Wu, Q.; Chen, Z.; Yao, S.; Huang, Y.; Wu, J. An Extended Minimum Spanning Tree method for characterizing local urban patterns. Int. J. Geogr. Inf. Sci. 2018, 32, 450–475. [Google Scholar] [CrossRef]
- Yang, L.; Yang, X.; Zhang, H.; Ma, J.; Zhu, H.; Huang, X. Urban morphological regionalization based on 3D building blocks—A case in the central area of Chengdu, China. Comput. Environ. Urban Syst. 2022, 94, 101800. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, X.; Yang, X.; Chen, Y.; Zhang, H.; Na, J. A new hierarchical analysis framework of building heights: Towards a more intuitive understanding of 3D urban structure. Trans. GIS 2024, 28, 40–57. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Yin, H. A graph convolutional neural network for classification of building patterns using spatial vector data. ISPRS J. Photogramm. Remote Sens. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Wu, S.; Sumari, N.S.; Dong, T.; Xu, G.; Liu, Y. Characterizing urban expansion combining concentric-ring and grid-based analysis for Latin American cities. Land 2021, 10, 444. [Google Scholar] [CrossRef]
- Xu, G.; Dong, T.; Cobbinah, P.B.; Jiao, L.; Sumari, N.S.; Chai, B.; Liu, Y. Urban expansion and form changes across African cities with a global outlook: Spatiotemporal analysis of urban land densities. J. Clean. Prod. 2019, 224, 802–810. [Google Scholar] [CrossRef]
- Xu, Z.; Jiao, L.; Lan, T.; Zhou, Z.; Cui, H.; Li, C.; Xu, G.; Liu, Y. Mapping hierarchical urban boundaries for global urban settlements. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102480. [Google Scholar] [CrossRef]
- Malik, K.; Robertson, C.; Roberts, S.A.; Remmel, T.K.; Long, J.A. Computer vision models for comparing spatial patterns: Understanding spatial scale. Int. J. Geogr. Inf. Sci. 2023, 37, 1–35. [Google Scholar] [CrossRef]
- Yang, C.; Li, Q.; Hu, Z.; Chen, J.; Shi, T.; Ding, K.; Wu, G. Spatiotemporal evolution of urban agglomerations in four major bay areas of US, China and Japan from 1987 to 2017: Evidence from remote sensing images. Sci. Total Environ. 2019, 671, 232–247. [Google Scholar] [CrossRef]
- Wu, W.-B.; Ma, J.; Banzhaf, E.; Meadows, M.E.; Yu, Z.-W.; Guo, F.-X.; Sengupta, D.; Cai, X.-X.; Zhao, B. A first Chinese building height estimate at 10 m resolution (CNBH-10 m) using multi-source earth observations and machine learning. Remote Sens. Environ. 2023, 291, 113578. [Google Scholar] [CrossRef]
- Cao, Y.; Huang, X. A deep learning method for building height estimation using high-resolution multi-view imagery over urban areas: A case study of 42 Chinese cities. Remote Sens. Environ. 2021, 264, 112590. [Google Scholar] [CrossRef]
- Stipek, C.; Hauser, T.; Adams, D.; Epting, J.; Brelsford, C.; Moehl, J.; Dias, P.; Piburn, J.; Stewart, R. Inferring building height from footprint morphology data. Sci. Rep. 2024, 14, 18651. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Liu, H.; Wang, S.; Yu, B.; Beck, R.; Hinkel, K. A localized contour tree method for deriving geometric and topological properties of complex surface depressions based on high-resolution topographical data. Int. J. Geogr. Inf. Sci. 2015, 29, 2041–2060. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Wu, Q.; Huang, Y.; Chen, Z.; Wu, J. Individual tree crown delineation using localized contour tree method and airborne LiDAR data in coniferous forests. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 82–94. [Google Scholar] [CrossRef]
- Peng, J.; Cheng, X.; Hu, Y.; Corcoran, J. A landscape connectivity approach to mitigating the urban heat island effect. Landsc. Ecol. 2022, 37, 1707–1719. [Google Scholar] [CrossRef]
- Lauri, J. Subgraphs as a Measure of Similarity. In Structural Analysis of Complex Networks; Dehmer, M., Ed.; Birkhäuser: Boston, MA, USA, 2011; pp. 319–334. [Google Scholar]
- Ehrlich, H.-C.; Rarey, M. Maximum common subgraph isomorphism algorithms and their applications in molecular science: A review. WIREs Comput. Mol. Sci. 2011, 1, 68–79. [Google Scholar] [CrossRef]
- Raymond, J.W.; Willett, P. Maximum common subgraph isomorphism algorithms for the matching of chemical structures. J. Comput. Aided Mol. Des. 2002, 16, 521–533. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Yao, S.; Wu, Q.; Chen, Z.; Wu, J. A surface network based method for studying urban hierarchies by night time light remote sensing data. Int. J. Geogr. Inf. Sci. 2019, 33, 1377–1398. [Google Scholar] [CrossRef]
- Xie, X.; Liu, X.; McNay, I. One country with two systems: The characteristics and development of higher education in the Guangdong–Hong Kong–Macau Greater Bay Area. Humanit. Soc. Sci. Commun. 2023, 10, 1. [Google Scholar] [CrossRef]
- Osman, T. Land use regulations and the dispersion of the IT Industry in the San Francisco Bay area. Pap. Reg. Sci. 2020, 99, 1301–1317. [Google Scholar] [CrossRef]
- Jasiewicz, J.; Netzel, P.; Stepinski, T.F. Landscape similarity, retrieval, and machine mapping of physiographic units. Geomorphology 2014, 221, 104–112. [Google Scholar] [CrossRef]
- Dark, S.J.; Bram, D. The modifiable areal unit problem (MAUP) in physical geography. Prog. Phys. Geogr. 2007, 31, 471–479. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Rosier, J.F.; Verburg, P.H.; van Vliet, J. Global maps of 3D built-up patterns for urban morphological analysis. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103048. [Google Scholar] [CrossRef]
- Xu, Z.; Coors, V. Combining system dynamics model, GIS and 3D visualization in sustainability assessment of urban residential development. Build. Environ. 2012, 47, 272–287. [Google Scholar] [CrossRef]
- Wei, Y.D.; Ewing, R. Urban expansion, sprawl and inequality. Landsc. Urban Plan. 2018, 177, 259–265. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Liu, P.; Wu, X.; Zhang, J.; Zhang, D.; Liu, X.; Yao, Y. Accurate estimation of the proportion of mixed land use at the street-block level by integrating high spatial resolution images and geospatial big data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6357–6370. [Google Scholar] [CrossRef]
- Liu, Y.; Fang, F.; Li, Y. Key issues of land use in China and implications for policy making. Land Use Policy 2014, 40, 6–12. [Google Scholar] [CrossRef]
- Wu, X.; Ou, J.; Wen, Y.; Liu, X.; He, J.; Zhang, J. Developing a data-fusing method for mapping fine-scale urban three-dimensional building structure. Sustain. Cities Soc. 2022, 80, 103716. [Google Scholar] [CrossRef]
- Chen, F.; Wittkopf, S.K.; Khai Ng, P.; Du, H. Solar heat gain coefficient measurement of semi-transparent photovoltaic modules with indoor calorimetric hot box and solar simulator. Energy Build. 2012, 53, 74–84. [Google Scholar] [CrossRef]
- Wang, C.; Song, J.; Shi, D.; Reyna, J.L.; Horsey, H.; Feron, S.; Zhou, Y.; Ouyang, Z.; Li, Y.; Jackson, R.B. Impacts of climate change, population growth, and power sector decarbonization on urban building energy use. Nat. Commun. 2023, 14, 6434. [Google Scholar] [CrossRef]
- Hui, Y.; Tang, Y.; Yang, Q.; Mochida, A. Numerical study on influence of surface vegetation on aerodynamics of high-rise buildings. Sustain. Cities Soc. 2024, 107, 105407. [Google Scholar] [CrossRef]
- Al-Kodmany, K. Greenery-covered tall buildings: A review. Buildings 2023, 13, 2362. [Google Scholar] [CrossRef]
- Sandifer, P.A.; Sutton-Grier, A.E.; Ward, B.P. Exploring connections among nature, biodiversity, ecosystem services, and human health and well-being: Opportunities to enhance health and biodiversity conservation. Ecosyst. Serv. 2015, 12, 1–15. [Google Scholar] [CrossRef]
- Xikai, M.; Lixiong, W.; Jiwei, L.; Xiaoli, Q.; Tongyao, W. Comparison of regression models for estimation of carbon emissions during building’s lifecycle using designing factors: A case study of residential buildings in Tianjin, China. Energy Build. 2019, 204, 109519. [Google Scholar] [CrossRef]
- Hesslerová, P.; Pokorný, J.; Huryna, H.; Seják, J.; Jirka, V. The impacts of greenery on urban climate and the options for use of thermal data in urban areas. Prog. Plan. 2022, 159, 100545. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, H.; Mao, S.; Zhang, G.; Jin, Y.; Luo, Y.; Huo, W.; Pan, Z.; An, P.; Lun, F. Exploring surface urban heat island (SUHI) intensity and its implications based on urban 3D neighborhood metrics: An investigation of 57 Chinese cities. Sci. Total Environ. 2022, 847, 157662. [Google Scholar] [CrossRef]
- Gao, H.; Liu, J.; Lin, P.; Li, C.; Xiao, Y.; Hu, G. Pedestrian level wind flow field of elevated tall buildings with dense tandem arrangement. Build. Environ. 2022, 226, 109745. [Google Scholar] [CrossRef]
- Shui, T.; Cao, L.; Xiao, T.; Zhang, S. Influence of building-height variability on urban ventilation and pollutant dispersion characteristics. Atmosphere 2025, 16, 614. [Google Scholar] [CrossRef]
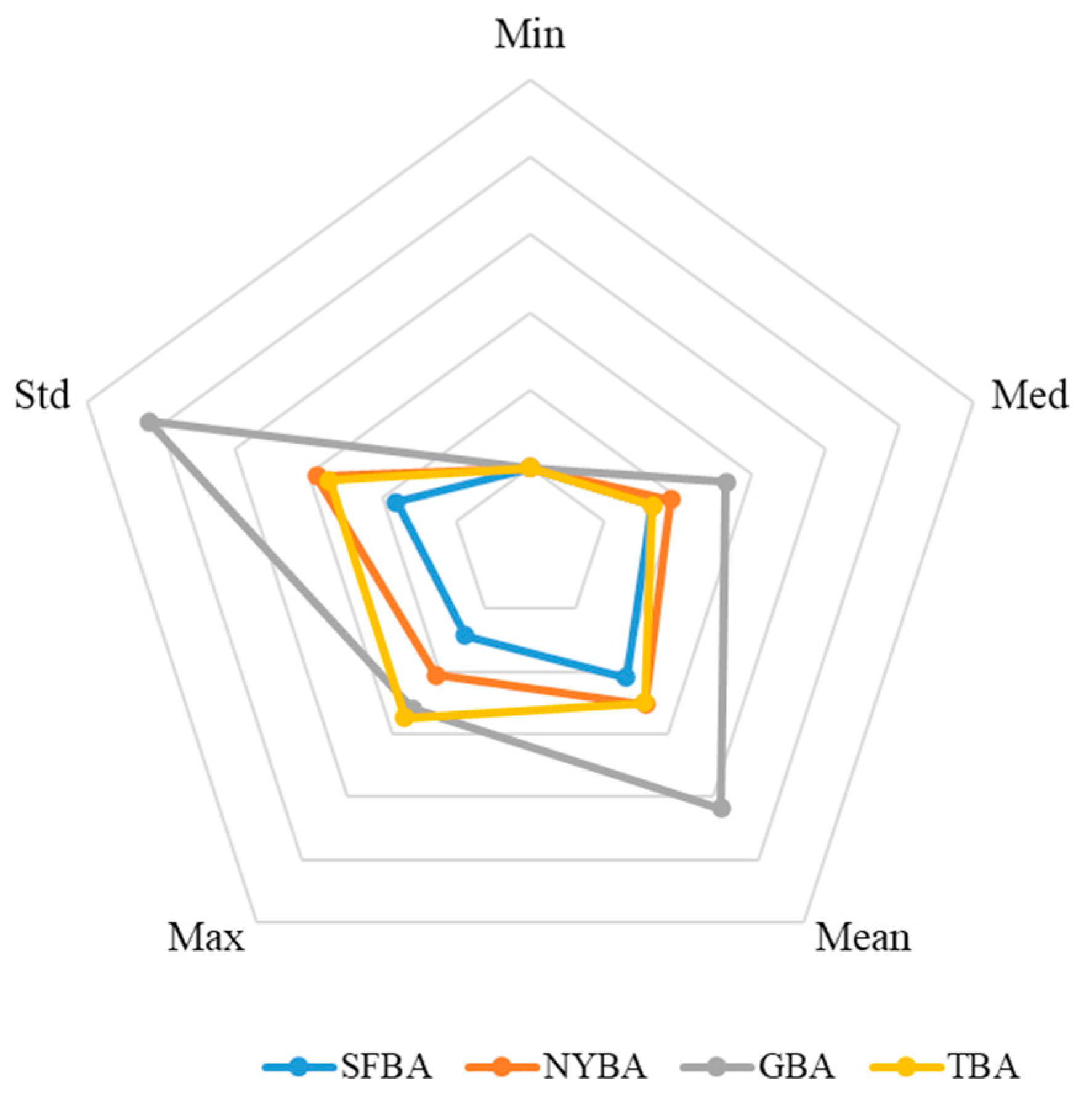
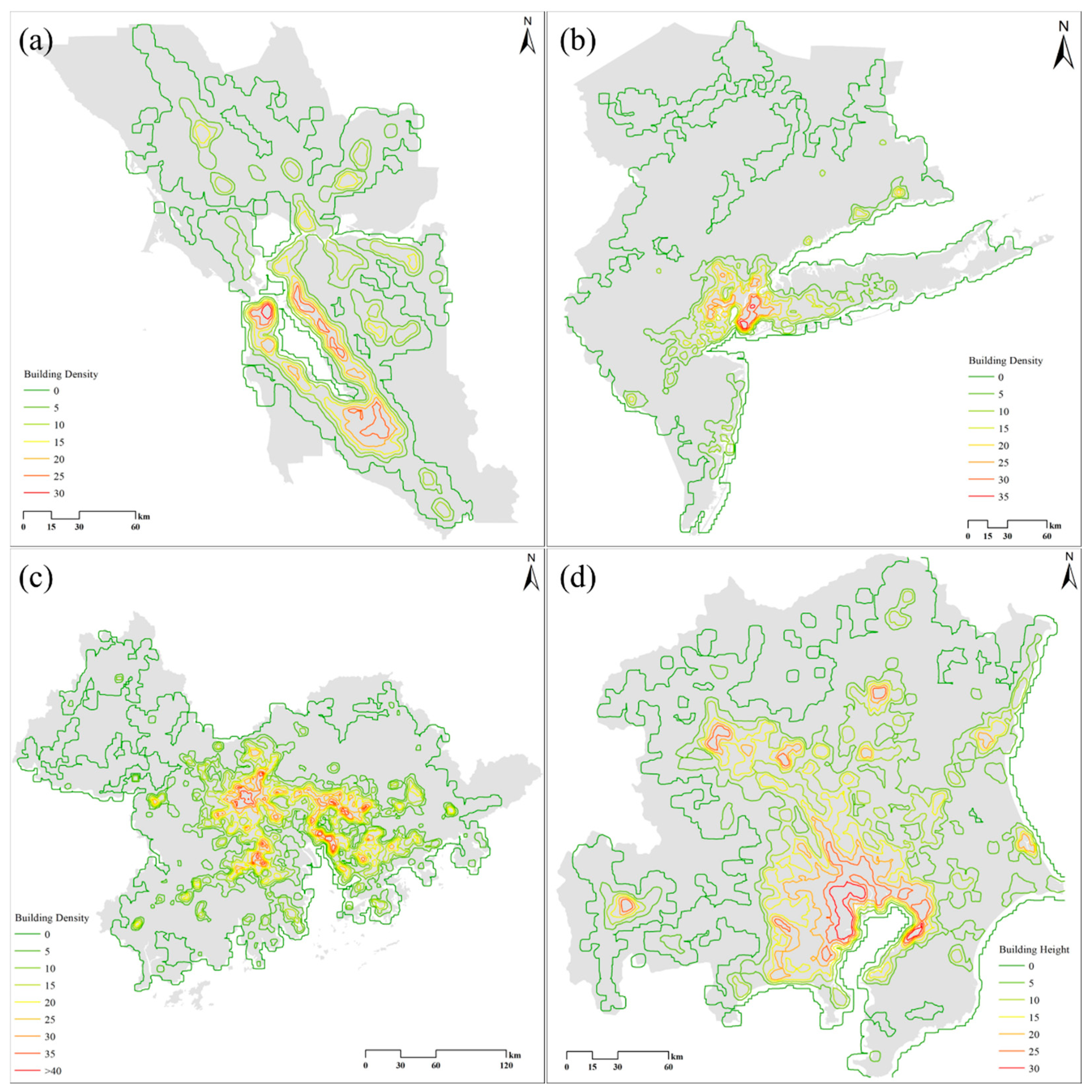
| SFBA | NYBA | GBA | TBA | |
|---|---|---|---|---|
| SFBA | / | 0.49 | 0.17 | 0.48 |
| NYBA | 0.49 | / | 0.34 | 0.74 |
| GBA | 0.17 | 0.34 | / | 0.36 |
| TBA | 0.48 | 0.74 | 0.36 | / |
| Metrics | SFBA | NYBA | GBA | TBA |
|---|---|---|---|---|
| Min | 0.20 | 0.20 | 0.20 | 0.20 |
| Med | 3.30 | 3.80 | 5.30 | 3.30 |
| Mean | 4.21 | 5.04 | 8.35 | 4.99 |
| Max | 285.30 | 413.00 | 518.14 | 548.91 |
| Std | 3.63 | 5.77 | 10.31 | 5.45 |
| Metrics | Building Density | Building Area (m2) | Building Volume (m3) |
|---|---|---|---|
| SFBA | 15.88 | 941.02 | 4581.71 |
| NYBA | 8.41 | 476.96 | 3808.78 |
| GBA | 18.73 | 1293.53 | 12,642.64 |
| TBA | 15.97 | 969.31 | 6128.31 |
| Contour Interval | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|
| SFBA-NYBA | 0.47 | 0.49 | 0.49 | 0.36 | 0.28 | 0.30 | 0.30 | 0.33 | 0.33 | 0.33 |
| SFBA-GBA | 0.14 | 0.17 | 0.17 | 0.09 | 0.08 | 0.08 | 0.08 | 0.04 | 0.04 | 0.06 |
| SFBA-TBA | 0.45 | 0.48 | 0.48 | 0.43 | 0.33 | 0.37 | 0.37 | 0.27 | 0.27 | 0.33 |
| NYBA-GBA | 0.32 | 0.34 | 0.34 | 0.27 | 0.27 | 0.25 | 0.25 | 0.13 | 0.13 | 0.18 |
| NYBA-TBA | 0.71 | 0.73 | 0.74 | 0.84 | 0.84 | 0.83 | 0.83 | 0.82 | 0.82 | 1.00 |
| GBA-TBA | 0.34 | 0.36 | 0.36 | 0.23 | 0.23 | 0.21 | 0.21 | 0.16 | 0.16 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Wu, B. A Novel Method for Comparing Building Height Hierarchies. Buildings 2025, 15, 2295. https://doi.org/10.3390/buildings15132295
Xie J, Wu B. A Novel Method for Comparing Building Height Hierarchies. Buildings. 2025; 15(13):2295. https://doi.org/10.3390/buildings15132295
Chicago/Turabian StyleXie, Jun, and Bin Wu. 2025. "A Novel Method for Comparing Building Height Hierarchies" Buildings 15, no. 13: 2295. https://doi.org/10.3390/buildings15132295
APA StyleXie, J., & Wu, B. (2025). A Novel Method for Comparing Building Height Hierarchies. Buildings, 15(13), 2295. https://doi.org/10.3390/buildings15132295







