Numerical and Experimental Multi-Approach Models for a Stone Pinnacle Reinforcement

Abstract

The church of Saint Felix in Girona (Spain) is crowned by an octagonal bell tower with a stone pinnacle at each corner. It was built using dry-joint stone masonry, a technique that involves laying stones in a precise pattern to create a solid and durable structure. In order to strengthen the connection between the stone blocks of the pinnacles, a wooden bar was placed through a central hole carved in the stone structure. Today, the inner structure has completely disappeared. During maintenance and repair work, it was decided to restore the functionality of the disappeared reinforcement by installing a titanium bar in its place. Due to the uncertainty associated with the pinnacle’s behaviour and the lack of both, a proper numerical model of the monument, and an extensive characterization of the materials, a strategy based on multiple approaches was designed. The proposed strategy was based on combining numerical and experimental models, the final objective being to determine the length and mechanical properties of the metallic inclusion, considering the effects of gravity, wind, and seismic forces. A scale model of the pinnacle was evaluated in laboratory conditions. The results were used to calibrate a numerical model representing the scale specimen. After calibration, the results were extrapolated to a full-scale numerical model. The experimental and numerical results showed that the pinnacles needed to be reinforced along their entire height. The tensile stresses cause by wind and seismic forces at different levels, could not be compensated without the contribution of the titanium bar inserted into the pinnacle.

1. Introduction

The bell tower of the church of Saint Felix, together with the Cathedral, forms part of Girona’s skyline. The construction of this Gothic tower began in 1368 under the direction of master stonemason Pere Sacoma. In the building records, the Saint Felix church appears cited as Pere Sacoma, Pere ça Coma, Pere de Coma, or Pere de Comes, and the ground plan of the bell tower, drawn by the same architect, has also survived [1,2]. He worked on the church and in the bell tower until around 1391. The construction of this building can be fully traced through the accounts, which detail day by day the work carried out, the materials used, the workers and their salaries, the tools used, and other details relating to its construction [3]. The bell tower was finally completed at the end of the 16th century (probably in 1572), as it appears on the keystone of the last level with the participation of at least three different master masons, Joan de Bellojch, Enric Gelabert, and Pere Boris.

Despite the date of its completion, the entire structure of the Saint Felix belfry follows Gothic typology. The tower was built in three phases. The first, which reached the level of the church roof, was built under the supervision of Pere Sacoma. The second, built in the middle of the 16th century, reached the level of the bells. And finally, in the last phase, the construction reached the level where the truncated spire begins, together with the pinnacles. Thus, the type of bell tower, with an irregular plan, is made up of three stepped bodies supported by eight buttresses crowned by pinnacles and a truncated central spire [4].

Inadequate maintenance and management of architectural heritage endangers both its conservation and public safety. In their research [5], the authors propose a methodology for evaluating the factors that threaten heritage conservation. Until the intervention described in this article was carried out, only one previous intervention on the bell tower of Saint Felix, dating from 1924, was known. This date appears in graffiti inside the spire. According to the reports in the press of the city of Girona, the accident may have been caused by lightning striking the top of the bell tower. Work was carried out on the spire but not on the pinnacles. Undoubtedly, there was a risk, as any part of the pinnacles falling could have affected neighbouring buildings or fallen directly onto the public road, endangering pedestrians.

Numerical modelling of the contact between courses has been a key issue. The properties that enable the interaction between these interfaces depends on whether the analysis is performed on a micro-, meso-, or macroscale. In [6], the specifics of this question when applied to dry-joint masonry structures are described.

The use of multi-approach strategies has been a successful tool in choosing the scale to analyze numerical models. In [7], a two-step strategy considering limit analysis and FE models describing the structure at a micro- and macroscale is presented.

The failure mechanism of different dry-joint masonry structural members has been tested in a laboratory. In [8], the particular case of overturning masonry walls was simulated. Two types of local stone—one calcareous and the other basaltic—were used in the tests. For this purpose, a tilting platform rotating on a horizontal axis parallel to the length of the specimen was used as a destabilizing factor. In [9], the behaviour of dry-joint masonry was tested in a scaled-up set of arches. The triggering effect for the instability of the structure involved imposed displacements at the lateral restrains. Similar tests performed using different materials were summarized in this report.

Another important issue to be considered when deciding how to carry out such an intervention is how to address issues such as reversibility or which materials are more suitable for restoration [10,11,12]. In the case studied, the element used to reinforce the pinnacle remains unseen. However, its design and implementation are not a trivial choice. In the available literature, the use of different types of stainless-steel alloys and other materials with similar properties, applied as a reinforcement of historic masonry, is extensively described. An excellent example of their use can be found in the pinnacles of the Jaen cathedral [13,14]. The confinement techniques of various masonry elements, based on fibre-reinforced polymer (FRP), fibre-reinforced cementitious matrix (FRCM), or carbon fibre-reinforced polymer (CFRP), which have been extensively studied in the literature, are not applicable, as the pinnacles cannot be coated [15,16,17,18,19].

On the other hand, we have reinforcement based on carbon fibre rods and with titanium alloy rods. The main advantage of carbon fibre bars, apart from their corrosion resistance, is their high strength-to-weight ratio and their good bonding to the cement-based matrix [20]. Titanium alloy rods are being used in the reinforcement of structural elements due to their high corrosion resistance and high strength [21,22].

There are several strategies for evaluating the nonlinear behaviour of this type of structure under seismic demands. It is common practice to use simplified models. Some of them are presented in [23]. In [24,25], the effect of seismic forces on this type of structure is evaluated, considering two possible failure mechanisms. The effect of horizontal forces on nonstructural elements or isolated elements that are part of more complex structures can be quantified using the procedures presented in [26].

The aim of this article is to analyze the behaviour of the pinnacles of the bell tower of the Saint Felix church, some of which are in poor condition, under the combined influence of self-weight, wind, and seismic forces. Their behaviour is evaluated using numerical and scaled models. The scaled real model was used to calibrate a numerical model. Once the calibration is complete, the model can reproduce the load test performed in the scaled real model under laboratory conditions, and a new numerical model of the real pinnacle is defined, including the properties updated in the previous step. A new reinforcement is proposed to replace the wooden rod that was previously placed in the central core of the pinnacles (Figure 1). The possible existence of sliding and overturning phenomena between the vertical distributed stone rings that make up the pinnacles are used as verification criteria.

2. Structural Analysis

2.1. Basics

Lateral stability and, to some extent, the transfer of load between the different layers of stone were previously ensured by a wooden bar located in the central part of the pinnacles. Restorations carried out during the 20th century on the pinnacles of other buildings, such as the church of Santiago de Jerez de la Frontera or the Palace of Westminster documented the presence of metal reinforcing bars inside the pinnacles [27,28]. Due to the passage of time, environmental conditions, and biotic agents, the rudimentary connection between the successive rings that form the pinnacles of the church of Saint Felix no longer exists.

After evaluating various alternatives, the restoration team decided to use a titanium rod—instead of other commonly used materials such as CRFP (carbon fibre-reinforced polymers) or BFRP (basalt fibre-reinforced polymers)—to replace the function performed by the old connector due to its high strength, fracture toughness, plasticity, and low crack propagation rate [21,22]. Functional issues, as well as the cost of purchasing and installing this element, justified the study of how to minimize the length of this reinforcement.

The self-weight of stone structures of this nature rarely represents a critical state and generally has a stabilizing effect. As emphasized in [29], the theory of limit analysis applied to masonry structures states that the allowable compressive stress can be considered infinite. Although this statement was mentioned in the specific context of arches and vaults, it can also be applied to the pinnacles, since these can be considered as belonging to masonry structures working at low tension.

Due to its location, the pinnacle is mainly affected by horizontal forces of wind and seismic activity. The value of these forces has been calculated using Spanish regulations [30,31]. These forces introduce bending moments and shear forces into the structure.

Due to the lack of continuity between the constituent elements—stone masonry laid with dry joints (without mortar)—this type of structure cannot transmit tensile forces. Stability is therefore provided by equilibrium, ensuring that the resultant load remains in the central core defined by the middle third rule.

The failure modes considered in the study are sliding (horizontal displacement between layers of masonry stone) and overturning (rotation of the section due to the presence of excessive tensile stress).

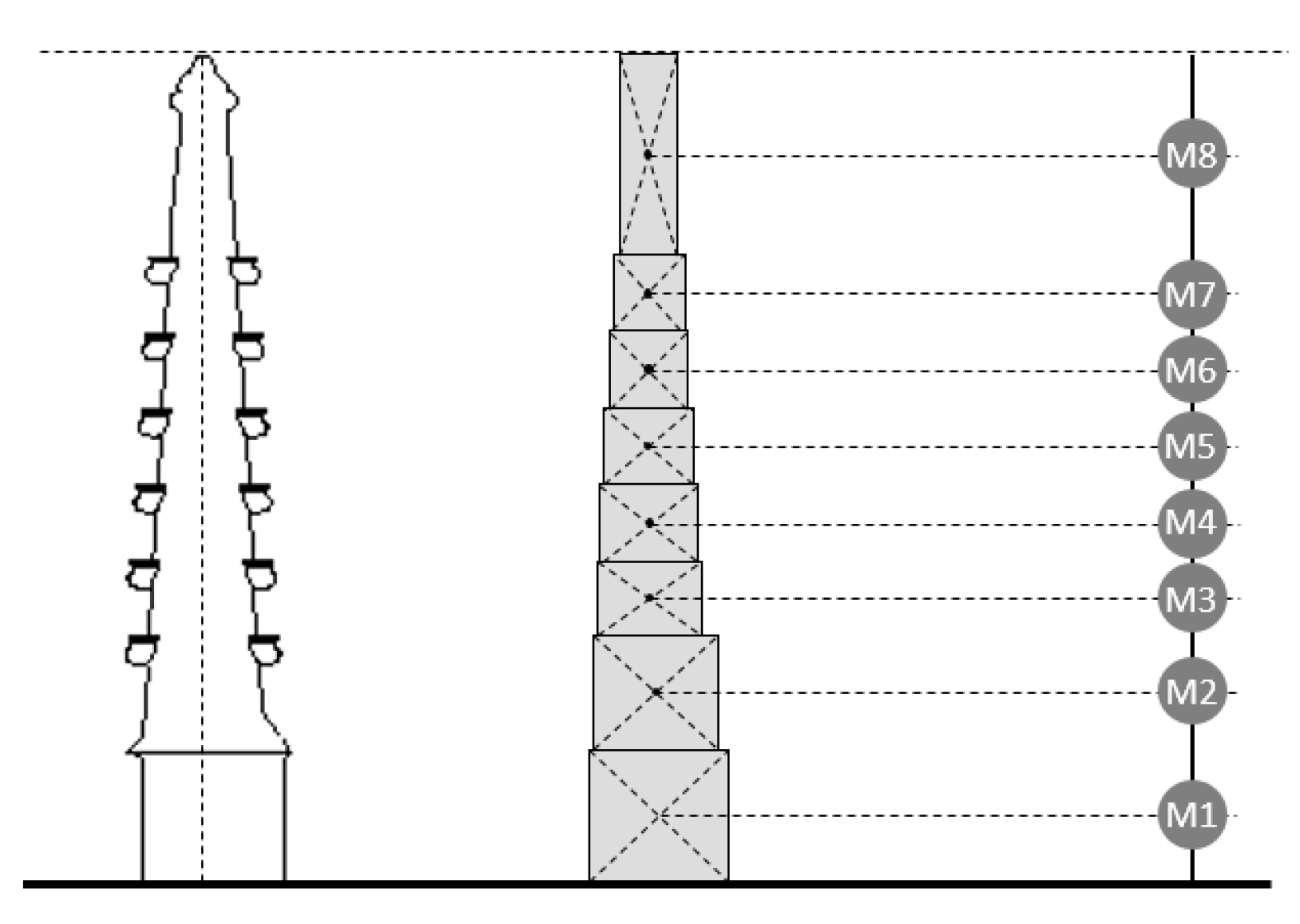
2.2. Geometry

The plan projection of the bell tower of the church of Saint Felix consists of an octagon with irregular sides. A sudden change in the elevation dimension allows one to define the geometry of the upper part of the tower and accommodate the eight pinnacles under study.

The pinnacles are approximately eight metres high. The chosen model of the pinnacle is composed of 32 courses of Girona stone ashlars of various dimensions, averaging 24 cm in height. The cross-section of the pinnacles at the starting point corresponds to a rectangle measuring 1.25 × 1.11 m. The pinnacle’s cross-section decreases in height. The cross-sectional dimensions at the highest point are approximately 0.54 × 0.53 m (Figure 2).

2.3. Stone of Girona

The bell tower of the Saint Felix church was built with a limestone known as “Girona stone”. It is a compact, coherent, and relatively homogeneous nummulitic limestone rock formed in the Middle Eocene period (Lutecian). It has a massive microcrystalline appearance where fossilized nummulites ranging from 0.5 to 6 cm in diameter stand out. Nummulites are an extinct genus of benthic foraminifera (unicellular organisms that lived in the depths of seas and oceans). They are well preserved to the present day because they had a fairly resistant calcareous shell.

Girona’s stone has three main varieties, but its chemical composition is mainly made up of the following minerals: calcite (83.00%), dolomite (2.50%), feldspar (9.50%), and quartz (5.00%). It has a low open porosity, a low and a relatively slow absorption capacity, a slow rate of drying, a high resistance to compression, and a medium modulus of elasticity [32].

Table 1. Properties of Girona stone.

Property	Value
density	27.00 kN/m3
absorption coefficient	0.30%
compression strength (generic value)	73.20 MPa
bending strength	9.00 MPa

show the properties of the stone used in the pinnacle construction.

Compression stress and flexural stress, determined using a four-point test, for different varieties of Girona’s stone were determined in [33] in an extensive experimental campaign. The results are shown in

Table 2. Compression strength (for different types of stone).

Direction of Effort	Compression Values
	White Stone [MPa]	Blue Stone [MPa]	Grey Stone [kMPa]
Perpendicular to the vein	100.60	131.60	111.90
Parallel to the vein	84.40	95.30	108.00

and

Table 3. Flexural strength (for different types of stone).

	Flexural Stress Values
	White Stone [MPa]	Blue Stone [MPa]	Grey Stone [kMPa]
Parallel to the vein	9.50	12.00	10.20

.

Additional tests were carried out to characterize some of the critical properties. The most relevant was the friction coefficient. No information was available on this variable. This prompted a testing campaign to determine it. The result was 0.66. Although there are many tests to determine this value, for the sake of simplicity, the one chosen was the so-called tilt test.

The Poisson ratio was considered to be 0.20. The Young’s modulus value was 1.0 × 10³ Mpa. Both values were within the range of those proposed by other authors. As indicated in [9], the Young’s modulus of stone as a material differs considerably from that corresponding to dry-joint masonry. For reference, the relationship between them is around 3.5–7.5%.

2.4. Load Estimation

2.4.1. Gravitational Forces

Gravitational forces are primarily due to self-weight. The density of the material was determined experimentally and compared with values available in the literature. The volume was calculated from the graphic documentation included in the restoration project.

2.4.2. Wind Forces

Wind is a dynamic phenomenon that can be described by decoupling it into different effects. A rigorous analysis of the wind affecting the pinnacle using tunnel wind tests is beyond the scope of the project. It is therefore a matter of carefully choosing the hypotheses to be used in the calculation to guarantee that the intervention to be carried out is safe enough.

Stone pinnacles have been studied in wind tunnel tests [34]. The static wind forces are expressed using the standard drag equation:

$$F_{wind}=\left({\displaystyle \frac{1}{2}}·{\rho }_{air}·v^2\right)·C_d·A$$

(1)

where ρ_air is the density of the air, υ is the wind speed, and A is frontal area over which the force of the wind is applied.

The drag coefficient (C_d) was established using the results of the wind tunnel tests through back-calculation from measured strains. The chosen values range between 1.20–1.50. The values are according to the literature [35,36].

The study concludes that, for this kind of structure, the dynamic effects are small. In [37], the vibrating behaviour of stone pinnacles was studied, arriving at a similar conclusion. The basic value of the dynamic pressure of wind was determined similarly in [38]. The basic velocity of wind to be applied is 29 m/s. The standard drag equation will be used in this study.

2.4.3. Seismic Forces

For the sake of simplicity, the pinnacle is considered as a cantilever structure, fixed at the base, as if the bell tower is not attached to the building. This consideration defines an unfavourable scenario which will result in a conservative estimate of the seismic forces.

In [39], a non-destructive test to determine the fundamental natural frequencies of the colonnade of the Dome of the Siena Cathedral was carried out. A similar approach was used in the monumental complex of Sacro Monte in Ghiffa (Italy) [40]. These analyses were performed in the upper colonnades. The influence of these elements on the overall behaviour of the building due to the mass ratio between them is negligible.

In [41], the influence on the dynamic behaviour of a belfry depending on its relative position with respect to the rest of the church is briefly explained. The slenderness of these structures makes them especially vulnerable to the effects of horizontal forces. Therefore, their connection to the main body of the church both protects and enhances their ability to withstand such forces.

The simplified method proposed In the regulations [30], where the structure can be compared to a pendulum with concentrated masses, was considered sufficiently representative for this study (Figure 3).

The eight-block discretization (see Figure 3) was chosen for its suitability for representing the three distinct zones that characterizes the pinnacle’s geometry. The model produces sufficiently accurate results. This geometric simplification has also been used in the equilibrium approach presented in Section 3.7.

The basic seismic acceleration to be applied in Girona is 0.08 ag/b, and the contribution coefficient equals 1.00. Therefore, the seismic constraints are not extremely demanding. The problem stems from the position of the element and its weakness against horizontal forces.

The church of Saint Felix is founded on rock. The soil coefficient considered is 1.00. Live loads are negligible compared to dead loads. Consequently, the mass considered in the calculations will correspond mainly to its self-weight. The parameters affecting ductility must be chosen carefully, considering that this type of structure is incapable of dissipating energy.

The fundamental period of the tower was calculated applying the procedures described in [30], and the result was approximately 0.40 s. Accordingly, the contribution of a single mode shape has been considered when determining the seismic forces. The effect of the seismic forces on the pinnacle has been calculated considering the total height of the bell tower.

3. Analysis Approaches

3.1. Introduction

To analyze the pinnacle’s behaviour, numerical and experimental models were combined. The first approach consists of calibrating the problem using a scaled real model (scale 1:5) under laboratory conditions. The scale model had the same number of courses as the real one, although the ornamental details were omitted. Once a representative numerical model of the scaled structures will be available, the analysis will be transferred to a real-life situation (Figure 4).

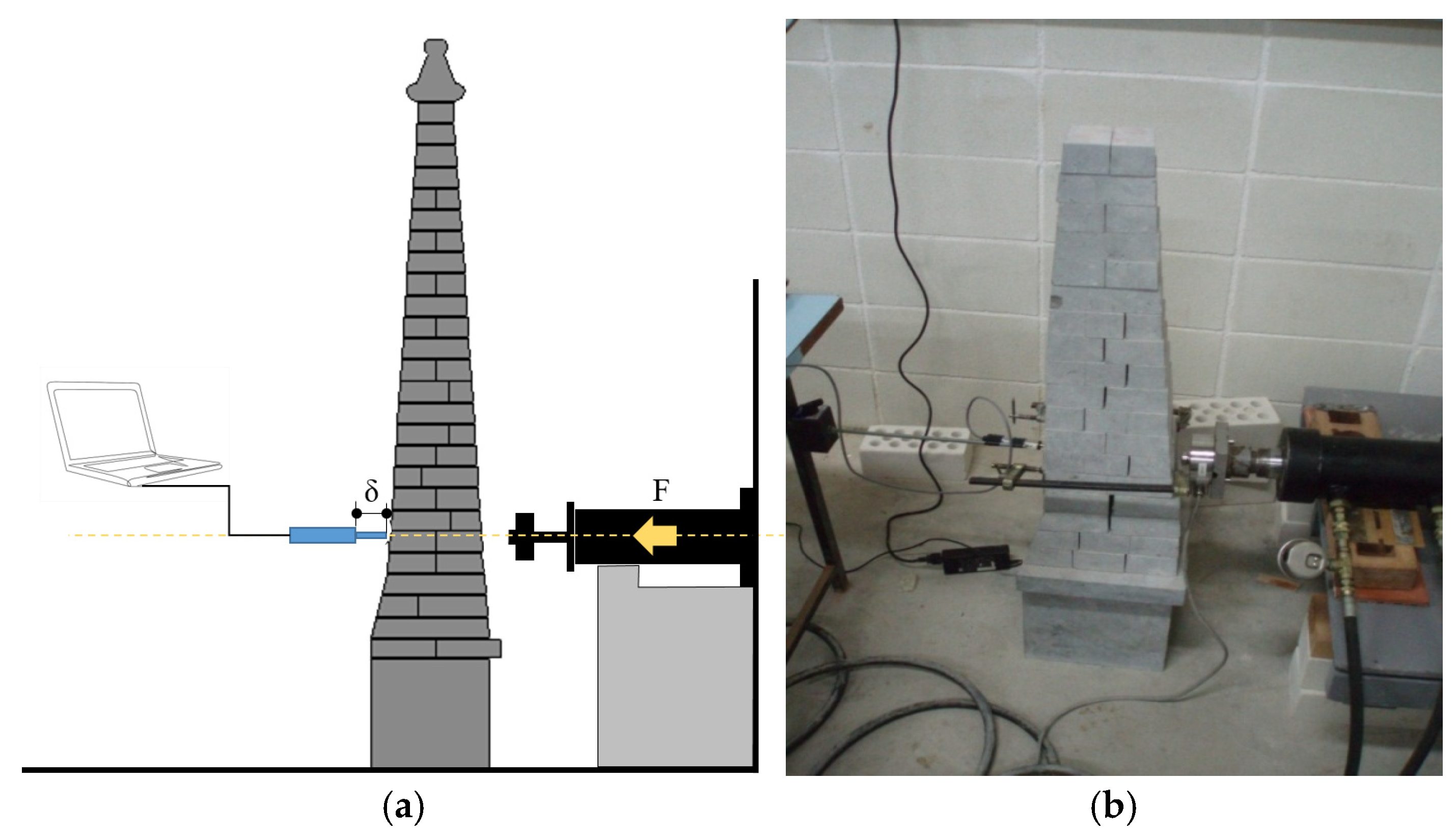
3.2. Experimental Scaled Model

A 1:5 scaled model of the pinnacle (Figure 5) was made using the same material and construction method. This model was used to simulate the effect of horizontal forces on it. For this purpose, a laboratory test was designed.

A step-by-step procedure was followed. It consisted of successively applying to each course the resultant of all the forces present above its position. The resultant force was applied by using a hydraulic piston.

A displacement transducer was used to identify the start of the ring’s displacement. In this way, it was possible to experimentally evaluate the behaviour of the pinnacle against sliding caused by horizontal loads.

Two tests were used to calibrate the numerical model as follows:

a

A horizontal load was applied to the fifth course starting from the top of the scale model until sliding was detected. A force of 340 N was obtained.

b

A horizontal load was applied to the top of the base until a vertical displacement—due to rotation—of 1.0 mm relative to the ground, was measured. The applied force was 330 N.

These tests were subsequently simulated on the scale numerical model to calibrate it.

3.3. Numerical Scaled Model

Once the experimental scaled model response was determined, an equivalent numerical model was calibrated. Masonry components were modelled using SOLID185 from ANSYS^® (Canonsburg, PA, USA). It is an eight-node solid element, with three degrees of freedom at each node (translations in nodal x, y, and z directions). It supports plasticity, stress stiffening, large deflection, and large strain [Ansys].

The variables to calibrate were related to the behaviour of the contact surface between the rings. Such contact surface was represented using CONTA174 and TARGET170.

3.4. Frictional Model

The frictional model was based on Coulomb’ law:

τ_lim = μ·P + b,

(2)

where μ = coefficient of friction for isotropic friction; P = contact normal pressure; and b = cohesion.

The limit condition is represented by

||τ|| ≤ τ_lim,

(3)

It was considered that cohesion could not be guaranteed. Then the original formula for Coulomb’s law is

τ_lim = μ·P,

(4)

where μ was assigned according to the experimentally determined value.

3.5. Contact Model

The contact model is based on augmented Lagrange, a penalty-based formulation where the contact stiffness is used to determine the degree of penetration between two consecutive courses. In this contact formulation, the contact stiffness value depends on the stress level in the material. The requirement for zero penetration between bodies is imposed, in which the augmented Lagrange multiplier is used to improve deconvergence. In this kind of nonlinear problem—where the contact properties vary during the process—this strategy allows for a gradual transition, enhancing the stability and the quality of the solution.

The numerical model’s ability to reproduce both the sliding and rotation of the courses was checked. The preliminary results are presented below (Figure 6).

3.6. Scale Model Adjustments and Full-Scale Model

A scaled real model was used to calibrate a numerical model. Once the calibration is complete, the model can reproduce the load test performed in the real model under laboratory conditions, and a full-scale numerical model of the real pinnacle is defined, including the properties updated in the previous step.

Only slight changes were necessary in the numerical model to achieve a satisfactory similarity with the experimental results. The updated parameter was the material’s density. Its value was reduced by approximately a 6% compared to the initial estimate.

After the calibration, the calculated forces due to the influence of wind and earthquakes were applied to the full-scale model. The model’s response was compared with the results of the equilibrium approach. Good agreement was observed between the two approaches.

3.7. Equilibrium Approach

An equilibrium approach based on the middle third rule has been used as a complementary tool to verify the quality of the results. The aim is to identify the loss of contact between consecutive layers of stone masonry based on the appearance of tensile stresses in the area of interest.

As a work hypothesis, it is assumed that the area has no capacity to cope with this kind of stress. This assumption is consistent with the physical reality of a masonry structure without mortar in the joints.

In

Table 4. Geometric eccentricities.

Element	Height (m)	X Dimension (m)	Y Dimension (m)	Volume (m3)	Weight (KN)	Accumulated (KN)	egeometric (m)
1	1.28	1.11	1.32	1.88	50.64	169.02	0.10
2	1.11	1.06	1.18	1.38	37.31	118.38	0.05
3	0.74	0.96	0.97	0.69	18.51	81.07	0.00
4	0.74	0.88	0.90	0.58	15.74	62.57	0.00
5	0.74	0.80	0.82	0.48	13.02	46.83	0.00
6	0.74	0.71	0.74	0.39	10.50	33.80	0.00
7	0.74	0.63	0.67	0.31	8.37	23.31	0.00
8	1.97	0.52	0.54	0.55	14.94	14.94	0.00

,

Table 5. Wind eccentricities.

Element	Force Wind (m)	Bending Moment Wind (kNm)	ewind (m)
1	2.10	33.49	0.20
2	1.80	21.16	0.19
3	1.10	14.83	0.14
4	1.00	10.54	0.16
5	0.90	7.28	0.17
6	0.80	4.66	0.18
7	0.70	2.81	0.19
8	1.50	1.44	0.20

The concept “force wind” expresses the force on each of the elements due to wind pressure. The notion “bending moment wind” expresses the accumulated bending moment due to the forces located above the base of the element in question.

and

Table 6. Seismic eccentricities.

Element	H (m)	ϕ	Weight (kN)	η1	S1	F1 (KN)	M1 (kNm)	eseismic [m]
1	56.30	0.02	50.64	0.96	0.08	4.10	39.05	0.23
2	57.50	0.02	37.31	0.97	0.08	3.00	23.88	0.20
3	58.40	0.02	18.51	0.97	0.08	1.50	15.01	0.19
4	59.10	0.02	15.74	0.97	0.08	1.30	10.27	0.16
5	59.90	0.02	13.02	0.98	0.08	1.10	6.83	0.15
6	60.60	0.02	10.50	0.98	0.08	0.90	4.21	0.12
7	61.30	0.02	8.37	0.99	0.08	0.70	2.47	0.11
8	62.70	0.02	14.94	1.00	0.08	1.30	1.25	0.08

Where H is the height of the centroid of the element with respect to the ground; ϕ, η1, and S1 are parameters to calculate the equivalent seismic forces [42]; F1 is the equivalent seismic force; and M1 is the bending moment at the base of every single element, applying the same criteria than those in Table 6.

, the eccentricities induced by geometry and the horizontal forces (wind and earthquakes) are determined. Afterwards, these elemental hypotheses are combined.

Once the elemental cases were analyzed, the most feasible combinations were studied. The combination corresponding to a transitory situation (C_transitory) is proposed as follows:

C_transitory = γ_G · e_geometric + γ_Q · e_wind,

(5)

where γ_G = 1.35 and γ_Q = 1.50 represent the value of the safety coefficients corresponding to dead loads and live loads, respectively.

The combination corresponding to an accidental situation (C_accidental) is proposed as follows:

C_accidental = γ_G · e_geometric + γ_Q · e_wind + γ_A · e_seismic,

(6)

where γ_A represents the value of the safety coefficient of the accidental loads.

3.8. Result of Overturning Analysis

In

Table 7. Persistent or transitory combination.

Element	egeometric (m)	ewind (m)	Combination (m)	emax * (m)
1	0.10	0.20	0.30	0.22
2	0.05	0.19	0.24	0.20
3	0.00	0.18	0.18	0.16
4	0.00	0.17	0.17	0.15
5	0.00	0.16	0.16	0.14
6	0.00	0.14	0.14	0.12
7	0.00	0.12	0.12	0.11
8	0.00	0.10	0.10	0.08

* Maximum eccentricity for the middle third rule.

and

Table 8. Accidental combination.

Element	egeometric (m)	ewind (m)	eseismic (m)	Combination	emax * (m)
1	0.10	0.20	0.23	0.53	0.22
2	0.05	0.19	0.20	0.44	0.20
3	0.00	0.18	0.19	0.37	0.16
4	0.00	0.17	0.16	0.33	0.15
5	0.00	0.16	0.15	0.30	0.14
6	0.00	0.14	0.12	0.26	0.12
7	0.00	0.12	0.11	0.23	0.11
8	0.00	0.10	0.08	0.18	0.08

* Maximum eccentricity for the middle third rule.

, the eccentricity due to two different combinations is calculated (e_max) and compared with the maximum allowable eccentricity before the appearance of tensile stresses in the plane studied (middle third rule). The enveloping hypothesis gives the result that the allowable eccentricity is exceeded at each level considered. This result implies—assuming that no tensile stresses can be transmitted through the stone rings—that the titanium bar must be installed along the entire height of the pinnacle.

3.9. Result of Sliding Analysis

Equilibrium in the horizontal direction provides the necessary information to determine whether sliding is a critical failure mode. The horizontal component of wind and seismic forces has been determined and accumulated. The horizontal response of the masonry components depends on the friction that the surface under analysis is capable of developing under the effect of incident vertical loads.

A general overview of dry block masonry and the kinematic phenomena affecting it is given in [42]. In [43], the coefficient of friction is determined experimentally for the case of dry block masonry walls. Rocking-sliding mechanisms have been detected depending on the point where the force was applied. The coefficient of friction determined experimentally is similar to the one proposed in this study.

In

Table 9. Sliding verification.

Element	Horizontal Forces		Vertical Forces
	Wind [kN]	Seismic [kN]	Acum. Resultant [kN]	Gravitational [kN]	Friction Comp. [kN]
1	2.10	4.10	23.80	169.02	111.55
2	1.80	3.00	17.60	118.38	78.17
3	1.10	1.50	12.80	81.07	53.55
4	1.00	1.30	10.20	62.57	41.29
5	0.90	1.10	7.90	46.83	30.80
6	0.80	0.90	5.90	33.80	22.30
7	0.70	0.70	4.20	23.31	15.38
8	1.50	1.30	2.80	14.94	9.86

, the balance between horizontal forces is stablished. The result confirms that the stability of the pinnacle does not depend on its safety against the sliding phenomenon.

4. Design of Reinforcement

4.1. Inner Bar

A titanium bar was chosen as the material for reinforcing the pinnacles. The reasons for choosing this material are its exceptional durability, very high specific strength, a coefficient of thermal expansion similar to that of construction materials, and low weight density [42]. In addition, its resistance to alkaline agents present in masonry, without the need for complementary protections, was considered a fundamental issue. These properties make this material extremely suitable for achieving the requirements of durability, compatibility, and reversibility.

Prior to its selection, other materials such as steel alloys or FRP (fibre-reinforced polymers) were considered. FRP bars were rejected due to their poor durability without additional protection. Titanium was preferred to steel alloys because of its elastic strength and its performance in terms of corrosion.

To determine the required cross-section, the design axial force that the titanium bar must withstand was previously calculated (

Table 10. Force in titanium bar (F) and stresses in masonry (due to bending moment).

Element	D (m)	X Dimension (m)	Y Dimension (m)	A (m2)	Bending M (KNm)	F (kN)	Cstress (MPa)
1	0.20	0.13	1.11	0.07	2.68	13.23	0.18
2	0.25	0.17	1.06	0.11	5.27	21.08	1.91
3	0.28	0.18	0.96	0.13	8.87	31.67	2.43
4	0.30	0.20	0.88	0.16	11.12	37.00	2.31
5	0.34	0.22	0.80	0.20	20.81	61.20	3.06
6	0.36	0.24	0.71	0.23	29.83	80.00	3.48
7	0.44	0.29	0.63	0.31	51.96	118.10	3.81
8	0.50	0.33	0.52	0.36	89.45	178.90	4.96

) and then the required diameter was determined based on the properties of the material to be used (

Table 11. Mechanical properties of titanium bar.

Alloy	Young’s Modulus (GPa)	Yield Strength (MPa)	Ultimate Strength (MPa)	Ultimate Strain (%)
Ti-6AI-7Nb	114.00	880.00	900.00	8.00

). The most restrictive combination was chosen as a calculation hypothesis.

D is the distance between the compressed zone and the position of the titanium bar, A equals the compressed area (b multiplied by the length of the perpendicular edge (L_edge)), F is the force supported by the reinforcement, and C_stress is the compression stress in the masonry specimen due to the bending moment:

$$C_{stress}={\displaystyle \frac{F}{b·L_{edge}}}$$

The geometry of the approach can be seen in Figure 7. To determine it, the combination that resulted in a higher bending moment was chosen, which was the accidental combination.

The result indicates that the pinnacle remains precariously stable under the loading states represented by the elementary hypotheses. However, the calculations indicate that the pinnacle cannot withstand the combined hypotheses.

Inserting a titanium bar with a diameter of 20 mm in the centre of the pinnacle, surrounded by a fibre-reinforced mortar filling the surrounding space of roughly 100 mm, was enough to reinforce the pinnacle. The stability analysis performed indicated that the reinforcement solution should be as long as the pinnacle itself.

Determining its cross-section is straightforward. The usage of the concepts of admissible stress and area and applying a safety coefficient of 1.50 for actions and 1.10 for the material, results in the following:

593.00 MPa < 800.00 MPa

(7)

4.2. Filler

The last step consists of verifying the interface between the mortar surrounding the titanium bar and the perimeter of the hole made inside the pinnacle. Some studies exist that affirm that when repairing stone monuments, the strength of the mortar used for this purpose must be lower than that of the stone support [44]. Pull-out tests were used to define the adhesion strength between surfaces.

Although the pull-out tests present better results when the contact surface is pretreated (i.e., sandblasted or water jet blasted), the values corresponding to untreated surfaces were used in the calculations. This is because it was unfeasible to apply such treatments to the pinnacles.

The averaged value for adhesion was 0.22 ± 0.04 Mpa [44]. This value was used to verify the described situation. In [45], similar results were achieved.

There is not a standard procedure for evaluating the adhesion of the mortar to the inner faces of the cavities created in the pinnacles. To evaluate it, it was assimilated into the geotechnical verification corresponding to the failure due to pulling out of the injected zone of an anchor to the ground.

In [46,47], the formulation to determine the slip resistance is as follows:

$$F=L_b·P_T·{\displaystyle \frac{{\tau }_{lim}}{{\gamma }_R}}$$

(8)

where L_b is the necessary contact length to transfer the effort, P_T is the contact perimeter—the average diameter in this case is 65 mm, τ_lim corresponds to the average value for adhesion, and γ_R, is a safety factor (1.20 in the reference).

Isolating the necessary contact length, (L_b) can be determined as follows:

$$L_b={\displaystyle \frac{F·{\gamma }_R}{P_T·{\tau }_{lim}}}$$

(9)

The result indicates that in the worst case, the contact length would be around 4.75 m, a value compatible with the total injected length (the entire height of the pinnacle).

5. Conclusions

Dynamic effects have been analyzed as a quasi-static phenomenon. This is a simplified description of the physical process. Based on the work of other researchers who have studied this type of structure, it can be concluded that the resulting loss of accuracy does not invalidate the analysis.

In ill-defined situations involving a high degree of uncertainty where comprehensive studies incorporating numerical models of the entire monument and complete material characterizations are unavailable, a multi-approach procedure based on the combination of experimental and numerical models has proven to be a powerful tool.

The effects of wind and earthquakes were simulated under laboratory conditions on a scale model of the pinnacle. The results were then used to calibrate a numerical model in two steps. First, a model representing the scale pinnacle was calibrated. After adjusting the selected design variables—density, Young’s modulus, and contact between courses—the results were transferred to a numerical model representing the real pinnacle.

As a complementary and subsequent verification tool, manual calculations based on equilibrium conditions were made. Good agreement was found between numerical models and handmade approximations.

Therefore, to guarantee the stability of a pinnacle exposed to wind and seismic loads, it is necessary to reinforce it along its entire length with a 20 mm diameter titanium bar. The transfer of the titanium bar to the courses was also verified, resulting in a transfer lower than that required for other considerations (overturning and sliding).

From the study carried out, it can be concluded that the stability of a pinnacle is mainly related to its capacity to withstand the overturning phenomenon, with sliding between stone layers being a secondary issue.