Next Article in Journal
Integrating Backscattered Electron Imaging and Multi-Feature-Weighted Clustering for Quantification of Hydrated C3S Microstructure
Next Article in Special Issue
Numerical and Experimental Multi-Approach Models for a Stone Pinnacle Reinforcement
Previous Article in Journal
Impact of Wood on Perception of Transient and Steady-State Indoor Thermal Environments
Previous Article in Special Issue
A Proposal for Reinforcement of Historical Masonry Minarets: Gaziantep Kabasakal Mosque Minaret
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 15
Issue 10
10.3390/buildings15101700
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Influence of Stone Cladding Elements on the Seismic Behaviour of a Bell Tower

by
Luciana Di Gennaro
1,*,
Mariateresa Guadagnuolo
1,
Mariano Nuzzo
1,2 and
Giuseppe Faella
1
1
Department of Architecture and Industrial Design, University of Campania “Luigi Vanvitelli”, Abbazia di San Lorenzo ad Septimum, Via S. Lorenzo 1, 81031 Aversa, Italy
2
Ministry for Cultural Heritage and Activities and Tourism, Archaeological Park of Pompeii, 80045 Pompeii, Italy
*
Author to whom correspondence should be addressed.
Buildings 2025, 15(10), 1700; https://doi.org/10.3390/buildings15101700
Submission received: 23 March 2025 / Revised: 23 April 2025 / Accepted: 11 May 2025 / Published: 17 May 2025
(This article belongs to the Special Issue Mechanics of Masonry Towers)
Browse Figures
Versions Notes

Abstract

Bell towers, due to their slender geometry and structural configuration, are among the buildings most susceptible to deterioration from weathering and seismic events. These aspects influence the structural assessment of these historic towers, which is essential for their conservation and maintenance. The “Carmine Maggiore” bell tower in Naples (Italy) has been an important and prominent landmark of the city for centuries. It is square in plan and 72 m high. Over time, it suffered extensive damage and was severely damaged by the earthquake of 1456. Reconstruction began in the first decade of the 17th century and the original design was modified, adding two stories and changing the shape of the plan to octagonal. In the centuries that followed, the structure was damaged again and further interventions were carried out, adding tie-rods and replacing damaged elements. Today, the bell tower has very elaborate façades with mouldings and decorations, so that the supporting structure appears to be covered with plaster, stucco, and stone elements. This paper describes the results of FEM analyses of the bell tower, obtained from models with different levels of complexity to evaluate the influence of stone cladding elements on the seismic behaviour. In particular, the difference in the IS safety indices, calculated as the ratio of capacity to demand, exceeds 15%, due to the mechanical consistency of the cladding elements, which contribute significantly to both stiffness and strength.

1. Introduction

Bell and masonry towers are a very typical type of structure in Italian and European cities. The importance of cultural heritage requires procedures aimed at preventing degradation phenomena and structural safety. In fact, most historical structures are degraded due to environmental factors, which are also aggravated by inadequate conservation.
Recent earthquakes in Italy have highlighted the high seismic vulnerability of bell towers, especially those with large openings and slender columns. It depends mainly on the slenderness, the effectiveness of the wall connection, the action of the bells, the presence of gables and projecting battlements, the presence of adjacent structures in the lower part, but also on the absence of dead loads in addition to own weight, which does not guarantee an adequate capacity of the horizontal sections of the tower and stabilising effects against overturning and out-of-plane mechanisms [1,2,3,4].
Italian technical standards provide information on analysing and strengthening existing masonry structures [5]. In particular, the National Guidelines [6] provide three approaches for the analysis of the seismic behaviour of historic masonry buildings, labelled LV1, LV2, and LV3. The LV1 method provides simplified models and analysis procedures [7], the LV2 approach concerns the analysis of out-of-plane kinematic mechanisms [3], while the LV3 approach, used in this paper, requires refined models for the analysis of the seismic response of the whole building [8].
In recent years, the growing interest in bell towers has stimulated scientific research at both the territorial [9,10,11] and structural levels, with finite element (FE) models being the most effective approach for evaluating seismic response [12,13,14,15,16,17,18]. Many papers have focused on dynamic identification [19,20,21,22,23,24,25,26], prediction of fundamental frequencies [27,28,29,30,31], and experiments [32,33,34], through which numerical models of the structure are then built using finite element (FE) modelling to analyse the response of the structure.
The foundation problems of bell towers are obvious, so soil flexibility is an area of research for these structures, especially when their dynamic and seismic response needs to be investigated [35,36,37,38].
It should also be mentioned that some research has been performed on the interaction effects between historic masonry towers and surrounding structures [22,39,40,41,42,43,44], but this topic is not discussed in this paper.
The type of model differs according to the analysis method used: linear or non-linear static analysis (pushover) and linear or non-linear time-history analysis [14,15,16,45,46,47,48]. With regard to the modelling technique, the finite element technique is the most widely used, as it allows the physical geometry of the tower to be accurately reproduced, and the different models differ according to their level of complexity and geometric discretisation [14,49].
In the context of historical masonry structures, non-structural components—such as cladding elements, architectural ornaments, and decorative facings—are often overlooked in structural analyses. However, their mass, stiffness, and degree of mechanical integration can significantly affect the global seismic response, particularly in tall and slender buildings. As highlighted in the recent literature, the accurate modelling of such elements and their connections could be essential for a realistic simulation of the structure’s dynamic behaviour, as they alter both the amount and distribution of mass throughout the structure, potentially affecting modal shapes, local stiffness, and internal force paths [50,51,52].
The aim of this paper is to evaluate the influence of stone cladding elements, such as façade decorations, on the dynamic behaviour and structural performance of the bell tower of the Basilica of “Carmine Maggiore” in Naples (Italy). A comparative finite element analysis was carried out using two numerical models with different levels of geometric and structural detail, in order to assess how the presence or absence of these elements affects the seismic response of the tower. The innovative aspect of the study consists of treating the stone cladding not merely as architectural mass, but as an active structural component, explicitly modelled and integrated in the numerical analysis—an approach rarely adopted in the seismic assessment of historic towers.

2. Objectives and Methods

Based on the geometric and diagnostic studies’ results, a very detailed finite element model of the tower (FEM1) was developed and analysed. The modelling of the stone cladding components is very refined, not only does it take into account their weights and masses in relation to their actual positions but also because they significantly impact the overall stiffness of the tower.
A second, less detailed finite element model (FEM2) was developed and analysed without modelling the stone cladding components. In particular, the covering elements in piperno present on the lower floors, the pilasters in piperno are present throughout the bell tower, the window frames in travertine and piperno, the cornices in Piperno, and the volutes in tuff.
Linear dynamic and pushover analyses were carried out to evaluate their influence on the static and seismic behaviour.

3. The Bell Tower of the Basilica Sanctuary of “Carmine Maggiore” in Naples (Italy)

The bell tower is part of the monumental complex of the Basilica of the Sanctuary of “Maria Santissima” of the “Carmine Maggiore” and the Convent of the Confraternity of “Santa Maria della Misericordia” and “Sant’Angelo Custode”. The bell tower borders the church to the north, the convent to the east and an urban building to the south (Figure 1).
The bell tower, 72 m high, has dominated the city of Naples for centuries and is one of the symbols of the city (Figure 1). The bell tower underwent a complex construction process between the 14th and 17th centuries, combining structural elements of different periods, geometries, and materials [53]. The base in piperno dates back to the 14th century, while the three quadrangular floors and the two octagonal upper levels were added in the 17th century by Conforto and Fra’Nuvolo, respectively. The upper part, lighter and more articulated, includes a higher number of openings and decorative elements. The structure had thirteen floors, in addition to the ground floor, with tuff and barrel vaults [53]. The structure ends with a pear-shaped polygonal spire in majolica, surmounted by a copper sphere. The decorative elements described, such as the rusticated piperno, the pediments and the volutes, cover the main load-bearing structure of the bell tower.
A four-flight wooden staircase led to the priests’ dormitory through a 15th-century wooden door. On the third floor level, there are five bells: four bells are placed in the side windows, while the largest is placed in the middle of the floor.
Numerous lightning strikes damaged the bell tower during the first centuries, and several strengthenings were necessary, mainly tie-rods [53].

Geometric and Diagnostic Survey of the Bell Tower

The studies carried out for the restoration and consolidation showed, in accordance with [54,55,56,57], that the structure has a rectangular plan up to the fourth floor with walls in yellow Neapolitan tuff, covered at the base with piperno ashlar. This traditional construction technique, which arranges more resistant and heavier materials at the base, can also be found in later buildings [11].
The walls of the octagonal upper part are in clay bricks up to the level of the cornice that delimits the last octagon at about 57 m from the base. The structure is completed by a pear-shaped cusp covered in green and yellow earthenware with eight ribs. Above the cusp is a sphere with a metal cross.
Today, the bell tower has six levels at 8.89 m, 18.98 m, 29.57 m, 40.19 m, 50.10 m, and 57.17 m above the ground. The thickness of the walls varies from 4 m at the base to about 1 m at the top.
The bell tower is joined to the church on the left side, up to the eaves of the church roof, and to the convent on the right and rear sides, up to the roof of the convent. The main façade facing the square is completely open. From the bell tower, access is gained to the cloister behind the convent. Historical sources indicate that the church and bell tower were originally separate and that the current configuration is due to later modifications.
As already stated, over time, the tower has undergone remarkable reconstructions that have modified its façades and structural behaviour, even in relation to the neighbouring buildings. In particular, some of the original masonry vaults were replaced by reinforced concrete floors. The upper part of the timber staircase was replaced by a reinforced concrete staircase, well connected to the masonry walls. This staircase connects the masonry walls, stiffening the bell tower in the upper levels where the walls are thinner.
Between the bell tower’s 18 m and 56 m levels, there are around 60 steel tie-rods, most of which pass through the walls and are anchored to the outside by a steel bar or plate. Some of the bars are from the 19th century, and others are probably from the 20s and 30s. The tie-rods have a diameter ranging between 35 and 50 mm. Later, in the 1970s, additional steel strand tie-rods with six wires of 4 mm diameter were placed to improve the degree of connection of the walls. After the 1980 earthquake, further strengthening injections were carried out on the floors above the fourth floor, and in 2008, fibreglass tie-rods with stainless steel anchor plates were installed at a level of about 55.70 m. A detailed description of all the interventions to consolidate the bell tower can be found in [57,58].

4. The Structural Models

Modelling the structure of a bell tower involves architectural and structural considerations and may include consideration of which elements of a very slender structure may positively or negatively affect its seismic behaviour and relative safety.
Bell tower structures can be modelled in different ways, depending on the approach and purpose of the analysis (wind analysis, seismic analysis, analysis under vibrations induced by the swinging of the bells, etc.), material considerations, and structural behaviour. The shell/plate model is often used to represent walls and floors and is considered adequate for assessing historic masonry towers’ wind and seismic resistance. Solid models, on the other hand, are generally only used for detailed stress and material failure analysis. However, they are often considered essential for detailed crack analysis in stone/brick towers.

4.1. Materials

Two types of masonry are present in the tower: tuff blocks or solid bricks with lime mortar.
The mechanical parameters of two types of masonry and cladding, chosen according to [5] and based on experimental tests, are given in Table 1.
Where:
  • fm is the mean compressive strength;
  • ft is the mean tensile strength;
  • τo is the mean shear strength;
  • E is the longitudinal modulus of elasticity;
  • G is the shear modulus of elasticity.
The partial coefficient for the resistances was assumed to be γm = 2 in the linear analyses and γm = 1 in the non-linear analyses

4.2. Loads of Structural and Stone Cladding Materials

The structural analyses were carried out using the unit load values summarised below. The s automatically computes the self-weight of the structural materials as a function of the density (w) of the materials and the geometry and spatial development of each structural element.
Masonry of soft stone ashlars (tuff): w = 16 kN/m3;
Masonry of solid bricks and lime mortar: w = 18 kN/m3;
Piperno (covering): w = 27 kN/m3;
Hard limestone (covering): w = 22 kN/m3;
Concrete: w = 25 kN/m3;
Stainless steel (tie-rods): w = 79 kN/m3.
In the bell tower, there are horizontal walkways supported by vaulted structures, except for one supported by a reinforced concrete floor. It was assumed that these structures would be subjected to a live load of 0.50 kN/m2 due to their use.

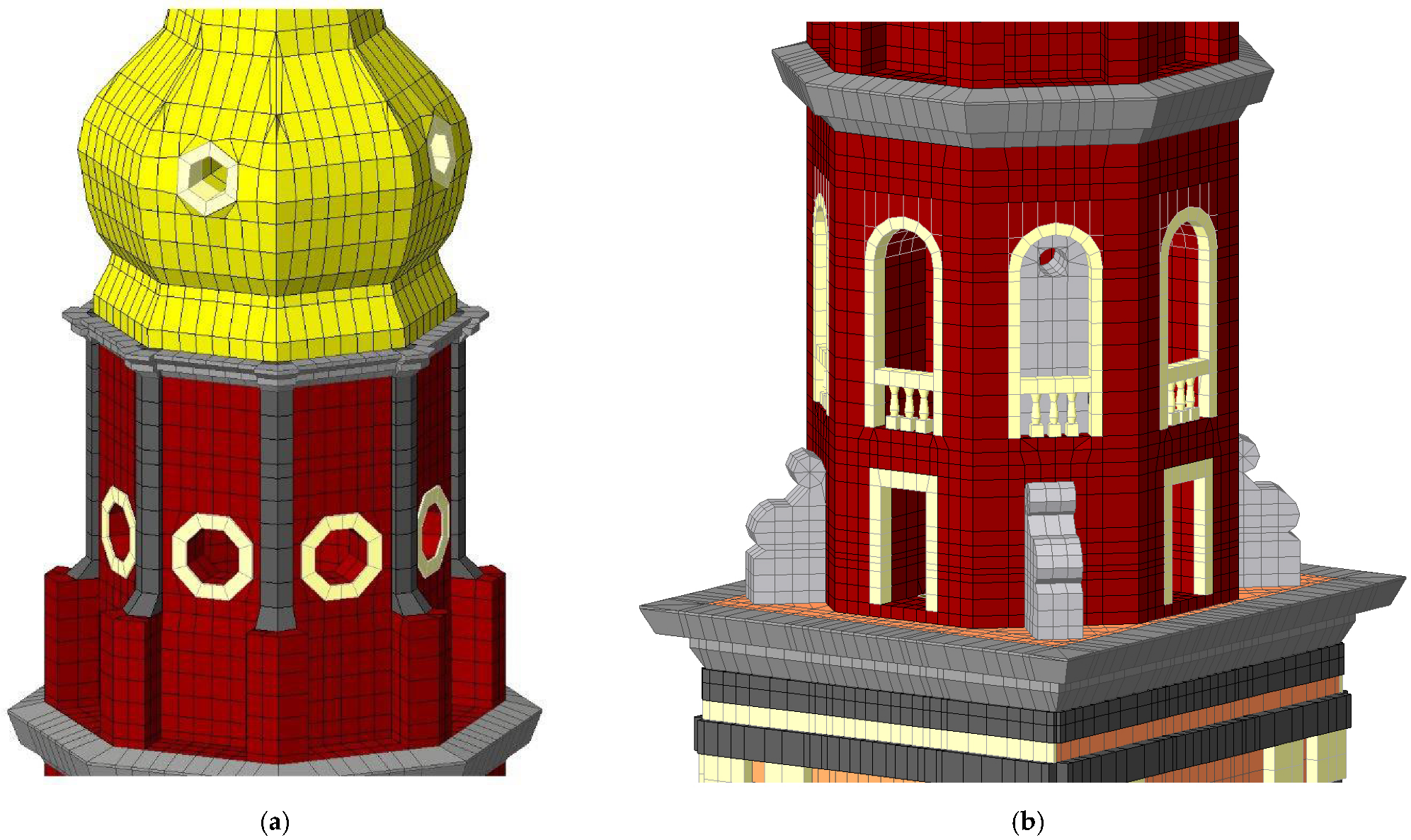
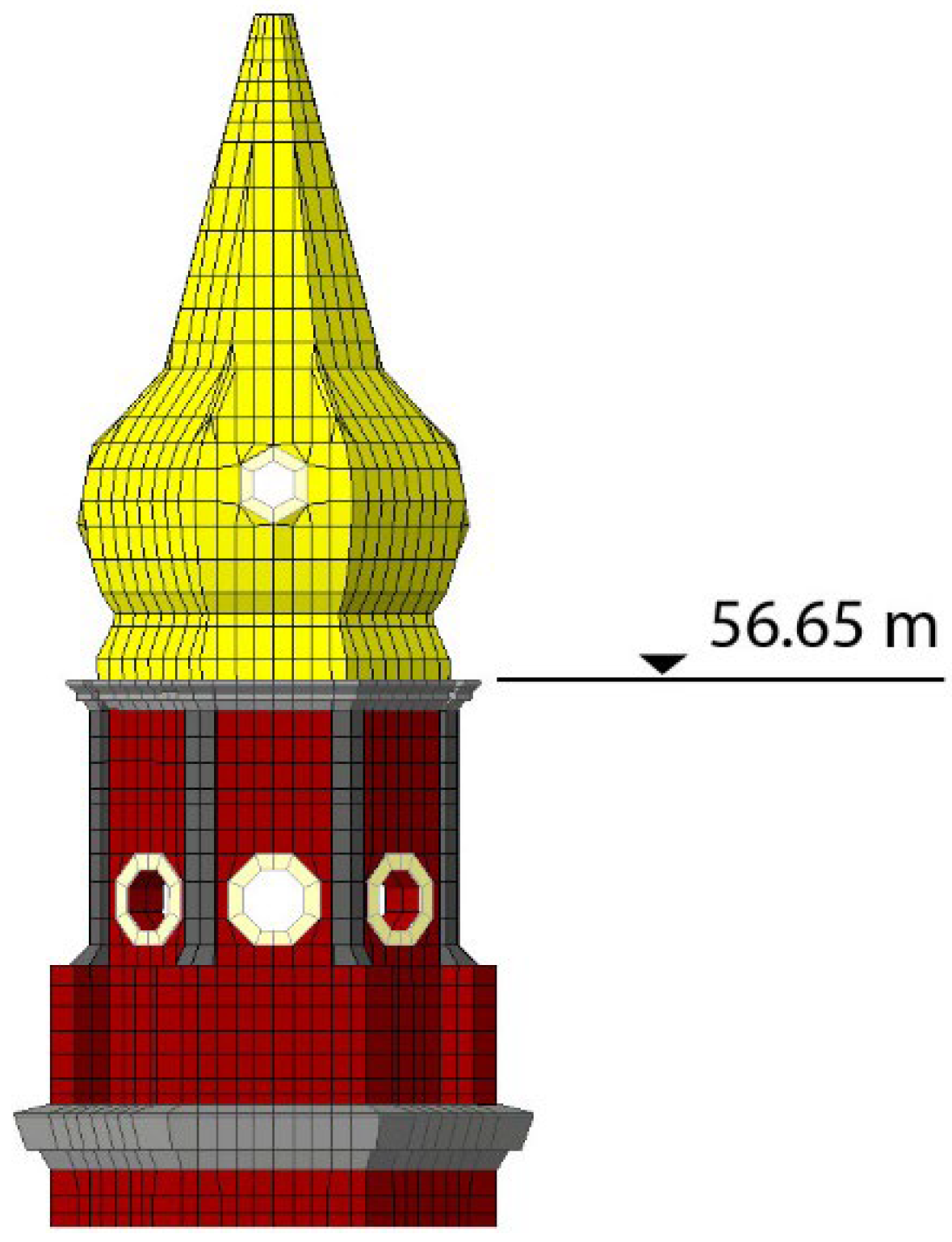
4.3. FEM Modelling

For the analyses, a finite element modelling approach was adopted, whose validity in the seismic assessment of masonry structures is well established in the literature [50,59,60,61,62,63,64,65].
On the basis of the detailed geometric survey available, two finite element models of the bell tower (FEM1 and FEM2) were developed: the structure was schematised using an integral spatial model, into which all the main components of the bell tower were inserted, and in FEM1 also the stone cladding elements. The latter were inserted both to take account of weights and masses in their actual position (given the non-negligible weight) and because they have a non-negligible effect on the overall stiffness of the bell tower. In FEM2, the weight of the stone cladding elements is distributed evenly over the height of the bell tower (Figure 2). More specifically, the claddings were not geometrically modelled in FEM2, but their masses were applied in order to account for their inertial effects without affecting the stiffness.
In particular, the masonry walls and the vault have been modelled with finite elements, using solid elements with 8, 6, and 4 nodes, in order to reproduce with a high degree of approximation the progressive changes in geometry and thickness along the height and the different openings, also taking into account the compatibility with the modelling of the main stone cladding elements, where present. In the FEM1 model, the stone cladding elements were mostly modelled with two-dimensional (plate) elements, or three-dimensional (solid) where necessary (Figure 3 and Figure 4). Table 2 shows the number of nodes and elements that make up the two different models.
A reference system (X, Y, and Z) was adopted, assuming Z as the bell tower’s longitudinal (vertical) axis and X and Y as axes contained in the section of the bell tower itself. In particular, the X direction is north–south (Church-Congregation), and the Y direction is East–West (Square-Cloister), as shown in Figure 2.
Structures with actual geometries and stiffnesses at the storey levels (vaulted or slab structure) were included in the model. The structure of the internal staircase was also included in the model, modelled by a slab of equivalent thickness; the tie-rods were modelled using one-dimensional (beam) elements. Furthermore, the structure was assumed to be monolithic, i.e., the model assumes that the different parts are well connected and able to transmit seismic actions. Therefore, local collapse mechanisms, which are not the subject of this paper, are not considered to be activable. The boundary conditions consist solely of external constraints, with only translational degrees of freedom prevented. The ground nodes were considered constrained in terms of translational displacements only. The other external nodes are also constraints that block only translation in the three directions.

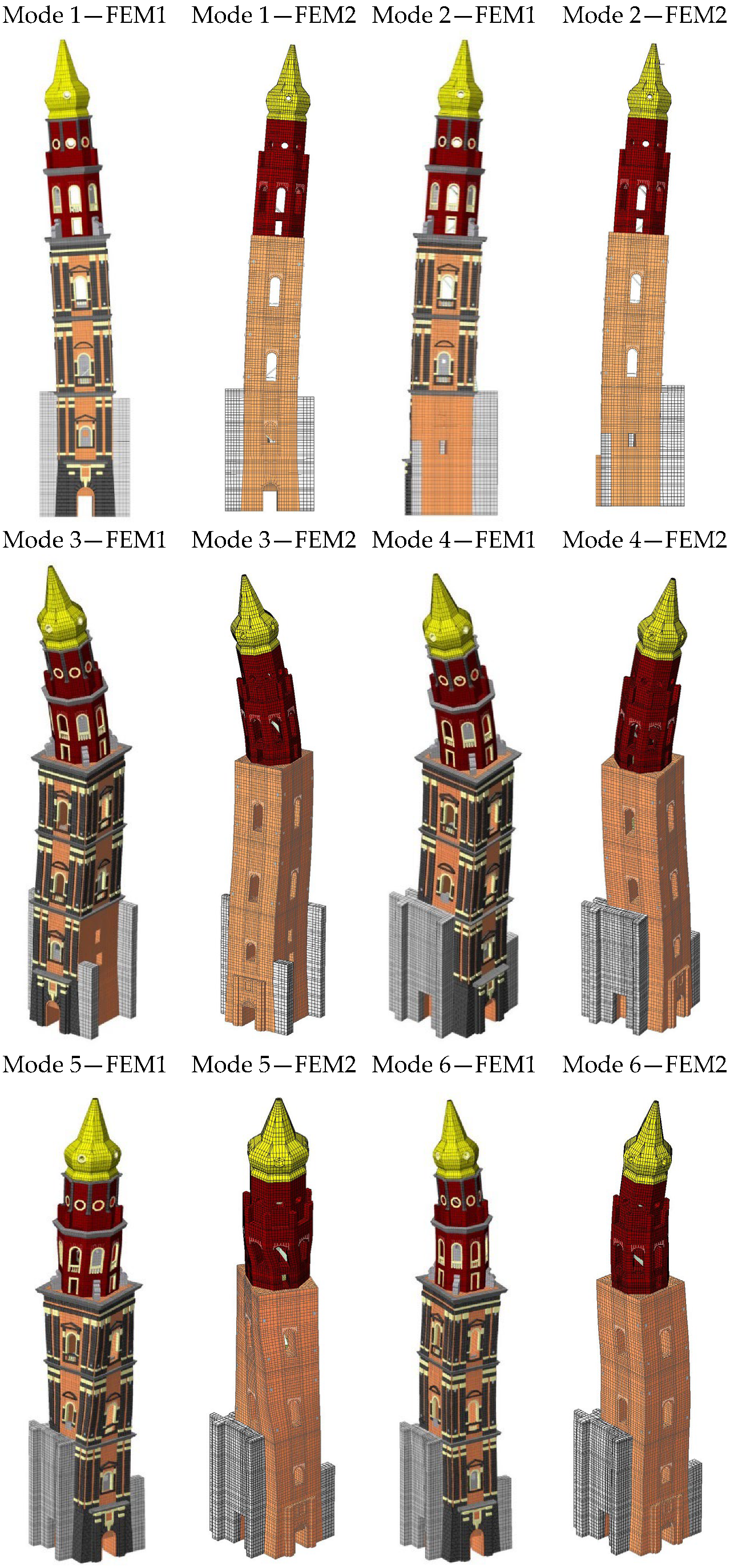
5. Eigenvalue Analysis

The response of historic masonry towers to earthquake loading is somewhat different from that of other old buildings, mainly due to their geometry. Adequate knowledge of the dynamic characteristics (frequencies and modal shapes) is an important starting point for a reliable seismic analysis. Therefore, the eigenvalues and eigenvectors of the structural system were first determined.
The natural frequencies of the system have been computed by evaluating the contribution of the masses concerning the self-weight, the dead loads and part of the live loads, according to the simultaneity coefficients provided by regulations in force, as previously reported.
In order to assess possible differences due to the bell tower modelling, the periods of vibration were computed beforehand. Table 3 shows the calculated values and shows that there are some differences in the X and Y directions.
The comparison of the vibration periods highlights the influence of the stone cladding elements. FEM1 exhibits systematically lower periods than FEM2, with differences of about 10% in the first two modes and significantly higher discrepancies in the higher modes. This indicates that the contribution of the cladding becomes more relevant in localised or higher-frequency deformations, where mass and stiffness distribution play a greater role.
The modal shapes are shown in Figure 5.
The results of both models show that the first two mode shapes are predominantly translational in one direction only, the third and fourth are translational in both directions, the fifth is torsional, and the sixth is translational in the z-direction.
The first two mode shapes are decoupled and have similar values of the main frequencies, while the third is three times larger than the first two in model FEM1 [29] and two times larger in model FEM2, showing the different influences of the upper modes due to the different deformability of the bell tower structure.
It is also noted, as expected, that the first two mode shapes are characterised by a deformation similar to that of a shelf, while the third and fourth display a flexural deformation with a visible point of curvature.

6. Non-Linear Static Analysis (Pushover)

The non-linear static (pushover) analyses were carried out using the MidasGen software 2025 [66]. The masonry is analysed as an equivalent homogeneous material, where the homogenisation technique provides the relationship to be used for the masonry, starting from a representative elementary volume with different constitutive relations for blocks vertical and horizontal mortar joints. The homogenisation technique proposed by Pande [67] is based on the equality of deformation energy. This approach makes it possible to study the behaviour of the masonry, taking into account the micromechanisms that actually occur.
In the pushover analysis, the loads were applied to the structure in two steps. First, the vertical loads were applied and then the lateral loads were monotonically increased. Lateral load distribution was assumed to be proportional to mass in height. No accidental eccentricity was considered when performing the pushover analysis.
As a precaution, the control point was taken at the centre of mass of the last floor present, i.e., at a height of 56.65 m, as shown in Figure 6.
The safety assessment was carried out using the capacity spectrum method, applying the response spectrum designed for Napoli, Piazza del Carmine (Latitude: 40.84676, Longitude 14.26745) at the limited state of life safety (soil type C, topographic category T1, Vn nominal life Vn = 50 years, use class Cu = 2, peak ground acceleration ag = 0.168 g, Fo = 2.378, soil coefficient S = 1.46, TB = 0.17 s, TC = 0.509 s, TD = 2.272 s).

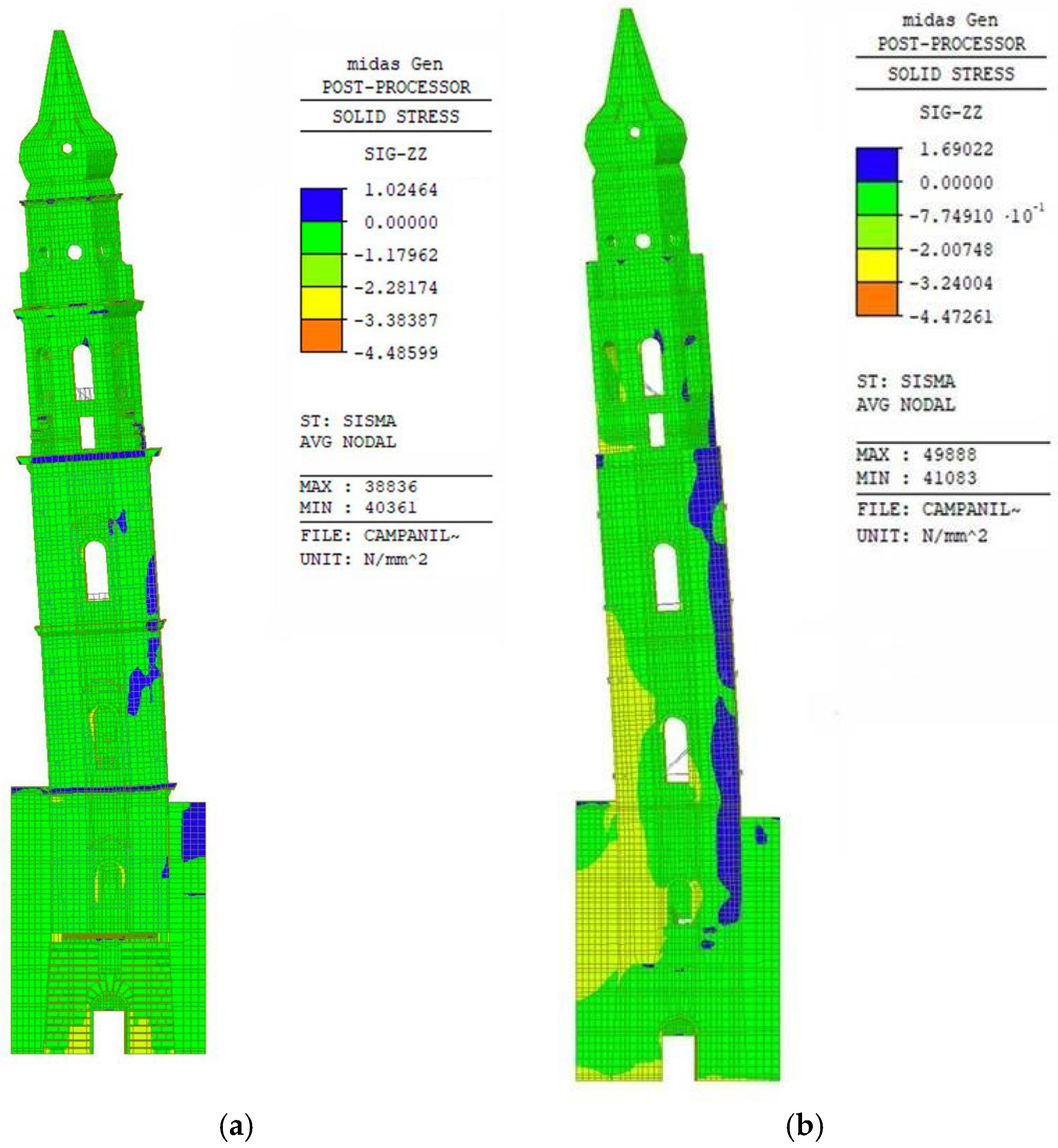
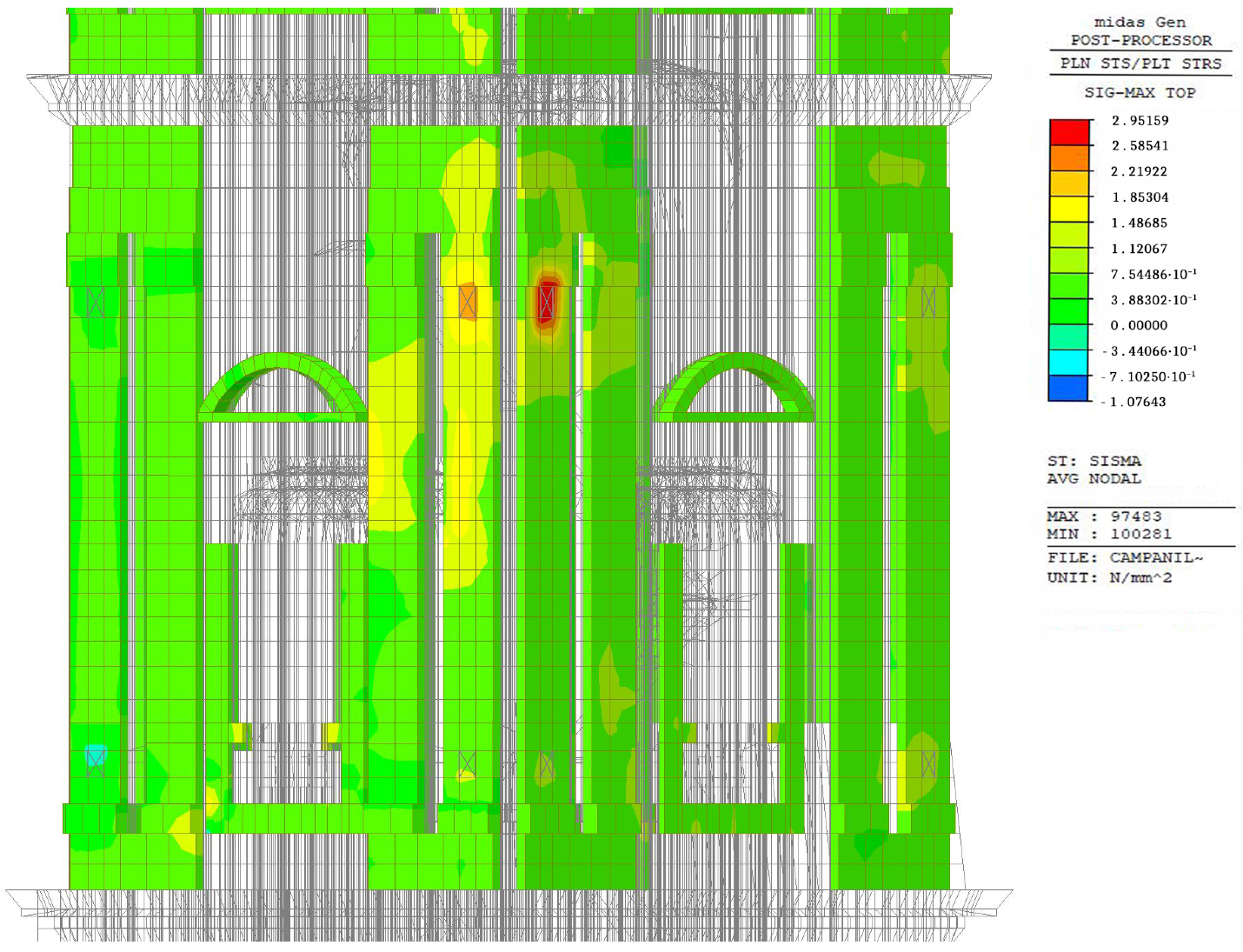
6.1. Results of Non-Linear Static Analyses

Figure 7 shows the deformed configuration and the distribution of normal stresses for the two models at the last step of displacement in the X-direction. In FEM1, the tensile stresses (calculated at the last pushover step and represented by positive values) affect only a few elements of the bell tower from the base to a height of approximately 40 m, corresponding to the change in the section from rectangular to octagonal (Figure 7). In FEM2, the tensile stresses affect the same part of the tower but are much more extensive.
Figure 8 shows the distribution of maximum principal stresses in the plate elements of the FEM1 model, which reproduce the cladding stone elements. Some stress concentrations can be seen, particularly at the tie-rod plates, which are reduced in the rear tuff elements due to an obvious distribution effect. In some cases, the stress concentration may be relevant if it induces local collapses of the elements concerned and, of course, can only be clearly detected if the modelling of the bell tower includes the cladding elements.

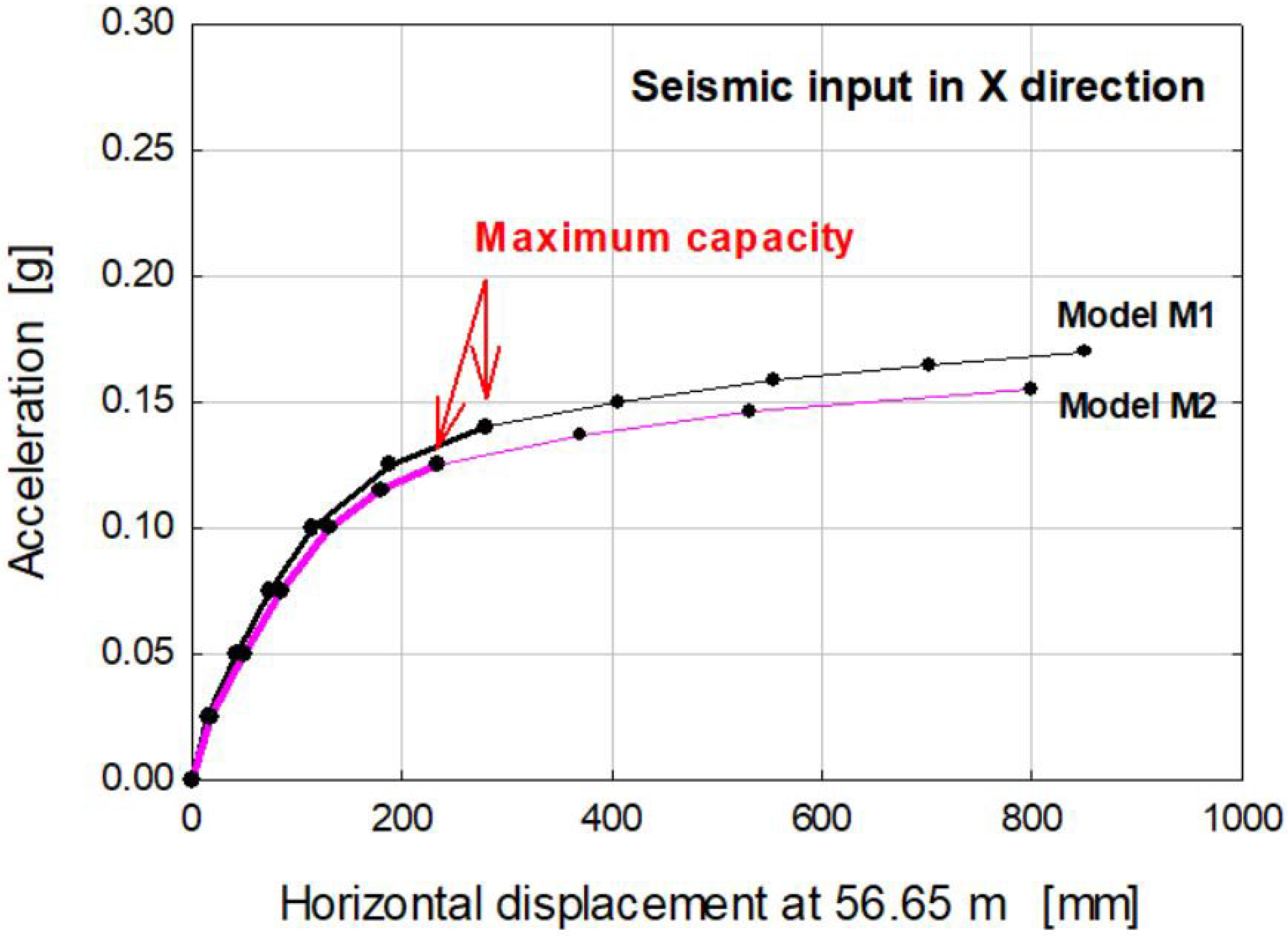
6.2. Seismic Capacity of the Bell Tower

The displacement capacity of masonry structures significantly influences and limits the ULS safety check in non-linear static analyses [68]. It mainly depends on the type of masonry, the failure mode (shear failure mechanisms generally provide low deformation capacity) and the level of axial load (frequently, the higher the axial load, the lower the displacement capacity of the walls).
The analysis was carried out using the capacity spectrum method, which compares the capacity of the structure with the earthquake demand in terms of displacements. In the case of the solid element modelling, the displacement capacity of the building could be identified on the basis of the achievement of the maximum displacements in the walls or the maximum equivalent (effective) stresses, but it was considered more appropriate to identify it as that corresponding to the achievement of the maximum load capacity in a masonry pier. Specifically, flexural failure was identified by comparing the bending moment obtained by integrating the stresses acting on the section with the resistant moment, while shear failure was assumed to coincide with the achievement of the shear strength calculated using the equation proposed by Turnsek, Sheppard (1981) [69].
Figure 9 shows the capacity curves obtained from the two models of the bell tower (acceleration displacement of the control point) for the X-direction of the application of the horizontal forces.
For both models, the response of the bell tower in terms of capacity in the two main directions is essentially identical due to the considerable symmetry of the tower, although some differences can be seen due to the different constraint conditions at the base due to the presence of the bell tower coupling with the adjacent buildings in the lower part. The absence of stone cladding elements in FEM2 reduces the capacity in terms of resistance and displacement, and consequently, the safety index is lower because the stone cladding elements are considered only as weight and not as contributing elements in terms of strength.
Table 4 shows the results of the verification of the bell tower for forces applied in the X- and Y+ directions, carried out using the capacity spectrum method [5,70] for both models. In particular, the difference in the IS safety indices, calculated as the ratio of capacity to demand, exceeds 15% due to the consistency of the stone cladding elements in this case, which are stiff and strength.

7. Impact on Retrofit Design and Conservation Strategies

The results of the study indicate that stone cladding elements, although often considered non-structural, can influence the dynamic response of historic masonry towers. The comparison between the two models highlights how the inclusion of these components affects the stiffness and mass distribution of the structure.
In the context of conservation, this suggests the need to consider the mechanical role of cladding elements when assessing the seismic behaviour of historic towers. Their removal, alteration, or isolation during retrofit interventions should be evaluated with respect to their structural contribution and potential safety implications.
From a retrofit design perspective, structural models of existing buildings are frequently used to guide decisions on strengthening interventions. If the safety index is found to be lower than one, retrofit measures—potentially invasive—are usually required to ensure structural safety. In this study, although both models produced safety indices greater than one, the value obtained from FEM2, which does not include the cladding elements, was more than 15% lower than that of FEM1. This difference opens a broader discussion on the level of refinement to be adopted in structural modelling. In cases where the safety index is close to the threshold, such modelling discrepancies could lead to fundamentally different decisions, such as recommending strengthening where it may not be necessary. Greater attention to the role of non-structural but mechanically relevant elements is therefore advised, in order to avoid over-conservative retrofit designs based on overly simplified models. Including these elements in the numerical analysis may lead to more accurate estimations of modal parameters and potential collapse mechanisms, which can inform the design of appropriate strengthening measures.

8. Discussion and Conclusions

The study evaluates the influence of the level of detail in the structural modelling of bell towers on their seismic behaviour and safety, with particular attention to the role of stone cladding elements. The analyses were conducted on the bell tower of the Basilica Sanctuary of “Carmine Maggiore” in Naples, where these elements are particularly widespread and structurally integrated.
The seismic behaviour of the bell tower was analysed using two detailed models: one including detailed cladding components as part of the structure (FEM1) and one excluding them (FEM2). In the case of FEM1, contrary to the usual practice the travertine or piperno cladding elements, they were considered to have a structural role.
While both models presented similar failure mechanisms, the differences in stiffness, displacement capacity and safety indices were non-negligible. These quantitative differences, although not extreme, reveal the contribution of façade complexity to the global dynamic response of the tower. Notably, the IS safety index, defined as the ratio between capacity and seismic demand, varied by over 15% between the two models, underlining the mechanical significance of the cladding elements in this specific case.
The findings confirm that structural modelling which does not explicitly include heavy architectural elements may lead to an underestimation of the tower’s stiffness and a less accurate assessment of its overall seismic vulnerability. This is particularly relevant for tall and slender historical constructions, where the presence of projecting features and ornamental masses influences not only the modal parameters but also the stress distribution during seismic events.
The results highlight the relevance of detailed modelling in assessing the seismic vulnerability of heritage structures. This approach enables a more realistic simulation of deformation patterns and internal force redistribution, which are often altered by non-structural but mechanically significant components. Beyond structural accuracy, the inclusion of cladding components also has implications for public safety, as potential detachment and local failure may go undetected in simplified representations. In the event of an earthquake, even non-structural elements can represent a hazard to occupants and bystanders if not properly anchored or accounted for in the analysis.
From a broader perspective, the study supports the adoption of advanced numerical models in the preservation of cultural heritage buildings, particularly when such structures are located in seismic areas and attract significant public presence. Although more time-consuming, detailed modelling proves to be a more reliable approach in evaluating the behaviour of bell towers subjected to seismic actions. It also offers a better foundation for the design of tailored reinforcement and monitoring strategies aimed at safeguarding both the built heritage and the community.
Future developments of this research may include non-linear time-history analyses to capture the dynamic response in greater detail, as well as in situ investigations to validate the numerical assumptions. Moreover, the modelling approach adopted here could be extended to historic towers with different geometries, materials, and construction typologies, in order to further assess its general applicability.

Author Contributions

Conceptualization, methodology G.F., M.G. and L.D.G.; software, validation, G.F.; formal analysis, investigation, data curation M.G. and L.D.G.; resources, writing—original draft preparation, writing—review and editing, visualisation, M.G., M.N. and L.D.G.; supervision, project administration, G.F.; funding acquisition, L.D.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Acknowledgments

This study has been developed within the national project PRIN 2022 PNRR “Safe Motion-Structural Assessment and development of innovative saFEguard Measures fOr hisTOrIcal masONry towers”.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Gesualdo, A.; Iannuzzo, A.; Monaco, M.; Savino, M.T. Dynamic Analysis of Freestanding Rigid Blocks. In Proceedings of the Twelfth International Conference on Computational Structures Technology, Naples, Italy, 2–5 September 2014; Volume 106. [Google Scholar] [CrossRef]
  2. Gesualdo, A.; Iannuzzo, A.; Monaco, M.; Penta, F. Rocking of a Rigid Block Freestanding on a Flat Pedestal. J. Zhejiang Univ. A 2018, 19, 331–345. [Google Scholar] [CrossRef]
  3. Guadagnuolo, M.; Aurilio, M.; Tafuro, A.; Faella, G. Analysis of Local Mechanisms through Floor Spectra for the Preservation of Historical Masonries. A Case Study. In Proceedings of the COMPDYN Proceedings, Crete, Greece, 24–26 June 2019; Volume 1, pp. 1501–1513. [Google Scholar]
  4. Frunzio, G.; Di Gennaro, L. The out of Plane Behaviour of Masonry Infilled Frames. J. Phys.: Conf. Ser. 2021, 2090, 012148. [Google Scholar] [CrossRef]
  5. MIT Norme Tecniche per Le Costruzioni, D.M. Official Bulletin n. 49, 17 January 2018. (In Italian)
  6. MIT Valutazione e Riduzione Del Rischio Sismico Del Patrimonio Culturale Con Riferimento Alle Norme Tecniche per Le Costruzioni Di Cui al Decreto Del Ministero Delle Infrastrutture e Dei Trasporti Del 14 Gennaio 2008. (11A02374). S.OOfficial Bulletin n. 54. 9 February 2011. Available online: https://dgspatrimonioculturale.beniculturali.it/wp-content/uploads/2020/08/Valutazione-e-riduzione-rischio-sismico-patrimonio-culturale-Direttiva-PdCM-09_02_2011.pdf (accessed on 22 March 2025). (In Italian).
  7. Guadagnuolo, M.; Aurilio, M.; Faella, G. Retrofit Assessment of Masonry Buildings through Simplified Structural Analysis. Frat. Ed Integrita Strutt. 2020, 14, 398–409. [Google Scholar] [CrossRef]
  8. Ferraioli, M.; Miccoli, L.; Abruzzese, D.; Mandara, A. Dynamic Characterisation and Seismic Assessment of Medieval Masonry Towers. Nat. Hazards 2017, 86, 489–515. [Google Scholar] [CrossRef]
  9. Curti, E.; Parodi, S.; Podestà, S. Simplified Models for Seismic Vulnerability Analysis of Bell Towers. Structural Analysis of Historic Construction: Preserving Safety and Significance. In Proceedings of the 6th International Conference on Structural Analysis of Historic Construction, SAHC08, Bath, UK, 2–4 July 2008; pp. 1237–1244. [Google Scholar]
  10. Formisano, A.; Ciccone, G.; Mele, A. Large Scale Seismic Vulnerability and Risk Evaluation of a Masonry Churches Sample in the Historical Centre of Naples. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2017; p. 090003. [Google Scholar]
  11. Guadagnuolo, M.; Nuzzo, M.; Faella, G. The Corpus Domini Bell Tower: Conservation and Safety. In Proceedings of the Procedia Structural Integrity, Hyderabad, India, 25–27 July 2018; Volume 11, pp. 444–451. [Google Scholar]
  12. Carpinteri, A.; Invernizzi, S.; Lacidogna, G. Numerical Assessment of Three Medieval Masonry Towers Subjected to Different Loading Conditions. Masonry 2006, 19, 65–76. [Google Scholar]
  13. Riva, P.; Perotti, F.; Guidoboni, E.; Boschi, E. Seismic Analysis of the Asinelli Tower and Earthquakes in Bologna. Soil Dyn. Earthq. Eng. 1998, 17, 525–550. [Google Scholar] [CrossRef]
  14. Bernardeschi, K.; Padovani, C.; Pasquinelli, G. Numerical Modelling of the Structural Behaviour of Buti’s Bell Tower. J. Cult. Herit. 2004, 5, 371–378. [Google Scholar] [CrossRef]
  15. Peña, F.; Lourenço, P.B.; Mendes, N.; Oliveira, D.V. Numerical Models for the Seismic Assessment of an Old Masonry Tower. Eng. Struct. 2010, 32, 1466–1478. [Google Scholar] [CrossRef]
  16. Milani, G.; Casolo, S.; Naliato, A.; Tralli, A. Seismic Assessment of a Medieval Masonry Tower in Northern Italy by Limit, Nonlinear Static, and Full Dynamic Analyses. Int. J. Arch. Herit. 2012, 6, 489–524. [Google Scholar] [CrossRef]
  17. Di Gennaro, L.; Guadagnuolo, M.; Monaco, M. Rocking Analysis of Towers Subjected to Horizontal Forces. Buildings 2023, 13, 762. [Google Scholar] [CrossRef]
  18. Massaro, L.; Di Gennaro, L.; Guadagnuolo, M.; Frunzio, G. Strengthening of Masonry Arches: The “Santa Maria Delle Grazie”. In COMPDYN Proceedings; National Technical University of Athens: Zografou, Athens, 2023. [Google Scholar] [CrossRef]
  19. Gentile, C.; Saisi, A. Ambient Vibration Testing of Historic Masonry Towers for Structural Identification and Damage Assessment. Constr. Build. Mater. 2007, 21, 1311–1321. [Google Scholar] [CrossRef]
  20. Ivorra, S.; Pallarés, F.J. Dynamic Investigations on a Masonry Bell Tower. Eng. Struct. 2006, 28, 660–667. [Google Scholar] [CrossRef]
  21. Ramos, L.F.; Marques, L.; Lourenço, P.B.; De Roeck, G.; Campos-Costa, A.; Roque, J. Monitoring Historical Masonry Structures with Operational Modal Analysis: Two Case Studies. Mech. Syst. Signal Process. 2010, 24, 1291–1305. [Google Scholar] [CrossRef]
  22. Pieraccini, M.; Dei, D.; Betti, M.; Bartoli, G.; Tucci, G.; Guardini, N. Dynamic Identification of Historic Masonry Towers through an Expeditious and No-Contact Approach: Application to the “Torre Del Mangia” in Siena (Italy). J. Cult. Herit. 2014, 15, 275–282. [Google Scholar] [CrossRef]
  23. Chisari, C.; Zizi, M.; De Matteis, G. Dynamic Model Identification of the Medieval Bell Tower of Casertavecchia (Italy). Eng. Fail. Anal. 2025, 167, 109055. [Google Scholar] [CrossRef]
  24. Nastri, E.; D’Apice, A.; Todisco, P. Dynamic Validation and Assessment of a Historical Bell Tower. Procedia Struct. Integr. 2024, 64, 153–160. [Google Scholar] [CrossRef]
  25. Degli Abbati, S.; Sivori, D.; Cattari, S.; Lagomarsino, S. Ambient Vibrations-Supported Seismic Assessment of the Saint Lawrence Cathedral’s Bell Tower in Genoa, Italy. J. Civ. Struct. Heal. Monit. 2024, 14, 121–142. [Google Scholar] [CrossRef]
  26. De Angelis, A.; Lourenço, P.B.; Sica, S.; Pecce, M.R. Influence of the Ground on the Structural Identification of a Bell-Tower by Ambient Vibration Testing. Soil Dyn. Earthq. Eng. 2022, 155, 107102. [Google Scholar] [CrossRef]
  27. Shakya, M.; Varum, H.; Vicente, R.; Costa, A. Empirical Formulation for Estimating the Fundamental Frequency of Slender Masonry Structures. Int. J. Arch. Herit. 2016, 10, 951796. [Google Scholar] [CrossRef]
  28. Ranieri, C.; Fabbrocino, G. Il Periodo Elastico Delle Torri in Muratura: Correlazioni Empiriche per La Previsione. In Proceedings of the XIV Convegno ANIDIS, L’Ingegneria Sismica in Italia, Bari, Italy, 18–22 September 2011. [Google Scholar]
  29. Diaferio, M.; Foti, D.; Potenza, F. Prediction of the Fundamental Frequencies and Modal Shapes of Historic Masonry Towers by Empirical Equations Based on Experimental Data. Eng. Struct. 2018, 156, 433–442. [Google Scholar] [CrossRef]
  30. Bartoli, G.; Betti, M.; Marra, A.M.; Monchetti, S. On the Role Played by the Openings on the First Frequency of Historic Masonry Towers. In Proceedings of the Bulletin of Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2020; Volume 18. [Google Scholar]
  31. Testa, F.; Barontini, A.; Lourenço, P.B. Development and Validation of Empirical Formulations for Predicting the Frequency of Historic Masonry Towers. Int. J. Arch. Herit. 2024, 18, 1164–1184. [Google Scholar] [CrossRef]
  32. Anzani, A.; Binda, L.; Carpinteri, A.; Invernizzi, S.; Lacidogna, G. A Multilevel Approach for the Damage Assessment of Historic Masonry Towers. J. Cult. Herit. 2010, 11, 459–470. [Google Scholar] [CrossRef]
  33. Pallarés, F.J.; Betti, M.; Bartoli, G.; Pallarés, L. Structural Health Monitoring (SHM) and Nondestructive Testing (NDT) of Slender Masonry Structures: A Practical Review. Constr. Build. Mater. 2021, 297, 123768. [Google Scholar] [CrossRef]
  34. Binda, L.; Zanzi, L.; Lualdi, M.; Condoleo, P. The Use of Georadar to Assess Damage to a Masonry Bell Tower in Cremona, Italy. NDT E Int. 2005, 38, 171–179. [Google Scholar] [CrossRef]
  35. Manos, G.C.; Pitilakis, K.D.; Sextos, A.G.; Kourtides, V.; Soulis, V.; Thauampteh, J. Field Experiments for Monitoring the Dynamic Soil–Structure–Foundation Response of a Bridge-Pier Model Structure at a Test Site. J. Struct. Eng. 2015, 141. [Google Scholar] [CrossRef]
  36. Manos, G.C.; Kourtides, V.; Soulis, V.; Sextos, A.; Renault, P. Study of the Dynamic Response of a Bridge Pier Model Structure at the Volvi—Greece European Test Site. In Proceedings of the 8th US National Conference on Earthquake Engineering 2006, San Francisco, CA, USA, 18–22 April 2006; Volume 8. [Google Scholar]
  37. Manos, G.C.; Kourtides, V.; Soulis, V.J. The Dynamic and Earthquake Response of a Bridge Pier Model at the Volvi European Test Site. In Proceedings of the WIT Transactions on the Built Environment; 2005; Volume 81. Available online: https://www.witpress.com/books/978-1-84564-018-7 (accessed on 22 March 2025).
  38. Manos, G.C. Study of the Influence of Underlying Soft-Soil Layers on the Dynamic and Earthquake Response of Bell Towers. In Proceedings of the COMPDYN Proceedings, Athens, Greece, 28–30 June 2021; Volume 2021. [Google Scholar]
  39. Degli Abbati, S.; D’Altri, A.M.; Ottonelli, D.; Castellazzi, G.; Cattari, S.; de Miranda, S.; Lagomarsino, S. Seismic Assessment of Interacting Structural Units in Complex Historic Masonry Constructions by Nonlinear Static Analyses. Comput. Struct. 2019, 213, 51–71. [Google Scholar] [CrossRef]
  40. Magrinelli, E.; Acito, M.; Bocciarelli, M. Numerical Insight on the Interaction Effects of a Confined Masonry Tower. Eng. Struct. 2021, 237, 112195. [Google Scholar] [CrossRef]
  41. Erdogan, Y.S.; Kocatürk, T.; Demir, C. Investigation of the Seismic Behavior of a Historical Masonry Minaret Considering the Interaction with Surrounding Structures. J. Earthq. Eng. 2019, 23, 1309725. [Google Scholar] [CrossRef]
  42. De Angelis, A.; Maddaloni, G.; Pecce, M.R. Numerical and Operational Modal Analyses of a Masonry Bell-Tower Inserted in a Building Aggregate. In Proceedings of the COMPDYN Proceedings, Athens, Greece, 12–14 June 2023. [Google Scholar]
  43. Buzzetti, M.; Acito, M.; Chesi, C.; Serra, F. Semi-Automatic Calibration of Numerical Models for the Seismic Safety Assessment of Masonry Towers Embedded in Building Aggregates. Eng. Struct. 2024, 316, 118553. [Google Scholar] [CrossRef]
  44. Formisano, A.; Milani, G. Seismic Vulnerability Analysis and Retrofitting of the SS. Rosario Church Bell Tower in Finale Emilia (Modena, Italy). Front. Built Environ. 2019, 5, 70. [Google Scholar] [CrossRef]
  45. Casolo, S. A Three-Dimensional Model for Vulnerability Analyses of Slender Masonry Medieval Towers. J. Earthq. Eng. 1998, 2, 487–512. [Google Scholar] [CrossRef]
  46. D’Ambrisi, A.; Mariani, V.; Mezzi, M. Seismic Assessment of a Historical Masonry Tower with Nonlinear Static and Dynamic Analyses Tuned on Ambient Vibration Tests. Eng. Struct. 2012, 36, 210–219. [Google Scholar] [CrossRef]
  47. Casolo, S.; Milani, G.; Uva, G.; Alessandri, C. Comparative Seismic Vulnerability Analysis on Ten Masonry Towers in the Coastal Po Valley in Italy. Eng. Struct. 2013, 49, 465–490. [Google Scholar] [CrossRef]
  48. Ferrante, A.; Clementi, F.; Milani, G. Advanced Numerical Analyses by the Non-Smooth Contact Dynamics Method of an Ancient Masonry Bell Tower. Math. Methods Appl. Sci. 2020, 43, 7706–7725. [Google Scholar] [CrossRef]
  49. Pavlovic, M.; Baraldi, D.; De Nardi, C. Analisi Modale Del Campanile Di Santa Maria Gloriosa Dei Frari: Un Caso Studio Di Struttura Muraria Come Materiale Composito. TECNOLOGOS 2014, 24. [Google Scholar]
  50. Roca, P.; Cervera, M.; Gariup, G.; Pela’, L. Structural Analysis of Masonry Historical Constructions. Classical and Advanced Approaches. Arch. Comput. Methods Eng. 2010, 17, 299–325. [Google Scholar] [CrossRef]
  51. Puncello, I.; Caprili, S. Seismic Assessment of Historical Masonry Buildings at Different Scale Levels: A Review. Appl. Sci. 2023, 13, 1941. [Google Scholar] [CrossRef]
  52. Torelli, G.; D’Ayala, D.; Betti, M.; Bartoli, G. Analytical and Numerical Seismic Assessment of Heritage Masonry Towers. Bull. Earthq. Eng. 2020, 18, 969–1008. [Google Scholar] [CrossRef]
  53. Filangieri, G. Chiesa e Convento Del Carmine Maggiore in Napoli. Descrizione Storica Ed Artistica. In Documenti per la Storia le arti e le Industrie Delle Provincie Napoletane, Diretta da Michele De Rubertis; Tipografia del’’accademia reale delle scienze: Napoli, Italy, 1885. [Google Scholar]
  54. de Silva, F.; Ceroni, F.; Sica, S.; Pecce, M.; Silvestri, F. L’interazione Terreno-Struttura Sotto Azione Sismica: Il caso di studio del Campanile del Carmine a Napoli. In Proceedings of the XXV Convegno Nazionale di Geotecnica “La Geotecnica nella Difesa del Territorio e delle Infrastrutture dalle Calamità Naturali”, Baveno, Italy, 4–6 June 2014; pp. 109–116. [Google Scholar]
  55. Ceroni, F.; Pecce, M.R.; Silvestri, F. Analisi Sismica Del Campanile Del Carmine in Napoli. In Proceedings of the atti del 12° Convegno Nazionale ANIDIS, Ascoli Piceno, Italy, 15–19 September 2007. [Google Scholar]
  56. Voto, S. Seismic Retrofitting and Restoration of Historical Buildings Using Innovative Materials: The Case of Carmine’s Bell Tower in Naples. Ph.D. Thesis, Università degli Studi di Napoli Federico II, Napoli, Italy, 2009. [Google Scholar]
  57. Ceroni, F.; Pecce, M.; Voto, S. Historical, Architectonic and Structural Investigations of the Bell Tower of Santa Maria Del Carmine Church. J. Build. Apprais. 2007, 3, 155–179. [Google Scholar] [CrossRef]
  58. Nuzzo, M.; Faella, G. The Carmine Maggiore Bell Tower: An Inclusive and Sustainable Restoration Experience. Sustainability 2021, 13, 1445. [Google Scholar] [CrossRef]
  59. Addessi, D.; Marfia, S.; Sacco, E.; Toti, J. Modeling Approaches for Masonry Structures. Open Civ. Eng. J. 2014, 8, 288–300. [Google Scholar] [CrossRef]
  60. Betti, M.; Galano, L.; Vignoli, A. Finite Element Modelling for Seismic Assessment of Historic Masonry Buildings. In Earthquakes and Their Impact on Society; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
  61. Kujawa, M.; Lubowiecka, I.; Szymczak, C. Finite Element Modelling of a Historic Church Structure in the Context of a Masonry Damage Analysis. Eng. Fail. Anal. 2020, 107, 104233. [Google Scholar] [CrossRef]
  62. Wang, M.L.; Liu, M.; Zhu, F.S.; Li, N. Application of Finite Element Analysis in Masonry Structures. Shenyang Jianzhu Daxue Xuebao (Ziran Kexue Ban)/J. Shenyang Jianzhu Univ. (Nat. Sci.) 2006, 22. [Google Scholar]
  63. Tzamtzis, A.; Asteris, P. Finite Element Analysis of Masonry Structures: Part II—Proposed 3-D Nonlinear Microscopic Model. In Proceedings of the 9th North American masonry conference, Clemson, SC, USA, 1–4 June 2003. [Google Scholar]
  64. Tzmatzis, A.; Asteris, P. Finite Element Analysis of Masonry Structures: Part I—Review of Previous Work. In Proceedings of the 9th North American masonry conference, Clemson, SC, USA, 1–4 June 2003. [Google Scholar]
  65. Lourenço, P.B.; Milani, G.; Tralli, A.; Zucchini, A. Analysis of Masonry Structures: Review of and Recent Trends in Homogenization Techniques. Can. J. Civ. Eng. 2007, 34, 1443–1457. [Google Scholar] [CrossRef]
  66. Midas FEA. Advanced Nonlinear and Detail Program. Analysis and Algorithm. 1989. Available online: https://www.midasuser.com/en/product/gen (accessed on 10 May 2025).
  67. Pande, G.N.; Liang, J.X.; Middleton, J. Equivalent Elastic Moduli for Brick Masonry. Comput. Geotech. 1989, 8, 243–265. [Google Scholar] [CrossRef]
  68. Montuori, M. Campanile della Basilica del Corpus Domini. In Architettura e Preesistenze; Balzani, M.R., Ed.; Dalla University of Naples Federico Negra: Milan, Italy, 2017; pp. 124–127. [Google Scholar]
  69. Turnsek, V.; Sheppard, P. The shear and flexural resistance of masonry walls. In Proceedings of the International Research Conference on Earthquake Engineering, Skopje, Yugoslavia, 29 June–2 July 1980. [Google Scholar]
  70. MIT Circolare 21 Gennaio 2019, n. 7 C.S.LL.PP. Istruzioni per l’applicazione Dell’aggiornamento Delle “Norme Tecniche per Le Costruzioni” Di Cui al Decreto Ministeriale 17 Gennaio 2018. Official Bullettin n. 35. 11 February 2019. Available online: https://www.gazzettaufficiale.it/eli/id/2019/02/11/19A00855/sg (accessed on 22 March 2025).
Buildings 15 01700 g001
Figure 1. Complex of “Carmine Maggiore” in Naples: (a) overhead sight and (b) the bell tower by night.
Figure 1. Complex of “Carmine Maggiore” in Naples: (a) overhead sight and (b) the bell tower by night.
Buildings 15 01700 g001
Buildings 15 01700 g002
Figure 2. Bell tower: (a) architectural survey of west façade; (b) meshed FEM1; and (c) meshed FEM2.
Figure 2. Bell tower: (a) architectural survey of west façade; (b) meshed FEM1; and (c) meshed FEM2.
Buildings 15 01700 g002
Buildings 15 01700 g003
Figure 3. Meshed FEM1 octagonal portion: (a) upper dome-like crowing; (b) intermediate level.
Figure 3. Meshed FEM1 octagonal portion: (a) upper dome-like crowing; (b) intermediate level.
Buildings 15 01700 g003
Buildings 15 01700 g004
Figure 4. The meshed FEM1 quadrangular portion: (a) intermediate level and (b) ground level.
Figure 4. The meshed FEM1 quadrangular portion: (a) intermediate level and (b) ground level.
Buildings 15 01700 g004
Buildings 15 01700 g005
Figure 5. The modal shapes.
Figure 5. The modal shapes.
Buildings 15 01700 g005
Buildings 15 01700 g006
Figure 6. The control point height is used in non-linear static analyses.
Figure 6. The control point height is used in non-linear static analyses.
Buildings 15 01700 g006
Buildings 15 01700 g007
Figure 7. Normal stresses for seismic input in X direction: (a) FEM1 and (b) FEM2.
Figure 7. Normal stresses for seismic input in X direction: (a) FEM1 and (b) FEM2.
Buildings 15 01700 g007
Buildings 15 01700 g008
Figure 8. FEM1, the maximum principal stresses in the cladding elements.
Figure 8. FEM1, the maximum principal stresses in the cladding elements.
Buildings 15 01700 g008
Buildings 15 01700 g009
Figure 9. Capacity curves for forces applied in the X direction.
Figure 9. Capacity curves for forces applied in the X direction.
Buildings 15 01700 g009
Table 1. The material parameters of two types of masonry and cladding.
Table 1. The material parameters of two types of masonry and cladding.
fm (N/mm2)ft (N/mm2)τo (N/mm2)E (N/mm2)G (N/mm2)
Tuff masonry1.400.070.0281080360
Brick masonry2.400.120.0601500500
Claddings3.000.150.09027001000
Table 2. The elements numbers of two models.
Table 2. The elements numbers of two models.
N°NodesSolid ElementsPlate ElementsBeam Elements
M1 model108,35896,3603926229
M2 model102,08491,19534516
Table 3. Comparison of vibration periods between FEM1 and FEM2.
Table 3. Comparison of vibration periods between FEM1 and FEM2.
FEM1 [s]FEM2 [s]Difference [%]
Mode 11.5821.74610.37
Mode 21.48771.63710.83
Mode 30.4200.984134.29
Mode 40.4030.964139.21
Mode 50.3290.963192.71
Mode 60.2310.962316.45
Table 4. Safety indices IS for both models.
Table 4. Safety indices IS for both models.
FEM1FEM2Difference [%]
Demand [mm]Capacity [mm]ISDemand [mm]Capacity [mm]IS
X- failure1442801.941502341.5619.6
Y+ failure1342641.971392321.6814.7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Di Gennaro, L.; Guadagnuolo, M.; Nuzzo, M.; Faella, G. The Influence of Stone Cladding Elements on the Seismic Behaviour of a Bell Tower. Buildings 2025, 15, 1700. https://doi.org/10.3390/buildings15101700

AMA Style

Di Gennaro L, Guadagnuolo M, Nuzzo M, Faella G. The Influence of Stone Cladding Elements on the Seismic Behaviour of a Bell Tower. Buildings. 2025; 15(10):1700. https://doi.org/10.3390/buildings15101700

Chicago/Turabian Style

Di Gennaro, Luciana, Mariateresa Guadagnuolo, Mariano Nuzzo, and Giuseppe Faella. 2025. "The Influence of Stone Cladding Elements on the Seismic Behaviour of a Bell Tower" Buildings 15, no. 10: 1700. https://doi.org/10.3390/buildings15101700

APA Style

Di Gennaro, L., Guadagnuolo, M., Nuzzo, M., & Faella, G. (2025). The Influence of Stone Cladding Elements on the Seismic Behaviour of a Bell Tower. Buildings, 15(10), 1700. https://doi.org/10.3390/buildings15101700

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop