Stability of Non-Uniform Soils Slope with Tension Cracks Under Unsaturated Flow Conditions
Abstract
1. Introduction
2. Problem Description and Methodology
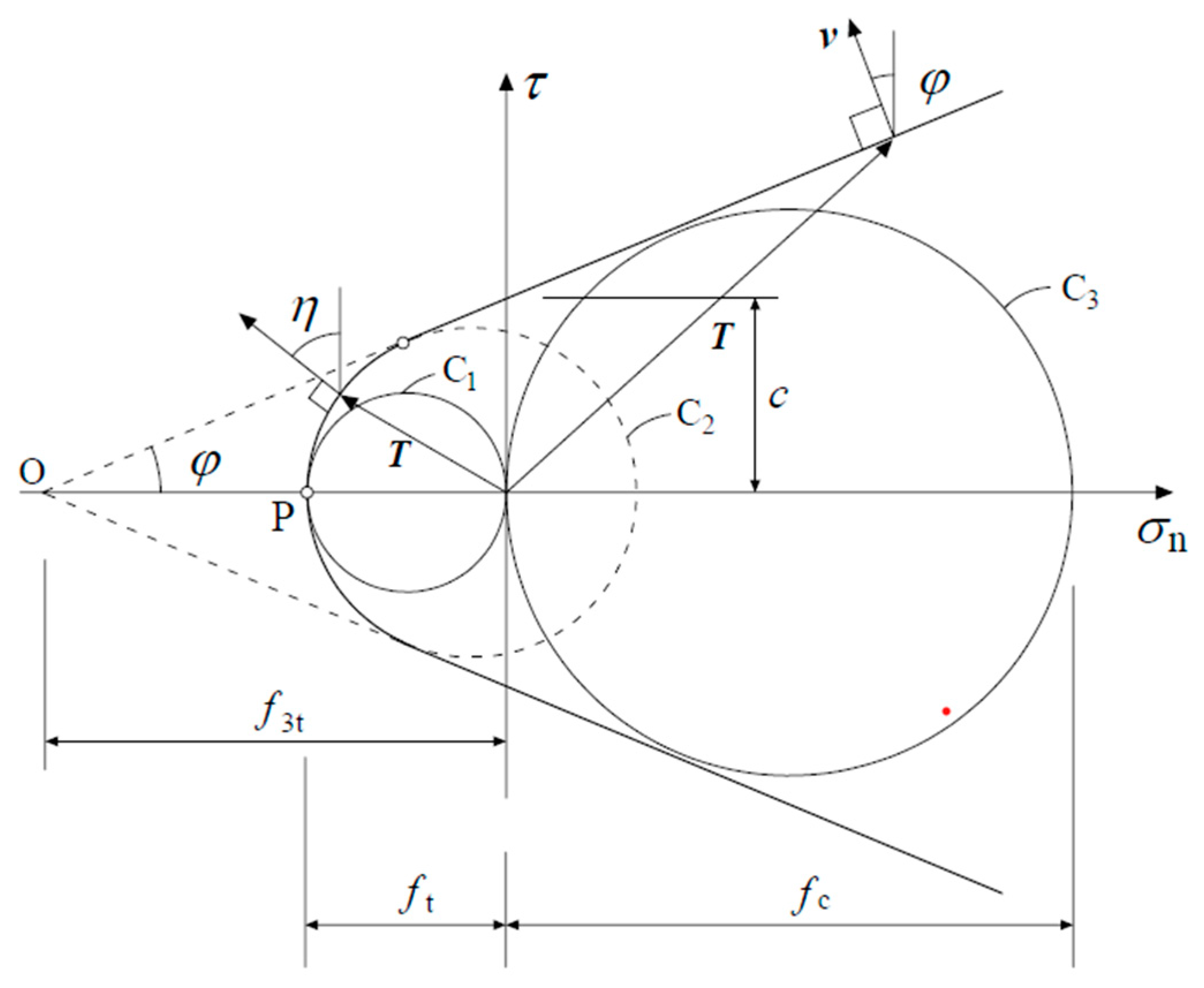
2.1. Suction Stress Distribution
2.2. Upper-Bound Theorem of Limit Analysis
3. Kinematic Analysis of Slope Stability
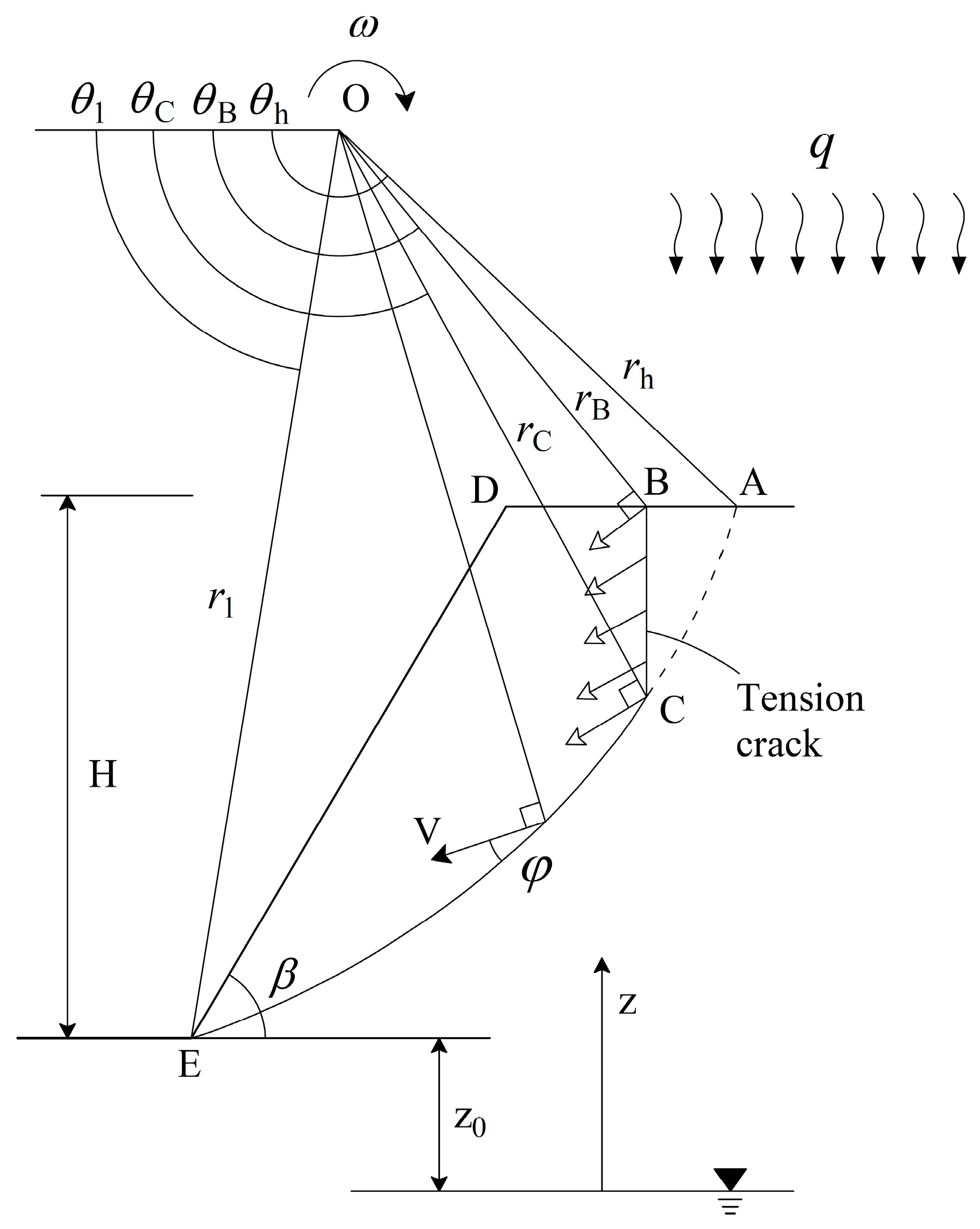
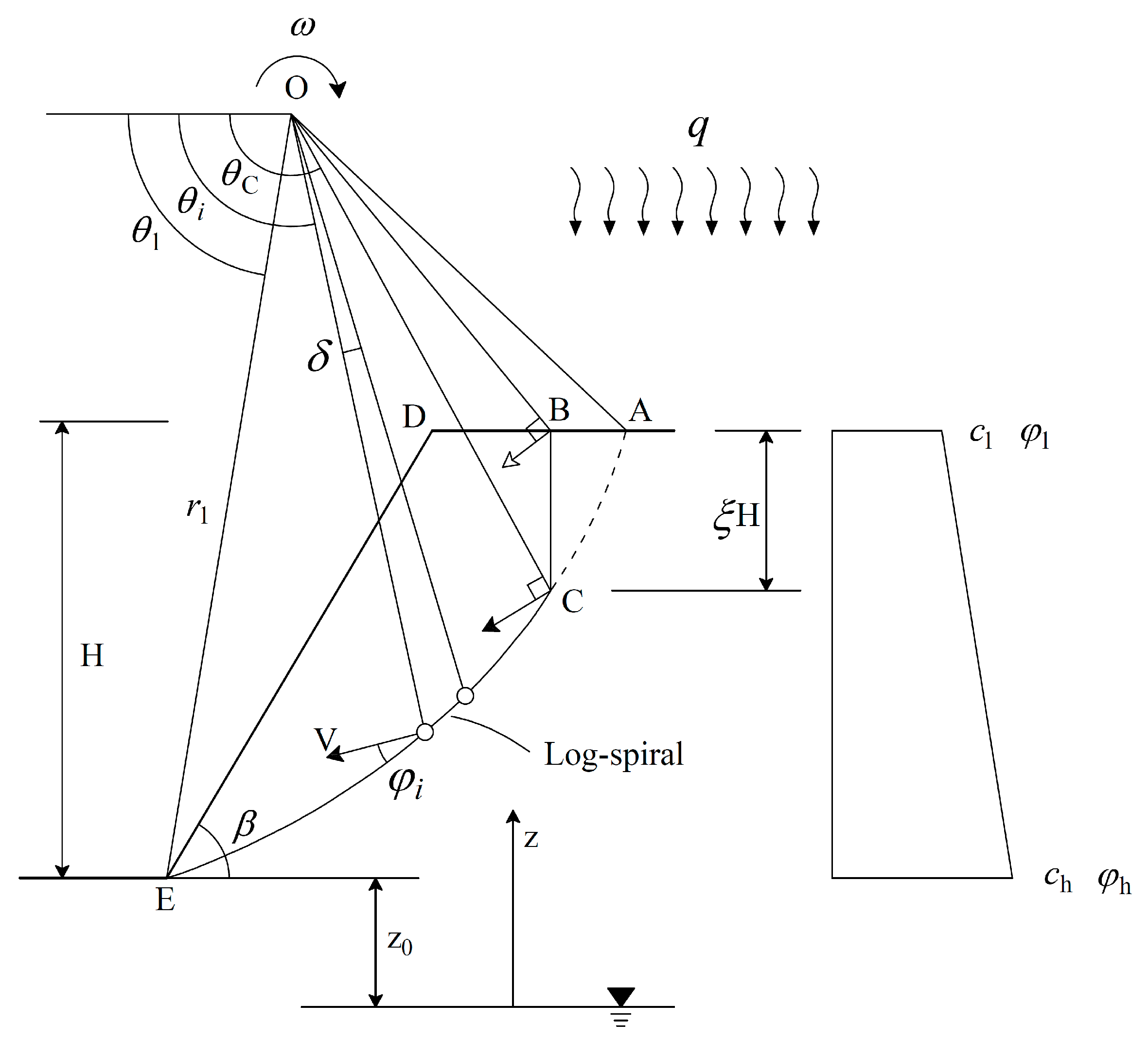
3.1. Failure Mechanism of Nonuniform Slope with Cracks
3.2. Maximum Depth of Cracks
3.3. Work–Energy Balance Equation
3.4. Factor of Safety
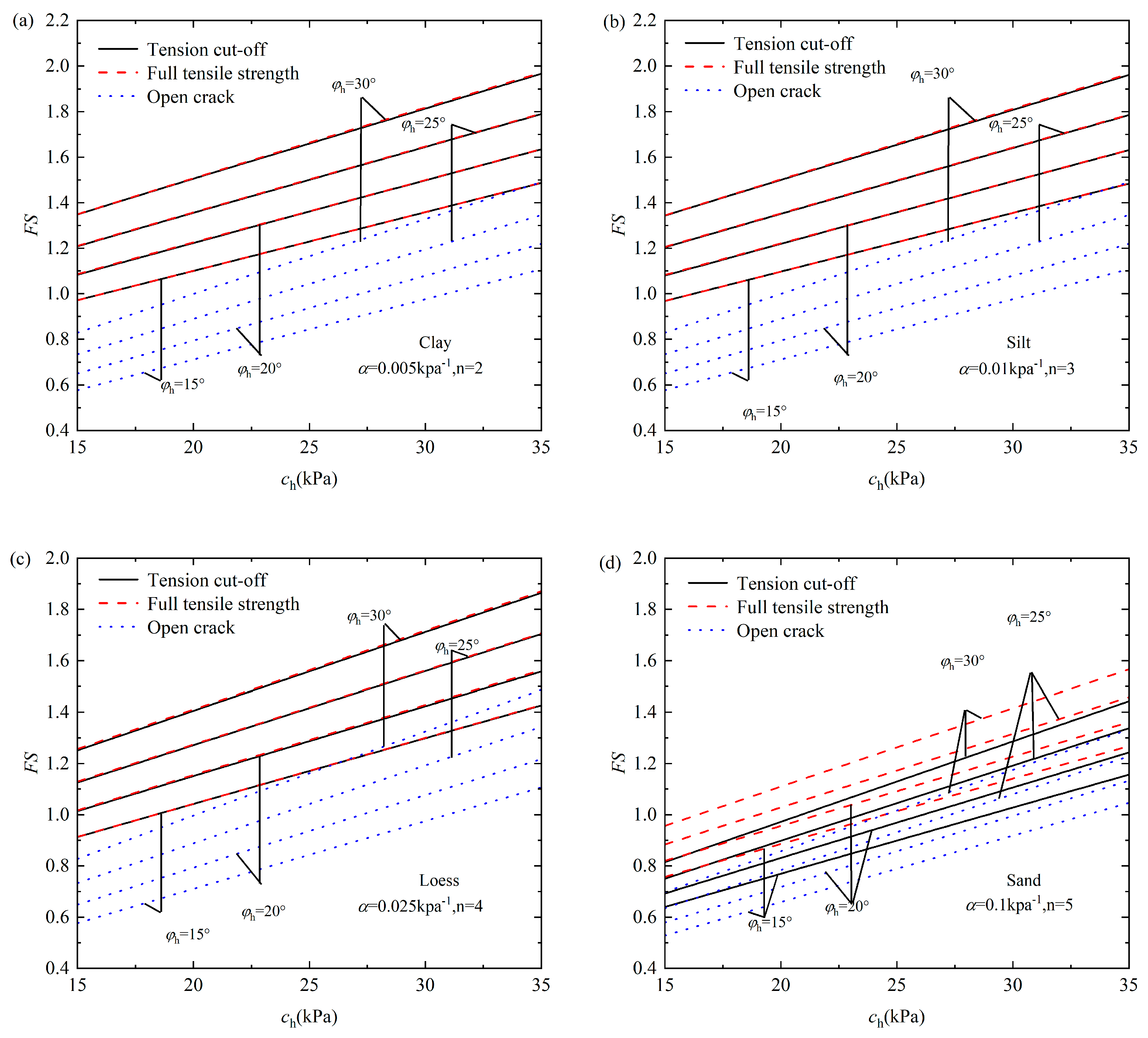
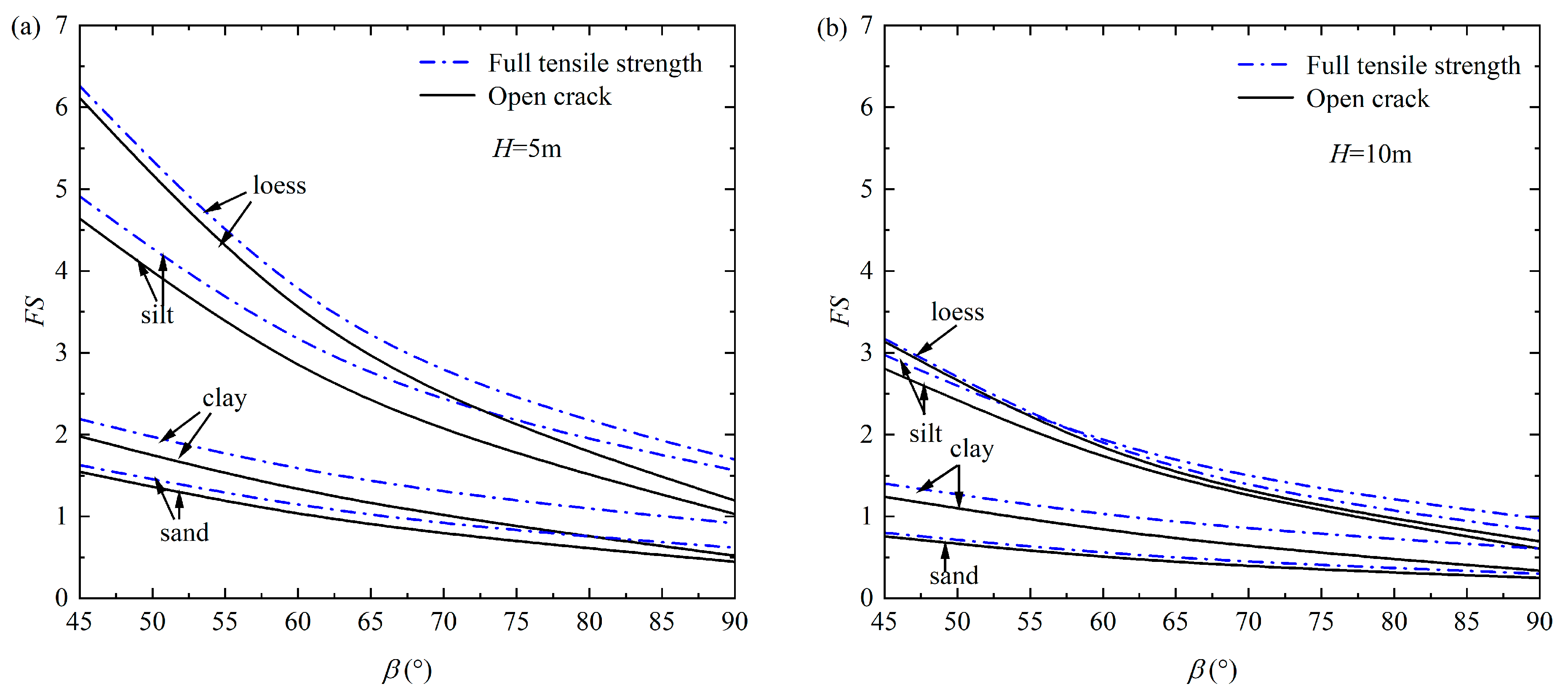
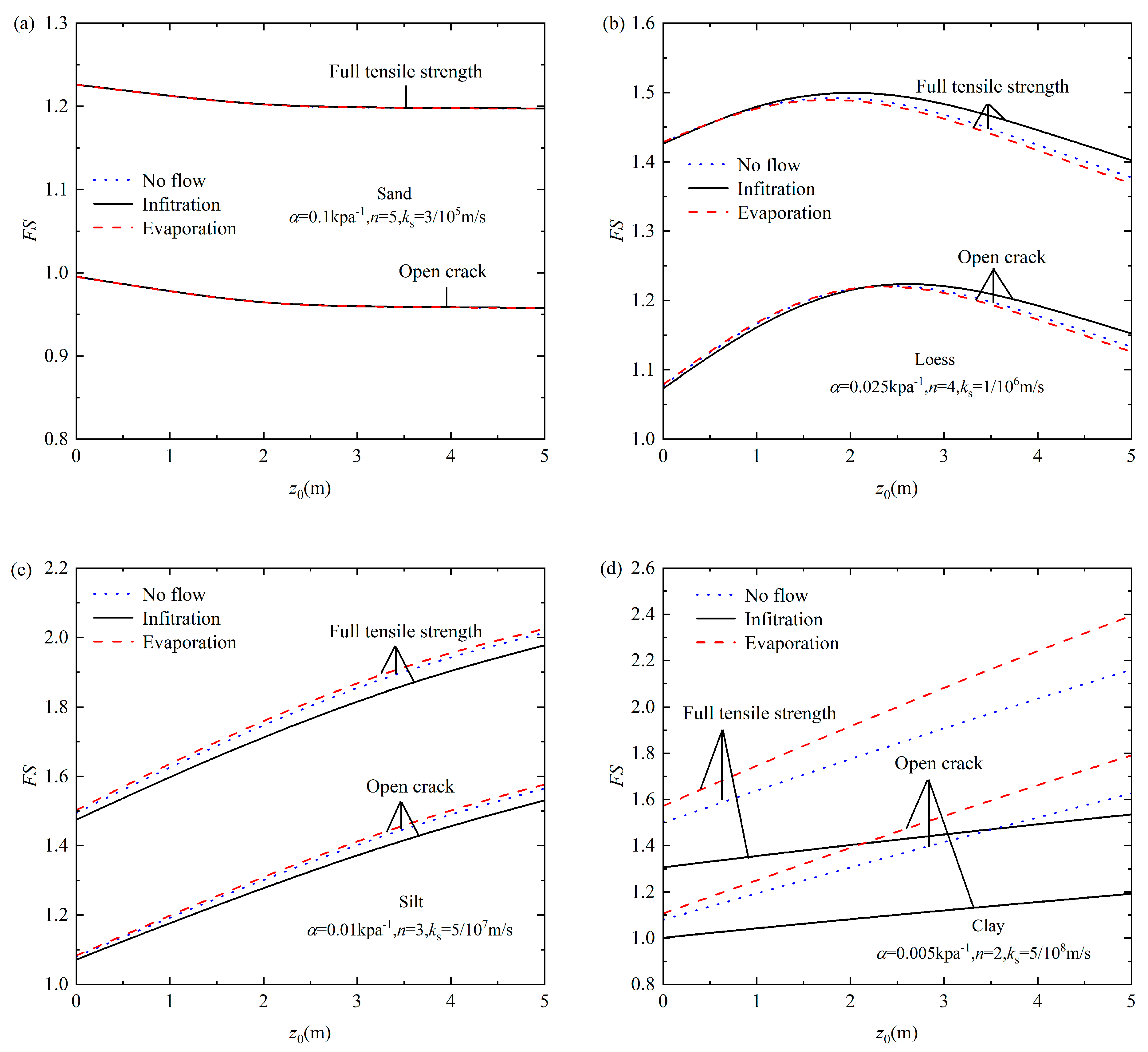
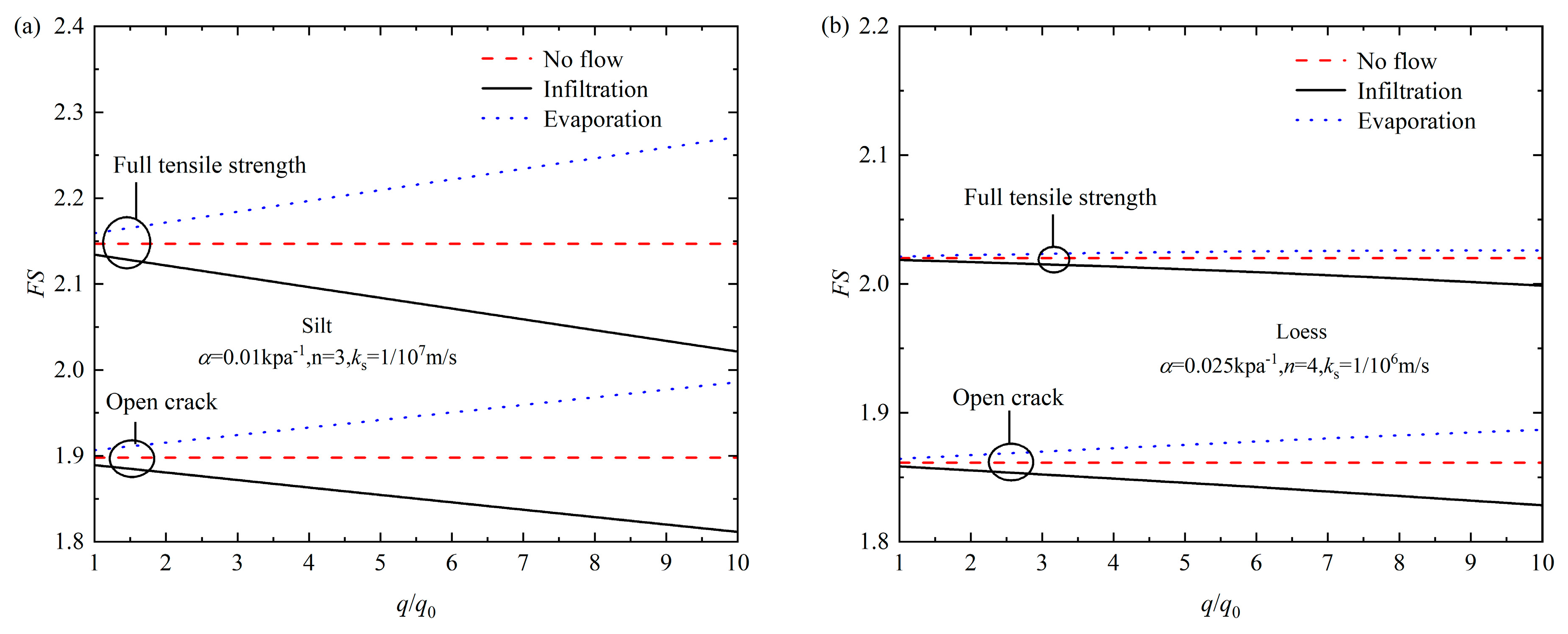
4. Parametric Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Calculation of Maximum Depth of Cracks
Appendix B. Some Equations
References
- Matsui, T.; San, K.C. Finite element slope stability analysis by shear strength reduction technique. Soils Found. 1992, 32, 59–70. [Google Scholar] [CrossRef]
- Zheng, H.; Tham, L.G.; Liu, D. On two definitions of the factor of safety commonly used in the finite element slope stability analysis. Comput. Geotech. 2006, 33, 188–195. [Google Scholar] [CrossRef]
- Alkasawneh, W.; Malkawi, A.I.H.; Nusairat, J.H. A comparative study of various commercially available programs in slope stability analysis. Comput. Geotech. 2008, 35, 428–435. [Google Scholar] [CrossRef]
- Yang, X.L.; Li, L.; Yin, J.H. Seismic and static stability analysis for rock slopes by a kinematical approach. Geotechnique 2004, 54, 543–549. [Google Scholar] [CrossRef]
- Yang, X.L.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek-Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Sloan, S.W. Geotechnical stability analysis. Géotechnique 2003, 63, 531–571. [Google Scholar] [CrossRef]
- Yang, X.L.; Du, D.C. Upper bound analysis for bearing capacity of nonhomogeneous and anisotropic clay foundation. KSCE J. Civ. Eng. 2016, 20, 2702–2710. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. Upper-bound analysis on the face stability of a non-circular tunnel. Tunn. Undergr. Space Technol. 2017, 62, 96–102. [Google Scholar] [CrossRef]
- Sorbino, G.; Nicotera, M.V. Unsaturated soil mechanics in rainfall-induced flow landslides. Eng. Geol. 2013, 165, 105–132. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Morgenstern, N.R.; Widger, R.A. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A.; Fredlund, M.D.; Barbour, S.L. The relationship of the unsaturated soil shear to the soil-water characteristic curve. Can. Geotech. J. 1996, 33, 440–448. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L. Three-dimensional active earth pressure for retaining structures in soils subjected to steady unsaturated seepage effects. Acta Geotech. 2020, 15, 2017–2029. [Google Scholar] [CrossRef]
- Vo, T.; Russell, A.R. Slip line theory applied to a retaining wall–unsaturated soil interaction problem. Comput. Geotech. 2014, 55, 416–428. [Google Scholar] [CrossRef]
- Vahedifard, F.; Leshchinsky, B.A.; Mortezaei, K. Active earth pressures for unsaturated retaining structures. J. Geotech. Geoenviron. 2015, 141, 04015048. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L.; Li, T.Z. Face stability analysis of tunnels under steady unsaturated seepage conditions. Tunn. Undergr. Space Technol. 2017, 93, 103095. [Google Scholar] [CrossRef]
- Li, T.Z.; Dias, D.; Li, Z.W. Failure potential of a circular tunnel face under steady-state unsaturated flow condition. Comput. Geotech. 2020, 117, 103231. [Google Scholar] [CrossRef]
- Wu, H.; Liao, H.; Wu, C. Stability of 3D tunnel face under steady unsaturated seepage coupled multi-layer soil suction head distributions. Alex. Eng. J. 2025, 117, 609–623. [Google Scholar] [CrossRef]
- Zhang, G.R.; Qian, Y.J.; Wang, Z.C.; Zhao, B. Analysis of rainfall infiltration law in unsaturated soil slope. Sci. World J. 2014, 2014, 567250. [Google Scholar] [CrossRef]
- Huang, W.; Leong, E.C.; Rahardjo, H. Upper-bound limit analysis of unsaturated soil slopes under rainfall. J. Geotech. Geoenviron. 2018, 144, 04018066. [Google Scholar] [CrossRef]
- Tang, G.; Huang, J.; Sheng, D.; Sloan, S.W. Stability analysis of unsaturated soil slopes under random rainfall patterns. Eng. Geol. 2018, 245, 322–332. [Google Scholar] [CrossRef]
- Meyerhof, G.G. The ultimate bearing capacity of foundations on slopes. Int. Conf. Soil Mech. Found. Eng. 1957, 1, 384–386. [Google Scholar]
- Utili, S. Investigation by limit analysis on the stability of slopes with cracks. Geotechnique 2013, 63, 140–154. [Google Scholar] [CrossRef]
- Michalowski, R.L. Stability assessment of slopes with cracks using limit analysis. Can. Geotech. J. 2013, 50, 1011–1021. [Google Scholar] [CrossRef]
- Li, Y.X.; Yang, X.L. Stability analysis of crack slope considering nonlinearity and water pressure. KSCE J. Civ. Eng. 2016, 20, 2289–2296. [Google Scholar] [CrossRef]
- Yang, X.L.; Zhang, S. Stability analysis of 3D cracked slope reinforced with piles. Comput. Geotech. 2020, 122, 103544. [Google Scholar] [CrossRef]
- Rao, P.; Wu, J.; Chen, Q.; Nimbalkar, S. Three-dimensional assessment of cracked slopes with pore water pressure using limit analysis. Environ. Earth Sci. 2021, 80, 645. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L. Active earth pressure for soils with tension cracks under steady unsaturated flow conditions. Can. Geotech. J. 2018, 55, 1850–1859. [Google Scholar] [CrossRef]
- Li, T.Z.; Yang, X.L. Three-dimensional face stability of shallow-buried tunnels with tensile strength cut-off. Comput. Geotech. 2019, 110, 82–93. [Google Scholar] [CrossRef]
- Li, T.Z.; Yang, X.L. Stability of plane strain tunnel headings in soils with tensile strength cut-off. Tunn. Undergr. Space Technol. 2020, 95, 103138. [Google Scholar] [CrossRef]
- Hou, C.T.; Yang, X.L. Seismic stability of 3D tunnel face considering tensile strength cut-off. KSCE J. Civ. Eng. 2020, 24, 2232–2243. [Google Scholar] [CrossRef]
- Qin, C.; Chian, S.C. Bearing capacity analysis of a saturated non-uniform soil slope with discretization-based kinematic analysis. Comput. Geotech. 2018, 96, 246–257. [Google Scholar] [CrossRef]
- Sun, Z.; Shu, X.; Dias, D. Stability analysis for nonhomogeneous slopes subjected to water drawdown. J. Cent. South Univ. 2019, 26, 1719–1734. [Google Scholar] [CrossRef]
- Guardiani, C.; Enrico, S.; Wu, W. Time-dependent reliability analysis of unsaturated slopes under rapid drawdown with intelligent surrogate models. Acta Geotech. 2022, 17, 1071–1096. [Google Scholar] [CrossRef]
- Waris, K.A.; Basha, B.M.; Alluri, H.R.; Munwar, B. Pseudo-static slope stability analysis using explainable machine learning techniques. Nat. Hazards. 2025, 121, 485–517. [Google Scholar] [CrossRef]
- Waris, K.A.; Basha, B.M. Detection and prediction of slope stability in unsaturated finite slopes using interpretable machine learning. Model. Earth Syst. Environ. 2025, 11, 273. [Google Scholar] [CrossRef]
- Asgari, A.; Bagheripour, M.H.; Mollazadeh, M. A generalized analytical solution for a nonlinear infiltration equation using the exp-function method. Sci. Iran. 2011, 18, 28–35. [Google Scholar] [CrossRef]
- Lu, N.; Likos, W.J. Suction stress characteristic curve for unsaturated soil. J. Geotech. Geoenviron. 2006, 132, 131–142. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46, 567–573. [Google Scholar] [CrossRef]
- Vahedifard, F.; Leshchinsky, D.; Mortezaei, K.; Lu, N. Effective stress-based limit equilibrium analysis for homogeneous unsaturated slopes. Int. J. Geomech. 2016, 16, D4016003. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lu, N. Unsaturated slope stability analysis with steady infiltration or evaporation using elasto-plastic finite elements. Int. J. Numer. Anal. Methods 2005, 29, 249–267. [Google Scholar] [CrossRef]
- Chen, W.F. Limit Analysis and Soil Plasticity; Elsevier: Amsterdam, The Netherlands, 1957. [Google Scholar]
- Donald, I.B.; Chen, Z. Slope stability analysis by the upper bound approach: Fundamentals and methods. Can. Geotech. J. 1997, 34, 853–862. [Google Scholar] [CrossRef]
- Yang, X.L. Upper bound limit analysis of active earth pressure with different fracture surface and nonlinear yield criterion. Theor. Appl. Fract. Mech. 2007, 47, 46–56. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. The effect of pore water pressure on tunnel face stability. Int. J. Numer. Anal. Methods 2016, 40, 2123–2136. [Google Scholar] [CrossRef]
- Abd, A.; Utili, S. Design of geosynthetic-reinforced slopes in cohesive backfills. Geotext. Geomembr. 2017, 45, 627–641. [Google Scholar] [CrossRef]

| Soil Type | α (kPa−1) | n | ks (m/s) | c/γD | φ(°) |
|---|---|---|---|---|---|
| Sand | 0.1 | 5 | 3 × 10−5 | 0 | 30 |
| Loess | 0.025 | 4 | 1 × 10−6 | 0.001 | 28 |
| Silt | 0.01 | 3 | 5 × 10−7 | 0.03 | 25 |
| Clay | 0.005 | 2 | 5 × 10−8 | 0.05 | 30 |
| Flow State | q (mm/day) | q (m/s) |
|---|---|---|
| High infiltration | −2.73 | −3.14 × 10−8 |
| No flow | 0 | 0 |
| High evaporation | 1.00 | 1.15 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Dong, J.; Zhao, Y.; Wang, Y.; Cheng, Y. Stability of Non-Uniform Soils Slope with Tension Cracks Under Unsaturated Flow Conditions. Buildings 2025, 15, 2123. https://doi.org/10.3390/buildings15122123
Zhang J, Dong J, Zhao Y, Wang Y, Cheng Y. Stability of Non-Uniform Soils Slope with Tension Cracks Under Unsaturated Flow Conditions. Buildings. 2025; 15(12):2123. https://doi.org/10.3390/buildings15122123
Chicago/Turabian StyleZhang, Jing, Jinyu Dong, Ying Zhao, Yukai Wang, and Yang Cheng. 2025. "Stability of Non-Uniform Soils Slope with Tension Cracks Under Unsaturated Flow Conditions" Buildings 15, no. 12: 2123. https://doi.org/10.3390/buildings15122123
APA StyleZhang, J., Dong, J., Zhao, Y., Wang, Y., & Cheng, Y. (2025). Stability of Non-Uniform Soils Slope with Tension Cracks Under Unsaturated Flow Conditions. Buildings, 15(12), 2123. https://doi.org/10.3390/buildings15122123





