Analytical Investigation of Dynamic Response in Cracked Structure Subjected to Moving Load
Abstract
1. Introduction
2. Theoretical Model
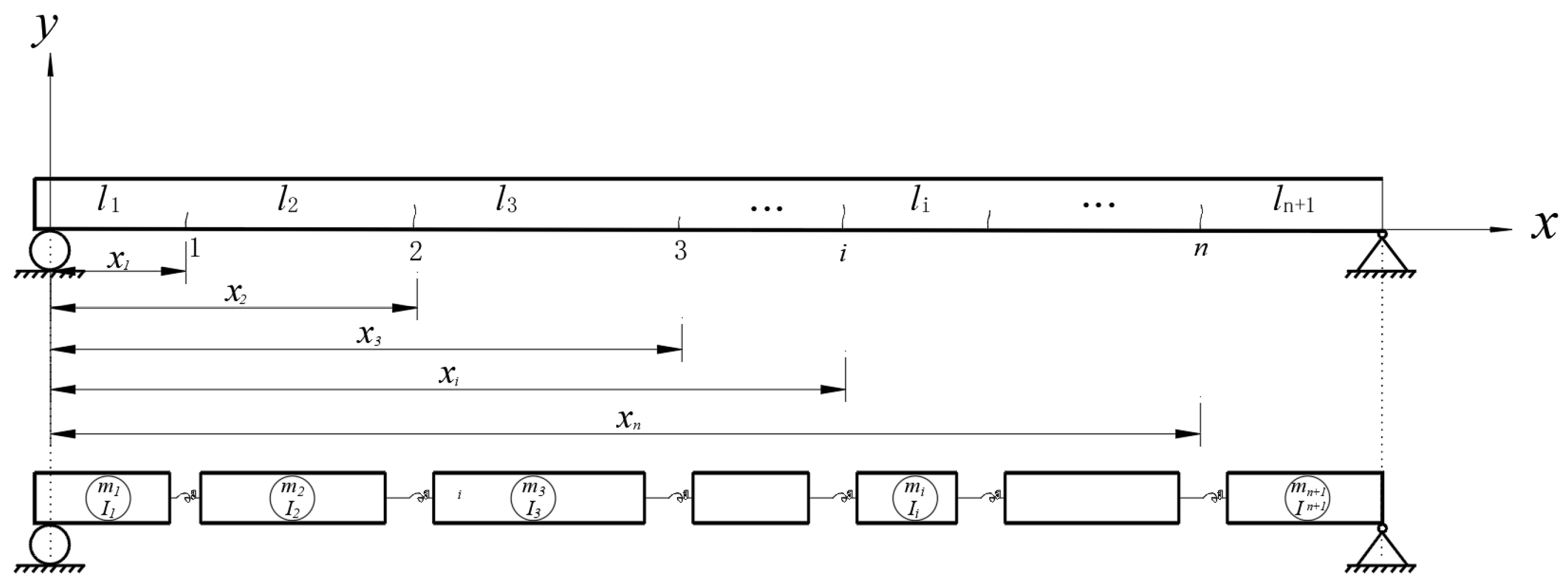
2.1. Mode Shape Function of a Damaged Beam with Cracks
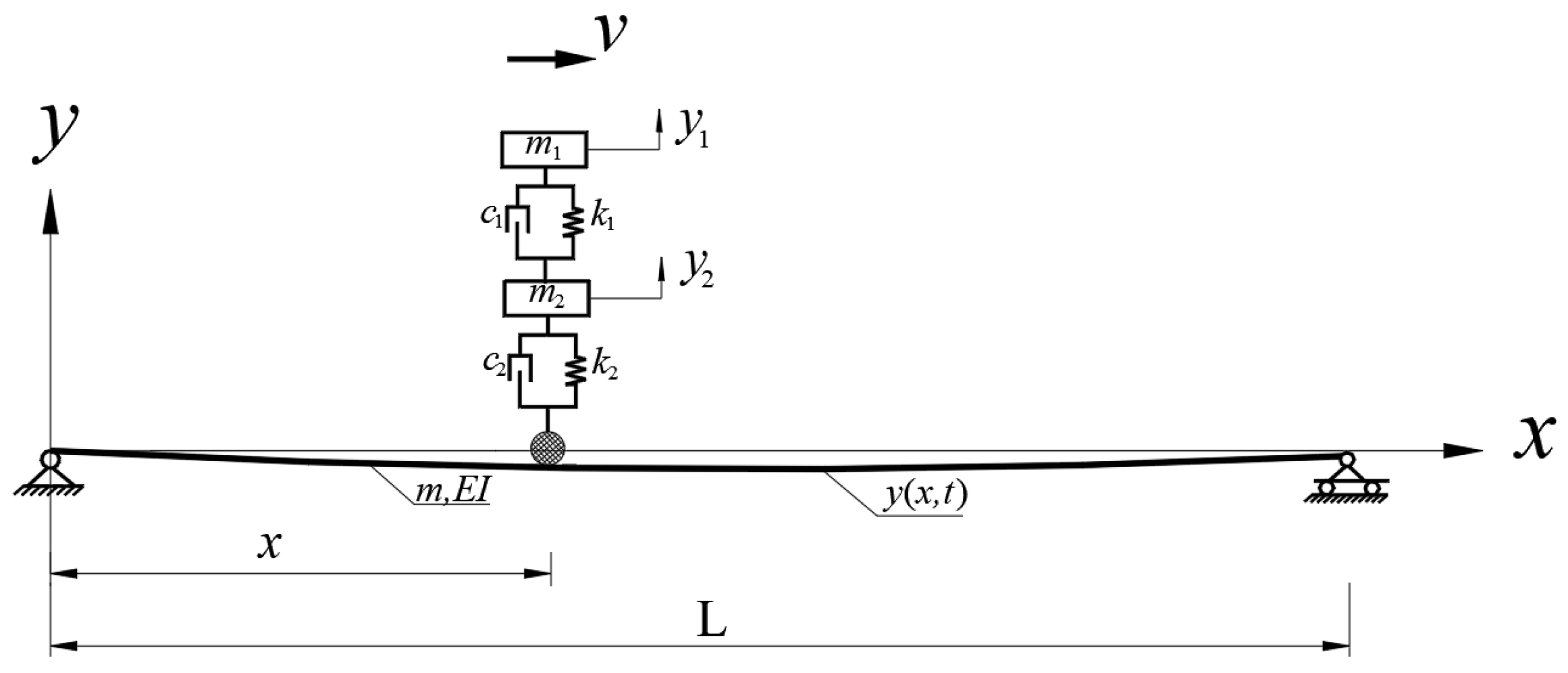
2.2. Analytical Model of Vehicle—Cracked Beam Bridge Coupled System
2.3. Algorithm for Coupled Analysis of Cracked Beam Bridge–Vehicle Interaction
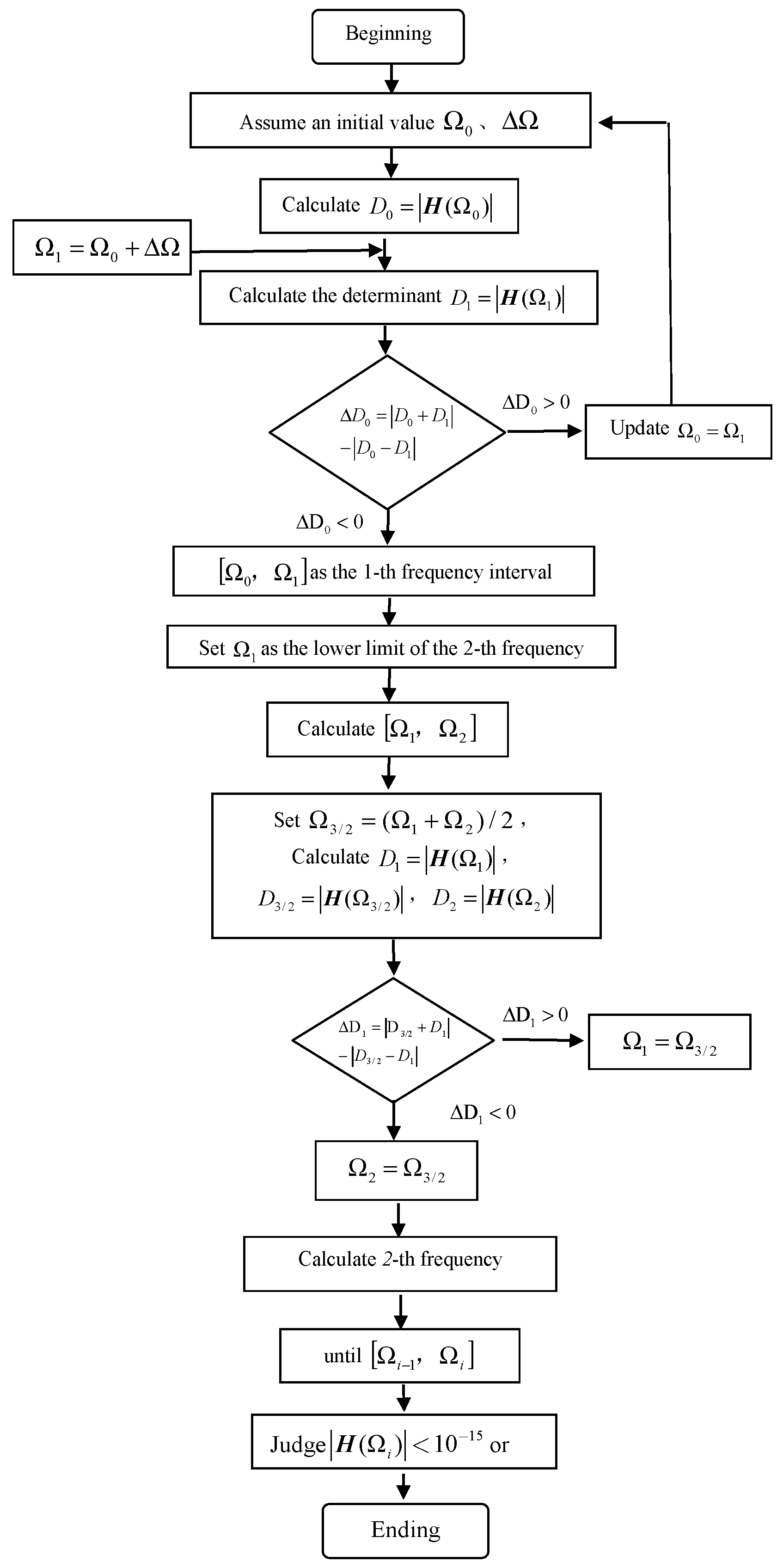
2.3.1. Semi-Interval Iterative Method for Analyzing Dynamic Characteristics of Cracked Beam Bridges
2.3.2. Algorithm Analytical for the Coupled System of Vehicle–Cracked Beam Bridge
3. Numerical Simulation and Discussions
3.1. Numerical Validation for Cracked Beam Subjected to Moving Load
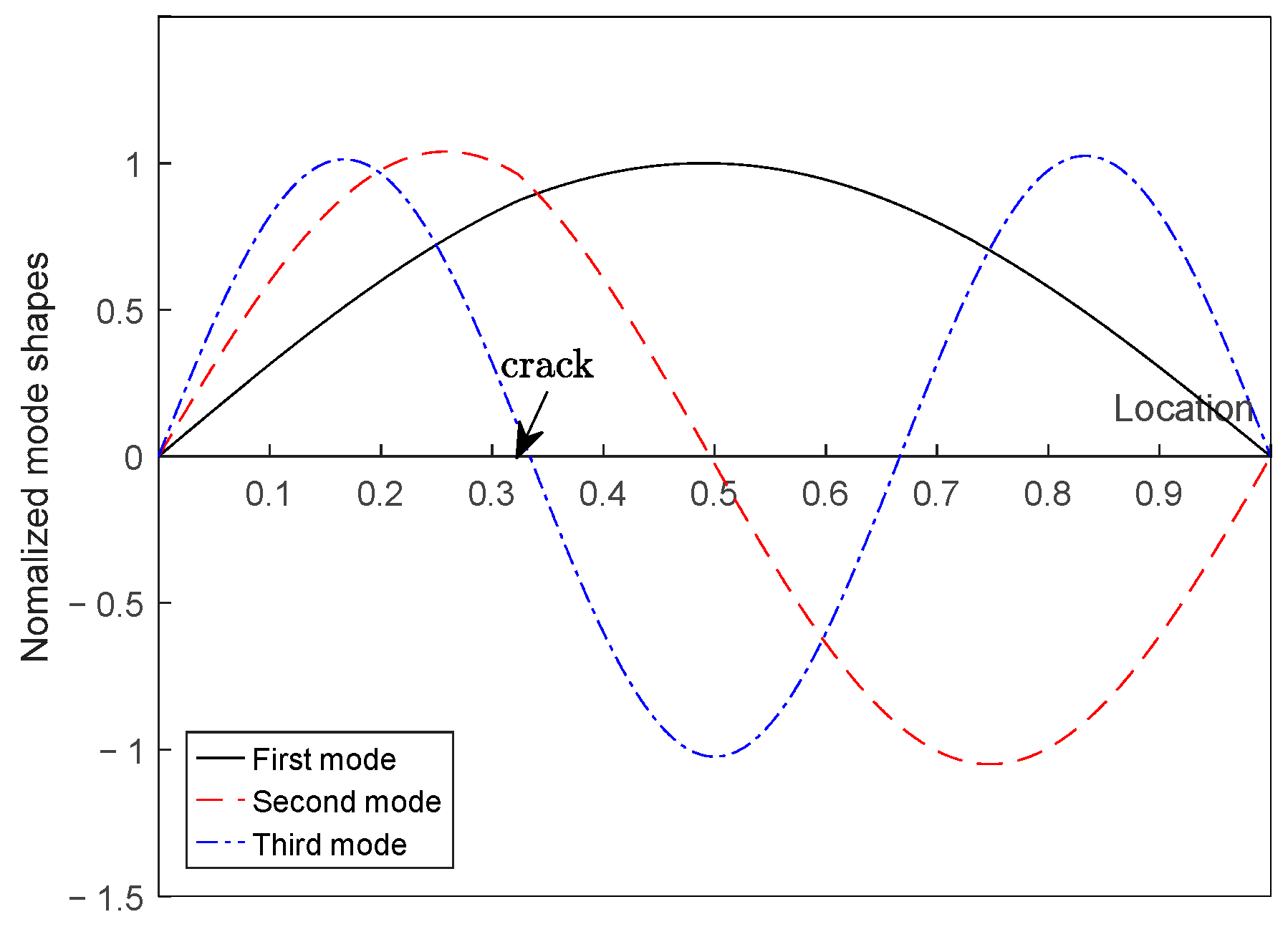
3.1.1. Cracked Beam Eigenfrequency Validation
3.1.2. Verification of Vehicle–Cracked Beam Coupling
3.2. Analysis of Time History Curve
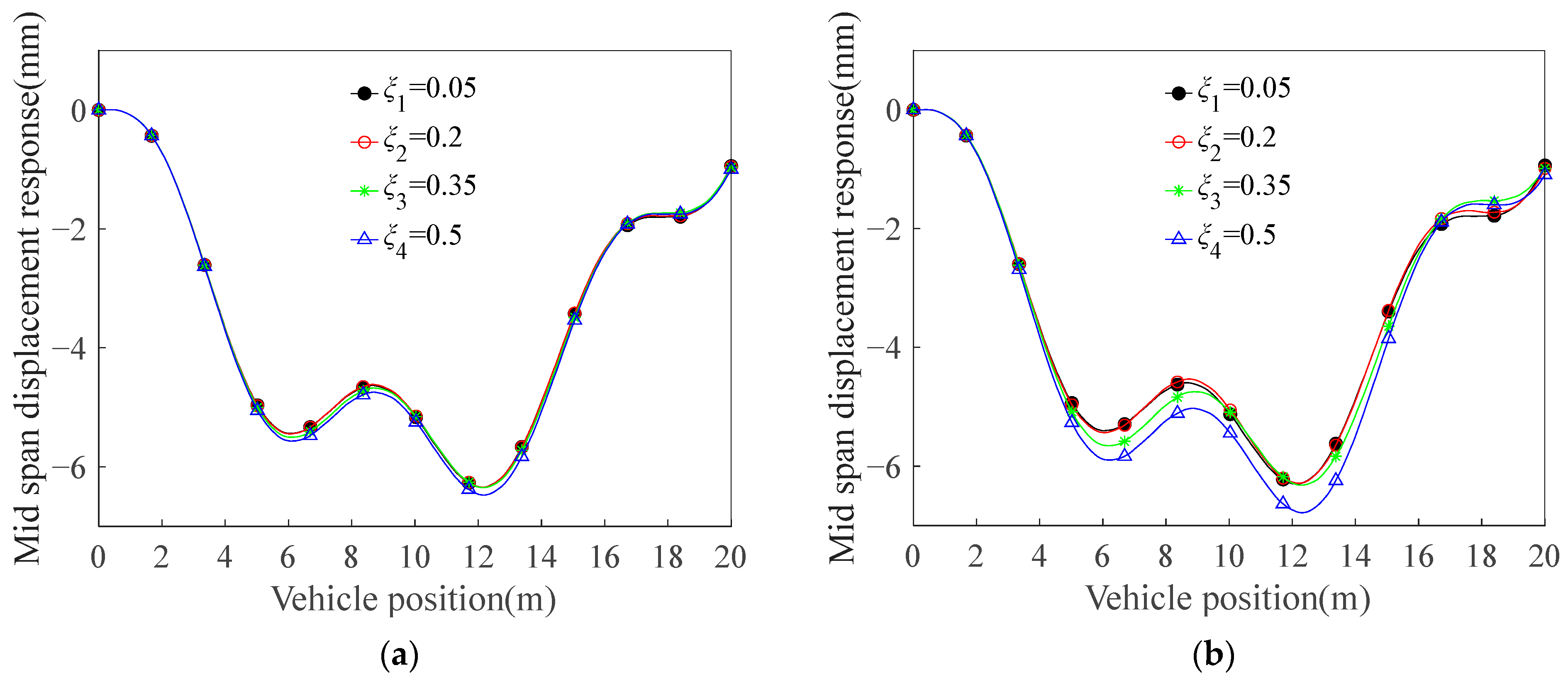
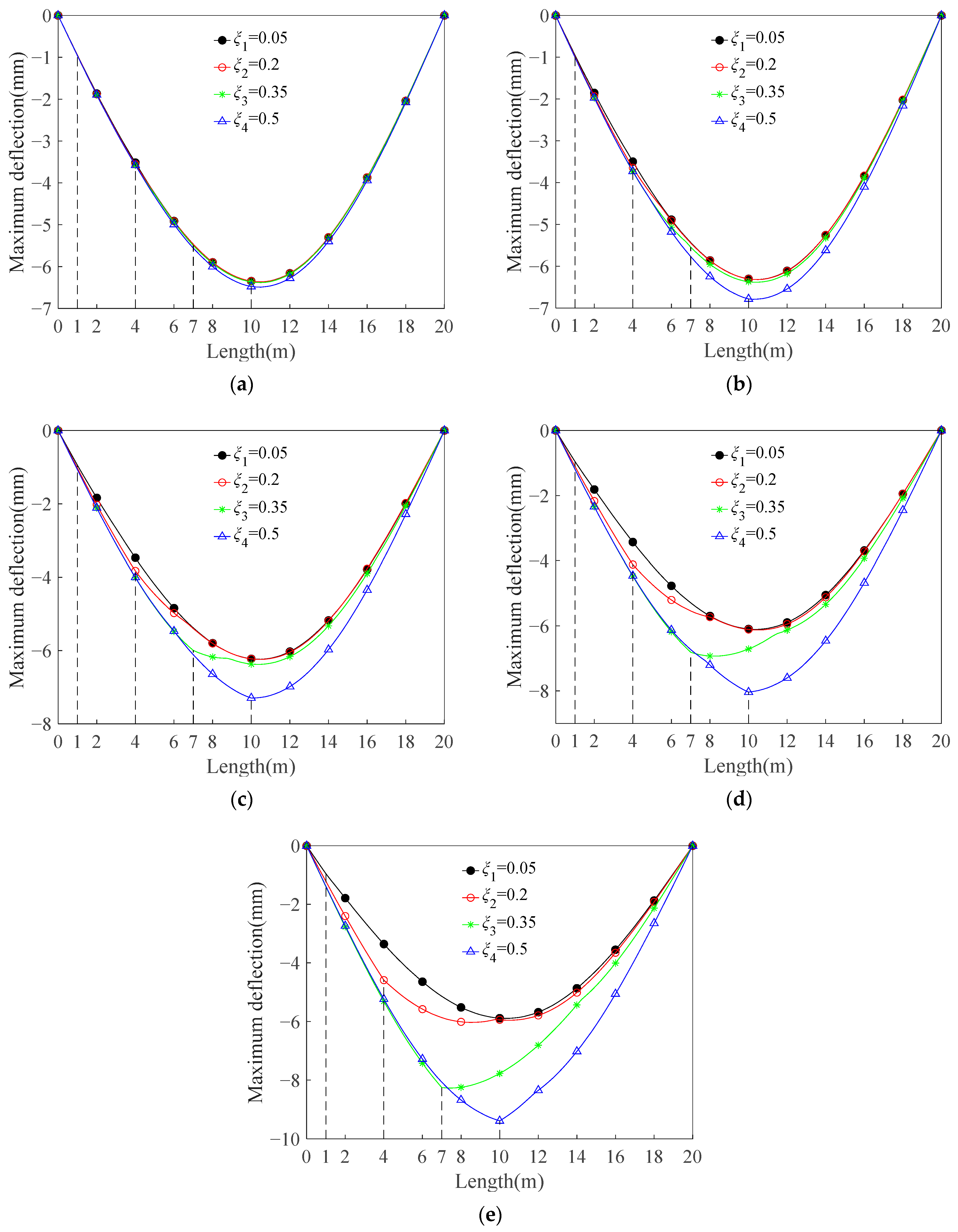
3.2.1. Influence of the Crack Depth
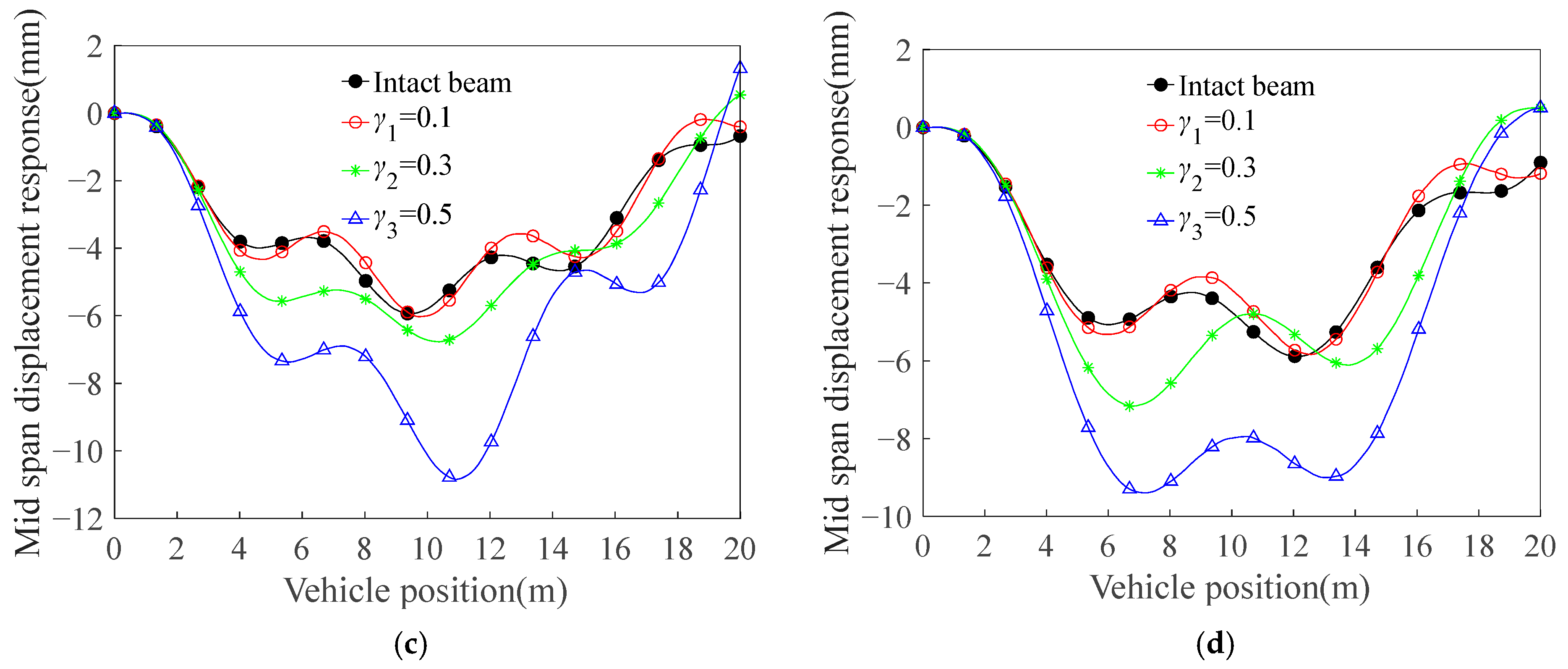
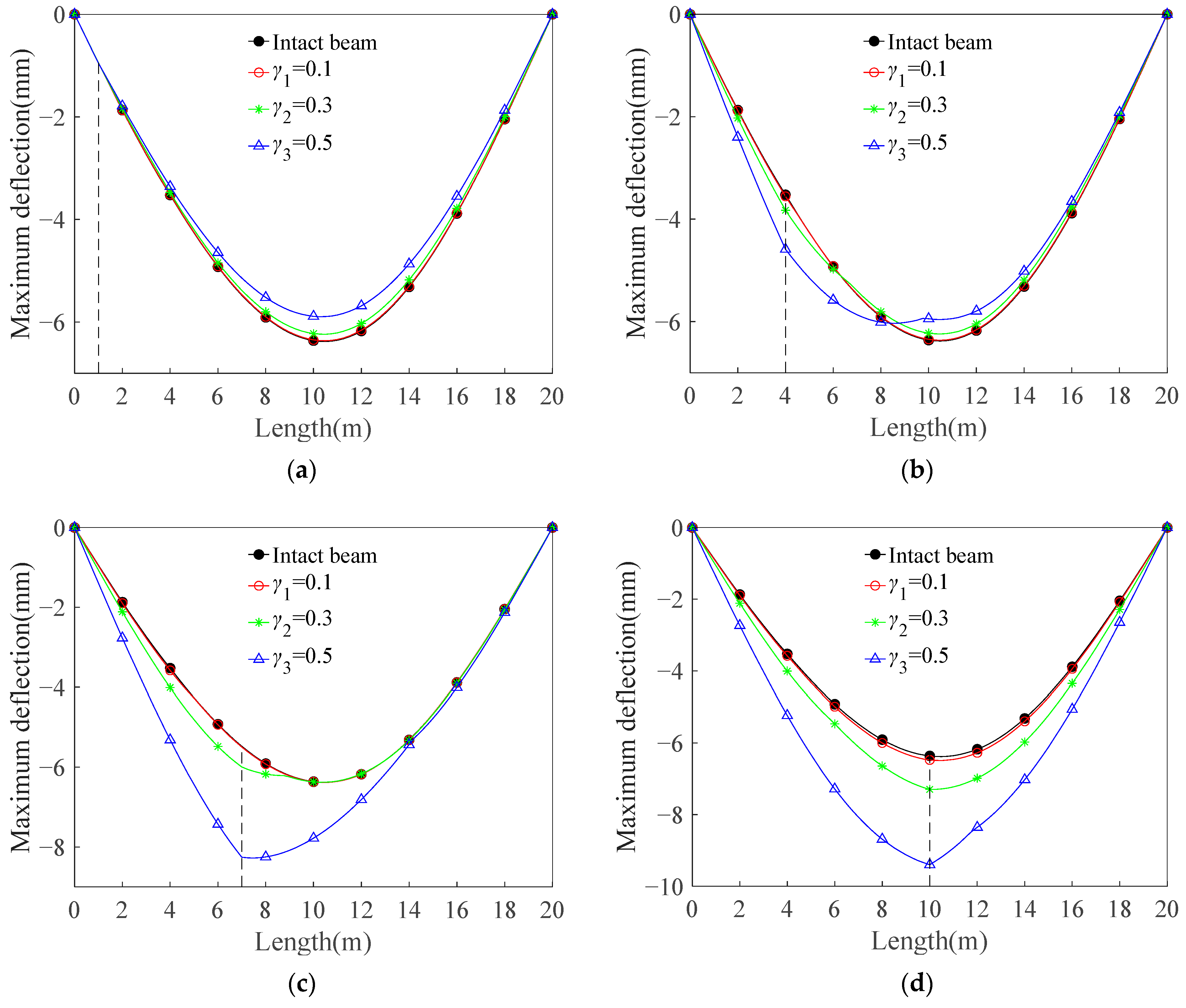
3.2.2. Influence of the Crack Location
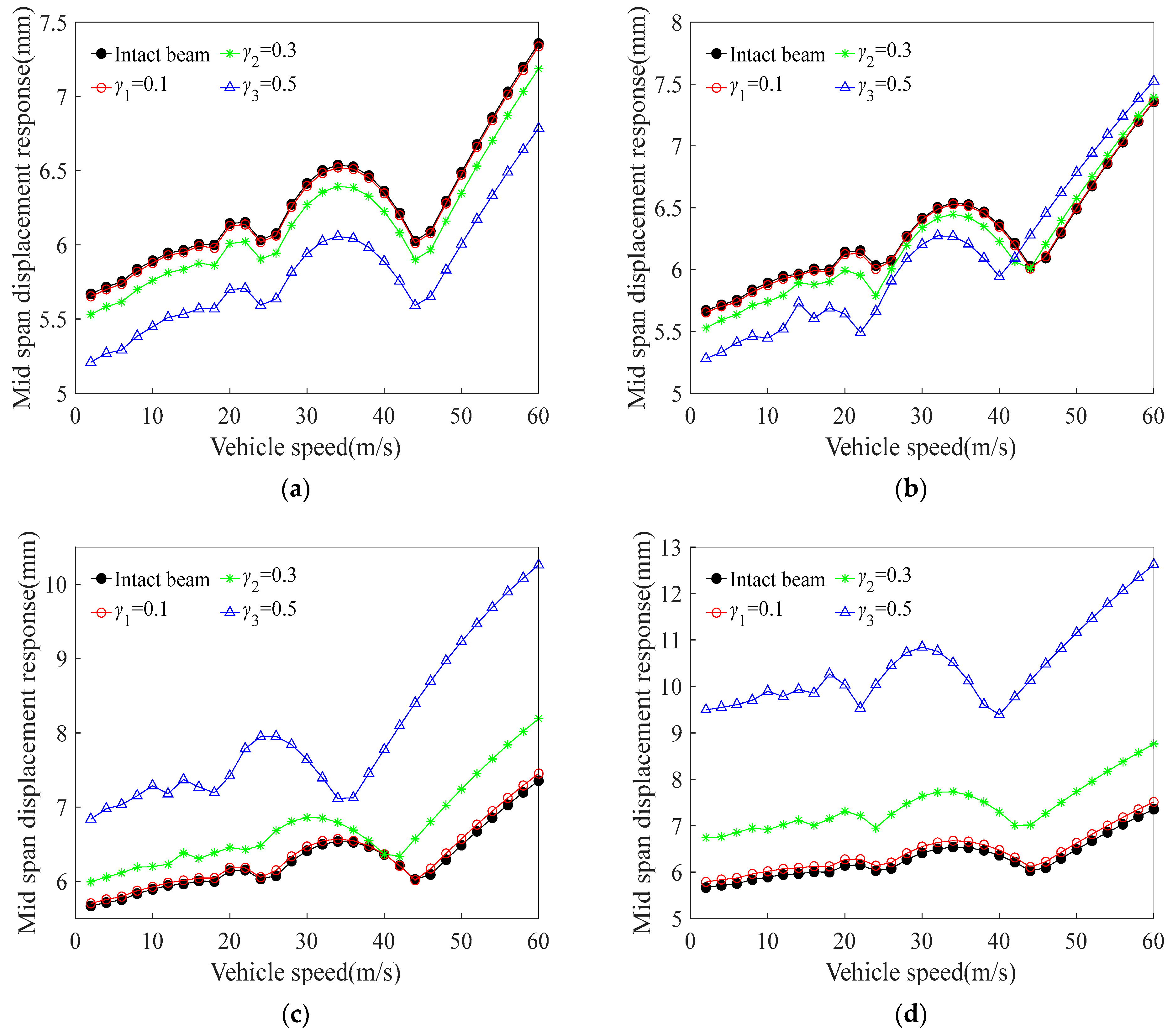
3.3. Maximum Deflection Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Y.; Zhao, Y.; Yao, H.; Jing, Y. Full-Scale Experimental Investigation of the Static and Dynamic Stiffness of Prestressed Concrete Girders. Shock Vib. 2019, 2019, 7646094. [Google Scholar] [CrossRef]
- Zheng, K.; Zhou, S.; Zhang, Y.; Wei, Y.; Wang, J.; Wang, Y.; Qin, X. Simplified evaluation of shear stiffness degradation of diagonally cracked reinforced concrete beams. Materials 2023, 16, 4752. [Google Scholar] [CrossRef] [PubMed]
- Tan, G.; Shan, J.; Wu, C.; Wang, W. Free vibration analysis of cracked Timoshenko beams carrying spring-mass systems. Struct. Eng. Mech. A Int. J. 2017, 63, 551–565. [Google Scholar]
- Yang, J.; Chen, Y.; Xiang, Y.; Jia, X.L. Free and forced vibration of cracked inhomogeneous beams under an axial force and a moving load. J. Sound Vib. 2008, 312, 166–181. [Google Scholar] [CrossRef]
- Lin, H.-P.; Chang, S.-C. Forced responses of cracked cantilever beams subjected to a concentrated moving load. Int. J. Mech. Sci. 2006, 48, 1456–1463. [Google Scholar] [CrossRef]
- Zheng, T.; Ji, T. An approximate method for determining the static deflection and natural frequency of a cracked beam. J. Sound Vib. 2012, 331, 2654–2670. [Google Scholar] [CrossRef]
- Dimarogonas, A.D. Vibration of cracked structures: A state of the art review. Eng. Fract. Mech. 1996, 55, 831–857. [Google Scholar] [CrossRef]
- Zhong, S.; Oyadiji, S.O. Analytical predictions of natural frequencies of cracked simply supported beams with a stationary roving mass. J. Sound Vib. 2008, 311, 328–352. [Google Scholar] [CrossRef]
- Aydin, K. Free vibration of functionally graded beams with arbitrary number of surface cracks. Eur. J. Mech. A-Solid. 2013, 42, 112–124. [Google Scholar] [CrossRef]
- Li, Q.S. Free vibration analysis of non-uniform beams with an arbitrary number of cracks and concentrated masses. J. Sound Vib. 2002, 252, 509–525. [Google Scholar] [CrossRef]
- Chondros, T.G.; Dimarogonas, A.D.; Yao, J. A continuous cracked beam vibration theory. J. Sound Vib. 1998, 215, 17–34. [Google Scholar] [CrossRef]
- Lin, H.P.; Chang, S.C.; Wu, J.D. Beam vibrations with an arbitrary number of cracks. J. Sound Vib. 2002, 258, 987–999. [Google Scholar] [CrossRef]
- Bakhtiari-Nejad, F.; Khorram, A.; Rezaeian, M. Analytical estimation of natural frequencies and mode shapes of a beam having two cracks. Int. J. Mech. Sci. 2014, 78, 193–202. [Google Scholar] [CrossRef]
- Lin, H.P. Direct and inverse methods on free vibration analysis of simply supported beams with a crack. Eng. Struct. 2003, 26, 427–436. [Google Scholar] [CrossRef]
- Lee, J.W.; Lee, J.Y. A transfer matrix method capable of determining the exact solutions of a twisted Bernoulli–Euler beam with multiple edge cracks. Appl. Math. Model 2017, 41, 474–493. [Google Scholar] [CrossRef]
- Nguyen, K.V. Mode shapes analysis of a cracked beam and its application for crack detection. J. Sound Vib. 2014, 333, 848–872. [Google Scholar] [CrossRef]
- Liu, D.; Jiang, J.; Han, H.; Sun, G.; Huo, R.; Zhou, D. Free vibration analysis of beams with an open crack at clamped end by the sub-domain Chebyshev–Ritz method. IJST-T Civ. Eng. 2023, 47, 415–430. [Google Scholar] [CrossRef]
- Huang, H.; Zheng, H.; Deng, J.; Li, W.; Li, Y. Random analysis of coupled vehicle–bridge systems with local nonlinearities based on explicit time-domain method. Nonlinear Dynam. 2022, 108, 81–95. [Google Scholar] [CrossRef]
- Law, S.S.; Zhu, X.Q. Bridge dynamic responses due to road surface roughness and braking of vehicle. J. Sound Vib. 2005, 282, 805–830. [Google Scholar] [CrossRef]
- Yu, P.; Yu, C.; Ren, Z.; Wang, L. Vehicle–Bridge Coupling Vibration of Long-Span Concrete-Filled Steel Tubular Arch Bridge. Int. J. Struct. Stab. Dyn. 2025, 25, 2550064. [Google Scholar] [CrossRef]
- Zhang, Y.; Duan, J.; Liu, Y.; Chen, Z.; Su, Y.; Liu, S. Dynamic Analysis of a Vehicle–Bridge System Under Excitation of Random Road Irregularities. Buildings 2024, 14, 3413. [Google Scholar] [CrossRef]
- Mahmoud, M.A.; Abou Zaid, M.A. Dynamic response of a beam with a crack subject to a moving mass. J. Sound Vib. 2002, 256, 591–603. [Google Scholar] [CrossRef]
- Nguyen, K.V.; Tran, H.T. Multi-cracks detection of a beam-like structure based on the on-vehicle vibration signal and wavelet analysis. J. Sound Vib. 2010, 329, 4455–4465. [Google Scholar] [CrossRef]
- Law, S.S.; Zhu, X.Q. Dynamic behavior of damaged concrete bridge structures under moving vehicular loads. Eng. Struct. 2004, 26, 1279–1293. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, H. Response of cracked simply supported concrete beam with moving vehicle load. Struct. Concr. 2016, 17, 875–882. [Google Scholar] [CrossRef]
- Shafiei, M.; Khaji, N. Analytical solutions for free and forced vibrations of a multiple cracked timoshenk o beam subject to a concentrated moving load. Acta Mech. 2011, 221, 79–97. [Google Scholar] [CrossRef]
- Pala, Y.; Reis, M. Dynamic response of a cracked beam under a moving mass load. J. Eng. Mechasce 2013, 139, 1229–1238. [Google Scholar] [CrossRef]
- Saimi, A.; Bensaid, I.; Fellah, A. Effect of crack presence on the dynamic and buckling responses of bidirectional functionally graded beams based on quasi-3D beam model and differential quadrature finite element method. Arch. Appl. Mech. 2023, 93, 3131–3151. [Google Scholar] [CrossRef]
- Ghannadiasl, A.; Khodapanah Ajirlou, S. Dynamic analysis of multiple cracked Timoshenko beam under moving load–analytical method. J. Vib. Control 2022, 28, 379–395. [Google Scholar] [CrossRef]
- Wang, W.J.; Lv, Z.R.; Liu, J.K. The dynamic response and time-frequency analysis of the bridge with breathing cracks. J. Vib. Shock 2013, 32, 12–16. (In Chinese) [Google Scholar]
- Tan, G.J.; Liu, Z.Y.; Wang, L.L.; Wang, L.S.; Cheng, Y.C. Free vibration analysis of a small or medium-span cracked simply supported bridge considering bridge-vehicle interaction. J. Vib. Eng. 2016, 29, 831–841. (In Chinese) [Google Scholar]
- Gui, S.R.; Chen, S.S.; Xu, S.Q. Comparison of three models for vehicle-bridge coupled vibration of simple beam bridge subjected to moving load. J. East China Jiaotong Univ. 2007, 24, 35–39. (In Chinese) [Google Scholar]
- Shi, L.N.; Yan, W.M.; He, H.X.; Chen, Y.J. Sensitivity of natural frequency and dynamic characteristics of the beam with open cracks to crack parameters. J. Vib. Meas. Diagn. 2016, 36, 881–889+1022. (In Chinese) [Google Scholar]
- Luo, J.B.; Xiao, Y.G.; Qian, C.Z. Nonlinear dynamic characteristics analysis of cracked beams under moving vehicle loads. J. Railw. Sci. Eng. 2009, 6, 36–39. (In Chinese) [Google Scholar]




| Mode Order | Frequency/Hz | Error(%) [|(①−②)/②|] | |
|---|---|---|---|
| Transfer Matrix Method ① | Ref. [33] ② | ||
| 1 | 38.24 | 38.47 | 0.60 |
| 2 | 152.77 | 153.73 | 0.63 |
| 3 | 352.26 | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gui, S.; Zeng, H.; Gui, Z.; Tan, M.; Guo, Z.; Zhong, K.; Xiong, Y.; Fang, W. Analytical Investigation of Dynamic Response in Cracked Structure Subjected to Moving Load. Buildings 2025, 15, 2119. https://doi.org/10.3390/buildings15122119
Gui S, Zeng H, Gui Z, Tan M, Guo Z, Zhong K, Xiong Y, Fang W. Analytical Investigation of Dynamic Response in Cracked Structure Subjected to Moving Load. Buildings. 2025; 15(12):2119. https://doi.org/10.3390/buildings15122119
Chicago/Turabian StyleGui, Shuirong, Hongwei Zeng, Zhisheng Gui, Mingjun Tan, Zhongzhao Guo, Kai Zhong, Yongming Xiong, and Wangwang Fang. 2025. "Analytical Investigation of Dynamic Response in Cracked Structure Subjected to Moving Load" Buildings 15, no. 12: 2119. https://doi.org/10.3390/buildings15122119
APA StyleGui, S., Zeng, H., Gui, Z., Tan, M., Guo, Z., Zhong, K., Xiong, Y., & Fang, W. (2025). Analytical Investigation of Dynamic Response in Cracked Structure Subjected to Moving Load. Buildings, 15(12), 2119. https://doi.org/10.3390/buildings15122119





