Abstract
The renovation of old communities is a major measure taken to promote urban development and transformation and can improve the quality of urban space and the living environment of residents, as well as promote economic development and bring new economic growth to the city. Decision-making regarding the updating of old communities is the starting point of the whole renovation process, and can be classified into two aspects: resilience assessment and renewal-potential evaluation. In order to standardize the retrofit evaluation index system, enhance the guidance of renovation decision plans for community renewal practices, and consider the randomness of evaluation indicators and the visualization of evaluation results, this paper proposes a method for evaluating the potential of old-urban-community renovation from the perspective of resilience. Based on an analysis of the relationship of the PSR (pressure–state–response) model and community resilience, as well as literature statistics, an evaluation index for the potential of old-community renovation according to the PSR model is established. Furthermore, vague set theory is applied to reduce the initial evaluation index system; then, entropy weight and the g1 method are used to determine objective and subjective weights, respectively, before determining the combination weight value. And the cloud model comprehensive evaluation method is applied to determine the membership degrees of resilience levels for the indicator, sub-criteria, criteria, and target layer in sequence. Finally, taking Nanjing Yinlun Garden Community as an example, the proposed method is adopted to identify the community’s resilience and renovation priorities, verifying the applicability of the method.
1. Introduction
The renovation of old urban communities, shifting from an incremental growth mode to a focus on enhancing existing assets, represents a fundamental transformation in the urbanization process. This initiative is a crucial aspect of urban renewal and development. It not only improves the living conditions of residents but also fosters the coordinated advancement of the economy, society, culture, and the environment [1]. Since the initiation of pilot projects for the renovation of old communities in 15 cities across China in 2017, there has been a growing level of policy support for this initiative, resulting in significant achievements and valuable insights. However, several challenges persist, including unclear responsibilities and authorities, hasty and indiscriminate renovations, substantial disparities in renovation outcomes across regions, outdated policies, and a lack of systematic top-level design and scheduling [2]. In particular, ambiguous renovation objectives lead to unscientific decision-making [3].
The renovation of old communities is a dynamic and complex process. From a spatial perspective, it involves not only the physical refurbishment of buildings but also the enhancement of community functions, optimization of public spaces, improvement of infrastructure, and overall elevation of residents’ quality of life. From a time perspective, the renovation process encompasses decision-making planning, scheduling, implementation, and post-evaluation [4]. Renovation decision-making is the initial step in the total process. It serves as the foundation to determine the renovation plans. Currently, research on the renovation decision-making of old communities can be categorized into two main aspects: renovation-potential evaluation and the resilience assessment of old communities. The former focuses on assessing the feasibility and potential of renovating existing communities in terms of physical space and functional improvements, as well as enhancing the community’s management and organizational capabilities. From the perspective of research scope, the evaluation of renovation potential has evolved from a macro urban level to a focus on land-intensive utilization and further to the micro level concerning the “three olds” (old towns, old factories, and old villages), with research subjects becoming increasingly specific [1]. In terms of renovation objectives, the evaluation of renovation potential primarily emphasizes aspects such as sustainability potential [5], energy conservation and emission reduction potential [6], age-friendly adaptation [7], and comprehensive benefits related to renovation efficiency and output [8].
From the perspective of urban planning and disaster management, “resilience” is defined as the ability of a system, community, or society to respond, resist, manage, and recover from disasters, including maintaining and restoring basic structures and functions. As the basic unit of urban governance, the community is not only the place where risks are generated and perceived, but also the direct bearer of risk consequences. Community resilience refers to the ability of a community to mitigate disaster losses, quickly restore normal community life order, and learn from experiences to better cope with future similar events through its organizational capacity, resource allocation capacity, social cohesion, etc., when facing various internal and external risks and challenges such as natural disasters, socio-economic crises, public health events, etc. The resilience assessment of old communities concentrates on evaluating their capacity to respond to emergencies, including external impact and internal pressures. This assessment primarily focuses on the resilience of old communities in terms of disaster response and emergency management. Shang, utilizing the PSR model, developed an evaluation index system for flood resilience in old communities, employing BP neural networks to assess flood resilience and proposing improvement strategies for these communities [9]. Guo established a resilience evaluation system for old communities and suggested optimization strategies based on the framework of risk, vulnerability, and recovery capacity [10]. Liu S, following the PSR model and entropy method, constructed a public health event resilience evaluation model for communities to assess pandemic prevention and control measures, as well as the resilience of living environments [11]. Maskrey evaluated community resilience against flooding and flood-related disasters from four dimensions: problem-solving, goal achievement, behavior, and structural system effectiveness [12]. Daniel L. proposed a community resilience assessment framework based on self-organizing functions, utilizing seven dimensions and 29 indicators to evaluate the strength of community resilience [13].
In summary, two methods, renovation potential and resilience assessment, for assessing old-community renovation decision-making have already been explored. However, the two approaches are not connected with each other. Renovation potential focuses on uncovering future possibilities, while resilience assessment emphasizes “emergency” capabilities. Due to the varying interpretations of potentiality and the diverse goals of stakeholders, there is significant variation in the potential-evaluation index systems constructed by different authors, making the results of evaluations of potential less effective in guiding decision-making.
In the field of resilience assessment research, most studies focus on specific current events, with researchers typically adopting a particular perspective to build evaluation systems. There is a lack of exploration from a multidimensional perspective to identify and analyze different types of old communities, renovation contents, and goals during the renovation process. Furthermore, there is insufficient quantitative research that integrates the dynamic characteristics of old communities and their resilience requirements [3,8].
In essence, both renovation potential and resilience assessment for old communities aim to enhance the overall performance and sustainability of existing neighborhoods. While these two evaluations are interconnected, they also possess different characteristics. Renovation potential increment can enhance resilience, and the findings from resilience assessments can inform the details renovation plans. The evaluation of renovation potential is helpful for planning departments to formulate renewal plans, and to estimate the investment of renovation funds and the benefits obtained. Conversely, resilience assessment is utilized for emergency and risk management, encompassing aspects such as emergency planning, material reserves, and personnel training, which help to clarify renovation goals. By integrating these two methods, priority can be given to renovating communities with lower resilience while simultaneously improving their development potentiality by enhancing their resilience. This integrated approach addresses both immediate challenges and long-term development needs.
Therefore, this paper proposes an evaluation method for the renovation potential of aging communities from a resilience perspective. The indicators for renovation-potential evaluation are initially constructed based on the pressure–state–response (PSR) model and literature-based statistical methods. Vague set theory is applied to simplify these indicators. After determining the objective and subjective weights of the indicators using the G1 method and entropy method, a combined weight is established. A cloud model is then employed for comprehensive evaluation, sequentially determining the resilience membership degree at the indicator layer, sub-criterion layer, criterion layer, and target layer. Finally, the applicability of the proposed method is verified through case study examples.
2. Materials and Methods
2.1. Concept of Resilience of Old Communities (ROC)
The resilience of established communities refers to their ability to adapt to emergencies and recover from various shocks and pressures. Community resilience encompasses both tangible and social systems, which include infrastructure, social structures, institutions, and economic stability, among others. From the perspective of disaster management, community resilience involves the capacity to maintain stability, recover effectively, and adapt during and after a disaster [14].
As mentioned earlier, the evaluation of renewal decisions for old communities can be based on two perspectives: future potential and existing risk response capabilities, namely community resilience. Combining future potential with current issues for the evaluation of old-community renewal decisions not only helps standardize the evaluation index system, but also makes the renewal tasks more specific. The ROC (resilience of old communities) refers to the goal of updating old communities from a resilience perspective and considering their future potential. It serves as the target layer for evaluating old-community updates and should be updated when the ROC is lower.
2.2. The Intrinsic Relationship Between the PSR Model and the ROC
The decision-making process for the renovation of old communities exhibits typical pressure–state–response (PSR) characteristics. It is essential to consider the impacts of human activities on the natural environment, emphasizing the relationship between economic operations and environmental effects. This model aids in understanding the interactions between economic activities and environmental changes. The community resilience change process based on the PSR model is illustrated in Figure 1.
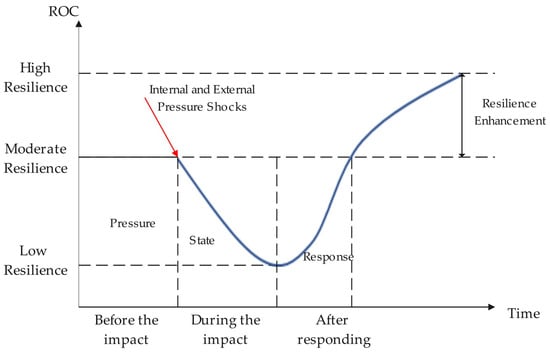
Figure 1.
ROC changes based on the PSR model.
Under social and environmental pressures, the resilience of the community system—encompassing economic, environmental, social, and infrastructure states—gradually declines. Once the resilience value reaches its limit, the system can no longer maintain self-consistency; therefore, external intervention is necessary to enhance the current system’s resilience. After implementing appropriate policy and economic responses, the community can restore its previous resilience value or even exceed its pre-impact resilience level. Figure 2 illustrates the topological relationship based on the PSR model, which includes the elements, characteristics, and identification methods of ROC.
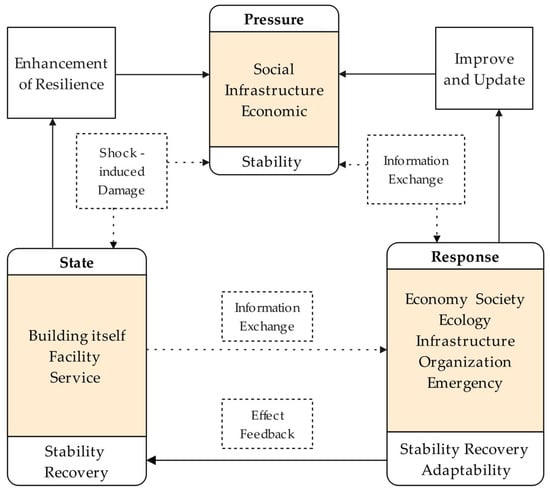
Figure 2.
Topological relationships between ROC and PSR.
The inner dashed rectangle in Figure 2 represents the information transmission relationships within the community when facing pressure. The outer solid rectangle depicts the enhanced community stability, adaptability, and recovery capacity following emergency responses. This diagram illustrates the underlying mechanisms by which internal and external influences lead to community stress, state changes, and responses. The contents of the external rectangular box with a “yellow” background correspond to the dependent variables of pressure, state, and response factors, and can also be seen as a sub-criterion for community renewal decisions. By using these factors as classification criteria and further analyzing their causes, observation indicators for these factors can be obtained.
2.3. ROC Assessment Indicator System Based on the PSR Model
The selection of resilience assessment indicators should adhere to the principles of generality, objectivity, scientific rigor, and applicability. Based on the topological relationships illustrated in Figure 2, a statistical analysis was conducted on the frequency of indicators extracted from 30 representative articles, both Chinese and international, including works such as the representative papers [2,3,9,10,12,14,15,16,17,18,19,20], among others. This analysis led to the development of an ROC assessment indicator system based on the PSR model, which comprises three criteria layers, eight sub-criteria layers, and 26 indicators, as detailed in Table 1. The indicator system is organized into four levels: the target layer, criteria layer, sub-criteria layer, and indicator layer. The indicators are classified into positive (+) and negative (−) types according to their influence on the target-ROC. The numbers in the last column of Table 1 represent the frequency of occurrence for each indicator. The indicator unit N represents a dimensionless parameter, and its value range is determined according to the corresponding specifications.

Table 1.
PSR-based resilience assessment indicators for existing older communities.
2.4. Vague Set-Based Indicator Simplification and Quantitative Classification of Indicators
Vague Set Theory is a methodology employed to manage uncertain information and reveal implicit knowledge, making it particularly effective for addressing the issue of indicator reduction [21]. Vague sets represent the membership degrees in terms of truth, falsity, and hesitation for each indicator, expressed as intervals. The function denotes the true membership function of Vague set A, indicating the extent to which x supports membership in set A. Correspondingly, represents the false membership function of Vague set A, indicating the degree to which x opposes membership in set A. The hesitation degree of Vague set A is defined by the function , which reflects the level of uncertainty regarding x’s membership in set A. The Vague value is represented by the closed interval , indicating the Vague value of set A at point x. The membership degree of the indicator is calculated according to Formula (1), and indicators are selected based on the criterion . When , the membership degree is calculated as follows:
In this study, ten experts in the fields of architecture and facility management were invited to provide three types of evaluations—support, opposition, and hesitation—regarding the indicators established in Table 1. Using the indicators included in the pressure (P) category as an example, the evaluation results are presented in Table 2. In Table 2, the values for indicators P13 and P33 are both less than 0.3; therefore, these two indicators have been removed from the pressure (P) criterion. After actual research, it was found that old urban communities are generally located far away from factories, as well as flammable and explosive facilities. Therefore, the p13 indicator has been removed. The correlation between the P33 and P12 indicators is extremely high; therefore, the P33 indicator has been excluded.

Table 2.
Vague set importance ranking of P-Criterion indicators.
The same method is employed to simplify the indicators of the state criteria (S) and response criteria (R). Indicators S24 and R23 have been removed, resulting in a streamlined PSR indicator system. Based on this reduced indicator system, the resilience evaluation results for older communities are categorized into five semantic levels: Low, Lower, Medium, Higher, and High, which correspond to the evaluation sets U = I, II, III, IV, and V. Each evaluation indicator is divided into five-level intervals according to the relevant standards, as illustrated in Table 3.

Table 3.
Simplified PSR indicator classification.
3. Cloud Model-Based Priority Decision-Making Framework for the Renovation of Old Communities
The cloud model facilitates the transformation between qualitative and quantitative representations of uncertainty. This model not only addresses the fuzziness of each evaluation indicator but also incorporates the randomness of the membership degree associated with these indicators. It visually and comprehensively presents the evaluation results and details in the form of a cloud map, making it an effective tool for multi-objective and multi-attribute decision-making and evaluation [22].
3.1. Cloud Model Evaluation Process
Taking the Characteristic ROC as the target, the cloud model evaluation process consists of the following three main steps, as illustrated in Figure 3:
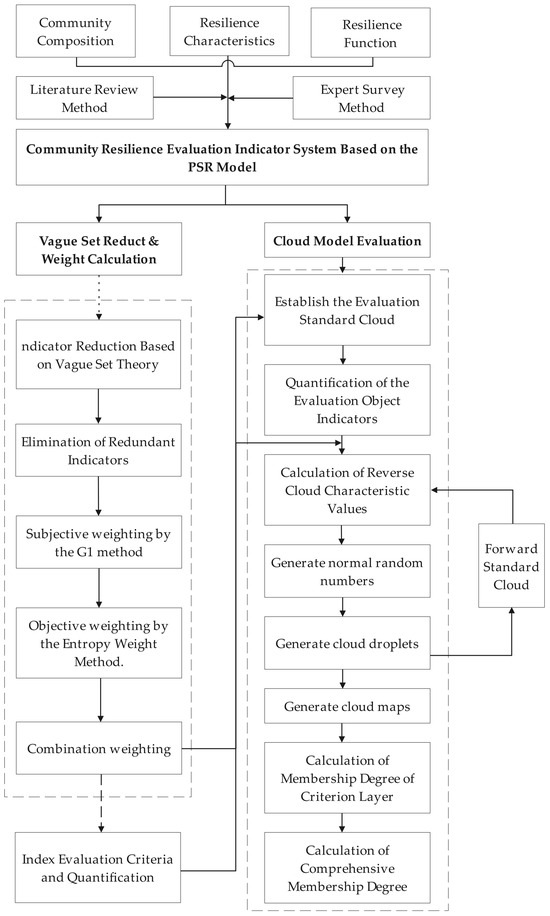
Figure 3.
The evaluation process of the resilience of old residential areas based on the cloud model.
- Preliminary determination of the ROC evaluation index system through a literature review and expert methods, and a reduction in indicators using vague set methods to determine the renovation evaluation index system for old communities.
- Using subjective and objective weighting methods to determine the combined weight of evaluation indicators.
- Using cloud model backward generators with the obtained weights to generate assessment cloud maps, comparing the backward cloud map with the forward standard cloud map, and determining the membership degree of the ROC value at each criterion on the principle of the maximum membership degree.
3.2. Combined Weighting Based on the G1 and Entropy Weight Methods
Scientifically determining the weights of evaluation indicators is essential for cloud model evaluation. This paper employs a combined weighting approach that integrates both subjective and objective methods. The subjective weighting method utilizes the G1 method, while the objective weighting method employs the entropy weight method.
- G1 Weighting MethodThe G1 weighting method, also known as the Sequence Relation Analysis Method, is a subjective weighting technique derived from the analytic hierarchy process (AHP). This method is logically straightforward, easy to compute, and does not require consistency checks, thereby enhancing the validity of the resulting weights [21]. The weights of each indicator are calculated according to Formula (2). In this formula, C represents the ranking of the relative importance of the indicators, denotes the weight of the indicator, and indicates the relative importance of the indicator, categorized into nine equal levels with values ranging from 1 to 1.8.
- Entropy Weight MethodThe entropy weight method calculates the weights of indicators by assessing the information entropy associated with each indicator, thereby facilitating the objective weighting of multi-indicator data. This process is specifically detailed in Formula (3). In this context, i represents the sample, j denotes the indicator, indicates the value of the sample and indicator, refers to the information entropy, and signifies the weight of the indicator.
- Combined WeightingThe weighting vectors of subjective and objective indicators are linearly combined according to Formula (4) to obtain the combined-weight vector. In Formula (4), and represent the coefficients of the subjective and objective weights, respectively. The weight coefficients are usually determined using methods such as the simple average, weighted average, analytic hierarchy process (AHP), etc.
3.3. Cloud Model Parameters and Membership Degree Calculation
After obtaining the combined weights of the evaluation indicators, the sequence for calculating the cloud model corresponds to Formulas (5) through (8). In Formula (5), K is a constant that typically ranges from 0.005 to 0.01 and is adjusted based on the fuzziness of the indicator. In Formula (7), represents the weight, while and are normally distributed random variables.
- Construct the forward standard cloud.
- Calculate the reverse cloud parameters for each evaluation indicator.
- Calculate the cloud level similarity.
- Calculate the cloud level membership degree
4. Case Study
4.1. Case Overview
Yinlun Garden Community, established in 2000, is situated on Huxi Street in the Jianye District of Nanjing, China. The community comprises 11 buildings, totaling 408 residential units, with an overall floor area of 8000 m² and a land area of 2162 m². Over the years, the community has encountered numerous issues, including weathering of the exterior walls, leading to significant water leakage; damaged roads; inadequate public facilities; and a shortage of parking spaces. Consequently, residents have expressed a strong desire for renovation. Before implementing the renovation, representatives from three categories—owners, property management companies, and community managers—were consulted. Given the high level of professionalism required for evaluating community renovations, a non-random survey method was employed. Two representatives with expertise in community renewal were selected from each survey group, and the scores were assigned based on the indicators listed in Table 3. A total of six data samples, derived from the indicator system and classification method established in Table 3, were collected, as shown in Table 4. In Table 4, the evaluation was conducted using a 1-to-5 rating scale with fuzzy assessments, and the results were quantified using the mean method.

Table 4.
Resilience evaluation results for Yinlun Garden indicators.
4.2. Establishment of a Cloud Model for the Evaluation Standards of Each Indicator
Based on the Golden Ratio method and the five-level classification standards for each indicator listed in Table 3, Formula (5) was employed to generate the forward standard cloud parameters for the indicators. With He set to 0.001, the parameters were obtained, as shown in Table 5. Using the negative indicator P11 and the positive indicator P12 as examples, an evaluation standard cloud map was generated in MATLAB utilizing the forward cloud generator, as illustrated in Figure 4.

Table 5.
Standard cloud parameters (Ex, En, He).
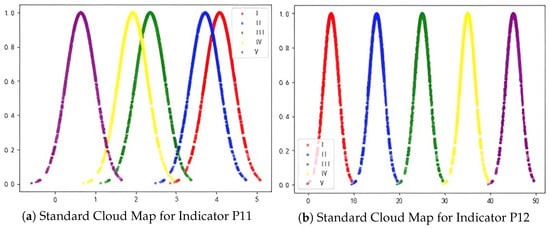
Figure 4.
Standard cloud maps for indicators.
In Figure 4, the horizontal axis represents the ROC range of the relevant indicator. For positive indicators, five levels from I to V are divided from left to right, corresponding to normal-distribution curves colored red, blue, green, yellow, and purple. For negative indicators, the order of the levels is exactly the opposite, but with the same color meanings. The vertical axis represents the degree of membership or certainty of the indicator value. Figure 4a shows a standard cloud map of five evaluation levels corresponding to the negative indicator P11, where the ROC value decreases from V to I from left to right. Figure 4b shows a standard cloud map of the positive indicator P12, where the ROC value increases from I to V from left to right. The other indicators’ standard cloud maps are similar to this, and will not be elaborated upon here.
4.3. Combined-Weight Calculation
- G1 Method for Weight Calculation
- Entropy Weight Method for Weight CalculationData from sixteen retrofitted communities in Nanjing, similar to the YinLun Garden community, were collected. Using Formula (3), the objective weights for the resilience evaluation of old communities were calculated.
- Combined-Weight CalculationAs illustrated in Figure 5, the entropy weight method and the G1 method assign significantly different weights to various indicators. The combined weighting method effectively mitigates the discrepancies arising from both subjective and objective weighting approaches. Given that the data sample utilized in the entropy weight method was relatively small, the weight coefficient was set at 0.4. The combined indicator weights were calculated using Formula (4). The results of the weight calculations are presented in Table 6, where W1 denotes the weight determined by the G1 method, W2 indicates the weight derived from the entropy weight method, and W0 with a bold font represents the combined weight.
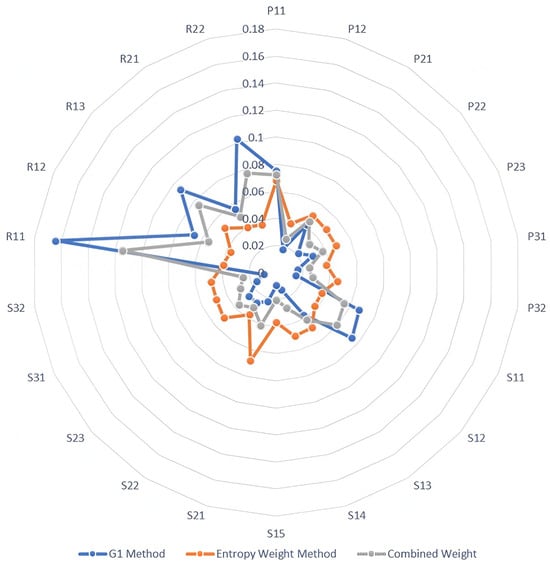 Figure 5. Radar chart comparing results of three weighting methods.
Figure 5. Radar chart comparing results of three weighting methods. Table 6. Weight calculation results of resilience evaluation indicators.
Table 6. Weight calculation results of resilience evaluation indicators.
4.4. Calculation of Indicator Membership Degree and Generation of Evaluation Cloud Map
Based on the results of the resilience sample survey conducted at Yinlun Garden, as presented in Table 4, MATLAB 2017 was utilized to calculate the inverse cloud parameters (Ex, En, He) of the evaluation samples according to Formula (6). Subsequently, Formula (7) was employed to determine the resilience cloud level similarity, while Formula (8) was applied to calculate the membership degree of the resilience cloud level. The results are displayed in Table 7.

Table 7.
Samples’ cloud parameters, cloud level similarity, and cloud level membership degree.
Based on the parameters generated from the inverse cloud model, MATLAB code was utilized to superimpose and generate 1000 cloud droplets within the standard cloud map for indicator evaluation. A comparison chart was created to illustrate the relationship between the indicators of the evaluation object and the standard cloud map. Using the indicators P11 and P12 as examples, a comparison between the cloud map of the evaluation object and the standard cloud map is presented in Figure 6.
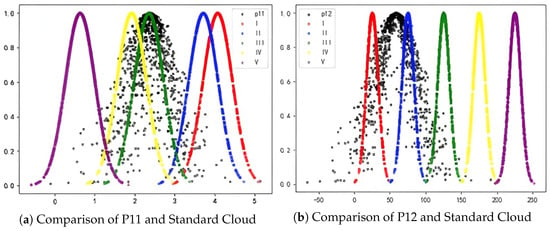
Figure 6.
Comparison of indicator cloud and standard cloud.
In Figure 6, the standard cloud map corresponds to the results presented in Figure 4. The black scatter plot illustrates the forward cloud map generated for the evaluation object’s indicators P11 (2.367, 0.452, 0.277) and P12 (14.5, 5.012, 1.918), which were calculated using the inverse cloud parameters. By comparing the indicator cloud map with the standard cloud map, the range of resilience levels for the indicators were initially determined as follows:
- We adopted a literature review and expert methods to preliminarily determine the ROC indicator system, and applied vague set methods to reduce the indicators for establishing the evaluation indicator system for old-community renovation.
- We adopted both subjective and objective weighting methods to establish the combined weights of the evaluation indicators.
- We treated the obtained combination weights as the probabilities of the resilience indicator’s occurrence, and we utilized the forward and reverse cloud generators of the cloud model to produce the cloud parameters. Based on the principle of the maximum membership degree, we calculated the membership degree values for different resilience levels of the ROC.
4.5. Calculation of Membership Degrees for Target, Criteria, and Sub-Criteria Layers
The cloud parameters for each evaluation indicator, calculated from the evaluation samples listed in Table 7, map the score levels for each indicator. By calculating the membership degree of the indicator with respect to score level j, the sub-criteria layer membership matrix is obtained. By integrating the combined weights for each indicator listed in Table 6, the membership degrees for the sub-criteria layer, criteria layer, and target layer can be calculated using Formula (9). The resilience level membership degree for the sub-criteria layer is presented in Table 8, while the resilience level membership degrees for the target and criteria layers are shown in Table 9. According to the principle of the maximum membership degree, the resilience levels for the sub-criteria, criteria, and target layers can be determined.

Table 8.
Sub-criteria resilience level membership degree.

Table 9.
Target and criteria resilience level membership degree.
5. Discussion and Suggestions
5.1. Discussion
According to Table 9, the comprehensive resilience membership degree of Yinlun Garden is 0.137, categorizing it within a lower resilience level. This indicates an urgent need for renovation within the community. The three criteria layers in the pressure–state–response (PSR) model also fall under the lower resilience level, with the pressure (P) and state (S) criteria layers exhibiting lower membership degrees than the response (R) criteria layer. This suggests that the community’s pressure and state resilience are significantly weaker than its response resilience. Consequently, the community’s state and the pressures it faces are both objective and pronounced, indicating that these issues cannot be resolved merely by implementing proactive measures to enhance resilience.
From the subordinate degree of resilience levels of the sub-criteria layer membership levels in Table 8, it is evident that in the pressure criteria layer, the P2 sub-criterion (which includes P21, P22, and P23) has a resilience membership degree of 0.51, indicating a “low” resilience level. Among these, as shown in Table 7, P23 has a membership degree of 0.83, also indicating “low” resilience, which suggests that the community’s health standards are very low. The P21 and P22 indicators have membership degrees of 0.60 and 0.46, respectively, clearly placing them in the “lower” resilience category. In the state criteria layer, the S2 sub-criterion (which includes S21, S22, and S23) has a membership degree of 0.049, indicating “low” resilience. Specifically, the S21 indicator has a membership degree of 1, signifying a critical issue with the community’s electricity supply. The S22 indicator, with a membership degree of 0.6, highlights significant drainage problems within the community. The S23 indicator has a resilience level of 0.83, suggesting that the community’s greening issues are less severe. In the response criteria layer, R2 falls within the lower resilience level, with the indicators R21 and R22 under R2 exhibiting membership degrees of 0.88 and 0.87, respectively, which also indicate lower resilience.
5.2. Suggestions
It can also be observed from the data analysis results that 75% of the indicators in the sub-criteria layer of Yinlun Garden fall within a lower resilience level, and 100% of the indicators in the criteria layer are categorized as having a lower resilience level. Consequently, the overall resilience of the community is classified as low, indicating that it should be prioritized for renovation and renewal projects this year.
Considering that the sub-criteria layers P2 and S2 exhibit extremely low resilience membership degrees, the renovation plan should prioritize the following indicators within the P criterion layer: enhancing the community’s flood drainage capacity during the rainy season (P21), improving traffic circulation and increasing road network density (P22), and enhancing community sanitation (P23). Additionally, attention should be paid to the indicators under the S sub-criterion layer: improving average power supply stability (S21), increasing drainage network density (S22), and expanding green space coverage (S23). Based on the resilience levels associated with the indicators presented in Table 7, it is clear that the P23 and S21 indicators are the most critical issues.
6. Conclusions and Limitations
6.1. Conclusions
- The decision-making process for renovating and evaluating older communities, viewed through a resilience perspective, effectively integrates current challenges with the potential for future development. This approach emphasizes goal orientation while also prioritizing sustainability. Notably, the resilience indicator classification system based on the pressure–state–response (PSR) model standardizes the evaluation indicators for renovation decisions, thereby enhancing the consistency and efficiency of the evaluation framework.
- The decision-making and evaluation method that employs the cloud model to calculate the resilience level membership degrees of various layers not only facilitates seamless conversion between qualitative language and quantitative values, but also accommodates the inherent randomness of the data. Moreover, through data visualization, it effectively illustrates the resilience levels of the different criteria layers within the evaluated community.
6.2. Limitations
- The weights of the resilience evaluation indicators based on the PSR model, as determined using the combined weighting method presented in this paper, require further validation to ensure their rationality and accuracy in practical applications. Additional research is needed to enhance the systematization and stability of the indicator system. The sample size utilized for determining the objective weights of the indicators through the entropy weight method is relatively small, and the number of experts surveyed to establish the subjective weights using the G1 method is also limited. Future research should focus on increasing both the sample size and the number of survey participants.
- Although a cloud model computation program based on MATLAB has been developed, the calculation process remains relatively complex. Future research will focus on further studies in areas such as the intelligent evaluation of renovation potential, automation of data acquisition, and visualization of evaluation results.
Author Contributions
Conceptualization, X.L.; methodology, X.L. and J.Z.; software, X.Z.; validation, X.L.; formal analysis, X.L.; investigation, X.L.; resources, X.Z. and J.Z.; data curation, X.L.; writing—original draft preparation, X.Z. and J.Z.; writing—review and editing, X.L.; visualization, X.Z.; supervision, X.L.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by (1) the Philosophy and Social Sciences Project of Jiangsu Province Universities “Research on Urban Smart Home Care Services Based on Demand Analysis”, grant number (2023SJYB0529), and (2) the Science and Technology Program Project of the Ministry of Housing and Urban-Rural Development “Innovative Research on the Path of Mass Participation in the Renovation of Older Neighborhoods under the Concept of “Co-Creation””, grant number (2019-R-009).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gu, Z.; Zhang, X. Framing social sustainability and justice claims in urban regeneration: A comparative analysis of two cases in Guangzhou. Land Use Policy 2021, 102, 105224. [Google Scholar] [CrossRef]
- Yi, H.; Wang, X. Research on the Current Status and Development Suggestions of Existing Residential Building Renovation in China. Build. Sci. 2021, 37, 121–127. [Google Scholar]
- Fan, Y.; Zhang, M.; Li, H.; Xu, J.; Chen, Y. Resilience evaluation system of the old community based on cloud model. J. Shandong Univ. (Eng. Sci.) 2023, 53, 1–9. [Google Scholar]
- Zhang, J.; Li, X. Evaluation of Urban Public Building Renovation Potential Based on Combination Weight Cloud Model—Case Study in China. Buildings 2024, 14, 3211. [Google Scholar] [CrossRef]
- Papadopoulos, A.M.; Theodosiou, T.G.; Karatzas, K.D. Feasibility of energy saving renovation measures in urban buildings: The impact of energy prices and the acceptable pay back time criterion. Energy Build. 2002, 34, 455–466. [Google Scholar] [CrossRef]
- Pietrapertosa, F.; Tancredi, M.; Giordano, M.; Cosmi, C.; Salvia, M. How to prioritize energy efficiency intervention in municipal public buildings to decrease CO2 emissions? A case study from Italy. Int. J. Environ. Res. Public Health 2020, 17, 4434. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Zhang, X. Assessing the adaptability of old community for renovation based on health sustainability. In Proceedings of the Institution of Civil Engineers-Engineering Sustainability; Emerald Publishing Limited: Leeds, UK, 2023; Volume 176, pp. 214–227. [Google Scholar]
- Zheng, C. Evaluation Study on the Comprehensive Benefits of the “Three Olds” Renovation in Tianhe District of Guangzhou City. Front. Humanit. Soc. Sci. 2023, 3, 92–98. [Google Scholar] [CrossRef]
- Shang, L.; Zhang, Y.; Zhang, D.; Zhong, Y. Disaster Resilience Evaluation of Old Communities under the Perspective of Rainstorm Flood Disasters: An Empirical Study Based on the PSR Model and BPNN. Sci. Technol. Eng. 2023, 23, 11338–11348. [Google Scholar]
- Guo, X.; Fei, Z.; Wang, Z. Rigidity, Flexibility, and Resilience in Urban Disaster Response. Urban Rural Plan 2021, 3, 35–42. [Google Scholar]
- Liu, S.; Wang, Y.; Li, Z.; Zhang, D.; Yu, K. Community resilience monitoring and evaluation under the prevention and control of public health emergencies. E3S Web Conf. 2021, 251, 03013. [Google Scholar] [CrossRef]
- Maskrey, S.; Vilcan, T.; O’Donnell, E.; Lamond, J. Using Learning and Action Alliances to build capacity for local flood risk management. Environ. Sci. Policy 2020, 107, 198–205. [Google Scholar] [CrossRef]
- Daniel, L.; Mazumder, R.K.; Enderami, S.A.; Sutley, E.J.; Lequesne, R.D. Community capitals framework for linking buildings and organizations for enhancing community resilience through the built environment. J. Infrastruct. Syst. 2022, 28, 04021053. [Google Scholar] [CrossRef]
- Zhang, X.; Luo, Y. Community Resilience from the Perspective of Disasters: International Research Progress and Implications. Secretary 2022, 40, 37–49. [Google Scholar]
- Yan, C.; Chen, J.; Duan, R.; Ren, W.; Lan, S. Evaluation System for Fireproof Resiliance of Urban Historical Blocks Based on Pressure-State-Response Model:A Case of Three Lanes and Seven Alleys in Fuzhou City. Sci. Technol. Eng. 2021, 21, 3290–3296. [Google Scholar]
- Hazbavi, Z.; Sadeghi, S.H.; Gholamalifard, M.; Davudirad, A.A. Watershed health assessment using the pressure–state–response (PSR) framework. Land Degrad. Dev. 2020, 31, 3–19. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Lin, G. Study on Rural Classification and Resilience Evaluation Based on PSR Model: A Case Study of Lvshunkou District, Dalian City, China. Sustainability 2024, 16, 6708. [Google Scholar] [CrossRef]
- Fan, H.; Yang, T. Study on the Path and Strategy of Upgrading Renovation of Old Community Based on the Residents’ Needs: A Case of Youdian Xincun Community, Wuhan. In Proceedings of the 2023 5th International Conference on Civil Architecture and Urban Engineering (ICCAUE 2023), Xiamen, China, 17–19 November 2023; Atlantis Press: Paris, France, 2024; pp. 309–324. [Google Scholar]
- Shen, T.; Yao, X.; Wen, F. The Urban Regeneration Engine Model: An analytical framework and case study of the renewal of old communities. Land Use Policy 2021, 108, 105571. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, M.; Xu, Z.; Ye, Y.; Chen, S.; Pan, Y.; Chen, J. The influence of Community Sports Parks on residents’ subjective well-being: A case study of Zhuhai City, China. Habitat Int. 2021, 117, 102439. [Google Scholar] [CrossRef]
- Guotai, C.; Zhichuan, Z.; Yuling, Z. The science and technology evaluation model based on entropy and G1 and empirical research of China. Stud. Sci. Sci. 2008, 26, 1210–1220. [Google Scholar]
- Deyi, L.; Changyu, L.; Juan, D.; Xu, H. Artificial Intelligence with Uncertainty. Software 2004, 15, 1583–1594. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).