Abstract
This study addresses a critical gap in blast-resistant design by investigating the influence of axial compression ratio—a previously underexplored parameter—on the dynamic response of reinforced concrete (RC) shear walls under close-in explosions. While existing research has focused on conventional loading scenarios, the interplay between axial compression and blast effects remains poorly understood, despite its practical significance for structural safety in high-risk environments. Through a combined experimental and numerical approach, three half-scale RC shear walls were tested under blast loading, complemented by simulations analyzing key parameters (aspect ratio, axial compression ratio, boundary conditions, and charge weight). The results demonstrate that a moderate axial compression ratio (around 0.3) enhances structural stiffness and reduces displacement, effectively helping to control wall damage. Boundary conditions were also found to affect failure modes: walls with stiffer end restraints exhibited reduced deformation but more brittle cracking. Lower aspect ratios (i.e., wider walls) improved blast resistance, and peak displacement progressively increased with the charge weight. These findings provide actionable insights for optimizing RC shear wall design in blast-prone infrastructures, balancing ductility and load capacity. By linking theoretical analysis to practical design criteria, this study advances blast-resistant engineering solutions.
1. Introduction
With the acceleration of urbanization, mid- to high-rise buildings and complex structures have become increasingly prevalent in modern cities. These buildings, often located in densely populated urban areas and serving critical social or symbolic functions, are more likely to become targets of terrorist attacks. Ensuring their structural safety is thus crucial for sustainable urban development and the protection of human life. In structural design, reinforced concrete (RC) shear walls are extensively employed in these buildings as primary lateral load-resisting components to withstand horizontal forces such as wind and seismic actions [1]. Moreover, given the rising incidence of terrorist attacks and accidental explosions in recent years [2,3,4,5,6], ensuring the blast resistance of such critical infrastructure has gained increasing attention from both academia and engineering practice [7,8,9,10,11,12,13,14]. RC shear walls, due to their high stiffness and strength, are particularly relevant for enhancing the blast resilience of high-occupancy or symbolically significant structures.
Concrete walls, as slab-type structural elements and vertical load-bearing components, play a critical role in preventing structural collapse under blast loading [15,16,17,18,19,20,21,22,23,24]. Ning et al. [12] investigated the damage patterns of concrete slabs subjected to TNT (Trinitrotoluene) explosions with varying charge weights and standoff distances. Milani and Lourenco [15] used a simplified rigid-plastic homogenization model to estimate the displacement of masonry walls with different thicknesses under various blast scenarios. Su et al. [16] conducted field tests comparing the dynamic responses of normal-strength and high-performance concrete slabs under blast loading. Arlery and Pontiroli [17] studied the response, damage mechanisms, and residual bearing capacity of RC columns subjected to explosions, finding that axial load enhances resistance at larger scaled distances but reduces it at shorter distances. Similarly, Shi et al. [18] observed that when the scaled distance exceeds a critical threshold, axial load increases residual strength; otherwise, it has a weakening effect. These studies highlight the importance of considering both standoff distance and axial load when evaluating the blast resistance of vertical load-bearing concrete members. Yu et al. [20] proposed a probabilistic method to predict failure of RC columns under blast loading, identifying axial force as a dominant factor affecting the failure probability of RC elements. Thai and Kim [21] recommended the use of the multi-material arbitrary Lagrangian–Eulerian (MM-ALE) method for blast modeling to investigate damage in RC members. The failure modes of RC elements under blast loads vary depending on the amount and rate of energy transfer [22]. Wu et al. [23] demonstrated that a properly constructed numerical model can reliably simulate the structural failure of RC slabs under blast effects. While some work has been conducted, reliability evaluations of other RC elements under blast loads—especially in stochastic domains—remain limited and often rely on simplified single-degree-of-freedom (SDOF) models.
Although the effects of axial compression ratio on the performance of reinforced concrete (RC) columns have been extensively studied, its role in RC shear walls remains relatively underexplored. Explosive charges are characterized by their instantaneous action and high energy release, which significantly increases the risk of severe structural damage under close-in detonation. Existing research [25] suggests that the axial compression ratio has a notable impact on the blast resistance of RC shear walls. Moreover, parameters such as edge restraints, aspect ratio, and explosive charge weight [26] also play important roles in influencing their dynamic response and failure mechanisms. However, further investigation is needed to clarify how these factors—particularly the axial compression ratio—affect the failure behavior of RC shear walls under blast loading conditions.
Notably, very few experimental studies have specifically addressed the behavior of RC shear walls subjected to blast loads while under axial compression. Furthermore, most existing blast tests on RC slabs or wall-like specimens have been conducted in a horizontal configuration, where specimens are laid flat on the ground [27,28]. This setup may not accurately capture the boundary conditions or load paths of shear walls in realistic vertical configurations used in actual structures. To bridge this gap, the present study adopts a more realistic testing configuration, in which half-scale RC shear walls are vertically anchored to the ground and subjected to both axial compression and close-in explosive loading. This arrangement more closely replicates the real-world structural context and allows for a better understanding of the interaction between axial force and blast-induced dynamic response.
In this study, dynamic response refers to the time-dependent structural behavior of shear walls during the blast event, including mid-span displacement, crack development, and damage evolution [29,30].
This study addresses this gap by combining experimental and numerical approaches. Three half-scale RC shear wall specimens were tested under close-in blast loading with varying axial compression levels and explosive charge weights. A validated 3D fluid–structure interaction (FSI) model was then developed to extend the analysis across different aspect ratios and boundary conditions. The findings contribute to a deeper understanding of shear wall behavior under blast threats and provide design references for improving blast resistance in structural systems.
2. Experimental Overview
2.1. Specimen Design
To investigate the dynamic response and damage characteristics of reinforced concrete (RC) shear walls under blast loading, a half-scale shear wall specimen was designed for testing [31]. The specimen consisted of three main components: the top beam, the shear wall panel, and the bottom beam. The total height of each specimen was 2100 mm, which corresponds to a 1:2 scale of a typical single-story RC shear wall with a full-scale story height of approximately 4.2 m. This scaling approach is consistent with common practice in blast-resistance experiments for structural walls [27,28] and allows meaningful evaluation of wall behavior while maintaining manageable testing dimensions. The top beam measured 1400 mm in length, 250 mm in width, and 250 mm in height. The shear wall panel was 1500 mm high, 800 mm wide, and 100 mm thick. The bottom beam measured 1400 mm in length, 250 mm in width, and 350 mm in height. The concrete cover thickness was 10 mm.
The concrete used was of strength grade C40, provided by Zhejiang Guangtian Component Group Co., Ltd., Taizhou, China. The reinforcement bars were procured from a local commercial supplier in Ningbo, China. The reinforcement design of the RC shear walls was based on the Code for Design of Concrete Structures (GB 50010-2010) [31]. Boundary zones were reinforced with vertical bars to resist axial compression and bending moment, while the web area adopted distributed horizontal and vertical reinforcement arranged in double layers along the wall thickness. The reinforcement ratio met the minimum code requirement of 0.2%, ensuring ductile failure and preventing premature local buckling. Distribution bars, stirrups, and bracing ties were fabricated from HPB300-grade steel, while the longitudinal bars in the confined boundary elements used HRB400-grade steel. The longitudinal reinforcement was fully anchored into the top and bottom boundary beams to ensure adequate force transfer and structural continuity. Detailed reinforcement configurations are illustrated in Figure 1.
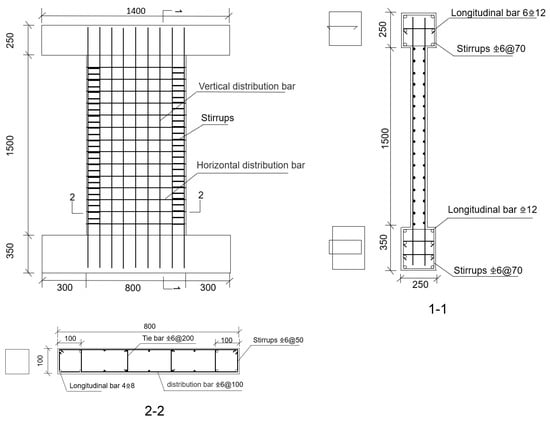
Figure 1.
Geometric and reinforcement details of the RC shear wall (unit: mm).
To evaluate the compressive strength of the concrete, three standard cubic specimens measuring 150 mm × 150 mm × 150 mm were cast and tested, with the results presented in Table 1. Two types of reinforcement bars were used in the experiment. For each type, three specimens were randomly selected to assess their mechanical properties, and the test results are summarized in Table 2.

Table 1.
Properties of concrete.

Table 2.
Properties of rebar.
2.2. Loading Device
In accordance with the experimental requirements, a self-equilibrating axial loading device was designed to simulate axial force conditions under blast loading, as illustrated in Figure 2. A hydraulic cylinder was installed at the top of the specimen to apply a uniaxial downward axial load along the vertical direction of the wall, simulating the gravitational effect of upper structures. The magnitude of the axial force could be adjusted by controlling the pressure within the hydraulic system. This configuration ensured that the axial load remained constant and uniformly distributed during the blast event.
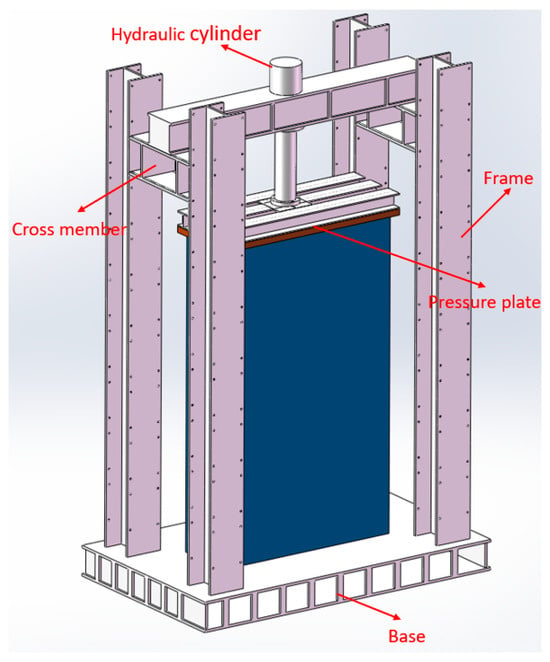
Figure 2.
Schematic diagram of the loading device.
2.3. Test Condition
Three reinforced concrete (RC) shear wall specimens, labeled A1 to A3, were fabricated with identical geometric dimensions. The specimens were designed to investigate the effects of explosive charge weight and axial compression ratio on blast-induced damage. Specifically, specimens A1 and A2 were used to examine the influence of charge weight under the same axial load, while specimens A1 and A3 were used to assess the effect of axial compression by varying the applied axial load under identical charge conditions. The detailed test configurations are summarized in Table 3.

Table 3.
Test condition of RC shear wall specimens.
The tests were conducted on a half-scale RC shear wall specimen. According to the similitude law for structural blast experiments, the applied axial load of 320 kN [32] corresponds to approximately 2.56 MN in the full-scale prototype (assuming a geometric scaling ratio of 1:2 and load scaling factor of λ3 = 8). This prototype-level axial force approximates the cumulative gravity load from 6 to 8 typical floors in a mid-rise RC building based on an assumed tributary floor area of 25–30 m2 per wall and a representative floor load of 10–12 kN/m2 [33].
After 28 days of standard curing, the RC shear walls were transported to the test site for contact blast experiments. As shown in Figure 3a, all three specimens were subjected to the same boundary conditions: the top was approximately simply supported, realized by clamping the top beam with steel plates and anchor bolts; the bottom was considered nearly free, with the rear side of the bot-tom beam propped by a support to prevent backward displacement. An approximately spherical emulsion explosive charge was suspended in front of the RC shear wall and detonated at its geometric center.

Figure 3.
Test setup diagram.
Due to the destructive nature of near-field and contact blast loading, pressure sensors placed too close to the charge may suffer damage, leading to inaccurate or lost data and increased testing costs. To address this issue, a pressure sensor was installed 65 cm to the left of the explosive charge to indirectly capture pressure information, as illustrated in Figure 3b.
The overpressure measurements were carried out using DFS-50 MPa-type pressure sensors. This sensor operates based on the strain gauge principle, where blast-induced pressure causes elastic deformation of the sensing element, and the resulting strain is converted into an electrical signal proportional to the applied pressure.
2.4. Test Results
2.4.1. Blast Load
Simoens [34] reported that the peak overpressure generated by emulsion explosives is equivalent to that produced by an equal mass of trinitrotoluene (TNT). The dynamic response of structural components under blast loading is primarily governed by the magnitude of the impulse. In terms of impulse, however, the energy output of emulsion explosives is approximately 70% that of TNT. Therefore, 1 kg of emulsion explosive is considered equivalent to 0.7 kg of TNT [35].
Figure 4 presents the time history of the reflected overpressure caused by the blast loading. The results show that the pressure rises sharply upon the arrival of the shock wave at the sensor, followed by an exponential decay over time. Additionally, there is a hump in the overpressure, which is caused by the detonation waves reflected from the expanding detonation products. This phenomenon is particularly prominent under conditions of close-in detonations with relatively large charge weights [18,36].
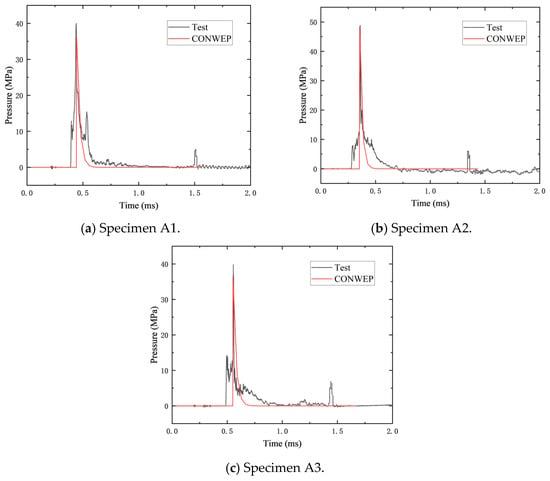
Figure 4.
Comparison of the experimental and predicted results of the peak pressure.
According to the UFC 3-340-02 guidelines, the CONWEP model was used to estimate the theoretical peak overpressure for comparison with measured results. This model is based on empirical data from spherical TNT explosions and provides a standard approach to blast load prediction [37]. Table 4 compares the peak reflected overpressures obtained from experimental measurements and CONWEP calculations. The discrepancies between the CONWEP results and the experimental measurements were all within 10%, indicating good agreement.

Table 4.
Comparison between the measured and predicted pressures.
2.4.2. Failure Modes
The experimental results of specimen A1 are presented in Figure 5. Specimen A1 developed a distinct horizontal damage band originating near the center of the blast-facing surface and extending upward. Severe concrete spalling occurred in this region, with localized loss of aggregates and mortar, exposing the internal reinforcement. The damaged zone had an average width of 12 cm, with a central width of 10 cm, a maximum width of 16 cm, and a minimum width of 8 cm. No cracks were observed in the upper or lower portions of the wall.

Figure 5.
Damage of RC shear wall specimen A1 under blast loading.
On the rear face, a main through-crack developed at the center, with a secondary branch crack extending from the upper right region. The overall failure mode was classified as flexural. A residual out-of-plane displacement of 1 cm was recorded at mid-span, and the support rotation angle reached 0.76°. Despite visible damage, the wall did not suffer through-thickness failure and remained structurally intact.
The experimental results of specimen A2 are shown in Figure 6. specimen A2 experienced severe horizontal cracking in the mid-span region, nearly separating the upper and lower portions of the wall. Extensive concrete spalling occurred, with partial exposure of reinforcement. Although some longitudinal bars remained connected, the wall had essentially lost its load-bearing capacity, indicating that the central portion was violently displaced during the explosion, resulting in significant structural damage.

Figure 6.
Damage of RC shear wall specimen A2 under blast loading.
On the blast-facing side, the horizontal spalling zone in the mid-region had an average width of 24 cm, with a central crack width of 15 cm, a maximum width of 27 cm, and a minimum width of 12 cm. No vertical propagation of the crack was observed. Cracking was also found in the upper region, while the lower portion remained relatively intact. On the rear face, a primary horizontal crack developed, accompanied by a circular spall crater on the left side, from which radial cracks extended outward. The concrete spalling followed an inverted triangular pattern in depth, and all tensile reinforcement in the affected zone was fractured.
The overall failure mode was characterized as flexural–shear. Prominent delamination was observed in the upper region, and a large residual out-of-plane displacement of 31 cm occurred at mid-span, with a support rotation angle of 22.4°. Although partial reinforcement continuity remained, the wall was effectively severed at the center and had lost its structural integrity.
As shown in Figure 7, specimen A3 developed a horizontal damage band with an average width of 15 cm, extending upward from the mid-height of the wall. In the central region of the blast-facing side, large-scale concrete spalling occurred, with partial exposure and bending of the reinforcement. The spalling zone was concentrated in the shear-damaged area near mid-span. Multiple cracks appeared along the side surfaces, and a prominent diagonal crack developed near the top of the wall, propagating upward through the thickness.

Figure 7.
Damage of RC shear wall specimen A3under blast loading.
On the rear face, a horizontal fracture zone was located approximately 10 cm above the central axis. Cracking was primarily concentrated below this fracture line, and reinforcement in the horizontal rupture zone was fractured. The overall failure mode was identified as flexural–shear. Cracks were also observed in the upper region of the wall.
A residual out-of-plane displacement of 16.5 cm was recorded at the mid-span, and the support rotation angle was measured as 12.4°.
2.5. Summary of Experimental Results
The results from specimens A1 and A2 indicate that a 50% increase in explosive charge weight (from 4 kg to 6 kg) under close-in detonation significantly elevates the peak overpressure and impulse. This sudden amplification of tensile, shear, and flexural effects at the moment of blast loading intensifies the damage, particularly in the mid-span region of the wall.
A comparison between A1 and A3 further shows that the application of axial compression modifies the height of the compression zone and the internal force distribution. This contributes to flexural equilibrium and enhances the wall’s bending resistance under blast loading.
The observed failure modes in the experiments differed from the conventional panel-type response, where localized cratering typically occurs at the center of impact. This deviation can be attributed to the geometry of the specimens—walls with a height of 1500 mm and a thickness of only 100 mm—making them slender vertical elements. Under such proportions, blast loading tends to induce overall out-of-plane bending rather than localized punching damage.
Repeated observations during testing revealed the formation of through-thickness horizontal cracks and, in some cases, complete mid-span fracture. These results confirm that the dominant failure mechanism was global flexural failure, rather than localized surface damage.
3. Finite Element Model
The numerical simulations in this study were conducted using LS-DYNA R11 (LSTC, Livermore, CA, USA, 2021), a nonlinear explicit finite element software widely used in dynamic impact and blast analysis. LS-DYNA provides robust capabilities for solving highly nonlinear transient dynamic problems involving fluid–structure interaction (FSI), material failure, and large deformation. It was selected for this study due to its ability to implement coupled Arbitrary Lagrangian–Eulerian (ALE) and Lagrangian formulations, which are essential for accurately capturing the interaction between the explosive detonation products and the reinforced concrete structure. The software’s extensive material libraries and erosion models also support detailed damage evolution modeling in blast-loaded concrete members.
3.1. Solid Model
A three-dimensional finite element (FE) model of a reinforced concrete (RC) shear wall under blast loading was developed based on the actual geometric dimensions of the experimental specimens, as shown in Figure 8. The model consisted of five material components: concrete, reinforcement, steel plates, air, and explosive. Concrete, steel plates, air, and explosive were modeled using SOLID164 solid elements, while the reinforcement was represented using BEAM161 elements to simulate its structural behavior. The element types were selected based on their suitability for modeling blast-related phenomena. SOLID164, an 8-node brick element, was used for modeling concrete, air, steel plates, and explosive materials because of its compatibility with the ALE formulation and its ability to capture large deformation and wave propagation. BEAM161 elements were used for reinforcement modeling as they effectively simulate the mechanical behavior of embedded steel bars under dynamic loads, while also allowing efficient coupling with the surrounding concrete through constraint equations.
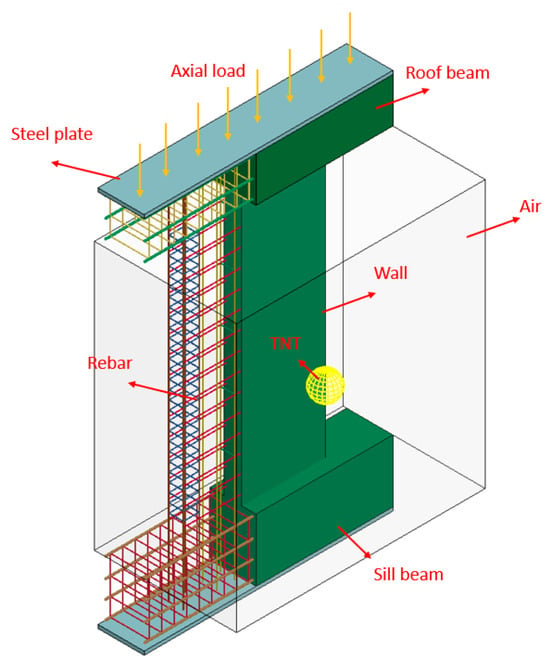
Figure 8.
Finite element model of shear wall.
The *AUTOMATIC_SURFACE_TO_SURFACE algorithm refers to a general surface-to-surface contact method used in finite element analysis to define mechanical interactions between contacting parts. The contact interaction between the steel plates and the concrete wall surfaces was defined using the *AUTOMATIC_SURFACE_TO_SURFACE contact algorithm to accurately simulate the constraints at the top and bottom boundaries. By replicating the experimental clamping setup in the numerical model, similar boundary conditions were ensured, thereby enhancing the comparability between the simulation and test results, as shown in Figure 9.
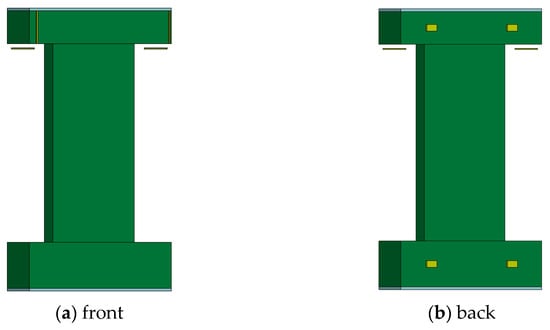
Figure 9.
Schematic diagram of boundary conditions in the simulation.
Both the reinforcement and concrete were modeled using the Lagrangian description, and their interaction was achieved through Lagrangian coupling within the solid domain. *BOUNDARY_PRESCRIBED_MOTION_SET is used in finite element analysis to apply a predefined motion (displacement, velocity, or acceleration) to a specific set of nodes. In our study, it was utilized to simulate the axial compression by applying a constant displacement at the top nodes of the shear wall specimen. This method ensures that the axial load remains stable during the blast event, thereby reproducing the boundary condition observed in the physical tests.
To avoid artificial reflections from the boundaries of the air domain, non-reflecting boundary conditions were applied to its outer surfaces, allowing for the effective simulation of wave propagation in an infinite medium.
A Lagrangian formulation was used for the concrete and reinforcement, while the air and explosive domains were modeled using the Arbitrary Lagrangian–Eulerian (ALE) approach. A fluid–structure interaction (FSI) algorithm was implemented to simulate the dynamic interaction between the solid and fluid media [38].
MAT_ADD_EROSION is an erosion criterion in LS-DYNA that allows for element deletion based on user-defined failure thresholds, such as maximum principal strain or effective plastic strain. To account for possible large deformation or severe distortion of concrete elements under blast effects, the *MAT_ADD_EROSION keyword was applied. A principal strain failure threshold of 0.3 was defined for concrete; elements exceeding this value were automatically deleted to maintain computational stability and prevent mesh distortion.
Mesh sizes of 10 mm, 20 mm, and 30 mm were tested, as shown in Figure 10. The simulation errors for 10 mm and 20 mm meshes were 6.3% and 9.3%, respectively, while the 30 mm mesh yielded a 15% error. To balance computational efficiency and accuracy, a mesh size of 20 mm was selected for the air domain, while a finer mesh of 10 mm was used for the concrete and reinforcement. This ensured both accurate stress wave propagation and reliable capture of localized structural responses.
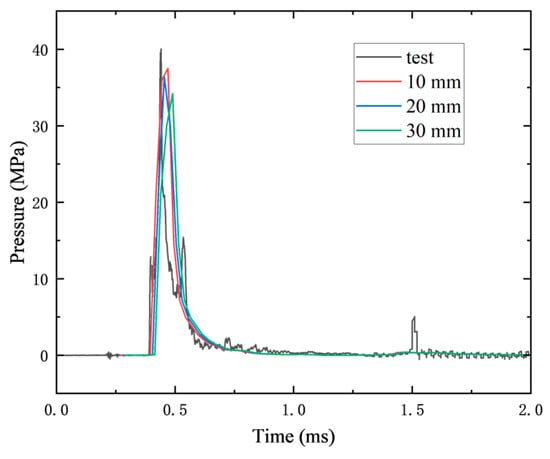
Figure 10.
Overpressure curves of different grids.
3.2. Material Model
In this study, the RHT (Riedel–Hiermaier–Thoma) concrete model was adopted to represent the dynamic behavior of concrete under blast loading. This model accounts for pressure-dependent strength, strain-rate effects, damage accumulation, and post-failure softening. It is particularly effective for simulating high strain-rate phenomena and has been validated in many previous studies involving impact and explosion scenarios. This model incorporates a p–α equation of state, the RHT strength model [39,40,41,42], a damage model, and an erosion algorithm. The RHT strength model defines three surfaces—the elastic-plastic yield surface, failure surface, and residual strength surface—which together characterize the concrete’s yield strength, peak strength, and residual strength. This allows the model to realistically capture the entire behavior of concrete from elastic deformation to failure, making it particularly suitable for simulating the dynamic properties of concrete under blast and impact loading.
The model also utilizes the Mie–Grüneisen equation of state in combination with the p–α compaction model to describe volumetric compaction effects. The specific material parameters used are listed in Table 5.

Table 5.
Concrete material parameters.
The strength criterion of the RHT model describes the yield and failure behavior of concrete under different stress states through the following equations:
where represents the dimensionless equivalent strength, denotes the elastic strength of the material, refers to the material strength considering damage, and represents the material strength under complete failure conditions.
Within the framework of a macroscopic model, the rate-dependent strength of concrete is typically modeled by expanding the failure surface using a Dynamic Increase Factor (). In the standard RHT model, as implemented in AUTODYN, the for both tension and compression is expressed as a linear function of the logarithm of the strain rate, as follows [43]:
where d and a are constants. The quasi-static strain rate is taken as for tension and for compression.
The reinforcement was modeled using the MAT_PLASTIC_KINEMATIC material model (MAT_003), which accounts for high strain rate effects [44,45]. The strain rate sensitivity was incorporated through the Cowper–Symonds model. In this formulation, the vertical reinforcement and ties in the RC shear wall were treated as isotropic plastic materials with kinematic hardening behavior. The model defines the yield stress as a function of the following parameters:
where represents the strain rate. The detailed reinforcement parameters are listed in Table 6.

Table 6.
Reinforcement material parameters.
Air was modeled using the MAT_NULL material model in combination with the EOS_LINEAR_POLYNOMIAL equation of state. The equation of state is expressed as follows:
where is the pressure; is the compression ratio; and are the current and initial densities, respectively; is the internal energy per unit volume; and , , , , , , and are material constants. The material parameters for air are provided in Table 7 [46].

Table 7.
Explosive material parameters.
Since No. 2 rock emulsion explosive [47] was used in the experiments, its equivalent pressure was scaled by a coefficient of 0.7 to convert the rock emulsion explosive into TNT equivalent for numerical simulation [34,48]. TNT explosive was modeled using the MAT_HIGH_EXPLOSIVE_BURN material model in conjunction with the Jones–Wilkins–Lee (JWL) equation of state. The JWL equation of state is expressed as follows:
where is the pressure, is the specific volume, and are the specific volume, is the internal energy per unit volume, and , , , , and are material-specific constants. The material parameters are provided in Table 8 [49].

Table 8.
Air material parameters.
3.3. Verification of Numerical Model
To validate the accuracy of the numerical model, the simulated reflected overpressure, damage morphology, and final displacement at the wall center were compared against the experimental results.
Figure 11 compares the experimental and numerical results of the reflected overpressure. The reliability of the numerical model was verified by comparing the simulated and experimental results of reflected overpressure for three specimens (A1–A3). As shown in Table 9, all relative errors between measured and predicted peak pressures were within 10%, demonstrating the acceptable accuracy and reliability of the simulation.
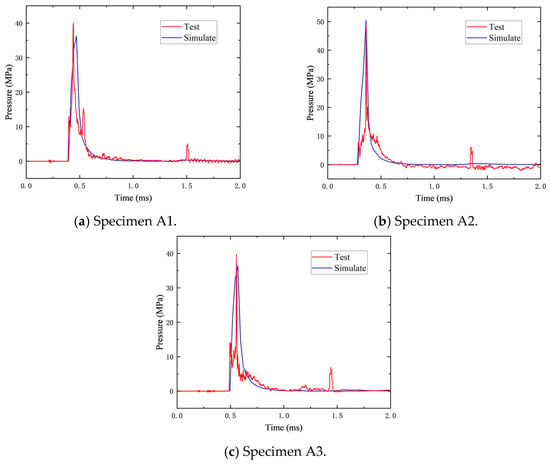
Figure 11.
Comparison of the experimental and numerical results of the peak pressure.

Table 9.
Comparison of the experimental and numerical results of the peak pressure.
The simulated damage pattern of specimen A1 showed good agreement with the experimental results in Figure 12. A pronounced flexural failure developed at mid-height, with a primary crack approximately 13 cm wide on the front face and a through-thickness crack at the rear center. The numerically predicted residual deflection at mid-span was 1.1 cm, slightly higher than the experimental value, with a deviation of about 10%.

Figure 12.
Comparison of test and simulation results for specimen A1.
The numerically simulated damage pattern of specimen A2 is shown in Figure 13. A clear shear failure developed at the wall center, with a primary crack approximately 30 cm wide on the front face. The simulated residual mid-span deflection was 30 cm, slightly less than the experimental value of 31 cm, resulting in a deviation of 3%. A circular spall crater also appeared on the rear face in the simulation, with a diameter of 25 cm—slightly larger than the 23 cm measured in the experiment—corresponding to an 8% error. This difference may be attributed to the uniform application of axial load in the numerical model.


Figure 13.
Comparison of test and simulation results for specimen A2.
The numerically simulated damage pattern of A3 is shown in Figure 14. The simulated residual mid-span deflection was 17.5 cm, slightly higher than the experimental value, with a deviation of approximately 6%. The location of the rear-face fracture was consistent with that observed in the experiment.

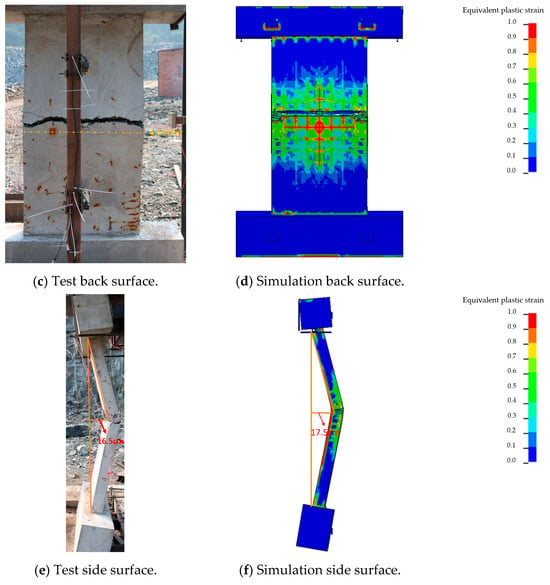
Figure 14.
Comparison of test and simulation results for specimen A3.
The simulation results were generally consistent with the experimental observations, capturing the main deformation and failure characteristics of the RC shear wall under blast loading.
After validating the numerical model against the experimental results, it was subsequently employed to perform a series of parametric analyses. The influence of key factors—including boundary conditions, aspect ratio, axial compression ratio, and explosive charge weight—on the blast response and failure behavior of RC shear walls was systematically investigated.
4. Parametric Analysis
4.1. Effect of Boundary Conditions
To investigate the influence of boundary conditions on the damage behavior of RC shear walls under blast loading, simulations were conducted by varying the end restraints while keeping the explosive charge and standoff distance constant.
As shown in Figure 15, when both the top and bottom ends were not fully constrained, the RC shear wall exhibited significant global bending deformation. A horizontal crack formed at mid-span, and wide cracks appeared on the rear face of the wall. Due to the minimal boundary constraints, the cracks remained relatively shallow, and the wall was able to dissipate part of the blast energy through ductile bending. The resulting damage level was classified as severe.
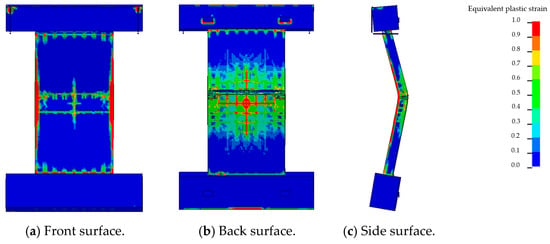
Figure 15.
One end simply supported and one end hinged.
In contrast, Figure 16 shows that when both ends were fully restrained, out-of-plane deformation was significantly suppressed. No large-scale bending was observed, and a transverse crushing zone appeared at mid-height. The rear face displayed a larger concrete damage area, with cracks concentrated around the center of the wall. The maximum mid-span displacement was 3.97 cm, and the support rotation angle was 3.03°, corresponding to a moderate damage level.
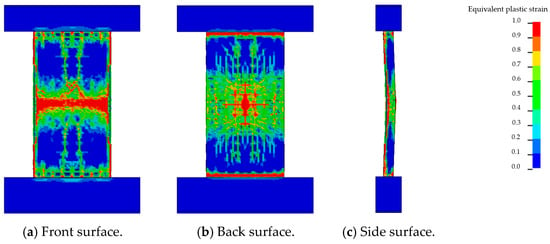
Figure 16.
Fixed support at both ends.
These results demonstrate that boundary conditions not only govern the out-of-plane stiffness and deformation capacity of RC shear walls but also significantly influence crack distribution and failure modes under blast loading. In practical engineering applications, most RC shear walls are fixed at both ends. Therefore, fully fixed boundary conditions were adopted in all subsequent numerical simulations.
4.2. Effect of Aspect Ratio
To investigate the influence of aspect ratio on the damage behavior of RC shear walls under identical blast conditions, the wall height was kept constant while the wall width (, defined as the wall width) was varied to adjust the aspect ratio. Figure 17 shows the damage patterns of RC shear walls subjected to a 5 kg emulsion explosive (equivalent to 3.5 kg TNT) at a standoff distance of 40 cm.
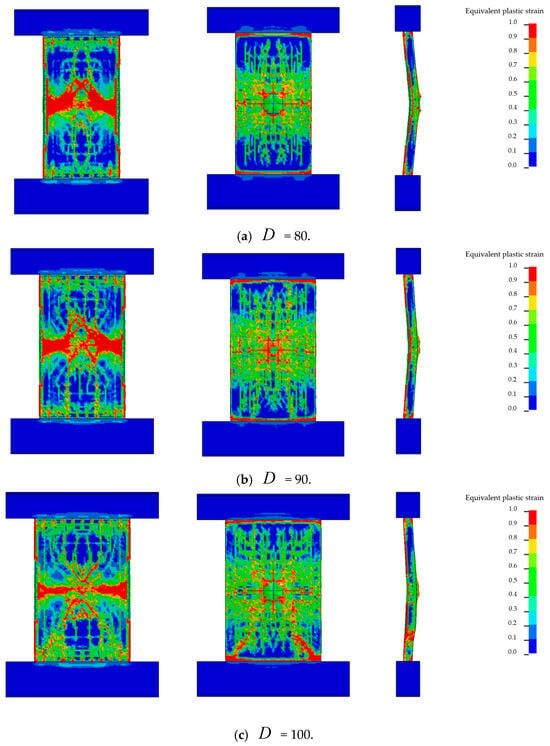
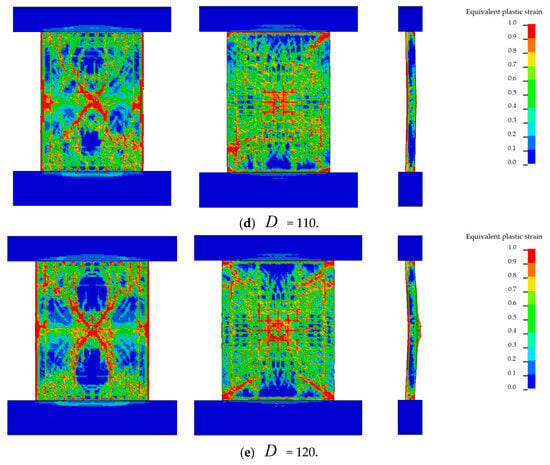
Figure 17.
Effect of aspect ratio on damage of RC shear walls.
As illustrated in Figure 17, the failure mode of the RC shear walls changes noticeably with decreasing aspect ratio under the same explosive charge and standoff conditions. When the wall width was 80 cm, a prominent horizontal concrete spalling zone appeared on the blast-facing side, while the rear face exhibited a circular crushed area. Due to the relatively low out-of-plane stiffness, the wall was more susceptible to large deflections under short-duration high-intensity blast loading, resulting in the formation of pronounced horizontal cracks.
As the wall width increased to 90 cm and 100 cm, the spalling zone on the front face became significantly narrower, and the rear face developed localized cracking at the center. When the width further increased to 110 cm and 120 cm, the horizontal spalling zone disappeared entirely, replaced by an X-shaped failure pattern. The cracking region on the rear face expanded, but the overall wall exhibited stronger out-of-plane flexural resistance. The blast energy was distributed over a wider area, resulting in more superficial spalling and non-penetrating cracks.
In addition, to further analyze the influence of aspect ratio on the damage mode of RC shear walls under identical blast loading, Figure 18 summarizes the central displacement responses of the walls subjected to different explosive charges. Here, the maximum displacement of the RC shear wall is used as an indicator of the overall displacement response.
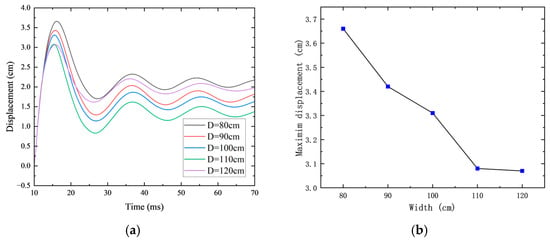
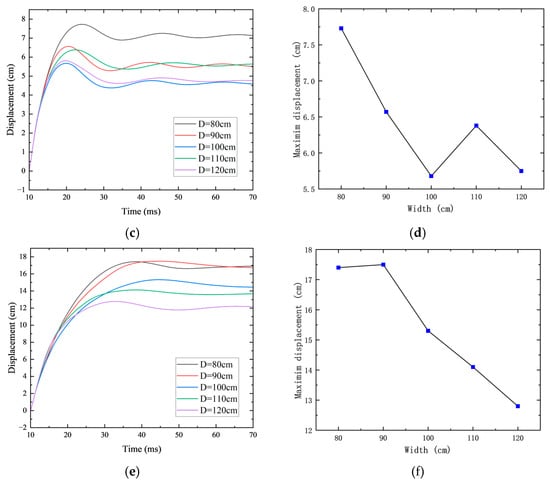
Figure 18.
Effect of aspect ratio on displacement response. (a) Displacement–time history curves under different aspect ratios at 2.8 kg TNT charge; (b) maximum displacement under different aspect ratios at 2.8 kg TNT charge; (c) displacement–time history curves under different aspect ratios at 3.5 kg TNT charge; (d) maximum displacement under different aspect ratios at 3.5 kg TNT charge; (e) displacement–time history curves under different aspect ratios at 4.2 kg TNT charge; (f) maximum displacement under different aspect ratios at 4.2 kg TNT charge.
Under the 2.8 kg explosive charge, the maximum displacement gradually decreased as the wall width increased, from 3.66 cm at D = 80 cm to 3.07 cm at D = 120 cm. This indicates that wider walls possess higher out-of-plane stiffness, which enhances their resistance to blast loads and results in smaller displacements.
At the 3.5 kg charge level, the maximum displacement decreased steadily from 7.73 cm at D = 80 cm to 5.68 cm at D = 100 cm, confirming that increased wall width improves out-of-plane stiffness and reduces displacement under blast loading. However, a rebound in displacement was observed at D = 110 cm, where the maximum displacement increased to 6.38 cm before decreasing again to 5.75 cm at D = 120 cm. As shown in Figure 17, the damage mode at D = 110 cm shifted from global to local failure, with the central region bulging outward, resulting in a larger out-of-plane deflection. At D = 120 cm, despite similar damage, the increased width enhanced the out-of-plane stiffness, leading to a reduction in maximum displacement.
Under a 4.2 kg explosive charge, the maximum central displacements at D = 80 cm and D = 90 cm were similar, indicating a transition from global to local failure modes. From D = 90 cm to D = 120 cm, the maximum displacement continued to decrease with increasing wall width. This further confirms that greater wall width improves out-of-plane stiffness and effectively suppresses excessive displacement under high-intensity blast loading.
4.3. Effect of Axial Load
To investigate the influence of axial compression on the damage characteristics and dynamic response of RC shear walls under blast loading, the aspect ratio, explosive charge, and standoff distance were kept constant. The axial compression ratio was varied by adjusting the applied axial load while maintaining consistent specimen geometry and blast conditions. Figure 19 compares the damage patterns of RC shear walls subjected to a 3.5 kg emulsion explosive at a standoff distance of 40 cm under different axial compression ratios . The axial compression ratio is defined as the ratio between the applied axial load and the axial load-carrying capacity of the wall section, expressed as:
where is the applied axial load; is the axial compressive strength of concrete; and is the cross-sectional area of the wall.
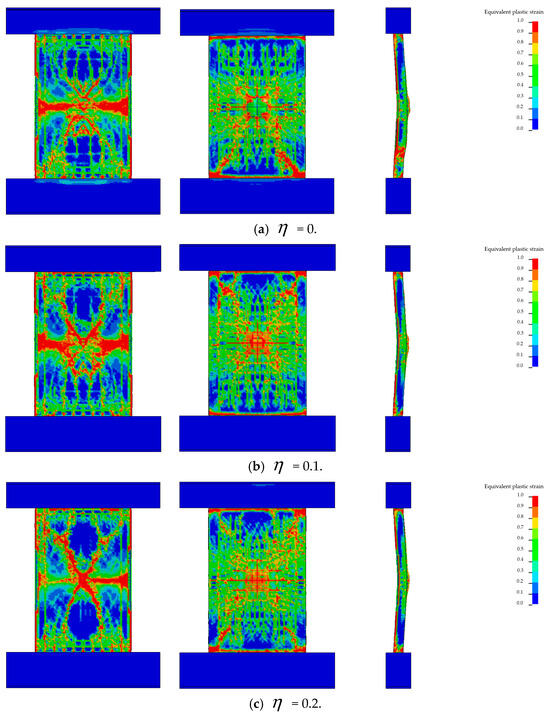
Figure 19.
Effect of axial loads on damage of RC shear walls.
When the axial load = 0, the RC shear wall exhibited global failure. On the blast-facing side, a long vertical strip of concrete damage developed, while the rear face showed a circular spalling zone. When the axial load increased to = 0.1, the failure mode shifted from global to local. The front face displayed both a vertical strip and an emerging X-shaped damage zone, while the spalling zone on the rear face disappeared.
At = 0.2, a more distinct X-shaped damage pattern formed on the blast-facing side, and the damaged area on the rear face was further reduced. When the axial load was increased to = 0.3, the X-shaped damage zone became more concentrated at the wall center, and rear-face damage continued to diminish.
However, when the axial load reached = 0.4, both a vertical strip-shaped damage zone and an X-shaped damage pattern reappeared on the blast-facing side, indicating a transition from localized to global failure in the RC shear wall. On the rear face, more cracks were observed, further reflecting the increase in overall structural damage.
Figure 20 presents the time–history curves of mid-span displacement for RC shear walls under different axial load levels. As shown in the figure, with increasing axial load, the displacement oscillation period becomes shorter, indicating an increase in wall stiffness due to the enhanced axial compression.
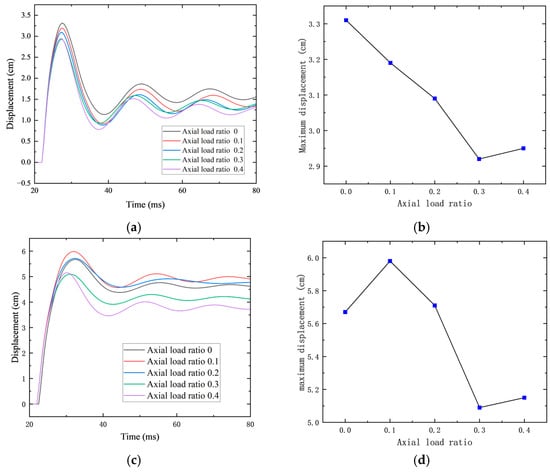
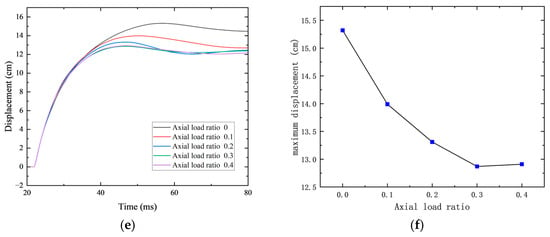
Figure 20.
Effect of axial load on displacement response. (a) Displacement–time history curves under different axial loads at 2.8 kg TNT charge; (b) maximum displacement under different axial loads at 2.8 kg TNT charge; (c) displacement–time history curves under different axial loads at 3.5 kg TNT charge; (d) maximum displacement under different axial loads at 3.5 kg TNT charge; (e) displacement–time history curves under different axial loads at 4.2 kg TNT charge; (f) maximum displacement under different axial loads at 4.2 kg TNT charge.
Under a 2.8 kg explosive charge, the maximum displacement at the wall center gradually decreased from 3.39 cm to 2.92 cm as the axial load increased from 0 to 0.3. This is attributed to the fact that moderate axial compression places the wall cross-section under pre-compressive stress, which improves the out-of-plane stiffness and overall stability. As a result, the wall’s resistance to blast-induced deformation is enhanced, and both out-of-plane bending and crack propagation are suppressed. However, when the axial load was further increased to 0.4, the maximum displacement slightly rebounded to 2.95 cm. This is likely because although a higher axial load provides greater stiffness and initially smaller deformation, once local cracking or spalling occurs, brittle fracture may trigger a redistribution of internal forces, leading to localized deflection increases and further crack propagation.
Under a 3.5 kg explosive charge, the axial load ratio increase from 0 to 0.1 led to a rise in displacement from 5.67 cm to 5.98 cm. As the ratio increased from 0.1 to 0.2, the displacement slightly decreased to 5.71 cm, which was still above the value for the uncompressed case. As shown in Figure 19, applying axial compression increases wall stiffness and induces stress concentration, which shifts the damage pattern from global to local failure. When the axial load ratio increased from 0.2 to 0.3, the wall’s flexural–shear resistance was significantly enhanced, leading to a marked decrease in displacement. This suggests that the “locking effect” of axial compression became dominant, suppressing large deflection and concentrating cracks before rapid propagation. However, when the axial load was further increased to 0.4, the wall became more susceptible to localized brittle failure. Once initial cracks formed, stress redistribution occurred, leading to locally intensified damage and a slight rebound in displacement.
Under a 4.2 kg explosive charge, as the axial load ratio increased from 0 to 0.3, the out-of-plane displacement was significantly reduced from 15.32 cm to 12.87 cm, passing through intermediate values of 13.99 cm and 13.31 cm. When the axial load ratio further increased to 0.4, the maximum displacement slightly rose to 12.91 cm. This trend is consistent with that observed under the 4 kg explosive condition.
4.4. Effect of Explosive Charge
To investigate the damage mechanisms of reinforced RC shear walls under close-in blast loading with different explosive charge weights, numerical simulations were carried out on walls with a fixed width of 100 cm. The standoff distance was kept constant at 40 cm, and the structural response under varying TNT charge weights was analyzed. The corresponding damage patterns are shown in Figure 21, and detailed simulation parameters are summarized in Table 10. The scaled distance is defined as:
where is the scaled distance; is the standoff distance from the charge to the target; and is the TNT equivalent charge weight.
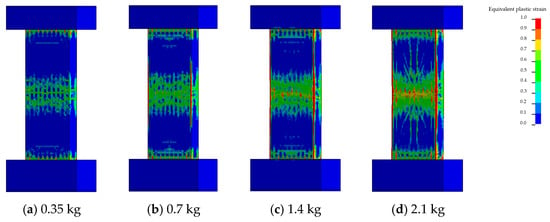
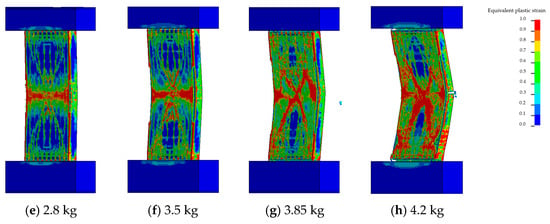
Figure 21.
Effect of explosive charge on damage of RC shear walls.

Table 10.
Different charge mass conditions.
When the charge weight was 0.35 kg, the wall remained intact with no visible damage. The reinforcement did not undergo deformation, and the maximum central displacement was 0.48 cm, within the elastic range. At 0.7 kg, minor surface cracks appeared on the blast-facing side, and a through-thickness crack was observed at the center of the rear face. The maximum central displacement increased to 0.73 cm.
At 2.8 kg, a noticeable concrete crushing zone formed on the blast-facing side, and the center of the rear face bulged outward. The through-crack deepened and became more concentrated. The maximum central displacement reached 3.31 cm, indicating slight flexural damage. At 3.5 kg, both vertical and X-shaped damage bands appeared on the blast-facing side, and a spall crater formed on the rear face. The maximum displacement increased to 5.67 cm, and the wall exhibited clear flexural failure.
When the charge weight was 3.85 kg, a prominent X-shaped damage zone developed on the blast-facing side, and the rear crater expanded. The maximum displacement rose to 8.90 cm, accompanied by minor cracking at the connection between the wall and the top beam. The wall showed signs of combined flexural–shear failure. At 4.2 kg, a large X-shaped damage zone formed on the front face, and extensive concrete spalling occurred on the rear face. Cracking appeared at both the top and bottom beam connections, and the wall experienced a clearly defined flexural–shear failure with a maximum central displacement of 15.32 cm.
Figure 22 presents the displacement–time curves at the center of the reinforced concrete shear wall under different scaled distances. As the blast occurred, with the standoff distance kept constant, the increase in TNT equivalent resulted in a decrease in scaled distance, leading to a larger maximum displacement at the wall center. Additionally, the time required to reach the peak displacement increased with the charge weight.
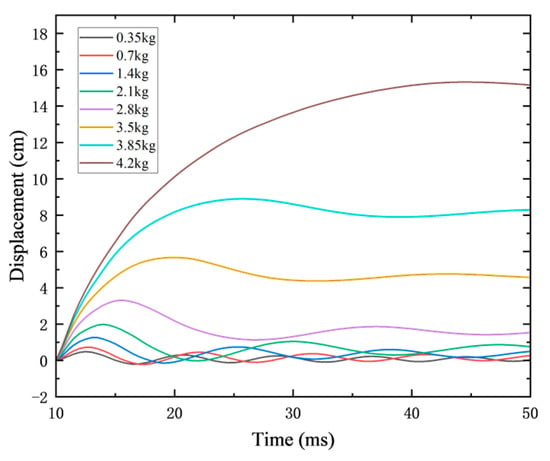
Figure 22.
Displacement–time history curves under different TNT charge weights.
Figure 23 further illustrates the relationship between peak central displacement and TNT charge weight. A curve is fitted using the least squares method , where represents the peak displacement and is the charge weight, as shown in the figure. The coefficient of determination () is 0.982, indicating a strong correlation and a good fit.
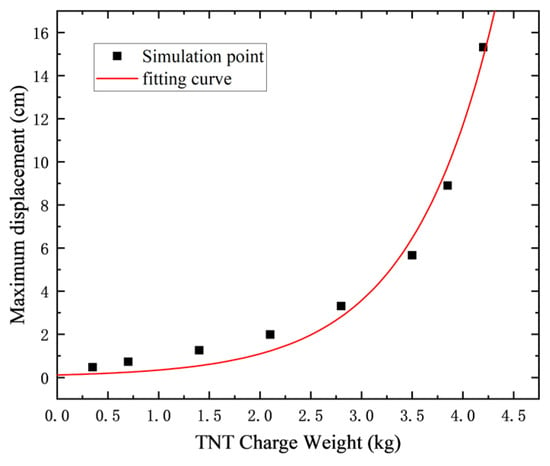
Figure 23.
Fitted curve of maximum displacement versus TNT charge weight.
For the RC shear wall model with a width of 100 cm (discussed in Section 4.2), the fitted curve in Figure 13 can be used to predict the maximum displacement at the wall center for TNT charge weights ranging from 0 to 4.2 kg.
To better interpret the damage mechanisms, Figure 24 illustrates the time–history evolution of kinetic energy, internal energy, and total energy under the 4.2 kg TNT blast scenario. Immediately following the detonation, the kinetic energy rapidly peaks and is subsequently converted into internal energy as the shear wall undergoes deformation. The total energy remains nearly constant throughout the simulation, indicating that energy conservation is well maintained. The progressive rise in internal energy represents the energy absorbed by the structure through plastic deformation and cracking, which aligns with the observed damage patterns.
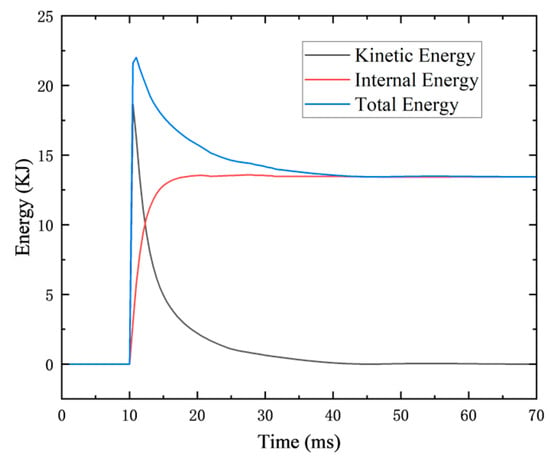
Figure 24.
Time–history curves of energy.
Figure 25 presents the relationship between the absorbed internal energy and TNT charge weight. As the explosive charge increases, the internal energy absorbed by the wall also increases nonlinearly. This trend indicates that more energy is transferred into the structure during higher-intensity blasts, leading to more significant plastic deformation and damage. The absorbed energy can be used as a quantitative indicator of the wall’s damage level, providing a complementary metric to displacement-based assessments.
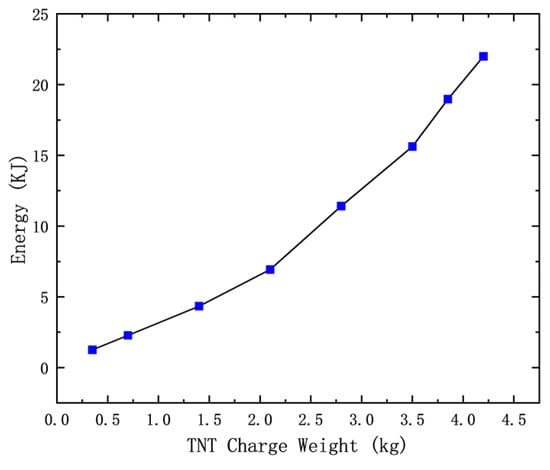
Figure 25.
Variation of absorbed internal energy with TNT charge weight.
Under blast loading, the failure modes of RC shear walls are primarily characterized by flexural failure or combined flexural–shear failure. Therefore, the support rotation angle is considered a more appropriate parameter for evaluating the damage level of shear walls. Based on the recommendations in Reference [50], the damage level assessment parameter for RC shear walls is defined as follows:
where denotes the maximum mid-span displacement of the shear wall, and represents the shortest distance between the wall center and the support. The corresponding relationship between the damage level of the RC shear wall and the support rotation angle as well as the mid-span displacement is presented in the table.
Based on the numerical simulation results, the damage phenomena associated with five typical failure modes are described as follows:
(1) No Damage: The wall remains within the elastic range under blast loading, with no impact on structural function. The support rotation angle is less than 0.5°.
(2) Minor Damage: A small number of fine cracks appear on the wall surface, with limited width and no through-thickness penetration. Localized concrete spalling may occur, but no visible perforation is formed. Overall deformation is small, and mid-span deflection remains within acceptable limits. The residual load-bearing capacity is essentially intact, and the structural function remains unaffected. The support rotation angle is between 0.5° and 2°.
(3) Moderate Damage: Significant radial and circumferential cracks develop on the wall surface, some penetrating the full thickness. Concrete spalling is more severe, with shallow craters or localized perforations possible. Overall deformation is considerable, and mid-span deflection exceeds allowable limits. Some residual load-bearing capacity remains, though structural function is partially impaired. The support rotation angle is between 2° and 6°.
(4) Severe Damage: Numerous through-thickness cracks appear, accompanied by extensive concrete spalling. Deep craters or large perforations form. The wall exhibits large overall deformation, and mid-span deflection significantly exceeds allowable limits. Residual capacity is greatly reduced. Collapse or blowout may occur on the rear face, with concrete fragments projected outward. Structural function is severely compromised. The support rotation angle is between 6° and 12°.
(5) Complete Failure: The wall completely fractures or collapses, losing all load-bearing capacity. Concrete is heavily fragmented, and reinforcement is exposed or ruptured. Rear-face blowout and through-failure are extremely severe, with wide debris scattering. Structural function is entirely lost. The support rotation angle exceeds 12°.
5. Discussion
Although this study employed 1:2 scale RC shear wall specimens, it is acknowledged that material behavior under high strain rates may not be fully captured at a reduced scale. While geometric similitude was maintained, the strain-rate sensitivity of concrete and steel may exhibit scale-dependent discrepancies. To improve the applicability of the findings to real-world scenarios, future research is encouraged to apply similitude laws (e.g., dimensional analysis-based scaling laws) or strain-rate correction models to bridge the gap between scaled and full-scale behavior. Full-scale experimental validation is also recommended to enhance the robustness and generalizability of the conclusions.
It is acknowledged that the boundary conditions adopted in the experiments—simply supported at the top and nearly free at the bottom—may not fully reflect the fixity conditions of shear walls in actual buildings. To address this limitation, the numerical simulations were conducted with fixed–fixed boundary conditions to better represent realistic structural constraints. The comparative results indicate that boundary conditions significantly influence the deformation patterns and failure modes of RC shear walls. Future research is recommended to explore more representative boundary fixities, such as frame-integrated or continuous systems, in both physical testing and numerical simulations, in order to improve the applicability of the findings to real-world engineering design.
In this study, axial load was applied statically before the blast, which simplifies the real scenario in which axial forces may fluctuate during an explosion. This approach is commonly used in experimental setups but may not fully capture dynamic interactions. While it still provides valuable insights into the role of axial compression, future studies are encouraged to adopt dynamic axial loading methods to better reflect real structural responses under blast conditions.
This study employed deterministic simulations without incorporating uncertainty analysis. To better reflect real-world variability in material properties and loading conditions, future work should introduce stochastic modeling approaches such as Monte Carlo simulation. Additionally, fragility curves could be developed to assess the probability of damage under varying blast intensities.
It was observed that under different charge weights, the damage mode of the shear wall transitioned from horizontal band-like cracking to X-shaped diagonal cracking. However, the critical aspect ratio at which this transition occurred varied depending on the explosive intensity. This indicates that the interaction between charge weight and aspect ratio affects the failure mechanisms in a non-linear manner. Further systematic studies are needed to identify the threshold aspect ratios corresponding to various blast intensities.
This study focused on the blast response of RC shear walls under axial compression, without considering conventional lateral forces such as seismic or wind loads. This simplification was made to isolate the effects of blast loading, which differs greatly from other lateral loads in terms of intensity and duration. However, in real structures, combined loading may occur. Future work should consider the interaction of blast with other lateral forces to improve design reliability.
Due to the extreme and instantaneous nature of blast loading, the peak displacement occurred within a few milliseconds, with timing varying across charge weights. However, the displacement and acceleration sensors detached during testing, limiting our ability to continuously track the damage evolution. Based on visual inspections and residual deformation observations, the majority of damage appeared to develop during the initial blast impact phase.
For specimens subjected to larger charge weights, damage included severe spalling, reinforcement exposure, and significant residual deformation—indicating potential irreparability. In contrast, specimens under lower charge weights displayed only moderate cracking, suggesting that repair might be feasible using grouting or surface patching methods.
Future studies should incorporate high-fidelity damage monitoring technologies such as high-speed photography or Digital Image Correlation (DIC) systems to better assess the reparability and progressive damage development of blast-loaded RC walls.
6. Conclusions
This study investigated the damage behavior of reinforced concrete (RC) shear walls subjected to close-in blast loading through a combination of experimental testing and validated numerical simulations. The key findings are summarized as follows:
(1) The finite element model showed good agreement with experimental results, with prediction errors for residual displacement and spalling length within 10%, confirming the model’s accuracy and applicability.
(2) Boundary conditions significantly influence failure modes. Stiffer supports reduce large deflections but may lead to brittle cracking, while more flexible supports enhance ductility but increase residual deformation.
(3) Aspect ratio plays a critical role in blast performance. Walls with higher aspect ratios (i.e., slender configurations) suffered increased out-of-plane displacement and concentrated damage, whereas lower aspect ratios (i.e., wider walls) exhibited better blast resistance and more distributed damage patterns.
(4) Moderate axial compression ratios (around 0.3) improve stiffness and reduce displacement, effectively helping to control wall damage. However, excessive axial compression (>0.3) increases brittleness and the likelihood of sudden failure under blast loading.
(5) Peak displacement at the wall center increased with TNT charge weight, indicating a strong correlation between blast intensity and structural response.
These findings provide valuable guidance for the design of blast-resistant RC shear walls, particularly in protective or defense-related structures. However, the study was limited to scaled specimens and simplified loading and boundary conditions. Future work should investigate full-scale structures, incorporate more realistic material heterogeneity, and evaluate the effectiveness of reinforcement detailing and retrofit methods under varied blast scenarios.
Author Contributions
Formal analysis, W.L.; Investigation, W.L.; Writing—original draft, W.L.; Writing—review and editing, R.Z., W.W. and C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gültepe, E.; Çömlekoğlu, H.G.; Öztürk, B.; Dönmez, C. Discussion on the Causes of the Observed Damages in the 2023 Kahramanmaraş Earthquakes. In Lecture Notes in Civil Engineering, Proceedings of the 7th International Conference on Earthquake Engineering and Seismology (ICEES 2023), Antalya, Türkiye, 6–10 November 2023; Springer: Cham, Germany, 2024; Volume 488. [Google Scholar] [CrossRef]
- Smith, P.D.; Mays, G.C.; Elliott, C.L. The protection of buildings against terrorism and disorder. Struct. Build. 1992, 94, 287–297. [Google Scholar] [CrossRef]
- Luccioni, B.M.; Ambrosini, R.D.; Danesi, R.F. Analysis of building collapse under blast loads. Eng. Struct. 2004, 26, 63–71. [Google Scholar] [CrossRef]
- Ha, T.; Ko, J.; Lee, S.; Kim, S.; Jung, J.; Kim, D.-J. A Case Study on the Rehabilitation of a Fire-Damaged Structure. Appl. Sci. 2016, 6, 126. [Google Scholar] [CrossRef]
- Wang, W.; Yang, G.; Yang, J.C.; Wang, Y.; Liu, F. Experimental and numerical research on reinforced concrete slabs strengthened with POZD coated corrugated steel under contact explosive load. Int. J. Impact Eng. 2022, 170, 104256. [Google Scholar] [CrossRef]
- Wang, W.; Song, X.; Yang, J.; Liu, F.; Gao, W. Experimental and numerical research on the effect of ogive-nose projectile penetrating UR50 ultra-early-strength concrete. Cem. Concr. Compos. 2023, 136, 104852. [Google Scholar] [CrossRef]
- Ginsburg, S.; Kirsch, U. Design of Protective Structures Against Blast. J. Struct. Eng. 1983, 109, 1490–1506. [Google Scholar] [CrossRef]
- Zineddin, M.Z. Blast effects and protective structures: An interdisciplinary course for military engineers. Saf. Secur. Eng. III 2009. [CrossRef]
- Makhutov, A.N.; Baecher, B.G.; Zineddin, M. Antiterrorism Protection and Protective Engineering Design. NATO Sci. Peace Secur. Ser. E Hum. Soc. Dyn. 2012, 102, 184–189. [Google Scholar]
- Jayasooriya, R.; Thambiratnam, P.D.; Perera, J.N.; Reid, S.R. Blast and residual capacity analysis of reinforced concrete framed buildings. Eng. Struct. 2011, 33, 3483–3495. [Google Scholar] [CrossRef]
- Alaoui, S.; Oswald, C.C. Blast-resistant design considerations for precast, prestressed concrete structures. PCI J. 2007, 52, 53–66. [Google Scholar] [CrossRef]
- Ning, J.; Yang, S.; Ma, T.; Xu, X. Fragment behavior of concrete slab subjected to blast loading. Eng. Fail. Anal. 2022, 138, 106313. [Google Scholar] [CrossRef]
- Wang, W.; Xu, Z.; Li, Y.; Zhang, Y. Experimental and numerical investigation of polyurea reinforced concrete thick slab under contact explosion. Eng. Fail. Anal. 2025, 171, 109349. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, C.; Yang, G. Anti-explosion Performance of a New Type of Polyurea-Coated Corrugated Steel Plate Reinforced Concrete Slab. Int. J. Concr. Struct. Mater. 2024, 18, 1–13. [Google Scholar] [CrossRef]
- Milani, G.; Lourenco, B.P. Blast Analysis of Enclosure Masonry Walls Using Homogenization Approaches. Int. J. Multiscale Comput. Eng. 2009, 7, 91–113. [Google Scholar] [CrossRef]
- Su, Q.; Wu, H.; Sun, H.S.; Fang, Q. Experimental and numerical studies on dynamic behavior of reinforced UHPC panel under medium-range explosions. Int. J. Impact Eng. 2021, 148, 103761. [Google Scholar] [CrossRef]
- Arlery, M.; Pontiroli, C. Residual bearing capacity of reinforced concrete columns after close-in detonations: Experimental and numerical. Int. J. Saf. Secur. Eng. 2019, 9, 38–49. [Google Scholar] [CrossRef]
- Shi, Y.; Hu, Y.; Chen, L.; Li, Z.; Xiang, H. Experimental investigation into the close-in blast performance of RC columns with axial loading. Eng. Struct. 2022, 268, 114688. [Google Scholar] [CrossRef]
- Wang, W.; Xu, Z.; Wang, Y.; Xu, X.; Huo, Q.; Song, X.; Yang, G. Influence of Explosive Shape on the Response of Steel Plates under Blast Loading. J. Struct. Eng. 2024, 150, 18. [Google Scholar] [CrossRef]
- Yu, R.; Chen, L.; Fang, Q.; Huan, Y. An improved nonlinear analytical approach to generate fragility curves of reinforced concrete columns subjected to blast loads. Adv. Struct. Eng. 2018, 21, 396–414. [Google Scholar] [CrossRef]
- Duc-Kien, T.; Seung-Eock, K. Numerical investigation of the damage of RC members subjected to blast loading. Eng. Fail. Anal. 2018, 92, 350–367. [Google Scholar] [CrossRef]
- Tsai, Y.K.; Krauthammer, T. Energy based load-impulse diagrams with multiple failure modes for blast-loaded reinforced concrete structural elements. Eng. Fail. Anal. 2019, 104, 830–843. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, Y.; Zhang, R.; Liu, C.; Zhang, Z. Numerical simulation of reinforced concrete slab subjected to blast loading and the structural damage assessment. Eng. Fail. Anal. 2020, 118, 104926. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, C.; Zhang, Z.; Li, L.; Wei, J. Experimental and numerical simulation study on flexural performance of high-strength reinforced concrete beams under static loading. Structures 2024, 63, 106482. [Google Scholar] [CrossRef]
- Wei, X.; Ren, X. Failure assessment of concrete shear walls under close-in blast based on viscous damage model. Eng. Fail. Anal. 2024, 156, 107858. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, C.; Zhao, Q. Experimental and Numerical Investigation on Dynamic Response of Reinforced Concrete Shear Walls under Near-field Explosion. J. Phys. Conf. Ser. 2024, 2891, 082025. [Google Scholar] [CrossRef]
- Cai, R.; Li, Y.; Zhang, C.; Cao, H.; Qi, H.; Mao, J. Size effect on reinforced concrete slabs under direct contact explosion. Eng. Struct. 2022, 252, 113656. [Google Scholar] [CrossRef]
- Tian, S.; Yan, Q.; Du, X.; Chen, F.; Zhang, B. Experimental and numerical studies on the dynamic response of precast concrete slabs under blast load. J. Build. Eng. 2023, 70, 106425. [Google Scholar] [CrossRef]
- Jafari, A.; Beheshti, M.; Shahmansouri, A.A.; Akbarzadeh Bengar, H. Plastic hinge length for coupled and hybrid-coupled shear walls. Steel Compos. Struct. 2023, 48, 367–383. [Google Scholar] [CrossRef]
- Jafari, A.; Beheshti, M.; Shahmansouri, A.A.; Akbarzadeh Bengar, H. Cyclic response and damage status of coupled and hybrid-coupled shear walls. Structures 2024, 61, 106010. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
- Zhou, F.; Cui, F.; Guo, A. Structural Response and Protection Under Blast Loading; National Defense Industry Press: Beijing, China, 2004. (In Chinese) [Google Scholar]
- GB 50009-2012; Load Code for the Design of Building Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China/China Planning Press: Beijing, China, 2012. (In Chinese)
- Simoens, B.; Lefebvre, M.H. Influence of different parameters on the TNT-equivalent of an explosion. Cent. Eur. J. Energetic Mater. 2011, 8, 3–17. [Google Scholar]
- Zhang, Z.; Wang, X.; Deng, Y. Dynamic response of square recycled aggregate concrete-filled steel tube columns subjected to close-range blast loads. J. Build. Eng. 2022, 52, 104427. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, L.; Fang, Q.; Xiang, H. Blast loading model of the RC column under close-in explosion induced by the double-end-initiation explosive cylinder. Eng. Struct. 2018, 175, 304–321. [Google Scholar] [CrossRef]
- UFC-3-340-02; Structures to Resist the Effects of Accidental Explosions. USA Department of Defense: Washington, DC, USA, 2008.
- Wang, W.; Wang, Y.; Yang, J.; Wang, J.; Wang, X. Investigation on air blast resistance of POZD-coated composite steel plates: Experiment and numerical analysis. Compos. Part B Eng. 2022, 237, 109858. [Google Scholar] [CrossRef]
- Riedel, W.; Thoma, K.; Hiermaier, S. Penetration of Reinforced Concrete by BETA-B-500 Numerical Analysis using a New Macroscopic Concrete Model for Hydrocodes. Energy Power Eng. 1999, 9, 315–322. [Google Scholar]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Chen, M.; Zhao, J. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses. Tunn. Undergr. Space Technol. 2017, 66, 19–33. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Wang, J.; Wang, S.; Wang, H.; Yin, Y.; Li, F. Effect of confining pressure on damage accumulation of rock under repeated blast loading. Int. J. Impact Eng. 2021, 156, 103961. [Google Scholar] [CrossRef]
- Borrvall, T.; Riedel, W. The RHT Concrete Model in LS-DYNA. In Proceedings of the 8th European LS-DYNA Users Conference, Strasbourg, France, 23–24 May 2011; pp. 23–24. [Google Scholar]
- Tu, Z.; Lu, Y. Modifications of RHT material model for improved numerical simulation of dynamic response of concrete. Int. J. Impact Eng. 2010, 37, 1072–1082. [Google Scholar] [CrossRef]
- LS-DYNA, Keyword User’s Manual, Version 971; Livermore Software Technology Corporation: Livermore, CA, USA, 2007.
- Wang, R.; Han, L.-H.; Hou, C.-C. Behavior of concrete filled steel tubular (CFST) members under lateral impact: Experiment and FEA model. J. Constr. Steel Res. 2013, 80, 188–201. [Google Scholar] [CrossRef]
- Material Models. In Ls-Dyna. Keyword User’s Manual; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2001; Volume 2.
- Cudzilo, S.; Kohlicek, P.; Trzcinski, V.A.; Zeman, S. Performance of Emulsion Explosives. Combust. Explos. Shock. Waves 2002, 38, 463–469. [Google Scholar] [CrossRef]
- Locking, P. TNT Equivalence-Experimental Comparison Against Prediction. In Proceedings of the 27th International Symposium on Ballistics, Freiburg, Germany, 22–26 April 2013. [Google Scholar]
- Chen, C.; Zhu, X.; Hou, H.; Shen, X.L.; Tang, T. Deformation and failure modes of clamped square plates under close-range air blast loads. Explos. Shock. Waves 2012, 32, 368–375. (In Chinese) [Google Scholar]
- Bai, Z.; Hu, Y.; Qian, B.; Yao, S.; Li, X.; Guo, X. Experimental study on cumulative damage of shear wall under multiple internal blast loads. Acta Armamentarii 2023, 44 (Suppl. 1), 50–58. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).