Grey-Box Model for Efficient Building Simulations: A Case Study of an Integrated Water-Based Heating and Cooling System
Abstract
1. Introduction
1.1. Context
1.2. Literature Review
1.3. Research Gaps and Research Objective
- Creation and validation of a detailed building model of a campus building at the Campus Inffeldgasse of Graz University of Technology using data from IoT sensors for calibration and validation;
- Development and comprehensive comparison of a GB model based on physical laws, incorporating a water-based heat distribution system for both cooling and heating purposes;
- A comprehensive comparison of the GB model with the detailed building model and measurement data, focusing on heat flows, room temperatures, and return temperatures of the radiator system;
- Evaluation of the model’s robustness through simulations with alternative control methods and weather files;
- A sensitivity analysis using the Morris Method to identify key model parameters for calibration and discussion of the model’s applicability to various building types and district heating systems.
2. Modeling Approach
2.1. Reference Building
2.2. Metrics
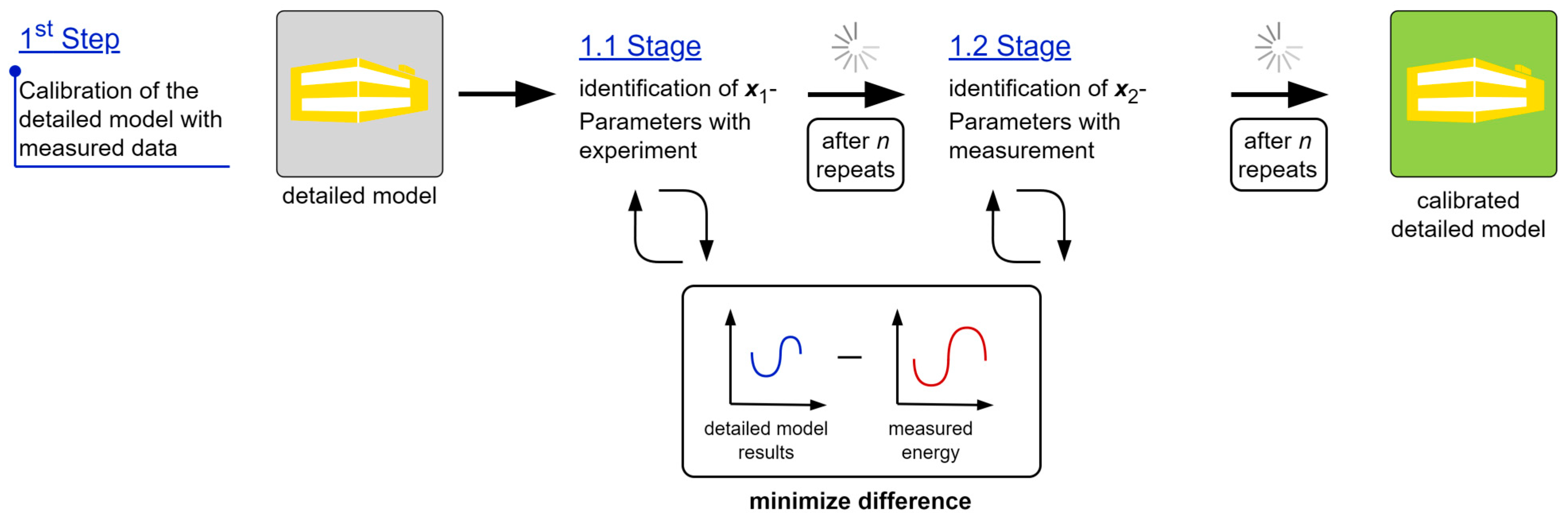
2.3. Step 1: Detailed Building Model
2.3.1. Modelling Approach
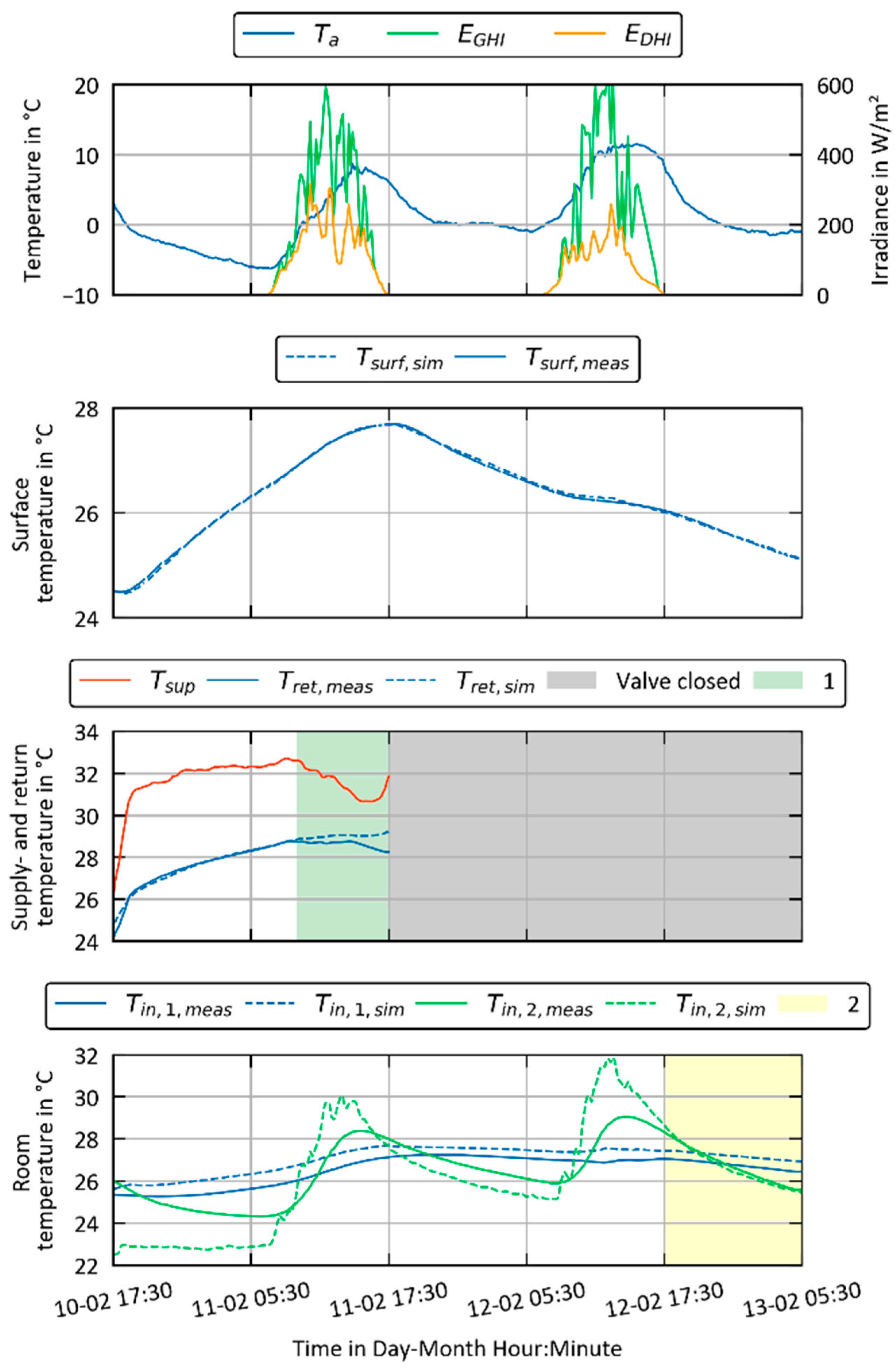
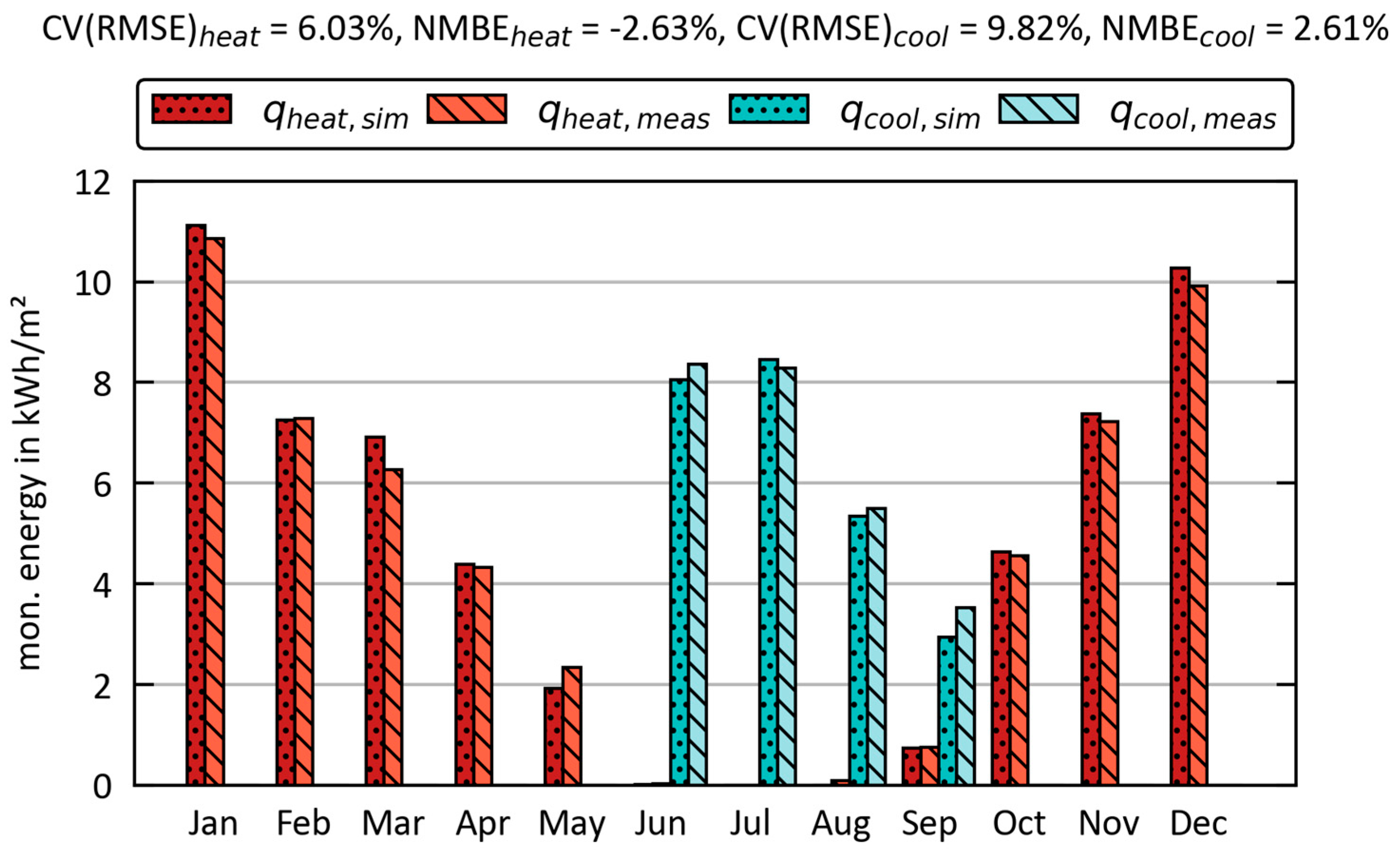
2.3.2. Calibration of the Model Using Experimental Data
2.4. Grey-Box Model
2.4.1. Model Formulation
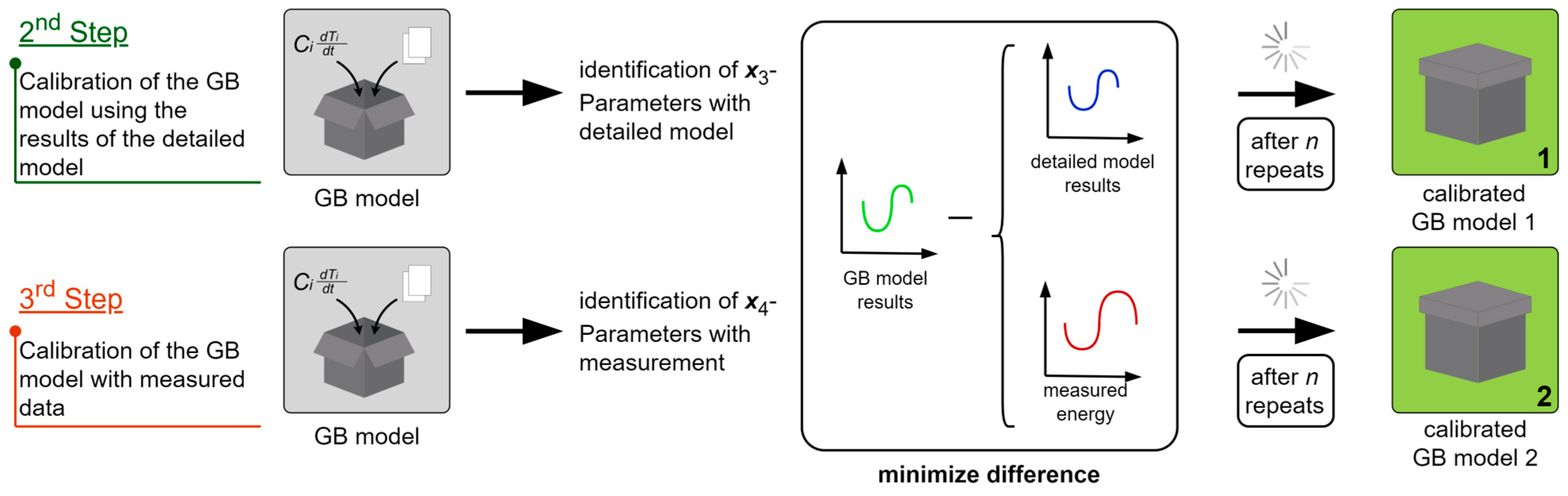
2.4.2. Step 2: Parameter Identification Based on Simulation Results
2.4.3. Step 3: Parameter Identification Based on Measurements
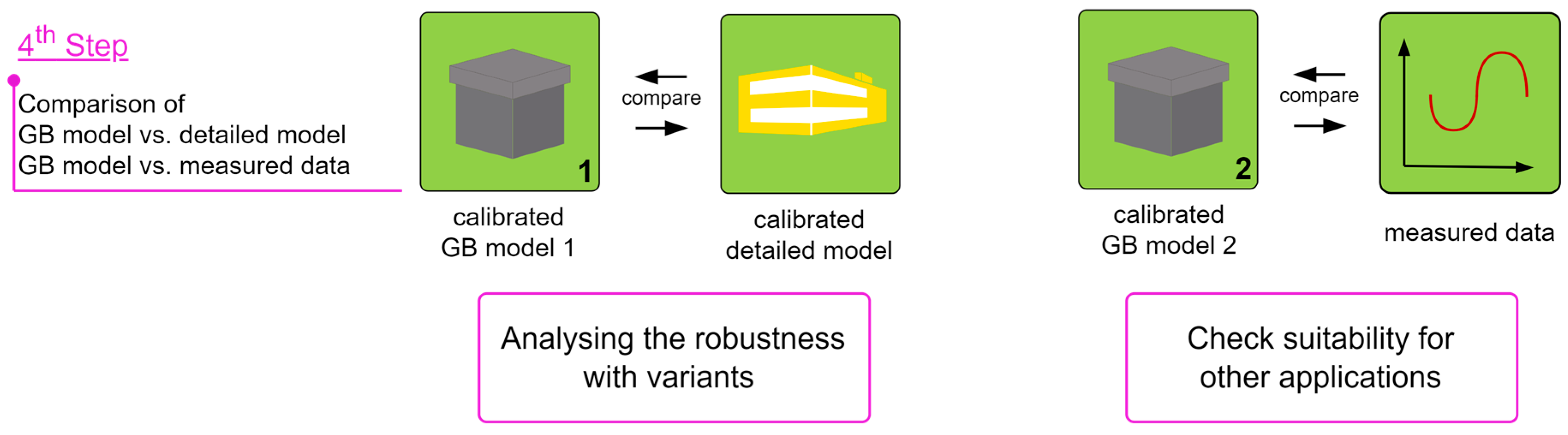
2.5. Step 4: Assessment of Robustness
- Reference case: Involved simulations of both the GB1 and detailed models using 2021 weather data and the default control strategy with the identified parameters;
- Weather case: Included simulations using 2019 weather data, while maintaining the parameters identified for the GB1 model;
- Control case: Applied an alternative control strategy to the simulations, again maintaining the identified parameters.
3. Model Evaluation
3.1. Detailed Model vs. Experimental Data
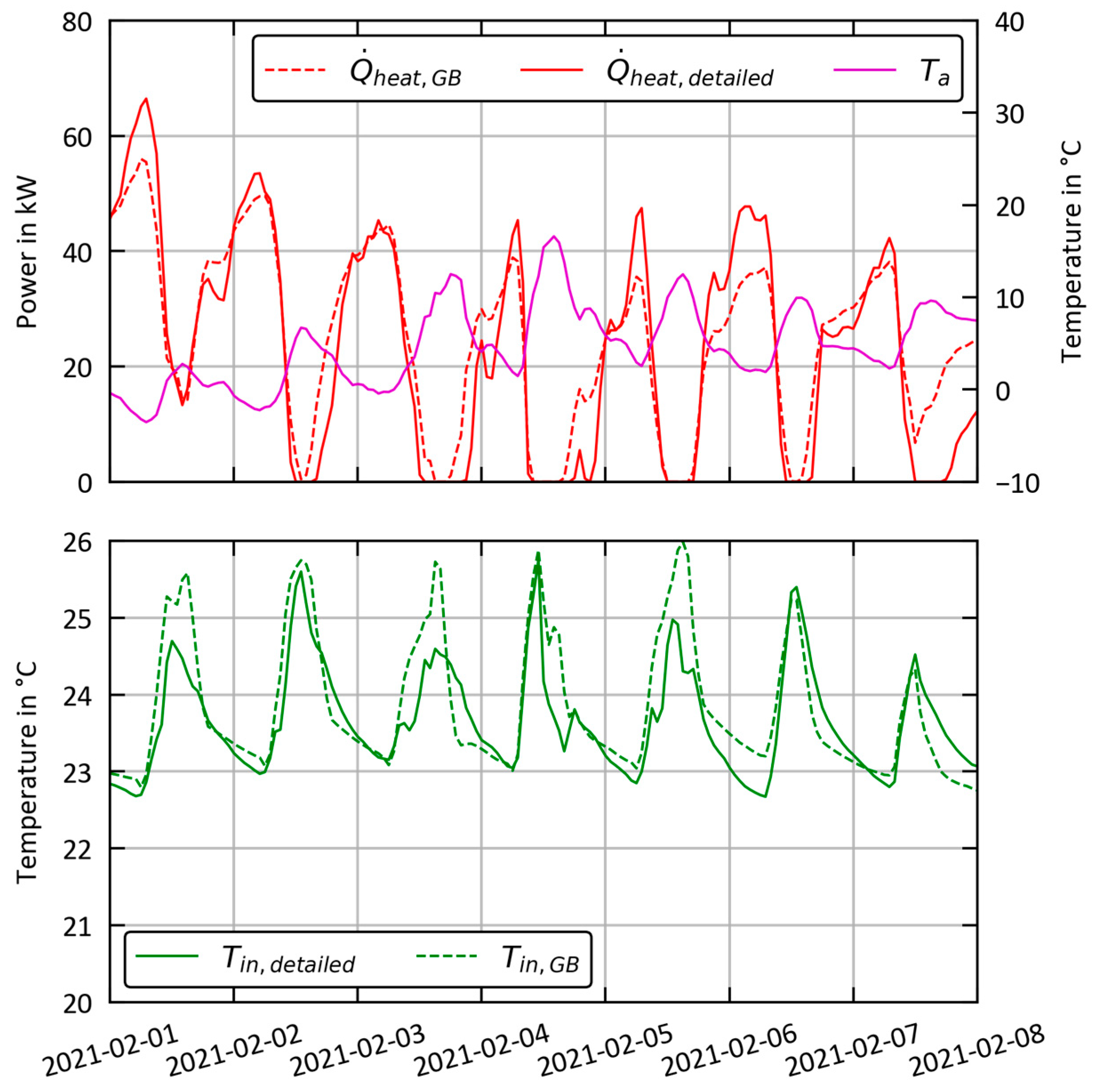
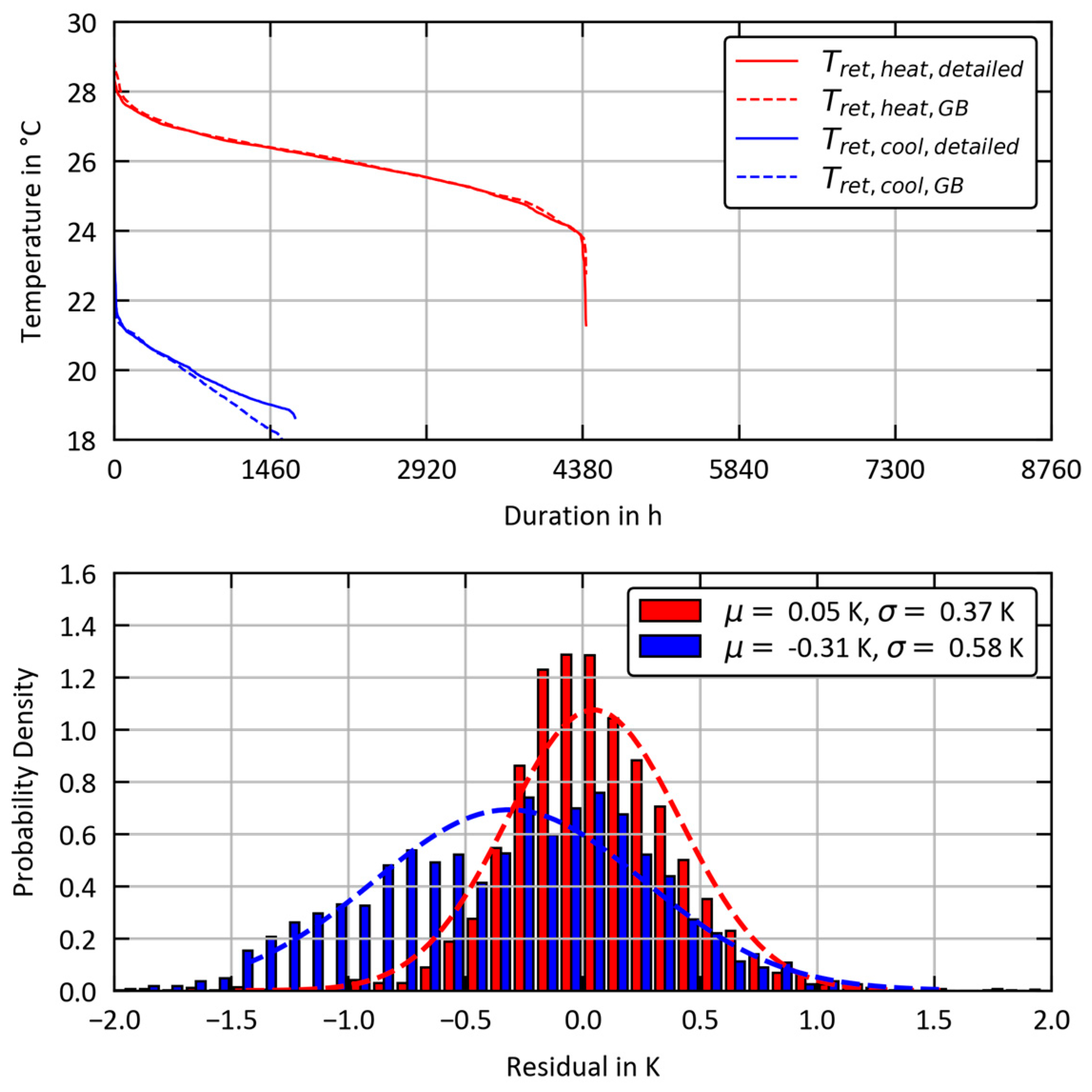
3.2. Grey-Box vs. Detailed Model
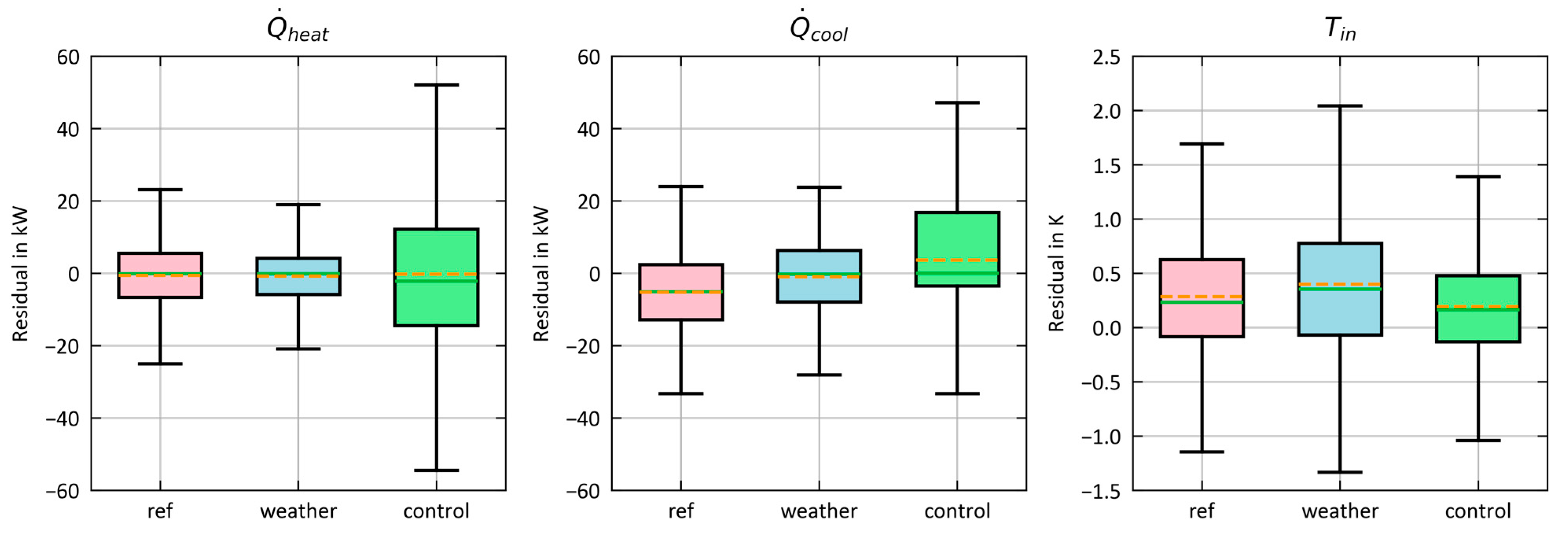
3.3. Analysis of the Robustness
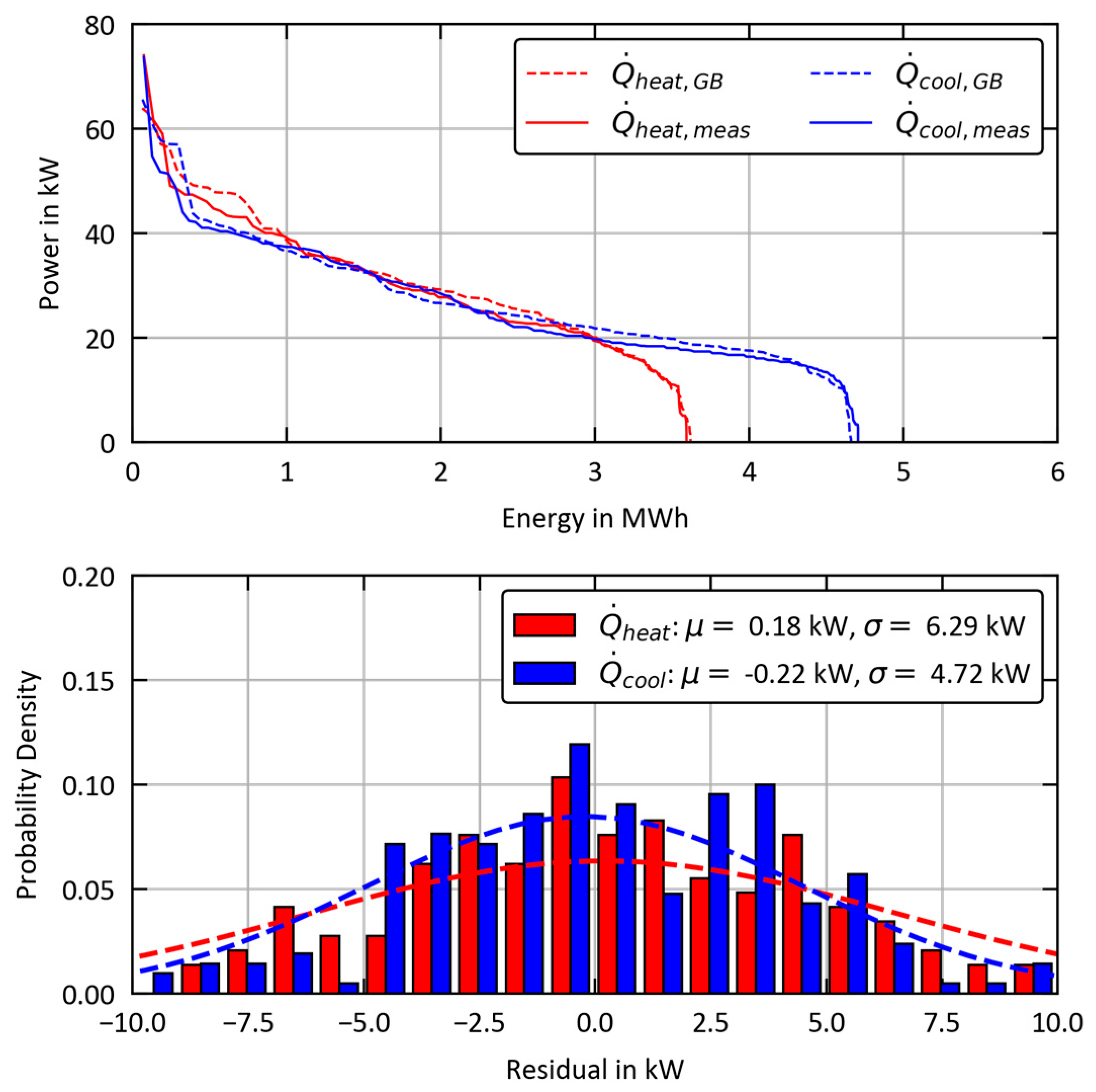
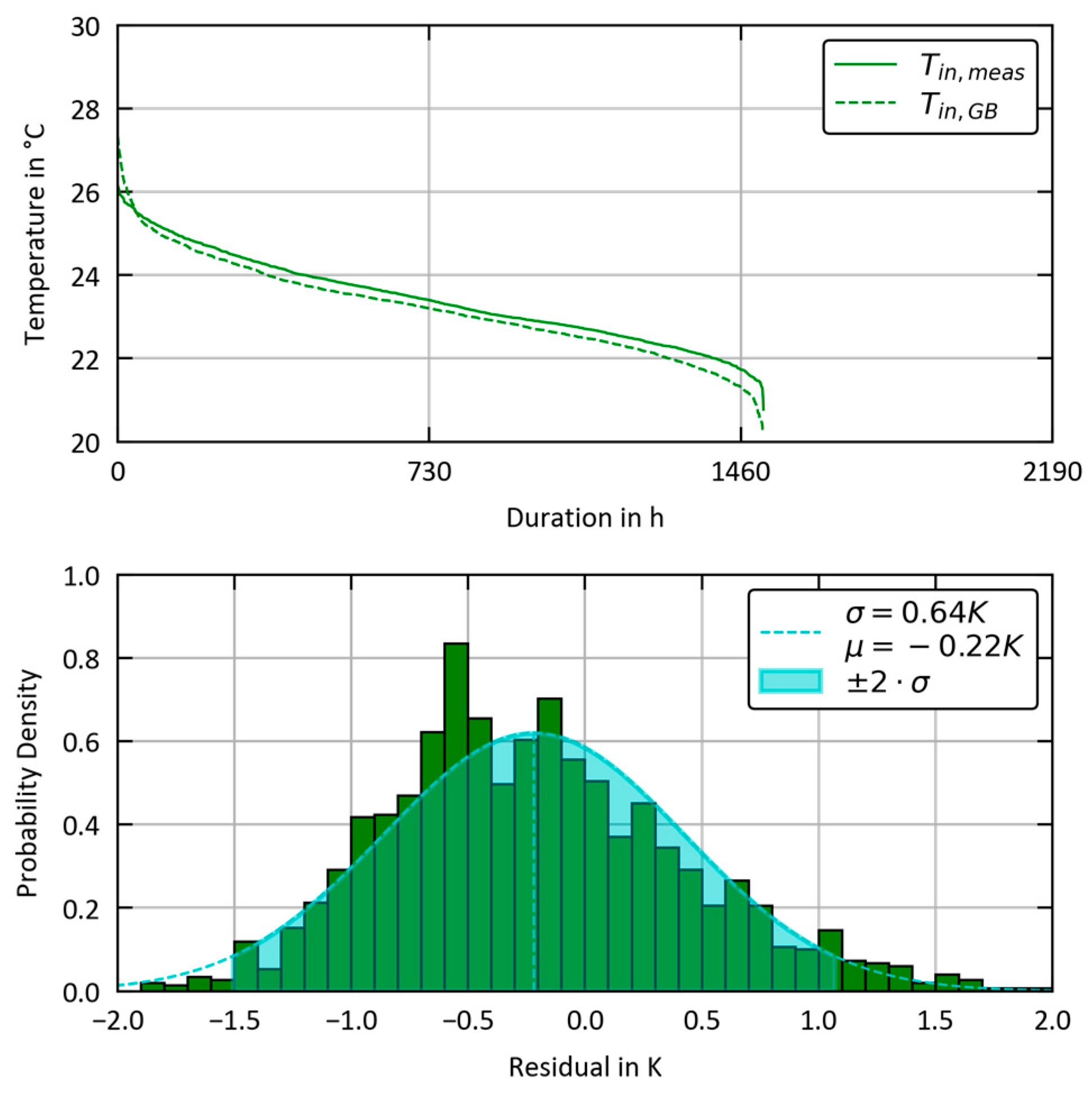
3.4. Grey Box vs. Measurement
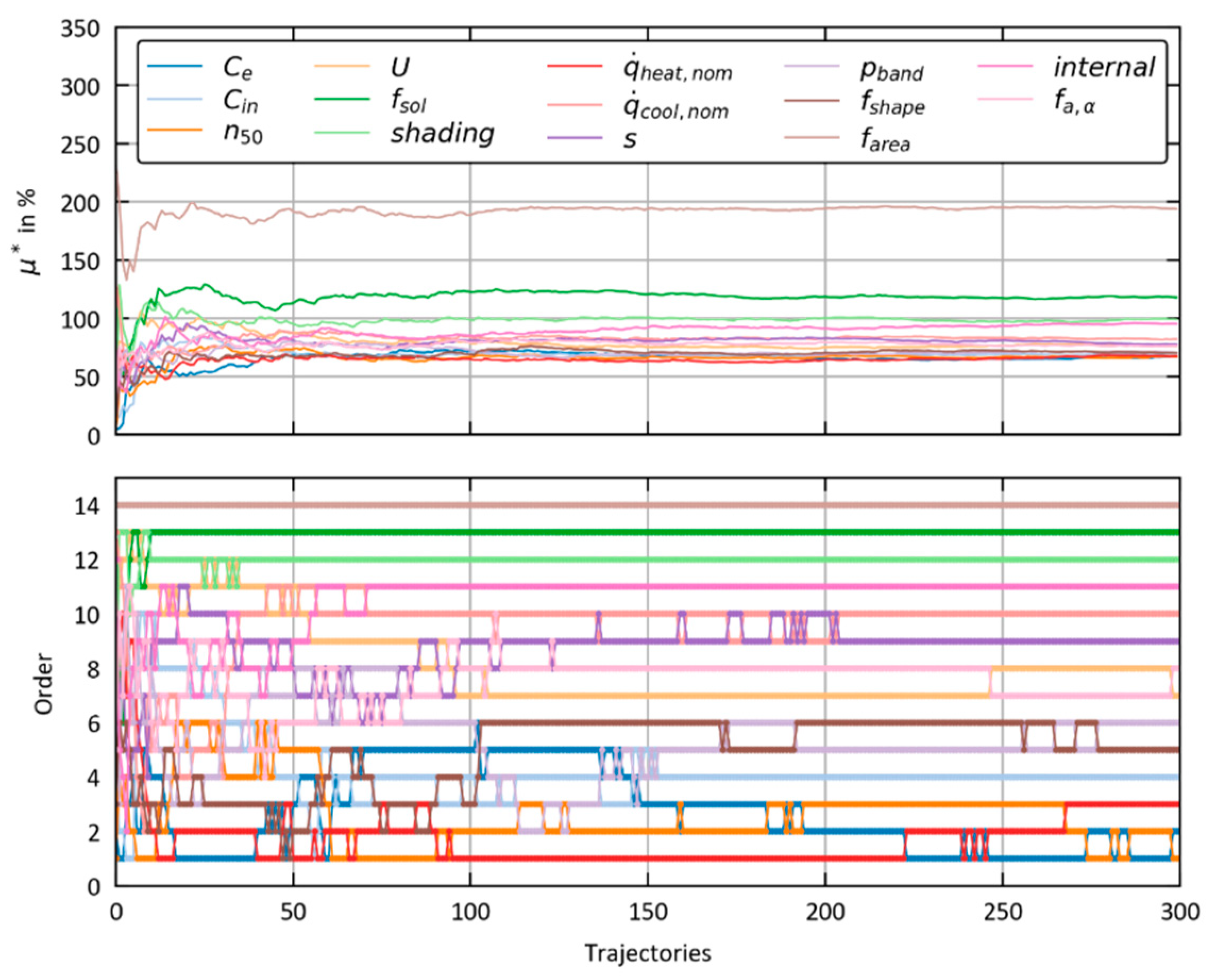
3.5. Sensitivity Analysis
4. Conclusions and Outlook
4.1. Scientific Contributions and Practical Implications
- Extensive validation and integration of a water-based heat emission system: The GB model includes a water-based heating and cooling system capable of predicting thermal power and return temperatures with sufficient accuracy. Its development involved a thorough validation process, comparing it to a detailed physical model and real-world measurement data;
- Minimal input requirements: A notable feature of the GB model is that it requires only a few input parameters for effective parameterization. This aspect enhances its usability and accessibility to a wide range of users;
- Demonstration of the optimization process: An exemplary optimization process to identify the model parameters was demonstrated, including a sensitivity analysis, showing the practical application and versatility in real-world scenarios.
- Urban building energy modeling (UBEM): The model could be used in UBEM scenarios, where parameterization requires only basic system design conditions and monthly measured values for heating and/or cooling demand. This makes it a suitable replacement for detailed models, which are much more time-consuming and for which, usually, not all necessary data is available for many buildings. Parameterization with monthly data leads to a loss of accuracy in comparison. However, for studies involving a large number of buildings, this should be manageable, as the energy demand is considered correctly. Additionally, the heat dissipation system and dynamic behavior are taken into account;
- Demand-side management and model predictive control: The model could also be applicable to the demand-side management of buildings and could serve as a foundational element for model predictive control systems, enabling the more accurate and responsive control of building energy systems. For these applications, additional measurement data are required for effective model training. These include data such as a time series of the average indoor air temperature and heating/cooling heat flows. These data can come either from a more detailed model or from measurements.
4.2. Study Limitations and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Variables and parameters | Tin | Room air temperature, °C | |
| A | Area, m2 | Tin, set | Room air set temperature, °C |
| ACH | Air exchange rate, 1/h | Tret | Return water temperature, °C |
| albedo | Reflection coefficient from the environment | Tsup | Supply/forward water temperature, °C |
| c | Simultaneity factor of direct normal radiation | U | Heat transfer coefficient, W/(m2K) |
| Ce | Heat capacity of the exterior/thermally active storage mass, J/K | V | Air volume of the building, m3 |
| Cin | Heat capacity of the indoor air, J/K | v | Vectorial wind speed, m/s |
| cp,a | Specific heat capacity of the air, J/(kgK) | z | Height, m |
| Cp,v | Mean pressure coefficient over the building | af | Absorption coefficient of the outer wall |
| cp,w | Specific heat capacity of water, J/(kgK) | Δp | Pressure difference between inside and outside, Pa |
| EDHI | Specific diffuse irradiance on the horizontal surface, W/m2 | ϑ | Temperature difference between fluid and room air temperature, K |
| EDNI | Specific direct normal irradiance, W/m2 | ϑ0 | Temperature difference between supply water and room air temperature, K |
| EGHI | Specific global irradiance on the horizontal surface, W/m2 | ϑlog | Logarithmic mean temperature difference between water and room air temperature, K |
| fa,α | Ratio of af and ha | Θm | Dimensionless mean temperature |
| farea | Ratio of net floor area and gross floor area | κ | Coefficient of performance |
| feff | Factor for the effectiveness of air exchange caused by pressure difference | µi* | The absolute mean of elementary effects |
| ρa | Mass density of the air, kg/m3 | ||
| fshape | Ratio of vertical and horizontal surface area | Φ | Sun position: azimuth, ° |
| fsignal | Overall control signal for heating or cooling | Indices | |
| fsol | Solar factor | b | Buoyancy effect |
| fvalve | Control signal for mass flow control | bui | Building |
| ha | Heat transfer coefficient between outer wall and environment, W/(m2K) | hor | Horizontal |
| hconv | Convective heat transfer coefficient, W/(m2K) | nom | Nominal/design conditions |
| k | Heat transfer coefficient, W/(m2K) | occ | Occupied |
| Mass flow of the water-based radiator system, kg/s | surf | Surface | |
| n | Heater exponent | ver | Vertical |
| n50 | Air exchange rate at a pressure difference of 50 Pa, 1/h | win | Window ventilation |
| nx | Air exchange rate caused by a pressure difference, 1/h | Abbreviations | |
| pa | Air pressure, Pa | AutoMOO | Automatic Multi-Objective Optimization |
| pband | Proportional band of the mass flow control, K | BEM | Building energy modeling |
| Heat flow from the heating system to the room node, W | BIM | Building Information Modeling | |
| Heat flow due to air exchange, W | C | Capacities | |
| Heat flow from the room node to the cooling system, W | CV(RMSE) | Coefficient of Variation of the Root-Mean-Square Error | |
| Heat flow due to pressure differences, W | GB | Grey-box | |
| Heat flow due to internal gains, W | GFA | Gross floor area | |
| Heat flow due to solar radiation, W | GHG | Greenhouse gas | |
| Ra | Gas constant of the air, J/(kgK) | IFC | Industry Foundation Classes |
| Re,a | Heat transfer resistance between the thermally activated storage mass and the equivalent outdoor air temperature, K/W | IoT | Internet-of-things |
| Rin,a | Heat transfer resistance between the outdoor temperature and the room air temperature, K/W | NFA | Net floor area |
| Rin,e | Heat transfer resistance between the two nodes, K/W | NMBE | Normalized-Mean-Bias Error |
| s | Radiative fraction of heat transfer of the heating and cooling system | R | Resistances |
| Ta | Outdoor air temperature, °C | RSE | Root-Square Error |
| Ta,eq | Equivalent outdoor air temperature, °C | SHGC | Solar heat gain coefficient, g-value |
| Te | Thermally active storage mass temperature, °C | UBEM | Urban Building Energy Simulation Models |
Appendix A
Appendix A.1. Detailed Model Boundary Conditions
| Utilization Number | |
|---|---|
| DIN 277 | SIA 2024 |
| NF7.1 | 12.06 |
| NF1.2 | 4.02 |
| NF2.1 | 3.01 |
| NF2.3 | 3.03 |
| NF3.3 | 9.03 |
| NF3.8 | 12.05 |
| NF4.1 | 12.04 |
| NF4.2 | 12.04 |
| NF5.2 | 4.01 |
| NF5.4 | 4.03 |
| TF8.4 | 12.04 |
| TF8.9 | 12.04 |
| VF9.1 | 12.01 |
| VF9.2 | 12.03 |
| VF9.3 | 12.04 |
| VF9.9 | 12.01 |
Appendix A.2. Sensor Positioning
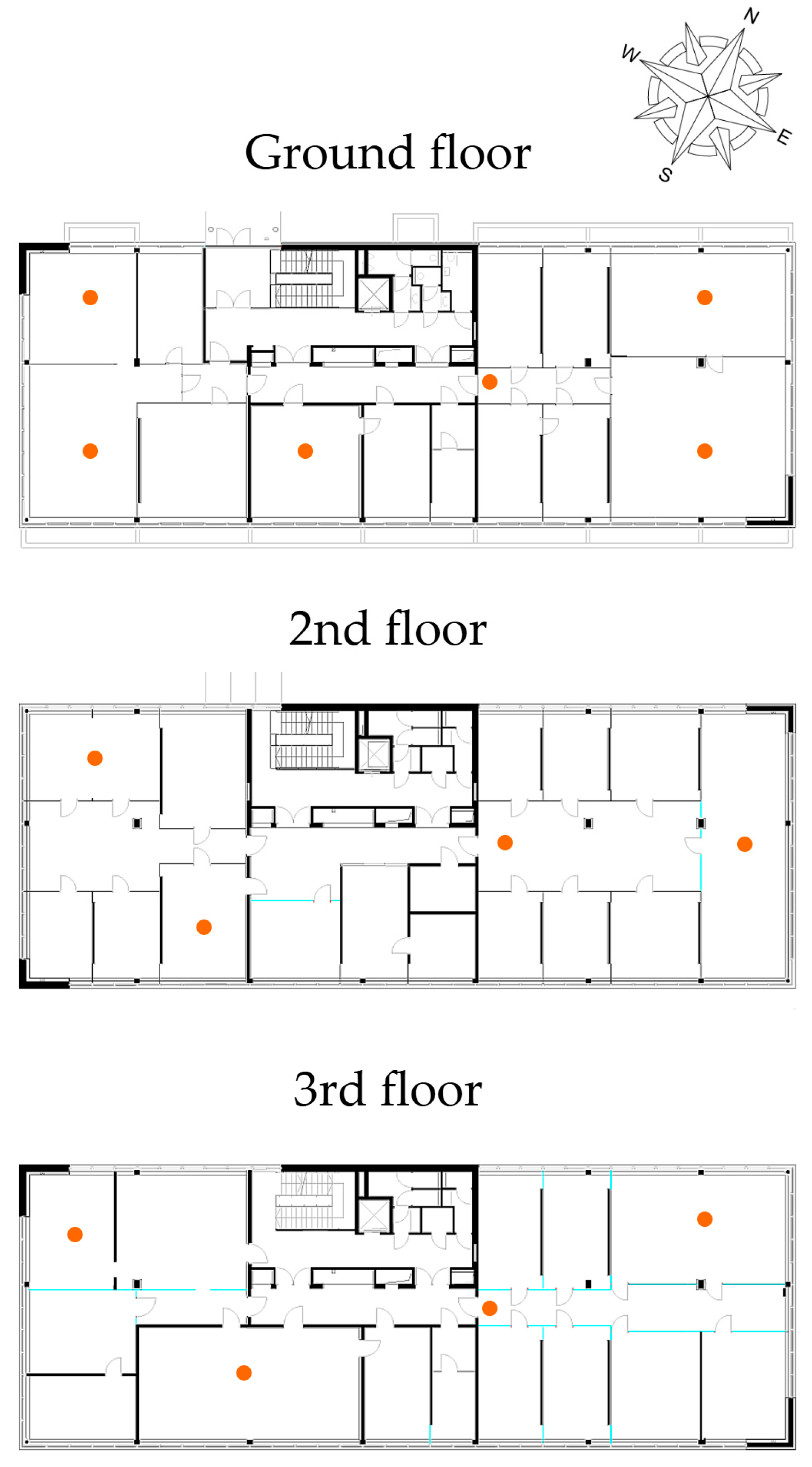
Appendix A.3. Morris Convergence Analysis
References
- Nejat, P.; Jomehzadeh, F.; Taheri, M.M.; Gohari, M.; Majid, M.Z.A. A global review of energy consumption, CO2 emissions and policy in the residential sector (with an overview of the top ten CO2 emitting countries). Renew. Sustain. Energy Rev. 2015, 43, 843–862. [Google Scholar] [CrossRef]
- IPCC Working Group I. IPCC Sixth Assessment Report, Climate Change 2021: The Physical Science Basis; The Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2021. [Google Scholar]
- Yin, R.; Xu, P.; Piette, M.A.; Kiliccote, S. Study on Auto-DR and pre-cooling of commercial buildings with thermal mass in California. Energy Build. 2010, 42, 967–975. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, S.; Xu, X.; Xiao, F. A grey-box model of next-day building thermal load prediction for energy-efficient control. Int. J. Energy Res. 2008, 32, 1418–1431. [Google Scholar] [CrossRef]
- Lee, K.; Braun, J.E. Model-based demand-limiting control of building thermal mass. Build. Environ. 2008, 43, 1633–1646. [Google Scholar] [CrossRef]
- Mirakhorli, A.; Dong, B. Model predictive control for building loads connected with a residential distribution grid. Appl. Energy 2018, 230, 627–642. [Google Scholar] [CrossRef]
- Fabre, A.; Thomas, R.; Duplessis, B.; Tran, C.-T.; Stabat, P. Dynamic modeling for evaluation of triple-pipe configuration potential in geothermal district heating networks. Energy Convers. Manag. 2018, 173, 461–469. [Google Scholar] [CrossRef]
- Kim, E.-J.; Plessis, G.; Hubert, J.-L.; Roux, J.-J. Urban energy simulation: Simplification and reduction of building envelope models. Energy Build. 2014, 84, 193–202. [Google Scholar] [CrossRef]
- Heidarinejad, M.; Mattise, N.; Dahlhausen, M.; Sharma, K.; Benne, K.; Macumber, D.; Brackney, L.; Srebric, J. Demonstration of reduced-order urban scale building energy models. Energy Build. 2017, 156, 17–28. [Google Scholar] [CrossRef]
- Edtmayer, H.; Nageler, P.; Heimrath, R.; Mach, T.; Hochenauer, C. Investigation on sector coupling potentials of a 5th generation district heating and cooling network. Energy 2021, 230, 120836. [Google Scholar] [CrossRef]
- Drgoňa, J.; Arroyo, J.; Figueroa, I.C.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L.; et al. All you need to know about model predictive control for buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar] [CrossRef]
- American Society of Heating, Refrigerating and Air Conditioning Engineers, Inc. ASHRAE Handbook-Fundamentals; D&R International, Ltd.: McLean, VA, USA, 2013. [Google Scholar]
- Coakley, D.; Raftery, P.; Keane, M. A review of methods to match building energy simulation models to measured data. Renew. Sustain. Energy Rev. 2014, 37, 123–141. [Google Scholar] [CrossRef]
- Shahcheraghian, A.; Madani, H.; Ilinca, A. From White to Black-Box Models: A Review of Simulation Tools for Building Energy Management and Their Application in Consulting Practices. Energies 2024, 17, 376. [Google Scholar] [CrossRef]
- Zhang, Y.; O’Neill, Z.; Dong, B.; Augenbroe, G. Comparisons of inverse modeling approaches for predicting building energy performance. Build. Environ. 2015, 86, 177–190. [Google Scholar] [CrossRef]
- Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Berthou, T.; Stabat, P.; Salvazet, R.; Marchio, D. Comparaison de Modèles Linéaires Inverses Pour la Mise en Place de Stratégies D’effacement. In Proceedings of the Rencontres AUGC-IBPSA, Chambéry, France, 6–8 June 2012. [Google Scholar]
- Attoue, N.; Shahrour, I.; Mroueh, H.; Younes, R. Determination of the Optimal Order of Grey-Box Models for Short-Time Prediction of Buildings’ Thermal Behavior. Buildings 2019, 9, 198. [Google Scholar] [CrossRef]
- Bacher, P.; Madsen, H. Identifying suitable models for the heat dynamics of buildings. Energy Build. 2011, 43, 1511–1522. [Google Scholar] [CrossRef]
- Brastein, O.M.; Perera, D.; Pfeifer, C.; Skeie, N.-O. Parameter estimation for grey-box models of building thermal behaviour. Energy Build. 2018, 169, 58–68. [Google Scholar] [CrossRef]
- Ghosh, S.; Reece, S.; Rogers, A.; Roberts, S.; Malibari, A.; Jennings, N.R. Modeling the Thermal Dynamics of Buildings. ACM Trans. Intell. Syst. Technol. 2015, 6, 1–27. [Google Scholar] [CrossRef]
- Arroyo, J.; Spiessens, F.; Helsen, L. Identification of multi-zone grey-box building models for use in model predictive control. J. Build. Perform. Simul. 2020, 13, 472–486. [Google Scholar] [CrossRef]
- González, V.G.; Ruiz, G.R.; Bandera, C.F. Empirical and Comparative Validation for a Building Energy Model Calibration Methodology. Sensors 2020, 20, 5003. [Google Scholar] [CrossRef]
- Yousaf, S.; Bradshaw, C.R.; Kamalapurkar, R.; San, O. A gray-box model for unitary air conditioners developed with symbolic regression. Int. J. Refrig. 2024, 168, 696–707. [Google Scholar] [CrossRef]
- Reynders, G.; Diriken, J.; Saelens, D. Quality of grey-box models and identified parameters as function of the accuracy of input and observation signals. Energy Build. 2014, 82, 263–274. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Gray-box modeling and validation of residential HVAC system for control system design. Appl. Energy 2015, 137, 134–150. [Google Scholar] [CrossRef]
- Hu, J.; Karava, P. A state-space modeling approach and multi-level optimization algorithm for predictive control of multi-zone buildings with mixed-mode cooling. Build. Environ. 2014, 80, 259–273. [Google Scholar] [CrossRef]
- Li, Y.; O’Neill, Z.; Zhang, L.; Chen, J.; Im, P.; DeGraw, J. Grey-box modeling and application for building energy simulations—A critical review. Renew. Sustain. Energy Rev. 2021, 146, 111174. [Google Scholar] [CrossRef]
- Kramer, R.; van Schijndel, J.; Schellen, H. Inverse modeling of simplified hygrothermal building models to predict and characterize indoor climates. Build. Environ. 2013, 68, 87–99. [Google Scholar] [CrossRef]
- Afshari, A.; Liu, N. Inverse modeling of the urban energy system using hourly electricity demand and weather measurements, Part 2: Gray-box model. Energy Build. 2017, 157, 139–156. [Google Scholar] [CrossRef]
- Thilker, C.A.; Bacher, P.; Bergsteinsson, H.G.; Junker, R.G.; Cali, D.; Madsen, H. Non-linear grey-box modelling for heat dynamics of buildings. Energy Build. 2021, 252, 111457. [Google Scholar] [CrossRef]
- Harb, H.; Boyanov, N.; Hernandez, L.; Streblow, R.; Müller, D. Development and validation of grey-box models for forecasting the thermal response of occupied buildings. Energy Build. 2016, 117, 199–207. [Google Scholar] [CrossRef]
- Berthou, T.; Stabat, P.; Salvazet, R.; Marchio, D. Development and validation of a gray box model to predict thermal behavior of occupied office buildings. Energy Build. 2014, 74, 91–100. [Google Scholar] [CrossRef]
- EQUA Simulation AB. IDA ICE 5 Beta 28-Simulation Software|EQUA. Available online: https://www.equa.se/de/ida-ice (accessed on 11 November 2023).
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Herman, J.; Usher, W. SALib: An open-source Python library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Guideline 14-2014: Measurement of Energy, Demand and Water Savings; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2014. [Google Scholar]
- DIN 277-1:2021-08; Areas and volumes in building construction—Part 1: Terms, definitions and calculation principles. Deutsches Institut für Normung (DIN): Berlin, Germany, 2021.
- SIA 2024:2021; Raumnutzungsdaten für die Energie- und Gebäudetechnik. Schweizerischer Ingenieur- und Architektenverein (SIA): Zürich, Switzerland, 2021.
- B 8110-7; Wärmeschutz im Hochbau: Teil 7: Tabellierte wärmeschutztechnische Bemessungswerte. Austrian Standards International: Wien, Austria, 2013.
- Mörth, M. Analyse und Transformation von Quartiers-Energiesystemen am Beispiel Innovation District Inffeld. MSc, Institut für Wärmetechnik, Technischen Universität Graz, Graz, 2022. Available online: https://online.tugraz.at/tug_online/wbAbs.showThesis?pThesisNr=76874&pOrgNr=2267# (accessed on 9 April 2024).
- Bundesanstalt für Geologie. Geophysik, Klimatologie und Meteorologie—GeoSphere. Available online: https://data.hub.geosphere.at/ (accessed on 19 November 2023).
- Gouda, M.M.; Danaher, S.; Underwood, C.P. Building thermal model reduction using nonlinear constrained optimization. Build. Environ. 2002, 37, 1255–1265. [Google Scholar] [CrossRef]
- Vivian, J.; Zarrella, A.; Emmi, G.; de Carli, M. An evaluation of the suitability of lumped-capacitance models in calculating energy needs and thermal behaviour of buildings. Energy Build. 2017, 150, 447–465. [Google Scholar] [CrossRef]
- Loutzenhiser, P.G.; Manz, H.; Felsmann, C.; Strachan, P.A.; Frank, T.; Maxwell, G.M. Empirical validation of models to compute solar irradiance on inclined surfaces for building energy simulation. Sol. Energy 2007, 81, 254–267. [Google Scholar] [CrossRef]
- EN ISO 52016-1; Energetische Bewertung von Gebäuden—Berechnung des Energiebedarfs für Heizung und Kühlung, Innentemperaturen Sowie der Heiz- und Kühllast in Einem Gebäude oder Einer Gebäudezone: Teil 1: Berechnungsverfahren. Austrian Standards International: Vienna, Austria, 2018.
- Großmann, H.; Böttcher, C. Pkw-Klimatisierung: Physikalische Grundlagen und Technische Umsetzung; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Sprenger, E.; Albers, K.-J.; Recknagel, H. (Eds.) Taschenbuch für Heizung und Klimatechnik: Einschließlich Trinkwasser- und Kältetechnik Sowie Energiekonzepte, 78th ed.; DIV Deutscher Industrieverlag GmbH: Munich, Germany, 2017. [Google Scholar]
- Zürcher, C.; Frank, T. Bauphysik: Bau und Energie, 5th ed.; vdf Hochschulverlag AG an der ETH Zürich: Zürich, Switzerland, 2018; Available online: https://enbau-online.ch/bauphysik/ (accessed on 10 April 2024).
- Zeller, J. Abschätzung der Infiltration nach DIN 1946-6 “Lüftung von Wohnungen”: Vergleich mit Anderen Verfahren und Würdigung der Ergebnisse. 8. Internationales BUILDAIR-Symposium, 2013. Available online: https://www.aivc.org/sites/default/files/Zeller_Buildair2013_de.pdf (accessed on 10 April 2024).
- Kaisermayer, V.; Muschick, D.; Horn, M.; Schweiger, G.; Schwengler, T.; Mörth, M.; Heimrath, R.; Mach, T.; Herzlieb, M.; Gölles, M. Predictive building energy management with user feedback in the loop. Smart Energy 2024, 16, 100164. [Google Scholar] [CrossRef]
- Petersen, S.; Kristensen, M.H.; Knudsen, M.D. Prerequisites for reliable sensitivity analysis of a high fidelity building energy model. Energy Build. 2019, 183, 1–16. [Google Scholar] [CrossRef]





| Building Envelope Designation | Area [m2] | U-Value [W/(m2K)] | UA-Value [W/K] | Share [%] |
|---|---|---|---|---|
| Walls in contact with the air | 590.72 | 0.30 | 180.17 | 10.17% |
| Walls in contact with the ground | 207.24 | 0.23 | 47.96 | 2.71% |
| Roof | 591.26 | 0.13 | 76.85 | 4.34% |
| Floor in contact with the ground | 633.66 | 0.16 | 98.95 | 5.59% |
| Windows | 724.90 | 1.53 | 1105.76 | 62.42% |
| Thermal bridging | 261.84 | 14.78% | ||
| Total | 2747.78 | 0.64 | 1771.53 | 100.00% |
| Metrics in % | GB1 Model | |||
|---|---|---|---|---|
| Reference | Weather | Control | Controladj | |
| CV(RMSE)heat | 8.409 | 11.170 | 7.824 | 7.956 |
| NMBEheat | −2.627 | −5.108 | −0.326 | 1.774 |
| CV(RMSE)cool | 10.340 | 6.699 | 19.390 | 10.690 |
| NMBEcool | −3.906 | −1.220 | 11.040 | 4.990 |
| Parameter | Order | ||
|---|---|---|---|
| Name | Unit | NMBEheat | NMBEcool |
| shading | - | 12 | 3 |
| Ce | J/(m2K) | 11 | 13 |
| Cin | J/(m2K) | 13 | 11 |
| fsol | - | 7 | 2 |
| s | - | 9 | 6 |
| pband | - | 14 | 9 |
| n50 | 1/h | 3 | 14 |
| U | W/(m2K) | 2 | 8 |
| W/m2 | 5 | 12 | |
| W/m2 | 10 | 5 | |
| fshape | m2/m2 | 8 | 10 |
| farea | - | 1 | 1 |
| internal | % | 4 | 4 |
| fa,α | m2K/W | 6 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mörth, M.; Heinz, A.; Heimrath, R.; Edtmayer, H.; Mach, T.; Kaisermayer, V.; Gölles, M.; Hochenauer, C. Grey-Box Model for Efficient Building Simulations: A Case Study of an Integrated Water-Based Heating and Cooling System. Buildings 2025, 15, 1959. https://doi.org/10.3390/buildings15111959
Mörth M, Heinz A, Heimrath R, Edtmayer H, Mach T, Kaisermayer V, Gölles M, Hochenauer C. Grey-Box Model for Efficient Building Simulations: A Case Study of an Integrated Water-Based Heating and Cooling System. Buildings. 2025; 15(11):1959. https://doi.org/10.3390/buildings15111959
Chicago/Turabian StyleMörth, Michael, Andreas Heinz, Richard Heimrath, Hermann Edtmayer, Thomas Mach, Valentin Kaisermayer, Markus Gölles, and Christoph Hochenauer. 2025. "Grey-Box Model for Efficient Building Simulations: A Case Study of an Integrated Water-Based Heating and Cooling System" Buildings 15, no. 11: 1959. https://doi.org/10.3390/buildings15111959
APA StyleMörth, M., Heinz, A., Heimrath, R., Edtmayer, H., Mach, T., Kaisermayer, V., Gölles, M., & Hochenauer, C. (2025). Grey-Box Model for Efficient Building Simulations: A Case Study of an Integrated Water-Based Heating and Cooling System. Buildings, 15(11), 1959. https://doi.org/10.3390/buildings15111959







