Stability Analysis of Removal of Steel Supports in Variable-Section Pits
Abstract
1. Introduction
2. Project Overview and Finite Element Model Construction
2.1. Project Overview
2.2. Finite Element Modelling
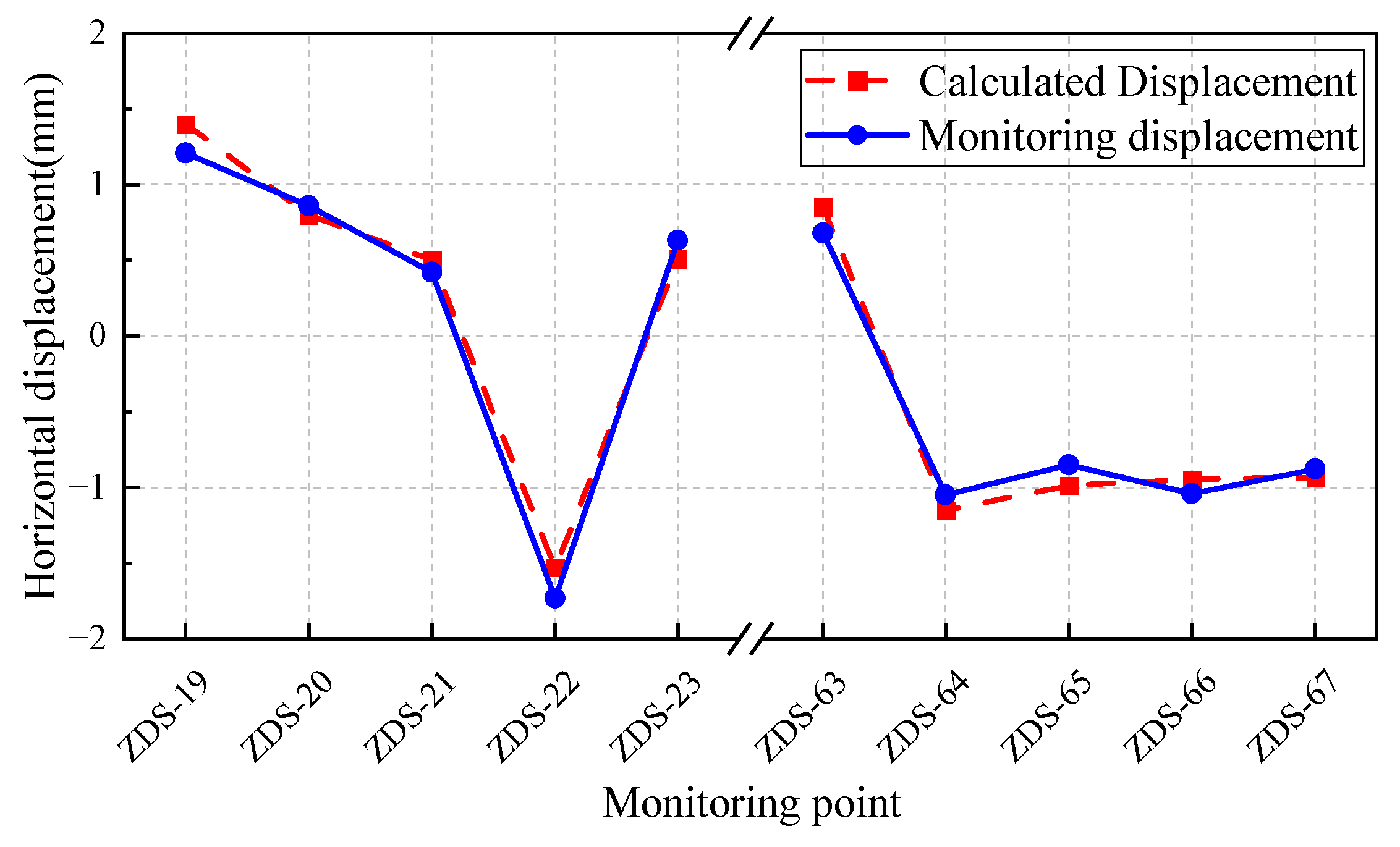
2.3. Finite Element Model Validation
3. Demolition Support Scheme Design
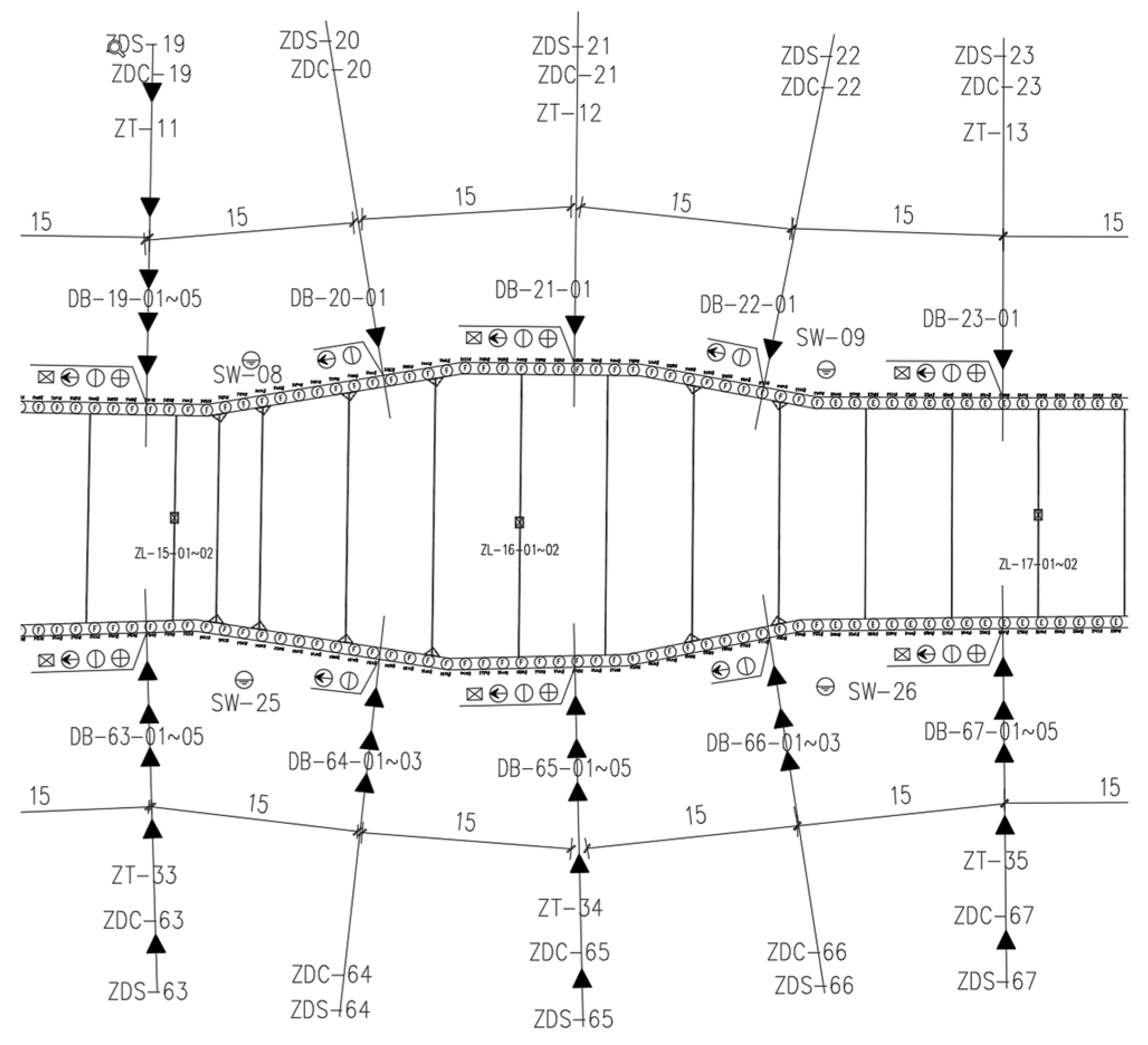
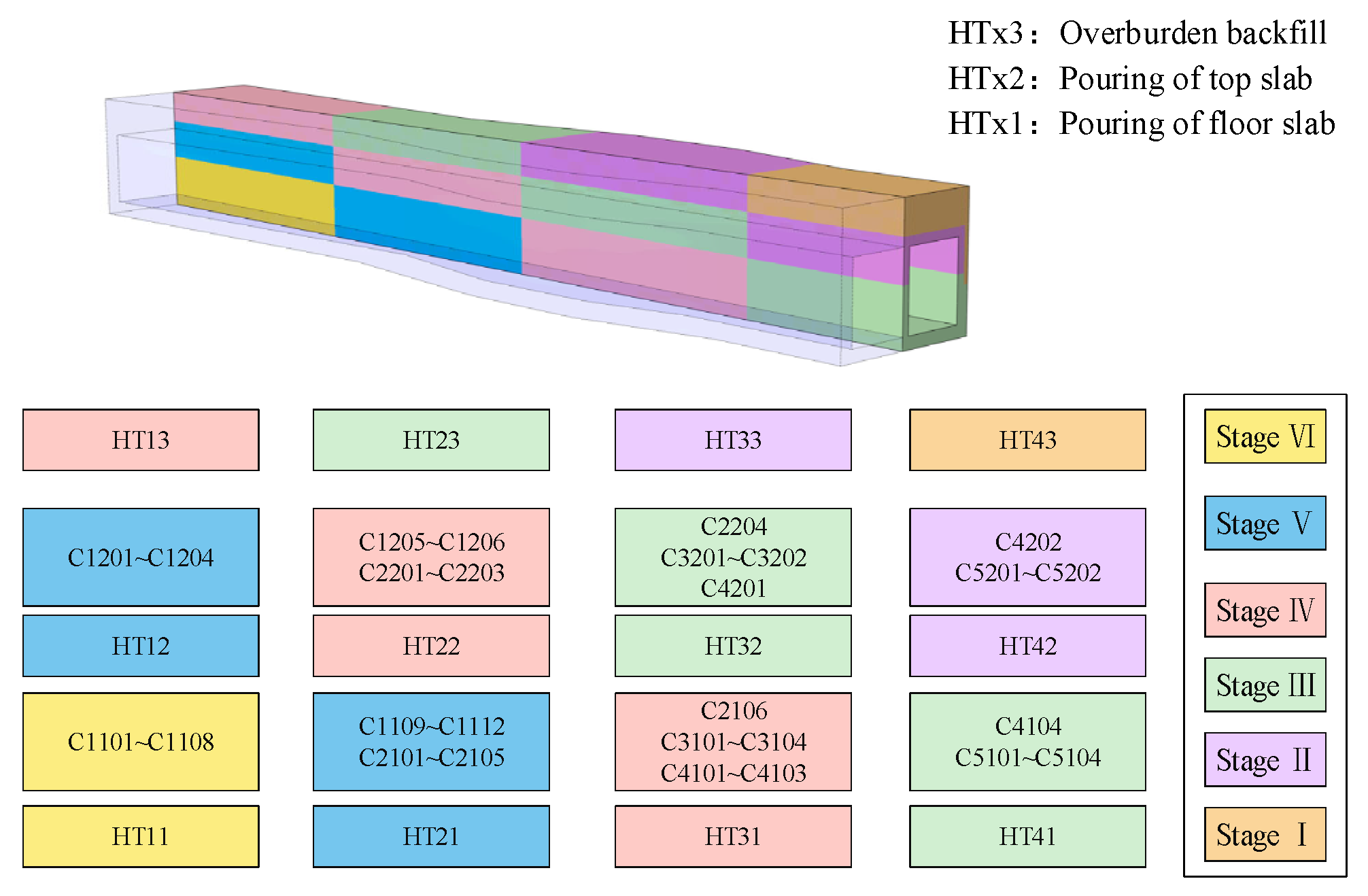
3.1. Steel Support Numbering
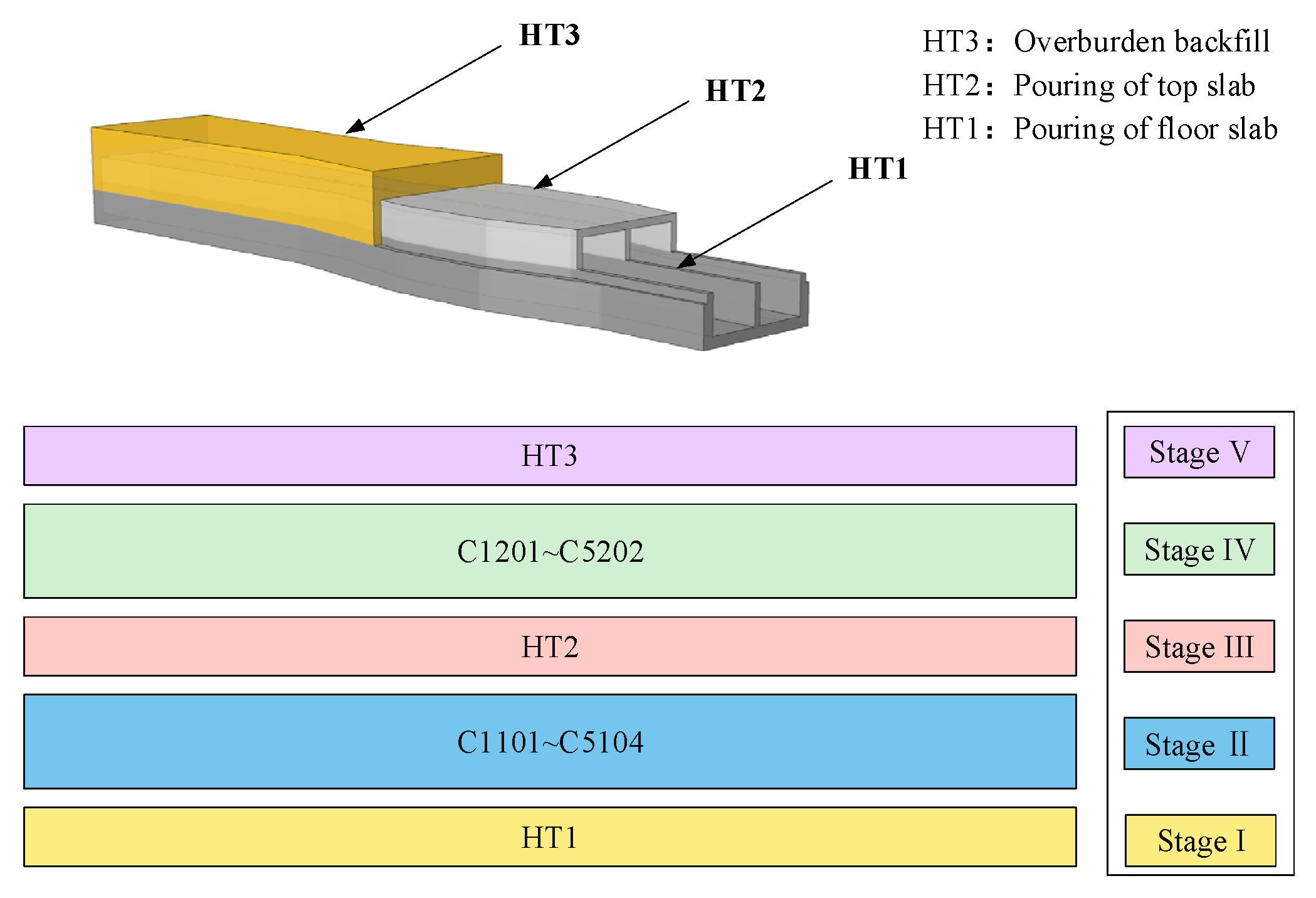
3.2. Layered Backfill and De-Bracing Programme
3.3. Stepped Backfill and De-Bracing Programme
3.4. Supplementary Finite Element Model Analysis Steps for the Disassembly and Bracing Stage
4. Stability Analysis of Layered Backfill and Demolition Support Design Options
4.1. Sedimentation Analysis
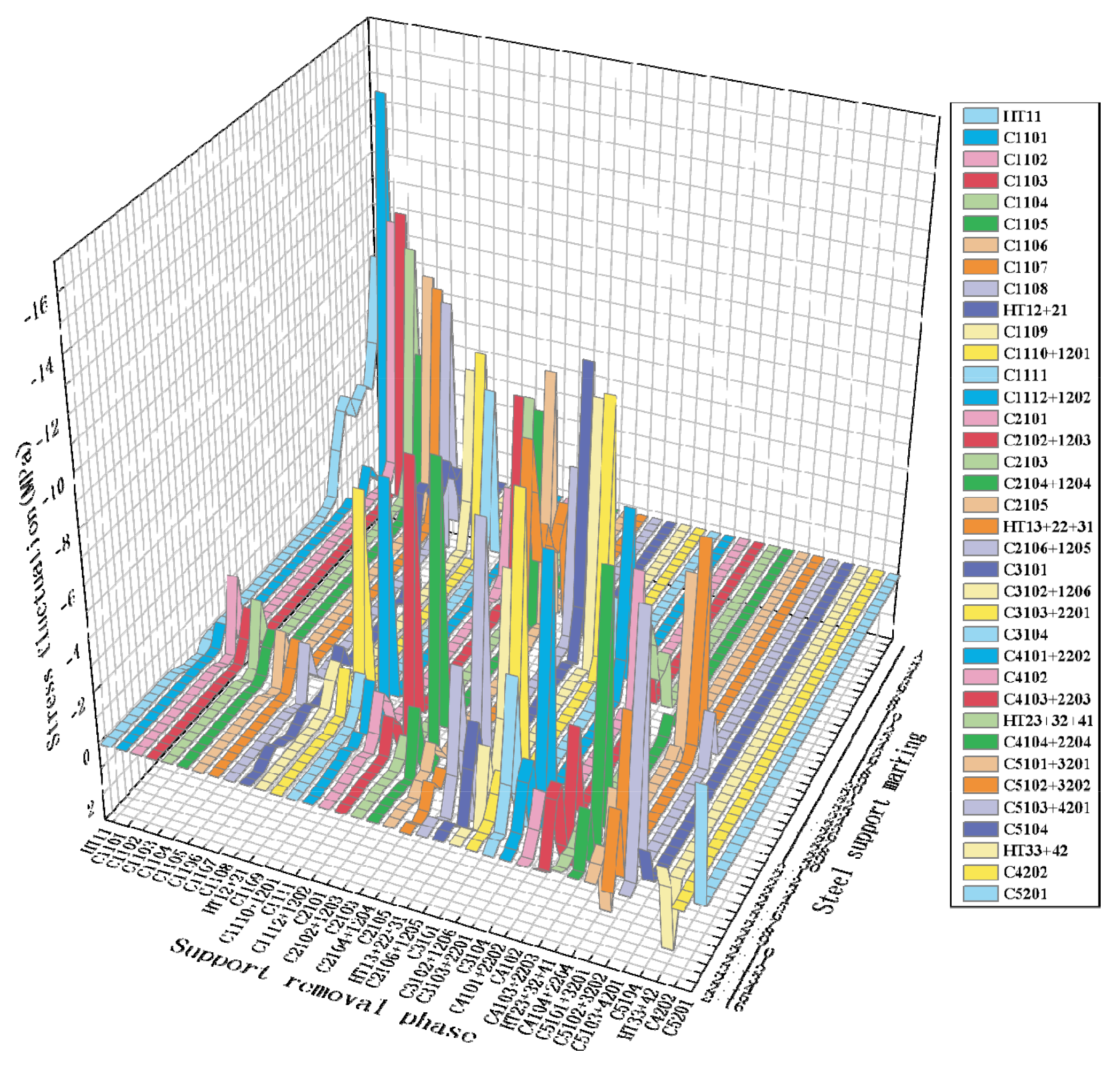
4.2. Axial Force Analysis
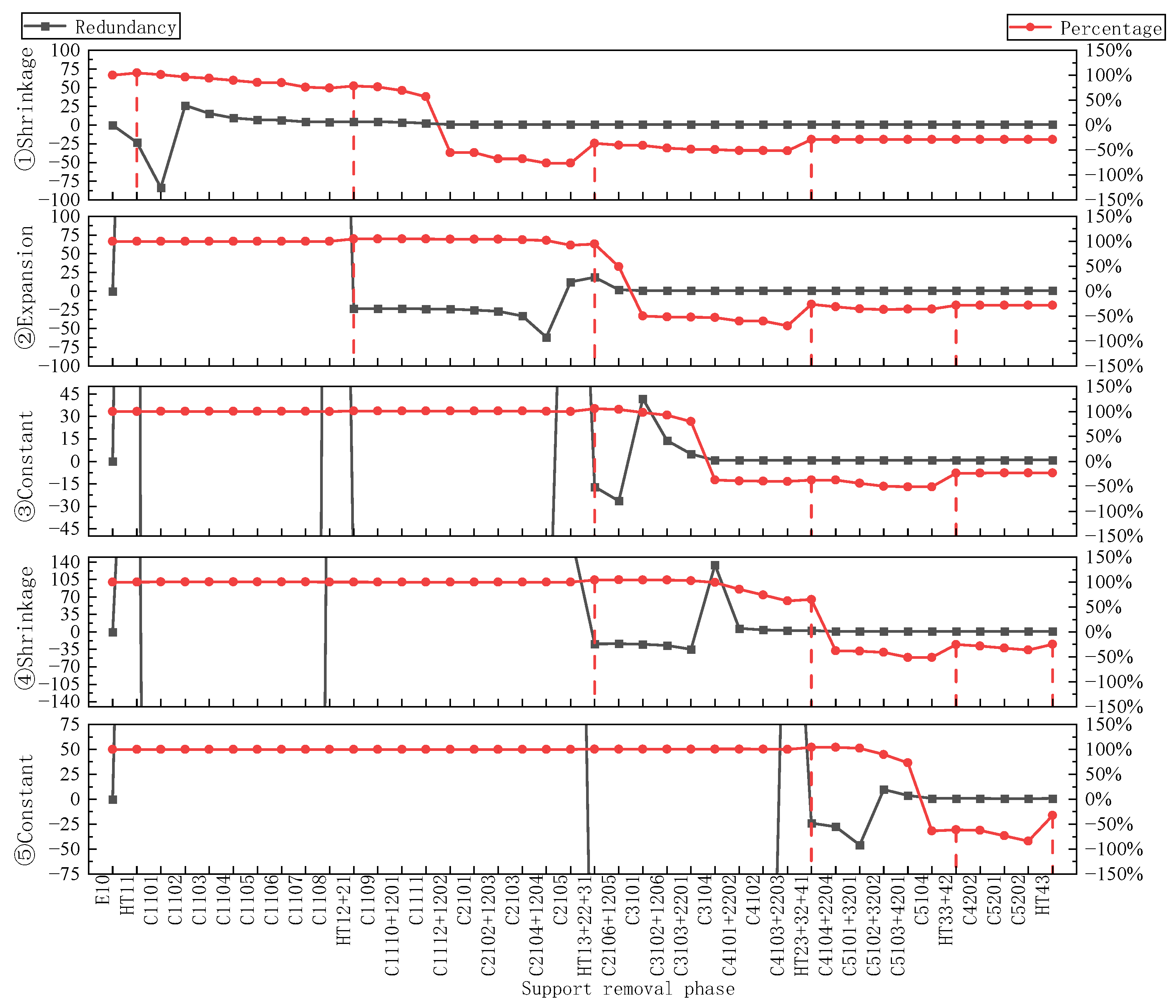
4.3. Redundancy Analysis
5. Stability Analysis of the Stepped Backfill and Demolition Bracing Design Options
5.1. Sedimentation Analysis
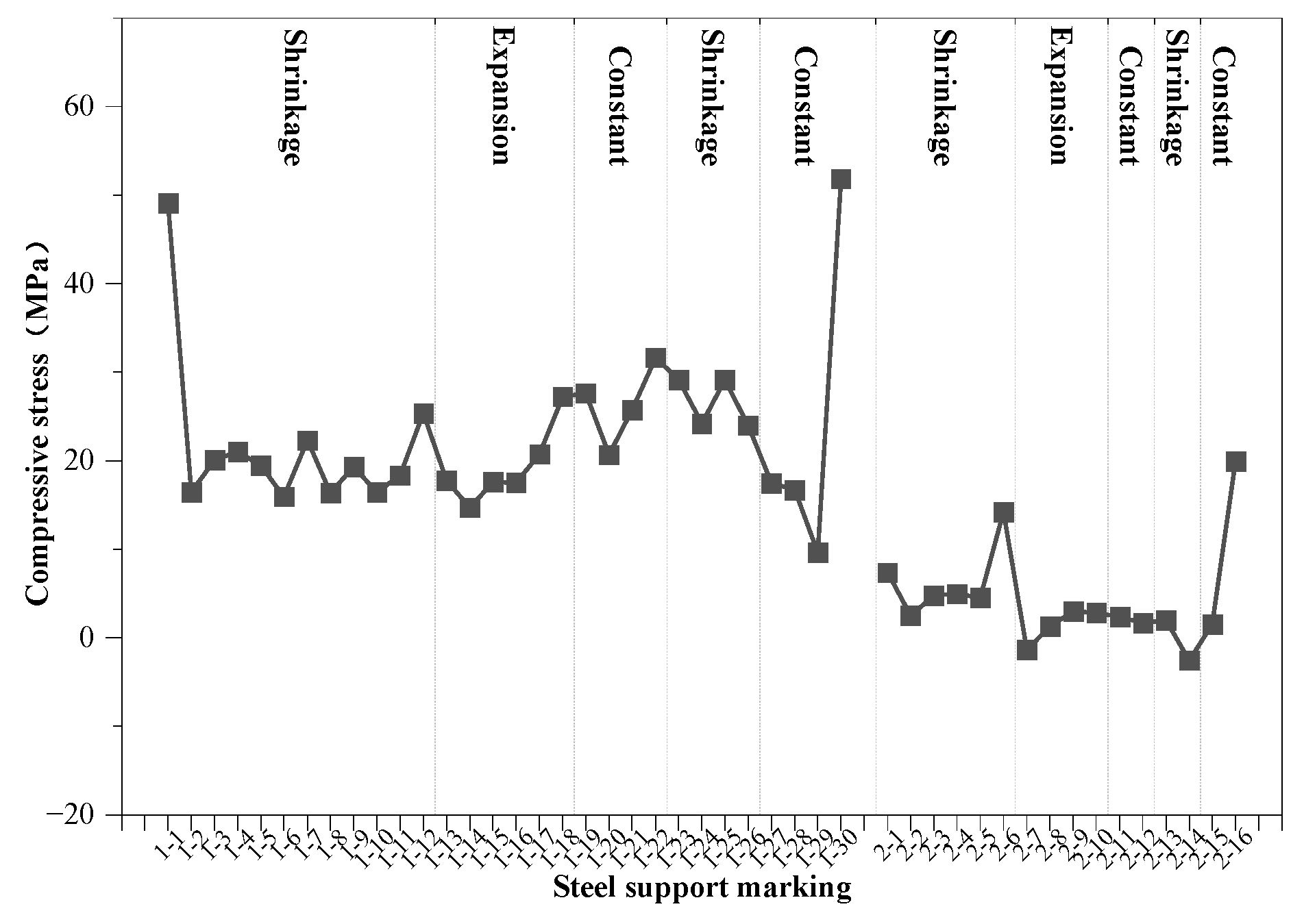
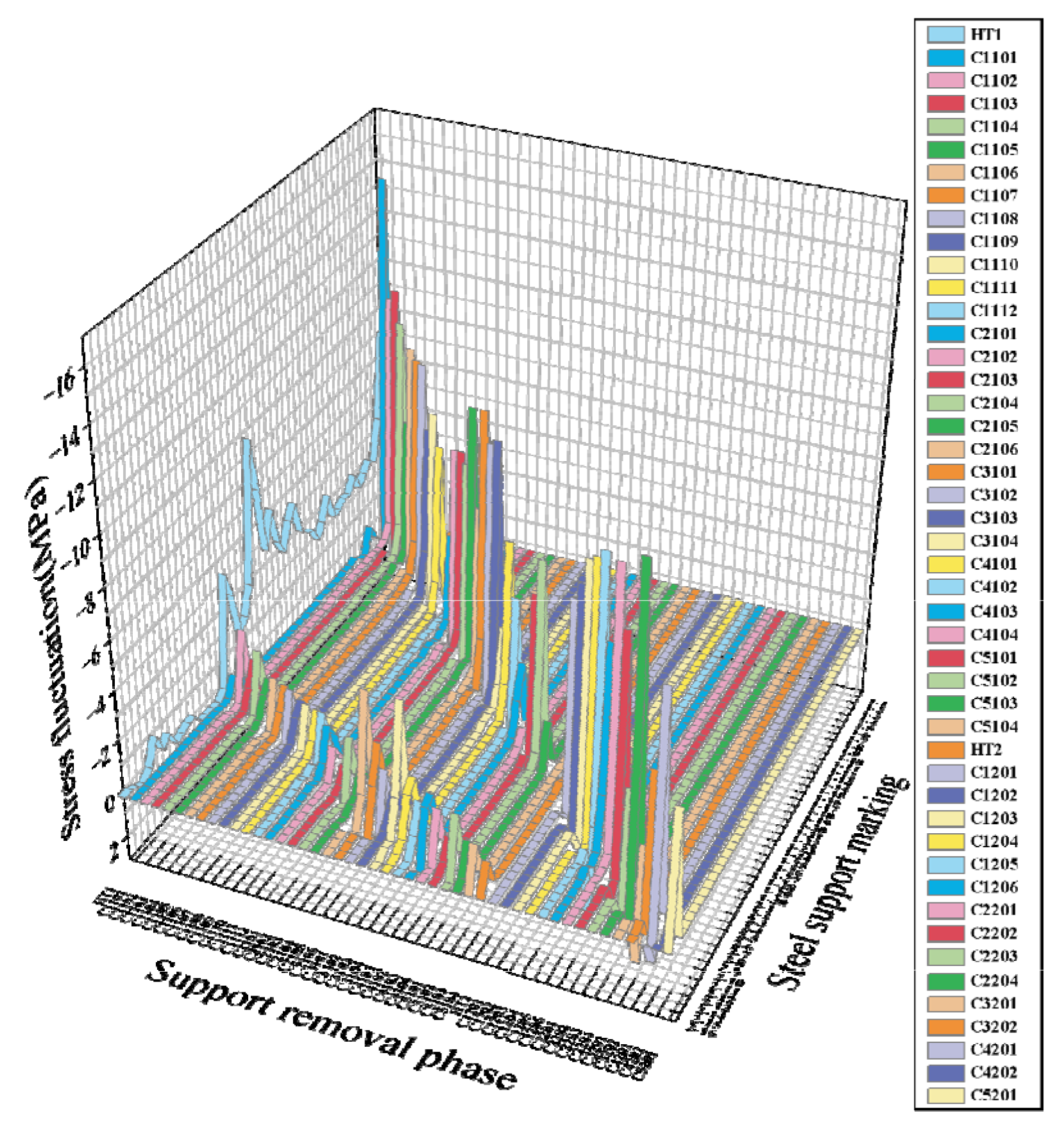
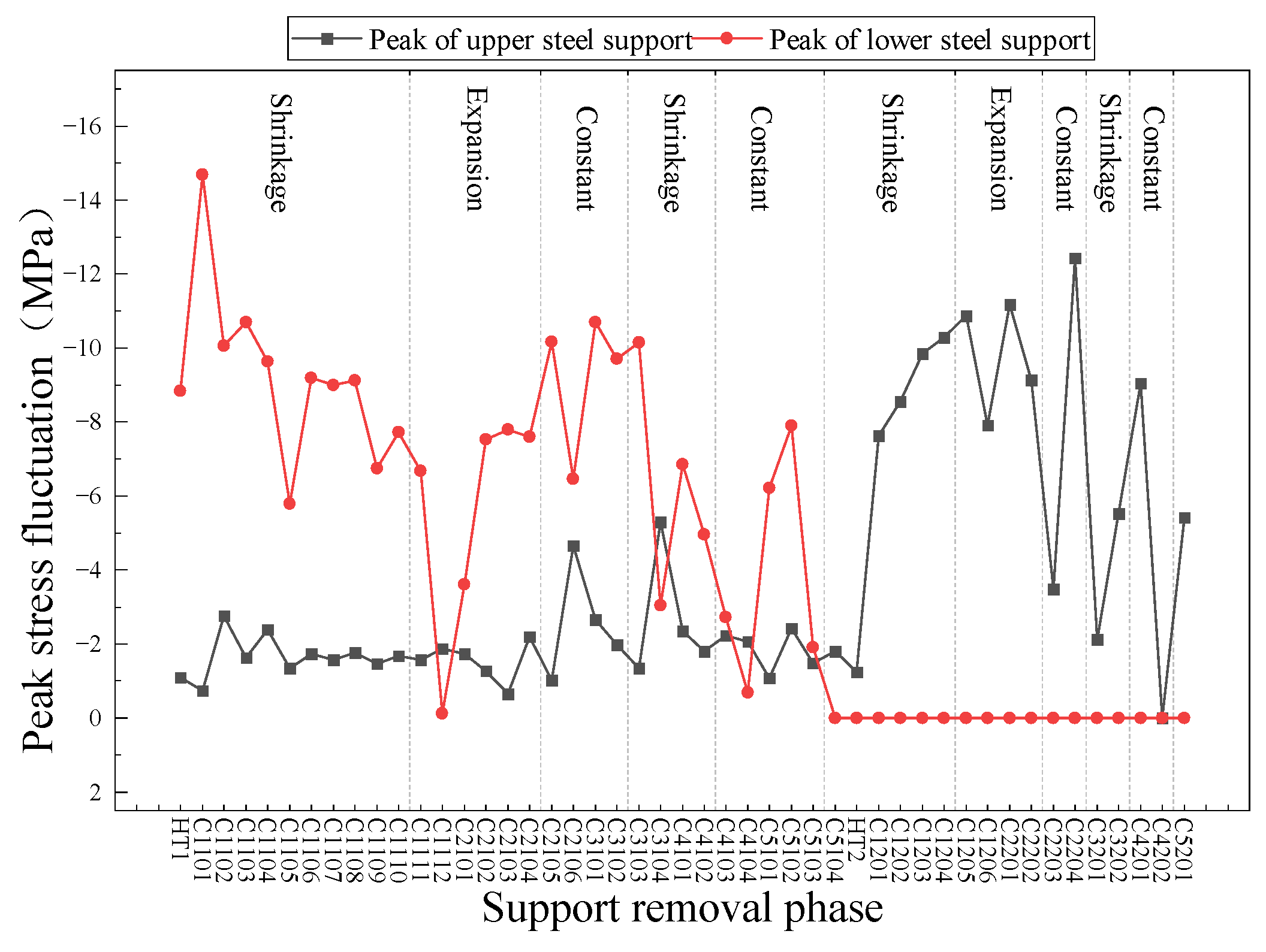
5.2. Axial Force Analysis
5.3. Redundancy Analysis
5.4. Backfilling and De-Bracing Options
6. Conclusions
- Compared with the stepped backfill and split support scheme, the laminar scheme offers more convenience in observing the changing patterns of settlement values and axial forces at different stages, but it is not as good as the stepped scheme in terms of the redundancy of the support structure.
- The redundancy R and relative deformation P effectively reflect the stability of the variable-section pit during each stage of de-bracing. In all five variable-section areas, the minimum redundancy value in the stepped scheme is greater than that in the laminated scheme, with an average increase of 0.03. In addition, the minimum relative deformation is reduced by an average of 5%, with a maximum reduction of 10.52%.
- The stepped removal of braces stabilises the axial force transfer path and controls the range of stress fluctuations, especially during root-by-root removal of steel braces, showing higher redundancy capacity and lower deformation increments. In the lower steel support removal stage, the maximum axial force fluctuation peak value under the stepped solution is only −6.5 MPa, which is smaller than the −8.84 MPa observed in the laminar solution.
- The stepped backfill approach effectively blocks the deformation extension effect between sections and improves the stability of the demolition support in the narrow opening and its distal structural region. In section ①, Pmin increased from −86.9% to −76.38% and Rmin increased to 0.567, which significantly reduced the deformation accumulation effect of the support system.
- The practical significance and engineering value of this study will be further enhanced if scaling experiments on similar models are carried out for validation and analysis in subsequent work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, X.; Rong, C.; Cheng, H.; An, G.; Wu, Q.; Zheng, L. Stability Analysis of Deep Foundation Pit with a Double-Row Cast-in-Place Piles and Diagonal Steel Lattice Braces under Sloped Excavation Conditions. Sci. Rep. 2024, 14, 22761. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Wu, G.; Yang, J.; Liu, Q. Stability Investigation of Fully Recycled Support System of Steel-Pipe-Anchored Sheet Pile in Soft Soil Excavation. Appl. Sci. 2024, 14, 5485. [Google Scholar] [CrossRef]
- Zheng, G.; Lei, Y.W.; Cheng, X.S.; Li, X.Y.; Wang, R.Z. Experimental Study on Progressive Collapse Mechanism in Braced and Tied-Back Retaining Systems of Deep Excavations. Can. Geotech. J. 2021, 58, 540–564. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, R.Z.; Cheng, X.S.; Lei, Y.W.; Li, X.Y.; Zhou, Q. Mechanism and Control of Progressive Collapse of Tied-Back Excavations Induced by Local Anchor Failure. Acta Geotech 2024, 19, 763–781. [Google Scholar] [CrossRef]
- Zheng, Y.; Hu, Z.; Ren, X.; Wang, R.; Zhang, E.; Long, Z. Effects of Partial Supporting Pile Removal from Deep Foundation Pits by Shallow Excavation Method in Loess Areas. Adv. Mater. Sci. Eng. 2021, 2021, 9934113. [Google Scholar] [CrossRef]
- Xie, Z.; Liu, X.; Niu, X.; Jian, J.; Xu, C.; Liao, J. Study on the Influence of the Performance Weakening of the Disconnectable Coupling (DC) Joint of Steel Support on the Retaining Structure of a Foundation Pit. Buildings 2024, 14, 1330. [Google Scholar] [CrossRef]
- Jin, Y.; Zhao, H.; Zheng, C.; Liu, J.; Ding, C. Effect of Steel Support Cross-Section and Preloaded Axial Force on the Stability of Deep Foundation Pits. Buildings 2024, 14, 2532. [Google Scholar] [CrossRef]
- Lu, T.S.; Liu, S.Y.; Cai, G.J.; Wu, K.; Xia, W.J. Study on the Disturbance and Recompression Settlement of Soft Soil Induced by Foundation Pit Excavation. Rock Soil Mech. 2021, 42, 565–573. [Google Scholar] [CrossRef]
- Xing, T.; Jing, Y.; Ye-xiang, J.; Xing-wang, L.; Ying, L. Calculation of Layered Unloading Additional Stress of Foundation Pit Based on Mindlin Solution and the Analysis of Multiple Factors Influencing the Rebound Deformation. Rock Soil Mech. 2020, 41, 2432–2440. [Google Scholar] [CrossRef]
- Song, D.; Chen, Z.; Dong, L.; Tang, G.; Zhang, K.; Wang, H. Monitoring Analysis of Influence of Extra-Large Complex Deep Foundation Pit on Adjacent Environment: A Case Study of Zhengzhou City, China. Geomat. Nat. Hazards Risk 2020, 11, 2036–2057. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.; Ankit, G.; Singh, Y.J. Deformation Monitoring Analysis and Numerical Simulation in a Deep Foundation Pit. Soil Mech. Found. Eng. 2021, 58, 56–62. [Google Scholar] [CrossRef]
- Qiu, H.; Zhou, Y.; Ayasrah, M. Impact Study of Deep Foundations Construction of Inclined and Straight Combined Support Piles on Adjacent Pile Foundations. Appl. Sci. 2023, 13, 1810. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, D.; Wang, W.; Ma, P.; Jiang, S. Deformation Law and Spatial Effect of Deep Foundation Pits for Subway Construction in Soil-Rock Composite Strata in Seasonally Frozen Areas. Teh. Vjesn.-Tech. Gaz. 2023, 30, 1315–1325. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, X. Construction Pit Deformation Measurement Technology Based on Neural Network Algorithm. J. Intell. Syst. 2023, 32, 20220292. [Google Scholar] [CrossRef]
- Zhu, Y.; Qin, H.; Zhang, X.; Wei, D.; Zhai, L.; Hu, L. Innovative Three-Row Pile Support System of Ultra-Deep Foundation Pit and Cooperative Construction Technology with Basement for High-Rise Tower Structures. Buildings 2024, 14, 1003. [Google Scholar] [CrossRef]
- Liu, J.Y.; Li, B.; Liu, Y.; Cai, S.B. Design Method of Redundancy of Brace-Anchor Sharing Supporting Based on Cooperative Deformation. IOP Conf. Ser. Earth Environ. Sci. 2017, 94, 012202. [Google Scholar] [CrossRef]
- Shadabfar, M.; Mahsuli, M.; Zhang, Y.; Xue, Y.D.; Ayyub, B.M.; Huang, H.W.; Medina, R.A. Resilience-Based Design of Infrastructure: Review of Models, Methodologies, and Computational Tools. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A-Civ. Eng. 2022, 8, 03121004. [Google Scholar] [CrossRef]
- Yi, F.; Su, J.; Zheng, G.; Cheng, X.S.; Zhang, J.T.; Lei, Y.W. Overturning Progressive Collapse Mechanism and Control Methods of Excavations Retained by Cantilever Piles. Eng. Fail. Anal. 2022, 140, 106591. [Google Scholar] [CrossRef]
- Sarmiento, S.; Thons, S.; Gonzalez-Libreros, J.; Bjornsson, I.; Sas, G. Comparison and Joint Evaluation of Importance, Redundancy and Robustness Indicators Applied to Aging Prestressed Concrete Bridges. Nord. Concr. Res. 2024, 70, 147–171. [Google Scholar] [CrossRef]
- Li, S.; Wang, F.; Le, Y.; Que, Q.; Su, Y.; Lin, H. Design and Deformation Pattern Simulation of Deep Excavation Support Structures. Front. Earth Sci. 2024, 12, 1416957. [Google Scholar] [CrossRef]
- Kim, J.; Yi, S.; Park, J.; Kim, T. Efficient System Reliability-Based Disaster Resilience Analysis of Structures Using Importance Sampling. J. Eng. Mech. 2024, 150, 4024081. [Google Scholar] [CrossRef]
- Wu, J.; Ye, S.H.; Wang, Z.Q.; Yang, D. Application and Automatic Monitoring and Analysis of Hybrid Support Structure in Ultra-DEEP Foundation Pit Engineering in the Lanzhou Area under Complex Environmental Conditions. Water 2023, 15, 1335. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, C.; Wu, J. Industry Foundation Class-Based Building Information Modeling Lightweight Visualization Method for Steel Structures. Appl. Sci. 2024, 14, 5507. [Google Scholar] [CrossRef]
- Ke, C.; Fan, Y.; Jiang, J. Influence of Staggered Truss on Progressive Collapse-Resistant Behavior of Steel Frame Structures. Buildings 2024, 14, 931. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, H.; Bhattacharya, B.; El-Tawil, S.; Agrawal, A.K.; Wong, W. Reliability-Based Framework for Structural Robustness Evaluation of Bridges. J. Bridge Eng. 2024, 29, 4024035. [Google Scholar] [CrossRef]
- Chen, Y.; Liao, Y.; Zhu, L.; Chen, L.; Chen, Y. Robustness of a Steel Truss Bridge Subjected to Sudden Member Breakage during the Continuous-to-Simply-Supported Transition. Buildings 2024, 14, 3035. [Google Scholar] [CrossRef]
- You, X.; Zhou, Q.; Xiao, Y.; Tong, L.; Yang, Q. Numerical Study on the Coupling Effect on a Retaining Structure of a Complex Deep Foundation Pit Group Excavation in a Soft-Soil Area. Appl. Sci. 2023, 13, 3263. [Google Scholar] [CrossRef]
- Di, H.G.; Guo, H.J.; Zhou, S.H.; Chen, J.M.; Wen, L. Investigation of the Axial Force Compensation and Deformation Control Effect of Servo Steel Struts in a Deep Foundation Pit Excavation in Soft Clay. Adv. Civ. Eng. 2019, 2019, 5476354. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, C. Analysis of Deep Foundation Pit Construction Monitoring in a Metro Station in Jinan City. Geotech. Geol. Eng. 2019, 37, 813–822. [Google Scholar] [CrossRef]
- Lu, B.; Zhao, W.; Du, X.; Li, S.; Guan, Y.; Wang, Z. Analysis of Ultimate Bearing Capacity and Parameters of Steel Support Cutting Pipe Roofing Structure. Transp. Res. Rec. 2022, 2676, 348–366. [Google Scholar] [CrossRef]
- Cheng, X.; He, J.; Li, X.; Xia, Q.; Su, H.; Chen, C. Deformation rule of bored pile & steel support for deep foundation pit in sandy pebble geology. Stavební Obz.-Civ. Eng. J. 2023, 33, 282–297. [Google Scholar] [CrossRef]
- Wang, X.; Song, Q.; Gong, H. Research on Deformation Law of Deep Foundation Pit of Station in Core Region of Saturated Soft Loess Based on Monitoring. Adv. Civ. Eng. 2022, 2022, 7848152. [Google Scholar] [CrossRef]
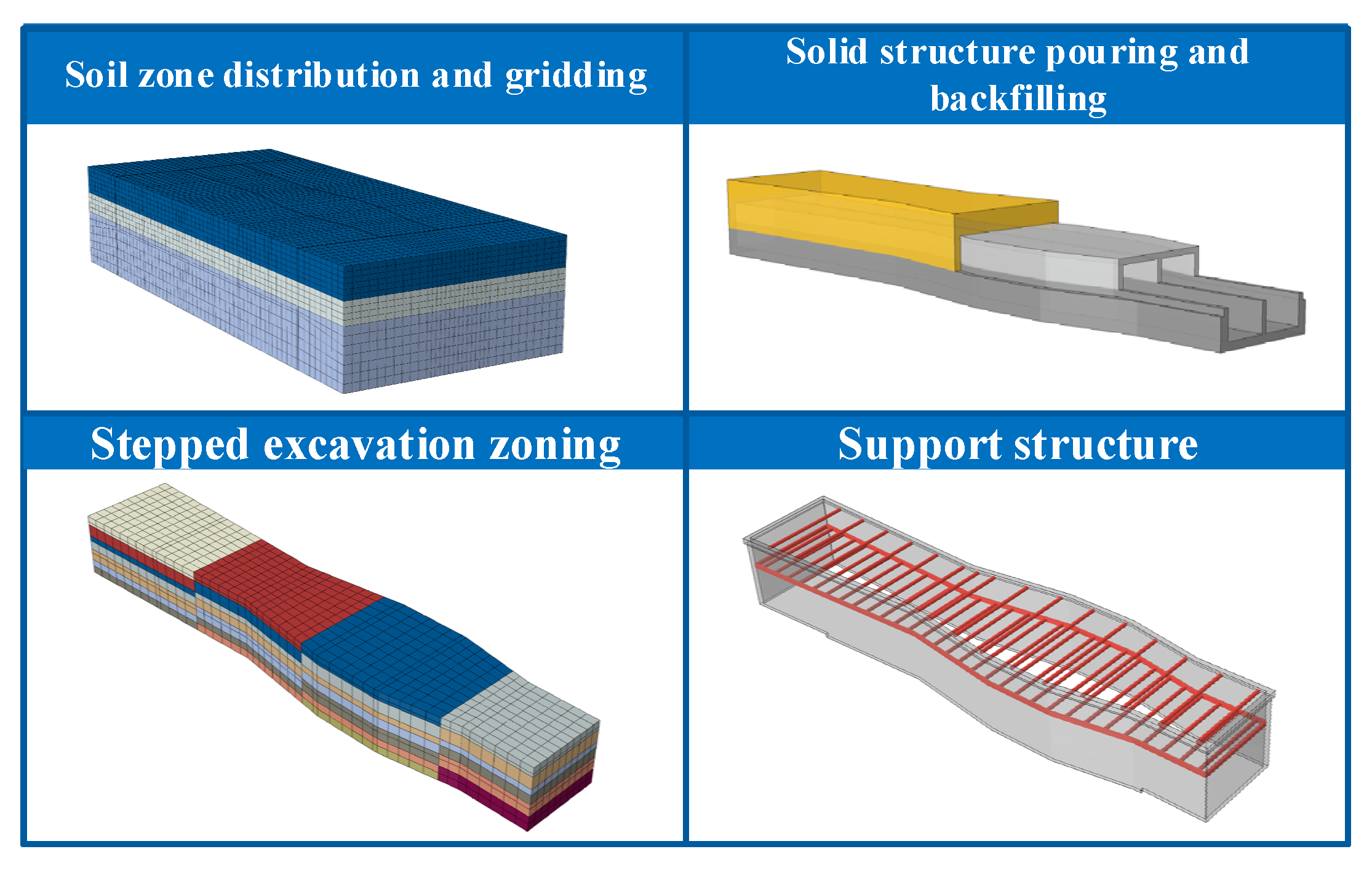






| Soil Layer Name | Density (kg/m3) | Angle of Internal Friction (°) | Cohesion (kPa) | Poisson’s Ratio | Elastic Modulus (MPa) |
|---|---|---|---|---|---|
| silty clay | 2000 | 20 | 33 | 0.2 | 21.5 |
| shale | 2500 | 25 | 50 | 0.2 | 6000 |
| conglomerates | 2140 | 28 | 40 | 0.2 | 15,500 |
| Makings | Density (kg/m3) | Modulus of Elasticity (MPa) | Poisson’s Ratio |
|---|---|---|---|
| C15 concrete | 2240 | 22,000 | 0.2 |
| C20 concrete | 2360 | 25,500 | 0.2 |
| C30 concrete | 2450 | 30,000 | 0.25 |
| Q235B steel | 7850 | 200,000 | 0.3 |
| No. | Content of the Analysis Step | No. | Content of the Analysis Step |
|---|---|---|---|
| 1 | Ground stress equilibrium | 11 | Step 5 Excavation |
| 2 | Enclosure construction | 12 | Erection of second and first steel supports for Step 5 |
| 3 | Step 1 Excavation | 13 | Step 6 Excavation |
| 4 | Erection of first steel support for Step 1 | 14 | Erection of second and first steel supports for Step 6 |
| 5 | Step 2 Excavation | 15 | Step 7 Excavation |
| 6 | Erection of first steel support for Step 2 | 16 | Erection of second and first steel supports for Step 7 |
| 7 | Step 3 Excavation | 17 | Step 8 Excavation |
| 8 | Erection of second and first steel supports for Step 3 | 18 | Step 9 Excavation |
| 9 | Step 4 Excavation | 19 * | Step 10 Excavation |
| 10 | Erection of second and first steel supports for Step 4 | ||
| No. | Analysis Step | No. | Analysis Step | No. | Analysis Step | No. | Analysis Step | No. | Analysis Step | No. | Analysis Step | No. | Analysis Step |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | HT1 | 27 | C1107 | 34 | C2102 | 41 | C3103 | 48 | C5102 | 55 | C1204 | 62 | C3201 |
| 21 | C1101 | 28 | C1108 | 35 | C2103 | 42 | C3104 | 49 | C5103 | 56 | C1205 | 63 | C3202 |
| 22 | C1102 | 29 | C1109 | 36 | C2104 | 43 | C4101 | 50 | C5104 | 57 | C1206 | 64 | C4201 |
| 23 | C1103 | 30 | C1110 | 37 | C2105 | 44 | C4102 | 51 | HT2 | 58 | C2201 | 65 | C4202 |
| 24 | C1104 | 31 | C1111 | 38 | C2106 | 45 | C4103 | 52 | C1201 | 59 | C2202 | 66 | C5201 |
| 25 | C1105 | 32 | C1112 | 39 | C3101 | 46 | C4104 | 53 | C1202 | 60 | C2203 | 67 | C5202 |
| 26 | C1106 | 33 | C2101 | 40 | C3102 | 47 | C5101 | 54 | C1203 | 61 | C2204 | 68 | HT3 |
| No. | Analysis Step | No. | Analysis Step | No. | Analysis Step | No. | Analysis Step | No. | Analysis Step | No. | Analysis Step |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | HT11 | 27 | C1107 | 34 | C2101 | 41 | C3101 | 48 | HT23+32+41 | 55 | C4202 |
| 21 | C1101 | 28 | C1108 | 35 | C2102+1203 | 42 | C3102+1206 | 49 | C4104+2204 | 56 | C5201 |
| 22 | C1102 | 29 | HT12+21 | 36 | C2103 | 43 | C3103+2201 | 50 | C5101+3201 | 57 | C5202 |
| 23 | C1103 | 30 | C1109 | 37 | C2104+1204 | 44 | C3104 | 51 | C5102+3202 | 58 | HT43 |
| 24 | C1104 | 31 | C1110+1201 | 38 | C2105 | 45 | C4101+2202 | 52 | C5103+4201 | - | - |
| 25 | C1105 | 32 | C1111 | 39 | HT13+22+31 | 46 | C4102 | 53 | C5104 | - | - |
| 26 | C1106 | 33 | C1112+1202 | 40 | C2106+1205 | 47 | C4103+2203 | 54 | HT33+42 | - | - |
| Variable Cross-Section Area | Scheme for Removal of Steel Support and Layered Backfill | Scheme for Removal of Steel Support and Stepped Backfill | ||
|---|---|---|---|---|
| Rmin | Pmin | Rmin | Pmin | |
| I Constant section | 0.537 | −86.9% | 0.567 | −76.38% |
| II Expansion section | 0.573 | −74.59% | 0.588 | −69.96% |
| III Constant section | 0.649 | −54.18% | 0.662 | −51.14% |
| IV Contraction section | 0.630 | −58.75% | 0.660 | −51.44% |
| V Constant section | 0.525 | −90.50% | 0.544 | −83.98% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Yao, X.; Wu, J.; Fan, X.; Jin, Y.; Zheng, C. Stability Analysis of Removal of Steel Supports in Variable-Section Pits. Buildings 2025, 15, 1903. https://doi.org/10.3390/buildings15111903
Huang Q, Yao X, Wu J, Fan X, Jin Y, Zheng C. Stability Analysis of Removal of Steel Supports in Variable-Section Pits. Buildings. 2025; 15(11):1903. https://doi.org/10.3390/buildings15111903
Chicago/Turabian StyleHuang, Qi, Xinyu Yao, Jingjiang Wu, Xiaohu Fan, Yang Jin, and Chuanfeng Zheng. 2025. "Stability Analysis of Removal of Steel Supports in Variable-Section Pits" Buildings 15, no. 11: 1903. https://doi.org/10.3390/buildings15111903
APA StyleHuang, Q., Yao, X., Wu, J., Fan, X., Jin, Y., & Zheng, C. (2025). Stability Analysis of Removal of Steel Supports in Variable-Section Pits. Buildings, 15(11), 1903. https://doi.org/10.3390/buildings15111903





