Experimental and Theoretical Investigation on Cracking Behavior and Influencing Factors of Steel-Reinforced Concrete Deep Beams
Abstract
1. Introduction
2. Experimental Setup
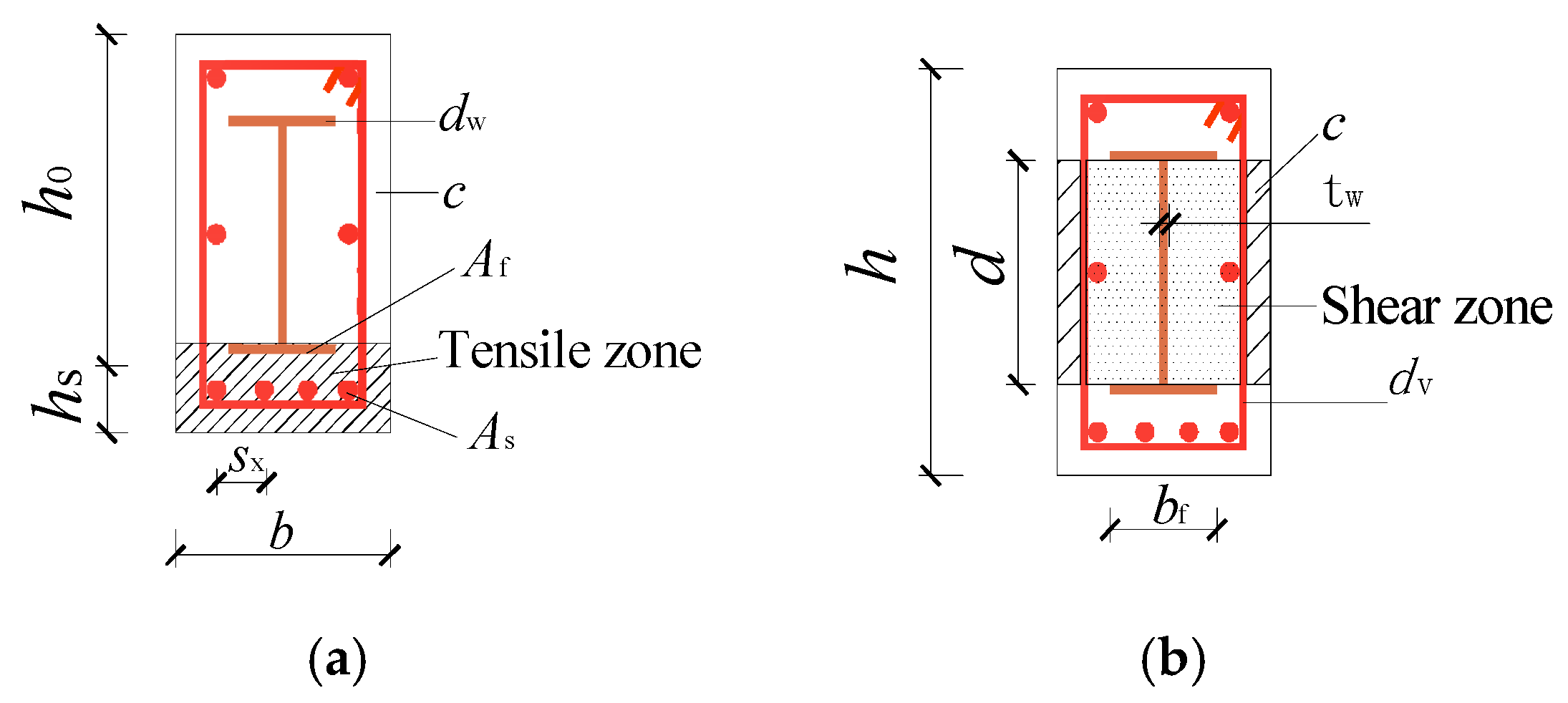
2.1. Specimen Details
2.2. Material Properties
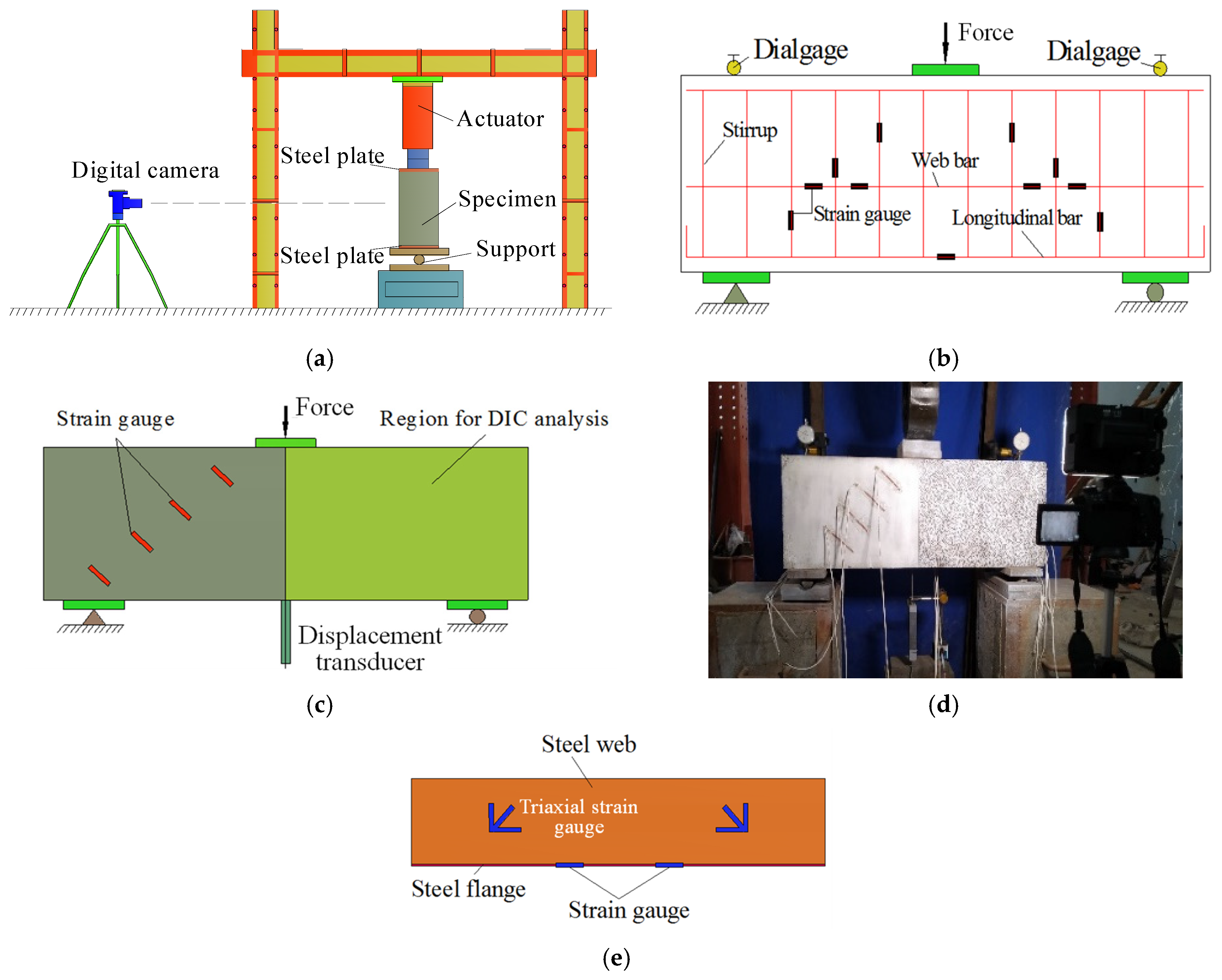
2.3. Test Setup
2.4. Digital Image Correlation Technique (DIC)
3. Test Results
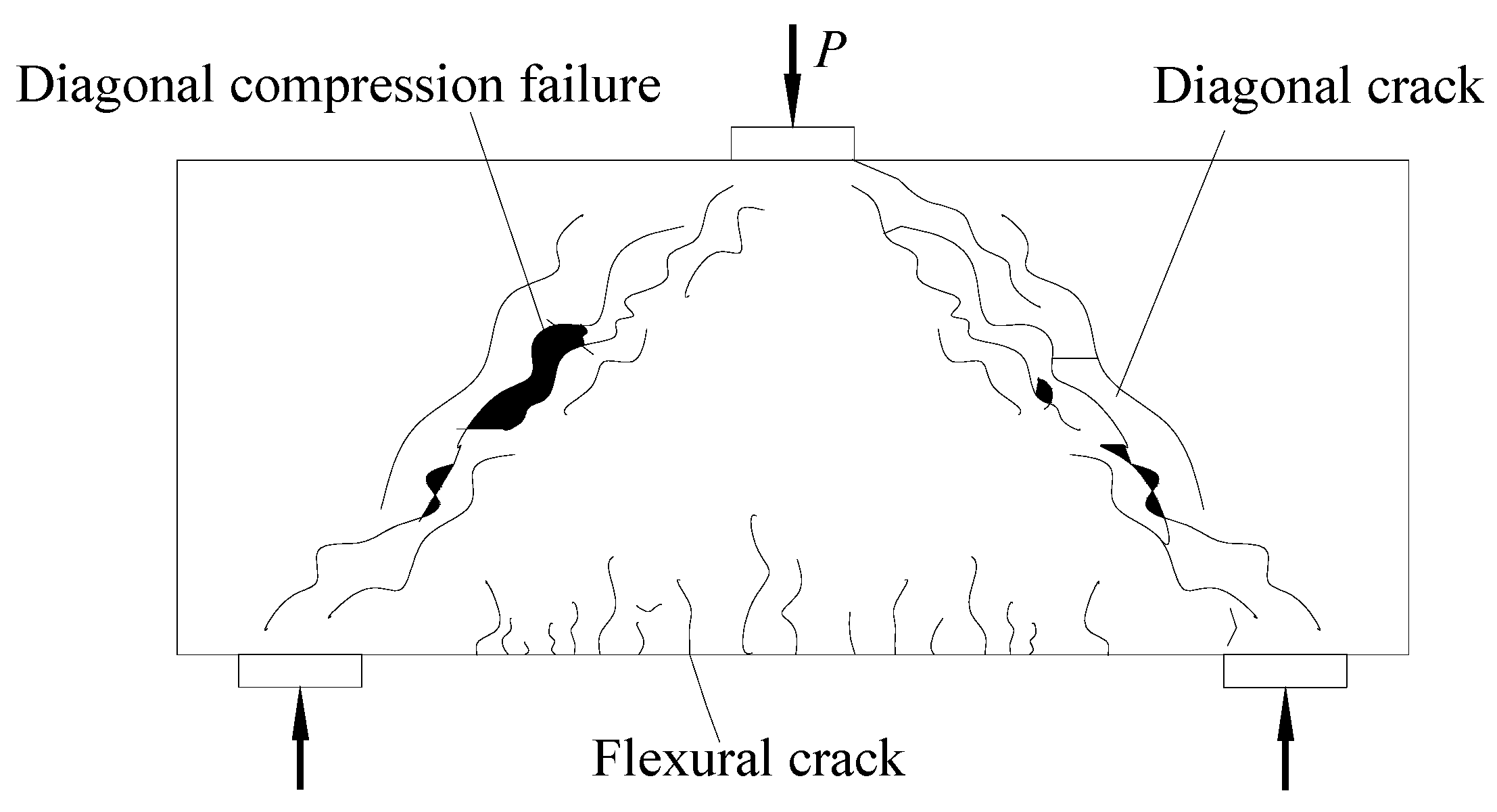
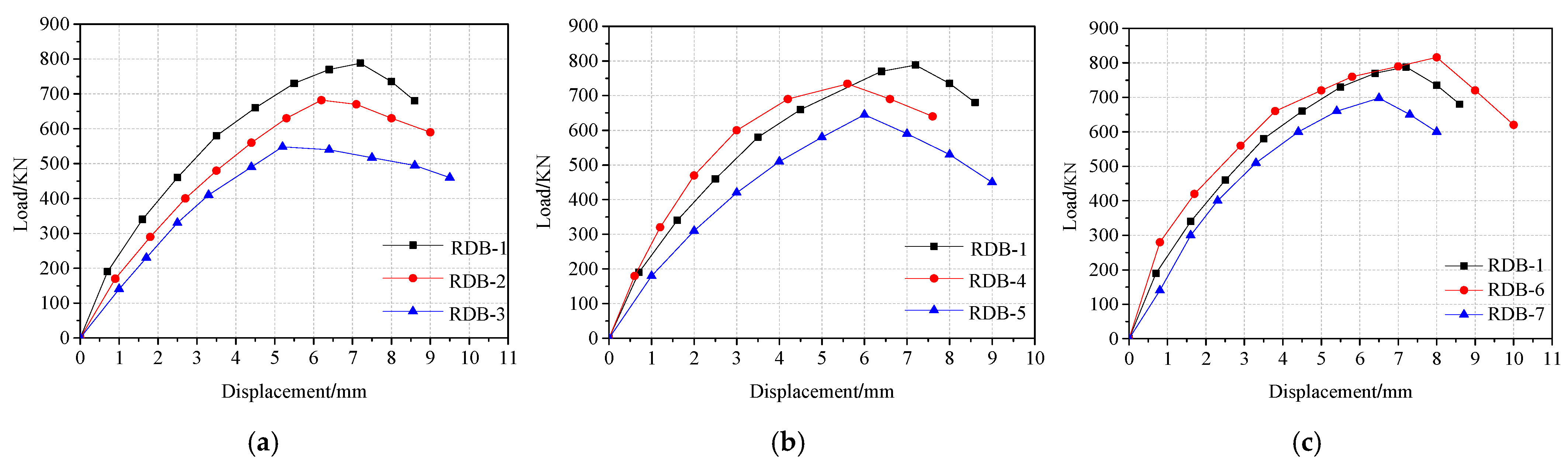
3.1. General Behavior and Failure Mode
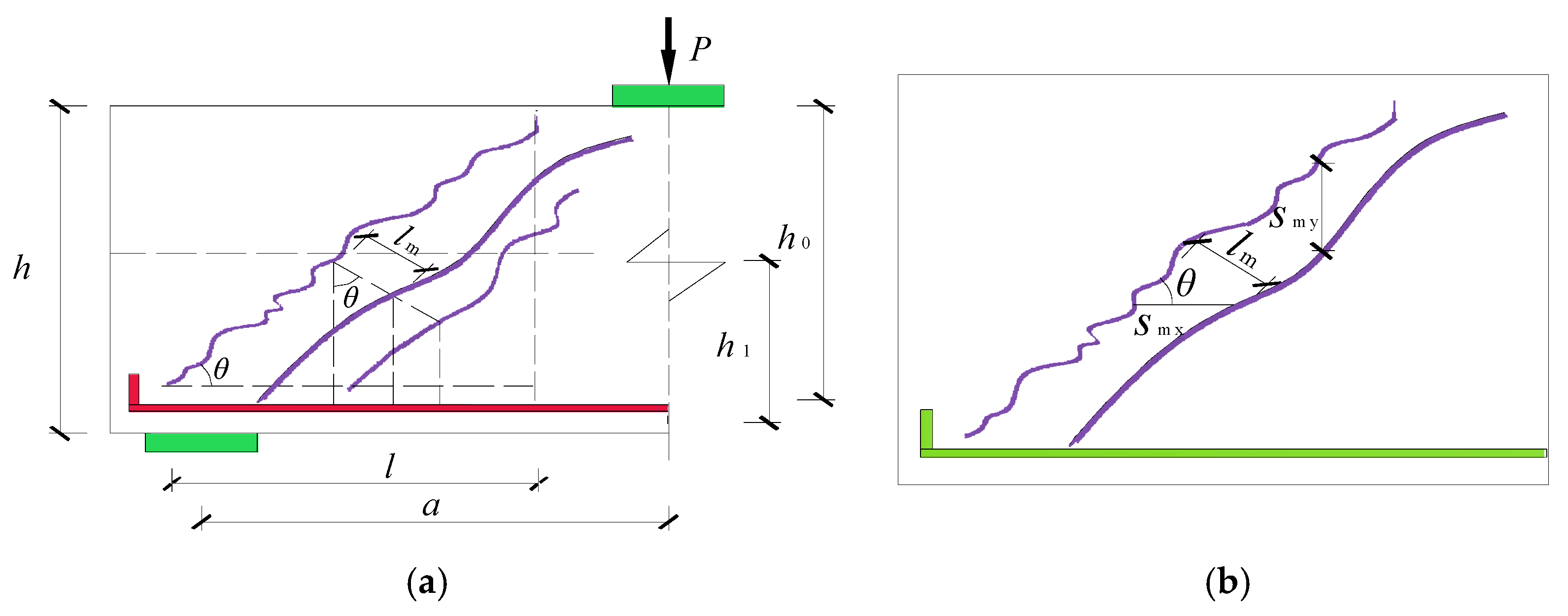
3.2. Diagonal Crack Spacing
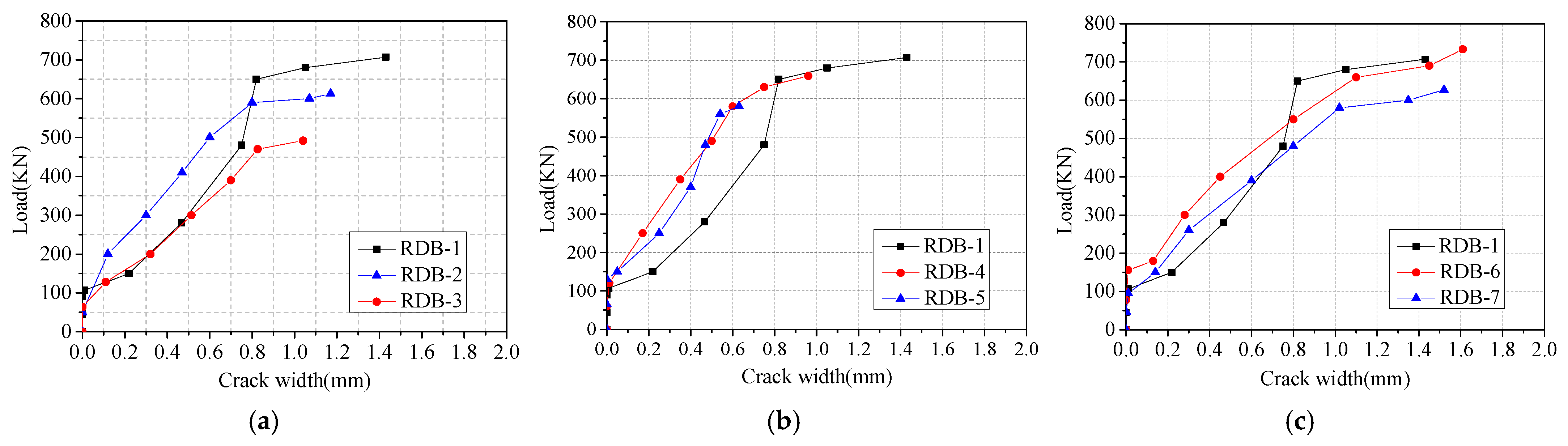
3.3. Diagonal Crack Width
4. Derivation of Diagonal Crack Width Calculation Method
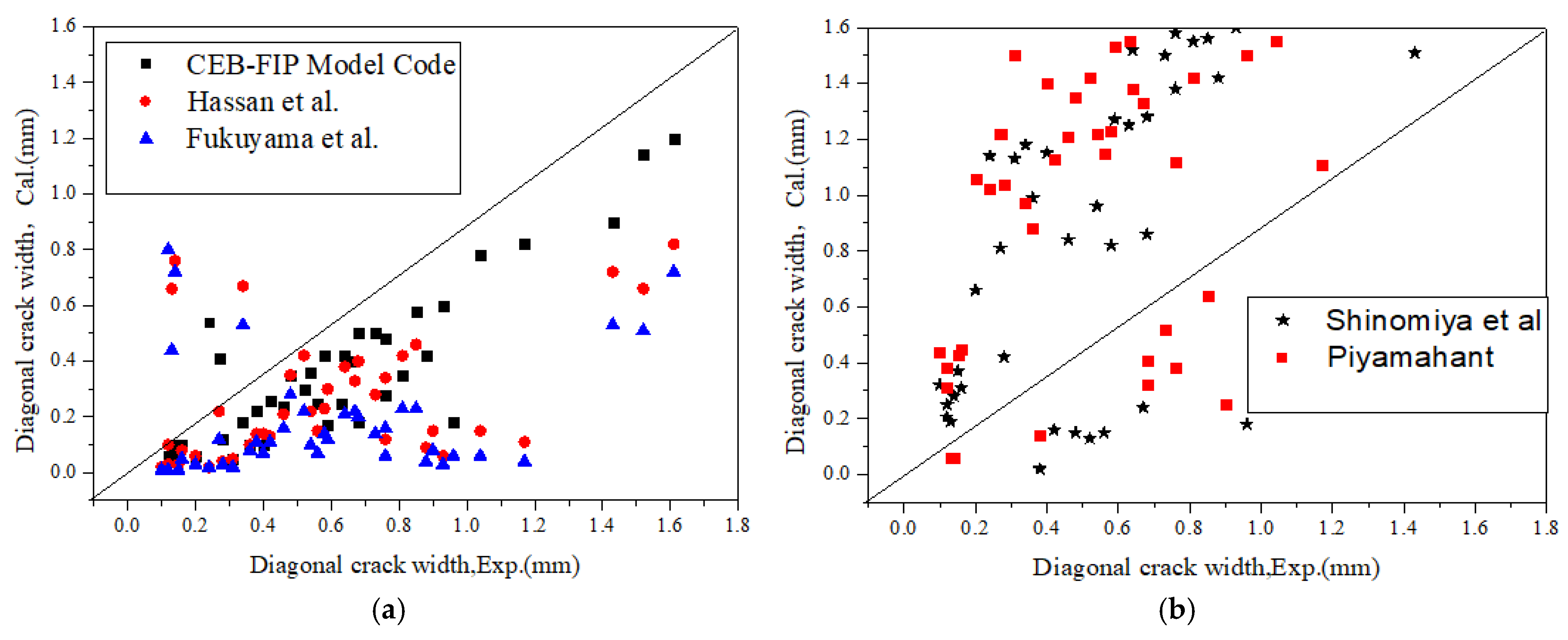
4.1. Diagonal Crack Width Formula
4.2. Diagonal Crack Spacing Model of SRC Deep Beam
5. Conclusions
- DIC is a suitable tool for evaluating cracking behavior as well as crack development. It can be used for full-field deformation measurements and is useful for the continuous tracking of critical shear cracks. In addition, DIC can accurately record the load at the first crack and can be used to better understand the appearance, development, and final shape of the cracks.
- When the increased from 1.1 to 1.4 and 1.7, the ultimate bearing capacity decreased by 13.3% and 30.4%, respectively. Increasing the section size of the steel skeleton can significantly improve the bearing capacity of the specimens. When the height ratio increases by 0.15 and 0.3, the ultimate bearing capacity increases by 13.7% and 22%, and when the width ratio increases by 0.17 and 0.34, the ultimate bearing capacity increases by 12.8% and 17%.
- The spacing of diagonal cracks decreases with the increase of the . When the increased from 1.1 to 1.4, the diagonal crack spacing reduced by 11.3 mm; when the increased from 1.4 to 1.7, the diagonal crack spacing reduced by 6.4 mm.
- The diagonal crack width is mainly affected by the height of the steel web and the , and the steel skeleton flange is slightly affected. When the steel skeleton flange width ratio increased from 0.33 to 0.5 and then to 0.67, the average crack width increased by 0.02 mm and 0.05 mm, respectively.
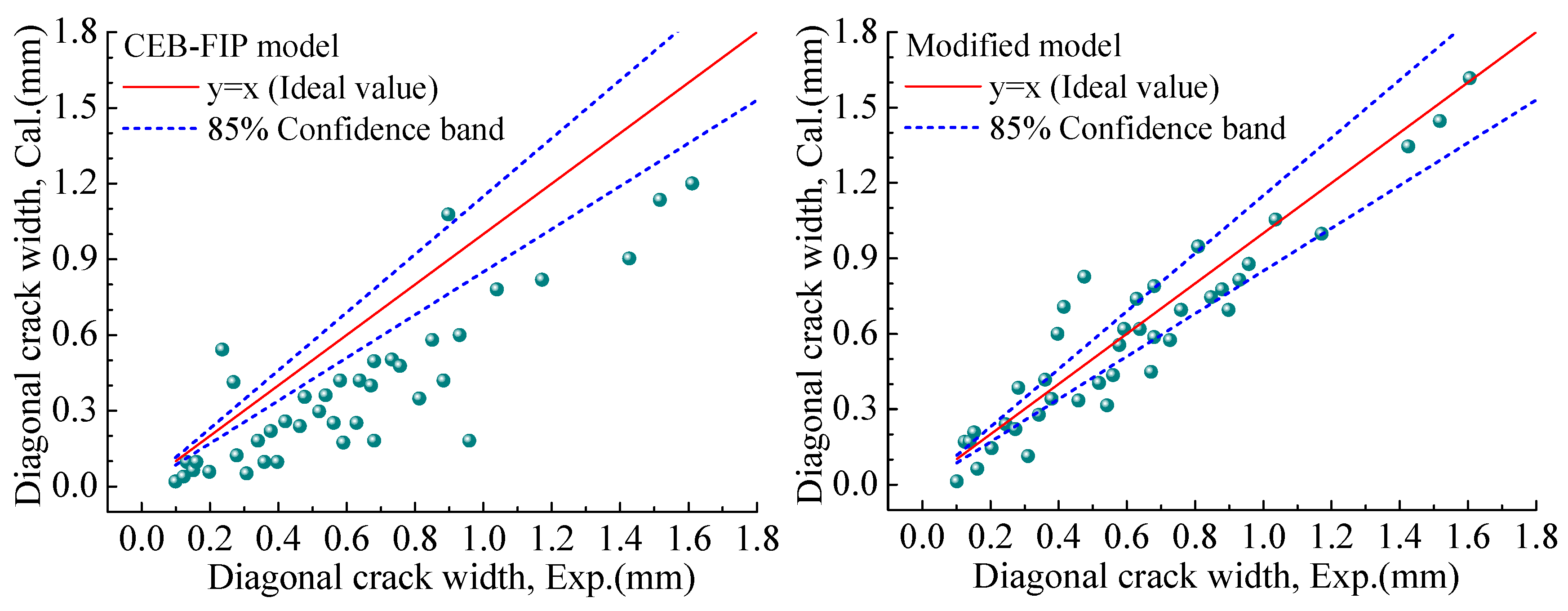
- The accuracy of the modified model for calculating the diagonal crack width is better than other models. The calculated results are in good agreement with the experimental results. Therefore, the modified model proposed in this paper can be used to estimate the diagonal crack width of an SRC deep beam. However, considering that the research and result verification in this article are based on a limited number of specimen experiments, readers should fully recognize that the effective range and accuracy of the model still need further and more comprehensive demonstration before being applied to practical engineering.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tong, L.W.; Xiao, S.; He, L.; Zhang, Y.F. Fatigue behavior of steel reinforced concrete (SRC) beams with different shear span-to-depth ratios. Eng. Struct. 2018, 166, 339–353. [Google Scholar] [CrossRef]
- Zeng, L.; Xiang, S.; Liu, Y.H.; Chen, J. Experimental study on the dynamic behavior of T-shaped steel reinforced concrete columns under impact loading. Eng. Struct. 2020, 208, 110307. [Google Scholar]
- Zeng, L.; Ren, W.T.; Zou, Z.T.; Chen, Y.G.; Xie, W.; Li, X.J. Experimental study on seismic behavior of frame structures composed of concrete encased columns with L-shaped steel section and steel beams. Earthq. Struct. 2019, 16, 97–107. [Google Scholar]
- Yue, J.G.; Qian, J.; Beskos, D.E. Seismic damage performance levels for concrete encased steel columns using acoustic emission tests and finite element analysis. Eng. Struct. 2019, 189, 471–483. [Google Scholar] [CrossRef]
- Yue, J.G.; Kunnath, S.K.; Xiao, Y. Uniaxial concrete tension damage evolution using acoustic emission monitoring. Constr. Build. Mater. 2020, 232, 117282. [Google Scholar] [CrossRef]
- Tong, L.W.; Liu, B.; Zhao, X.L. Numerical study of fatigue behaviour of steel reinforced concrete (SRC) beams. Eng. Fract. Mech. 2018, 166, 339–353. [Google Scholar] [CrossRef]
- Wu, K.; Chen, F.; Chen, C.; Zheng, H.; Xu, J. Load-transfer mechanism and bond-stress components in steel and steel fiber–reinforced concrete structure. J. Struct. Eng. 2019, 145, 04019160. [Google Scholar] [CrossRef]
- Chen, C.C.; Chen, C.C. Flexural behavior of steel encased composite. J. Chin. Inst. Civ. Hydraul. 2001, 13, 263–275. (In Chinese) [Google Scholar]
- Zeng, L.; Xiao, Y.F.; Chen, J.; Chen, Y.G. Quasi-static cyclic test on a concrete-encased frame-reinforced concrete tube building model. Shock Vib. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Chen, C.C.; Lin, K.T.; Chen, Y.J. Behavior and shear strength of shape reinforced concrete deep beams. Eng. Struct. 2018, 175, 425–435. [Google Scholar] [CrossRef]
- Weng, C.C.; Wang, H.S. Shear strength of steel reinforced concrete (SRC) deep beam. J. Chin. Inst. Civ. Hydraul. Eng. 2004, 16, 403–414. (In Chinese) [Google Scholar]
- Wight, J.K. Reinforced Concrete Mechanics and Design; Pearson Education South Asia Pte Ltd.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Zeng, L.; Cui, Z.; Xiao, Y.; Jin, S.; Wu, Y. Cyclical Behavior of Concrete-Encased Composite Frame Joints with High Strength Concrete. Adv. Mater. Sci. Eng. 2015, 6, 1–13. [Google Scholar] [CrossRef]
- Xiao, Y.F.; Zeng, L.; Cui, Z.K.; Jin, S.Q.; Chen, Y.G. Experimental and analytical performance evaluation of steel beam to concrete-encased composite column with unsymmetrical steel section joints. Steel Compos. Struct. 2017, 23, 17–29. [Google Scholar] [CrossRef]
- Chen, H.; Yi, W.J.; Hwang, H.J. Cracking strut-and-tie model for shear strength evaluation of reinforced concrete deep beams. Eng. Struct. 2018, 163, 396–408. [Google Scholar] [CrossRef]
- Araba, A.M.; Ashour, A.F. Flexural performance of hybrid GFRP-Steel reinforced concrete continuous beams. Compos. Part B-Eng. 2018, 154, 321–336. [Google Scholar] [CrossRef]
- Rahal, K.N.; Alrefaei, Y.T. Shear strength of recycled aggregate concrete beams containing stirrups. Constr. Build. Mater. 2018, 191, 866–876. [Google Scholar] [CrossRef]
- Demir, A.; Caglar, N.; Ozturk, H. Parameters affecting diagonal cracking behavior of reinforced concrete deep beams. Eng. Struct. 2019, 184, 217–231. [Google Scholar] [CrossRef]
- Birrcher, D.; Tuchscherer, R.; Huizinga, M.; Bayrak, O.; Wood, S.; Jirsa, J. Strength and Serviceability Design of Reinforced Concrete Deep Beams; Center for Transportation Research the University of Texas: Austin, TX, USA, 2009. [Google Scholar]
- Barris, C.; Torres, L.; Vilanova, I.; Miàs, C.; Llorens, M. Experimental study on crack width and crack spacing for glass-FRP reinforced concrete beams. Eng. Struct. 2017, 131, 231–242. [Google Scholar] [CrossRef]
- Lu, W.Y. Shear strength prediction for steel reinforced concrete deep beams. J. Constr. Steel Res. 2006, 62, 933–942. [Google Scholar] [CrossRef]
- Comité Euro International Du Béton. CEB-FIP Model Code; Thomas Telford Service Ltd.: London, UK, 1990. [Google Scholar]
- Khan, R.M.A.; Shafighfard, T.; Ali, H.Q.; Mieloszyk, M.; Yildiz, M. Strength prediction and experimental damage investigations of plain woven CFRPs with interacting holes using multi-instrument measurements. Polym. Composite. 2015, 44, 3594–3609. [Google Scholar] [CrossRef]
- Sabau, C.; Gonzalez-Libreros, J.H.; Sneed, L.H.; Sas, G.; Pellegrino, C.; Täljsten, B. Use of image correlation system to study the bond behavior of FRCM-concrete joints. Mater. Struct. 2017, 50, 172. [Google Scholar] [CrossRef]
- Mo, J.X.; Zeng, L.; Liu, Y.; Ma, L.; Cheng, G. Mechanical properties and damping capacity of polypropylene fiber reinforced concrete modified by rubber powder. Constr. Build. Mater. 2020, 242, 118111. [Google Scholar] [CrossRef]
- GB/T50107-2010; Standard for Evaluation of Concrete Compressive Strength. China Architecture and Building Press: Beijing, China, 2010. (In Chinese)
- GB/228.1-2010; Metallic Materials-Tensile Testing-Part: Method of Test at Room Temperature. Chinese Specification Press: Beijing, China, 2011. (In Chinese)
- Ivanov, D.; Ivanov, S.; Lomov, S.; Verpoes, I. Strain mapping analysis of textile composites. Opt. Laser Eng. 2009, 47, 360–370. [Google Scholar] [CrossRef]
- Paepegem, W.V.; Shulev, A.A.; Roussev, I.R.; Pauw, S.D.; Degrieck, J.; Sainov, V.C. Study of the deformation characteristics of window security film by digital image correlation techniques. Opt. Laser Eng. 2009, 47, 390–397. [Google Scholar] [CrossRef]
- Hassan, H.M.; Farghaly, S.A.; Ueda, T. Displacement at shear crack in beams with shear reinforcement under static and fatigue loadings. Proc. JSCE 1991, 15, 215–222. [Google Scholar] [CrossRef][Green Version]
- Fukuyama, H.; Suwada, H.; Iso, M.; Matsuzaki, Y.; Nakano, K.; Kasahara, M. Evaluation of damage limit state of RC element due to shear crack width. Proc. Archit. Inst. Jpn. 2000, C-2, 13–14. [Google Scholar]
- Shinomiya, K.; Watanabe, F. Study on prediction of shear crack width for reinforced concrete beams. Archit. Inst. Jpn. 2002, C-2, 295–296. [Google Scholar]
- Piyamahant, S. Shear Behavior of Reinforced Concrete Beams with a Small Amount of Web Reinforcement. Master’s Dissertation, Kochi University of Technology, Kochi, Japan, 2002. [Google Scholar]
- Silva, S.D.; Mutsuyoshi, H.; Witchukreangkrai, E. Evaluation of shear crack width in I-shaped prestressed reinforced concrete beams. J. Adv. Concr. Technol. 2008, 6, 443–458. [Google Scholar] [CrossRef]
- Zakaria, M.; Ueda, T.; Wu, Z.; Meng, L. Experimental investigation on shear cracking behavior in reinforced concrete beams with shear reinforcement. J. Adv. Concr. Technol. 2009, 7, 79–96. [Google Scholar] [CrossRef]
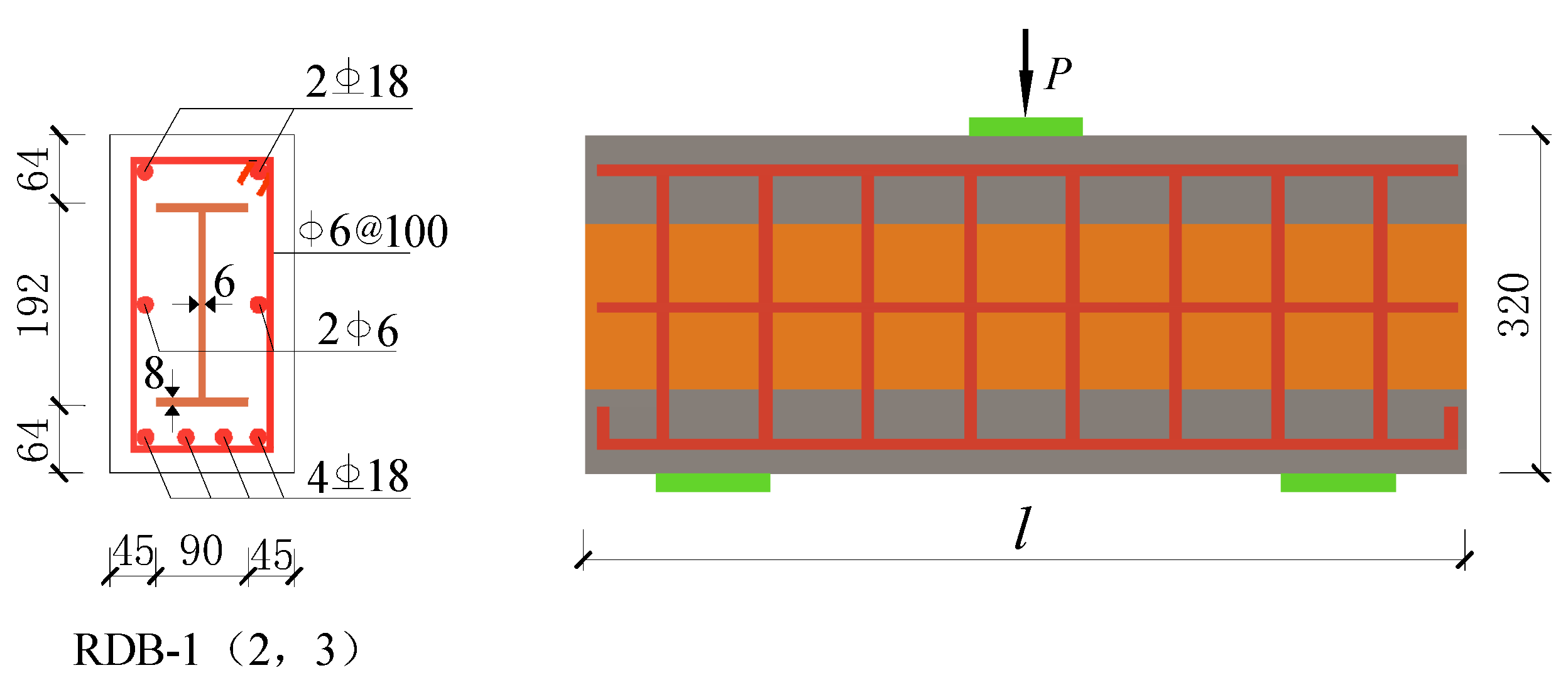


| Specimen Number | Specimen Length (mm) | Width Ratio | Height Ratio | Cross-Section of Steel Size (mm) | |
|---|---|---|---|---|---|
| RDB-1 | 860 | 1.1 | 0.5 | 0.6 | 192 × 90 × 6 × 8 |
| RDB-2 | 1020 | 1.4 | 0.5 | 0.6 | 192 × 90 × 6 × 8 |
| RDB-3 | 1200 | 1.7 | 0.5 | 0.6 | 192 × 90 × 6 × 8 |
| RDB-4 | 860 | 1.1 | 0.5 | 0.45 | 144 × 90 × 6 × 8 |
| RDB-5 | 860 | 1.1 | 0.5 | 0.3 | 96 × 90 × 6 × 8 |
| RDB-6 | 860 | 1.1 | 0.67 | 0.6 | 192 × 120 × 6 × 8 |
| RDB-7 | 860 | 1.1 | 0.33 | 0.6 | 192 × 60 × 6 × 8 |
| Steel Type | Thickness or Diameter/mm | /MPa | Ultimate Strength fu/MPa | /MPa |
|---|---|---|---|---|
| HPB300 | 6 | 313 | 534 | 2.1 × 105 |
| HRB335 | 18 | 440 | 515 | 2.1 × 105 |
| Q235 | 6 | 272 | 406 | 2.1 × 105 |
| 8 | 315 | 430 | 2.0 × 105 |
| Specimen Number | First Flexural Crack Load (KN) | First Shear Crack Load (KN) | Peak Load (KN) | Failure Mode |
|---|---|---|---|---|
| RDB-1 | 90 | 110 | 788 | diagonal compression |
| RDB-2 | 60 | 100 | 682 | diagonal compression |
| RDB-3 | 70 | 130 | 548 | diagonal compression |
| RDB-4 | 100 | 120 | 734 | diagonal compression |
| RDB-5 | 100 | 130 | 645 | diagonal compression |
| RDB-6 | 110 | 160 | 816 | bearing |
| RDB-7 | 60 | 100 | 698 | diagonal compression |
| Specimen Number | Minimum Spacing (mm) | Maximum Spacing (mm) | Mean Spacing (mm) |
|---|---|---|---|
| RDB-1 | 29 | 82 | 56.4 |
| RDB-2 | 21 | 74 | 45.1 |
| RDB-3 | 20 | 62 | 38.7 |
| RDB-4 | 27 | 72 | 48.3 |
| RDB-5 | 32 | 71 | 46.9 |
| RDB-6 | 33 | 78 | 57 |
| RDB-7 | 20 | 64 | 35.8 |
| Specimen Number | Minimum Width (mm) | Maximum Width (mm) | Mean Width (mm) |
|---|---|---|---|
| RDB-1 | 0.12 | 1.43 | 0.9 |
| RDB-2 | 0.15 | 1.17 | 0.76 |
| RDB-3 | 0.10 | 1.04 | 0.68 |
| RDB-4 | 0.12 | 0.96 | 0.59 |
| RDB-5 | 0.16 | 0.63 | 0.27 |
| RDB-6 | 0.14 | 1.61 | 0.93 |
| RDB-7 | 0.13 | 1.52 | 0.88 |
| Model | RDB-1 | RDB-2 | RDB-3 | RDB-4 | RDB-5 | RDB-6 | RDB-7 |
|---|---|---|---|---|---|---|---|
| CEB-FIP Model Code | 0.63 | 0.48 | 0.85 | 0.58 | 0.67 | 0.60 | 0.72 |
| Shinomiya | 0.57 | 0.51 | 0.78 | 0.48 | 0.64 | 0.56 | 0.49 |
| Piyamahant | 0.43 | 0.47 | 0.74 | 0.61 | 0.78 | 0.65 | 0.64 |
| Modified model | 0.87 | 0.82 | 0.77 | 0.85 | 0.86 | 0.91 | 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Zeng, L.; Chen, B.; Teng, S. Experimental and Theoretical Investigation on Cracking Behavior and Influencing Factors of Steel-Reinforced Concrete Deep Beams. Buildings 2025, 15, 1812. https://doi.org/10.3390/buildings15111812
Hu G, Zeng L, Chen B, Teng S. Experimental and Theoretical Investigation on Cracking Behavior and Influencing Factors of Steel-Reinforced Concrete Deep Beams. Buildings. 2025; 15(11):1812. https://doi.org/10.3390/buildings15111812
Chicago/Turabian StyleHu, Gaoxing, Lei Zeng, Buqing Chen, and Shuai Teng. 2025. "Experimental and Theoretical Investigation on Cracking Behavior and Influencing Factors of Steel-Reinforced Concrete Deep Beams" Buildings 15, no. 11: 1812. https://doi.org/10.3390/buildings15111812
APA StyleHu, G., Zeng, L., Chen, B., & Teng, S. (2025). Experimental and Theoretical Investigation on Cracking Behavior and Influencing Factors of Steel-Reinforced Concrete Deep Beams. Buildings, 15(11), 1812. https://doi.org/10.3390/buildings15111812







