Back-Silting Characteristics of Foundation Trench Excavation in an Ultra-Wide Inland Immersed Tunnel and Its Impacts on Slope Stability: A Case Study of the Tanzhou Waterway in Shunde

Abstract

During the construction of a large immersed tunnel crossing an ultra-wide inland river, the long drying time after the excavation of the foundation trench and changes in river flow velocity result in the river carrying a large amount of sediment into the foundation trench and the slope, increasing installation difficulties and threatening construction safety. This study investigates the back-silting characteristics and their impacts on foundation trench slope stability during an ultra-wide immersed tunnel excavation at LunGui Road in Foshan City, China. Numerical simulations reveal the spatiotemporal distribution patterns of deposited sediments at the trench bottom and side slopes, with distinct behaviors identified between the flood season and dry season. Siltation predominantly occurs at the trench bottom, with deposition thickness decreasing almost linearly from the bottom to the slope crest. Hydroperiod variations considerably influence the spatiotemporal distribution of back-silting. Then, the Morgenstern–Price method was employed to analyze slope stability under varying back-silting and dredging conditions, quantifying the relationship between safety factor and sediment thickness. Furthermore, the evolution of critical failure surfaces and the safety factor under different dredging strategies was systematically examined. The critical values of back-silting thickness corresponding to different dredging slope ratios are provided. The research findings provide valuable insights for formulating engineering strategies for trench excavation of extra-wide immersed tube tunnels in inland waterways.

1. Introduction

Most regions in southern China are located in subtropical monsoon climate zones characterized by abundant annual precipitation. This climatic condition has resulted in numerous rivers and lakes with intricate waterway networks throughout the southern territories. Taking Guangdong Province as a representative case, the area features a crisscrossing river system. When implementing urban road construction projects, engineers inevitably encounter multiple river crossings. Moreover, Guangdong’s proximity to the Pearl River estuary enhances its inland connectivity and contributes to a highly developed water transport system. To maintain normal waterway operations during construction, immersed tube tunnels have become the preferred solution for river-crossing road projects [1]. In the construction process of ultra-wide inland river immersed tube tunnels, the excavation and maintenance of the foundation trench are key factors determining whether the immersed tube can be safely placed. After the excavation of the foundation trench, due to prolonged exposure, the river carries a large amount of sediment that accumulates at the bottom of the trench, posing a threat to the placement of the immersed tube. Therefore, exploring the sedimentation patterns in the trench section and formulating a reasonable dredging plan are crucial for the construction of immersed tube tunnels.

Previous researchers have explored the siltation pattern of submerged grooves through monitoring and field tests, which provides a reference for the numerical simulation in this paper. Zheng [2] determined the distribution pattern of siltation thickness in the foundation trench through various methods, including multibeam monitoring, silt density detection, measurement of sediment bulk density, and manual diving exploration. The removal standard after siltation is proposed, which provides a reference for the siltation law and the removal of silt after siltation in this paper. Liu and Zeng [3] analyzed the variation in sediment concentration and the vertical variation in sediment concentration under different discharges in summer and winter, which provides an idea for the simulation of siltation in wet and dry seasons. Lee et al. [4] explored the siltation patterns in the North Port of Incheon, Korea, and examined the harbor ditch deposition rates to provide a control for the instream base channel deposition rates in this paper. Based on the fluid dynamics and sedimentary conditions, Restrepo et al. [5] analyzed the sedimentation and erosion patterns at the bottom of the channel, which provides a reference for the selection of the migration formula.

Field monitoring and laboratory experiments are often associated with prolonged research cycles and substantial workloads. In recent years, with the advancement of computer technology, an increasing number of scholars have opted to employ numerical simulation methods to investigate the sedimentation patterns of underwater foundation trenches [6,7,8]. To ensure the accuracy of numerical simulations, it is essential to establish a correct mathematical model that aligns with the actual field conditions. He and Xin [9] employed a water–sediment mathematical model to inversely analyze the diffusion and transport processes of turbid water masses formed by sand mining activities upstream of Neilingding Island under tidal action. Santos-Ferreira et al. [10] proposed a hydrodynamic model for coastal areas, identifying the causes of port siltation. Gomes Jr. et al. [11] developed the HydroHP-1D tool and applied it to estimate 1D steady and unsteady hydrodynamics. Xu et al. [12] developed a numerical model based on the interMixingFoam solver in OpenFOAM to study the interaction between water and silt. HEC-RAS (Hydraulic Engineering Center—River Analysis System), as a hydrodynamic numerical simulation software, offers high simulation accuracy and is suitable for rivers with flat terrain and minimal cross-sectional variations [13]. Consequently, many scholars have utilized this software to investigate sediment transport and deposition patterns in river channels. Li et al. [14] simulated the sediment discharge at the outlet section of a watershed during a heavy rain event using HEC-RAS. Rahman and Chakrabarty [15] developed a model suitable for river sediment transport by utilizing artificial neural networks in conjunction with the one-dimensional hydrodynamic model HEC-RAS. Li et al. [16] employed HEC-RAS to determine sediment transport capacity and estimate erosion, deposition, and riverbed changes. Pratama et al. [17] simulated sediment transport and siltation in a reservoir over a decade using HEC-RAS, thereby determining the reduction in reservoir capacity. Tadesse and Dai [18] integrated the SWAT model with the HEC-RAS model to calculate sediment deposition in reservoirs.

After the excavation of the foundation trench, the siltation and dredging of the underwater slope can affect its stability, posing a threat to the placement and installation of the immersed tunnel. To ensure the stability of the foundation trench slope, the excavation must adhere to rational design principles [19,20] and investigate the failure modes of underwater slopes. Consequently, numerous scholars have conducted research on the stability of underwater slopes. Lin et al. [21] explored the failure and computational models of foundation trench slopes, adopting an integration method based on the slice principle to replace the conventional slice method for calculating the appropriate slope ratio. Li et al. [22] discussed the stability of underwater slopes based on the strength reduction method. Fang et al. [23] conducted research on the optimal slope ratio for the immersed tube tunnel trench of the Hong Kong–Zhuhai–Macao Bridge, providing crucial references for the selection of slope ratios. Jiang et al. [24] investigated the stability of embankment slopes by considering the weak layer between the underwater embankment and the original mountain mass, as well as the influence of water level fluctuations. Luo et al. [25] employed the strength reduction method to analyze the effects of slope level, slope ratio, and platform width on the stability of multi-level slopes. Chen et al. [6] performed a numerical study on the stability of foundation trench slopes under wave action, particularly examining the impacts of sediment deposition and dredging activities. The limit equilibrium method is a commonly used approach for studying slope failure. Based on this method, Li et al. [26] horizontally and obliquely divided the soil, analyzed the stresses, and established potential failure mechanisms for multi-level slopes under both global and local failure modes. Utilizing the plane strain strength equations and limit analysis methods of limit equilibrium, Ye et al. [27] developed a new model for calculating the bearing capacity of foundations near slopes and derived the ultimate bearing capacity formula for slope foundations. Based on the previous research, this paper utilizes the Geo-Studio finite element numerical simulation software to simulate and analyze slope stability with the SLOPE/W module—a widely used method for calculating slope stability and deformation characteristics [28,29]. Li et al. [30] utilized the software to analyze real-time data such as slope deformation and displacement.

Although there is a relatively substantial body of research on the sedimentation patterns of foundation trenches and the stability of underwater slopes, the majority of these studies focus on coastal areas, reservoirs, or lake regions, particularly on foundation trenches or ports. Research on the sedimentation patterns of ultra-wide inland river foundation trenches and the integration of sedimentation with slope stability to explore reasonable dredging schemes is comparatively scarce. In contrast to the former studies, ultra-wide inland rivers experience significant seasonal variations in flow and unstable flow velocities, leading to relatively complex and uncertain sedimentation patterns in the foundation trench slopes. Therefore, investigating the sedimentation patterns of ultra-wide inland river foundation trenches is crucial for the safe construction of immersed tunnels. Based on the previous research, this study employs numerical simulations to explore the sedimentation characteristics of foundation soils after trench excavation and analyzes the distribution differences between the wet and dry seasons. Additionally, the study examines the impact of sedimentation and dredging methods on the stability of foundation trench slopes, providing on-site dredging recommendations based on the safety factor of slope stability.

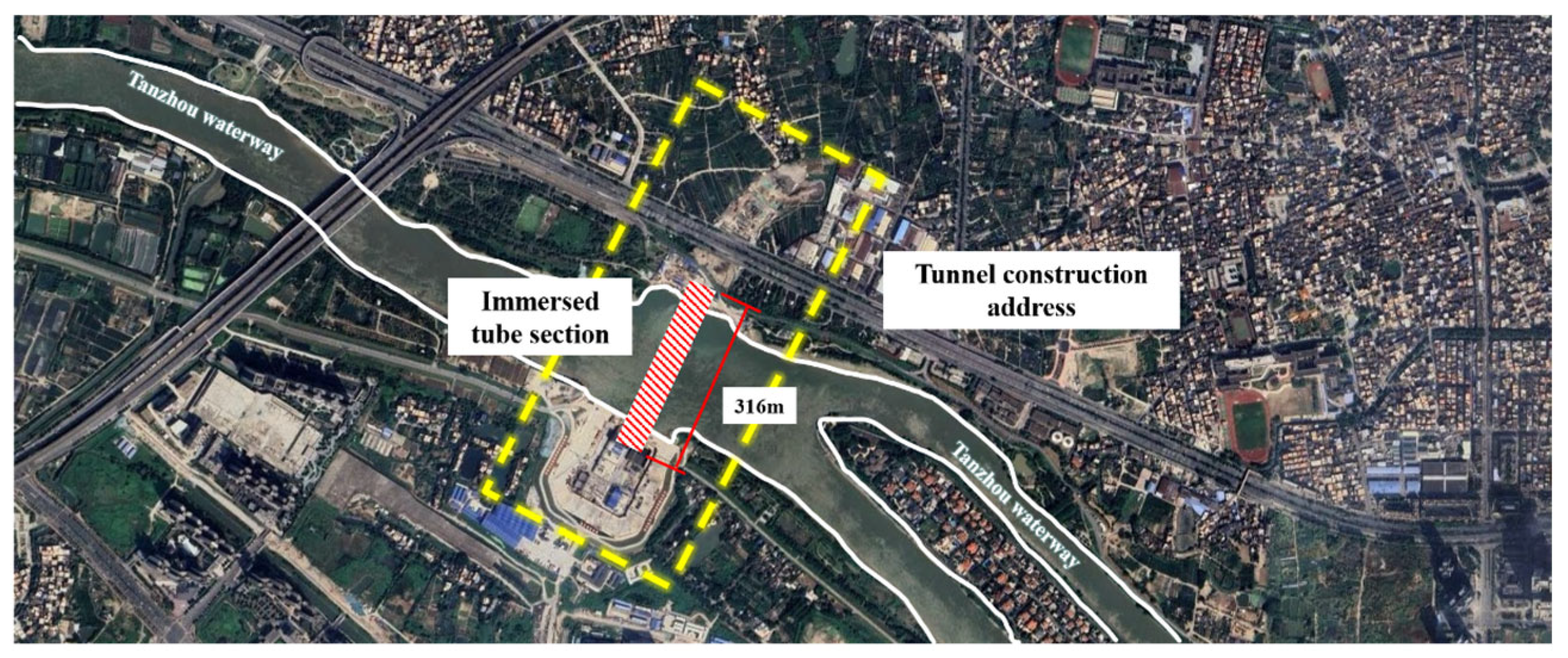
2. Project Overview

The Lungui Road Immersed Tunnel is located in Shunde District, Foshan City, China, crossing beneath the Tanzhou Waterway. The tunnel has a total length of 1220 m and comprises three distinct sections, i.e., a 316 m immersed tube section (Figure 1), a 504 m buried cut-and-cover section, and a 400 m open-cut section. To authentically replicate actual construction conditions and ensure the reliability of experimental parameters and numerical simulation results, comprehensive field investigations and laboratory tests on undisturbed soil samples were conducted. These efforts yielded critical engineering geological and hydrological data specific to the immersed tube section.

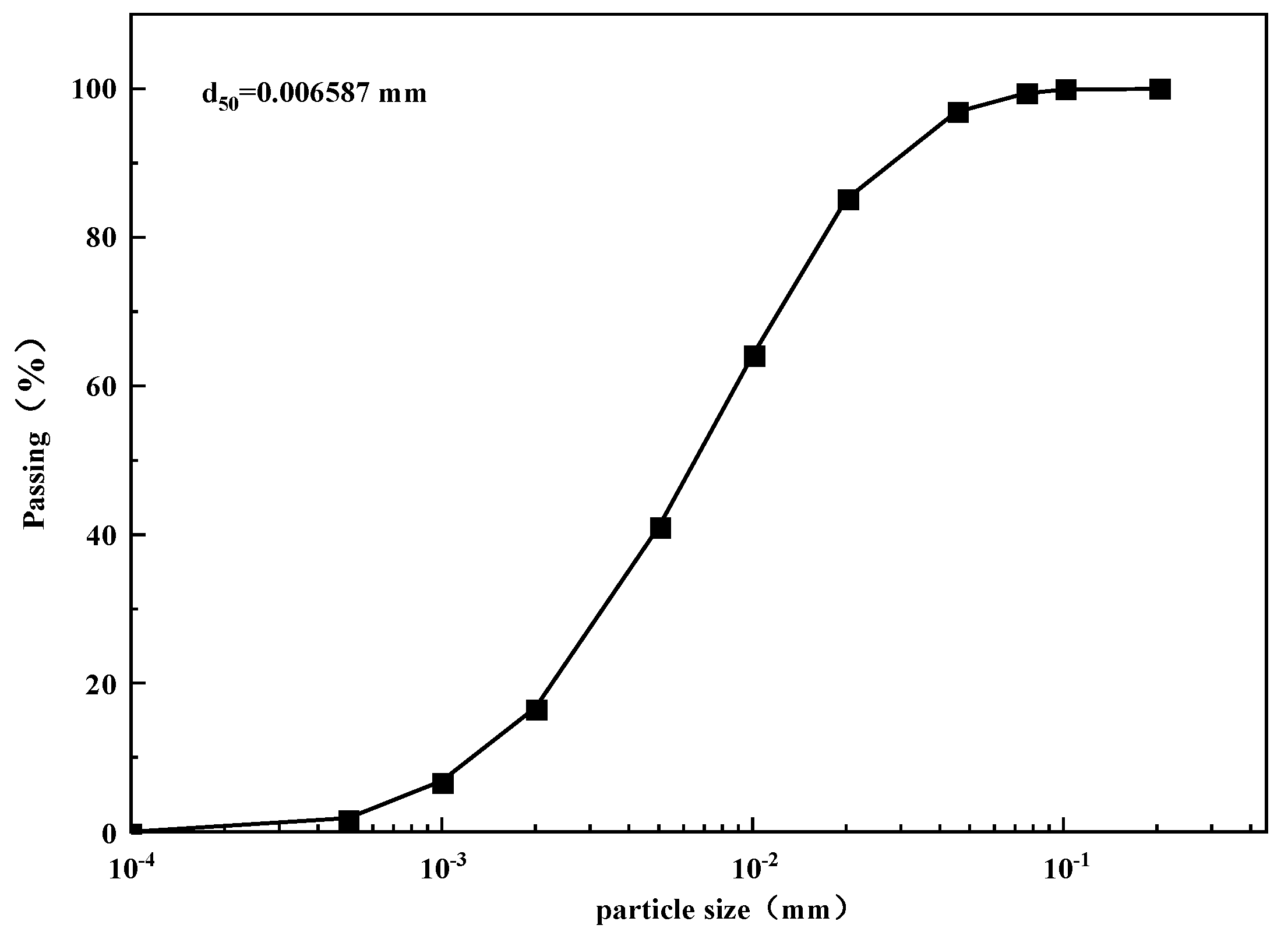
2.1. Engineering Geological Conditions

The Tanzhou Waterway is situated in the heart of the Pearl River Delta, characterized by an alluvial plain landscape with low and flat terrain, predominantly covered by Quaternary loose sediments. According to drilling data, the strata within the exploration depth primarily consist of the artificial fill layer of the Holocene Series of the Quaternary System (Q4ml), the marine–terrestrial interaction sedimentary layer of the Holocene Series of the Quaternary System (Q4mc), and the mudstone–siltstone of the Lower Cretaceous bedrock (K1b). The specific stratigraphy of the site is detailed in

Table 1. Stratigraphic conditions.

Stratum	Types of Soil	Roof Elevation (m)	Floor Elevation (m)	Soil Thickness (m)
Filling layer	Artificial fill	0.91~6.24	−2.89~4.64	0.50~5.00
Quaternary Holocene interbedded marine and terrestrial deposits (Q4mc)	Silt	−20.43~4.64	−26.23~0.62	1.00~18.30
	Silty clay	−20.43~1.90	−23.23~0.42	0.90~3.80
	Siltstone fine sand	−9.39~0.77	−13.47~−2.93	1.90~10.70
	Fine sand	−20.11~0.87	−23.36~−5.53	1.00~18.40
	Alumina	−21.72~−7.67	−24.52~−13.19	1.10~9.50
Bedrock	Strongly weathered muddy siltstone	−26.23~−9.89	−55.70~−12.99	0.50~40.20
	Moderately weathered muddy siltstone	−55.44~−12.99	−83.51~−23.46	2.20~59.90

Roof elevation: elevation of the top of the current soil layer. Floor elevation: elevation of the bottom of the current soil layer.

.

Based on the on-site drilling data, the special soils in the site mainly include artificial fill, silt, and weathered rock. Due to the location of these soils at the bottom of the river channel, they exhibit high moisture content, predominantly in a fluid–plastic state, with low shear strength and poor bearing capacity. This makes the excavation of foundation trench slopes prone to instability, which is detrimental to slope stability. The soil layers exposed at the bottom of the river channel are primarily silt and fine sand, serving as the main source of river sediment transport. Along the survey site, the main types of groundwater include perched water, pore phreatic water, pore confined water, and bedrock fissure water, with pore-confined water having the most significant impact on the proposed project.

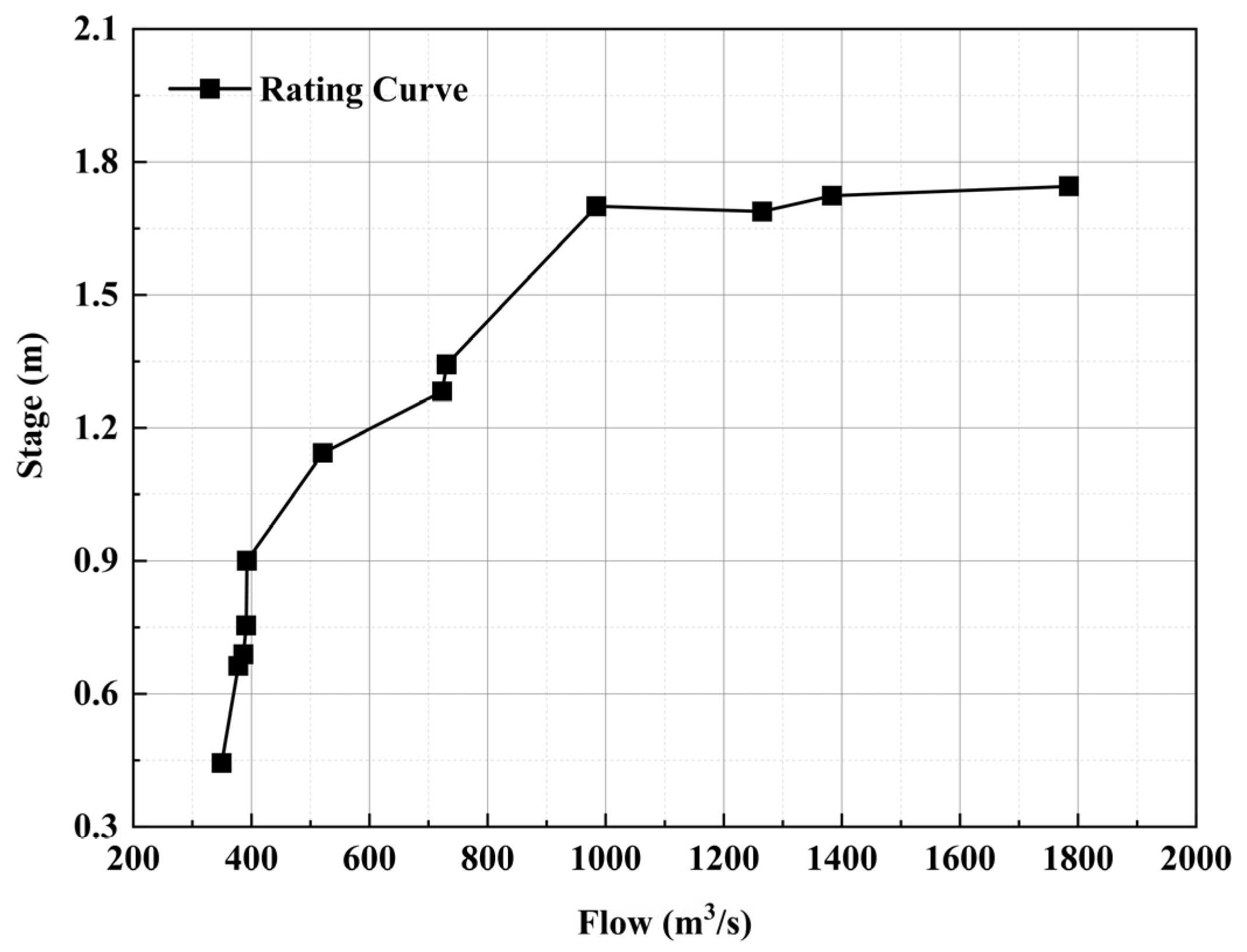
2.2. Hydrological Conditions

The Tanzhou Waterway spans 37 km in total length. The region features a subtropical monsoon climate dominated by the subtropical high-pressure system. Influenced by flood seasons and storm surges, the highest tidal levels generally occur between June and September, while the lowest tidal levels are typically observed from December to February. The river section at the tunnel site is fully subjected to tidal influence only during the dry season.

For the proposed project, the maximum flow velocity during flood periods reaches 2–3 m/s or higher upstream and downstream. During dry seasons, the maximum cross-sectional flow velocity measures approximately 1.0 m/s, with an average velocity around 0.5 m/s. The tidal level characteristics are summarized in

Table 2. Table of mean tide levels in the Tanzhou Channel.

Typology	Tide Level (m)
Multi-year mean tide level	1.294
Multi-year average high tide level	1.724
Multi-year mean low tide level	0.864
Mean tide level in low water	0.934
Average high tide level during dry periods	1.414
Mean low water level during dry season	0.444

Tide level: water surface elevation.

.

The average sand content of the river is 0.18 kg/m³, the maximum sand content is 0.32 kg/m³ (in 1972 and 1988), and the average sand transport is about 8 × 10⁶ t. The inter- and intra-annual distribution of sand transport is very uneven, and the change in sand transport is basically the same as the change in runoff. The river transports large amounts of sand during years of abundant water, whereas sand transport is minimal during years of low water availability.

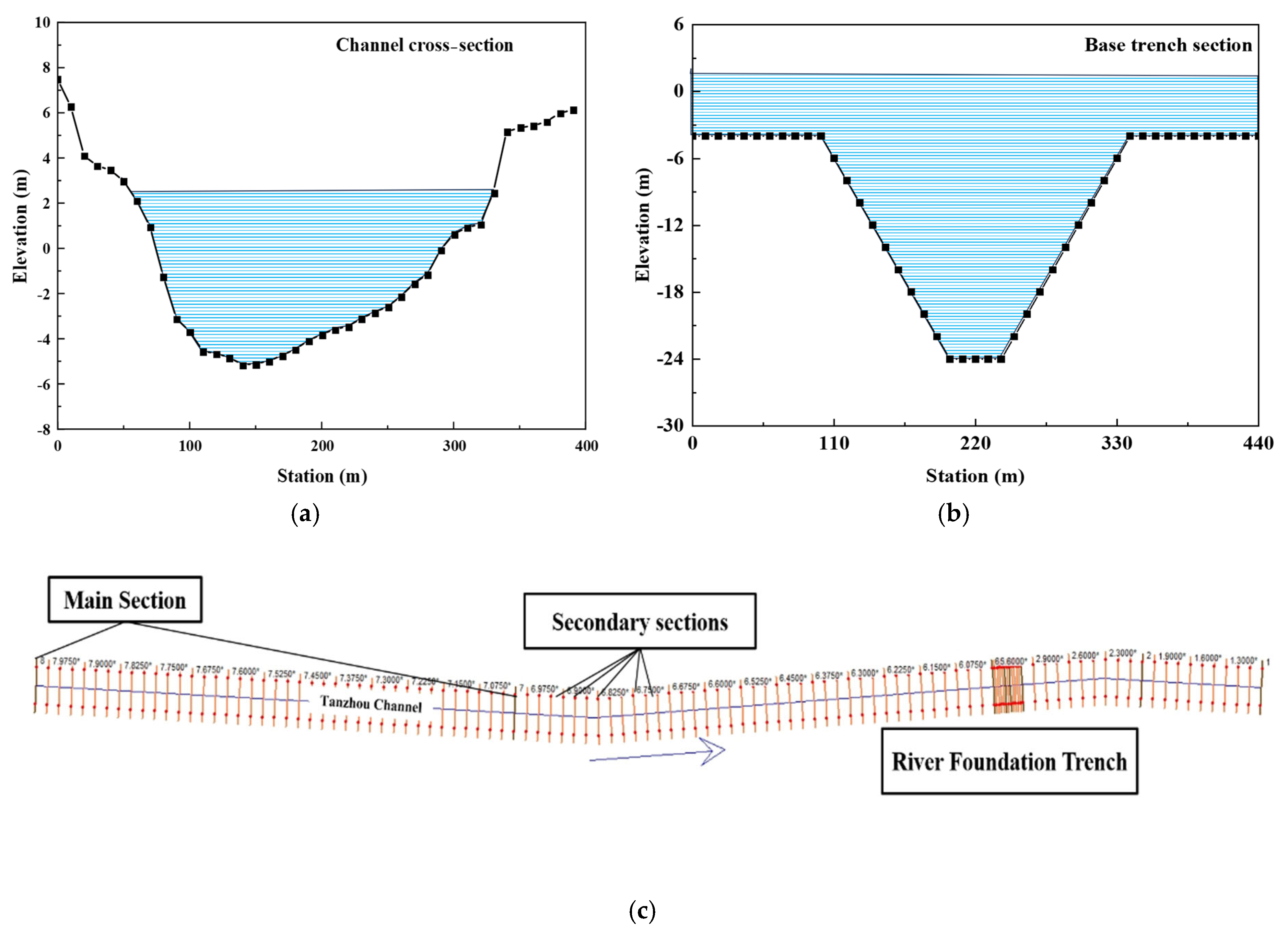
3. Study on the Siltation Pattern of Underwater Foundation Trench

As the primary carrier of immersed tube tunnels, the foundation trench demands high safety standards. Situated at the riverbed, the foundation trench is significantly influenced by water flow and river sediment. Progressively accumulated sediment carried by the river tends to accumulate on the slopes and bottom of the foundation trench. If not promptly cleared, this sediment can adversely affect subsequent rock dumping and leveling operations, as well as the lowering of the immersed tube, thereby posing a threat to the project’s safety. This chapter employs the HEC-RAS software 6.3.1 to establish a one-dimensional river channel and underwater foundation trench model. The sediment transport module of the software is utilized to determine the sedimentation patterns within the underwater foundation trench.

3.1. Modeling Methodology

HEC-RAS is a software package developed by the United States Army Corps of Engineers’ Hydrologic Engineering Center, designed to analyze one-dimensional steady/unsteady flow, as well as sediment transport and deposition in natural or artificial river networks. In order to restore the field conditions to the greatest extent possible, we carried out the extrapolation of the flow at different stages of the Tanzhou Waterway in one year. Meanwhile, we conducted field surveys on the bottom topography of the river channel to obtain the elevation data of the river cross-section, and obtained the basic physical properties of the sediments through indoor experiments. Finally, the above results were imported into the model to project the sediment siltation inside the base channel, and the specific modeling process is shown in Figure 2. The establishment of the model includes three main parts, i.e., channel modeling, water temperature modeling, and sediment simulation.

The establishment of a river channel model requires consideration of both the cross-section and longitudinal profile of the river. The Tanzhou Waterway generally runs in a northwest–southeast direction. Based on field survey data of the Tanzhou Waterway, the width of the river cross-section is 390 m. Therefore, we considered taking elevation points at 10 m intervals from southwest to northeast, totaling 40 points. Each elevation point is connected with a smooth curve in order to form the river cross-section. In river modeling, it is generally considered that the demarcation area between river water and land is the two banks of the river. Based on the monitoring data of water level at the gauging station, we take the elevation points corresponding to the average water level of the river. Manning’s roughness coefficient is a key empirical parameter used in hydraulics to quantify the roughness of the bed or sidewall of an open channel, which is an important parameter in the hydrological modeling process of this paper. The Tanzhou waterway belongs to the large plain rivers, which are affected by the upstream flooding all the year round. The bottom of the river has many kinds of sedimentary materials and complexity, and is full of large cobbles and gravel particles, which are poor in homogeneity. Therefore, based on the table of natural channel roughness values prepared by Holton, U.S.A., the Manning’s coefficient of roughness is taken to be 0.1 in this model.

A total of eight primary cross-sections were designed in the model, and in order to ensure the homogeneity and accuracy of the model, we designed secondary cross-sections between each primary cross-section every 100 m using linear interpolation. By controlling the distance between the cross-sections, the primary and secondary cross-sections are combined to obtain the longitudinal section of the river. The base channel section of the immersed tube tunnel is determined according to the slope rate given in the ground investigation report, which is proposed to be set at 1:5. The established river model is shown in Figure 3:

A one-dimensional nonconstant flow module, which is controlled by Equations (1) and (2), is selected for this hydrologic model:

$${\displaystyle \frac{\partial A}{\partial t}}+{\displaystyle \frac{\partial Q}{\partial x}}=q_l=0$$

(1)

$${\displaystyle \frac{\partial Q}{\partial T}}+{\displaystyle \frac{\partial (QV)}{\partial x}}+gA\left({\displaystyle \frac{\partial z}{\partial x}}+S_f\right)=0$$

(2)

where A is the area of the cross-section; t is the time; x is the calculated length of the upstream and downstream sections; q_l is the single-width flow S_f is the friction slope; Q is the flow rate; and V is the flow velocity.

The establishment of a hydrological model requires the control of two boundary conditions at the upstream and downstream of the river. The upstream boundary, which serves as the primary source of river water, is controlled by inputting river discharge. In this model, determining the upstream discharge is relatively complex due to the lack of measured data from hydrological stations. We surveyed the water levels and flow velocities of the Tanzhou Waterway across different seasons and determined the cross-sectional area of the river channel through double integration. The upstream boundary data were then established using the flow rate formula. Since the river’s flow velocity and water level vary by season, the seasonal flow rates of the river are illustrated in Figure 4a. The downstream boundary of the river is determined by the stage–discharge relationship curves at various downstream gauging stations (Figure 5). Consequently, the Manning equation and Chézy formula are crucial for this section, and the following results are derived from these two formulas:

$$Q={\displaystyle \frac{A{R}^{2/3}}{n}}\sqrt{i}$$

(3)

where R is the hydraulic radius; n is the riverbed roughness; and i is the hydraulic gradient.

According to the principle that the calculation step does not exceed the duration, we take the calculation step as 3 h. In addition, the river water temperature affects the viscous force of the fluid and is set as shown in Figure 4b.

According to the results of field investigation, the soil layer covering the river surface is mainly silt layer, and the main sediment at the bottom of the foundation channel and the slope is also mainly silt, so we take silt as the main sediment source. Through the dredger at the project site, we obtained the silt at a depth of 3~5 m on the riverbed surface and scanned the silt soil particle gradation by a BT-9300S laser particle sizer (Figure 6). The HEC-RAS software provides eight different transport functions, including Ackres–White, Engelund–Hansen, Laursen (Copeland), Tofflaleti, etc. The Engelund–Hansen (1967) formula, denoted by Equation (4), was selected for this model by synthesizing the plains river conditions and the basic physical properties of the sediments. In river systems, coarser particles (d50) play a dominant role in bed stability and bedload transport, while finer particles represented by d10 are more susceptible to suspension and may lead to overestimations of sand transport rates. Therefore, d50 is selected as the key parameter in this formula. And the Rubey formula, denoted by Equation (5), was adopted for the sediment deposition:

$$g_s=0.05{\gamma }_s{V}^2\times \sqrt{{\displaystyle \frac{d_{50}}{g({\gamma }_s/\gamma -1)}}}{\left[{\displaystyle \frac{{\tau }_0}{\left({\gamma }_s-\gamma \right)d_{50}}}\right]}^{3/2}$$

(4)

where τ₀ represents the bed shear stress.

$$\omega =\sqrt{{\left(13.95{\displaystyle \frac{v}{d}}\right)}^2+1.09{\displaystyle \frac{{\gamma }_s-\gamma }{\gamma }}}gd-13.95{\displaystyle \frac{v}{d}}$$

(5)

where $\mathsf{\omega }$ is the settling velocity; d is the sediment diameter; v denotes the river flow velocity; and $\mathsf{\gamma }$ is the unit weight. γ_s is the dry unit weight.

Following this, set the sediment boundary conditions on both sides of the river and design a deposition depth of 20 m. The design effect diagram of the sediment is shown in Figure 7.

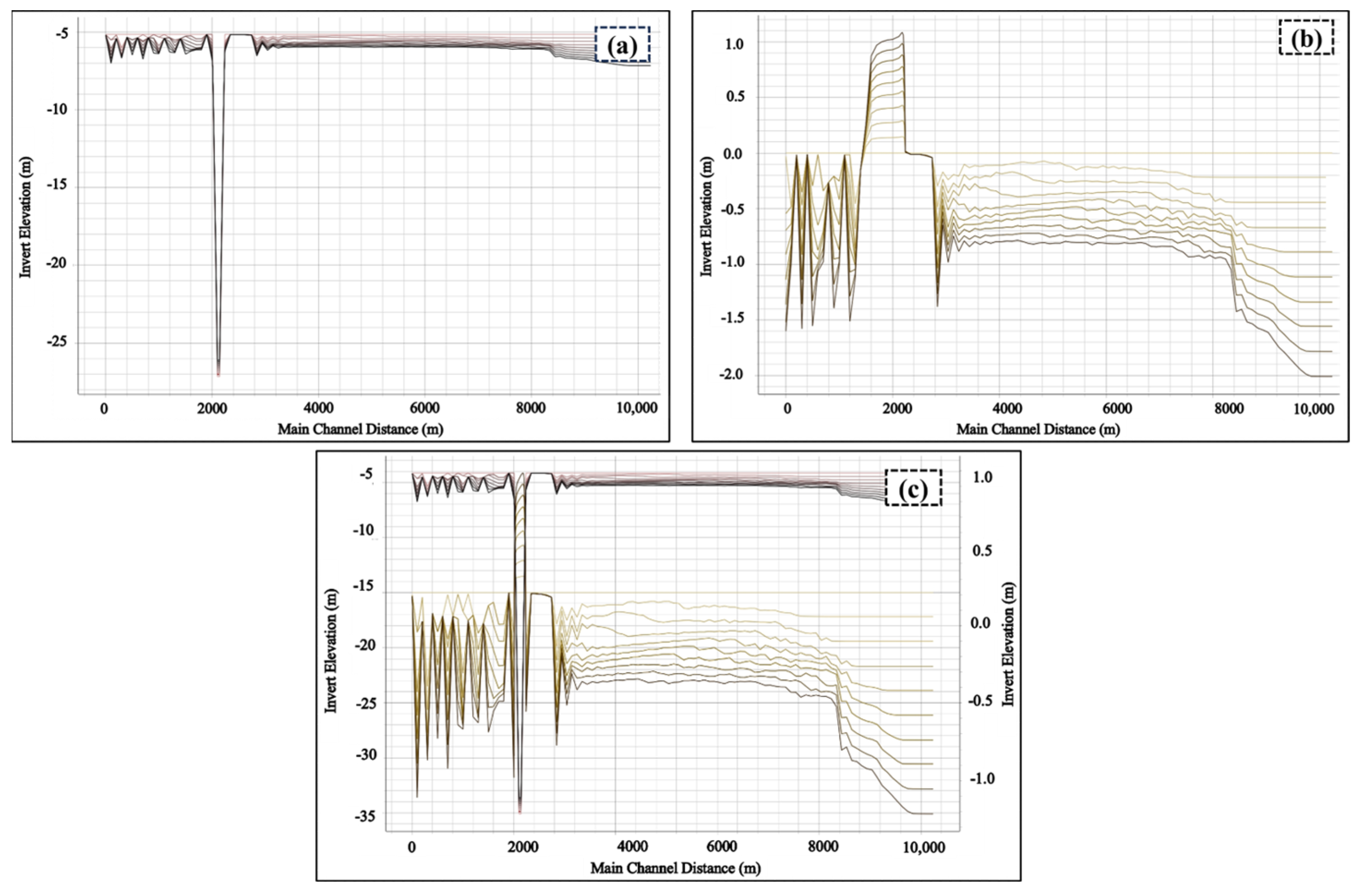
3.2. Analysis of Base Trench Dredging Results

Using the HEC-RAS software, a 90-day simulation prediction of sediment deposition inside the foundation trench of the immersed tunnel was conducted. The calculation time step is set at 3 h, with sediment deposition data recorded every 10 days. The recorded results are illustrated in Figure 8, in which the right side and left side present the upstream boundary and downstream boundary of the river, respectively. The depressed area is the immersed tube tunnel base channel section. It can be seen that the surrounding areas of the foundation trench and the upstream regions of the river are predominantly subjected to erosion processes. From day 0 to day 90 (Figure 8a), the ground elevation of the riverbed continuously decreases. According to Figure 8b,c, the elevation of the upstream section decreased by about 1~2 m in 90 d—the closer to the upstream boundary, the stronger the erosion, and the upstream channel topography is generally gentle. Compared with the upstream section of the base channel, the channel surface of the downstream section is more undulating and jagged, and the decrease in elevation is between 0 and 1.5 m. In the upstream section, the river channel is less eroded by the river, and the surface elevation hardly changes significantly.

The river channels on both sides of the foundation trench are subjected to intense erosion, providing a continuous supply of sediment for the trench section. As shown in Figure 8b, the bottom of the foundation trench is primarily dominated by sedimentation. From day 0 to day 90, the amount of sediment deposition at the riverbed ranges approximately from 1.06 to 1.83 m, with an average daily deposition of about 1.18 to 2.03 cm. This is roughly consistent with the observations from the sedimentation boxes deployed at the immersed tunnel project site.

From the bottom to the top of the foundation trench, the thickness of back-silting decreases linearly. The thickness of back-silting gradually decreases as it moves upward along the slope, diminishing to zero at a distance of 2 m from the slope crest, which is designated as the demarcation point. Above the demarcation point, river erosion becomes the primary process, whereas below it, river siltation dominates. The simulation results of this part are similar to the field test results of back silting in the trial trench by Cao et al. [31].

To further analyze the sediment deposition within the foundation trench, elevation points were taken every 5 m and plotted as shown in Figure 9. Simultaneously, the sedimentation thickness curves for each cross-section were also obtained (Figure 10a). The middle section of the foundation trench is designated as the dividing line for convenience, then segmenting the trench into an upstream section and a downstream section. Compared to the downstream section of the foundation trench, the upstream section exhibits a relatively greater thickness of sediment deposition at the bottom, approximately 1.07 m, which is about 0.04 to 0.06 m higher. And this difference increases progressively over time.

The sediment distribution at the bottom of the base trench is relatively uniform, with an average thickness of 1.06~1.83 m. The erosion process predominantly affects the crests of both the upstream and downstream slopes of the foundation trench. The elevation of the upstream slope varies approximately between 1.07 and 1.23 m, while the downstream slope experiences a more significant reduction in elevation, ranging from 1.65 to 1.92 m. Compared to the upstream, the downstream crest of the foundation trench is subjected to more severe water erosion. Curves 1 to 10 in Figure 10b illustrate the variation in sedimentation height over time at elevation points taken every 5 m along the slope of the foundation trench. By integrating the observations from Figure 9d and Figure 10b, it is evident that the thickness of back-silting decreases progressively from the bottom to the top of the slope. Additionally, the back-silting thickness in the middle section of the slope is relatively uniform, exhibiting an approximately linear distribution.

As the immersed tube tunnel project is located in the monsoon climate zone, the Tanzhou Waterway experiences periods of low and high water levels due to precipitation. To understand the sedimentation patterns during different periods, we simulated the sedimentation within the foundation trench by controlling the variations in river flow for both periods, and the simulation results are shown in Figure 11. During the dry season, the distribution of sediments at the bottom of the foundation trench is relatively uniform, with minimal surface undulations, as shown in Figure 11a,b. The sedimentary material accumulates layer by layer over time.

However, there is a significant difference in the sedimentation pattern at the bottom of the foundation trench during the abundant water period compared to the dry season. Based on the variations in ground elevation, we obtained the curves depicting the changes in the back-silting height over time at different periods and locations along the base of the foundation trench (Figure 12). From Figure 11b,d and Figure 12a,b compared to the dry season, the uniformity of sediment deposition thickness at the bottom of the foundation trench during the wet season is small, primarily manifested in the significant difference in deposition height between the upstream and downstream sections, with a maximum difference of up to 0.79 m. The maximum siltation height during the abundant water period occurs in the middle section of the foundation trench, which is about 1.18–2.01 m at 90 d and larger than that in the dry water period. However, the siltation thickness at the bottom of the base channel in this period is not accumulated sequentially, whereas both siltation and erosion phenomena coexist. From 0 d to 40 d, the siltation thickness gradually increased. From 40 d to 60 d, fluvial erosion led to a progressive decrease in siltation thickness by about 0.2 m. Subsequently, from 60 to 90 days, siltation thickness increased again, and its distribution along main channel distance is relatively uneven. Therefore, during actual engineering construction, it is recommended to excavate the foundation trench during the dry season of the river. This allows for the prediction of sediment deposition patterns at the bottom of the foundation trench, ensuring the safe lowering of the immersed tunnel.

Figure 13 illustrates the velocity distribution curve of the river flow. As depicted in the graph, when the flow passes through the foundation trench section, the velocity within the river channel decreases rapidly from an initial speed of 0.38 m/s to 0.067 m/s. This observation indicates that as the upstream river carries a substantial amount of sediment through the base channel section, the flow velocity diminishes quickly, leading to a gradual reduction in the kinetic energy of the sediment. Consequently, this results in the deposition of sediment at the bottom of the base channel.

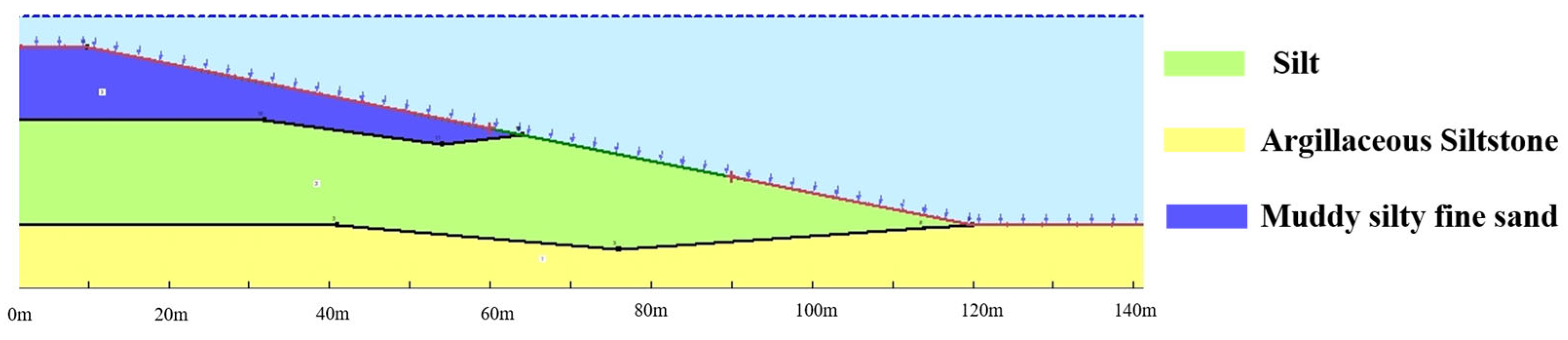
4. The Impact of Back-Silting on Slope Stability

4.1. Modeling Methodology

After the trench excavation of an immersed tunnel, back-silting is inevitable, which may prevent the immersed tube from settling accurately at the predetermined elevation and planar position, potentially causing deviation or tilting. Additionally, the uneven hardness of the silt layer can lead to localized subsidence or slippage during the lowering of the tube, increasing the difficulty of leveling adjustments. In some cases, repeated lifting and repositioning may be required, which raises safety risks during construction. Therefore, the proper removal of back-silted materials inside the trench is crucial for the safe construction of immersed tunnels. The SLOPE/W module of the Geo-Studio finite element software is utilized to investigate the foundation trench slope stability by introducing the back-silting simulation results during the dry season. By adjusting the dredging height and slope ratio, a safe and economical dredging method is derived.

Given that the geological conditions on both sides of the trench are identical, the upstream portion of the slope is selected for simulation for simplification. The geological conditions of the area to be modeled are complex, and most of them are saturated soft soil. In order to obtain the distribution of strata and the basic parameters of soil in this area, we use a combination of field survey and laboratory tests. The determination of the soil layer distribution is mainly determined by the drill pipe sampler, which is shown in Figure 14. According to the cross-sectional trend of the immersed tunnel slope, we set up 13 boreholes from left to right with an interval of about 22.3 m and a depth of 47.5–55.4 m. Based on borehole data, the slope strata are mainly composed of silt, fine sand and argillaceous siltstone. The soil taken by the drill pipe is undisturbed. In order to reduce the disturbance of the soil sample, the undisturbed soil is taken back to the laboratory with the drill pipe, and the basic physical properties and indoor triaxial tests are carried out. The specific test parameters are shown in

Table 3. Mechanical properties of soils.

Soil Type	Cohesion/kPa	Friction Angle
Silt	12.8	7°
Muddy silty fine sand	10.8	24°
Argillaceous Siltstone	45	30°
Back-silted material	1.62	0.4°

and

Table 4. Basic physical properties of soils.

Soil Type	Silt	Muddy Silty Fine Sand	Argillaceous Siltstone	Back-Silted Material
Unit weight kN/m3	19.2	18.5	24.4	12.348

.

The foundation trench slope has a gradient of 1:5 (V:H) with a total height of 30 m. The established foundation trench slope model is illustrated in Figure 15. The Morgenstern–Price theory is selected for analysis. In slope stability analysis, the Morgenstern–Price method simultaneously satisfies the horizontal force equilibrium, vertical force equilibrium, and moment equilibrium conditions. Compared to the Swedish slice method and Bishop’s simplified method, it yields more accurate and reliable computational results. Furthermore, this method is applicable for slope stability assessments across diverse geological conditions and demonstrates exceptional performance in complex slope scenarios. The potential sliding direction of the slope failure is defined as left-to-right, and the slip surface is determined by specifying entry and exit zones.

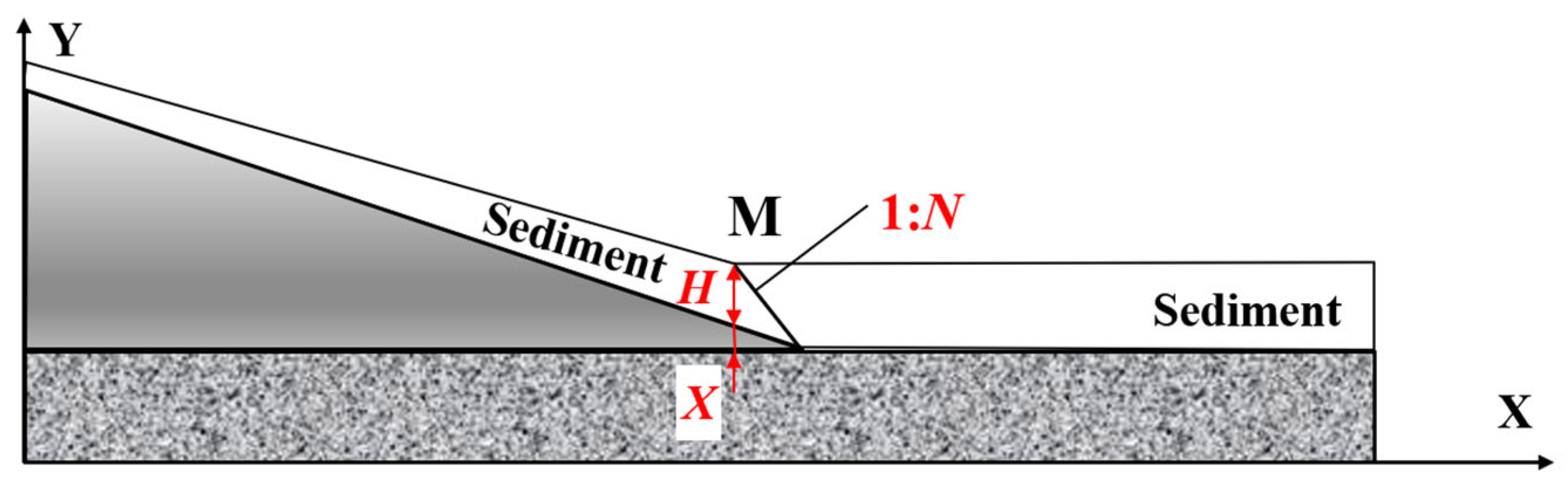
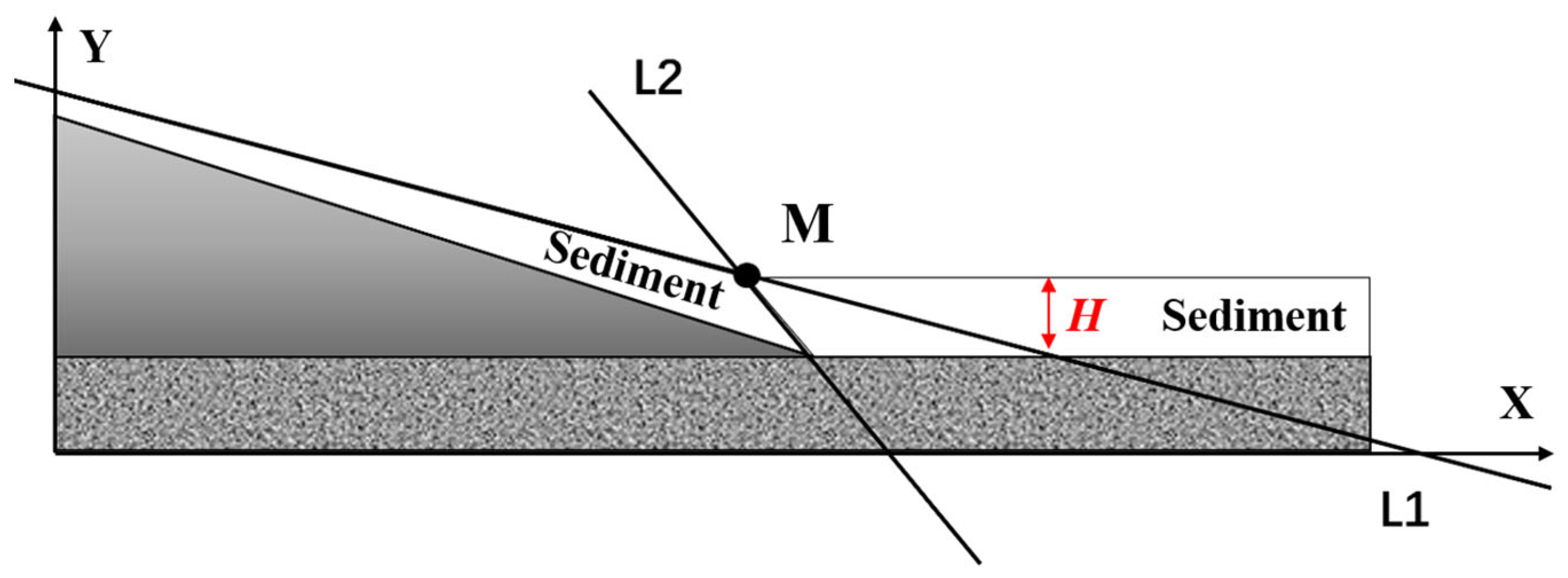
4.2. Influence of Back-Silting Depth on Subaqueous Slope Stability

To investigate the influence of back-silted materials on slope stability, a back-silting slope model (Figure 16) was established based on the sedimentation patterns described in Chapter 3. In this model, the back-silting thickness at the trench bottom is defined as the overall sedimentation height. Nine back-silting heights (0, 0.4, 0.8, 1.2, 1.6, 2, 2.4, 2.8, and 3.2 m) were selected for parametric analysis. Identify the most critical slip surface and obtain the curve of the safety factor for the slope under different siltation heights, as Figure 17 and Figure 18, respectively. The slope safety factor exhibited a slight increase from 1.566 to 1.613 with rising back-silting thickness. This phenomenon may be attributed to the reduced effective slope angle due to sediment deposition. Consequently, silt accumulation in the trench slope does not compromise slope stability.

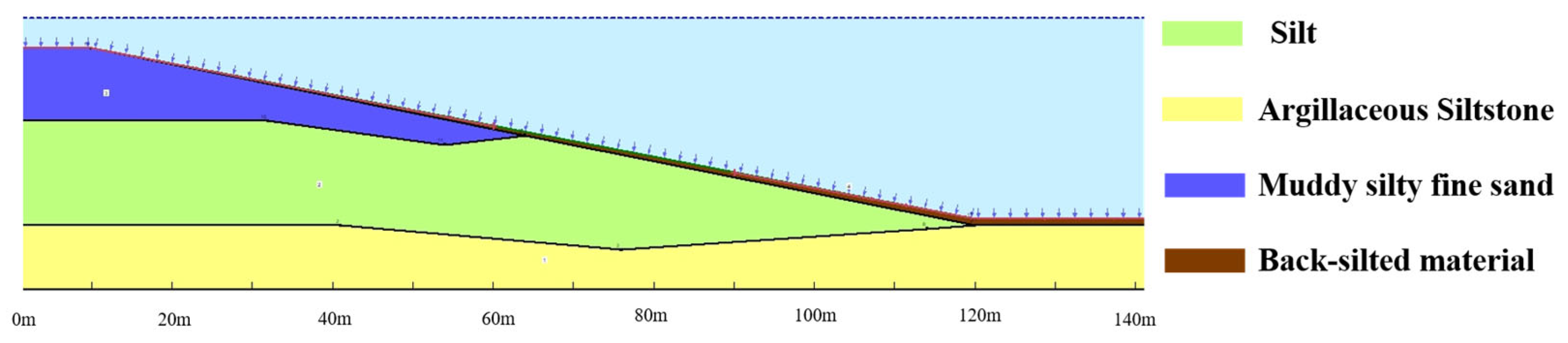
4.3. Dredging Method

A slope-grading dredging method is adopted to address the back-silting issue of foundation trench slopes. Comparison between pre-dredging and post-dredging conditions is illustrated in Figure 19. By establishing the entire slope within a Cartesian coordinate system, two critical parameters must be determined during the dredging simulation process, i.e., the dredging slope ratio and the position of the dredging initiation point M (as shown in Figure 20 and Figure 21). Two alternative methodologies are considered for determining the coordinates of point M. The first method involves specifying the dredging height H and the horizontal distance X from point M to the slope crest, then calculating the coordinates of point M by applying the dredging slope ratio, original slope gradient, and incorporating the geometric relationships defined in Equations (6) and (7):

$$x={\displaystyle \frac{5NH}{5-N}}$$

(6)

$$y={\displaystyle \frac{NH}{5-N}}+H$$

(7)

Another method involves introducing two intersecting straight lines and determining the coordinates of point M by solving the simultaneous linear equations, with specific computational procedures detailed in Equations (8) and (9).

$$x={\displaystyle \frac{b_2-b_1}{k_2-k_1}}$$

(8)

$$y=k_1\times x_1+b_1$$

(9)

where k₁ and k₂ represent the slopes of lines L₁ and L₂, while b₁ and b₂ denote the y-intercepts of these two straight lines, respectively.

Two fundamental concepts must be clarified regarding these two methodologies. In the first method, the dredging height (H in Figure 20) is determined by measuring the vertical distance from the dredging point to the slope toe after dredging. In the second method, the back-silting height (H in Figure 21) refers specifically to the sediment accumulation thickness at the trench bottom. For practical engineering applications, direct measurement of the back-silting height proves more operationally efficient than calculating linear distances through slope ratios. The back-silting height can be conveniently obtained through real-time field monitoring of sedimentation data. Therefore, the second method is employed to determine the position of point M in the modeling establishment, as it better reflects actual construction conditions and allows for direct incorporation of measurable site data into the simulation model.

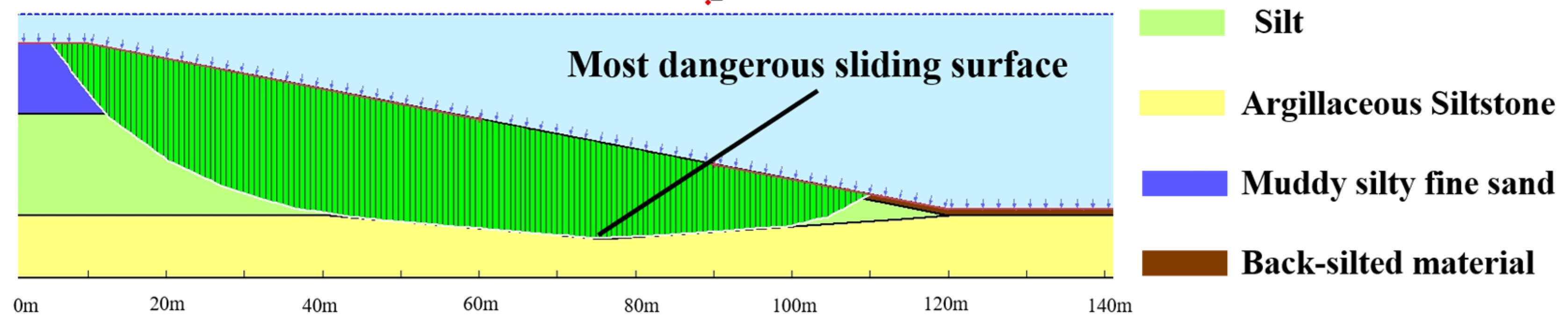
4.4. Slope Stability in Dredged Trenches: Effects of Siltation and Gradient

Two variable conditions, i.e., the dredging slope ratio and the back-silting thickness, are considered in the slope numerical model. The stability analysis evaluates five different trench slope ratios, i.e., 1:3, 1:2.5, 1:2, 1:1.5, and 1:1. The back-silting height ranges from 0 to 4.8 m with an interval of 0.4 m, totaling 65 simulation cases. The simulated slope failure surfaces and corresponding safety factors are presented in Figure 22 and Figure 23, respectively, in which the slope ratio represents the dredging slope ratio, and the height indicates the back-silting height of the foundation trench. To better highlight the variation in the most unfavorable sliding surface, we take a higher siltation height of 4.4 m and keep it constant, while examining changes in the slope safety factor by adjusting the slope ratio.

The most critical slip surface of the slope shifts accordingly as the safety factor undergoes significant changes. When there is no back-silting or the back-silting height is relatively small, such as 0~2 m, the safety factor of the dredged slope remains high, and the most critical slip surface is located within the trench slope body. As the back-silting thickness increases, the position of the most critical slip surface gradually shifts into the newly deposited sediment. This is due to the low strength and poor cohesion of the newly formed sediments, with the direct shear and quick shear indices being only 50% of those of the slope soil. As the safety factor of the sliding surface in the newly formed sediment is smaller than that in the trench slope, the position of the most unfavorable sliding surface may be shifted. Moreover, as the dredging slope ratio increases, the area of the most critical slip surface gradually decreases and continuously contracts toward the toe of the slope. As shown in Figure 22, the failure surface nearly penetrates the entire deposited sediment when the slope ratio is 1:3. However, when the slope ratio increases to 1:1, the most critical slip surface has already contracted to the slope toe. This is similar to the conclusion of Zhou et al. [32] that the destabilization location of underwater slopes is mainly concentrated at the foot of the slope through centrifugal experiments, and suggests that underwater slopes should pay full attention to the stabilization of the foot of the slope in the construction stage.

One can see from Figure 23 that within a specific dredging depth range, the slope safety factors at four different dredging gradients remain stable at approximately 1.57, comparable to the pre-dredging safety factor. According to China’s “Technical code for building slope engineering”. [33], the design value of the safety factor for grade I slopes typically ranges from 1.3 to 1.5. When the back-silting height exceeds 2.0 m, the safety factors of 1:1 gradient slope begin to decrease, falling below the critical threshold at 2.4 m. Consequently, the back-silting height should be maintained below 2.4 m for 1:1 gradient. As the slope gradient gradually changes from 1:1 to 1:3, the back-silting height corresponding to the onset of safety factor reduction increases progressively. Notably, for gentler slopes with gradients of 1:3 or less, significant safety factor variations only emerge when the back-silting height surpasses 3.6 m, necessitating control within 4.0 m. These results clearly demonstrate that under identical back-silting conditions, gentler dredging gradients produce higher safety factors. The intrinsic mechanism can be explained by the classical soil mechanics theory, based on the theory of limit equilibrium, the safety coefficient depends on the ratio of the anti-slip moment to the downward sliding moment. When the slope gradient increases, it will directly lead to an increase in the downward force component of the soil self-weight along the slope surface, while the normal force component perpendicular to the slope surface decreases, reducing the shear strength. Secondly, the foot of the steep slope due to the formation of geometric mutation shear stress concentration area, the maximum shear stress and slope ratio is inversely proportional to the more likely to exceed the soil body shear strength and thus damage. Therefore, when dealing with foundation trench slopes of fixed height and gradient, increased back-silting thickness requires the implementation of progressively gentler dredging gradients to ensure stability. The findings suggest an inverse relationship between back-silting thickness and optimal dredging gradient—greater sediment accumulation necessitates flatter slope angles to maintain structural integrity.

5. Conclusions

This study preliminarily investigated the back-silting patterns in underwater foundation trenches after excavation and evaluated the effect of slope dredging on trench slope safety factor. The main conclusions are summarized as follows:

(1)

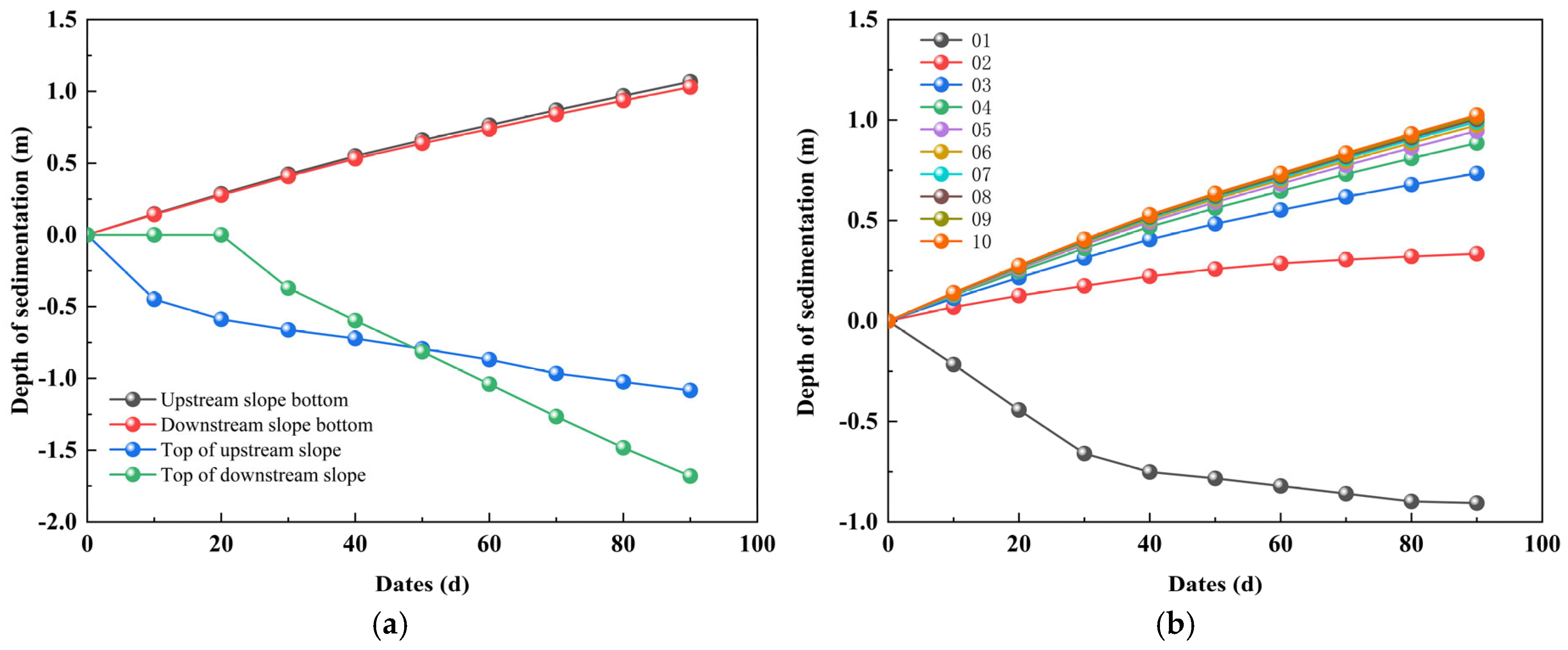
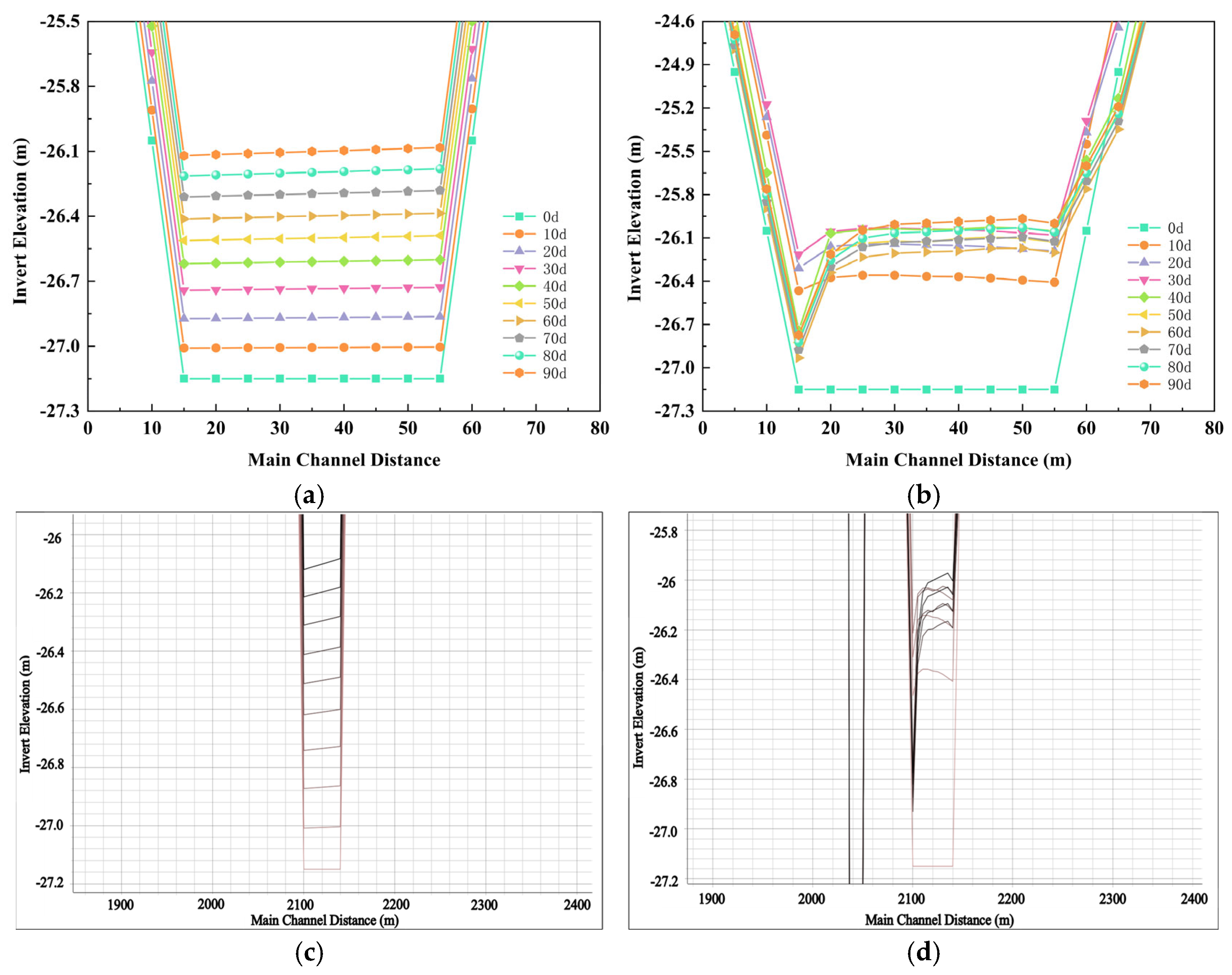
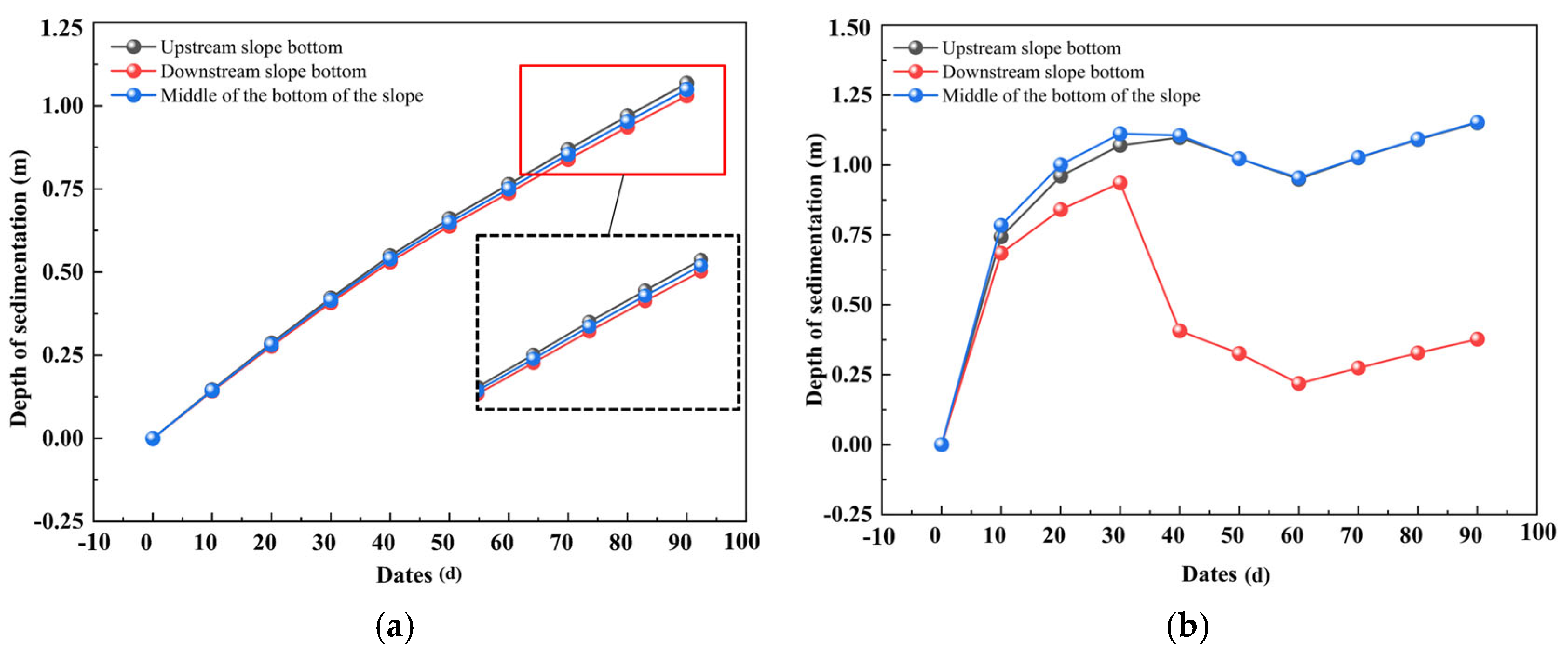
The river back-silting process exhibits distinct spatial heterogeneity. Sediment deposition primarily occurs at the foundation trench bottom, and the back-silting thickness follows an approximately linear trend from the slope toe to the slope crest. The slope crest area is predominantly influenced by fluvial hydrodynamic erosion, forming a well-defined erosion–deposition interface. The back-silting height at the upstream section of the trench bottom is slightly greater than that at the downstream section.

(2)

Hydroperiod variations significantly influence the spatiotemporal distribution of back-silting. During the dry season, the sedimentation process demonstrates stable hydrodynamic conditions with smooth sediment surfaces, and the deposition thickness increases almost linearly over time following a steady-state sedimentation pattern. In contrast, the flood season exhibits greater overall sedimentation intensity but with highly dynamic variations, characterized by alternating “deposition–erosion–redeposition” cycles that correlate strongly with hydrodynamic fluctuations (e.g., flow velocity and sediment concentration). From an engineering practice perspective, it is suggested that the optimal timing for immersed tube trench excavation should prioritize dry season operations.

(3)

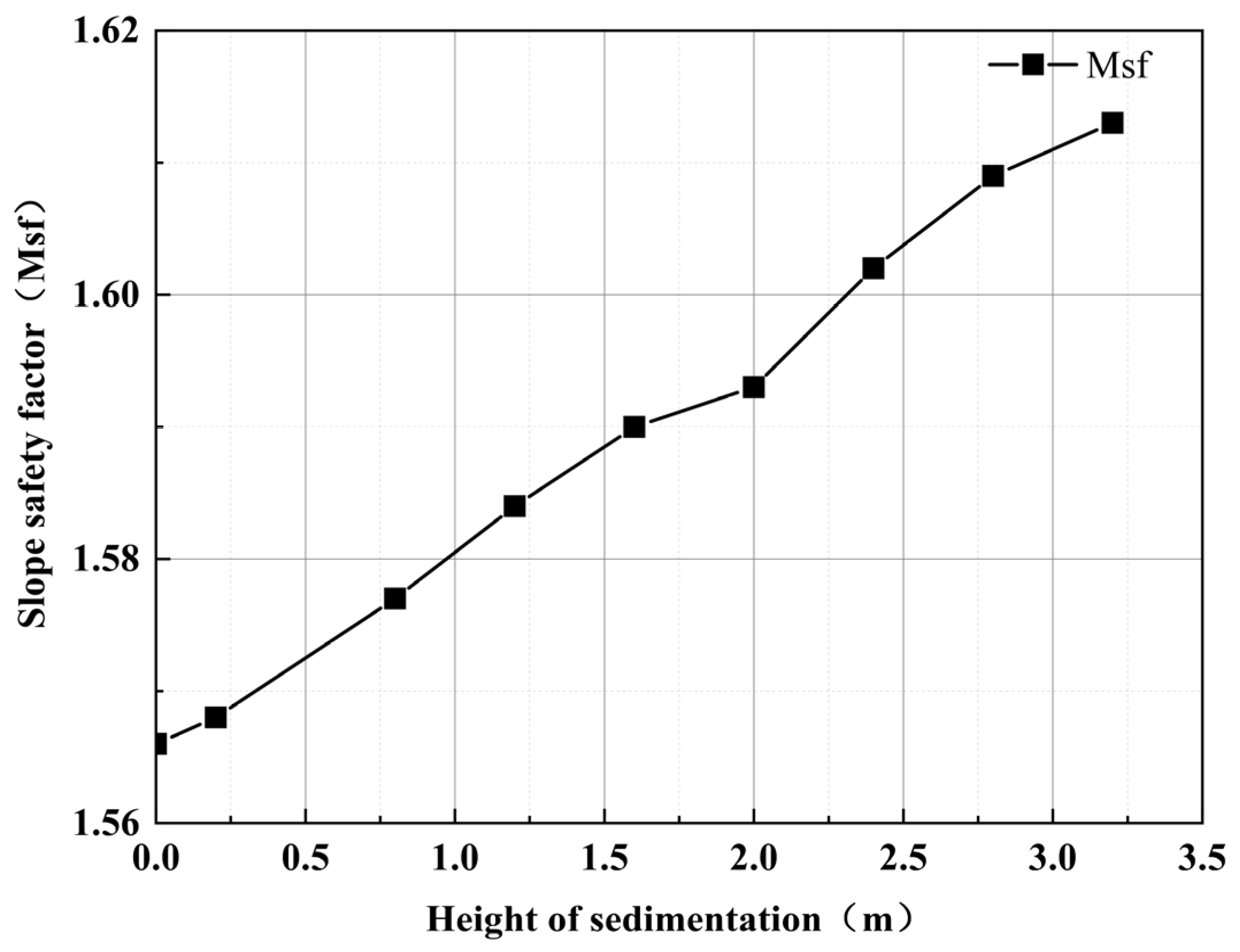
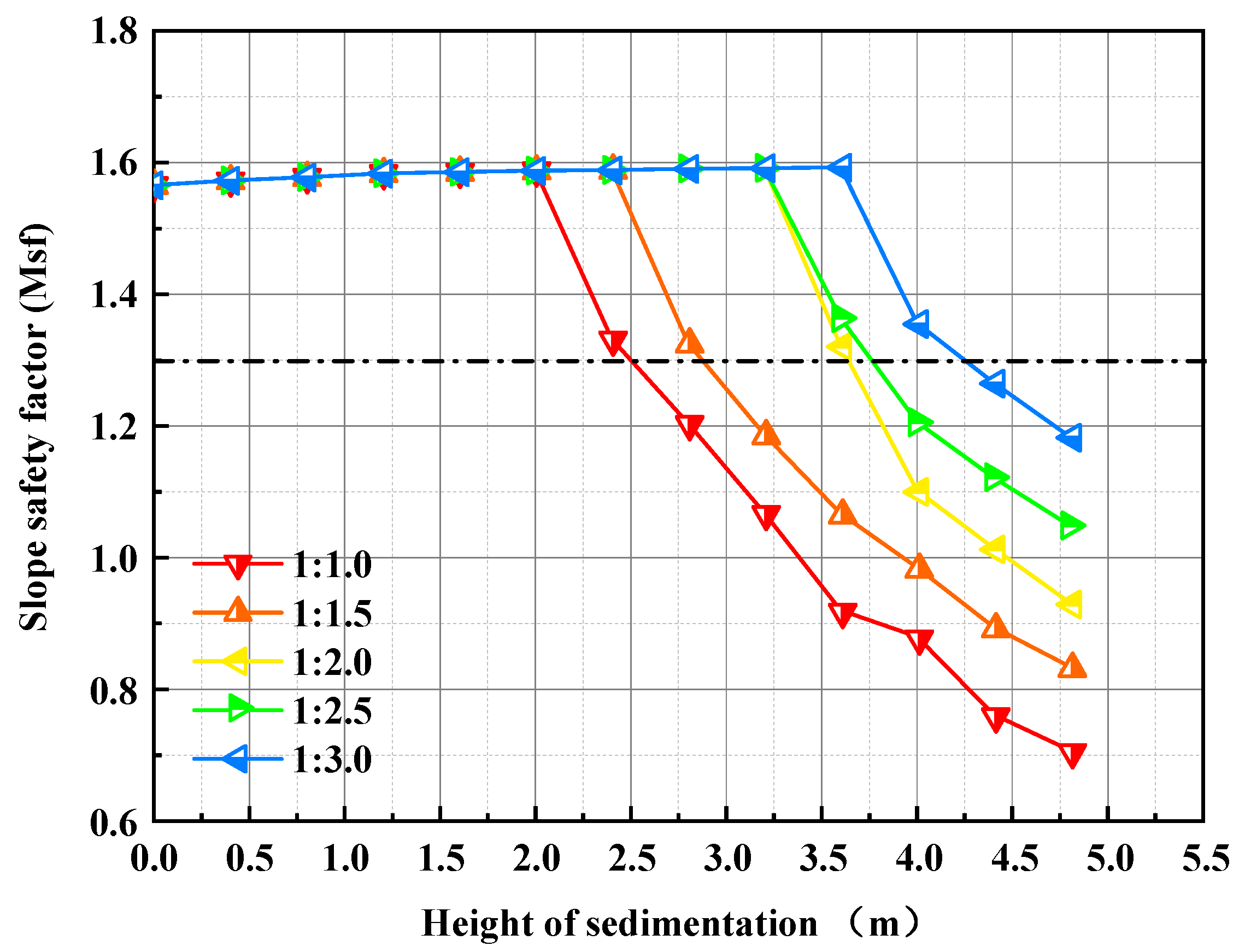
The back-silting process within the foundation trench exhibits a marginally positive influence on slope stability. The overall safety factor of trench slopes shows a slightly increasing trend with progressive back-silting thickness accumulation. Quantitative evaluation reveals that for every 3.2 m of sediment deposition, the safety factor experiences a nominal enhancement of approximately 0.05. This minimal variation suggests that back-silting deposition exerts negligible impact on the inherent stability of the slopes themselves.

(4)

The dredging simulation results reveal a progressive outward migration of the critical failure surface from the interior slope body to the newly deposited sediment layer with increasing back-silting thickness. Notably, steeper dredging gradients lead to a systematic reduction in the spatial distribution of critical slip surfaces, which progressively localize near the slope toe. This phenomenon substantiates the synergistic control mechanism between back-silting thickness and dredging gradient on slope failure patterns, providing a theoretical foundation for stability assessment in immersed tube foundation trench engineering.

(5)

For the proposed dredging method in this study, under identical foundation trench slope height and gradient, a greater back-silting height necessitates a gentler dredging slope gradient. Specifically, when the dredging slope ratio is 1:1, the back-siltation height should be controlled within 2.4 m. Correspondingly, for dredging slope ratios of 1:1.5, 1:2, 1:2.5, and 1:3, the allowable back-siltation heights should be limited to 2.8 m, 3.6 m, 3.6 m, and 4.0 m, respectively.