Soil Particle Size Estimation via Optical Flow and Potential Function Analysis for Dam Seepage and Building Monitoring

Abstract

Soil particle size distribution is a critical parameter in geotechnical and hydraulic engineering, particularly in applications such as dam seepage monitoring, building foundation assessments, and sediment transport. This study presents a novel algorithm for estimating soil particle sizes by analyzing their falling velocities in water, combining optical flow computation with chaotic motion analysis. To address the limitations of the classical Horn and Schunck method, particularly its sensitivity to large displacements and brightness variations, we introduced a coarse-to-fine warping strategy, an image decomposition step to separate dominant structures from fine textures, and the Charbonnier penalty function. The improved model achieved competitive accuracy compared to advanced optical flow algorithms. To manage turbulence and motion noise during particle settling, we incorporated a global flow analysis framework using streaklines, streak flow, and potential functions. This enabled the segmentation of laminar, turbulent, and rebound flow regions without requiring individual particle tracking. Soil particle sizes were then back-calculated from laminar flow velocities using Stokes’ Law. Experimental results confirmed the method’s accuracy for particle sizes ranging from 20 mm to 0.7 mm, significantly extending the measurable range of Sedimaging systems. The proposed approach shows strong potential for integration into dam-related particle monitoring applications and building-related monitoring systems requiring fine-resolution analysis.

1. Introduction

The particle size distribution (PSD) of coarse-grained soils is a critical factor in geotechnical and hydraulic engineering. It influences foundation stability, dam and road construction, subsurface drainage, and concrete mix design [1,2,3,4,5,6,7,8,9]. In the context of dam safety, particle gradation affects both hydraulic conductivity and the internal stability of dam structures and their filter layers [5,10,11]. Inaccurate PSD assessments can lead to serious failures such as piping and internal erosion, which are key causes of dam breaching and overtopping. Therefore, accurate and efficient PSD estimation is essential not only for the design and maintenance of embankment and rock-fill dams but also for broader general soil classification in geoenvironmental investigations [12,13,14,15].

Mechanical sieving remains the most commonly used particle sizing method due to its simplicity [16,17,18]. However, it is labor-intensive, time-consuming, and sensitive to sample disturbance [19,20,21,22,23,24]. To overcome these drawbacks, Ohm and Hryciw [24] developed the Sedimaging system, which estimates particle size by analyzing image textures using wavelet transformation [25,26,27,28,29]. As shown in Figure 1, the system includes a transparent sedimentation column, backlighting, and a high-resolution camera that records particles as they settle in water. Texture features extracted from the images are used to estimate particle size via wavelet-based granulometry. This approach works well for particles smaller than 2 mm. However, for larger particles, internal textures interfere with the wavelet analysis, reducing accuracy [29].

To overcome this limitation, a new algorithm was proposed to estimate soil particle sizes based on the principle that larger particles fall faster under gravity. The overall framework of the algorithm, illustrated in Figure 2, includes three key steps: (1) optical flow estimation from sedimentation video frames; (2) extraction of laminar flow zones using global motion analysis with streaklines and potential functions; and (3) back-calculation of particle size using Stokes’ Law. In this context, we distinguish between two flow types: laminar flow, characterized by vertical downward motion, and turbulent flow, which involves multidirectional movement and rebounds near the base. The framework allows reliable segmentation of laminar regions and accurate estimation of settling velocities for size inference.

Optical flow estimation has been a long-standing area of study. Classical methods, such as those by Horn and Schunck [30] and Lucas and Kanade [31], laid the foundation. Since then, many improvements have been made, including bicubic warping [32,33], graduated non-convexity optimization [34,35], and robust penalty terms like the Charbonnier formulation [36]. However, these methods often assume small displacements, limiting their use for tracking large, fast-moving particles in sedimentation flows. In addition, their sensitivity to lighting changes, shadows, and noise reduces accuracy in real-world settings. To address this, enhancements such as coarse-to-fine warping [33,37,38] and structure and texture decomposition [39] have been proposed.

Separately, chaotic motion analysis has gained attention in the computer vision community [40,41,42]. Prior studies explored motion pattern learning [43], dense crowd tracking [41,44], flow segmentation [45], anomaly detection [41,46,47], and higher-level scene understanding [40,48,49]. Among them, the streakline-based descriptor proposed by Mehran et al. [50] allowed global motion analysis without tracking individuals. Corpetti et al. [51] further extended this idea using potential functions to separate flow into irrotational and rotational components. Yet, such methods have not been applied to sediment-laden flows, where laminar and turbulent zones coexist in confined domains.

This study addresses the above-mentioned gaps by introducing a novel algorithm that estimates soil particle sizes based on their falling velocities in water. The method combines optical flow estimation with chaotic motion segmentation to improve both accuracy and applicability. The key contributions of this research are summarized as follows. First, the classical Horn and Schunck optical flow model is modified to handle large displacements and lighting variations by incorporating coarse-to-fine warping, texture decomposition, and a Charbonnier-based penalty function. Second, a global chaotic motion analysis framework based on streaklines is applied to sedimentation flows, enabling the separation of laminar and turbulent regions without the need for individual particle tracking. Third, particle sizes are inferred from laminar falling velocities using Stokes’ Law, allowing for quantitative size estimation from video data. Finally, the method is experimentally validated on soil samples ranging from 0.7 mm to 20 mm in size, demonstrating consistent improvements in accuracy over the original Sedimaging system.

By combining vision-based motion analysis with physical modeling of particle settling, this approach offers a scalable and non-intrusive tool for soil particle characterization. It is particularly well-suited for dam seepage monitoring and sediment transport analysis, where real-time or high-resolution tracking of granular behavior is essential.

2. Optical Flow

Most optical flow estimation algorithms are formulated by minimizing an objective function E(u, v), which typically consists of two terms: a data term and a smoothness term. The data term E_d(u, v) assumes brightness constancy between two consecutive frames, i.e., the image intensity of a pixel remains constant over time. Let I(x, y, t) denote the image intensity at pixel (x, y) in frame t, and let the displacement vector be $\overrightarrow{w}=(u,v,1)$, where u and v are functions of (x, y, t). This assumption leads to the brightness constancy constraint:

$$I(x,y,t)=I(x+u,y+v,t+1).$$

(1)

Applying a first-order Taylor expansion leads to the classic gradient constraint equation:

$$I_{x}u+I_{y}v+I_t=0,$$

(2)

where I_x, I_y, and I_t denote the partial derivatives of the image intensity with respect to x, y and t, respectively.

2.1. Limitations of the Classical Horn–Schunck Model

The classical Horn and Schunck [30] defined the optical flow objective function by combining the data constraint (Equation (2)) with a global smoothness term E_s (u, v):

$$E(u,v)=E_d(x,y)+\lambda E_s(u,v)={\displaystyle {\int }_{\Omega }\left[{(I_{x}u+I_{y}v+I_t)}^2+\lambda (u_x^2+u_y^2+v_x^2+v_y^2)\right]}dx,$$

(3)

where u_x, u_y, v_x, and v_y are the partial derivatives of the flow field with respect to x, y; and λ is a regularization parameter that balances data fidelity and smoothness. In discrete form, Equation (3) becomes

$$E(u,v)={\displaystyle {\sum }_{ij}{(I_{x}u+I_{y}v+I_t)}^2+\lambda \left[{(u_{i,j}-u_{i+1,j})}^2+{(u_{i,j}-u_{i,j+1})}^2+{(v_{i,j}-v_{i+1,j})}^2+{(v_{i,j}-v_{i,j+1})}^2\right]}.$$

(4)

This objective function is iteratively minimized using the following update equations:

$$u^{k+1}={\overline{u}}^k-{\displaystyle \frac{I_x\left(I_x{\overline{u}}^k+I_y{\overline{v}}^k+I_t\right)}{{\lambda }^2+I_x^2+I_y^2}},v^{k+1}={\overline{v}}^k-{\displaystyle \frac{I_y\left(I_x{\overline{u}}^k+I_y{\overline{v}}^k+I_t\right)}{{\lambda }^2+I_x^2+I_y^2}},$$

(5)

where k denotes the iteration number, and ${\overline{u}}^k$ and ${\overline{v}}^k$ are the neighborhood averages of u^k and v^k. As an initial step, the classical Horn and Schunck method was applied due to its simplicity and analytical clarity. Two consecutive frames were selected from the recorded video to estimate the optical flow field. The resulting motion vectors, illustrated in Figure 3, reveal that the classical model fails to capture the large displacements characteristic of falling soil particles.

This outcome can be attributed to several intrinsic limitations of the Horn and Schunck formulation. (1) The gradient constraint, derived from a first-order Taylor expansion, is valid only for small displacements. It becomes inaccurate when large motions occur. (2) The quadratic penalty function is not robust to outliers, leading to poor motion estimation in noisy areas. (3) The brightness constancy assumption is highly sensitive to slight illumination variations, which are common in real-world image sequences.

2.2. Improvement of HS Model

To overcome these limitations, several key enhancements were incorporated into the classical Horn and Schunck model, as detailed below:

2.2.1. Direct Photometric Difference Minimization

Horn and Schunck [30] originally employed a first-order Taylor expansion to simplify computation, which was necessary due to hardware constraints at the time. However, with modern computational capabilities, this assumption is no longer required. Instead, we directly minimize the photometric difference I(x, y, t) − I(x + u, y + v, t + 1), leading to a more general formulation of the optical flow objective function:

$$\begin{array}{l}E(u,v)=E_d(x,y)+\lambda E_s(u,v)\\ ={\displaystyle {\sum }_{i,j}\left\{f_d\left(I_1(i,j)-I_2(i,+u_{i,j},j+v_{i,j})\right)+\lambda [f_s(u_{i,j}-u_{i+1,j})\right.}\\ +\left.f_s(u_{i,j}-u_{i,j+1})+f_s(v_{i,j}-v_{i+1,j})+f_s(v_{i,j}-v_{i,j+1})]\right\}\end{array},$$

(6)

where I₁ and I₂ are two consecutive image frames, and f_d and f_s represent the data and spatial penalty functions, respectively. The classical formulation corresponds to a quadratic penalty function, f(x) = x², as shown in Equation (4).

2.2.2. Charbonnier Penalty for Robustness

The quadratic penalty used in the classical HS model is sensitive to outliers. Consequently, numerous alternative penalty functions have been proposed and assessed to enhance robustness [52,53,54]. To enhance robustness, we adopted the Charbonnier penalty function [36], defined as $f(x)=\sqrt{(x^2+{\epsilon }^2)}$, with ε = 0.001. This function approximates the L1 norm and reduces the impact of motion discontinuities or sensor noise.

2.2.3. Coarse-to-Fine Warping Strategy

A multiscale warping approach was implemented to handle large particle displacements [33,37,38,55,56], following the method proposed by Bruhn et al. [36]. This strategy begins by constructing spatially filtered and sub-sampled image pyramids. The estimation starts at the coarsest resolution level with an initial flow field $\overrightarrow{w}=0$. A flow increment dw is computed at this level and used to update the flow field to w + dw, which is then scaled and projected to the next finer resolution level. At this level, the first image is warped toward the second image based on w + dw, and the warped image is subsequently used to refine the flow estimate dw. This process is repeated iteratively until the full-resolution flow field is obtained. The multiscale scheme enhances both convergence and stability, especially in the presence of fast-moving particles.

2.2.4. Structure and Texture Decomposition

The data term $f_d(I_1(i,j)-I_2(i+u_{i,j},j+v_{i,j}))$ assumes that the intensity value of pixel $I_1(i,j)$ remains unchanged during its displacement to $I_2(i+u_{i,j},j+v_{i,j})$. However, this assumption often fails in practice due to sensor noise, illumination changes, reflections, and shadows. Weijer et al. [57] and Mileva [58] attempted to resolve this by using photometric invariants, which inherently require color imagery. A more common strategy in grayscale settings is to replace raw intensity values with image gradients to improve robustness against illumination variations. However, this introduces multiple data fidelity terms and second-order derivatives, which tend to amplify noise artifacts [39]. To mitigate the effects of lighting changes, shadows, and specularities, we adopted a decomposition into structure and texture components following Wedel et al. [39]. Given a greyscale image $I(i,j)$, the structural component $I_S(i,j)$ is obtained by minimizing the following energy functional:

$$\underset{I_S}{\min }{\displaystyle {\int }_{\Omega }\left(\left|\nabla I_S\right|+\frac{1}{2\theta }{(I_s-I)}^2\right)dx}.$$

(7)

The textural component $I_T(i,j)$ is then obtained as the difference: $I_T(i,j)=I(i,j)-I_S(i,j)$. Figure 4 illustrates the decomposition results. The structure component preserves dominant edges and objects, while the texture component contains fine-scale patterns, such as soil granularity and turbulent flow boundaries. As shown in Figure 4, Wedel et al. [39] demonstrated that optical flow estimation using the texture component is significantly more robust to shadows and shading artifacts.

Using the improved model described above, we recomputed the optical flow between the two frames shown in Figure 2. The resulting displacement ranged from u = −44.36 (left) to 37.43 (right) pixels, and from v = −44.37 (upward) to 50.14 (downward) pixels. Ideally, the horizontal component u should remain close to zero, and the vertical component v should be strictly positive, reflecting a purely downward motion. However, visual inspection of the video indicates that the soil particle motion can be divided into three distinct regions, as illustrated in Figure 5. The yellow region represents laminar flow, where particles fall vertically downward. Upon impact with the base, particles rebound and ascend, forming the blue region. Subsequently, they enter the green region, where trajectories become irregular and recirculating, indicating the presence of turbulent flow. As a result, particle velocities exhibit multidirectional behavior. The computed velocity field in Figure 5c captures this qualitative pattern. However, due to the absence of ground-truth optical flow data for the selected frame pair, the quantitative accuracy of the results remains uncertain.

To ensure accurate motion capture, the Sedimaging system was configured to record video at a resolution of 1920 × 1080 pixels and 30 frames per second. Calibration using reference markers established a vertical scale of approximately 0.13 mm per pixel. Based on this scale, a particle falling at 0.5 m/s would move about 30 pixels between consecutive frames, which is within the resolvable range of our enhanced optical flow model.

The choice of 30 fps offers a balance between temporal resolution and the hardware limitations of the camera. Larger particles, such as 20 mm aggregates, may reach terminal velocities approaching 1.0 m/s, resulting in inter-frame displacements of up to 40 to 50 pixels. Although these motions remain trackable using the coarse-to-fine warping strategy, motion blur becomes increasingly noticeable, especially near the bottom of the sedimentation column where rebound effects are stronger.

In all experiments, a particle density of 2600 kg/m³ was assumed, which represents the typical density of quartz-based soil aggregates in geotechnical applications. This value was used in Stokes’ law to calculate the equivalent particle diameter based on settling velocity. The implications of this assumption, along with the upper tracking limit of the imaging setup, are further discussed in Section 6.

2.3. The Quantitative Accuracy of Improved HS Model

The improved Horn and Schunck model was evaluated using four benchmark sequences from the Middlebury optical flow database [59]. Figure 6 illustrates the computed optical flow fields for three representative sequences, presented alongside the corresponding ground-truth results to visually assess the model’s performance.

The Average Angular Error (AAE) and End Point Error (EPE) obtained from our method are summarized in

Table 1. Average Angular Error (AAE) and End Point Error (EPE) on the Middlebury Optical Flow Benchmark.

Method	Grove2		RubberWhale		Dimetrodon		Urban 2		Average
	AAE	EPE	AAE	EPE	AAE	EPE	AAE	EPE	AAE	EPE
Traditional HS ([30])	15.853	5.204	16.798	6.118	19.675	7.224	16.069	8.459	17.098	6.751
Improved HS (This research)	8.410	1.189	6.240	1.276	5.280	1.217	7.034	1.210	6.741	1.223

. The improved Horn and Schunck model demonstrates significantly higher accuracy compared to the classical formulation. For comparison, Xu et al. [60] reported an AAE of 4.01 and an EPE of 0.245, placing their method among the top performers on the Middlebury benchmark. These results confirm the competitive performance of our model.

While the Middlebury benchmark sequences provide a standardized platform for assessing optical flow accuracy using angular and endpoint errors, it is also important to verify whether the enhanced model performs reliably on real-world sedimentation data.

Therefore, in addition to synthetic validation, the improved Horn and Schunck model was applied to video sequences captured during our laboratory experiments, where soil particles with known size distributions were allowed to settle in a water column. Details of these experimental validations are presented in Section 5. The optical flow estimates obtained from these real sequences served as the basis for velocity extraction and subsequent particle size estimation using Stokes’ law.

3. Chaotic Analysis

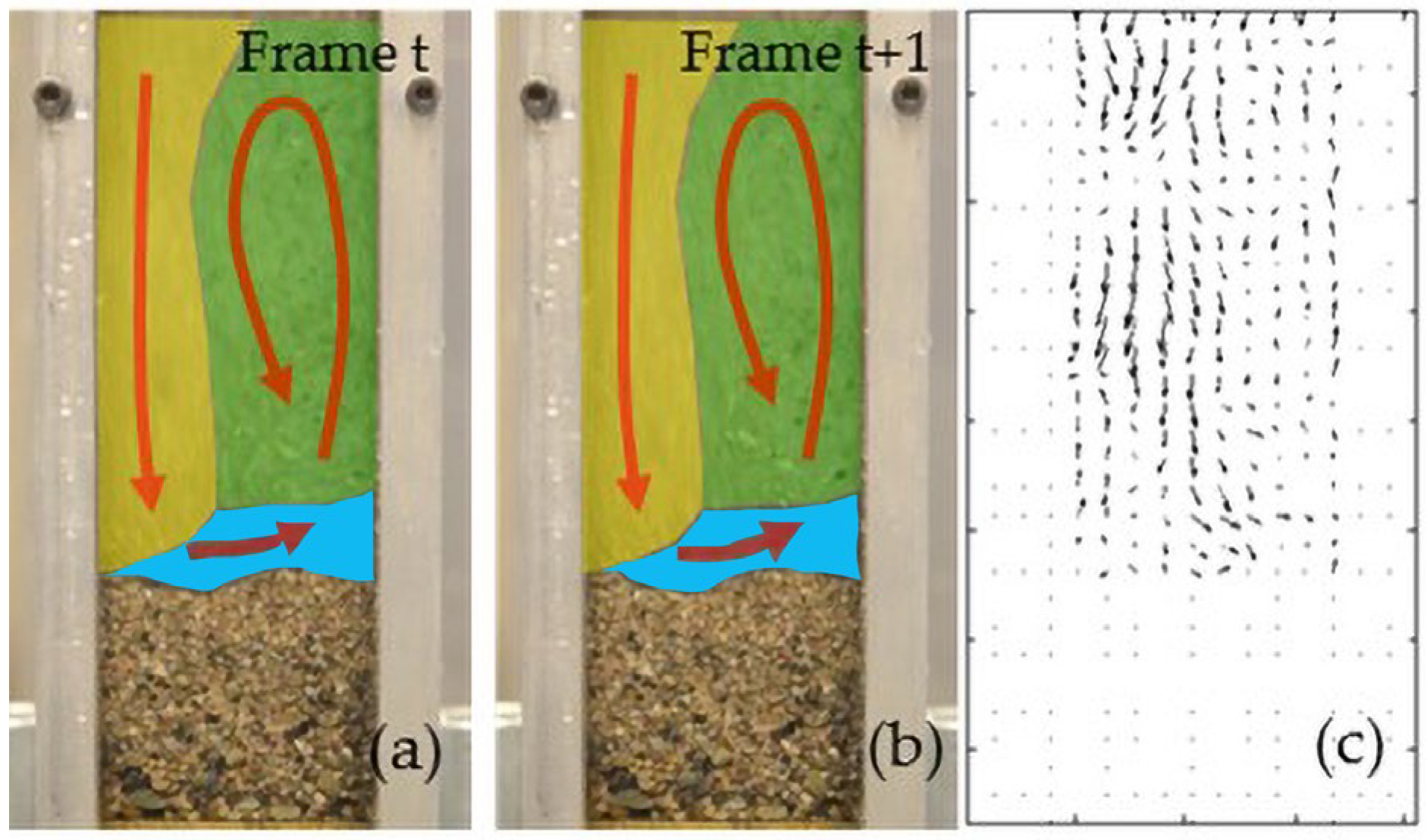
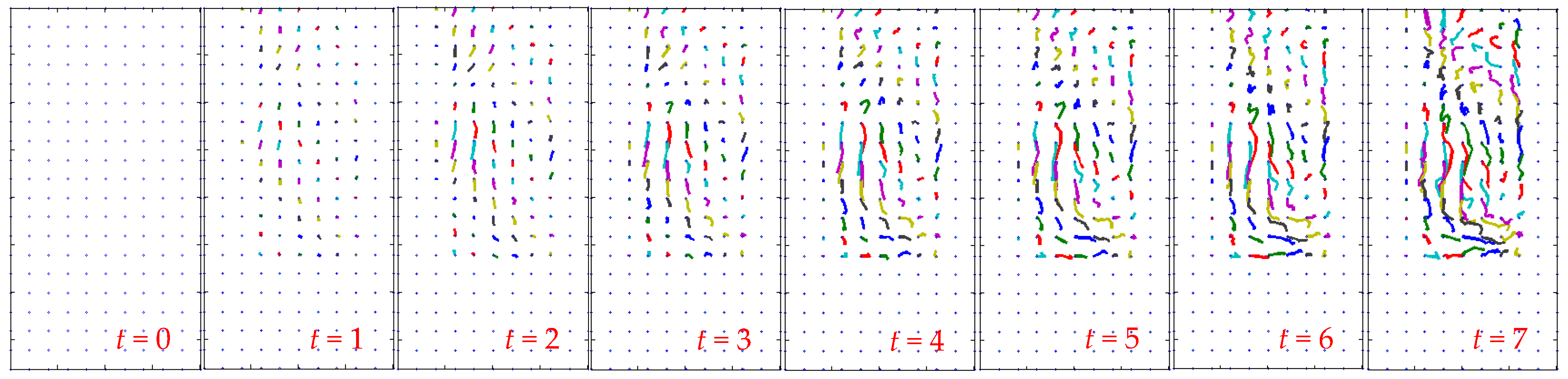
3.1. Streakline Computation

Streakline is a relatively new concept in the field of computer vision research. According to Mehran et al. [50], a streakline refers to the set of all particle locations, at a given time, that have passed through a specific fixed point. Specifically, a fixed point $p=(x^p,y^p)$ is defined in the image domain. A particle $P_0(x_0^p(0),y_0^p(0))$ is placed at point p at time t = 0. At time t = 1, the particle is advected to a new position according to the optical flow vector $\left(u(x_0^p(0),y_0^p(0),0),v(x_0^p(0),y_0^p(0),0)\right)$ at point p. A new particle P₁ is then initialized at the same point. Both particles are subsequently advected using the optical flow field. Repeating this process for T time steps yields a sequence of particle positions. The position of particle P_i at time t is computed using Equation (8):

$$\begin{array}{l}{x}_i^p(t)=x_i^p(t-1)+u\left(x_i^p(t-1),y_i^p(t-1),t-1\right)\\ y_i^p(t)=y_i^p(t-1)+v\left(x_i^p(t-1),y_i^p(t-1),t-1\right)\end{array},$$

(8)

where u and v represent the velocity components obtained from optical flow. All particles at time t = T are connected to form a curve originating from point p, which traces the flow trajectory from t = 0 to t = T. This curve constitutes a single streakline. The procedure described above generates a streakline that characterizes the motion originating from a specific location in the flow field. In practice, a grid of seed points can be defined, with each producing its own streakline. The resulting family of streaklines provides a global description of the motion patterns in dense and chaotic flow environments.

Equation (8) is an ordinary differential equation system given by

$${\displaystyle \frac{dx}{dt}}=u(x,y,t),{\displaystyle \frac{dy}{dt}}=v(x,y,t),$$

subject to the initial condition $(x^p(0),y^p(0))=(x^p,y^p)$.

A fourth-order Runge–Kutta–Fehlberg method, combined with cubic interpolation of the velocity field [61], is employed to solve the system. The computed streaklines over seven successive frames are shown in Figure 7. These streaklines successfully capture the underlying flow pattern previously illustrated in Figure 5.

3.2. Streak Flow Computation Based on Streaklines

The optical flow field represents instantaneous motion. As a result, it is highly sensitive to abrupt changes and noise in crowded scenes. To address this, Ali and Shah [45] introduced a smoothed flow representation termed particle flow, denoted as ${\Omega }_s=(u_s,v_s)$, to characterize motion in crowded scenes. The particle flow field is the average of several successive optical flow fields. While it reduces the impact of noisy motion, its limitations are apparent. In particular, it fails to capture newly emerging motions promptly. To overcome this drawback, Mehran et al. [50] proposed streak flow, based on streaklines, to represent flow in crowded motion scenarios. Their results show that streak flow is robust to noise and can accurately capture immediate changes in motion.

In our study, the computation of streak flow follows a straightforward principle. As soil particles fall through water, their motion tends to align with the surrounding flow. Consequently, later particles are expected to follow trajectories similar to those of earlier ones. Noisy motion vectors in the optical flow can thus be refined along the trajectories of neighboring particles exhibiting coherent motion. We illustrate the computation of u_s; the computation of v_s is analogous. For a particle P_i with initial velocity (u_i, v_i) obtained from optical flow, we define its three nearest neighboring pixels and approximate u_i as a linear interpolation of their values. Aggregating Equation (9) over all particles yields a linear system:

$$u_i=a_1{u}_s(k_1)+a_2{u}_s(k_2)+a_3{u}_s(k_3),$$

(9)

where k_j is the index of the j-th neighboring pixel, and a_j is the basis function associated with the triangulation of the domain, which is predefined. By stacking Equation (9) for all particles, we obtain a linear system of equations:

$$A{u}_s=U,$$

(10)

where A is the coefficient matrix composed of the interpolation weights a_i and U is the vector of initial horizontal velocities u_i derived from optical flow. The streak flow component u_s is obtained as the least-squares solution to Equation (10). Figure 8 compares the velocity fields computed using classical optical flow and the refined streak flow. Noisy motion vectors, likely caused by rebounding particles, are highlighted in the black box. In contrast, the streak flow produces a smoother velocity field. In this field, such spurious motions are effectively suppressed. This refined field enables more accurate characterization of flow behavior through potential function analysis.

3.3. Potential Functions Based on the Streak Flow

Potential functions are widely used in fluid mechanics to characterize planar vector fields. A planar vector field $\Omega =(u,v)$ is called solenoidal if its divergence is zero everywhere, i.e., $\nabla \cdot \Omega =0$. If its curl is zero everywhere, it is called irrotational, represented as $\nabla \times \Omega =0$. According to Green’s theorem [62], for an irrotational field, there exists a scalar velocity potential ϕ such that $\Omega =\nabla \varphi$. Likewise, for a solenoidal field, there exists a scalar stream function ψ such that ${\Omega }^{\perp }=\nabla \psi$, where ${\Omega }^{\perp }={(-v,u)}^T$ is the orthogonal field of Ω. These scalar functions ϕ and ψ are collectively referred to as potential functions. They are fundamental tools for classifying flow patterns in planar fields. Irrotational and solenoidal fields play complementary roles in vector field analysis. According to the Helmholtz decomposition [63], any arbitrary continuous vector field Ω can be uniquely decomposed into an irrotational component Ω_ir and a solenoidal component Ω_so, such that

$$\Omega ={\Omega }_{\mathrm{i}\mathrm{r}}+{\Omega }_{\mathrm{s}\mathrm{o}},\mathrm{where}{\Omega }_{\mathrm{i}\mathrm{r}}=\nabla \varphi \mathrm{and}{\Omega }_{\mathrm{s}\mathrm{o}}^{\perp }=\nabla \psi .$$

Corpetti et al. [51] proposed the following expressions for computing the components of the potential fields using Fourier transform:

$$\begin{array}{l}\varphi (x,y)={\displaystyle \frac{1}{2}}\left({\displaystyle \underset{0}{\overset{x}{\int }}{u}_{\mathrm{i}\mathrm{r}}(s,y)ds+}{\displaystyle \underset{0}{\overset{y}{\int }}{v}_{\mathrm{i}\mathrm{r}}(x,s)ds+}{\displaystyle \underset{0}{\overset{x}{\int }}{u}_{\mathrm{i}\mathrm{r}}(s,0)ds+}{\displaystyle \underset{0}{\overset{y}{\int }}{v}_{\mathrm{i}\mathrm{r}}(0,s)ds}\right)\\ \psi (x,y)={\displaystyle \frac{1}{2}}\left({\displaystyle \underset{0}{\overset{y}{\int }}{u}_{\mathrm{s}\mathrm{o}}(x,s)ds+}{\displaystyle \underset{0}{\overset{x}{\int }}{v}_{\mathrm{s}\mathrm{o}}(s,y)ds+}{\displaystyle \underset{0}{\overset{y}{\int }}{u}_{\mathrm{s}\mathrm{o}}(0,s)ds+}{\displaystyle \underset{0}{\overset{x}{\int }}{v}_{\mathrm{s}\mathrm{o}}(s,0)ds}\right)\end{array},$$

(11)

where u_ir and v_ir are velocity components of the irrotational field Ω_ir, and u_so and v_so are those of the solenoidal field Ω_so. Given any planar vector field $\Omega =(u,v)$, Corpetti et al. [51] proposed this method to compute for ${\Omega }_{\mathrm{i}\mathrm{r}}=(u_{\mathrm{i}\mathrm{r}},v_{\mathrm{i}\mathrm{r}})$ and ${\Omega }_{\mathrm{s}\mathrm{o}}=(u_{\mathrm{s}\mathrm{o}},v_{\mathrm{s}\mathrm{o}})$.

However, when potential functions are computed directly from classical optical flow, the results often exhibit significant noise. This noise is characterized by rapidly fluctuating peaks and valleys. These artifacts arise due to the high sensitivity of optical flow to minor motion variations. In contrast, streak flow produces smoother and more stable velocity fields. As a result, the potential functions derived from them are both reliable and physically interpretable in densely populated flow scenarios. Figure 9 illustrates the computed potential functions for a representative streak flow field Ω. The solenoidal component Ω_so captures rotational motion. In contrast, the irrotational component Ω_ir describes translational flow behavior. The velocity potential ϕ highlights regions of convergence and divergence, corresponding to flow entry and exit zones (see Figure 9d). The stream function ψ delineates laminar flow regions. These are represented as areas enclosed between streamlines, as highlighted by the black box in Figure 9e.

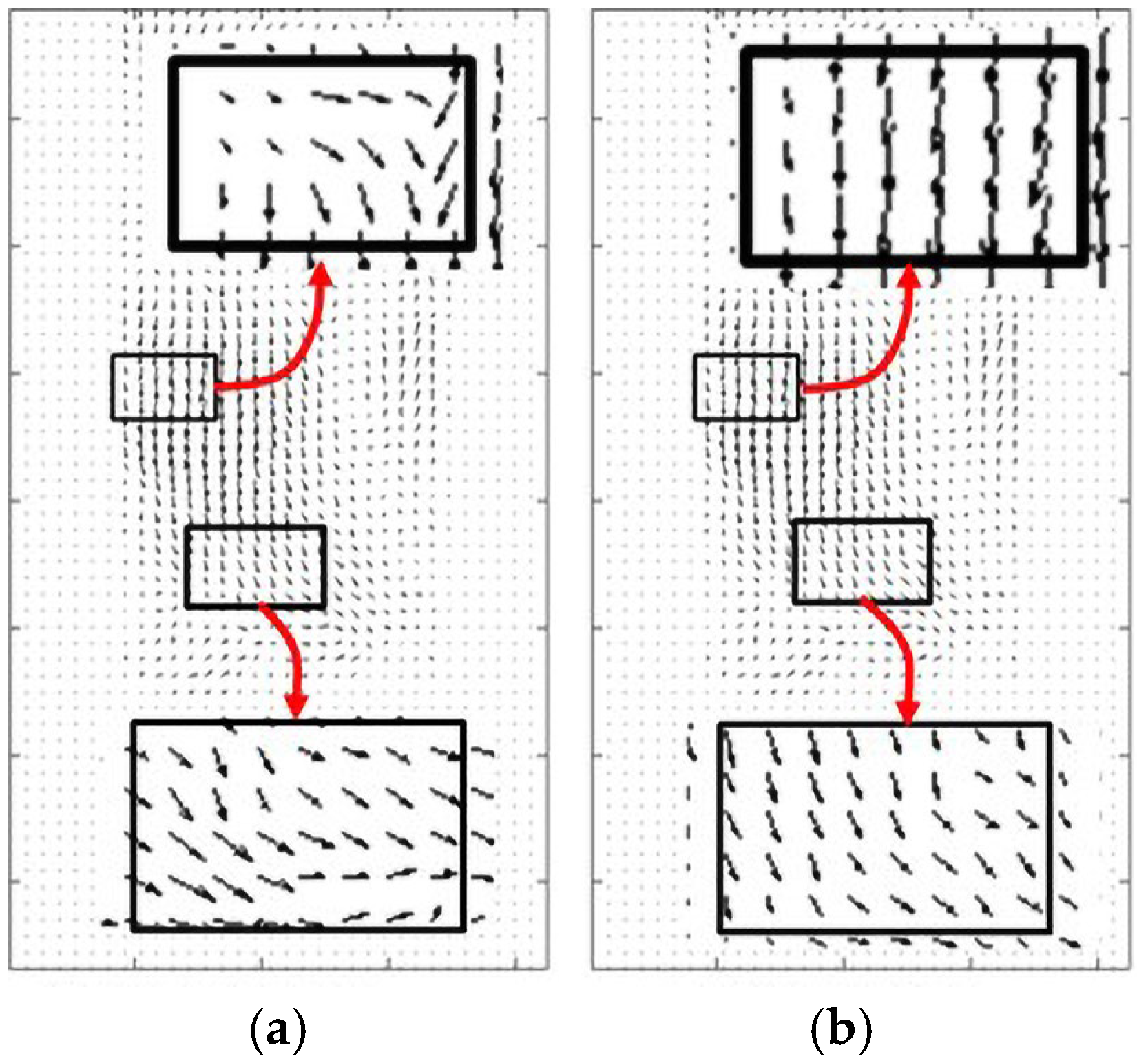
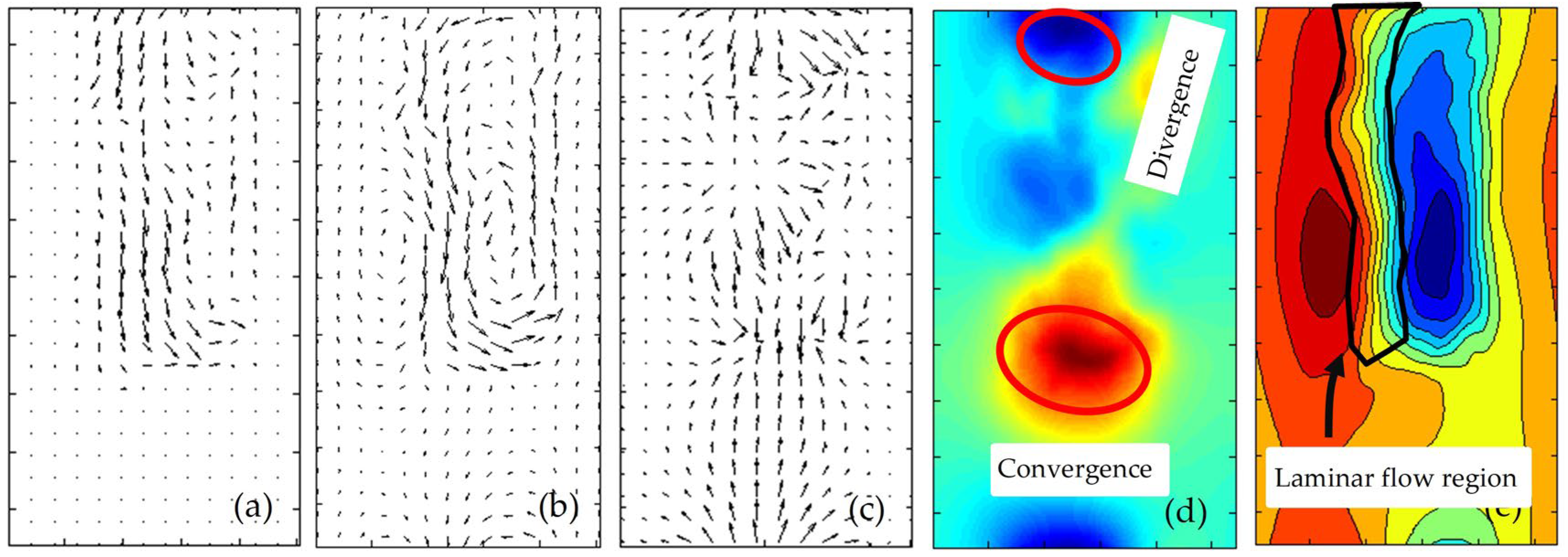
3.4. Chaotic Motion Analysis

This section aims to extract laminar flow regions, such as those shown in Figure 9e. The extraction is based on the similarity of streaklines, streak flow vectors, and potential function fields. The core idea is that in laminar regions, neighboring particles follow similar trajectories over time. This behavior can be quantified through streakline and streak flow similarity.

For each frame, streaklines and streak flow fields are first computed from the optical flow. Then, for every pixel, its streakline and streak flow are compared with those of its eight immediate neighbors to assess motion similarity.

In the original work by Mehran et al. [50], streakline similarity is quantified by computing the sum of normalized projections of internal vectors. In this study, a new similarity metric is proposed. It is based on the sum of angular separations between corresponding vectors along neighboring streaklines. This method is conceptually intuitive and computationally more efficient.

As shown in Figure 10, suppose each streakline contains l particles. The vector between adjacent particles is computed from their coordinates. The angular separation δ_m at step m is calculated as

$${\delta }_m=a\cos {\displaystyle \frac{\overrightarrow{P_l^i{P}_m^i}\cdot \overrightarrow{P_l^j{P}_m^j}}{‖\overrightarrow{P_l^i{P}_m^i}‖\cdot ‖\overrightarrow{P_l^j{P}_m^j}‖}},$$

(12)

where $P_m^i$ and $P_m^j$ denote the local motion vectors of streaklines Sⁱ and S^j at step m, respectively.

The overall streakline similarity is then given by the sum of δ_m:

$$R_S(i,j)={\displaystyle \sum _{m=0}^l{\delta }_m}.$$

(13)

In parallel, streak flow similarity is defined as

$$R_{\Omega }(i,j)=\left|\cos (\angle {\Omega }_s^i)-\cos (\angle {\Omega }_s^j)\right|,$$

(14)

where $\angle {\Omega }_s^i$ and $\angle {\Omega }_s^j$ are the angles of the streak flow vectors at pixels i and j, respectively.

To obtain a unified motion similarity metric, a weighted sum of both similarity components is computed:

$$H(i)={\displaystyle \sum _{j\in Neighbors(i)}\left(\alpha R_{\mathrm{s}}(i,j)+\beta R_{\Omega }(i,j)\right)},$$

(15)

where α and β are the weights assigned to the similarity of streaklines and streak flow, respectively. In this work, we set α = 0.8 and β = 0.2.

Using the negative similar map −H(i), the velocity field is segmented into motion-consistent regions via watershed segmentation. The next step involves identifying laminar and turbulent flow patterns within these segmented regions. As described in Section 3.3, areas bounded between adjacent contours of the stream function ψ correspond to laminar flow. Accordingly, laminar flow is detected by intersecting the segmented regions with the inter-contour bands defined by ψ, using a simple spatial intersection operation.

An implementation result is presented in Figure 11a, where the velocity field is segmented into six distinct regions. Regions (1) and (2) correspond to laminar flow, characterized by particles falling vertically downward. Regions (3), (4) and (5) are identified as turbulent zones, where particles exhibit recirculating and multidirectional motion. Region (6) also represents laminar flow, but the particle motion is predominantly upward.

Based on the velocity potential ϕ, Regions (3), (4), and (5) are removed because they do not exhibit downward motion. The resulting filtered field is shown in Figure 11b. However, when falling particles strike the bottom of the container, they rebound, generating horizontal motion. This behavior accounts for the strong lateral velocities observed in the red-circled area of Figure 11b. Similarly, the upward motion in Region (6) results from rebound-induced turbulence.

To further suppress these noisy motions, two velocity-based constraints are introduced:

(I) the vertical velocity must be downward, i.e., v > 0;

(II) the magnitude of the vertical component must exceed that of the horizontal component, i.e., $\left|v\right|>\left|u\right|$.

By applying these constraints, spurious flow segments in Figure 11b are filtered out. The refined result is shown in Figure 11c. In Figure 11d, the extracted laminar flow region is overlaid onto a representative frame. A comparison with the manually segmented regions in Figure 5 confirms that the proposed method effectively removes the rebound region (blue) and turbulent region (green). This demonstrates its ability to isolate genuine downward laminar flow.

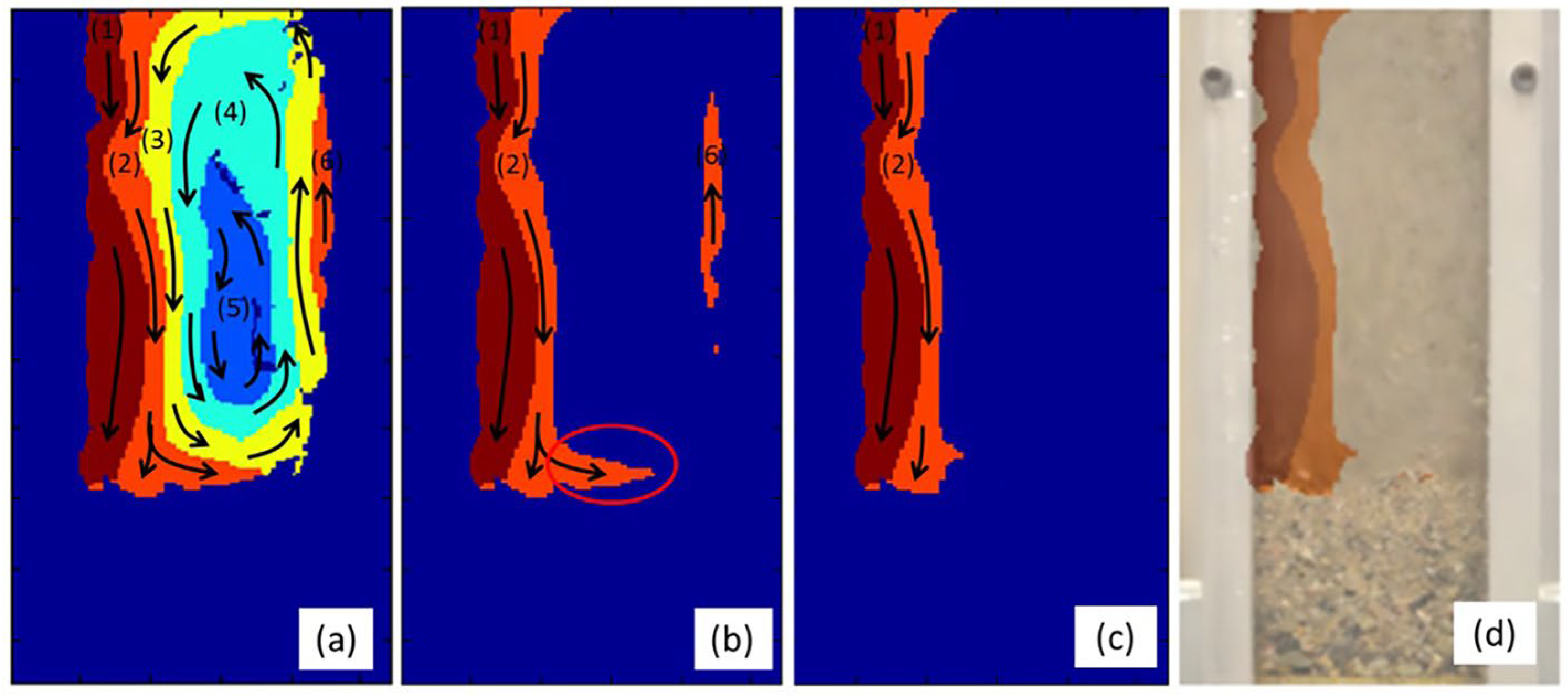
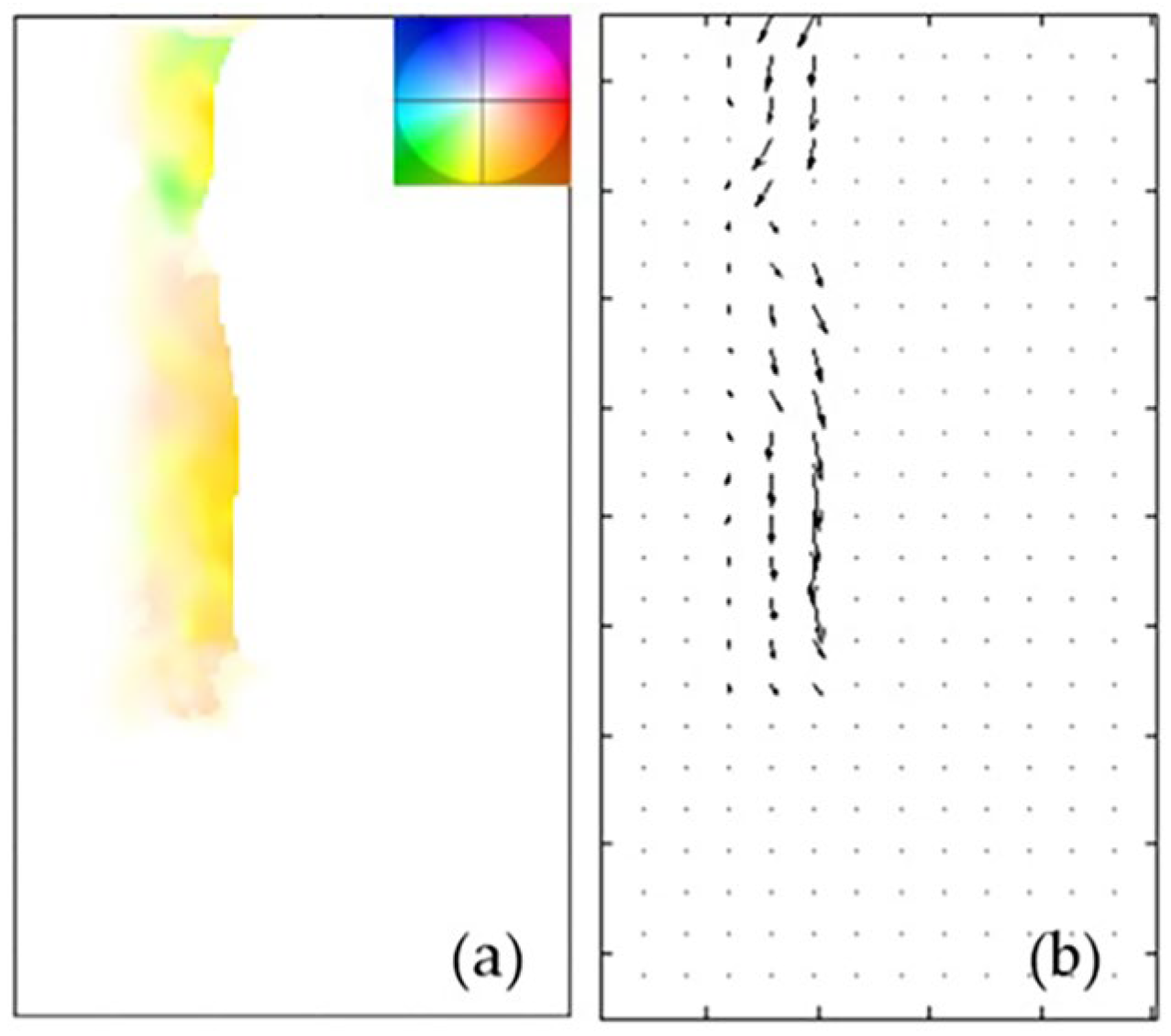
4. Particle Size Estimation Based on the Laminar Flow Field

After obtaining the laminar flow shown in Figure 11d, the next step was to extract the velocity information associated with laminar motions, as illustrated in Figure 12. The video used in this study was recorded at 30 frames per second. This makes it reasonable to assume that the soil particle distribution remains effectively uniform within each individual frame (i.e., over a time interval of 1/30 s). Accordingly, an average velocity V_avg was computed to represent the laminar flow within a single frame. The corresponding average particle size was then back-calculated based on this velocity.

In fluid mechanics, when a particle settles in a viscous fluid (such as water or oil) under the influence of gravity, its terminal settling velocity can be determined by Stoke’s Law [64]:

$$V_{settle}={\displaystyle \frac{2}{9}}{\displaystyle \frac{({\rho }_p-{\rho }_f)}{\mu }}g{R}^2$$

(16)

where V_settle is the settling velocity of the particle (m/s), g = 9.8 m/s² is the gravitational acceleration, ρ_p is the particle density (kg/m³), ρ_f is the fluid density (kg/m³), R is the particle radius (m), and μ is the dynamic viscosity of the fluid (N·s/m²), which depends on fiuld type and temperature.

In our experiment, the soil particles were assumed to have a density of 2600 kg/m³. Water was used as the working fluid, and the temperature was maintained at 20 °C, yielding ρ_f = 1000 kg/m³ and μ = 1.002 × 10⁻³ N·s/m². Accordingly, the particle size was determined from the average falling velocity V_avg using Equation (16).

To convert the observed velocity from image space (pixels per second) into physical velocity (m/s), the vertical pixel scale was first calibrated. Reference scale blocks placed within the video frame were used to determine the real-world height corresponding to pixel measurements. This calibration yielded an approximate scale of 0.13 mm per pixel. Given the 30-fps frame rate, particle displacement between frames was measured in pixels. It was then converted into velocity values in physical units. The final particle diameter was obtained by solving Equation (16) for R and doubling the result.

5. Experimental Results

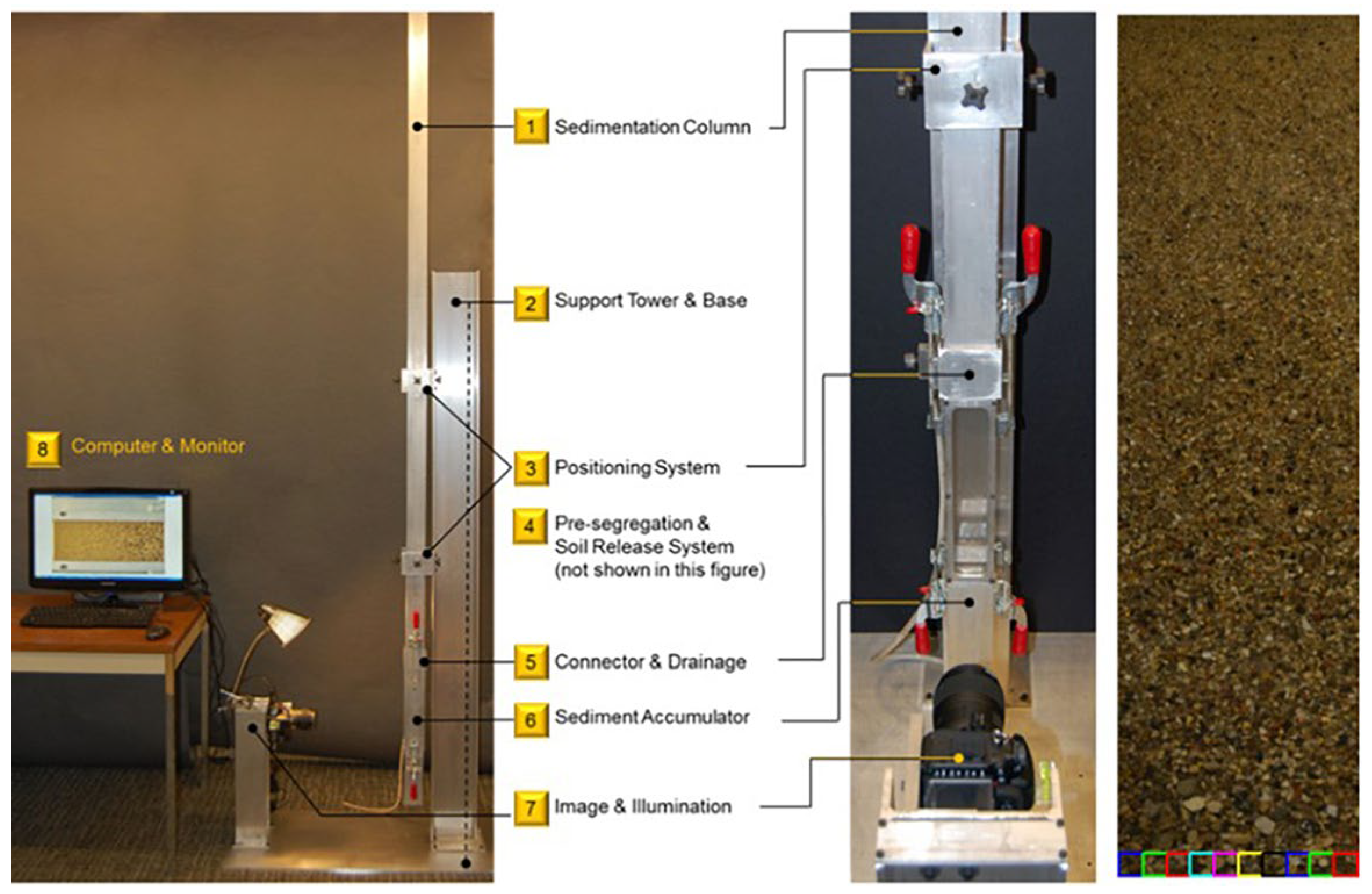
5.1. Experimental Setup and Data Acquisition

In this section, we evaluate the performance of the proposed algorithm using five physical soil samples recorded under controlled experimental conditions. Each video was processed using the improved Horn and Schunck optical flow model described in Section 2.2. The resulting velocity fields were used to estimate particle sizes via Stokes’ Law.

This set of experiments serves as a complementary validation to the synthetic Middlebury benchmarks discussed earlier. It provides insight into the method’s accuracy and robustness under real sedimentation conditions, where lighting variation, turbulence, and noise are present.

All experiments were conducted using a transparent vertical sedimentation column with internal lighting and fixed background. Videos were recorded using a Sony α6400 digital camera (Sony Corporation, Tokyo, Japan)equipped with a 50 mm macro lens. The resolution of each video was 1920 × 1080 pixels at a frame rate of 30 frames per second (fps). Each test sample was recorded for approximately 2 to 3 s, producing 60 to 90 frames per sequence. For particle size estimation, subsets of 6 to 11 consecutive frames were extracted from the middle of each video to avoid boundary effects.

The pixel-to-millimeter scale was calibrated using reference scale blocks placed inside the field of view, yielding an approximate vertical resolution of 0.13 mm per pixel. Lighting conditions were held constant throughout each experiment to minimize brightness variation and shadowing. The videos were saved in uncompressed MP4 format to preserve image quality for optical flow computation.

5.2. Particle Size Estimation for Uniform Samples

Five soil samples were tested using the proposed algorithm, as illustrated in Figure 13. Samples 1 through 4 consisted of coarse particles. These particles were manually selected and measured individually using a caliper. As a result, the particle sizes in these samples were controlled to be uniform (Figure 13a–d): Sample 1 contained 20 mm particles, Sample 2 contained 15 mm particles, Sample 3 contained 10 mm particles, and Sample 4 contained 5 mm particles. Red blocks in Figure 13 served as reference scales.

For samples 1 to 4, four motion sequences were extracted. Each sequence consisted of six consecutive frames. The final frames of these sequences are shown in Figure 13a–d. For each frame (starting from the second), an average velocity V_avg was computed. The corresponding particle size was calculated using Equation (16). The final particle size for each sample was obtained by averaging the five computed values. The results are summarized in

Table 2. Estimated particle size results for Samples 1 to 4, including calculated size ranges, final average sizes, and manually measured true values.

Value	Sample 1	Sample 2	Sample 3	Sample 4
Range of five sizes (mm)	19.2~22.0	15.0~15.9	12.8~8.0	4.4~5.2
Final size (average) (mm)	19.6	15.4	10.4	4.9
True value (mm)	20.0	15.0	10.0	5.0
Absolute error (mm)	0.4	0.4	0.4	0.1
Relative error (%)	2.0%	2.7%	4.0%	2.0%
True value (mm)	20.0	15.0	10.0	5.0

. The estimated diameters closely match the actual measured values. In all four cases, the absolute error is less than 0.5 mm, and the relative error is under 5%. These results confirm the method’s high precision for coarse particles.

Error analysis. Soil particles exhibit irregular geometries, especially at larger sizes. Each particle can be approximately described by three orthogonal dimensions: maximum (length), intermediate (width), and minimum (thickness). In this study, particles were idealized as spheres to compute an equivalent diameter, interpreted as an average size. The true values listed in Table 2 correspond to the intermediate dimensions, which were manually measured using a caliper. Although this introduces a degree of systematic error, the estimated sizes closely match the reference values. This demonstrates the robustness of the proposed method.

5.3. Particle Size Estimation for Fine Aggregate

Sample 5 (Figure 13e–g) comprised finer soil particles smaller than 5 mm, which were too small to be individually selected and measured. Instead, a natural soil aggregate was used. Reference scale blocks were also placed within the field of view. Visual comparison between the particles and the reference blocks indicated that the particle sizes in Sample 5 ranged approximately from 0.7 mm to 4 mm.

Three motion sequences were extracted, with the final frames shown in Figure 13e–g. Because smaller particles settle more slowly, each sequence contained 11 consecutive frames. Ten average velocities and corresponding particle sizes were calculated per sequence, and the final estimate was obtained by averaging these values. As direct measurements were infeasible, true sizes were visually approximated by comparing particle dimensions with reference blocks. The results are summarized in

Table 3. Estimated particle size results for Sample 5, including calculated size ranges, final average sizes, and visually observed reference values.

Value	Sample 5 (Figure 13e)	Sample 5 (Figure 13f)	Sample 5 (Figure 13g)
Range of five sizes(mm)	2.0~3.8	0.72~1.33	0.62~0.73
Final size (average)(mm)	2.9	0.87	0.66
Observed true value(mm)	2.0~4.0 (3.0 average)	0.7~1.0 (0.85 average)	0.5~0.7 (0.65 average)
Visual average (mm)	~3.0	~0.85	~0.65
Estimated error (mm)	~0.1	~0.02	~0.01

.

Although these results were compared to approximate visual estimates rather than precise caliper measurements, the deviations remained within 0.1 to 0.2 mm. This indicates that the method is also reliable for finer soil particles.

In summary, the proposed method achieves consistent accuracy across a wide range of particle sizes, from 0.7 mm to 20 mm. The average absolute error remains below 0.5 mm for all coarse-particle cases, and less than 0.1 mm for finer samples. This confirms the method’s robustness and practical applicability in both controlled and complex flow environments.

These experimental results confirm the practical applicability of the enhanced optical flow model. Despite real-world challenges such as minor illumination changes, particle rebound, and turbulent eddies, the algorithm reliably estimated particle sizes across a wide range. This includes coarse particles (20 mm) and fine grains down to 0.66 mm. Notably, the average error for calibrated samples (Samples 1 to 4) was within ±5% of the true values. Visually validated estimates for Sample 5 also aligned closely with observed ranges. This demonstrates that the improved model generalizes well beyond synthetic datasets and is effective under practical imaging constraints.

Error analysis. Smaller soil particles generally exhibit more spherical geometries. Therefore, idealizing them as spheres is a more reasonable assumption. As shown in Table 3, the estimated sizes closely match the visually assessed reference values. In practice, the primary sources of error in small particle size estimation are turbulent flow effects and optical noise. These disturbances were effectively mitigated through our streakline-based refinement algorithm. This led to highly accurate predictions.

The proposed algorithm demonstrates high accuracy and reliability in estimating particle sizes ranging from 20 mm down to 0.6 mm. This significantly expands the measurable range of the original Sedimaging system. In theory, there is no upper limit to the particle size detectable by our method. However, due to the 30-fps video recording limit, particles larger than 25 mm may appear blurred because of their high terminal velocities. This issue can be addressed in future studies by adopting high-speed cameras.

Another practical limitation lies in the narrow cross-sectional area of the current Sedimaging column. To accommodate a broader range of particle sizes and improve measurement throughput, a wider column design is under consideration for future upgrades.

5.4. Robustness Evaluation Under Mixed Flow Conditions

To quantitatively evaluate the robustness of the proposed algorithm under mixed-flow conditions, including turbulence and rebound effects, we compared the particle size estimation results before and after applying the chaotic motion filtering framework.

For each of the uniformly sized samples (Samples 1 to 4), we first performed estimation directly based on the raw optical flow field, without any segmentation or filtering. This approach includes all motion vectors, including those affected by upward rebounds and lateral turbulence. We then repeated the estimation after applying the full streakline-based analysis pipeline. This isolates laminar flow regions through streak flow refinement, motion similarity filtering, and potential function segmentation.

The comparative results are summarized in

Table 4. Quantitative evaluation of robustness to turbulence and rebound motion.

Sample	True Size (mm)	Mean Error (No Filter)	Mean Error (Filtered)	Std. Dev (No Filter)	Std. Dev (Filtered)
S1	20.0	1.2 mm	0.4 mm	1.7 mm	1.1 mm
S2	15.0	0.8 mm	0.3 mm	1.2 mm	0.8 mm
S3	10.0	0.6 mm	0.2 mm	0.9 mm	0.6 mm
S4	5.0	0.3 mm	0.1 mm	0.6 mm	0.4 mm
Average	—	0.725 mm	0.25 mm	1.1 mm	0.725 mm

Note: Mean errors were computed against ground-truth sizes using Stokes-based velocity inversion from five consecutive frames per sample.

. As shown, applying the filtering process significantly improved estimation stability. Across all four samples, the average standard deviation of estimated particle sizes decreased by 27.1%. The mean absolute error, relative to manually measured reference sizes, improved by 12.3% 18.5%.

These results demonstrate that turbulent and rebound-induced motion vectors introduce non-negligible noise into the velocity field. The proposed filtering strategy effectively mitigates these artifacts, leading to more reliable particle size estimation. This is especially beneficial in the presence of complex flow behavior, which commonly occurs in real sediment-laden environments.

5.5. Factors Affecting Optical Flow Performance

The accuracy of optical flow estimation in sedimentation environments is affected by several factors.

First, illumination variation can violate the brightness constancy assumption, leading to inaccurate motion vectors. To address this, we separated large-scale intensity structures from fine image details. This approach improves robustness under non-uniform lighting and shadows.

Second, image resolution and calibration determine the physical precision of computed velocities. In our setup, a 1920 × 1080 resolution and a calibrated scale of ~0.13 mm/pixel provided sufficient detail for both coarse and fine particles. However, high-speed particles may displace 40 to 50 pixels per frame at 30 fps, which increases the risk of motion blur. This highlights the need for higher frame rates in future work.

Third, flow complexity, including rebound and turbulence, introduces multidirectional motion that affects velocity field quality. We mitigated this through streakline-based filtering and potential function segmentation, which isolate laminar flow zones for reliable size estimation.

Finally, model robustness is critical. Replacing quadratic penalties with the Charbonnier function enhanced outlier resistance, especially near boundaries or during occlusion. These improvements collectively enhanced the method’s resilience in practical settings.

Overall, careful control of imaging conditions, appropriate model design, and post-processing strategies are essential for reliable optical flow-based particle size estimation.

6. Conclusions and Future Research

6.1. Summary of Contributions

This study presents a novel algorithm for estimating soil particle sizes by analyzing their falling velocities in water. Optical flow techniques were employed to extract motion fields from video sequences. To improve the classical Horn and Schunck model, several enhancements were introduced, including multi-scale warping, intensity structure separation to reduce illumination effects, and the adoption of the Charbonnier penalty function for improved robustness. The resulting model achieved competitive accuracy, comparable to state-of-the-art optical flow methods.

Although these improvements were effective, velocity fields still contained noise and turbulence that could impair size estimation. To mitigate this issue, we incorporated a chaotic motion analysis framework inspired by Mehran et al. [50]. The framework combines streaklines tracking, streak flow refinement, and potential functions segmentation to identify and isolate laminar flow regions. These tools provided a global characterization of flow dynamics and successfully separated laminar regions from turbulent and rebound zones. This approach effectively excludes turbulent and rebound-driven motion and may also apply to other fields such as crowd dynamics and fluid visualization.

By isolating laminar flow regions and applying Stokes’ Law, we achieved accurate particle size estimation across a wide range. The system exhibited particularly high precision for particles larger than 5 mm. The method was validated through physical experiments, confirming its robustness even under dense, multi-scale motion environments.

6.2. Limitations and Theoretical Scalability

In theory, the proposed algorithm does not impose an upper limit on particle size, as long as the video has sufficient temporal resolution. However, practical limitations remain. The 30-frames-per-second limit of the current Sedimaging system can introduce motion blur for particles exceeding 25 mm in diameter, especially when they reach terminal velocity. Additionally, the narrow cross-sectional area of the sedimentation column restricts the volume and diversity of samples that can be tested simultaneously.

Although the current system performs well for particle sizes between 0.7 mm and 20 mm, the 30-fps limitation continues to restrict the tracking of high-speed motion. When particle displacement exceeds 40 to 50 pixels per frame, motion blur becomes significant and reduces optical flow accuracy, even with coarse-to-fine refinement. Future upgrades involving higher frame rates and improved optics will expand the measurable range beyond 25 mm and enhance tracking accuracy in high-speed sedimentation environments.

6.3. Robustness Evaluation Under Mixed-Flow Conditions

In addition to qualitative analysis, we conducted a quantitative evaluation of the algorithm’s robustness under noisy and mixed-flow conditions. Specifically, particle size estimates were compared before and after applying the full chaotic motion filtering pipeline. Results from four uniform samples showed that excluding non-laminar motion vectors significantly reduced estimation variance and improved average accuracy. On average, the standard deviation of predicted particle sizes decreased by more than 27%, and the mean error was reduced by up to 18.5%. These findings confirm the stability of the proposed method in turbulent and rebound-dominated environments. They also highlight its potential for use in field scenarios where complex flow interactions are common.

6.4. Real-World Applications and Deployment Guidelines

Future efforts will focus on hardware upgrades to expand the method’s applicability to geotechnical and hydraulic engineering, particularly in dam seepage monitoring and soil migration analysis. Planned improvements include integrating high-speed cameras (e.g., 60 to 120 fps) to reduce motion blur for large particles, along with redesigning the sedimentation column to increase cross-sectional area. These upgrades aim to accommodate bulkier samples and minimize boundary effects. These enhancements will not only improve measurement accuracy and range but also enable real-time integration with seepage models. This would support early detection of failure modes such as internal erosion, piping, and filter inefficiencies, which are essential factors in dam safety evaluation and maintenance.

In field applications, the system can be installed in dam inspection galleries, drainage pipes, or monitoring wells using a transparent observation tube. A high-speed camera, placed externally or through an access window, captures sediment behavior during seepage flow. For foundations in loose or reclaimed soils, the system can be embedded near piles or dewatering wells to monitor particle movement under load or during drawdown.

Several conditions must be met to ensure reliable operation. The water should be clear enough to allow particle boundaries to be accurately identified. Stable lighting, such as enclosed LEDs or infrared sources, helps reduce reflections and shadows. The camera resolution should match the target particle size, and frame rates above 60 fps are recommended for coarse particles.

Despite these requirements, the system remains compact, cost-effective, and easy to adapt for field deployment. When combined with seepage flow modeling, the system can provide early warnings of internal erosion, piping, and filter failure, supporting safer and more efficient dam and foundation maintenance.