From Density to Efficiency: Exploring Urban Building Use Efficiency in 35 Large Chinese Cities
Abstract
1. Introduction
2. Data Collection and Research Methodology
2.1. Study Area
2.2. Data Preprocessing
2.2.1. Data Sources
2.2.2. Identification of UBUE
2.3. The Power Function and Linear Function Fitting
2.4. Scale-Adjusted Metropolitan Indicator (SAMI)
3. Results
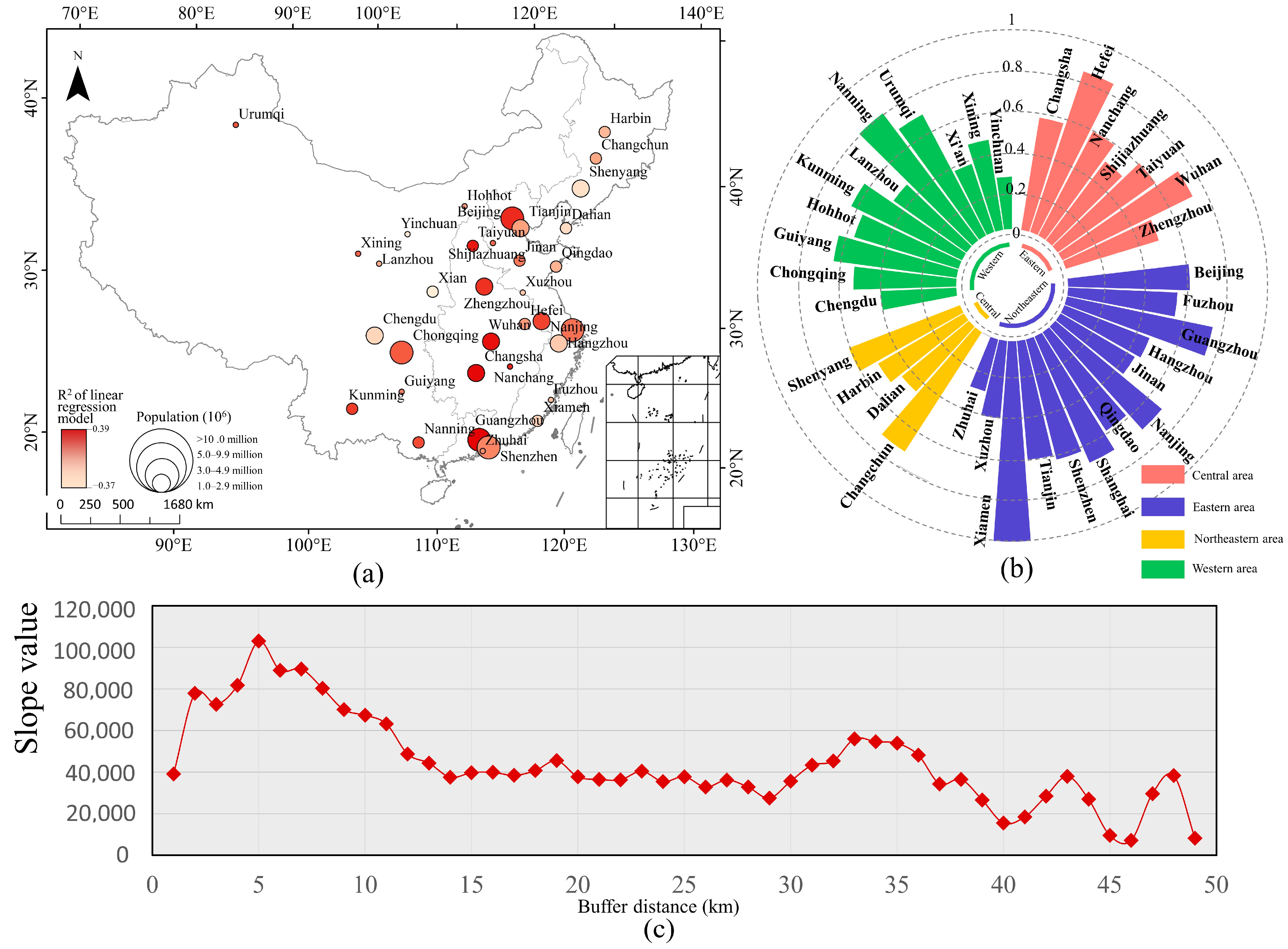
3.1. The Distribution of UBUE
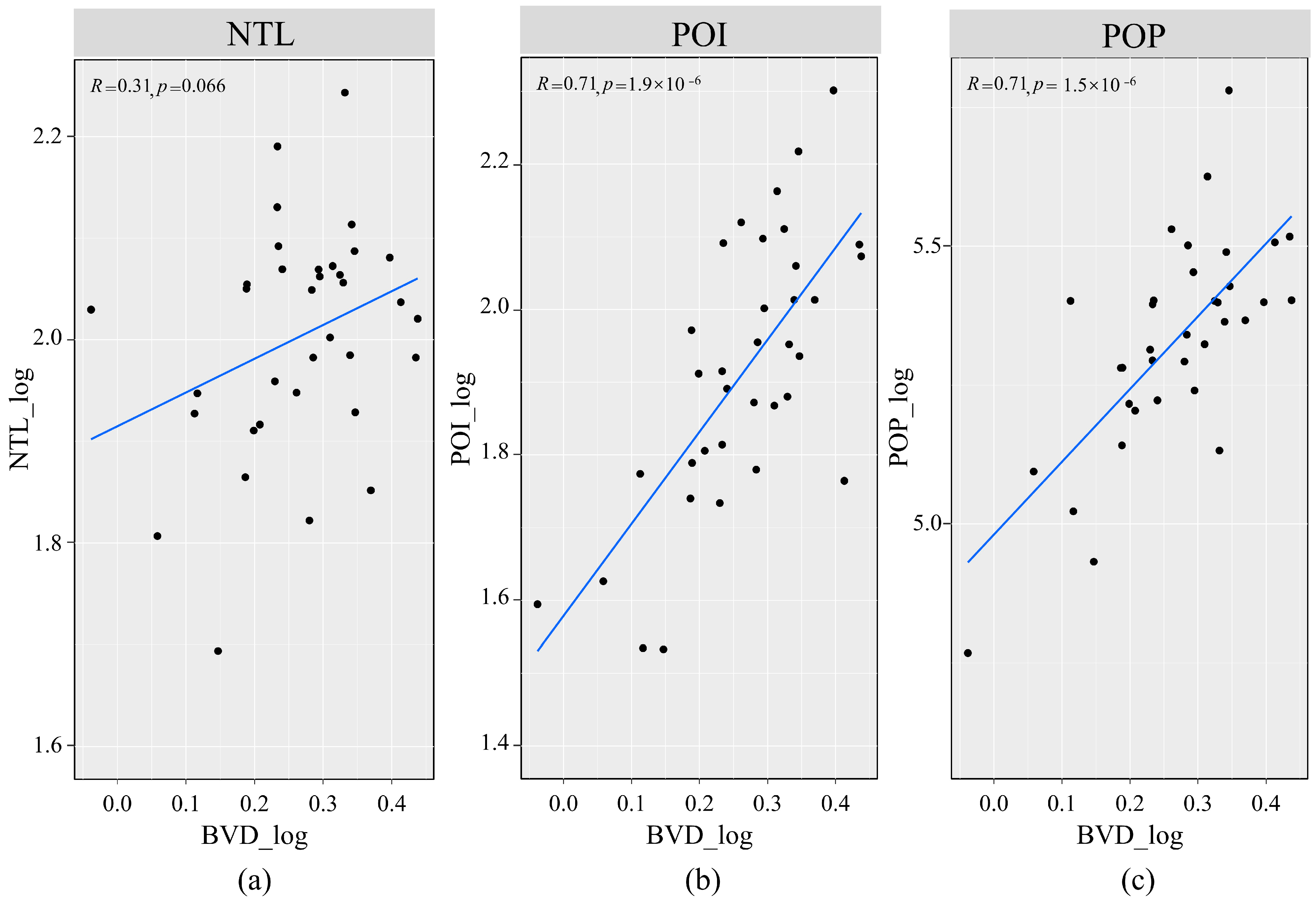
3.2. The Relationship Between UFI and BVD
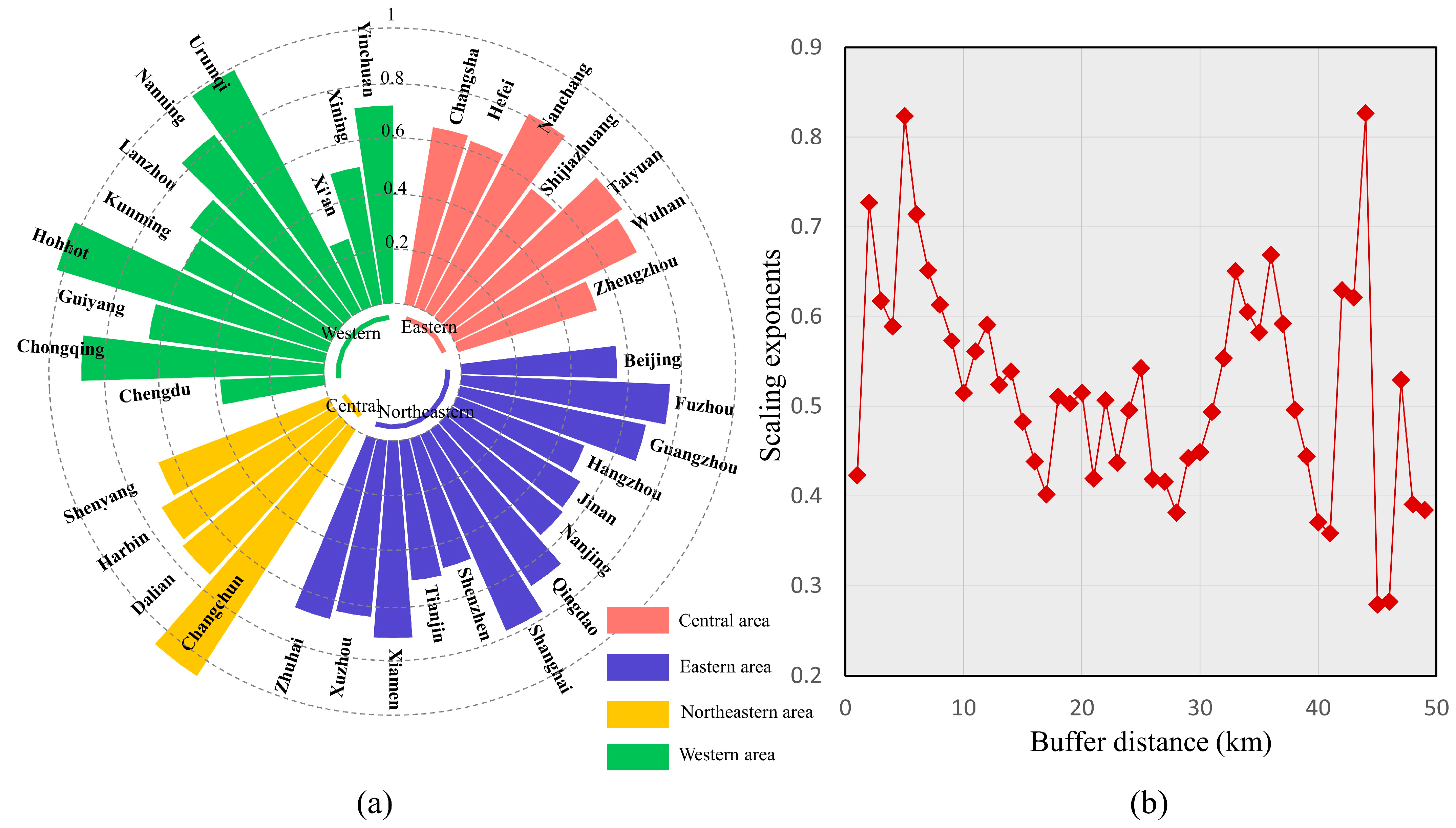
3.3. Spatial Heterogeneity of Scaling Exponents
4. Discussion
4.1. Theoretical Understanding of UBUE Spatial Variation
4.2. Implication for Land Development Rights at the National Scale
4.3. Urban Growth Strategies at the Urban Scale
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UBUE | Urban building use efficiency |
| BVD | Building volume density |
| UFI | Urban function intensity |
| POI | Point of interest |
| NTL | Nighttime light |
References
- Zhao, P. Managing Urban Growth in a Transforming China: Evidence from Beijing. Land. Use Policy 2011, 28, 96–109. [Google Scholar] [CrossRef]
- Li, J.; Li, C.; Zhu, F.; Song, C.; Wu, J. Spatiotemporal Pattern of Urbanization in Shanghai, China between 1989 and 2005. Landsc. Ecol. 2013, 28, 1545–1565. [Google Scholar] [CrossRef]
- Huq, S.; Kovats, S.; Reid, H.; Satterthwaite, D. Reducing Risks to Cities from Disasters and Climate Change. Environ. Urban. 2007, 19, 3–15. [Google Scholar] [CrossRef]
- Liu, Z.; He, C.; Zhou, Y.; Wu, J. How Much of the World’s Land Has Been Urbanized, Really? A Hierarchical Framework for Avoiding Confusion. Landsc. Ecol. 2014, 29, 763–771. [Google Scholar] [CrossRef]
- Klotz, M.; Kemper, T.; Geiß, C.; Esch, T.; Taubenböck, H. How Good Is the Map? A Multi-Scale Cross-Comparison Framework for Global Settlement Layers: Evidence from Central Europe. Remote Sens. Env. 2016, 178, 191–212. [Google Scholar] [CrossRef]
- Laroche, P.C.S.J.; Schulp, C.J.E.; Kastner, T.; Verburg, P.H. Telecoupled Environmental Impacts of Current and Alternative Western Diets. Glob. Environ. Change 2020, 62, 102066. [Google Scholar] [CrossRef]
- Gao, J.; O’Neill, B.C. Mapping Global Urban Land for the 21st Century with Data-Driven Simulations and Shared Socioeconomic Pathways. Nat. Commun. 2020, 11, 2302. [Google Scholar] [CrossRef] [PubMed]
- Assembly, G. Resolution Adopted by the General Assembly on 11 September 2015; United Nations: New York, NY, USA, 2015. [Google Scholar]
- Gao, J.; Chen, W.; Yuan, F. Spatial Restructuring and the Logic of Industrial Land Redevelopment in Urban China: I. Theoretical Considerations. Land. Use Policy 2017, 68, 604–613. [Google Scholar] [CrossRef]
- Lin, J.; Wan, H.; Cui, Y. Analyzing the Spatial Factors Related to the Distributions of Building Heights in Urban Areas: A Comparative Case Study in Guangzhou and Shenzhen. Sustain. Cities Soc. 2020, 52, 101854. [Google Scholar] [CrossRef]
- Mahtta, R.; Mahendra, A.; Seto, K.C. Building up or Spreading out? Typologies of Urban Growth across 478 Cities of 1 Million+. Environ. Res. Lett. 2019, 14, 124077. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhou, W.; Wang, J.; Hu, X.; Qian, Y. Sixty-Year Changes in Residential Landscapes in Beijing: A Perspective from Both the Horizontal (2D) and Vertical (3D) Dimensions. Remote Sens. 2017, 9, 992. [Google Scholar] [CrossRef]
- Shen, L.; Shu, T.; Liao, X.; Yang, N.; Ren, Y.; Zhu, M.; Cheng, G.; Wang, J. A New Method to Evaluate Urban Resources Environment Carrying Capacity from the Load-and-Carrier Perspective. Resour. Conserv. Recycl. 2020, 154, 104616. [Google Scholar] [CrossRef]
- Huang, Z.; He, C.; Zhu, S. Do China’s Economic Development Zones Improve Land Use Efficiency? The Effects of Selection, Factor Accumulation and Agglomeration. Landsc. Urban. Plan. 2017, 162, 145–156. [Google Scholar] [CrossRef]
- Du, J.; Thill, J.-C.; Peiser, R.B. Land Pricing and Its Impact on Land Use Efficiency in Post-Land-Reform China: A Case Study of Beijing. Cities 2016, 50, 68–74. [Google Scholar] [CrossRef]
- Huang, Z.; Bao, Y.; Mao, R.; Wang, H.; Yin, G.; Wan, L.; Qi, H.; Li, Q.; Tang, H.; Liu, Q. Big Geodata Reveals Spatial Patterns of Built Environment Stocks across and within Cities in China. Engineering 2024, 34, 143–153. [Google Scholar] [CrossRef]
- Banister, D.; Watson, S.; Wood, C. Sustainable Cities: Transport, Energy, and Urban Form. Environ. Plann B Plann Des. 1997, 24, 125–143. [Google Scholar] [CrossRef]
- Katsavounidou, G. Life between Buildings: Using Public Space: The History of Jan Gehl’s Book and the Legacy of Its Philosophy for Designing Cities at Human Scale. In The Future of Central Urban Areas: Sustainable Planning and Design Perspectives from Thessaloniki, Greece; Institutionelles Repositorium der Leibniz Universität Hannover: Hanover, Germany, 2023; pp. 21–37. [Google Scholar]
- Jane, J. The Life and Death of Great American Cities; Random House: New York, NY, USA, 1961. [Google Scholar]
- Zhong, C.; Schläpfer, M.; Müller Arisona, S.; Batty, M.; Ratti, C.; Schmitt, G. Revealing Centrality in the Spatial Structure of Cities from Human Activity Patterns. Urban. Stud. 2017, 54, 437–455. [Google Scholar] [CrossRef]
- Xia, C.; Yeh, A.G.; Zhang, A. Analyzing Spatial Relationships between Urban Land Use Intensity and Urban Vitality at Street Block Level: A Case Study of Five Chinese Megacities. Landsc. Urban. Plan. 2020, 193, 103669. [Google Scholar] [CrossRef]
- Ruan, L.; He, T.; Xiao, W.; Chen, W.; Lu, D.; Liu, S. Measuring the Coupling of Built-up Land Intensity and Use Efficiency: An Example of the Yangtze River Delta Urban Agglomeration. Sustain Cities Soc. 2022, 87, 104224. [Google Scholar] [CrossRef]
- Lee, J.H.; Lim, S. The Selection of Compact City Policy Instruments and Their Effects on Energy Consumption and Greenhouse Gas Emissions in the Transportation Sector: The Case of South Korea. Sustain. Cities Soc. 2018, 37, 116–124. [Google Scholar] [CrossRef]
- Kremer, P.; Haase, A.; Haase, D. The Future of Urban Sustainability: Smart, Efficient, Green or Just? Introduction to the Special Issue. Sustain. Cities Soc. 2019, 51, 101761. [Google Scholar] [CrossRef]
- Burger, M.; Meijers, E. Form Follows Function? Linking Morphological and Functional Polycentricity. Urban. Stud. 2012, 49, 1127–1149. [Google Scholar] [CrossRef]
- Chen, Z.; Tang, J.; Wan, J.; Chen, Y. Promotion Incentives for Local Officials and the Expansion of Urban Construction Land in China: Using the Yangtze River Delta as a Case Study. Land. Use Policy 2017, 63, 214–225. [Google Scholar] [CrossRef]
- Chen, K. Ghost Cities of China. The Story of Cities Without People in the World’s Most Populated Country. Eur.-Asia Stud. 2017, 69, 998–999. [Google Scholar] [CrossRef]
- Lin, J.; Lu, S.; He, X.; Wang, F. Analyzing the Impact of Three-Dimensional Building Structure on CO2 Emissions Based on Random Forest Regression. Energy 2021, 236, 121502. [Google Scholar] [CrossRef]
- Zitti, M.; Ferrara, C.; Perini, L.; Carlucci, M.; Salvati, L. Long-Term Urban Growth and Land Use Efficiency in Southern Europe: Implications for Sustainable Land Management. Sustainability 2015, 7, 3359–3385. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Xu, Y.; Zhou, P.; Yeh, C.-H. Evaluating Urban Land Use Efficiency with Interacting Criteria: An Empirical Study of Cities in Jiangsu China. Land. Use Policy 2020, 90, 104292. [Google Scholar] [CrossRef]
- Wu, C.; Wei, Y.D.; Huang, X.; Chen, B. Economic Transition, Spatial Development and Urban Land Use Efficiency in the Yangtze River Delta, China. Habitat. Int. 2017, 63, 67–78. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, B.; Wang, J.; Wu, Q.; Wei, Y.D. How Does Industrial Agglomeration Affect Urban Land Use Efficiency? A Spatial Analysis of Chinese Cities. Land. Use Policy 2022, 119, 106178. [Google Scholar] [CrossRef]
- Cui, X.; Wang, X. Urban Land Use Change and Its Effect on Social Metabolism: An Empirical Study in Shanghai. Habitat. Int. 2015, 49, 251–259. [Google Scholar] [CrossRef]
- Ye, Y.; Li, D.; Liu, X. How Block Density and Typology Affect Urban Vitality: An Exploratory Analysis in Shenzhen, China. Urban. Geogr. 2018, 39, 631–652. [Google Scholar] [CrossRef]
- Moroni, S. Urban Density after Jane Jacobs: The Crucial Role of Diversity and Emergence. City Territ. Archit. 2016, 3, 1–8. [Google Scholar] [CrossRef]
- Wang, Y.; Yue, X.; Li, C.; Wang, M.; Zhang, H.; Su, Y. Relationship between Urban Three-Dimensional Spatial Structure and Population Distribution: A Case Study of Kunming’s Main Urban District, China. Remote Sens. 2022, 14, 3757. [Google Scholar] [CrossRef]
- Pickett, S.T.A.; Cadenasso, M.L.; Childers, D.L.; Mcdonnell, M.J.; Zhou, W. Evolution and Future of Urban Ecological Science: Ecology in, of, and for the City. Ecosyst. Health Sustain. 2016, 2, e01229. [Google Scholar] [CrossRef]
- Xu, G.; Xiu, T.; Li, X.; Liang, X.; Jiao, L. Lockdown Induced Night-Time Light Dynamics during the COVID-19 Epidemic in Global Megacities. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102421. [Google Scholar] [CrossRef]
- Wu, B.; Yang, C.; Chen, Z.; Wu, Q.; Yu, S.; Wang, C.; Li, Q.; Wu, J.; Yu, B. The Relationship between Urban 2-D/3-D Landscape Pattern and Nighttime Light Intensity. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 15, 478–489. [Google Scholar] [CrossRef]
- Kuang, W.; Liu, J.; Dong, J.; Chi, W.; Zhang, C. The Rapid and Massive Urban and Industrial Land Expansions in China between 1990 and 2010: A CLUD-Based Analysis of Their Trajectories, Patterns, and Drivers. Landsc. Urban. Plan. 2016, 145, 21–33. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, Y.; Seto, K.C.; Stokes, E.C.; Deng, C.; Pickett, S.T.A.; Taubenböck, H. Understanding an Urbanizing Planet: Strategic Directions for Remote Sensing. Remote Sens. Environ. 2019, 228, 164–182. [Google Scholar] [CrossRef]
- Li, K.; Li, Y.; Yang, X.; Liu, X.; Huang, Q. Comparing the Three-Dimensional Morphologies of Urban Buildings along the Urban-Rural Gradients of 91 Cities in China. Cities 2023, 133, 104123. [Google Scholar] [CrossRef]
- Gong, P.; Li, X.; Wang, J.; Bai, Y.; Chen, B.; Hu, T.; Liu, X.; Xu, B.; Yang, J.; Zhang, W. Annual Maps of Global Artificial Impervious Area (GAIA) between 1985 and 2018. Remote Sens. Environ. 2020, 236, 111510. [Google Scholar] [CrossRef]
- Wu, W.-B.; Ma, J.; Banzhaf, E.; Meadows, M.E.; Yu, Z.-W.; Guo, F.-X.; Sengupta, D.; Cai, X.-X.; Zhao, B. A First Chinese Building Height Estimate at 10 m Resolution (CNBH-10 m) Using Multi-Source Earth Observations and Machine Learning. Remote Sens. Environ. 2023, 291, 113578. [Google Scholar] [CrossRef]
- Wu, L.; Gong, C.; Yan, X. Taylor’s Power Law and Its Decomposition in Urban Facilities. R. Soc. Open Sci. 2019, 6, 180770. [Google Scholar] [CrossRef]
- Xu, R.; Yue, W.; Wei, F.; Yang, G.; He, T.; Pan, K. Density Pattern of Functional Facilities and Its Responses to Urban Development, Especially in Polycentric Cities. Sustain. Cities Soc. 2021, 76, 103526. [Google Scholar] [CrossRef]
- Li, X.; Gong, P.; Zhou, Y.; Wang, J.; Bai, Y.; Chen, B.; Hu, T.; Xiao, Y.; Xu, B.; Yang, J. Mapping Global Urban Boundaries from the Global Artificial Impervious Area (GAIA) Data. Environ. Res. Lett. 2020, 15, 94044. [Google Scholar] [CrossRef]
- Tatem, A.J. WorldPop, Open Data for Spatial Demography. Sci. Data 2017, 4, 170004. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wei, Y.; Shi, K.; Zhao, Z.; Wang, C.; Wu, B.; Qiu, B.; Yu, B. The Potential of Nighttime Light Remote Sensing Data to Evaluate the Development of Digital Economy: A Case Study of China at the City Level. Comput. Environ. Urban. Syst. 2022, 92, 101749. [Google Scholar] [CrossRef]
- Jiao, L. Urban Land Density Function: A New Method to Characterize Urban Expansion. Landsc. Urban. Plan. 2015, 139, 26–39. [Google Scholar] [CrossRef]
- Tan, X.; Huang, B.; Batty, M.; Li, W.; Wang, Q.R.; Zhou, Y.; Gong, P. The Spatiotemporal Scaling Laws of Urban Population Dynamics. Nat. Commun. 2025, 16, 2881. [Google Scholar] [CrossRef]
- Barthelemy, M. The Statistical Physics of Cities. Nat. Rev. Phys. 2019, 1, 406–415. [Google Scholar] [CrossRef]
- Bettencourt, L.M.A. The Origins of Scaling in Cities. Science (1979) 2013, 340, 1438–1441. [Google Scholar] [CrossRef]
- Xu, G.; Zhu, M.; Chen, B.; Salem, M.; Xu, Z.; Li, X.; Jiao, L.; Gong, P. Settlement Scaling Law Reveals Population-Land Tensions in 7000 + African Urban Agglomerations. Habitat. Int. 2023, 142, 102954. [Google Scholar] [CrossRef]
- Lobo, J.; Bettencourt, L.M.A.; Smith, M.E.; Ortman, S. Settlement Scaling Theory: Bridging the Study of Ancient and Contemporary Urban Systems. Urban. Stud. 2020, 57, 731–747. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Z.; Xu, G.; Tian, Z. Built-up Land Efficiency in Urban China: Insights from the General Land Use Plan (2006–2020). Habitat. Int. 2016, 51, 31–38. [Google Scholar] [CrossRef]
- Alonso, W. Location and Land Use: Toward a General Theory of Land Rent; Harvard University Press: Cambridge, MA, USA, 1964; ISBN 0674729560. [Google Scholar]
- Li, M.; Verburg, P.H.; van Vliet, J. Global Trends and Local Variations in Land Take per Person. Landsc. Urban. Plan. 2022, 218, 104308. [Google Scholar] [CrossRef]
- Yan, S.; Peng, J.; Wu, Q. Exploring the Non-Linear Effects of City Size on Urban Industrial Land Use Efficiency: A Spatial Econometric Analysis of Cities in Eastern China. Land. Use Policy 2020, 99, 104944. [Google Scholar] [CrossRef]
- He, T.; Lu, Y.; Yue, W.; Xiao, W.; Shen, X.; Shan, Z. A New Approach to Peri-Urban Area Land Use Efficiency Identification Using Multi-Source Datasets: A Case Study in 36 Chinese Metropolitan Areas. Appl. Geogr. 2023, 150, 102826. [Google Scholar] [CrossRef]
- Hosseini, A.; Pourahmad, A.; Taeeb, A.; Amini, M.; Behvandi, S. Renewal Strategies and Neighborhood Participation on Urban Blight. Int. J. Sustain. Built Environ. 2017, 6, 113–121. [Google Scholar] [CrossRef]
- Ahmed, S.; Bramley, G. How Will Dhaka Grow Spatially in Future?-Modelling Its Urban Growth with a near-Future Planning Scenario Perspective. Int. J. Sustain. Built Environ. 2015, 4, 359–377. [Google Scholar] [CrossRef]
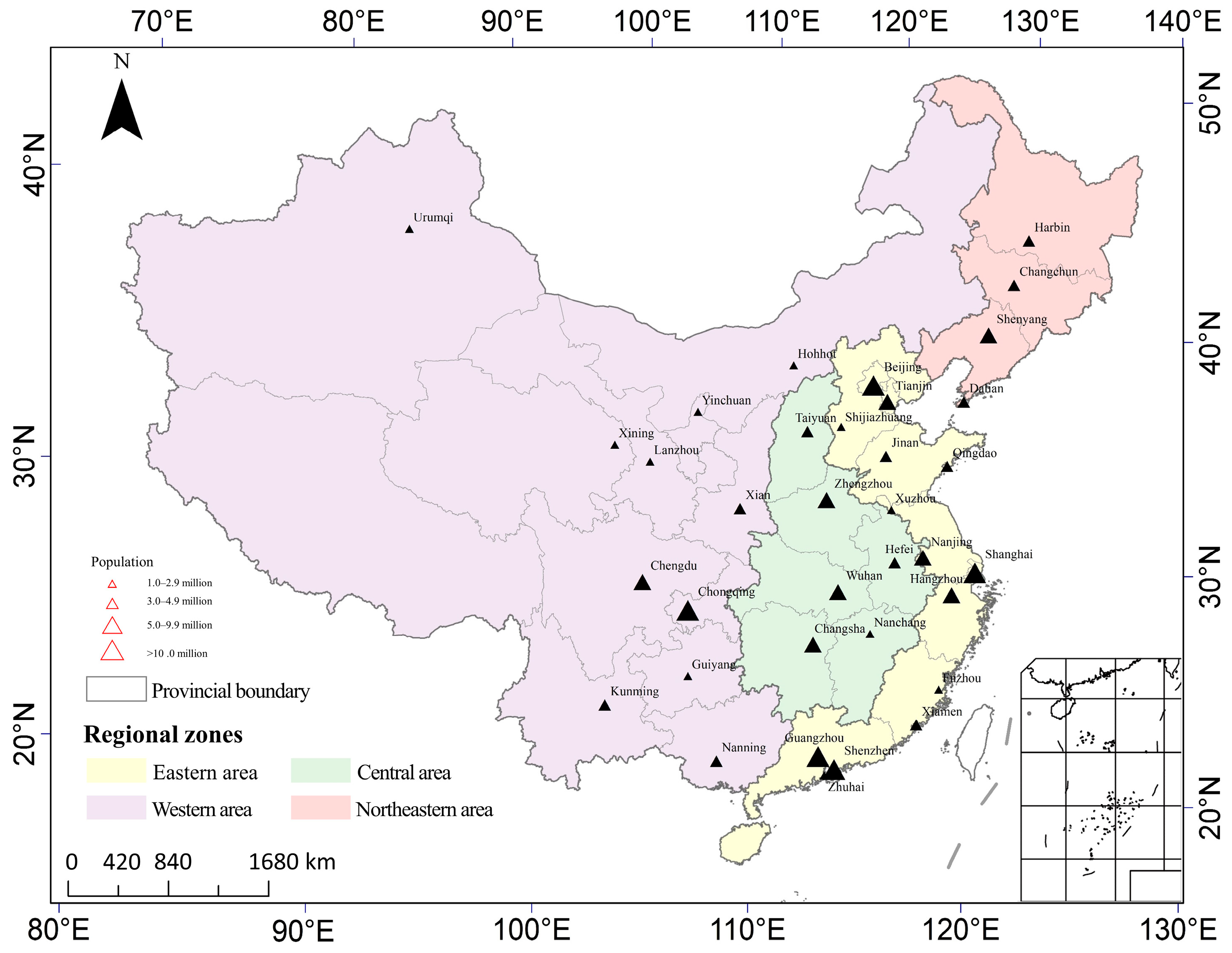
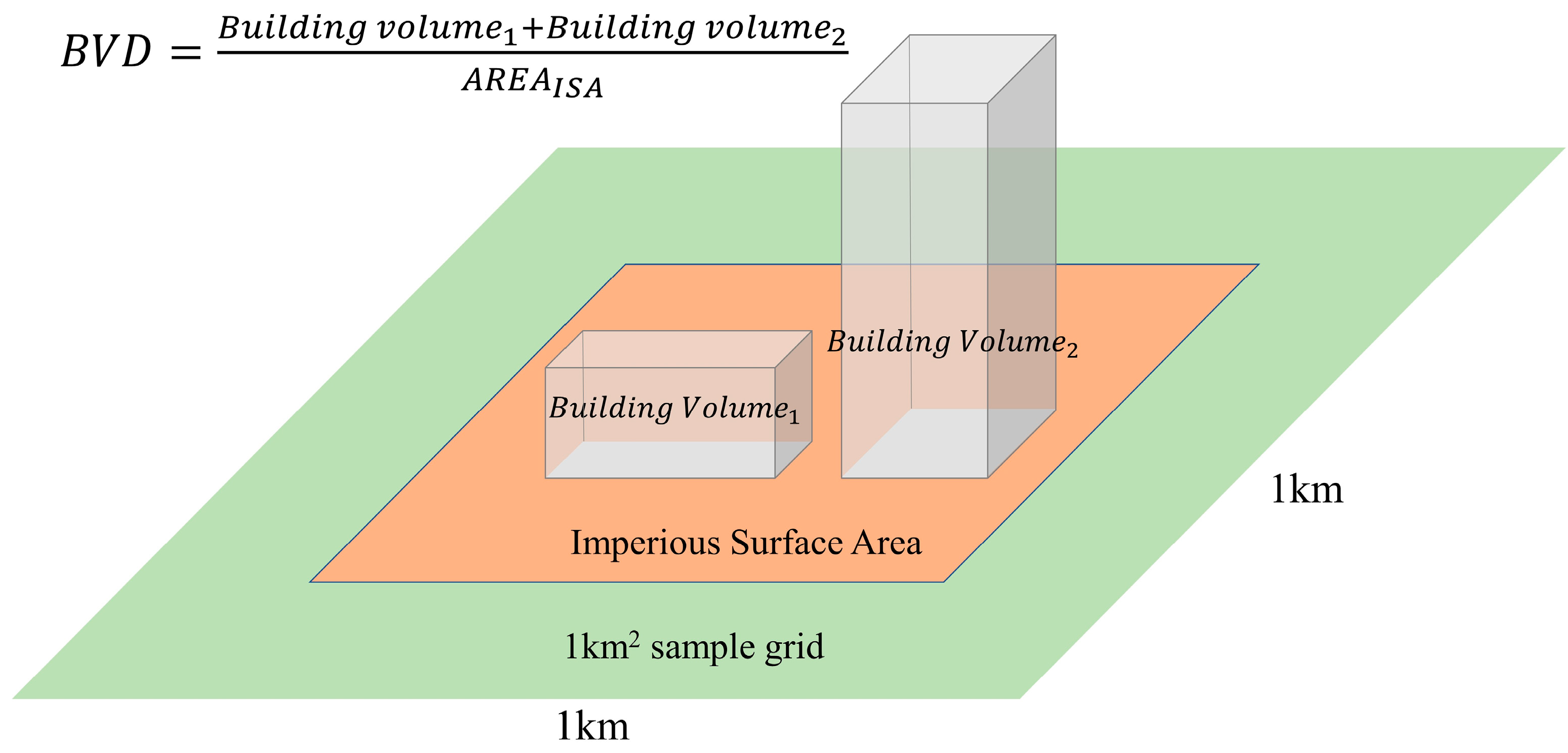

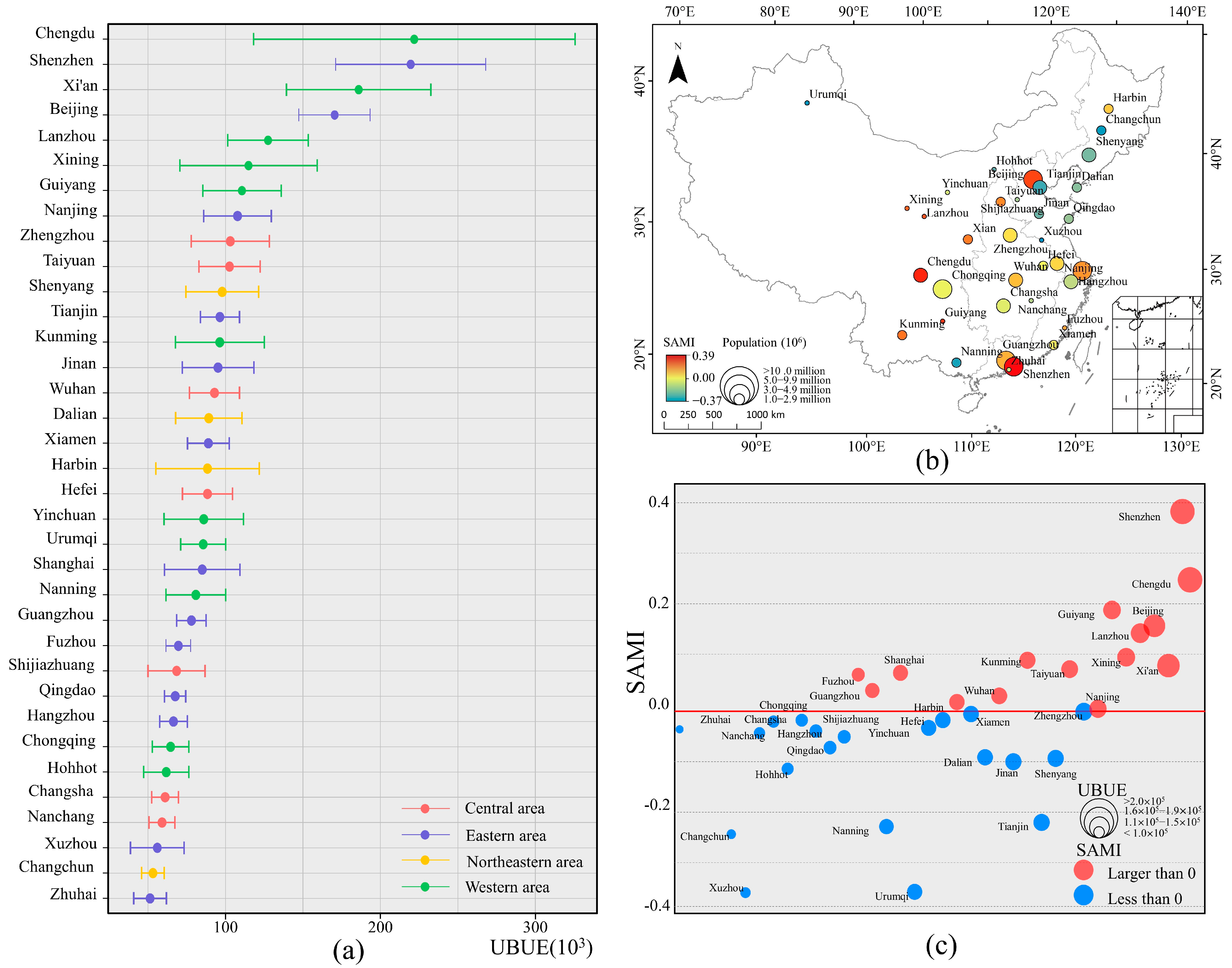
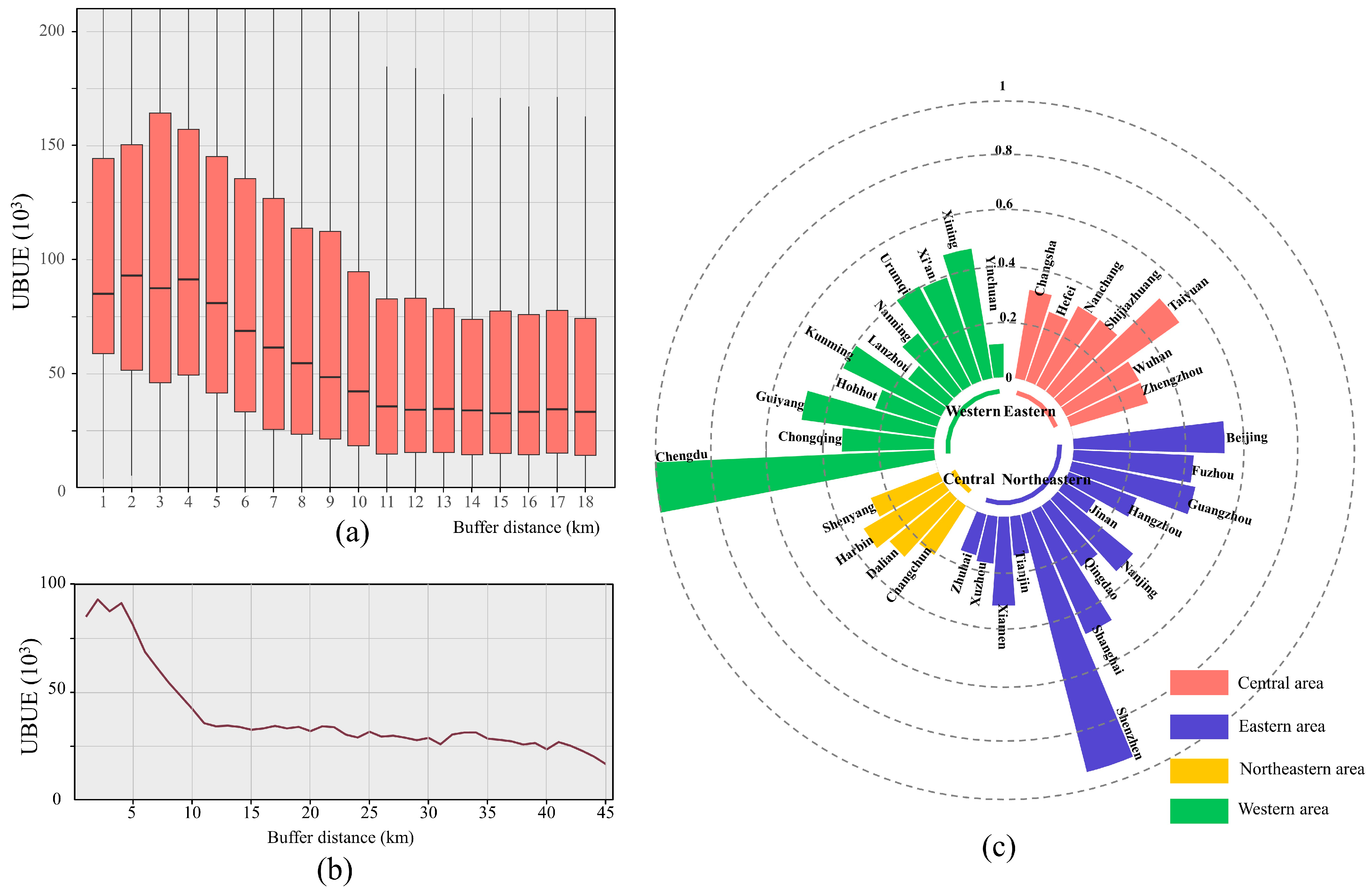



| Description | Time | Spatial Resolution | Reference and Sources |
|---|---|---|---|
| Urban area boundary | 2018 | 30 m | [47] |
| Building volume | 2020 | 10 m | [44] |
| Built-up land | 2018 | 30 m | [43] |
| Population data | 2020 | 100 m | [48] |
| Nighttime light data | 2020 | 500 m | [49] |
| Point of interest | 2018 | - | [46] |
| GDP | 2017 | - | Ministry of Housing and Urban–Rural Development of the People’s Republic of China |
| Public budget expenditure | 2017 | - | Ministry of Housing and Urban–Rural Development of the People’s Republic of China |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, T.; Cao, S.; Lu, Y.; Zhang, M.; Guo, A.; Liu, B. From Density to Efficiency: Exploring Urban Building Use Efficiency in 35 Large Chinese Cities. Buildings 2025, 15, 1803. https://doi.org/10.3390/buildings15111803
He T, Cao S, Lu Y, Zhang M, Guo A, Liu B. From Density to Efficiency: Exploring Urban Building Use Efficiency in 35 Large Chinese Cities. Buildings. 2025; 15(11):1803. https://doi.org/10.3390/buildings15111803
Chicago/Turabian StyleHe, Tingting, Shanshan Cao, Youpeng Lu, Maoxin Zhang, Andong Guo, and Boyu Liu. 2025. "From Density to Efficiency: Exploring Urban Building Use Efficiency in 35 Large Chinese Cities" Buildings 15, no. 11: 1803. https://doi.org/10.3390/buildings15111803
APA StyleHe, T., Cao, S., Lu, Y., Zhang, M., Guo, A., & Liu, B. (2025). From Density to Efficiency: Exploring Urban Building Use Efficiency in 35 Large Chinese Cities. Buildings, 15(11), 1803. https://doi.org/10.3390/buildings15111803







