Effect of Steel Slag Fine Aggregate on the Seismic Behavior of Reinforced Concrete Columns with Steel Slag Sand
Abstract
1. Introduction
2. Experimental Program
2.1. Materials
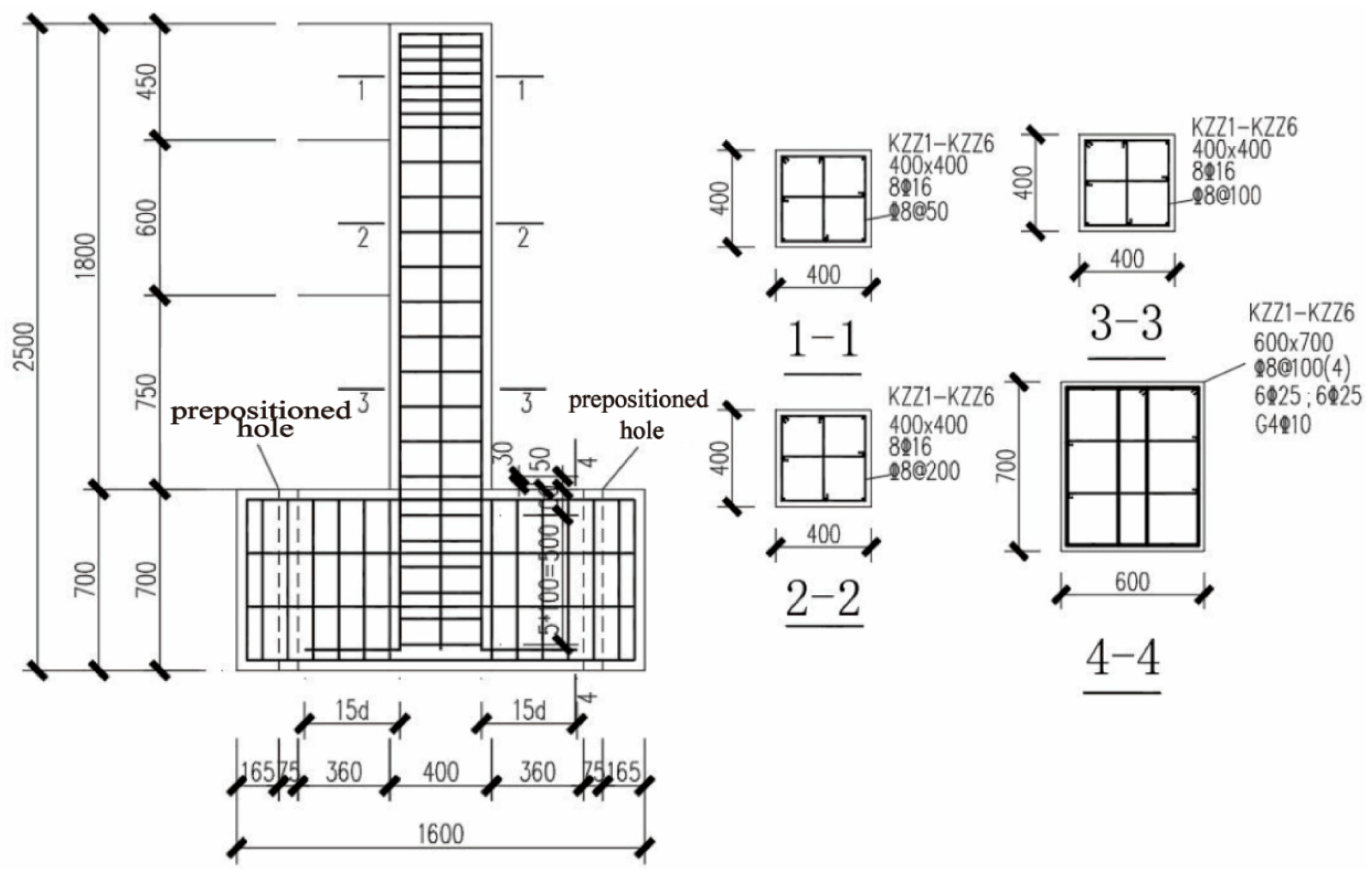
2.2. Experimental Design
2.3. Concrete Mix Design
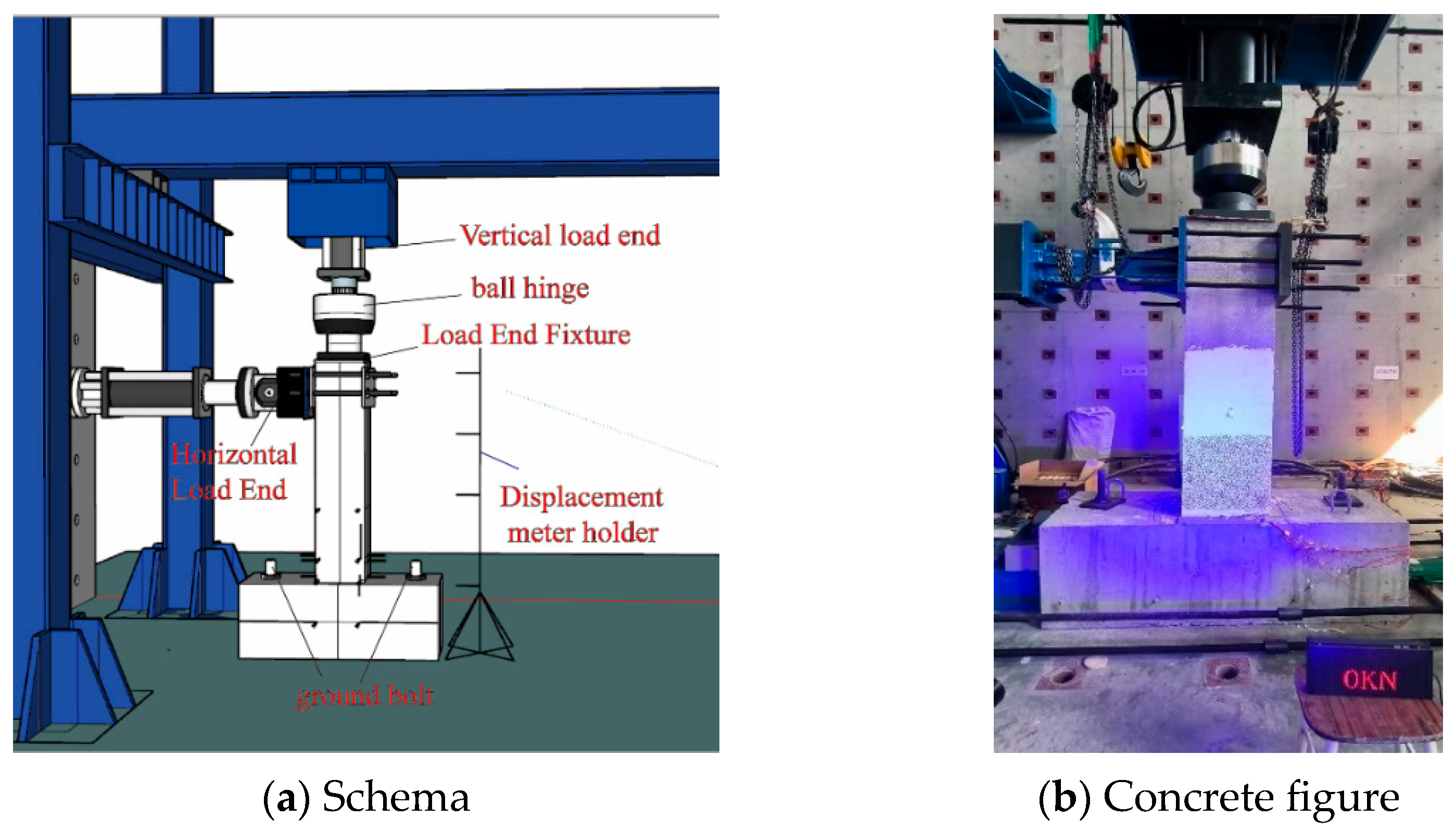
2.4. Testing Procedure
2.4.1. Loading Scheme
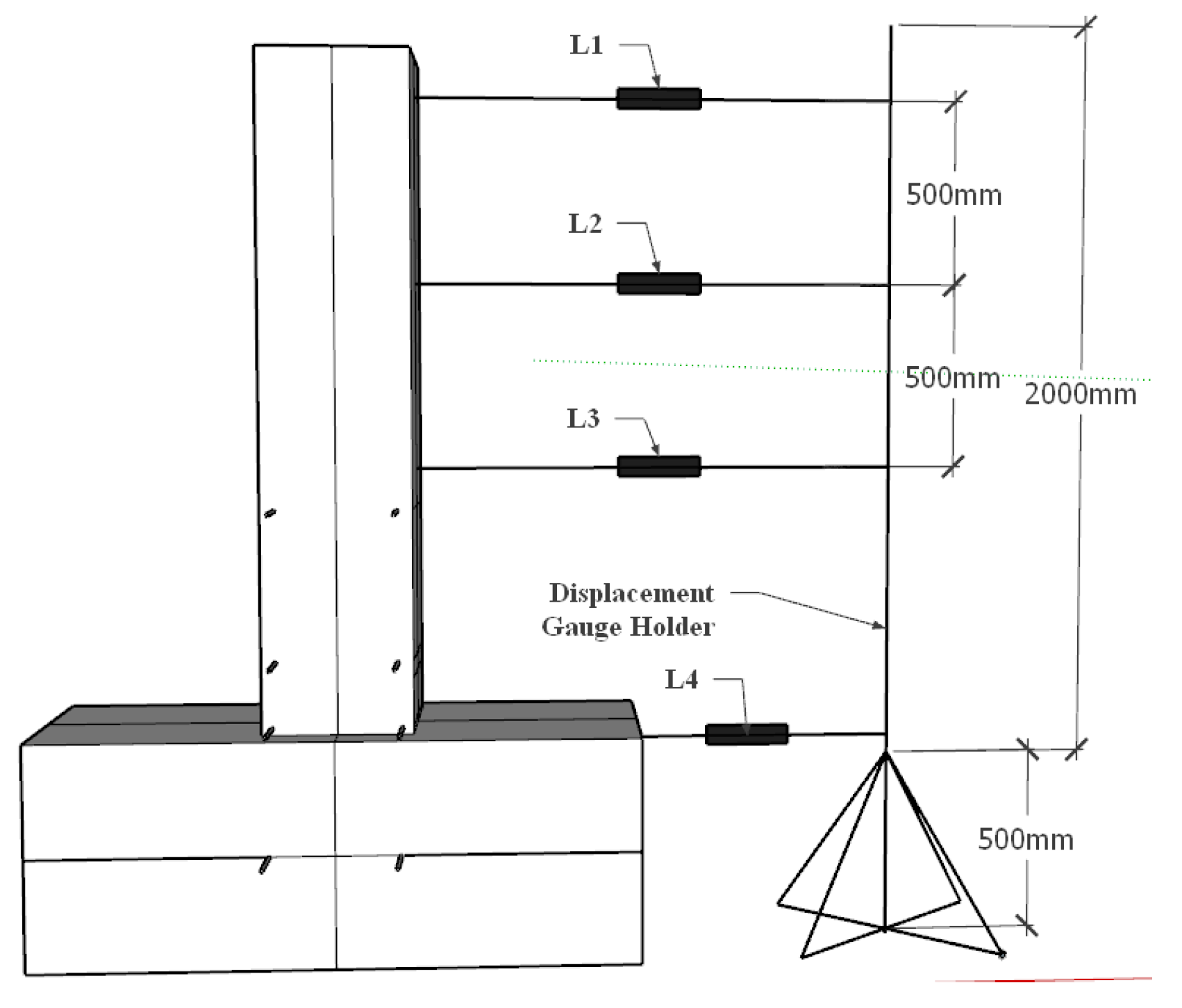
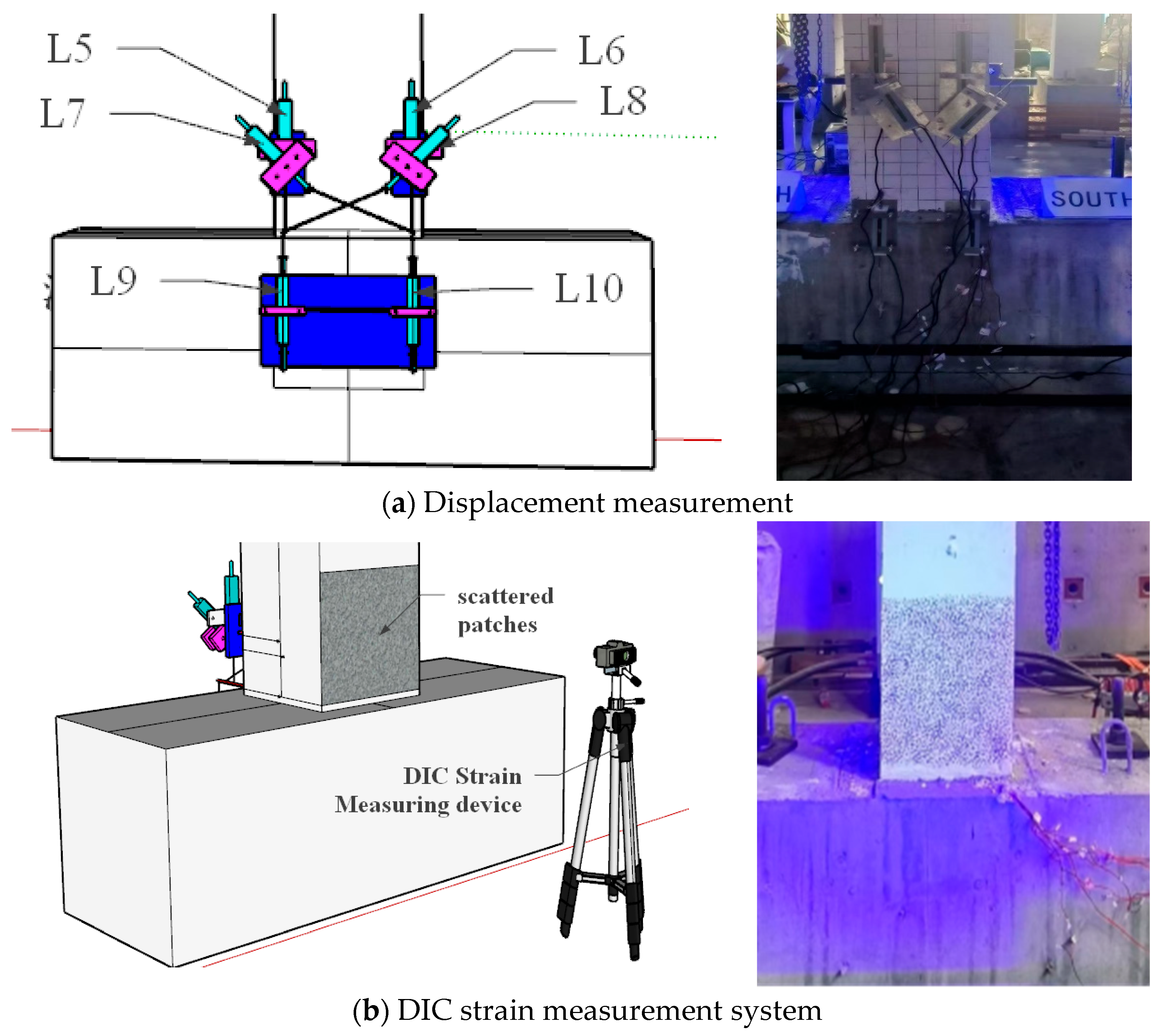
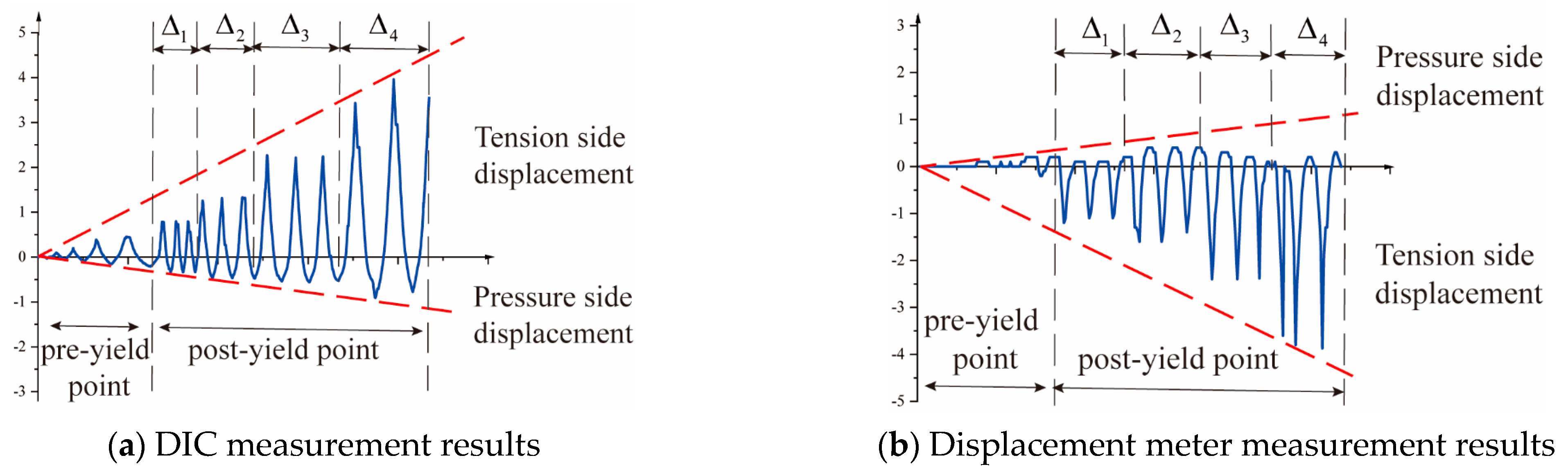
2.4.2. Measurement Scheme for Concrete Column Deformations
- (1)
- Measurement of Specimen Deformations
- (2)
- Measurement of Plastic Hinge Deformation
- (3)
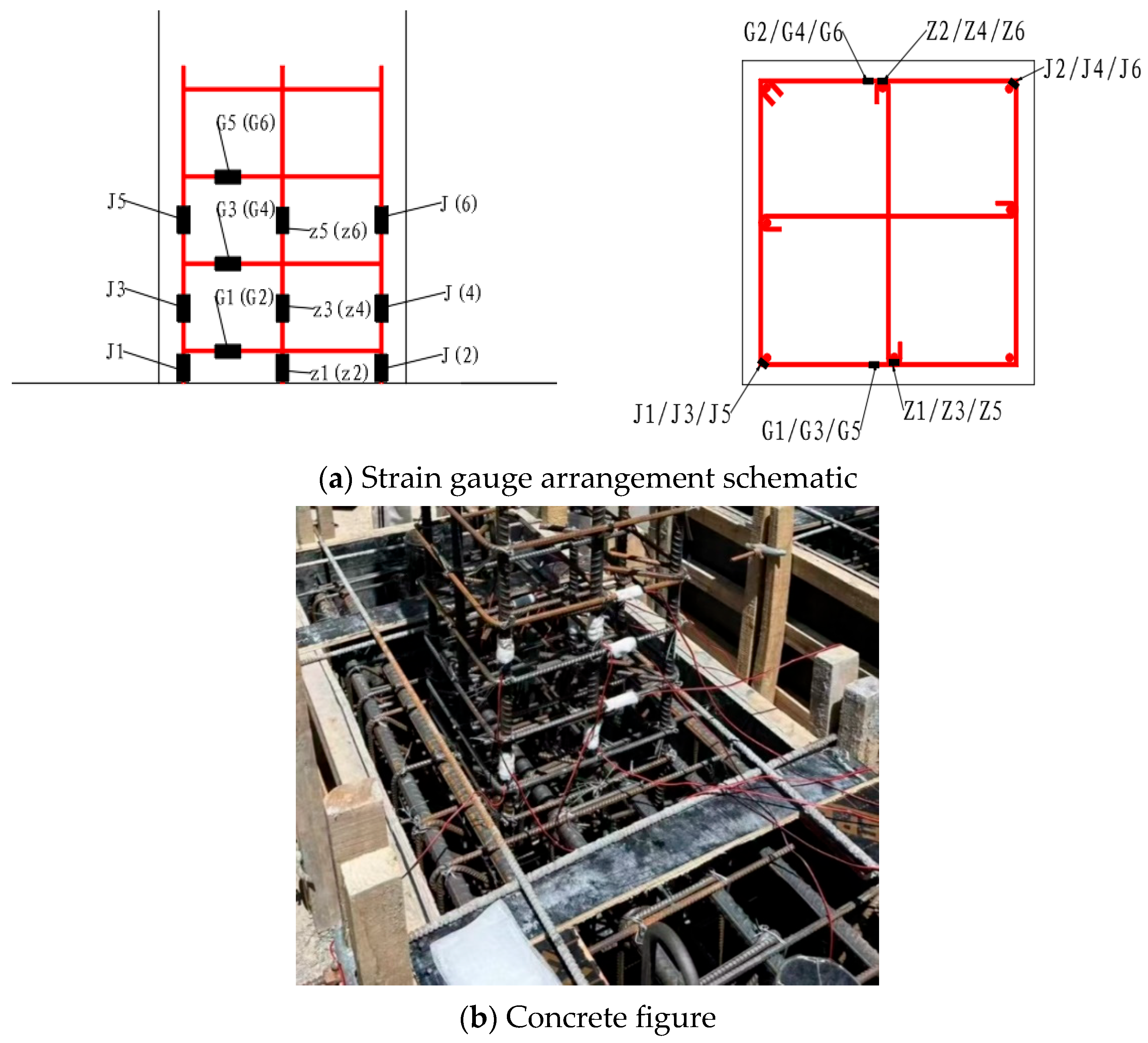
- Reinforcement Strain Measurement
3. Experimental Results and Analysis
3.1. Basic Mechanical Properties of Steel Slag Sand Concrete (SSC)
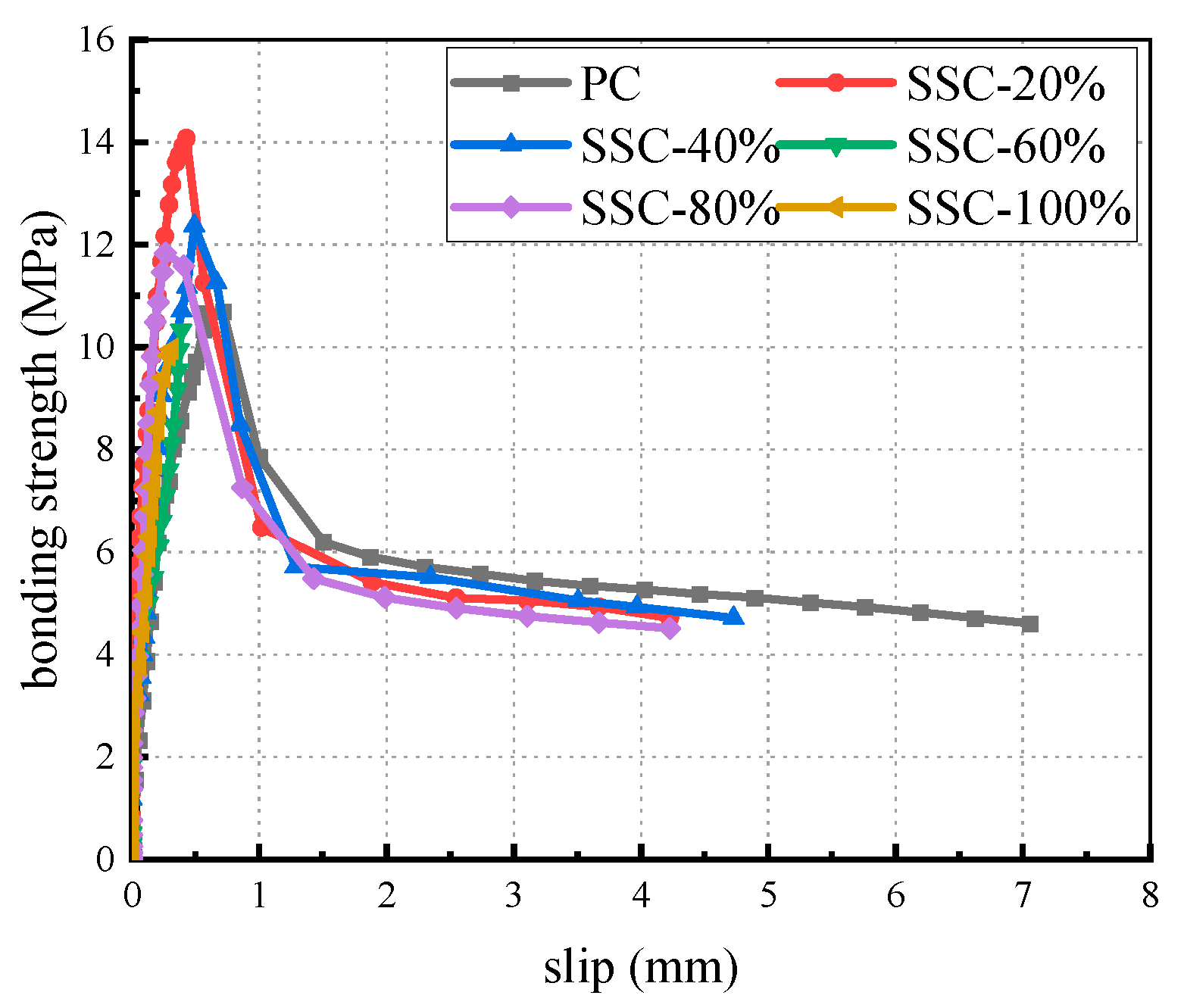
3.2. Bond–Slip Properties of SSC with Steel Bars
3.3. Destruction Patterns of SSCC
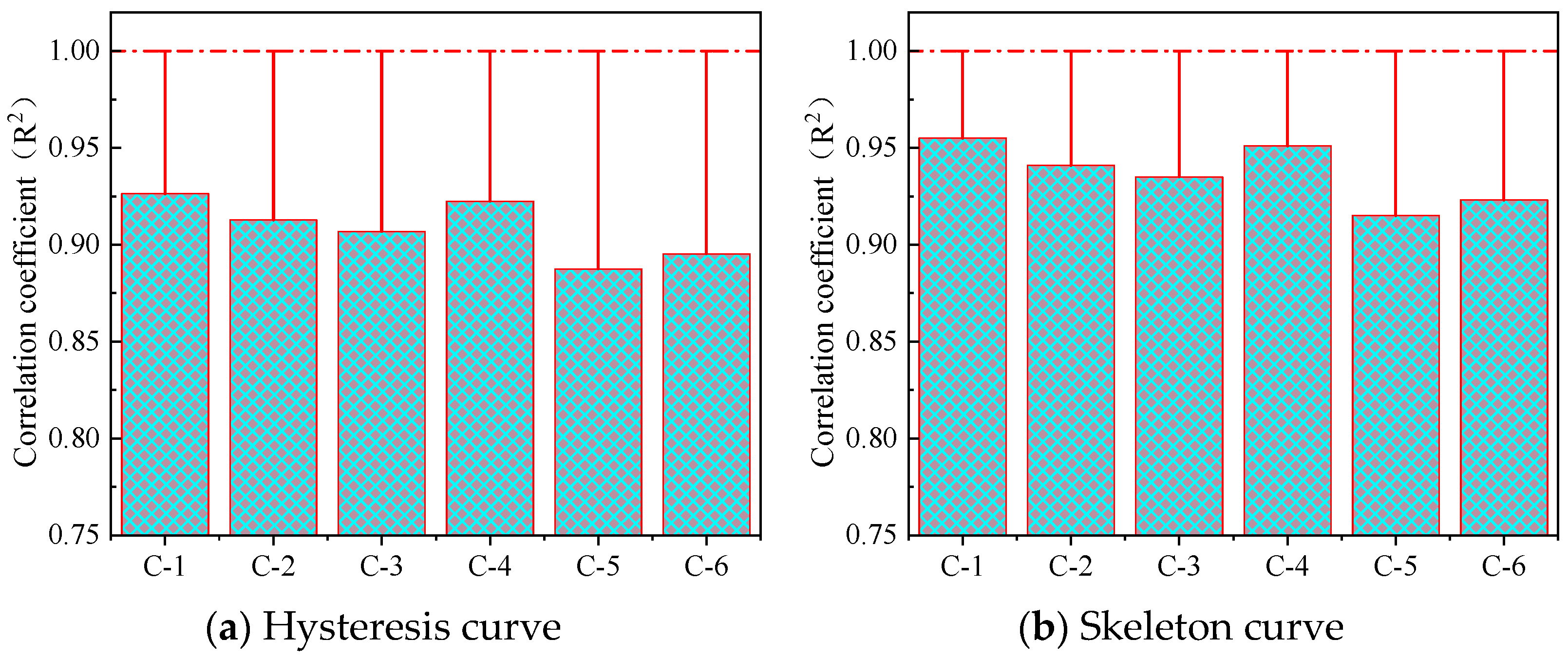
3.4. Seismic Performance Analysis of SSC Columns
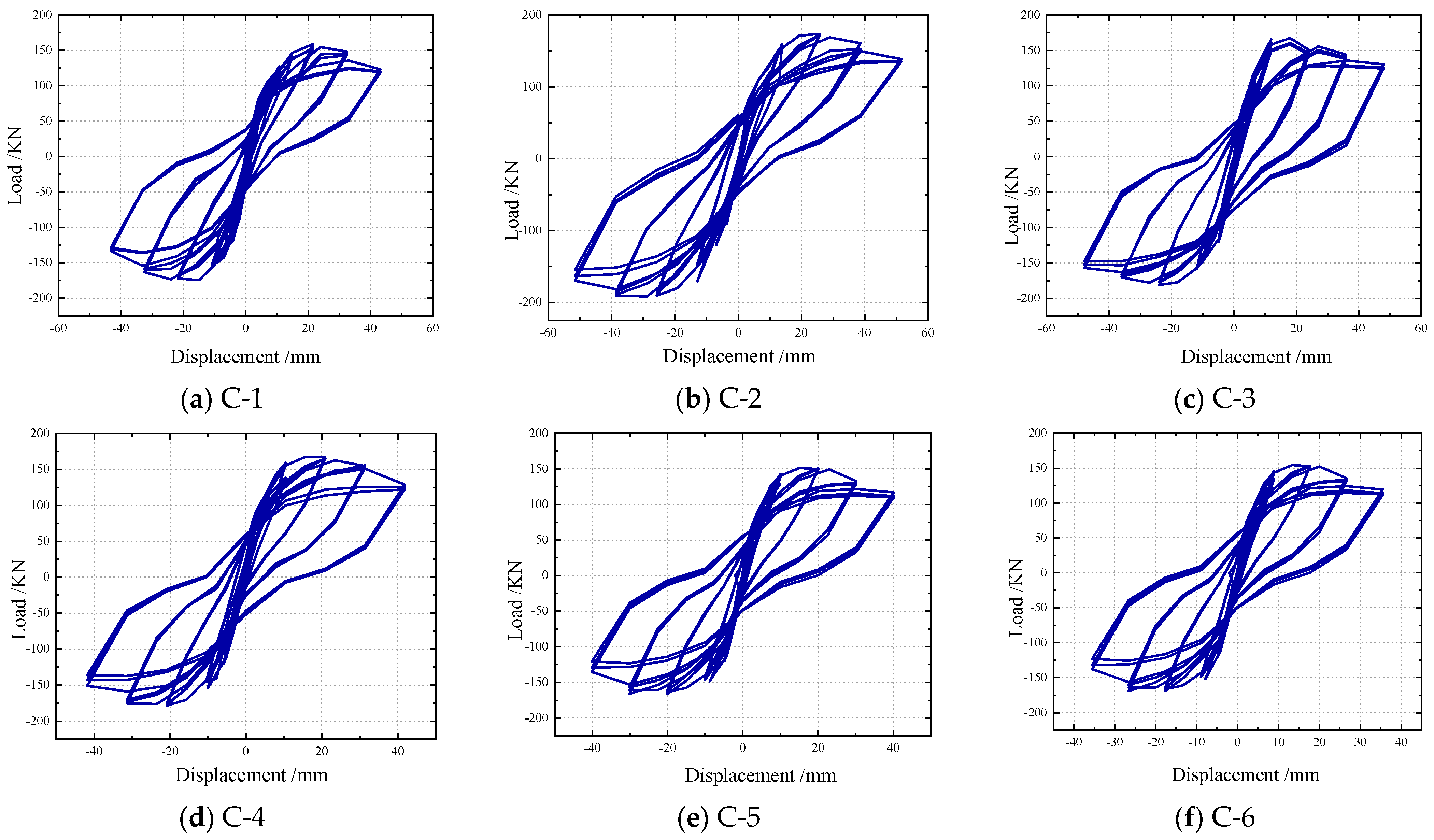
- (1)
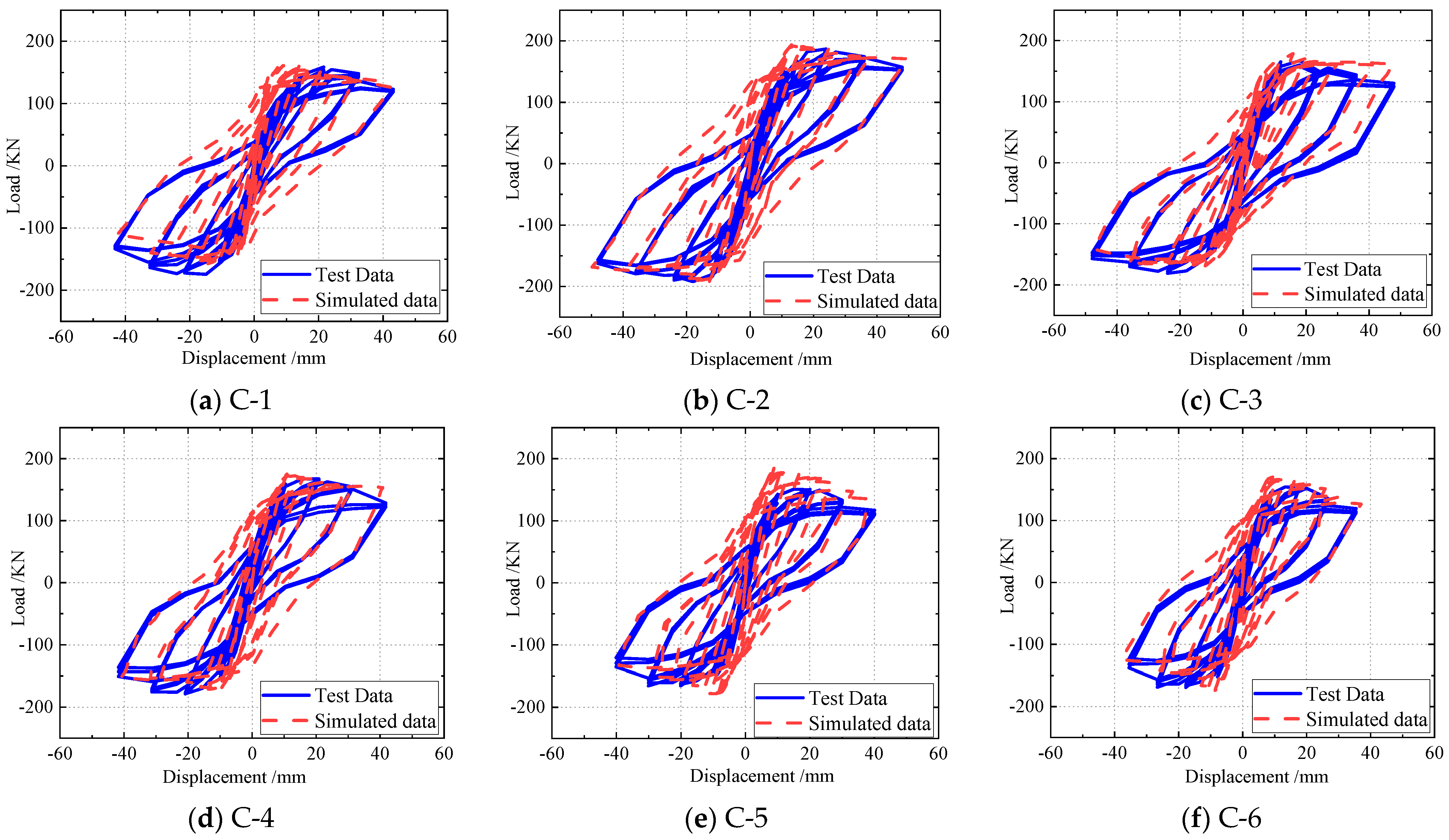
- SSCC load–displacement hysteresis curve analysis
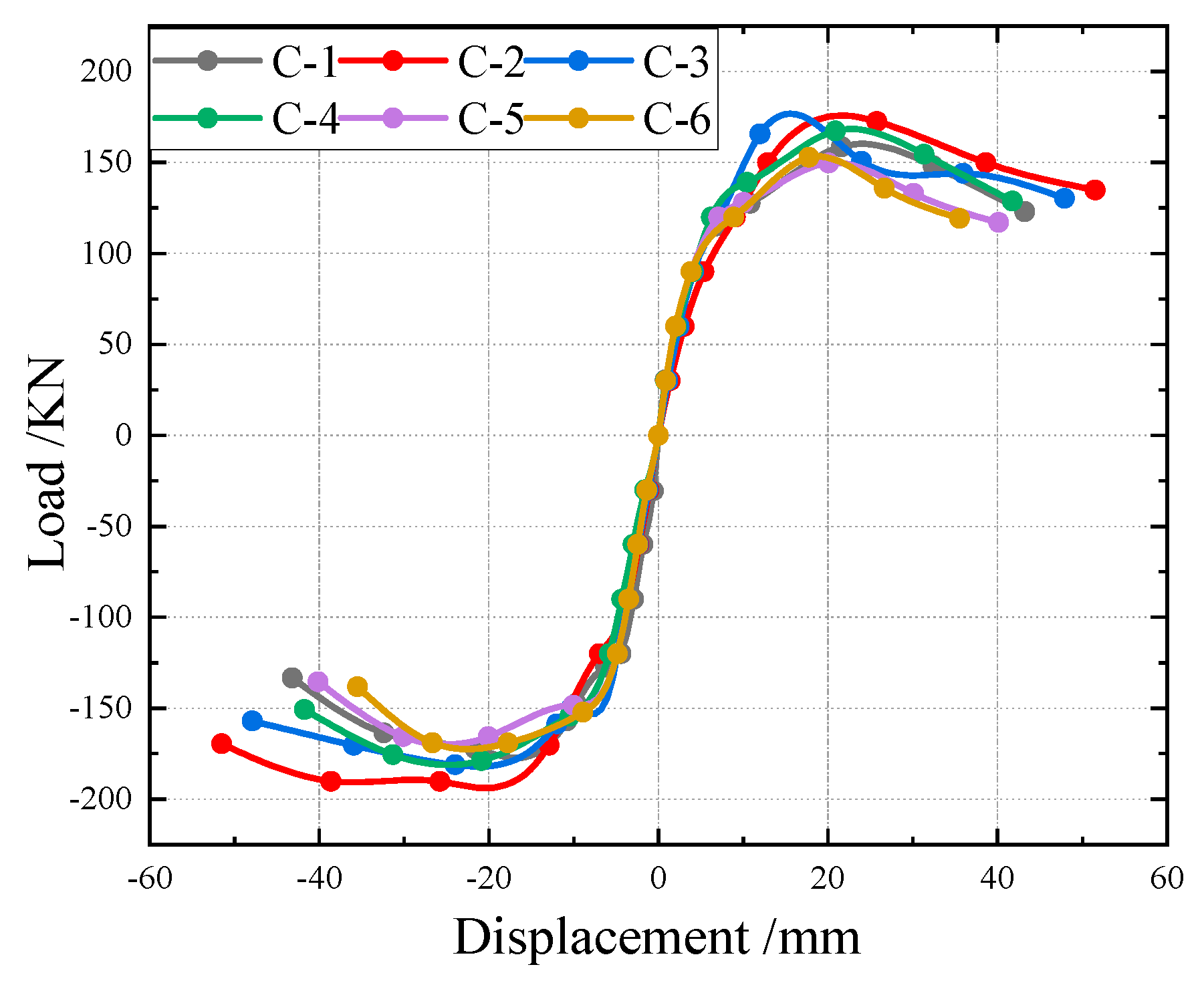
- (2)
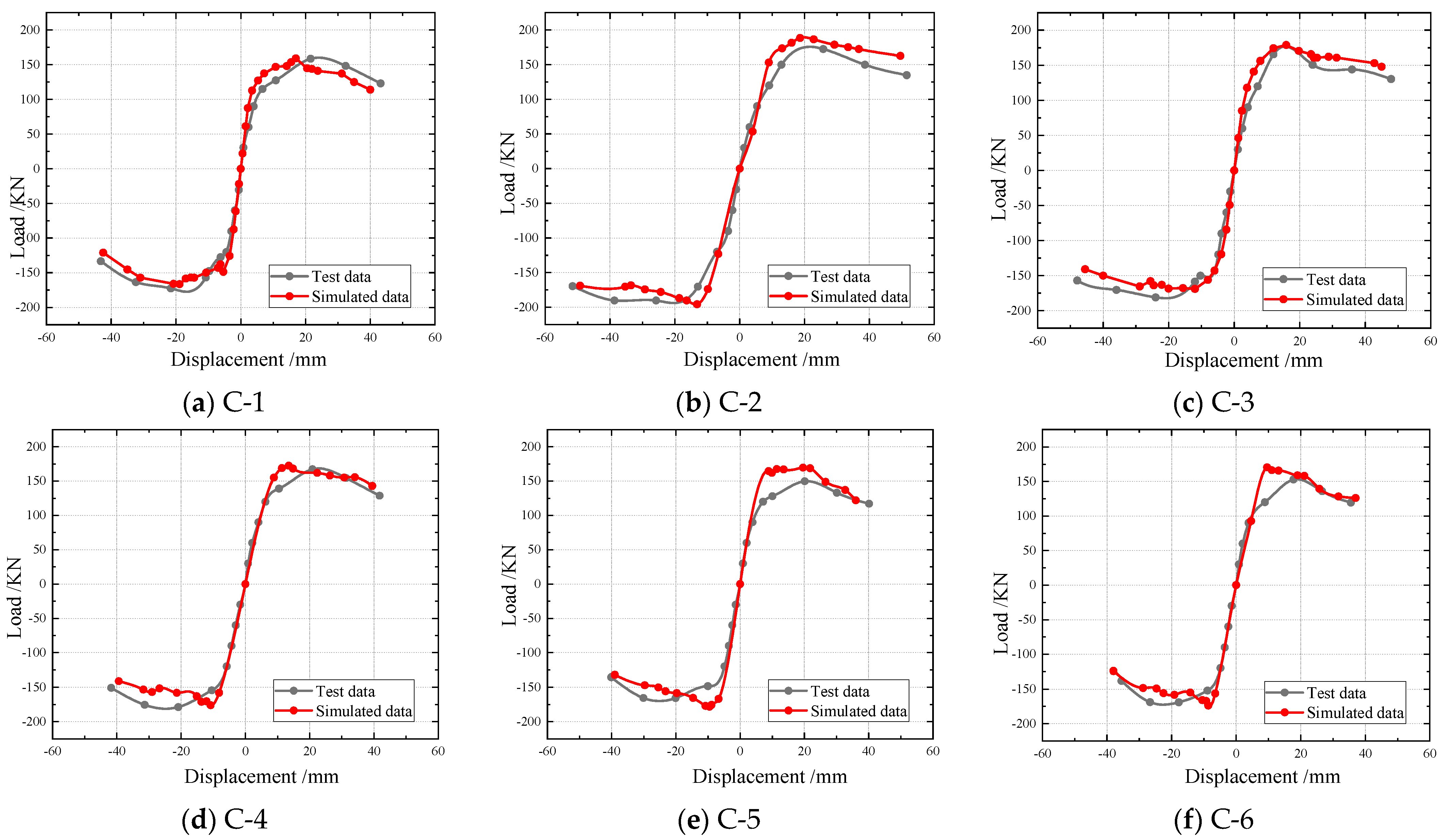
- SSCC skeleton curve analysis
- (3)
- SSCC Ductility and Stiffness Degradation Analysis
- (4)
- SSCC energy dissipation analysis
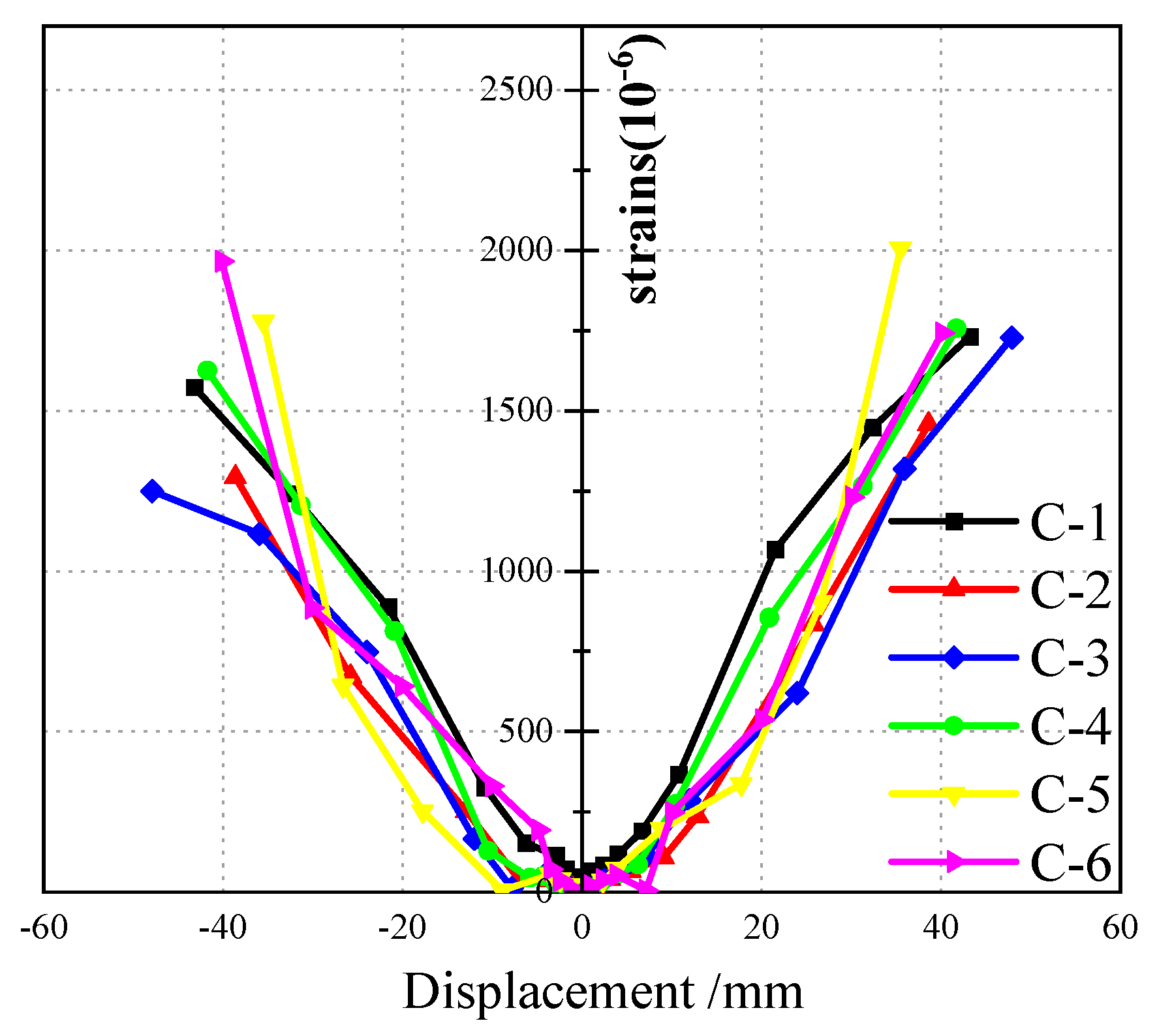
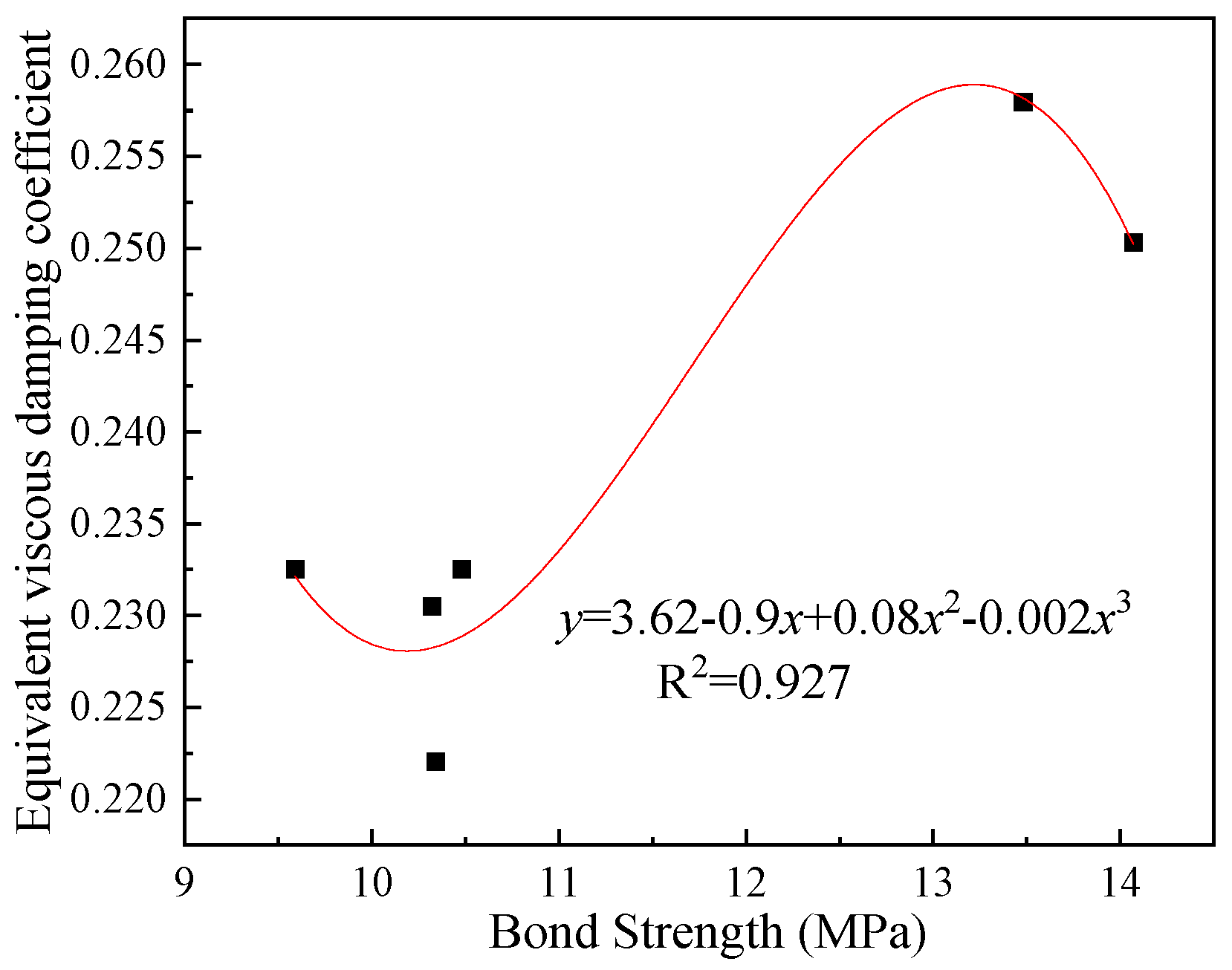
3.5. Strain Analysis of SSCC Reinforcement
- (1)
- Strain analysis of longitudinal reinforcement
- (2)
- Strain analysis of hoop reinforcement
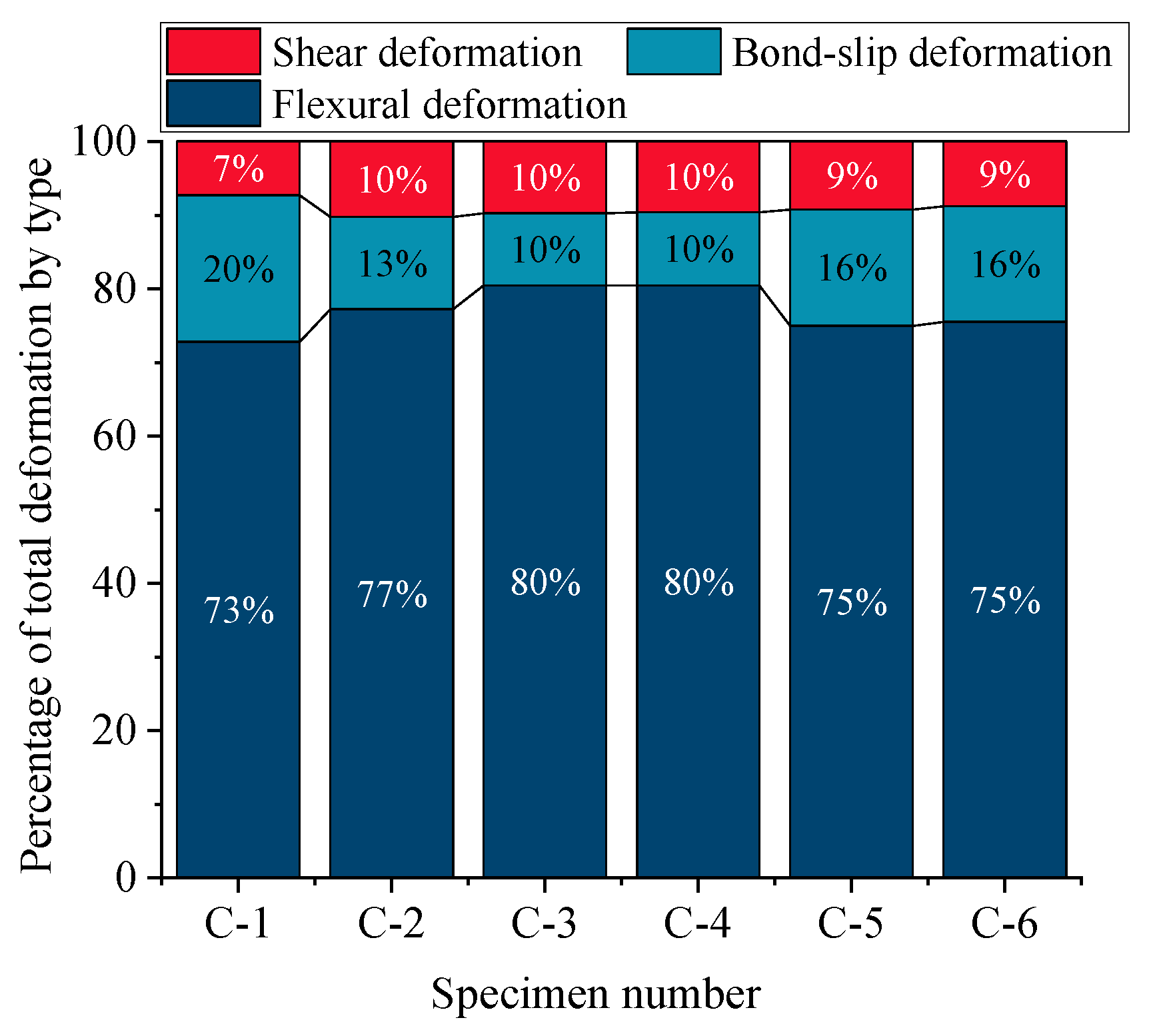
3.6. Deformation Analysis of Plastic Hinge Region
4. Finite Element Analysis
4.1. Material Eigenmodel
- (1)
- Concrete material principal structure
- (2)
- Reinforcing material principal structure
- (3)
- SSC bond–slip ontological relationship
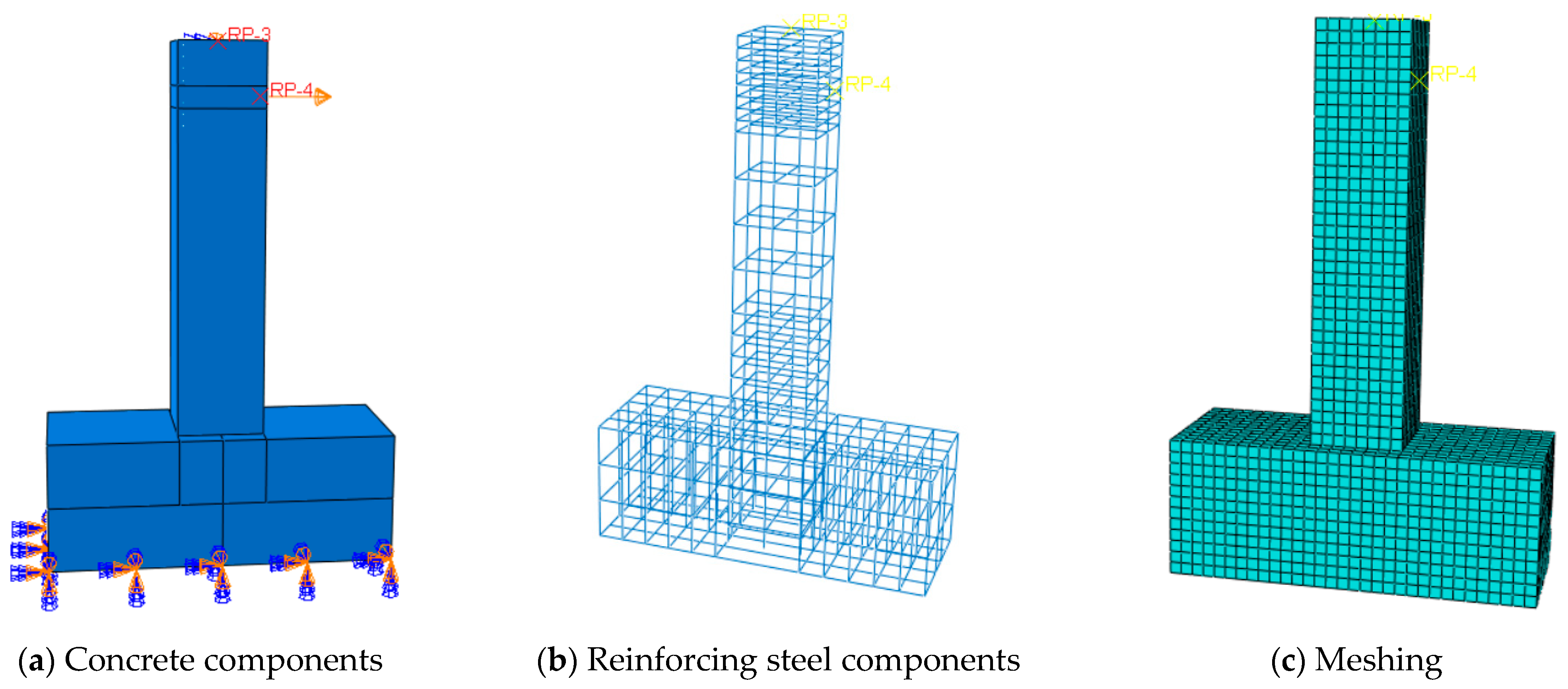
4.2. Finite Element Modeling
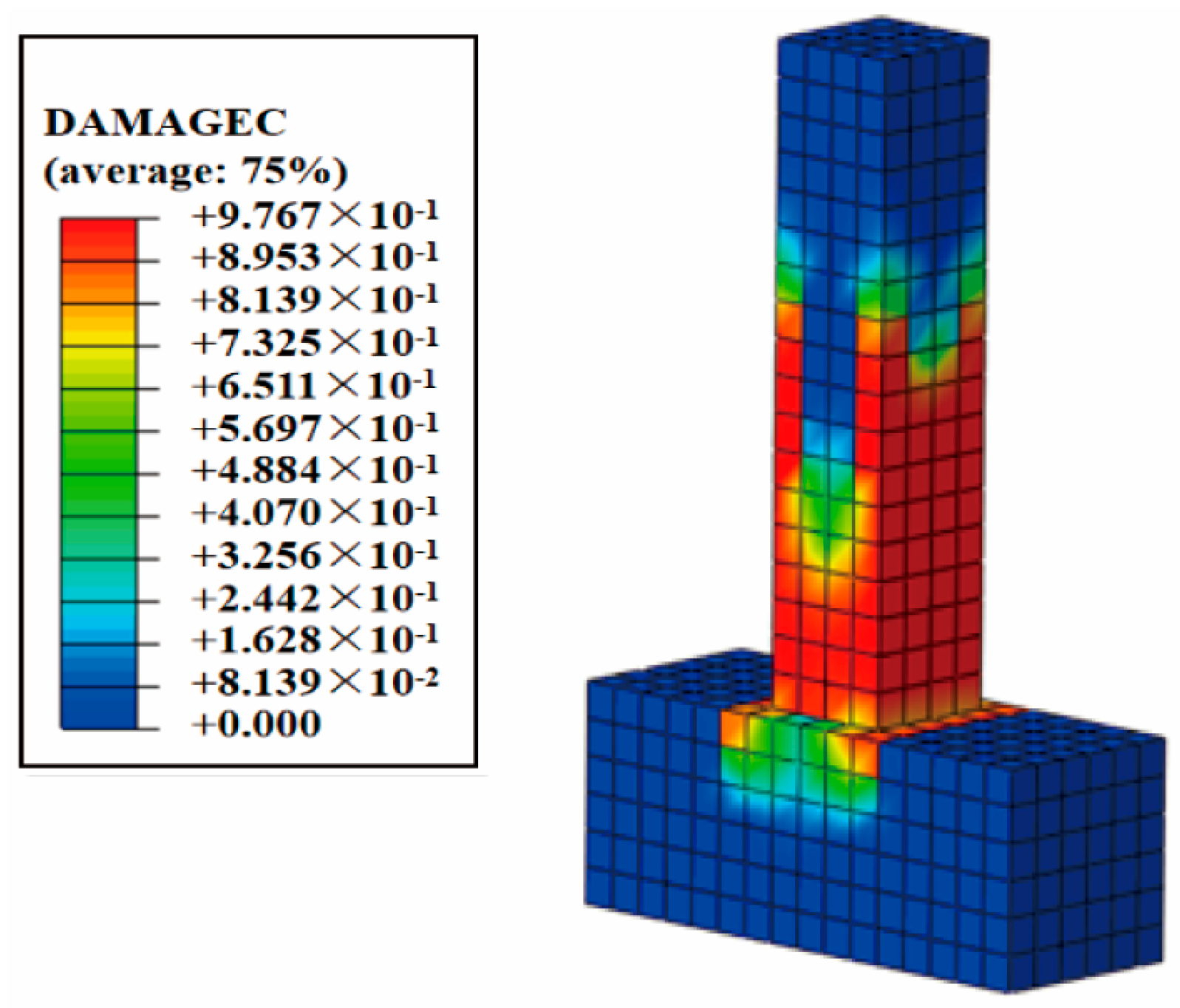
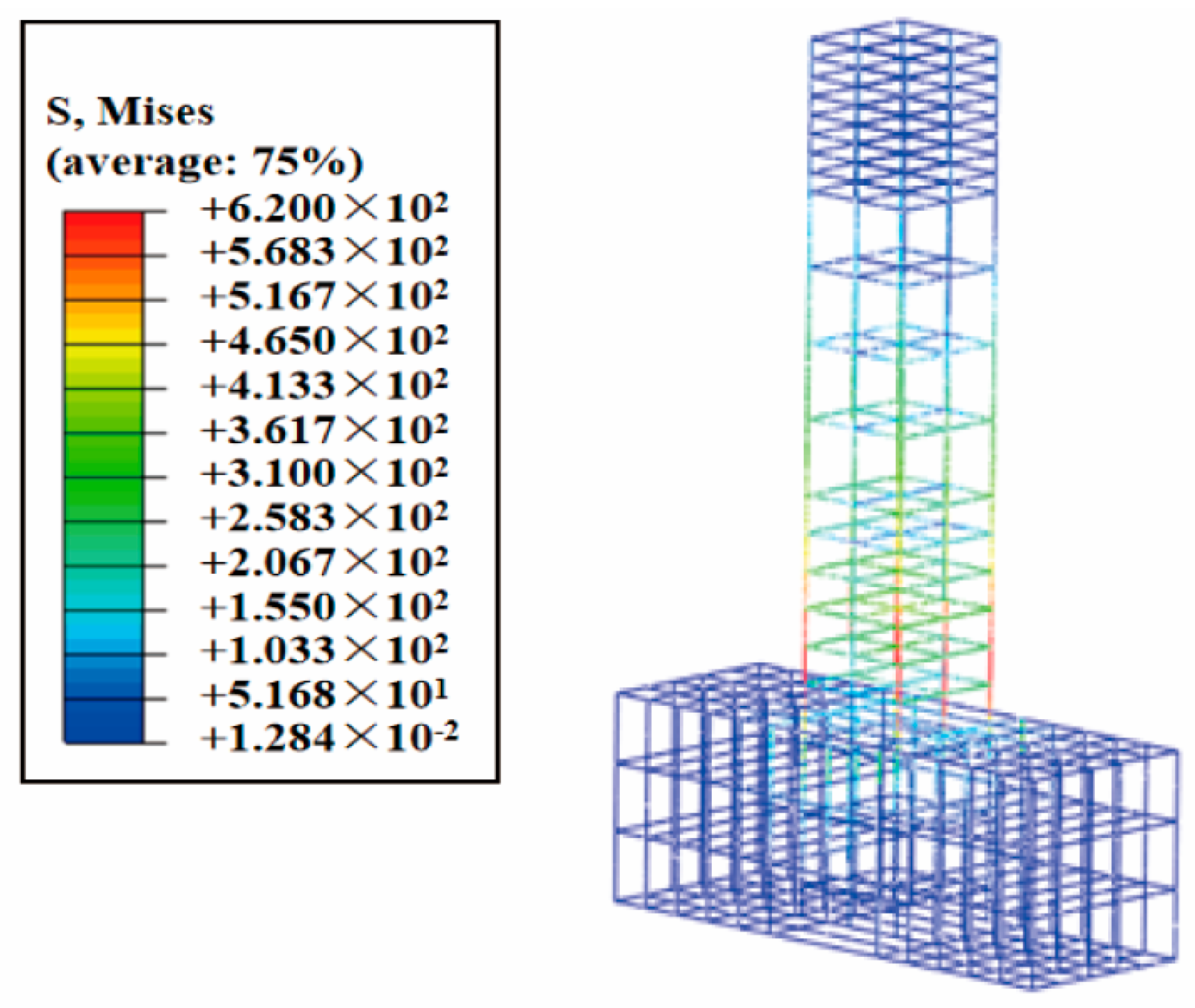
4.3. Simulation Results and Analysis
5. Conclusions
- (1)
- As the steel slag sand substitution rate increases, the cube compressive strength (fcu), axial compressive strength (fc), and bond strength of the concrete initially increase and then decrease. Optimal mechanical properties are observed at substitution rates of 20–40%. Notably, the improvement in bond strength is more pronounced than in fcu and fc.
- (2)
- The incorporation of steel slag sand markedly improves the seismic performance of the columns. Compared with conventional plain concrete (PC) columns, the SSCCs demonstrate superior seismic characteristics under cyclic loading. The experimental results reveal that at a 40% replacement ratio, the SSCCs exhibit an 11.3% increase in energy dissipation capacity, a 10% reduction in bond–slip deformation within the plastic hinge region, and a 9% improvement in flexural deformation capacity relative to PC. Furthermore, the SSCCs exhibit more stable and fuller hysteresis loops, higher ductility coefficients, and larger ultimate drift ratios, all indicative of enhanced energy dissipation capability and seismic resilience.
- (3)
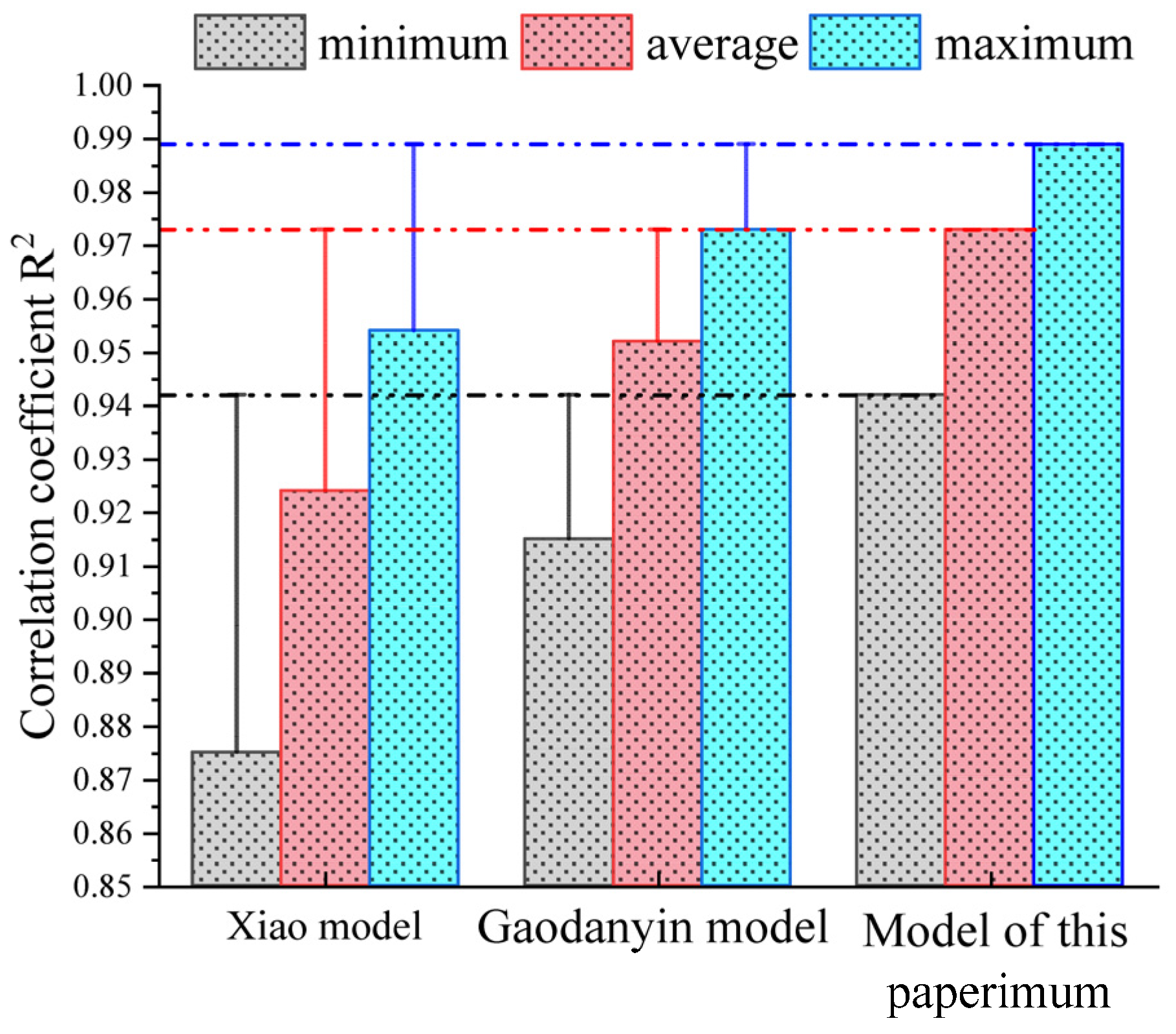
- The study proposes the bond–slip relationship between SSC and reinforcing steel and develops a finite element (FE) model to simulate the seismic response of SSCCs. The model incorporates bond–slip effects to accurately capture the load–displacement behavior under cyclic loading. Although the model does not fully reproduce the pinching effect observed in the experimental hysteresis curves, its predictions of load capacity and ductility show strong agreement with experimental results, validating the effectiveness of the FE approach for evaluating and designing the seismic performance of steel slag aggregate concrete structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gencel, O.; Karadag, O.; Oren, O.H.; Bilir, T. Steel slag and its applications in cement and concrete technology: A review. Constr. Build. Mater. 2021, 283, 122783. [Google Scholar] [CrossRef]
- Ye, G.; Yuen, K.-V.; Jin, Q.; Zhou, M.; Yin, C.; Jiang, Q.; Zhao, S.; Su, W. Evaluation method for uniformity of steel slag concrete aggregate based on improved YOLOv8. J. Build. Eng. 2024, 98, 111046. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, G.; Chen, X.; Tan, J.; Gu, X. Recycling of steel slag aggregate in portland cement concrete: An overview. J. Clean. Prod. 2021, 282, 124447. [Google Scholar] [CrossRef]
- Wang, C.; Ye, G.; Jin, Q.; Zhou, Z.; Hu, D.; Wei, Y. The uniaxial compressive stress-strain relations of steel slag fine aggregate concrete under steam curing. Constr. Build. Mater. 2025, 459, 139820. [Google Scholar] [CrossRef]
- Guo, Y.; Xie, J.; Zheng, W.; Li, J. Effects of steel slag as fine aggregate on static and impact behaviours of concrete. Constr. Build. Mater. 2018, 192, 194–201. [Google Scholar] [CrossRef]
- Zhou, Z.; Jin, Q.; Hu, D.; Zhu, L.; Li, Z.; Su, W. Long-term volume stability of steel slag sand mortar and concrete. Case Stud. Constr. Mater. 2025, 22, e04179. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, P.; Yang, J.; Zhang, B. Influence of steel slag on mechanical properties and durability of concrete. Constr. Build. Mater. 2013, 47, 1414–1420. [Google Scholar] [CrossRef]
- Lai, M.; Lin, Y.; Jin, Y.; Fei, Q.; Wang, Z.; Ho, J. Uni-axial behaviour of steel slag concrete-filled-steel-tube columns with external confinement. Thin-Walled Struct. 2023, 185, 110562. [Google Scholar] [CrossRef]
- Lu, L.; Zhang, T.; Liang, T.; Ren, Q. Axial compressive behavior of circular concrete-filled steel tube stub columns with steel slag coarse aggregate. Structures 2023, 51, 1893–1905. [Google Scholar] [CrossRef]
- Pang, Y.; Cai, L.; Ouyang, H.; Zhou, X. Seismic performance assessment of different fibers reinforced concrete columns using incremental dynamic analysis. Constr. Build. Mater. 2019, 203, 241–257. [Google Scholar] [CrossRef]
- Bu, S.; Yu, F.; Chen, T.; Fang, Y.; Qin, Y. Experimental study on seismic behavior of circular steel tube confined reinforced self-stressing steel slag concrete columns. Struct. Concr. 2023, 24, 1102–1117. [Google Scholar] [CrossRef]
- Lu, L.; Liang, T.; Zhang, T.; Ren, Q.; Wang, Q.; Wang, S. Axial compressive behaviors of circular steel slag concrete-filled steel tube slender columns. Struct. Concr. 2023, 24, 6953–6972. [Google Scholar] [CrossRef]
- Cai, R.; Zhang, J.; Liu, Y.; Tao, X. Seismic behavior of recycled concrete columns reinforced with ultra-high-strength steel bars. Eng. Struct. 2023, 279, 115633. [Google Scholar] [CrossRef]
- Liu, K.; Yan, J.; Zou, C. A pilot experimental study on seismic behavior of recycled aggregate concrete columns after freeze-thaw cycles. Constr. Build. Mater. 2018, 164, 497–507. [Google Scholar] [CrossRef]
- Chen, Z.; Jing, C.; Xu, J.; Zhang, X. Seismic performance of recycled concrete-filled square steel tube columns. Earthq. Eng. Eng. Vib. 2017, 16, 119–130. [Google Scholar] [CrossRef]
- Baili, J.; Raza, A.; Azab, M.; Ali, K.; El Ouni, M.H.; Haider, H.; Farooq, M.A. Experiments and predictive modeling of optimized fiber-reinforced concrete columns having FRP rebars and hoops. Mech. Adv. Mater. Struct. 2023, 30, 4913–4932. [Google Scholar] [CrossRef]
- Liu, J.; Yu, B.; Wang, Q. Application of steel slag in cement treated aggregate base course. J. Clean. Prod. 2020, 269, 121733. [Google Scholar] [CrossRef]
- Gong, W.; Chen, Q.; Miao, J. Bond behaviors between copper slag concrete and corroded steel bar after exposure to high temperature. J. Build. Eng. 2021, 44, 103312. [Google Scholar] [CrossRef]
- Montgomery, D.; Wang, G. Instant-chilled steel slag aggregates in concrete—Strength related properties. Cem. Concr. Res. 1991, 21, 1083–1091. [Google Scholar] [CrossRef]
- Olonade, K.; Kadiri, M.; Aderemi, P. Performance of Steel Slag as Fine Aggregate in Structural Concrete. Nig. J. Technol. 2015, 34, 452. [Google Scholar] [CrossRef]
- Yu, F.; Chen, T.; Niu, K.; Wang, S.; Kong, Z.; Fang, Y. Study on Bond-Slip Behaviors of Self-Stressing Steel Slag Concrete-Filled Steel Tube. KSCE J. Civ. Eng. 2020, 24, 3309–3319. [Google Scholar] [CrossRef]
- Faleschini, F.; Santamaria, A.; Zanini, M.A.; José, J.-T.S.; Pellegrino, C. Bond between steel reinforcement bars and Electric Arc Furnace slag concrete. Mater. Struct. 2017, 50, 170. [Google Scholar] [CrossRef]
- Hui, S. Mechanical Properties and Volumetric Stability of Steel Slag Concrete. Master’s Thesis, Inner Mongolia University of Science and Technology, Baotou, China, 2023. [Google Scholar]
- Sun, Y. Mechanical Properties and Microstructure of Steel Slag Concrete. Master’s Thesis, Guangzhou University, Guangzhou, China, 2022. [Google Scholar]
- Yu, F.; Qin, Y.; Yao, C.; Bu, S.; Fang, Y. Experimental investigation on the seismic behavior of self-stressing steel slag CFST column. Struct. Concr. 2022, 23, 1492–1507. [Google Scholar] [CrossRef]
- Alkhawaldeh, S. FE Modelling of the Bond-Slip Behaviour and Its Effects on the Seismic Performance of RC Framed Structures. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2019. [Google Scholar]
- Qin, X.C.; Ding, M.B.; Lu, J.H.; Liu, D.; Hao, Y. Quasi-static test study on railway gravity piers with unbonded steel bars. J. Nat. Disasters 2022, 31, 134–141. [Google Scholar]
- Pan, S.; Chen, D.; Chen, X.; Ge, G.; Su, D.; Liu, C. Experimental Study on the Workability and Stability of Steel Slag Self-Compacting Concrete. Appl. Sci. 2020, 10, 1291. [Google Scholar] [CrossRef]
- GB/T 228.1-2010; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Tensile Testing of Metallic Materials—Part 1: Methods of Test at Room Temperature. China Standards Press: Beijing, China, 2011.
- GB/T 50010-2010; Ministry of Housing and Urban-Rural Development of the People’s Republic of China, Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010.
- GB 50011-2010; Ministry of Housing and Urban-Rural Development of the People’s Republic of China, Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010.
- JGJ 55-2011; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Concrete Mixes. China Architecture & Building Press: Beijing, China, 2011.
- JGJ/T 101-2015; Ministry of Housing and Urban-Rural Development of the People’s Republic of China, Standard for Seismic Isolation Design of Buildings. China Architecture & Building Press: Beijing, China, 2015.
- Zhao, X.; Wu, Y.-F.; Leung, A.; Lam, H.F. Plastic Hinge Length in Reinforced Concrete Flexural Members. Procedia Eng. 2011, 14, 1266–1274. [Google Scholar] [CrossRef]
- Pokhrel, M.; Bandelt, M.J. Plastic hinge behavior and rotation capacity in reinforced ductile concrete flexural members. Eng. Struct. 2019, 200, 109699. [Google Scholar] [CrossRef]
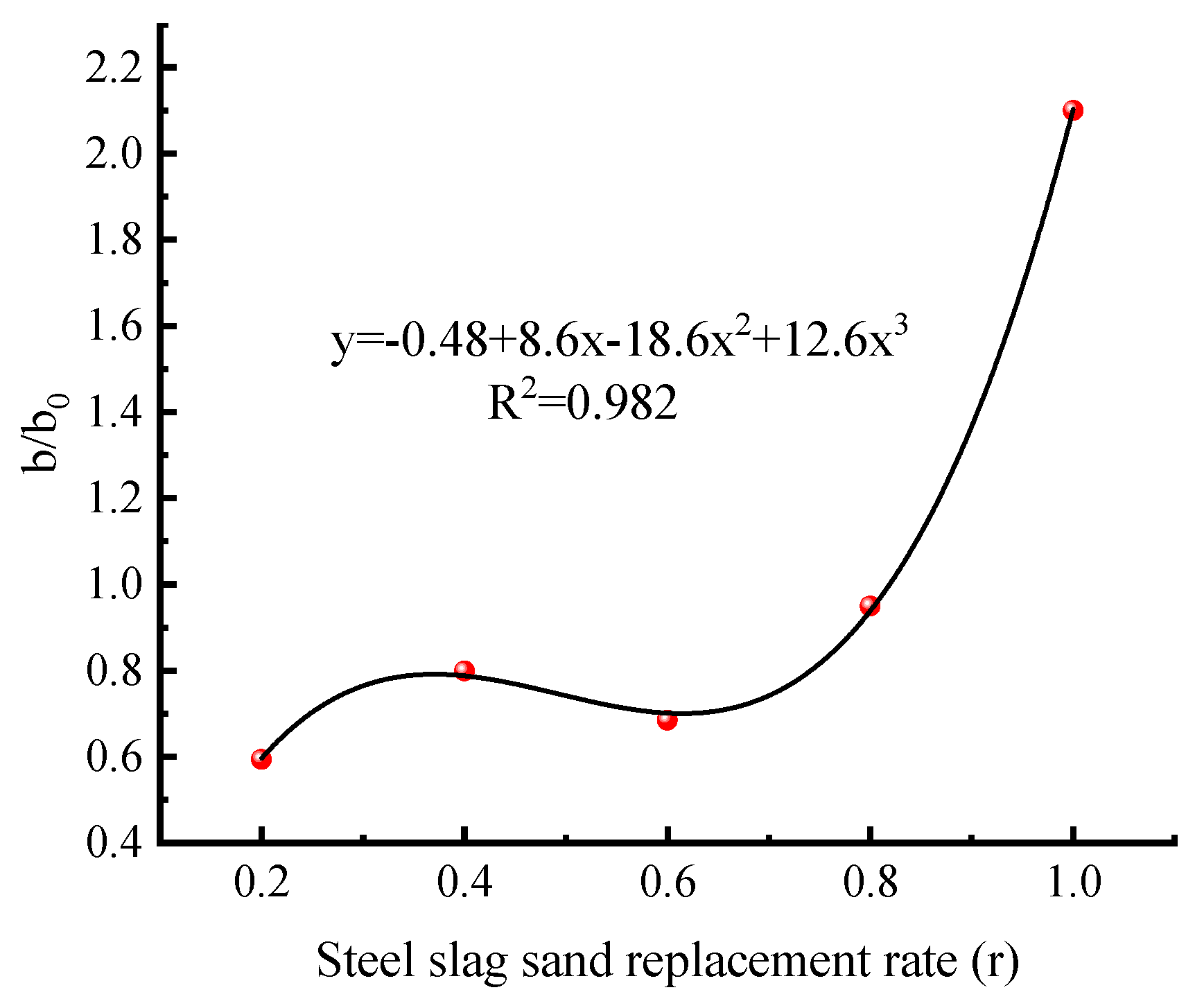
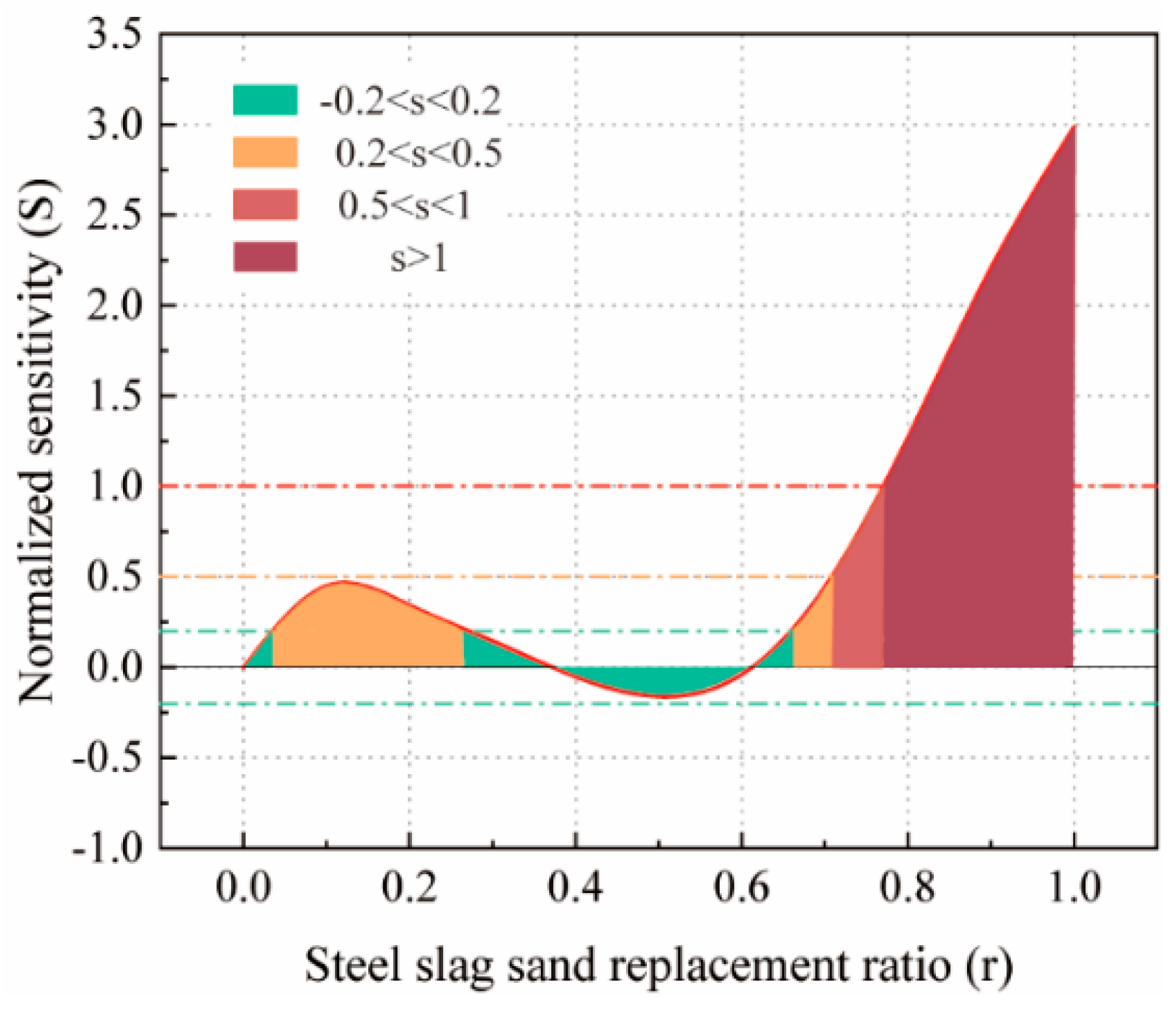
- Xue, G.; Fu, Q.; Xu, S. Macroscopic mechanical properties and microstructure characteristics of steel slag fine aggregate concrete. J. Build. Eng. 2022, 56, 104742. [Google Scholar] [CrossRef]
- Pan, Z.; Zhou, J.; Jiang, X. Investigating the effects of steel slag powder on the properties of self-compacting concrete with recycled aggregates. Constr. Build. Mater. 2019, 200, 570–577. [Google Scholar] [CrossRef]
- Gu, X.; Wang, H.; Zhu, Z.; Liu, J.; Xu, X.; Wang, Q. Synergistic effect and mechanism of lithium slag on mechanical properties and microstructure of steel slag-cement system. Constr. Build. Mater. 2023, 396, 131768. [Google Scholar] [CrossRef]
- Zghair, H.H. Optimization of mechanical characteristics of cement mortar incorporating hybrid nano-sustainable powders. J. Mech. Behav. Mater. 2024, 33, 20240008. [Google Scholar] [CrossRef]
- Valikhani, A.; Jahromi, A.J.; Mantawy, I.M.; Azizinamini, A. Experimental evaluation of concrete-to-UHPC bond strength with correlation to surface roughness for repair application. Constr. Build. Mater. 2020, 283, 117753. [Google Scholar] [CrossRef]
- Lee, H.-S.; Noguchi, T.; Tomosawa, F. Evaluation of the bond properties between concrete and reinforcement as a function of the degree of reinforcement corrosion. Cem. Concr. Res. 2002, 32, 1313–1318. [Google Scholar] [CrossRef]
- Yuan, T.; Mao, Y. A review of pinch analysis techniques and extended application in power systems. Renew. Sustain. Energy Rev. 2024, 202, 114684. [Google Scholar] [CrossRef]
- He, H.; Cheng, S.; Chen, Y. Earthquake damage assessment model based on differential ratio of elastic–plastic dissipated energy. Bull. Earthq. Eng. 2022, 20, 2719–2749. [Google Scholar] [CrossRef]
- Le Minh, H.; Khatir, S.; Wahab, M.A.; Cuong-Le, T. A concrete damage plasticity model for predicting the effects of compressive high-strength concrete under static and dynamic loads. J. Build. Eng. 2021, 44, 103239. [Google Scholar] [CrossRef]
- Ren, Z.; Li, D. Uniaxial compressive behavior study of normal-strength concrete using waste steel slag aggregate through laboratory tests and numerical simulation. J. Build. Eng. 2024, 85, 108720. [Google Scholar] [CrossRef]
- Xiao, Y.; Chen, Z.; Zhou, J.; Leng, Y.; Xia, R. Concrete plastic-damage factor for finite element analysis: Concept, simulation, and experiment. Adv. Mech. Eng. 2017, 2017, 168781401771964. [Google Scholar] [CrossRef]
- Mohemmi, M.; Broujerdian, V.; Rajaeian, P. An Equivalent Method for Bar Slip Simulation in Reinforced Concrete Frames. Int. J. Civ. Eng. 2020, 18, 851–863. [Google Scholar] [CrossRef]
- Gao, D.; Xie, J.; Li, C. Basic issues of bond behavior of fiber-reinforced polymer bars in concrete. J. Zhengzhou Univ. (Eng. Sci. Ed.) 2002, 23, 1–5. [Google Scholar]
- Bai, G.; Liu, B. Nonlinear finite element analysis of bond-slip performance of recycled aggregate concrete filled circular steel tube. J. Adhes. Sci. Technol. 2019, 33, 1294–1319. [Google Scholar] [CrossRef]
- Xiao, J.; Falkner, H. Bond behaviour between recycled aggregate concrete and steel rebars. Constr. Build. Mater. 2007, 21, 395–401. [Google Scholar] [CrossRef]
- Zou, J.-F.; Wu, Q.-H. Three-dimensional elastoplastic analysis of strain-softening surrounding rock based on the non-linear bond-slip relationship considering hydraulic-mechanical coupling. Eur. J. Environ. Civil Eng. 2024, 28, 3567–3586. [Google Scholar] [CrossRef]
- Cao, S.; Wang, Y.; Wang, J. Influence of bond-slip behavior on seismic performance of reinforced concrete columns. Eng. Struct. 2020, 207, 110254. [Google Scholar]
- Saatcioglu, M.; Razvi, S.R. Strength and ductility of confined concrete. J. Struct. Eng. 1992, 118, 1590–1607. [Google Scholar] [CrossRef]






| SiO2 | Al2O3 | Fe2O3 | CaO | MgO | SO3 | Na2O | K2O | Loss |
|---|---|---|---|---|---|---|---|---|
| 24.96 | 4.88 | 3.58 | 60.97 | 1.19 | 0.95 | 0.13 | 0.78 | 2.56 |
| Cement Grade | Specific Gravity (g/cm3) | Blaine Surface Area (m2/kg) | Water Requirement of Standard Consistency (%) | Setting Time (min) | Flexural Strength (MPa) | Compressive Strength (MPa) | |||
|---|---|---|---|---|---|---|---|---|---|
| Initial Setting | Final Setting | 3 d | 28 d | 3 d | 28 d | ||||
| 42.5R | 3.13 | 346 | 27.8 | 147 | 208 | 5.1 | 7.3 | 26.7 | 49.8 |
| Aggregates | Apparent Relative Density (kg/m3) | Bulk Density (Kg/m3) | Water Absorption (%) | Crush Value (%) | Fineness Modulus |
|---|---|---|---|---|---|
| Natural stone | 2588 | 1438 | 0.72 | 8.74 | |
| Natural sand | 2659 | 1596 | 0.97 | 7.25 | 2.71 |
| Steel slag sand | 3322 | 1925 | 1.2 | 4.37 | 2.86 |
| Chemical Composition | SiO2 | CaO | MgO | Fe2O3 | P2O5 | Al2O3 | MnO | f-CaO | Other |
|---|---|---|---|---|---|---|---|---|---|
| Content (%) | 12.97 | 42.63 | 8.44 | 20.3 | 4.33 | 0.94 | 0.73 | 2.3 | 7.36 |
| Diameter (mm) | Area (mm2) | Yield Strength (MPa) | Yield Strain (με) | Ultimate Strength (MPa) | Poisson’s Ratio | |
|---|---|---|---|---|---|---|
| Nominal | Measured | |||||
| 8 | 50.27 | 50.68 | 413 | 1915 | 590 | 0.3 |
| 16 | 201.1 | 211.05 | 454 | 2185 | 621 | 0.3 |
| Sample ID | Cement (kg/m3) | NAS (kg/m3) | Steel Slag Sand (kg/m3) | NAC (kg/m3) | Water (kg/m3) | WRA (kg/m3) |
|---|---|---|---|---|---|---|
| C-1 | 375 | 852 | - | 1017 | 169 | 3.00 |
| C-2 | 681.6 | 207.57 | 3.225 | |||
| C-3 | 511.2 | 415.15 | 3.45 | |||
| C-4 | 340.8 | 622.72 | 3.675 | |||
| C-5 | 170.4 | 830.29 | 3.90 | |||
| C-6 | - | 1037.87 | 4.125 |
| Sample ID | fcu, 7d (MPa) | fcu, 28d (MPa) | fc (MPa) | fts, 28d (MPa) | τ (MPa) | fc/fcu |
|---|---|---|---|---|---|---|
| PC | 27.7 | 36.1 | 28.2 | 3.26 | 10.34 | 0.78 |
| SSC-20 | 33.5 | 42.8 | 33.2 | 3.56 | 14.07 | 0.78 |
| SSC-40 | 29.7 | 39.3 | 30.9 | 3.83 | 13.48 | 0.79 |
| SSC-60 | 29.9 | 37.0 | 28.4 | 2.88 | 10.32 | 0.77 |
| SSC-80 | 29.0 | 35.0 | 26.8 | 2.65 | 10.48 | 0.76 |
| SSC-100 | 28.0 | 35.6 | 27.6 | 2.26 | 9.59 | 0.80 |
| Calculation Parameters | Load Direction | C-1 | C-2 | C-3 | C-4 | C-5 | C-6 |
|---|---|---|---|---|---|---|---|
| Peak load (KN) | Positive | 152.7 | 176.5 | 165.6 | 167.3 | 149.8 | 152.9 |
| Negative | 166.4 | 198.3 | 181.1 | 178.0 | 165.7 | 169.1 | |
| Averages | 159.5 | 185.4 | 173.4 | 172.7 | 157.8 | 161.0 | |
| Yield load (KN) | Positive | 129.0 | 151.6 | 140.9 | 140.1 | 126.3 | 126.1 |
| Negative | 143.2 | 167.9 | 159.1 | 154.5 | 143.9 | 151.0 | |
| Averages | 136.1 | 159.8 | 150.0 | 147.3 | 135.1 | 138.6 | |
| Yield displacement (mm) | Positive | 11.3 | 13.0 | 10.4 | 10.8 | 10.2 | 9.4 |
| Negative | 10.3 | 12.6 | 11.3 | 11.4 | 9.6 | 8.7 | |
| Averages | 10.8 | 12.8 | 10.85 | 11.1 | 9.9 | 9.1 | |
| Ultimate load (KN) | Positive | 123.0 | 134.8 | 130.3 | 128.8 | 117.1 | 119.4 |
| Negative | 133.3 | 169.5 | 157.0 | 151.0 | 135.4 | 138.2 | |
| Averages | 128.2 | 152.2 | 143.7 | 139.9 | 126.3 | 128.8 | |
| Ultimate displacement (mm) | Positive | 43.2 | 51.5 | 47.9 | 41.8 | 40.1 | 35.5 |
| Negative | 43.2 | 51.5 | 47.9 | 41.8 | 40.1 | 35.5 | |
| Averages | 43.2 | 51.4 | 47.9 | 41.8 | 40.1 | 35.5 |
| Sample ID | Load Direction | Yield Displacement (mm) | Ultimate Displacement (mm) | Ductility Coefficient | Average | Ultimate Displacement Angle (%) | Average (%) |
| C-1 | Positive | 11.3 | 43.2 | 3.8 | 3.95 | 1.200 | 1.200 |
| Negative | 10.3 | 43.2 | 4.1 | 1.200 | |||
| C-2 | Positive | 13.0 | 51.5 | 4.0 | 4.05 | 1.422 | 1.427 |
| Negative | 12.6 | 51.5 | 4.1 | 1.431 | |||
| C-3 | Positive | 10.4 | 47.9 | 4.6 | 4.4 | 1.331 | 1.331 |
| Negative | 11.3 | 47.9 | 4.2 | 1.331 | |||
| C-4 | Positive | 10.8 | 41.8 | 3.9 | 3.8 | 1.160 | 1.160 |
| Negative | 11.4 | 41.8 | 3.7 | 1.160 | |||
| C-5 | Positive | 10.2 | 39.6 | 3.8 | 3.95 | 1.115 | 1.114 |
| Negative | 9.6 | 39.6 | 4.1 | 1.114 | |||
| C-6 | Positive | 9.4 | 35.5 | 3.8 | 3.9 | 0.987 | 0.987 |
| Negative | 8.7 | 35.5 | 4.1 | 0.987 |
| Sample ID | Characteristic Point | Δf/mm | /mm | /mm | % |
|---|---|---|---|---|---|
| C-1 | Yield point | 7.02 (65.4) | 0.66 (6.2) | 1.29 (10.1) | 83.2 |
| Peak point | 15.04 (66.3) | 1.45 (6.4) | 3.87 (15.2) | 89.4 | |
| Limit point | 29.46 (68.2) | 3.02 (7.1) | 8.21 (17.7) | 94.2 | |
| C-2 | Yield point | 8.62 (67.2) | 1.03 (8.0) | 1.26 (9.8) | 84.8 |
| Peak point | 18.36 (67.2) | 2.45 (9.1) | 2.73 (10.9) | 86.2 | |
| Limit point | 35.54 (69.3) | 4.73 (9.2) | 5.77 (11.2) | 89.4 | |
| C-3 | Yield point | 8.56 (71.5) | 0.71 (6.0) | 0.63 (5.3) | 82.8 |
| Peak point | 16.2 (72.7) | 1.62 (7.2) | 1.53 (6.8) | 85.8 | |
| Limit point | 35.46 (74.5) | 4.26 (8.9) | 4.26 (10.9) | 91.8 | |
| C-4 | Yield point | 7.64 (72.2) | 0.70 (6.8) | 0.72 (6.9) | 86.9 |
| Peak point | 13.72 (72.4) | 1.32 (7.3) | 1.36 (7.5) | 90.2 | |
| Limit point | 30.02 (73.7) | 3.59 (8.6) | 3.72 (11.9) | 94.2 | |
| C-5 | Yield point | 6.82 (68.8) | 0.87 (8.7) | 0.96 (9.6) | 86.3 |
| Peak point | 12.24 (69.8) | 1.61 (9.2) | 2.19 (12.5) | 91.5 | |
| Limit point | 29.02 (72.3) | 3.33 (8.3) | 5.69 (14.2) | 94.8 | |
| C-6 | Yield point | 5.57 (69.3) | 0.35 (4.2) | 0.87 (9.8) | 87.8 |
| Peak point | 9.49 (72.5) | 1.65 (4.2) | 1.95 (12.3) | 88.2 | |
| Limit point | 24.99 (72.1) | 2.92 (5.4) | 5.19 (13.8) | 93.2 |
| Dilation | Eccentricity | fcb/fc0 | K | μ |
|---|---|---|---|---|
| 30 | 0.1 | 1.16 | 0.0067 | 0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Zhang, D.; Jin, Q.; Li, S.; Liu, X. Effect of Steel Slag Fine Aggregate on the Seismic Behavior of Reinforced Concrete Columns with Steel Slag Sand. Buildings 2025, 15, 1769. https://doi.org/10.3390/buildings15111769
Zhao T, Zhang D, Jin Q, Li S, Liu X. Effect of Steel Slag Fine Aggregate on the Seismic Behavior of Reinforced Concrete Columns with Steel Slag Sand. Buildings. 2025; 15(11):1769. https://doi.org/10.3390/buildings15111769
Chicago/Turabian StyleZhao, Tianhai, Dongling Zhang, Qiang Jin, Sen Li, and Xuanxuan Liu. 2025. "Effect of Steel Slag Fine Aggregate on the Seismic Behavior of Reinforced Concrete Columns with Steel Slag Sand" Buildings 15, no. 11: 1769. https://doi.org/10.3390/buildings15111769
APA StyleZhao, T., Zhang, D., Jin, Q., Li, S., & Liu, X. (2025). Effect of Steel Slag Fine Aggregate on the Seismic Behavior of Reinforced Concrete Columns with Steel Slag Sand. Buildings, 15(11), 1769. https://doi.org/10.3390/buildings15111769






