Dynamic Simulation of Solar-Assisted Medium-Depth Ground Heat Exchanger Direct Heating System

Abstract

The global challenges of rising energy consumption and carbon emissions underscore the urgent need for efficient and sustainable heating solutions in the building sector. The implementation of high-performance buildings that envelope insulation and the increasing adoption of low-temperature radiant heating systems have significantly reduced the water temperature required from heat sources, enabling greater compatibility with renewable energy systems. In this study, we propose a renewable energy heating system incorporating a solar-assisted medium-depth ground heat exchanger (MDGHE). A dynamic simulation model of the solar-assisted MDGHE system was developed in TRNSYS, featuring a novel MDGHE module specifically developed to improve simulation accuracy. A case study of a residential building in China was conducted to evaluate the performance of the proposed system. The simulation results demonstrate that while the standalone MDGHE covers 71.9% of the building’s heating demand, integrating solar collectors with the MDGHE can increase this coverage to 99.9%, enabling full compliance with heating requirements without relying on conventional heat pumps. The results revealed that the system’s COP reached 9.26. Compared with the traditional medium-depth ground source heat pump system with the COP of 4.84, the energy efficiency of this system has been enhanced by 47.7%. A static payback period of 7 years has been obtained compared with the cost of central heating service for residential buildings. These findings highlight the potential of solar-geothermal hybrid systems as a sustainable alternative to traditional heating methods.

1. Introduction

The global demand for climate change mitigation has driven nations worldwide to establish ambitious carbon neutrality commitments. In this context, China’s building sector emerges as a critical energy consumer, with recent data indicating an annual energy use figure exceeding 1 Gtce (gigaton of coal equivalent), representing nearly one-quarter of national energy consumption. Notably, space heating in northern urban areas contributes over one-fifth of the total building-related energy demand [1]. These consumption patterns present significant challenges to China’s dual goals of reaching peak carbon emissions before 2030 and achieving carbon neutrality by 2060. As a result, the decarbonization of space-heating systems has become a critical priority within the nation’s broader energy transition strategy.

Among renewable alternatives, geothermal energy has emerged as a sustainable solution for space heating and cooling in buildings because of its abundant availability and high efficiency. Based on the extraction depth, geothermal energy can be categorized into shallow geothermal energy (0–200 m deep) and medium-depth geothermal energy (2000–3500 m deep). In order to use geothermal energy more efficiently, it is critical to establish accurate and effective ground heat exchanger models.

As for the shallow geothermal energy applications, researchers have developed a variety of numerical and analytical solution models to analyze the heat transfer characteristics of ground heat exchangers. A numerical simulation is based on employing discretized numerical calculations to solve a problem. The finite volume method (FVM) [2], finite element method (FEM) [3], and finite difference method (FDM) [4] are mainly used to analyze the heat transfer of underground temperature fields. On the other hand, Kelvein [5] proposed a linear heat source theory model, which laid the foundations for heat transfer analysis in ground heat exchangers. Subsequently, Carslaw and Jaeger [6] introduced an infinite-length cylindrical heat source model, simplifying the structure within the borehole to an infinitely long linear or cylindrical heat source distributed along the axis. Philippe [7] further developed a three-dimensional transient far-field boundary heat transfer model, constructed based on the principle of energy balance. As research continues to deepen, theoretical models have been further optimized and refined. For example, Bandos [8] proposed a three-dimensional finite line source model for borehole heat exchangers (BHEs), which can be used for the design of complex borehole structures. Jia [9] built an infinite-line source model (ILSM), considering the non-uniformity of specific heat flux along the vertical direction of the borehole wall, and developed an enhanced variable-heat-flux density model using the superposition method.

However, shallow geothermal energy is typically utilized via heat pump technology, and it is well-suited to buildings with relatively balanced heating and cooling loads due to its character of relatively low energy density [10,11]. In comparison, medium-depth geothermal systems offer greater energy quality and storage capacity, making them particularly suitable for heating-dominated buildings in northern areas. While conventional U-tube ground heat exchangers (GHEs) are widely employed in shallow geothermal systems, coaxial GHEs are often preferred in medium-depth geothermal systems because of their superior structural stability and enhanced heat transfer performance in deep boreholes exceeding 2000 m [12].

Over the past decade, medium-depth ground heat exchangers (MDGHEs) have emerged as a transformative geothermal technology in China, undergoing significant advancements in both practical applications and theoretical research. Deng [13] demonstrated that ground-source heat pump (GSHP) systems incorporating MDGHEs achieved significantly better thermal performance than conventional shallow geothermal systems. Under continuous 48 h operational testing, the system exhibited heat extraction rates per unit borehole length that were 1.5–3.6 times higher than the shallow counterparts. To enhance the performance of MDGHEs, Jiankai Dong [14] reviewed the effects of multiple factors on the thermal performance of deep-borehole heat exchangers, aiming to guide the design and use of MDGHEs. The results of their study demonstrate that there is a strong positive correlation between inlet and outlet temperatures in MDGHEs. Under high-inlet-temperature conditions (23 °C), these systems consistently deliver elevated outlet temperatures (35 °C), making direct heating possible. Compared to indirect heating systems using medium-depth GSHPs, the direct utilization of circulating fluid from MDGHEs can significantly improve operational efficiency by eliminating the need to activate the heat pump when the fluid temperature is sufficiently high, such as over 30 °C. The direct utilization of MDGHEs for heating purposes has been successful in several developed countries. As shown in

Table 1. Summary of international case studies on medium-depth geothermal heating technologies [15].

Location	Borehole Depth (m)	Ground Temperature at the Bottom of the Borehole (°C)	Inlet Water Temperature (°C)	Outlet Water Temperature (°C)
Penzlau, Germany	2786	108	35	70
Aachen, Germany	2500	85	40	25~55
Weggis, Switzerland	2300	78	32	45
Hawaii, United States	1962	110	30	98

, critical operational parameters, such as the ground temperatures at the bottom of the borehole and the water temperatures during the initial operation period, from different projects were documented. These data provide essential benchmarks for evaluating the technical feasibility and thermal performance of MDGHE systems in direct heating applications.

Currently, research on MDGHEs focuses on using them as low-temperature heat sources for heat pump units, which then indirectly provide heating to the end-user [16]. However, studies on direct heating systems using MDGHEs remain relatively scarce. In fact, during the initial heating phase, the outlet water temperature of medium-depth buried pipes can exceed 30 °C, a temperature range that is particularly suitable for low-temperature terminal devices such as radiant floors [15]. Therefore, MDGHEs can be an excellent direct heat source for heating systems. When their outlet water temperature is too low to meet the heating needs of the terminal users, they can be considered for combined heating with other heat sources. Wang [17] established a model of MDGHEs using MATLAB and coupled it with TRNSYS software to design a direct heating system for MDGHEs. He found that in the first few days of the heating season, the MDGHEs could provide direct heating. Liu [18] established a simulation model for a deep buried-pipe heat pump heating system based on TRNSYS software. According to water supply temperature conditions, the model achieved switching control between direct heating and indirect heating under different load ratios. Yuan [19] addressed the issue of the seasonal imbalance in energy supply and demand by constructing a simulation model that dynamically couples solar cross-seasonal thermal storage with deep buried ground-source heat pump systems.

It is well known that continuous heat extraction leads to a progressive decline in the outlet water temperature from MDGHEs. This phenomenon significantly impacts the long-term viability of direct heating systems utilizing MDGHEs. A viable approach to overcoming this technical constraint is using solar energy for seasonal thermal storage and supplementary heating during the winter [20,21,22]. As the price of solar thermal collectors drops, solar-assisted GSHP heating systems will offer increasingly better cost-effectiveness.

At present, research on solar-assisted buried-pipe heating mainly focuses on the composite-system heating provided by solar-assisted ground-source heat pump systems [23]. The integration of shallow geothermal and solar thermal energy has been widespread, offering a promising solution for maintaining consistent heating performance throughout operational cycles [24]. Recent research has revealed a particular interest in solar-assisted GSHP configurations, especially in challenging climatic conditions. Turan [25] used TRNSYS software to model a solar-assisted ground-source heat pump (SAGSHP) composite system, conducting a 20-year simulation study in six U.S. cities with different climate conditions. The results showed that the system demonstrates significant economic and energy-saving benefits in regions primarily focused on heating. Bakker [26] used TRNSYS software to simulate a solar-assisted ground-source heat pump coupled heating system equipped with a 25 m² solar energy collector. Their research revealed that this system not only meets the heating needs of single-family residences but also maintains stable soil temperatures by injecting excess solar energy into the ground, effectively avoiding the issue of COP decline during the long-term operation of a heat pump. Reda [27] investigated system performance in Finland’s cold climate through comprehensive TRNSYS simulations comparing conventional GSHP systems with solar-enhanced inter-seasonal heat storage (SEIHS-GSHP) systems. Their findings revealed that properly designed SEIHS-GSHP systems achieve superior performance when optimal borehole configurations are paired with appropriately selected solar collectors. Furthermore, strategic optimization of solar thermal utilization was shown to enhance key performance indicators, including both the Seasonal Performance Factor (SPF) and Primary Energy Ratio (PER), by significant margins. Mehrpanahi et al. [28] conducted a comprehensive study on system configuration optimization for a solar-assisted GSHP (SAGSHP) in Tehran’s distinct climate, developing tailored control strategies to effectively meet buildings’ thermal demands. In order to address the problem of heating loads being higher than cooling loads in cold climates, a comprehensive investigation of the long-term performance of single U-tube and double U-tube GHEs for SAGSHPs was carried out, and the results were compared with those obtained for a conventional GSHP [29]. The results showed that the yearly average heating coefficient of performance (COP) increased by a factor of 1.21 and 1.18 for the single and double U-tube SAGSHPs, respectively, when compared with that of the conventional GSHP. Sun Chang [30] addressed the issue of decreasing soil temperatures over time in GSHP applications in northwestern rural areas by integrating a solar–GSHP system. Through comprehensive TRNSYS modeling, their work not only validated the system’s technical feasibility but also established optimal operational protocols for maximizing performance.

While existing studies have extensively explored solar-assisted shallow geothermal systems, significant knowledge gaps remain regarding the direct heating applications of MDGHEs in hybrid solar–geothermal configurations. A particularly underexplored area is the system behavior under transient operating conditions and variable building thermal demands. This study introduces an innovative direct heating system that synergistically combines MDGHE technology with a solar thermal collector, eliminating the need for a conventional heat pump. Through comprehensive parameter optimization, we demonstrate the technical feasibility of achieving fully renewable heating for buildings by using the proposed solar-assisted MDGHE system. The research outcomes provide critical insights for implementing such systems in practical engineering applications, addressing both performance characteristics under dynamic loads and operational strategies for maximizing renewable energy utilization.

2. Development of a Module for the Medium-Depth Ground Heat Exchanger

The conventional heat transfer model for GHEs in TRNSYS (i.e., the Type 557d module) exhibits several computational constraints when used for MDGHE simulations. Key limitations in this regard include (1) the inability to define the ground heat flux boundary conditions, (2) restricted nodal resolution in numerical discretization, and (3) the assumption of uniform thermal conductivity for both the inner and outer pipes. To overcome these modeling deficiencies, we developed and implemented a novel TRNSYS simulation module specifically tailored for coaxial MDGHE systems.

The thermal performance of GHEs, serving as the primary equipment for subsurface energy extraction, requires both operational stability and high thermodynamic efficiency. Two configurations are commonly employed in current engineering practices: U-tube and coaxial-casing designs. Comparative analysis has revealed that coaxial-type exchangers offer distinct advantages, including (1) an enhanced heat transfer surface area per unit installation volume, (2) improved structural integrity due to a concentric pipe arrangement, and (3) a superior heat exchange capacity. These characteristics make coaxial systems particularly suitable for medium-depth applications.

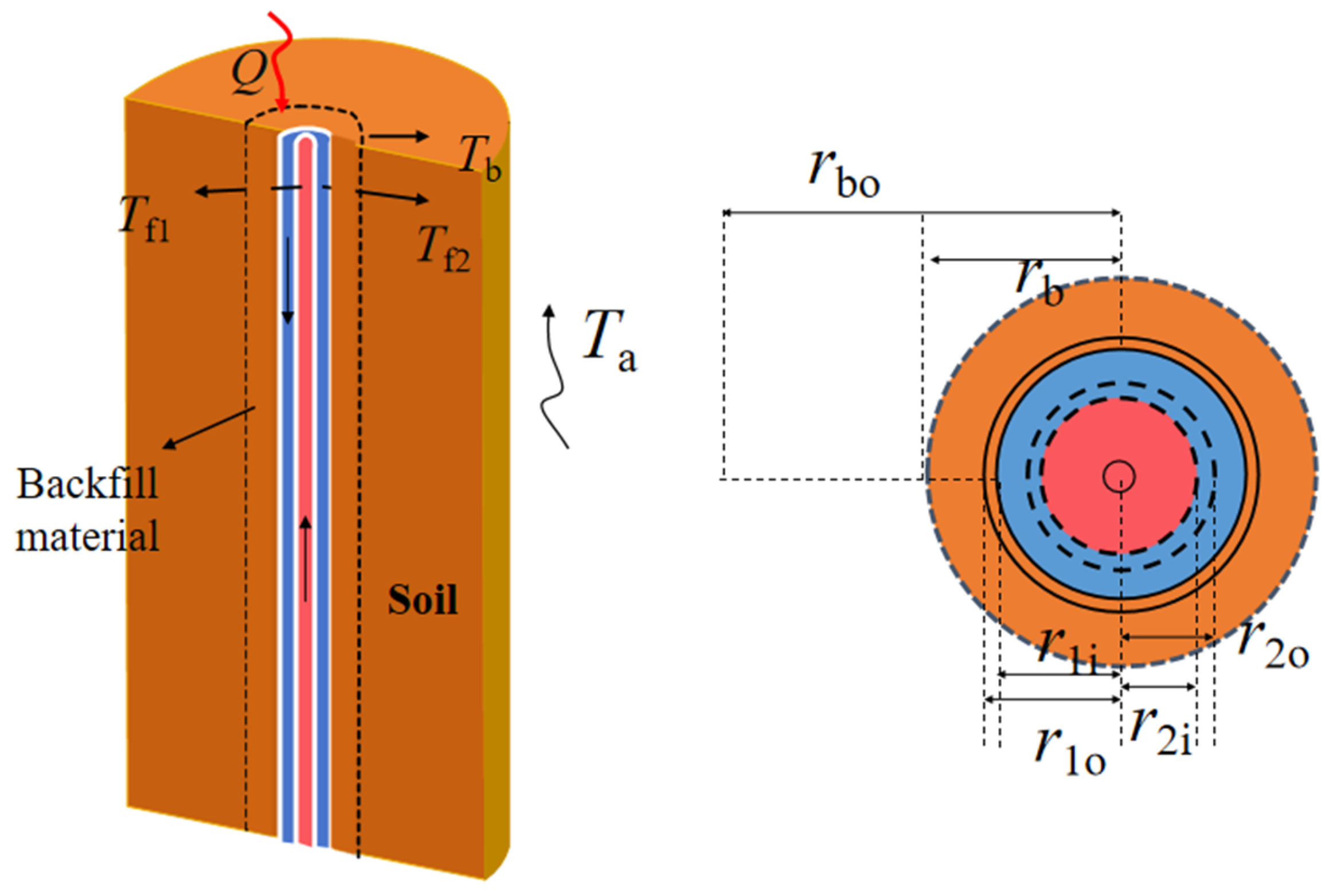
In this study, a coaxial-casing heat exchanger utilizing water as the circulating fluid within the sleeve was employed. Figure 1 presents a detailed rendering of the structure of the MDGHE.

Cylindrical coordinate systems are employed in the thermal analysis of MDGHEs to exploit the inherent axisymmetric characteristics of both the borehole and surrounding geological formations. In order to simplify the calculation process, the following assumptions are made: (1) the radial fluid temperature is uniform; (2) the thermal properties of the circulating fluid, borehole, and underground remain stable and are unaffected by temperature; (3) the underground medium is stratified, with each layer being homogeneous; (4) the temperature of the ground surface remains constant; (5) radial heat conduction within the borehole can be ignored; and (6) geothermal heat flow through the entire medium remains constant.

2.1. Governing Equations for the Medium-Depth Ground Heat Exchanger

Based on the aforementioned modeling assumptions, the heat transfer mechanism in the coaxial borehole can be mathematically described using the following governing equations. Taking advantage of the axial symmetry characteristic, the heat conduction equation for each geological layer is expressed as

$$\begin{array}{c}{\displaystyle \frac{1}{{\mathrm{a}}_{\mathrm{s}}}}{\displaystyle \frac{\partial \mathrm{T}}{\partial \mathsf{\tau }}}={\displaystyle \frac{1}{\mathrm{r}}}{\displaystyle \frac{\partial }{\partial \mathrm{r}}}\left(\mathrm{r}{\displaystyle \frac{\partial \mathrm{T}}{\partial \mathrm{r}}}\right)+{\displaystyle \frac{\partial {\mathrm{T}}^2}{\partial {\mathrm{z}}^2}}\end{array}$$

(1)

where α_s is the thermal diffusivity of the geological layer, in m²/s; T is the temperature of the geological layer, in °C; τ is the time step, which is one hour in this study; and r and z represent the radial and vertical coordinate variables, in m.

When the circulating fluid follows an “outer-in, inner-out” pattern, the governing equations for the outer and inner pipes are as follows:

$$\begin{array}{c}\left\{\begin{array}{c}{\mathrm{C}}_1{\displaystyle \frac{\partial {\mathrm{T}}_{\mathrm{f}1}}{\partial \mathsf{\tau }}}={\displaystyle \frac{{\mathrm{T}}_{\mathrm{f}1}-{\mathrm{T}}_{\mathrm{f}2}}{{\mathrm{R}}_2}}+{\displaystyle \frac{{\mathrm{T}}_{\mathrm{b}}-{\mathrm{T}}_{\mathrm{f}1}}{{\mathrm{R}}_1}}-C{\displaystyle \frac{\partial {\mathrm{T}}_{\mathrm{f}1}}{\partial \mathrm{z}}}\\ {\mathrm{C}}_2{\displaystyle \frac{\partial {\mathrm{T}}_{\mathrm{f}2}}{\partial \mathsf{\tau }}}={\displaystyle \frac{{\mathrm{T}}_{\mathrm{f}1}-{\mathrm{T}}_{\mathrm{f}2}}{{\mathrm{R}}_2}}+C{\displaystyle \frac{\partial {\mathrm{T}}_{\mathrm{f}2}}{\partial \mathrm{z}}}\end{array}\right.\end{array}$$

(2)

In these equations,

$${\mathrm{C}}_1=\pi \left({\mathrm{r}}_{1\mathrm{i}}^2-{\mathrm{r}}_{2\mathrm{o}}^2\right)\rho c+\pi \left({\mathrm{r}}_{1\mathrm{o}}^2-{\mathrm{r}}_{1\mathrm{i}}^2\right){\mathsf{\rho }}_2{\mathrm{c}}_2+\pi \left({\mathrm{r}}_{\mathrm{b}}^2-{\mathrm{r}}_{1\mathrm{o}}^2\right){\mathsf{\rho }}_{\mathrm{g}}{\mathrm{c}}_{\mathrm{g}}$$

$${\mathrm{C}}_2=\mathsf{\pi }{\mathrm{r}}_{2\mathrm{i}}^2\mathsf{\rho }\mathrm{c}+\mathsf{\pi }\left({\mathrm{r}}_{2\mathrm{o}}^2-{\mathrm{r}}_{2\mathrm{i}}^2\right){\mathsf{\rho }}_1{\mathrm{c}}_1$$

$${\mathrm{R}}_1={\displaystyle \frac{1}{2\mathsf{\pi }{\mathrm{r}}_{1\mathrm{i}}{\mathrm{h}}_1}}+{\displaystyle \frac{1}{2\mathsf{\pi }{\mathrm{k}}_{\mathrm{p}1}}}\ln \left({\displaystyle \frac{{\mathrm{r}}_{1\mathrm{o}}}{{\mathrm{r}}_{1\mathrm{i}}}}\right)+{\displaystyle \frac{1}{2\mathsf{\pi }{\mathrm{k}}_{\mathrm{g}}}}\ln \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{b}}}{{\mathrm{r}}_{1\mathrm{o}}}}\right)$$

$${\mathrm{R}}_2={\displaystyle \frac{1}{2\mathsf{\pi }{\mathrm{r}}_{2\mathrm{i}}{\mathrm{h}}_2}}+{\displaystyle \frac{1}{2\mathsf{\pi }{\mathrm{k}}_{\mathrm{p}2}}}\ln \left({\displaystyle \frac{{\mathrm{r}}_{2\mathrm{o}}}{{\mathrm{r}}_{2\mathrm{i}}}}\right)+{\displaystyle \frac{1}{2\mathsf{\pi }{\mathrm{r}}_{2\mathrm{o}}{\mathrm{h}}_1}}$$

Here, ${\mathrm{k}}_{\mathrm{g}}$, ${\mathrm{k}}_{\mathrm{p}1}$, and ${\mathrm{k}}_{\mathrm{p}2}$ represent the thermal conductivity of the backfill material, outer pipe, and inner pipe, respectively, in W/(m·K); ${\mathrm{r}}_{\mathrm{b}}$, ${\mathrm{r}}_{\mathrm{i}}$, and ${\mathrm{r}}_{\mathrm{o}}$ denote the borehole radius, inner diameter, and outer diameter of the pipe, respectively, in m, with the specific structure shown in Figure 1; ${\mathrm{h}}_1$ and ${\mathrm{h}}_2$ represent the convective heat transfer coefficients for the outer and inner pipes, in W/(m²·K); and C represents the heat capacity flow rate of the circulating fluid, in kJ/(s·K).

2.2. Initial and Boundary Conditions

Under the assumption of a constant geothermal gradient and constant ground heat flow, the initial temperature distribution in each underground layer can be mathematically described using the following equation:

$$\mathrm{T}\left(\mathrm{r},\mathrm{z},\mathsf{\tau }\right)={\mathrm{T}}_{\mathrm{a}}+{\displaystyle \frac{{\mathrm{q}}_{\mathrm{g}}}{{\mathrm{h}}_{\mathrm{a}}}}+\sum _{\mathrm{j}=1}^{\mathrm{m}-1}{\displaystyle \frac{{\mathrm{q}}_{\mathrm{g}}}{{\mathrm{k}}_{\mathrm{j}}}}\left({\mathrm{H}}_{\mathrm{j}}-{\mathrm{H}}_{\mathrm{j}-1}\right)+{\displaystyle \frac{{\mathrm{q}}_{\mathrm{g}}}{{\mathrm{k}}_{\mathrm{m}}}}(\mathrm{z}-{\mathrm{H}}_{\mathrm{m}-1})$$

(3)

$$\mathsf{\tau }=0,0\le \mathrm{z}\le \mathrm{\infty },\hspace{1em}\hspace{1em}{\mathrm{r}}_{\mathrm{b}}\le \mathrm{r}<\infty$$

where ${\mathrm{T}}_{\mathrm{a}}$ is the surface air temperature, in °C; ${\mathrm{q}}_{\mathrm{g}}$ is the ground heat flux, in W/m²; ${\mathrm{h}}_{\mathrm{a}}$ is the convection heat transfer coefficient between the surface air and ground, in W/(m²·K); ${\mathrm{k}}_{\mathrm{j}}$ and ${\mathrm{k}}_{\mathrm{m}}$ are the thermal conductivity of ground in the j-th and m-th layers, in W/(m·K); the m-th layer extends downward to the bottom of the borehole (with depth given in m); ${\mathrm{H}}_{\mathrm{j}}$ and ${\mathrm{H}}_{\mathrm{m}}$ are the coordinates of the j-th and m-th layers; and ${\mathrm{r}}_{\mathrm{b}}$ is the borehole radius, in m.

At the radial boundary, the first-type boundary condition is applied, assuming that the temperature distribution remains unaffected by the heat extraction of the GHE. At the surface boundary, the third-type boundary condition is applied, assuming that the air temperature ${\mathrm{T}}_{\mathrm{a}}$ near the ground surface and the convective heat transfer coefficient ${\mathrm{h}}_{\mathrm{a}}$ remain constant.

$${\mathrm{k}}_{\mathrm{g}}{\displaystyle \frac{\partial \mathrm{T}}{\partial \mathrm{z}}}={\mathrm{h}}_{\mathrm{a}}({\mathrm{T}}_{\mathrm{g}}-{\mathrm{T}}_{\mathrm{a}}),\mathsf{\tau }\ge 0,\mathrm{z}=0,\mathrm{r}\to \mathrm{\infty }$$

(4)

The radial boundary is positioned at r = r_bnd, with r_bnd set to be significantly larger than the casing radius to ensure boundary independence. At this far-field boundary, a constant temperature (Dirichlet) condition is imposed:

$$\mathrm{T}\left({\mathrm{r}}_{\mathrm{b}\mathrm{n}\mathrm{d}},\mathsf{\tau }\right)={\mathrm{T}}_{\mathrm{a}}+{\displaystyle \frac{{\mathrm{q}}_{\mathrm{g}}}{{\mathrm{h}}_{\mathrm{a}}}}+\sum _{\mathrm{j}=1}^{\mathrm{m}-1}{\displaystyle \frac{{\mathrm{q}}_{\mathrm{g}}}{{\mathrm{k}}_{\mathrm{j}}}}\left({\mathrm{H}}_{\mathrm{j}}-{\mathrm{H}}_{\mathrm{j}-1}\right)+{\displaystyle \frac{{\mathrm{q}}_{\mathrm{g}}}{{\mathrm{k}}_{\mathrm{m}}}}(\mathrm{z}-{\mathrm{H}}_{\mathrm{m}-1})$$

(5)

$$\mathrm{r}={\mathrm{r}}_{\mathrm{b}\mathrm{n}\mathrm{d}},{\mathrm{H}}_{\mathrm{m}-1}\le \mathrm{z}\le {\mathrm{H}}_{\mathrm{m}},\mathsf{\tau }\ge 0$$

Consistent with the radial boundary treatment, the far-field boundary facing downward toward the bottom of the borehole is positioned at a depth of H_m below the bottom of the borehole. This boundary similarly employs a Dirichlet condition, assuming a constant temperature.

The initial fluid temperature within the inner and outer pipes is assumed to equilibrate with the in situ ground temperatures at corresponding depths; that is, the initial temperature is as follows:

$${\mathrm{T}}_{\mathrm{f}1}={\mathrm{T}}_{\mathrm{f}2}={\mathrm{T}}_{\mathrm{a}}+{\displaystyle \frac{{\mathrm{q}}_{\mathrm{g}}}{{\mathrm{h}}_{\mathrm{a}}}}+\sum _{\mathrm{j}=1}^{\mathrm{m}-1}{\displaystyle \frac{{\mathrm{q}}_{\mathrm{g}}}{{\mathrm{k}}_{\mathrm{j}}}}\left({\mathrm{H}}_{\mathrm{j}}-{\mathrm{H}}_{\mathrm{j}-1}\right)+{\displaystyle \frac{{\mathrm{q}}_{\mathrm{g}}}{{\mathrm{k}}_{\mathrm{m}}}}(\mathrm{z}-{\mathrm{H}}_{\mathrm{m}-1})$$

(6)

$${\mathrm{H}}_{\mathrm{m}-1}\le \mathrm{z}\le {\mathrm{H}}_{\mathrm{m}},\mathsf{\tau }=0$$

For the flow direction from outside the pipe to inside the pipe, the boundary conditions for the partial differential equation are

$$\left\{\begin{array}{c}{\mathrm{T}}_{\mathrm{f}1}={\mathrm{T}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{i}},\hspace{1em}\mathrm{z}=0\\ {\mathrm{T}}_{\mathrm{f}1}={\mathrm{T}}_{\mathrm{f}2},\hspace{1em}\mathrm{z}=\mathrm{H}\end{array}\right.$$

(7)

Here, ${\mathrm{T}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{i}}$ is the inlet fluid temperature, in °C.

2.3. Model Solution

The schematic of mesh discretization and boundary conditions is shown in Figure 2. An important feature in solving this problem is that both the radial temperature gradient and heat flux are concentrated near the center of the borehole, while they approach zero in the vicinity of the radial boundary. Therefore, our model adopts a variable step size in the radial direction and replaces it with a new coordinate.

$$\mathsf{\sigma }=\mathrm{l}\mathrm{n}\left({\displaystyle \frac{\mathrm{r}}{{\mathrm{r}}_{\mathrm{b}}}}\right)$$

(8)

The heat conduction equation in the new coordinate system can be written as

$${\displaystyle \frac{1}{{\mathsf{\alpha }}_{\mathrm{s}}}}{\displaystyle \frac{\partial \mathrm{T}}{\partial \mathsf{\tau }}}={\displaystyle \frac{1}{{\mathrm{r}}^2}}{\displaystyle \frac{{\partial }^2\mathrm{T}}{\partial {\mathsf{\sigma }}^2}}+{\displaystyle \frac{{\partial }^2\mathrm{T}}{\partial {\mathrm{z}}^2}}$$

(9)

If the uniform step size σ of the coordinate is Δσ, the corresponding r coordinate forms a geometric progression. The expression for the radial node ratio γ is

$${\displaystyle \frac{{\mathrm{r}}_{\mathrm{i}+1}}{{\mathrm{r}}_{\mathrm{i}}}}={\displaystyle \frac{{\mathrm{r}}_1}{{\mathrm{r}}_{\mathrm{b}}}}=\mathrm{e}\mathrm{x}\mathrm{p}(∆\mathsf{\sigma })=\mathsf{\gamma }$$

(10)

Here, a_s is the thermal diffusivity of different soils/rocks, in m²/s; ${\mathrm{r}}_{\mathrm{i}+1}$ and ${\mathrm{r}}_{\mathrm{i}}$ are radial coordinates at node numbers i+1 and i, respectively, given in m; and $\mathsf{\gamma }$ is the radial node ratio, set as 1.2 in this study.

When solving the two-dimensional transient coupled heat transfer problem, if an implicit finite difference method is used, the node equations for non-boundary points typically involve five unknowns, and the process of achieving an iterative solution is time-consuming. Thus, in this study, we employed the alternating time step method to establish the node equations which were shown in Appendix A. Finally, the model was compiled in TRNSYS software to simulate the temperature distribution of the MDGHE. A detailed numerical simulation of heat transfer analysis in an MDGHE using finite difference methods (including mathematical descriptions and node equation formulations) can be found in our previous studies [31].

2.4. Module Development in TRNSYS

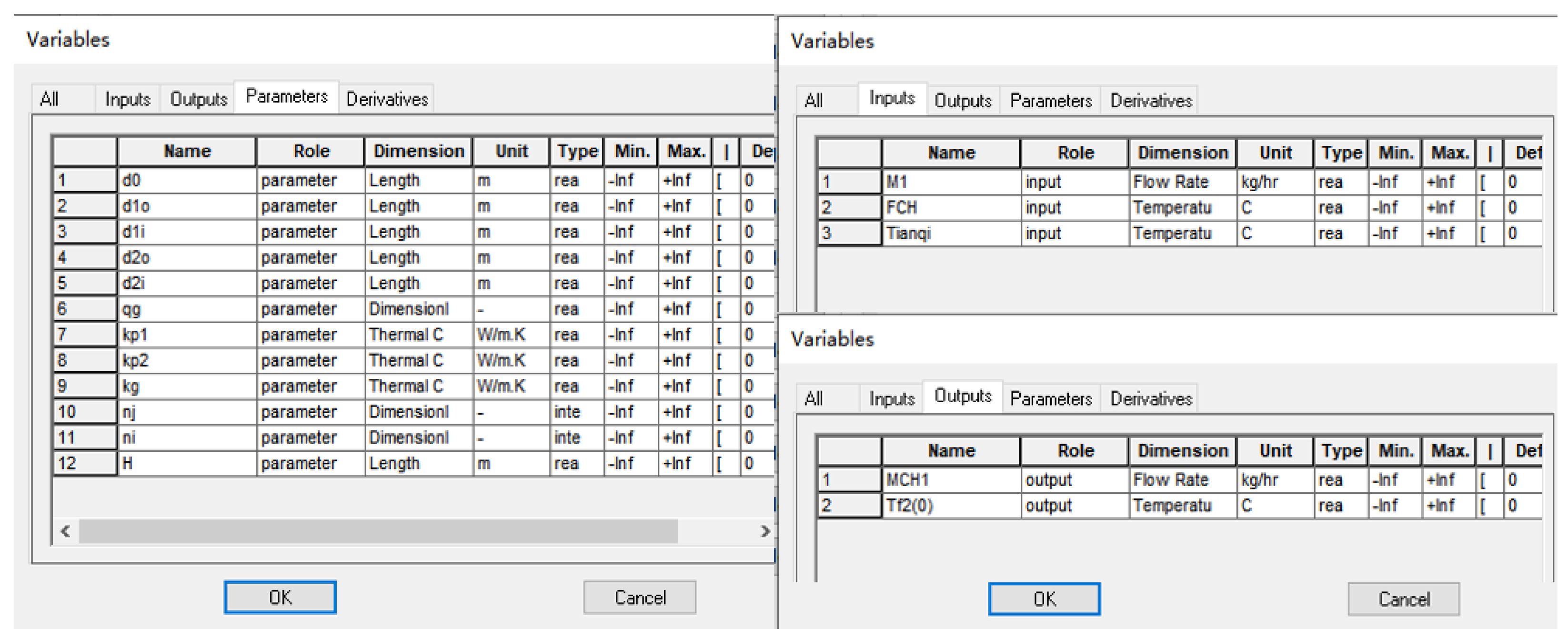
In order to allow the compiled program to successfully transfer data with other modules in TRNSYS, it is necessary to reasonably design the interface for data transfer between modules. The interface includes three tabs, as shown in Figure 3.

There are three variables in the input tab: “FCH” represents the inlet water temperature; “M1” represents the flow rate of the circulating water; and “Tianqi” represents the local outdoor temperature.

There are two variables in the output tab: “MCH1” represents the flow rate of the circulating water, and “Tf2(0)” represents the outlet water temperature.

There are twelve variables in the Parameters tab: “d0” represents the diameter of the borehole; “d1o” represents the outer diameter of the outer pipe; “d1i” represents the inner diameter of the outer pipe; “d2o” represents the outer diameter of the inner pipe; “d2i” represents the inner diameter of the inner pipe; “qg” represents ground heat flow; “kp1” represents the thermal conductivity of the outer pipe; “kp2” represents the thermal conductivity of the inner pipe; “kg” represents the thermal conductivity of the geotechnical layers; “ni” represents the number of transverse nodes; “nj” represents the number of longitudinal nodes; and “H” represents the well depth of the buried-pipe heat exchanger.

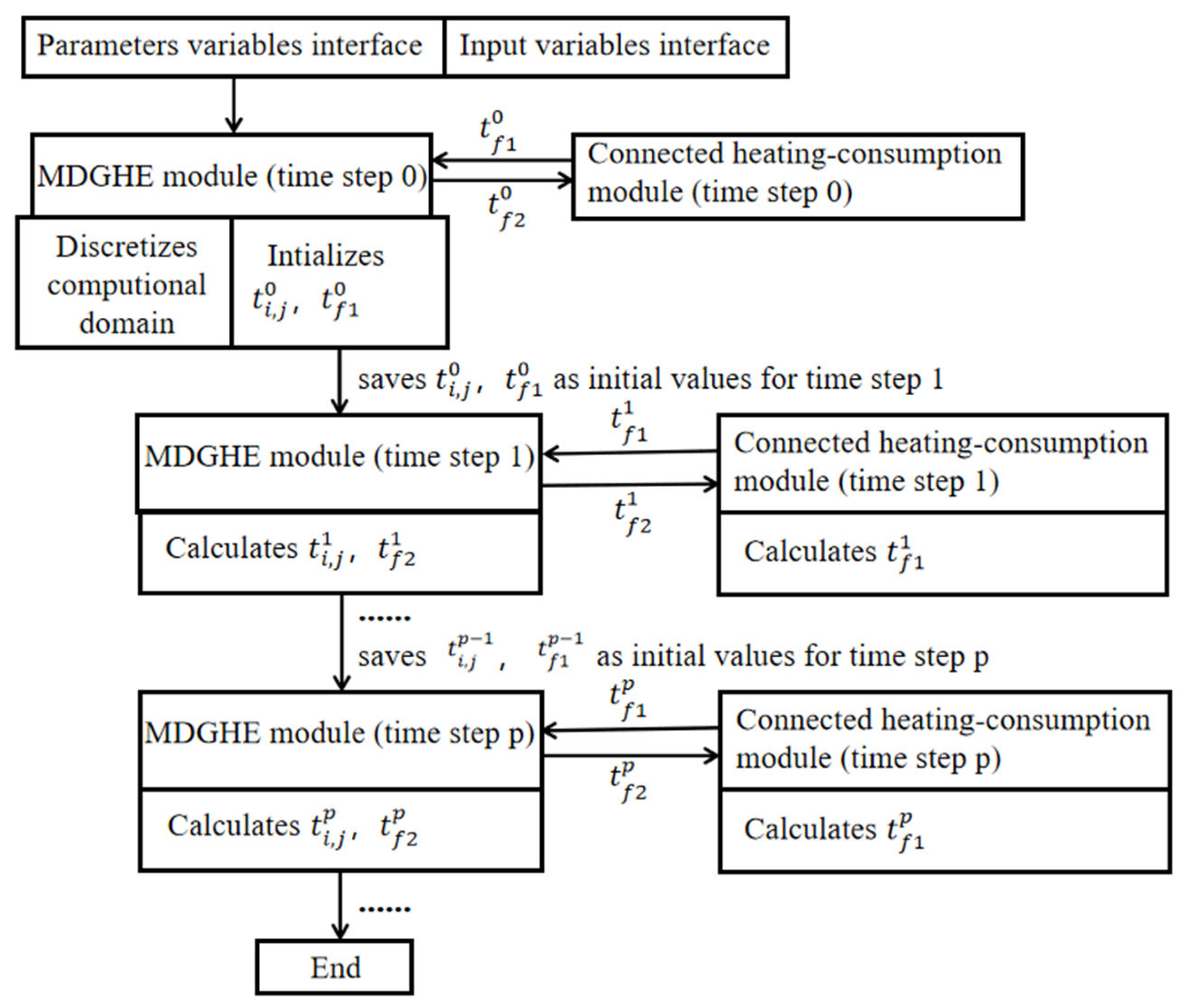
Upon configuring the parameters of the buried-pipe heat exchanger, we successfully established the Type282 module within the Type Studio environment of TRNSYS. A computational flowchart of the module within the TRNSYS environment is depicted in Figure 4. The following steps were conducted:

• At time step 0, the MDGHE module reads data from its parameter variables and input variables interfaces. A heating consumption module is connected to the MDGHE module. The outlet water temperature $t_{f2}^0$ is transferred from the MDGHE module to the heating consumption module, and the water temperature $t_{f1}^0$ is returned to the MDGHE module after heating is consumed in the heating consumption module. $T_{i,j}$ is the temperature of a discrete point with the transverse serial number i and longitudinal serial number j. $t_{f1}^0$ and $t_{f2}^0$ are assigned to be 0 and saved as the initial values for time step 1.$T_{i,j}^0$ is assigned to be the original temperature of the geotechnical layers and saved as the initial value for time step 1.
• At time step 1, the MDGHE module calculates $t_{f2}^1$ and $T_{i,j}^1$ based on $t_{f1}^0$ and $T_{i,j}^0$. $t_{f2}^1$ is transferred from the MDGHE module to the heating consumption module, and the water temperature $t_{f1}^1$ is returned to the MDGHE module after heating is consumed in the heating-consumption module; this temperature is calculated based on $t_{f2}^0$ and the heating load. $t_{f1}^1$, $t_{f2}^1$, and $T_{i,j}^1$ are saved as the initial values for time step 2.
• Continuing the process, at time step p, the MDGHE module calculates $t_{f2}^p$ and $T_{i,j}^p$ based on $t_{f1}^{p-1}$ and $T_{i,j}^{p-1}$. Then, $t_{f2}^p$ is transferred from the MDGHE module to the heating-consumption module, and the water temperature $t_{f1}^p$ is returned to the MDGHE module after heating is consumed in the heating consumption module; this temperature is calculated based on $t_{f2}^{p-1}$ and the heating load. $t_{f1}^p$, $t_{f2}^p$, and $T_{i,j}^p$ are saved as the initial values for time step p+1.

2.5. Experimental Validation

In this study, the accuracy of the simulation results was validated using data obtained from a field experiment conducted in the Liuhong community, Dezhou City, Shandong Province.

The experimental system was built based on the MDGHE ground source heat pump system in the studied case, to be rebuilt as a solar-assisted MDGHE system for direct heating. The in situ experimental system comprised the middle-depth ground heat exchanger (MDGHE), the automatic control system, and other equipment located in the plant room, as illustrated in Figure 5. It should be noted that this experiment only uses the operation data of the MDGHE to verify the developed heat transfer model of MDGHE.

The MDGHE was retrofitted from a decommissioned geothermal well with a depth of 2829 m. As depicted in Figure 6, the ground heat exchanger is composed of four sections. The structural parameters for these four sections are detailed in

Table 2. Structural parameters of the four-section coaxial ground heat exchanger.

Location of the Buried Pipe	Depth of the Buried Pipe (m)	Diameter of the Borehole (m)	Diameter of the Outer Pipe (m)	Diameter of the Inner Pipe (m)	Thermal Conductivity of Geotechnical Layers (W/(m·K))
The first section	455	0.4445	0.3397	0.3204	2.8
The second section	2017	0.3112	0.2445	0.2266	2.8
The third section	2626	0.2159	0.1778	0.1594	3.0
The fourth section	2829	0.1524	0.1397	0.1213	3.5

.

The remaining parameters were configured as follows: The outer pipe was made of steel and had a thermal conductivity of 43 W/(m·K). The circulating medium within the buried pipe was water, flowing at a rate of 20 m³/h. The average ambient temperature was maintained at 15 °C. The backfill material has a thermal conductivity of 1.5 W/(m·K). For the inner pipe, PVC was selected, which has a thermal conductivity of 0.17 W/(m·K).

The in situ measurement of underground soil temperature was carried out using fiber optic sensors. These sensors are capable of four-channel fiber optic temperature sensing. Each channel has a detection distance of over 5 km and offers a temperature measurement accuracy of ±0.5 °C. The distributed temperature sensing (DTS) system was installed along the borehole, with temperature sensing points spaced every 0.5 m, enabling continuous monitoring down to a depth of 800 m. The ground temperature gradient was estimated to be 0.027 °C/m through data fitting, as illustrated in Figure 7. Based on this gradient, the temperature at a depth of 2829 m was inferred to be 79.8 °C, extrapolated from the temperature measured at a depth of 800 m.

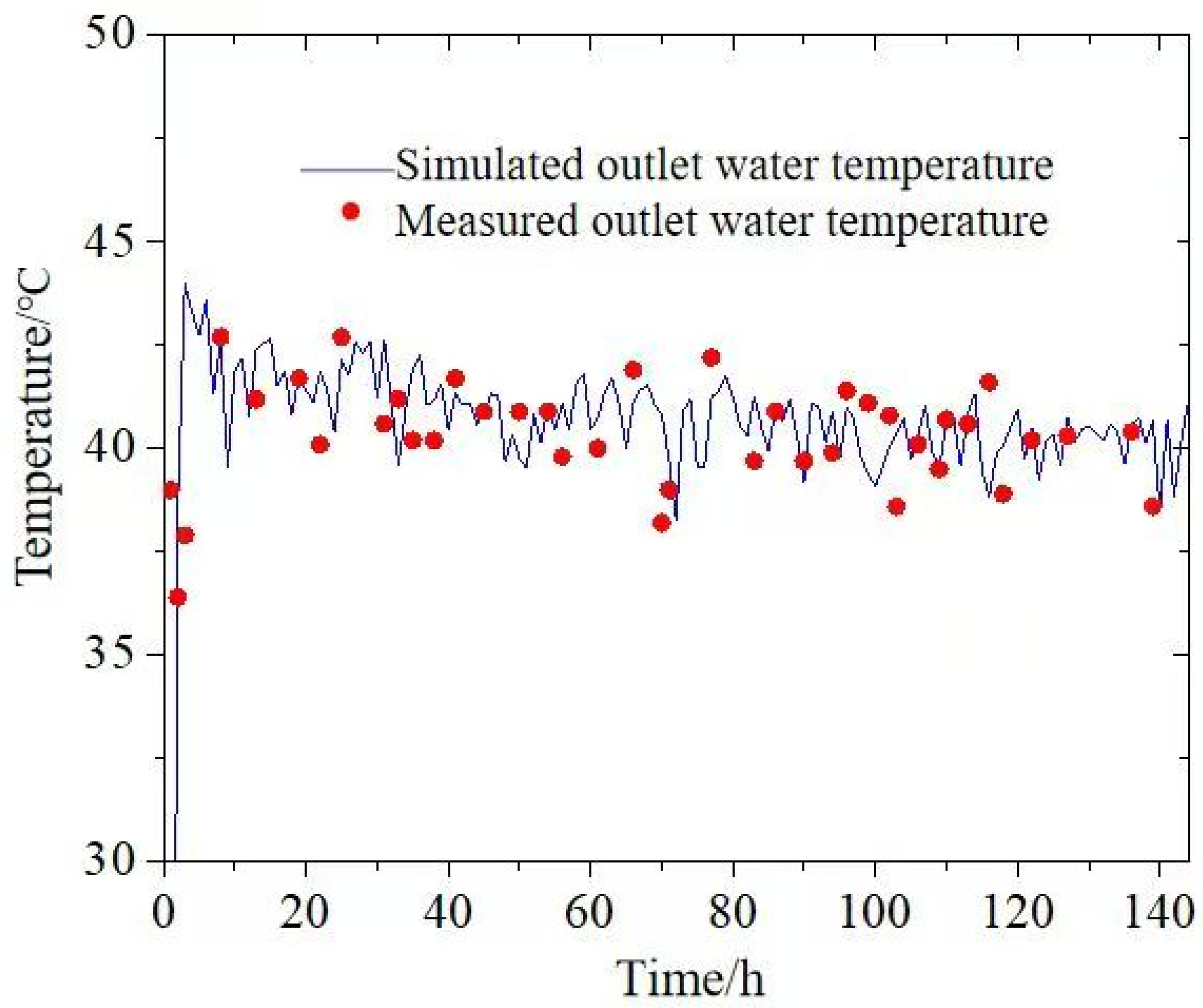
In this demonstration project, an automatic inspection system was designed and implemented within the PLC automatic control cabinet (as shown in Figure 5). This system automatically recorded the inlet water temperature, outlet water temperature, and circulating water flow rate of the MDGHE. Based on these recorded data, the capacity of the heat exchanger under heating conditions was calculated. Additionally, on the load side, the supply temperature, return temperature, circulating water flow rate, and circulating pump power were also automatically recorded. The same parameters used in the experimental system were input into the TRNSYS module for simulation and analysis. A load-based outlet temperature validation method was employed in this study. The validation process involved the following steps: (1) The instantaneous thermal load was calculated from the measured inlet and outlet water temperatures and the flow rate. (2) This calculated heat load was used as input for the numerical module to estimate the corresponding outlet water temperature. (3) The calculated outlet temperature was then compared with the experimentally measured value to assess the model’s accuracy. Figure 8 presents a comparison between the simulated and measured outlet water temperatures. The results indicate that the error range is within ±2.5 °C except for the initial 5 h, which is caused by initial static water temperature. This demonstrates the acceptable accuracy of the developed TRNSYS module for MDGHE simulations. The potential errors of this experiment may come from the following aspects: (1) The measurement accuracy of the optical fiber sensor has affected the accuracy. (2) Due to the relatively short experimental period, some thermal inertial response processes were not fully reflected in the data. (3) Although the pipeline has been insulated, due to the large fluctuations in outdoor temperature, heat loss still exists, and there will be errors in the calculation process.

2.6. The Model’s Limitations and a Sensitivity Analysis

2.6.1. The Model’s Limitations

This study focused on heat transfer in a single deep borehole with coaxial tubes. The following assumptions were taken into account in the model:

• The soil and rock surrounding the DBHE is regarded as one or a few horizontal layers of homogeneous media, whose thermal properties do not change with temperature.
• The domain studied is considered semi-infinite; for numerical simulation, however, boundaries are set far away from the DBHE, where temperature distributions are assumed to be uninfluenced by DBHE operation in the period concerned.
• Groundwater infiltration is neglected, and pure conduction is considered the only mechanism of heat transfer in the soil/rock.
• The fluctuation in the temperature of the atmosphere and its influence on the top layer of the soil are ignored, so the air temperature above the ground surface remains constant.
• A uniform geothermal heat flux exists throughout the media.
• Convective heat transport by circulating water in pipes is the dominant mechanism of heat transfer in the longitudinal direction within the borehole; conduction by grout, pipe walls, and water in the borehole is neglected in this direction.
• The thermal capacity of the grout, pipe walls, and water in pipes is counted in the model; the temperature of the grout and pipe walls, however, is assumed to be the same as that of the water in the same section of the pipe.

2.6.2. Sensitivity Analysis

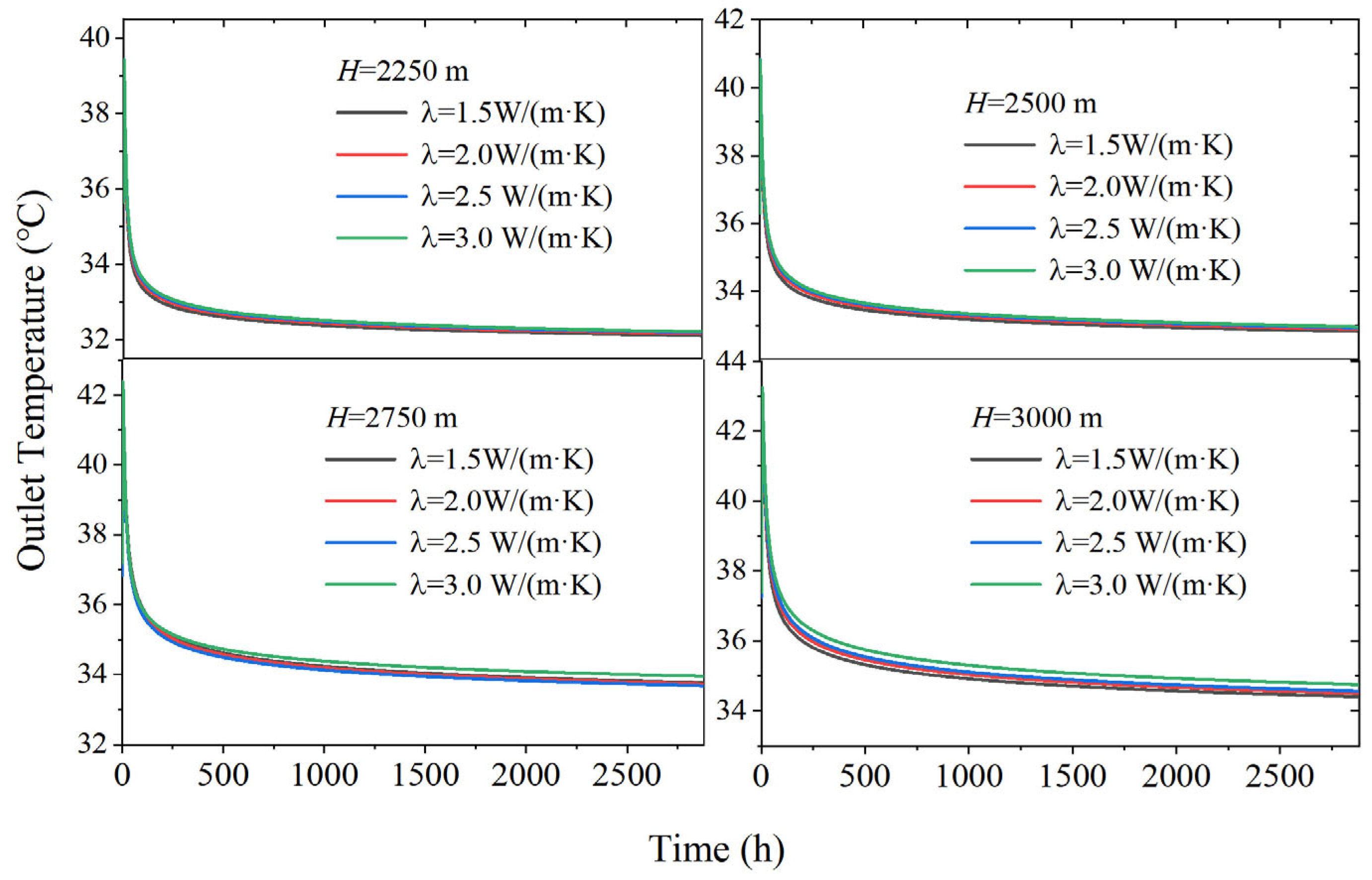
The effects of two key parameters, borehole depth and soil thermal conductivity, on the variation in the outlet water temperature of an MDGHE were investigated, clarifying the importance of the role of each parameter in the thermal response of the system. The parameters of the MDGHE were set to be the same as those in Table 2. The inlet water temperature was taken to be 30 °C, and the flow rate was 60 m³/h.

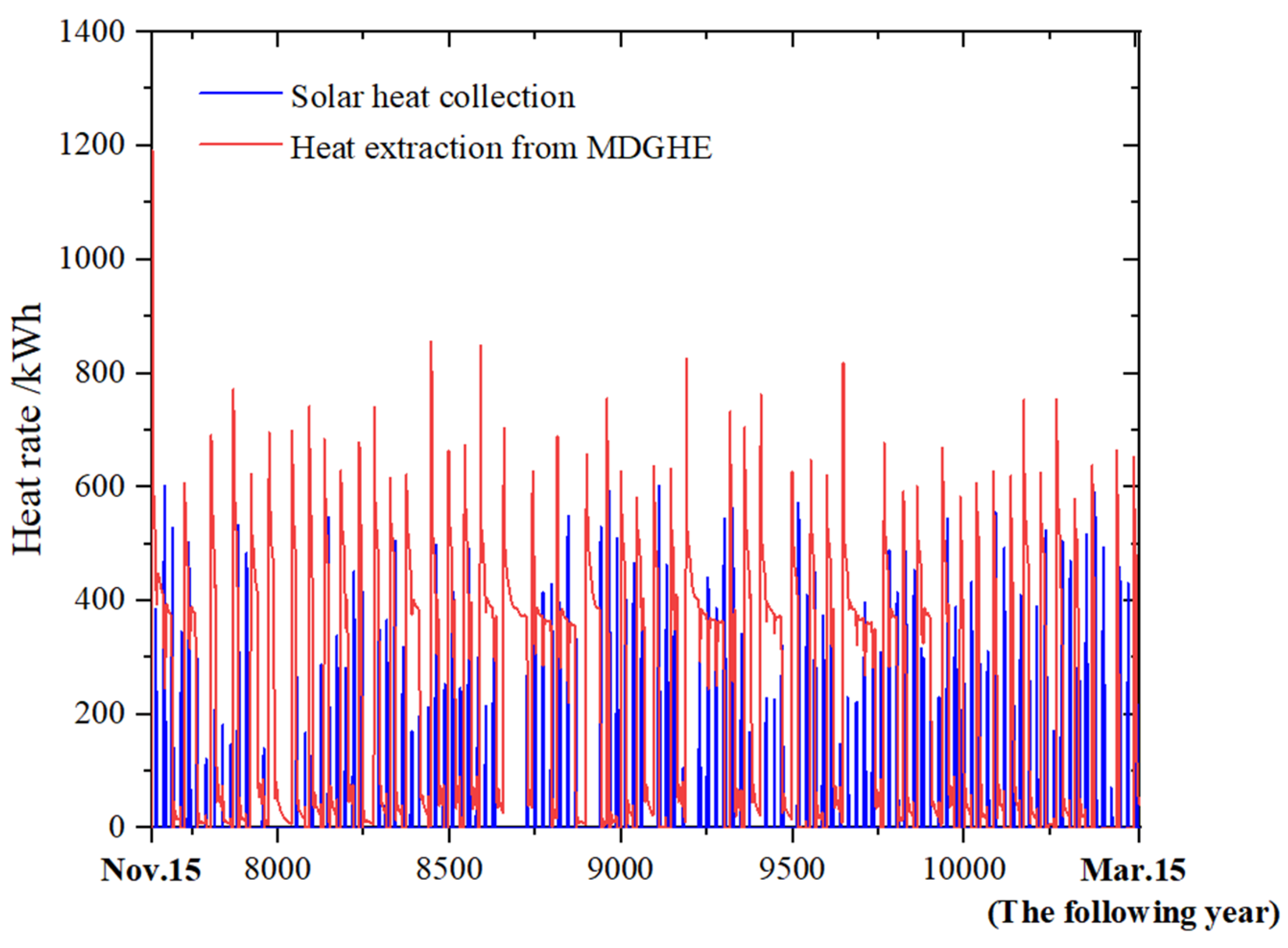
The trend of the system outlet water temperature over the operating time can be clearly observed by comparing the simulation results at different depths (2250–3000 m) and under different soil thermal conductivity (1.5–3.0 W/(m·K)) conditions, see Figure 9. The results of the analysis show that the outlet water temperature exhibited a trend of rapidly increasing in the early stage of system operation, but with the increase in the heat extraction time, the outlet water temperature of the buried-pipe heat exchanger gradually decreased and eventually stabilized. This phenomenon indicates that the heat exchange between the soil and the fluid stabilizes, and the system can reach thermal dynamic equilibrium when it operates for longer periods of time. It can also be seen from the figure that the effect of borehole depth on outlet water temperature is particularly significant, with a maximum temperature rise 3.6 °C. This phenomenon is due to the fact that as depth increases, the temperature of the geothermal field gradually rises, thus enhancing the heat exchange capacity between the fluid in the pipe and the surrounding soil.

In contrast, the effect of soil thermal conductivity on the thermal performance of the system was relatively weak. Increasing the thermal conductivity from 1.5 W/(m·K) to 3.0 W/(m·K) at the same depth resulted in an increase of 0.2 °C in outlet water temperature. Although the increase in thermal conductivity can accelerate the rate at which thermal energy is conducted through the soil to the fluid, the effect on the outlet water temperature is significantly weakened by the fact that the ground temperature gradient is mainly determined by the natural conditions of the ground and the fact that the heat transfer time is relatively long. Overall, the outlet water temperature is highly sensitive to the depth of the borehole, and the response to the change in soil thermal conductivity is weak. Therefore, in the design and optimization of medium-depth buried-pipe heat transfer systems, the depth of the borehole should be considered a key parameter that must be prioritized, and geothermal heat collection efficiency should be improved by reasonably increasing the depth of the borehole to achieve a higher energy utilization rate.

3. Development of a TRNSYS Simulation Framework for a Solar-Assisted MDGHE Direct Heating System

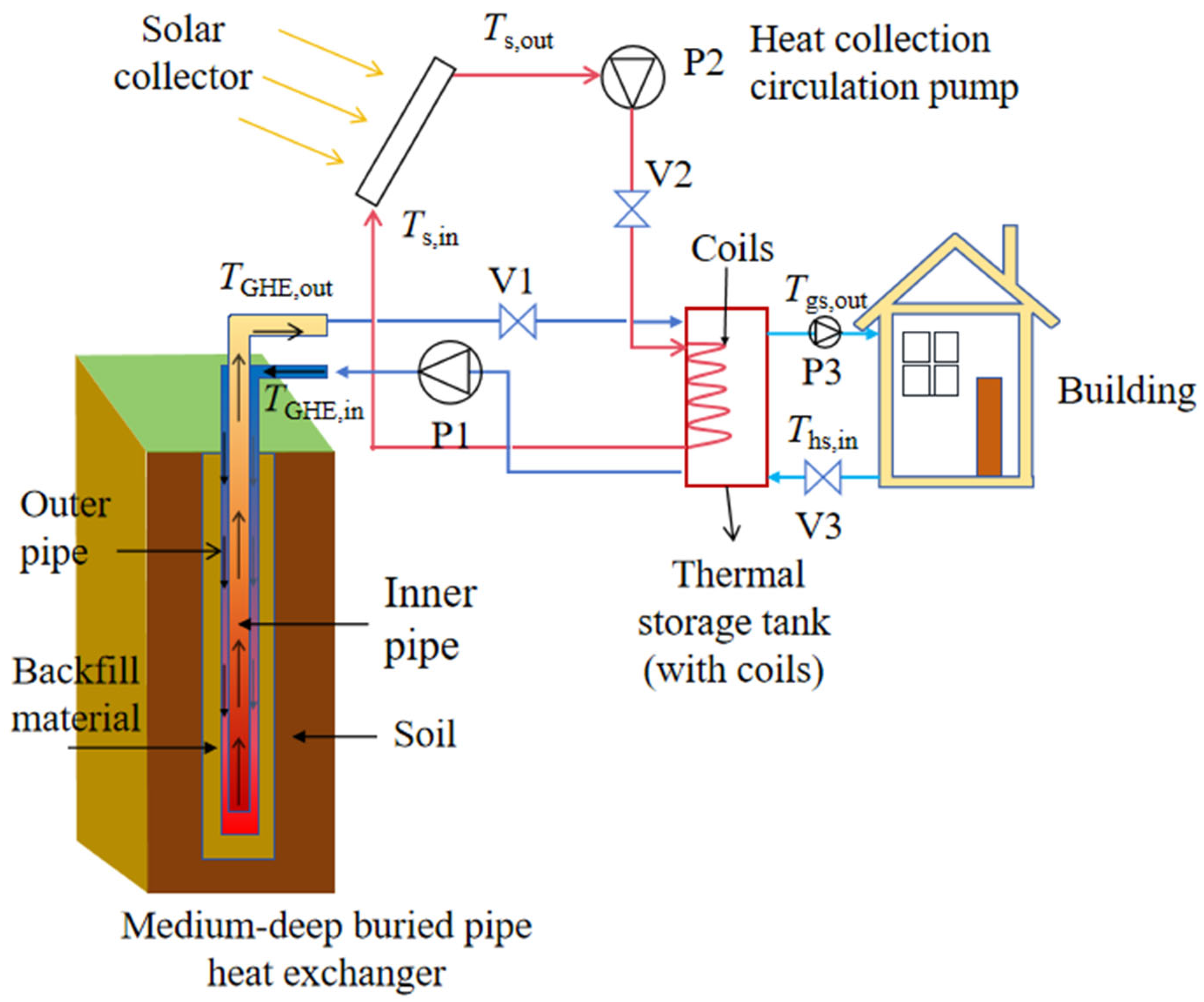
Following the development of the MDGHE model, we aimed to evaluate the performance of the solar-assisted MDGHE direct heating system by integrating the newly developed module into the TRNSYS simulation framework. Figure 10 is a schematic diagram of the solar-assisted MDGHE direct heating system. The integrated heating system incorporates four core subsystems: (1) an MDGHE, (2) flat-plate solar collectors, (3) a stratified thermal storage unit with an internal heat exchanger, and (4) low-temperature radiant heating terminals.

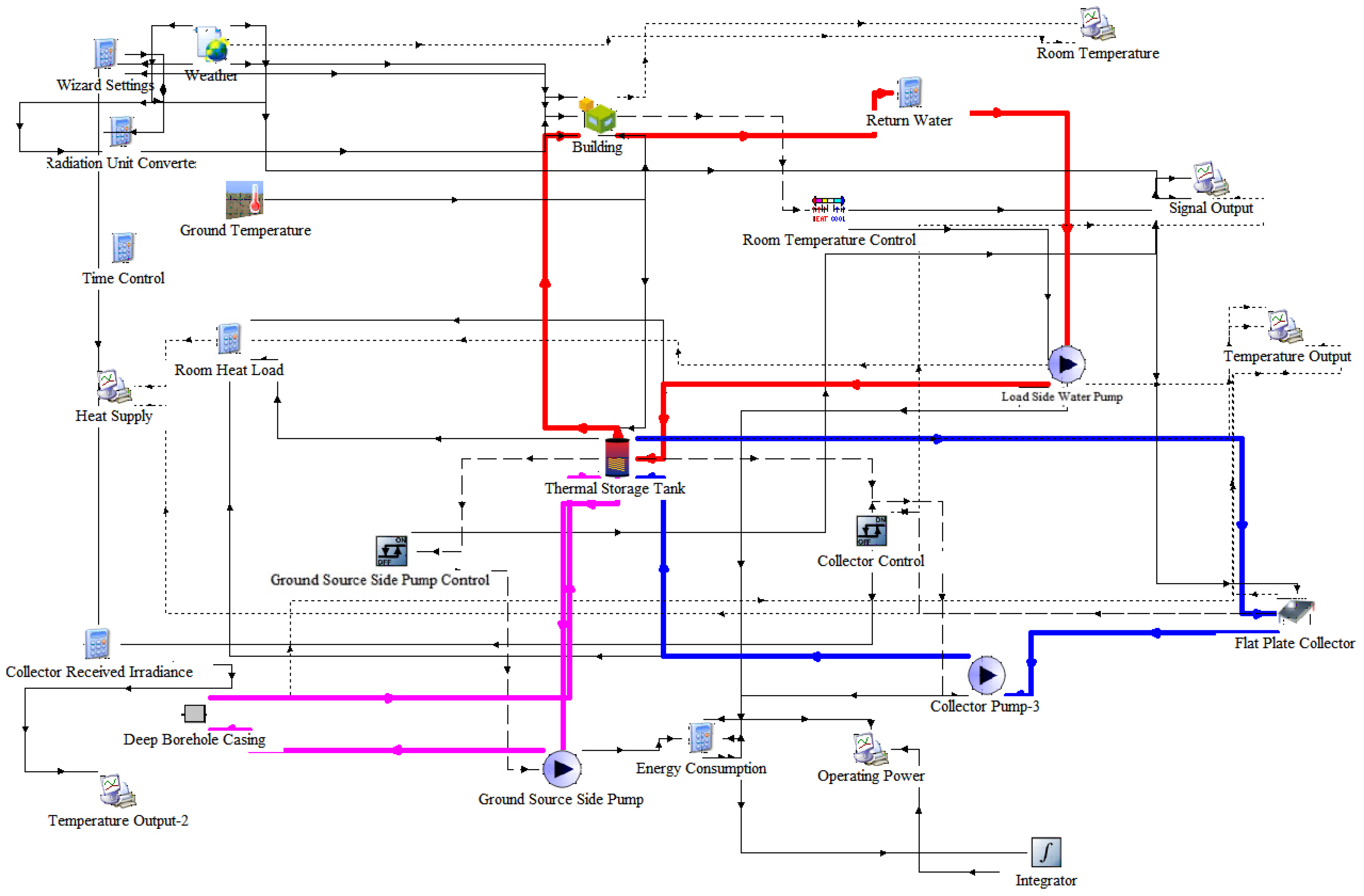
Following the system design specifications, the corresponding components were systematically selected and interconnected within the TRNSYS simulation environment in order to develop a comprehensive numerical model. As illustrated in Figure 11, the implemented model consists of the following parts:

(1)

Component selection: accurate matching of numerical modules with physical components, along with customized parameterization for each subsystem.

(2)

System integration: thermodynamic coupling of all energy transfer processes, hydraulic connection establishment, and control logic implementation.

(3)

Model configuration: time-step optimization, convergence criteria setting, and output parameter definition.

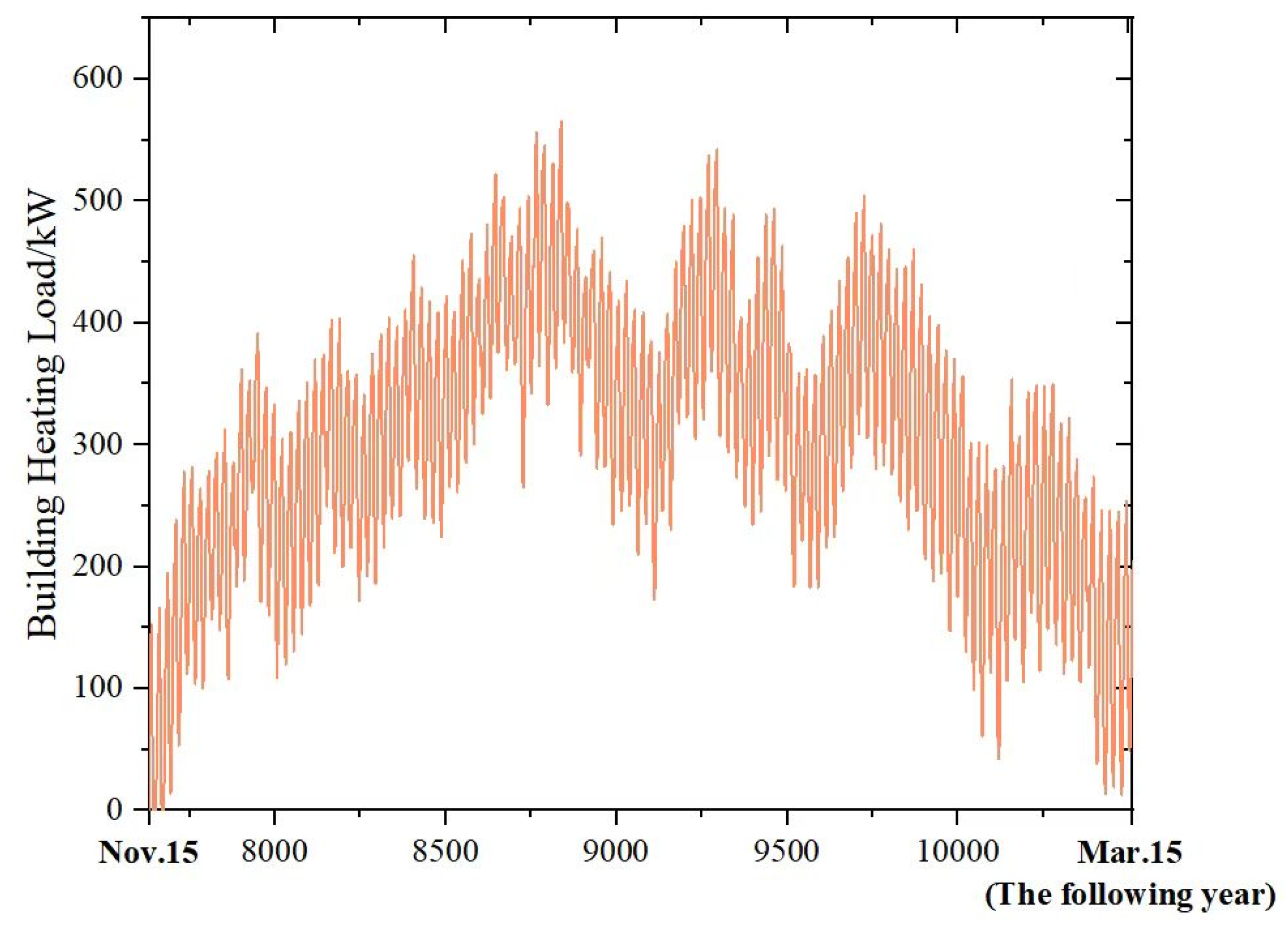
3.1. Building Heating Load Simulation

The heating load profile of a residential building with an area of 12,000 m² was simulated using the Type 56 module in TRNSYS. The accuracy of simulation results largely depends on the appropriateness of a model’s boundary conditions and parameter settings. The conditions and parameter settings used for the simulation are presented below.

(1)

Outdoor meteorological parameters

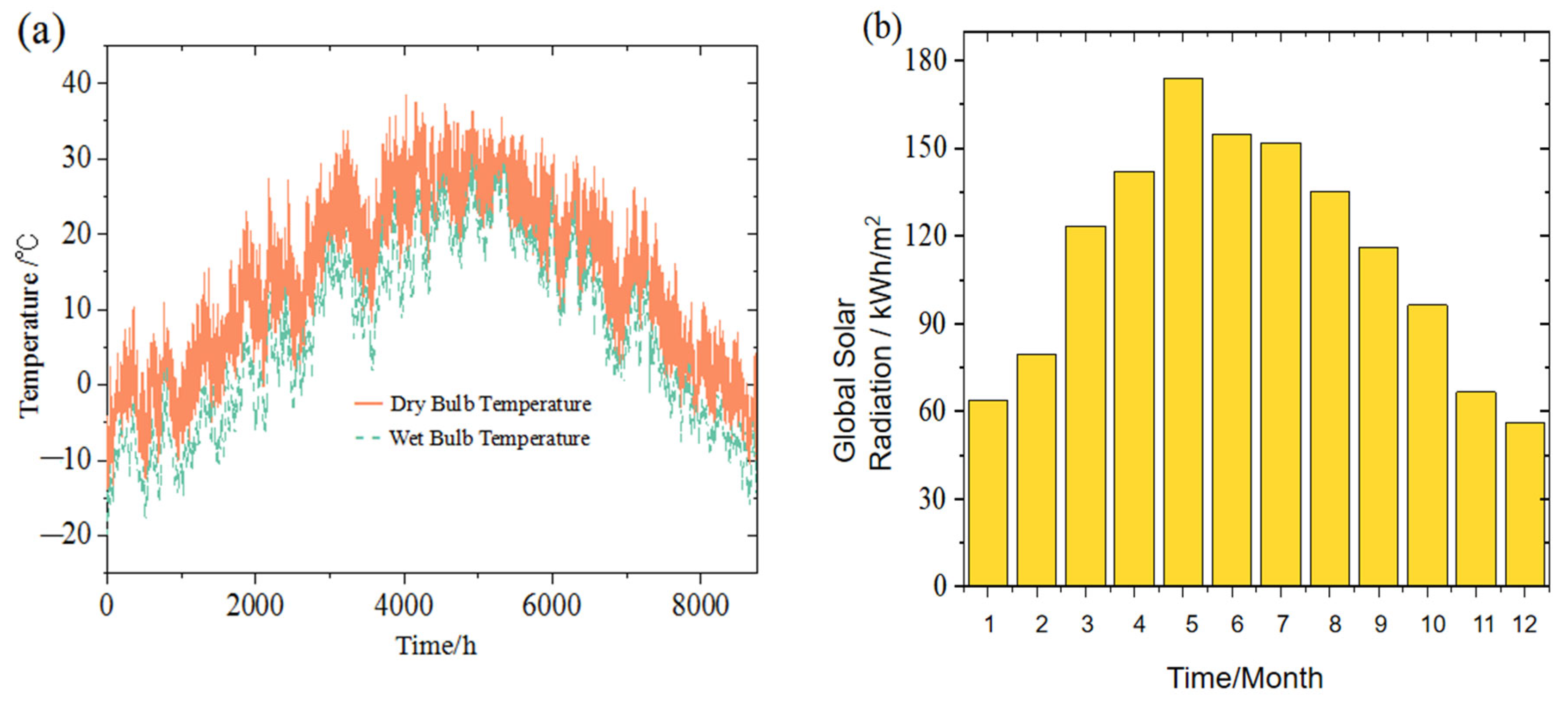
Load simulations were conducted using Typical Meteorological Year (TMY) data. The TMY was determined by statistically analyzing the monthly averages of meteorological data over the past 30 years, selecting the most representative year from the most recent decade that best approximated the 30-year monthly averages. The geolocation settings for the software were set to Dezhou, Shandong Province, to extract local meteorological data.

Dezhou (37°45′ N, 116°3′ E), located in the central region of Shandong Province, has a warm temperate semi-humid continental monsoon climate, characterized by hot, rainy summers and cold, dry winters. The multi-year average temperature is 14.3 °C. The seasonal variations in outdoor temperature and solar radiation intensity are illustrated in Figure 12.

(2)

Building Envelope Parameters

The configuration of the envelope and the window-to-wall ratios (WWRs) for each orientation are detailed in the following sections.

Table 3. Thermal parameters of typical building envelope components.

Building Envelope Components	Structural Configuration	Thermal Conductivity W/(m·K)
Exterior wall	Cement mortar (4 mm) + reinforced concrete (50 mm) + XPS board (5 mm) + cement mortar (4 mm)	K = 0.456
Exterior window	Double-glazed Low-E windows (20% frame + 80% glazing)	K = 1.896
Roof	Cement mortar (20 mm) + reinforced concrete (150 mm) + gravel-aggregate concrete (50 mm) + cement mortar (15 mm)	K = 1.8

presents the thermal parameters of the residential building envelope, while

Table 4. Window-to-wall ratios according to orientation.

Orientation	East	South	West	North
Window-to-wall ratio	0.29	0.5	0	0.3

specifies the WWR values across various facades.

(3)

Additional parameter configurations

The indoor thermal conditions were controlled, with indoor temperature and relative humidity setpoints of 20 °C and 50%, respectively. Standard fluorescent lamps were selected for lighting, with radiant and convective heat fluxes set at 5.4 kW·h/m² and 3.6 kW·h/m², respectively. Electrical appliances were set to a power density of 280 W, while the ventilation system operated at an air exchange rate of 0.5/h. Continuous 24 h heating operation was implemented, with a simulated occupant load of three people for heating load calculations.

3.2. Determination of Equipment Capacity

The developed numerical algorithms for the MDGHE were computationally implemented as a customized TRNSYS simulation module. The detailed parameters of the MDGHE module, which can solve 70% of the peak heating load, are shown in

Table 5. Parameters of medium-depth ground heat exchanger.

Parameter	Value
Borehole depth, m	2800
Ground thermal conductivity, W/(m·K)	2.0
Ground heat capacity, kJ/(m3·K)	2.06
Outer-pipe inner and outer diameter, m	0.38/0.34
Inner-pipe inner and outer diameter, m	0.15/0.12
Inner- and outer-pipe heat capacity, kJ/(m3·K)	1200/3400
Backfill material thermal conductivity, W/(m·K)	1.5
Borehole diameter, m	0.45
Outer-pipe thermal conductivity, W/(m·K)	52
Inner-pipe thermal conductivity, W/(m·K)	0.45
Geothermal heat flow, W/m2	0.068

.

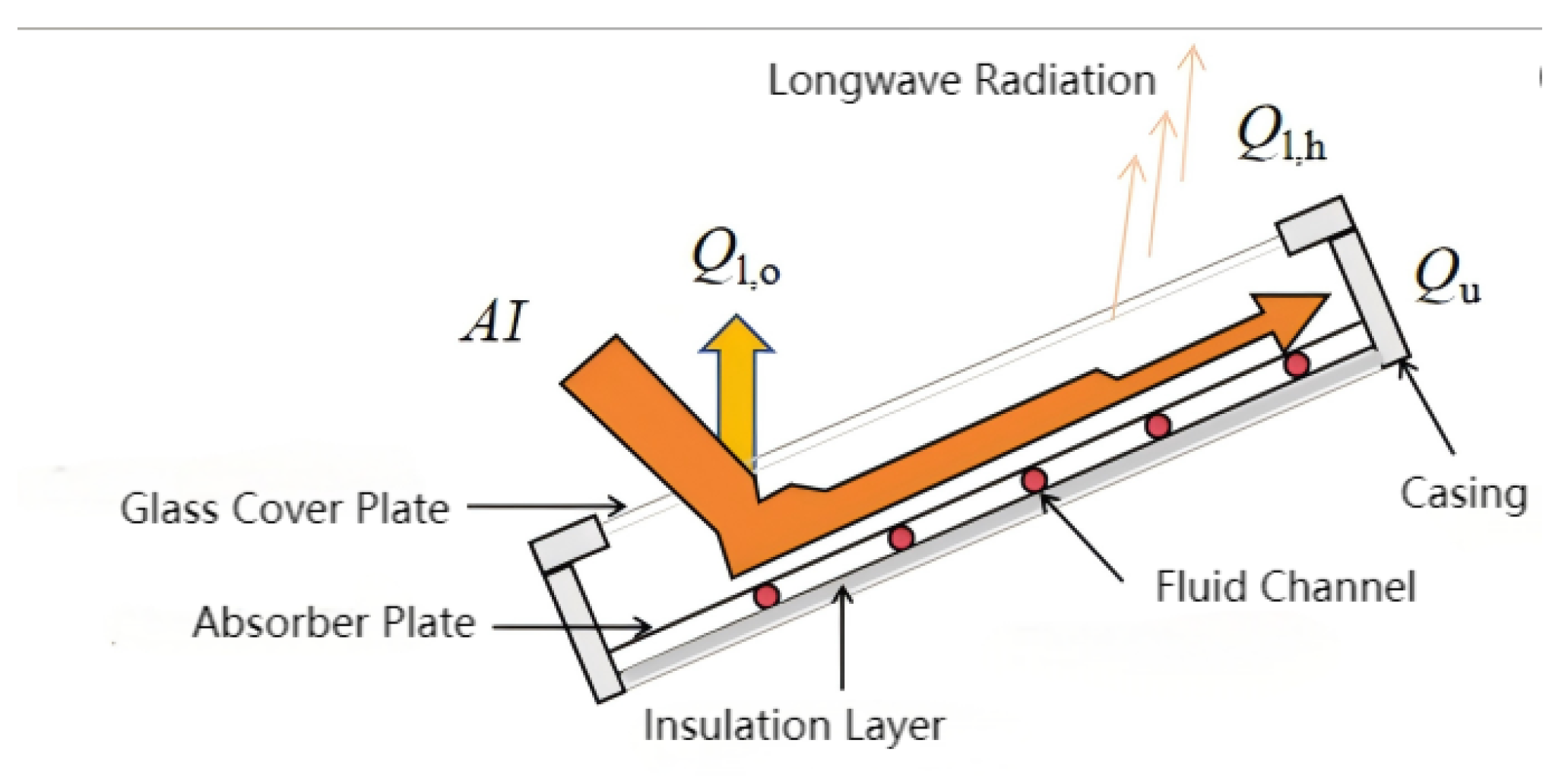
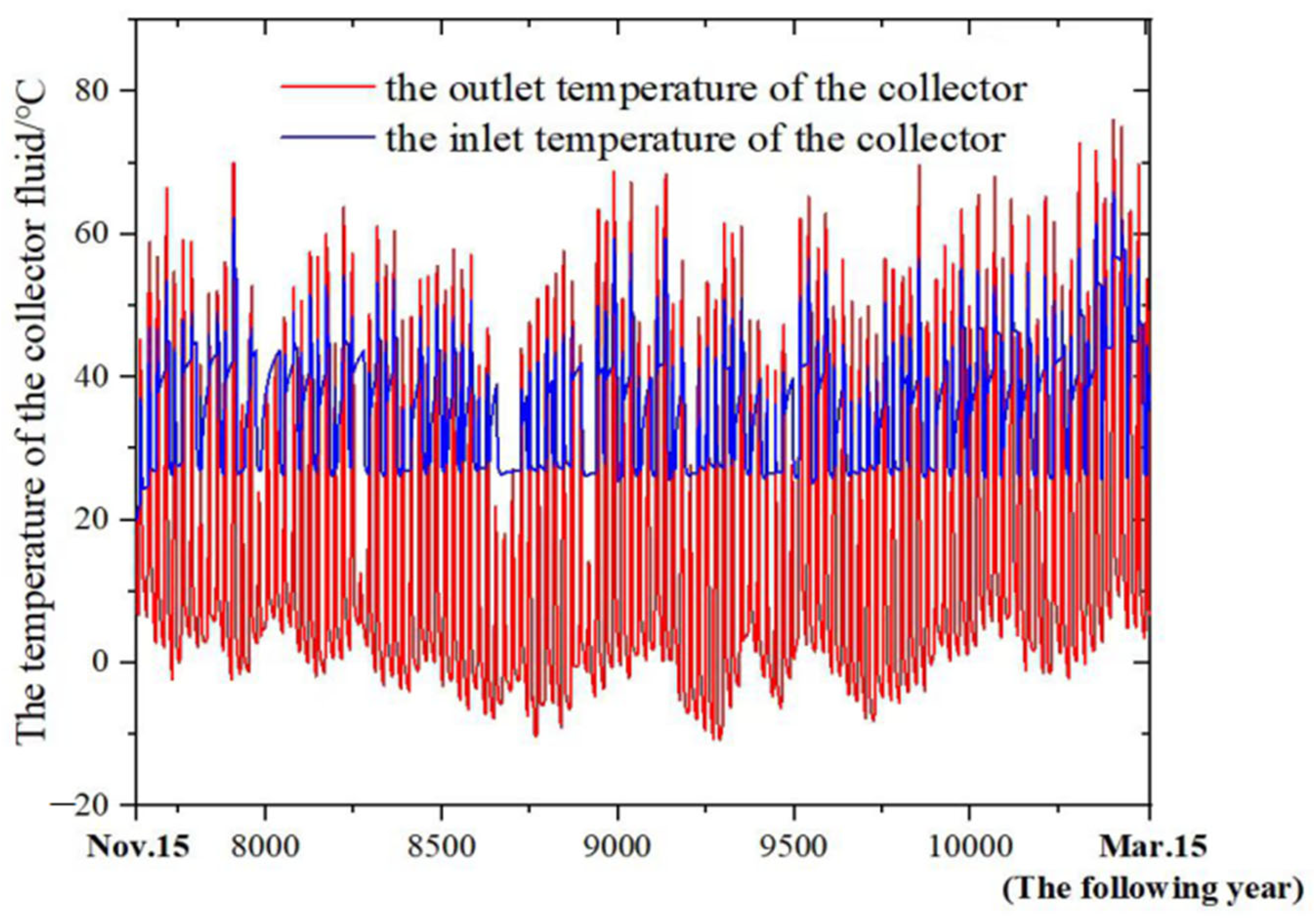
A type 1b component was used to simulate a flat-plate solar collector. The thermal performance of the flat-plate collector array depends on the number of connected collectors and the thermal performance of each individual collector. The collector component allows users to customize parameters such as the total collector area, installation angle, collection efficiency, and circulating fluid flow rate.

The collector outlet fluid temperature can be calculated by incorporating the known basic parameters of the collector together with the local hourly solar radiation intensity and the inlet fluid temperature (as shown in Figure 13).

The gradually increasing solar collector area was integrated with the MDGHE, and the area measuring 1231 m² was selected when indoor temperature reached over 99.9% of the heating time. The parameters of the flat-plate solar collector are shown in

Table 6. Solar collector parameters.

Parameter	Value
Collector area, m2	1231
Solar guarantee rate	30%
Average collector efficiency	50%
Heat loss, m	15%
Instantaneous efficiency intercept	0.79
First-order heat loss coefficient	4.7
Second-order heat loss coefficient	0

.

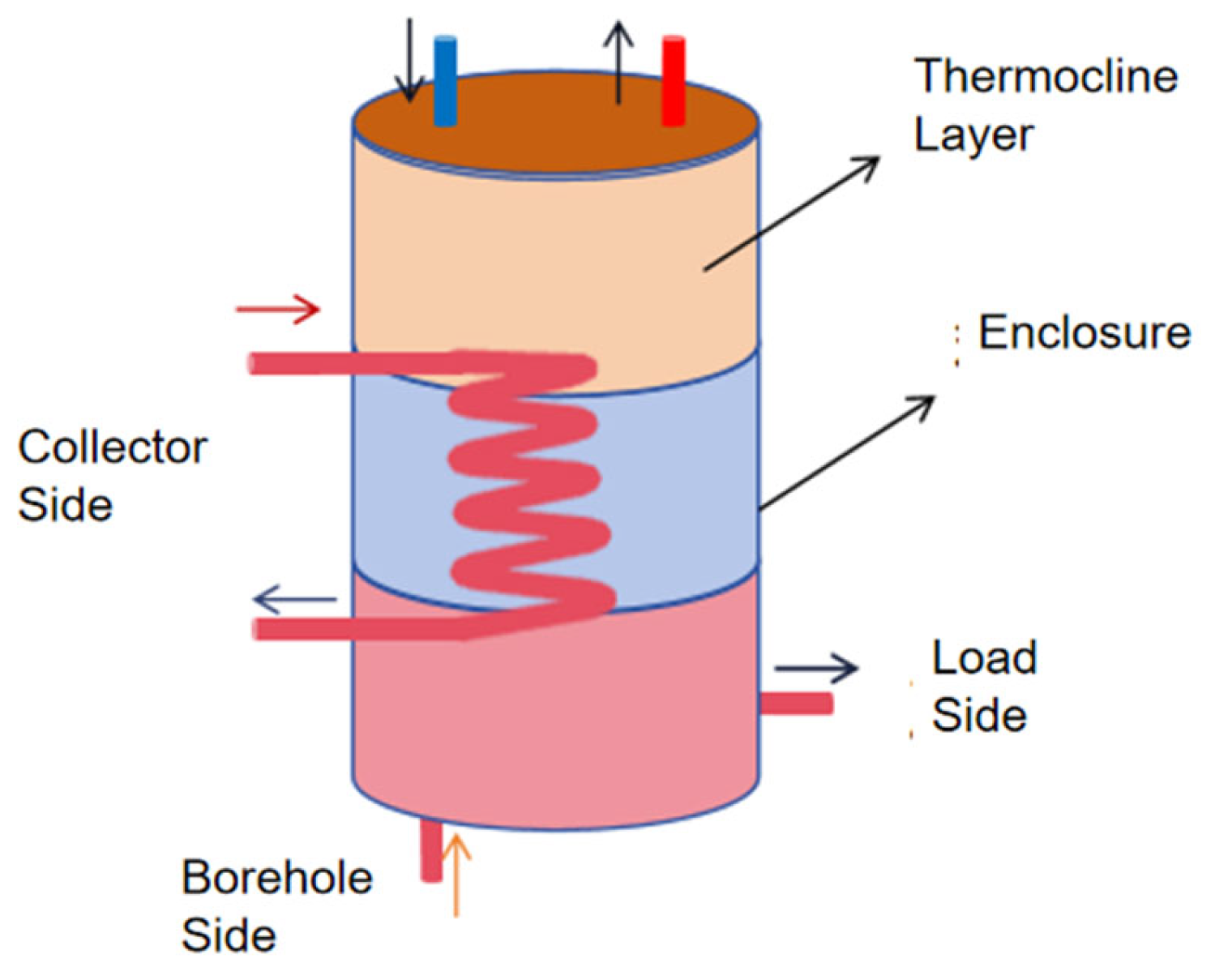
In this study, antifreeze was used as a circulating fluid to prevent freezing in the solar collectors. Pure water was used as the heat exchange medium in the storage tank. To prevent the mixing of the antifreeze and water, a storage tank with an internal coil heat exchanger was used in the system. The heat storage tank with a coil heat exchanger is shown in Figure 14.

The volume of a storage tank is typically selected based on the unit area of the collector. Typically, the range is between 40 L/m² and 300 L/m², as recommended by the Chinese “Technical standard for solar heating system (GB50495-2019)” [32]. In this study, we assumed that the volume of the storage tank is equal to 100 L per square meter of collector area. The detailed parameters of the thermal storage tank are shown in

Table 7. Thermal storage tank parameters.

Parameter	Value
Tank volume (m3)	123.1
Tank height (m)	2
Heat exchange coil diameter (m)	0.02
Heat exchange coil length (m)	1000
Thermal conductivity of the heat exchange coil (W/(m·K))	0.5

.

The parameters of circulating pumps on solar side, MDGHE side and load side are shown in

Table 8. Circulating pump parameters.

	Water Flow Rate, m3/h	Power, kW	Head, mH2O
Circulating pump on the solar side	53.52	4.5	20
Circulating pump on the MDGHE side	60	35	125
Circulating pump on the load side	60	5.5	20

.

3.3. Control Strategies

The performance of a solar-assisted MDGHE system can be significantly influenced by the applied control strategies. In this study, optimized operational control strategies for essential components were developed to ensure heating stability and comfort while maximizing energy efficiency. The details of these strategies are presented below.

(1)

Control strategies for the circulating pumps on the solar side: We employed a temperature-difference-based control strategy in which pump operation is regulated by monitoring the temperature difference between the temperature of the solar collector and the temperature of the return water of the water tank. Specifically, when the temperature of the solar collector exceeds the water tank return water temperature by 8 °C, the circulating pump is activated to transfer the collected solar heat to the water tank. Conversely, when the temperature difference drops below the set threshold of 2 °C, the circulating pump is deactivated to prevent heat backflow, which would otherwise reduce the system’s energy efficiency.

(2)

Control strategies for the circulating pumps on the MDGHE side: The system establishes a minimum water supply temperature of 35 °C to meet the requirements for direct heating. When the solar heating contribution is inadequate, resulting in the heat storage tank temperature falling below 35 °C, the system will activate the pipe circulation pump on the MDGHE side to introduce geothermal energy into the heating process.

(3)

Control strategies for circulating pumps on the load side: The indoor temperature is carefully controlled and maintained between 19 and 21 °C. When the temperature drops below 19 °C, the circulating pumps on the load side are activated to heat the room. Conversely, when the temperature rises above 21 °C, the circulating pumps on the load side are deactivated to prevent overheating.

4. Results

4.1. Energy Analysis

Figure 15 shows the hourly variation in the heating load of the residential building studied. The results indicate a peak heating load of 565 kW and a heating index of 47.1 W/m². According to the local heating schedule, the heating season extends from 15 November through 15 March of the following year.

The hourly supply and return water temperatures for the building were simulated over the entire heating period, as shown in Figure 16. Because of the greater depth of the MDGHE and the presence of a geothermal temperature gradient, the outlet water temperature from the MDGHE (the supply water temperature) is relatively high, satisfying the temperature requirement from the load side. Figure 17 shows the inlet and outlet temperature of the solar collector, and Figure 18 presents the heating rates collected by the solar collector and MDGHE. Evidently, the maximum heat extraction rate and total heat extraction for the MDGHE are 1192.1 kW and 629.8 MWh, respectively, while the maximum heat collection rate and total collected heat for the solar collector are 602.5 kW and 244.9 MWh, respectively.

Figure 19 presents the energy performance metrics of the integrated heating system, quantifying both the thermal output and energy consumption over the entire heating season.

The Solar Fraction (SF) serves as a critical performance metric for evaluating the integration of renewable energy in hybrid heating systems. This dimensionless parameter characterizes the proportion of solar thermal energy contributing to the total space-heating demand and is mathematically expressed as follows [24]:

$$\mathrm{S}\mathrm{F}={\displaystyle \frac{{\mathrm{Q}}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r}}}{{\mathrm{Q}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}}\times \mathrm{100\%}$$

(11)

Here, Q_solar is solar thermal energy, and Q_total is the total space-heating requirement.

The results indicate that over the course of the heating season, the solar collector supplied 28% of the total heating demand. Although the system was originally designed with a target solar energy contribution of 30%, its actual performance fell slightly short of this value. This discrepancy may be attributed to the design being based on long-term average data or assumed optimal weather conditions.

In contrast, there was significant weather variability during actual operation, resulting in reduced solar energy availability. However, the findings also highlight the system’s reliance on solar energy, which helps decrease its dependence on the medium-depth ground heat exchanger and, consequently, contributes to cost savings.

The System Satisfaction Index (η_sys) serves as a critical performance indicator for evaluating the effectiveness of space-heating systems in meeting buildings’ thermal demands. This quantitative metric is defined as follows:

$${\mathsf{\eta }}_{\mathrm{s}\mathrm{y}\mathrm{s}}={\displaystyle \frac{{{\mathrm{Q}}_{\mathrm{M}\mathrm{D}\mathrm{G}\mathrm{H}\mathrm{E}}+\mathrm{Q}}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r}}}{{\mathrm{Q}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}}\times \mathrm{100\%}$$

(12)

where Q_MDGHE + Q_solar represents the actual thermal energy supplied by the heating system, encompassing the heat from both the solar collector and the medium-depth geothermal heat exchanger, and Q_total denotes the building’s heating demand.

Quantitative analysis yielded an exceptional System Satisfaction Index, namely, 99.9%, demonstrating that the integrated renewable energy heating system successfully meet the building’s heat requirements. This outstanding performance confirms the reliability of this system.

The coefficient of the performance (COP) serves as a critical thermodynamic indicator for assessing the overall efficiency of an integrated renewable energy heating system. The proposed hybrid configuration achieves superior energy efficiency through the elimination of mechanical vapor compression, resulting in a fundamentally different COP calculation paradigm. In this direct heating architecture, the system COP is principally determined as follows:

$$\mathrm{C}\mathrm{O}\mathrm{P}={\displaystyle \frac{{{\mathrm{Q}}_{\mathrm{M}\mathrm{D}\mathrm{G}\mathrm{H}\mathrm{E}}+\mathrm{Q}}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r}}}{{\mathrm{P}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}}\times \mathrm{100\%}$$

(13)

where P_total is the total energy consumption of the system, including the energy consumption of the load-side circulation pump, the geothermal-side circulation pump, and the solar-collector-side circulation pump. The average COP calculated for this system is 9.26. This means that for every unit of energy consumed by the system, 9.26 units of heat are produced. Compared with the traditional medium-depth ground source heat pump system which has a COP value of approximately 4.84 [33], the energy efficiency of this system has been enhanced by 47.7%. This remarkable improvement significantly reduces energy consumption and delivers an exceptional energy-saving effect.

4.2. Payback Calculation

The initial investment of the system mainly consists of equipment costs, installation and commissioning cost and the modification cost of the MDGHE, and the cost of each item is shown in

Table 9. The cost of the equipment.

Equipment	Unit Price	Quantity	Cost, Thousand RMB
Solar collectors	500	1231 m2	615.5
Storage tanks	800	123.1 m3	98.4
Pumps	0.5	33.52 kW	16.8
Installation and commissioning			109.61
Total			730.7

and

Table 10. Rehabilitation costs for an abandoned well.

Cost Category	Unit Price	Quantity	Cost, Thousand RMB
Clean-up of abandoned wells	-	1	20
Installation of casing material	200 RMB/m	2829 m	565.8
Backfill slurry and construction	100 RMB/m	2829 m	282.9
System testing and commissioning	-	10	10
Pipe connection and insulation	-	-	10
Total cost			898.7

. The total initial investment cost of this composite heating system is 1739.01 thousand RMB.

The annual operating and maintenance cost of the system during heating season is

$$\mathrm{W}=({\mathrm{P}}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r}}+{\mathrm{P}}_{\mathrm{M}\mathrm{D}\mathrm{G}\mathrm{H}\mathrm{E}}+{\mathrm{P}}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}})\ast \mathrm{Y}+\mathrm{M}$$

(14)

where ${\mathrm{P}}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r}}$ represents the electricity consumption of the pump on solar side, kWh. ${\mathrm{P}}_{\mathrm{M}\mathrm{D}\mathrm{G}\mathrm{H}\mathrm{E}}$ represents the electricity consumption of the pump on ground side, kWh. ${\mathrm{P}}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$ represents the electricity consumption of the pump on load side, kWh. $\mathrm{Y}$ represents the time-of-use electricity price in Shandong Province, which is shown in

Table 11. The time-of-use electricity price in Shandong Province.

Time	Price of Electricity, RMB/kWh
8:00–22:00	0.58
22:00–8:00 (next day)	0.37

. M represents the annual maintenance cost, taken as 3000 RMB.

The system’s annual O&M cost is 4.45 RMB/m², while the unit price of central heating service for residential buildings is 26.7 RMB/m² in Shandong. Energy-saving benefit is RMB 267,000 every year. A static payback period of 7 years has been obtained, which is shown in

Table 12. Calculation of the static payback period.

The Total Initial Investment Cost, Thousand RMB	The Annual Saved O&M Cost, Thousand RMB	The Static Payback Period, Year
1739.01	267	7

.

5. Conclusions

This study proposes a renewable energy heating system based on a solar-assisted MDGHE. Unlike conventional geothermal or solar-assisted heat pump systems, the proposed configuration eliminates all vapor compression components and maximizes the utilization of renewable energy for space heating and cooling in buildings. A dynamic simulation model was developed using the TRNSYS platform to simulate the system’s performance. To increase the accuracy of the simulation, a novel TRNSYS module for MDGHE was developed and integrated into the simulation model. A case study based on a residential building in Shandong Province, China, was conducted to evaluate the performance of the proposed system. The key findings of this study are summarized below.

(1)

The hybrid solar-assisted MDGHE system demonstrates excellent thermal stability performance. During the peak heating season, the integration of solar thermal input significantly increases the outlet water temperature, keeping it consistently above 35 °C. This capacity compensates for the limitations of the standalone MDGHE system, which is subject to a notable decline in outlet temperature due to continuous heat extraction and cannot fully meet the building’s thermal demand on its own.

(2)

The dynamic simulation results indicate that the standalone MDGHE meets 71.9% of the total heating demand of buildings, whereas the hybrid configuration achieves 99.9% coverage. This demonstrates the feasibility of the solar-assisted MDGHE direct heating system and offers a valuable reference for future engineering applications.

(3)

This system can provide stable and continuous heating for a building with a total area of 12,000 m². The integration of the solar collector significantly enhances the system’s heating capacity and effectively compensates for the deficiencies of medium-depth geothermal energy. The results revealed that the system’s COP reached 9.26, demonstrating excellent performance in terms of energy utilization efficiency. Compared with the traditional medium-depth ground source heat pump system that has a COP value of 4.84, the energy efficiency ratio of this system has been enhanced by 47.7%. This remarkable improvement significantly reduces energy consumption and delivers an exceptional energy-saving effect.

In conclusion, this combined heating system, which focuses on energy saving and efficient utilization of renewable energy, offers an efficient and environmentally friendly solution for heating systems in cold regions. This study highlights the great potential of combining solar and geothermal energy for building heating and demonstrates this commination’s promising economic benefits. Future work will focus on system optimization, practical validation, and adaptability analysis under different climatic conditions to facilitate the widespread adoption of this sustainable heating technology.