Future Climate Projections and Uncertainty Evaluations for Frost Decay Exposure Index in Norway
Abstract
1. Introduction
1.1. Background
1.2. Objectives and Scope
- How have the FDEI values developed in Norway over the last normal period, and what are the likely future developments?
- What additional uncertainties are introduced in the FDEI by using future climate projections?
- How can we use the FDEI and uncertainty information as design tools for moisture safety design in building projects?
1.3. Climate-Related Uncertainties
1.4. Climate-Based and Response-Based Indices
1.5. Climate Adaptation of Buildings Using Precalculated Climate Indices and Qualitative Risk Analysis
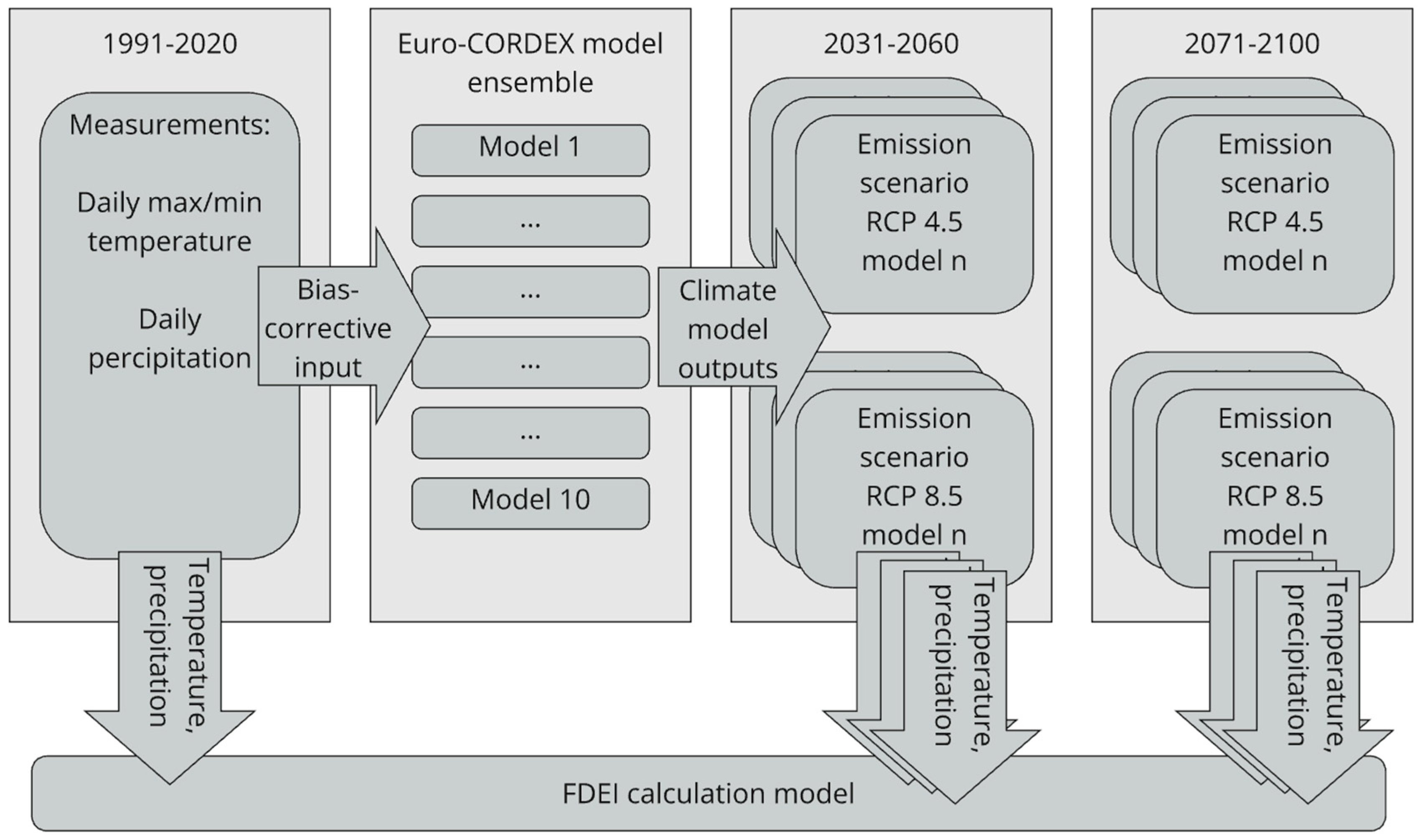
2. Materials and Methods
2.1. Frost Decay Exposure Index (FDEI)
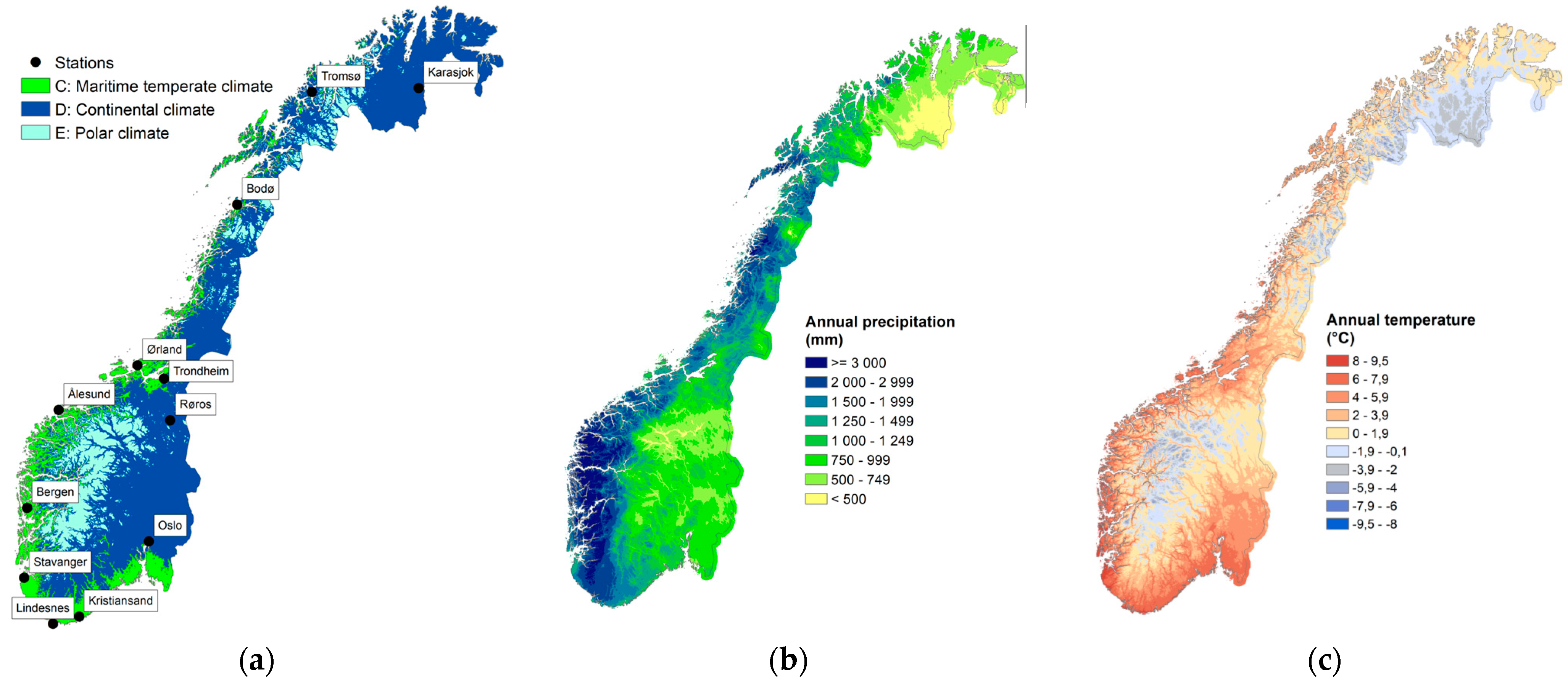
2.2. Locations and Climate Variations
2.3. Temporal Resolution of Historical Measurements
2.4. Future Climate Scenarios
2.5. Evaluation and Analysis Methodology
3. Results
3.1. Evaluation of Climate Model Ensemble

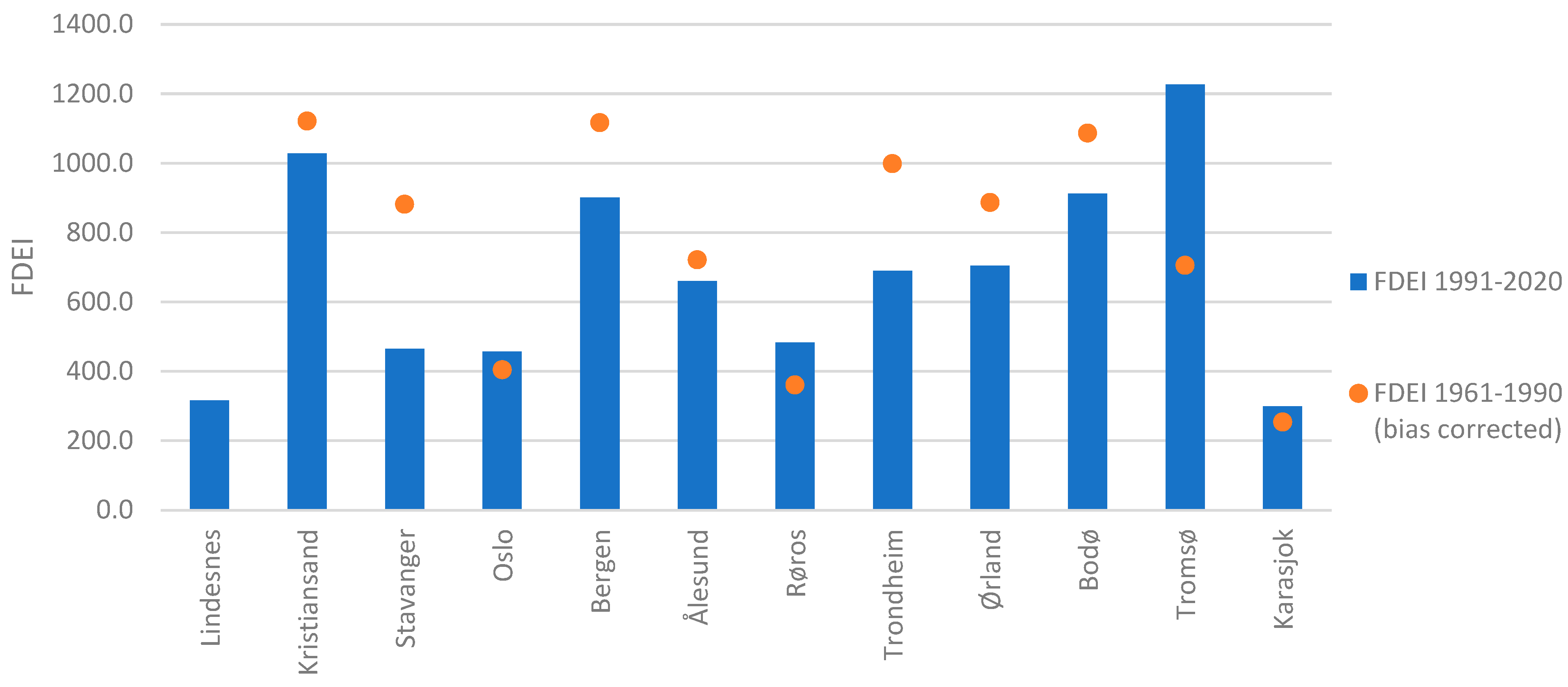
3.2. FDEI Based on Historical Observations (1991–2020)—Influence of Temporal Variations and Comparisons with 1961–1990 Data
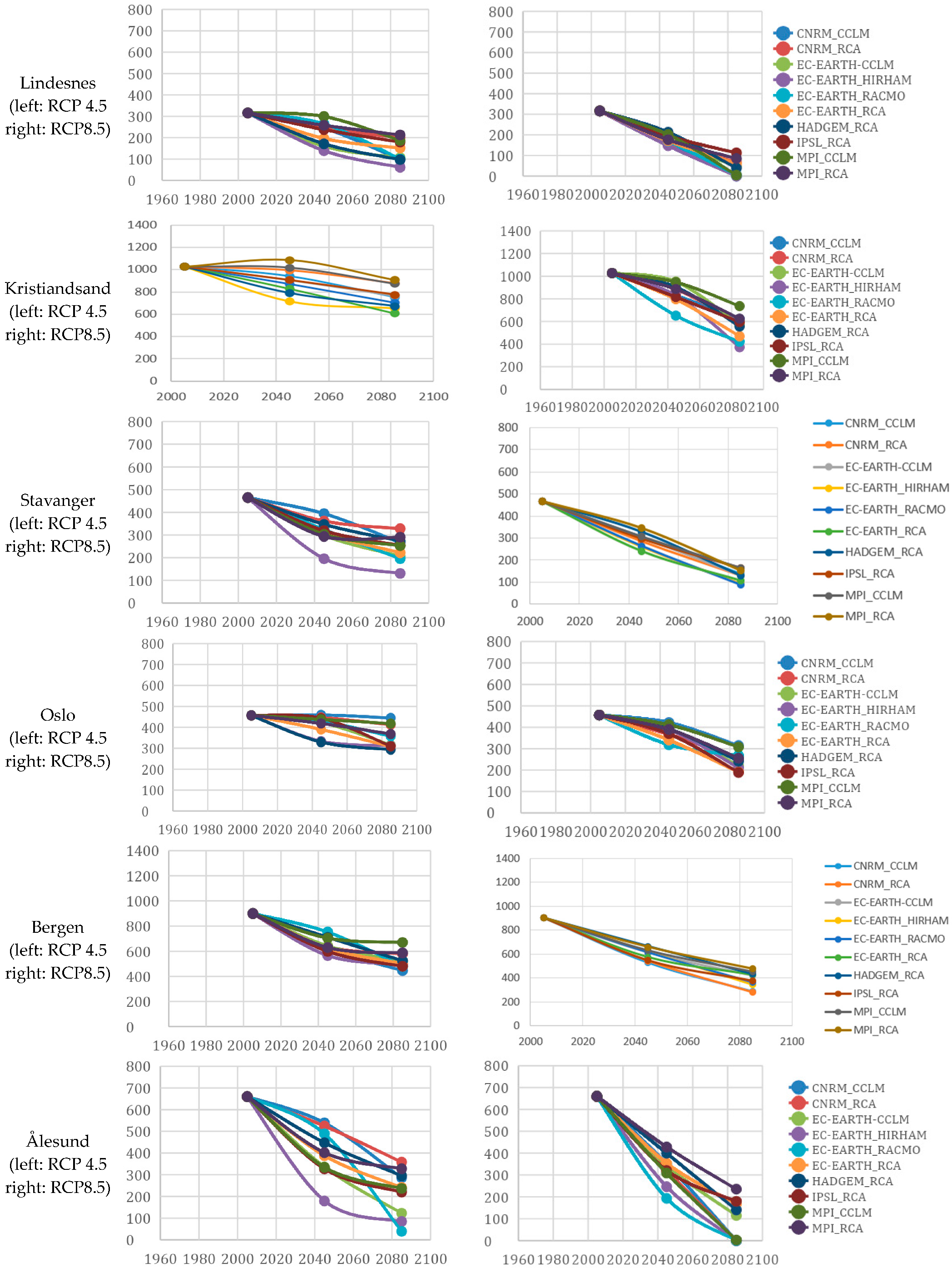
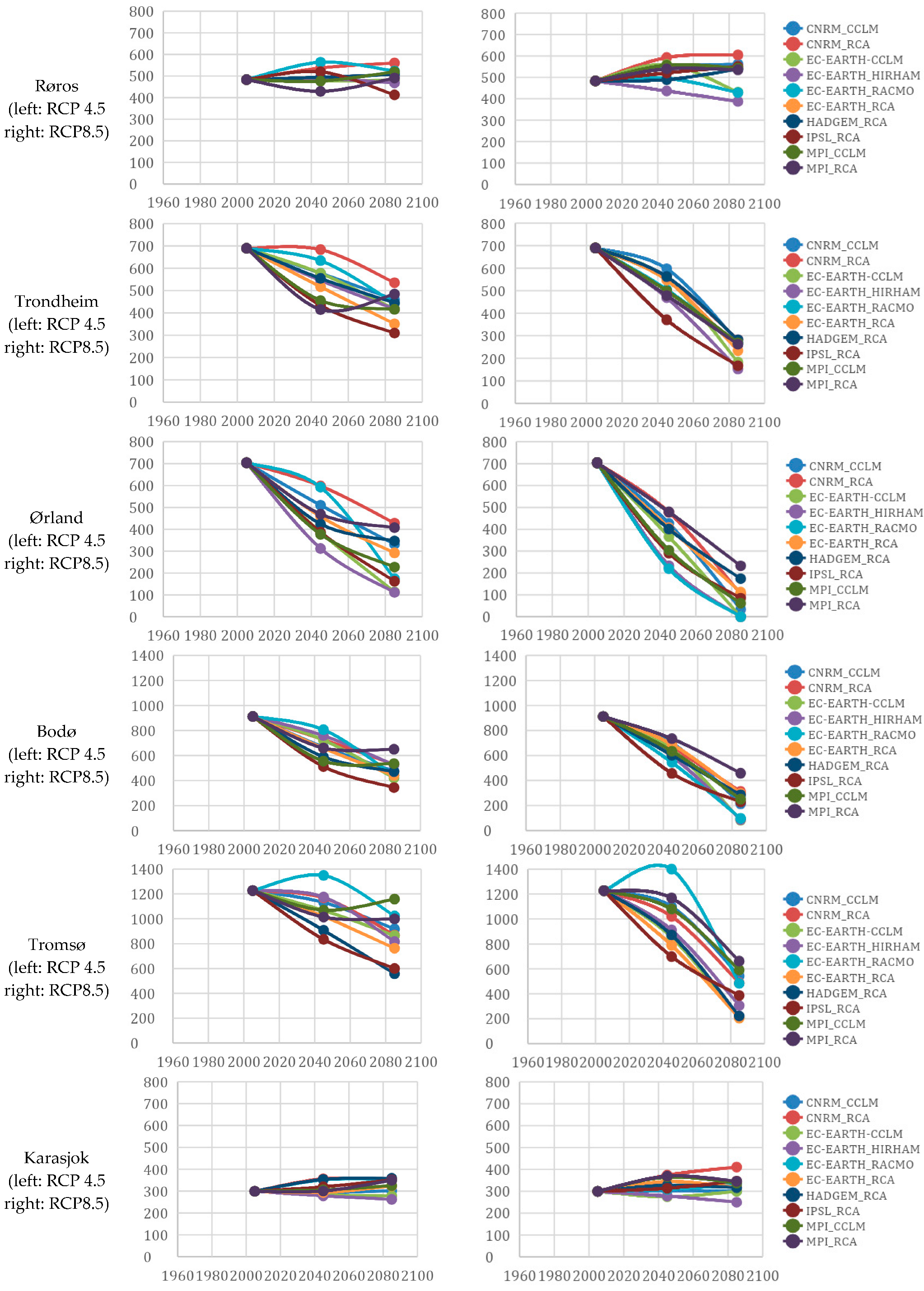
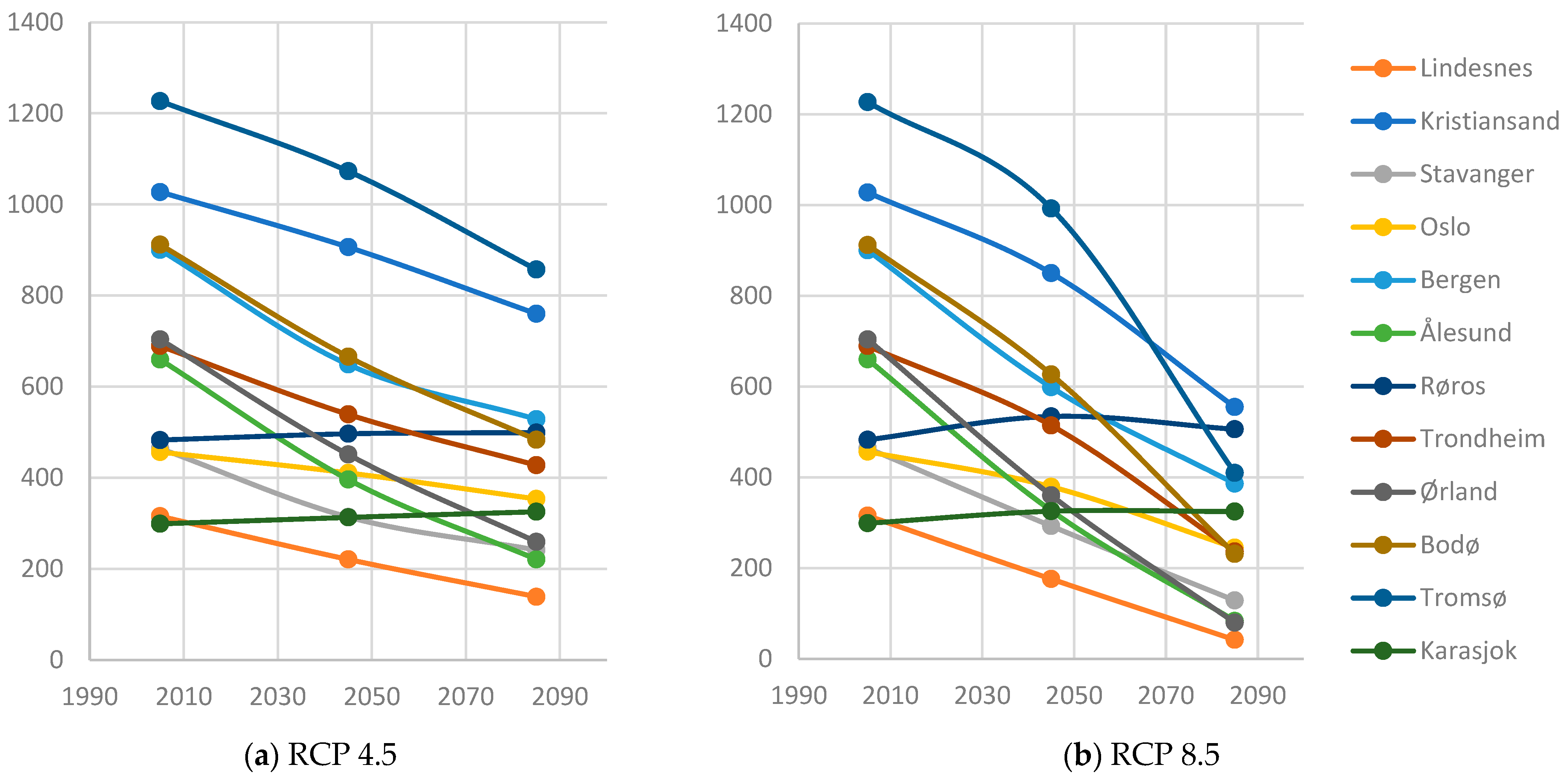
3.3. Estimated Future Development of FDEI Based on Climate Models (2031–2100)
3.4. Climate Model Uncertainty Analysis and Design Values of FDEI
4. Discussion
4.1. Historical and Future Developments of FDEI in Norway
4.2. Uncertainties Originating from Future Climate Projections
4.3. FDEI as a Design Tool in Building Design
4.4. Limitations and Scope for Further Research
5. Conclusions
- The development of FDEI values in Norway over the last decades have declined when comparing climate data from 1961–1990 to 1991–2020, due to increasing winter temperatures from climate changes. Notable exceptions to the trend are found in the coldest locations (Røros, Karasjok, Tromsø, Oslo), where the net effect of increased winter temperatures and increased precipitation leads to an increase in FDEI values. In the future, the overall reduction in FDEI values is expected to continue for all locations except Røros and Karasjok, where annual freezing-point crossings are relatively stable even when considering the RCP 8.5 2071–2100 scenario, leading to an increase in FDEI values.
- Additional uncertainties in the calculation of FDEI values are introduced when using future climate projections. A comparison of the 10 climate models revealed significant variations, demonstrating that introducing future estimates increases the level of uncertainty in such calculations. In particular, the results show that longer timeframes increase the variance between the model chains, independent of emission scenario forcing, and more extreme emission scenario forcings further increase the variance. Therefore, assessments of future climate scenarios should be calculated using an ensemble of models and emission scenarios to assess the uncertainty of the results.
- For the index to be useful as a design tool, design values and information describing design value uncertainty must be defined. The proposed design value for each location is conservatively defined as the highest average FDEI value in the data set for each location (either from the 1991–2020 period or from one of the four future scenarios). The coefficient of variance, CV, for each design value calculation is defined, as well as the estimated future development trend for the location. A comparison of the index value for the given location relative to other locations in the set indicates whether the location is a high- or low-risk area for frost decay, and evaluating CV and development trends allows for an uncertainty analysis of the conclusion. This approach enables a quick-to-use qualitative comparative risk analysis for climate adaptation purposes, in line with the climate risk and vulnerability assessment required in the EU Taxonomy Regulation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. FDEI Curves for Each Calculated Location, Timestep, Climate Model and Emission Scenario
References
- Grynning, S.; Wærnes, E.; Kvande, T.; Time, B. Climate adaptation of buildings through MOM-and upgrading-State of the art and research needs. Energy Procedia 2017, 132, 622–627. [Google Scholar] [CrossRef]
- Häkkinen, T.; Belloni, K. Barriers and drivers for sustainable building. Build. Res. Inf. 2011, 39, 239–255. [Google Scholar] [CrossRef]
- Singh, C.; Iyer, S.; New, M.G.; Few, R.; Kuchimanchi, B.; Segnon, A.C.; Morchain, D. Interrogating ‘effectiveness’ in climate change adaptation: 11 guiding principles for adaptation research and practice. Clim. Dev. 2022, 14, 650–664. [Google Scholar] [CrossRef]
- Lisø, K.R.; Kvande, T.; Time, B. climate adaptation framework for moisture-resilient buildings in Norway. Energy Procedia 2017, 132, 628–633. [Google Scholar] [CrossRef]
- Bunkholt, N.S.; Gullbrekken, L.; Time, B.; Kvande, T. Process induced building defects in Norway—Development and climate risks. J. Phys. Conf. Ser. 2021, 2069, 012040. [Google Scholar] [CrossRef]
- Rydock, J.P.; Lisø, K.R.; Førland, E.J.; Nore, K.; Thue, J.V. A driving rain exposure index for Norway. Build. Environ. 2005, 40, 1450–1458. [Google Scholar] [CrossRef]
- Pakkala, T.A.; Lahdensivu, J. Wind-driven rain load in Finland in present and future projected climates. J. Phys. Conf. Ser. 2023, 2654, 012012. [Google Scholar] [CrossRef]
- Gaur, A.; Lu, H.; Lacasse, M.; Ge, H.; Hill, F. Future projected changes in moisture index over Canada. Build. Environ. 2021, 199, 107923. [Google Scholar] [CrossRef]
- Gaarder, J.E.; Andenæs, E.; Astrup, I.; Lacasse, M.; Time, B.; Kvande, T. Comparing Canadian and Norwegian moisture indices for building climate adaptation. J. Phys. Conf. Ser. 2023, 2654, 012013. [Google Scholar] [CrossRef]
- Lisø, K.R.; Kvande, T.; Hygen, H.O.; Thue, J.V.; Harstveit, K. A frost decay exposure index for porous, mineral building materials. Build. Environ. 2007, 42, 3547–3555. [Google Scholar] [CrossRef]
- Lehner, F.; Deser, C.; Maher, N.; Marotzke, J.; Fischer, E.M.; Brunner, L.; Knutti, R.; Hawkins, E. Partitioning climate projection uncertainty with multiple large ensembles and CMIP5/6. Earth Syst. Dyn. 2020, 11, 491–508. [Google Scholar] [CrossRef]
- Sahlin, U.; Helle, I.; Perepolkin, D. “This Is What We Don’t Know”: Treating Epistemic Uncertainty in Bayesian Networks for Risk Assessment. Integr. Environ. Assess. Manag. 2021, 17, 221–232. [Google Scholar] [CrossRef] [PubMed]
- Gaarder, J.E.; Hygen, H.O.; Bohne, R.A.; Kvande, T. Building Adaptation Measures Using Future Climate Scenarios—A Scoping Review of Uncertainty Treatment and Communication. Buildings 2023, 13, 1460. [Google Scholar] [CrossRef]
- Gaarder, J.E.; Høien Clausen, R.; Næss, R.; Kvande, T. Barriers to Climate Adaptation in Norwegian Building Projects–Insights from Moisture Safety Designers’ Perspective. Clim. Risk Manag. 2024, 43, 100590. [Google Scholar] [CrossRef]
- Kvande, T.; Tajet, H.T.T.; Tunheim, K. Klimadata for dimensjonering mot regnpåkjenning. In SINTEF, Building Research Design Guides; SINTEF AS: Oslo, Norway, 2023; Available online: https://www.byggforsk.no/sok/2?sources=1&source=1&q=Klimadata+for+dimensjonering+mot+regnp%C3%A5kjenning (accessed on 4 September 2024).
- Kvande, T.; Tajet, H.T.T.; Hygen, H.O. Klimadata for termisk dimensjonering og frostsikring. In SINTEF, Building Research Design Guides; SINTEF AS: Oslo, Norway, 2023; Available online: https://www.byggforsk.no/sok/2?sources=1&source=1&q=Klimadata+for+termisk+dimensjonering+og+frostsikring (accessed on 4 September 2024).
- WMO. Guidelines on analysis of extremes in a changing climate in support of informed decisions for adaptation. World Meteorol. Organ. 2009, 1500, 72. [Google Scholar]
- Tveito, O.E. Norwegian Standard Climate Normals; Norwegian Meteorological Institute: Oslo, Norway, 2021. [Google Scholar]
- Hanssen-Bauer, I.; Tveito, O.E.; Tajet, H.T.T.; Skaland, R.G. Temperatur- og Nedbør-Regioner i Norge; Norwegian Meteorological Institute: Oslo, Norway, 2022. [Google Scholar]
- Berkhout, F.; Hertin, J.; Gann, D.M. Learning to adapt: Organisational adaptation to climate change impacts. Clim. Chang. 2006, 78, 135–156. [Google Scholar] [CrossRef]
- Bevan, L.D. The ambiguities of uncertainty: A review of uncertainty frameworks relevant to the assessment of environmental change. Futures 2022, 137, 102919. [Google Scholar] [CrossRef]
- Manning, M.; Lawrence, J.; King, D.N.; Chapman, R. Dealing with changing risks: A New Zealand perspective on climate change adaptation. Reg. Environ. Chang. 2015, 15, 581–594. [Google Scholar] [CrossRef]
- Shen, M.; Chen, J.; Zhuan, M.; Chen, H.; Xu, C.-Y.; Xiong, L. Estimating uncertainty and its temporal variation related to global climate models in quantifying climate change impacts on hydrology. J. Hydrol. 2018, 556, 10–24. [Google Scholar] [CrossRef]
- Opoku, D.-G.J.; Ayarkwa, J.; Agyekum, K. Barriers to environmental sustainability of construction projects. Smart Sustain. Built Environ. 2019, 8, 292–306. [Google Scholar] [CrossRef]
- Simonet, G.; Leseur, A. Barriers and drivers to adaptation to climate change—A field study of ten French local authorities. Clim. Chang. 2019, 155, 621–637. [Google Scholar] [CrossRef]
- Haarhaus, T.; Liening, A. Building dynamic capabilities to cope with environmental uncertainty: The role of strategic foresight. Technol. Forecast. Soc. Chang. 2020, 155, 120033. [Google Scholar] [CrossRef]
- Stanton, M.C.B.; Roelich, K. Decision making under deep uncertainties: A review of the applicability of methods in practice. Technol. Forecast. Soc. Chang. 2021, 171, 120939. [Google Scholar] [CrossRef]
- Clarke, D.; Murphy, C.; Lorenzoni, I. Barriers to Transformative Adaptation: Responses to Flood Risk in Ireland. J. Extreme Events 2016, 3, 1650010. [Google Scholar] [CrossRef]
- Ryan, B.; Bristow, D.N. Climate Change and Hygrothermal Performance of Building Envelopes: A Review on Risk Assessment. Int. J. Technol. 2023, 14, 1461–1475. [Google Scholar] [CrossRef]
- Vandemeulebroucke, I.; Kotova, L.; Caluwaerts, S.; Van Den Bossche, N. Degradation of brick masonry walls in Europe and the Mediterranean: Advantages of a response-based analysis to study climate change. Build. Environ. 2023, 230, 109963. [Google Scholar] [CrossRef]
- Kvande, T.; Lisø, K.R. Climate adapted design of masonry structures. Build. Environ. 2009, 44, 2442–2450. [Google Scholar] [CrossRef]
- Ojo, B. Strategies for the Optimization of Critical Infrastructure Projects to Enhance Urban Resilience to Climate Change. J. Sci. Eng. Res. 2024, 11, 107–123. [Google Scholar]
- EU. Regulation (EU) 2020/852 of the European Parliament and of the Council of 18 June 2020 on the establishment of a framework to facilitate sustainable investment, and amending Regulation (EU) 2019/2088. Off. J. Eur. Union 2020, 198, 13–43. [Google Scholar]
- Janssens, K.; Marincioni, V.; Van Den Bossche, N. Improving hygrothermal risk assessment tools for brick walls in a changing climate. J. Phys. Conf. Ser. 2023, 2654, 012024. [Google Scholar] [CrossRef]
- Pakkala, T.A.; Köliö, A.; Lahdensivu, J.; Kiviste, M. Durability demands related to frost attack for Finnish concrete buildings in changing climate. Build. Environ. 2014, 82, 27–41. [Google Scholar] [CrossRef]
- Mandinec, J.; Johansson, P. Microclimate modelling and hygrothermal investigation of freeze-thaw degradation under future climate scenarios. J. Phys. Conf. Ser. 2023, 2654, 012146. [Google Scholar] [CrossRef]
- Köppen, W. Das geographische System der Klimate. In Handbuch der Klimatologie, s. 46; Borntraeger: Stuttgart, Germany, 1936. [Google Scholar] [CrossRef]
- MET. Norwegian Meteorological Institute. 2024. Available online: https://www.seklima.met.no (accessed on 1 April 2024).
- Venter, Z.S.; Krog, N.H.; Barton, D.N. Linking green infrastructure to urban heat and human health risk mitigation in Oslo, Norway. Sci. Total Environ. 2020, 709, 136193. [Google Scholar] [CrossRef] [PubMed]
- Lussana, C. seNorge observational gridded datasets. seNorge_2018, version 20.05. arXiv 2020, arXiv:2008.02021. [Google Scholar]
- Lussana, C.; Tveito, O.E.; Dobler, A.; Tunheim, K. seNorge_2018, daily precipitation, and temperature datasets over Norway. Earth Syst. Sci. Data 2019, 11, 1531–1551. [Google Scholar] [CrossRef]
- Wong, W.K.; Nilsen, I.B. Bias-Adjustment of Maximum and Minimum Temperatures for Norway; Norwegian Water Resources and Energy Directorate: Oslo, Norway, 2019. [Google Scholar]
- Wong, W.K.; Haddeland, I.; Lawrence, D.; Beldring, S. Gridded 1 × 1 km Climate and Hydrological Projections for Norway; Norwegian Water Resources and Energy Directorate: Oslo, Norway, 2016. [Google Scholar]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of IPCC the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Giorgi, F.; Mearns, L.O. Introduction to special section: Regional Climate Modeling Revisited. J. Geophys. Res. Atmos. 1999, 104, 6335–6352. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in projections of regional precipitation change. Clim. Dyn. 2011, 37, 407–418. [Google Scholar] [CrossRef]
- Martel, J.-L.; Brissette, F.P.; Lucas-Picher, P.; Troin, M.; Arsenault, R. Climate Change and Rainfall Intensity–Duration–Frequency Curves: Overview of Science and Guidelines for Adaptation. J. Hydrol. Eng. 2021, 26, 03121001. [Google Scholar] [CrossRef]
- Fischer, E.M.; Sedláček, J.; Hawkins, E.; Knutti, R. Models agree on forced response pattern of precipitation and temperature extremes. Geophys. Res. Lett. 2014, 41, 8554–8562. [Google Scholar] [CrossRef]
- Vandemeulebroucke, I.; Caluwaerts, S.; Van Den Bossche, N. Factorial Study on the Impact of Climate Change on Freeze-Thaw Damage, Mould Growth and Wood Decay in Solid Masonry Walls in Brussels. Buildings 2021, 11, 134. [Google Scholar] [CrossRef]
- Choidis, P.; Coelho, G.B.A.; Kraniotis, D. Assessment of frost damage risk in a historic masonry wall due to climate change. Adv. Geosci. 2023, 58, 157–175. [Google Scholar] [CrossRef]
- Loli, A.; Bertolin, C. Indoor Multi-Risk Scenarios of Climate Change Effects on Building Materials in Scandinavian Countries. Geosciences 2018, 8, 347. [Google Scholar] [CrossRef]
- Hanssen-Bauer, I.; Drange, H.; Førland, E.J.; Roald, L.A.; Børsheim, K.Y.; Hisdal, H.; Lawrence, D.; Nesje, A.; Sandven, S.; Sorteberg, A. Climate in Norway 2100. In Background Information to NOU Climate Adaptation (In Norwegian: Klima i Norge 2100. Bakgrunnsmateriale til NOU Klimatilplassing); Norsk klimasenter: Oslo, Norway, 2017. [Google Scholar]
- Scheffer, T.C. A climate index for estimating potential for decay in wood structures above ground. For. Prod. J. 1971, 21, 25–31. [Google Scholar]
- Grossi, C.M.; Brimblecombe, P.; Harris, I. Predicting long term freeze–thaw risks on Europe built heritage and archaeological sites in a changing climate. Sci. Total Environ. 2007, 377, 273–281. [Google Scholar] [CrossRef]
- Lisø, K.R.; Hygen, H.O.; Kvande, T.; Thue, J.V. Decay potential in wood structures using climate data. Build. Res. Inf. 2006, 34, 546–551. [Google Scholar] [CrossRef]
- Gaur, A.; Lacasse, M.; Armstrong, M. Climate Data to Undertake Hygrothermal and Whole Building Simulations Under Projected Climate Change Influences for 11 Canadian Cities. Data 2019, 4, 72. [Google Scholar] [CrossRef]
- Smith, D.M.; Scaife, A.A.; Eade, R.; Athanasiadis, P.; Bellucci, A.; Bethke, I.; Bilbao, R.; Borchert, L.F.; Caron, L.-P.; Counillon, F.; et al. North Atlantic climate far more predictable than models imply. Nature 2020, 583, 796–800. [Google Scholar] [CrossRef]
- Jeong, D.I.; Cannon, A.J. Projected changes to moisture loads for design and management of building exteriors over Canada. Build. Environ. 2020, 170, 106609. [Google Scholar] [CrossRef]
- Dukhan, T.; Sushama, L. Understanding and modelling future wind-driven rain loads on building envelopes for Canada. Build. Environ. 2021, 196, 107800. [Google Scholar] [CrossRef]
- Calle, K.; Van Den Bossche, N. Analysis of Different Frost Indexes and Their Potential to Assess Frost Based on HAM Simulations. In Proceedings of the 14th International Conference on Durability of Buildings Materials and Components, Ghent, Belgium, 29–31 May 2017; RILEM Publications SARL: Paris, France, 2017; pp. 61–62. Available online: http://hdl.handle.net/1854/LU-8525026 (accessed on 4 September 2024).
| Station Name | Station Number | Latitude | Longitude | Annual Normal Temperature (1961–1990) | Annual Normal Temperature (1991–2020) | Annual Normal Precipitation (1961–1990) | Annual Normal Precipitation (1991–2020) |
|---|---|---|---|---|---|---|---|
| Lindesnes | SN41770 | 57.9815 | 7.048 | 7.4 | 8.6 | 1159 | 1245 |
| Kristiansand | SN39040 | 58.2000 | 8.0767 | 6.6 | 7.6 | 1299 | 1384 |
| Stavanger | SN44560 | 58.8843 | 5.637 | 7.4 | 8.4 | 1180 | 1257 |
| Oslo | SN18700 | 59.9423 | 10.72 | 5.7 | 7.0 | 763 | 837 |
| Bergen | SN50540 | 60.383 | 5.3327 | 7.6 | 8.4 | 2250 | 2496 |
| Ålesund | SN60990 | 62.5617 | 6.115 | 6.9 | 7.9 | 1310 | 1451 |
| Røros | SN10380 | 62.5773 | 11.3518 | 0.3 | 1.1 | 504 | 531 |
| Trondheim | SN69100 | 63.4597 | 10.9305 | 5.3 | 6.1 | 892 | 823 |
| Ørland | SN71550 | 63.7045 | 9.6105 | 5.8 | 6.8 | 1048 | 994 |
| Bodø | SN82290 | 67.2723 | 14.3816 | 4.5 | 5.5 | 1020 | 1118 |
| Tromsø | SN90450 | 69.6537 | 18.9368 | 2.5 | 3.4 | 1031 | 1091 |
| Karasjok | SN97251 | 69.4635 | 25.5023 | −2.4 | −1.2 | 366 | 417 |
| Institute | Global Climate Model (GCM) | Regional Climate Model (RCM) | Combination |
|---|---|---|---|
| Climate Limited-area Modelling Community | CNRM-CM5 | CCLM-4-8-17 | CNRM_CCLM |
| Swedish Meteorological and Hydrological Institute | CNRM-CM5 | RCA4 | CNRM_RCA |
| Climate Limited-area Modelling Community | EC-EARTH | CCLM4-8-17 | EC-venterEARTH_CCLM |
| Danish Meteorological Institute | EC-EARTH | HIRHAM5 | EC-EARTH_HIRHAM |
| Royal Netherlands Meteorological Institute | EC-EARTH | RACMO22E | EC-EARTH_RACMO |
| Swedish Meteorological and Hydrological Institute | EC-EARTH | RCA4 | EC-EARTH_RCA |
| Swedish Meteorological and Hydrological Institute | HadGEM2-ES | RCA4 | HADGEM_RCA |
| Swedish Meteorological and Hydrological Institute | IPSL-CM5A-MR | RCA4 | IPSL_RCA |
| Climate Limited-area Modelling Community | MPI-ESM-LR | CCLM | MPI_CCLM |
| Swedish Meteorological and Hydrological Institute | MPI-ESM-LR | RCA4 | MPI_RCA |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FDEImax/min 1 | 315.9 | 1027.4 | 464.8 | 456.9 | 900.4 | 659.9 | 483.1 | 689.5 | 703.9 | 911.8 | 1226.8 | 299.3 |
| FDEIhourly | 175.2 | 650.0 | 346.1 | 282.3 | 647.1 | 348.2 | 324.8 | 477.9 | 453.5 | 583.2 | 689.0 | 193.4 |
| FDEISynoptic 2 | 144.2 | 488.0 | 234.1 | 248.5 | 525.1 | 243.6 | 222.2 | 348.1 | 319.2 | 402.8 | 551.9 | 135.3 |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FPCmax/min 1 | 29.5 | 82.8 | 51.4 | 75.5 | 46.2 | 38.7 | 102.3 | 82.8 | 60.9 | 72.0 | 87.4 | 91.3 |
| FPChourly | 15.3 | 49.4 | 35.4 | 45.7 | 30.4 | 20.6 | 78.5 | 53.6 | 35.3 | 43.0 | 48.9 | 57.3 |
| FPCSynoptic 2 | 13.2 | 38.5 | 25.5 | 38.6 | 26.6 | 14.7 | 58.3 | 40.0 | 25.5 | 29.4 | 36.8 | 38.8 |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CNRM_CCLM | 244.2 | 941.4 | 394.6 | 459.2 | 622.6 | 539.3 | 484.7 | 577.9 | 510.2 | 667.8 | 1131.3 | 292.9 |
| CNRM_RCA | 244.5 | 995.3 | 361.4 | 446.9 | 636.9 | 524.5 | 537 | 683.9 | 598.4 | 727.1 | 1167.6 | 356.6 |
| EC-EARTH-CCLM | 159.8 | 906.3 | 297.5 | 423 | 641.8 | 335.6 | 477 | 577.6 | 386.2 | 723.7 | 1066.1 | 282.3 |
| EC-EARTH_HIRHAM | 138.8 | 714.9 | 195.2 | 333.5 | 565.5 | 179.2 | 487.5 | 545.6 | 312 | 759.1 | 1175.1 | 278.5 |
| EC-EARTH_RACMO | 264.5 | 872 | 323.8 | 429.6 | 753.6 | 489.1 | 563.9 | 634.3 | 593.1 | 806.8 | 1349.2 | 351.7 |
| EC-EARTH_RCA | 195.9 | 828.8 | 309.5 | 389.8 | 623.9 | 387.8 | 500.5 | 517.1 | 458.2 | 658.8 | 1018.8 | 293.6 |
| HADGEM_RCA | 171.3 | 789.2 | 347 | 329.3 | 711.3 | 447.4 | 494.3 | 554.4 | 424.3 | 589.5 | 907.7 | 353.5 |
| IPSL_RCA | 237.6 | 907.7 | 318.9 | 443.7 | 598.8 | 327 | 519.7 | 433.5 | 386.7 | 511.7 | 834.7 | 319.4 |
| MPI_CCLM | 299.3 | 1019.4 | 302.9 | 437.8 | 705 | 334.3 | 476.6 | 455.2 | 377.1 | 555.2 | 1068.1 | 305.2 |
| MPI_RCA | 257.9 | 1088.5 | 293.5 | 418.5 | 629.5 | 401.7 | 428.6 | 414.6 | 469.1 | 660.4 | 1013.1 | 300.2 |
| Average | 221 | 906 | 314 | 411 | 649 | 397 | 497 | 539 | 452 | 666 | 1073 | 313 |
| Maximum | 299 | 1089 | 395 | 459 | 754 | 539 | 564 | 684 | 598 | 807 | 1349 | 357 |
| Minimum | 139 | 715 | 195 | 329 | 566 | 179 | 429 | 415 | 312 | 512 | 835 | 279 |
| Std dev | 52 | 112 | 53 | 46 | 57 | 109 | 37 | 87 | 94 | 93 | 145 | 30 |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CNRM_CCLM | 97.4 | 752.8 | 266 | 444.8 | 446.4 | 286.2 | 511.1 | 459.5 | 331.7 | 476.7 | 918.4 | 301.9 |
| CNRM_RCA | 199.5 | 880.6 | 328 | 412.1 | 579 | 358.1 | 560.4 | 535.2 | 428.3 | 530.4 | 870.2 | 354 |
| EC-EARTH-CCLM | 106.6 | 767.9 | 206.9 | 316.2 | 522.3 | 123 | 480.9 | 417.3 | 113.8 | 420.5 | 865.3 | 278.1 |
| EC-EARTH_HIRHAM | 61.3 | 653 | 130.6 | 312.5 | 495.8 | 84.8 | 468.1 | 417.2 | 111.5 | 525.8 | 817.5 | 262.2 |
| EC-EARTH_RACMO | 100.2 | 704.8 | 195.5 | 357.2 | 479.5 | 39.2 | 523.4 | 443.9 | 174.2 | 441.5 | 1022.1 | 353.9 |
| EC-EARTH_RCA | 151.7 | 608.9 | 221.9 | 308.2 | 502.6 | 241.6 | 521.3 | 350.8 | 292 | 441.1 | 763.5 | 322.8 |
| HADGEM_RCA | 96.9 | 672.4 | 273.6 | 293.7 | 524.6 | 295.4 | 506.7 | 444.9 | 347 | 471.5 | 558.4 | 358.6 |
| IPSL_RCA | 179.2 | 776.3 | 254.2 | 309.4 | 480.1 | 220.2 | 412.7 | 309.7 | 162.4 | 344.3 | 600.8 | 351.4 |
| MPI_CCLM | 186.9 | 876.2 | 253.1 | 417.9 | 670.7 | 237.1 | 519.5 | 416 | 227.4 | 535.7 | 1158.5 | 324.7 |
| MPI_RCA | 212.8 | 910.2 | 290.7 | 368.1 | 587.7 | 327.8 | 490.9 | 484.3 | 407.5 | 650.3 | 998.5 | 349.5 |
| Average | 139 | 760 | 242 | 354 | 529 | 221 | 500 | 428 | 260 | 484 | 857 | 326 |
| Maximum | 213 | 910 | 328 | 445 | 671 | 358 | 560 | 535 | 428 | 650 | 1159 | 359 |
| Minimum | 61 | 609 | 131 | 294 | 446 | 39 | 413 | 310 | 112 | 344 | 558 | 262 |
| Std dev | 53 | 103 | 56 | 55 | 66 | 106 | 40 | 64 | 118 | 83 | 185 | 35 |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CNRM_CCLM | 155.5 | 830.2 | 303.9 | 422.2 | 525.3 | 351.1 | 546.8 | 597.6 | 426.6 | 700.1 | 1099.6 | 302.7 |
| CNRM_RCA | 162.5 | 884.3 | 283.8 | 366.8 | 542.3 | 321.2 | 593 | 558.6 | 477.8 | 660.5 | 1020.5 | 373.5 |
| EC-EARTH-CCLM | 169.6 | 952.9 | 304.3 | 392.8 | 614.1 | 343.4 | 560.2 | 554.1 | 366.1 | 650.7 | 855.4 | 274.5 |
| EC-EARTH_HIRHAM | 147.2 | 830.1 | 258.8 | 389.8 | 618.9 | 246.6 | 436.5 | 469.2 | 232.8 | 595 | 911.4 | 277.9 |
| EC-EARTH_RACMO | 170.1 | 651.5 | 262.9 | 318.4 | 612.1 | 192.8 | 494.8 | 504.9 | 219.4 | 544.7 | 1427.8 | 308.6 |
| EC-EARTH_RCA | 171.5 | 796.5 | 240.5 | 340.8 | 573.9 | 354.1 | 607.4 | 547.2 | 407 | 689 | 789.8 | 344 |
| HADGEM_RCA | 212.9 | 904.6 | 327.2 | 392.6 | 663.4 | 399.6 | 489.2 | 562.5 | 400.9 | 602.5 | 873.8 | 327.1 |
| IPSL_RCA | 194.9 | 816.2 | 295.6 | 369.4 | 547.7 | 321.2 | 520.7 | 370.8 | 290.6 | 457.1 | 699 | 313.1 |
| MPI_CCLM | 201.2 | 947.2 | 306.6 | 411.6 | 628.8 | 309.2 | 557 | 499.6 | 304 | 634.7 | 1079.4 | 365 |
| MPI_RCA | 176.4 | 886 | 344.3 | 389.8 | 658.3 | 428.3 | 539.7 | 478.7 | 479 | 734.6 | 1168.1 | 368.8 |
| Average | 176 | 850 | 293 | 379 | 598 | 327 | 535 | 514 | 360 | 627 | 992 | 326 |
| Maximum | 213 | 953 | 344 | 422 | 663 | 428 | 607 | 598 | 479 | 735 | 1428 | 374 |
| Minimum | 147 | 652 | 241 | 318 | 525 | 193 | 437 | 371 | 219 | 457 | 699 | 275 |
| Std dev | 21 | 88 | 32 | 31 | 49 | 68 | 51 | 65 | 94 | 81 | 213 | 36 |
| Lindesnes | Kristiansand | Stav-ager | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CNRM_CCLM | 0 | 622.9 | 138 | 314.5 | 285.1 | 0 | 561.9 | 273.5 | 33.8 | 214.5 | 543.4 | 301 |
| CNRM_RCA | 68.4 | 586 | 127.9 | 255.5 | 281.4 | 0 | 605.1 | 282.6 | 104.3 | 312.6 | 488.7 | 410 |
| EC-EARTH-CCLM | 48.9 | 566.9 | 130.5 | 218.9 | 422.4 | 114.5 | 430.9 | 183 | 0 | 82.6 | 206.4 | 299.4 |
| EC-EARTH_HIRHAM | 0 | 372.9 | 90.2 | 210.6 | 343.5 | 0 | 387.7 | 152.9 | 0 | 88 | 306.1 | 250 |
| EC-EARTH_RACMO | 5.7 | 421.6 | 86.7 | 268.1 | 362.5 | 0 | 429.3 | 264.5 | 0 | 97.8 | 483.5 | 328.5 |
| EC-EARTH_RCA | 61.2 | 470.3 | 107.2 | 190.7 | 427.8 | 167.9 | 481 | 234.2 | 112 | 297.1 | 205.2 | 317.5 |
| HADGEM_RCA | 38.7 | 554.7 | 129.1 | 241.1 | 431.7 | 140.4 | 538.4 | 282.4 | 173.8 | 286.1 | 221.6 | 316 |
| IPSL_RCA | 112.7 | 594.9 | 162.3 | 189.3 | 378.9 | 180.1 | 550.8 | 166.8 | 84.9 | 229.2 | 387 | 346 |
| MPI_CCLM | 4.6 | 735.4 | 165.4 | 307.8 | 452.2 | 2.9 | 543 | 268.8 | 61.5 | 250.8 | 592.1 | 336.7 |
| MPI_RCA | 85.2 | 624.9 | 152.3 | 256 | 477 | 235 | 535.3 | 262.2 | 232.7 | 458.6 | 663.4 | 345.5 |
| Average | 43 | 555 | 129 | 245 | 386 | 84 | 506 | 237 | 80 | 232 | 410 | 325 |
| Maximum | 113 | 735 | 165 | 315 | 477 | 235 | 605 | 283 | 233 | 459 | 663 | 410 |
| Minimum | 0 | 373 | 87 | 189 | 281 | 0 | 388 | 153 | 0 | 83 | 205 | 250 |
| Std dev | 40 | 107 | 28 | 44 | 68 | 93 | 70 | 50 | 78 | 119 | 169 | 41 |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1991–2020 | 316 | 1027 | 465 | 457 | 900 | 660 | 483 | 690 | 704 | 912 | 1227 | 299 |
| RCP 4.5 2031–2060 | 221 | 906 | 314 | 411 | 649 | 397 | 497 | 539 | 452 | 666 | 1073 | 313 |
| RCP 4.5 2071–2100 | 139 | 760 | 242 | 354 | 529 | 221 | 500 | 428 | 260 | 484 | 857 | 326 |
| RCP 8.5 2031–2060 | 176 | 850 | 293 | 379 | 598 | 327 | 535 | 514 | 360 | 627 | 992 | 326 |
| RCP 8.5 2071–2100 | 43 | 555 | 129 | 245 | 386 | 84 | 506 | 237 | 80 | 232 | 410 | 325 |
| Max avg value | 316 | 1027 | 465 | 457 | 900 | 660 | 535 | 690 | 704 | 912 | 1227 | 326 |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1991–2020 | 30 | 83 | 51 | 76 | 46 | 39 | 115 | 83 | 61 | 72 | 87 | 91 |
| RCP 4.5 2031–2060 | 21 | 74 | 40 | 71 | 33 | 25 | 114 | 72 | 45 | 58 | 83 | 99 |
| RCP 4.5 2071–2100 | 16 | 65 | 34 | 63 | 27 | 16 | 112 | 62 | 34 | 47 | 74 | 99 |
| RCP 8.5 2031–2060 | 19 | 71 | 38 | 68 | 30 | 22 | 115 | 69 | 41 | 55 | 80 | 102 |
| RCP 8.5 2071–2100 | 7 | 49 | 22 | 48 | 15 | 5 | 106 | 44 | 19 | 30 | 54 | 99 |
| Max avg value | 30 | 83 | 51 | 76 | 46 | 39 | 115 | 83 | 61 | 72 | 87 | 102 |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1991–2020 | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a | n/a |
| RCP 4.5 2031–2060 | 0.23 | 0.12 | 0.17 | 0.11 | 0.09 | 0.28 | 0.07 | 0.16 | 0.21 | 0.14 | 0.14 | 0.10 |
| RCP 4.5 2071–2100 | 0.38 | 0.14 | 0.23 | 0.15 | 0.13 | 0.48 | 0.08 | 0.15 | 0.45 | 0.17 | 0.22 | 0.11 |
| RCP 8.5 2031–2060 | 0.12 | 0.10 | 0.11 | 0.08 | 0.08 | 0.21 | 0.10 | 0.13 | 0.26 | 0.13 | 0.21 | 0.11 |
| RCP 8.5 2071–2100 | 0.93 | 0.19 | 0.21 | 0.18 | 0.18 | 1.11 | 0.14 | 0.21 | 0.98 | 0.51 | 0.41 | 0.13 |
| Max coeff. of var. | 0.93 | 0.19 | 0.23 | 0.18 | 0.18 | 1.11 | 0.14 | 0.21 | 0.98 | 0.51 | 0.41 | 0.13 |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RCP 4.5 2031–2060 | 0.36 | 0.21 | 0.32 | 0.16 | 0.14 | 0.45 | 0.14 | 0.25 | 0.32 | 0.22 | 0.24 | 0.12 | 0.24 |
| RCP 4.5 2071–2100 | 0.54 | 0.20 | 0.41 | 0.21 | 0.21 | 0.72 | 0.15 | 0.26 | 0.61 | 0.32 | 0.35 | 0.15 | 0.34 |
| RCP 8.5 2031–2060 | 0.19 | 0.18 | 0.18 | 0.14 | 0.12 | 0.36 | 0.16 | 0.22 | 0.36 | 0.22 | 0.37 | 0.15 | 0.22 |
| RCP 8.5 2071–2100 | 1.32 | 0.33 | 0.31 | 0.26 | 0.25 | 1.40 | 0.21 | 0.27 | 1.45 | 0.81 | 0.56 | 0.25 | 0.62 |
| All scenarios | 0.60 | 0.23 | 0.30 | 0.19 | 0.18 | 0.73 | 0.16 | 0.25 | 0.68 | 0.39 | 0.38 | 0.17 | 0.36 |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CNRM_CCLM | 0.98 | 0.20 | 0.47 | 0.18 | 0.36 | 0.92 | 0.07 | 0.34 | 0.73 | 0.47 | 0.32 | 0.02 | 0.42 |
| CNRM_RCA | 0.52 | 0.24 | 0.42 | 0.26 | 0.35 | 0.87 | 0.06 | 0.39 | 0.61 | 0.37 | 0.38 | 0.07 | 0.38 |
| EC-EARTH-CCLM | 0.50 | 0.24 | 0.37 | 0.30 | 0.20 | 0.50 | 0.13 | 0.46 | 0.89 | 0.68 | 0.57 | 0.04 | 0.41 |
| EC-EARTH_HIRHAM | 0.85 | 0.36 | 0.50 | 0.29 | 0.27 | 0.97 | 0.11 | 0.50 | 0.95 | 0.68 | 0.54 | 0.05 | 0.51 |
| EC-EARTH_RACMO | 0.96 | 0.34 | 0.55 | 0.24 | 0.35 | 1.36 | 0.13 | 0.40 | 1.20 | 0.75 | 0.44 | 0.07 | 0.57 |
| EC-EARTH_RCA | 0.46 | 0.27 | 0.46 | 0.32 | 0.18 | 0.38 | 0.12 | 0.38 | 0.55 | 0.38 | 0.59 | 0.08 | 0.35 |
| HADGEM_RCA | 0.67 | 0.24 | 0.40 | 0.24 | 0.24 | 0.48 | 0.05 | 0.30 | 0.37 | 0.32 | 0.54 | 0.06 | 0.33 |
| IPSL_RCA | 0.34 | 0.20 | 0.30 | 0.39 | 0.22 | 0.28 | 0.14 | 0.42 | 0.65 | 0.37 | 0.36 | 0.06 | 0.31 |
| MPI_CCLM | 0.85 | 0.16 | 0.27 | 0.17 | 0.21 | 0.75 | 0.08 | 0.28 | 0.65 | 0.39 | 0.29 | 0.09 | 0.35 |
| MPI_RCA | 0.47 | 0.26 | 0.36 | 0.23 | 0.15 | 0.28 | 0.11 | 0.27 | 0.31 | 0.22 | 0.26 | 0.10 | 0.25 |
| All models | 0.66 | 0.25 | 0.41 | 0.26 | 0.25 | 0.68 | 0.10 | 0.37 | 0.69 | 0.46 | 0.43 | 0.06 | 0.39 |
| Lindesnes | Kristiansand | Stavanger | Oslo | Bergen | Ålesund | Røros | Trondheim | Ørland | Bodø | Tromsø | Karasjok | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FDEId | 316 | 1027 | 465 | 457 | 900 | 660 | 535 | 690 | 704 | 912 | 1227 | 326 |
| CV | 0.93 | 0.19 | 0.23 | 0.18 | 0.18 | 1.11 | 0.14 | 0.21 | 0.98 | 0.51 | 0.41 | 0.13 |
| Trend | +/− | +/− | − | +/− | − | − | + | +/− | − | − | +/− | + |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaarder, J.E.; Tajet, H.T.T.; Dobler, A.; Hygen, H.O.; Kvande, T. Future Climate Projections and Uncertainty Evaluations for Frost Decay Exposure Index in Norway. Buildings 2024, 14, 2873. https://doi.org/10.3390/buildings14092873
Gaarder JE, Tajet HTT, Dobler A, Hygen HO, Kvande T. Future Climate Projections and Uncertainty Evaluations for Frost Decay Exposure Index in Norway. Buildings. 2024; 14(9):2873. https://doi.org/10.3390/buildings14092873
Chicago/Turabian StyleGaarder, Jørn Emil, Helga Therese Tilley Tajet, Andreas Dobler, Hans Olav Hygen, and Tore Kvande. 2024. "Future Climate Projections and Uncertainty Evaluations for Frost Decay Exposure Index in Norway" Buildings 14, no. 9: 2873. https://doi.org/10.3390/buildings14092873
APA StyleGaarder, J. E., Tajet, H. T. T., Dobler, A., Hygen, H. O., & Kvande, T. (2024). Future Climate Projections and Uncertainty Evaluations for Frost Decay Exposure Index in Norway. Buildings, 14(9), 2873. https://doi.org/10.3390/buildings14092873






