Analysis of the Bearing Capacity of Concrete-Filled Thin-Walled Square Steel Tubes with Helical Stiffening Based on Local Buckling
Abstract
1. Introduction
2. Axial Compression Test
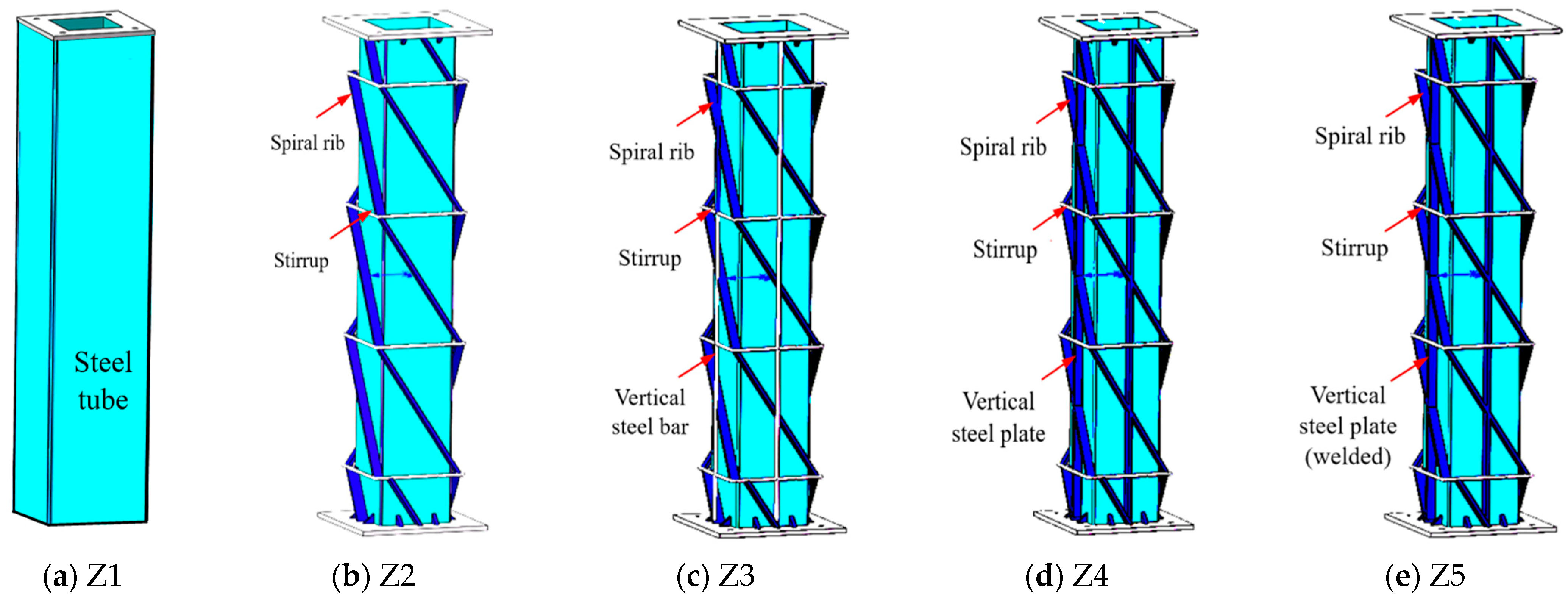
2.1. Specimen Design and Loading Device
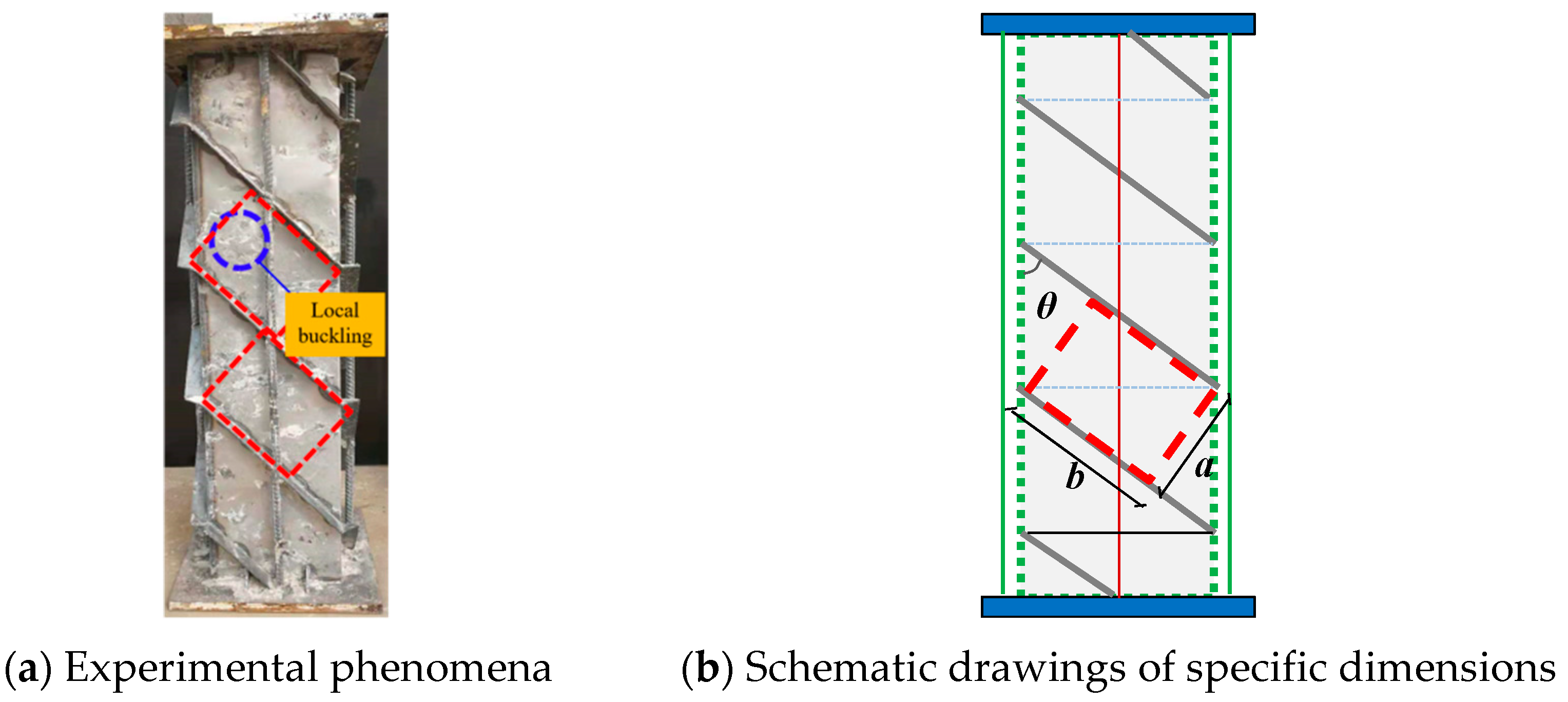
2.2. Damage Phenomenon
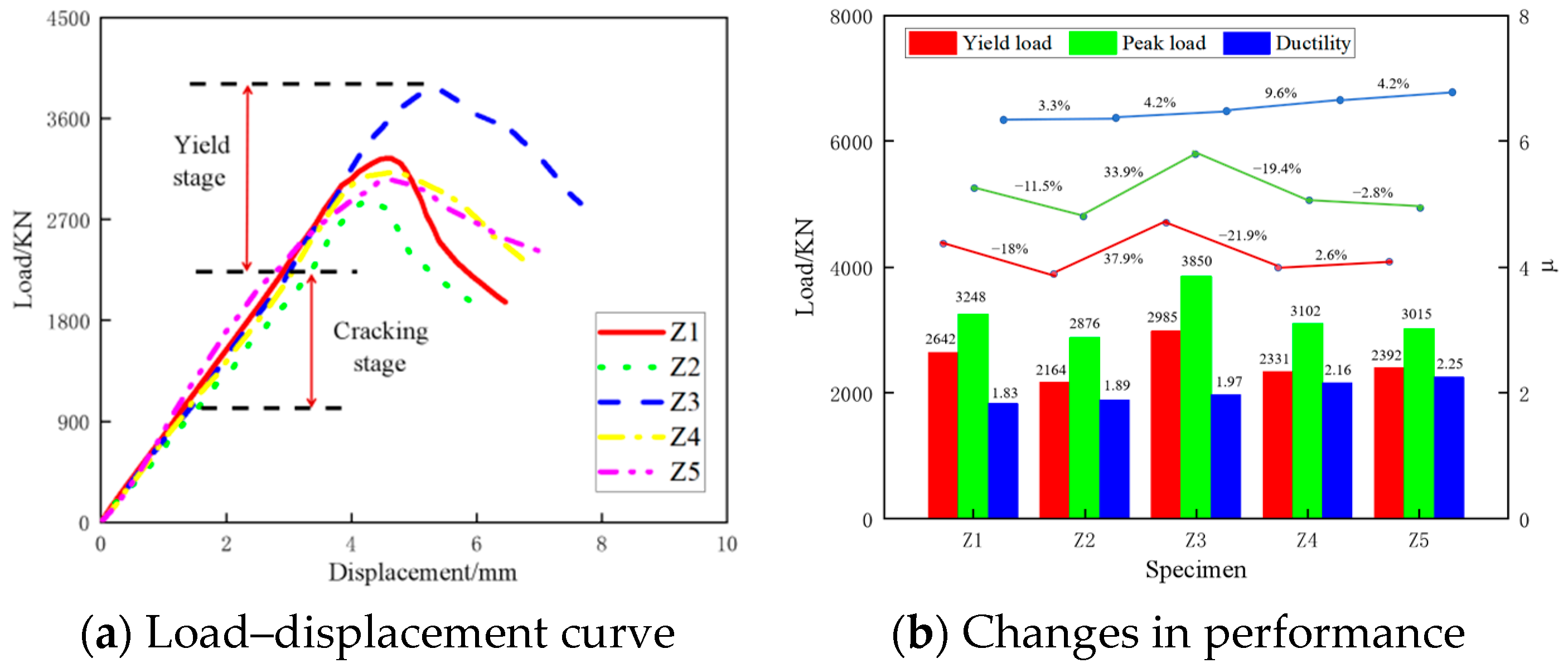
2.3. Load–Displacement Curve
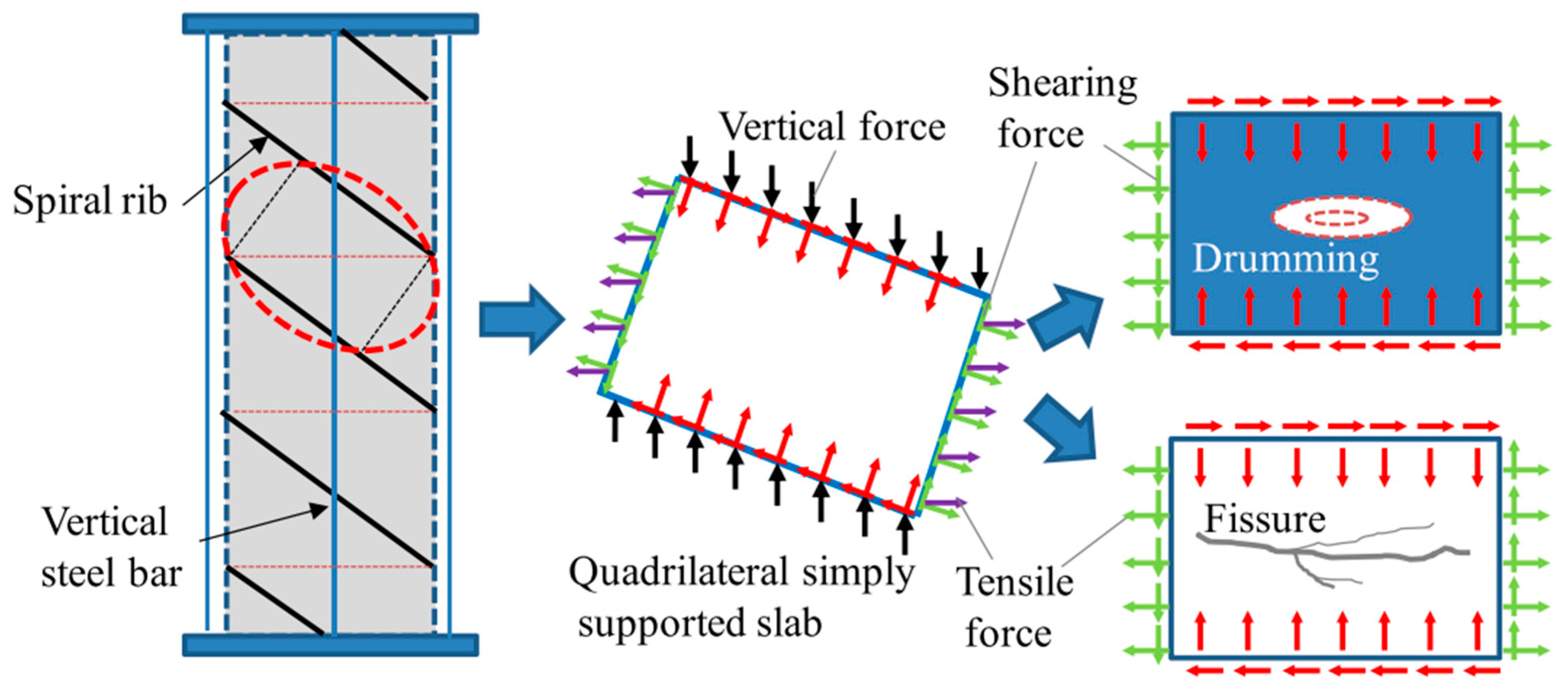
2.4. Mechanism of Spiral Rib Confinement
3. Spiral Rib Steel Tube Buckling Analysis
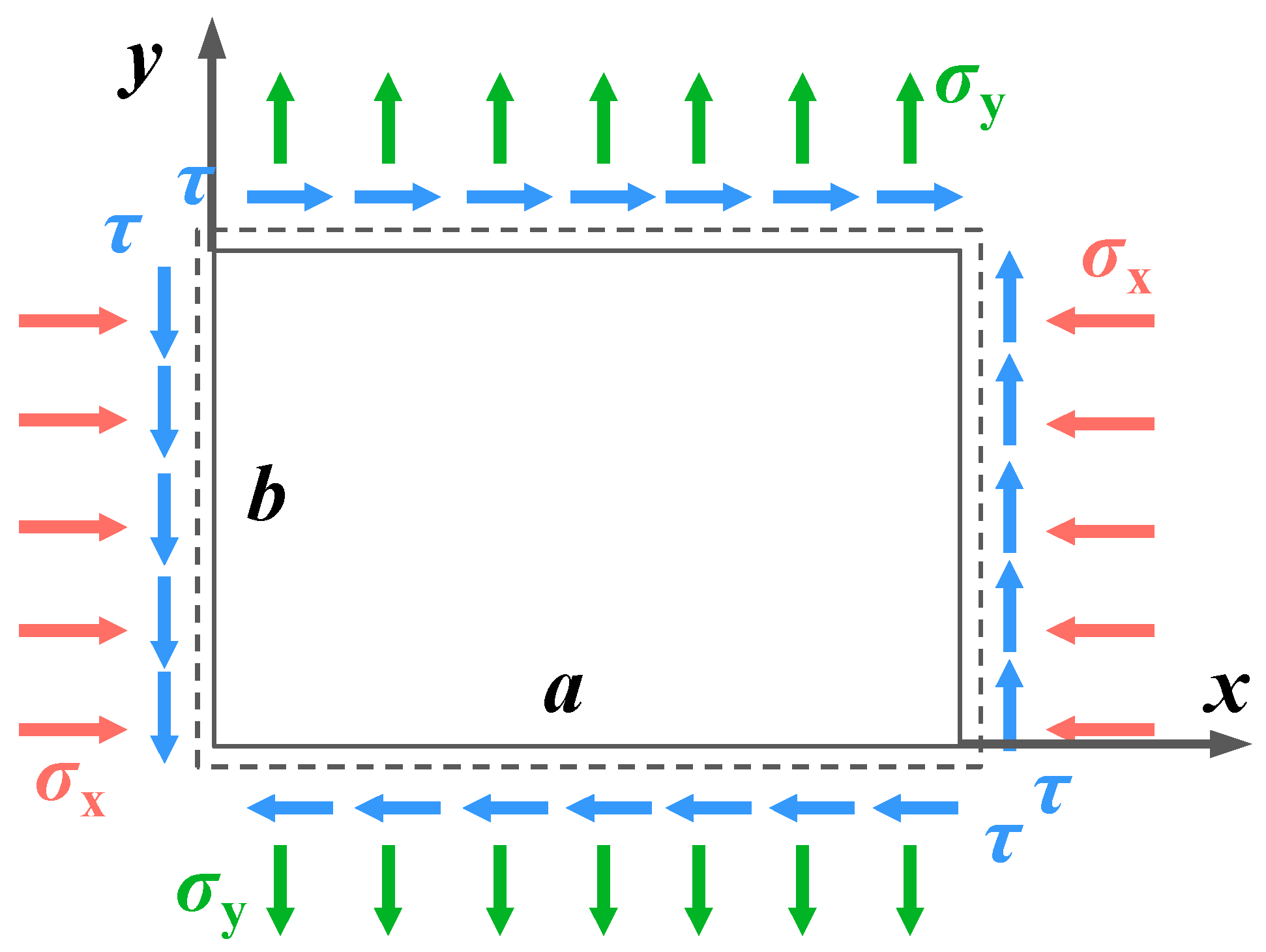
3.1. Theoretical Analysis Method
3.1.1. Mechanical Model
3.1.2. Assumptions of Thin Plate Stability Theory
- (1)
- The linear strain of the mid-surface normal direction is not taken into consideration, which results in εz = 0:
- (2)
- The minor stress components τzx, τzy, and σz are significantly smaller compared to the other stress components. Therefore, the shear strains (γzx, γzy) and normal strain (εz) induced by these components are neglected. This simplification transforms the problem of small deflection bending of the thin plate into a plane stress problem, governed by the following physical equations:
- (3)
- In the context of small deflection bending of a thin plate, longitudinal displacements along the mid-surface of the plate are neglected. When the mid-surface of the plate undergoes bending deformation, its projected shape, including its line segments and area, remains unchanged on the xoy plane:
3.1.3. Thin Plate Bending Equation
3.1.4. Critical Buckling Stress
3.2. Numerical Analysis
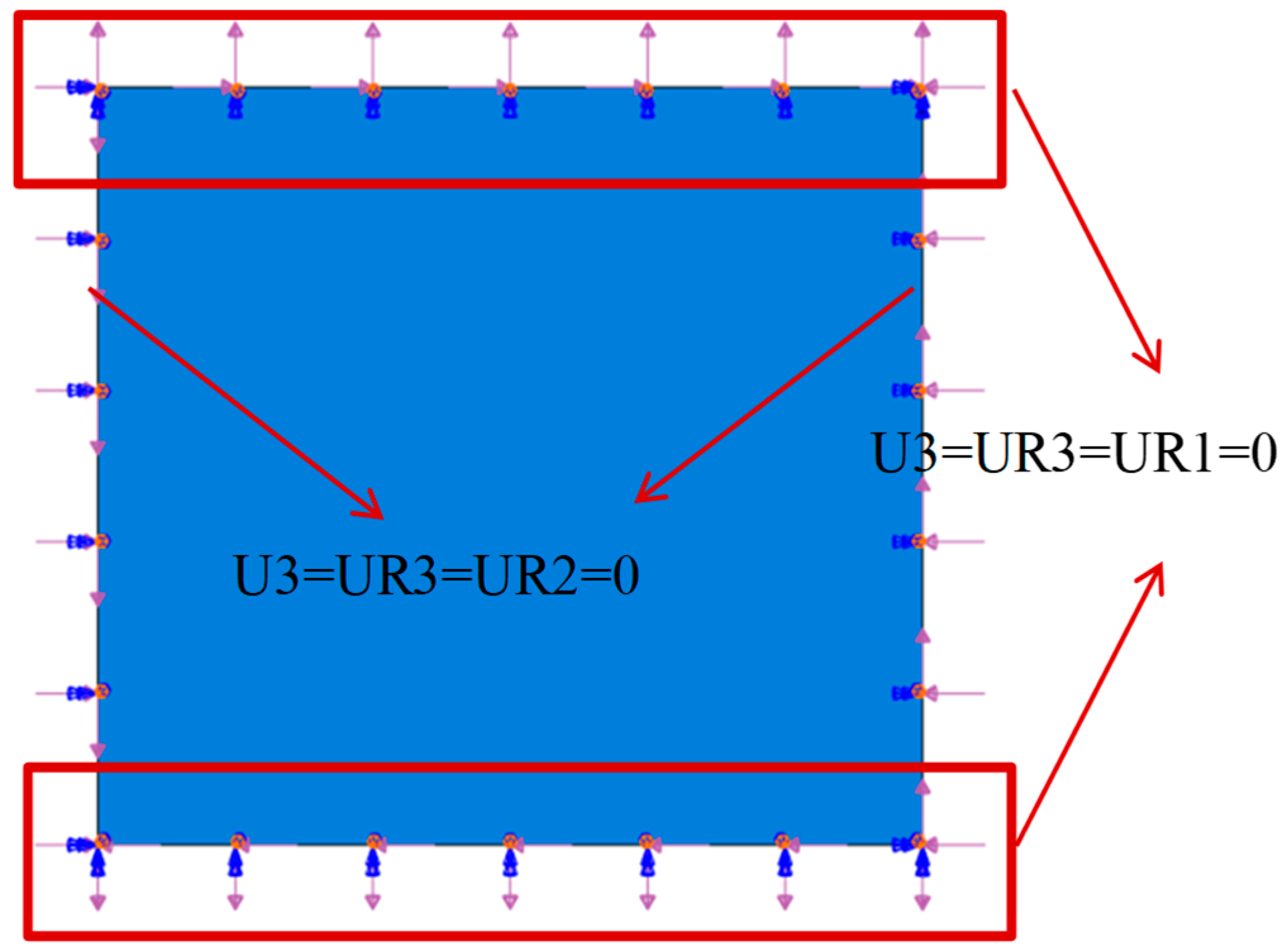
3.2.1. Linear Buckling Model
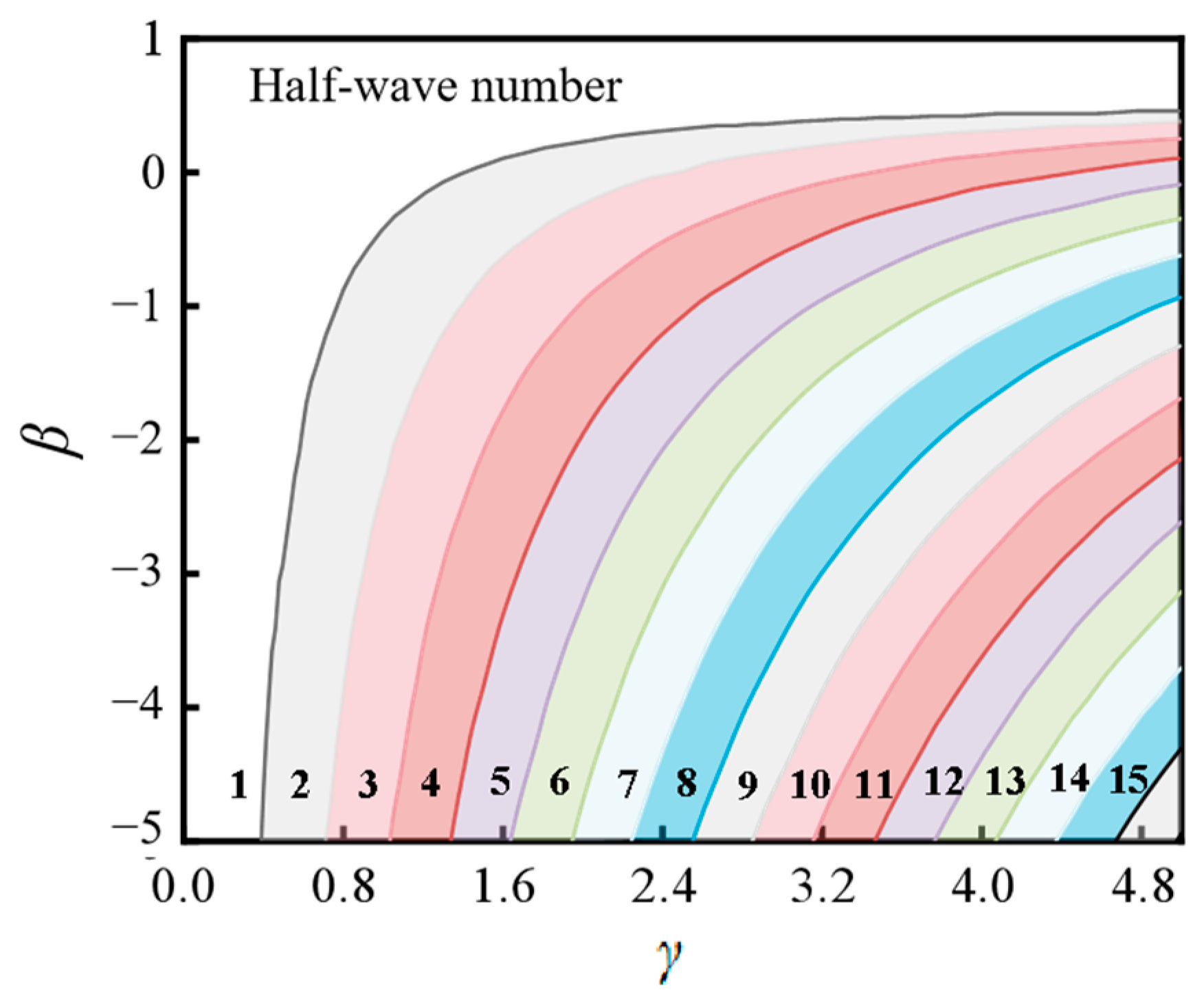
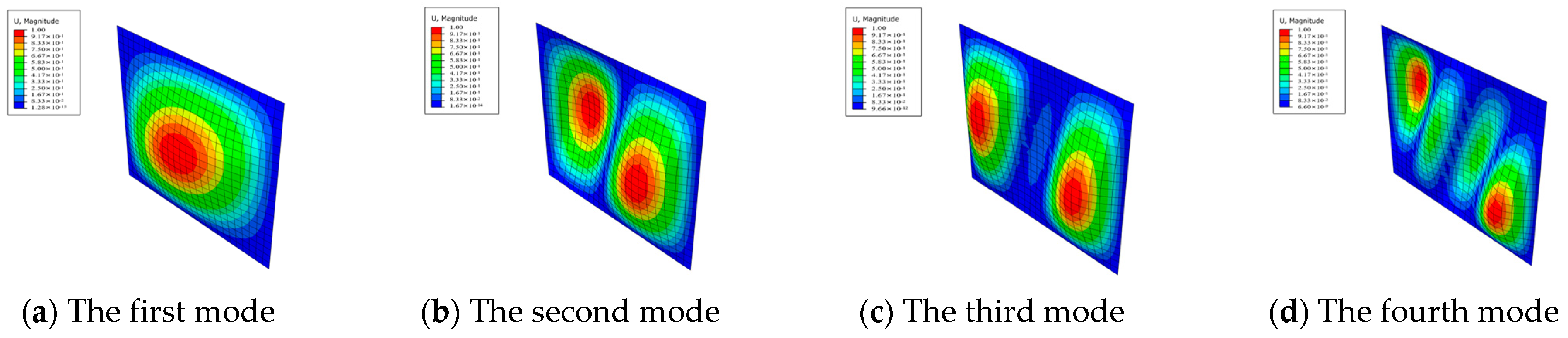
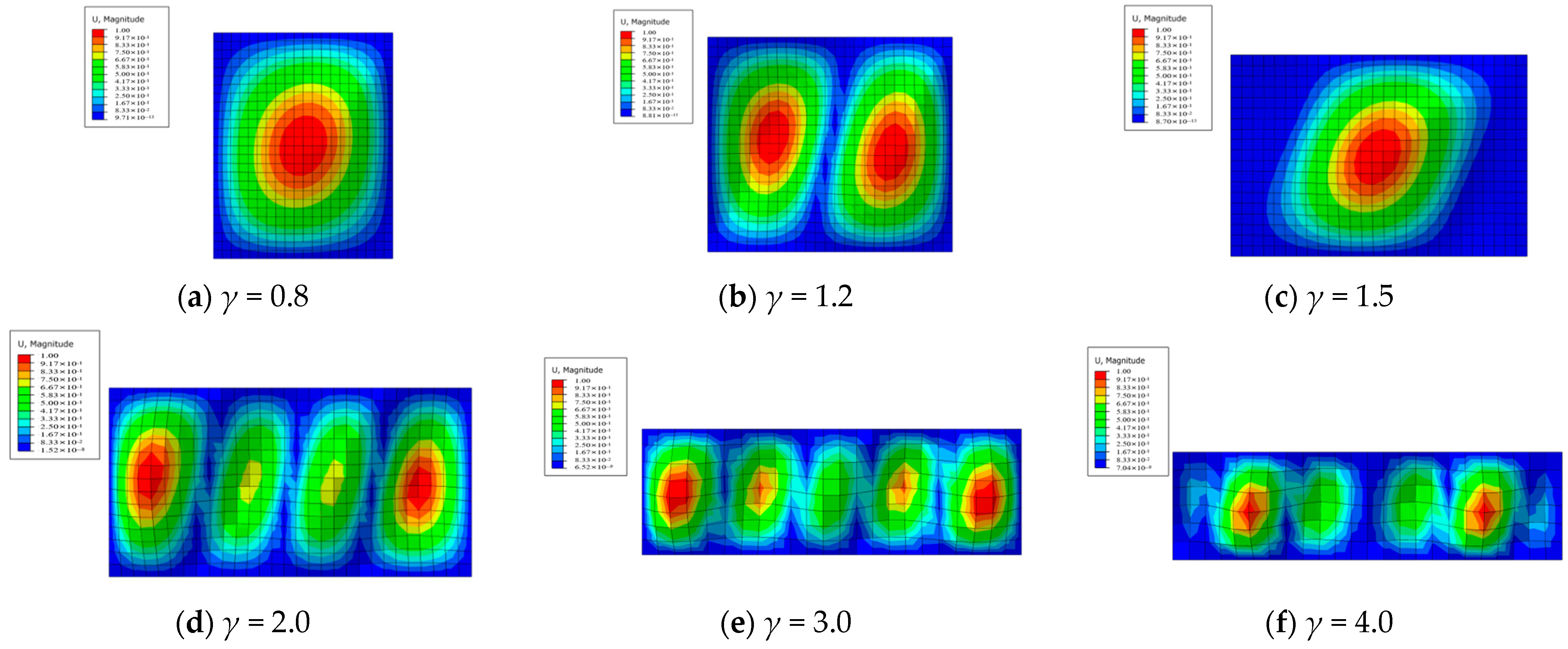
3.2.2. Buckling Mode Calculation
- (1)
- (2)
- (3)
- (4)
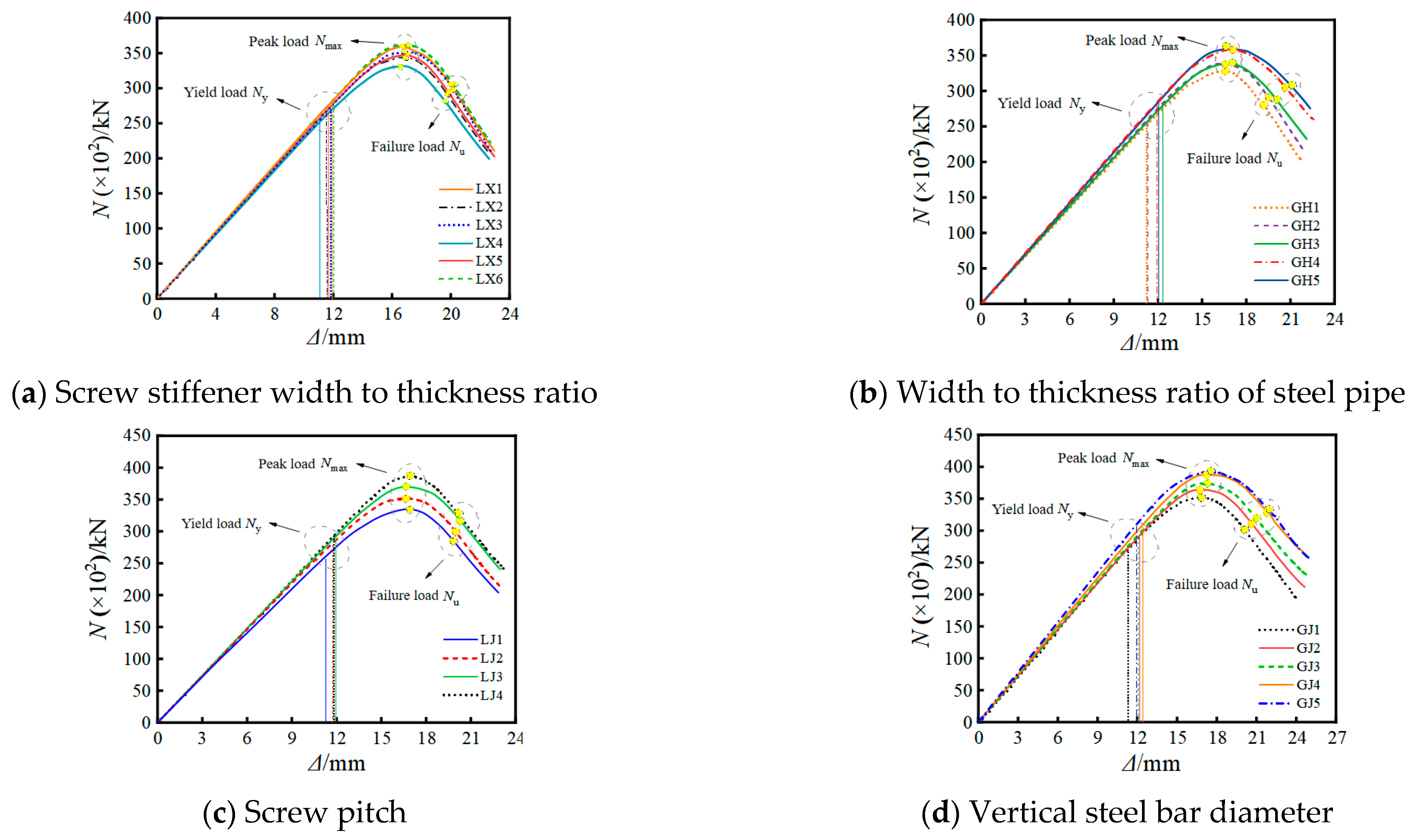
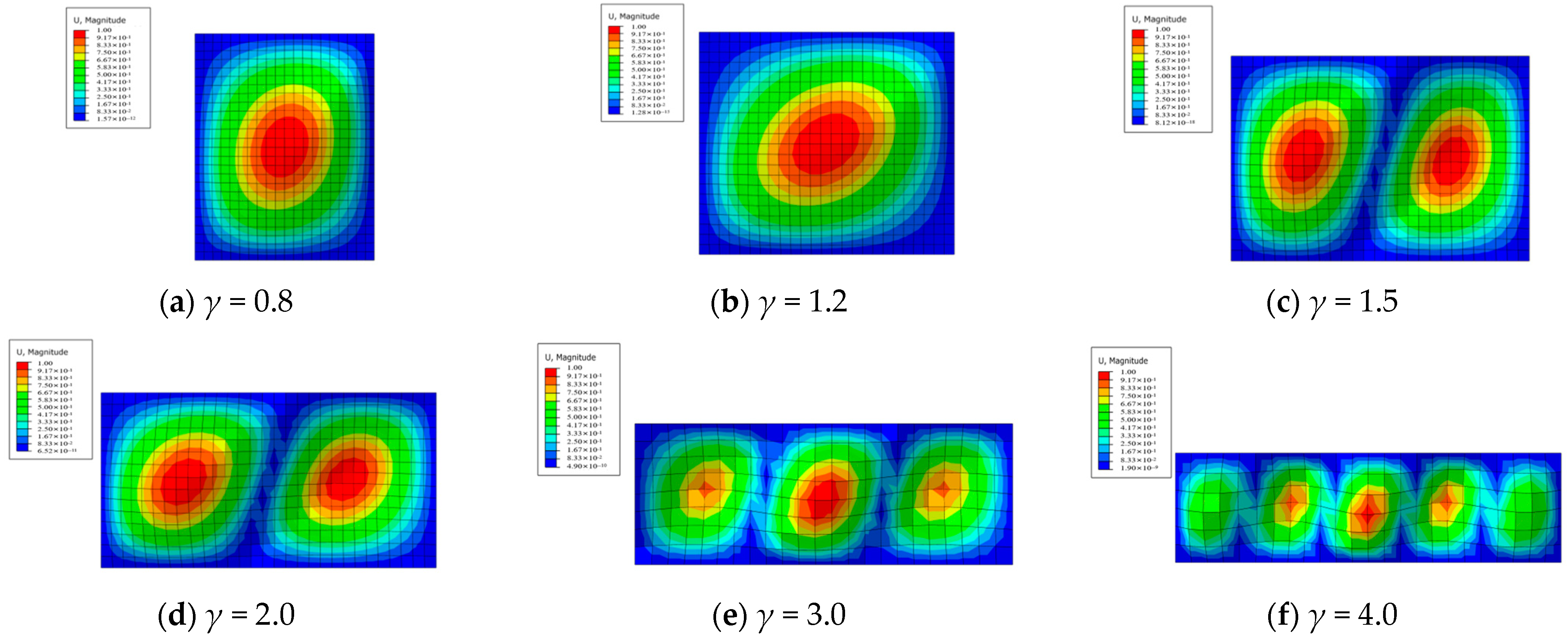
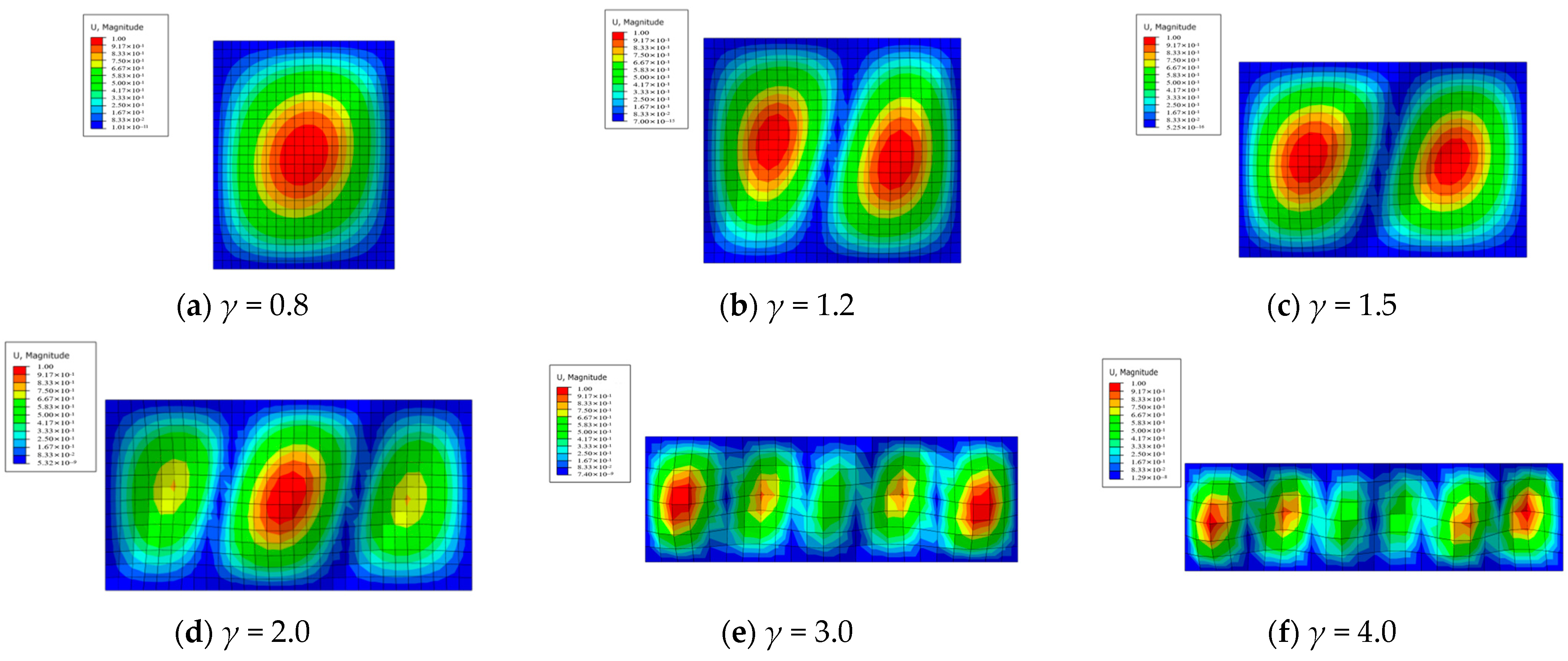
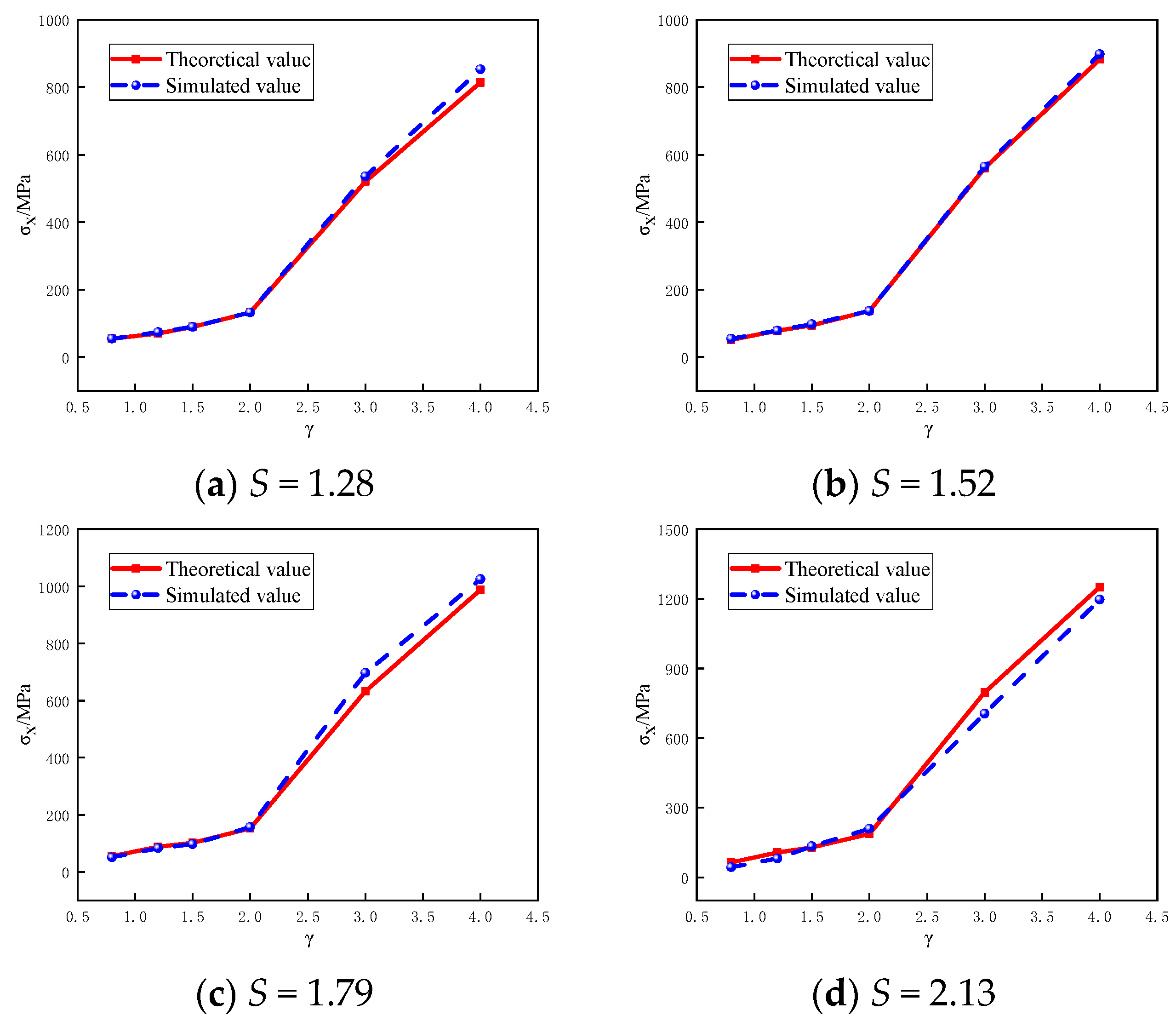
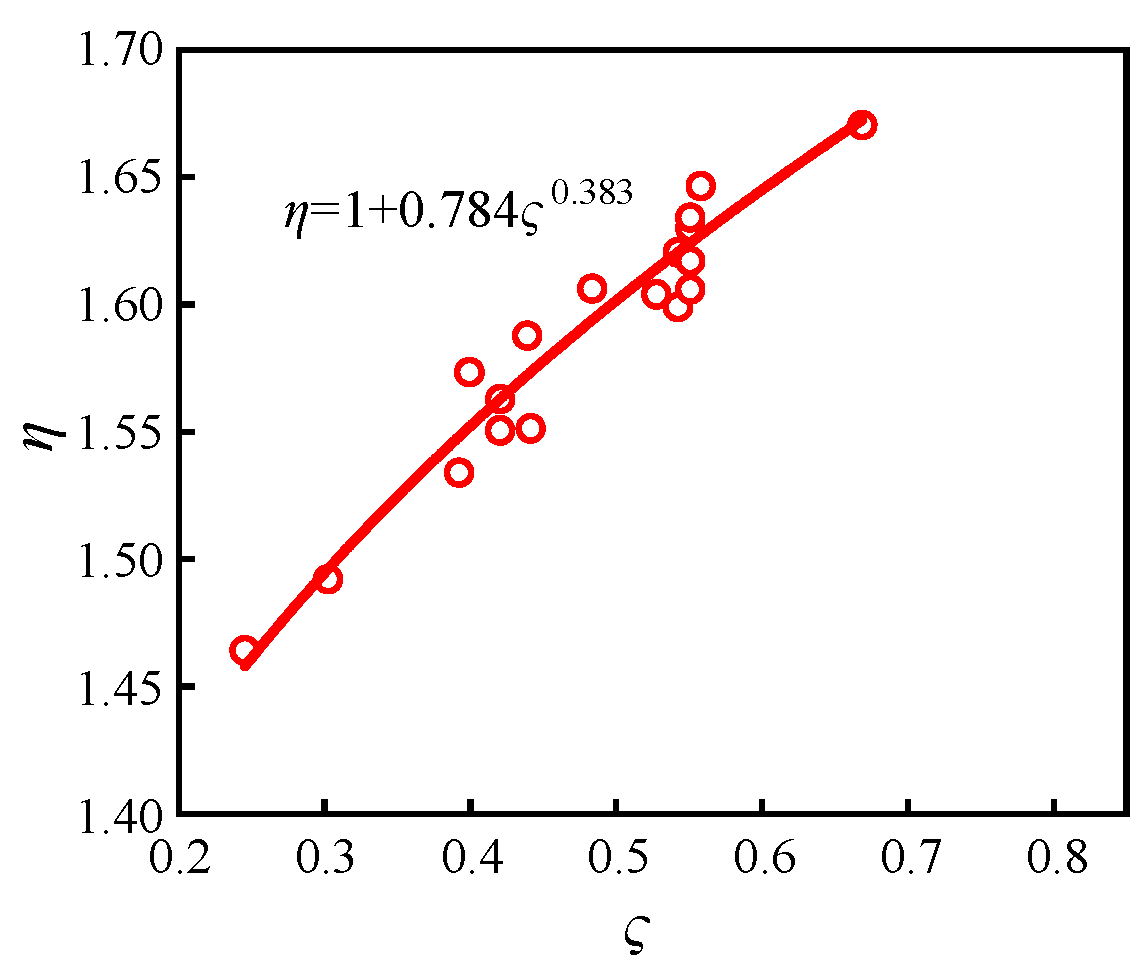
3.3. Critical Buckling Capacity
4. Bearing Capacity
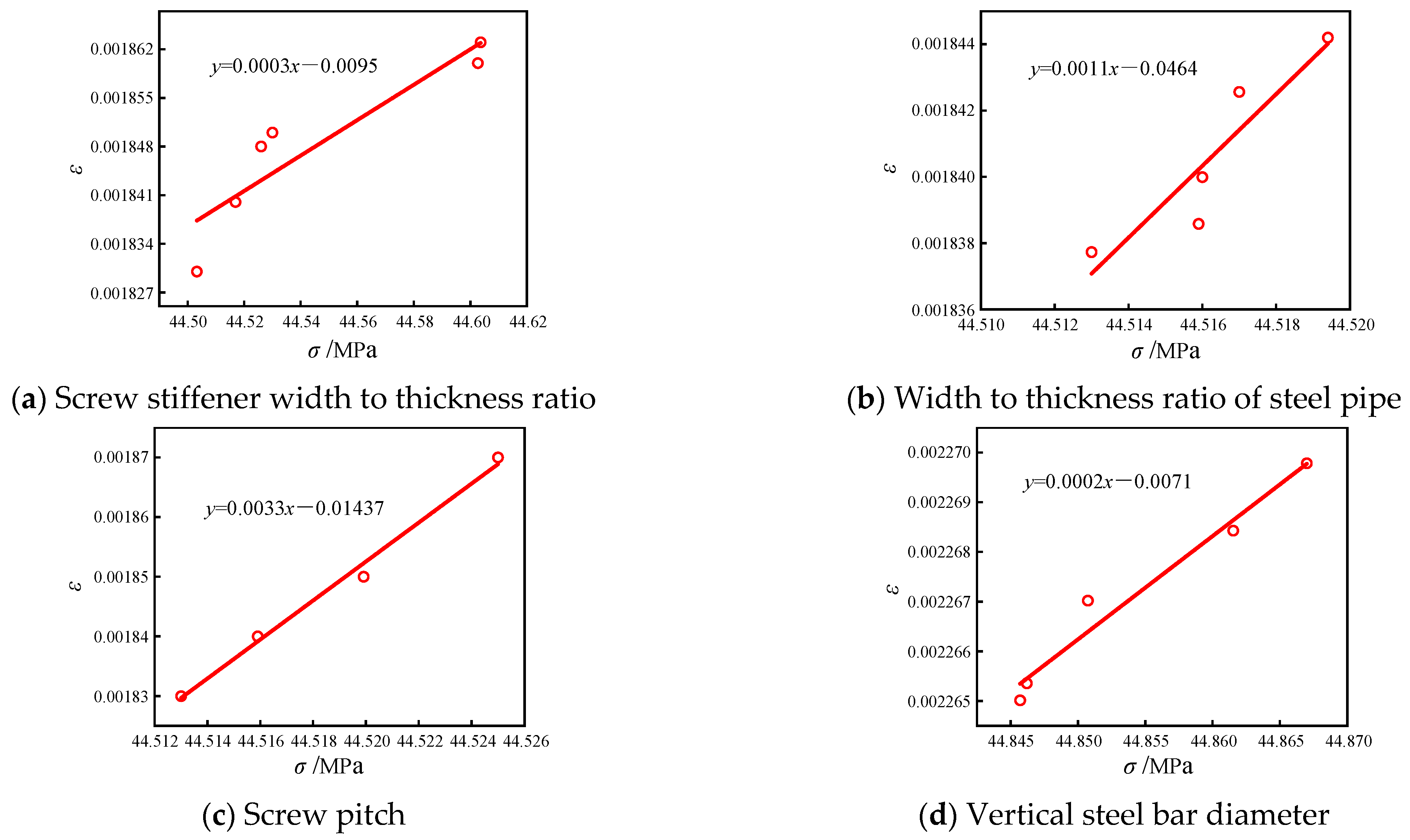
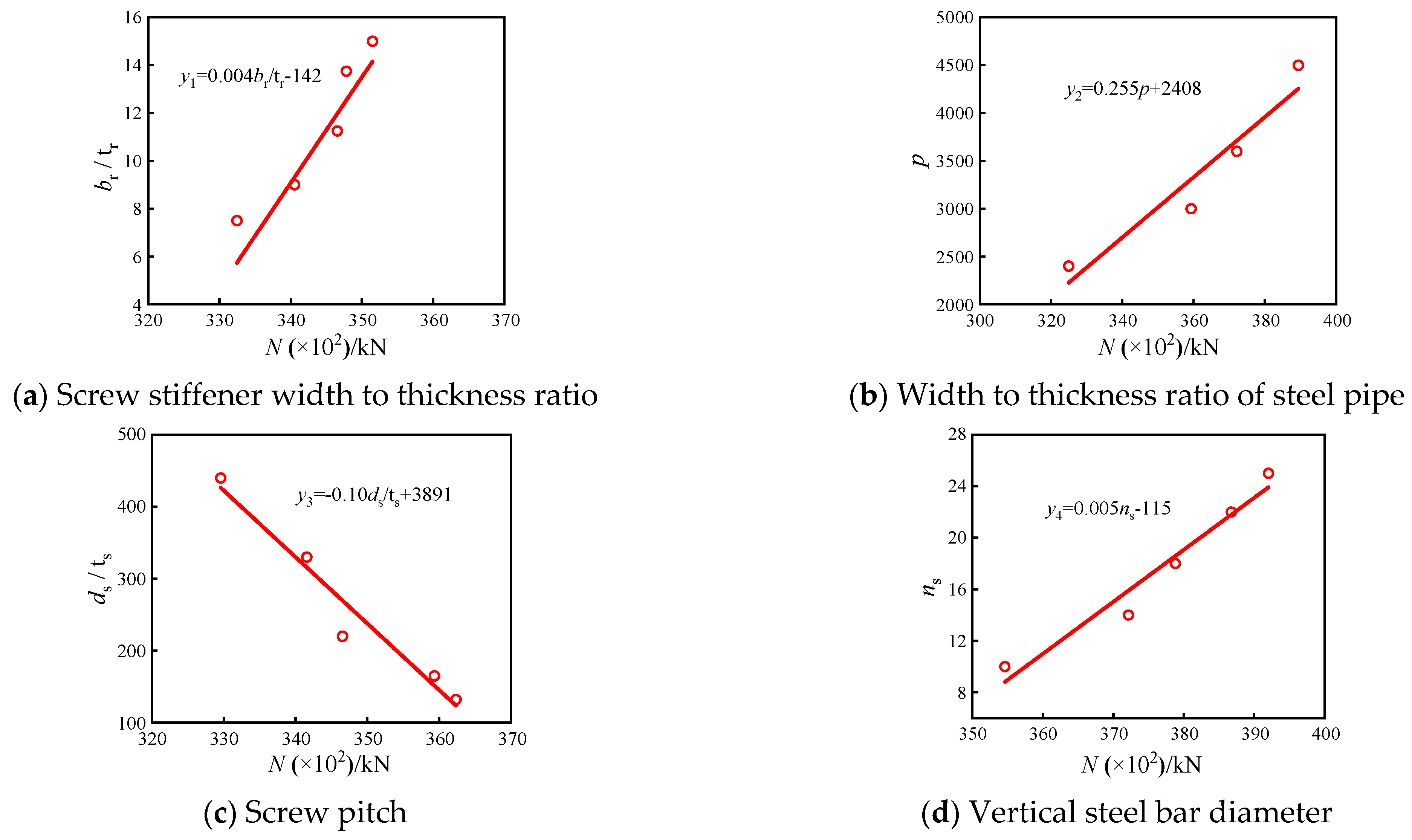
4.1. Impact Parameters
4.2. Bearing Capacity of Outsourced Concrete
4.3. Core Concrete Bearing Capacity
4.4. Axial Compressive Capacity of Composite Column
5. Conclusions
- (1)
- The failure mode of steel tube concrete columns under axial compression typically involves the crushing of the core concrete and the outward buckling of the steel tube. In the case of spiral rib-reinforced composite columns, the external concrete casing tends to crack diagonally along the direction of the spiral ribs. The buckling of the steel tube wall occurs predominantly between the spiral ribs. Spiral ribs significantly enhance the ability of thin-walled steel tube concrete components to resist local buckling;
- (2)
- In comparison to ordinary steel tube concrete columns, using a single spiral rib restraint enhances the ductility of the structure but can reduce its load-bearing capacity. However, when spiral ribs are combined with steel bars (welded), the load-bearing capacity and ductility of the structure increase by 18.5% and 7.7%, respectively. Spiral ribs effectively delay the buckling of thin-walled steel tubes, thereby enhancing both the load-bearing capacity and deformation capability of the structure to a certain extent;
- (3)
- The mechanism of spiral rib confinement works as follows: spiral ribs on the outer wall of the steel tube divide the concrete and the steel tube into several spiral band-like structures. Under an axial compressive load, the vertical force is converted into shear force along the direction of the spiral ribs and vertical pressure. The component undergoes a combined compression–shear stress pattern, thereby restricting the buckling of the steel tube and lateral deformation;
- (4)
- The axial compressive load capacity of spiral rib-reinforced steel tube concrete composite columns is influenced by the spiral ribbed steel tube, external concrete, core concrete, and vertical steel bars. Based on the eigenvalue buckling mode method, a formula for the critical buckling stress of spiral rib-reinforced steel tubes is proposed. By applying the superposition principle, the experimental and numerical simulations and the theoretical calculations show that the load-bearing capacities of the composite columns are generally consistent.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, J.; Wu, H.; Zhao, X. Current situation and discussion of structural design for super high-rise buildings above 250 m in China. J. Build. Struct. 2014, 35, 1–7. [Google Scholar] [CrossRef]
- Lee, H.J.; Choi, I.R.; Park, H.G. Eccentric Compression Strength of Rectangular Concrete-Filled Tubular Columns Using High-Strength Steel Thin Plates. J. Struct. Eng. 2016, 143, 04016228. [Google Scholar] [CrossRef]
- Wang, Z.-B.; Tao, Z.; Yu, Q. Axial compressive behaviour of concrete-filled double-tube stub columns with stiffeners. Thin Walled Struct. 2017, 120, 91–104. [Google Scholar] [CrossRef]
- Xu, B.; Wu, F.; Xu, G.; Kong, H.; Gu, G.; Yu, X. Experimental study on the axial compressive performance of CFST short columns with different stiffeners. Sichuan Build. Sci. 2018, 44, 43–46. [Google Scholar] [CrossRef]
- Al-Zubaidi, I.; Abdel-Jaber, M.; Hunaiti, Y.; El-Nimri, R. Behavior of light-gauge steel short columns filled with normal and lightweight aggregate concrete under cincentrte under concentric axial loading. J. Appl. Eng. Sci. 2022, 20, 1040–1052. [Google Scholar] [CrossRef]
- Sulaiman, A.; Hunaiti, Y.; Abdel-Jaber, M.; Abdel-Jaber, M. Compressive behavior of light-gauge steel tubes filled with concrete containing recycled aggregates. Int. Rev. Appl. Sci. Eng. 2022, 13, 185–196. [Google Scholar] [CrossRef]
- Zuo, Z.L.; Liu, D.X.; Cai, J.; Yang, C.; Chen, Q.J. Experiment on T-Shaped CFT Stub Columns with Binding Bars Subjected to Axial Compression. Adv. Mater. Res. 2013, 838–841, 439–443. [Google Scholar] [CrossRef]
- Zuo, Z.-L.; Cai, J.; Chen, Q.-J.; Liu, X.-P.; Yang, C.; Mo, T.-W. Performance of T-shaped CFST stub columns with binding bars under axial compression. Thin Walled Struct. 2018, 129, 183–196. [Google Scholar] [CrossRef]
- Ge, Q.; Yang, F.; Dong, W.; Bian, Z. Unified solutions on axial bearing capacity of T-shaped concrete-filled steel tube short columns with binding bars. IOP Conf. Ser. Earth Environ. Sci. 2021, 636, 012024. [Google Scholar] [CrossRef]
- Ding, F.-X.; Luo, L.; Wang, L.; Cheng, S.; Yu, Z.-W. Pseudo-static tests of terminal stirrup-confined concrete-filled rectangular steel tubular columns. J. Constr. Steel Res. 2018, 144, 135–152. [Google Scholar] [CrossRef]
- Tan, Q.; Chen, Z.; Jing, C. Experimental investigation on mechanical performance and bearing capacity calculation of spiral stirrup-reinforced concrete-filled square steel tubular columns under eccentric compression. J. Build. Struct. 2020, 41, 102–109. [Google Scholar] [CrossRef]
- Teng, J.; Wang, J.; Lin, G.; Zhang, J.; Feng, P. Compressive behavior of concrete-filled steel tubular columns with internal high-strength steel spiral confinement. Adv. Struct. Eng. 2021, 24, 1687–1708. [Google Scholar] [CrossRef]
- Ding, F.-X.; Lu, D.-R.; Bai, Y.; Zhou, Q.-S.; Ni, M.; Yu, Z.-W.; Jiang, G.-S. Comparative study of square stirrup-confined concrete-filled steel tubular stub columns under axial loading. Thin Walled Struct. 2016, 98, 443–453. [Google Scholar] [CrossRef]
- Long, Y.; Zeng, L.; Wang, Y.; Cai, J. Elastic-plastic local buckling model of rectangular CFT columns under axial compression. Sci. Sin. Technol. 2019, 49, 35–43. [Google Scholar] [CrossRef][Green Version]
- Liu, J.; Wang, K. Bending of anisotropic rectangle plates with four free edges on elastic foundation. Chin. J. Appl. Mech. 2003, 20, 103–106. [Google Scholar]
- Batista, M. New analytical solution for bending problem of uniformly loaded rectangular plate supported on corner points. IES J. Part A Civ. Struct. Eng. 2010, 3, 75–84. [Google Scholar] [CrossRef]
- Xu, T.; Xing, Y. Exact solutions for free vibrations of rectangular thin plates on the winkler foundation. Eng. Mech. 2014, 31, 43–48. [Google Scholar]
- Li, R.; Zheng, X.; Wang, H.; Xiong, S.; Yan, K.; Li, P. New analytic buckling solutions of rectangular thin plates with all edges free. Int. J. Mech. Sci. 2018, 144, 67–73. [Google Scholar] [CrossRef]
- Li, R.; Wang, B.; Lv, Y.; Zhang, Q.; Wang, H.; Jin, F.; Teng, F.; Wang, B. New analytic solutions for static problems of rectangular thin plates point-supported at three corners. Meccanica 2017, 52, 1593–1600. [Google Scholar] [CrossRef]
- Ullah, S.; Wang, H.; Zheng, X.; Zhang, J.; Zhong, Y.; Li, R. New analytic buckling solutions of moderately thick clamped rectangular plates by a straightforward finite integral transform method. Arch. Appl. Mech. 2019, 89, 1885–1897. [Google Scholar] [CrossRef]
- Tang, Z.; Fu, Z.; Fan, C. Generalized finite difference method for solving kirchhoff plate and winkler plate bending problems. Chin. J. Solid Mech. 2018, 39, 419–428. [Google Scholar] [CrossRef]
- Mijušković, O.; Ćorić, B.; Šćepanović, B. Accurate buckling loads of plates with different boundary conditions under arbitrary edge compression. Int. J. Mech. Sci. 2015, 101–102, 309–323. [Google Scholar] [CrossRef]
- Nazarimofrad, E.; Zahrai, S.M.; Kholerdi, S.E.S. Effect of rotationally restrained and Pasternak foundation on buckling of an orthotropic rectangular Mindlin plate. Mech. Adv. Mater. Struct. 2018, 25, 592–599. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture Industry Press: Beijing, China, 2015.
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture Industry Press: Beijing, China, 2017.
- Wang, Z.-S.; Han, J.-Y.; Wei, J.; Lu, J.-L.; Li, J.-L. The axial compression mechanical properties and factors influencing spiral-ribbed thin-walled square concrete-filled steel tube composite members. Case Stud. Constr. Mater. 2022, 17, e01510. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Wei, J.; Lu, J.; Li, X. The Eccentric Compression Performance of Spirally Stiffened Thin-Walled Square Concrete-Filled Steel Tubular Laminated Composite Members. Buildings 2022, 12, 1151. [Google Scholar] [CrossRef]
- Coskun, S.B.; Ozturk, B. Elastic Stability Analysis of Euler Columns Using Analytical Approximate Techniques. Adv. Comput. Stab. Anal. 2012, 6, 115–132. [Google Scholar] [CrossRef]
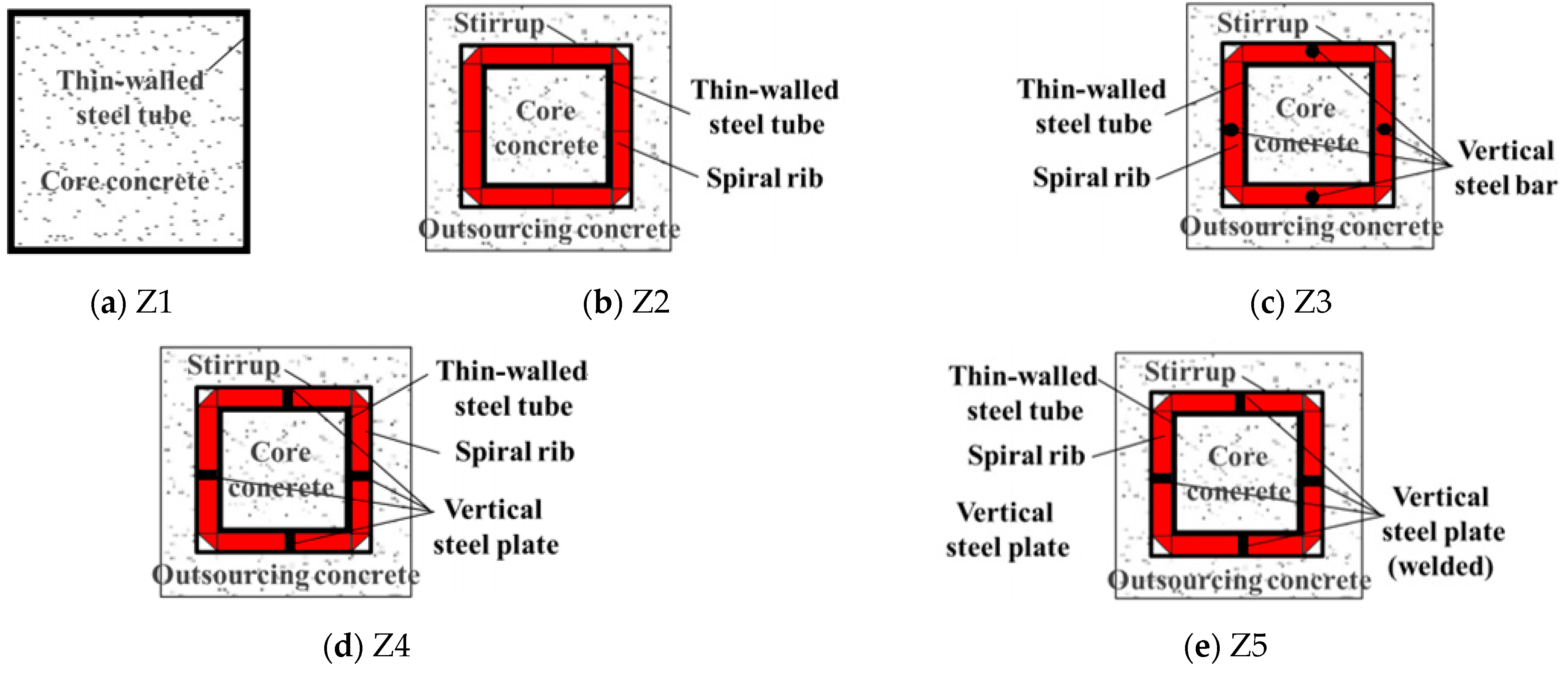


| Specimen Number | Column (H × Bt) | Steel Tube (ds × ts) | Spiral Rib (br × tr) | Steel Plate (bp × tp) | Steel Bar (ns) | Constraint Measures |
|---|---|---|---|---|---|---|
| Z1 | 1000 × 340 | 340 × 1 | - | - | - | None |
| Z2 | 1000 × 340 | 220 × 1 | 30 × 3 | - | - | Spiral rib |
| Z3 | 1000 × 340 | 220 × 1 | 30 × 3 | - | 14 | Spiral-ribbed steel bar |
| Z4 | 1000 × 340 | 220 × 1 | 30 × 3 | 30 × 5 | - | Spiral-ribbed steel plate |
| Z5 | 1000 × 340 | 220 × 1 | 30 × 3 | 30 × 5 | - | Spiral-ribbed steel plate (weided) |
| Category | Yield Strength/MPa | Ultimate Strength/MPa | Yield Ratio | Elongation/% |
|---|---|---|---|---|
| Steel tube | 278.70 | 388.93 | 0.72 | 27.3% |
| Spiral rib | 256.94 | 363.79 | 0.71 | 25.7% |
| Steel plate | 252.65 | 359.26 | 0.70 | 22.7% |
| Steel bar | 462.95 | 625.30 | 0.74 | 24.6% |
| Strength Grade | Specimen Label | fcu,k/MPa | fck/MPa | Fc/MPa | Ec/GPa |
|---|---|---|---|---|---|
| C30 | 1 | 34.6 | 23.1 | 27.3 | 24.7 |
| 2 | 33.8 | 22.6 | 26.7 | 24.4 | |
| 3 | 33.5 | 22.4 | 26.5 | 24.3 | |
| Average | 34.0 | 22.7 | 26.8 | 24.5 |
| γ | S | R | k3 | k1 | σx/MPa |
|---|---|---|---|---|---|
| 0.8 | 1.28 | −0.256 | 3.45 | 4.44 | 49.30 |
| 1.2 | 1.28 | −0.256 | 3.84 | 4.97 | 77.96 |
| 1.5 | 1.28 | −0.256 | 3.13 | 4.08 | 87.15 |
| 2.0 | 1.28 | −0.256 | 3.00 | 3.95 | 125.85 |
| 3.0 | 1.28 | −0.256 | 2.91 | 3.91 | 517.47 |
| 4.0 | 1.28 | −0.256 | 2.87 | 3.93 | 812.63 |
| 0.8 | 1.52 | −0.304 | 2.97 | 4.61 | 51.21 |
| 1.2 | 1.52 | −0.304 | 3.12 | 4.88 | 77.91 |
| 1.5 | 1.52 | −0.304 | 2.77 | 4.36 | 93.05 |
| 2.0 | 1.52 | −0.304 | 2.67 | 4.24 | 135.11 |
| 3.0 | 1.52 | −0.304 | 2.62 | 4.24 | 561.83 |
| 4.0 | 1.52 | −0.304 | 2.59 | 4.27 | 884.10 |
| 0.8 | 1.79 | −0.358 | 2.57 | 5.02 | 55.80 |
| 1.2 | 1.79 | −0.358 | 2.74 | 5.39 | 84.48 |
| 1.5 | 1.79 | −0.358 | 2.44 | 4.83 | 103.12 |
| 2.0 | 1.79 | −0.358 | 2.37 | 4.73 | 150.80 |
| 3.0 | 1.79 | −0.358 | 2.34 | 4.76 | 630.12 |
| 4.0 | 1.79 | −0.358 | 2.31 | 4.78 | 989.05 |
| 0.8 | 2.13 | −0.426 | 2.19 | 6.16 | 68.43 |
| 1.2 | 2.13 | −0.426 | 2.38 | 6.73 | 105.49 |
| 1.5 | 2.13 | −0.426 | 2.12 | 6.02 | 128.68 |
| 2.0 | 2.13 | −0.426 | 2.07 | 5.92 | 188.90 |
| 3.0 | 2.13 | −0.426 | 2.05 | 5.96 | 789.15 |
| 4.0 | 2.13 | −0.426 | 2.04 | 6.02 | 1245.01 |
| Mode | Eigenvalue | Critical Buckling Load (MPa) |
|---|---|---|
| First mode | 296.98 | 74.25 |
| Second mode | 329.88 | 82.47 |
| Third mode | 542.30 | 135.58 |
| Fourth mode | 812.71 | 203.18 |
| γ | Eigenvalue | Critical Buckling Load (MPa) |
|---|---|---|
| 0.8 | 198.68 | 49.67 |
| 1.2 | 283.68 | 70.92 |
| 1.5 | 362.05 | 90.51 |
| 2.0 | 509.43 | 127.36 |
| 3.0 | 2130.20 | 532.55 |
| 4.0 | 3405.20 | 851.30 |
| γ | Eigenvalue | Critical Buckling Load (MPa) |
|---|---|---|
| 0.8 | 202.83 | 50.71 |
| 1.2 | 296.98 | 74.25 |
| 1.5 | 376.26 | 94.07 |
| 2.0 | 535.24 | 133.81 |
| 3.0 | 2249.50 | 562.38 |
| 4.0 | 3586.30 | 896.58 |
| γ | Eigenvalue | Critical Buckling Load (MPa) |
|---|---|---|
| 0.8 | 205.98 | 51.50 |
| 1.2 | 338.56 | 84.64 |
| 1.5 | 387.62 | 96.91 |
| 2.0 | 616.82 | 154.21 |
| 3.0 | 2776.40 | 694.10 |
| 4.0 | 4094.60 | 1023.65 |
| γ | Eigenvalue | Critical Buckling Load (MPa) |
|---|---|---|
| 0.8 | 208.50 | 52.13 |
| 1.2 | 345.73 | 86.43 |
| 1.5 | 529.73 | 132.43 |
| 2.0 | 840.45 | 210.11 |
| 3.0 | 2847.2 | 1423.6 |
| 4.0 | 4792.6 | 1198.15 |
| Specimen Number | Buckling Capacity/kN | Error Value/% | |
|---|---|---|---|
| Test or Simulation | Formula Calculation | ||
| Z3 | 2700.0 | 2560.0 | −5.2% |
| LX1 | 27,992.0 | 28,831.8 | 3.0% |
| LX2 | 26,302.0 | 27,406.7 | 4.2% |
| LX3 | 27,117.6 | 27,470.1 | 1.3% |
| LX4 | 24,889.7 | 23,645.2 | −5.0% |
| LX5 | 26,739.1 | 25,589.3 | −4.3% |
| LX6 | 27,736.0 | 28,679.1 | 3.4% |
| GH1 | 24,933.1 | 26,628.6 | 6.8% |
| GH2 | 25,798.9 | 25,102.3 | −2.7% |
| GH3 | 27,992.0 | 30,007.5 | 7.2% |
| GH4 | 28,033.7 | 28,314.1 | 1.0% |
| GH5 | 28,391.4 | 27,454.5 | −3.3% |
| LJ1 | 25,831.2 | 23,764.7 | −8.0% |
| LJ2 | 28,033.7 | 28,314.0 | 1.0% |
| LJ3 | 28,936.8 | 29,891.7 | 3.3% |
| LJ4 | 29,324.3 | 28,503.2 | −2.8% |
| GJ1 | 26,833.6 | 27,423.9 | 2.2% |
| GJ2 | 28,936.8 | 27,750.4 | −4.1% |
| GJ3 | 29,172.5 | 28,880.7 | −1.0% |
| GJ4 | 30,748.3 | 31,763.0 | 3.3% |
| GJ5 | 30,944.2 | 32,429.6 | 4.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, P.; Wang, Z.; Wang, K.; Niu, J.; Xie, Z.; Liu, K. Analysis of the Bearing Capacity of Concrete-Filled Thin-Walled Square Steel Tubes with Helical Stiffening Based on Local Buckling. Buildings 2024, 14, 2122. https://doi.org/10.3390/buildings14072122
Tian P, Wang Z, Wang K, Niu J, Xie Z, Liu K. Analysis of the Bearing Capacity of Concrete-Filled Thin-Walled Square Steel Tubes with Helical Stiffening Based on Local Buckling. Buildings. 2024; 14(7):2122. https://doi.org/10.3390/buildings14072122
Chicago/Turabian StyleTian, Penggang, Zhenshan Wang, Kai Wang, Jianhui Niu, Zhixun Xie, and Kangning Liu. 2024. "Analysis of the Bearing Capacity of Concrete-Filled Thin-Walled Square Steel Tubes with Helical Stiffening Based on Local Buckling" Buildings 14, no. 7: 2122. https://doi.org/10.3390/buildings14072122
APA StyleTian, P., Wang, Z., Wang, K., Niu, J., Xie, Z., & Liu, K. (2024). Analysis of the Bearing Capacity of Concrete-Filled Thin-Walled Square Steel Tubes with Helical Stiffening Based on Local Buckling. Buildings, 14(7), 2122. https://doi.org/10.3390/buildings14072122