A Safety Risk Analysis of a Steel-Structure Building Using an Improved Controlled Interval and Memory Model
Abstract
1. Introduction
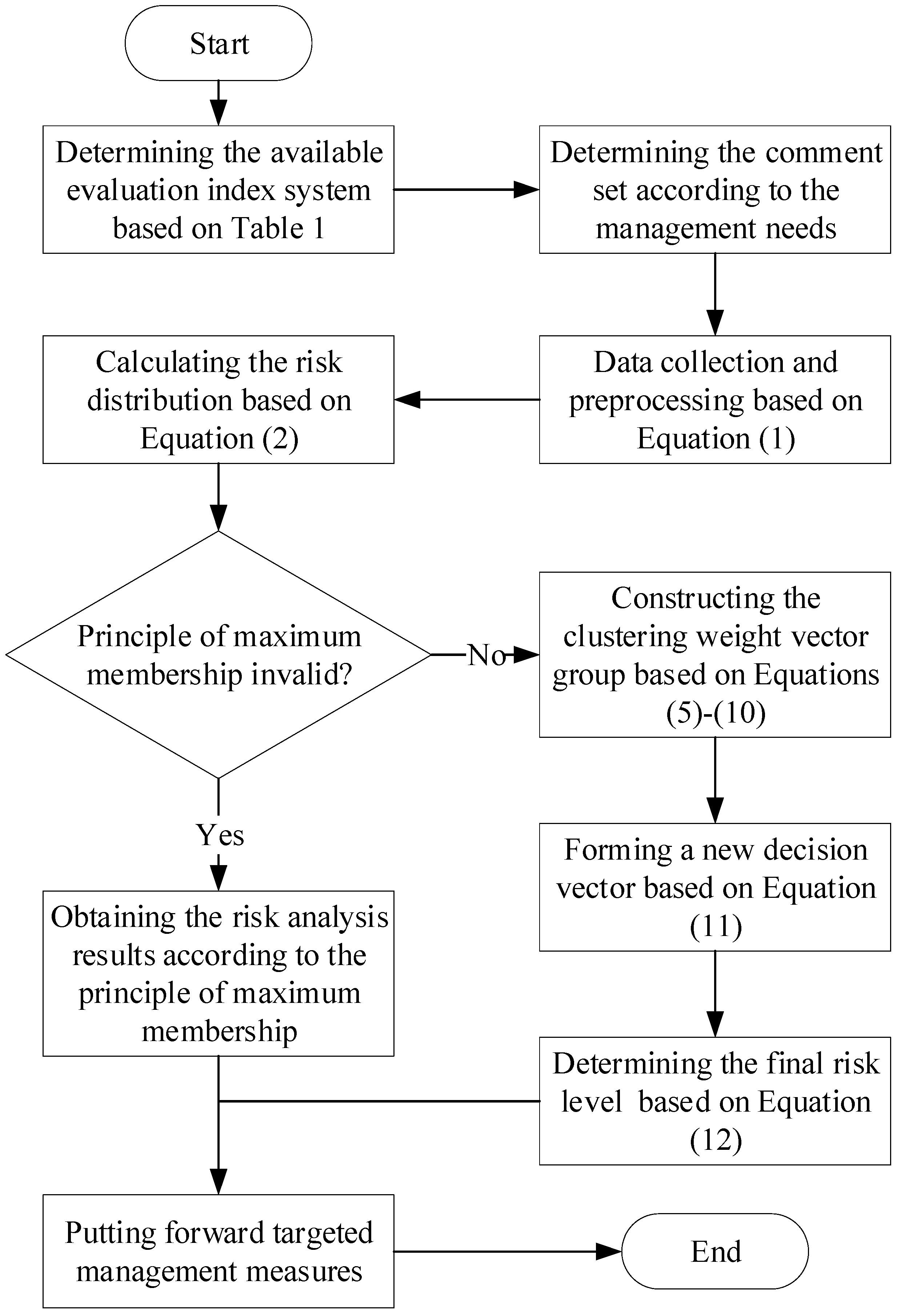
2. Methods
2.1. The Proposed Index System
2.2. The Proposed Safety Risk Analysis Model
2.2.1. The Standard CIM Model
2.2.2. The Proposed Improvement Strategy
2.3. The Proposed Model
3. Case Study
3.1. Project Overview
3.2. Risk Level Calculation
4. Discussion
4.1. Comparison of the Standard and Improved CIMs
4.2. Model Adaptability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alekseytsev, A. Optimal design of steel frame structures subject to level of mechanical safety. Build. Reconstr. 2020, 3, 89. [Google Scholar] [CrossRef]
- Bhardwaj, U.; Teixeira, A.P.; Guedes Soares, C. Uncertainty in the estimation of partial safety factors for different steel-grade corroded pipelines. J. Mar. Sci. Eng. 2023, 11, 177. [Google Scholar] [CrossRef]
- Risco, G.; Zania, V.; Giuliani, L. Numerical assessment of post-earthquake fire response of steel buildings. Saf. Sci. 2023, 157, 105921. [Google Scholar] [CrossRef]
- Cao, Y.; Jiang, J.; Lu, Y.; Chen, W.; Ye, J. Progressive collapse of steel structures exposed to fire: A critical review. J. Constr. Steel Res. 2023, 207, 107985. [Google Scholar] [CrossRef]
- Hu, S.; Fang, Y.; Moehler, R. Estimating and visualizing the exposure to tower crane operation hazards on construction sites. Saf. Sci. 2023, 160, 106044. [Google Scholar] [CrossRef]
- Leu, S.-S.; Chang, C.-M. Bayesian-network-based safety risk assessment for steel construction projects. Accid. Anal. Prev. 2013, 54, 122–133. [Google Scholar] [CrossRef] [PubMed]
- Sanni-Anibire, M.O.; Mahmoud, A.S.; Hassanain, M.A.; Salami, B.A. A risk assessment approach for enhancing construction safety performance. Saf. Sci. 2020, 121, 15–29. [Google Scholar] [CrossRef]
- Ning, X.; Qi, J.; Wu, C. A quantitative safety risk assessment model for construction site layout planning. Saf. Sci. 2018, 104, 246–259. [Google Scholar] [CrossRef]
- Dyckhoff, H.; Souren, R. Integrating multiple criteria decision analysis and production theory for performance evaluation: Framework and review. Eur. J. Oper. Res. 2022, 297, 795–816. [Google Scholar] [CrossRef]
- Miao, C.; Teng, J.; Wang, J.; Zhou, P. Population vulnerability assessment of geological disasters in China using CRITIC–GRA methods. Arab. J. Geosci. 2018, 11, 268. [Google Scholar] [CrossRef]
- Chodur, G.M.; Zhao, X.; Biehl, E.; Mitrani-Reiser, J.; Neff, R. Assessing food system vulnerabilities: A fault tree modeling approach. BMC Public Health 2018, 18, 817. [Google Scholar] [CrossRef]
- Wu, X.; Hu, F. Analysis of ecological carrying capacity using a fuzzy comprehensive evaluation method. Ecol. Indic. 2020, 113, 106243. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, H.; Fan, L.; Yi, J. Dynamic modulus prediction model and analysis of factors influencing asphalt mixtures using gray relational analysis methods. J. Mater. Res. Technol. 2022, 19, 1312–1321. [Google Scholar] [CrossRef]
- Tian, S.; Zhang, P.; Liu, T. Application of cont rolled interval s and memory model in risk evaluation of expressway investment. J. Wuhan Univer Sity Technol. (Transp. Sci. Eng.) 2009, 33, 483–486. [Google Scholar]
- Zhang, N.M.; Luo, F.L.; Bi, L.; Hu, L.X. Cost risk assessment for large hydropower project based on the probability distribution. Appl. Mech. Mater. 2012, 212, 1015–1019. [Google Scholar] [CrossRef]
- Kavikumar, R.; Sakthivel, R.; Kwon, O.; Kaviarasan, B. Faulty actuator-based control synthesis for interval type-2 fuzzy systems via memory state feedback approach. Int. J. Syst. Sci. 2020, 51, 2958–2981. [Google Scholar] [CrossRef]
- Chen, X.; Ye, Y.; Xu, X.; Huang, J.Z. A feature group weighting method for subspace clustering of high-dimensional data. Pattern Recognit. 2012, 45, 434–446. [Google Scholar] [CrossRef]
- Franek, L.; Jiang, X. Ensemble clustering by means of clustering embedding in vector spaces. Pattern Recognit. 2014, 47, 833–842. [Google Scholar] [CrossRef]
- Lu, Y.E.; Wu, Y. Redundancy of bridge piers with pile foundations under lateral load. Disaster Adv. 2012, 5, 484–488. [Google Scholar]
- Pham, H.V.; Yakel, A.; Azizinamini, A. Experimental investigation of redundancy of twin steel box-girder bridges under concentrated loads. J. Constr. Steel Res. 2021, 177, 106440. [Google Scholar] [CrossRef]
- Urban, S.; Strauss, A.; Macho, W.; Bergmeister, K.; Dehlinger, C.; Reiterer, M. Concrete structures under cyclic loading—Robustness and redundancy considerations for residual lifetime optimization. Bautechnik 2012, 89, 737–752. [Google Scholar] [CrossRef]
- Chen, L.M.; Hu, D.; Deng, H.; Cui, Y.H.; Zhou, Y.Y. Optimization of the construction scheme of the cablestrut tensile structure based on error sensitivity analysis. Steel Compos. Struct. 2016, 21, 1031–1043. [Google Scholar] [CrossRef]
- Keykha, A.H. Investigation of the Effect of CFRP Strengthening on the Behavior of Deficient Steel Members under Combined Lateral and Torsional Loading. Jordan J. Civ. Eng. 2018, 12, 590–602. [Google Scholar]
- Keykha, A.H. Structural performance evaluation of deficient steel members strengthened using CFRP under combined tensile, torsional and lateral loading. J. Build. Eng. 2019, 24, 100746. [Google Scholar] [CrossRef]
- Wang, Q.J.; Gong, H.Y.; Fu, Z.H.; Zhang, D.W. Automatic detection of carbon steel corrosion degree based on image identification. Comput. Mater. Sci. 2024, 233, 112717. [Google Scholar] [CrossRef]
- Zhu, W.J.; Francois, R.; Poon, C.S.; Dai, J.G. Influences of corrosion degree and corrosion morphology on the ductility of steel reinforcement. Constr. Build. Mater. 2017, 148, 297–306. [Google Scholar] [CrossRef]
- Bezerra, L.M.; Cavalcante, O.O.; Chater, L.; Bonilla, J. V-shaped shear connector for composite steel-concrete beam. J. Constr. Steel Res. 2018, 150, 162–174. [Google Scholar] [CrossRef]
- Qiu, S.Y.; Guo, Y.T.; Nie, X.; Fan, J.S.; Tao, M.X. Experimental study on shaped steel shear connectors used in large-scale composite structures. J. Constr. Steel Res. 2020, 172, 106201. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Wang, Y.H.; Zhai, X.M. Tensile resistance of novel interlocked angle connectors used in steel-concrete-steel sandwich structures. Constr. Build. Mater. 2022, 341, 127774. [Google Scholar] [CrossRef]
- Chen, M.C.; Fang, W.; Yang, C.; Xie, L. Bayesian prediction and probabilistic model of fatigue cracks in steel structures. Eng. Fail. Anal. 2019, 103, 335–346. [Google Scholar] [CrossRef]
- Yu, Z.C.; Wu, J.Y.; Ma, K.J.; Zhong, C.J.; Jiang, C.Y. Fatigue Crack Calculation of Steel Structure Based on the Improved McEvily Model. Appl. Sci. 2022, 12, 6344. [Google Scholar] [CrossRef]
- Jiang, L.Z.; Qi, J.J.; Scanlon, A.; Sun, L.L. Distortional and local buckling of steel-concrete composite box-beam. Steel Compos. Struct. 2013, 14, 243–265. [Google Scholar] [CrossRef]
- Li, W.; Dong, J.; Qu, H.; Wang, L.Q.; Zhao, K. Local Buckling Development of H-Section Steel Core of Buckling-Restrained Brace. Buildings 2022, 12, 227. [Google Scholar] [CrossRef]
- Seif, M.; Schafer, B.W. Local buckling of structural steel shapes. J. Constr. Steel Res. 2010, 66, 1232–1247. [Google Scholar] [CrossRef]
- Liu, Z.S.; Jiang, A.T.; Zhang, A.S.; Xing, Z.Z.; Du, X.L. Intelligent Prediction Method for Operation and Maintenance Safety of Prestressed Steel Structure Based on Digital Twin Technology. Adv. Civ. Eng. 2021, 2021, 6640198. [Google Scholar] [CrossRef]
- Schiltz, P.; Brühwiler, E. Monitoring based fatigue safety verification of the riveted steel structure of a railway bridge. Bautechnik 2021, 98, 785–792. [Google Scholar] [CrossRef]
- Wieclaw-Bator, L.; Mocko, W.; Chmielewski, R.; Kruszka, L. Minimazing the occurance of factors affecting the acceleration of degradation process of steel bridge structures. Roads Bridges-Drog. I Mosty 2016, 15, 315–328. [Google Scholar] [CrossRef]
- Feier, A.; Gruin, A.; Enache, F. Sustainable old steel structure at corrosion protection. In Proceedings of the 15th International Multidisciplinary Scientific Geoconference (SGEM), Albena, Bulgaria, 18–24 June 2015; pp. 607–612. [Google Scholar]
- Guo, J.B.; Wang, N.; Su, H. Research on quantitative assessment of corrosion and mechanical properties of hydraulic steel structure. In Proceedings of the International Conference on Advances in Materials and Manufacturing Processes, Shenzhen, China, 6–8 November 2010; pp. 1132–1137. [Google Scholar]
- Lazorenko, G.; Kasprzhitskii, A.; Nazdracheva, T. Anti-corrosion coatings for protection of steel railway structures exposed to atmospheric environments: A review. Constr. Build. Mater. 2021, 288, 123115. [Google Scholar] [CrossRef]
- Tian, S.B.; Zhang, P.L.; Liu, T.X. Application of Controlled Intervals and Memory Model in Risk Evaluation of Expressway Investment. In Proceedings of the 5th International Conference on Innovation & Management, Maastricht, The Netherlands, 10–11 December 2008; Volumes I and II, pp. 1696–1701. [Google Scholar]
- Luo, D.; Zhang, M.; Zhang, H. Two-stage grey cloud clustering model for drought risk assessment. Grey Syst.-Theory Appl. 2019, 10, 68–84. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.; Yang, Y. On paradox of rule of maximum value and its solution. Syst. Eng.-Theory Pract. 2018, 38, 1830–1835. [Google Scholar]
- GB 50011-2016; Code for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.

| Index | References |
|---|---|
| : Load redundancy | [19,20,21] |
| : Construction error of steel members | [22,23,24] |
| : Steel corrosion degree | [25,26] |
| : Integrity of connectors | [27,28,29] |
| : Fatigue crack of connector | [30,31] |
| : Local buckling of steel members | [32,33,34] |
| : Regular inspection and maintenance | [35,36,37] |
| : Unfavorable Operating Environment | [38,39,40] |
| No. | Working Years | Professional Title | Number of Similar Projects in Which the Experts | Evaluation of the Index System |
|---|---|---|---|---|
| (1) | 12 | Senior engineer | 17 | No need to modify |
| (2) | 15 | Senior engineer | 23 | No need to modify |
| (3) | 8 | Associate professor | 11 | No need to modify |
| (4) | 14 | Professor | 24 | No need to modify |
| (5) | 15 | Senior engineer | 20 | |
| (6) | 32 | Senior engineer | 35 | No need to modify |
| (7) | 25 | Professor | 21 | No need to modify |
| (8) | 27 | Senior engineer | 13 | No need to modify |
| (9) | 16 | Senior engineer | 9 | No need to modify |
| (10) | 29 | Professor | 36 | No need to modify |
| (11) | 31 | Senior engineer | 23 | No need to modify |
| Factor | Extremely High | High | Medium | Low | Extremely Low |
|---|---|---|---|---|---|
| Level | Probability |
|---|---|
| Extremely high | 0.122 |
| High | 0.340 |
| Medium | 0.289 |
| Low | 0.249 |
| Extremely low | 0 |
| Level | Standard CIM | Improved CIM | ||
|---|---|---|---|---|
| 11 Experts in Case Study | 10 New Experts | 11 Experts in Case Study | 10 New Experts | |
| Extremely high | 0.122 | 0.133 | 0.222 | 0.216 |
| High | 0.340 | 0.282 | 0.227 | 0.232 |
| Medium | 0.289 | 0.323 | 0.219 | 0.206 |
| Low | 0.249 | 0.257 | 0.204 | 0.197 |
| Extremely low | 0 | 0.005 | 0.178 | 0.149 |
| Research Environments | Standard CIM | Improved CIM | ||
|---|---|---|---|---|
| 11 Experts in Case Study | 10 New Experts | 11 Experts in Case Study | 10 New Experts | |
| Original index system | II | III | II | II |
| Delete | II | II | II | II |
| Delete | II | II | II | II |
| Delete | II | II | II | III |
| Delete | III | III | III | III |
| Delete | II | II | II | II |
| Delete | II | II | II | II |
| Delete | III | III | III | III |
| Delete | II | II | II | II |
| Add: | III | II | II | II |
| Add: | II | II | II | II |
| Add and | III | II | II | II |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhou, L.; Liu, Y.; Wang, Y. A Safety Risk Analysis of a Steel-Structure Building Using an Improved Controlled Interval and Memory Model. Buildings 2024, 14, 1553. https://doi.org/10.3390/buildings14061553
Chen J, Zhou L, Liu Y, Wang Y. A Safety Risk Analysis of a Steel-Structure Building Using an Improved Controlled Interval and Memory Model. Buildings. 2024; 14(6):1553. https://doi.org/10.3390/buildings14061553
Chicago/Turabian StyleChen, Jinhua, Lihong Zhou, Yipeng Liu, and Yajie Wang. 2024. "A Safety Risk Analysis of a Steel-Structure Building Using an Improved Controlled Interval and Memory Model" Buildings 14, no. 6: 1553. https://doi.org/10.3390/buildings14061553
APA StyleChen, J., Zhou, L., Liu, Y., & Wang, Y. (2024). A Safety Risk Analysis of a Steel-Structure Building Using an Improved Controlled Interval and Memory Model. Buildings, 14(6), 1553. https://doi.org/10.3390/buildings14061553






