Stochastic Response of Composite Post Insulators under Seismic Excitation
Abstract
1. Introduction
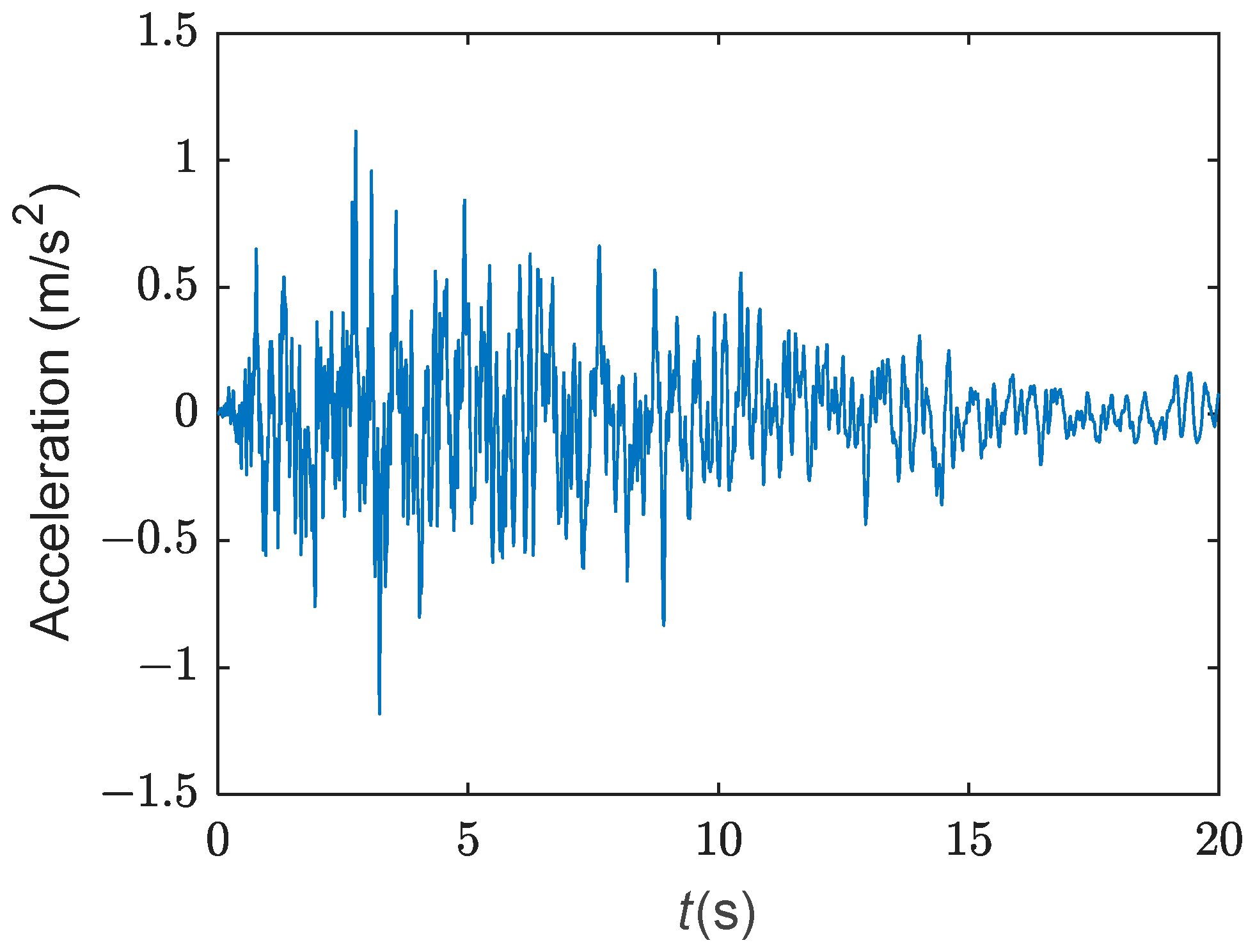
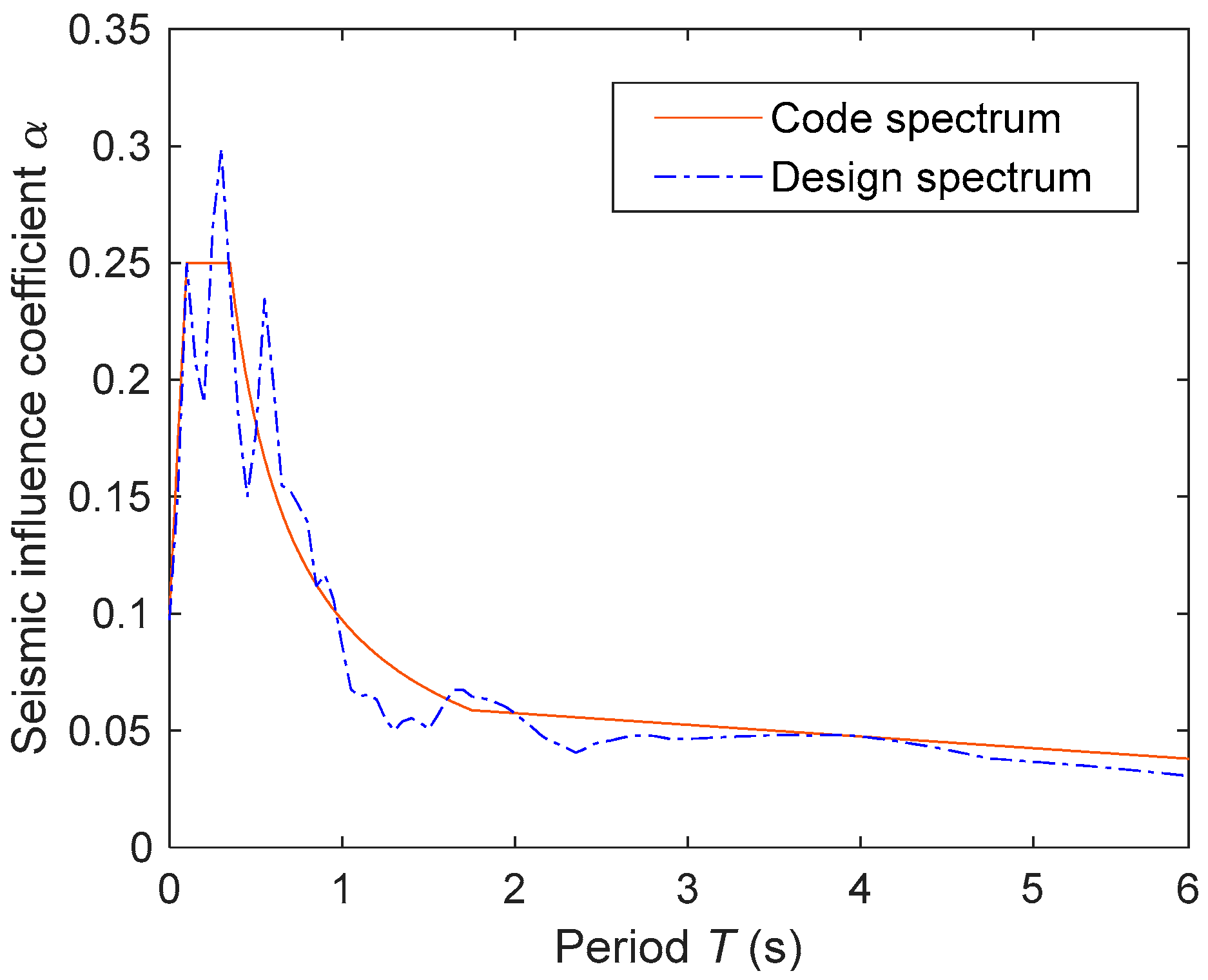
2. Stochastic Ground Motion Model
3. Dynamic Model of Composite Post Insulators under Earthquake
4. Analytical Study
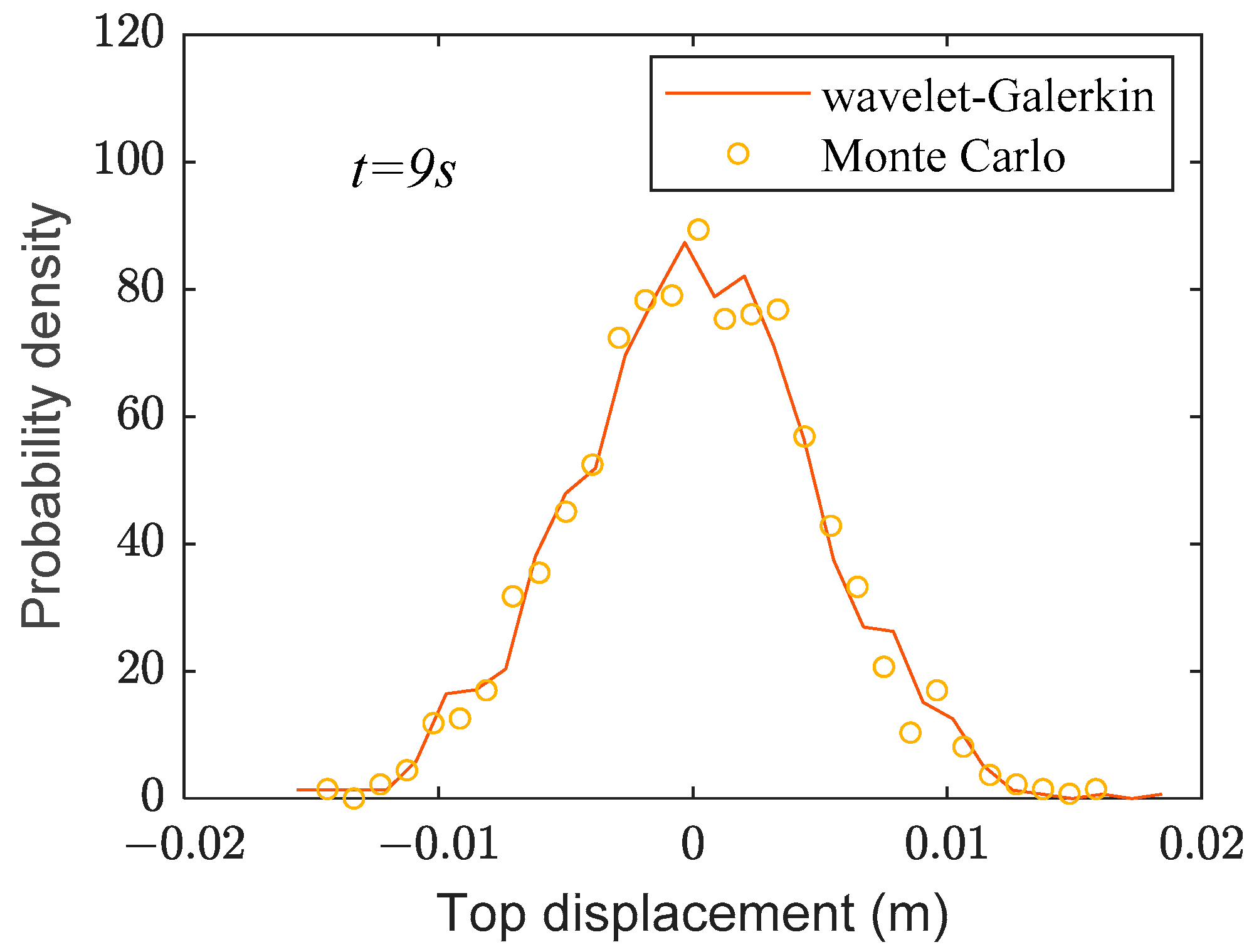
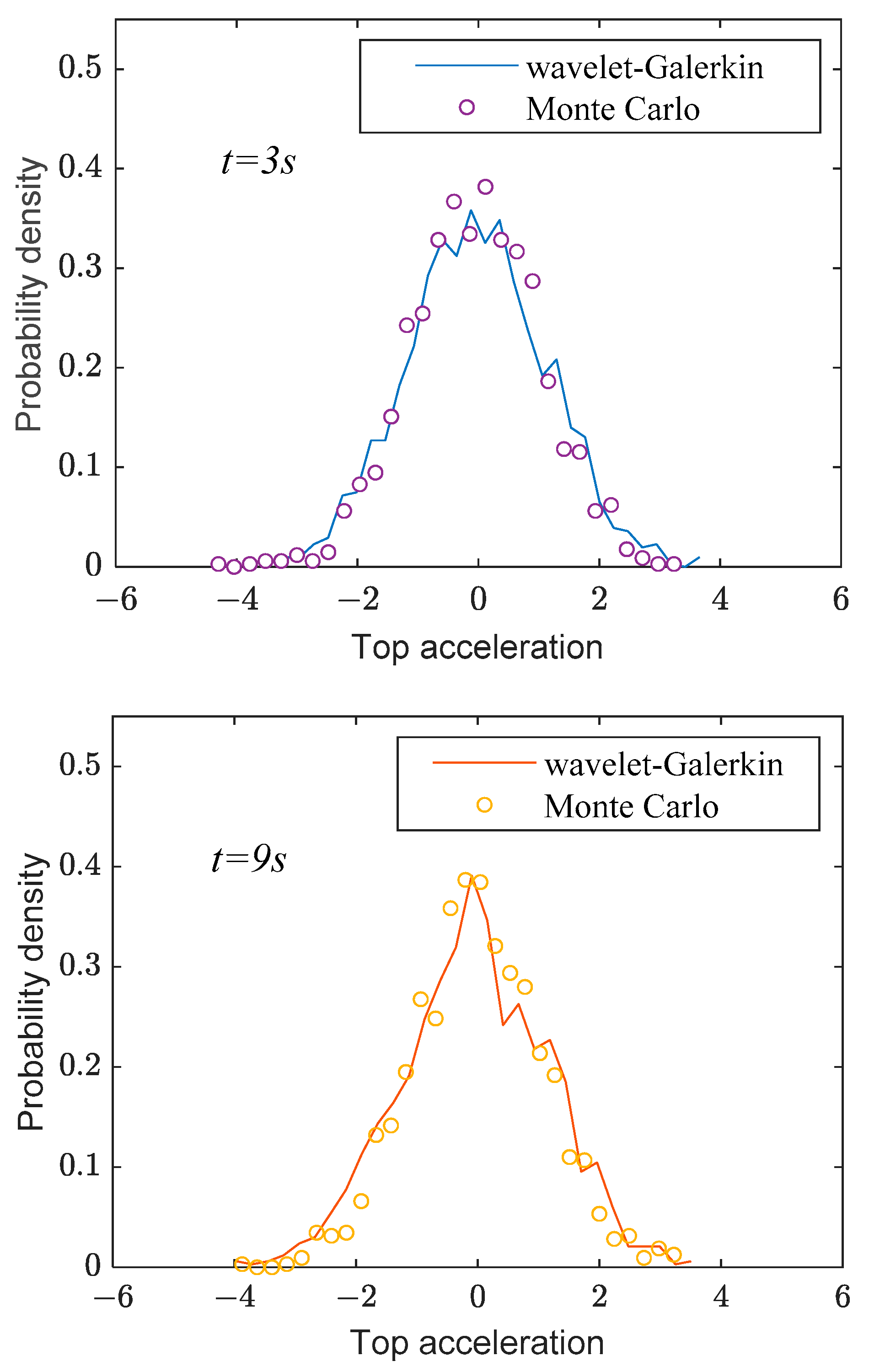
4.1. Seismic Response
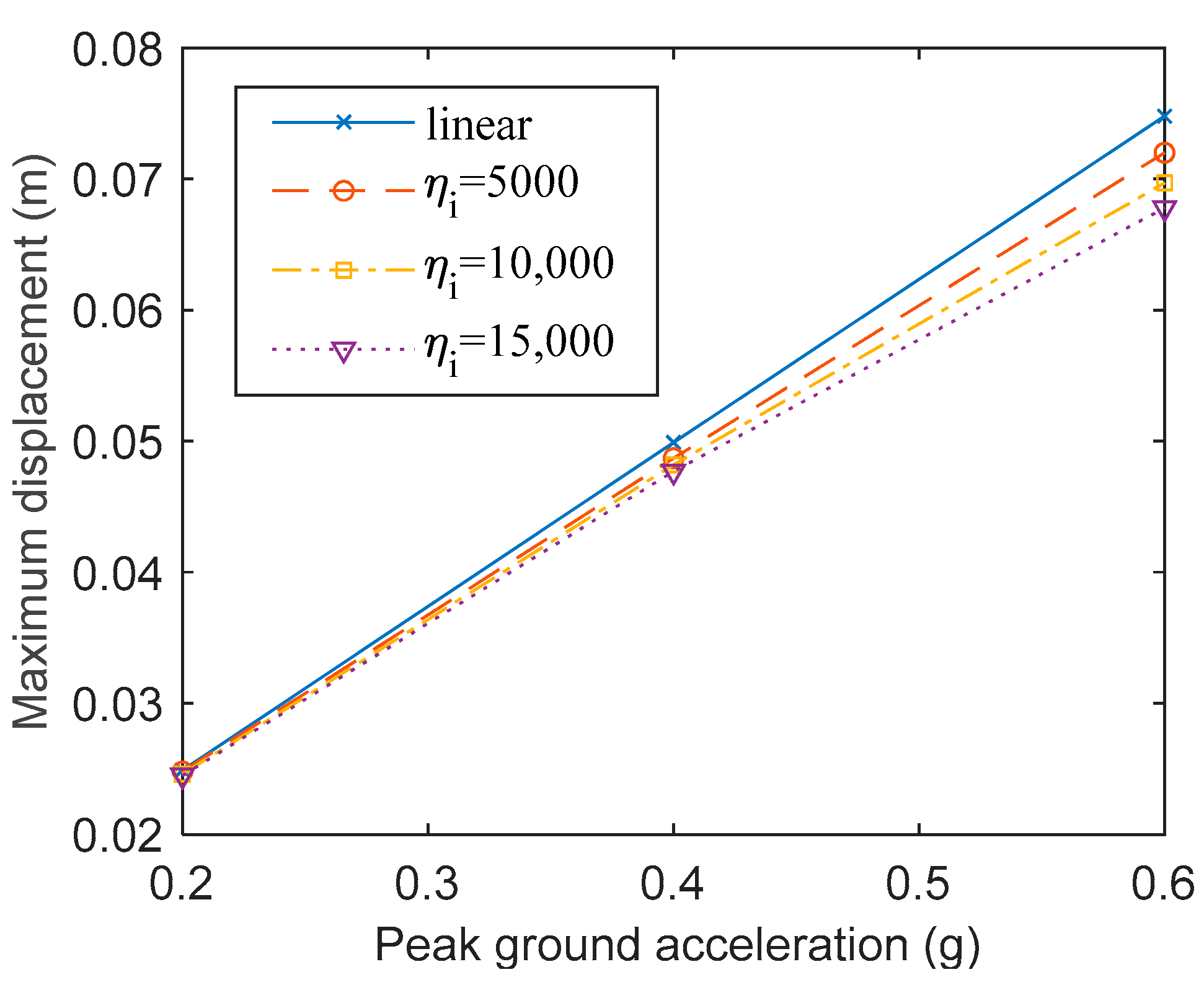
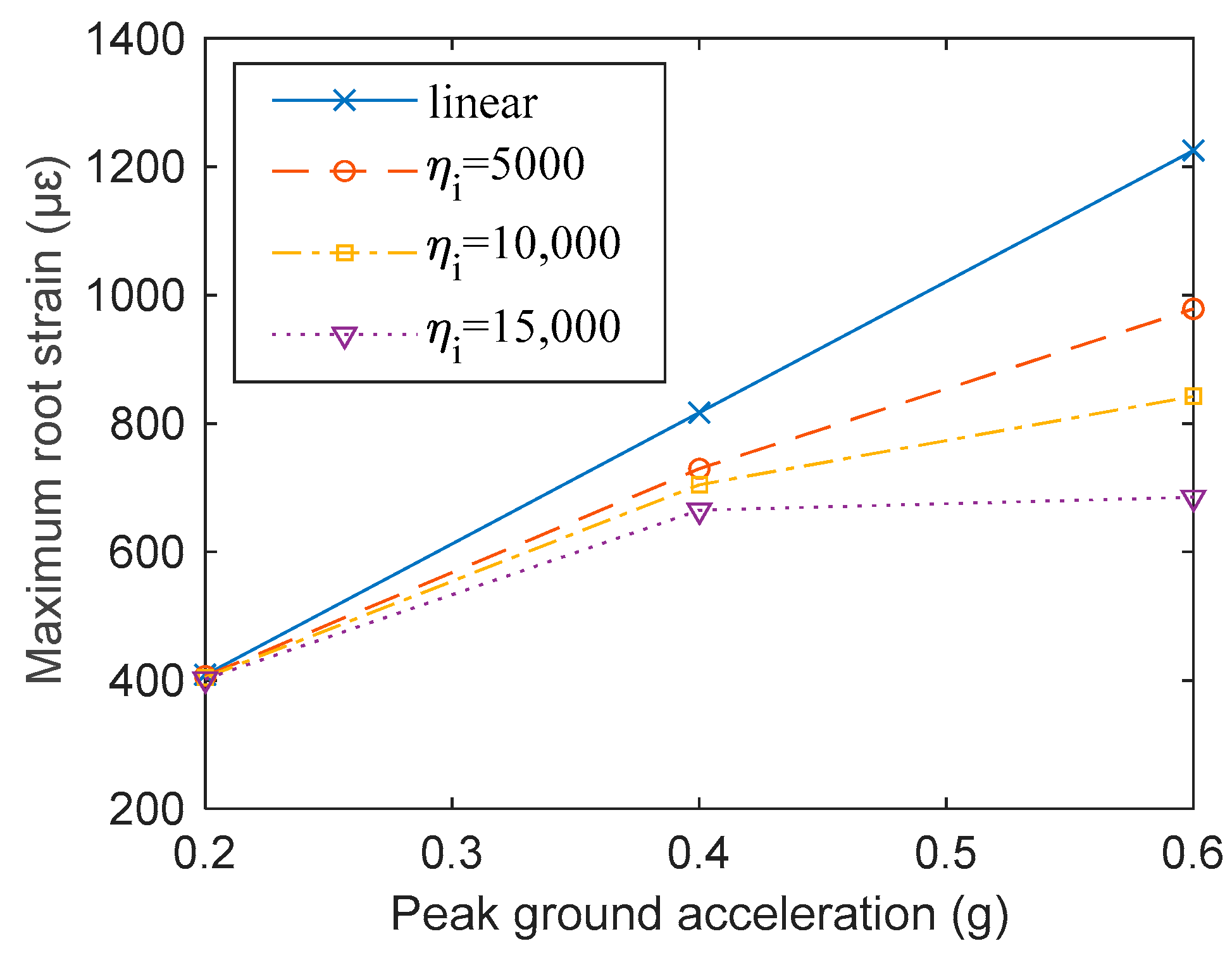
4.2. The Impact of Nonlinearity on System Response
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ying, Z.G.; Ni, Y.Q.; Ko, J.M. Semi-active optimal control of linearized systems with multi-degree of freedom and application. J. Sound. Vib. 2005, 279, 373–388. [Google Scholar] [CrossRef]
- Qian, J.; Yang, J.P.; Xia, Y.; Yan, Y.X.; Zhou, J.T. Rapid damage assessment of regional beam bridges after earthquake based on simplified models and different seismic inputs. Structures 2023, 57, 105306. [Google Scholar] [CrossRef]
- Kempner, L.; Scott, M.S.; Haldar, A.K. Seismic Effects on Transmission Lines and Their Major Components. Electr. Transm. Substn. Struct. 2018, 2018, 132–145. [Google Scholar]
- He, C.; Xie, Q.; Yang, Z.Y.; Xue, S.T. Seismic evaluation and analysis of 1100-kVUHV porcelain transformer bushings. Soil Dyn. Earthq. Eng. 2019, 123, 498–512. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Y.; Lu, Z.; Zhu, Z. Shaking Table Test of a ±1100 k V Composite Post Insulator. Insul. Surg. Arrest. 2018, 138–144. [Google Scholar]
- Kanai, K. Semi-Empirical Formula for the Seismic Characteristics of the Ground. Bull. Earthq. Res. Inst. Univ. Tokyo 1957, 35, 309–325. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures. McGraw-Hill Book, Co.: New York, NY, USA, 1975. [Google Scholar]
- Ou, J.P.; Niu, D.T. Parameters in the Random Process Models of Earthquake Ground Motion and their Effects on the Response of Structures. J. Harbin Eng. Univ. 1990, 23, 24–34. [Google Scholar]
- Liu, Z.J.; Liu, Z.H.; Liu, W. Probability Model of Fully Non-stationary Ground Motion with the Target Response Spectrum Compatible. J. Vib. Shock 2017, 36, 32–38. [Google Scholar]
- Gumus, E.; Ozturk, B.; Mohamed Nazri, F. Scaling method application for seismic design along the central Anatolian fault zone. Adv. Civ. Eng. 2022, 2022, 1963553. [Google Scholar] [CrossRef]
- GB50260-2013; Code for Seismic Design of Electrical Installations. Ministry of Housing and Urban-Rural Development: Beijing, China, 2013.
- Han, X.; Pagnacco, E. Response EPSD of chain-like MDOF nonlinear structural systems via wavelet-Galerkin method. Appl. Math. Model. 2022, 103, 475–492. [Google Scholar] [CrossRef]
- Hashemi AMosalam, K.M. Shake-table experiment on reinforced concrete structure containing masonry infill wall. Earthq. Eng. Struct. D 2006, 35, 1827–1852. [Google Scholar] [CrossRef]
- John, D.; Aochi, H. A survey of techniques for predicting earthquake ground motions for engineering purposes. Surv. Geophys. 2008, 29, 187–220. [Google Scholar]
- Wilson, E.; Der Kiureghian, A.; Bayo, E.P. A Replacement for The Srss Method Inseismic Analysis. Earthq. Eng. Struct. D 1981, 9, 187. [Google Scholar] [CrossRef]
- Shinozuka, M.; Sato, Y. Simulation of nonstationary random processes. ASCE J. Eng. Mech. Div. 1967, 93, 11–40. [Google Scholar] [CrossRef]
- Jun, X.; Wang, J.; Wang, D. Evaluation of the probability distribution of the extreme value of the response of nonlinear structures subjected to fully nonstationary stochastic seismic excitations. J. Eng. Mech. 2020, 146, 06019006. [Google Scholar]
- Fabio, S.; Antonio, P.; Gabriele, F.; Giovanni, L.; Lucia, L. Simulation of non-stationary stochastic ground motions based on recent Italian earthquakes. Bull. Earthq. Eng. 2021, 19, 3287–3315. [Google Scholar]
- Xue, Y.; Cheng, Y.; Zhu, Z.; Li, S.; Liu, Z.; Guo, H.; Zhang, S. Study on Seismic Performance of Porcelain Pillar Electrical Equipment Based on Nonlinear Dynamic Theory. Adv. Civ. Eng. 2021, 2021, 8816322. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, L.; Cheng, Y.; Guo, H.; Lu, Z. On the Nonlinear Seismic Responses of Shock Absorber-Equipped Porcelain Electrical Components. Math. Probl. Eng. 2020, 2020, 9026804. [Google Scholar] [CrossRef]
- Paolacci, F.; Giannini, R. Seismic reliability assessment of a high-voltage disconnect switch using an effective fragility analysis. J. Earthq. Eng. 2009, 13, 217–235. [Google Scholar] [CrossRef]
- Roh, H.; Nicholas, D.O.; Andrei, M.R. Experimental test and modeling of hollow-core composite insulators. Nonlinear Dynam. 2012, 69, 1651–1663. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, Y.; Lu, Z.; Zhu, Z.; Li, S. Study on the Flexural Behavior of ± 1100 kV Composite Post Insulators. Insul. Surg. Arrest. 2018, 207–214. [Google Scholar]

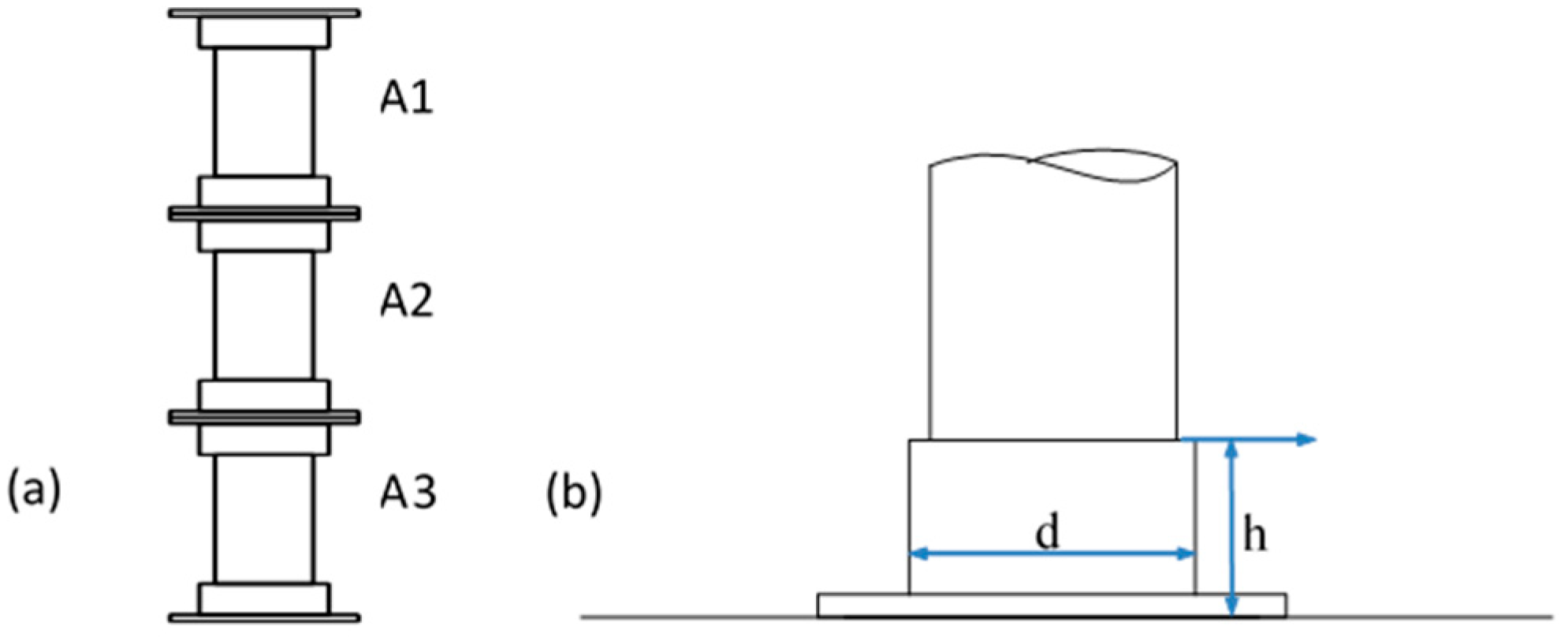
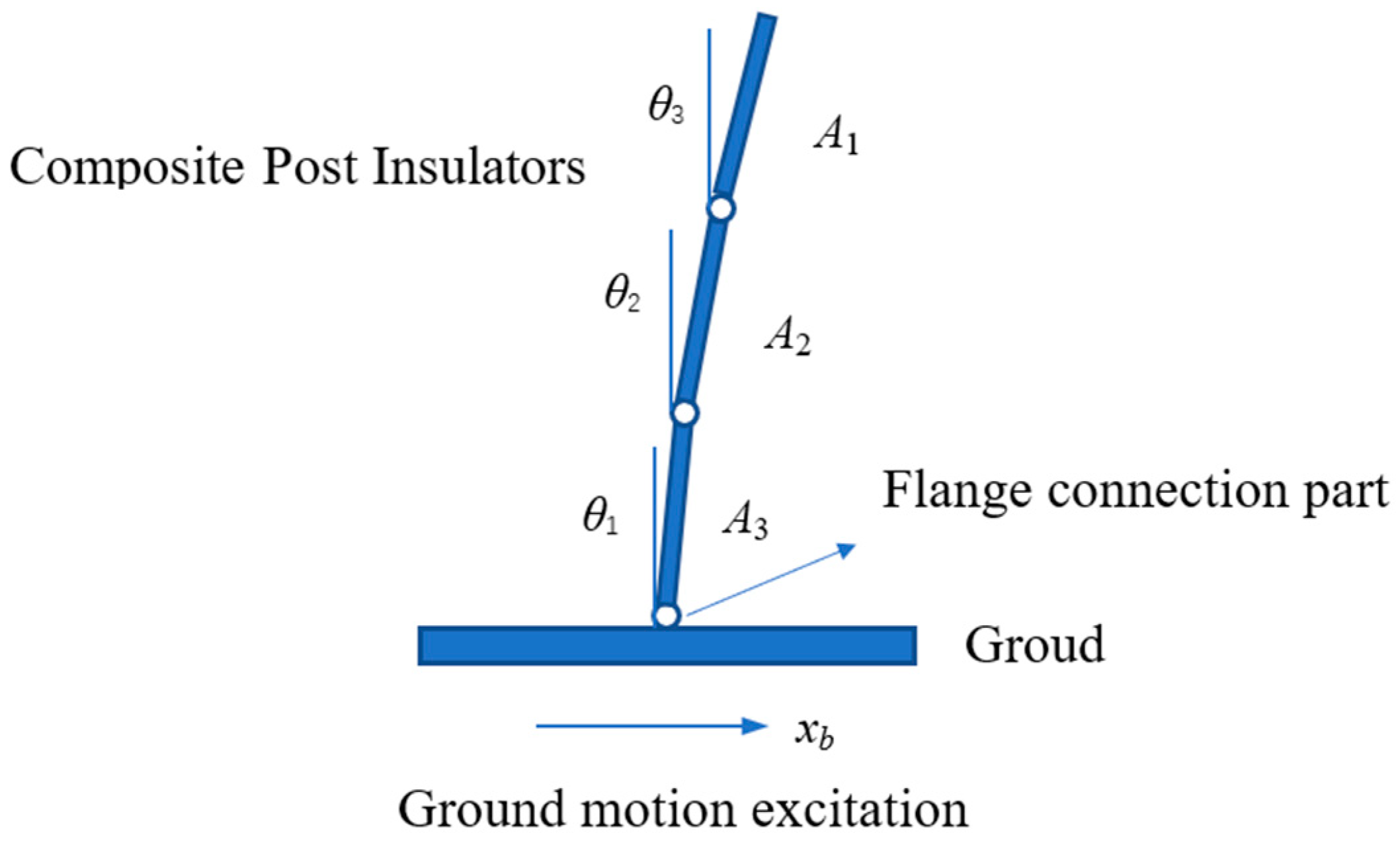
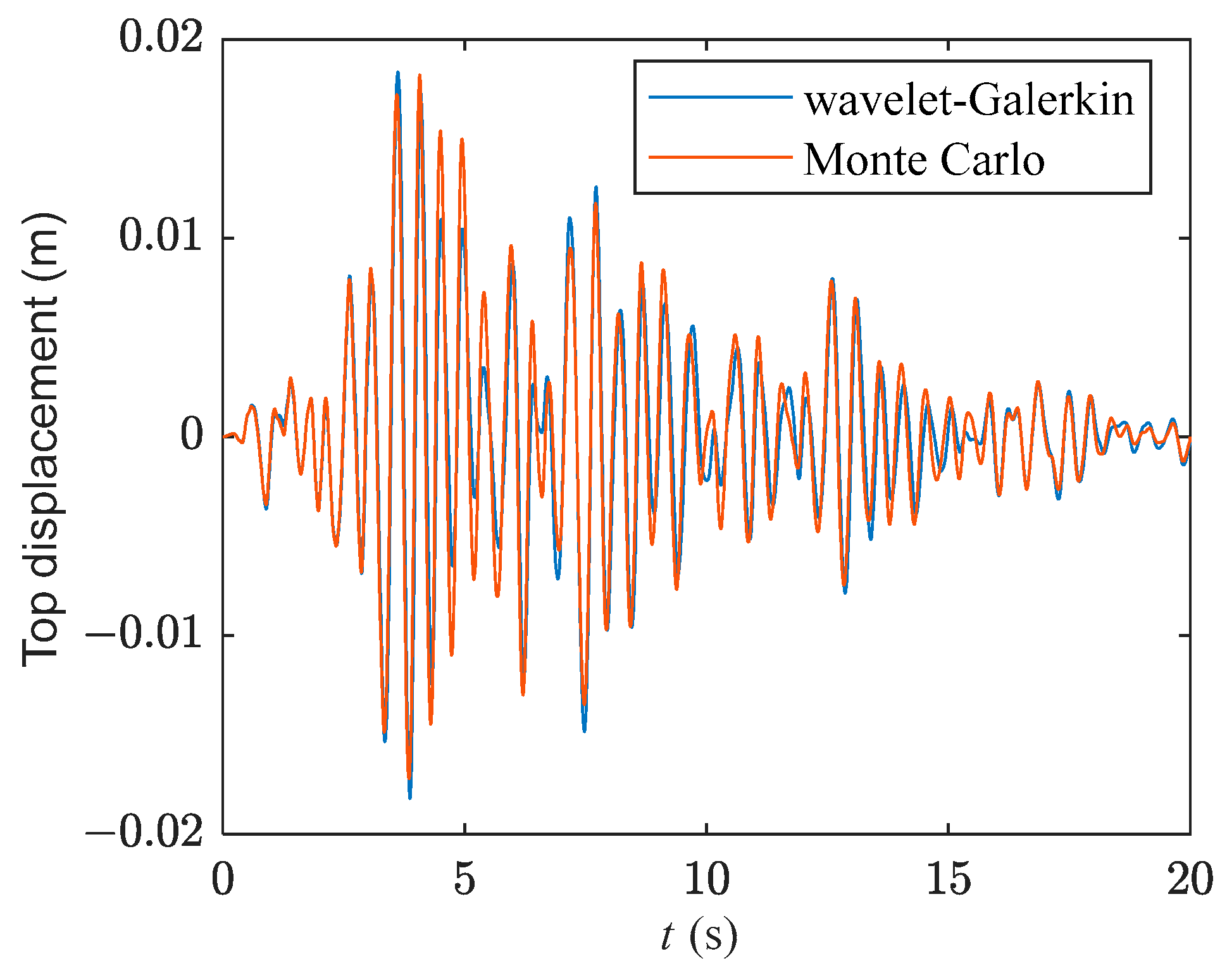
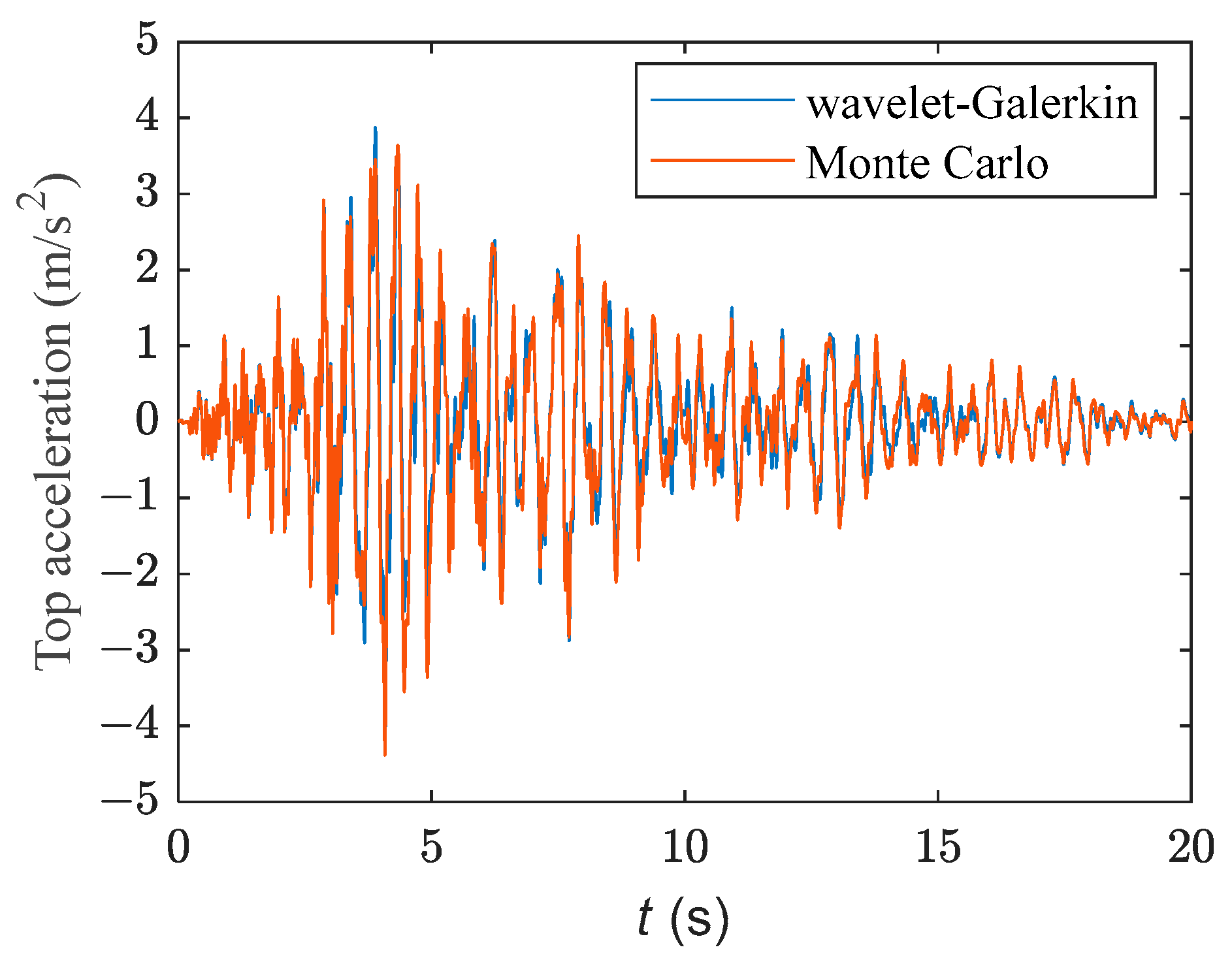
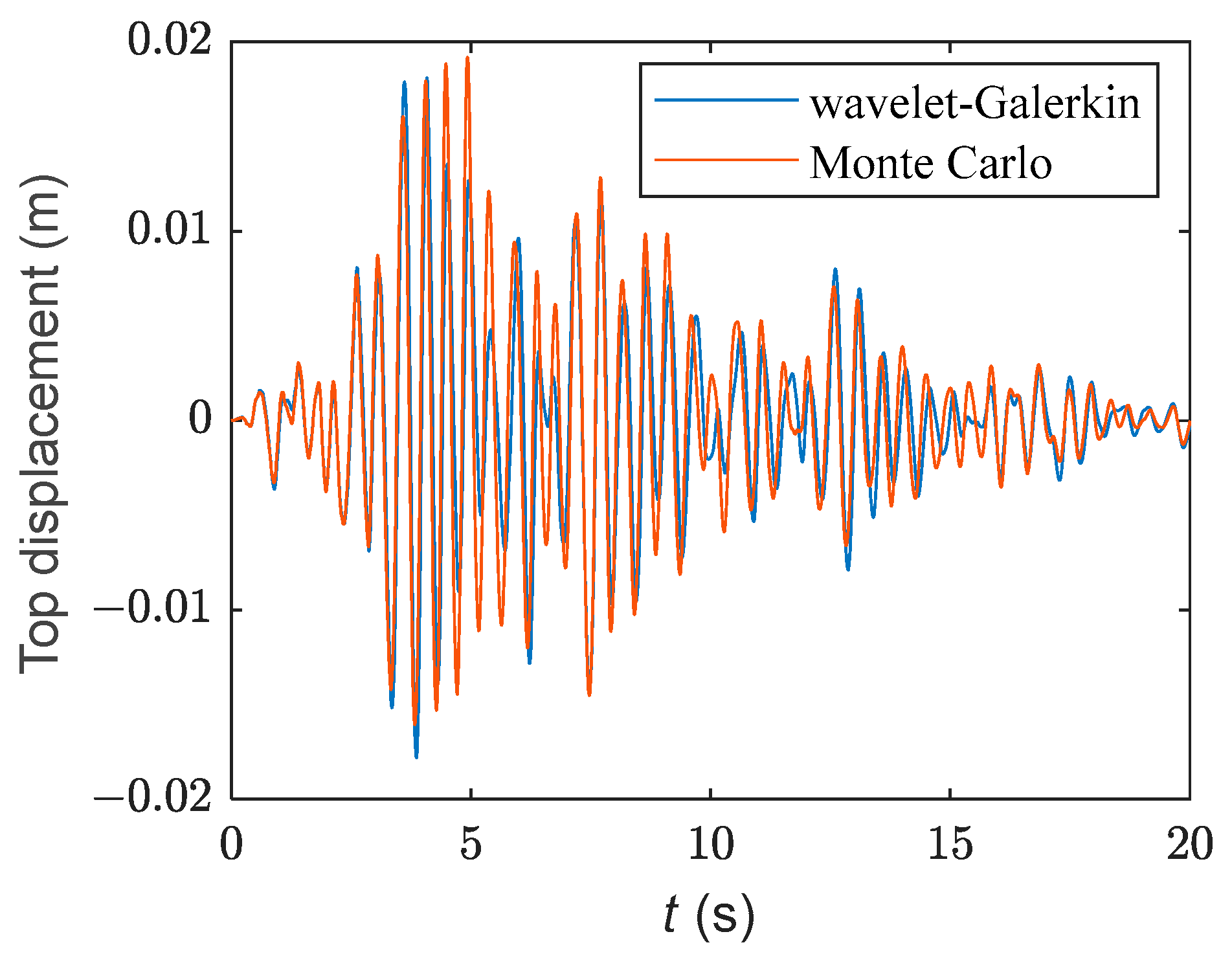
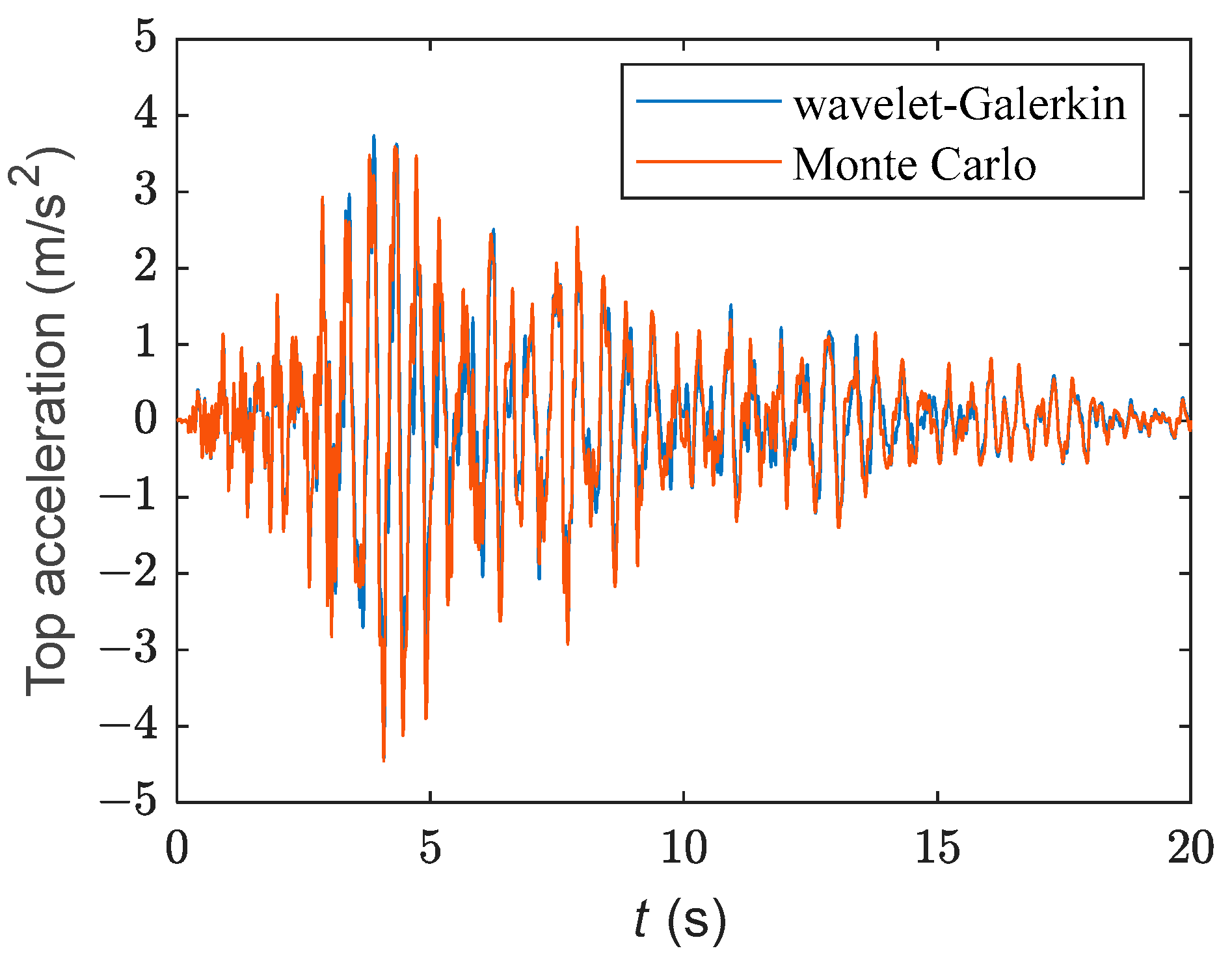

| Section | Length (mm) | Mass (kg) | Section Diameter (mm) | Flange Height h (mm) | Outer Diameter of Flange d (mm) |
|---|---|---|---|---|---|
| A1 | 3225 | 710 | 300 | 150 | 340 |
| A2 | 2425 | 585 | 300 | 150 | 340 |
| A3 | 2465 | 590 | 300 | 180 | 340 |
| Section | hc (m) | dc (m) | Ec (GPa) | Kc (N.m/rad) | λc |
|---|---|---|---|---|---|
| A1 | 0.15 | 0.34 | 68.7 | 3.7373 × 107 | 5.8213 × 1018 |
| A2 | 0.15 | 0.34 | 65.5 | 3.8179 × 107 | 5.6645 × 1018 |
| A3 | 0.18 | 0.34 | 67.8 | 4.9244 × 107 | 6.3052 × 1018 |
| Difference Range ((Linear − Nonlinear)%/Linear) | |||||
|---|---|---|---|---|---|
| Seismic Excitation | ηi = 5000 | ηi = 10,000 | ηi = 15,000 | ||
| Top displacement | 0.2 g | 0.4 | 0.8 | 1.6 | |
| 0.4 g | 2.4 | 3.4 | 4.4 | ||
| 0.6 g | 3.7 | 6.8 | 9.4 | ||
| Root strain | 0.2 g | 0.5 | 10.7 | 20.1 | |
| 0.4 g | 1 | 13.8 | 31.3 | ||
| 0.6 g | 1.6 | 18.6 | 44.1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Cheng, Y.; Lu, Z.; Huan, R.; Lü, Q.; Liu, Z. Stochastic Response of Composite Post Insulators under Seismic Excitation. Buildings 2024, 14, 1539. https://doi.org/10.3390/buildings14061539
Wang H, Cheng Y, Lu Z, Huan R, Lü Q, Liu Z. Stochastic Response of Composite Post Insulators under Seismic Excitation. Buildings. 2024; 14(6):1539. https://doi.org/10.3390/buildings14061539
Chicago/Turabian StyleWang, Haibo, Yongfeng Cheng, Zhicheng Lu, Ronghua Huan, Qiangfeng Lü, and Zhenlin Liu. 2024. "Stochastic Response of Composite Post Insulators under Seismic Excitation" Buildings 14, no. 6: 1539. https://doi.org/10.3390/buildings14061539
APA StyleWang, H., Cheng, Y., Lu, Z., Huan, R., Lü, Q., & Liu, Z. (2024). Stochastic Response of Composite Post Insulators under Seismic Excitation. Buildings, 14(6), 1539. https://doi.org/10.3390/buildings14061539





