A Review of Levitation Control Methods for Low- and Medium-Speed Maglev Systems

Abstract

Maglev transportation is a highly promising form of transportation for the future, primarily due to its friction-free operation, exceptional comfort, and low risk of derailment. Unlike conventional transportation systems, maglev trains operate with no mechanical contact with the track. Maglev trains achieve levitation and guidance using electromagnetic forces controlled by a magnetic levitation control system. Therefore, the magnetic levitation control system is of utmost importance in maintaining the stable operation performance of a maglev train. However, due to the open-loop instability and strong nonlinearity of the control system, designing an active controller with self-adaptive ability poses a substantial challenge. Moreover, various uncertainties exist, including parameter variations and unknown external disturbances, under different operating conditions. Although several review papers on maglev levitation systems and control methods have been published over the last decade, there has been no comprehensive exploration of their modeling and related control technologies. Meanwhile, many review papers have become outdated and no longer reflect the current state-of-the-art research in the field. Therefore, this article aims to summarize the models and control technologies for maglev levitation systems following the preferred reporting items for systematic reviews and meta-analysis (PRISMA) criteria. The control technologies mainly include linear control methods, nonlinear control methods, and artificial intelligence methods. In addition, the article will discuss maglev control in other scenarios, such as vehicle–guideway vibration control and redundancy and fault-tolerant design. First, the widely used maglev levitation system modeling methods are reviewed, including the modeling assumptions. Second, the principle of the control methods and their control performance in maglev levitation systems are presented. Third, the maglev control methods in other scenarios are discussed. Finally, the key issues pertaining to the future direction of maglev levitation control are discussed.

1. Introduction

In recent decades, railway transportation has experienced rapid global development due to its energy efficiency and increased transport capacity during operation [1]. Nevertheless, conventional wheel-based rail transport systems face several technical challenges associated with noise, adhesion, rail–wheel wear, and vibration [2]. Maglev train systems have emerged as innovative railway transport systems in response to the increasing demand for higher speeds and enhanced comfort in intercity travel. They offer various advantages, including non-contact operation, minimal vibration, low noise, no risk of derailment, flexible route selection, and cost-effective construction. As a result, maglev trains have garnered significant attention for their development and implementation in countries such as Japan, Korea, and China [3].

Based on the levitation mechanism, maglev train systems can be broadly categorized into electromagnetic levitation (EMS) and electrodynamic levitation (EDS) [3]. The EDS-type system utilizes repulsive forces for levitation and is inherently stable due to the proportional relationship between the repulsive force and the gap. When the gap decreases, the repulsive force increases, which ensures a stable levitation state [4]. However, the EDS-type requires sufficient speed to acquire sufficient induced currents for levitation. Unlike the EDS-type system, the EMS-type system achieves levitation by utilizing the magnetic attraction force between the guideway and electromagnets. Such levitation is unstable due to the nature of the magnetic circuit, and precise control is necessary to maintain the uniform airgap. Nonetheless, the EMS-type maglev system has a significant advantage compared with the EDS-type in that it can provide an attractive force at zero or low speed [5]. Currently, commercial maglev train lines primarily utilize EMS-type systems, such as the Changsha Maglev line in China and the EcoBee line in South Korea. These systems are predominantly designed for low- to medium-speed operations. Given the substantial impact of the dynamic performance of the magnetic levitation system on the overall performance of maglev trains, the implementation of an active levitation control system is crucial to ensure the safety and stability of EMS-type maglev trains. Therefore, this paper focuses on reviewing the active magnetic levitation control systems of EMS-type low- and medium-speed maglev trains, which have more extensive and practical significance.

The maglev levitation system models for control design in the literature can mainly be divided into two categories: dynamic equation-based modeling and data-driven-based modeling. In dynamic equation-based methods, numerical models are built based on Newton’s law and Kirchhoff’s law. The parameters of the models are predefined using the mechanical properties of the maglev levitation system, and uncertainties associated with the system and environmental disturbances, such as wind load, can be updated using the measured data. Unlike dynamic equation-based modeling, data-driven-based modeling directly uses historic data for training. In the future, a magnetic levitation controller could be designed based on these models.

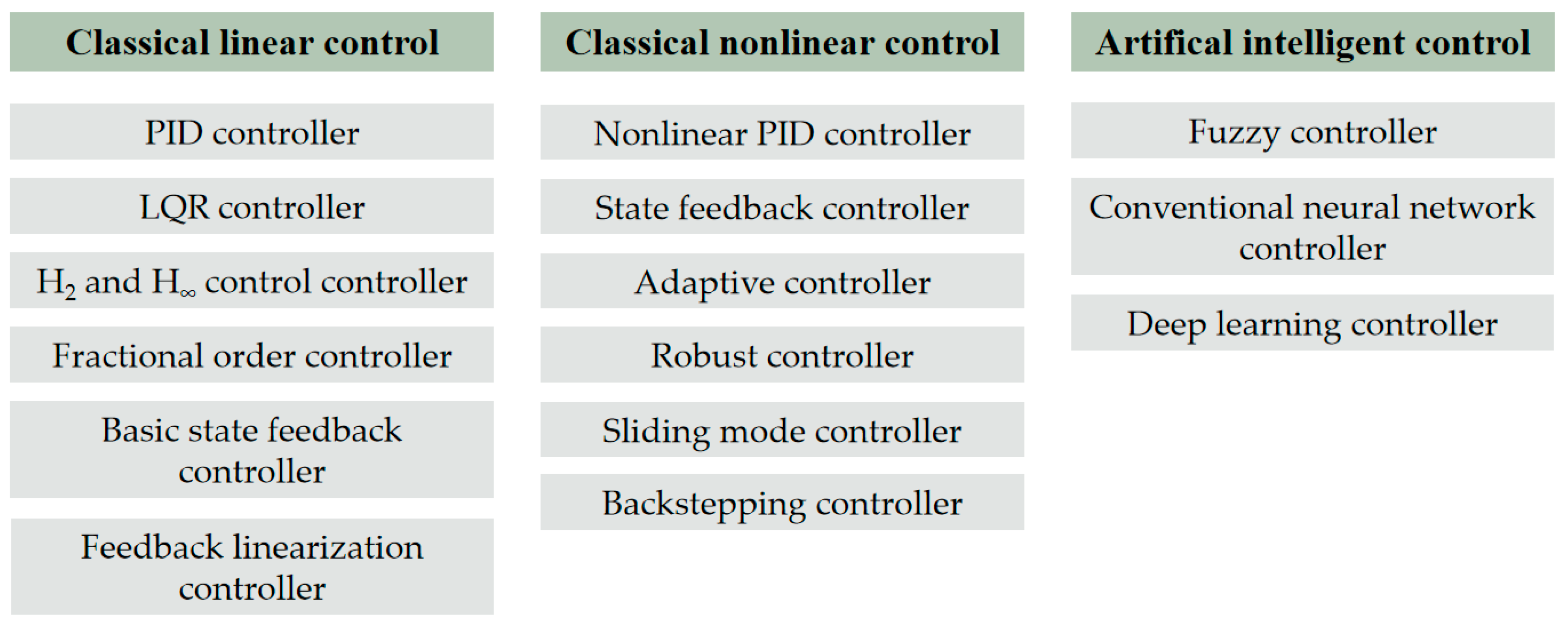
The levitation control techniques discussed in this paper are classified into three categories according to the control algorithms: classical linear control methods, classical nonlinear control methods, and artificial intelligence control methods. In general, a linearized model of an EMS-type system is established around the equilibrium point and controlled using linear control algorithms, such as the proportional–integral–derivative (PID) [6,7] and linear quadratic regulator (LQR) [8,9,10] theories. Nevertheless, it is worth noting that maglev levitation controllers based on linearized models are typically implemented within proximity to the equilibrium point. Due to the inherently strong nonlinearity of the magnetic levitation system, controllers based on linear simplified designs may become unstable or ineffective when the system is subjected to external disturbances. To enable the designed levitation controller to handle external disturbances as smoothly and efficiently as possible, advanced levitation controllers based on different nonlinear control theories have been proposed to improve the overall performance of the control system, such as robust control [11,12,13], adaptive control [14,15], and sliding mode control (SMC) [16,17,18]. However, most of these control strategies degrade in performance when there are disturbances because they rely on a precise model and detailed information about the system. Artificial intelligent control methods, including the fuzzy logic method [19,20], neural networks (NN) [21,22,23,24,25], deep belief networks (DBN) [26], and deep reinforcement learning (DRL) [27], have been implemented to increase the robustness of the control system by automatically adjusting the parameters in the controller or directly acting as a controller.

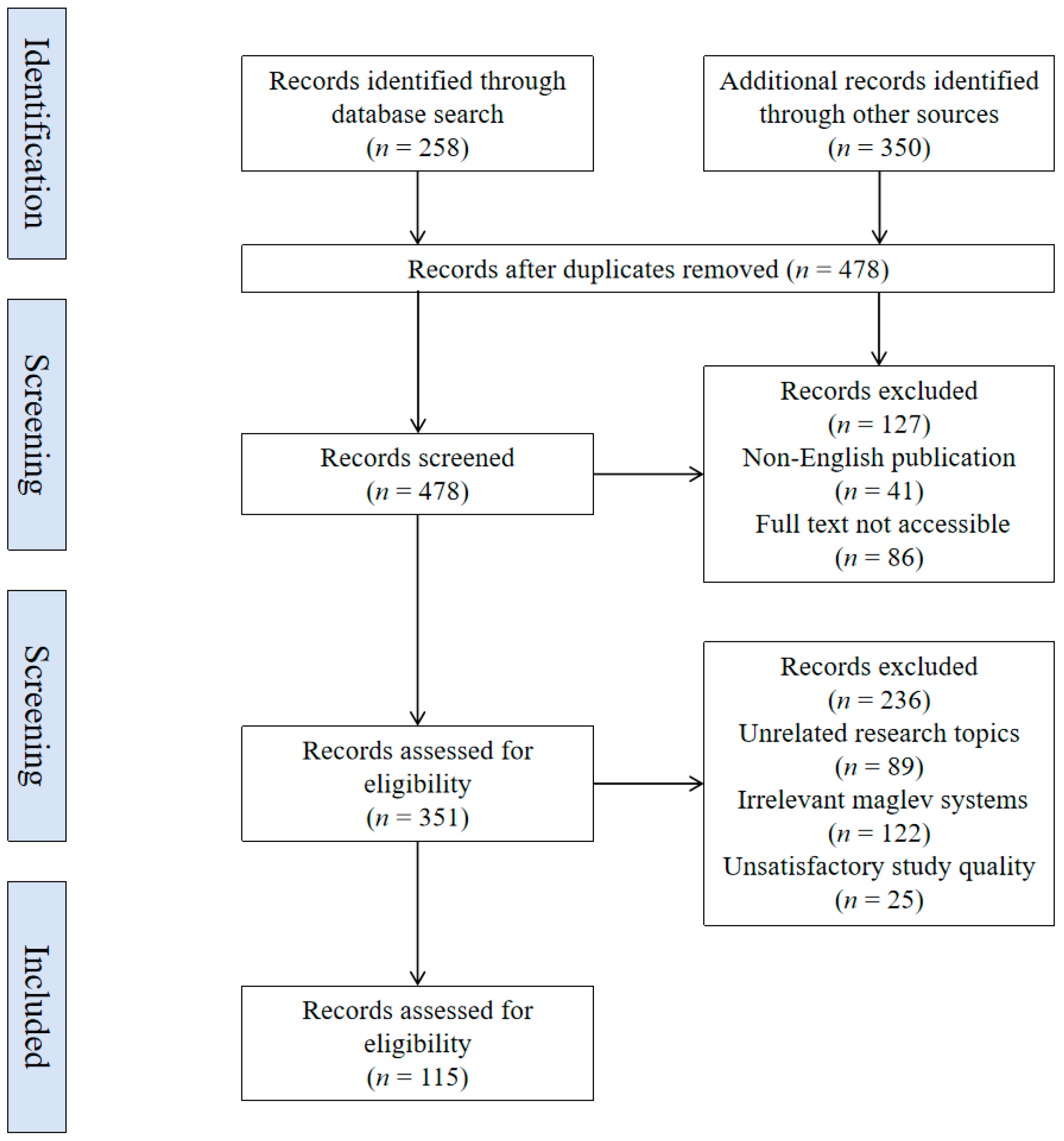
Although several review papers on maglev levitation systems and control methods have been published over the last decade, there are currently no in-depth investigations of their modeling or their related control technologies [28,29,30]. This paper presents a comparative study of maglev levitation system modeling and different maglev levitation control methods implemented on an EMS-type maglev levitation system. In addition, uncertainty factors, such as the time delay and disturbance of EMS-type maglev trains, are reviewed. The effect of the controller on the guideway vibration and fault-tolerant control had not been published before. As the speed of EMS-type maglev trains continues to improve, modeling and levitation control play a fundamental role in the advancement of EMS-type maglev train technology. The research records reviewed in this paper were selected following the preferred reporting items for systematic reviews and meta-analysis (PRISMA) criteria, as shown in Figure 1. This review serves as a valuable resource for researchers in this field and offers a systematic and comprehensive compilation of materials. The primary contributions of this review are as follows:

(1)

The magnetic levitation system modeling for levitation control is reviewed in detail, including the modeling based on dynamic equations and data. Specific problems in modeling, such as the coupling of two levitation points and electromagnet-guideway coupling, are also discussed.

(2)

The advantages and disadvantages of levitation control techniques and uncertainty factors in the control system are analyzed.

(3)

Recent studies on the effect of levitation control on the guideway vibration and fault-tolerant control design are also summarized.

The remainder of this paper is organized as follows. Section 2 describes the history and background of the EMS-type maglev system development. Section 3 introduces the modeling of the EMS-type maglev system for levitation control. Section 4 discusses the classical linear control methods, classical nonlinear control methods, and artificial intelligence control methods for maglev levitation systems. Section 5 summarizes the effect of the maglev levitation control on the guideway vibration and fault-tolerant control. Section 6 presents the discussion. The conclusions and prospects are outlined in Section 7.

2. History Background of the EMS-Type Maglev Train System

The development of maglev trains can be traced back to 1934, when Hermann Kemper of Germany patented the concept. In 1969, the German company Krauss-Maffei achieved a significant milestone by developing the first prototype model of a Maglev train in their laboratory, known as Transrapid (TR) 01. In the early 1970s, the German government initiated a high-speed maglev train transportation development plan, leading Krauss-Maffei to develop subsequent models, namely, TR02 and TR04, based on the TR01 prototype. In 1991, the German government conducted an evaluation of the TR07 model and deemed it ready for practical application. Following this, the development of the TR08 and TR09 maglev trains took place. The TR08 model achieved a significant milestone, as it became the first commercially operational maglev train in the world. It was successfully implemented in the joint Germany and China project, connecting Shanghai Pudong Airport to Longyang Road subway station.

In 1974, Japan Airlines (JAL) made a significant investment by purchasing the TR04 model from Krauss-Maffei. Building upon this technology, JAL developed a series of low-speed maglev trains and high-speed surface transport (HSST) systems based on the TR04 model. The bogie structure utilized in the HSST-05 design became widely adopted in subsequent low-speed maglev train designs. Based on the HSST-05, two models were developed, HSST-100S and HSST-100L, capable of reaching speeds of up to 100 km/h. The HSST-100L model was implemented on the Linimo line in Nagoya, Japan, showcasing its practical application. The Japanese National Railways (JNR) have also made significant contributions to maglev train research. In 1972, they successfully developed the ML100 model, followed by the ML500, which set a world record speed of 517 km/h in 1979. The MLX01, developed in 1997, achieved a remarkable speed of 550 km/h. Furthermore, Japan’s efforts in maglev train technology extended to the development of the low-temperature superconducting electric maglev vehicle known as L0. Tested on the Yamanashi test line, the L0 achieved a remarkable world record speed of 603 km/h, highlighting Japan’s advancements in high-speed maglev train capabilities.

Korea has also made notable advancements in the development of low-speed maglev trains, intending to address traffic congestion issues in major cities. The improvement of the urban air mobility (UTM)-01 took place in 1999, leading to the subsequent development of UTM-02. In 2004, a study focusing on the commercial operation of UTM-02-based low-speed maglev trains commenced. The demonstration line for this study was chosen to be located at Incheon International Airport. However, it took until 2016 for the commercial line to be officially put into operation, serving as a solution to the city’s transportation needs.

China initiated research on maglev trains in the 1980s, with various educational institutions and research institutes actively participating in the field. Notable contributors include many universities and institutes, like the National University of Defense Technology, the Chinese Academy of Sciences, etc. Several organizations embarked on the development of a hybrid magnet maglev train, achieving success in 2012. A 425 m long test line was constructed in Chengdu, and a low-speed electromagnetic maglev train was developed. This train underwent testing on the line in 2006. Later, a 1500 m long low-speed maglev test line was established in Shanghai, resulting in the development of a low-speed maglev train. Additionally, the China Southern Railway Corporation Limited group (CSR) began studying low-speed maglev train technologies, establishing a test line at the Zhuzhou Railway Vehicle Factory.

3. EMS-Type Maglev Train System and Modeling

In this section, we consider a standard EMS-type maglev train system and will firstly introduce the main components and their functions. Then, we will review different modelling approaches for the EMS-type levitation system for control objective. Specific problems in modeling, such as the coupling of two levitation points and electromagnet-guideway coupling, will be emphasized in this section.

3.1. Overview of EMS-Type Maglev Train System

The EMS-type maglev train is suspended on the track via an electromagnetic force instead of the wheel–rail contact force in conventional rail transport systems. The electromagnet is adopted in the maglev train for both levitation and guidance functions, and the linear motor is utilized for the traction function. In general, EMS-type maglev trains consist of five main components: levitation and guidance, traction, bogie, braking, and rail–bridge systems.

• Linear motors are used in the traction system of the EMS-type maglev trains: long-stator linear synchronous motor (LSM) and short-stator linear-induced motors (LIM) are commonly selected depending on the speed requirements of the train.
• The bogie system serves as a crucial component for mounting the levitation system and guiding the electromagnets and traction motors in maglev trains.
• The braking system ensures the safe operation of maglev trains; braking systems can be divided into common, fast, emergency, and holding brake methods.
• The levitation and guidance mechanisms are achieved using electromagnets installed on the levitation bogie and an F-type rail. The electromagnets are energized to attract the F-type rail to levitate the vehicle. Precise control of the current in the electromagnets ensures that the train remains stably suspended within a dynamic stability range, which is typically 8–12 mm.
• The difference in the supporting and guidance functions between the maglev train system and the conventional rail transport system results in a difference in the guideway design. The construction cost of the rail-bridge system exceeds 60–70% of the total initial investment in a maglev train. For EMS-type maglev trains, the guideway structures can be divided into three types: steel sleeper-based rail structures, direct-connected rail structures without sleepers, and integral bed rail structures.

3.2. The Modelling of EMS-Type Maglev Train System

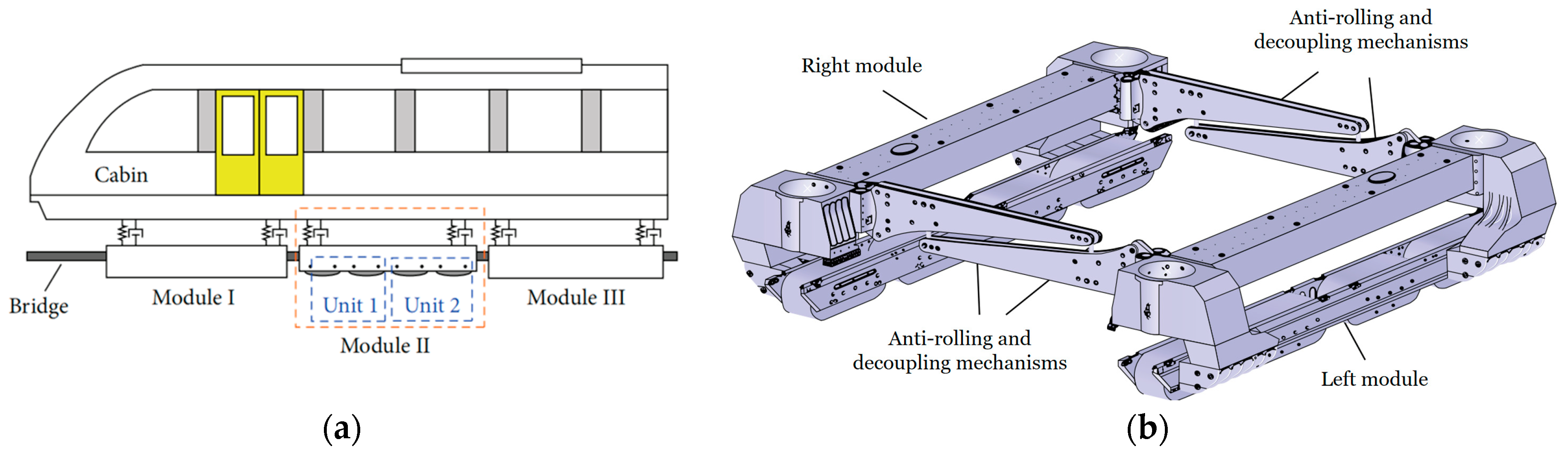
The EMS-type maglev train consists of cabins, levitation bogies, secondary levitations, and guidance electromagnets. The vehicle body of the maglev train is supported by multiple bogies using air springs as buffers and supporters. As shown in Figure 2, each bogie consists of two levitation units, and each unit contains two pairs of adjacent electromagnets controlled by decentralized single-input single-output (SISO) controllers. The modelling of the magnetic levitation system in the literature can be divided into dynamic equations and data-driven based methods. The flowchart for this part is as in Figure 3.

3.2.1. Dynamic Equations-Based Modeling

For dynamic equations-based model ing, some assumptions are usually made to simplify the magnetic levitation system. Specifically, these numerical models are divided into single-point levitation, multi-point levitation, electromagnet-guideway coupling system, and vehicle–guideway coupling system models.

▪

Single-point levitation system modeling

The single-point levitation module is the simplest levitation module. The four levitation modules of a bogie can be decoupled by the anti-rolling beams [33]. Using the mechanical decoupling strategy, each electromagnet can be controlled independently. Thus, the levitation performance of maglev levitation systems relies on the control performance of a single electromagnet. In addition, the mass and stiffness of the guideways on the current maglev line are designed to be very large. Hence, the F-type rail on the guideway is generally regarded as a rigid beam. The levitation control problem for a maglev levitation system can be simplified as a single electromagnet levitation control system consisting of a single electromagnet, rigid F-type rail, and levitation controller. Figure 4 shows the configuration of the single electromagnet levitation control system, in which the magnetic force is adjusted by changing the coil current.

In the single-point levitation model, it is assumed that (a) the magnetic field distribution in the air gap is uniform, and (b) both the iron core and the F-type rail act as ideal magnetic conductors. Based on these assumptions, a fundamental single electromagnet levitation model can be derived using Newton’s law and Kirchhoff’s law [34,35,36,37,38].

▪

Multi-point levitation system modeling

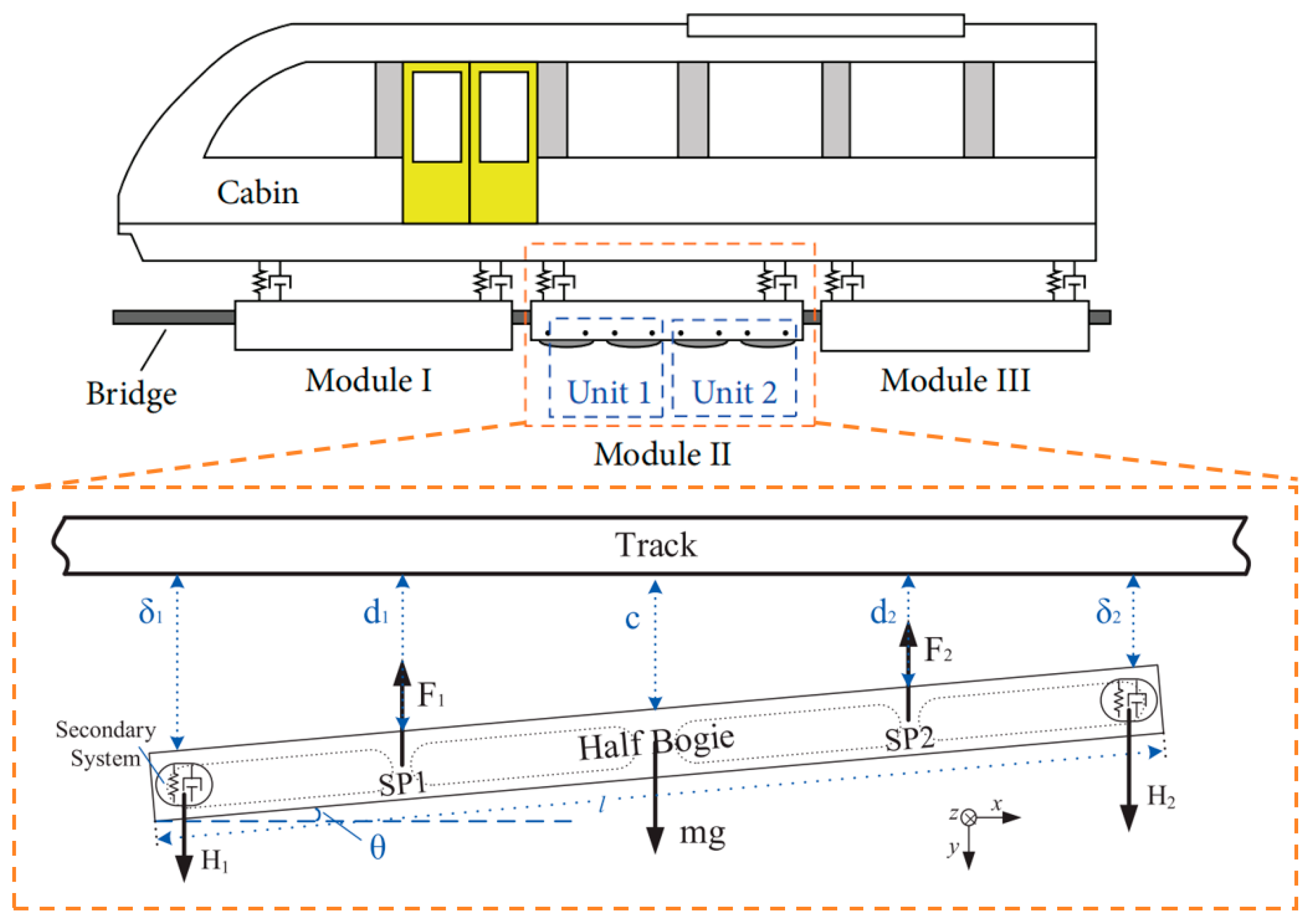
Although we attempted to decouple the levitation system in the structure by using mechanical decoupling, it was found in a series of experiments that the coupling effect between the two levitation points in a module is too strong to be ignored [39]. Hence, a multi-point levitation model must be considered when designing a levitation controller [39,40,41,42,43,44]. The multi-point levitation control system generally consists of two electromagnet levitation points, an F-type rail, and a levitation controller. A schematic of a half bogie for the two-point levitation model is shown in Figure 5. To simplify the modeling procedure, it is normally assumed that (a) the leakage flux can be neglected, (b) the magnetic saturation is ignored, (c) magneto-resistance in the core and track is ignored, (d) the rolling and yawing motion between the electromagnets and the track is negligible, (e) the elastic vibration or dynamic deformation of the track is negligible, (f) the half bogie structure is simplified as a uniform mass rod, where the gravity center and geometric center coincide, and (g) the electromagnetic force at each levitation point is equivalent to the concentrating force [40].

▪

Electromagnet-guideway coupling system modeling

In the aforementioned single-point levitation system and multi-point levitation systems, the F-type rail is regarded as a rigid beam. However, a small deformation of the guideway cannot be eliminated for precise controller design. Thus, the electromagnet-guideway coupling model is established [45,46,47,48,49], where the guideway is simplified as a Bernoulli–Euler beam. This simplification is justified because the length of the guideway is significantly larger than its other dimensions. The nonlinear behavior of the guideway is disregarded due to the small amplitude of vibration in comparison to the span of the guideway. The maglev electromagnet-guideway coupling system model is illustrated in Figure 6.

In addition, irregularity has been considered when establishing the maglev electromagnet-guideway coupling model [51].

▪

Vehicle–guideway coupling system modeling

In order to investigate the accurate dynamic response, it is essential to construct a vehicle–guideway coupling model that incorporates the guideway, actively controlled electromagnets, air springs, and vehicle cabins [52]. When establishing the vehicle model, several common assumptions are typically considered: (a) the vehicle cabin and levitation bogie are simplified as a rigid cubic body with five degrees of freedom, encompassing vertical, lateral, yaw, pitch, and rotation movements; (b) the air spring is treated as a combination of a linear spring and a linear damper; and (c) the mass densities of the vehicle cabin and levitation bogie are assumed to be uniform.

3.2.2. Data-Driven-Based Modeling

Due to aging, weather conditions, and failure of system components during operation, modeling based on dynamic equations sometimes cannot represent the real maglev levitation system well, which may lead to failure in maglev levitation control. Data-driven modeling is concerned with the meaning of every term, such as the mass of the vehicle and the stiffness of the beam; however, it can, although it seldom does, require a sufficiently accurate black-box based on historical data [53].

▪

Interactive learning method

Wen et al. [54] used a data-driven interactive inversion learning (IIL) control method to approximate the nonlinear maglev levitation system using the history data of the levitation system.

▪

Takagi–Sugeno fuzzy model

He et al. [19], Chen et al. [20], and Su et al. [34] used a mathematical tool named Takagi–Sugeno (T–S) fuzzy model [55] to build fuzzy models of the nonlinear system. Then, controllers were designed based on these fuzzy models.

▪

Neural network-based model

Machine learning (ML) and deep learning (DL) have already been used for data-driven modeling in various fields, such as robotics [56] and civil structures [57]. For the maglev system, Zhao et al. [58] directly trained a DRL controller using the dataset collected from the medium–low-speed maglev trains in Changsha, China. Sun et al. [26] trained a deep belief network (DBN) controller to combine with an output constraint controller to handle the unmeasurable air gap velocity and disturbance. The projection recurrent neural network (PRNN) [59] and radial basis function (RBF) [60] have also been used.

The two types of modeling methods can be combined. Chen et al. [40] designed a feedback controller to stabilize the nominal dynamic equation-based system model and proposed a data-driven new extended state observer (ESO) to estimate the unknown system states. A model reference method was adopted to address uncertainties in control systems and is normally combined with adaptive control [61,62].

3.2.3. Summary of Models

The maglev levitation system models used for controller design can thus be categorized in two ways, as model fidelity and model type. Model fidelity involves the specific problems considered during modeling, such as coupling of two levitation points, coupling of electromagnet and guideway, etc. Model type can be generally classified into dynamic equations-based and data-driven-based models. Specifically, data-driven-based models can be divided based on the method to represent the system, such as interactive model, neural network, and T–S fuzzy model.

4. Maglev System Control Methods

With the availability of various control methods, they have been applied to control the electromagnetic levitation system in the maglev train (Figure 7). The control methods developed in recent years will be discussed in this section.

4.1. Linear Control Methods on Maglev Levitation Systems

The conventional levitation controller for maglev trains uses linear control methods based on a linearized maglev train system [6,7]. These methods are generally based on the single-point levitation model and assume that the levitation electromagnet and guideway are in a stable position [6]. Based on the linearized system model, this section introduces typical control methods, such as the proportional–integral–differential (PID) control [6,7,63,64], linear quadratic regulator control (LQR) [8,9,10], and state feedback control [2,37,38].

However, when the air gap is far from the equilibrium point, the stability of the control system based on these linear control methods significantly decreases. To solve this problem, a feedback linearization method, which is a first-order derivative transformation process for a nonlinear system at the desired inputs, was proposed [65]. Section 4.1.6 introduces the feedback linearization method and its state-feedback controller in detail.

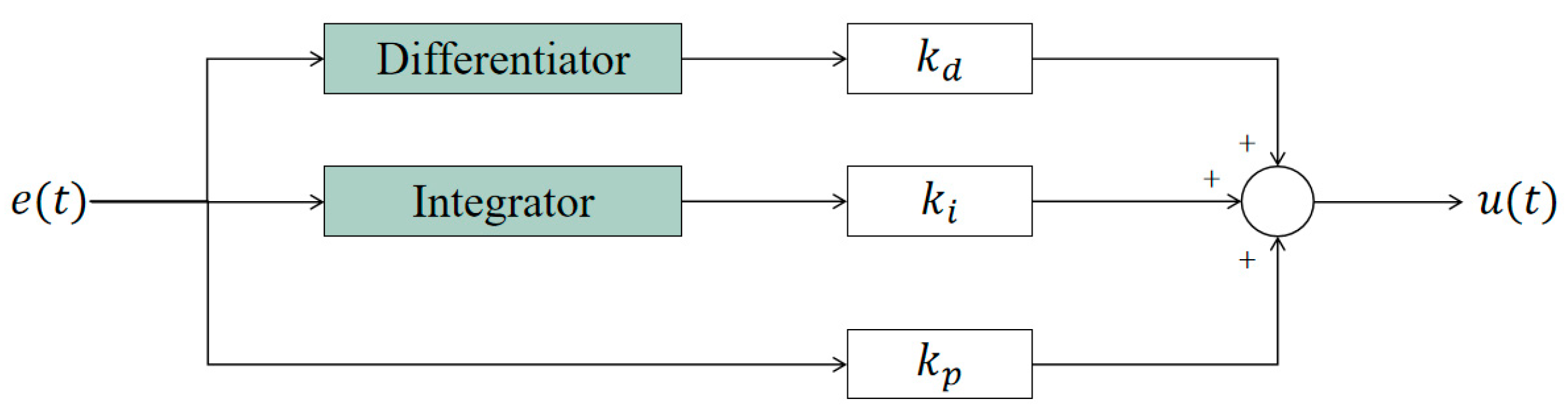
4.1.1. PID Control Algorithms

PID control is a widely used control method in various industrial applications (Figure 8). The typical transfer function of a PID controller is commonly expressed as follows

$$G_{PID}\left(s\right)=K_P+K_I\frac{1}{s}+K_{D}s$$

(1)

where $K_P$, $K_I$, and $K_D$ are the proportional, integral, and differential coefficients, respectively, and $s$ is a complex number after Laplace transform. The coefficient values significantly affect the control performance [41]. Hence, many methods, such as the Ziegler–Nichols step response method, the Ziegler–Nichols frequency response method, the internal model control (IMC) method, and the Cohen–Coon method, and new tuning approaches, such as the time domain optimization method, frequency domain shaping, and optimal control method, have been adopted to obtain PID parameters [28].

Due to its simplicity and effectiveness, PID control can be applied to various models, and it has been widely used in maglev levitation control [6,7]. To improve the control performance of PID, innovations and improvements have been made by combining other algorithms, such as internal model control (IMC) [63,64] and fuzzy control [6,66], to simplify the parameter tuning, shorten the stable time, or suppress the overshoot. Based on a single levitation point system, Duka et al. [63] adopted an IMC-based PID controller to achieve stable levitation of a ferromagnetic object at predetermined distances. The controller used the magnetic field generated by a coil to control the levitation process. The performance of the designed controller was verified by introducing a step change in the magnetic levitation system in the simulation. The IMC control strategy operates on the principle that when a model of the controlled system is available, it should be explicitly utilized in the design of the controller. The IMC specifications simplify the tuning process of a PID controller by modifying a single parameter known as the closed-loop time constant instead of adjusting three individual coefficients in the PID controller [64]. Yang et al. [6] designed a composite fuzzy–PID controller consisting of PID and fuzzy controllers for maglev levitation system control. The efficiency of the proposed fuzzy–PID controller was verified by comparing it with the classical PID controller and fuzzy controller in both overshooting and stable times. Ma et al. combined fuzzy control and an immune algorithm to adjust the PID coefficients [66]. Based on the principle of immune feedback, as depicted in Figure 9, B cells are stimulated by Th cells and inhibited by Ts cells, which results in a reverse response due to antigen invasion [67]. After a period of time, the system tends to become balanced. The proposed controller is better than the fuzzy–PID controller in tracking various signals with external interference in the maglev transportation system.

Considering the existing coupling in the levitation control system, He et al. [39] utilized a modified adjoint transfer matrix as a decoupler to partition the levitation control system into two separate SISO control systems. They then designed a compensated controller to meet the required loop performance and robustness criteria for the levitation control system. The controller was then transformed into a PID-type controller through model reduction. This transformation was carried out to prevent the resultant controller from becoming excessively high-order. By employing this approach, the researchers aimed to achieve effective control of the levitation system while maintaining a manageable and practical controller structure. To validate the efficacy of the proposed controller, simulations and experiments were performed on a full-scale single bogie of the CMS-04 maglev train.

PID also works well with an uncertain maglev system model. Xu et al. [68] designed a controller mechanism utilizing PID as a nominal controller. A reduced-order residual generator was then adopted to achieve real-time levitation performance optimization.

4.1.2. Linear Quadratic Regulator Algorithms

Although PID control shows efficiency and simplicity in maglev levitation control, its parameter selection remains a significant challenge. The problem caused by parameter setting can be solved using linear quadratic regulator (LQR). Assuming that all state variables are accessible for feedback, the LQR design process begins by selecting a specified set of states that are to be controlled. These chosen states serve as the basis for developing the control strategy using the LQR approach. By focusing on these specific states, the LQR design method aims to optimize the control system’s performance and achieve desired control objectives. A system model is represented in the state-space form as $\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)$, where A and B are the state matrix and input matrix, respectively. The Riccati equation is given as

$$A^{T}P+PA-PB{R}^{-1}{B}^{T}P+Q=0$$

(2)

where $Q$ and $R$ are the weighting matrices of the state variables, and $P$ can be solved using the Riccati equation defined. The LQR feedback can be obtained as $K=R^{-1}{B}^{T}P$.

Unni et al. [8] designed an LQR controller for a maglev system and compared the results of the LQR controller with a classical PID controller and a fuzzy logic controller. It was shown that the LQR controller is more efficient than the PID controller in settling time. Long et al. [9] applied the LQR controller to a newly designed structure of levitation module. In this particular design, each controller was responsible for controlling a specific electromagnet within the system. During the operation, the active fault-tolerant control problem of the newly designed levitation module structure was studied by cutting the control channels. To reduce disturbances during operation and improve the robustness of the controller against load variation, Yang et al. [10] proposed a new control method based on the LQR. The newly designed controller extended the applicability of the disturbance observer-based control (DOBC) to the “mismatching” disturbance condition. Xu et al. [69] introduced a functionalized control structure by attaching an incremental controller gain system, with an LQR controller and Q-learning involved.

4.1.3. H₂ and H_∞ Control

$H_2$ and $H_{\mathrm{\infty }}$ norms are commonly used performance measures in optimal control theory. These norms are defined in the frequency domain for a stable transfer matrix $G\left(s\right)$ as [70]

$${‖G‖}_2={\left(\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left[G\left(j\omega \right)\ast G\left(j\omega \right)\right]d\omega \right)}^{1/2}$$

(3)

$${‖G‖}_{\mathrm{\infty }}={\mathrm{s}\mathrm{u}\mathrm{p}}_{\omega }{\sigma }_{max}\left[G\left(j\omega \right)\right]({\sigma }_{max}=\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m}\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e})$$

(4)

where $j$ denotes a complex number and $\omega$ stands for the frequency. The ${‖G‖}_{\mathrm{\infty }}$ norm is particularly relevant when the exogenous signals are assumed to be either fixed or have a fixed power spectrum. On the other hand, ${‖G‖}_2$ is more suitable when considering balls of exogenous signals. Bittar and Sales [35] adopted the $H_2$ and $H_{\mathrm{\infty }}$ method for maglev system control. The method worked by finding a stabilizing controller $K\left(s\right)$ for the closed-loop transfer function matrix. The transfer function was firstly minimized using an $H_2$ controller. Then, an $H_{\mathrm{\infty }}$ controller was utilized to make the transfer function smaller than a given parameter.

Li and Shen [71] adopted the $H_{\mathrm{\infty }}$ controller to regulate the linearized track–vehicle coupling system. When designing the controller, they took into account the vibration requirement of the magnet vehicle, ensuring that it met the specified vibration criteria. The focus was on achieving robust control performance even in the presence of track irregularities.

4.1.4. Fractional Order Control

Fractional calculus has emerged as a valuable tool for simulating and controlling a wide range of physical systems. On the basis of the fractional order theory, researchers have extensively explored the design and application of controllers. In general, fractional order control is combined with other traditional control methods, such as PD control [36], PID control, and sliding mode control [72], to improve control performance. Compared with the transfer function of the conventional PID control in (1), the fractional order PID (FOPID) control adds two additional fractional order parameters: fractional integral value $\lambda$ and fractional derivative value $\mu$ as

$$G_{FOPID}\left(s\right)=K_P+K_I\frac{1}{s^{\lambda }}+K_D{s}^{\mu }$$

(5)

For fractional order sliding mode control (FOSMC), the fractional calculus operator $D_t^{\alpha }$ is employed. The sliding surface $S_f\left(t\right)$ can be represented as

$$S_f\left(t\right)=c_1{D}_t^{\alpha }e\left(t\right)+c_{2}e\left(t\right)$$

(6)

where $c_1$ and $c_2$ are the weighting parameters determining the slope of the sliding manifold, respectively, and $e\left(t\right)$ denotes the tracking error of the system. As for the fractional order fuzzy–PID (FOFPID) control, the differentiation and integration coefficients in the conventional fuzzy–PID controller [6] are replaced by fractional integral value $\lambda$ and derivative value $\mu$.

Yu et al. [36] adopted the fractional order PD (FOPD) control in the maglev levitation system and compared the proposed controller with a classical controller using LQR. The FOPD had better dynamic performance and robustness, particularly for uncertain loads and operating gaps in the simulation results. Ataşlar-Ayyıldız et al. [72] used FOPID, FOSMC, and FOFPID in a maglev system. They further proposed a tuning method for these controllers using a hybrid approach based on the gray wolf optimization (GWO) and particle swarm optimization (PSO) algorithms, known as the GWO–PSO algorithm. The simulation results indicate that the proposed GWO–PSO-based FOFPID controller exhibits several advantages in terms of the stabilization, trajectory tracking, and control of the maglev system. These advantages include robustness, improved performance, and disturbance rejection capabilities in a closed-loop control system.

4.1.5. Basic State Feedback Control

The state feedback controller is designed using state-space models and has been adopted as a part of the feedback linearization controller design [65]. In a state feedback control system, the control signals are determined by multiplying the state variables by a feedback controller gain matrix [73]. The system dynamics are assumed to be described by the following state-space equation

$$\left\{\begin{array}{l}\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)\\ y\left(t\right)=Cx\left(t\right)\end{array}\right.$$

(7)

where $A$, $B$, and $C$ are state matrix, input matrix, and output matrix, respectively. Additionally, $x\left(t\right)$ and $y\left(t\right)$ denote the state and output of the system, respectively. Assuming there are n state variables and a single input variable, the control signal $u\left(t\right)$ can then be calculated as a linear combination of the n state variables

$$u\left(t\right)=-\left(k_1{x}_1\right(t)+k_2{x}_2(t)+\cdots +k_n{x}_n(t\left)\right)=-\mathit{K}x\left(t\right)$$

(8)

where $\mathit{K}$ denotes the control gain.

Based on the state feedback control, Sun et al. [7] designed a state feedback controller considering the guideway flexibility. The state feedback vector of the controller comprises specific variables related to the guideway and the electromagnet in the control system. These variables include modal coordinate of the guideway, the differentiation of the guideway, and the vertical displacement, velocity, and acceleration of the electromagnet. The control system incorporates the vibration of the guideway, and the simulation results validate that the designed controller achieves two key outcomes. Firstly, it ensures a consistent and stable suspension of the electromagnet. Secondly, it successfully eliminates the vibrations present in the guideway. Xia et al. [37] employed the velocity fusion estimation method (VFE) in conjunction with state feedback control. The proposed controller can precisely control the air gap and effectively counteract disturbances.

A state feedback controller can also be incorporated with a state observer or a model predictive method to improve the control performance. He et al. [38] proposed a novel approach involving the design of a state observer integrated with a state feedback controller. This approach aims to mitigate the adverse effects of time delays resulting from various factors, such as sending processing, controller area network (CAN) bus access waiting, and receiving processing. Zhang et al. [74] implemented a model predictive control (MPC) strategy for a maglev system, incorporating a two-level state feedback approach. This strategy leverages measurable state variables, including the air gap, electromagnet acceleration, and control current. In this approach, the first-level nonlinear state feedback is utilized to linearize the inherently unstable nonlinear maglev levitation system. Furthermore, the second-level linear state feedback is employed to enhance system stability and improve dynamic performance. The simulation results validate the effectiveness of the proposed strategy. It demonstrates that the MPC approach, incorporating the two-level state feedback, ensures precise control of the air gap. Additionally, the strategy exhibits favorable disturbance resistance, indicating its ability to mitigate the impact of external disturbances on the system.

4.1.6. Feedback Linearization Control Algorithms

As the state-space function of the system can be written in linear form in feedback linearization control, it is classified as a linear control method in this study. For a nonlinear system, the form of feedback linearization control can be written as

$$\dot{\mathit{x}}=f(\mathit{x},\mathit{u})$$

(9)

where $\mathit{x}$ is the state, $\mathit{u}$ is the input, and $f(·)$ is a continuous differentiable nonlinear function. The control function is $\mathit{u}=-\mathit{K}\mathit{x}$ (state feedback control), and $\mathit{K}$ is the controller gain. Applying the Taylor series to (9), we obtain

$$\dot{\mathit{x}}=\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{x}}(\mathit{x}-{\mathit{x}}_d)+\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{u}}(\mathit{u}-{\mathit{u}}_d)+r$$

(10)

where ${\mathit{x}}_{\mathit{d}}$ is the desired state and ${\mathit{u}}_{\mathit{d}}$ is the desired input; ${\mathit{x}}_{\mathit{d}}$ and ${\mathit{u}}_{\mathit{d}}$ are considered to be zero, and $r$ is a residue. Then, (10) can be rewritten as

$$\begin{gathered} \dot{\mathit{x}}=\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{x}}\mathit{x}+\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{u}}\mathit{u}+r+\left({\left.\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{x}}\right|}_{\mathit{x}=0,\mathit{u}=0}\right)\mathit{x}+\left({\left.\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{u}}\right|}_{\mathit{x}=0,\mathit{u}=0}\right)\mathit{u} \\ -\left({\left.\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{x}}\right|}_{\mathit{x}=0,\mathit{u}=0}\right)\mathit{x}-\left({\left.\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{u}}\right|}_{\mathit{x}=0,\mathit{u}=0}\right)\mathit{u} \end{gathered}$$

(11)

Equation (11) can be rewritten as

$$\dot{\mathit{x}}=A\mathit{x}+B\mathit{u}+\tilde{A}\mathit{x}+\tilde{B}\mathit{u}+r=A\mathit{x}+B\mathit{u}+\delta ,\delta =\tilde{A}\mathit{x}+\tilde{B}\mathit{u}+r$$

(12)

where

$$\begin{gathered} \mathrm{A}=\left({\left.\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{x}}\right|}_{\mathit{x}=0,\mathit{u}=0}\right),B=\left({\left.\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{u}}\right|}_{\mathit{x}=0,\mathit{u}=0}\right) \\ \tilde{A}=\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{x}}-{\left.\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{x}}\right|}_{\mathit{x}=0,\mathit{u}=0},\tilde{B}=\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{u}}-{\left.\frac{\partial f(\mathit{x},\mathit{u})}{\partial \mathit{u}}\right|}_{\mathit{x}=0,\mathit{u}=0} \end{gathered}$$

Utilizing $A$ and $B$, the controllability of the system can be estimated by comparing the rank of the controllability matrix ($\mathbb{C}=\left[\begin{array}{cc}\begin{array}{cc}B& AB\end{array}& \begin{array}{ccc}{A}^{2}B& \cdots & A^{n-1}B\end{array}\end{array}\right]$) with $n$. Then, the controller gains can be obtained by designing the characteristic polynomial functions. Replacing the control functions into (12), we can obtain

$$\dot{\mathit{x}}=A\mathit{x}+B(-\mathit{K}\mathit{x})+\delta =(A-B\mathit{K})\mathit{x}+\delta =A_C\mathit{x}+\delta$$

(13)

The eigenvalue of $A_C$ is ${\lambda }_i$. Then the characteristic polynomial of the selected eigenvalues is as

$$P_{\lambda }=(s-{\lambda }_1)\cdots (s-{\lambda }_n)=s^n+b_{n-1}{s}^{n-1}+\cdots +b_{1}s+b_0$$

(14)

where $b_{n-1},\dots ,b_0$ denote the constant terms. The characteristic polynomial of $A_C$ is

$$P_{A_C}=\mathrm{d}\mathrm{e}\mathrm{t}(sI-A_C)=s^n+a_{n-1}\left(\mathit{K}\right)s^{n-1}+\cdots +a_1\left(\mathit{K}\right)s+a_0$$

(15)

where $a_{n-1}\left(\mathit{K}\right),\dots ,a_0$ denote the constant terms. Let (14) be equal to (15), and the controller gains $\mathit{K}$ can be calculated.

Based on the feedback linearization method, Leng et al. [42] developed a decoupling controller to address the coupling effects between two points of the module levitation system. The primary objective of this controller design is to minimize the gap fluctuation that occurs when the module levitation system traverses track steps. The simulation results demonstrate the superior effectiveness of the proposed control algorithm compared with PID control. Meanwhile, the experimental results show that the proposed control approach substantially reduced the levitation gap error of a single point and reached a maximum improvement of 49.6% compared with PID control. In addition, the system significantly enhanced the transition time and fluctuation.

Zhang et al. [75] proposed an improved multi-equilibrium point feedback linearization method to address the variation of the inductance value in the levitation system. This method involves substituting the rated operating point air gap with a measurable air gap and disregarding the impact of nonlinear factors, such as leakage inductance. Zhang et al. [46] adopted the feedback linearization method in a vehicle–bridge interaction system to establish a linearized levitation system model and designed a levitation control method. To validate the performance of the proposed method, experiments were conducted on a levitation platform characterized by low track stiffness. The experimental results substantiate the effectiveness of the proposed method. By implementing the proposed method, unwanted vibrations due to the interaction between the vehicle and the guideway were effectively minimized or eliminated. Furthermore, the method demonstrated satisfactory levitation control even in scenarios characterized by extremely low track stiffness. Li et al. [76] designed a controller based on feedback linearization and extended state observer (ESO) techniques to suppress inner coupling effects within the system while mitigating the impact of uncertainties. Han et al. [77] proposed a disturbance-observer-based tube model predictive levitation control (DO-TMPLC) scheme based on a linearized feedback model with bounded disturbance.

4.2. Nonlinear Control Methods on Maglev Levitation Systems

The maglev levitation system is a strong nonlinear system, and the aforementioned linear control methods based on the linearized maglev levitation model show poor robustness and low practicality. In recent years, many researchers have applied nonlinear control methods, including adaptive control, backstepping control, and sliding mode control (SMC), to solve maglev levitation control problems.

4.2.1. Nonlinear PID Control Algorithms

The PID control method is a model-free method, and the control performance of the PID mainly relies on the state of the system and three coefficients. PID control can also be used in nonlinear models. By addressing the issues of stability loss and nonlinear coupled vibration in maglev systems, Li et al. [78] utilized the tuned mass damper (TMD) control method to prevent the Hopf bifurcation in vehicle–bridge vibration. Subsequently, they employed a conventional PID controller to control the maglev levitation system. Xu et al. [43] developed a PID controller for the maglev train. The developed controller takes the coupling effect between the electromagnet coils, as well as its impact on the levitation performance into account. The controller design was based on a characteristic model specific to the maglev train. However, it was found that although conventional PID control is easy to tune, the stiffness and performance of the control conflict when applied to the maglev levitation system. To improve the PID control performance in a nonlinear maglev system, Liu et al. [79] adopted the exponential function of PID. The exponential function of PID can increase the stiffness of the system when the system is apart from the equilibrium point. The control signal of the nonlinear PID is adopted as

$$u=K_P{x}_1^a+K_D{x}_2^b$$

(16)

where $x_1=x-x_{eq}$, $x_2={\dot{x}}_1$ and $u=i-i_{eq}$. Here, $x$ denotes the air gap, $x_{eq}$ and $i_{eq}$ are the air gap and current at the equilibrium point, respectively, and $K_P$ and $K_D$ are the proportional and differential coefficients obtained from the linear PID controller, respectively. Parameters $a$ and $b$ were obtained from experiments.

Wai et al. [41] designed a real-time particle-swarm-optimization (PSO)-based PID control scheme for the nonlinear maglev system. The coefficients of the PID are obtained using the PSO method. The fitness functions for the proposed control scheme are defined as

$$\left\{\begin{array}{l}{f}_p^j=\frac{1}{1+e_j^2}\\ f_i^j=\frac{1}{1+{\int }_0^{\mathrm{\infty }}{e}_j^{2}dt}\\ f_d^j=\frac{1}{1+{\dot{e}}_j^2}\end{array}\right.$$

(17)

where $f_p^j$, $f_i^j$, and $f_d^j$ denote the $j$th element ($j=1,2,3,4,5)$ in the fitness function vectors and $e_j$ denotes j th element in the error state vector. These five elements represent the central levitation height, rolling angle, pitching angle, bending angle, and platform position, respectively. The PSO process utilizes the fitness functions to determine the coefficients of the PID corresponding to each state. The proposed controller is then compared with both the sliding mode control (SMC) and PSO–PID controllers for performance evaluation [80]. Both the simulation and experimental results demonstrate superior performance of the proposed controller.

Owing to the flexibility of the track, self-excited vibrations may occur during maglev train operation. Zhou et al. [47] applied the harmonic balance method to analyze and determine the amplitude of the self-excited vibration. Based on this analysis, they developed a controller that regulates the vibration amplitude at a specific level. Liu et al. [81] applied a nonlinear PD controller to the single-point levitation system. Uncertainties like periodic unsteady aerodynamic disturbance and varying carriage mass were taken into consideration. The stiffness bifurcation of the system was also analyzed.

4.2.2. State Feedback Control Algorithms

State feedback control can be directly adopted in nonlinear systems. Xu and Zhou et al. [82] adopted the state feedback control method to replace the nonlinear part in the nonlinear maglev system. The electromagnetic force was decomposed into four parts for controller design. The proposed control method was proved to have better performance than the PID controller through the experiment.

In the experimental setup of the maglev system, a time delay is inherent in both the control and execution processes. Consequently, it becomes essential to examine the dynamic behavior of maglev systems that incorporate time delays. Zhang and Zhang [83] investigated the time-delay problem by taking the time delay as a bifurcation parameter. To solve the time-delay problems, Zhang et al. [84] applied state feedback control to the port voltage of the electromagnet. They considered the presence of time delays in all the feedback control variables within their approach. Furthermore, a linear stability analysis was conducted to establish the limitations on the feedback gains and time delay. Xu et al. [85] proposed a double time-delay feedback controller for a maglev train operating on a flexible guideway. Their controller takes into account the time-delayed position feedback signal, as well as the velocity feedback signal. The proposed controller was validated through field experiments.

Disturbance is also a key factor affecting maglev system control. Li et al. [52] firstly adopted a feedback linearization method with a disturbance-observer-incorporated controller for a maglev levitation system. However, it was found that the error generated by this approach was deemed unacceptable, especially in the presence of high-frequency disturbances. To address this limitation, they subsequently devised a novel nonlinear acceleration feedback controller. The devised controller was specifically designed to enhance the system’s ability to attenuate fast-varying disturbances. By implementing this new controller, Li et al. achieved superior performance compared to the traditional feedback linearization controller. Furthermore, the proposed controller demonstrated robustness in the presence of disturbances. Qiang et al. [33] developed a nonlinear state feedback controller for the maglev system. The developed controller was able to accurately represent the electromagnet force. This controller was designed to estimate and compensate for both nonlinear and periodic bounded disturbances that occur in the system. To further improve disturbance compensation, they extended the controller by integrating an online frequency estimator. This online frequency estimator allowed the controller to estimate the frequency of exogenous nonlinear periodic disturbances. Chen et al. [40] designed a model-guided data-driven controller using both the measured data and knowledge of the model. The control strategy was composed of two components to effectively handle system uncertainties and disturbances while ensuring system stability. The first controller is a standard feedback controller aimed at stabilizing the system using the information provided by the system model. The second controller attempts to cancel the effects of uncertainties and disturbances on the system to maintain stability. This controller estimates the uncertainties and disturbances online in real-time. Sun et al. [86] adopted a state feedback controller for a vehicle–guideway coupling maglev system. The primary objective was to investigate the influence of guideway parameters on the vibration and coupling behavior between the vehicle and the guideway. To achieve this, they conducted simulations and experiments to analyze the impact of various guideway parameters.

Instead of solving the state feedback gains through simulations or Riccati equations, parameter optimization methods have been studied. Wang et al. [87] developed a full-state feedback controller based on the air gap and the current signals. The PSO algorithm was utilized to optimize the control gains in the state feedback controller. The effectiveness of the proposed method was verified through simulations and experiments. The results indicate that the controller performs well even under conditions of violent external disturbances.

4.2.3. Adaptive Control Algorithms

Adaptive control is a promising technology for enhancing the performance of control systems when faced with uncertainties stemming from various factors, such as degradation and modeling uncertainty [14,88]. Adaptive control can be categorized into two main types: direct and indirect. The direct adaptive controller can be mathematically represented as follows

$$u=k_x\left(t\right)x+k_r\left(t\right)r$$

(18)

where $k_x\left(t\right)$ and $k_r\left(t\right)$ are the control gains to be adjusted, $x$ denotes the state, and $r$ represents reference state. In direct adaptive control, the control gains are adjusted using an adaptive law. This adaptive law enables the direct adaptation of the feedback control mechanism within the control system. The primary objective of this adaptation is to counteract and cancel out any undesired system uncertainty. By directly adjusting the feedback control mechanism, direct adaptive control aims to restore the performance of the control system even in the presence of significant uncertainty. This allows the control system to effectively regain its desired performance and maintain stability and accuracy under challenging operating conditions. In contrast, an indirect adaptive controller achieves the same objective by adjusting the control gains in an indirect manner, specifically through a parameter estimation process.

$$u=k_x\left(p\right(t\left)\right)x+k_r\left(p\right(t\left)\right)r$$

(19)

where $p\left(t\right)$ are system parameters that are estimated online to update the control gains.

Based on the advantages of adaptive control, Zhou et al. [51] designed an adaptive controller that could receive air gap signals from two sensors. The designed controller can be self-tuned to effectively eliminate the vibration of the rear levitation unit, specifically under the excitation of a single-frequency sinusoidal track profile. The adaptive controller first samples the air gap and vertical accelerations at the front terminal of the electromagnet obtained by the front sensors and estimates the track displacement based on the collected data. Following the estimation of the track information, a tuned finite impulse response (FIR) filter is used to compensate for the rear controller. The effect of the proposed controller was verified considering typical track irregularities, such as random track irregularity and sinusoidal track profile. The results demonstrate the effectiveness of the designed controller in significantly reducing the vibration of the rear levitation gap across various situations. Zhang and Li [15] focused on the real-time adaptive control of the maglev system, with a particular focus on situations where the load mass experienced significant changes. The relationship between the optimal control parameters of the controller and the steady-state current was deduced by observing the real-time steady-state levitation current as the load mass changed. Sun et al. [89] proposed an adaptive fuzzy cooperative control strategy for a multi-point levitation system. They focused on addressing challenges related to uncertainties, dead-zone, and saturation effects in the control system.

In addition, some researchers have adopted model-assisted and reference-adaptive control for maglev systems. Sinha and Pechev [61] developed a model reference adaptive controller for a maglev system, designing the controller using the stable maximum descent criterion, and its main objective was to reduce the air gap error between the reference model and the actual system. To validate the effectiveness of the proposed controller, Sinha and Pechev conducted experiments under various operating conditions, including the payload mass, disturbance force, and air gap set-point during the operation. Bidikli [90] developed a controller with a nonlinear velocity observer to enable control without directly measuring the system velocity. It can adaptively compensate for parametric uncertainties that may arise during the control process. Dalwadi et al. [62] designed a position-stabilizing control strategy for a maglev system operating under highly uncertain parametric conditions. The control strategy used a reference model governed by a reference stabilizer with a nonlinear adaptive control structure. Then, the control performance was verified by a simulation and compared with the conventional nonlinear control.

4.2.4. Robust Control Algorithms

In reality, it is common for mathematical models of systems to include uncertain components. The objective of the robust theory is to establish an efficient and high-performance design approach that uses uncertainty information. Various approaches have been proposed within the field of robust control to address the challenge of model uncertainty. These approaches include the small-gain approach, positive real Lyapunov method, robust regional pole placement, and gain scheduling [11].

Three major difficulties in maglev control systems must be considered, namely, (1) the state is a bounded state, (2) unilateral control input, and (3) the system fails to meet the matching condition. To solve these problems, Xu et al. [12,13] adopted robust control in a transformed system considering fast time-varying uncertainty. Liu et al. [91] proposed a robust immersion and invariance (I&I) adaptive synchronization controller based on a disturbance observer. This controller was specifically designed for an output-constrained uncertain maglev module that experiences mismatched disturbances. The effectiveness of the proposed synchronization controller was verified using numerical simulation results. Ren et al. [92] designed a robust adaptive control method by merging neural networks. The designed control can deal with magnetic saturation and eddy current effect of the maglev system with uncertainties. Specifically, a radial basis function (RBF) neural network is chosen to approximate the unknown function of the model. Then, a robust adaptive controller is established without requiring precise information.

4.2.5. Sliding Mode Control Algorithms

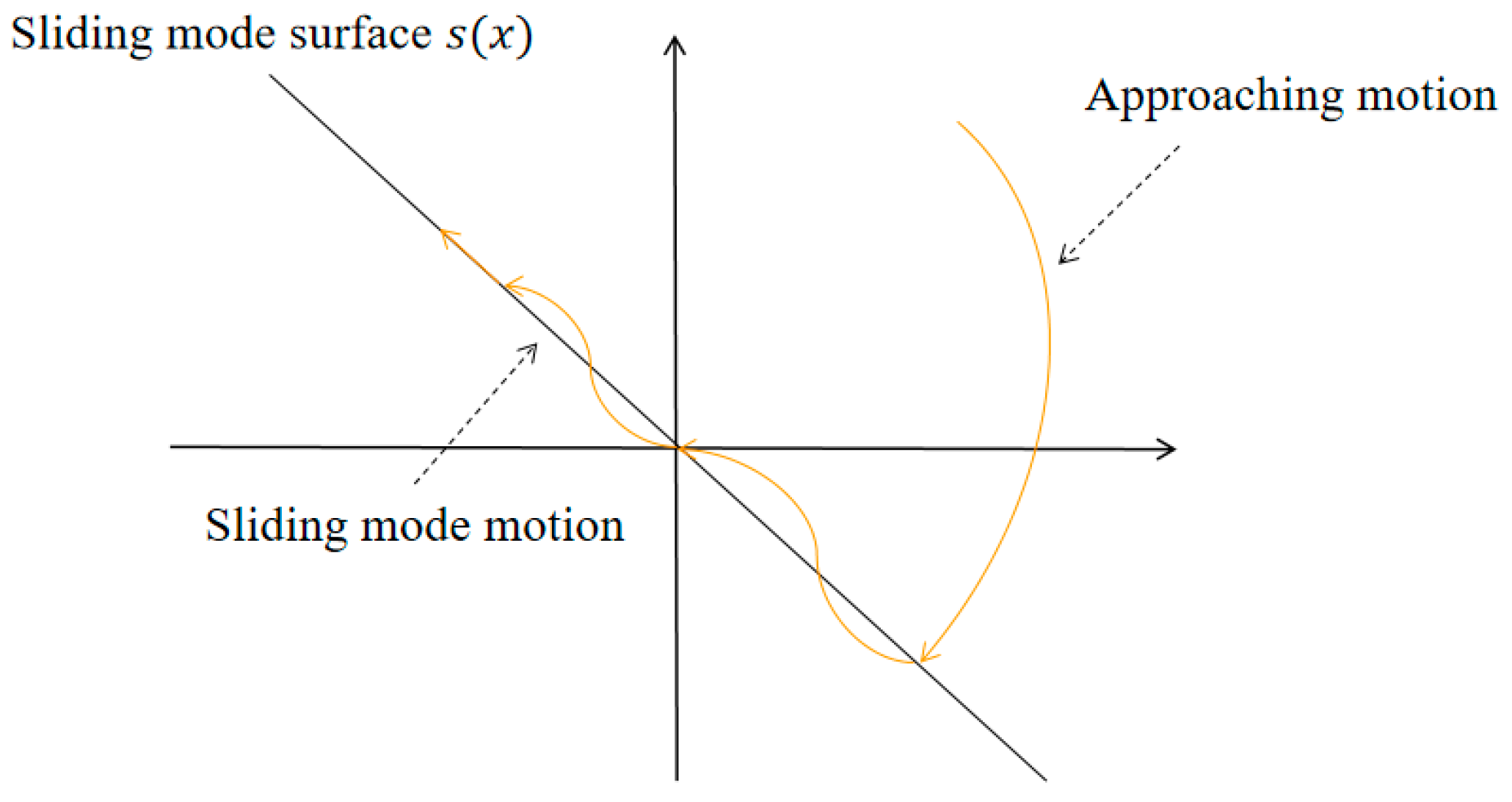
Sliding mode control (SMC) is a nonlinear control algorithm known for its simple physical implementation, rapid response, and robustness. This powerful control algorithm is commonly applied to handle the complexities associated with nonlinear systems. Consider a nonlinear system described as $\dot{x}=f(x,u,t)$, where $x$ represents the state vector and $u$ denotes the control input. The sliding mode surface is characterized by a specific equation, denoted as $s\left(x\right)$. In this context, the switching surface is defined as $s\left(x\right)=0$, which divides the state space into two distinct regions. These regions are determined by the sign of $s\left(x\right)>0$ and $s\left(x\right)<0$ corresponding to the two respective regions. A schematic diagram of the state motion process is depicted in Figure 10. As can be seen, the state motion process of the sliding mode control system can be divided into two distinct parts: (1) the state point undergoes a phase of approaching the sliding mode surface and (2) the state point transitions to a phase of moving along the sliding mode surface. The reaching law characterizes the process by which a system progresses from an initial state, which is often distant from the sliding mode surface, toward the sliding mode surface itself.

Kong et al. [16] constructed a computational model to capture the dynamic characteristics of an actively controlled magnetically suspended system that operated on a flexible guideway. Furthermore, they devised a Kalman-filter-based sliding mode controller specifically tailored for this computational model. The simulation results demonstrate the effectiveness of the proposed controller in mitigating the airgap fluctuation and vertical acceleration of the vehicle, and it outperformed the conventional Kalman-filter-based LQR regulator. To enhance the robustness of the controller, the state observer was integrated with the SMC technique. Zhu et al. [17] introduced an adaptive sliding mode control approach utilizing a linear extended state observer to improve the system’s response speed, robustness, and anti-interference capability, as well as to minimize the detrimental effects of external disturbances on the stability of the levitation process.

Modifications have been made to SMC for various purposes. To achieve global fast-tracking control of the maglev system during the startup and stable processes, Li et al. [18] built a second-order flux linkage model. They proposed a global fast-terminal integral sliding mode controller (GFTISMC) with a recursive structure to enhance the system’s overall fast response speed and minimize the steady-state error. The design of the GFTISMC has two parts: (1) the sliding surface design with a recursive structure was employed to enable the system to rapidly approach the desired sliding surface and (2) an integral term was incorporated to mitigate the steady-state error. Alain et al. [93] designed a control strategy utilizing a precise model of nonsingular robust sliding mode control. The primary objective of this strategy was to minimize the upper bound of both uncertainty and interference in the sliding mode controller. Zhang et al. [94] designed a modified sliding mode controller that effectively addressed the chattering phenomenon that arose from hardware limitations and time delays in the control units. This modified controller combines an exponential reaching law with continuous control laws to mitigate the adverse effects of chattering.

Sliding model control can also be combined with other control algorithms or optimization algorithms to improve control performance. Sun et al. [95] introduced a fuzzy sliding mode control law for the dynamic maglev nonlinear model. They devised a novel sliding surface that facilitated stable point convergence within a finite time and utilized the fuzzy inference method to decrease the crossing speed of system states across the sliding surface. Through simulations, they demonstrated that their proposed control method achieved global robustness against external disturbances and parameter perturbations while significantly reducing the chattering phenomenon. To reduce the chattering in the SMC while preserving the fast response speed and robustness of the fuzzy PID, a new hybrid control method based on the PSO sliding mode and fuzzy PID was proposed by Zhang et al. [96]. The proposed controller utilizes PSO to optimize the SMC. It employs the exponential approach law method to determine the optimal parameters for the sliding mode surface and coefficients for the exponential approach rate. The objective is to reduce the time required for the nonlinear system to approach the stable region, particularly when it is initially far from the stable point. During the system’s approach to the stable point, the proposed controller seamlessly transitions to fuzzy PID control, which effectively mitigates the chattering phenomenon associated with SMC. The proposed controller was verified through simulations and experiments, and the results demonstrate that it effectively weakened chattering and exhibited adaptability to external disturbances and state variable transitions. Teklu et al. [97] proposed a genetic-algorithm-tuned super-twisting SMC on a vehicle guideway coupling model with varying load and external random disturbances.

4.2.6. Backstepping Control

The backstepping control method is a recursive design procedure. It establishes a connection between the selection of a control Lyapunov function and the design of a feedback controller [98]. This method ensures the global asymptotic stability of strict feedback systems.

In maglev levitation control, Zhang et al. [44] presented a novel collaborative levitation controller based on the backstepping controller. The proposed controller focused on preventing physical contact to ensure the safety of the air gap. To better estimate the unknown parameters in the control system, Huang et al. [99] derived a multi-input–multi-output (MIMO) adaptive backstepping controller. The controller was specifically designed to address decoupling nonlinearities and eliminating uncertainties. The experimental results demonstrate that the designed controller outperformed adaptive control methods without backstepping, particularly in terms of its ability to effectively decouple nonlinearities in the maglev system. The proposed controller also provided high rigidity in the experiment.

The backstepping method can also be combined with SMC to enhance control performance, such as fast response and robustness. Adil et al. [100] introduced two innovative sliding mode controllers, namely, the supertwisting and integral backstepping sliding mode controllers (ST-SMC and IBS-SMC). The main objective of these controllers was to maintain the air gap at the desired value. At the same time, chattering phenomenon can also be reduced. Additionally, these controllers aimed to track the magnetic flux and momentum to their respective reference values. Yaseen et al. [101] proposed three nonlinear controllers for airgap tracking, adaptive terminal sliding mode control (AT-SMC), adaptive backstepping sliding mode control (ABS-SMC), and adaptive integral backstepping sliding mode control (AIBS-SMC), to track the airgap. Simulations and experiments were performed for comparison.

4.3. Artificial Intelligent Control Methods on Maglev Levitation Systems

Artificial intelligence control methods have been introduced in modern control engineering for its self-adaptation, self-learning, and self-optimization characteristics. For systems containing uncertain parameters, artificial intelligence control methods, like fuzzy control, neural network control, and DL control, have proved their superiority versus conventional linear and nonlinear control methods [102]. Specifically, artificial neural networks are highly interconnected networks that excel in representing complex nonlinear functions with exceptional accuracy through the process of training. The weighting parameters of a neural network can be adjusted to approximate any desired nonlinear function with the necessary accuracy. This capability allows neural networks to effectively represent complex nonlinear system models or unknown systems [103]. With the development of DL networks in recent decades, some DL methods, such as DBNs and convolutional neural networks (CNN), have also been used for controller design. Instead of using networks to represent the system structure, DRL methods can interact with the environment to obtain the optimal series of control signals.

4.3.1. Fuzzy Logic Control Algorithms

Fuzzy control is capable of dealing with high-order processes, systems with a long dead time, or systems with oscillatory modes [104]. Fuzzy logic control uses sentences in the form of rules to control the process. The input of the fuzzy controller is not limited and it can include expert knowledge [105]. 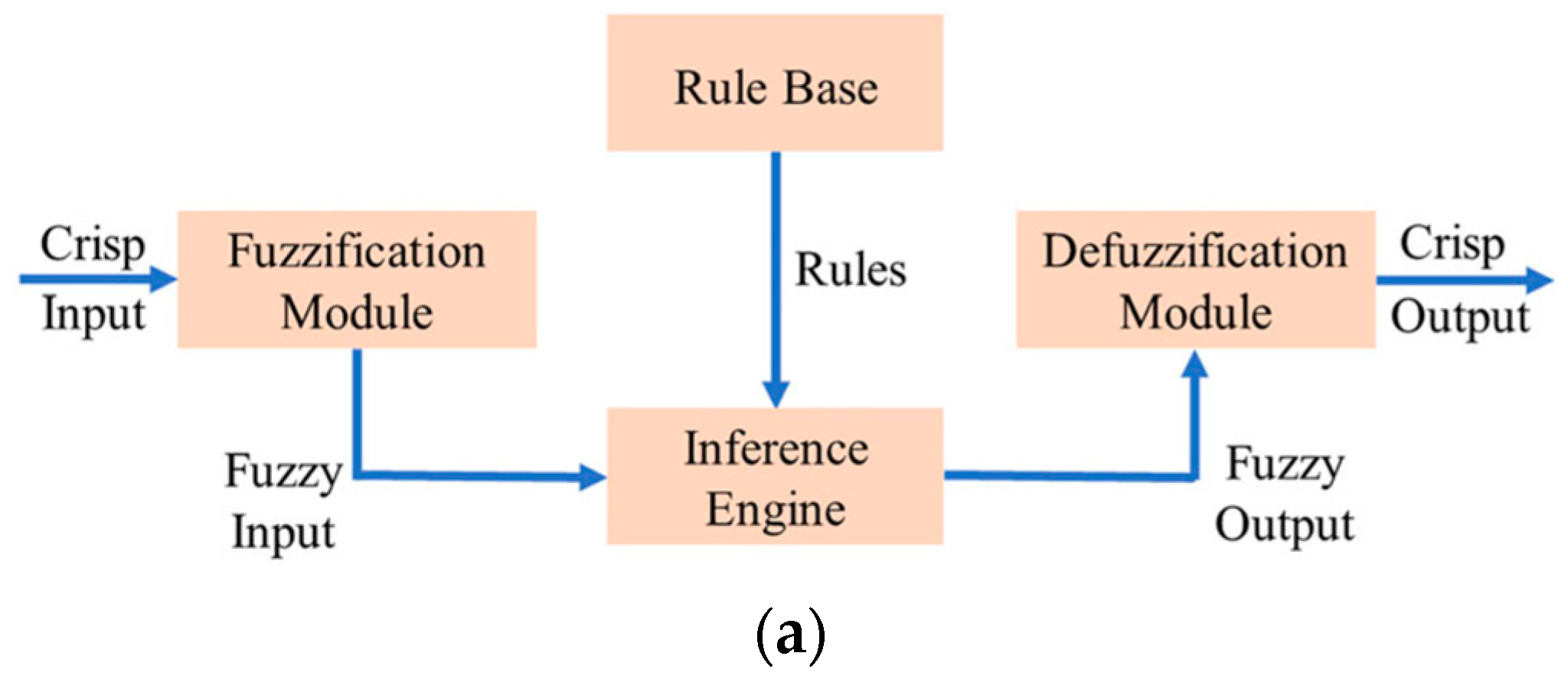Fuzzy logic control can be categorized into type-1 fuzzy logic control and advanced type-2 fuzzy logic control [106], as shown in Figure 11. It can be observed from Figure 11a that type-1 fuzzy logic control is composed of four primary components: fuzzifier, rules, inference engine, and defuzzifier. Compared with type-1 fuzzy logic control, type-2 fuzzy logic control adds a type reducer between the defuzzifier and the inference engine, as in Figure 11b.

Innovation and modifications have been made in fuzzy control to enhance the control ability of maglev levitation systems. In the composite PID–fuzzy controller proposed by Yang et al. [6], the inputs of the fuzzy controller are vehicle displacement and velocity, and the output is the desired actuator voltage. The control process can be divided into three stages: fuzzification, fuzzy inference, and defuzzification. Each stage plays a crucial role in transforming real-number input values into appropriate controller outputs. The first stage, fuzzification, involves converting crisp and real-number input values into fuzzy values. The second stage, fuzzy inference, utilizes the fuzzified input data and processes it using a fuzzy inference engine. The final stage, defuzzification, converts the outputs of the second stage into real numbers.

Due to the reliance on human operator experience and control engineer knowledge in fuzzy controller design, operators often find it challenging to linguistically describe the specific actions they take in particular situations. Takagi and Sugeno [55] developed a mathematical method to build a system fuzzy model, named the Takagi–Sugeno (T–S) fuzzy control method. The T–S fuzzy control method has already been adopted in maglev levitation control [19,20]. He et al. [19] proposed a T–S fuzzy parallel distributed compensation (PDC) state feedback controller. The proposed controller utilizes T–S fuzzy models to represent the discrete-time linear system and considered the model parameter uncertainties. The effectiveness of the proposed method was demonstrated through numerical simulations and physical experiments. The experiments were carried out on a full-scale single bogie of a CMS-04 maglev train developed by the National University of Defense Technology.

Considering the tracking performance of the system control parameters and the parameter optimization time when faced with external disturbances, a PSO-assisted fuzzy controller was proposed by Chen et al. [20]. In their work, the T–S fuzzy model was firstly utilized to decompose the non-linear model of the maglev system into multiple sub-models that exhibit linear characteristics. Subsequently, the PDC method was employed to design fuzzy control laws for each of these models. To enhance the control accuracy of the system, the PSO algorithm was utilized to optimize the fuzzy rules and associated domains. In the numerical simulation, the performance of the PSO–fuzzy controller was compared with that of the PID control and fuzzy control methods. The results highlighted several advantages of the PSO–fuzzy controller over the other two methods. Firstly, the PSO–fuzzy controller exhibited the smallest overshoot compared to the PID control and fuzzy control. Secondly, the PSO–fuzzy controller demonstrated the strongest robustness. Additionally, the PSO–fuzzy controller achieved the fastest system response without a steady-state error. The control capability of the PSO–fuzzy controller was also verified by a series of experiments on low- and medium-speed maglev trains with parameter perturbations and external disturbances. The experimental results validate the strong robustness of the PSO–fuzzy controller under an external disturbance. In addition, the method can effectively maintain the levitation performance and improve the equipment service life, as well.

Fuzzy control can also be adopted for nonlinear system control. Considering that the ${\mathcal{l}}_2-{\mathcal{l}}_{\mathrm{\infty }}$ control can better achieve the desired system performance and constrain the controlled output in presence of energy-bounded noise input, Su et al. [34] proposed a ${\mathcal{l}}_2-{\mathcal{l}}_{\mathrm{\infty }}$ fuzzy controller for a maglev levitation system. Using the established nonlinear maglev system, a discrete-time T–S fuzzy model was employed to approximate the original nonlinear equations. Subsequently, the Lyapunov–Krasovskii technique was employed to establish sufficient ${\mathcal{l}}_2-{\mathcal{l}}_{\mathrm{\infty }}$ performance conditions for the maglev system. These conditions were formulated in terms of linear matrix inequalities (LMIs). The feasibility and effectiveness of the designed controller were verified through simulations.

For nonlinear control, fuzzy control can be combined with PID to adjust the PID coefficients online under different operational disturbances. Sun et al. [48] applied the fuzzy adaptive tuning PID controller to the maglev train system to solve the problem of vehicle–guideway interaction vibration. The proposed controller mitigates the vehicle–guideway interaction vibration and prevents the closed-loop system from reaching the Hopf bifurcation point. This approach involves automatically adjusting the control parameters based on the identification of disturbances or changes in the system parameters. In a subsequent study by Sun et al. [49], an improved approach was introduced where fuzzy inference rules were utilized to modify the PID coefficients online. This modification was based on two inference benchmarks: the air gap error and the air gap error changing rate.

4.3.2. Conventional Neural Network Algorithms

Neural networks (NNs), a conventional type of intelligent method, have been widely adopted for maglev system control. NNs are characterized as highly interconnected networks of simple elements and are designed to operate in a massively parallel manner. These networks exhibit a hierarchical organization to mimic the observed interactions in biological nervous systems when interacting with real-world objects [107].

In maglev levitation control, NNs are typically combined with conventional control methods to improve the performance. Wai et al. [21] designed a model-free adaptive fuzzy-neural-network controller (AFNNC) for a maglev levitation system. Notably, their approach aimed to address the control challenges without requiring auxiliary compensate controllers, strict constraints, or control transformations. All the network parameters in the FNN were automatically tuned using adaptation laws derived from stability analysis. The FNN consists of different layers, each of which serves a specific purpose within the fuzzy system. The input and membership layers belong to the premise part of the fuzzy system. The rule and output layers of the FNN belong to the consequent part of the fuzzy system. Based on the FNN, Wai et al. proposed a robust FNN controller (RFNNC) [22], a backstepping FNN controller (BFNNC) [23], and an observer-based adaptive FNN controller (OAFNNC) [24] for the maglev system. Sun et al. [25] proposed an adaptive neural-fuzzy sliding mode controller (ANFSMC) to address problems such as unmatched disturbance, parameter perturbations, and chattering in the SMC. The simulation and experimental results demonstrate the effectiveness of the proposed ANFSMC. The ANFSMC exhibited several desirable characteristics, including not overshooting, good robustness, a fast dynamic response, and the ability to effectively mitigate chattering in the SMC. The proposed method addresses two significant challenges in maglev train control: unmatched disturbances and parameter perturbations. These challenges can have a detrimental impact on the control performance and system stability. However, the proposed method effectively handles these issues while ensuring a large regulating speed, so it satisfies the control quality requirements of maglev trains.

The radial basis function (RBF) network has several advantages: the ability to approximate a nonlinear function, a simple structure, and fast convergence speed. Therefore, the control performance can be effectively improved against the large uncertainty of the system. Sun et al. [108] designed an SMC approach for the maglev system using an established affine nonlinear mathematical model. To approximate the unknown functions within the SMC, they proposed the use of an RBF neural network with a minimum parameter learning method. Chen et al. [109] applied a complex RBF network adaptive robust SMC algorithm to a vehicle-flexible guideway interaction system. Load change and track irregularity were considered in the simulations and experiments. Ma et al. [110] designed an RBF–PID controller for a nonlinear maglev system. The RBF–PID controller used an RBF network to identify the system information and subsequently used this information to dynamically adjust the parameters of the PID controller based on the actual external conditions and the system’s working status. Chen et al. [111] introduced a novel approach to control the maglev system by combining an RBF neural network and an output-constrained inversion controller (OCIC). To estimate the system state variable matrix and output state in real time, Chen et al. introduced an RBF neural network. The RBF network, which is known for its ability to approximate complex functions, was used to model and estimate the system’s state variables and output state. By leveraging the RBF network’s approximation capabilities, the estimated states could be obtained in real time and provide valuable information for control purposes. In conjunction with the estimated states, they used an OCIC to regulate the maglev system. The OCIC is a control strategy that takes into account the output constraints and ensures that the controlled system operates within predefined limits. By incorporating the OCIC into the control design, Chen et al. aimed to guarantee that the maglev system adhered to specific output constraints while achieving satisfactory control performance. Sun et al. [60] designed a neural-network-based supervisor controller (NNBSC) for control systems. The NNBSC was designed to mitigate the controller output saturation by incorporating an amplitude saturation controller (ASC). In addition, an RBF neural network was introduced as a supervisory compensator to enhance the performance of the ASC. Sun et al. [112] focused on addressing uncertainties in the nonlinear maglev system, such as the time-varying mass and external disturbances. They proposed a neural network-based adaptive control approach to stabilize the air gap, which is a critical parameter in maglev systems.

The projection recursive neural network (PRNN) is inspired by the Hopfield network, which is a type of recurrent neural network. The Hopfield network is known for its ability to store and retrieve patterns through the convergence of its network dynamics to equilibrium points [113]. Unlike the former function of NNs in maglev system control, Fatemimoghadam et al. [59] used a PRNN to represent a combination of a first-order dynamic equation and an algebraic equation. This representation was used to develop a real-time optimizer to solve constrained quadratic programming (QP) problems. First, they formulated the backstepping control approach as a constrained optimization problem. By formulating the backstepping control in this manner, they aimed to satisfy the control constraint and convert the performance index into a constrained QP problem. This formulation enabled them to leverage the capabilities of the PRNN to solve the constrained QP problem and optimize the control performance.

4.3.3. Deep Learning Algorithms

Deep learning (DL) is a subfield of machine learning that is concerned with the development and application of large neural network models. These models, often called deep neural networks, are designed to learn and make data-driven decisions by automatically extracting relevant features and patterns from input data. The basic DL models include the deep belief network (DBN) [114], stacked autoencoder (SAE) [115], convolutional neural network (CNN) [116], recurrent neural network (RNN) [117], and generative adversarial network (GAN) [118]. The distinctive ability of DL with traditional machine learning is an approach that considers feature design. DL offers distinct advantages over conventional machine learning methods. Notably, DL excels at learning valuable features directly from raw data at a low level. As a result, the need for labor-intensive manual feature engineering is minimized or eliminated entirely [119]. Nowadays, DL has already been adopted in maglev systems by some researchers.

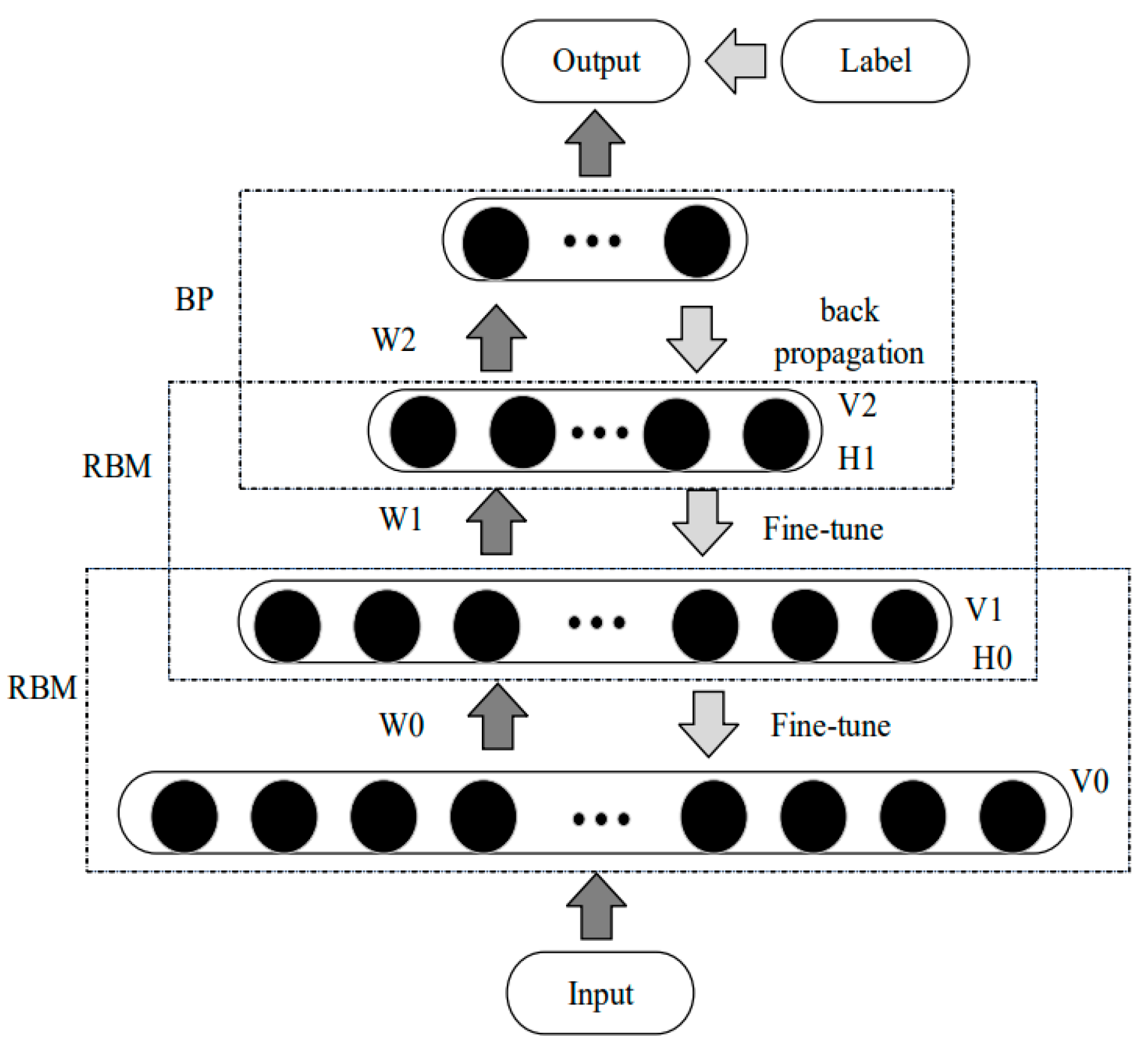
Sun et al. [26] used a DBN to design a controller for the maglev vehicle to primarily address the challenges posed by uncertainty in the system. The DBN model was trained using a technique that involved stacking multiple layers of a restricted Boltzmann machine (RBM), which is a type of generative neural network. The training process of the DBN started by training individual RBM layers. Each RBM layer learned to represent and capture important features of the data. By stacking these RBM layers, the DBN model gained the ability to learn hierarchical representations of the input data. To further refine the DBN model and enhance its performance, a supervised reverse iterative layer was added to the final layer. This additional layer facilitated the fine tuning of the overall network by incorporating feedback from a supervised learning approach. This fine-tuning process enabled the DBN model to adapt and optimize its parameters based on the desired control objectives and encountered uncertainty in the maglev vehicle system. Figure 12 illustrates the structure of the DBN.

Unlike supervised or unsupervised learning, the first objective of reinforcement learning (RL) is to extrapolate or generalize responses of systems so that they act correctly in situations that are not present in the training set, and the second objective is to maximize a reward signal [121]. The fundamental principle of RL revolves around learning through interactions. In RL, the agent interacts with its environment and adapts its behavior based on the rewards that it receives and the observed consequences of its actions. This process involves the agent learning to optimize its actions to maximize cumulative rewards over time. With its inherent function approximation capabilities, deep learning is commonly employed in RL agents. Neural networks, which are known for their ability to approximate complex functions, are well-suited for regressing functions within RL frameworks. Using deep learning techniques, RL agents can effectively learn and represent the relationships between states, actions, and rewards, which enables them to make informed decisions and improve their performance over time. In recent years, DRL has emerged as a highly promising approach for addressing real-world problems, such as optimal control of nonlinear systems [122], pedestrian regulation [123], and traffic grid signal control [58]. Zhao et al. 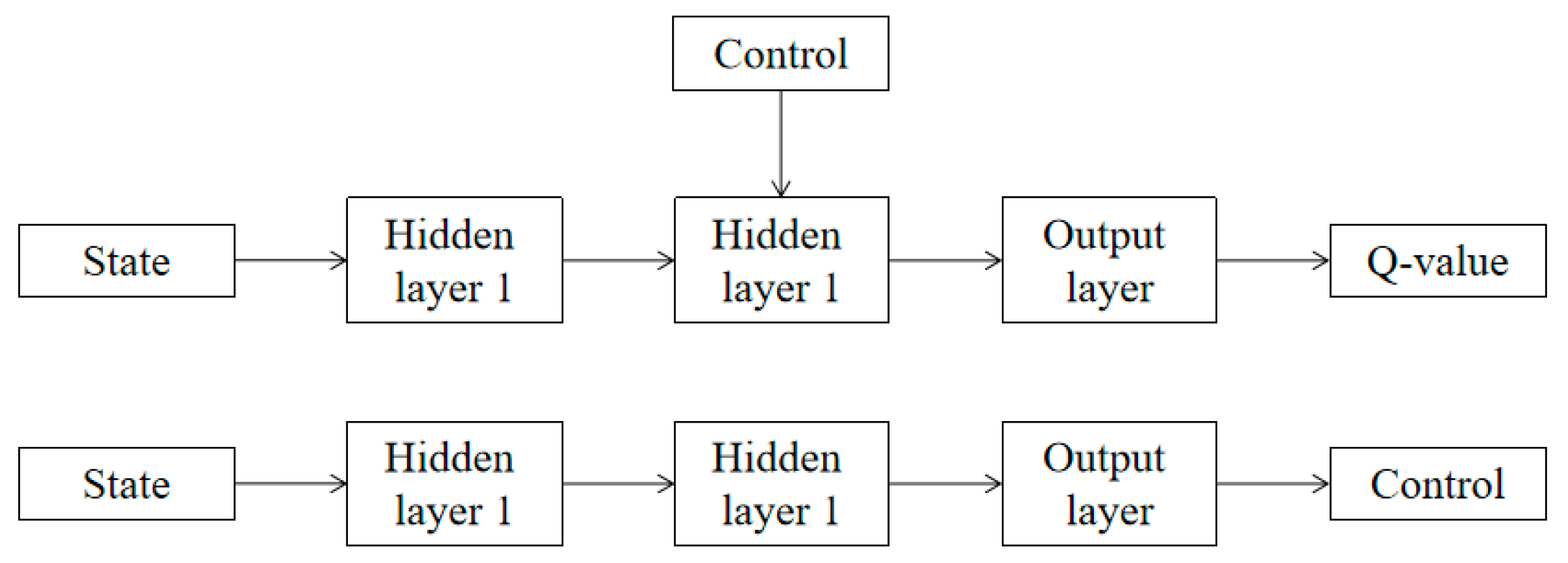[27] modeled the maglev system control into a continuous Markov decision process problem (MDP) and adopted the deep deterministic policy gradient (DDPG) algorithms for levitation regulation. The network structure of the DDPG algorithm is as in Figure 13. To evaluate the effectiveness of the proposed controllers, simulations and experiments were conducted, comparing their performance with that of PID and LQR controllers.

4.4. Control Item Design and Uncertainty Factors

In the levitation control system, choppers play a crucial role in supplying power to the levitation electromagnet by regulating the current flowing through it. Hence, the controller design primarily focuses on the current loop. Consequently, when designing the controller for the maglev levitation system, the state-space function can be simplified by excluding the current state from consideration.

A control loop can also be designed to improve the controller or to simplify system modeling. For instance, Xu et al. [124] found that the magnetic flux loop exhibits exceptional robustness and is a favorable alternative to the current loop when high levels of robustness are required. Sun et al. [125] adopted ${\left[\frac{i\left(t\right)}{x\left(t\right)}\right]}^2$ ($i\left(t\right)$) is the current and $x\left(t\right)$ is the measured air gap) for controller design to simplify the modeled system.

In addition, uncertainties, like track irregularity, passenger fluctuation, parameter perturbation, and delayed signal transmission, have also been considered in controller design. When considering the track irregularity factor for controller design, sinusoidal track profile, random track profile, and track steps are usually adopted for track irregularity simulations [51]. The disturbance force is simulated using a sinusoidal load [124,125]. Passenger fluctuation and parameter perturbation can be simulated by adding an uncertainty term to the mass. The time delay in the signal transmission can be introduced by adding a time-delay state function to the entire dynamic model [125]. The impact of time delay on the dynamic response under the influence of a PID controller has been analyzed, including an examination of the relationships between running speed, control parameters, and response regularities [126]. To deal with the factors illustrated above, observers, such as disturbance observers [52] and flux density observers [124], combined with adaptive algorithms are usually adopted. Some researchers have directly used robust and artificial intelligence algorithms to achieve the same goal [125].

4.5. Summary

A comparative study of the different control methods adopted for maglev levitation systems was conducted and is described in this section. The advantages and disadvantages of these control methods are concluded.

4.5.1. Linear Control Methods

Linear control methods are based on the linearized maglev levitation model.

• The PID control algorithm is easy to apply, and the choice of the three coefficients is of great importance for designing the proper PID controller. However, there are two disadvantages in PID: (1) compared with other controllers, such as the LQR controller, the PID controller exhibits larger peak overshoot and settling time, and (2) the disturbance cannot be ignored in real applications. Real-time changes in the three coefficients are required to adapt to different scenarios. Therefore, the fuzzy logic and IMC methods have been used in PID control to better tune the coefficients in the PID controller.
• The LQR controller assumes that all state variables are accessible for feedback. However, in a maglev system, it is widely recognized that the velocity of the air gap cannot be directly measured, and the presence of disturbances significantly influences the system’s behavior. Thus, the state estimation and DOBC can be combined to improve the performance of the LQR controller.
• $H_2$ and $H_{\mathrm{\infty }}$ control algorithms use the $H_2$ and $H_{\mathrm{\infty }}$ norms, which are two popular measures in optimal control theory for control design and are robust when there are disturbances.
• The fractional order control algorithm is normally combined with other methods, such as PID and sliding mode control, by introducing additional fractional order parameters in the control design. With additional parameters, the traditional controllers show better performance in terms of robustness and disturbance rejection.
• The basic state feedback control algorithm uses the state variables of the system for control design. The state variables of the controller must be carefully selected to improve the accuracy and robustness of the controller, and the state observer or model predictive method can be combined to obtain sufficient state variables for controller design.

4.5.2. Nonlinear Control Methods

Nonlinear control methods were directly applied to the maglev levitation model. It comprises a state feedback control algorithm, an adaptive control algorithm, a robust control algorithm, and a sliding mode control algorithm.

• The PID control algorithm applied to nonlinear system control must be carefully designed. For example, it is necessary to change the conventional transfer function into an exponential function to increase the stiffness of the system when it is apart from the operating point or combine it with other methods, such as TMD, to decrease the system vibration and PSO to optimize the coefficients of the PID.
• The state feedback control algorithm can address the time delay of the system and real-time disturbances, such as nonlinear and periodic bounded disturbances and uncertainties. It can combine with an optimal method, such as PSO, to improve the controller parameters.
• The adaptive control algorithm shows great potential in enhancing the performance of control systems, particularly when handling uncertainties caused by factors such as degradation and modeling inaccuracies. In addition to directly applying adaptive control algorithms to maglev levitation systems, model-assisted/reference-adaptive control algorithms are implemented.
• A robust control algorithm can address the uncertain part of the system and develop an effective design method that considers uncertainty information. The robust controller can also be combined with a disturbance observer to increase robustness to disturbances.
• SMC is a type of nonlinear control algorithm widely employed in the field of nonlinear control due to its straightforward physical implementation, rapid response, and robustness. Modifications can be made to the SMC for various purposes. For example, the designed GFTISMC improves the global fast response speed of the maglev system and reduces the steady-state error. The nonsingular robust SMC reduces the upper bound of the uncertainty and interference of the SMC. The SMC can also combine with other control algorithms or optimization algorithms, such as the fuzzy logic control method and PSO method.
• The backstepping control algorithm is typically adopted to decouple nonlinearities and eliminate uncertainties. It can be combined with SMC to reduce the chattering of the SMC and improve the dynamic response of the system.

4.5.3. Artificial Intelligent Control Methods

Artificial intelligent control methods are capable of dealing with the complex nonlinear problem of maglev levitation systems and are classified into conventional neural network algorithms and deep learning algorithms in this study.

• The fuzzy logic control algorithm can use expert knowledge to obtain the output control signal, which has better control performance than the PID controller and can be directly applied to nonlinear systems. However, traditional fuzzy logic controllers are designed based on human operator experience and cannot linguistically determine the exact action for the output. The T–S fuzzy control method was proposed as a mathematical tool to overcome this problem. In addition, optimization methods such as PSO can be combined to better tune the parameters of the controller. It can also combine the ${\mathcal{l}}_2-{\mathcal{l}}_{\mathrm{\infty }}$ control to ensure that the controlled output is less than a prescribed level and PID to optimally adjust the coefficients and restrain the coupled vibration of the vehicle and guideway.
• The conventional neural network algorithm can address complex nonlinear problems that have the characteristics of approximation of nonlinear functions, a simple structure, and fast convergence. This solution can effectively improve the control performance against large uncertainties in the system. In maglev levitation control, conventional neural network algorithms are commonly used as controllers to output the control item or optimize the parameters of other controllers, such as PID and state feedback controllers.
• The deep learning algorithm places emphasis on designing and evaluating training algorithms and model architectures for contemporary neural networks. These networks can better represent the intricate features of complex problems. Although few studies have investigated deep-learning-based maglev levitation control, the application of DBN and DRL has demonstrated the robustness and effectiveness of the deep-learning algorithm in the maglev levitation area.

5. Maglev Train Controller in Other Situations

In this section, maglev train controllers in other situations are reviewed and discussed. The scenarios mainly include vehicle–guideway vibration suppression control and redundancy and fault-tolerant design. For vehicle–guideway vibration suppression control, the vehicle–guideway system models and related suppression controllers are reviewed. For redundancy and fault-tolerant design, electrical redundancy will be emphasized.

5.1. Vehicle–Guideway Vibration Suppression Control Design

Due to the small levitation air gap and strong nonlinear behavior of the maglev control system, the acceleration amplitudes of a series of maglev trains will be significantly amplified [127] and may cause failure in maglev control. In addition, the resonance phenomenon of vehicle–guideway vibration is frequently observed in commercial lines [128] and affects the ride comfort and safety of the maglev train. To suppress the vehicle–guideway vibration, many studies have been conducted to analyze the dynamic performance of the vehicle–guideway coupling system and design appropriate controllers to reduce the vibration fluctuation.

For the vibration analysis of vehicle–guideway coupling models, Lengyel et al. [129] used a simply supported beam connected with a free beam on distributed springs and dampers to describe the guideway and coupled maglev vehicle, and they analyzed dynamic behaviors, such as the deflection and acceleration of the guideway and the deformation of the vehicle with different speeds. Kim et al. [130] developed an integrated model of a UTM vehicle that incorporated a 3-dimensional (3D) full vehicle model, including the bodies, joints, and force elements derived from prototyping. A 2-dimensional (2D) flexible guideway and feedback controllers were also included to accurately represent all electromagnet levitation units. This integrated model offers a more realistic representation of the UTM vehicle system. The established model was investigated under standstill and low-speed operation scenarios. Min et al. [131] proposed a 3D mathematical maglev system model of the UTM vehicle, compared its dynamic performance with a 2D model, and analyzed the effect of the lateral and vertical track irregularities. For the single electromagnet-guideway coupling model [50,132], full vertical dynamic coupling vibration model of an HSST type low-speed maglev train [133], and mathematical model of the low-speed maglev test car of Tongji University [86,134], the effect of the time-delay [85,133], levitation current perturbation, and control gain [133] on vibration behavior were studied. The Hopf bifurcation theory was adopted by researchers to analyze the mechanism of a fundamental theory of vehicle–guideway coupling vibration [50,86].

Numerous controllers have been proposed to reduce the vibration of the vehicle–guideway coupling system. Some researchers used extra controllers to suppress the vibration. Li et al. [78] adopted a tuned mass damper (TMD) installed at the guideway to avoid the Hopf bifurcation phenomenon of the train-switch vibration. Wang et al. [135] introduced a novel approach to address resonant phenomena encountered by a vehicle traversing guideway girders. They proposed the use of an additional feedback controller based on the condensed virtual dynamic absorber (C-VDA) scheme. This approach aims to mitigate the resonant effects and enhance the overall stability of the vehicle’s motion on the guideway girders.

Instead of using extra controllers, Yau et al. [127] proposed a neural-PI control using a back-propagation (BP) neural network to train the PI controller. The authors demonstrated that the proposed controller effectively regulated the acceleration amplitude of running maglev vehicles to ensure that it remained within an acceptable range. Yau et al. [136,137] also proposed an LQR+PID controller to reduce the substantial amplification of the acceleration amplitude, which running maglev vehicles at higher speeds experience due to aerodynamic forces. Furthermore, they addressed the dynamic response of maglev trains that travel over suspension bridges subjected to horizontal earthquakes. Kong et al. [16] proposed a Kalman-filter-based SMC to reduce the vibration response. They discovered that the fluctuation of the air gap and vertical acceleration of the cabin’s center of gravity (CG) was significantly influenced by the vehicle speed and guideway irregularity. However, they observed only minimal effects on these factors due to variations in vehicle mass. Wang et al. [87] developed a full-state feedback controller and used the PSO to optimize the control gains; then, they verified the performance of the proposed controller through a simulation and test rig even under violent external disturbances. Zhou et al. [47] found that the vibration amplitude depended on the voltage supplied by the power source. To address this issue, they proposed a vibration amplitude control method utilizing a PI controller. This method can control the vibration amplitude by adjusting the voltage of the power supply. Zhou et al. [51] presented an effective novel approach for vibration suppression under various common track irregularities, including sinusoidal track profiles, random track irregularities, and track steps. Their proposed method uses a pair of mirror FIR filters alongside an adaptation mechanism controller. Sun et al. [48] developed a fuzzy adaptive tuning PID controller, for which the controller gains were adjusted according to the identified disturbance or changes in the system parameters.

In [49], Sun et al. employed an enhanced version of the Apriori algorithm to extract and process data from a stored historical database. This process facilitated the establishment of a reliable database, based on which the researchers developed an improved fuzzy adaptive controller. The proposed controller was verified on a full-scale Internet of Things (IoT) maglev train system at Tongji University. In addition, sliding mode robust adaptive control [109], robust control [71], feedback linearization control [46], double loop PID considering control gain perturbation [86], and GA tuned super-twisting-SMC (ST-SMC) [97] have been proposed to suppress the vibration of the coupling system.

5.2. Redundancy and Fault-Tolerant Design

Redundancy and fault-tolerant design refers to mechanical redundancy (adding components or improving structure) or electrical redundancy (adding hardware circuits or optimizing control algorithms) [138]. In this part, research on fault-tolerant control will be emphasized.

Long et al. [9] designed a new levitation module, and each controller in the module can control only one electromagnet. Based on the new structure, a cascade control theory-based current loop was proposed, and an optimal controller was constructed. The proposed levitation system was proved to be more effective through simulation. Zhang et al. [139] considered the failure of the accelerometer and proposed a sensor-fault diagnosis system based on an unscented Kalman filter. An improved PID regulator with tracking differentiators was then adopted to tolerate the accelerometer failure. Li et al. [38] designed a switch strategy-based active fault-tolerant controller. When sensor fault (time-delay) happens, the system switched to a state observer to obtain signals so as to keep stability. Zhou et al. [140] developed a new and efficient redundant levitation controller. The experiment results indicate that the proposed controller could successfully remove the interactions between the redundant actuator and general actuators, as well as maintain good robustness under disturbance.

5.3. Summary

At present, there are vulnerable theoretical results related to vehicle–guideway coupling modeling and controller design. However, there is no systematic proposal to guide the field design. In addition, the effect of factors like aerodynamics, linear motors, etc., is relatively lacking. In the future, these factors can be incorporated into vehicle–guideway coupling analysis and control design to improve the vehicle–guideway coupling model and control algorithms.

As for the redundant and fault-tolerant design, mechanical redundancy and electrical redundancy can be combined to achieve stability of the system in the future. Especially for low- and medium-speed maglev systems, most related research mainly uses controllers and actuators to improve system redundancy. In the future, mechanical redundancy and combination of these two methods can be further researched.

6. Discussion

Maglev levitation system control plays a vital role in maintaining the stability of maglev train operation. Presently, the maglev levitation system models utilized for controller design can mainly be divided into dynamic-equation-based and data-driven models. Due to the presence of different scenarios, dynamic-equation-based models are commonly divided into single-point levitation, multi-point levitation, electromagnet-guideway coupling system, and vehicle–guideway coupling system types. Dynamic equations and data-driven methods can also be combined to establish more accurate models in some studies [40].

Based on maglev levitation system models, a comparative study of different control methods for the systems was conducted.

(1)

Linear control methods: The maglev levitation systems are first linearized using Taylor expansion or feedback linearization methods. The linear control methods can normally be classified into state feedback methods and optimal control methods based on the principle of control. To achieve better control performance, the conventional linear control methods are combined with other methods, such as fuzzy logic and IMC.

(2)

Nonlinear control methods: Compared with linear control methods, nonlinear control methods can be directly applied to the maglev levitation models. Nonlinear control methods, such as robust control and adaptive control, show great potential in enhancing the performance of control systems, especially in handling uncertainties caused by factors such as degradation and modeling inaccuracies.

(3)

Artificial intelligence control methods: Artificial intelligence control methods can handle the complex nonlinear problem of maglev levitation systems. In particular, deep learning control algorithms, such as deep reinforcement learning, can simultaneously achieve the advantage of model-based control and data-driven control.

In addition, vehicle–guideway vibration suppression control, redundancy, and fault tolerance were reviewed. There is no systematic proposal to guide the field design for vehicle–guideway vibration suppression control. For redundancy and fault-tolerant design, the mechanical redundancy and combination of mechanical redundancy and electrical redundancy can be further developed.

7. Conclusions and Prospects

The maglev levitation system is a key component in the maglev train, but its control remains a challenge due to the open-loop control and strong nonlinearity of the system. Therefore, this paper summarizes the models and control technologies for maglev levitation systems. The models for maglev levitation systems control are categorized into dynamic-equation-based and data-driven models. The reviewed control technologies mainly cover linear control methods, nonlinear control methods, and artificial intelligence methods. In addition, this paper discussed maglev control in other scenarios, such as vehicle–guideway vibration control, redundancy, and fault-tolerant design. The reviewed research involved in this paper follows the PRISMA criteria. The main contributions of this paper can be concluded as (1) a detailed review of magnetic levitation system modeling for levitation control; (2) analyzing the advantages and disadvantages of different kinds of levitation control techniques; (3) summarizing recent studies on the effect of the levitation control on the guideway vibration and fault-tolerant control design. In addition, uncertainty factors in maglev levitation control are also discussed.

7.1. Theoretical and Practical Implications

This paper reviewed different maglev levitation system modeling techniques (including those based on dynamic equations and data-driven modeling) and different control methods adopted in maglev levitation systems (including linear control methods, nonlinear control methods, and artificial intelligence methods). Most studies have focused on the performance of the proposed controller. However, uncertainties such as load change, track irregularity, and time delay cannot be ignored in the real application of these controllers. More research must focus on the robustness of the proposed controllers to these uncertainties, and deep learning as a new trend in recent years can be further studied and applied to maglev levitation system control.

This paper has also investigated maglev control in other situations, such as vehicle–guideway coupling vibration control, redundancy control, and fault-tolerant control. Different types of vehicle–guideway coupling models, vibration suppression controllers, redundant structures, and fault-tolerant controllers were reviewed. More factors similar to aerodynamics should be included in the vibration model analysis, and more studies on artificial intelligence methods can be conducted for fault-tolerant controller design.

7.2. Future Prospects

Future research on low- and medium-speed EMS-type maglev levitation control algorithms should transition from models of decentralized and independent levitation units to complex models that are more similar to real maglev trains, such as the 3D UTM model in Section 5.2. To enhance the realism of theoretical research, more studies should consider issues such as time delay, network transmission, and fault tolerance. To address more complex problems and make the control sufficiently robust for disturbances, artificial intelligence methods should be used for nonlinear control algorithms, such as SMC and backstepping control, to enable nonlinear control. In addition, the designed levitation control algorithms should be evaluated on testbeds or actual maglev trains to verify their practicality. For other situations of control in the maglev system, more artificial intelligence methods and factors from outside the environment should be taken into consideration in the control design.

There is a trend that transportation is required to offer environmentally friendly solutions to combat traffic-related pollution [141]. In this way, maglev trains are promising transportation for the future for their advantages over conventional trains in both capacity and energy efficiency, as aforementioned. Maglev trains and control methods can also contribute to sustainable development goals (SDGs) [142,143] as outlined below:

(1)

Maglev trains and advanced control methods can contribute to the development of sustainable and innovative transportation infrastructure.

(2)

Maglev trains can enhance accessibility, reduce dependence on fossil fuel-based transportation, and promote sustainable urban mobility. The use of efficient control methods can improve the safety of the maglev trains, as well as contribute to the development of sustainable cities and communities.

(3)

Maglev trains are energy-efficient and have low carbon emissions. Thus, energy consumption can be optimized, further reducing greenhouse gas emissions and supporting climate action initiatives.

(4)

The development and implementation of maglev train control methods require collaboration and partnerships between governments, research institutes, and industry stakeholders. Such collaboration can foster knowledge sharing, technology transfer, and capacity building, contributing to the achievement of SDGs.