Unsteady Numerical Simulation of Two-Dimensional Airflow over a Square Cross-Section at High Reynolds Numbers as a Reduced Model of Wind Actions on Buildings
Abstract
1. Introduction
2. Materials and Methods
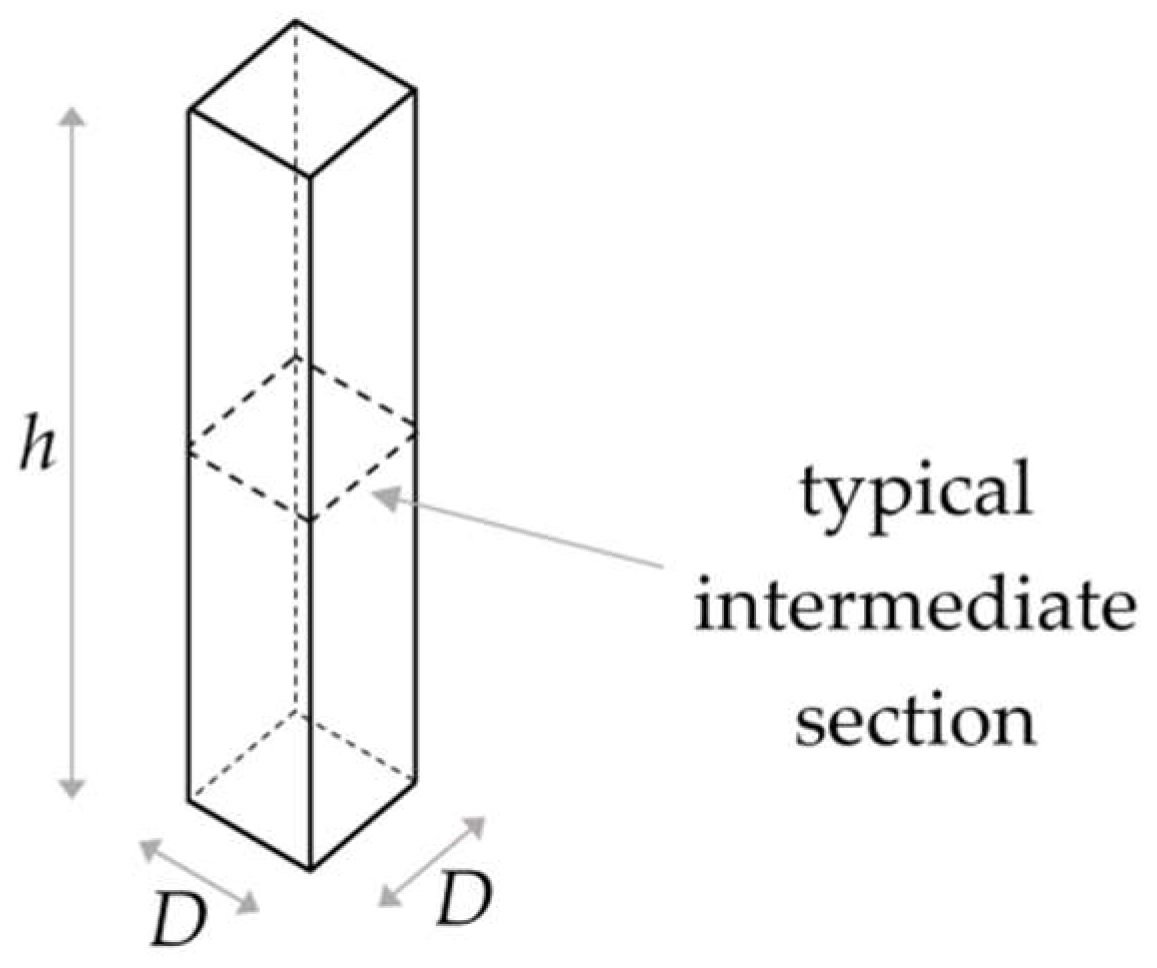
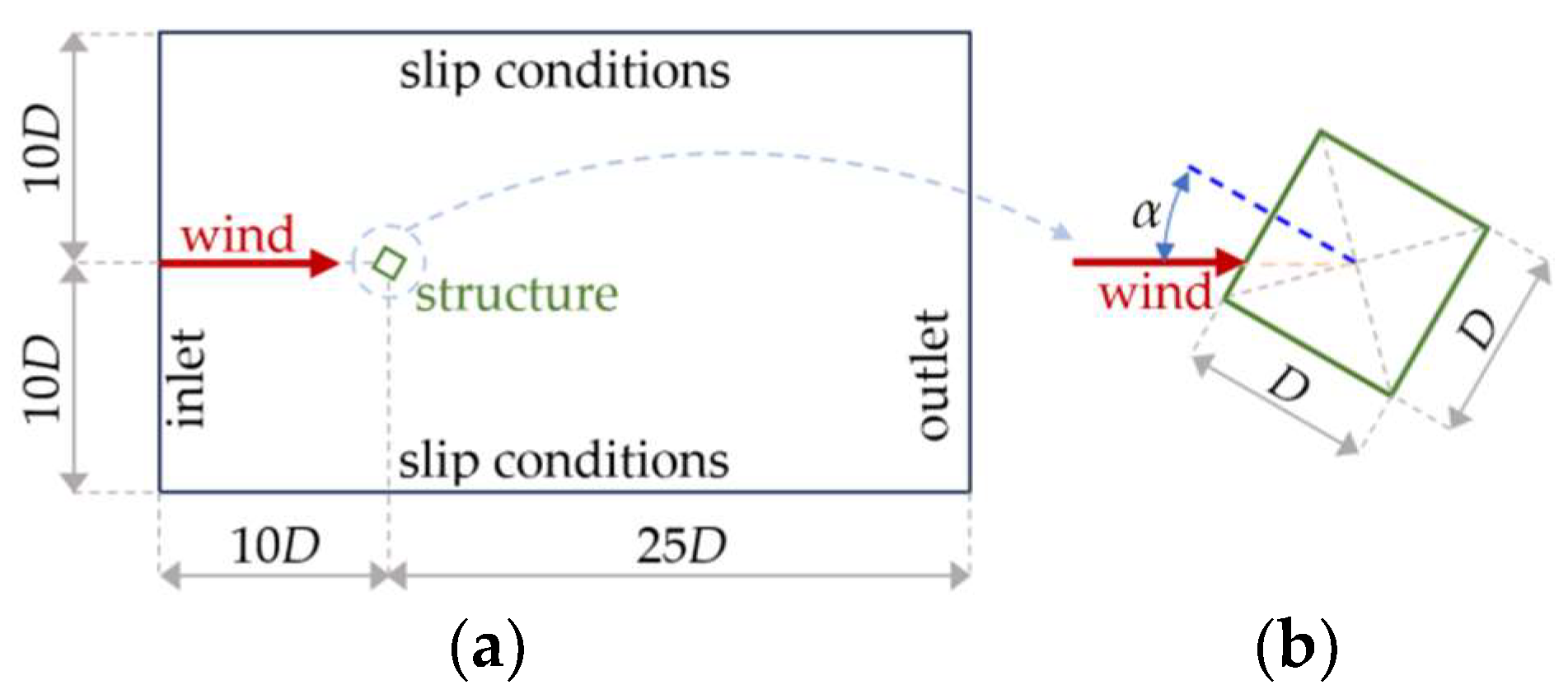
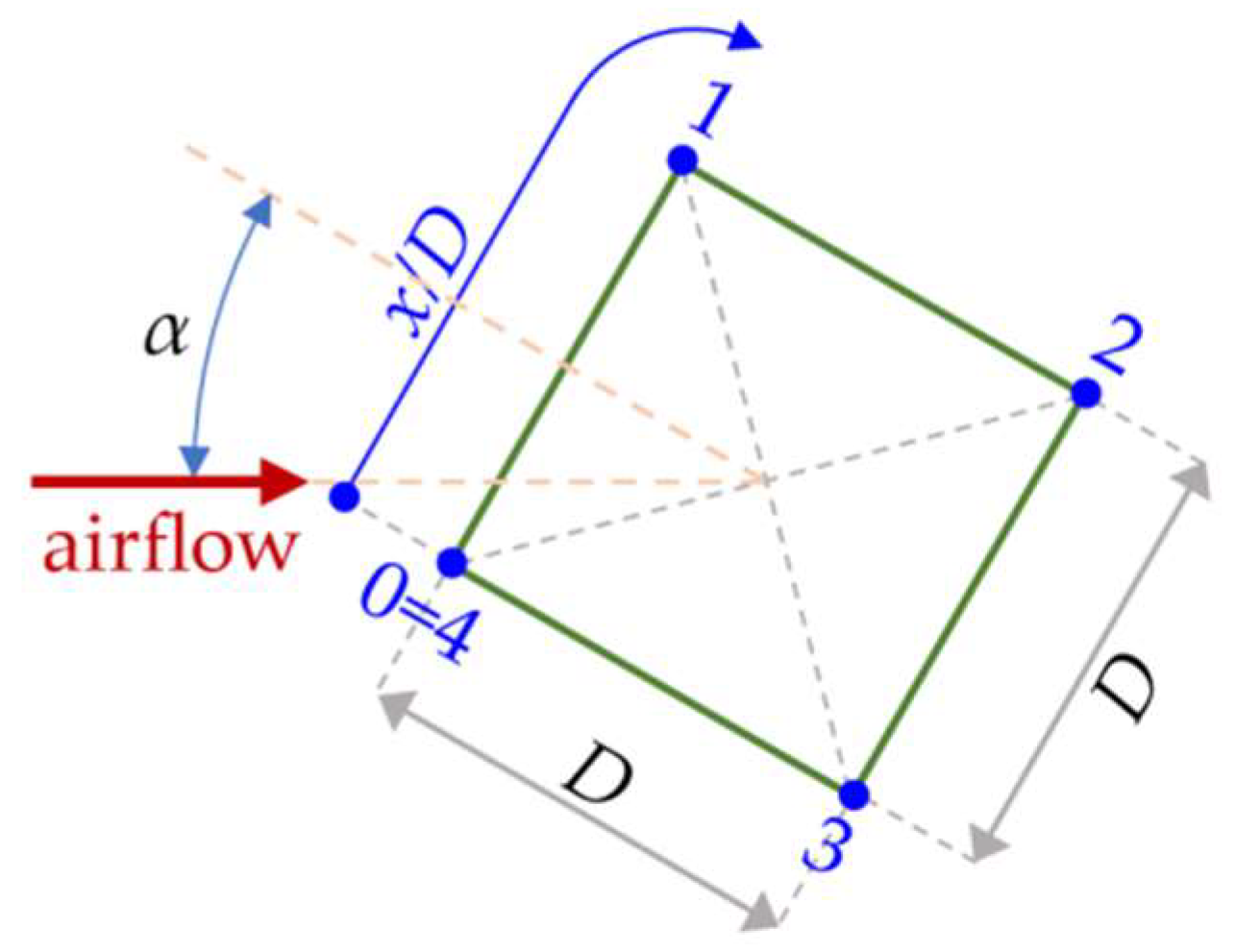
2.1. Computational Model
2.2. Aerodynamic Parameters
3. Results
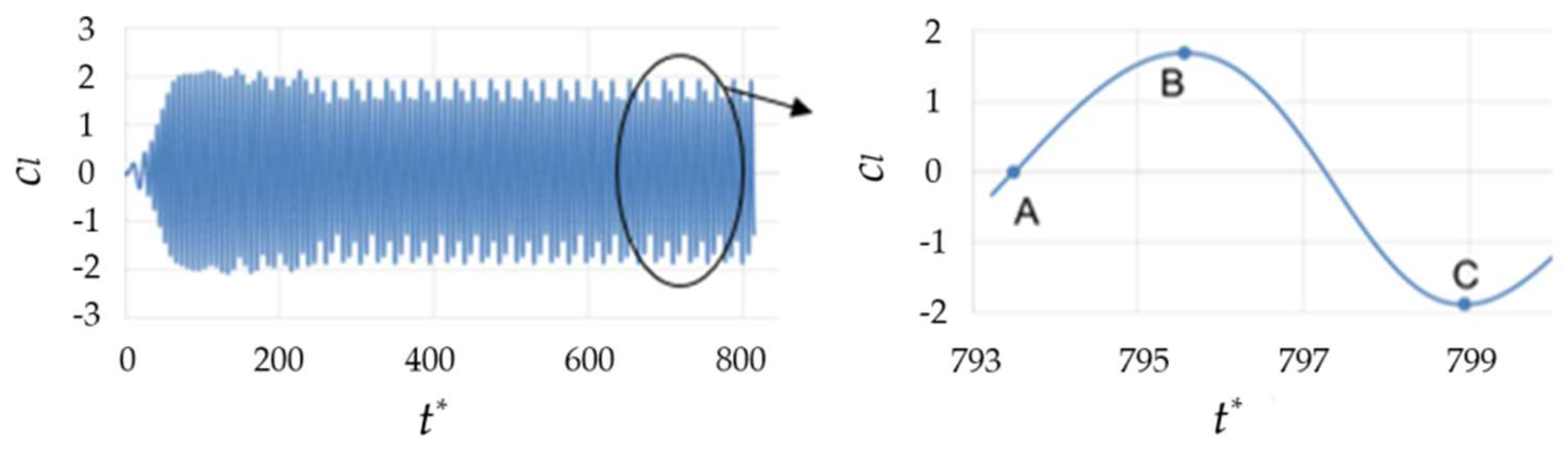
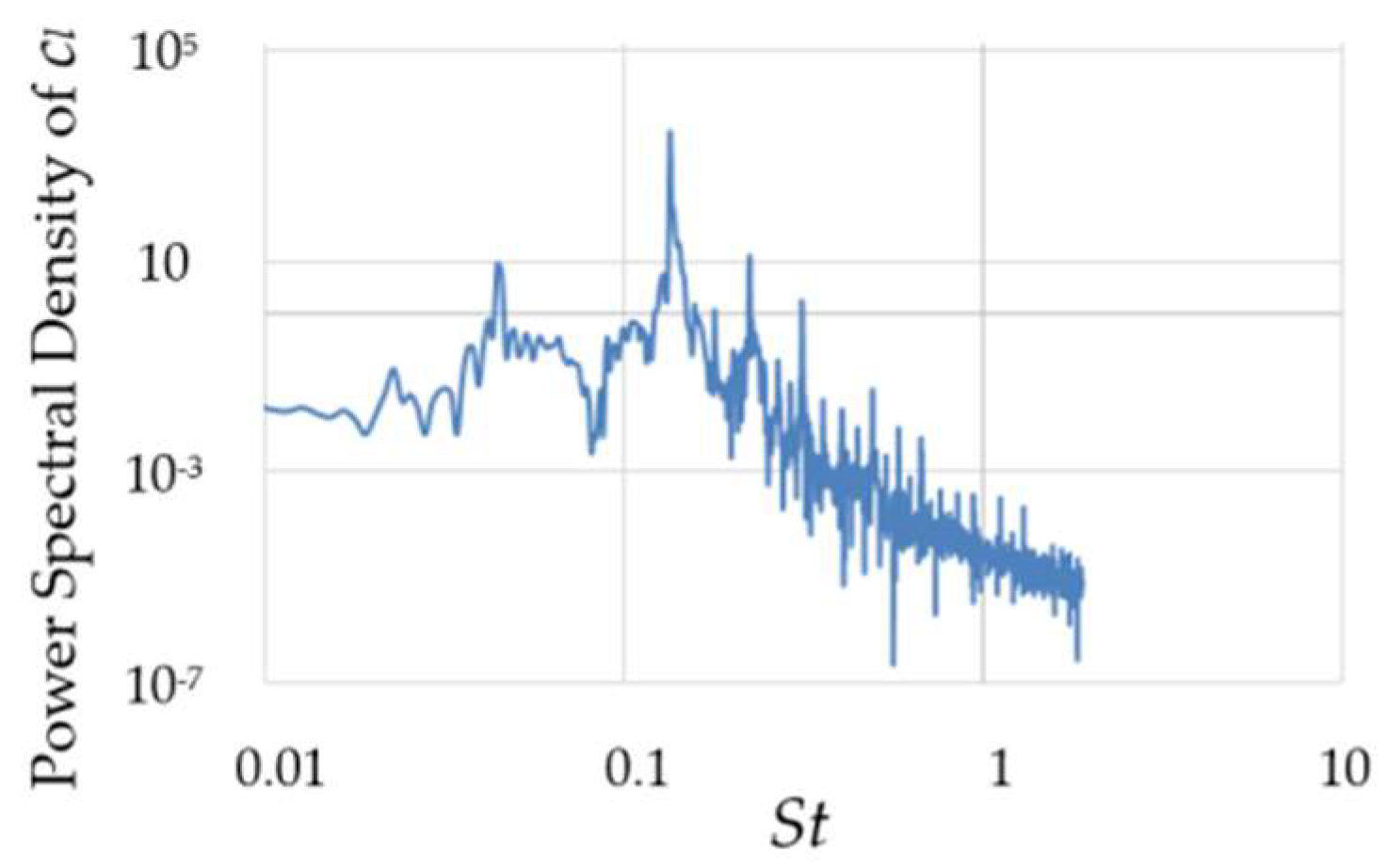
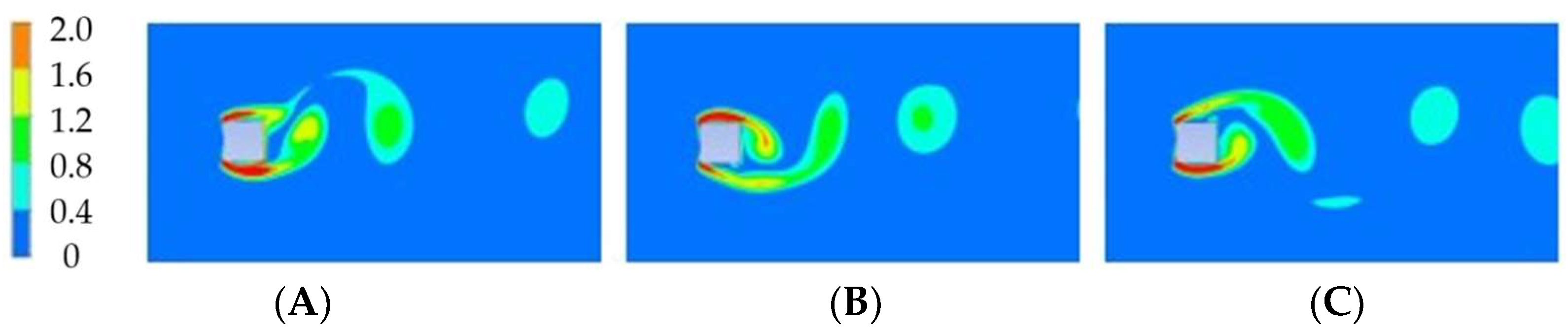
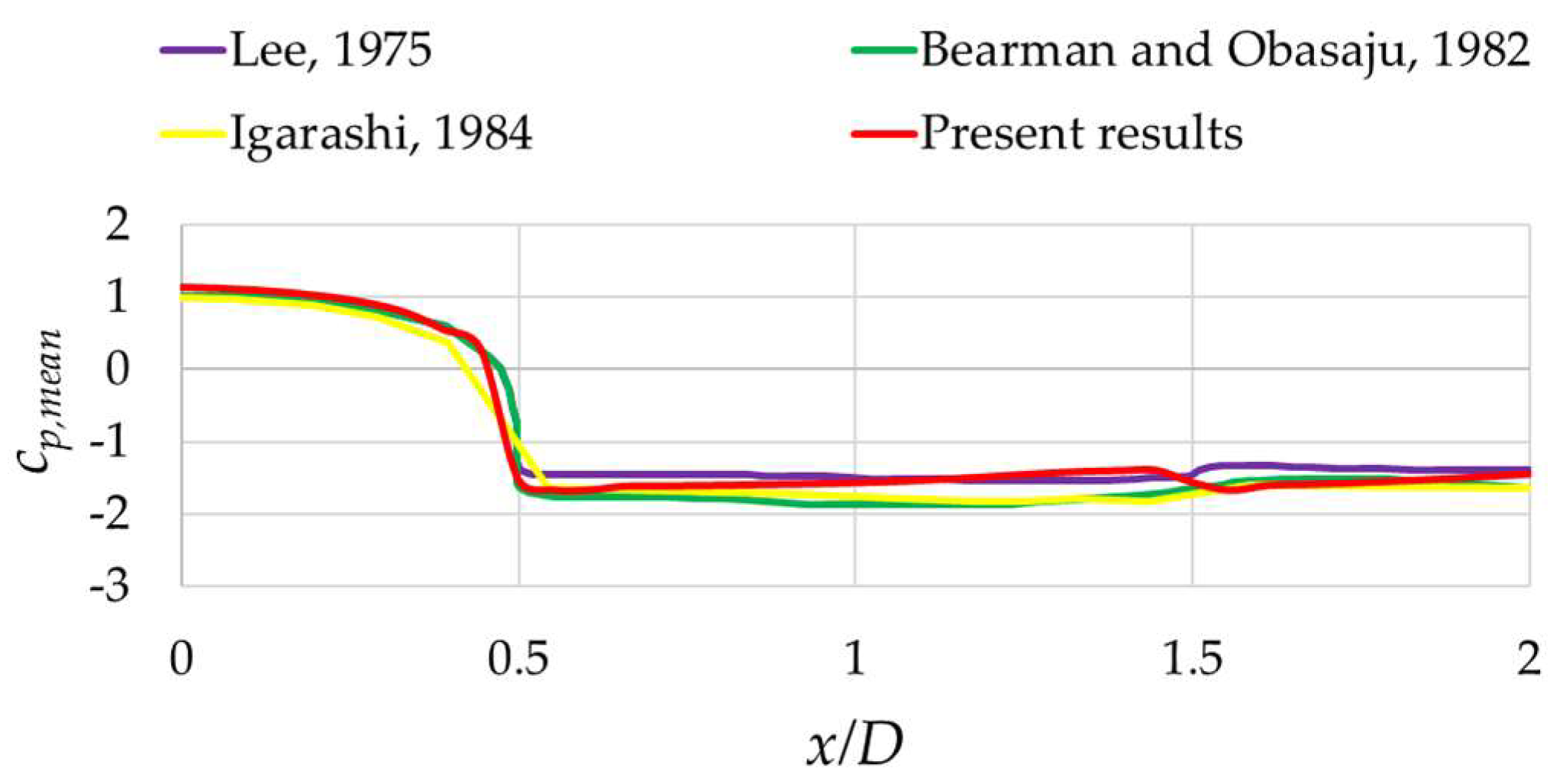
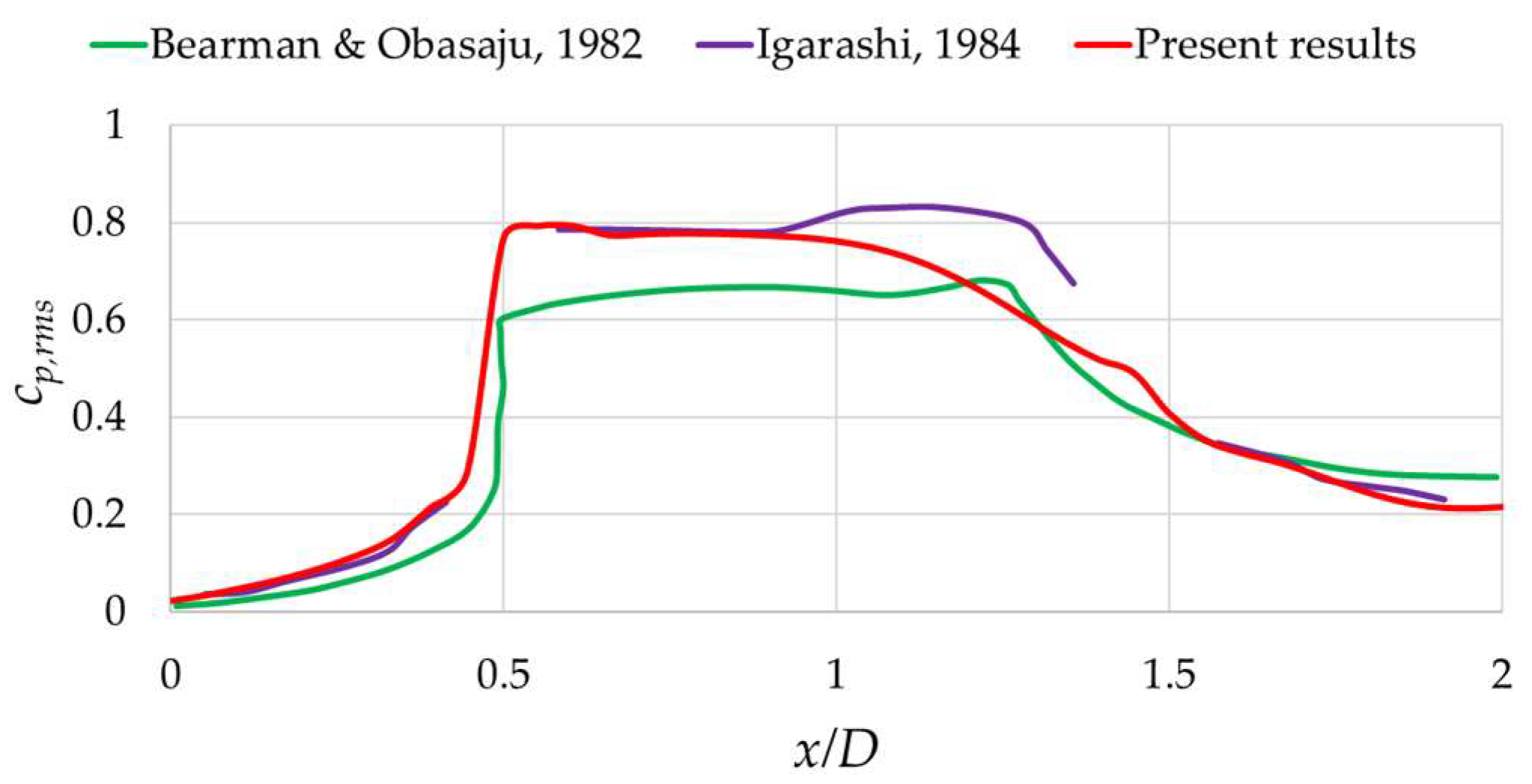
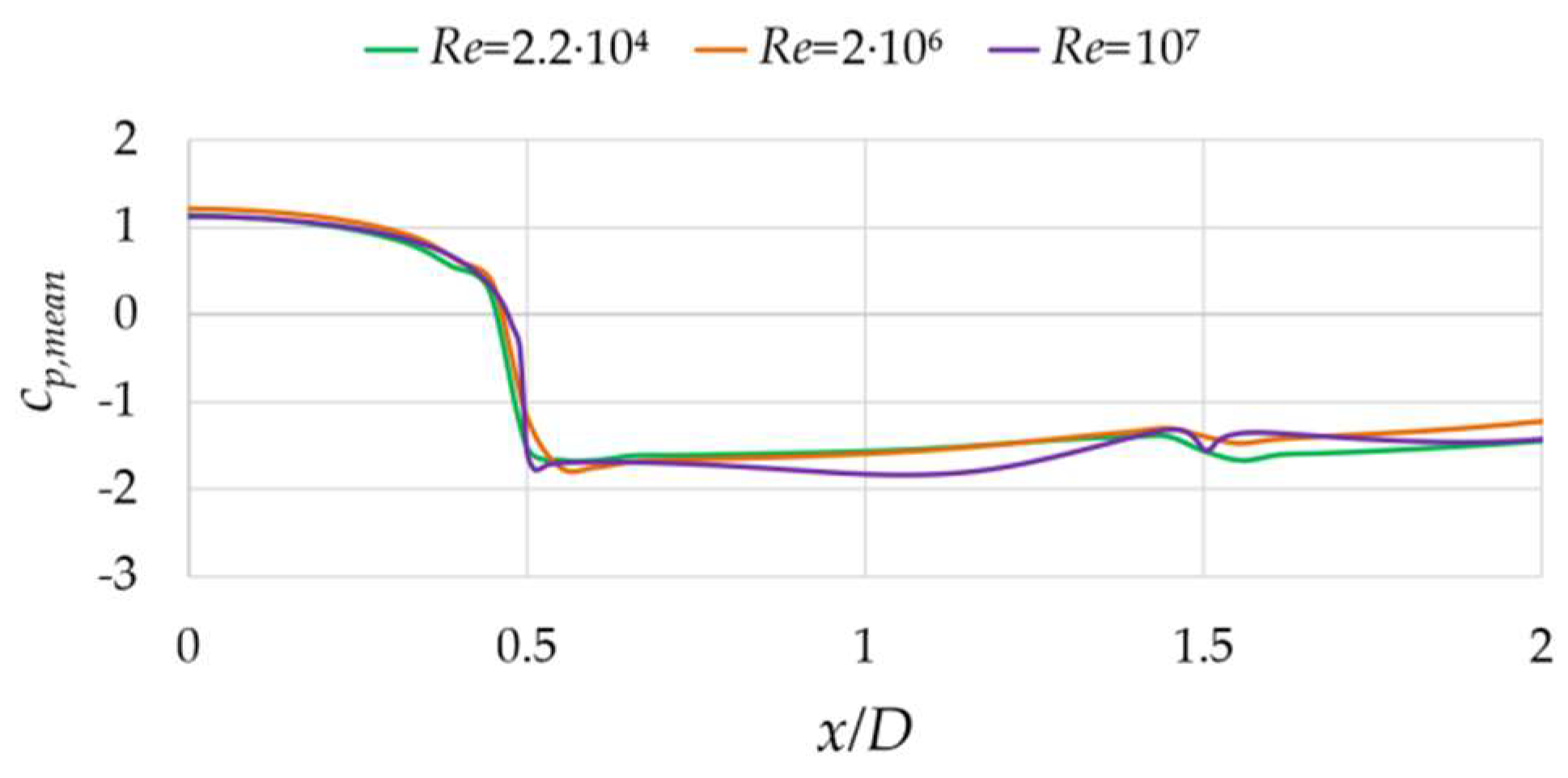
3.1. Numerical Results for Re = 2.2 × 104 and Model Validation
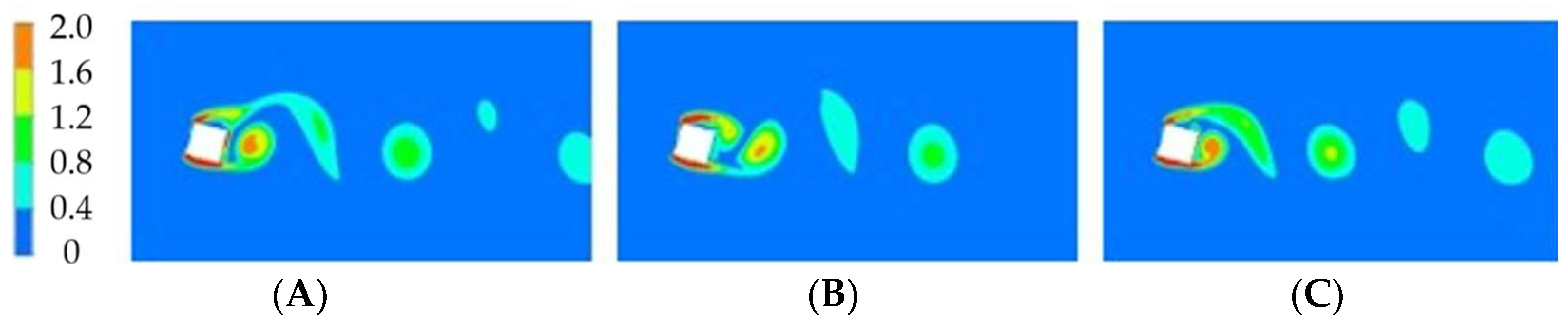
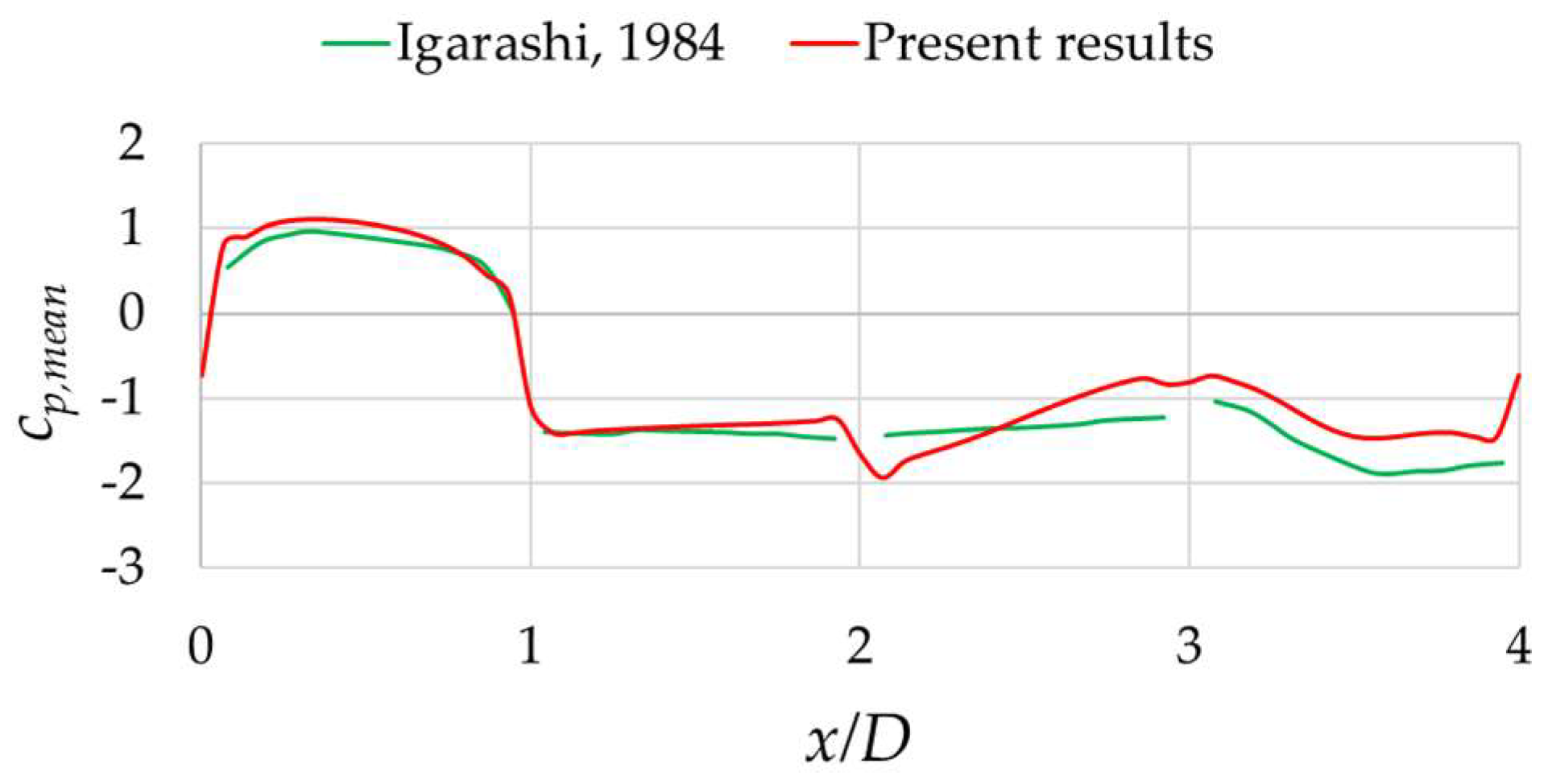
3.1.1. Zero-Degrees Angle of Incidence
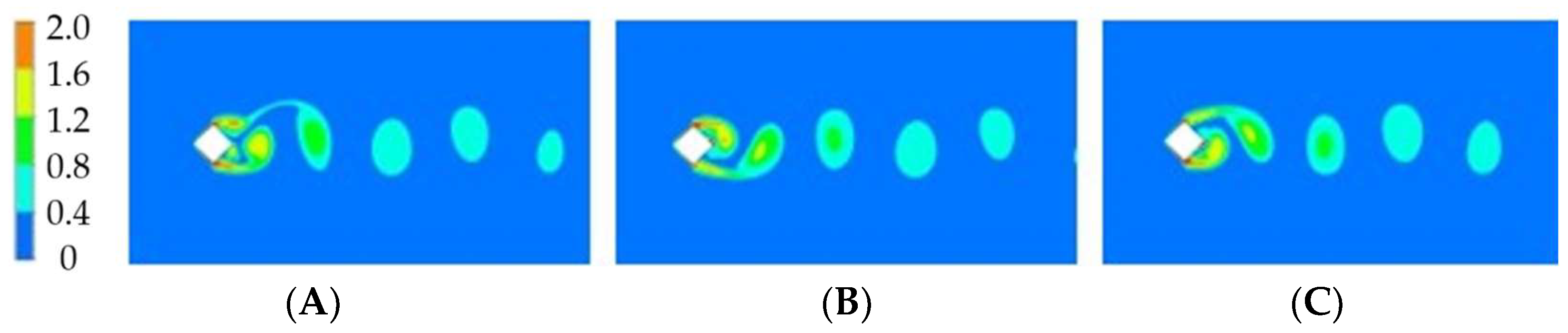
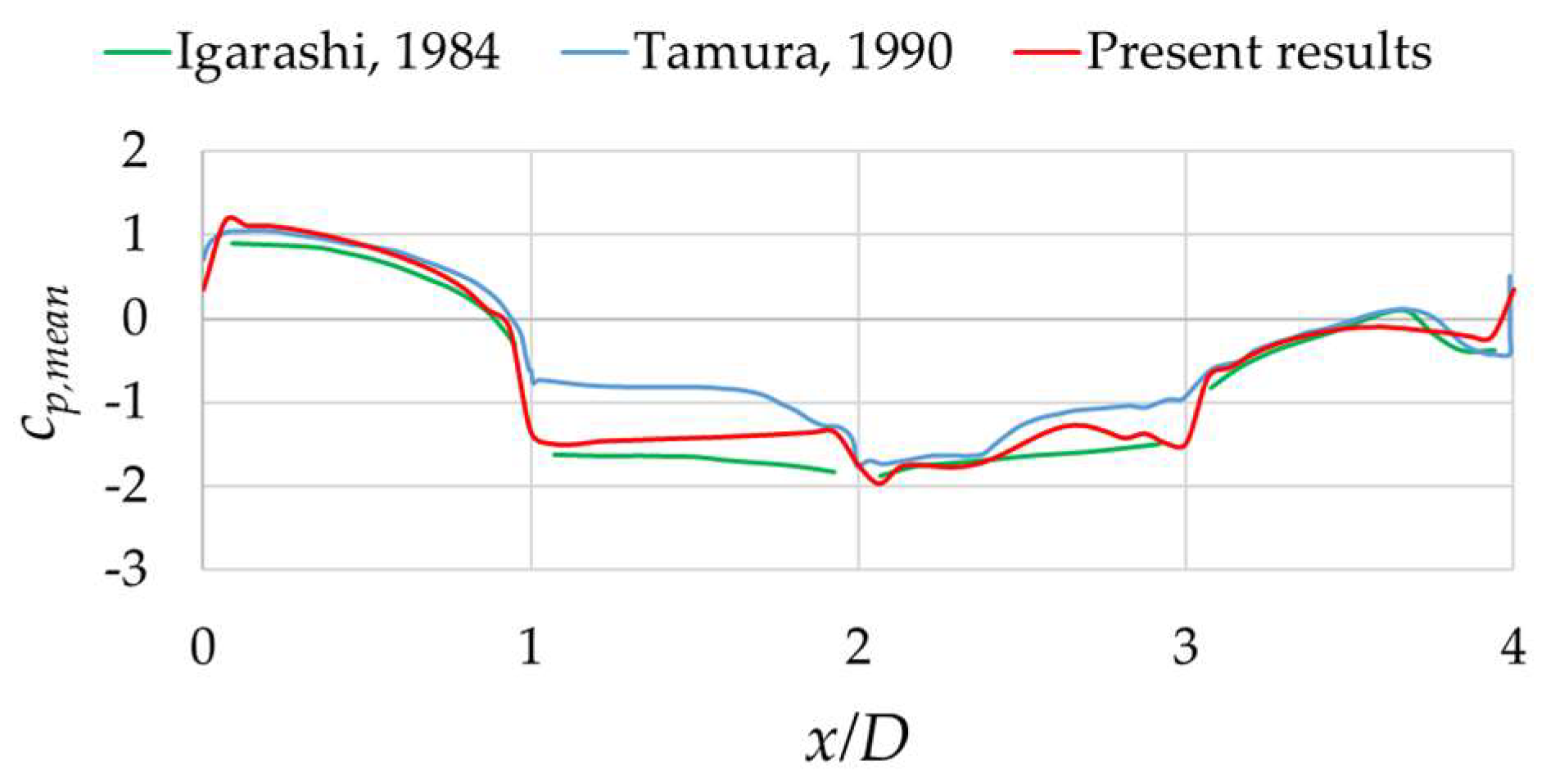
3.1.2. Nonzero Angles of Incidence
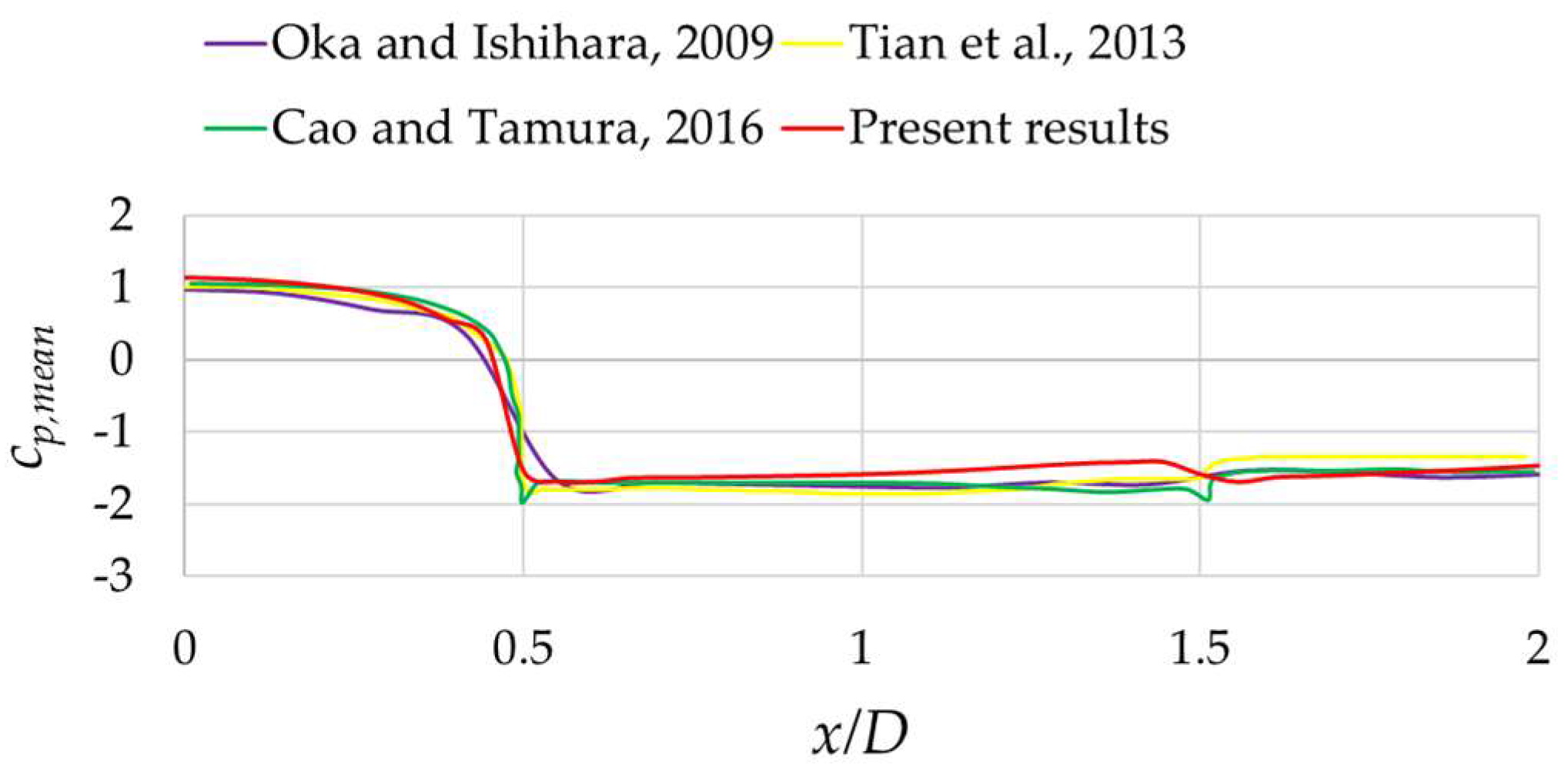
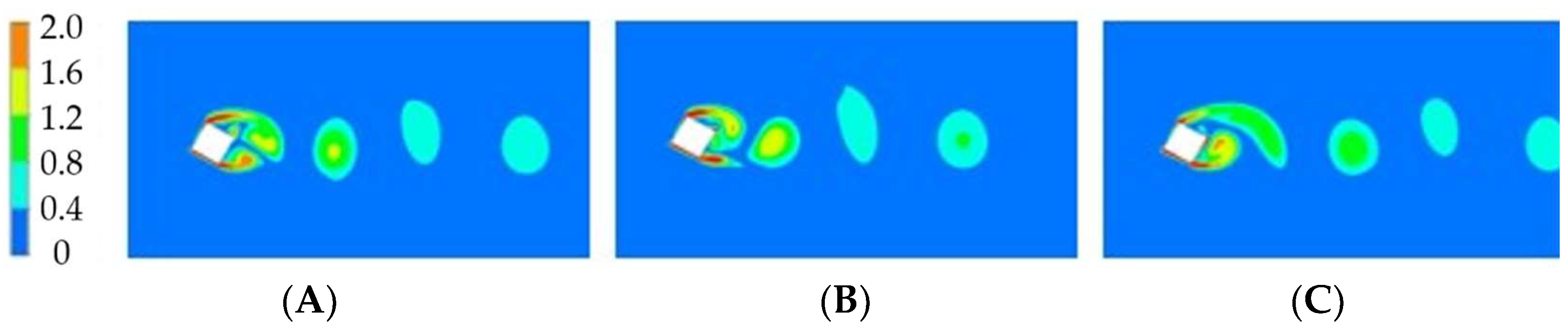
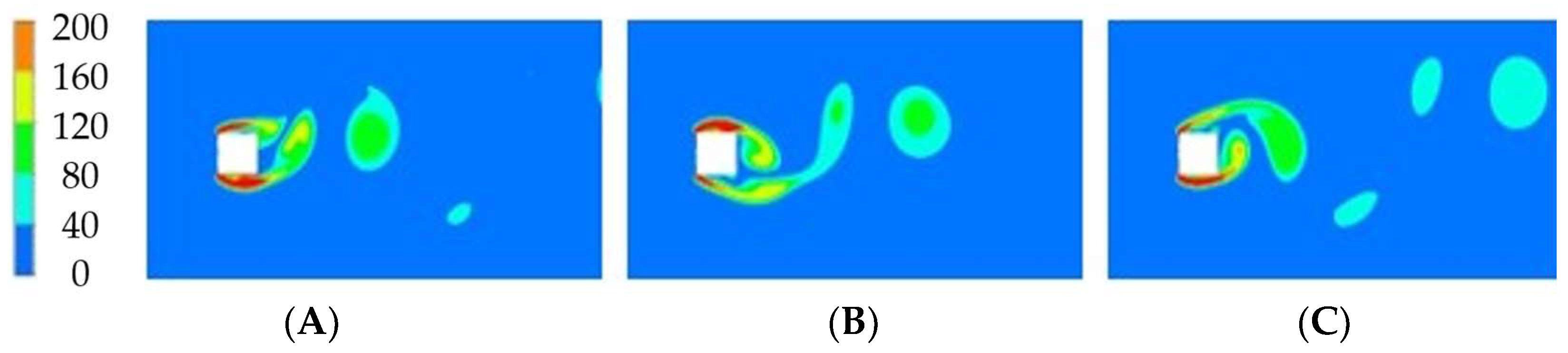
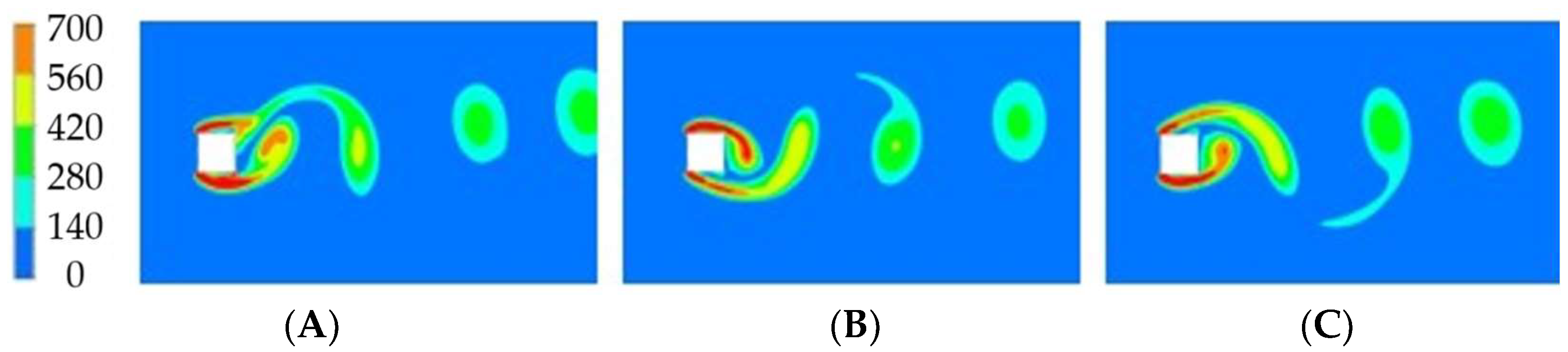
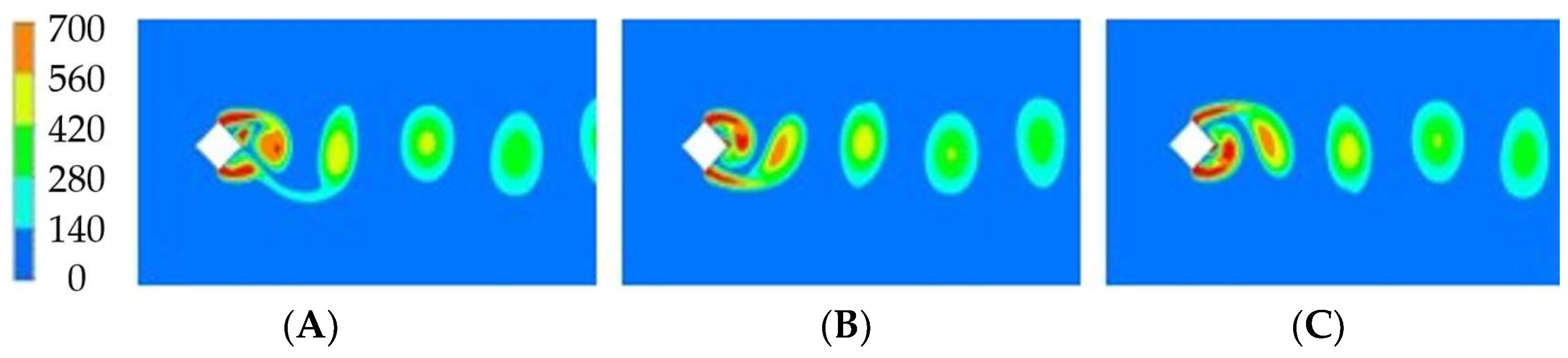
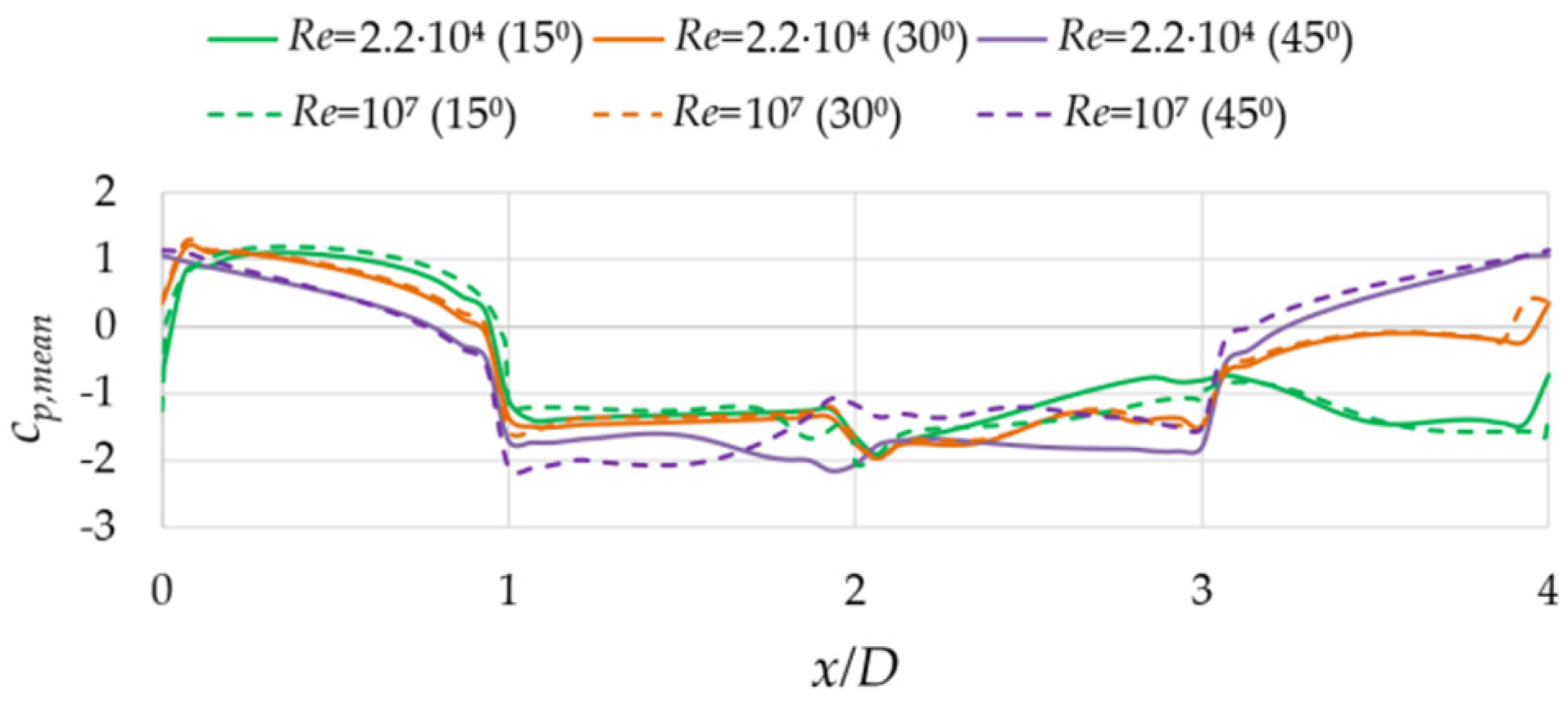
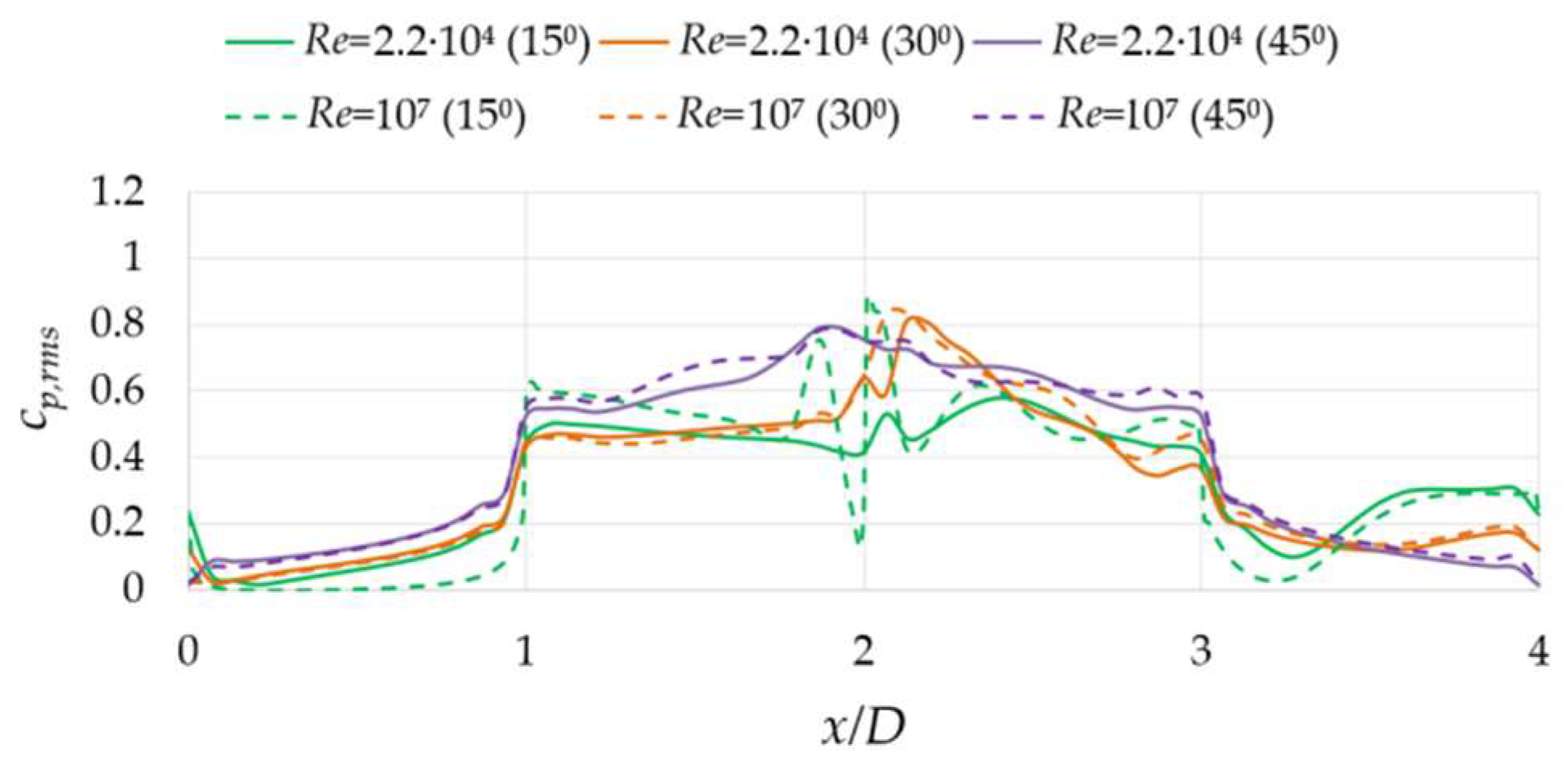
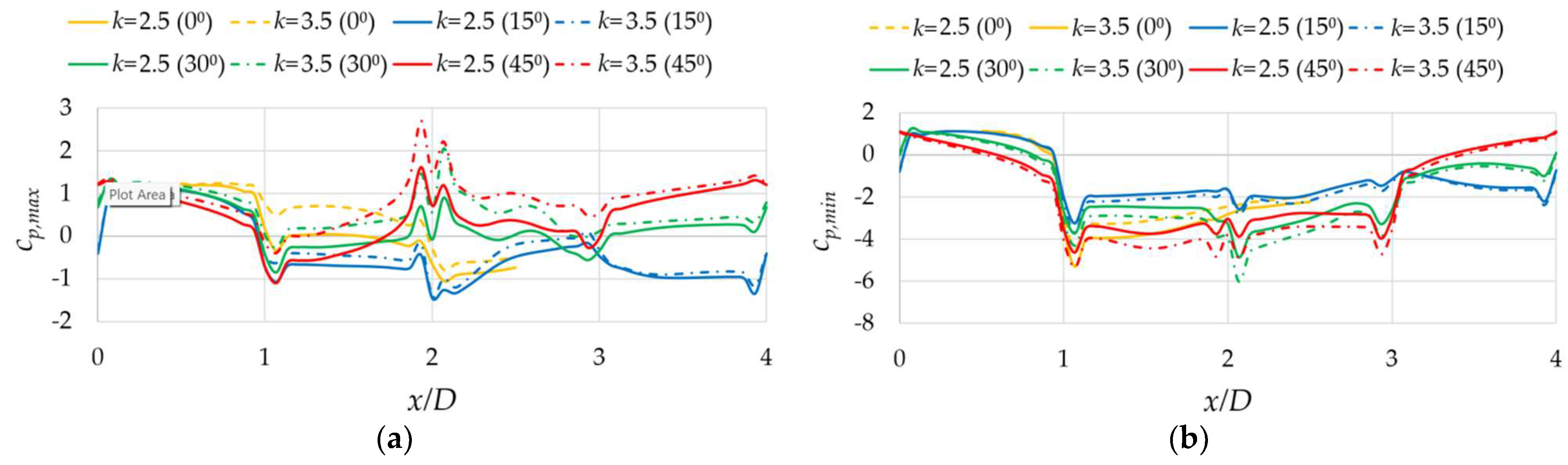
3.2. Numerical Results for High Reynolds Numbers
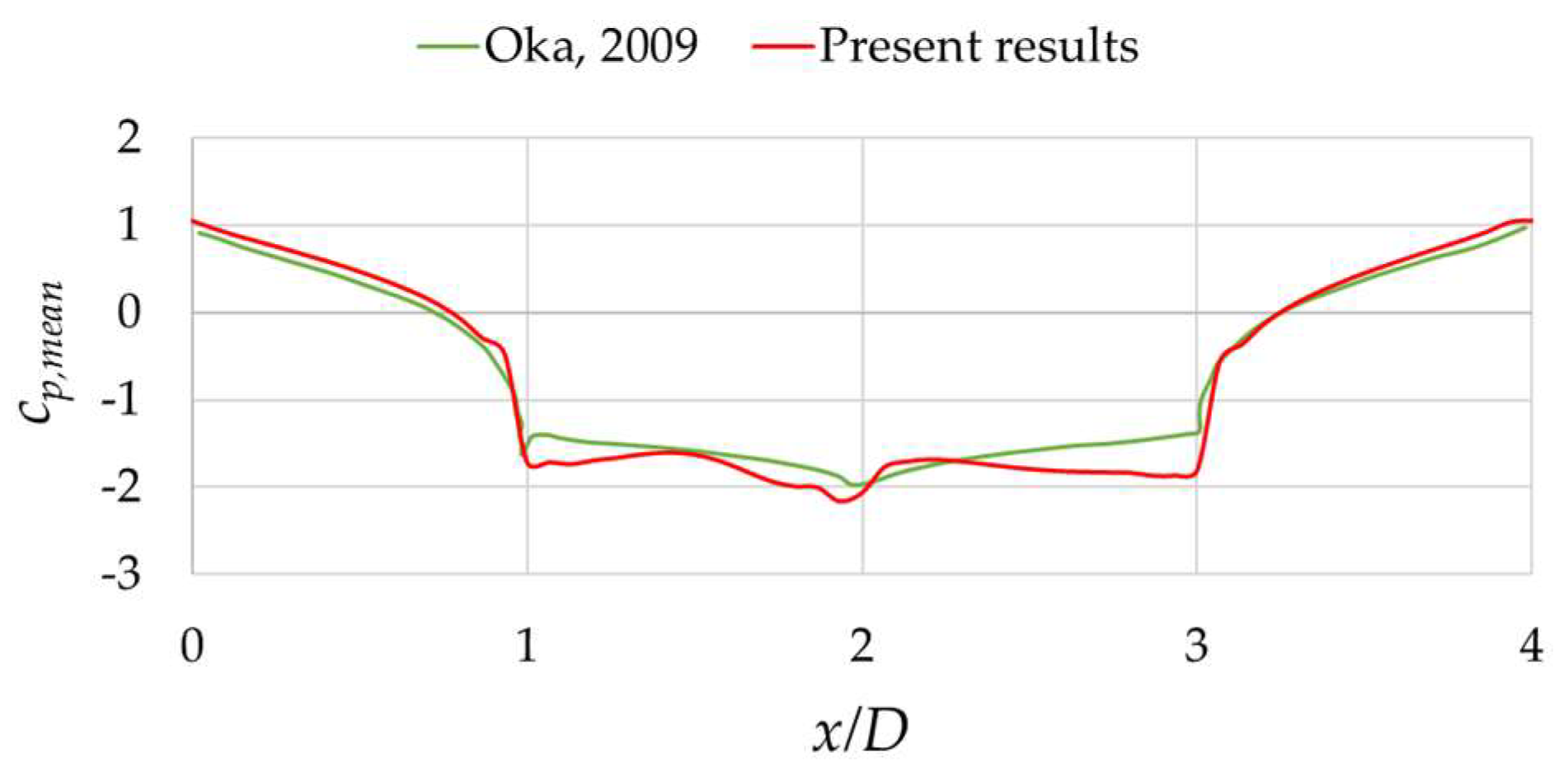
3.2.1. Zero-Degrees Angle of Incidence
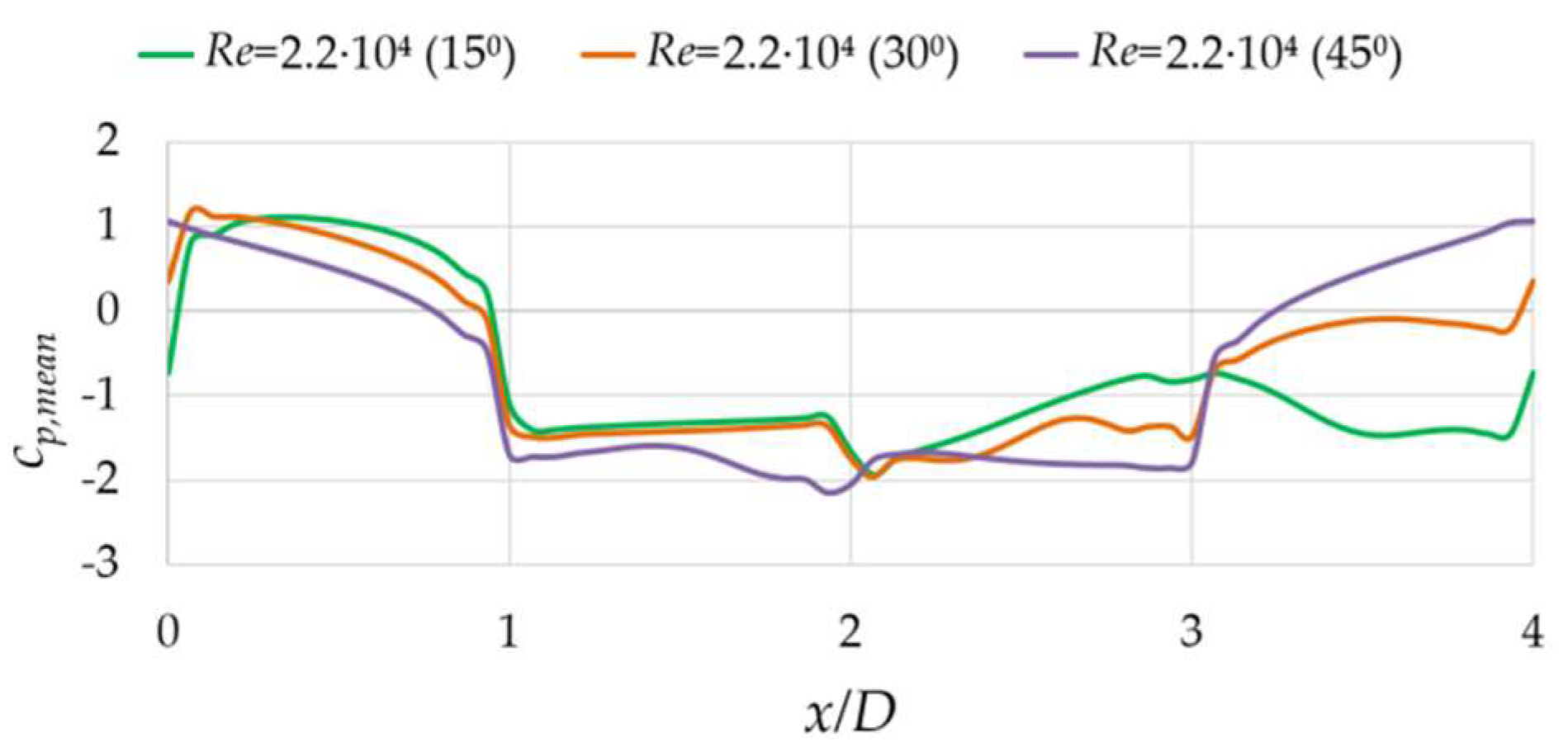
3.2.2. Nonzero Angles of Incidence
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cook, N.; Mayne, J. A novel working approach to the assessment of wind loads for equivalent static design. J. Wind Eng. Ind. Aerodyn. 1979, 4, 149–164. [Google Scholar] [CrossRef]
- Cook, N.; Mayne, J. A refined working approach to the assessment of wind loads for equivalent static design. J. Wind Eng. Ind. Aerodyn. 1980, 6, 125–137. [Google Scholar] [CrossRef]
- Cook, N. Calibration of the quasi-static and peak-factor approaches to the assessment of wind loads against the method of Cook and Mayne. J. Wind Eng. Ind. Aerodyn. 1982, 10, 315–341. [Google Scholar] [CrossRef]
- Harris, R. An improved method for the prediction of extreme values of wind effects on simple buildings and structures. J. Wind Eng. Ind. Aerodyn. 1982, 9, 343–379. [Google Scholar] [CrossRef]
- Kwok, K. Cross-wind response of tall buildings. Eng. Struct. 1982, 4, 256–262. [Google Scholar] [CrossRef]
- Wacker, J.; Plate, E. Local peak wind pressure coefficients for cuboidal buildings and corresponding pressure gust factors. J. Wind Eng. Ind. Aerodyn. 1993, 50, 183–192. [Google Scholar] [CrossRef]
- Zhou, Y.; Kijewski, T.; Kareem, A. Aerodynamic Loads on Tall Buildings: Interactive Database. J. Struct. Eng. 2003, 129, 394–404. [Google Scholar] [CrossRef]
- Stathopoulos, T.; Baniotopoulos, C. Wind Effects on Buildings and Design of Wind-Sensitive Structures; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Holmes, J.D. Wind Loading of Structures; Taylor & Francis: London, UK, 2007. [Google Scholar]
- Petrini, F.; Ciampoli, M. Performance-based wind design of tall buildings. Struct. Infrastruct. Eng. 2012, 8, 954–966. [Google Scholar] [CrossRef]
- Dagnew, A.; Bitsuamlak, G. Computational evaluation of wind loads on a standard tall building using LES. Wind Struct. 2014, 18, 567–598. [Google Scholar] [CrossRef]
- Rizzo, F.; D’Alessandro, V.; Montelpare, S.; Giammichele, L. Computational study of a bluff body aerodynamics: Impact of the laminar-to-turbulent transition modelling. Int. J. Mech. Sci. 2020, 178, 105620. [Google Scholar] [CrossRef]
- Rizzo, F.; Huang, M. Peak value estimation for wind-induced lateral accelerations in a high-rise building. Struct. Infrastruct. Eng. 2021, 18, 1317–1333. [Google Scholar] [CrossRef]
- Rizzo, F. Sensitivity Investigation on the Pressure Coefficients Non-Dimensionalization. Infrastructures 2021, 6, 53. [Google Scholar] [CrossRef]
- Petrini, F.; Li, H.; Bontempi, F. Basis of design and numerical modeling of offshore wind turbines. Struct. Eng. Mech. 2010, 36, 599. [Google Scholar] [CrossRef]
- Zou, Q.; Li, Z.; Wu, H.; Kuang, R.; Hui, Y. Wind pressure distribution on trough concentrator and fluctuating wind pressure characteristics. Sol. Energy 2015, 120, 464–478. [Google Scholar] [CrossRef]
- Delany, N.K.; Sorensen, N.E. Low-Speed Drag of Cylinders of Various Shape; National Advisory Committee for Aeronautics: Washington, DC, USA, 1953. [Google Scholar]
- Vickery, B.J. Fluctuating lift and drag on a long cylinder of square cross-section in a smooth and in a turbulent stream. J. Fluid Mech. 1966, 25, 481–494. [Google Scholar] [CrossRef]
- Lee, B.E. The effect of turbulence on the surface pressure field of a square prism. J. Fluid Mech. 1975, 69, 263–282. [Google Scholar] [CrossRef]
- Bearman, P.W.; Obasaju, E.D. An experimental study of pressure fluctuations on fixed and oscillating square-section cylinders. J. Fluid Mech. 1982, 119, 297–321. [Google Scholar] [CrossRef]
- Igarashi, T. Characteristics of the Flow around a Square Prism. Bull. JSME 1984, 27, 1858–1865. [Google Scholar] [CrossRef]
- Knisely, C.W. Strouhal numbers of rectangular cylinders at incidence: A review and new data. J. Fluids Struct. 1990, 4, 371–393. [Google Scholar] [CrossRef]
- Norberg, C. Flow around rectangular cylinders: Pressure forces and wake frequencies. J. Wind Eng. Ind. Aerodyn. 1993, 49, 187–196. [Google Scholar] [CrossRef]
- Luo, S.; Yazdani, M.; Chew, Y.; Lee, T. Effects of incidence and afterbody shape on flow past bluff cylinders. J. Wind Eng. Ind. Aerodyn. 1994, 53, 375–399. [Google Scholar] [CrossRef]
- Lyn, D.A.; Einav, S.; Rodi, W.; Park, J.-H. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. J. Fluid Mech. 1995, 304, 285–319. [Google Scholar] [CrossRef]
- Tamura, T.; Miyagi, T. The effect of turbulence on aerodynamic forces on a square cylinder with various corner shapes. J. Wind Eng. Ind. Aerodyn. 1999, 83, 135–145. [Google Scholar] [CrossRef]
- van Oudheusden, B.; Scarano, F.; van Hinsberg, N.; Roosenboom, E. Quantitative visualization of the flow around a square-section cylinder at incidence. J. Wind Eng. Ind. Aerodyn. 2008, 96, 913–922. [Google Scholar] [CrossRef]
- Carassale, L.; Freda, A.; Marrè-Brunenghi, M. Experimental investigation on the aerodynamic behavior of square cylinders with rounded corners. J. Fluids Struct. 2014, 44, 195–204. [Google Scholar] [CrossRef]
- van Hinsberg, N.P.; Schewe, G.; Jacobs, M. Experiments on the aerodynamic behaviour of square cylinders with rounded corners at Reynolds numbers up to 12 million. J. Fluids Struct. 2017, 74, 214–233. [Google Scholar] [CrossRef]
- Sohankar, A. Flow over a bluff body from moderate to high Reynolds numbers using large eddy simulation. Comput. Fluids 2006, 35, 1154–1168. [Google Scholar] [CrossRef]
- Oka, S.; Ishihara, T. Numerical study of aerodynamic characteristics of a square prism in a uniform flow. J. Wind Eng. Ind. Aerodyn. 2009, 97, 548–559. [Google Scholar] [CrossRef]
- Ying, X.; Zhang, Z. Prediction of Unsteady Flow around a Square Cylinder Using RANS. Appl. Mech. Mater. 2011, 52–54, 1165–1170. [Google Scholar]
- Tian, X.; Ong, M.C.; Yang, J.; Myrhaug, D. Unsteady RANS simulations of flow around rectangular cylinders with different aspect ratios. Ocean Eng. 2013, 58, 208–216. [Google Scholar] [CrossRef]
- Cao, Y.; Tamura, T. Large-eddy simulations of flow past a square cylinder using structured and unstructured grids. Comput. Fluids 2016, 137, 36–54. [Google Scholar] [CrossRef]
- Zhang, L.Z. Numerical Simulation of Flows past a Circular and a Square Cylinder at High Reynolds Number, and a Curved Plate in Transitional Flow. Master’s Thesis, Washington University, St. Louis, MO, USA, 2017. [Google Scholar]
- Dai, S.S.; Younis, B.A.; Zhang, H.Y. Prediction of Turbulent Flow Around a Square Cylinder With Rounded Corners. J. Offshore Mech. Arct. Eng. 2017, 139, 031804. [Google Scholar] [CrossRef]
- EN1991-1-4:2005/AC:2010 (E); Eurocode 1: Actions on Structures—Part 1–4: General Actions—Wind Actions. European Standard (Eurocode); European Committee for Standardization (CEN): Bruxelles, Belgium, 2010.
- AS/NZS, 1170,2:2002; Structural Design Actions, Part 2: Wind Actions. Standards Australia: Sydney, Australia; Standards New Zealand: Wellington, New Zealand, 2002.
- Okamoto, S.; Uemura, N. Effect of rounding side-corners on aerodynamic forces and turbulent wake of a cube placed on a ground plane. Exp. Fluids 1991, 11, 58–64. [Google Scholar] [CrossRef]
- McClean, J.; Sumner, D. An Experimental Investigation of Aspect Ratio and Incidence Angle Effects for the Flow Around Surface-Mounted Finite-Height Square Prisms. J. Fluids Eng. 2014, 136, 081206. [Google Scholar] [CrossRef]
- Fluent, ANSYS FLUENT 19.2 Theory Guide; Ansys Inc.: Canonsburg, PA, USA.
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal two equation kw turbulence models for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar]
- Argyropoulos, C.D.; Markatos, N.C. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Elshaer, A.; Aboshosha, H.; Bitsuamlak, G.; El Damatty, A.; Dagnew, A. LES evaluation of wind-induced responses for an isolated and a surrounded tall building. Eng. Struct. 2016, 115, 179–195. [Google Scholar] [CrossRef]
- Elshaer, A.; Bitsuamlak, G.; El Damatty, A. Enhancing wind performance of tall buildings using corner aerodynamic optimization. Eng. Struct. 2017, 136, 133–148. [Google Scholar] [CrossRef]
- Sun, X.; Liu, H.; Su, N.; Wu, Y. Investigation on wind tunnel tests of the Kilometer skyscraper. Eng. Struct. 2017, 148, 340–356. [Google Scholar] [CrossRef]
- Tamura, T.; Ohta, I.; Kuwahara, K. On the reliability of two-dimensional simulation for unsteady flows around a cylinder-type structure. J. Wind Eng. Ind. Aerodyn. 1990, 35, 275–298. [Google Scholar] [CrossRef]






| Author | Re ( ×104) | cf,mean | cf,rms | cl,rms | St |
|---|---|---|---|---|---|
| Vickery [18] | 10 | 2.05 | 0.17 | 1.30 | 0.12 |
| Lee [19] | 17.6 | 2.04 | 0.22 | 1.19 | 0.122 |
| Bearman and Obasaju [20] | 2.2 | 2.10 | - | 1.20 | 1.13 |
| Norberg [23] | 1.3 | 2.11 | - | - | 0.131 |
| Luo et al. [24] | 3.4 | 2.21 | 0.18 | 1.21 | 0.13 |
| Lyn et al. [25] | 2.14 | 2.10 | - | - | 0.132 |
| Tamura and Miyagi [26] | 3 | 2.10 | - | 1.05 | 0.13 |
| Van Oudheusden et al. [27] | 2 | 2.19 | - | - | - |
| Carassale et al. [28] | 37 | 2.06 | - | 1.02 | 0.125 |
| Our study | 2.2 | 2.09 | 0.158 | 1.17 | 0.134 |
| Author | Method | Re (×104) | cf,mean | cf,rms | cL,rms | St |
|---|---|---|---|---|---|---|
| Sohankar [30] | LESs | 2.2 | 2.25 | 0.200 | 1.50 | 0.130 |
| Oka and Ishihara [31] | LESs | 1 | 2.06 | 0.140 | 1.26 | 0.125 |
| Xu and Zhang [32] | URANS | 2.14 | 2.09 | - | 1.39 | 0.121 |
| Tian et al. [33] | URANS | 2.14 | 2.06 | - | 1.49 | 0.138 |
| Cao and Tamura [34] | LESs | 2.2 | 2.21 | 0.205 | 1.26 | 0.132 |
| Zhang [35] | URANS | 2.2 | 2.20 | - | - | - |
| Dai et al. [36] | URANS | 2 | 2.00 | 0.204 | 1.13 | 0.130 |
| Our study | URANS | 2.2 | 2.09 | 0.158 | 1.17 | 0.134 |
| Re | Variable | Our Study | Delany et al. [17] | Sohankar [30] | EN1991-1-4 [37] |
|---|---|---|---|---|---|
| 5 × 103–5 × 104 | cf,mean | 2.09 | 1.9 | 2.24 | 2.1 |
| cf,rms | 0.16 | - | 0.2 | - | |
| cl,rms | 1.17 | - | 1.45 | - | |
| St | 0.134 | - | 0.123 | 0.12 | |
| 3 × 105–3 × 106 | cf,mean | 2.28 | 1.95 | 2.29 | 2.1 |
| cf,rms | 0.18 | - | 0.18 | - | |
| cl,rms | 1.61 | - | 1.51 | - | |
| St | 0.1 | - | 0.128 | 0.12 | |
| 4 × 106–107 | cf,mean | 2.35 | - | 2.24 | 2.1 |
| cf,rms | 0.15 | - | 0.2 | - | |
| cl,rms | 1.37 | - | 1.58 | - | |
| St | 0.1 | - | 0.124 | 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karvelis, A.C.; Dimas, A.A.; Gantes, C.J. Unsteady Numerical Simulation of Two-Dimensional Airflow over a Square Cross-Section at High Reynolds Numbers as a Reduced Model of Wind Actions on Buildings. Buildings 2024, 14, 561. https://doi.org/10.3390/buildings14030561
Karvelis AC, Dimas AA, Gantes CJ. Unsteady Numerical Simulation of Two-Dimensional Airflow over a Square Cross-Section at High Reynolds Numbers as a Reduced Model of Wind Actions on Buildings. Buildings. 2024; 14(3):561. https://doi.org/10.3390/buildings14030561
Chicago/Turabian StyleKarvelis, Aggelos C., Athanassios A. Dimas, and Charis J. Gantes. 2024. "Unsteady Numerical Simulation of Two-Dimensional Airflow over a Square Cross-Section at High Reynolds Numbers as a Reduced Model of Wind Actions on Buildings" Buildings 14, no. 3: 561. https://doi.org/10.3390/buildings14030561
APA StyleKarvelis, A. C., Dimas, A. A., & Gantes, C. J. (2024). Unsteady Numerical Simulation of Two-Dimensional Airflow over a Square Cross-Section at High Reynolds Numbers as a Reduced Model of Wind Actions on Buildings. Buildings, 14(3), 561. https://doi.org/10.3390/buildings14030561










