Abstract
Non-engineered buildings (NEBs) are prone to earthquake damage. One type of damage that often occurs in NEBs is the separation of beam and column elements owing to joint failures. Strengthening joints with steel plates is expected to improve the seismic performance of this type of building. Strengthening with steel plates is cheap and easy to apply, so it will be a preferable choice in preventing damage to the NEB due to earthquake loads. This study investigated the seismic performance of reinforced concrete frames, representing an NEB whose beam–column joints were strengthened with L-shaped steel plates. Two widths of L-shaped steel plates were proposed: 75 mm (NEB-075) and 100 mm (NEB-100). An NEB without strengthening (NEB-000) was used as a control. Both experimental and numerical investigations were performed to determine the seismic performance of NEBs. The results showed that damage to the NEB-000 and NEB-075 models occurred at the joints, but less damage was observed in NEB-075 than in NEB-000. Furthermore, damage in the NEB-100 model occurred at the column. The undamaged limit levels of the NEB-000, NEB-075, and NEB-100 models were 56.49, 81.54, and 82.46%, respectively. These results show that strengthening the NEB with steel plates effectively improves its seismic performance. According to an analysis of the performance of the tested models, the NEB-100 model exhibited the best seismic performance.
1. Introduction
Indonesia is prone to earthquakes as it lies between three active tectonic plates: the Eurasian, Indo-Australian, and Pacific plates. Boen T. [1] reported that earthquakes occur almost annually in various regions of Indonesia. Most damage caused by earthquakes occurs in lower-class residential houses because these are usually non-engineered buildings (NEBs). These buildings fail to meet the technical requirements of earthquake-resistant buildings, as they are constructed based on local customs, using poor quality materials and by workers lacking understanding of the technical requirements of earthquake-resistant buildings. These construction practices are prevalent among lower-class communities that cannot afford to build structures meeting standardized requirements.
The seismic damage in NEBs is mainly due to poor concrete quality, an insufficient reinforcement ratio, unsatisfactory spacing of shear reinforcements, and inadequate development length of the longitudinal reinforcements, as shown in Figure 1. An insufficient longitudinal reinforcement length fails to satisfy anchorage requirements. Hence, the column and beam sections that constitute a building do not form integrated elements [2].

Figure 1.
(a) Insufficient reinforcement ratios of column in non-engineered building and (b) inadequate shear reinforcement and development lengths/anchorage of longitudinal reinforcements.
The noncompliant reinforcement at the joints, coupled with low-quality concrete, render the joint area the weakest point of the NEB structure against earthquake loads. A weak joint cannot distribute the internal stress. Consequently, it breaks, causing the column and beam sections to separate, even under low- to medium-intensity earthquakes. The separation of elements at the beam and column joints in an NEB causes a total collapse, leading to a large number of casualties and substantial economic losses [3].
The government and stakeholders of the Republic of Indonesia have taken the initiative in disaster mitigation, particularly concerning earthquake-resistant structures in low-income housing; this initiative involves issuing guidelines for earthquake-resistant residential construction [4]. Additionally, they provide technical training to construction workers to familiarize them with the fundamentals of constructing earthquake-resistant buildings. However, owing to the extensive regions that need to be covered, many areas still do not have access to the required education or knowledge regarding the basics of earthquake-resistant building construction. Therefore, low-income housings are built without adequate technical knowledge. Additionally, numerous buildings from the past have been constructed without considering earthquake-resistant building criteria. Therefore, structural engineers are obliged to help communities by providing technical advice for improving the seismic performance of existing NEBs. The improved performance lowers the probability of seismic damage of existing NEBs and subsequently increases the resilience of lower-class communities against future earthquakes.
One way to improve the seismic performance of existing NEBs is structural strengthening. Various materials and methods of strengthening, including the use of carbon fiber-reinforced polymer (CFRP) [5,6,7,8], glass fiber-reinforced polymer (GFRP) [9,10,11], aramid fiber-reinforced polymer (AFRP) [5], textile-reinforced mortar (TRM) [12,13,14,15], and steel plates [16,17,18], can be employed in such cases. Some of these materials have been used to strengthen joints and improve the seismic performance of reinforced-concrete structures. The AFRP, GFRP, and AFRP are widely used in strengthening engineered buildings. However, these materials are unsuitable for strengthening NEBs, especially in developing countries, because they are expensive. The materials for strengthening NEBs should be cheap and easy to implement, and must perform well. The material that meets these criteria is steel plates. Therefore, this research uses steel plates as a strengthening material for beam and column joints in NEBs.
Joint strengthening is intended to increase the joint’s strength and stiffness. A strengthened joint must be more robust than the connected elements, such that the failure of the joint does not precede the failure of the beam or column to which the joint is connected. The strengthened joint must also be sufficiently rigid to distribute the internal stress from one element to another, so that the structure can adequately withstand external loads. Ultimately, strengthening the joint should effectively improve the seismic performance of the structure, thus lowering the probability of damage or failure [18].
The probability of damage or failure can be quantified by constructing fragility curves. A fragility curve is a graphical representation of the relationship between the intensity of a natural hazard, such as an earthquake, and the resulting damage to or performance of a structure. This graph typically begins at the origin and increases as the hazard intensity increases. This provides essential insights into the probabilities of different levels of damage or performance for a particular hazard intensity. Strengthening the joints is expected to reduce the probability of damage to NEB structures [19].
The strengthening of NEBs necessitates the selection of strengthening materials with specific criteria, primarily considering the ease of application and affordability, for an effective increase in the seismic performance. Based on these considerations, a steel plate is a good choice, as it is affordable for low-income families. This material can be easily applied to strengthen the underrated beam–column joints of NEBs. Previous research has indicated that steel plates are adequate for increasing the capacity of strengthened structures [18]. In the current research, further investigation is carried out to determine not only the increase in the structural capacity of the strengthened structures, but also the influence of a joint strengthened using steel plates on the progressive damage of the structures, especially on the reduction in joint damage. The identified progressive damage is then used to define the damage-state levels using the criteria established by FEMA [20,21,22]. To the best of our knowledge, no study has defined the seismic damage state levels of NEBs whose joints are strengthened using steel plates. The damage state levels defined in this study were used to determine the seismic fragility curves of the strengthened structures. The curves are presented and compared with those of the unstrengthened structure to demonstrate the effective use of steel plates for improving the seismic performance of NEBs.
2. Materials
This study employed both experimental and numerical investigations. An experimental investigation was conducted by testing models of reinforced concrete (RC) frames that represent NEBs. The concrete used to construct this model was of substandard quality and did not meet the technical requirements of the structural concrete regulations for buildings. The steel reinforcements used for the construction of the models are typically used for residential building constructions in Indonesia and are widely available on the market. Table 1 lists the properties of the materials used to construct the model, including the steel plates used to strengthen the joints.

Table 1.
Properties of the materials utilized for constructing the structural models.
3. Methods
3.1. RC Frame Structure Model
The experiments utilized three distinct RC frame structure models:
- An NEB portal model without joint strengthening (NEB-000);
- An NEB model with beam–column joint strengthening using a 75 mm wide plate (NEB-075);
- An NEB model with beam–column joint strengthening using a 100 mm wide steel plate (NEB-100).
The portal models consisted of columns with dimensions of 150 mm × 150 mm and a total height of 2500 mm. The column used four longitudinal reinforcements with diameters of 10 mm (4D10) and shear reinforcements with diameters of 6 mm at a distance of 200 mm (D6-200). The beams had widths, heights, and total lengths of 150, 200, and 3000 mm, respectively. The beams were reinforced with four longitudinal reinforcements 10 mm in diameter (4D10) and shear reinforcements 6 mm in diameter at a distance of 200 mm (D6-200). For NEB-075 and NEB-100, both sides of the beam–column joints were reinforced with steel plates bonded to the concrete surface using Sikadur 31 CF adhesive. A glue thickness of ±5 mm was applied, and the steel plates were then connected with six fischer bolts with diameters of 8 mm and lengths of 60 mm. Three bolts were installed in the column direction and three beam directions. The bolt installation distance from the edge was 50 mm, and the distance between bolts was 200 mm. Subsequently, the steel plates and concrete were clamped for seven days to ensure that the steel plates were fully attached to the concrete surface with no signs of separation. Figure 2 and Table 2 present the specifications of the RC-frame structure models.
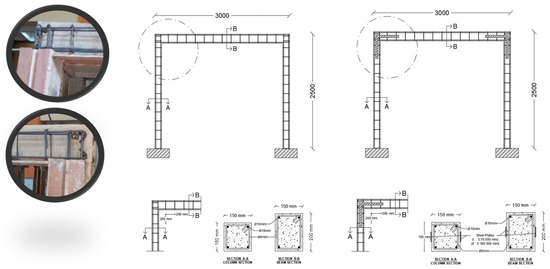
Figure 2.
Specifications of the RC frame models.

Table 2.
Types of the RC frame structure models.
3.2. Loading Protocol
Several researchers have carried out many cyclic and non-cyclic tests with the loading speed and strain response that occurs [23,24,25,26]. The loading protocol for the experiment followed the ACI standard 374.1-05 [27]. The loading cycle, shown in Figure 3, can be explained as follows.
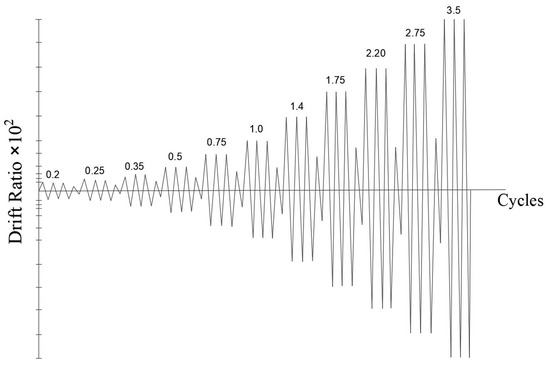
Figure 3.
Loading cycle based on displacement, controlled following ACI TI 374.1-05 [27].
The specimens were loaded with a sequence of displacement control cycles, representative of the drift expected to occur in the joint during an earthquake.
- Three complete cycles were applied for each drift ratio.
- The initial drift ratio was 0.002 (0.2%) in the test, and it was within the range of the linear elastic behavior of the specimen. The subsequent drift ratios were at least 1.25 times, but not more than 1.5 times, the previous drift ratio.
- The test was conducted by gradually increasing the drift ratio until a minimum drift ratio of 0.035 (3.5%) was achieved.
3.3. Experimental Setup
Experimental testing of the structural model was performed via dynamic pseudo-loading. The load was applied using a hydraulic jack (capacity: 250 kN), with a load cell attached to its end. The experimental setup is illustrated in Figure 4.
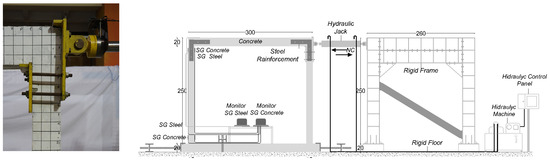
Figure 4.
Experimental setup of the structural model.
4. Numerical Investigation
A numerical investigation of the structural model was conducted to complement the laboratory investigation and obtain more detailed data related to the progressive damage occurring in the structural model, such as when cracking began to appear, the subsequent development and propagation of cracks with increasing load, the pattern of the cracks, and the yielding of the reinforcement. The numerical investigation used the advanced tool for engineering nonlinear analysis (ATENA) software v5.9.0. The modeling implemented the following materials, as defined in ATENA: 3D Nonlinear Cementitious 2 for the concrete elements, 3D nonlinear steel von Mises for the steel plate elements, and reinforcement for the longitudinal and shear reinforcement elements. This numerical test used a global element size of 4 cm × 4 cm.
In ATENA, 3D Nonlinear Cementitious 2 is a fracture–plastic constitutive model that combines two separate models to simulate the tensile (fracturing) and compressive (plastic) behaviors of concrete. This fracture model is based on the Rankine failure criterion and exponential softening, whereas the hardening/softening plasticity model is derived from the Menétree–Willam failure surface. This model is designed to handle cases in which the failure surfaces of both models are active and can be used to simulate concrete cracking, crushing under high confinement, and crack closure owing to crushing in other material directions. The concrete material parameters based on the ATENA software v5.9.0 manual [28,29,30,31] are listed in Table 3.

Table 3.
Parameters of concrete material according to ATENA (adapted from ATENA Program Documentation Part 1 Theory [30] (p. 33)).
The 3D bilinear steel von Mises plasticity model is widely used to simulate the plastic deformation behavior of materials, particularly metals and alloys. This is based on the von Mises yield criterion, which is widely accepted for predicting the onset of plastic deformation in materials. Figure 5 shows the parameters of the model applied to the steel plates.
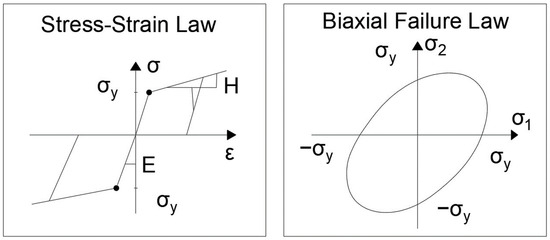
Figure 5.
Parameters of the model applied to the steel plates.
The reinforcement can be discretely modeled as bars and represented by truss elements. The multilinear law, which consists of four lines, is used to model all four stages of steel behavior: elastic state, yield plateau, hardening, and fracture. A multiline is defined by the four points that the input can specify. The software also provides the option of using a simpler constitutive model in the form of a bilinear model with hardening. In this study, the bilinear hardening models of the longitudinal and shear reinforcements are shown in Figure 6.
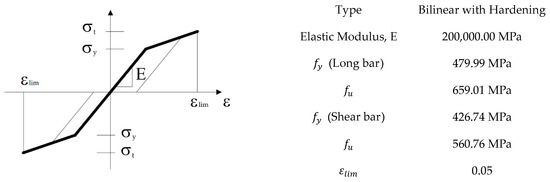
Figure 6.
Parameters of the model applied for reinforcement.
Unlike the experimental investigation, which applied a pseudo-dynamic load, the loading on the structural model in the numerical investigation was performed by applying a lateral static load to the joint at certain increments until the structure collapsed. The application of a static load was sufficient to obtain the necessary information on the behavior of the structure in terms of the global response and progressive damage that occurs in it.
The bond between the concrete and reinforcement is affected by the quality of the concrete and the confinement of the stirrup. The bond model used in this numerical test was a perfect connection.
5. Results and Analysis
5.1. Load Displacement
The structural models were tested with pseudo-dynamic loading and displacement envelopes were generated, as illustrated in Figure 7a. The peak loads and their corresponding displacements at each cycle during the compressive and tensile loading were used to create the envelope curves. Figure 7b shows a comparison of the load–displacement curves obtained from the numerical investigation (ATENA) with the experimental test, Figure 7a. In the figure, the load–displacement graphs resulting from the numerical investigation are directly compared with the envelope curves of compressive loading obtained from the experimental investigation. The essential parameters extracted from these curves are the maximum load values and their corresponding displacements. These values are listed in Table 4.
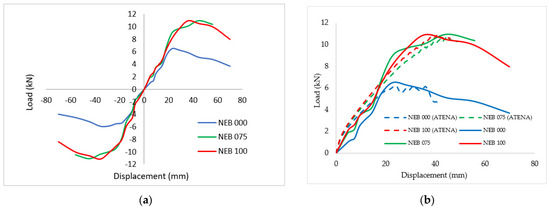
Figure 7.
(a) Envelope curves obtained from the experimental investigation and (b) comparison of the load-displacement curves obtained from the numerical investigation with the compressive envelop curves.

Table 4.
Maximum load and its corresponding displacement.
Figure 7 and Table 4 suggest that strengthening the joints of the structural models using steel plates (NEB-075 and NEB-100) can significantly improve the load capacity. The NEB-075 model showed a 68.92% increase in the load capacity (from 6.50 kN to 10.98 kN), while the NEB-100 model experienced a 68.31% increase (from 6.50 kN to 10.95 kN). Although the NEB-100 model exhibited nearly the same increase as that of NEB-075, it exhibited improved ductility. This improved ductility indicates that NEB-100 can better maintain the integrity of the beam and column elements.
5.2. Crack Pattern
The crack pattern at the final level of experimental testing and numerical testing is shown in Figure 8, Figure 9 and Figure 10. Figure 8 shows the failure pattern on a normal test specimen, while Figure 9 and Figure 10 show the failure pattern of a test object reinforced with a 75 mm wide steel plate and 100 mm. Based on Figure 8, Figure 9 and Figure 10, it can be seen that the collapse pattern initially occurred in the joint area, subsequently moving to the column area. This shows the effectiveness of steel plate reinforcement, which is able to maintain the integrity of the beam and column elements, thereby reducing the destruction of the NEB structure.

Figure 8.
Damage observed in NEB-000, (a) right joint and (b) left joint.
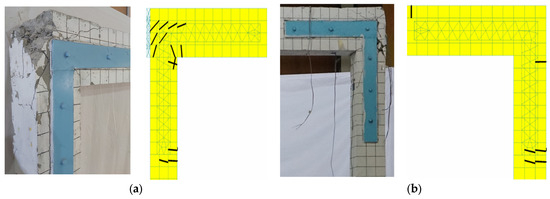
Figure 9.
Damage observed in NEB-075, (a) right joint and (b) left joint.

Figure 10.
Damage observed in NEB-100, (a) right joint and (b) left joint.
5.2.1. NEB-000 Model
Both the experimental and numerical investigations indicate a concentrated crack pattern at the joints of the NEB-000 model (Figure 8). This confirms that, without strengthening, the joints are fragile; thus, portal collapse originates from severe damage in this region. Hence, under seismic loading, the NEB-000 experienced a complete collapse.
5.2.2. NEB-075 Model
Figure 9 shows the crack patterns that occurred in NEB-075. At the left joint, the cracks were concentrated in the joint area, but with less intensity than those of NEB-000. However, no concentrated cracks were observed in the right joint. Instead, the crack shifted to the beam and column regions at the right at the end of the steel plate. These cracks confirm that the steel plates can modify the collapse pattern and subsequently increase the capacity of the portal to withstand seismic loads. Additionally, even in the case of substantial damage to the left joint, the steel plate can distribute the stress among the beam–column elements; thus, the structure can withstand a higher load.
5.2.3. NEB-100 Model
Figure 10 shows the cracks and damage that occurred on NEB-100. Lower crack intensity was observed in this portal compared to other portals. On the NEB-100 portal, the damage did not come from the joint, but rather a crack in the end column of the steel plate. The cracks in this section widened as the load increased, ultimately causing serious damage to the column. The yield stress of the reinforcement was reached at 480.9 MPa (at stage 71) at a drift ratio of 1.51%. Damage to NEB-100 occurred in the column section, while damage to NEB-000 and NEB 075 occurred in the beam–column connection section. This difference shows that the NEB 100 model succeeded in transferring damage that was more global in nature, namely, that which occurred at joints, to parts that were more local in nature, namely, column elements. Damage to this part of the column initiated the failure of the NEB-100 before it completely collapsed (Figure 10). These results show that variations in strengthening with steel plates at column–beam joints have resulted in better strengthening than that of the model. These results corroborate the conclusion that joint strengthening can change the collapse mode and increase the portal capacity against seismic loading.
5.3. Energy Dissipation
Ground shaking during an earthquake causes the structure to vibrate, owing to lateral dynamic forces which it experiences. These forces can be destructive; however, the energy transferred to the structure can be reduced by energy-dissipating mechanisms. Energy dissipation refers to the ability of a structure to absorb and disperse the energy released during an earthquake. Energy dissipation can be quantified using the area under the load–displacement behavior of the structure (Figure 7). Table 5 presents the results.

Table 5.
Energy dissipation of the NEB models.
Table 5 indicates that strengthening the joints with 100 mm wide steel plates resulted in a 76.19% increase in energy dissipation compared to the structural model without joint strengthening. In comparison, 75 mm steel plates only increased the energy dissipation by 37.02%. Consequently, 100 mm steel plates were more effective than 75 mm plates in enhancing the energy dissipation of NEBs.
5.4. Damage State
The HAZUS-MZ standard [32] classifies the level of damage to buildings into four distinct categories: light (DS1/Slight), medium (DS2/Moderate), near-collapse (DS3/Near Collapse), and collapse (DS4/Collapse). Several engineering demand parameters have been proposed to assess the damage limit state accurately. In this study, the damage state was determined using the FEMA guidelines for reinforced concrete frames (C1) [32]. Table 6 outlines the criteria of the HAUZ-MZ standard [32] for assessing the extent of each damage state.

Table 6.
Description of the structural damage states of a reinforced concrete frame (C1) (adapted from Hazus Earthquake Model Technical Manual [32] (pp. 5–15)).
Based on the criteria in Table 6, the displacement load data from experimental testing and steel yield stress data based on numerical testing can determine the damage state of the test object model. Values of load displacement to define hysteresis characteristic parameters are shown in Table 7; for example, DS1 indicates that the first crack occurred at a load of 1.37 kN and a displacement of 3.69 mm, as well as for other points. Furthermore, these capacity curves can be converted into ADRS curves that correlate spectral displacement (Sd) to spectral acceleration (Sa) following the provisions of ATC–40 to determine the damage state. The damage state values are shown in Table 8. Figure 11 shows the points on the capacity curve where damages at the DS1–DS4 levels occurred. This facilitated the expression of damage limit states in terms of Sa or Sd values (Table 8 and Figure 12).

Table 7.
Load displacement to define hysteresis characteristic parameters.

Table 8.
Damage limit state of NEBs expressed in terms of Sa and Sd.
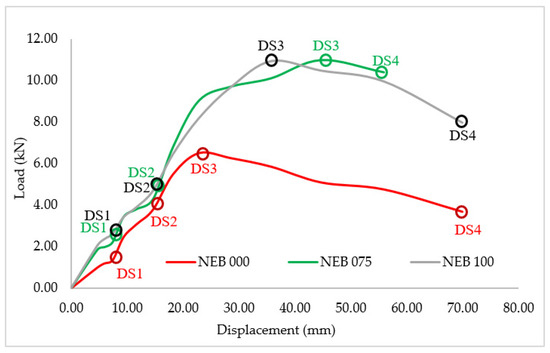
Figure 11.
Capacity curve of the NEBs with points representing the load or displacement in various damage states.
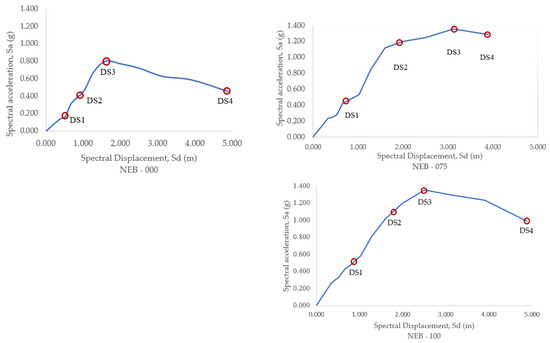
Figure 12.
Spectrum capacity of the NEBs with points representing Sa or Sd in various damage states.
5.5. Structural Uncertainty
Structural engineers must consider a range of uncertain factors when conducting seismic analysis. This includes the material properties, construction methods, and environmental conditions that affect the performance of the structure. A comprehensive understanding and quantification of these sources of uncertainty are essential for establishing the reliability of the analysis. This realm of uncertainty, commonly referred to as structural uncertainty, encompasses a variety of factors that can influence the response of a structure to loading. Investigating and addressing these uncertainties is imperative for determining the probable damage state. The FEMA formula was used to determine the uncertainty value [27].
Here, βSds is the lognormal standard deviation that describes the total variability for the structural damage state, ds. βC is the lognormal standard deviation parameter that describes the variability of the capacity curve, calculated by Equation (1). βD is the lognormal standard deviation parameter that describes the variability of the demand spectrum. βD is set to 0.45 for a short period and 0.50 for a long period. is the median value of the spectral displacement of structural components for the damage state, ds. is the lognormal standard deviation parameter that describes the uncertainty in the estimated median value of the structural damage state threshold. βM(Sds) is taken as 0.40. The function “CONV” in Equation (1) implies a complex process of convolving probability distributions of the demand spectrum and capacity curve. From Equation (2), s is the standard deviation of the structure’s spectral acceleration capacity and m is the average of the structure’s spectral acceleration capacity. The results of the structural uncertainty calculation are presented in Table 9.

Table 9.
The structural uncertainty of the NEBs.
5.6. Fragility Analysis
5.6.1. Fragility Curve of NEBs
The fragility curve shows the changes in the probability of structural damage with respect to various demand parameters. This probability can be calculated according to the formula provided by FEMA [27], as follows:
where is the standard normal cumulative distribution function. βds is the standard deviation of the natural logarithm of spectral displacement for the damage state, ds. is the median value of the spectral displacement at which the building reaches the threshold of the damage state, ds. The resulting fragility curves of the NEBs are shown in Figure 13.
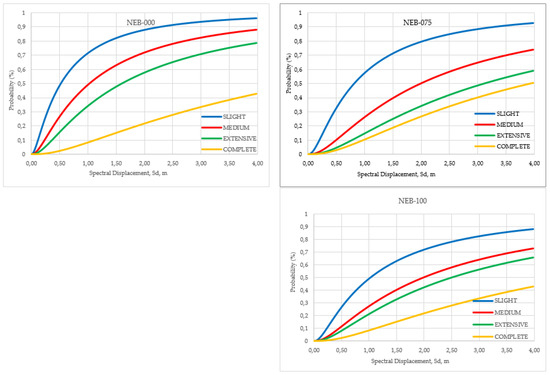
Figure 13.
Fragility curves of the NEBs.
5.6.2. Discrete Damage of NEBs
Figure 13 was analyzed to determine the discrete damage, representing the probability of damage at each level. In this study, the discrete damage of the NEB models was assessed by applying earthquake loads with a 500-year return period (DBE) and 2500-year return period (MCE) in the Surakarta area of Central Java, Indonesia. The results of the discrete damage analysis of the NEB model are presented in Table 10.

Table 10.
Discrete damage of the NEB models.
Based on Table 10, the undamaged values of the NEB models without joint strengthening and with joint strengthening using 75 and 100 mm wide plates were 56.49, 81.54, and 82.46%, respectively. These values indicate that strengthening the beam–column joint section with steel plates improves the seismic performance. There was also a tendency for joint strengthening to result in less damage at medium to complete levels. The best performance was achieved by strengthening with 100 mm wide steel plates.
6. Conclusions
This research resulted in the following conclusions:
- The NEB model without joint strengthening tended to experience severe damage in the joint area. This joint damage could potentially cause the beam and column elements to break. The NEB model with joint strengthening using 75 mm wide steel plates reduced the level of joint damage, whereas the NEB model with 100 mm wide steel plates transferred the damage from the joint areas to the column sections at the end of the steel plates. These findings confirm that steel plates can maintain the integrity of beam and column elements and reduce the severity of damage.
- Strengthening the joints of the NEBs using 75 and 100 mm wide steel plates increased the load-bearing capacity by 68.92 and 68.31%, respectively. Compared to using 75 mm wide steel plates, strengthening the joints of NEBs with 100 mm wide steel plates was more effective in preserving the integrity of the beam–column elements. This improved the ductility and energy dissipation of the structure.
- Strengthening the joints of NEBs with 75 and 100 mm wide steel plates can change the damage limit states of NEBs. Subsequently, it also improves the seismic performance of the structure, as the structure exhibited higher undamaged values than the NEBs without joint strengthening.
- The use of steel plates as strengthening materials in NEB effectively improved the seismic performance and integrity of the structural elements. This material is relatively affordable for lower-class communities and easy to apply.
Author Contributions
E.P. contributed to the research concept, modeling, testing, data processing, and drafting the manuscript, S.A.K. contributed to refining the concept, reviewing the testing, data processing, and the manuscript, S.S. contributed to refining the concept and the manuscript, H.A.S. contributed to reviewing the testing and the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Sebelas Maret University (grant number 254/UN27.22/PT.01.03/2022).
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Boen, T. Earthquake Resistant Design of Non-Engineered Buildings in Indonesia; Building Trust International: Jakarta, Indonesia, 2001; p. 34. Available online: https://www.researchgate.net/publication/238659833 (accessed on 2 November 2019).
- Santiago, W.C.; Beck, A. A study of brazilian concrete strength (non-)compliance and its effects on reliability of short columns. IBRACON Struct. Mater. J. 2011, 4, 663–676. [Google Scholar]
- Kristianto, A.; Imran, I.; Suarjana, M.; Pane, I. Confinement of Reinforced-Concrete Columns with Non-Code Compliant Confining Reinforcement plus Supplemental Pen-Binder. ITB J. Eng. Sci. 2012, 44, 220–237. [Google Scholar] [CrossRef]
- Badan Standarisasi Nasional. Persyaratan Beton Struktural untuk Bangunan Gedung SNI 2847-2013; Badan Standarisasi Nasional: Jakarta, Indonesia, 2013; p. 265. [Google Scholar]
- Ha, G.-J.; Ha, Y.-J.; Kang, H.-W. Improvement and Evaluation of Seismic Performance of Reinforced Concrete Exterior Beam-Column Joints Retrofitting with Fiber Reinforced Polymer Sheets and Embedded CFRP Rods. J. Korea Inst. Struct. Maint. Insp. 2015, 19, 151–159. [Google Scholar] [CrossRef]
- Le-Trung, K.; Lee, K.; Lee, J.; Lee, D.H.; Woo, S. Experimental study of RC beam–column joints strengthened using CFRP composites. Compos. Part B Eng. 2010, 41, 76–85. Available online: https://www.sciencedirect.com/science/article/pii/S135983680900119X (accessed on 31 October 2019). [CrossRef]
- Ilia, E.; Mostofinejad, D. Seismic retrofit of reinforced concrete strong beam–weak column joints using EBROG method combined with CFRP anchorage system. Eng. Struct. 2019, 194, 300–319. [Google Scholar] [CrossRef]
- Tafsirojjaman, T.; Fawzia, S.; Thambiratnam, D.P. Structural behaviour of CFRP strengthened beam-column connections under monotonic and cyclic loading. Structures 2021, 33, 2689–2699. [Google Scholar] [CrossRef]
- Meenakshi, B.; Suguna, K.; Raghunath, P. Effect of confinement on concrete beams under cyclic loading with GFRP laminates. Mater. Today Proc. 2021, 45, 6633–6637. [Google Scholar] [CrossRef]
- Roy, B.; Laskar, A.I. Cyclic Performance of Beam-Column Subassemblies with Construction Joint in Column Retrofitted with GFRP. Structures 2018, 14, 290–300. [Google Scholar] [CrossRef]
- Madupu, L.S.; Ram, K.S. Performance of axially loaded reinforced concrete rectangular columns strengthened with GFRP strips. Mater. Today Proc. 2020, 43, 1784–1791. [Google Scholar] [CrossRef]
- Koutas, L.; Pitytzogia, A.; Triantafillou, T.C.; Bousias, S.N. This is a repository copy of Strengthening of infilled reinforced concrete frames with TRM: Study on the development and testing of textile-based anchors. J. Compos. Constr. 2014, 18, 1–33. [Google Scholar] [CrossRef]
- Koutas, L.; Bousias, S.N.; Triantafillou, T.C. Seismic Strengthening of Masonry-Infilled RC Frames with TRM: Experimental Study. J. Compos. Constr. 2015, 19, 1–33. [Google Scholar] [CrossRef]
- Koutas, L.N.; Bournas, D.A. Confinement of masonry columns with textile-reinforced mortar jackets. Constr. Build. Mater. 2020, 258, 120343. [Google Scholar] [CrossRef]
- Giese, A.C.H.; Giese, D.N.; Dutra, V.F.P.; Filho, L.C.P.D.S. Flexural behavior of reinforced concrete beams strengthened with textile reinforced mortar. J. Build. Eng. 2021, 33, 101873. [Google Scholar] [CrossRef]
- Deng, B.-Y.; Liu, X.; Yu, K.-Q.; Li, L.-Z.; Chen, Y. Seismic retrofitting of RC joints using steel cage and haunch with bolted steel plate. Structures 2022, 43, 285–298. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, X.; Wu, R.; Li, L.; Lu, Z.; Yu, K. Seismic retrofit of large-scale interior RC beam-column-slab joints after standard fire using steel haunch system. Eng. Struct. 2022, 252, 113585. [Google Scholar] [CrossRef]
- Rahmi, Y.; Saputra, A.; Siswosukarto, S. Numerical Modelling of Interior RC Beam-Column Joints for Non-Engineered Buildings Strengthened Using Steel Plates. MATEC Web Conf. 2017, 138, 02007. [Google Scholar] [CrossRef][Green Version]
- Purwanto, E.; Adri, P.A.; Kristiawan, S.A.; Sangadji, S.; Alfisa, S.H. Strengthening of Non-engineered Building Beam-Column Joint to Increase Seismic Performance with Variation of Steel Plate Width BT. In Proceedings of the 5th International Conference on Rehabilitation and Maintenance in Civil Engineering, Surakarta, Indonesia, 8–9 July 2021; Kristiawan, S.A., Gan, B.S., Shahin, M., Sharma, A., Eds.; Springer Nature Singapore: Singapore, 2023; pp. 215–224. [Google Scholar]
- FEMA. HAZUS-MH MR4 Multi-Hazard Loss Estimation Methodology—Earthquake Model: Technical Manual; Department of Homeland Security/FEMA: Washington, DC, USA, 2003. [Google Scholar]
- FEMA. Technical and User’s Manual of Advanced Engineering Building Module (AEBM) “Hazus MH 2.1.”; FEMA: Washington, DC, USA, 2015. [Google Scholar]
- FEMA. Hazus–MH 2.1: Technical Manual; FEMA: Washington, DC, USA, 2012. [Google Scholar]
- Wang, C.; Xiao, J. Evaluation of the stress-strain behavior of confined recycled aggregate concrete under monotonic dynamic loadings. Cem. Concr. Compos. 2018, 87, 149–163. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, J.; Qi, C.; Li, C. Rate sensitivity analysis of structural behaviors of recycled aggregate concrete frame. J. Build. Eng. 2022, 45, 103634. [Google Scholar] [CrossRef]
- Wang, C.; Wu, H.; Li, C. Hysteresis and damping properties of steel and polypropylene fiber reinforced recycled aggregate concrete under uniaxial low-cycle loadings. Constr. Build. Mater. 2022, 319, 126191. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, J.; Liu, W.; Ma, Z. Unloading and reloading stress-strain relationship of recycled aggregate concrete reinforced with steel/polypropylene fibers under uniaxial low-cycle loadings. Cem. Concr. Compos. 2022, 131, 104597. [Google Scholar] [CrossRef]
- ACI374.1; Acceptance Criteria for Moment Frames Based on Structural Testing and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2005; p. 13.
- Cervenka Consulting. ATENA Program Documentation; Cervenka Consulting: Prague, Czech Republic, 2007. [Google Scholar]
- Cervenka, J.; Libor, J. ATENA Program Documentation; Part 6; Cervenka Consulting: Prague, Czech Republic, 2015. [Google Scholar]
- Červenka, J. ATENA Program Documentation Part 2-1 User’s Manual for ATENA 2D. In ATENA Program Documentation Part 4-1 Tutorial for Programme ATENA 2D; Červenka Consulting: Prague, Czech Republic, 2015; Volume 4–1, pp. 1–62. [Google Scholar]
- Cervenka, V.; Jendele, L.; Cervenka, J. ATENA Program Documentation Part 1 Theory; Atena: Prague, Czech Republic, 2012; pp. 1–282. [Google Scholar]
- Federal Emergency Management Agency (FEMA). Hazus Earthquake Model Technical Manual; Hazus 4.2.; FEMA: Washington DC, USA, 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).