Prediction of the Compressive Strength of Vibrocentrifuged Concrete Using Machine Learning Methods
Abstract
1. Introduction
- -
- An in-depth examination of the existing machine learning techniques for determining the physical and mechanical attributes of concrete.
- -
- Justification of the need to supplement traditional methods for determining the strength of vibrocentrifuged concrete with forecasting tools based on machine learning methods;
- -
- Preparation of empirical data obtained during real physical experiments;
- -
- Using Feature Engineering technology to improve the accuracy of the model by adding a new feature with information about cluster membership to the original data set;
- -
- Description of the selected machine learning models, their implementation in order to compare of the data of their prediction with experimental results based on the main quality metrics of regression models.
2. Materials and Methods
2.1. Materials for Concrete
- (1)
- Portland cement CEM I 52.5N (Serebryakovcement, Mikhailovka, Russia) with a specific surface area of 340 m2/kg, compressive strength after 28 days of hardening—56.0 MPa;
- (2)
- Crushed sandstone (Sokolovsky quarry, Novoshakhtinsk, Russia) with grain sizes from 5 to 20 mm;
- (3)
- River sand (Kagalnitsky quarry, Kagalnik, Russia) with a fineness modulus of 1.43 and a bulk density of 1400 kg/m3
2.2. Preparation Parameters and Composition of Vibrocentrifuged Concrete
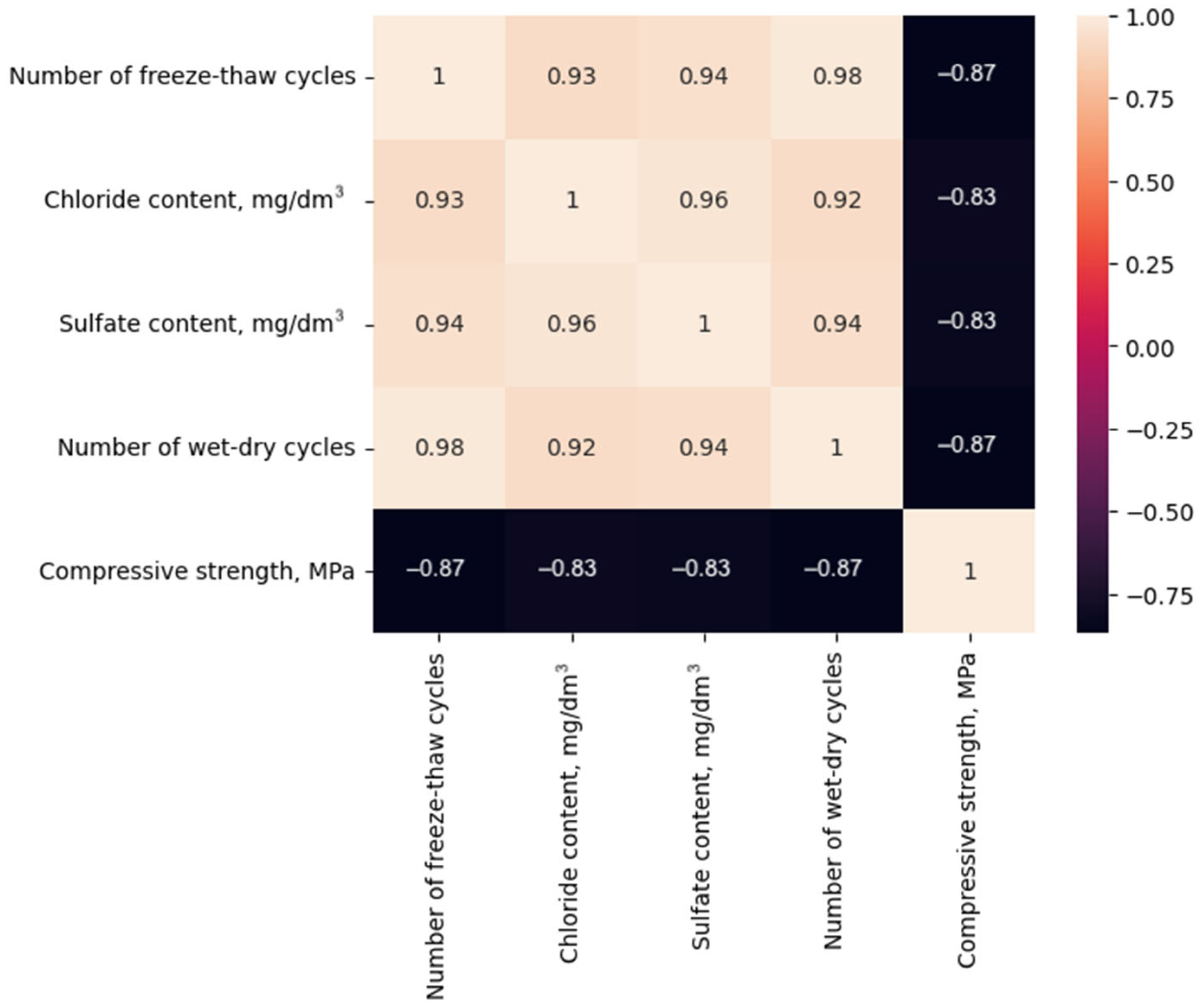
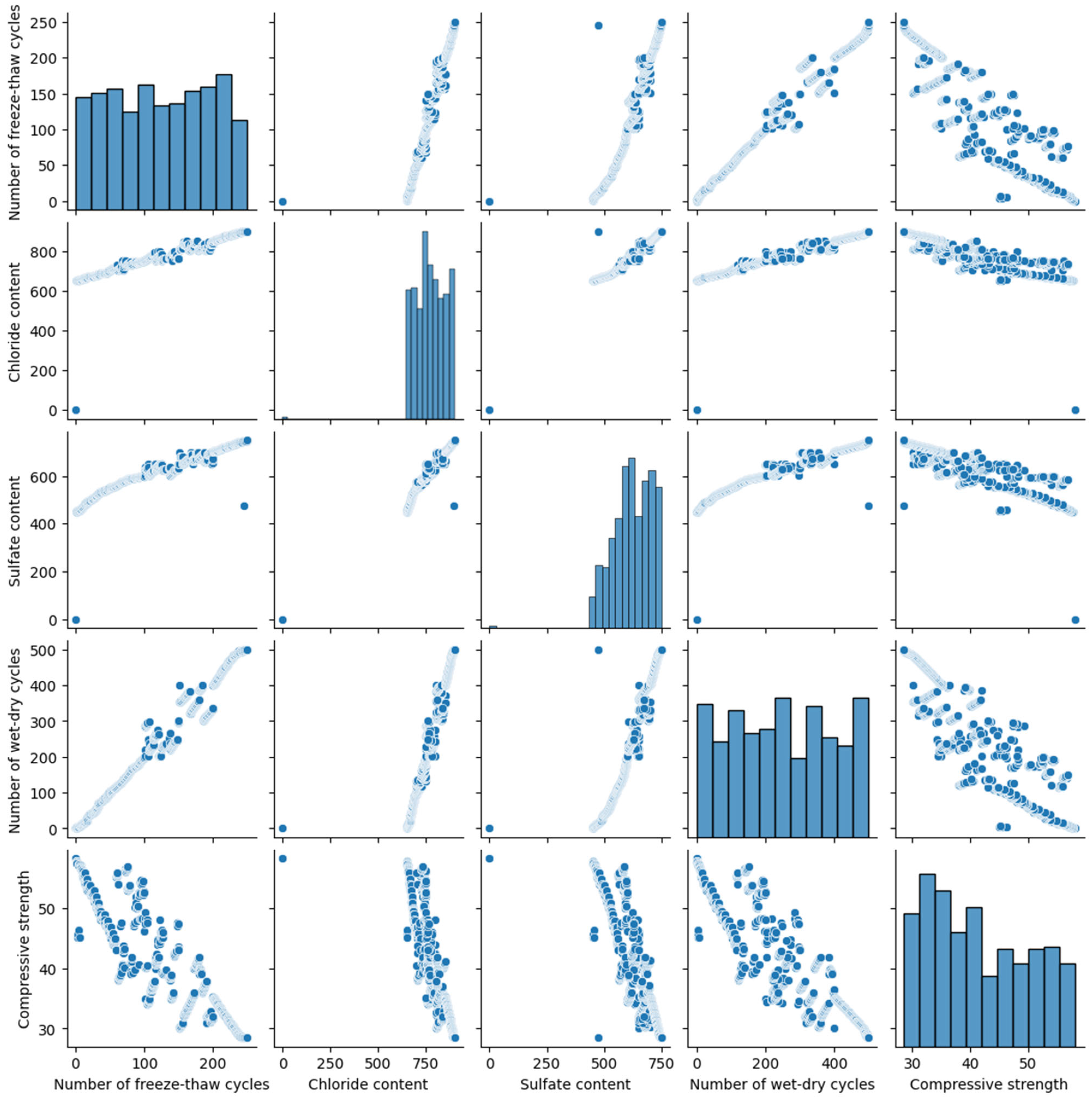
2.3. Dataset Description
2.4. Feature Engineering
2.5. Description of Machine Learning Methods Chosen for the Study
2.5.1. Linear Regression
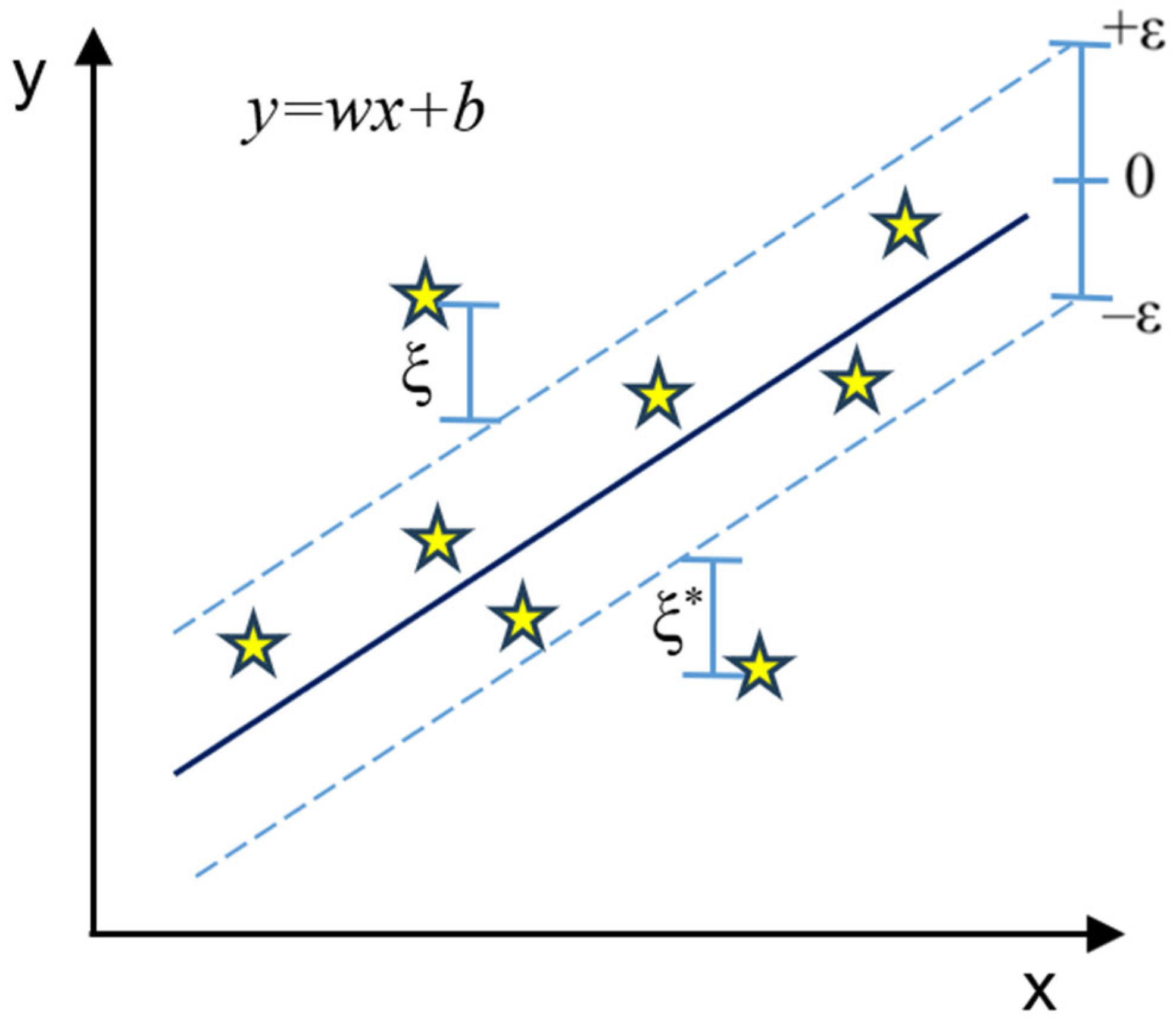
2.5.2. Support Vector Regression (SVR)
- SVR has a specific parameter ε (epsilon). This parameter determines “the width of the tube around the function” being evaluated (hyperplane). Predictions that fall within this “tube” are considered correct.
- Support vectors comprise points located outside the pipe, not exclusively those on the edge, as observed in classification problems.
- By modifying the regularization parameter C, one can control the value of the additional sliding variable (ξ), which serves as a measure of the distance to points situated outside the pipe.
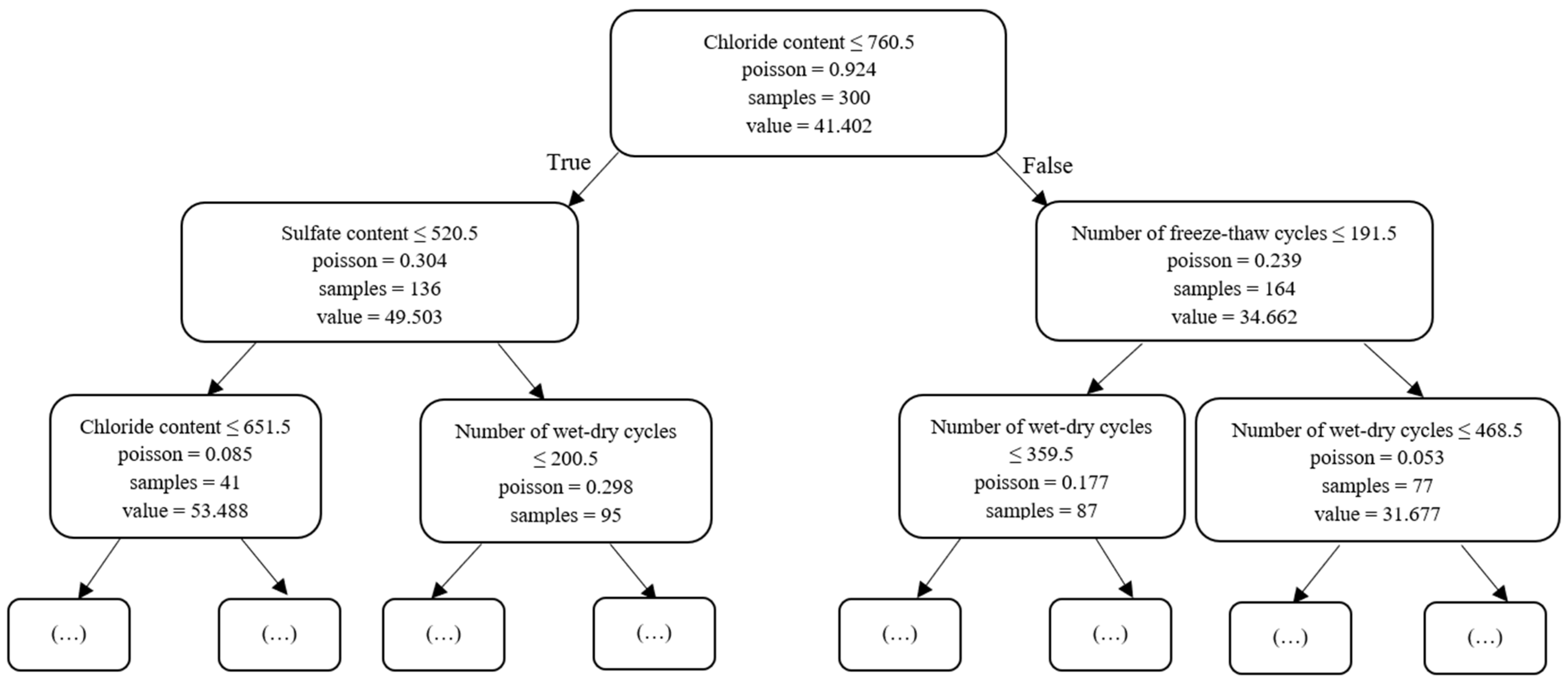
2.5.3. Random Forest Regression
2.5.4. CatBoost Regressor
2.6. Performance-Evaluation Methods
3. Results and Discussion
4. Conclusions
- (1)
- An empirical database has been compiled that includes information on the strength of vibrocentrifuged concrete, taking into account the influence of the number of freeze–thaw cycles, the content of chlorides and sulfates, and the number of wetting-drying cycles.
- (2)
- In order to enhance the model’s accuracy, Feature Engineering technology was utilized. This involved proposing and validating a hypothesis regarding the potential division of data into clusters. Additionally, a new feature was incorporated, containing details about membership in the corresponding cluster within the original dataset.
- (3)
- Implementation and comparison of four machine learning algorithms based on Linear Regression, Support Vector Regression, Random Forest, and CatBoost were carried out.
- (4)
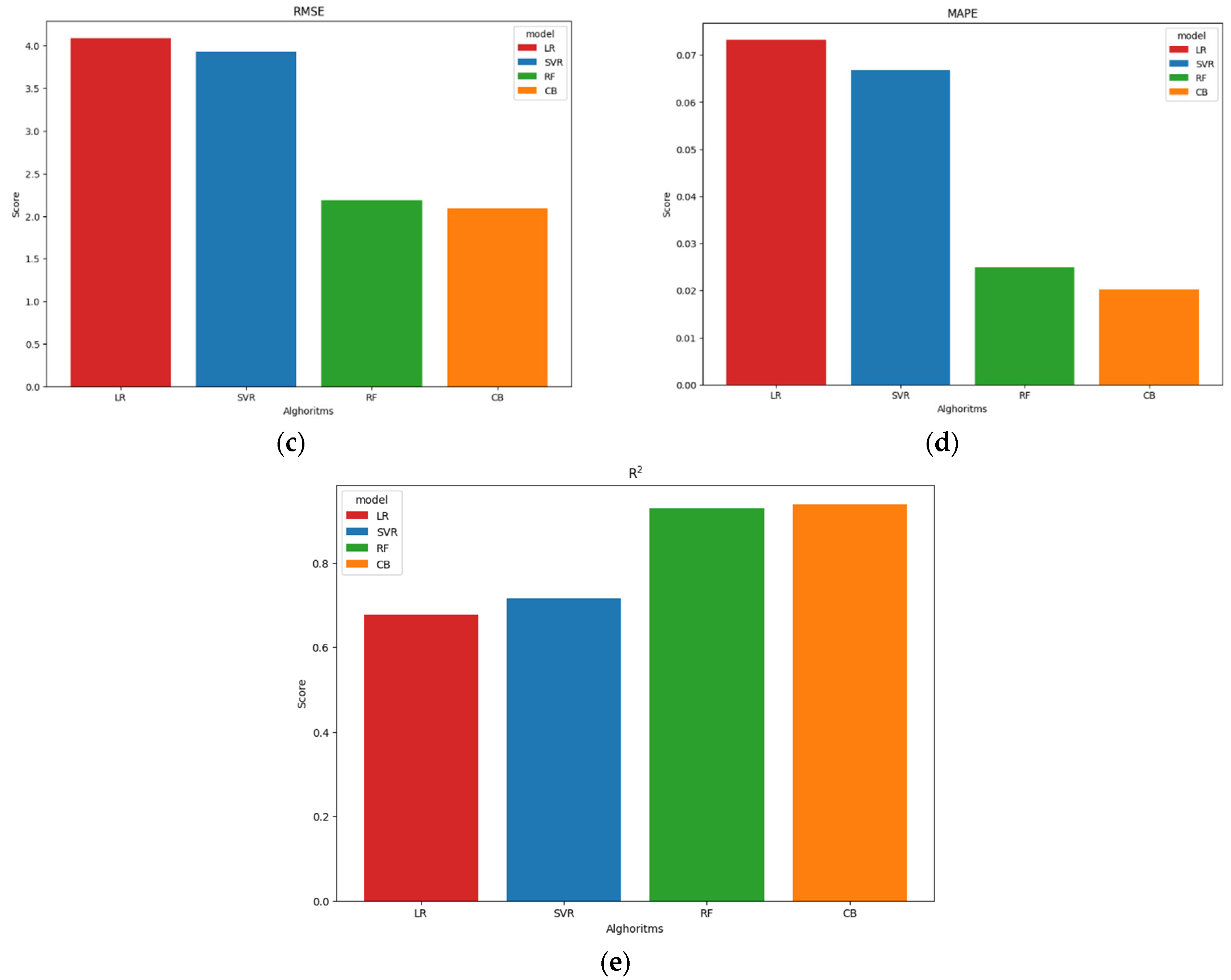
- The CatBoost model showed the best results: MAE = 0.89, MSE = 4.37, RMSE = 2.09, MAPE = 2% and R2 = 0.94.
- (5)
- It has been determined that machine learning techniques exhibiting a MAPE value ranging from 2 to 7% on a test sample are deemed suitable for implementation. This level of model error is comparable to the standards set forth in normative documents for concrete. Feature engineering and feature selection technologies will help reduce the error. Additionally, also with an increase in the data set, it will be possible to use more complex models.
- (6)
- The developed models can be offered to civil engineers, specialists in the field of materials science and materials technology as an additional source of information for making informed decisions regarding the development of improved concrete mix compositions and construction methods. These models can also be used for other materials that are exposed to aggressive environments. When changing materials and wanting to take into account a diverse range of their properties, it is advisable to use the technology of data drift, concept drift and domain adaptation. These methods will allow you to take into account new connections in the data without losing quality.
- (7)
- The limitation is that we can have confidence in the results presented within the range reported in vitro. However, we believe that it reflects real-world conditions as closely as possible. The developed intelligent models can become part of a large-scale forecasting system. Continuation of the research is planned in the direction of increasing the number of data in order to track the impact of additional factors influencing the strength characteristics of vibrocentrifuged concrete, as well as testing other machine learning models for prediction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shufrin, I.; Pasternak, E.; Dyskin, A. Environmentally Friendly Smart Construction—Review of Recent Developments and Opportunities. Appl. Sci. 2023, 13, 12891. [Google Scholar] [CrossRef]
- Yang, G.; Yang, R.; Zhang, J. Prediction and Interpretation of Residual Bearing Capacity of Cfst Columns under Impact Loads Based Interpretable Stacking Fusion Modeling. Buildings 2023, 13, 2783. [Google Scholar] [CrossRef]
- Bazhenov, Y.M.; Murtazaev, S.A.Y.; Alaskhanov, A.H.; Saydumov, M.S.; Bataev, D.K.S.; Murtazaeva, T.S.A. High-strength concretes based on anthropogenic raw materials for earthquake resistant high-rise construction. Eng. Solid Mech. 2021, 9, 335–346. [Google Scholar] [CrossRef]
- Kliukas, R.; Lukoševičienė, O.; Jaras, A.; Jonaitis, B. The Mechanical Properties of Centrifuged Concrete in Reinforced Concrete Structures. Appl. Sci. 2020, 10, 3570. [Google Scholar] [CrossRef]
- Mailyan, L.R.; Stel’makh, S.A.; Shcherban’, E.M.; Khalyushev, A.K.; Smolyanichenko, A.S.; Sysoev, A.K.; Parinov, I.A.; Cherpakov, A.V. Investigation of Integral and Differential Characteristics of Variatropic Structure Heavy Concretes by Ultrasonic Methods. Appl. Sci. 2021, 11, 3591. [Google Scholar] [CrossRef]
- Abbas, Y.M.; Khan, M.I. Robust Machine Learning Framework for Modeling the Compressive Strength of SFRC: Database Compilation, Predictive Analysis, and Empirical Verification. Materials 2023, 16, 7178. [Google Scholar] [CrossRef] [PubMed]
- Leonovich, S.N.; Shalyi, E.E.; Kim, L.V. Reinforced Concrete under the Action of Carbonization and Chloride Aggression: A Probabilistic Model for Service Life Prediction. Sci. Tech. 2019, 18, 284–291. [Google Scholar] [CrossRef]
- Shcherban’, E.M.; Stel’makh, S.A.; Beskopylny, A.N.; Mailyan, L.R.; Meskhi, B.; Elshaeva, D.; Chernil’nik, A. Physical and Mechanical Characteristics of Variotropic Concrete during Cyclic and Continuous Sulfate Attack. Appl. Sci. 2023, 13, 4386. [Google Scholar] [CrossRef]
- Shcherban’, E.M.; Stel’makh, S.A.; Beskopylny, A.N.; Mailyan, L.R.; Meskhi, B.; Varavka, V.; Chernil’nik, A.; Elshaeva, D.; Ananova, O. The Influence of Recipe-Technological Factors on the Resistance to Chloride Attack of Variotropic and Conventional Concrete. Infrastructures 2023, 8, 108. [Google Scholar] [CrossRef]
- Beskopylny, A.N.; Shcherban, E.M.; Stel’makh, S.A.; Mailyan, L.R.; Meskhi, B.; Chernil’nik, A.; El’shaeva, D. Influence of Variatropy on the Evaluation of Strength Properties and Structure Formation of Concrete under Freeze-Thaw Cycles. J. Compos. Sci. 2023, 7, 58. [Google Scholar] [CrossRef]
- Kovačević, M.; Hadzima-Nyarko, M.; Grubeša, I.N.; Radu, D.; Lozančić, S. Application of Artificial Intelligence Methods for Predicting the Compressive Strength of Green Concretes with Rice Husk Ash. Mathematics 2024, 12, 66. [Google Scholar] [CrossRef]
- Qin, X.; Kaewunruen, S. Eco-Friendly Design and Sustainability Assessments of Fibre-Reinforced High-Strength Concrete Structures Automated by Data-Driven Machine Learning Models. Sustainability 2023, 15, 6640. [Google Scholar] [CrossRef]
- Nizina, T.A.; Nizin, D.R.; Selyaev, V.P.; Spirin, I.P.; Stankevich, A.S. Big data in predicting the climatic resistance of building materials. I. Air temperature and humidity. Constr. Mater. Prod. 2023, 6, 18–30. [Google Scholar]
- Abramyan, S.G.; Klyuev, S.V.; Polyakov, V.G.; Sabitova, T.A.; Akopyan, G.O.; Guseynov, K.M. Specifics of information model development for functional conversion of offshore oil platforms. Constr. Mater. Prod. 2023, 6, 42–57. [Google Scholar] [CrossRef]
- Farooq, F.; Nasir Amin, M.; Khan, K.; Rehan Sadiq, M.; Faisal Javed, M.; Aslam, F.; Alyousef, R. A Comparative Study of Random Forest and Genetic Engineering Programming for the Prediction of Compressive Strength of High Strength Concrete (HSC). Appl. Sci. 2020, 10, 7330. [Google Scholar] [CrossRef]
- Stel’makh, S.A.; Shcherban’, E.M.; Beskopylny, A.N.; Mailyan, L.R.; Meskhi, B.; Razveeva, I.; Kozhakin, A.; Beskopylny, N. Prediction of Mechanical Properties of Highly Functional Lightweight Fiber-Reinforced Concrete Based on Deep Neural Network and Ensemble Regression Trees Methods. Materials 2022, 15, 6740. [Google Scholar] [CrossRef]
- Khodaparasti, M.; Alijamaat, A.; Pouraminian, M. Prediction of the concrete compressive strength using improved random forest algorithm. J. Build. Rehabil. 2023, 8, 92. [Google Scholar] [CrossRef]
- Thi Mai, H.-V.; Nguyen, T.-A.; Ly, H.-B.; Tran, V.Q. Prediction Compressive Strength of Concrete Containing GGBFS using Random Forest Model. Adv. Civ. Eng. 2021, 2021, 6671448. [Google Scholar] [CrossRef]
- Hasanzadeh, A.; Vatin, N.I.; Hematibahar, M.; Kharun, M.; Shooshpasha, I. Prediction of the Mechanical Properties of Basalt Fiber Reinforced High-Performance Concrete Using Machine Learning Techniques. Materials 2022, 15, 7165. [Google Scholar] [CrossRef]
- Tang, F.; Wu, Y.; Zhou, Y. Hybridizing Grid Search and Support Vector Regression to Predict the Compressive Strength of Fly Ash Concrete. Adv. Civ. Eng. 2022, 2022, 3601914. [Google Scholar] [CrossRef]
- Ding, B.; Wang, Q.; Ma, Y.; Shi, H. Prediction of compressive strength of concrete for high-performance concrete using two combined models, SVR-AVOA and SVR-SSA. Multiscale Multidiscip. Model. Exp. Des. 2023, 23, 00226. [Google Scholar] [CrossRef]
- Rajczakowska, M.; Szeląg, M.; Habermehl-Cwirzen, K.; Hedlund, H.; Cwirzen, A. Interpretable Machine Learning for Prediction of Post-Fire Self-Healing of Concrete. Materials 2023, 16, 1273. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Li, H.; Zhou, Y. Compressive Strength Prediction of Fly Ash Concrete Using Machine Learning Techniques. Buildings 2022, 12, 690. [Google Scholar] [CrossRef]
- Sai, G.; Singh, V. Prediction of Compressive Strength Using Support Vector Regression. Mendel 2019, 25, 51–56. [Google Scholar] [CrossRef]
- Lin, C.-J.; Wu, N.-J. An ANN Model for Predicting the Compressive Strength of Concrete. Appl. Sci. 2021, 11, 3798. [Google Scholar] [CrossRef]
- Chopra, P.; Sharma, R.K.; Kumar, M. Artificial Neural Networks for the Prediction of Compressive Strength of Concrete. Int. J. Appl. Sci. Eng. 2015, 13, 187–204. [Google Scholar] [CrossRef]
- Chopra, P.; Sharma, R.K.; Kumar, M. Prediction of Compressive Strength of Concrete Using Artificial Neural Network and Genetic Programming. Adv. Mater. Sci. Eng. 2016, 2016, 7648467. [Google Scholar] [CrossRef]
- Almeida, T.A.d.C.; Felix, E.F.; de Sousa, C.M.A.; Pedroso, G.O.M.; Motta, M.F.B.; Prado, L.P. Influence of the ANN Hyperparameters on the Forecast Accuracy of RAC’s Compressive Strength. Materials 2023, 16, 7683. [Google Scholar] [CrossRef]
- Ahmad, M.M.; Elahi, A.; Barbhuiya, S. Comparative Analysis of Reinforced Concrete Beam Behaviour: Conventional Model vs. Artificial Neural Network Predictions. Materials 2023, 16, 7642. [Google Scholar] [CrossRef]
- Beskopylny, A.N.; Stel’makh, S.A.; Shcherban’, E.M.; Mailyan, L.R.; Meskhi, B.; Razveeva, I.; Chernil’nik, A.; Beskopylny, N. Concrete Strength Prediction Using Machine Learning Methods CatBoost, k-Nearest Neighbors, Support Vector Regression. Appl. Sci. 2022, 12, 10864. [Google Scholar] [CrossRef]
- Tran, V.-L.; Lee, T.-H.; Nguyen, D.-D.; Nguyen, T.-H.; Vu, Q.-V.; Phan, H.-T. Failure Mode Identification and Shear Strength Prediction of Rectangular Hollow RC Columns Using Novel Hybrid Machine Learning Models. Buildings 2023, 13, 2914. [Google Scholar] [CrossRef]
- Taheri, E.; Mehrabi, P.; Rafiei, S.; Samali, B. Numerical Evaluation of the Upright Columns with Partial Reinforcement along with the Utilisation of Neural Networks with Combining Feature-Selection Method to Predict the Load and Displacement. Appl. Sci. 2021, 11, 11056. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, G.; Zhang, H.; Zhang, Y.; Yang, X. Predicting the Compressive Strength of Environmentally Friendly Concrete Using Multiple Machine Learning Algorithms. Buildings 2024, 14, 190. [Google Scholar] [CrossRef]
- Khan, S.; Ali Khan, M.; Zafar, A.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Predicting the Ultimate Axial Capacity of Uniaxially Loaded CFST Columns Using Multiphysics Artificial Intelligence. Materials 2022, 15, 39. [Google Scholar] [CrossRef] [PubMed]
- Atasham ul haq, M.; Xu, W.; Abid, M.; Gong, F. Prediction of Progressive Frost Damage Development of Concrete Using Machine-Learning Algorithms. Buildings 2023, 13, 2451. [Google Scholar] [CrossRef]
- Ismael Jaf, D.K. Soft Computing and Machine Learning-Based Models to Predict the Slump and Compressive Strength of Self-Compacted Concrete Modified with Fly Ash. Sustainability 2023, 15, 11554. [Google Scholar] [CrossRef]
- Shao, S.; Wang, R.; Gong, A.; Li, R.; Xu, J.; Wang, F.; Liu, F. Study and Neural Network Analysis on Durability of Basalt Fibre Concrete. Water 2023, 15, 1016. [Google Scholar] [CrossRef]
- Adamu, M.; Çolak, A.B.; Ibrahim, Y.E.; Haruna, S.I.; Hamza, M.F. Prediction of Mechanical Properties of Rubberized Concrete Incorporating Fly Ash and Nano Silica by Artificial Neural Network Technique. Axioms 2023, 12, 81. [Google Scholar] [CrossRef]
- Mhaya, A.M.; Shahidan, S.; Algaifi, H.A.; Zuki, S.S.M.; Benjeddou, O.; Ibrahim, M.H.W.; Huseien, G.F. Thermal Conductivity of Coconut Shell-Incorporated Concrete: A Systematic Assessment via Theory and Experiment. Sustainability 2022, 14, 16167. [Google Scholar] [CrossRef]
- Shah, H.A.; Yuan, Q.; Akmal, U.; Shah, S.A.; Salmi, A.; Awad, Y.A.; Shah, L.A.; Iftikhar, Y.; Javed, M.H.; Khan, M.I. Application of Machine Learning Techniques for Predicting Compressive, Splitting Tensile, and Flexural Strengths of Concrete with Metakaolin. Materials 2022, 15, 5435. [Google Scholar] [CrossRef]
- de-Prado-Gil, J.; Zaid, O.; Palencia, C.; Martínez-García, R. Prediction of Splitting Tensile Strength of Self-Compacting Recycled Aggregate Concrete Using Novel Deep Learning Methods. Mathematics 2022, 10, 2245. [Google Scholar] [CrossRef]
- Beskopylny, A.N.; Stel’makh, S.A.; Shcherban’, E.M.; Mailyan, L.R.; Meskhi, B.; Chernil’nik, A.; El’shaeva, D.; Pogrebnyak, A. Influence of Variotropy on the Change in Concrete Strength under the Impact of Wet–Dry Cycles. Appl. Sci. 2023, 13, 1745. [Google Scholar] [CrossRef]
- Korolev, E.V.; Bazhenov, Y.M.; Smirnov, V.A. Building Materials of Varitropic Frame Structure; National Research Moscow State University of Civil Engineering: Moscow, Russia, 2011; 304p. [Google Scholar]
- SP 28.13330.2017 Protection Against Corrosion of Construction. Available online: https://docs.cntd.ru/document/456069587 (accessed on 4 January 2024).
- Zhang, K.; Guo, A.; Yu, Y.; Yang, B.; Yu, B.; Xie, C. Freeze–Thaw Damage Degradation Model and Life Prediction of Air-Entrained Concrete in Multi-Year Permafrost Zone. Materials 2023, 16, 7703. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Dai, M.; Li, M.; Liu, F. Study of the Freeze–Thaw Resistance for Composite Fiber Recycled Concrete with Sulphate Attack Exposure. Buildings 2023, 13, 1037. [Google Scholar] [CrossRef]
- Casanova, L.; Ceriani, F.; Messinese, E.; Paterlini, L.; Beretta, S.; Bolzoni, F.M.; Brenna, A.; Diamanti, M.V.; Ormellese, M.; Pedeferri, M. Recent Advances in the Use of Green Corrosion Inhibitors to Prevent Chloride-Induced Corrosion in Reinforced Concrete. Materials 2023, 16, 7462. [Google Scholar] [CrossRef]
- El Inaty, F.; Marchetti, M.; Quiertant, M.; Omikrine Metalssi, O. Chemical Mechanisms Involved in the Coupled Attack of Sulfate and Chloride Ions on Low-Carbon Cementitious Materials: An In-Depth Study. Appl. Sci. 2023, 13, 11729. [Google Scholar] [CrossRef]
- Liu, J.; Zang, S.; Yang, F.; Zhang, M.; Li, A. Fracture Mechanical Properties of Steel Fiber Reinforced Self-Compacting Concrete under Dry–Wet Cycle Sulfate Attack. Buildings 2022, 12, 1623. [Google Scholar] [CrossRef]
- Baak, M.; Koopman, R.; Snoek, H.; Klous, S. A new correlation coefficient between categorical, ordinal and interval variables with Pearson characteristics. arXiv 2019, arXiv:1811.11440v2. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Visualizing High-Dimensional Data Using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. arXiv 2019, arXiv:1907.10902v1. [Google Scholar]
- Watanabe, S. Tree-Structured Parzen Estimator: Understanding Its Algorithm Components and Their Roles for Better Empirical Performance. arXiv 2023, arXiv:2304.11127v3. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Rathakrishnan, V.; Bt Beddu, S.; Ahmed, A.N. Predicting compressive strength of high-performance concrete with high volume ground granulated blast-furnace slag replacement using boosting machine learning algorithms. Sci. Rep. 2022, 12, 9539. [Google Scholar] [CrossRef] [PubMed]






| C (kg/m3) | W (l/m3) | CS (kg/m3) | S (kg/m3) | Density (kg/m3) | Slump (cm) |
|---|---|---|---|---|---|
| 375 | 185 | 1113 | 694 | 2367 | 3.5 |
| Parameter | Number of Freeze–Thaw Cycles | Chloride Content, mg/dm3 | Sulfate Content, mg/dm3 | Number of Wet-dry Cycles | Compressive Strength, MPa |
|---|---|---|---|---|---|
| mean | 124.08 | 773.09 | 620.59 | 248.84 | 41.50 |
| std | 71.72 | 78.41 | 83.04 | 148.57 | 8.60 |
| min | 0.00 | 0.00 | 0.00 | 0.00 | 28.50 |
| 25% | 61.00 | 714.75 | 563.75 | 119.75 | 34.00 |
| 50% | 120.00 | 768.00 | 626.00 | 237.50 | 40.20 |
| 75% | 187.25 | 836.00 | 690.25 | 372.25 | 48.73 |
| max | 250.00 | 900.00 | 750.00 | 500.00 | 58.20 |
| № | Parameter | Definition | Value |
|---|---|---|---|
| 1 | Kernel | Kernel type, which determines the type of hyperplane for data partitioning: either linear or nonlinear hyperplane can be used. | Linear kernel |
| 2 | C | Regularization parameter: The strength of regularization is inversely proportional to this parameter. | 27 |
| 3 | Epsilon (ε) | The epsilon-tube within which no penalty is associated in the training loss function with points predicted within a distance epsilon from the actual value | 0.1 |
| № | Parameter | Definition | Value |
|---|---|---|---|
| 1 | Number of estimators | Number of trees in the forest | 282 |
| 2 | Max depth | Maximum depth of one tree | 178 |
| 3 | Criterion | What criterion is used to construct each branch? | Poisson |
| 4 | Min samples split | Minimum number of objects in a sheet to split it | 4 |
| 5 | Min samples leaf | Minimum number of objects in a sheet for it to exist | 2 |
| № | Parameter | Definition | Value |
|---|---|---|---|
| 1 | Number of estimators | Number of trees in the forest | 1443 |
| 2 | Learning_rate | Learning rate | 0.034 |
| 3 | Depth | Tree depth | 9 |
| 4 | L2 | Coefficient for L2 regularization | 14.361 |
| 5 | Bootstrap_type | Defines the method for sampling the weights of objects | Bayesian |
| 6 | Bagging temperature | Bootstrap coefficient: In Bayesian bootstrap, each feature is assigned a random weight | 0.681 |
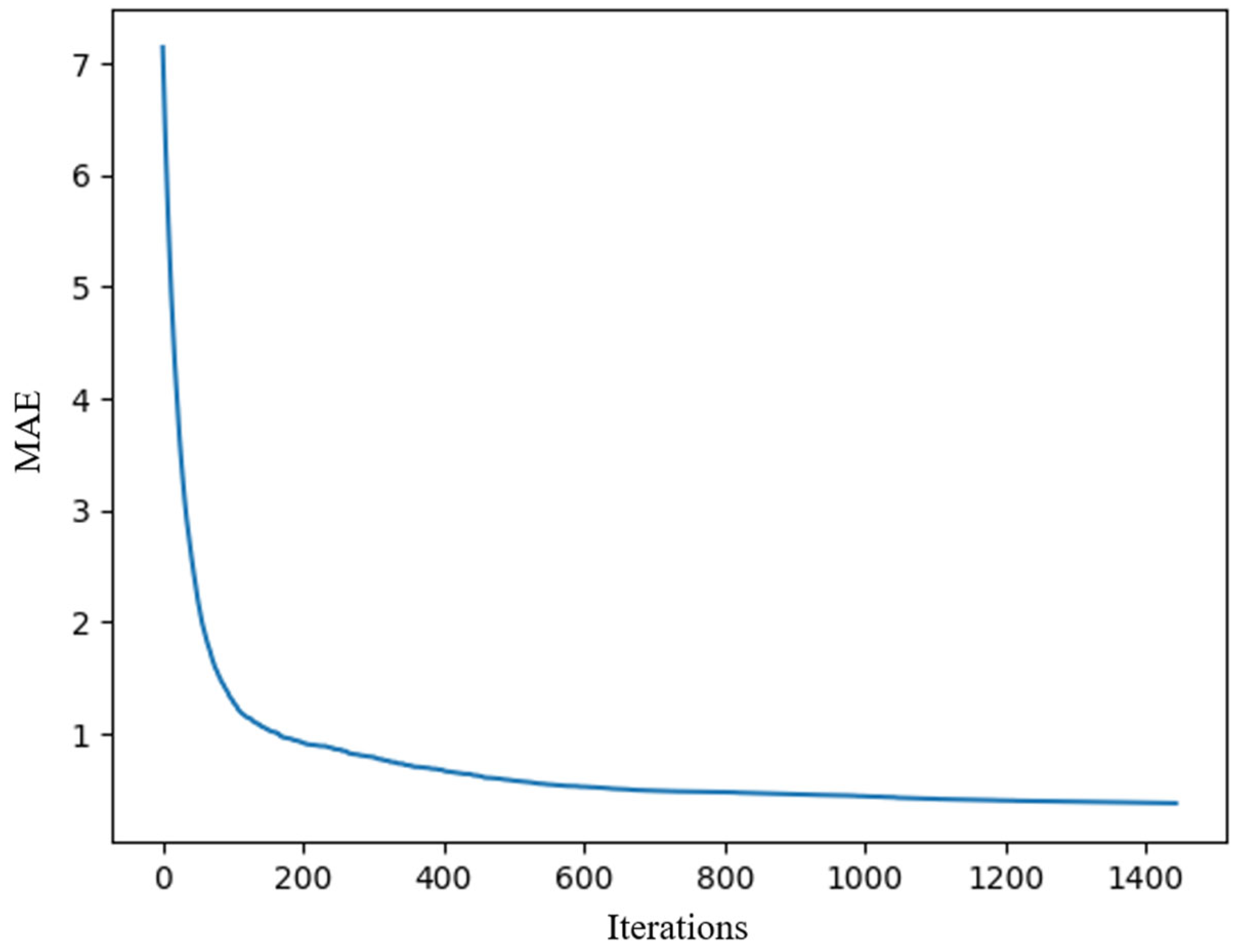
| 7 | Loss function | The metric to use in training | Mean Absolute Error (MAE) |
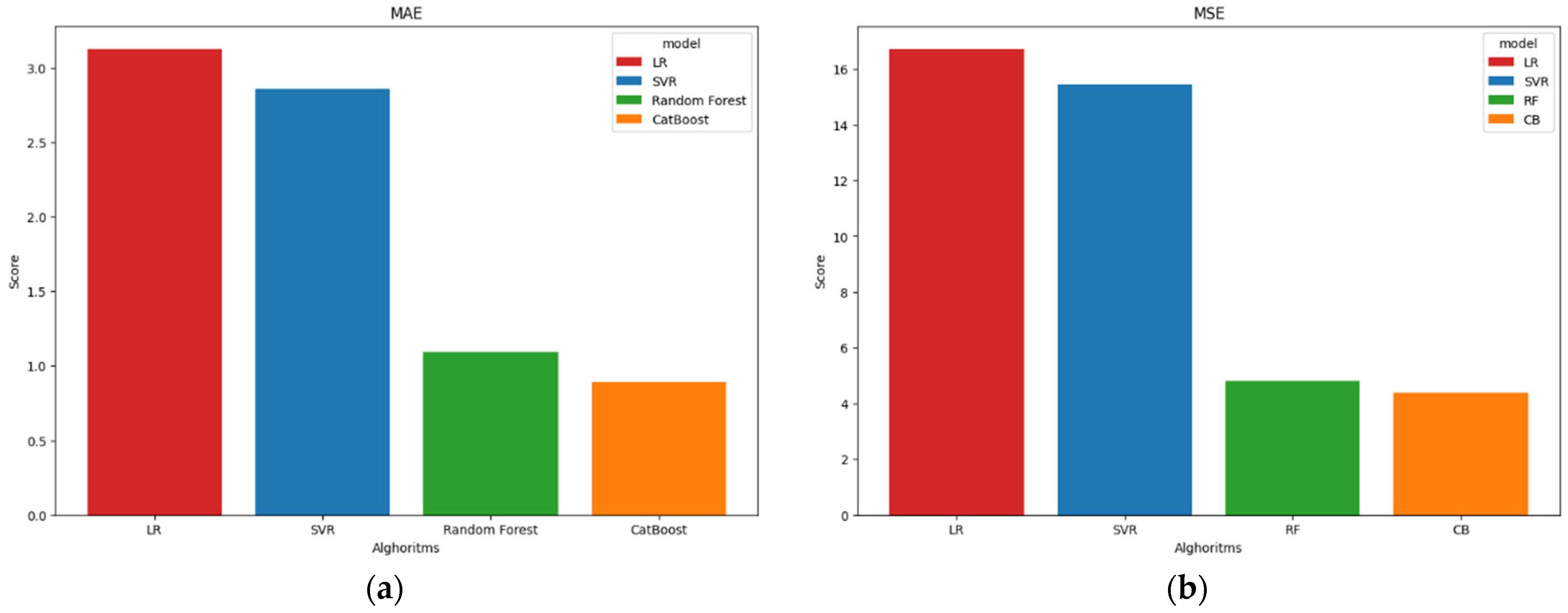
| № | Model | MAE | MSE | RMSE | MAPE, % | R2 |
|---|---|---|---|---|---|---|
| 1 | LR | 3.12 | 16.71 | 4.09 | 7 | 0.68 |
| 2 | SVR | 2.86 | 15.46 | 3.93 | 7 | 0.72 |
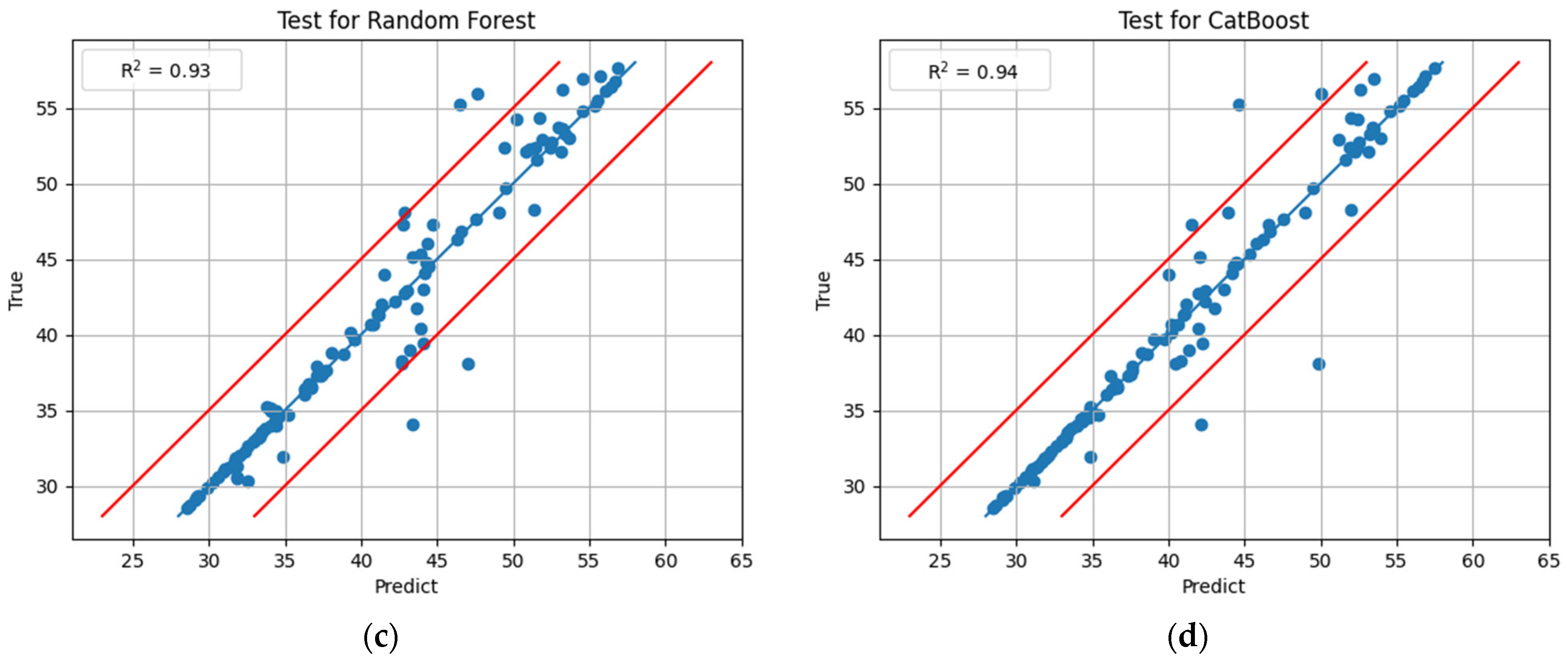
| 3 | RF | 1.10 | 4.79 | 2.19 | 2 | 0.93 |
| 4 | CB | 0.89 | 4.37 | 2.09 | 2 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beskopylny, A.N.; Stel’makh, S.A.; Shcherban’, E.M.; Mailyan, L.R.; Meskhi, B.; Razveeva, I.; Kozhakin, A.; Pembek, A.; Elshaeva, D.; Chernil’nik, A.; et al. Prediction of the Compressive Strength of Vibrocentrifuged Concrete Using Machine Learning Methods. Buildings 2024, 14, 377. https://doi.org/10.3390/buildings14020377
Beskopylny AN, Stel’makh SA, Shcherban’ EM, Mailyan LR, Meskhi B, Razveeva I, Kozhakin A, Pembek A, Elshaeva D, Chernil’nik A, et al. Prediction of the Compressive Strength of Vibrocentrifuged Concrete Using Machine Learning Methods. Buildings. 2024; 14(2):377. https://doi.org/10.3390/buildings14020377
Chicago/Turabian StyleBeskopylny, Alexey N., Sergey A. Stel’makh, Evgenii M. Shcherban’, Levon R. Mailyan, Besarion Meskhi, Irina Razveeva, Alexey Kozhakin, Anton Pembek, Diana Elshaeva, Andrei Chernil’nik, and et al. 2024. "Prediction of the Compressive Strength of Vibrocentrifuged Concrete Using Machine Learning Methods" Buildings 14, no. 2: 377. https://doi.org/10.3390/buildings14020377
APA StyleBeskopylny, A. N., Stel’makh, S. A., Shcherban’, E. M., Mailyan, L. R., Meskhi, B., Razveeva, I., Kozhakin, A., Pembek, A., Elshaeva, D., Chernil’nik, A., & Beskopylny, N. (2024). Prediction of the Compressive Strength of Vibrocentrifuged Concrete Using Machine Learning Methods. Buildings, 14(2), 377. https://doi.org/10.3390/buildings14020377











